Coevolutionary networks of splicing cis-regulatory elements

Abstract

Accurate and efficient splicing of eukaryotic pre-mRNAs requires recognition by trans-acting factors of a complex array of cis-acting RNA elements. Here, we developed a generalized Bayesian network to model the coevolution of splicing cis elements in diverse eukaryotic taxa. Cross-exon but not cross-intron compensatory interactions between the 5′ splice site (5′ss) and 3′ splice site (3′ss) were observed in human/mouse, indicating that the exon is the primary evolutionary unit in mammals. Studied plants, fungi, and invertebrates exhibited exclusively cross-intron interactions, suggesting that intron definition drives evolution in these organisms. In mammals, 5′ss strength and the strength of several classes of exonic splicing silencers (ESSs) evolved in a correlated way, whereas specific exonic splicing enhancers (ESEs), including motifs associated with hTra2, SRp55, and SRp20, evolved in a compensatory manner relative to the 5′ss and 3′ss. Interactions between specific ESS or ESE motifs were not observed, suggesting that elements bound by different factors are not commonly interchangeable. Thus, the splicing elements defining exons coevolve in a way that preserves overall exon strength, allowing specific elements to substitute for loss or weakening of others.

Choice of splice sites in nuclear pre-mRNA splicing involves a complex set of recognition events. Motifs at the 5′ splice site (5′ss), the polypyrimidine tract (PPT) and 3′ splice site (3′ss), and the branch point sequence (BPS) are required for splicing, but lack sufficient information content to define exon locations in most organisms (1). Auxiliary splicing regulatory elements (SREs), known as exonic splicing enhancers (ESEs), intronic splicing enhancers (ISEs), exonic splicing silencers (ESSs), and intronic splicing silencers (ISSs), are defined by their effects on adjacent splice sites, e.g., ESEs tend to promote inclusion and ESSs promote exclusion of the exons they reside in. SREs control splice site choice by recruitment of specific trans-acting factors to the pre-mRNA that function to either activate or repress splicing by interaction with other regulatory factors or core spliceosome components (reviewed in refs. 2 and 3).

A prominent feature of splicing regulation is the elaborate network of interactions that occur among and between core and auxiliary splicing factors (4). Two general models have been proposed for early spliceosome assembly (5). In the intron definition model, intron-spanning interactions between factors recognizing the 5′ss and the downstream 3′ss occur initially; this model is supported for transcripts with large exons and small introns (6, 7). In the exon definition model, exon-spanning interactions between factors that recognize the 5′ss and factors bound at the upstream 3′ss lead to formation of exon definition complexes before rearrangements that yield intron-spanning spliceosomes. Exon definition is thought to predominate in splicing of mammalian internal exons, which are typically moderately sized (≈50–250 bp) and often flanked by much larger introns (5, 8). Other interactions of general importance for splicing, including contacts between small nuclear ribonucleoprotein (snRNP) components bound to splice sites and proteins of the serine-arginine-rich (SR) protein family, most of which bind ESEs (9–11). Conversely, several heterogeneous nuclear ribonucleoproteins (hnRNPs) bind to ESSs and inhibit exon recognition or alter splice site choice by antagonizing the activity or interactions of SR protein and/or snRNP factors (12–14). These interactions among splicing factors appear vital to the robustness, precision, and adaptability of the splicing reaction.

Sequences involved in the splicing of constitutive exons are expected to be under selection to optimize the network of splicing factor interactions for accurate and efficient splicing. To understand how such selection influences gene evolution, we studied the coevolution of splicing cis-regulatory elements in orthologous exons and introns. For example, a mutation that eliminated a critical ESE in an exon might be compensated by a second mutation strengthening a splice site to restore efficient splicing (Fig. 1A). Because several distinct cis elements are involved in splicing of a typical constitutive exon (15, 16), pairwise analysis of elements is inadequate, and the system is better modeled as a network of interacting nodes, each representing a particular cis element.

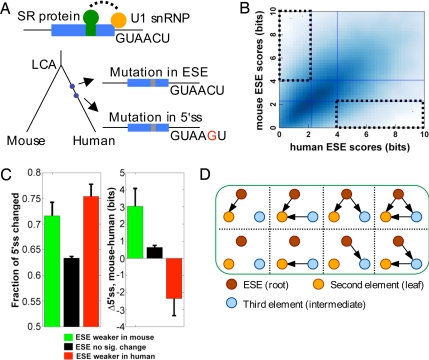
Fig. 1.

The PVSA method for inference of coevolutionary networks. (A) Evolution of a hypothetical exon (blue box) is shown. After the last common ancestor (LCA) of human and mouse, two mutations occur on the human lineage, the first disrupting an ESE, the second strengthening the 5′ss. (B) The PVS for ESE (dotted boxes) is defined as the set of exons whose ESE strength is in the upper 33% of one genome but in the lower 33% of the other genome. (C) Frequency of changes to 5′ss sequences (Left) and changes in 5′ss score (Right) (mean ± SE) in exons belonging to two subsets of the PVS-ESE (green, ESEs weaker in mouse; red, ESEs weaker in human) and to non-PVS-ESE exons (black). (D) Definition of subnetworks in the PVSA method. The subnetworks are rooted directed-acyclic graphs (e.g., with ESE as the root node). For simplicity, only subnetworks with a fixed leaf node (no outgoing edges) are listed.

Network formalisms are widely used for modeling sets of physical and functional interactions between proteins (e.g., refs. 17 and 18). Here, we developed a network formalism for modeling evolutionary relationships among cis elements, which we call principal variation-based subset analysis (PVSA). Applied to large sets of orthologous exon pairs from related organisms, PVSA identified major trends in splicing element coevolution that differ between mammals and other eukaryotic taxa and uncovered unexpected complexity in the interplay between splice sites and various types of SREs.

Results

Modeling Coevolution of cis Elements.

Splicing of a typical constitutive mammalian internal exon depends on a fairly broad set of cis elements, including the 5′ss, 3′ss/PPT, BPS, and multiple ESEs, and is often modulated by the presence of ESSs, ISEs and ISSs (3, 15, 16). Mutation of any of these elements may disrupt splicing, most often causing partial skipping of the mutated exon, thereby reducing the quantity of full-length mRNA and protein produced (19, 20). Substantial reduction in the level of a gene product is often deleterious, sometimes resulting in disease (reviewed in refs. 21 and 22). If only mildly deleterious, the mutant allele may survive for sufficient time to acquire secondary mutation(s) that suppress the disruptive effects of the original mutation, e.g., as illustrated in Fig. 1A.

Our goal was to understand the evolutionary relationships among the major categories of splicing cis elements (5′ss, 3′ss, ESE, ESS, etc.). For example, two elements X and Y (e.g., the 5′ss and 3′ss of exons) might have a “compensatory” relationship, with Y strengthening when X weakens, and vice versa. Alternatively, X and Y might have a “correlated” relationship, with strengthening of X associated with strengthening of Y, or have no direct relationship if changes in X and Y occur independently of one another. The PVSA approach considers network rather than pairwise relationships among splicing cis elements, with each node representing a specific category of cis element (5′ss, 3′ss, ESE, ESS, etc.), and with interactions between elements represented by directed edges between nodes. In PVSA, a subset of data called the principal variation subset for X (PVS, or PVS-X) is defined for each cis element X, by identifying exons or introns in which the strength of X changed dramatically between orthologous exons or introns in the genomes under study (Fig. 1B), using log-odds scoring of cis elements [supporting information (SI) Text]. Such large changes can be thought of as perturbations to the splicing network, analogous to the experimental perturbations (such as administration of a specific kinase inhibitor) typically used to infer directed edges in signaling networks (18, 23).

When such a large change has occurred, changes in other elements are often observed. For example, in human/mouse changes to 5′ss sequences occurred more often in exons belonging to the PVS for ESEs than in other exons, with the 5′ss stronger on average in the organism in which ESEs were substantially weaker (Fig. 1C). This pattern suggested that 5′ss strengthening can and often does compensate for ESE-disrupting mutations. However, consideration of additional relevant variables in a network model is essential to avoid potential artifacts. For example, the scenario in which Y compensates X, and Z compensates Y could lead a pairwise model to detect a spurious relationship between X and Z that could be avoided by inclusion of all three variables in a network. A simple pairwise analysis may also fail to detect significant relationships, e.g., in cases where one variable is compensated by several others.

In the PVSA method, patterns of change are analyzed by applying a Bayesian network inference procedure to the PVS for each element (see Materials and Methods). For each cis element X, the PVS-X is used to evaluate possible directed acyclic subnetworks that involve X as a root node (Fig. 1D and SI Fig. 5). Those subnetworks identified as significant (i.e., which have high likelihood of generating the observed patterns of association between the variables relative to controls) are then cascaded together to generate a final network that summarizes the relationships among the nodes (but which is not required to satisfy the acyclicity constraint of Bayesian networks). In this final network, an arrow X → Y indicates that large changes in element X were associated with significant changes in the strength of Y, with the color of the arrow indicating whether the changes tended to be in a compensatory (green) or correlated (red) direction (see Fig. 2 and SI Text).

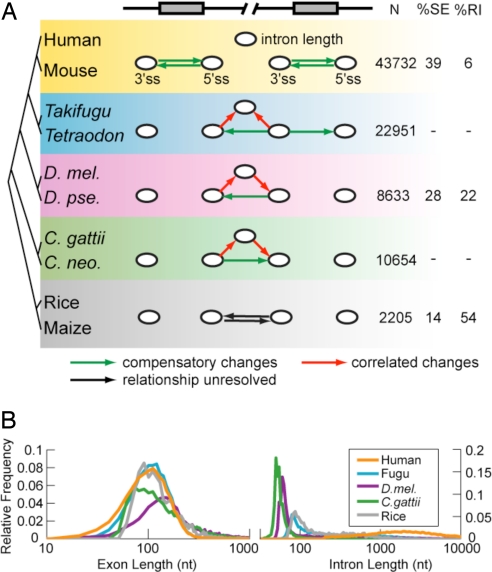
Fig. 2.

Coevolution of splice sites and introns in diverse eukaryotic taxa. (A) Using PVSA, the coevolution of five elements was modeled: the 3′ss and 5′ss of consecutive pairs of exons (all taxa) and intron length (all taxa except plants). An arrow from node X to node Y indicates significant covariation based on the PVS-X. Significant compensatory relationships are shown in green, correlated relationships are in red, and relationships with unresolved directionality are in black. The P value cutoff for all networks was 0.05 (allowing about one false positive network edge), except human–mouse, where a more stringent cutoff of P < 0.001 was used because the data were used in further network analyses (Fig. 3). The number of pairs of exons used (N), and the percentages of exon skipping and intron retention events among all alternative splicing events are also listed. (B) Semilog plot of exon and intron length distributions in five representative genomes. D. mel, Drosophila melanogaster; D. pse, D. pseudoobscura; C. gattii, Cryptococcus gattii; C. neo, C. neoformans; SE, skipped exon; RI, retained intron.

Widespread Constraints on Splicing Element Evolution Associated with Exon and/or Intron Definition.

Initially, the coevolution of the cis elements involved in splicing of constitutive exons and introns was studied in an evolutionarily diverse group of eukaryotes (SI Table 1). The 3′ss and 5′ss of pairs of consecutive constitutive exons (i.e., a total of four splice site variables) were considered. The length of the intervening intron was considered as a fifth variable (except in plants, where the sample size was insufficient), because intron length is known to influence splicing in a number of organisms (24, 25); exon length did not vary sufficiently between orthologs to merit consideration. Throughout this study, we have included the PPT as part of the 3′ss score and have excluded the BPS because for most introns the location of the BPS has not been mapped. The final networks resulting from PVSA analysis of available orthologous pairs of consecutive exons from five disparate eukaryotic taxa, including mammals, fish, insects, plants, and fungi are shown in Fig. 2A (P values shown in SI Fig. 6).

For human and mouse, significant bidirectional compensation was observed between the strength of the splice site pairs flanking the exons (P < 0.001), but not between splice site pairs flanking introns, or between splice site strength and intron length. Similar results were observed in these mammals when considering a larger set of variables including also SREs (SI Fig. 7A). These observations indicate that, for splicing, the exon rather than the intron is the fundamental evolutionary unit in mammals, with changes that weaken a 5′ss, for example, generally compensated by changes to the upstream (cross-exon) 3′ss rather than to the downstream (cross-intron) 3′ss. The existence of such cross-exon compensatory relationships suggests that pervasive exon definition in mammalian transcripts (5, 8) enforces an effective minimum “total strength” for exons, but not for introns.

Previously, large differences in intron length between orthologous mammalian introns were observed to be modestly associated with increased ESE density and splice site strength, using a pairwise analysis method that did not control for effects of sequence composition (26). Here, controlling for the effects of base composition (SI Text) using a network inference approach, no significant association between intron length and ESE or splice site strength was observed in mammals.

The PVSA network for the insect Drosophila (Fig. 2A; see also SI Fig. 7B for introns ≤250 bases in length) identified compensatory interactions across introns rather than exons, including interactions between intron length and the associated splice sites, suggesting that in Drosophila widespread intron definition leads to introns rather than exons being more fundamental evolutionary units. (Exon definition may also occur in some Drosophila genes but the subset of genes with small exons/large introns was too small to analyze separately or impact the overall results.) The pufferfishes Takifugu and Tetraodon represent an interesting intermediate case, with changes in 3′ss strength compensated by both the upstream and downstream 5′ss and by changes in intron length (P < 0.05). These observations suggested that intron definition has become prominent in pufferfishes, consistent with the ≈8-fold smaller average intron size in pufferfishes relative to mammals, but that exon definition may also occur for some exons or transcripts (see also ref. 27). In both the fishes and the flies, splice site strength changed in a correlated fashion with intron length, suggesting that shorter intron lengths increase splicing efficiency in both of these systems (25).

Application of PVSA to the intron-rich fungi of genus Cryptococcus, as well as the monocot plants rice and maize, identified compensatory relationships between 3′ss and 5′ss across introns but not across exons. Thus, the intron is the fundamental evolutionary unit in studied fungi and plants, consistent with a predominance of short introns and intron definition in these organisms (Fig. 2B and ref. 28). Weaker exon definition mechanisms may also affect splice site recognition in some cases (29).

Classically, exon definition and intron definition can be distinguished by observing the splicing phenotypes of mutations that disable splice sites, with exon definition commonly leading to exon skipping and intron definition to intron retention. Consistent with the PVSA results above for constitutive exons and introns, analyses of alternative splicing (AS) patterns based on available transcript data found a ≈7-fold bias for exon skipping over intron retention in mammals and a ≈4-fold bias for intron retention in plants (Fig. 2A), in agreement with previous studies of these and other mammals and plants (30, 31). Drosophila represented an interesting case, with slightly higher levels of exon skipping than intron retention detected, despite the predominant intron definition signature observed in splicing network analysis of constitutive introns. This observation suggests that intron definition may be favored in constitutively spliced Drosophila transcripts, with AS more common in situations involving exon definition, consistent with the long intron lengths associated with many known AS events in this organism (25).

Extensive Evolutionary Compensation Involving SREs in Mammals.

To understand how SREs interact with each other and with splice sites, we focused on analyses of human and mouse, taking advantage of the availability of reliable collections of mammalian SREs from recent screens (SI Text). For each pair of human/mouse orthologous constitutive exons, the scores of six classes of well characterized cis elements associated with the exon were analyzed: 5′ss, 3′ss, ESE, ESS, 5′ISE, and 3′ISE (SI Table 2). ISEs were represented by the canonical and abundant “G-triple” class (27, 32), and ISEs located near the 5′ss and 3′ss (designated 5′ISE and 3′ISE, respectively) were analyzed separately. Application of PVSA to these data identified a network containing a number of highly significant relationships between cis element classes, including all of the analyzed elements except 3′ISEs (Fig. 3A; P values listed in SI Table 3).

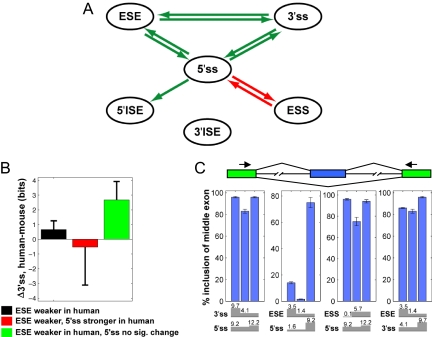
Fig. 3.

SRE coevolutionary network for human and mouse. (A) The network identified by using the PVSA method based on six classes of splicing cis elements is shown. For all edges P < 0.001. Arrows are colored as in Fig. 2. (B) Change in 3′ss strength (mean ± SE) for the set of PVS-ESE exons with weaker ESEs in human than mosue (black), and for subsets created by intersecting this set with the subset of the PVS-5′ss having weaker 5′ss in mouse (red) or the non-PVS-5′ss set (green). (C) Tests of bidirectional compensatory relationships detected in A used constructs containing combinations of stronger and weaker 5′ss, 3′ss, ESE, and ESS (with log-odds scores indicated) in the second exon. Inclusion of the second exon was assayed by body-labeled RT-PCR of total RNA from 293T cells transfected with each reporter by using primers targeted to the first and third exons. Blue bars indicate mean, and error bars indicate range of duplicated experiments.

Several features of the identified network are notable. First, the 5′ss appears to play a particularly central role, with compensatory or correlated relationships detected to four other elements in the network, whereas other elements had significant interactions with at most two other elements. This observation suggests that splicing of constitutive exons may be particularly sensitive to 5′ss strength, perhaps because 5′ss recognition by U1 snRNP occurs before other steps in spliceosome assembly (33, 34). Notably, all of the interactions detected are in the direction expected to result from selection acting to maintain a minimum exon “strength.” Compensatory interactions (Fig. 3A, green) occur between the 5′ss and the three other positively acting elements (3′ss, ESE, and 5′ISE), whereas a correlated interaction (Fig. 3A, red) was detected between the 5′ss and negatively acting ESSs.

Another prominent feature of the network is the set of mutually compensatory relationships among all combinations of 5′ss, 3′ss, and ESEs. The nature of these three-way interactions and the interpretation of the final PVSA network is illustrated in Fig. 3B. No significant change in 3′ss strength was observed for the set of exons in which ESEs were substantially weaker in human than mouse. However, a large increase in 3′ss strength was observed in the subset of this set for which 5′ss strength changed little or not at all, and a modest decrease in 3′ss strength was seen in the subset where 5′ss strength increased. Thus, the compensatory relationship between ESEs and the 3′ss is only readily observed when 5′ss changes are controlled, underlining the complex and multivariate nature of cis element relationships in mammals.

Three of the four interactions involving the 5′ss, as well as the compensatory relationship between ESEs and the 3′ss, were bidirectional, suggesting “functional symmetry,” with each element in the pair commonly able to rescue weakness in the other. This conclusion was supported by splicing reporter assays. For each of the four pairs of elements with bidirectional compensation relationships identified in Fig. 3A, three constructs were tested, representing a reference exon subjected to two successive mutations, weakening one element, then strengthening the other (Fig. 3C and SI Fig. 8). The results confirmed that, in each case, exon skipping resulting from weakening of one element could be rescued completely or partially by strengthening of the second element for each of these four pairs. The magnitudes of the changes in exon inclusion tended to be larger when the changes in log-odds scores of the affected elements were larger, supporting the relevance of these scores to splicing activity. Some of these compensatory relationships have also been supported by previous studies (35, 36).

The unidirectional arrow between 5′ss and 5′ISE in Fig. 3A indicated that large decreases in 5′ss strength between human and mouse were associated with increased ISE density in the downstream intron, but not vice versa. This asymmetry could indicate that large changes in 5′ss strength are more likely to impact splicing than are large changes in 5′ISEs and/or that the activity of these ISEs is highly context-dependent.

Evolutionary Relationships of Individual SREs.

In the network analysis of Fig. 3A, all ESE and ESS hexanucleotides derived from large screens were analyzed together. This approach therefore captures the average behavior of these classes of SREs, but could obscure any differences that may exist between ESE and ESS motifs recognized by different factors. Therefore, we also analyzed the evolutionary relationships among individual ESE and ESS motifs (Fig. 4, SI Fig. 9, and SI Tables 4–6). ESE motifs associated with specific SR proteins were obtained primarily from SELEX or functional SELEX experiments (10, 16, 37), and the ESS motifs were derived based on clustering of ESS oligonucleotides identified in a cell fluorescence-based screen (38), some of which correspond to known binding motifs of specific hnRNP proteins. To obtain the network shown in Fig. 4, subnetworks were first identified based on four nodes [the two splice sites and two regulatory element motifs (i.e., two ESE groups, two ESS groups or one ESE and one ESS group]. Given the seven ESE groups and six ESS groups, a total of 78 four-node networks were analyzed and combined together to form the final network. Analyzing no more than two ESE or ESS groups at a time was essential to reduce the search space; this approach implicitly assumes that indirect interactions of two SRE motifs through a third SRE motif are negligible. A P value cutoff of 0.001 was used, yielding an expectation of less than one false positive network edge in this analysis.

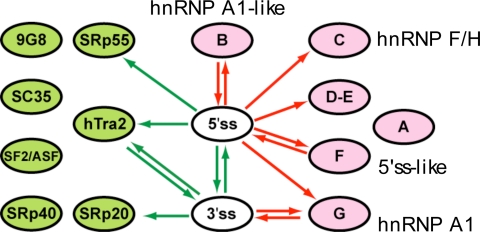
Fig. 4.

Evolutionary relationship among individual groups of ESE and ESS motifs. The splicing interaction network among ESE and ESS motifs resembling binding sites of SR proteins and hnRNPs is shown. All edges P < 0.001. Arrows are colored as in Fig. 2.

The results of this analysis yielded a very clear pattern, with extensive compensatory relationships between three ESE motifs (corresponding to hTra2, SRp20, and SRp55) and the 5′ss and/or 3′ss, and correlated relationships between ESS motifs and splice sites, principally the 5′ss (Fig. 4). These results reinforce those seen in Fig. 3A, suggesting that gain/loss, respectively, of several different ESE/ESS motifs can compensate for mutations that weaken splice sites. However, it was notable that no significant compensatory or correlated relationships were observed between different ESE or ESS motifs. Previously, evidence of selection against changes from one ESE sequence to another in recent primate evolution was obtained from analyses of single-nucleotide polymorphism data (39), and selection to conserve “neighborhood-inference” score (reflecting high similarity to other known ESEs) was observed over longer periods of mammalian evolution (40). The analysis here differs in that overlapping SREs were excluded to avoid artifacts in network inference (SI Text and SI Fig. 10), whereas the previous studies considered only overlapping SREs. The absence of compensatory interactions between ESE motifs observed here suggests that loss/gain of specific ESEs is more often compensated by changes in splice site strength than by gain/loss of another ESE bound by a different factor. This observation suggests that the in vivo activities of different mammalian ESE motifs are not commonly interchangeable.

The ESS motifs analyzed showed more consistent behavior than the ESEs, with almost all having significant correlated relationships to the 5′ss. These observations suggested that there is a major evolutionary dynamic between the 5′ss and ESSs, with emergence of new ESSs in constitutive exons (e.g., arising by drift or driven by selection at the protein level for specific codons that happen to create ESSs) very often requiring strengthening of the 5′ss to restore efficient splicing. Conversely, exons weakened or disabled by 5′ss mutations are likely under strong selection to eliminate ESSs. For one ESS motif, group G, which contains the core hnRNP A1 consensus motif UAGG, a correlated relationship with the 3′ss was also observed, which might indicate that A1 can commonly inhibit recognition of both splice sites (41). However, similar 3′ss correlations were not detected for any other ESS motifs, suggesting that most ESSs act primarily to inhibit productive association of factors with the 5′ss (consistent with Fig. 3A). Among ESEs, only the hTra2 motif had a compensatory relationship to both the 5′ss and 3′ss, suggesting that this element more commonly functions to enhance both splice sites than other ESEs.

Discussion

Splicing of constitutive exons represents a common evolutionary dynamic in which natural selection likely acts on a particular outcome (production of adequate amounts of accurately spliced mRNA) with little concern for how that outcome is achieved. Because splicing of a mammalian exon depends on recognition of several distinct cis elements, selection for efficient and accurate splicing can lead to complex dynamics in the evolution of splicing cis elements. Here, we have introduced a method, PVSA, that provides a framework for understanding coevolutionary networks of cis-regulatory elements. Coevolutionary networks inferred with PVSA are analogous to other network representations of biological systems such as protein interaction, signaling, and transcriptional regulatory networks (18, 42), in that they reflect functional relationships among proteins and/or nucleic acids, but PVSA requires no direct experimental data for network inference, instead using comparative genomic data. The PVSA method could, without difficulty, be applied to study the coevolution of transcriptional elements in core promoters or other evolutionary processes involving coordinated activity of diverse cis-regulatory elements.

The coevolutionary networks inferred for splicing in diverse eukaryotic taxa suggest that intron definition and exon definition models, sometimes regarded as abstractions, play fundamental roles in shaping gene evolution (5, 8). Incorporation of SREs into the splicing networks in mammals yielded a set of relationships describing which elements tend to compensate for mutations that weaken other elements. These rules may aid in determining which regions should be preferentially targeted in repairing mutations that contribute to disease through disruption of splicing (21). For example, the results of Fig. 4 suggest that exon skipping resulting from 5′ss mutations (a very common type of human disease mutation) in exons containing any of several ESS motifs may be commonly rescuable by inhibition of ESS recognition or other activities of specific splicing repressors.

The observation of common evolutionary compensation between ESEs and splice sites in mammals is also consistent with a recently proposed model for splicing evolution in which the emergence of SR proteins allowed evolutionary diversification of splicing signals across organisms and within organisms. This diversification, in turn, allowed versatility and flexibility in splice site recognition, enabling alternative splicing, and perhaps also increased robustness of constitutive exons to mutations (43, 44). The frequent covariation between exonic SREs and splice sites suggests that the constraints of accurate and efficient splicing may pose an effective speed limit on the rate of amino acid divergence in exons, with evolution of certain codon changes requiring prior or immediately subsequent splice site strengthening.

Materials and Methods

Exon and Intron Data Sets.

Constitutive human exons and introns were obtained from the HOLLYWOOD database (30). Orthologous mouse exons were identified by using multigenome alignment provided by the University of California Santa Cruz genome browser (45). Further details of data set construction for mammals and other organisms are given in SI Text.

The PVSA Method.

For all classes of cis elements, we evaluated their strength in the exons or introns of the two genomes under study (e.g., human and mouse). Specifically, 5′ss and 3′ss strength was scored by using a maximum entropy model (46). ESE, ESS and ISE elements were assigned log-odds scores reflecting their relative enrichment in exons and introns (SI Text). When included, the length of the intron was used directly as the “score” associated with the “intron length” node. For each cis element, the PVS consisted of human–mouse orthologous exons in which the score was in the lowest 33% of all exons in one genome and in the upper 33% in the other genome (Fig. 1B). The 33% cutoff was chosen by considering the tradeoff between the size of PVSs and the extent of variation in the cis elements. Use of different cutoffs within a reasonable range (e.g., 25%) yielded the same network structures.

To identify the subnetwork associated with the PVS for element X, all possible network structures with X as the root node were constructed (see Fig. 1D for examples of three-node rooted subnetworks with a fixed leaf). In this study, only network structures with a maximum depth of three were considered (i.e., one root node, arbitrary numbers of intermediate and leaf nodes, with no path longer than two edges). These subnetworks were then scored by using standard Bayesian inference methods (23), which calculate the likelihood of generating the observed data under a given Bayesian network structure. The high scored subnetworks (2% of subnetworks with highest likelihood) were averaged together to calculate a score for each edge between the root and the leaf nodes. The edge score was defined as the fraction of times that this edge is included in the high-scored networks.

Subsequently, a shuffling procedure was performed to obtain a P value for the edges in the final subnetwork. For each cis element in each exon (or intron), a control exon (or intron) was chosen randomly from among those whose differences in G+C content between human and mouse orthologs were similar to that of the exon (or intron) under study. The scores of the cis element in the control exon (or intron) in human and mouse genomes were substituted for the scores of the test exon (or intron) in the two genomes, respectively. This procedure was carried out independently for each cis element. The same PVSA method was applied to the shuffled data set to derive an averaged control network. The P value of each edge in the final subnetwork was calculated as the fraction of times that this edge received a higher score in the shuffled data than in the real data. Further details are provided in SI Text and SI Figs. 11 and 12.

Cell Culture and Splicing Reporter Assays.

293T cells were cultured and transfected with splicing reporter constructs, and splicing was assayed by radio-labeled RT-PCR, as described in SI Text.