Protein folding transition states probed by loop extension

Abstract

We propose a new way to characterize protein folding transition states by (1) insertion of one or more residues into an unstructured protein loop, (2) measurement of the effect on protein folding kinetics and thermodynamics, and (3) analysis of the results in terms of a rate-equilibrium free energy relationship, α_Loop. α_Loop reports on the fraction of molecules that form the perturbed loop in the transition state. Interpretation of the changes in equilibrium free energy using standard polymer theory can help detect residual structure in the unfolded state. We illustrate our approach with data for the model proteins CI2 and the alpha spectrin SH3 domain.

Protein folding transition states are transient ensembles of conformations that cannot be isolated for their study. Their structure must be characterized by indirect means, commonly rate-equilibrium free energy relationships (REFERs) (Leffler 1952; Sánchez and Kiefhaber 2003c). Briefly, we apply a perturbation ∂x to a protein folding reaction and measure the changes in the activation free energy for folding, 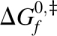, and the equilibrium free energy, ΔG ⁰. In a two-state folding reaction, these changes are linearly related and a proportionality constant, 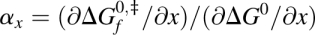, can be defined. We can obtain global information about the transition state using medium-induced REFERs and local information using structure-induced REFERs (Sánchez and Kiefhaber 2003c). Local structural perturbations used to date include mutation of residue side chains (ϕ-values) (Fersht et al. 1992), chemical modification of the protein backbone (Deechongkit et al. 2004), and engineering of metal binding sites (ψ-values) (Krantz and Sosnick 2001). Commonly, the transition state for folding of a protein is characterized at near-atomic resolution by measuring a large number of φ-, ψ-, or α_Backbone-values distributed throughout the structure. The φ-, ψ-, and α_Backbone-values for a given region of the protein are sometimes different (Deechongkit et al. 2004; Sosnick et al. 2004; Pandit et al. 2006), and there is currently no consensus on how to integrate them into a unified description of the transition state (Sosnick et al. 2004; Pandit et al. 2006). This puzzle prompts for the development of additional ways to characterize protein folding transition states.

Results and Discussion

Characterization of protein folding transition states

We propose a new structure-induced REFER. Let us consider the simple, two-state folding reaction of a protein that has an unstructured loop. The unstructured loop may be present in the wild-type protein or created by inserting two or more glycine residues into a structured loop. We can then insert one or more extra residues into the already unstructured loop using molecular biology techniques and measure the effect on the thermodynamics and kinetics of folding. This perturbation can be understood as a loop extension-induced REFER:

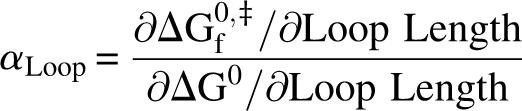We can give a physical interpretation to α_Loop using general concepts from polymer theory. The end-to-end distance of the chosen unstructured loop is strongly constrained in the native state and, in the absence of residual structure, unconstrained in the unfolded state. In this case, folding of the loop from the unfolded to the native state should have a free energy cost of purely entropic origin. Extension of the loop will increase this free energy cost because of a larger entropic penalty in the native state and an unchanged (null) entropic penalty in the unfolded state (Jacobson and Stockmeier 1950; Zhou 2004). This will lead to a change in ΔG ⁰. If the loop is constrained into a native-like conformation in the transition state, th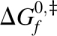e change in will be the same as the change in ΔG ⁰, and the α_Loop will be 1. If the loop is as unconstrained in the transition state as in the unfolded state, the change in 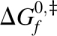will be 0 and the α_Loop = 0.

Many φ-, ψ-, and α_Backbone-values measured to date are fractional (Goldenberg 1999; Krantz and Sosnick 2001; Sánchez and Kiefhaber 2003d; Deechongkit et al. 2004; Krantz et al. 2004; Sosnick et al. 2004; Pandit et al. 2006). Unfortunately, their structural interpretation is ambiguous. They may arise from conformational heterogeneity in the transition state, from weakened interactions, or both (Fersht et al. 1992; Bodenreider and Kiefhaber 2005). To a first approximation, the change in free energy caused by extension of an unstructured loop that does not interact with the rest of the protein is independent of other interactions. In this case, the α_Loop can be read as the fraction of molecules in which the perturbed loop is constrained in the transition state in a native-like manner. However, nonnative-like conformations of the loop in the transition state are also possible. For example, partial opening of the loop neck may change the stiffness of the loop and its response to extension. Alternatively, additional residues may become unstructured and be incorporated into the loop. We can approximate the change in free energy for the addition of n residues to an unstructured loop of N residues as ΔΔG ⁰ = 1.5 · RT · ln(1 + n/N) (Jacobson and Stockmeier 1950). It follows that an extended nonnative-like loop in the transition state will have smaller values of 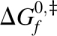and of the α_Loop than a native-like one. In this case, the α_Loop gives a lower limit for the fraction of loop-forming molecules (native-like or nonnative-like) in the transition state.

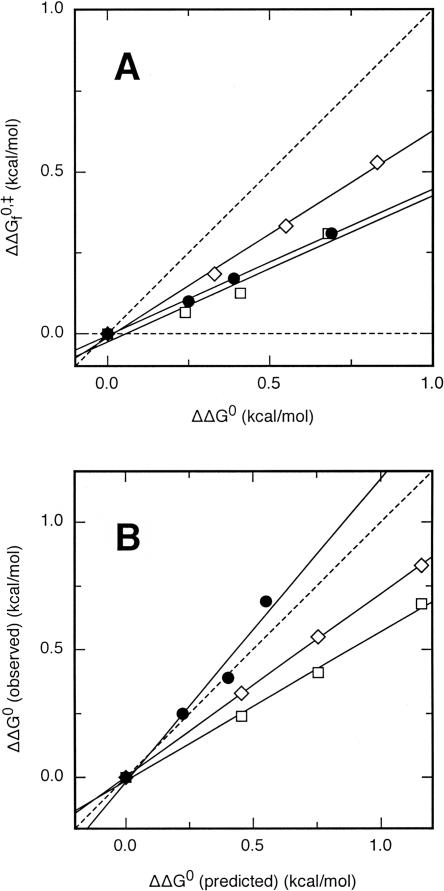
Several protein folding reactions have been perturbed by the extension of an unstructured protein loop. We will use these data to illustrate the use of the α_Loop. Figure 1A shows the effect of loop extension in the equilibrium and activation free energies for folding of CI2 and the S19P20 and N47D48 circular permutants of the spectrin SH3 domain (Ladurner and Fersht 1997; Viguera and Serrano 1997). The data for the three proteins are well described by a linear fit (R = 0.97 or higher), suggesting that the rate-limiting transition state is not altered by extension of the unstructured loop (Sánchez and Kiefhaber 2003b,a). The slope for each protein, i.e., the α_Loop-value, varies between 0.45 and 0.64 (Table 1). The fractional α_Loop-values indicate that the perturbed loops are formed in ∼45%–64% of the molecules in the transition states for folding of these proteins. The φ-values probing side chain interactions across the extended loop are significantly higher than zero in all three proteins (Itzhaki et al. 1995; Viguera et al. 1996), in agreement with our results.

Figure 1.

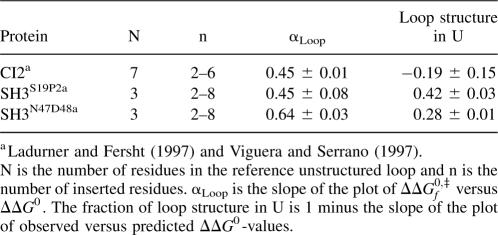
(A) Loop extension-induced REFERs for CI2 (●), SH3^S19P20 (□), and SH3^N47D48 (◊) (Ladurner and Fersht 1997; Viguera and Serrano 1997). The continuous lines are linear fits to the data. The dashed lines correspond to α_Loop-values of 0 and 1 and are shown as a reference. (B) Observed versus predicted effects of loop extension on ΔG ⁰ for CI2 (●), SH3^S19P20 (□), and SH3^N47D48 (◊) (Ladurner and Fersht 1997; Viguera and Serrano 1997). The continuous lines are linear fits to the data. The dashed line has a slope of 1 and corresponds to a negligible amount of residual structure in the unfolded state. The predicted ΔΔG ⁰-value for the addition of n residues to an unstructured loop of N residues is ΔΔG ⁰ = 1.5 · RT · ln(1 + n/N) (Jacobson and Stockmeier 1950). N = 7 and n = 2–6 for CI2; N = 3 and n = 2–8 for both SH3 domains.

Table 1.

Experimental results for CI2, SH3^S19P20, and SH3^N47D48

Detection of residual structure in the unfolded state

All REFERs take the free energy (and, consequently, the structure) of the unfolded state as a reference (Fersht et al. 1992). Many small proteins show substantial residual structure in the unfolded state (Sánchez and Kiefhaber 2003b), which puts a cautionary note to the interpretation of structure-induced REFERs (Cho and Raleigh 2006). Quantification of residual structure at each site probed by a φ-, ψ-, or α_Backbone-value is time consuming and rarely carried out. The equilibrium data collected in loop extension experiments can be used to detect residual structure in the unfolded state as follows: If a fraction of the protein molecules form the perturbed loop in the unfolded state, they will not pay an entropic penalty upon going from the unfolded to the native state and will not contribute to ΔΔG ⁰. The observed ΔΔG ⁰ will be reduced relative to the one predicted for a fully unfolded state in an amount proportional to the population of the loop. A plot of observed ΔΔG ⁰-values versus the ones predicted from polymer theory (Jacobson and Stockmeier 1950) will be linear, with a slope that can be read as the fraction of molecules that do not form a loop in the unfolded state.

Figure 1B shows the observed and predicted ΔΔG ⁰-values for CI2, SH3^S19P20, and SH3^N47D48 (Ladurner and Fersht 1997; Viguera and Serrano 1997). The data for the three proteins are well described by a linear fit (R = 0.98 or higher). The slope for CI2 is ∼1, indicating that the two halves of the protein separated by the extended loop, CI2^1–40 and CI2^41–64, are not in contact in the unfolded state. NMR experiments indeed show that residual structure in the unfolded state is confined to CI2^1–40 (Kazmirski et al. 2001). The slope of such a plot for a series of loop extension variants of the Rop protein (Nagi and Regan 1997) is also very close to 1 (Zhou 2004). On the other hand, the slopes for SH3^S19P20 and SH3^N47D48 are smaller than 1 (Table 1), suggesting the existence of a population with significant residual structure in the unfolded states of both proteins. NMR experiments found extensive residual structure in the unfolded state of the spectrin SH3 domain (Kortemme et al. 2000). This structure involves residues at both sides of the perturbed loop, in agreement with our results.

Applicability

In order to yield a meaningful α_Loop-value, the following conditions must be fulfilled: (1) Creation of an unstructured loop by the insertion of several glycine residues should not change the folding mechanism and (2) should not destabilize the protein drastically, so that the extension variants can be characterized. (3) The inserted sequence should be devoid of interactions with itself or the rest of the protein in the unfolded, native, or transition states. (4) The ΔΔG ⁰ caused by loop extension should be of entropic origin. The available experimental evidence for creation (Sondek and Shortle 1990; Ladurner and Fersht 1997; Viguera and Serrano 1997; Gordon-Smith et al. 2001) and extension (Martinez et al. 1999) of unstructured loops in the proteins CI2, SH3^S19P20, SH3^N47D48, and staphylococcal nuclease suggests that these conditions are often met, and that insertion of polyglycine or polyglutamine sequences into most protein loops will yield a useful α_Loop-value.

We have shown that loop extension-induced REFERs can give information about loop formation in protein folding transition states. α_Loop is an approximation for the fraction of loop-forming molecules in the transition state, a piece of information that can be directly compared with simulation. Additionally, interpretation of the results using standard polymer theory can help detect residual structure in the unfolded state. Since only a handful of loops in a protein will be suitable for extension experiments, α_Loop-values should be used in combination with other medium- and structure-induced REFERs in order to reach a unified description of the transition state.