Sequence-Level Population Simulations Over Large Genomic Regions

Abstract

Simulation is an invaluable tool for investigating the effects of various population genetics modeling assumptions on resulting patterns of genetic diversity, and for assessing the performance of statistical techniques, for example those designed to detect and measure the genomic effects of selection. It is also used to investigate the effectiveness of various design options for genetic association studies. Backward-in-time simulation methods are computationally efficient and have become widely used since their introduction in the 1980s. The forward-in-time approach has substantial advantages in terms of accuracy and modeling flexibility, but at greater computational cost. We have developed flexible and efficient simulation software and a rescaling technique to aid computational efficiency that together allow the simulation of sequence-level data over large genomic regions in entire diploid populations under various scenarios for demography, mutation, selection, and recombination, the latter including hotspots and gene conversion. Our forward evolution of genomic regions (FREGENE) software is freely available from www.ebi.ac.uk/projects/BARGEN together with an ancillary program to generate phenotype labels, either binary or quantitative. In this article we discuss limitations of coalescent-based simulation, introduce the rescaling technique that makes large-scale forward-in-time simulation feasible, and demonstrate the utility of various features of FREGENE, many not previously available.

SIMULATION of population genomic data is crucial for validating the analyses of many evolutionary and population genetics studies, and for assessing designs of genomewide association studies. As genotyping and resequencing technologies advance, it is important to simulate at the sequence level over large genomic regions, and under realistic models that include the effects of selection, both directional and balancing, and of gene conversion and crossover hotspots. The size of the region simulated will often need to be large, so that any boundary effects are minimized and to permit investigation of the long-range effects of multiple sites under different selection regimes on patterns of genetic variation such as linkage disequilibrium (LD).

There already exists a range of software tools for performing population genetic simulations. The development of coalescent methods in the 1980s and 1990s allowed researchers to trace only the observed sample backward in time, ignoring other members of the population. The resulting computational efficiency has led to coalescent-based approaches becoming widely used, implemented for example in MS (Hudson 2002), SELSIM (Spencer and Coop 2004), CoaSim (Mailund et al. 2005), and FastCoal (Marjoram and Wall 2006). However, coalescent methods have important limitations, and we argue here for a complementary role for forward-in-time approaches.

The first major limitation, both theoretical and practical, of coalescent methods, is in modeling large amounts of recombination. The coalescent with recombination is defined (Hudson 1983; Griffiths and Marjoram 1997) in terms of the limit as population size grows to infinity of a discrete-time Wright–Fisher model. Even without recombination, the coalescent process differs notably from the Wright–Fisher model for small population sizes (Fu 2006). With recombination, however, this discrepancy becomes much more marked because chromosomes that are ancestral to the observed sample are always assumed to recombine with nonancestral chromosomes. Working backward in time from the present, the number of chromosomes carrying ancestral material can increase rapidly in the presence of high recombination, before eventually reducing to one. Thus a fundamental assumption underpinning the coalescent with recombination is questionable even for moderately large population sizes, and appears untenable for small populations and for populations undergoing severe bottlenecks. The practical difficulty is that methods for simulating from the coalescent with recombination, such as CoaSim and MS, are only feasible for relatively small amounts of crossover and gene conversion, corresponding to at most a few megabases. FastCoal is, as the name suggests, fast, and can simulate very large genomic regions, but this is achieved by exploiting an approximation to the coalescent with recombination, and FastCoal does not incorporate gene conversion.

The second major limitation of coalescent approaches is that the repertoire of selection scenarios that they can accommodate is limited. Selsim does incorporate a general diploid selection model, but is limited to a single locus under selection, relatively small sample sizes and genomic regions, constant population size, and uniform recombination rate.

Forward-in-time approaches are extremely flexible; almost any population genetic model can be simulated subject to computational requirements. Even with the storage and processing power of today's computers this remains a serious limitation, because the entire population must be tracked forward in time. However, we illustrate below time-rescaling techniques that, together with efficient coding, make “brute force” forward-in-time methods feasible. Some forward-in-time population genetics simulation software is already available, for example FPG (Hey 2004) and simuPOP (Peng and Kimmel 2005). FPG is limited to 1000 sequences with each sequence restricted to 32 polymorphic sites. SimuPOP is implemented in Python; simple evolutionary models can be run interactively using a Python shell, while more complex models require user-written macros.

Our forward-in-time software forward evolution of genomic regions (FREGENE) provides advantages of modeling flexibility and computational efficiency over existing simulation software. FREGENE accommodates selection, both directional and balancing, affecting multiple sites so that the joint effect of different selection regimes can be investigated. It allows both crossovers and gene conversion (we use “recombination” to refer collectively to both these processes) including hotspots. FREGENE allows selfing, and incorporates growth and decline of population sizes, and population subdivision with migration. These can be combined to devise complex demographic scenarios. For example, FREGENE can be used to mimic global human genetic history, similar to the approach of Schaffner et al. (2005), including major features such as continental population structure with migration and bottlenecks. SimuPOP is also highly flexible, but FREGENE, because of its efficient coding in C++, required less than half the computational time for comparable models in our simulations, and the maximum feasible genomic region was about four times larger.

FREGENE is useful for the investigation of patterns of genomic variation under various selection regimes (see e.g., Charlesworth 2006). In addition, it is useful for investigating the properties of statistical methods to detect loci subject to selection (Nielsen et al. 2005; Voight et al. 2006), and fine-scale estimation of recombination rates (Crawford et al. 2004; McVean et al. 2004; Myers et al. 2005; Carvajal-Rodriguez et al. 2006), in particular the sensitivities of such estimates to other evolutionary factors. Perhaps most importantly, it allows both these phenomena to be studied jointly, which is important because the signal of recombination in polymorphism data can be confounded by selection, and vice versa.

The FREGENE package can also generate phenotype labels for the final generation of individuals, under a range of disease models that can include multiple causal variants. This facilitates the use of FREGENE to test statistical analysis strategies for genetic association studies, using either resequencing data or SNP genotypes and it has already been used for this purpose (Minichiello and Durbin 2006). Although simulation of entire human genomes in large populations remains infeasible, 10-Mb chromosomes in a population of 10,000 diploid individuals can be simulated within 2 days using a standard desktop work station (>2 GB RAM) and approximated in <1 hour using 10-fold rescaling, described below. Thus, direct simulation of the genetic history of population isolates that are of particular interest in gene mapping (Varilo and Peltonen 2004) is feasible, as is a good approximation of many aspects of global human genetic variation (Jobling et al. 2004). Further, a genomic interval of 10 Mb suffices for accurate extrapolation to genomewide studies, so that false discovery rates (Storey and Tibshirani 2003) and statistical significance thresholds can be investigated under various design options.

METHODS

The evolutionary models implemented are aimed at flexibility and simplicity, while maintaining computational efficiency.

Evolutionary models:

In FREGENE, a population of N individuals, each consisting of a pair of homologous sequences, evolves over discrete, nonoverlapping generations according to the Wright–Fisher model. The starting sequences are assigned by the user; they may all be empty lists, or the final state from a previous run of FREGENE.

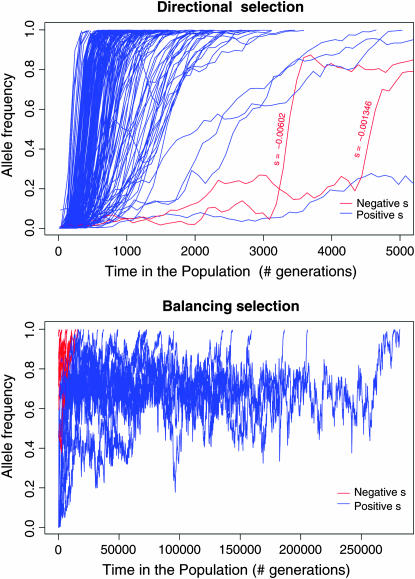
Each sequence is represented as a list of sites at which the minor allele is present—we track the minor rather than the derived allele to minimize memory usage and computation time. This is achieved by periodically (below every 100 unscaled generations) checking the population allele frequencies. If a minor allele has become the major allele at a site, the allele labels are “swapped” (swapping eliminates the site from sequences that previously included it, and includes it in sequences that previously did not). The swap status (derived or ancestral) of each minor allele is recorded so the identity of the derived allele is always known. The entire life history of all selected alleles can be tracked, allowing detailed study of the behavior of selected variants (Figure 1).

Figure 1.—

Trajectories of selected variants that reached fixation in simulation studies (Table 1). Red curves correspond to negatively selected alleles (s < 0).

Mutation:

FREGENE implements a two-allele, finite-sites mutation model, with mutation events occurring independently and at constant rate. It would be feasible to program a four-allele mutation model, corresponding to the four DNA bases, but our diallelic model provides a computationally efficient approximation that is accurate when mutations are rare and also when transversions are much less likely than transitions.

At each mutation event, a sequence and a site are chosen at random and the site is added to the minor allele list for that sequence, unless it is already there in which case it is removed. The latter case corresponds to a “back mutation,” in which a derived allele mutates back to the ancestral type. All “double hit” polymorphic sites can be recorded, whether they correspond to a back mutation or to a new mutation arising on an ancestral allele at a polymorphic site. Double-hit sites can confuse naive estimators of recombination rate and their rate is affected by the rescaling technique described below.

Reproduction, selection, and recombination:

Each sequence in a new generation is obtained from the two sequences of a parent, following recombination events that may include both crossovers and gene conversions. The two parents of an individual are chosen at random (selfing can be switched on, otherwise the parents are distinct), with probability proportional to fitness W, calculated as

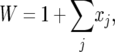(1)

where the summation is over nonneutral SNPs and

Recall that FREGENE records minor alleles for each sequence, so implementing Equation 1 requires checking the list of sites at which the derived allele is not the minor allele.

For computational efficiency we do not currently implement sexual dimorphism, but this would be straightforward. Also, in common with the standard Wright–Fisher model, each offspring arises from an independent mating so that full siblings rarely arise.

Recombination in FREGENE is specified by a C++ object that is readily modified or replaced to implement alternative models. The recombination models currently offered within FREGENE include uniform, a constant-intensity hotspot model, and varying-intensity hotspots within a hierarchical structure that models recombination rate heterogeneity at different genomic scales. The user can specify that the pattern of hotspots applies both to crossovers and to gene conversions or only to crossovers while the gene conversion rate is uniform. See the FREGENE web site for further details.

When mutation generates a novel allele, it is neutral with probability p_N. Otherwise selection coefficients s and h are each chosen from a mixture of two Gaussian (normal) distributions with means and variances assigned by the user. If 0 < h < 1, then positive (s > 0) or negative (s < 0) directional selection arise. If h < 0 or h > 1 then balancing selection can arise such that both alleles tend to be maintained at stable frequencies. For large population sizes, there is an equilibrium population proportion of the derived allele at

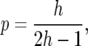(2)

irrespective of the value of s, but when sh < 0 the equilibrium is unstable and is rarely realized. Even a stable equilibrium will eventually be destroyed, either by drift or by a positively selected allele arising at a tightly linked site.

Population size:

The population size can be constant, or it can grow or decline exponentially. More complex demographic scenarios, involving for example bottlenecks, or periods of stasis between bouts of growth, or population splits or merges, can be implemented via multiple successive runs, the output of each being used as input for the subsequent run with new demographic parameters.

Simulation of a very large population, for example the current worldwide human population, may be constrained by computer memory to short genomic intervals. However, typical human effective population sizes are readily accommodated, and large populations can be approximated using rescaling, as described below.

Subdivided populations with migration:

FREGENE implements a symmetric island model, in which there is a common migration rate m in each direction and between each pair of islands. Different population sizes can be specified for each island, but if exponential growth is specified, the same growth rate applies to each island. If the population sizes are constant in a symmetric island model, users may specify instead of m the corresponding equilibrium value of F_st.

Migration of sequences occurs after pairing but before reproduction; each pair of sequences used to generate new sequences in an island is chosen locally with probability 1 – m, otherwise the source island is chosen uniformly from all the islands in the simulation. Since the local island can be chosen in the latter case, the effective migration rate is m(1 − 1/k).

Simulation size and run length:

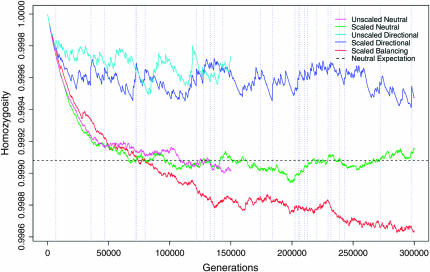
Users will typically wish to run FREGENE for the minimum time necessary to achieve approximate equilibrium, if there is one for the specified model, or more generally so that the initial conditions are “forgotten” with high probability. This occurs if, at almost every site, the entire final generation traces back to a unique sequence in the founding generation of the simulation. For a standard Wright–Fisher model of a constant-size, panmictic population under neutrality, the time since the most recent common ancestor at a site has a known distribution (Neuhauser 2007), and 10N and 12N generations suffice to ensure that the final generation will trace to a unique founder sequence at, respectively, almost 98 and >99% of sites in a large genomic interval. This will typically be adequate when the mutation rate is low; most of the remaining sites will trace back to two or three founders and, if the simulation were extrapolated backward in time, these would typically reach a common ancestor with no intervening mutation. Figure 2 illustrates that the equilibrium homozygosity under neutrality is reached well within 10N generations.

Figure 2.—

Per-site homozygosity over generations for simulations described in Table 1. The dashed horizontal line shows the theoretical equilibrium value for the neutral simulations. Vertical dotted lines indicate the generations at which, in the scaled directional simulation, selected sites with s > 0.05 went to fixation.

Rescaling approximations for computational efficiency:

The diffusion theory of population genetics (Ewens 2004) is founded on the principle that, for a wide range of models, populations of any (large) size are approximately equivalent—for example, allele frequencies and LD statistics have approximately the same distribution—provided that time is scaled by (effective) population size. Under this scaling, rate parameters such as mutation (μ) and recombination rates (R_c and R_g, for crossover and gene conversion), and also the selection coefficient s, are expressed as products with N. For example, the proportion of sequence pairs that have the same allele at a site, averaged over sites, is F = 1/(1 + 4Nμ). Further, t generations is equivalent to t/N scaled time units. Thus, if it is desired to simulate over t generations a population with parameter values N, μ, R_c, R_g, and s, then a simulation using instead N/λ, λμ, λR_c, λR_g, and λs, evolved for t/λ generations, for some λ > 1, will generate approximately the desired allele frequency distribution and patterns of LD.

Rescaling permits a dramatic reduction in computing time. For example, we found that simulation under neutrality of 10-Mb chromosomes in 10,000 individuals required nearly 2 days without rescaling, but <1 hr using 10-fold rescaling (λ = 10). This decrease is achieved because the number of generations is reduced by a factor of λ, and in each generation the number of individuals to be simulated is similarly reduced. Thus, rescaling could reduce the overall computing time by a factor of up to λ². In practice, because some aspects of the computation do not scale with λ, the achieved speed reduction is less than λ², particularly for λ large: we found that with λ = 5, 10, and 20 the computation time was reduced by factors of 20, 64, and 180, respectively. Run times for models involving balancing selection can be longer, while directional selection typically reduces run time compared with a neutral simulation. In either case, the relative time saving from rescaling is similar to that under neutrality.

Simple rescaling leaves fewer individuals in the final generation, but this can be avoided while retaining most of the computational gain by starting the simulation with 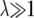, but gradually approaching λ = 1 as the simulation proceeds. For example, using λ = 10⁴/(10³ + g), where g is the generation number, for the first 9000 generations, and then continuing with λ = 1 for a further 11,000 generations, allowed us to simulate 10,000 pairs of 10-Mb chromosomes to near equilibrium in ∼10 hr.

One cost of rescaling is that double-hit sites become more frequent, which may be important for some applications such as the estimation of recombination rates, although double-hit sites are typically rare and a higher rate will often be unproblematic. If the user is concerned about double-hit sites, a possible solution is to replace N with N/λ but leave all the rate parameters unchanged and instead increase the genome length (number of sites) by λ. The mutation rate per site and hence the double-hit rate are unchanged; each site is less likely to be polymorphic but, because of the larger number of sites, the expected total number of polymorphic sites is unchanged. Alternatively, since double-hit sites are flagged in FREGENE, it may be appropriate to remove a proportion of 1 – 1/λ double-hit sites from the output.

Storage requirements:

For every copy of the minor allele at every SNP, an integer is required to store its genomic location. At equilibrium in a standard Wright–Fisher model, the total storage requirement (integers) for N diploid individuals is about 11N²μ. For N = 10,000 and μ = 2.3 × 10⁻⁸, the expected number of integers stored per site is ∼25. In practice, we found that ∼205 MB of RAM were required per megabase of sequence with N = 10,000 but only 27 MB/Mb when approximated using rescaling with λ = 10.

RESULTS

We simulated 10,000 individuals over a 3-Mb genomic region, using recombination and mutation models representative of those observed in humans (Table 1). Three selection scenarios were implemented: (a) neutrality; (b) predominantly directional selection, both positive and negative; and (c) predominantly balancing selection. The literature on realistic values for selection coefficients at typical human loci is sparse, and we chose illustrative rather than realistic values. We used scaling with λ = 10, so that only 30,000 FREGENE generations were required to mimic 300,000 actual generations, but as a check, simulations a and b were replicated without scaling (λ = 1) for 150,000 generations. For the scaled simulations, the generation counts reported below refer to unscaled equivalents.

TABLE 1.

Parameter values for the simulation models

	Target value	Scaled value λ = 10
No. chromosomes, N	20,000	2000
No. generations	300,000	30,000
Mutation rate, μ	2.3 × 10−8	2.3 × 10−7
Crossover rate, Rc	1.1 × 10−8	1.1 × 10−7
Gene conversion rate, Rg	1.2 × 10−8	1.2 × 10−7
Directional selection
Selection coefficient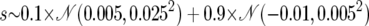
Dominance coefficient	h = 0.5
Balancing selection
Selection coefficient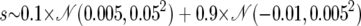
Dominance coefficient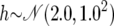

The top section applies to all simulations. For both nonneutral models, the proportion of the genome under selection is 5 × 10⁻⁴ (i.e., P_N = 0.9995). 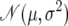denotes the Gaussian (normal) distribution with mean μ and standard deviation σ.

Figure 1 shows the trajectories of selected alleles that reach fixation. The majority of positively selected alleles (top) proceed rapidly to fixation, but two with small s values took more than 5000 (unscaled) generations. The two negatively selected variants reaching fixation both show a period of rapid increase in frequency corresponding to hitchhiking with a nearby positively selected allele. A small number of variants with s < 0 also reach fixation under the balancing selection model (bottom). For the parameters chosen here, the allele frequencies remain highly variable in the vicinity of the equilibrium value, so that some quasi-stable loci do reach fixation within this simulation.

Figure 2 shows the evolution of homozygozity for the three simulation scenarios, and also for the two unscaled replicates which, as expected, show a similar evolution to their scaled counterparts. The vertical dotted lines refer to simulation b; these correspond to the fixation of a positively selected allele, which usually generates a rapid local increase in homozygosity. The balancing simulation c has still not reached equilibrium after 300,000 generations; new balancing polymorphisms are arising more rapidly than they are being lost leading to a decline of homozygosity that is only gradually attenuating.

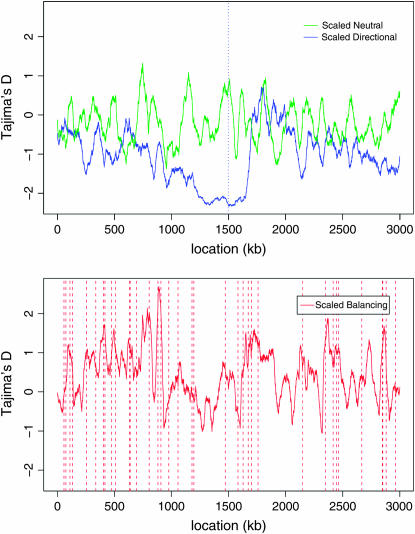
Figure 3 illustrates the capacity of Tajima's D (Tajima 1989) to detect a signature of selection (Carlson et al. 2005). Negative values of D indicate an excess of rare variants that may be due to positive selection, while the excess of common variants signaled by D > 0 may flag balancing selection. The definition of D implies that Var(D) = 1 under a simple neutral model, and |D| > 2 is usually interpreted as significant at level 0.05. Only one site reached fixation within the final 3000 generations of the directional simulation, generating the smallest, but only barely significant, D value. For the balancing simulation, stable polymorphisms sometimes generate a positive peak in Tajima's D but only once did this peak exceed 2. Note that our simulation includes some directionally selected alleles, which may (realistically) complicate the signal from Tajima's D relative to a simpler simulation.

Figure 3.—

Tajima's D in 50-kb windows after 300,000 generations (top) and 150,000 generations (bottom). The vertical dotted line (top) indicates the location of the unique site under positive selection that went to fixation within the final 3000 generations. The vertical dashed lines (bottom) indicate selected sites that were polymorphic throughout the preceding 10,000 generations.

DISCUSSION

High-throughput genotyping and resequencing technologies are revolutionizing population genetics, by providing data to study processes such as recombination and selection at high resolution on large genomic scales. Computationally efficient simulation tools that can explore complex demographic and selection scenarios over large genomic regions will be invaluable in making full use of these data. We have illustrated (Figure 1) how FREGENE can permit detailed tracking of selected variants, for example hitchhiking of negatively selected variants. We have also illustrated the utility of our FREGENE software to explore the behavior of a selection-monitoring statistic, Tajima's D, under complex selection scenarios, which has not been available to previous authors using this statistic.

Genomewide association studies using dense SNP maps are now a reality, and whole genome resequencing is beginning to emerge, so that researchers will want to evaluate its costs relative to its potential benefits, and for this a sophisticated simulation tool is required that can generate test data sets for evaluating different genotyping technologies and study designs. FREGENE has already been used for assessing an analysis tool for dense SNP-based studies, and it can also be used with resequencing data. For either data type, it will be particularly useful for the study of population isolates. The possibility of including selection in such simulations greatly enhances their realism. Recently, forward simulations have been used to investigate patterns of complex disease under different scenarios (Peng and Kimmel 2007; Peng et al. 2007). These authors use either a single locus under selection or a few unlinked loci, and the same loci affect penetrance. Use of FREGENE would allow the effects of interactions among many sites under selection to be incorporated, most of these not related to the penetrance for a specific phenotype. Although the final frequency of a selected variant cannot be predicted, the simulation of large genomic regions using FREGENE can allow many possibilities for selected variants in the final generation.

Forward simulators are memory and cpu intensive, but we have introduced here a rescaling technique that reduces the number of generations required for a simulation. With this technique, we believe that FREGENE will prove a valuable tool both for those developing methods to detect genomewide associations, and those exploring population genetic hypotheses. Source code, executables, and documentation are available from http://www.ebi.ac.uk/projects/BARGEN.