Consequences of localized frustration for the folding mechanism of the IM7 protein

Abstract

In the laboratory, IM7 has been found to have an unusual folding mechanism in which an “on-pathway” intermediate with nonnative interactions is formed. We show that this intermediate is a consequence of an unusual cluster of highly frustrated interactions in the native structure. This cluster is involved in the binding of IM7 to its target, Colicin E7. Redesign of residues in this cluster to eliminate frustration is predicted by simulations to lead to faster folding without the population of an intermediate ensemble.

For proteins to fold to an organized native ensemble, they have evolved to form a highly favorable, stabilizing set of native interactions (1). Proteins, it seems, have a funneled energy landscape toward the native state (1–3). However, real protein landscapes may not be perfectly funneled but probably display some landscape ruggedness because of the possibility of forming favorable but nonnative interactions during the folding process. Energy landscape theory shows that, if the landscape were too rugged, numerous long-lived intermediate states that energetically compete with the native state would become populated (4). The rarity of the experimental finding of such intermediates having significant nonnative structure strongly argues that proteins largely conform to the “principle of minimal frustration” (2).

When populated kinetic folding intermediates have been observed, it has generally turned out to be the case that these metastable thermodynamic states are not caused by energetic frustration but by a nonuniform compensation of the entropy and energy changes upon forming native contacts. The existence of such productive, on route, folding intermediates can be said to be topology-driven and can often be predicted from the native structure alone by using a perfectly funneled landscape (5–8).

IM7 is an 86-residue-long protein that is known to fold through an on-pathway intermediate state. An intermediate populated in the folding of IM7 has been shown to possess a nonnative packing of three of the four helices around a specific hydrophobic core (9). In this article, we explore the relationship between nonnative interactions, the presence of the stable folding intermediate, and the residual frustration found in the native structure. Our analysis suggests that this seeming exception to the pattern expected for minimally frustrated proteins is, in fact, consistent with the ideas of energy landscape theory touching on the behavior of frustrated, random heteropolymers.

We first demonstrate that the intermediate of IM7 is not a direct consequence of the topology of IM7 by simulating its folding with a sequence-independent energy function that yields a perfectly funneled landscape [a so-called Ḡ Hamiltonian (10)]. Not only is no intermediate observed with this Hamiltonian, but neither is an intermediate found when contact energetic heterogeneity or nonadditivity through many-body interactions are included. These more sophisticated Hamiltonians do not predict the existence of a stable intermediate. These results suggest that the experimentally observed intermediate may be a consequence of elements excluded in these purely topological simple models.

Can we establish how frustration changes the way the IM7 intermediate is formed? To study this, we performed simulations with a transferable Hamiltonian of the type used to predict protein structure de novo. This relatively realistic Hamiltonian turns out to predict not only the existence of a populated intermediate that is stabilized by nonnative interactions but also a structure of the intermediate ensemble that compares well to the observations of Capaldi et al. (9), who inferred the presence of a three-helix core of helices I, II, and IV. We note that this ensemble has numerous native-like interactions but also is stabilized by some nonnative interactions.

Equipped with an energy function that predicts the experimentally observed intermediate, we quantify the role frustration plays in the folding. Based on the same energy function used for the kinetic simulations, we employ the algorithm of Ferreiro et al. (11) to compute local frustration for all sites in the native structure and in the intermediates. We also use this scheme to predict mutants that should reduce the level of frustration so as to make the landscape less rugged and more funneled. We contrast two different redesign schemes, one based on the native state that alleviates the frustration in that structure and another redesign that attempts to specifically destabilize the intermediate states found in the IM7 simulation. When the redesigned mutants were simulated with the associative memory Hamiltonian with water-mediated interactions (AMW) model, the kinetic intermediate disappears when residual native-state frustration is reduced, confirming the role of localized native-state frustration in allowing this state to be populated.

Results and Discussion

Perfect Funnel Models.

We first examine whether the existence of an intermediate could follow from a perfectly funneled landscape. We simulated IM7 with a native topology-based model that takes into account only those interactions that are found in the folded protein. In the simplest funneled landscape, often called a Ḡ model after the form used in early lattice studies (10), all native contact energies are weighted equally. Intermediates and barriers in the free-energy profile in this case must arise from a nonuniform tradeoff between entropic terms describing the many conformations that the free chain can have and the stabilization energy of the specifically formed, native contacts. Simulations with this Hamiltonian suggest that IM7 would fold down-hill. The experimentally detected intermediate is not reproduced by using such a perfectly funneled Hamiltonian. When nonadditivity through many-body contact terms was included, IM7 folded in a two-state manner. There is neither a stable thermodynamic ensemble other than the folded and unfolded state nor any long-lived local energetic traps or any other signs of “topological frustration,” such as the observation of a bimodal distribution of the transition state φ values, often an indication of multiple, distinct folding pathways. Although inclusion of nonadditivity through many-body contact terms increased the barrier height, including such additional explicit cooperativity did not produce an intermediate state.

To study whether there may be an effect of energetic heterogeneity, the magnitude of all of the native interactions were scaled with the Miyazawa–Jernigan contact energies (12). A priori it is possible that the resulting inhomogeneous but still perfectly funneled model might account for the observation of a stable intermediate. Nevertheless, molecular dynamics simulations with this Hamiltonian both with and without explicit nonadditivity did not reveal any intermediates. The two-state folding behavior is preserved with no relevant traps being present. [see supporting information (SI) Fig. 4]. Moreover, the transition state φ values still exhibit unimodal probability distributions.

The intermediate experimentally observed in IM7 folding apparently cannot be captured by a perfectly funneled landscape. The absence of any populated intermediate state predicted even with heterogenous contact energies and many-body terms in funneled Hamiltonians conflicts with experiment and suggests strongly that the folding landscape of IM7 must be more rugged than these ideal models.

AMW–IM7 Folding Mechanism.

To predict the folding of IM7 with an energy function that yields a more rugged but still globally funneled energy landscape capable of folding the molecule, we carried out simulations with the AMW model. This nonadditive Hamiltonian has heterogeneous direct contact energies and nonadditive energy terms to capture solvent-mediated interactions but makes no use of native tertiary structure information and, thus, allows for possible nonnative tertiary interactions. To quantify the amount of local ruggedness of the energy landscape yielded by the AMW model (Fig. 1A), we compute the frustration indices for interacting residue pairs with the method presented by Ferreiro et al. (11) in this issue of PNAS. The energy of a site involving interacting residues at positions i and j depends only on their amino acid identities (λ_i and λ_j), densities (ρ_i and ρ_j), and pairwise distance r_ij. To measure how frustrated a site is (F_ij), we compute for each site the native energy and reference decoy site energies (see Methods for details). The ratio of the local contribution to the energy gap versus the standard deviation of the local decoy energies (the frustration index) then gives an estimate of how favorable the native interaction is relative to randomized interactions.

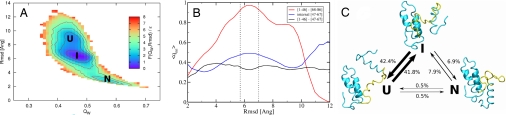
Fig. 1.

Characterization of the IM7 wild type folding thermodynamics and its intermediate features. (A) Free energy (in units of ε) of the IM7 at T̄ = 1.0 as a function of Q_W and rmsd. The wells correspond to the unfolded (U), intermediate (I), and native (N) states. (B) The average fraction of nonnative contacts as a function of the rmsd. In the red curve, we consider only the interactions between the first half of the protein (residues 1–46) with the fourth helix (residues 68–86). The blue curve shows the same ratio but only for the contacts internal to the helix III region (residues 47–67), and the black curve represents the contacts between the first half and the helix III region. Also displayed with vertical dotted lines are the boundaries used to define the intermediate state. (C) The percentage of the transitions observed between the three states U, I, and N suggests the intermediate to be on-pathway in the folding reaction. The states are operatively defined in terms of Q_W and rmsd as U = [0.43; 0.47] × [8.4; 9.7], I = [0.45; 0.51] × [5.7; 7.0] and U = [0.55; 0.60] × [2.5; 3.3], and a transition is counted every time the trajectory in Q_W, rmsd space leaves one state and enters another without passing through the third. The percentage of jumps are calculated out of 1,890 observed transitions during 40 independents simulations at T̄ = 1.0. Three representative snapshots of each state also are shown, with the helix III region highlighted in yellow.

We first calculate the frustration index for all interacting residue pairs in the crystal structure of IM7 (Protein Data Bank ID code 1AYI) to characterize the local energy landscape around the native basin. Also shown in the accompanying article by Ferreiro et al. (11), an extensive survey of local frustration in proteins provides us with an estimate of the typical fraction of minimally frustrated, frustrated, and highly frustrated contacts present in natural proteins. On the contact level, we find that IM7 is less minimally frustrated (i.e., more frustrated) than is a typical protein. Of the native contacts, 32% are minimally frustrated (Fig. 2A, green lines) compared with 37% in a typical protein. Still, like most proteins, the minimally frustrated contacts do form a cluster spanning most of the protein core. We also observe more frustrated sites in IM7 (36%) compared with the 32% ordinarily expected. Importantly, multiple, distinct, highly frustrated contact clusters (11% of the total, compared with the 9% expected) (Fig. 2A, red lines) are found in three distinct regions: the loop region between helices I and II, the helix III region, and the C-terminal residues in helix IV. In general, the separable topology and clustered nature of these frustrated interactions is the key to the nonnative intermediate formed. Taken together, IM7 has more frustrated contacts and fewer minimally frustrated contacts, suggesting a more rugged landscape than a typical protein.

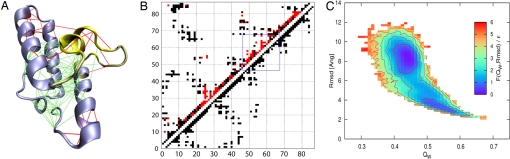
Fig. 2.

Native-state residual frustration and two-state behavior of the designed double mutant Y55R, Y56N. (A) Local frustration is depicted on the native IM7 wild-type structure (from Protein Data Bank ID code 1AYI). A large cluster of minimally frustrated contacts (green) defines the core of the protein, but some highly frustrated contacts (F_ij < −1) surround the core (indicated in red). (B) Native contacts of wild-type IM7 in the native (upper-left) and intermediate (lower-right) states. Highly frustrated contacts (red) are primarily local compared with all contacts present in the native state. Within region III (blue box), multiple frustrated contacts remain unformed in the intermediate. (C) Free energy (in units of ε) of the IM7 designed mutant at T̄ = 1.0 as a function of Q_W and rmsd. The minima correspond well to the unfolded (U) and native (N) states of the wild-type protein.

The presence of a larger amount of frustration in the native state of IM7 than usual seems to stem from the fact that, in nature, IM7 evolved not only to have a significantly funneled folding landscape but also a funneled binding landscape. When the frustration levels for IM7 bound to its binding partner are computed, most of the contacts that are frustrated in the monomeric native state become minimally frustrated in the bound form (SI Fig. 5).

To study the folding routes with a partially frustrated landscape, we extracted the free-energy profile from constant temperature molecular dynamics simulations of the AMW model with one memory term for the short-range, in-sequence interactions, the crystal structure of IM7. This memory term introduces a bias to form proper native secondary structure without biasing the long-range tertiary interactions. This term cooperates in ensuring that indeed the proper native state is formed. The free energy profile for this now frustrated landscape displayed as a function of two measures of the extent of folding [Q_W and rmsd; see SI Text for details] of IM7 exhibits, at equilibrium, three thermodynamically stable states: a native (N), an intermediate (I) and an unfolded ensemble (U) (Fig. 1A). We computed the radius of gyration R_g for members of the respective ensembles. The three ensembles all show a similar degree of compactness relative to the x-ray crystal structure of IM7. The unfolded state is unusually compact with an average radius of gyration of 〈R_g^U〉/R_g^X = 1.2. This can partly be understood by the bias of native, secondary structure in the Hamiltonian. Indeed, most of the secondary structure elements are already formed in the unfolded ensemble. Before reaching the native state, which has a crystal-structure-like compactness (〈R_g^N〉/R_g^X = 1.0), an intermediate ensemble becomes populated. At a simulation temperature of T̄ = 1.0, the intermediate is the most populated basin and is on-pathway in the folding route to the native state, which is evident from the relative percentage of the transitions observed between the three states (Fig. 1C). The observed intermediate ensemble with 〈R_g^I〉/R_g^X = 1.1 has an almost native-like compactness. It has been experimentally determined that the intermediate is nearly as compact as the native structure, consistent with the experiments of Friel et al. (13) who measured a Tanford value of β_T = 0.8 for the intermediate of IM7 relative to the native state.

The structures of the intermediate ensemble generally contain a three-helix core in which helix I (residues 12–24) and helix II (residues 32–45) and their interface are all natively formed. Helix IV (residues 66–79), however, interacts in a nonnative way with helix I. The presence of this highly structured core composed of helices I, II, and IV in the intermediate was inferred experimentally by Capaldi et al. (9) from φ value analysis. Specifically, in our simulations, residues 77–80 of helix IV and residues 12–24 of helix I form numerous nonnative contacts with high probability in this intermediate (Fig. 3B). Analyzing the frustration at a local level reveals that these nonnative contacts are minimally frustrated with respect to this core structure (see Fig. 3A, blue lines); that is, they stabilize the intermediate state through favorable contacts not found in the native ensemble. Interestingly, mutations of some of these residues (A77G, A78G, A13G, F15A, V16A, L18A, L19A, and I22V) are known from experiment to destabilize the intermediate state. From our simulations, we understand that these favorable but nonnative contacts must be lost upon transition to the native state (see Fig. 1B, red curve), prompting helix IV to trade some favorable nonnative contacts for native contacts that also are favorable.

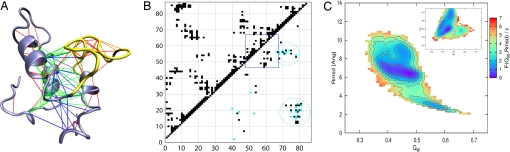
Fig. 3.

Specific intermediate state redesign. (A) Local frustration is depicted on a selected IM7 intermediate structure. Minimally frustrated contacts present in the crystal structure (green) are distinguished from those that are nonnative (blue). A distinct nonnative cluster can be observed involving interactions between helix IV and the helix I–II region. Native (red) and nonnative (orange) frustrated contacts surround the core. (B) Two clusters of minimally frustrated contacts (blue) characterize the nonnative contacts in the intermediate state (lower-right). The wild-type native-state contacts also are shown (upper-left). (C) Free energy (in units of ε) of the IM7 redesigned mutant K20Y, N79Y at T̄ = 1.0 as a function of Q_W and rmsd. (Inset) The free energy as a function of Q_W to the crystal structure and Q_W to a representative structure from the wild-type intermediate basin.

Besides favorable interactions, the intermediate also exhibits many frustrated contacts (Fig. 3A, red and orange lines). Whereas the three-helix core of helices I, II, and IV is stabilized both by favorable native and favorable nonnative interactions, the loop region (residues 47–67, which we refer to as the helix III region) surrounding helix III (residues 51–56) does not show any particular local structural preference (Fig. 3B, blue box). That is, native and nonnative contacts internal to the region occur in almost equal proportion. Moreover, no particularly favorable interactions and many highly frustrated interactions are found in this region. Both the frustrated interactions and the rugged landscape of the helix III region must therefore play an important role in the stabilization of the IM7 folding intermediate. Indeed, this region behaves very much in the way we would expect a random heteropolymer to act. Upon crossing the free-energy barrier separating the intermediate basin from the native one, the helix III region reduces its nonnativeness. The ratio of nonnative contacts over the total number of contacts decreases by almost 40% in making this transition (see Fig. 1B, blue curve). The helix III region also interacts nonnatively with helix IV. Unlike the interactions within the helix III region itself, many of these “external” interactions are favorable.

Reducing Native State Frustration.

Kinetic folding experiments on experimentally designed IM7 mutants have shown that the populations of the native and intermediate states can be shifted significantly with single- and double-residue mutations (14). Based on our site-specific localization of frustration, we devised two strategies to redesign the folding landscape. In the first design scheme, the goal is to find those double mutants that reduce the frustration in the native structure. Among the regions with significantly frustrated residues (Fig. 2B), we chose to focus our design strategy on the helix III region. In this frustrated region there is a large preponderance of competing nonnative interactions and an absence of several native contacts in the intermediate ensemble, making the helix III region an optimal target for redesign. The other regions, although frustrated locally in the native structure, are substantially native-like in the intermediate (Fig. 2B), making them less likely successful redesign targets to shift the population of observed structures toward having more native and less intermediate structures. We selected eight highly frustrated positions for designing a defrustrated native state and constructed a library of double mutants. For each pair of positions, the local frustration was computed for each of the 400 possible mutants (representing all combinations of amino acids). Approximately 76% (13,695 of 18,000) of the mutants had fewer frustrated sites than the native does.

To test whether the less-frustrated mutant sequences do in fact yield a less rugged energy landscape than the wild type, we selected two top designs for further AMW simulation studies (Table 1). The free-energy profile obtained from constant temperature simulations with the least-frustrated double mutant (Y55R, Y56N) is shown in Fig. 2C. The free-energy profile of this mutant sequence does indeed exhibit two-state folding behavior with no stable intermediate basin. This is a clear success for a design strategy focused on defrustrating the native state rather than specifically targeting the intermediate state with its manifold of competing nonnative interactions. Whereas the wild-type sequence folds through an intermediate stabilized by nonnative interactions, the designed sequence cooperatively folds from the unfolded ensemble to the low-energy native state without populating any intermediate traps. The average folding time τ for the wild-type sequence and the mutant sequences were computed. As a consequence of being less rugged and more funneled, the less frustrated, designed sequence displayed a 10-fold speed-up in folding despite the intermediate being “on-pathway” in the wild type (see SI Table 2). Making the “minor” change of two residues in the sequence minimizes frustration and yields an energy landscape that appears to be as funneled as the energy landscapes ordinarily obtained with the “flavored” Ḡ models having heterogeneous but only native contact energies.

Table 1.

Mutant design

Redesign of native state				Negative design of intermediate
Design	Positions	Native	Mutants	Design	Positions	Native	Mutants
1*	49, 55	D, Y	S, R	1	17, 59	Q, N	L, Y
2			L, S	2			F, A
3	50, 55	G, Y	M, S	3*	20, 79	K, N	Y, Y
4			S, N	4			D, Y
5	50, 56	G, Y	M, K	5	20, 81	K, K	Y, L
6			S, K	6			Y, R
7*	55, 56	Y, Y	R, N	7	24, 79	K, N	M, Y
8			N, K	8			W, Y

In total 18,000 mutants were evaluated for native state redesign (left side), and 7,600 were evaluated for specific negative design (right side). For each scheme, eight highly favorable double mutants are presented. Selected mutants used for AMW simulation studies are marked with an asterisk.

Attempted Specific Negative Design of Intermediate.

The goal of our second design study was to specifically destabilize the intermediate ensemble and eliminate the dominant thermodynamic trap. The specific negative design of the intermediate state is, however, a more difficult way to remove ruggedness from the energy landscape than is the reduction of the level of frustration in the native target structure. As expected from energy landscape theory, it is likely that even when such specific redesign succeeds in destabilizing the specific ensemble of structures, which constitutes the wild type IM7 intermediate, if the native state is still frustrated, one cannot exclude the emergence of still other thermodynamic, glassy traps. We evaluated the efficacy of a specific negative design approach by first identifying nonnative contacts present in the wild-type intermediate ensemble that are minimally frustrated by our site-specific measure (Fig. 3 A, blue lines, and B, blue contacts). From this analysis, a precise candidate set of contacts for modification emerged, namely those contacts that arise from the nonnative association of helix IV with both helix I and helix III regions. To disrupt these interactions, we need to find residues that frustrate the nonnative sites but do not also significantly frustrate native contacts. We mutated to all 400 possible pairs and measured the energy change over a representative set of the intermediate ensemble (500 structures). A selection of the top mutants for negative design is presented in Table 1.

Our results are consistent with the φ value data obtained by Capaldi et al. (9). In their study, mutations of residues in the ranges 3–19 and 72–78 were found to destabilize the intermediate state. Many of our top mutants involve residues in these ranges. One of the top mutants involves disrupting the interaction between Lys-20 and Asp-79. We ran AMW simulations on this mutant. The free energy of this double mutant (K20Y, N79Y), shown in Fig. 3C, still displays an intermediate state. This intermediate state turns out to be more widely dispersed in Q_W and rmsd than is the intermediate state of the wild type, but the landscape still contains a profound thermodynamic trap. The negative design scheme was successful in partially destabilizing the wild-type intermediate, but the mutant sequence nevertheless gave rise to an alternative folding route to the native state via a different stable intermediate. Due to this alternate route, the folding time was lengthened. To quantify the destabilization of the intermediate, we also plotted the free energy as a function of Q_W and Q_W^I, where Q_W^I is the structural similarity relative to a representative wild-type intermediate structure (Fig. 3C Inset). There are several low free-energy basins in the free-energy plot. The biggest basin corresponds to an intermediate state that is not found in the wild type intermediate (low Q_W^I value). Therefore, the folding route through this alternate intermediate structure turns out to be preferred for this modified sequence.

Conclusions

From its inception, the energy landscape theory acknowledged and highlighted the fact that many amino acid sequences would have frustrated interactions that could slow folding. Nevertheless, in keeping with the principle of minimal frustration, specifically structured, long-lasting nonnative intermediates like that observed in the IM7 folding seem to be rare. We have seen that the intermediate of IM7 is not captured by perfect funnel models, even when cooperativity and contact heterogeneity are added. Yet, from the landscape theoretic viewpoint, this result is not surprising due to the significant clusters of highly frustrated sites observed in the native state (Fig. 2). Frustrated interactions give rise to a rugged energy landscape wherein favorable nonnative interactions compete and give rise to a spectrum of stable but structurally disparate states. In the case of IM7, these significant traps from frustration give rise to an intermediate, which is observed both in experiment and in our AMW simulations. The structural features of the intermediate from our simulations compare well with the known experimental findings.

The observation of clusters of frustrated interactions in the native state points the way to a general mutational strategy to reduce the ruggedness of folding landscapes. Our redesign strategy based on minimizing native state frustration was a success and led to double mutants that eliminated any significant intermediate population during AMW simulations. As expected, specific negative design is not so easy or effective as was minimizing frustration in the native target structure. The mutant specifically redesigned to destabilize the wild-type intermediate did not fold without an intermediate but rather retained an intermediate having a different structure.

We note that the frustration in IM7 is relieved upon binding to its natural partner. In vivo, folding and binding may occur together and may be well described by a largely unfrustrated landscape. IM7, by itself, only marginally satisfies the minimal frustration principle, so the emergence of an intermediate with significant nonnative structure (accompanying many native interactions) beautifully resonates with the ideas of the energy landscape theory.

Methods

Localized Frustration Measurements and Design Procedures.

The details of the simulations are described in theSI Text. Standard procedures were followed for all simulations used for this study.

Our site-specific measure of local frustration serves to rationalize the role of specific interactions in the IM7 folding mechanism. It is used also to guide our mutational designs. The definition and procedures are described.

Local Frustration Index.

The local frustration index is a site-specific measure of the energetic fitness for a given set of residues λ_i and λ_j at residue positions i and j > i + 1. We used a simple definition of site-specific frustration based only on the sequence-specific components of the AMW energy function (ℋ_contact, ℋ_water, and ℋ_burial) (15). These terms depend on the identities (λ), densities (ρ), and interaction distances (r_ij) of the residues involved. The local frustration is defined as

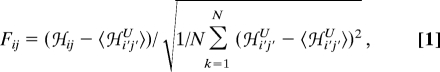where ℋ_ij = ℋ _contact^ij + ℋ _water^ij + ℋ _burialⁱ + ℋ _burial^j is the native site energy with native parameters (λ_i, λ_j, ρ_i, ρ_j, and r_ij). We obtain the average and standard deviation of a set of reference energies, ℋ_i′j′^U = ℋ _contact^i′j′ + ℋ _water^i′j′ + ℋ _burial^i′ + ℋ _burial^j′, by randomly selecting the parameters (λ′_i, λ′_j, ρ′_i, ρ′_j, and r′_ij) according to the native composition of the corresponding parameters. With this definition, for a given protein sequence composition and structure, the average and standard deviation of reference site energies are the same for all interacting residue pairs i, j.

When ℋ_ij = 〈ℋ_i′j′^U〉, the native site energy is not discriminated from a typical energy at a random site, and F_ij = 0. For the present study, frustrated sites are those where F_ij < 0. Highly frustrated sites have values of F_ij < −1. Arguments from theory suggest that an interaction is minimally frustrated when F_ij > 0.78. We use these cutoffs in this study. An article in this issue of PNAS (11) presents an extensive study of the concept of local frustration as well as alternative definitions for it.

To characterize the landscape generated by AMW simulations, we randomly selected 200 structures from the native basin and 500 structures from the intermediate basin. For each structure, we calculated F_ij for all pairs of residues whose C^β atoms (C^α for glycine) are within 9.5 Å.

Redesign Procedures.

In the first step of both a redesign based on minimally frustrating the native state and one based on specific negative design by destabilizing the intermediate state, residue pairs were selected based on the local frustration index. For redesign, all residues involved in highly frustrated interactions (Fig. 2A, red lines) in the helix region III were selected for mutation (10 residues). All pairwise combinations of these positions define our set of double-mutant positions (45 residue pairs). All possible combinations of residue types (400) were evaluated for each pair, resulting in a total of 18,000 distinct double mutants. For our specific negative design procedure, we identified 19 minimally frustrated interactions, involving 22 distinct residue positions, from the AMW wild-type intermediate ensemble. Unlike the design procedure based on minimizing native state frustration, we did not consider all combinations of these 22 positions but instead focused our efforts on the 19 pairs with minimally frustrated interactions. For these 19 pairs, we obtain a total of 7,600 distinct double mutants.

The second step involved selecting the best double mutants. In the design procedure, we evaluated the local frustration (F_ij) for all interacting pairs in the crystal structure. To check that this mutant does not destabilize the protein's total energy, we compute the total energy change of the contact (ℋ_contact and ℋ_water) and burial (ℋ_burial) terms upon mutation. To minimally frustrate the crystal structure, we filtered out double mutants with the fewest highly frustrated sites (F_ij < −1) and the most favorable total energy change. A similar procedure was used for specific negative design. The average local frustration and total energy change (over the intermediate ensemble) were calculated. Best candidates were those that not only minimized the number of nonnative minimally frustrated (F_ij > 0.78) sites over the intermediate ensemble but that also did not frustrate the native state interactions.