A Rabbit Ventricular Action Potential Model Replicating Cardiac Dynamics at Rapid Heart Rates

Abstract

Mathematical modeling of the cardiac action potential has proven to be a powerful tool for illuminating various aspects of cardiac function, including cardiac arrhythmias. However, no currently available detailed action potential model accurately reproduces the dynamics of the cardiac action potential and intracellular calcium (Ca_i) cycling at rapid heart rates relevant to ventricular tachycardia and fibrillation. The aim of this study was to develop such a model. Using an existing rabbit ventricular action potential model, we modified the L-type calcium (Ca) current (I_Ca,L) and Ca_i cycling formulations based on new experimental patch-clamp data obtained in isolated rabbit ventricular myocytes, using the perforated patch configuration at 35–37°C. Incorporating a minimal seven-state Markovian model of I_Ca,L that reproduced Ca- and voltage-dependent kinetics in combination with our previously published dynamic Ca_i cycling model, the new model replicates experimentally observed action potential duration and Ca_i transient alternans at rapid heart rates, and accurately reproduces experimental action potential duration restitution curves obtained by either dynamic or S1S2 pacing.

INTRODUCTION

Cardiac action potential (AP) models have led to important insights into cardiac arrhythmias at both the cellular and tissue levels. However, currently available cardiac AP models containing detailed formulations of biological ionic currents and intracellular Ca (Ca_i) cycling were originally developed to simulate cardiac properties at physiologic heart rates, rather than at the rapid heart rates relevant to tachyarrhythmias. When pushed into the rapid heart rate regime, these AP models fail to reproduce some key experimental findings important in cardiac arrhythmogenesis. For example, except for the early generation Luo-Rudy model (1), which does not contain detailed Ca_i cycling, and the more recent canine Fox model (2), other detailed models exhibit an unphysiologically flat action potential duration (APD) restitution slope (<1), and thereby fail to exhibit spontaneous breakup of induced rotors, as occurs in normal hearts (3). In addition, most of the latest generation ventricular AP models such as the LRd (4,5), Fox (2), Winslow (6), and Shannon et al. (7) models fail to exhibit Ca_i transient alternans during rapid pacing with a clamped AP waveform, as observed experimentally in isolated cardiac myocytes (8–10). This is an important limitation, since this Ca_i cycling instability is now believed to play a key role in the development of arrhythmogenic APD alternans, through its effects on Ca-sensitive currents such I_Ca,L and electrogenic Na-Ca exchange. The two exceptions are our previously reported Ca_i cycling model (11), which was subsequently incorporated into the Fox model (12), and a recently modified version of the LRd model (13) that adopts a qualitatively similar Ca_i cycling model to the one developed by Shiferaw et al. (11). The latter model has flat APD restitution properties, and both models utilize a Hodgkin-Huxley formulation of the L-type Ca current (I_Ca,L), which is suboptimal for representing the delicate cross-talk between I_Ca,L and sarcoplasmic reticulum (SR) Ca release.

To address these limitations, we used the Shannon et al. rabbit ventricular AP model (7) as a platform, and reformulated two key aspects:

1. A Markovian formulation of I_Ca,L, which plays a key role in Ca_i cycling, as well as in regulating the slope of APD restitution (14).

2. The Ca_i cycling component, to incorporate a phenomenological model emulating local control that produces the appropriate instability leading to Ca_i transient alternans at rapid heart rates.

We addressed the first aspect by experimentally characterizing I_Ca,L in patch-clamped isolated rabbit ventricular myocytes using the perforated patch configuration at 35–37°C to preserve its major physiological properties. We then used this data to generate a minimal seven-state Markovian model of I_Ca,L, which incorporates both voltage-dependent inactivation (VDI) and Ca-dependent inactivation (CDI) based on current biophysical interpretations of the underlying molecular mechanisms. We addressed the second aspect by implementing the Ca_i cycling model of Shiferaw et al. (11), tuned to replicate Ca_i alternans measured experimentally in rabbit ventricular myocytes (10). The modified model with new I_Ca,L and Ca_i cycling formulations was then tuned to replicate experimentally measured APD and Ca_i transient properties at rapid pacing rates.

METHODS

Experimental

All animal procedures conformed to the “Guiding Principles for Research Involving Animals and Human Beings” of the American Physiological Society.

Myocyte isolation

Rabbit cardiac myocytes were isolated as previously described (14). Briefly, the hearts were rapidly excised from 2 to 3 kg New Zealand white rabbits anesthetized with intravenous pentobarbital, and submerged in Ca-free Tyrode's solution containing (in mM) 140 NaCl, 5.4 KCl, 1 MgCl₂, 0.33 NaH₂PO₄, 10 glucose, and 5 HEPES adjusted to pH 7.4. The aorta was cannulated and the heart perfused retrogradely at 37°C on a Langendorff apparatus with Ca-free Tyrode's buffer containing 1.65 mg/mL collagenase and 0.8 mg/mL bovine serum albumin for 30–40 min. After washing out the enzyme solution, the hearts were removed from the perfusion apparatus and swirled in a beaker. Cells were isolated with the calcium concentration slowly being increased to 1.8 mmol/L. Ca-tolerant, rod-shaped ventricular myocytes with clear striations were randomly selected for electrophysiological studies.

Patch-clamp methods

Macroscopic ionic currents were recorded under the voltage- or current-clamp conditions using the whole cell perforated patch technique described by Rae et al. (15). The pipette solution contained (in mmol/L): 140 K-Aspartate, 5 NaCl, 10 HEPES, 1 EGTA, 5 MgATP, 5 creatine phosphate, and 0.05 cAMP; pH 7.2 with HCl for APD restitution experiments, with K being replaced by CsOH for the I_Ca,L experiments. A DigiData 1200 and pCLAMP software (Axon Instruments, Foster City, CA) were used to generate command pulses and acquire data. For Ca current measurement, rabbit ventricular myocytes were superfused with a HEPES-buffered Tyrode solution containing (in mM) 135 NaCl, 5.4 KCl, 1 MgCl, 2 CaCl₂, 5 HEPES, and 10 glucose, with pH adjusted to 7.3 with NaOH. For Ba current measurements, 1.8 mM Ba replaced Ca in the superfusate. Blocking the uptake and release of Ca from SR was achieved by preincubating the myocytes for 30–60 min with 10 μM ryanodine and 2 μM thapsigargin. All electrophysiology experiments were performed at physiologic temperatures (35–37°C).

Patch-clamp protocols and data analysis

Activation and inactivation kinetics of I_Ca,L were recorded using a standard rectangular pulse protocol that delivered test step pulses from −40 to +50 mV in 10-mV increments from a holding potential of −80 mV. Na currents were inactivated by a prepulse step (−80 mV to −40 mV for 40 ms) and by the addition of 10 μM tetrodotoxin to the superfusate. Recovery from inactivation was assessed using a standard recovery protocol in which a 250-ms voltage-clamp pulse to 10 mV (P1) was followed by repolarization to the holding potential (–100, −80, or −60 mV) for a variable time interval, after which a second pulse to 0 mV (P2) was delivered. Recovery from inactivation was calculated as the ratio of the peak P2/P1 currents, and plotted as a function of recovery interval.

I_Ca,L was also measured during AP clamps. Steady-state APs were first recorded at pacing cycle lengths (CL) of 1000 and 400 ms in the current-clamp mode. Switching to the voltage-clamp mode, the AP clamp waveforms were applied at the same respective pacing CL before and after exposure to 10 μM nifedipine. The nifedipine-sensitive current (determined by subtraction) was taken to represent I_Ca,L during the AP waveform.

APD restitution protocols

APD restitution was measured using two methods:

1. Extrastimulus (S1S2) method. The myocyte was paced at a CL of 400 ms for 10 beats, and then an extrastimulus (S2) was delivered at progressively shorter S1S2 coupling intervals (in 5–10 ms increments) until loss of capture.

2. Dynamic (rapid pacing) method. The myocyte was paced at a CL of 400 ms until steady-state APD was reached, after which the CL was progressively decreased by 5–20 ms every 12 beats until 2:1 block occurred.

APD was measured at 90% repolarization (APD₉₀), and the diastolic interval (DI) was calculated as CL minus APD₉₀. APD restitution curves were constructed by plotting APD₉₀ versus DI. The maximum APD restitution slope was calculated from the first derivative of the fitted monoexponential curve, at the shortest DI which elicited an action potential.

Mathematical modeling

Markovian model formulation of I_Ca,L

Based on the new experimental data from rabbit ventricular myocytes, and taking into consideration previously reported single channel properties (16), we formulated a model for I_Ca,L using a minimal Markovian scheme with seven states as shown in Fig. 1 B. We fitted the experimentally measured I_Ca,L directly to the Markovian model with a multidimensional least-squares algorithm using the software package Berkeley Madonna. All rate constants are chosen so that the model I_Ca,L was fitted to the experimental current traces at −20, −10, 0, +10, +20, and +30 mV, using a multidimensional least-squares algorithm. Microscopic reversibility was implemented by equating the product of all transition rates in the clockwise and anticlockwise direction for all closed loops. The rationale and features of the Markovian model, along with a description of our fitting strategy is described below:

FIGURE 1.

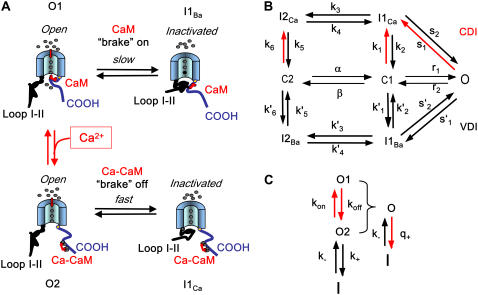
Schematic representation of Markovian model and Ca_i cycling machinery: (A) Seven-state Markovian model of the L-type Ca channel. The red lines denote Ca-dependent transitions to inactivated states. (B) Schematic illustration of the different conformational states corresponding to the VDI and CDI pathways. Domains III and IV of the L-type Ca channel are shown, with the pore in the middle. The I-II cytoplasmic linker connecting domains I and II (not shown) acts as the voltage-dependent inactivation gate (VDI), whose ability to inactivate the channel is inhibited by CaM tethered to the COOH terminus. The braking effect is removed when Ca binds to CaM, allowing the I-II linker to inactivate the channel more rapidly. (C) Demonstration that CDI can be minimally represented using a direct Ca-dependent transition to the inactivated state (see text for explanation). The single open state in panel B corresponds to a reduction of two physical states O1 and O2.

Voltage dependence of activation is controlled by transitions between closed states. It is well known that the voltage dependence of the L-type Ca channel activation is determined by transitions between closed states (17–19). At least four closed states (corresponding to gating movements in each of the four subunits) are thought to be present, and have been included in recent detailed formulations of I_Ca,L (6,20). However, for our minimal Markovian model, we found that two closed states were sufficient to model this effect (Fig. 1 B), such that the transitions between C2 and C1 are strongly voltage-dependent. The transitions from C1 to O are voltage-independent and determine the steady-state open probability. In this case, rate constants are adjusted so that the maximum open probability is roughly 5% (16).

Inactivation of I_Ca,L is biexponential when Ca is the charge carrier, and monoexponential when Ba is the charge carrier. We modeled the inactivation of I_Ca,L as occurring via two pathways, VDI and CDI (Fig. 1, A and B). With Ba as the charge carrier, inactivation occurs only via the VDI pathway, and a single time constant of inactivation is observed (Fig. 1 B, states labeled with the subscript Ba). When Ca is the charge carrier, two distinct time constants of inactivation, corresponding to VDI and CDI, respectively, are observed (Fig. 1 B, all states). According to this biophysical evidence, the VDI and CDI components physically reflect channels in which Ca is not (VDI), or is (CDI), interacting with Calmodulin (CaM) molecules tethered to the C-terminus of the channel. In the absence of Ca, the C-terminus-CaM complex is hypothesized to act as a brake on the ability of the inactivation gate, located in the cytoplasmic I-II linker, to inactivate the channel (Fig. 1 A). When Ca is present and binds to CaM, however, the Ca-induced conformational change in CaM displaces the C-terminus-CaM complex from its braking site, allowing the I-II linker to inactivate the channel more rapidly (Fig. 1 A). Thus, in this schema, which reflects current biophysical interpretations (21,22), inactivation gating by the I-II linker is fundamentally voltage-dependent, and CDI represents a Ca-dependent unbraking of this fast mode of VDI (Fig. 1 B). This physical picture can be modeled using two open states O1 and O2 (Fig. 1 C), in which the transitions between open states (k_on,k_off) are Ca-dependent, while the transitions from the open state to the inactivated state (k₊,k₋) are purely voltage-dependent. However, if the kinetics of binding of Ca to CaM is fast and has reached a quasi-steady state during the timescale of inactivation, then it is straightforward to show that the lumped open state, with open probability O = O1 + O2, transitions to the inactivated state at an effective rate q₊ = k_on/(k_on + k_off)k₊, that is both Ca- and voltage-dependent. Thus, the Ca-mediated braking of fast VDI can be effectively modeled by a direct Ca-mediated transition from a single open state to an inactivated state (Fig. 1, B and C). Hence, to model these features using a minimal approach, we split the Markovian scheme into two parallel sets of inactivated states: the I1_Ca, I2_Ca states, when Ca is bound to CaM and thereby relieving inhibition of inactivation; or the I1_Ba, I2_Ba states, when Ca is not bound to CaM and not relieving inhibition of inactivation. Although this mathematical formulation is consistent with the idea of Ca acting as an allosteric modulator (i.e., brake remover) of VDI (21,22), it is also mathematically equivalent to a scheme of separate VDI and CDI pathways entered from the same open state (5).

We found that two inactivated states (I1 and I2) in each limb were required to fit the voltage-clamp data at −10 and −20 mV. Specifically, the I2 states were required to drain the closed states, to prevent the closed C1 state (where most of the channels reside at these voltages) from repopulating the open state O. Physically, we can imagine that the I1_Ba state corresponds to an inactivated state in which the I-II linker has inactivated the channel, but the C-terminus-CaM complex is still in its usual inhibitory location. I2_Ba state might then represent a new conformation with the C-terminus-CaM complex displaced from its usual location.

Although other Markovian formulations of I_Ca,L with fewer inactivated states have been formulated for ferret and mouse ventricular AP models (23,24), the extra inactivated state could be eliminated in those models because the equivalent C1 to O transition was made voltage-dependent. In our model, however, the C1 to O transition is voltage-independent, to account for the experimental observation that the mean open time is voltage-independent (25).

We obtained our model parameters by fitting the voltage-dependence of VDI rate constants to the measured I_Ca,L when Ba was the charge carrier, and the SR was depleted, i.e., the primed rate constants indicated in Fig. 1 B. After determining the primed rate constants, these parameters were fixed and we then proceeded to fit the unprimed rate constants using current traces measured with Ca as the charge carrier, first with the SR depleted, and then without the SR depleted. In this way, the fitting procedure was constrained at each step based on the experimental data.

The time course of the recovery from inactivation is monoexponential. This feature is accounted for in our Markovian scheme by letting recovery depend only on rates from I2_Ca and I2_Ba to the closed state C2. The rate constants 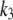and 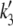were adjusted so that when the voltage dropped below −40 mV, transitions from I1_Ba and I1_Ca to I2_Ca and I2_Ba were much faster than the transition rates from I2_Ca and I2_Ba to the closed state C2. Thus, recovery is determined primarily by the latter relatively slow inactivation process. At depolarization voltages <−40 mV, we let k₅ = k′₅, and k₆ ≈ k′₆, so that recovery from inactivation is independent of the pathway of inactivation.

The Ca_i cycling model equations

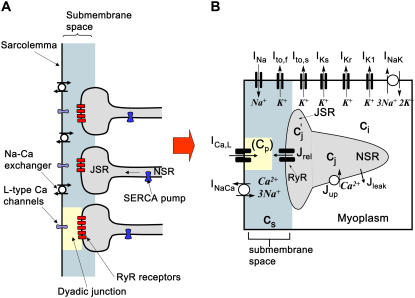
Ca-induced inactivation of I_Ca,L depends on Ca flowing through the pore of the channel as well as Ca released from the SR. This is challenging to model because of the additional fact that L-type Ca channels are spatially distributed in compartments which sense a different Ca concentration than that in the bulk cytoplasm. Specifically, most L-type Ca channels are localized in small (1–5 channels) clusters in close proximity to clusters of 50–200 SR Ca release channels (ryanodine receptors, RyR) which control the flow of Ca from the SR (26) (see Fig. 2). Interactions between L-type Ca channels and RyRs occur in a sub-micron-restricted space referred to as the dyadic junction (27,28). When the local RyR receptors open in response to trigger Ca from the L-type Ca channel, the Ca concentration within the junction can rise to levels much higher than in the bulk cytoplasm (>100 μM) (28). Therefore, during Ca release in the cell, the distribution of Ca concentrations is highly nonuniform.

FIGURE 2.

(A) Sketch of spatially distributed dyadic junctions where L-type Ca channels are in close proximity to RyR receptors which gate Ca flux from the JSR. (B) Reduced whole-cell model showing basic elements of Ca cycling machinery and membrane ion currents. Ca release is modeled phenomenologically by taking into account recruitment of discrete release events (Ca sparks). See text for further details.

To account for the complex spatiotemporal distribution of Ca during release from the SR, Shiferaw et al. (11) used a phenomenological approach to model the spatially averaged Ca concentrations within different compartments of the cell. In this approach, illustrated in Fig. 2, the cell was divided into four essential compartments, and differential equations were developed to describe the averaged Ca concentration within each compartment. Following Shiferaw et al., (11), the SR was divided into two compartments: the dyadic junctional SR (JSR) with averaged concentration c′_j, representing the average concentration of an ensemble of several thousand JSR compartments distributed inside the cell from which SR Ca release occurs; and the nonjunctional SR (NSR) with averaged concentration of c_j, where SR Ca uptake by SERCA pumps occurs. The time delay between SR Ca reuptake in the NSR and its availability for release from the JSR is given by the time constant τ_a, and plays a critical role in generating Ca_i alternans (see Discussion). The outside of the SR was divided into the bulk myoplasm with average Ca concentration c_i, and also a submembrane space, with averaged concentration c_s, which is a volume in close proximity to the cell membrane, as shown in Fig. 2, where all the Ca-sensitive channels deliver Ca via I_Ca,L and I_NaCa. Within this compartment, Ca is allowed to vary substantially faster than in the bulk myoplasm, consistent with the experimental findings that I_NaCa did not track the bulk concentration, but rather a faster Ca dynamics near the cell membrane (29). Note that this compartment does not directly correspond to the dyadic junction, where Ca concentrations can rise to even higher levels due to the further restriction of diffusion by the apposed SR membrane. The details of the Ca_i cycling equations for the averaged concentrations are given in the Appendix.

Formulation of averaged dyadic cleft Ca concentration

Given that L-type Ca channels are mainly located in dyadic junctions, neither the average cytoplasmic nor submembrane Ca concentrations directly control I_Ca,L inactivation rate. This is evident from experimental data, since the rate of I_Ca,L inactivation is more rapid during a voltage-clamp to −20 mV than to 0 mV, even though peak c_i (and therefore also c_s) is much smaller (Fig. 3). To estimate the effective Ca concentration which mediates the transitions to the inactivated states in our Markovian scheme, we phenomenologically represented the effective Ca concentration sensed by L-type Ca channels distributed throughout the cell (c_p), as a complex function of: 1), Ca permeation through the channel itself; 2), Ca permeation through neighboring channels in the cluster; 3), local SR Ca release via RyR channels nearby; 4), Ca that diffuses from the space outside of the dyadic cleft; and 5), binding to Ca buffers in the dyadic junction (Fig. 2). The equation for c_p is taken to obey

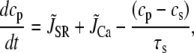(1)

where 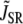and 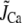are the components due to the Ca fluxes from the SR and L-type Ca channels, respectively, while the last term denotes the diffusion of Ca into the submembrane space. Given that the dyadic cleft is roughly 100–250 nm in diameter (30), and with an estimated diffusion of Ca of ∼100–300 (μm)²/s, this time constant is in the 0.1–0.5 ms range. In our simulations we used a time constant of τ_s = 0.5 ms. Equation 1 describes the averaged dynamics of the Ca concentration regulating inactivation of L-type Ca channels distributed throughout the cell. We denote terms on the right-hand side of the equation with a tilde since they do not represent fluxes into a single compartment, but rather, the average flux over an ensemble of dyadic clefts. Note that during a global Ca transient, a fraction of dyadic clefts sense Ca due to RyR Ca release, while the remainder see only the Ca due to the local L-type Ca channels. In our study we find that both contributions must be taken into account to fit the experimentally observed time course of I_Ca,L. Thus, the tildéd fluxes represent localized microdomain fluxes that differ from the global fluxes used in calculating flux balance. We use this multiscale approach as a convenient means to integrate subcellular local control events with the cellular scale Ca transient.

FIGURE 3.

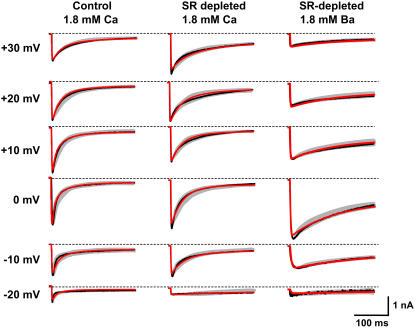
I_Ca,L traces along with model fits using Ba and Ca as charge carriers, and for intact and depleted SR. The black line represents a typical experimentally measured current trace. The red lines represent the best fit of that current trace to the Markovian model. The gray line represents the largest deviations from a sample of eight cells, where the peak has been normalized to the typical case. Dashed lines indicate zero current levels.

To assess the relative contributions to inactivation of Ca released from the SR and Ca flowing through the channel pore, we measured the I_Ca,L when SR release and uptake were blocked by incubating the cell with ryanodine and thapsigargin. The combined effect of these two agents was to eliminate the contribution of SR release to Ca-induced inactivation of I_Ca,L. This protocol allowed us to assess the effect of Ca entry via the channel pore on inactivation kinetics. In this case, the rate of inactivation was strongly correlated with the peak of whole cell I_Ca,L, i.e., the rate of inactivation followed a bell-shaped curve that mirrored the current amplitude (compare Fig. 4 B with Fig. 5 A). This effect is modeled phenomenologically by letting

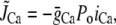(2)

with 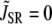in Eq. 1, since we do not expect any contribution from Ca due to SR release. Here P_o is the probability of finding an L-type Ca channel in the open state, and i_Ca is the unitary current through L-type Ca channels (which changes with voltage), while 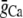is a constant determined by fitting to the current traces measured with thapsigargin + ryanodine. The choice of Eq. 2 ensures that the time course of Ca-induced inactivation mirrors I_Ca,L. Note that this choice is motivated directly from our experimental data, but it is not surprising since we expect the average dyadic cleft concentration to mirror whole cell Ca entry in the absence of SR release.

FIGURE 4.

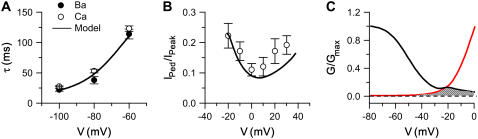
The kinetics of recovery of I_Ca,L. (A) Plot of the time constant of recovery from inactivation as a function of membrane voltage with either Ca or Ba as the charge carrier, obtained with a double pulse protocol (see Methods). The recovery time constant was estimated by fitting the recovery curve to a monoexponential function. Symbols represent the experimental measurements and lines correspond to the model fits. (B) Pedestal current remaining after 300-ms voltage-clamps to the potentials indicated, expressed as fraction of the peak current at that potential, illustrating the classic U-shaped relationship with Ca as the charge carrier and SR Ca release intact. Symbols show experimental data, lines show model fits. (C) Voltage dependence of activation (red) and quasi-steady-state inactivation after 300 ms (black) in the model, illustrating the region of I_Ca,L window currents between −30 and −10 mV.

FIGURE 5.

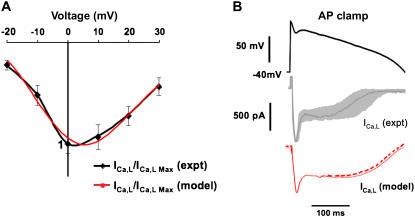
Experimental validation of Markovian model. (A) IV curve showing the peak I_Ca,L versus membrane voltage for experimental data (black) versus the model (red). (B) Comparison of nicardipine-sensitive current during an AP clamp in myocytes (black and gray) versus the model (red). Black trace is from a representative myocyte, and the gray zone indicates the range of nicardipine-sensitive currents recorded from eight myocytes, normalized to the same peak. The AP clamp was applied from −40 mV to inactivate the Na current. For the model, the solid red line shows the simulated nicardipine-sensitive current and the dashed red line shows I_Ca,L during the AP clamp in the model.

The contribution in Eq. 1 due to the SR Ca release is modeled using a phenomenological equation of the form

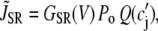(3)

where c′_j is the average Ca concentration in the JSR, G_SR(V) is a voltage-dependent gain function that is chosen to fit the experimental data, and P_o is the open probability of RyRs. This gain function emulates the experimental observation of Wier et al. (31), who showed that the gain of SR release to whole cell I_Ca,L increased as the membrane voltage decreased. This presumably is due to the larger single channel current amplitude of L-type Ca channels at less depolarized voltages, as a result of the increased driving force, which is more effective at triggering the opening of SR RyRs in the dyad. The function Q(c′_j) describes the dependence of SR Ca release on the Ca concentration in the SR lumen, which we have taken to be the same as that used by Shiferaw et al. (11) (see Appendix for a detailed description). Note that 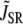also depends on the Ca_i concentration via the RyR open probability P_o. This is reasonable since we expect that the average dyadic Ca concentration (c_p) will depend on the number of sparks recruited, which in turn depends on c_s via its effect on the whole cell I_Ca,L, i.e., Ca-induced inactivation.

It is important to note that Eqs. 1–3 phenomenologically emulate a local control mechanism of Ca cycling, since they contain separate terms representing the number of sparks recruited, and their efficacy at inducing SR Ca release and Ca-induced inactivation. This is different from other models (7,20), in which the dynamics of Ca within a single common dyadic cleft is used to generate the whole cell Ca. Finally, we note that the effects of buffers contained in the dyadic junction are assumed to be accounted for by the phenomenological fluxes and Since the concentrations and kinetics of buffers within dyadic junctions are not known, we did not attempt to model them explicitly.

Formulation of Ca-induced inactivation

To proceed, Ca-induced inactivation is modeled by letting the inactivation rate constants (see Fig. 1 B) obey

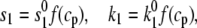(4)

where

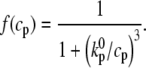(5)

Here, 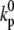is the Ca concentration at which the rate of Ca-induced inactivation is half-maximal, which we have arbitrarily set to be in the range 3–5 μM. The values 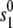and 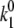are constants whose values are determined from the multidimensional fits.

The experimental current traces, shown in Fig. 3 A, reveal that under control conditions, I_Ca,L inactivates most rapidly at −20 mV. However, in this voltage range the open probability P_o is low, so that most of the channels are in the deeply closed state C2. To fit the rapid inactivation seen experimentally, we found it necessary to incorporate a Ca-dependence into the rate constant k₆. In this way, even at large negative voltages, I_Ca,L can inactivate rapidly as the open state is drained via transitions from C2 to I2_Ca. See Appendix for a detailed formulation of the transition rates.

The rabbit ventricular AP model

The new I_Ca,L formulation and our previously reported dynamic Ca_i cycling model (11) were introduced into a model whose currents resembled the currents in the Shannon et al. model (7). We adjusted parameter values of several currents to fit our model to the single cell dynamics which we observed experimentally. A list of all the currents with corresponding parameters and initial values is provided inAppendix Tables 1–6. The membrane voltage (V) is described mathematically according to the ordinary differential equation

(6)

where C_m = 1 μF/cm² is membrane capacitance, I_ion is total ionic current density across the cell membrane, and I_stim is the stimulus current. The full details of the model formulation are given in the Appendix. The model, which consists of 26 differential equations, was integrated using the Euler method with an adaptive time step ranging from 0.1 to 0.01 ms. We checked the accuracy of our numerical scheme by comparing the generated AP with that produced using an Euler scheme with a smaller time step of 0.001 ms.

TABLE 1.

SR release parameters

Parameter	Definition	Value
τr	Spark lifetime	30 ms
τa	NSR-JSR relaxation time	100 ms
gRyR	Release current strength	2.58 sparks cm2/mA
u	Release slope	11.3 ms−1
csr	Threshold for steep release function	90 μM/l cytosol
s	Release function parameter	(1-u)csr-50 μM/ms = 977 μM/ms
τd	Submembrane-myoplasm diffusion time constant	4 ms
τs	Dyadic junction-submembrane diffusion time constant	0.5 ms

TABLE 2.

Cytosolic buffering parameters

Parameter	Definition	Value
BT	Total concentration of Troponin C	70 μmol/l cytosol
BSR	Total concentration of SR binding sites	47 μmol/l cytosol
BCd	Total concentration of Calmodulin binding sites	24 μmol/l cytosol
Bmem	Total concentration of membrane binding sites	15.0 μmol/l cytosol
Bsar	Total concentration of sarcolemma binding sites	42.0 μmol/l cytosol
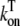	On rate for Troponin C binding	0.0327 (μM)−1 (ms)−1
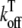	Off rate for Troponin C binding	0.0196 ms−1
KSR	Dissociation constant for SR binding sites	0.6 μM
KCd	Dissociation constant for Calmodulin binding sites	7 μM
Kmem	Dissociation constant for membrane binding sites	0.3 μM
Ksar	Dissociation constant for sarcolemma binding sites	13.0 μM

TABLE 3.

Exchanger, uptake, and SR leak parameters

Parameter	Definition	Value
cup	Uptake threshold	0.5 μM
vup	Strength of uptake	0.4 μM/ms
gNaCa	Strength of exchange current	0.84 μM/s
ksat	Constant	0.2
ξ	Constant	0.35
Km,Nai	Constant	12.3 mM
Km,Nao	Constant	87.5 mM
Km,Cai	Constant	0.0036 mM
Km,Cao	Constant	1.3 mM
cnaca	Constant	0.3 μM
gl	Strength of leak current	2.07 × 10−5 (ms)−1
kj	Threshold for leak onset	50 μM

TABLE 4.

L-type Ca current parameters

Parameter	Definition	Value
PCa	Constant	0.00054 cm/s
gCa	Strength of Ca current flux	182 mmol/(cm C)
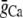	Strength of local Ca flux due to L-type Ca channels	9000 mmol/(cm C)
	Strength of local Ca flux due to RyR channels	26,842 mmol/(cm C)
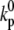	Threshold for Ca-induced inactivation	3.0 μM
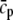	Threshold for Ca dependence of transition rate k6	3.0 μM
τpo	Time constant of activation	1 ms
r1	Opening rate	0.3 ms−1
r2	Closing rate	3 ms−1
s′1	Inactivation rate	0.00195 ms−1
k′1	Inactivation rate	0.00413 ms−1
k2	Inactivation rate	0.0001 ms−1
k′21	Inactivation rate	0.00224 ms−1
TBa	Time constant	450 ms

TABLE 5.

Physical constants and ionic concentrations

Parameter	Definition	Value
Cm	Cell capacitance	3.1 × 10−4μF
vi	Cell volume	2.58 × 10−5μl
vs	Submembrane volume	0.02 vi
F	Faraday constant	96.5 C/mmol
R	Universal gas constant	8.315 Jmol−1 K−1
T	Temperature	308K
[Na+]o	External sodium concentration	136 mM
[K+]i	Internal potassium concentration	140 mM
[K+]o	External potassium concentration	5.4 mM
[Ca2+]o	External calcium concentration	1800 μM

TABLE 6.

Ionic current conductances

Parameter	Definition	Value
gNa	Peak INa conductance	12.0 mS/μF
gto,f	Peak Ito,f conductance	0.11 mS/μF
gto,s	Peak Ito,s conductance	0.04 mS/μF
gKl	Peak IKl conductance	0.3 mS/μF
gKr	Peak IKr conductance	0.0125 mS/μF
gKs	Peak IKs conductance	0.1386 mS/μF
gNaK	Peak INaK conductance	1.5 mS/μF

RESULTS

Characterization of I_Ca,L in rabbit ventricular myocytes and in Markovian model

Isolated rabbit ventricular myocytes were studied under the following three experimental conditions:

1. Control, with 1.8 mM extracellular Ca present in the superfusate (n = 12).

2. SR-depleted (pretreatment with 2 μM thapsigargin and 10 μM ryanodine for 30–60 min) with 1.8 mM extracellular Ca present (n = 8).

3. SR-depleted with 1.8 mM Ba replacing extracellular Ca (n = 10).

To model the data, we developed the seven-state Markovian model shown in Fig. 1 B. The choice of model was motivated by our voltage-clamp data, along with single channel properties described by Rose et al. (16). Fig. 3 (black traces) shows representative traces of I_Ca,L elicited by 300 ms voltage-clamp pulses from a holding potential of −80 mV to various depolarized potentials under the three different experimental conditions. The gray areas indicate the range of current kinetics observed in different myocytes, with their peak current normalized to the peak of the black trace. Good fits of the model to the experimental data of I_Ca,L inactivation were obtained and are indicated by the red traces in Fig. 3. Under control and SR-depleted conditions with 1.8 mM extracellular Ca present, I_Ca,L inactivation was well-fit by a double exponential, whose fast and slow time constants and amplitudes are summarized in Table 7. The experimental I_Ca,L traces shown in Fig. 3 agree with the classical observations (32) that I_Ca,L inactivation has both Ca-dependent (CDI) and voltage-dependent (VDI) components, accounting for the fast and slow time constants of inactivation, respectively. Note that over a time course comparable to the APD (<300 ms), inactivation was not complete, with a residual pedestal current ranging from 10 to 20% of the peak current at different voltages (Fig. 3 and Fig. 4 B). Without SR depletion, inactivation of Ba currents was still biexponential (data not shown), suggesting contamination by residual SR Ca release. Under SR-depleted conditions with 1.8 mM extracellular Ba present, however, inactivation was generally well fit by a single exponential. Note that we did not consider ultraslow inactivation on timescales exceeding 300 ms, which have little or no impact at physiological heart rates.

TABLE 7.

Experimental values of I_Ca,L inactivation

	Ca 1.8 mMol (SR intact)			Ca 1.8 mMol (SR depleted)			Ba 1.8 mMol (SR depleted)
Voltage (mV)	Imax (pA)	τslow (ms)	τfast (ms)	Imax (pA)	τslow (ms)	τfast (ms)	Imax (pA)	τslow (ms)
−20	−467 ± 95	111 ± 10.5	10.3 ± 3.1	−296 ± 22	143 ± 14.3	22 ± 5.2	−228 ± 45	166 ± 11.4
−10	−1193 ± 226	78 ± 9.2	9.2 ± 0.8	−1075 ± 144	111 ± 12.7	14.6 ± 2.7	−989 ± 101	132 ± 14.2
0	−2071 ± 213	58 ± 5.3	11.1 ± 1.3	−1979 ± 178	78 ± 11.4	14.3 ± 3.3	−2057 ± 229	117 ± 9.7
10	−2135 ± 184	63 ± 6.0	11.9 ± 2.2	−1882 ± 125	91 ± 11.9	17.4 ± 3.5	−1689 ± 113	121 ± 14.1
20	−1665 ± 168	69 ± 4.9	13.6 ± 2.8	−1581 ± 114	114 ± 11.3	18.5 ± 3.4	−948 ± 85	132 ± 8.6
30	−1006 ± 105	87 ± 11.7	15.1 ± 3.3	−1031 ± 102	105 ± 11.6	20.2 ± 2.1	−630 ± 66	138 ± 11.9

Fig. 4 A illustrates the experimental results for the time constant of recovery from inactivation under control conditions with 1.8 mM extracellular Ca and in SR-depleted myocytes with 1.8 mM Ba present. Unlike I_Ca,L inactivation, recovery from inactivation at multiple voltages (–60, −80, and −100 mV) was monoexponential over the physiologically relevant range of diastolic intervals (<300 ms in the rabbit). The time constants of recovery from inactivation of I_Ca,L were similar (∼40 ms) when either Ca or Ba were used as charge carriers. The kinetics of recovery from inactivation of the Markovian I_Ca,L model under similar conditions are superimposed, and show good agreement. Fig. 4 B shows residual noninactivated pedestal current at the end of 300-ms square voltage-clamp pulses to various membrane potentials, expressed as the fraction of the peak current at that voltage. The graph illustrates the classic U-shaped dependence, paralleled by the U-shaped dependence of the inactivation time constants (Table 7). Fig. 4 C plots the steady-state activation curve and the quasi-steady state (300 ms) inactivation curve in the model, illustrating the I_Ca,L window current (cross-hatched area).

Fig. 5 A shows current-voltage (IV) curves illustrating the average peak current density at various voltages for the experimental I_Ca,L and model I_Ca,L. To validate that the Markovian model accurately reproduced the typical time course of I_Ca,L during the rabbit ventricular action potential, Fig. 5 B compares the experimentally measured nifedipine-sensitive current (primarily I_Ca,L) during an AP clamp at pacing CL of 400 ms to the simulated nifedipine-sensitive current when the same experimental AP waveform was applied to the Markovian model before and after setting the L-type Ca current conductance zero (red line in lower trace). The traces show reasonably close agreement, given that the experimental traces contain some uncertain degree of series resistance error. Fig. 5 B also shows I_Ca,L in the model (dashed red line in lower trace), illustrating that I_Ca,L is close, but not identical to the simulated nifedipine-sensitive current (solid red line), due to effects on other Ca-sensitive currents when I_Ca,L block suppressed the Ca_i transient.

Incorporation of the Markovian I_Ca,L into a detailed rabbit ventricular AP model

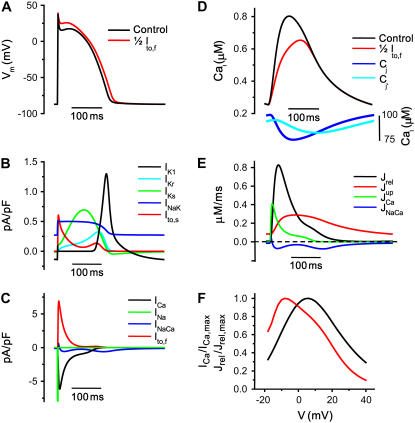
Using the Shannon et al. model as a platform, we replaced its Hodgkin-Huxley style I_Ca,L with our new Markovian I_Ca,L formulation, and also replaced its Ca_i cycling components with our dynamic Ca_i cycling model (11). The model was then tuned to reproduce physiological excitation-contraction (EC) coupling features at normal heart rates as well as experimentally observed nonlinear dynamics of the AP and Ca_i transient at rapid heart rates (10,14). Fig. 6 illustrates the AP (A) and Ca_i transient (D), various ionic currents (B and C), and Ca fluxes (E) during steady-state pacing at a CL of 400 ms. The red lines in Fig. 6, A and D, show the AP and Ca_i transient when I_to,f is blocked by 50%, causing loss of the early repolarization notch and consequent reduced driving force for Ca entry through L-type Ca channels, which produces less efficient SR Ca release and a smaller Ca_i transient, as has been reported experimentally (33,34). Fig. 6 F simulates rectangular voltage-clamp pulses, illustrating that the peak amplitude of the Ca_i transient is graded with respect to peak I_Ca,L, with a higher EC coupling gain at membrane voltages <0 mV than at >0 mV, as observed experimentally (31).

FIGURE 6.

Ionic currents and Ca concentrations in the model after steady-state pacing at 400 ms for 200 beats. (A) Action potential. The red line represents the AP after I_to,f was reduced by 50%, keeping all other model parameters the same. As expected the AP notch is reduced, and the APD increases slightly. (B) K currents during the AP. (C) Plots of I_Ca,L, I_NaCa, I_to,f, and I_Na. Note that I_Na has been truncated. (D) Ca concentrations in the various compartments. The black and red lines show the Ca_i transient with normal and reduced I_to,f. Other Ca concentrations correspond to the normal (control) I_to,f case. (E) Profile of Ca fluxes in the various compartments. (F) The voltage dependence of the peak I_Ca,L and peak SR Ca release flux (J_rel) (both normalized). The peak SR Ca release flux mirrors the voltage dependence of I_Ca,L, as required for graded release, and Ca-induced Ca release gain is higher at negative than positive voltages.

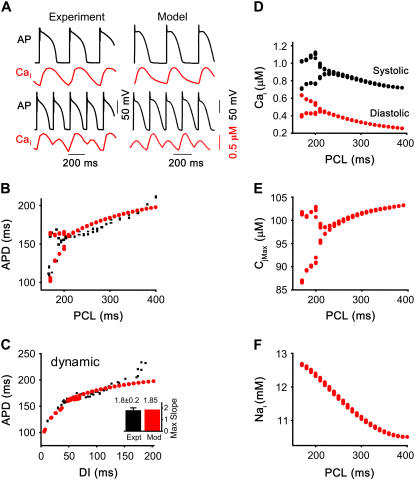
Fig. 7 shows rate-dependent features of the AP and Ca_i transient in rabbit ventricular myocytes versus the model. Fig. 7 A compares traces of the AP and Ca_i transient at two different pacing cycle lengths in a representative rabbit ventricular myocyte (under current-clamp conditions using the perforated patch configuration at 36°C) with the model. At a pacing CL of 400 ms, neither the AP nor Ca_i transient alternate, but at the shorter CL, they both alternate in phase with each other, such that the long APD is associated with the large Ca_i transient (i.e., electromechanically concordant alternans). Fig. 7 B compares APD versus pacing CL during the dynamic pacing protocol in another representative rabbit myocyte (black points) with the model (red trace). When the initial pacing CL of 400 ms (at steady state) was shortened every 10 beats by 2 ms until loss of 1:1 capture, the model developed APD alternans at a pacing CL of 210 ms, within the experimentally observed range in myocytes (190–240 ms, n = 8). The maximum amplitude of APD alternans (70 ms) also fell within the experimentally measured range (60–110 ms, n = 8). In Fig. 7 C, the dynamic APD restitution curve was constructed from the data in Fig. 7 B by plotting APD versus DI at the different heart rates. In the model, the maximum slope of the dynamic APD restitution and the range of DI with slope >1 were 2.1 and 25 ms, respectively, which fall within the experimentally observed range among eight myocytes characterized (1.4–2.5 and 20–45 ms). Also, note that the onset of APD alternans in the model occurred when the dynamic APD restitution slope was only 0.7 (corresponding to a DI of 70 ms), which is also consistent with experimental observations (14). Fig. 7 D shows the peak systolic and diastolic Ca_i levels in the model during the dynamic pacing protocol, which agrees with previously published experimental data from isolated rabbit ventricular myocytes (10). Fig. 7 E shows the corresponding rate dependence of the maximum (i.e., end-diastolic) Ca in the JSR in the model, and Fig. 7 F shows the rate-dependent changes in intracellular Na concentration during the dynamic pacing protocol.

FIGURE 7.

Rate-dependent features: dynamic pacing. (A) APs and Ca_i transients from a representative myocyte (left traces) and the model (right traces) at pacing cycle lengths (PCL) above (upper) and below (lower) the threshold for alternans. (B) APD versus heart rate during the dynamic pacing protocol in a representative myocyte (black points) versus the model (red line). Alternans developed at a PCL of 190 ms and 210 ms for the myocyte and model experiment, respectively. (C) The dynamic APD restitution curve. Same data as in panel B, but with APD plotted versus DI = PCL-APD. Inset compares the average maximum APD restitution slope in myocytes to that in the model. (D) Systolic and diastolic Ca_i versus PCL in the model. (E) Peak JSR Ca concentration versus PCL in the model. (F) Intracellular Na versus PCL in the model.

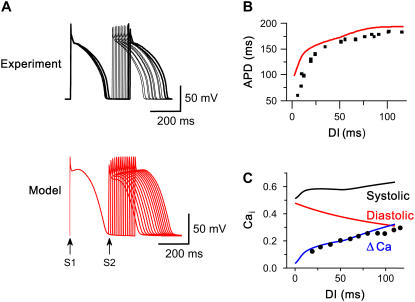
Fig. 8 compares APD restitution measured using the S1-S2 method in a representative myocyte with the model. The myocyte and model were paced at an S1-S1 CL of 400 ms and premature beats (S2) introduced at progressively shorter S1-S2 coupling intervals every 10 beats, as seen from the superimposed traces in Fig. 8 A. In Fig. 8 B, the APD of the S2 beat is plotted against the DI (i.e., the S1-S2 interval). Although the simulated APDs are slightly longer than the experimental APDs for this particular myocyte, they are well within the observed experimental range for five myocytes, and replicate the slope accurately. The maximum slopes of APD restitution (3.43) and the range of DI with slope >1 (17 ms) in the model fell in the experimentally observed range (within two standard deviations) for five myocytes, which averaged 3.1 ± 0.7 and 24 ± 4 ms, respectively (14). Fig. 8 C shows the Ca_i transient restitution of the model, which is also consistent with previously published experimental data (black dots) (14).

FIGURE 8.

Rate-dependent features: S1S2 pacing. (A) Superimposed APs from a representative myocyte (upper black traces) and the model (lower red traces) during the last paced S1 beat at 400 ms, and the S2 beats at progressively shorted S1S2 intervals. (B) The S1S2 APD restitution curve, showing the APD of the S2 beat versus the S1S2 interval in a representative myocyte (black points) versus the model (red line). (C) Peak systolic, diastolic and Ca_i transient amplitude (ΔCa) versus the S1S2 interval in the model. Black circles show ΔCa data points from a myocyte subjected to the same protocol, replotted from Goldhaber et al. (14).

DISCUSSION

In this study, we describe an improved rabbit ventricular AP model, whose major improvements consist of a new minimal Markovian I_Ca,L formulation, based directly on new experimental data from rabbit ventricular myocytes studied at physiological temperature using the perforated patch configuration to preserve intracellular signaling, and a dynamical model of Ca_i cycling. The Markovian I_Ca,L formulation reliably replicates CDI and VDI as well as recovery from inactivation. The dynamic Ca_i cycling model has the feature that SR Ca release is formulated to represent the summation of discrete release events (i.e., Ca sparks), phenomenologically emulating a local control system (31,35), as described previously (11). In this formulation, the instability responsible for Ca_i transient alternans naturally arises from a mechanism which depends on the amplitude and duration of local events on Ca_i cycling dynamics (11). The ventricular AP model incorporating these improved features reproduces APD and Ca_i transient alternans measured experimentally in rabbit ventricular myocytes using either the dynamic or S1S2 pacing methods. Because the model features both physiologically steep APD restitution and dynamically active Ca_i cycling, it will be useful for studying the interactions between voltage-driven and Ca_i-driven APD alternans.

Minimal Markovian model

I_Ca,L occupies a unique vantage point in modulating dynamic wave stability via both APD restitution slope and Ca_i cycling (36), and therefore may provide an attractive target for molecular-based antifibrillatory therapy. Genetic abnormalities in I_Ca,L inactivation also predispose to sudden cardiac death in the Timothy syndrome (37). To relate therapeutically desirable modifications of I_Ca,L to specific molecular interventions, it is essential to have a model of I_Ca,L with physiologically realistic VDI and CDI components representing the underlying molecular processes. Although current Hodgkin-Huxley formulations of I_Ca,L contain separate Ca- and voltage-dependent inactivation components, they are phenomenologically based, and not directly relatable to classic state diagram approaches used to represent ion channel biophysical properties in terms of molecular transitions between discrete conformational states. Moreover, the current Hodgkin-Huxley I_Ca,L formulations do not accurately reproduce the kinetics of inactivation and recovery from inactivation experimentally measured in rabbit ventricular myocytes in this study. Although they could in principle be refitted to do so, the process is not straightforward, since Ca- and voltage-dependent inactivation are expressed as the product of gating variables in these formulations, leading to a complex nonlinear interdependence.

A Markovian state diagram, on the other hand, can directly represent transitions between states of the channel corresponding to discrete molecular conformations of the channel, and is a more physiologically realistic way to separate Ca- and voltage-dependent kinetics. In principle, the effects of overexpressing gene products, drugs or genetic defects on the molecular transition rates can be measured and incorporated into the Markovian state diagram model, as, for example, has been done to explore the effects of Na and Ca channel mutations in genetic channelopathies (5,38). Markovian formulations of many ionic currents are currently available, and are being incorporated in the latest generation AP models, such as the I_Ca,L in several ventricular AP models (20,23,24), the Na current (I_Na) in the LRd model (38), and I_Kr in the LRd model (39). The recent mouse ventricular Markovian I_Ca,L model formulated by Winslow and co-workers (20) (with 12 states and 30 rate constants) and the new guinea pig ventricular Markovian I_Ca,L model by Faber et al. (5) (with 14 states and 42 rate constants) are both highly detailed. To facilitate large-scale tissue simulations, however, we designed a more computationally tractable minimal Markovian model to fit to our experimental data from rabbit ventricular myocytes. For example, we incorporated only two closed states (Fig. 1 B), although at least four exist corresponding to up/down positions of the activation gates in the channel's tetrameric structure. However, two closed states were sufficient to incorporate the strong voltage-dependence of transitions between closed states (leading to a low maximum open probability of ∼0.05 during depolarization as observed experimentally (16), coupled with a voltage-independent transition from the final closed state C1 to the open state O.

We based our I_Ca,L model on experimental data exploring the full range of voltages (−20 to +30 mV) over which I_Ca,L is active during an AP, and then directly validated that the fitted parameters accurately reproduced the time course of I_Ca,L in rabbit ventricular myocytes under AP clamp conditions (Fig. 6) (40,41). An advantage of our approach is that the full data set of I_Ca,L properties incorporated into the model were measured in the same preparation at physiological temperature, using the perforated patch configuration to minimize disturbance of the normal intracellular milieu. In contrast, other formulations typically have had to cull experimental data from multiple sources performed under variable experimental conditions, often at room temperature, requiring extrapolation to 37°C with an assumed Q₁₀ value.

Ca-induced inactivation

Our model for the Markovian state diagram was loosely based on the molecular schema of CDI and VDI proposed by Soldatov (21), in which VDI is the fundamental inactivation process and is allosterically modulated by Ca, which removes the brake on VDI imposed by calmodulin molecules tethered to the channel (Fig. 1 A). Our experimental results are fully consistent with this schema, as well as with prior findings (42) showing that I_Ca,L inactivates with a biexponential time course when Ca is the charge carrier (reflecting both VDI and CDI), but more slowly with a monoexponential time course when Ba, Sr, or Na are substituted for Ca as the charge carrier (reflecting VDI alone). In assessing VDI, we did not measure Sr or Na currents through L-type Ca channels, since previous studies in guinea pig ventricular myocytes showed that Ba, Sr, and Na all have quantitatively similar effects on I_Ca,L inactivation (43).

A novel aspect of our Markovian model is the explicit separation of CDI into two components, one related to Ca entry through the pore of the L-type Ca channel (corresponding to the experimental data in SR-depleted myocytes with Ca as the charge carrier), and the other to SR Ca release triggered by opening of the L-type Ca channels (corresponding to the additional component of Ca-induced inactivation in myocytes with intact SR and Ca as the charge carrier). The experimental data provides insights into the relative contributions of Ca entry through the pore and SR Ca release to I_Ca,L inactivation at different voltages. For example, Fig. 3 shows that under control conditions with intact SR, Ca-induced inactivation was much more rapid at −10 mV than at +20 or +30 mV, despite similar peak I_Ca,L amplitudes (see also Table 7). However, in SR-depleted myocytes with Ca as the charge carrier, the rates of fast inactivation at these voltages were similar. This observation suggests that fast inactivation at negative voltages is more strongly influenced by SR Ca_i release, consistent with the higher gain of SR Ca-induced Ca release at negative voltages. That is, although open probability is lower at negative voltages, the unitary current amplitude is larger due to the increased driving force, so that the peak macroscopic current is the same. However, the larger unitary Ca current at negative potentials also enhances the gain of SR Ca-induced Ca release, so that most L-type Ca channel openings trigger a Ca spark, causing SR Ca release to dominate Ca-induced inactivation of I_Ca,L. At positive voltages, on the other hand, the peak macroscopic I_Ca,L is the same due to the higher open probability, but the smaller single channel current amplitude is less effective at triggering SR Ca release. Thus, Ca flowing through the pore of the channel dominates Ca-induced inactivation at positive voltages, producing similar inactivation rates as in the absence of SR Ca release. In contrast, in the SR-depleted myocytes, Ca-induced inactivation rate tracked peak I_Ca,L independently of voltage. It is interesting that the single channel current amplitude of Ca entering through the pore at negative or positive voltages does not seem to have much influence on Ca-induced inactivation rate in SR-depleted myocytes, suggesting that its ability to enhance inactivation is already saturated at the small single channel amplitude associated with positive voltages. However, SR Ca release at negative voltages was still able to markedly further enhance Ca-induced inactivation, consistent with previous evidence that SR Ca has preferential access to the inactivating site on the L-type Ca channel (44). The minimal Markovian I_Ca,L model replicated all of these features of the experimental data.

Recovery from inactivation

In contrast to I_Ca,L inactivation, recovery from inactivation is monoexponential for the range of DIs (<500 ms) relevant to most physiological settings and tachyarrhythmias (although over longer time windows, a second long exponential component has been reported in human ventricular myocytes (45)). Moreover, the time constants were nearly identical with either Ca or Ba as the charge carrier (Fig. 4 A), indicating that recovery from inactivation is primarily voltage-dependent and Ca-insensitive. Our model incorporated this feature by making the rate-limiting rate constants for recovery from inactivation (i.e., the transitions from states I2_Ca→C2 and I2_Ba→C2 in Fig. 1 B) voltage-dependent, but Ca-insensitive. The measured time constant of recovery from inactivation of I_Ca,L under physiological conditions was ∼40 ms. This, in combination with the significant noninactivating component of I_Ca,L during the AP (Fig. 3), explains why I_Ca,L recovery from inactivation is a critical determinant of APD restitution slope in the range of DI (10–50 ms) which are typically visited during functional cardiac reentry. Among other late generation detailed models, only the Fox et al. (2) modification of the LRd model has a physiologically steep enough APD restitution slope to produce APD alternans. However, in this model, APD alternans is critically dependent on I_to, rather than on I_Ca,L or Ca_i cycling dynamics. In our Markovian model, both the time constant of recovery from inactivation and the noninactivating residual component of I_Ca,L over the time course of the AP were sufficient to replicate the steep APD restitution slope measured experimentally. It should be noted that APD restitution is also affected by other currents. I_Ca,L recovery from inactivation kinetics predominantly affects APD restitution slope for the intermediate range of DI values (10–50 ms). K-current deactivation kinetics and I_Na recovery from inactivation affect APD restitution slope at long DI values (>50 ms) and very short DIs (<10 ms), respectively. Restitution of the Ca_i transient (Fig. 8 C) also modulates Na-Ca exchange current at short DIs, influencing APD restitution slope.

Ca_i cycling features in the improved rabbit ventricular AP model

The introduction of detailed Ca_i cycling into late generation AP models has been immensely valuable for simulating EC coupling at normal heart rates (2,4,6,7). However, since these Ca_i cycling models were primarily designed to simulate cardiac function at normal heart rates, it is not surprising that at fast heart rates, most do not accurately reproduce experimentally documented features such as Ca_i alternans during pacing with a fixed voltage waveform (8–10). For this reason, in addition to reformulating I_Ca,L, we also replaced the Ca_i cycling formulation in the Shannon et al. rabbit ventricular AP model. We used our previously reported dynamic Ca_i cycling model (11), which was specifically developed to replicate Ca_i cycling dynamics in rabbit ventricular myocytes at rapid heart rates. In this model, Ca_i cycling emulates a local control system (31,35) by incorporating experimentally observed statistics on spark recruitment into Ca_i cycling, producing graded SR Ca release. Other detailed Ca_i cycling models are explicitly single pool models that do not represent SR Ca release as the summation of discrete SR Ca release events (i.e., Ca sparks).

Alternans

A major advantage of this model is that alternans can be induced via two distinct mechanisms. The first mechanism is the classic APD restitution mechanism where ionic current recovery kinetics lead to a steep dependence of APD on the previous DI. For a sufficiently steep slope, this can drive APD and Ca_i transient alternans (46). An alternative mechanism is via instabilities in the intrinsic dynamics of Ca_i cycling (10,14,47). In the Shiferaw et al. (11) model, this instability is induced by steepening the dependence of SR Ca release on the SR Ca load (Ca content), a feature which is consistent with several experimental studies documenting a steep relationship (8,48). During dynamic pacing, the cell gradually accumulates Ca, which loads the luminal SR Ca into a regime in which the release-versus-load relationship becomes steep. The second key additional feature required for alternans is a time delay (τ_a) between Ca uptake by SERCA pumps into the free SR (c_j space), and its availability for release through Ca release channels in the junctional SR (c′_j space) (Fig. 2). Physically, this time delay is consistent with either diffusional delay of Ca transport from uptake sites in the free SR to release sites in junctional SR, or refractoriness (adaptation) of Ca release channels after Ca release (in which case c′_j no longer represents the free Ca concentration in a physical space, but instead a refractory period regulated directly by c′_j). Recent evidence in rat ventricular myocytes favors the latter mechanism, since refilling of the local JSR stores (Ca blinks) had an average time constant of 29 ms, whereas the combination of JSR refilling plus RyR recovery had a time constant of 194 ms at room temperature (49). We used a temperature-corrected value of τ_a = 100 ms, assuming a Q₁₀ of 1.6 (50). This also matches the time course of Ca_i transient restitution in Fig. 8 (although the latter may also be affected by I_Ca,L recovery from inactivation). The refractory period could reflect either an intrinsic property of RyR, or, as currently favored (51), extrinsic regulation of RyR availability by SR luminal Ca-dependent molecular interactions with binding partners such as triadin, junctin, and calsequestrin. Mathematically, our formulation is consistent with any of these possibilities. Recent experimental observations suggest that Ca_i transient alternans can precede alternans in SR luminal Ca (52). In this version of our model alternation of cytoplasmic free Ca (c_i), c_j, and c′_j begin simultaneously. However, if c′_j is taken to represent Ca release channel refractoriness rather than junctional SR Ca concentration, so that c_j represents the free Ca in the lumen of junctional SR, then introduction of a buffer into the c_j space can produce c′_j alternation without c_j alternation at the onset of alternans (Restrepo and Karma, unpublished observations).

Livshitz and Rudy (13) have recently investigated the role of calmodulin kinase II on the regulation of Ca_i transient alternans in their guinea pig ventricular model using a mathematical formulation of SR Ca release that is closely analogous to the earlier formulation derived by Shiferaw et al. (11) based on a phenomenological description of a large ensemble of local Ca release events (Ca sparks). This formulation assumes that SR Ca release relaxes exponentially in time to a steady-state value that is the product of the whole cell L-type Ca current (consistent with the experimental observation that the spark recruitment rate is proportional to I_Ca,L) and a phenomenological function of JSR Ca concentration. The formulations of Livshitz and Rudy and Shiferaw et al. differ in the choice of this function and in the choice of the relaxation time of the SR release current to its steady-state value (equivalent to the sparks lifetime), which is chosen to be constant by Shiferaw et al. and dependent on JSR Ca concentration by Livshitz and Rudy. Despite these different choices, Ca alternans in both models arise from the identical mechanism, a steep dependence of fractional Ca release on SR load coupled with a time delay in RyR recovery.

Once Ca_i transient alternans begins, it causes APD alternans independently of the slope of the APD restitution curve. From our data in Fig. 6, A and B, we found that the onset of APD alternans occurred at a DI of roughly 70 ms. At this DI, the dynamic restitution slope was roughly 0.7, which is significantly less than the theoretically predicted slope > 1 required to induce alternans via steep APD restitution. Furthermore, at a DI of 70 ms, the S1S2 restitution curve is nearly flat, which implies that most ionic currents are fully recovered. This result is consistent with Fig. 4 A, which shows that at the resting potential of −85 mV, recovery from inactivation is fast (∼40 ms). Thus I_Ca,L can only contribute to APD restitution at pacing rates which engage a DI of roughly 50 ms or less. Hence, these considerations imply that Ca_i cycling must play an important role in inducing Ca_i transient and APD alternans. We tuned the model to reproduce these results by increasing the sensitivity of SR release on SR load, so that the steep portion was achieved during rapid pacing at a DI near 70 ms. When the model was rapidly paced with a clamped AP waveform, it is noteworthy that Ca_i transient alternans also occurred at a DI near 70 ms, proving that the Ca_i cycling instability was actively driving Ca_i transient alternans at the onset of APD alternans. However, it is important to point out that while a Ca_i cycling instability was essential for alternans at onset, APD restitution also plays a critical role in modulating the onset and amplitude of alternans. As shown by Shiferaw et al. (53), the bidirectional coupling between APD and the Ca_i transient ensures that the onset of alternans is dependent on both of these parameters. In the model implemented here, the dynamic restitution APD slope is not zero, and so it is dynamically active and works in conjunction with Ca_i cycling to induce alternans. Furthermore, at more rapid pacing rates (CL < 150 ms), APD restitution slope increases substantially as shorter DIs are engaged. In this regime, it is likely that APD restitution becomes the primary driver for alternans, although the Ca_i cycling instability is also active.

Bidirectional coupling between V and Ca_i

In our model, Ca_i transients are similar to experimental results with regard to their amplitude, time-to-peak, and decay time (41,54). Moreover, as SR Ca accumulates at rapid pacing rates, the nonlinear relationship between SR Ca load and SR Ca release becomes very steep, resulting in Ca_i transient alternans even when the AP is clamped (11). When the AP is allowed to run freely, the interaction between voltage and Ca_i cycling dynamics is bidirectional. For its current parameter settings, the influence of voltage on Ca_i release (APD→Ca_i coupling) is always positive, i.e., a larger I_Ca,L causes both a longer APD and a larger Ca_i transient, corresponding to electromechanically concordant APD alternans. The model also exhibits positive Ca_i→APD coupling, i.e., a larger Ca_i transient promotes a longer APD, since stimulation of electrogenic Na-Ca exchange outweighs greater Ca-induced inactivation of I_Ca,L for these parameter settings. These features are typical of rabbit ventricular myocytes under normal conditions, in which the dynamic Ca_i instability appears to develop first and drive APD alternans secondarily (14), as reported in other mammalian species (55). However, the model can also be readily tuned to produce negative Ca_i→APD coupling in which a larger Ca_i transient is associated with a shorter APD, corresponding to electromechanically discordant APD alternans. Different combinations of positive/negative bidirectional coupling have been shown to have important consequences on patterns of APD and Ca_i transient alternans (53), spatially discordant alternans (12), and even subcellular alternans (9,53,56), and are likely to have important effects on wave stability during reentry in tissue (36,57). Thus, this improved AP model may be very useful for understanding how such properties can be favorably manipulated by molecular interventions targeting L-type Ca channels or other ion channels and Ca_i cycling elements, to improve dynamic wave stability as an antiarrhythmic strategy (36).

Limitations

Although our improved rabbit ventricular AP model represents an advance over currently available late generation AP models for simulating cardiac AP and Ca_i cycling dynamics, the model has limitations that will need to be addressed in future versions. These include the need to formulate a physiologically plausible mechanism for spontaneous SR Ca release in Ca_i-overloaded conditions, which plays a major role in the pathogenesis of delayed afterdepolarizations and triggered activity. Other late generation AP models have incorporated this feature, although the accuracy with which spontaneous Ca release from a single pool accurately represents the underlying spatiotemporal complexity of Ca-induced Ca release waves remains unclear. In addition, we have modeled a generic rabbit ventricular myocyte AP, and the model parameters will need to be adjusted to represent APs and Ca_i cycling features specific to different regions of the myocardium. Also the model should ultimately incorporate the effects of β-adrenergic stimulation on I_Ca,L and Ca_i cycling dynamics, in view of the strong proarrhythmic influence of sympathetic stimulation, as well as simulate the electrical remodeling of the AP in the setting of heart failure and chronic ischemia. Despite these limitations, we hope that by realistically replicating dynamical behaviors of rabbit ventricle myocytes at rapid heart rates relevant to ventricular tachyarrhythmias, the new improved rabbit ventricular AP model will be useful in facilitating a better understanding of the roles of dynamic factors in acquired and congenital cardiac arrhythmias, and for designing and testing in silico potential molecular antifibrillatory targets, in conjunction with experimental approaches.

APPENDIX

Equations for Ca cycling

Ca_i cycling in the rabbit myocyte is described using a model by Shiferaw et al. (11). The currents implemented in the model are illustrated in Fig. 2 B in the main text. The equations for Ca cycling are

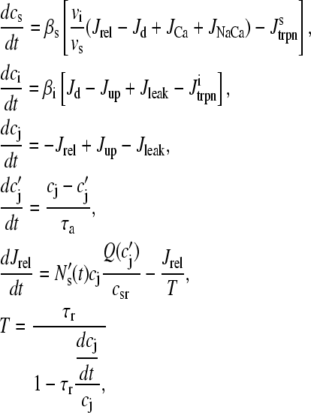(7)

where c_s, c_i, and c_j are the average concentrations of free Ca in a thin layer just below the cell membrane (the submembrane space), in the cytosol, and the SR, with volumes v_s, v_i, and v_sr, respectively. Equation 7 is identical to the Shiferaw model (59) with the exception of the relaxation time T of the whole-cell junctional SR (JSR) release current to its steady-state value. The modified expression accounts for the fact that the single spark release current is assumed to be proportional to the SR Ca load c_j and to decay exponentially in time after a spark is recruited (which prevents c_j from reaching negative values at low SR load). This release current differs from the one used to regulate Ca-induced inactivation of L-type Ca channel (c_p in Eq. 1, which is an effective concentration not used in calculating flux balance). Here the SR volume includes both the JSR and the free nonjunctional SR (NSR). Also c′_j can be defined alternatively as the average free [Ca] available for release in the JSR, or as the c_j-dependent refractory period of Ca release channels in the JSR. The concentrations c_s and c_i are in units of μM, whereas c_j and c′_j (for simplicity) are both in units of μM v_sr/v_i (μM/l cytosol). We take the volume of the submembrane space to be roughly 50 times less than the volume of the bulk myoplasm so that v_s/v_i = 0.02, which, following Weber et al. (58), ensures that membrane channels sense faster Ca concentration changes than that of the bulk myoplasm.

The current fluxes are:

• J_rel is the total release flux out of the SR via Ca release (RyR) channels;

• J_d diffusion of Ca from the submembrane space to the bulk myoplasm;

• J_up is the uptake current via SERCA pumps in the SR;

• J_Ca is the current flux into the cell via L-type Ca channels;

• J_NaCa is the current flux into the cell via the NaCa exchanger;

• J_leak is the leak current from the SR into the bulk myoplasm.

The release flux from the SR (J_rel) is formulated as the summation of elementary release fluxes corresponding to Ca sparks. Here, N′_s(t) corresponds to the rate of spark recruitment, Q(c′_j) is the peak flux due to a spark, which is dependent on c′_j, and finally τ_r is the spark lifetime. All Ca fluxes are divided by v_i and have units of μM/ms, which can be converted to units of μA/μF using the conversion factor nFv_i/C_m, where n is the ionic charge of the current carrier, C_m is the cell membrane capacitance, and F is Faraday's constant. Thus, ionic fluxes can be converted to membrane currents using

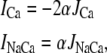(8)

where α = Fv_i/C_m, and where the ion currents are in units of μA/μF.

The dependence of Ca release on SR Ca load is determined by the peak flux due to a spark Q(c′_j), which is in units of 10⁻⁶ μM/ms. To reproduce the experimental data of Bassani et al. (59), where the SR release increases steeply with SR load at high loads, we make the local release flux depend on c′_j (representing either JSR Ca available for release, or alternatively RyR availability depending on which molecular mechanism is preferred—see Discussion) in a similar fashion. The assumption here is that at high SR loads the peak amplitude of the local release flux underlying a spark is sensitively dependent on SR load. The relationship can be implemented using the functional form

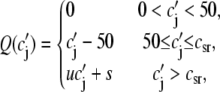(9)

where the parameter u controls the slope of the SR Ca release versus SR Ca load relationship at high loads (c′_j > c_sr). The parameter s is chosen so that the function Q(c′_j) is continuous at c_sr. Details for the motivation and form of the function are given in Shiferaw et al. (11).

The formulation of Ca release from the SR is modeled by computing the rate at which sparks are recruited in the whole cell. Spark recruitment occurs within dyadic junctions where an L-type Ca channel opening triggers the local cluster of Ca release channels (RyR receptors) to open via Ca-induced Ca release. This process occurs within thousands of dyadic junctions in the cell. To achieve computational tractability, following Shiferaw et al. (11), the rate at which sparks are recruited is modeled using a phenomenological approach. In this approach, the number of sparks recruited over the whole cell in a time interval Δt is given by ΔN_s, and the rate of spark recruitment is N′_s = ΔN_s/Δ_t. Since spark recruitment is initiated by the stochastic single channel opening of L-type Ca channels distributed throughout the cell, we expect that N′_s follows a voltage dependence similar to the whole cell Ca entry. Thus, we use a phenomenological expression for spark rate given by

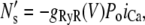(10)

where g(V) is the gain function, which controls the voltage dependence of Ca released into the SR in response to a trigger from the L-type Ca current. We choose a functional form for this expression so that graded release is achieved as demonstrated experimentally in Wier et al. (31). The voltage dependence is weak and has the form

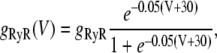(11)

where the parameters are chosen using the multidimensional fitting procedure.

The L-type Ca current flux

The Ca flux into the cell due to the L-type Ca current is given by

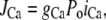(12)

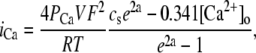(13)

where a = VF/RT, and where c_s is the submembrane concentration in units of mM.

Markovian model of the L-type Ca current

The open probability of L-type Ca channels is dictated by the kinetics of the Markovian model illustrated in Fig. 1 B and described in the previous section. The equations for the Markovian states are

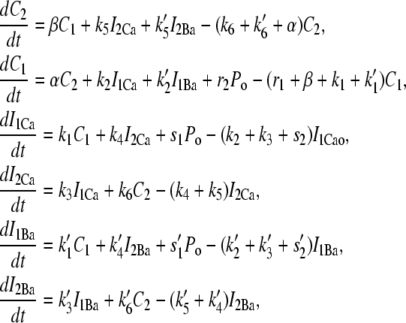(14)

where the open probability satisfies

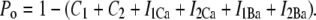(15)

The rates are given by

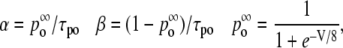(16)

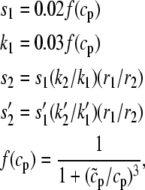(17)

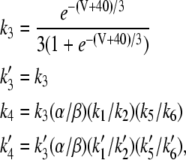(18)

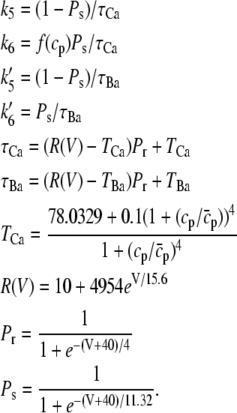(19)

Diffusive flux

Following Shiferaw et al. (11), the flux of Ca from the submembrane space to the bulk myoplasm is described by

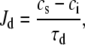(20)

where τ_d is the time constant for Ca diffusion from the submembrane space to the bulk myoplasm. For an effective Ca diffusion rate in the range of 250–350 μm²/s and for an average distance between the submembrane space and the center of the sarcomere of roughly 1 μm, we estimate τ_d to be roughly 4 ms.

Nonlinear buffering

Buffering of Ca is modeled by incorporating instantaneous buffering to SR, calmodulin, membrane, and sarcolemma binding sites. All buffering parameters are experimentally based and summarized in Shannon et al. (60). Parameters are given in Table 2. Note that new buffers were added to the original model to prevent Ca surge to very large values during fibrillation, and are described by

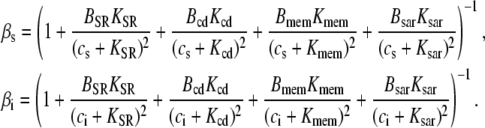(21)

Time-dependent buffering to Troponin C is described by

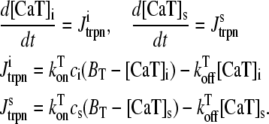(22)

NaCa exchange flux

The flux of Ca due to the NaCa exchanger is based on the well-established formulation of Luo and Rudy (4), with recent modifications (61). The equation is

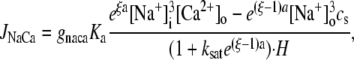(23)

where

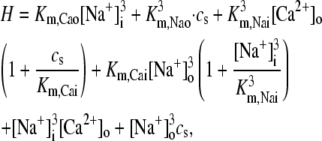(24)

and where

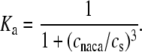(25)

The SERCA (uptake) pump

Following the Shiferaw et al. (11), the SERCA Ca pump is formulated using

(26)

where v_up denotes the strength of uptake and c_up is the pump threshold. The values of these quantities (given in Table 3) are adjusted to obtain a steady-state Ca transient similar in shape and magnitude as measured in experiments (10).

The SR leak flux

The leak flux from the SR is modeled as

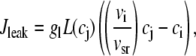(27)

where v_sr/v_i is the SR/cytoplasm volume ratio, and L(c_j) is a threshold function of the form

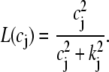(28)

Since leak from the SR is only appreciable at high SR loads, we chose the leak threshold to be roughly 50 μM/l cytosol. Thus, the leak current is appreciable only for large SR loads. Parameters of the leak flux are chosen so that a quiescent cell achieves physiological steady-state myoplasmic and SR Ca concentrations, after which the uptake flux loading the SR balances the leak flux. During rapid pacing, the leak flux does not play an important role in the dynamics, since under these conditions release is dominated by I_Ca,L.

Averaged Ca dynamics in the dyadic space

The average concentration in active dyadic clefts is modeled phenomenologically as

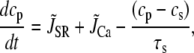(29)

where

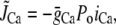(30)

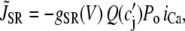(31)

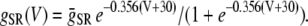(32)

As described in the main text 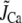and 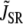denote average Ca fluxes into an ensemble of dyadic junctions, phenomenologically regulating the dynamics of the average dyadic cleft Ca concentration.

Na dynamics

Intracellular Na dynamics is given by

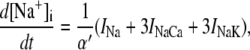(33)

where the factor 1/α′ converts membrane currents in μA/μF to Na fluxes in units of mM/ms. The conversion factor is given by α′ = 1000α, where α = Fv_i/C_m.

Ionic currents

The rate of change of the membrane voltage V is described by the equation

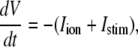(34)

where I_ion is the total membrane current due to ionic species, and where I_stim is the stimulus current driving the cell. The total membrane current is given by

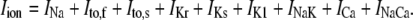(35)

Current kinetics are based on the Shannon et al. model (7).

The fast sodium current (I_Na)

We used the original formulation by Luo and Rudy as subsequently implemented in the Shannon et al. model:

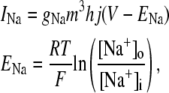(36)

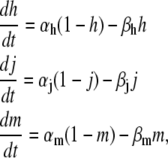(37)

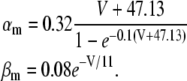(38)

For V ≥ −40 mV,

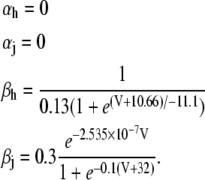(39)

For V ≤ −40 mV,

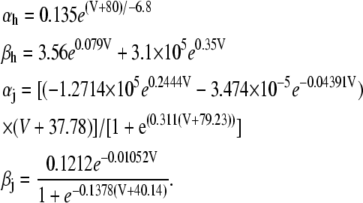(40)

Inward rectifier K⁺ current (I_K1)

We used the original formulation by Luo and Rudy as subsequently implemented in the Shannon et al. model:

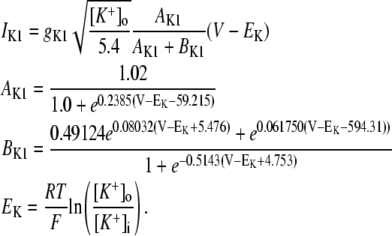(41)

The rapid component of the delayed rectifier K⁺ current (I_Kr)

We used the original formulation by Luo and Rudy, with modifications for the rabbit myocyte due to Puglisi et al. (62), as subsequently implemented in the Shannon et al. model:

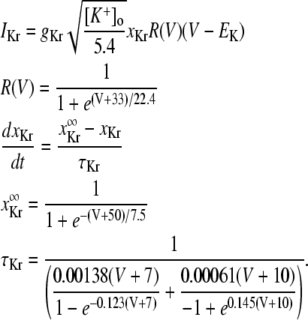(42)

The slow component of the delayed rectifier K⁺ current (I_Ks)

We used the original formulation by Luo and Rudy as subsequently implemented in the Shannon et al. model, and made a modification to the Ca dependence of the conductance to fit our dynamic restitution data:

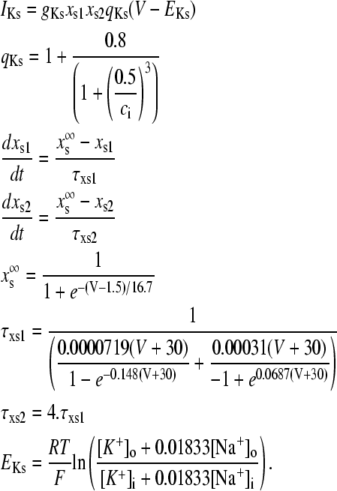(43)

Note that conductance of I_Ks has a Ca-sensitive component. This Ca dependence follows experimental findings of (63) and is also implemented in the Shannon et al. model (7). We have adjusted the Ca dependence here to fit our measured dynamic restitution curve.

The Na-K pump current (I_NaK)

As in the Shannon et al. model,

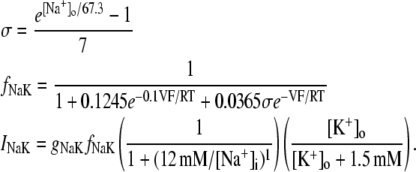(44)

The fast component of the rapid inward K⁺ current (I_to,f)

As in the Shannon et al. model,

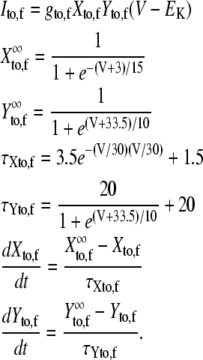(45)

The slow component of the rapid outward K⁺ current (I_to,s)

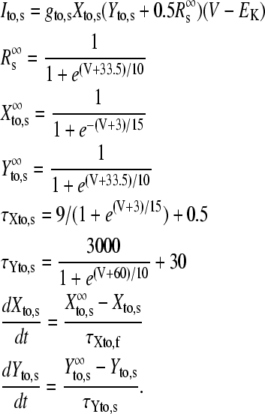(46)