Approximate Analytical Time-Dependent Solutions to Describe Large-Amplitude Local Calcium Transients in the Presence of Buffers

Abstract

Local Ca²⁺ signaling controls many neuronal functions, which is often achieved through spatial localization of Ca²⁺ signals. These nanodomains are formed due to combined effects of Ca²⁺ diffusion and binding to the cytoplasmic buffers. In this article we derived simple analytical expressions to describe Ca²⁺ diffusion in the presence of mobile and immobile buffers. A nonlinear character of the reaction-diffusion problem was circumvented by introducing a logarithmic approximation of the concentration term. The obtained formulas reproduce free Ca²⁺ levels up to 50 μM and their changes in the millisecond range. Derived equations can be useful to predict spatiotemporal profiles of large-amplitude [Ca²⁺] transients, which participate in various physiological processes.

INTRODUCTION

There is scarcely a reaction within the body that is not regulated, directly or indirectly, by Ca²⁺. It is a second messenger, which is injected into the cytoplasm after the opening of single channels in plasma membrane or internal stores. Concomitant increases in intracellular [Ca²⁺], [Ca²⁺]_i, are, in general, local and their patterns are determined by combined effects of Ca²⁺ diffusion and buffering in the cytoplasm (1). Such processes belong to a well-known reaction-diffusion problem of mathematical physics, which is a persistent stumbling block for theorists, cf. literature (2,3) for recent reviews. In the presence of N Ca²⁺ buffers in the cytoplasm, one needs to solve a set of 2N + 1 nonlinear parabolic partial differential equations (PDE)

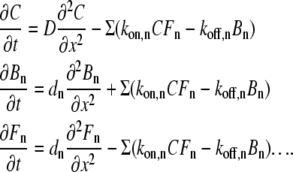(1)

Here C is the concentration of free Ca²⁺ and D is its diffusion coefficient, B_n and F_n are the concentrations of free and Ca²⁺-bound forms of the nth buffer, for which the diffusion coefficient is d_n, and k_on and k_off are the rate constants of Ca²⁺ binding to and dissociation from the buffer. The rate constants define the dissociation constant of the buffer, K_d = k_off/k_on, which determines its potency to bind Ca²⁺.

Due to the importance of Ca²⁺ signaling, many theoretical and experimental studies investigated the main characteristics of local [Ca²⁺]_i changes and their possible role in different physiological events. Hundreds of articles considered various aspects of the local [Ca²⁺]_i signals. Illustrative results include the analysis of the form (4,5) and modeling of the function of micro- and nanodomains (6,7), the measurements of spatial widths of [Ca²⁺]_i increases around the single channels (8–11), the effects of buffers on [Ca²⁺]_i oscillations (12,13) and waves (14–18), and Ca²⁺ dynamics in the dendritic compartments (19); also included are stochastic spreading and integration of intracellular Ca²⁺ release (20,21) and the effects of exogenous buffers on [Ca²⁺]_i transients (22) and waves (23). These and other studies delivered many important insights on spatiotemporal patterns of Ca²⁺ within neurons and other cell types that is also summarized in several reviews (1,24,25).

Ca²⁺ entry through discrete channels produces Ca²⁺ gradients around the exit lumen (6). Assuming that buffer is in excess, Neher (4) linearized the steady-state reaction-diffusion problem and estimated the widths of local stationary [Ca²⁺]_i increases as related to the rate of Ca²⁺ binding to the buffer. Normally the buffers are present in the cytoplasm at concentrations >0.1 mM and most of them bind Ca²⁺ with the time constant τ = 1/k_onF ≈ 1/[10⁸ M⁻¹s^{−1 .} (>0.1 mM)] < 0.1 ms. This is by 1–2 orders of magnitude smaller than the time constant of Ca²⁺ channel gating, therefore consideration of steady-state gradients of [Ca²⁺]_i provides a good first approximation for Ca²⁺ nanodomains. Single channels act as point sources and can produce big local [Ca²⁺]_i elevations that would saturate the buffer(s). The ways to obtain the steady-state solution of the resulting nonlinear problem have been delineated by Wagner and Keizer (12), who derived a transport equation for Ca²⁺ in the presence of multiple buffers. They estimated the effective Ca²⁺ diffusion coefficient and used it to describe a slow diffusion of Ca²⁺.

The results of recent experiments indicate that in most physiologically relevant situations, the local [Ca²⁺]_i levels exceed 10 μM (22,26,27). Such increases are implicated in various forms of cellular (especially neuronal) plasticity. Large-amplitude [Ca²⁺]_i transients can be correctly treated only in simulations that explicitly consider the effects of multiple buffers and the kinetics of Ca²⁺ binding (7,9,19,27,28). Due to the choice of particular models, these numerical experiments likely present special cases rather than giving insight into the ways in which buffers can change the qualitative behavior of a system. It is important to have a more general theory of the effects of buffers on the local transients that could be used to understand specific results in terms of a broader framework.

In this study, we propose an approximate treatment of the problem of Ca²⁺ diffusion/buffering, which is applicable in a wide range of Ca²⁺ and buffer concentrations. A nonlinear character of the problem was circumvented by introducing the variable ln(1 + C/K_d) and by expanding the reaction-diffusion equations in terms of this variable. We obtained explicit solutions that reproduce [Ca²⁺]_i changes up to 50 μM and underestimate them at [Ca²⁺]_i = 100 μM by ∼20%. The proposed approach can be useful in interpreting the local large-amplitude [Ca²⁺]_i transients in most physiologically relevant situations. The outline of the article is as follows: in “Ca²⁺ binding by a single mobile buffer” we consider [Ca²⁺]_i transients in the presence of single mobile Ca²⁺ buffer; in “Mobile and immobile Ca²⁺ buffers with the same K_d” we add an immobile buffer with the same dissociation constant; in “Mobile and immobile Ca²⁺ buffers with different K_d values” the general solution for mobile and fixed buffers is obtained; in “Propagating Ca²⁺ signals” the approach is applied to the propagating Ca²⁺ signals; and in “Rapid and slow Ca²⁺ buffers” we compare the properties of fast and slow buffers and discuss the applicability of the rapid buffer approximation. Appendix I recapitulates the linearized approximation for multiple buffers and extends it to quadratic terms, Appendix II presents a general formulation of the logarithmic approximation for several Ca²⁺ buffers, and Appendix III discusses the characteristics of the cytoplasmic buffers.

RESULTS

Ca²⁺ binding by a single mobile buffer

In all derivations below we consider a one-dimensional formulation of the diffusion problem but all algebra and formulas are readily transformed to the case of the three-dimensional radial diffusion that, e.g., corresponds to the spread up of Ca²⁺ from the channel lumen into a hemisphere. For this, one sets C = U/r that transforms a three-dimensional diffusion term (1/r²)∂(r²∂C/∂r) into a simple second derivative. The radial concentration profiles are then obtained by dividing the solution of the one-dimensional problem by the distance from the channel lumen.

When we add first two Eq. 1, this removes the reaction term and gives the equation of diffusion of total Ca²⁺

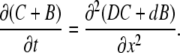(2)

We solve this equation using a rapid buffer approximation that assumes a fast binding of Ca²⁺ (see Introduction and “Rapid and slow Ca²⁺ buffers”) and defines the bound Ca²⁺ as

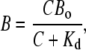(3)

where K_d is the dissociation constant and B_o is the total concentration of the buffer. We first obtain a solution for one mobile buffer. Normalizing K_d and all concentrations to B_o and using Eq. 3, we transform Eq. 2 into the nonlinear PDE for the variable y = (1 + c) = (1 + C/K_d)

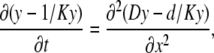(4)

where K = K_d / B_o. In the following, we drop or add appropriate constants in the derivatives when appropriate. Mathematically this changes nothing because these terms vanish after differentiation. Thus, Eq. 4 can be presented in the form of simple parabolic PDE as

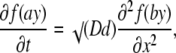(5)

for the function f(y) = (y − 1/y), where a = √K and b = √KD/d. The equation is only seemingly simple and it cannot be solved directly, because f(y) is generally not invariant to linear transformations. However, an explicit solution can be found by using the approximation f(y) ≈ 2.3lny, which follows from the expansion of both functions in the Taylor series around y = 1. Theoretical proportionality factor is 2, but empirically we found that the approximation is better when it is set to 2.3 (see the inset in Fig. 1). The quality of the approximation is determined by the parameters of Ca²⁺ buffering in the cytoplasm. For the typical values D = 200 μm²/s, d = 20 μm²/s, K_d = 0.3 μM, and B_o = 0.3 mM (see Table 1 in Appendix III), the nondimensional parameters are K = 0.001, a = 0.03, and b = 0.1. Function f(ay) is well fitted by the logarithm up to ay ≈ 3.5 (Fig. 1) that corresponds to C/K_d = 100 (the quality of approximation can be further improved by including quadratic logarithmic terms; see Appendix II). Replacement of f(y) by logarithm gives a linear diffusion equation

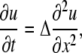(6)

for u = lny, where Δ = √Dd = 40 μm²/s is an apparent diffusion coefficient. The boundary condition is u_o = ln(1 + Q/K_d) at x, t = 0 and u_o = 0 otherwise (here Q is a surge of Ca²⁺ into the cytoplasm).

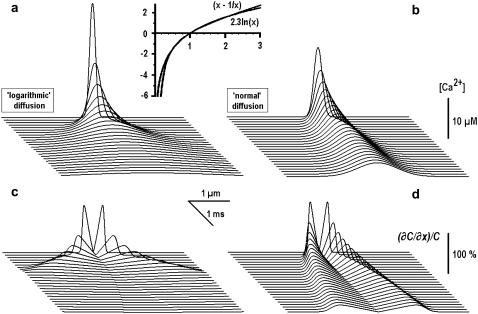
FIGURE 1.

“Logarithmic” and “normal” diffusion of Ca²⁺ from the point source. Shown are the time-dependent profiles of Ca²⁺ concentration, which were obtained from Eqs. 8 and 7, describing the fast (a) and the normal (b) diffusion, respectively. In both cases, the effective diffusion coefficient was 40 μm²/s and the same amplitude of point source was used. The inset (top) shows the approximation of “total [Ca²⁺]” term in Eqs. 4 and 5 by logarithm. Panels a and b depict [Ca²⁺] changes, and panels c and d present normalized spatial derivatives as indicators of the fronts of Ca²⁺ concentration.

TABLE 1.

Dissociation constants, cytoplasmic content, and the mobility of buffers

Buffer	Kd, μM	Concentration, mM	Diffusion coefficient, μm2/s
Calbindin*	0.7	0.16	20
Parvalbumin†	0.5	0.1	43
Fluo-4	0.3	0–0.4	200
Calmodulin	2	0.15	0
Troponin‡	0.5	0.07	0
Phospholipid	13	12	0
Fluo-3	0.4	0.1	100
ATP	200	0.26	320
Calmodulin	2.4	0.1	25
Not specified§	10	0.1–1	15
Calbindin¶	0.6	0.2	40
Parvalbumin	0.3	0.2	100

^*Data taken from Muller et al. (29).

^†Data taken from Goldberg et al. (9).

^‡Data taken from Michailova et al. (28).

^§Data taken from Sherman et al. (5).

^¶Data taken from Schmidt et al. (19).

Equation 6 is closely related to a famous porous equation (30,31). To show this, we introduce a new variable w = 1/y and neglect ay in the left-hand side of Eq. 5, which is usually smaller than 1/ay. This gives an equation for the logarithmic diffusion (32)

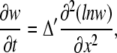which is a special case of the porous equation (see also “Mobile and immobile Ca²⁺ buffers with the same K_d” below and Appendix II).

Returning to Eq. 6, we note that it has a form of a common diffusion equation (33), which solution for a point source is

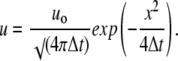(7)

Presenting Eq. 7 in terms of calcium concentration, we obtain

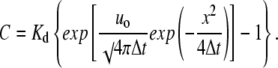(8)

Fig. 1 presents the [Ca²⁺] profiles for the “logarithmic” and the “normal” diffusion. In the calculations we used the same source amplitude and the apparent diffusion coefficient. The spatiotemporal patterns are clearly different and it is seen that in the case of the logarithmic diffusion, the changes in [Ca²⁺] spread out faster. This becomes more evident in the plots of normalized derivatives, (∂C/∂x)/C, which depict the fronts of Ca²⁺ concentration (Fig. 1, c and d).

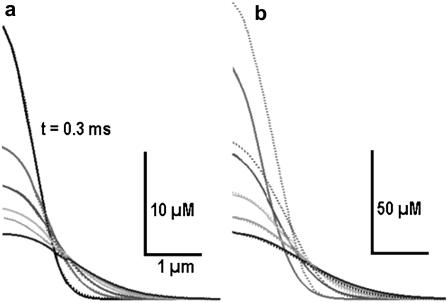
We checked the applicability of the derived approach to describe [Ca²⁺] transients by performing numerical integration of Eq. 1 using the Crank-Nicolson algorithm (33). Fig. 2 a shows that the approximation works well for the levels of [Ca²⁺] < 50 μM, and at [Ca²⁺] > 100 μM, the predictions underestimate exact values by ∼20% (Fig. 2 b).

FIGURE 2.

Exact Ca²⁺ transients and their approximation. Time-dependent Ca²⁺ concentration profiles obtained by numerical integration of reaction-diffusion system using the Crank-Nicolson algorithm (dotted curves) are approximated by the analytical solution for the logarithmic diffusion (solid curves). The diffusion coefficients were D_Ca = 200 μm²/s, d_Buffer = 20 μm²/s, the on- and off-rate constants were k_on = 10⁸ M⁻¹s⁻¹ and k_off = 100 s⁻¹ (K_d = 1 μM), and the total buffer concentration B_o = 1 mM. For the logarithmic diffusion the apparent diffusion coefficient Δ was 40 μm²/s. In panel b the amplitude of instantaneous Ca²⁺ source was seven times bigger than in panel a. Note a close correspondence between the two solutions (a) and underestimation of the large amplitude transients in the case of the logarithmic diffusion (b).

Mobile and immobile Ca²⁺ buffers with the same K_d

In the cellular environment, Ca²⁺ signals are shaped by multiple endogenous buffers. Each buffer is characterized by at least three parameters (concentration, dissociation constant, and diffusion coefficient). Buffers enter Eq. 1 in the same way, therefore their effects can be additive; that means that [Ca²⁺]_i transients may not be very sensitive to the variations in the characteristics of specific buffers. To show this, we first consider the case of two buffers with the same dissociation constant (K) and different diffusion coefficients (d₁ and d₂). Instead of Eq. 4 we now have

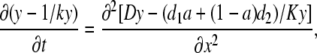(9)

where a = B_o1/B_o is the mol fraction of the first buffer and 1 − a = B_o2/B_o is the mol fraction of the second buffer. The equation can be put in the form of Eq. 6, where the apparent diffusion coefficient is now

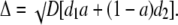(10)

When one buffer is immobile, the diffusion coefficient is simply Δ = √(aDd), where d = d₁.

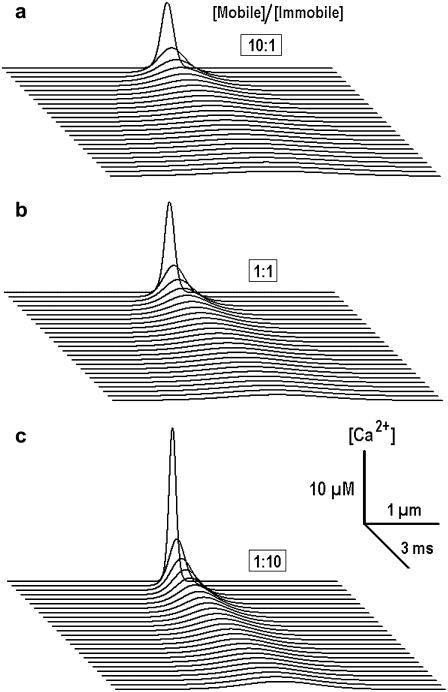
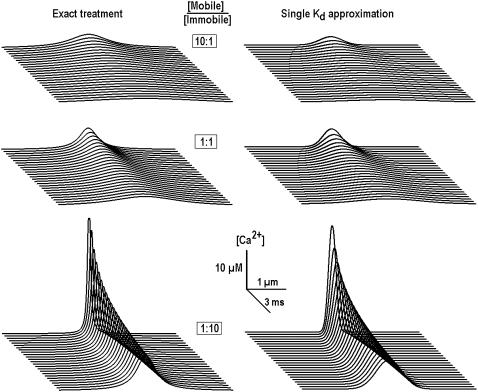
Fig. 3 shows the results of calculations for different mixtures of mobile and immobile buffers. It is seen that when the concentration of mobile buffer decreases, the transients appear more localized and decreases in widths of the transients are accompanied by increases in their amplitude.

FIGURE 3.

Ca²⁺ transients in the presence of mobile and immobile buffers of the same affinity. Calculations were performed at fixed total buffer concentration (1 mM) and the mol fraction of buffers was varied as indicated in each panel. The diffusion coefficient of mobile buffer was 20 μm²/s and the dissociation constant for both buffers was set to 0.3 μM. In the calculations, we used the effective diffusion coefficient, which depended on the [Mobile]/[Immobile] ratio; see Eq. 10. Note a sharpening of Ca²⁺ transients with the increase in the mol fraction of the immobile buffer.

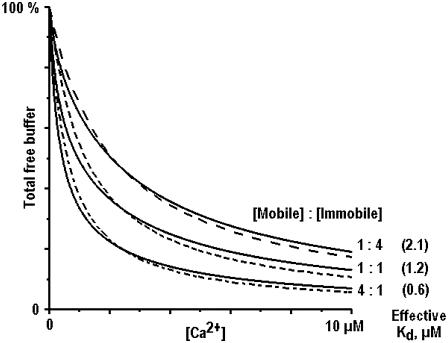
We noticed that a reasonably good description of the total Ca²⁺ buffering capacity can be obtained by using a model that consists of only two buffers with the same K_d, when it is allowed to change according to the composition of the mixture (Fig. 4). This reproduces well the general solution (Fig. 5) and it was used to approximate Ca²⁺ buffering properties of the cytoplasm (Appendix III).

FIGURE 4.

Effective dissociation constants in mixtures of mobile and immobile Ca²⁺ buffers. Solid traces indicate the Ca²⁺ binding capacity in the presence of two buffers with dissociation constants equal to 0.3 and 3 μM (see Appendix III). The dotted curves approximate the data by assuming the same dissociation constant for both buffers. Its values are given in parentheses (right of the curves) and depend on the mol ratio.

FIGURE 5.

Ca²⁺ transients in the presence of mobile and immobile Ca²⁺ buffers of different affinity. The panels show Ca²⁺ transients at different buffer mol ratios as indicated. The total buffer concentration was 1 mM, the dissociation constants of the mobile and the immobile buffers were 0.3 μM and 3 μM, respectively, and the diffusion coefficient for the mobile buffer was 20 μm²/s. The profiles in the left column were obtained by explicitly considering the effects of two buffers (Eq. 14). The profiles in the right column show the transients calculated by using effective dissociation constants (Fig. 4) and diffusion coefficients (Eq. 10), which both depended on the mol ratio. Note a close correspondence between the transients in the two sets of data.

Mobile and immobile Ca²⁺ buffers with different K_d values

A general solution in the case of multiple Ca²⁺ buffers is given in Appendix II. The derived equation corresponds to a quadratically nonlinear diffusion. For one mobile and one immobile buffer that have different K_d values, it can be presented as

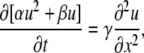(11)

where the coefficients α = (1 − a)A√K, β = a√k + (1 − a)B√K, and γ = a√(kDd). Here k and K are the normalized dissociation constants for mobile and immobile buffers (it is assumed that k < K; see Appendix III), u = ln(1 + c/k), a is the mol fraction of the mobile buffer, and the coefficients A and B are defined in Eq. B3. Rewriting Eq. 11 as

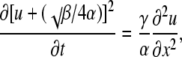(12)

and changing the variable u to w = [u + (√β/4α)]², we obtain

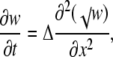(13)

where Δ is given by Eq. B4 (it is smaller or equal to √(Dd)). Equation 13 is also the porous equation, which describes a fast diffusion (34). Its general solution (32) is

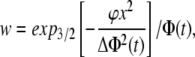(14)

where Φ(t) = [1.5ϕt]^2/3, ϕ is the normalization constant, and exp_q(z) =[1 + (1 − q)z]^1/(1−q) is the stretched exponential (at q = 1 it becomes a simple exponential). The concentration of free Ca²⁺ is obtained from Eq. 14 through the back transformation steps (w² → ln(u) → c ∼ exp(u)).

Fig. 5 presents the [Ca²⁺] transients that were calculated for a mixture of mobile and immobile Ca²⁺ buffers with different K_d values. It is seen that the amplitude of transients decreases with the mol fraction of the mobile buffer that resembles the behavior shown in Fig. 3. Notably, the data in the left panel are well reproduced by the profiles in the right panel that were obtained by using the same K_d for both buffers, which depended on the mol fraction.

Propagating Ca²⁺ signals

We next examined the effects of Ca²⁺ diffusion and buffering on the propagating Ca²⁺ signals. We considered a special case of Ca²⁺ waves that are supported by the Ca²⁺-induced Ca²⁺ release (CICR) from the internal stores (endoplasmic reticulum and/or mitochondria (35)) that have been documented in various cell types. We used a sort of “diffuse-and-fire” model (16,25), which assumes that at any time only one release channel is open and the activation of neighboring channel occurs only when the [Ca²⁺] level in its vicinity reaches a given threshold.

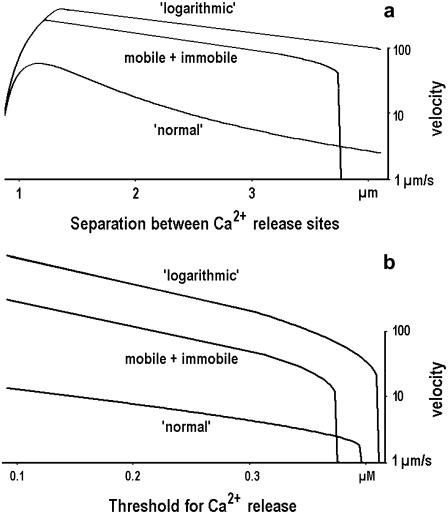
Wave velocities in the model were calculated as a ratio of distance between the channels and the time needed for [Ca²⁺] to reach the threshold at another site. In one set of calculations, we set a threshold to 0.2 μM (36) and varied the distance between the release sites. Ca²⁺ waves maintained about the same velocity up to the separation of ∼4 μm between the sites, after which a regenerative propagation ceased (Fig. 6 a). When CICR threshold increased, the velocity steadily declined (Fig. 6 b). It is seen that in both cases the velocity is bigger for the logarithmic diffusion. It becomes smaller when the immobile buffer was introduced (middle traces in Fig. 6), but the differences remain.

FIGURE 6.

Calculations of the velocity of Ca²⁺ waves due to regenerative Ca²⁺ release from internal stores. The velocities were obtained as the ratios of distances between the release sites and the times needed for a [Ca²⁺] transient to reach the threshold of release at the neighboring site. In panel a the threshold was set to 0.2 μM and the distance between the release sites was varied. In panel b the distance between the release sites was fixed at 1 μm and the threshold was varied. The parameters of intrinsic cytoplasmic buffer were B_o = 1 mM, K_d = 1 μM, and d = 20 μm²/s (mobile buffer). Middle curves in each panel correspond to the case when the concentrations of the mobile and immobile buffers were equal.

Rapid and slow Ca²⁺ buffers

The use of rapid Ca²⁺ buffering approximation has certain limitations. To assess its validity and restrictions, consider a bimolecular reaction of Ca²⁺ binding, which rate is

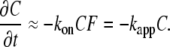(15)

Ca²⁺ binding to the most Ca²⁺ binding proteins occurs with the on-rate constant k_on ≈ 10⁸ M⁻¹s⁻¹, a so-called diffusion limit (37). When the buffer concentration is bigger than 0.1 mM, k_app > 10⁴ s⁻¹ corresponds to the reaction time below 0.1 ms. However, for some buffers such as parvalbumin and EGTA, the kinetics of Ca²⁺ binding is slower. Such effects of parvalbumin are implied in shaping long-lasting transients [Ca²⁺]_i during muscle contraction (38) and in some events that accompany neuronal plasticity (39). EGTA (alone or in comparison with another buffer, BAPTA) is often used as an exogenous buffer to examine the role of Ca²⁺ compartmentalization in various physiological responses (1). The trick is that despite the fact that the two buffers have similar Ca²⁺ affinities, EGTA binds Ca²⁺ hundreds of times slower than BAPTA and therefore does not considerably influence the fast local [Ca²⁺]_i transients (4).

From the physicochemical point of view, the classification of Ca²⁺ buffers into slow and fast deserves some comments. In contrast to BAPTA, EGTA binds Ca²⁺ with a high affinity only at alkaline pH, when all its four carboxyl residues are free. At physiological pH values, two out of four EGTA carboxyls are protonated and the affinity shifts into the millimolar range. The high-affinity form of EGTA is also present at neutral pH, but it comprises only 1% of total EGTA. According to Eq. 15, a 100-fold decrease in the concentration of the high-affinity form of EGTA would decrease k_app by ∼100-fold. This estimate is in line with the results of the stopped-flow experiments (40–42). Therefore, the observed slow Ca²⁺ binding by EGTA can be attributed to a low content of its high-affinity form. Ca²⁺ binding certainly shifts the equilibrium between the two forms of EGTA, but the high-affinity form is replenished slowly and, in the case of the fast local [Ca²⁺] transients, the reaction can be neglected. Parvalbumin binds Ca²⁺ slowly, because its binding sites are normally occupied by Mg²⁺ and, in this sense, parvalbumin mimics “slow” Ca²⁺ buffers (43).

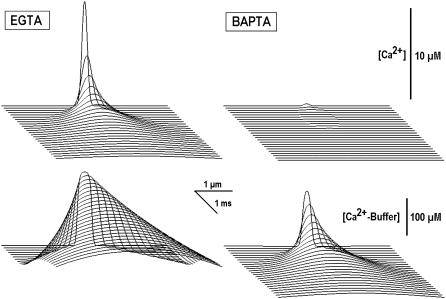
Fig. 7 shows the [Ca²⁺]_i transients that were calculated in the presence of intrinsic buffer (0.1 mM) and BAPTA and EGTA (either at 10 mM). For simplicity, we set K_d = 1 μM and the diffusion coefficients (20 μm²/s) the same for all buffers (see Table 1 in Appendix III). In the calculations, we considered only the high-affinity form of EGTA (0.1 mM) and used the effective concentrations of mobile buffers of 10.1 mM (BAPTA) and 0.2 mM (EGTA). Fig. 7 shows that the [Ca²⁺]_i peak in BAPTA had much smaller amplitude and it was more localized. This can explain why BAPTA (but not EGTA) inhibits such physiological responses, which require big [Ca²⁺] increases in nanodomains.

FIGURE 7.

Local [Ca²⁺] transients in the presence of “slow” (EGTA) and “fast” (BAPTA) buffers. Spatiotemporal profiles of free and bound Ca²⁺ were obtained by using Eq. 8 for the fast diffusion. The concentration of intrinsic buffer was 0.1 mM, K_d = 1 μM, and the diffusion coefficient was 20 μm²/s. Same K_d and d values were assumed for EGTA and BAPTA (both present at 10 mM). In the case of EGTA we considered the Ca²⁺ binding only to its high-affinity form (1% of total at physiological pH or 0.1 mM; see “Rapid and slow Ca²⁺ buffers”).

Another striking feature in Fig. 7 is that the changes in bound Ca²⁺ are much wider than those of free Ca²⁺. This seemingly presents a paradox as it contradicts the expected slow diffusion of the buffer. The following explanation can be suggested: the buffer readily captures Ca²⁺ at the front of its gradient and this reaction is transmitted faster than the spread of free Ca²⁺. Such effects can be important in the functioning of the cytoplasmic Ca²⁺ sensors. For example, calmodulin is both a Ca²⁺ buffer (see Table 1 in Appendix III) and the Ca²⁺ trigger, which activates various signaling pathways. Capturing Ca²⁺, these Ca²⁺ buffers/sensors would deliver Ca²⁺ messages faster than Ca²⁺ itself, which is in line with recent theoretical suggestions (17) and experimental findings (19).

DISCUSSION

Many theoretical studies in the last two decades witness an avalanche of theoretical and experimental investigations that describe various aspects of Ca²⁺ signaling in the cytoplasm (1,4–6,12–18,24,25,27). Due to the development of new methods of Ca²⁺ imaging and the refinement of old ones, the experimentalists are now able to monitor the [Ca²⁺] transients with high spatial (but not yet temporal) resolution (8,10,11). The theoretical predictions, which have been developed to describe the localization and propagation of the [Ca²⁺] transients, now need to be combined with new results. Openings of single channels in the plasma membrane or internal stores generate big local [Ca²⁺] transients, which can easily saturate both endogeneous Ca²⁺ buffers and Ca²⁺-sensitive probes. Therefore previous analytical approaches, based on the linearized and/or steady-state approximations, may not be accurate in this case, because their applicability is restricted to the transients of small amplitude (Appendix I). For the data interpretation an integration of the reaction-diffusion equations is required. Such numerical experiments need corresponding software, careful adjustment of model parameters, and perhaps lengthy analysis.

In this study we aimed to go beyond the linear and time-independent considerations and developed a simple analytical approach that works well within two decades of the Ca²⁺ concentrations. We obtained the solution for an instantaneous point source. It is important that it represents the Green function for the diffusion equation (33), therefore the derived equation also can be used to obtain solutions for other boundary conditions. We can reproduce exact results obtained by numerical integration of reaction-diffusion equations up to 50 μM (Fig. 2). For comparison, the linearized approximation can describe free [Ca²⁺]_i levels only up to ∼0.4K_d, which corresponds to 0.12 μM for a typical cytoplasmic buffer. The results of recent simulations indicate that local [Ca²⁺]_i increases may reach 100 μM (44,45). In this range, our approach underestimates the transients by ∼20%. However, it can be useful also in these cases, because such deviations would produce smaller variations in the activation of Ca²⁺-binding proteins, which translate the [Ca²⁺]_i changes into specific intracellular responses. Consider a protein with a single binding site with K_d = 100 μM. [Ca²⁺]_i variations around this level by ±20% (Fig. 2 b) change the site occupancy by ±5%. Calmodulin has four binding sites that cooperatively bind Ca²⁺, which is described by the Hill isotherm. In this case a 20%-error in [Ca²⁺]_i would change the degree of calmodulin activation by 8%. Perhaps such deviations can be tolerated in the analysis of the experimental data.

The equations derived in Appendix II are applicable in the case of multiple Ca²⁺ buffers with different characteristics. In the main text, we first considered the simplest case of one mobile buffer and then extended the approach to the case of one mobile and one immobile buffer. These two cases may provide a sufficiently good approximation of the experimental data. The reasoning is that the reaction-diffusion system for Ca²⁺ is likely “overdetermined” and it may well be that similar spatiotemporal patterns can be obtained for different Ca²⁺ buffering systems. This also means that such characteristics of cytoplasmic buffers as their content, dissociation constant, and diffusion coefficient are difficult to rigorously determine experimentally. Some literature data illustrate this notion. For example, the intrinsic Ca²⁺ buffers in dendrites of the hippocampal neurons are assumed to be either fixed (46) or mobile (29). In the modeling studies, various buffer cocktails with different characteristics have been used (5,9,19,28,29; Appendix III). The data indicate that at least in the heart cells and neurons it is possible to consider the cytoplasm as a mixture of one mobile buffer with K_d ≈ 0.4 μM and one immobile buffer with K_d ≈ 2 μM, which are taken in different proportions.

This study delivered some unexpected properties of Ca²⁺ signals as related to the presence of buffers. The main finding is that in the case of buffer saturation, the large-amplitude [Ca²⁺]_i transients can spread out faster than it is predicted for the “normal” diffusion (Fig. 1). This feature can be important for the propagating waves of Ca²⁺ in the cytoplasm. However, this issue needs further analysis because many parameters such as the geometry of cytoplasmic compartment, the kinetics, the distribution and type of release channels, the effects of Ca²⁺ influx, and clearance from cytoplasm can influence the wave velocity (11,13–17,20–25). Another interesting aspect concerns the effects of the immobile buffer on the form of the [Ca²⁺]_i transients (Figs. 3 and 5). When its content increases, the amplitude of the transients increases and their width decreases. Because immobile buffers cannot diffuse, they probably saturate first. Therefore their bigger K_d values may have “physiological” sense. Decreased buffer capacity is compensated by the bigger content of immobile buffers (see Appendix III). Combination of two effects would make Ca²⁺ buffering by fixed buffers comparable to that of the mobile buffers.

We investigated the spatiotemporal patterns of local Ca²⁺ transients, which are formed around single channels, the Ca²⁺ nanodomains (1). For consideration of global events in Ca²⁺ signaling, the model should be modified by first including the Ca²⁺ pumps. They would little affect the fast local [Ca²⁺]_i transients, but the pumps will gain importance in slow events in Ca²⁺ homeostasis (47). One possibility will be to split the reaction-diffusion problem into the fast and slow systems and treat the latter as perturbation (48). However, this will produce a nonlinear diffusion with a “source” term (49), which needs further analysis.

We would like to conclude that despite the fact that the explicit solutions derived in this study are approximate and describe only the actions of buffers, the derived formula cover about two decades of Ca²⁺ concentrations. Therefore we believe that the method (with discussed restrictions) can be helpful in interpreting physiologically relevant [Ca²⁺]_i transients and in revealing their possible functional role.

APPENDIX I: THE CASE OF MULTIPLE BUFFERS—A “NORMAL” DIFFUSION

Rewriting the rapid buffer approximation (Eq. 3) as CB_o/(C + K_d) = B_o[1 − 1/(1 + C/K_d)], we present Eq. 2 as

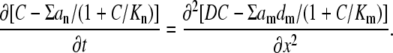(A1)

As in the main text, all concentration-dependent terms (C and K_d) are here normalized to B_o, the total buffer concentration. Each buffer is characterized by its normalized dissociation constant K_n, the diffusion coefficient d_n and its mol fraction a_n = B_on/B_o. Note also that the sum in the right-hand side (index m) runs only over mobile buffers. The left-hand and the right-hand sides are derivatives and therefore we took a liberty to neglect or to add appropriate constants that helped us to maintain a compact structure of equations.

Expanding each buffer term into the Taylor series as

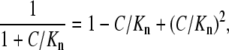(A2)

we obtain the equation of nonlinear diffusion

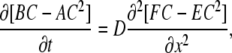(A3)

where A = Σ(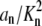), B = 1 + Σ(a_n/K_n), E = Σ(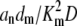), and F = 1 + Σ(a_md_m/K_mD). Changing the time and concentration variables to respectively T = DE/A and u = C − √(B/4A) + √(F/4E), we get the diffusion-advection equation

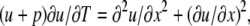which has polynomial solutions (34). Neglecting quadratic terms (note that this reasonably approximates Eq. A2 only when C < 0.4 K_n), we linearize Eq. A1 to

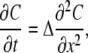(A4)

where the effective diffusion coefficient is

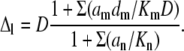(A5)

For one mobile buffer with d = 20 μm²/s, K_d = 0.3 μM, and B_o = 0.3 mM (the nondimensional K = 0.001), we obtain Δ ≈ d, indicating that Ca²⁺ predominantly diffuses in a bound form.

APPENDIX II: THE CASE OF MULTIPLE BUFFERS—A LOGARITHMIC APPROXIMATION

Applying the transformation used in the main text to derive Eq. 5 from Eq. 4, we can similarly simplify the general Eq. A1. For the reference, we choose the mobile buffer with the lowest dissociation constant (k). Dividing free [Ca²⁺] and dissociation constants of other buffers by k, we decompose each term in the derivative in the left-hand side of Eq. A1 and approximate it with the logarithm as

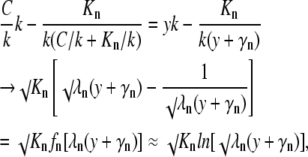where y = 1 + C/k, γ_n = K_n/k − 1 and λ_n = k/√K_n. Because the minimal k is chosen, all λ_n values are always smaller than √k, which determines the scaling terms a and b in Eq. 5. Thus, in comparison with the case of the single mobile buffer considered in “Mobile and immobile Ca²⁺ buffers with the same K_d”, the approximation of functions f_n(y) with logarithm (the last transformation step) is applicable in a wider range of Ca²⁺ concentrations. For the terms in the right-hand side we obtain a similar approximate expression √(K_mDd_m)ln[√η_m(y + γ_m)] where η_m = k√[D/(K_md_m)]. After dropping the constant terms λ_n and η_m in logarithms, we present Eq. A1 as

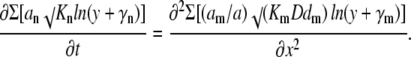(B1)

Note that the right-hand side contains only mobile buffers and therefore we normalized each coefficient a_m to their sum a = Σa_m < 1.

Because the arguments of logarithms contain different offset terms, Eq. B1 is not easier to solve than the original Eq. A1, but it can be done after approximating these terms with quadratic polynomials as ln(y + γ) = A lny² + B lny + C. Fig. 8 shows that the approximation works well for more than two decades of the normalized Ca²⁺ concentrations (from 0 to 200k_d or, in terms of Ca²⁺ concentration, up to 60 μM for k_d = 0.3 μM). In the fitting functions, we used the same coefficient A = 0.07 and different B coefficients (coefficients C do not play any role because they vanish after differentiation). Using these approximations, we present Eq. B1 as

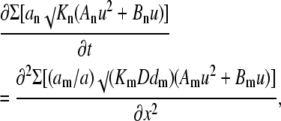(B2)

where u = lny. Collecting the coefficients at the same power of u, we obtain quadratically nonlinear diffusion equation

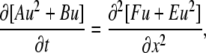(B3)

with the coefficients A = Σa_nA_n√K_n; B = Σa_nB_n√K_n; E = Σ(a_m/a)A_m√(K_mDd_m); F = Σ(a_m/a)B_m√(K_mDd_m). The equation has a form of Eq. A3 and it has polynomial solutions (34). In the main text, we present explicit solutions in the case of i), a single mobile buffer and ii), a mixture of mobile and immobile buffers. Both cases correspond to the equation of fast diffusion

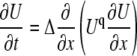with q = −1 (i) and q = −1/2 (ii), respectively.

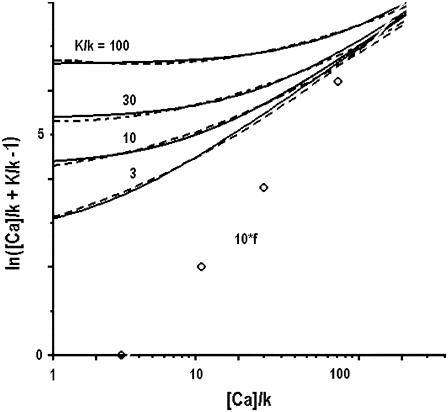
FIGURE 8.

Approximation of logarithm ln(y + γ) in Eq. B1 by quadratic polynomial A lny² + B lny + C. Solid lines show the original functions and the dotted lines indicate their approximations. In all fits, the coefficient A = 0.07 and the coefficients B were obtained from the empirical function f = 1.8 ln(K_n/k) − 4.2 (multiplied in plot by 10 to fit the scale).

For u < 1, we can neglect quadratic terms in Eq. B3 that gives a linear PDE with the effective diffusion coefficient

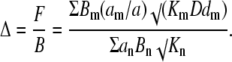(B4)

This expression clearly differs from that given by Eq. A5 for the “normal” diffusion.

APPENDIX III: CYTOPLASMIC CA²⁺ BUFFERING SYSTEMS

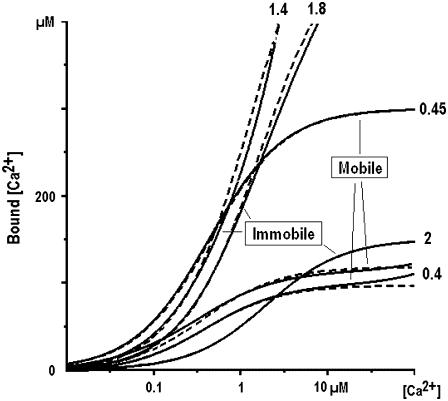
Table 1 lists representative Ca²⁺ buffering cocktails, which were used in literature to model Ca²⁺ homeostasis in different cell types. Ca²⁺-sensing probes were also included because they act as Ca²⁺ buffers. Fig. 9 shows that Ca²⁺ binding capacity in the mixture of mobile or immobile buffers is well reproduced by using only one buffer. For such mobile buffer the effective dissociation constant is about 0.4 μM and the concentration ranges from 0.1 to 0.3 mM. For the immobile buffer K_eff ≈ 2 μM and B_o is in the range from 0.2 to 0.6 mM.

FIGURE 9.

Binding capacity of cytoplasmic Ca²⁺ buffers and its approximation. The graphs are based on the representative literature data listed in Table 1. The amount of bound Ca²⁺ in the mixtures of mobile and immobile Ca²⁺ buffers is shown by continuous lines as indicated. The traces are approximated by considering only one buffer with the effective dissociation constants indicated near each curve.