Allelic association under map error and recombinational heterogeneity: A tale of two sites

Abstract

Recombination acts on the genetic map, not on the physical map. On the other hand, the physical map is usually more accurate. Choice of the genetic or physical map for positional cloning by allelic association depends on the goodness of fit of data to each map under an established model. Huntington disease illustrates the usual case in which the greater reliability of physical data outweighs recombinational heterogeneity. Hemochromatosis represents an exceptional case in which unrecognized recombinational heterogeneity retarded positional cloning for a decade. The Malecot model performs well for major genes, but no approach assuming either equilibrium or disequilibrium has been validated for oligogenes contributing to common disease. In this case of greatest interest, the power of allelic association relative to linkage is less clear than for major genes.

Linkage is measured by sex-specific recombination between two loci, without regard to genotype. Allelic association is measured by dependence of allelic frequencies at two loci, without regard to sex-specific recombination. We are interested in the case in which one locus is a polymorphic marker and the other locus has alleles that affect susceptibility to a particular disease but have not yet been characterized. In a dense marker map, the distance between the disease gene and the closest marker can approach zero. Then under simple assumptions, maximal association is expected to occur at the same location as minimal recombination. These two independent sources of information may be efficiently combined to identify a small candidate region for the disease gene preparatory to positional cloning and sequencing (1, 2). The relative efficiency of linkage and allelic association depends on map accuracy and density, sample composition, evolutionary history of disease genes, and their frequencies and effects. Map error and recombinational heterogeneity pose problems for allelic association that are addressed here.

METHODS

We suppose that haplotypes for the disease gene and marker i (i = 1, .., m) can be merged into a 2 × 2 table such that Q is both the current frequency of disease alleles and the frequency of haplotypes bearing a disease allele and a particular set of marker alleles in a hypothetical (usually much smaller) founder population that lacked haplotypes bearing a disease allele and the other marker alleles (2). Over time, the association caused by founder haplotypes is reduced by unknown rates of recombination, marker mutation, and immigration of other haplotypes, but we assume that the allele frequencies remain constant through mutation from the normal allele and immigration of susceptible haplotypes. Because only recombination is systematically related to distance d_i between loci, the expected probability of association that has not been disrupted by mutation or migration is ρ_i = (1 − L) M exp (−ɛd_i) + L, where L is the probability of spurious association through population stratification or the constraint ρ_i > 0 in the algorithm used to merge alleles, M is the proportion of disease alleles transmitted from founders (and so is 1 if disease alleles are monophyletic), and ɛ is proportional to the number of generations during which the haplotypes have been approaching equilibrium. This Malecot equation is the same as for kinship in linear space (3, 4). A simpler approximation is the Luria–Delbruck equation describing replicate bacterial cultures under recurrent mutation, which may be applied less realistically to recombination in a unique human population when the size and date of the founder population are known, all loci are diallelic, and the reproductive rate is constant (5).

However formulated, the object of this analysis is to estimate S_D, the location of the disease gene in the marker map, which is introduced by substituting d_i = δ_i (S_i − S_D), where S_i is the location of marker i and δ_i = 1 if S_i ≥ S_D or −1 else. This unconventional use of δ assures the correct sign for the derivative with respect to S_D. The Malecot model with four parameters (L, M, ɛ, S_D) is fitted from composite likelihood that is a function of the estimated ρ_i and its amount of information K_i, which depends on sampling error and accumulated stochastic variation over an evolutionary history with many unknown parameters, including duration, population size in each generation, migration, and allele-specific mutation rates. Estimation of these multiple parameters from allelic association is impractical when the location of the disease gene is unknown (6). Allelic association usually gives multiple local maxima, with a global maximum becoming dominant asymptotically. Maximum likelihood is therefore only a rough guide in small samples, for which exact theory is not feasible. Accordingly, if deviations from the model with smallest residual χ² with n degrees of freedom are formally significant, γ = n/χ² may be taken as a scaling factor for information and tests of subhypotheses of the Malecot model, which is equivalent to multiplying the standard errors attributed to sampling by 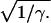The lod Z₁ testing the null hypothesis that ρ_i = 0 for all i is derived from the difference between total χ²_m and residual χ²_n for the accepted model (2).

Map Error in Huntington Disease (HD).

Although recombination acts on the genetic map, the physical map may be nearly proportional, z = w/c, where w is the physical length of the candidate region in megabases (Mb) and c is the length in centimorgans (cM). A rough rule of thumb, often misleading, equates z to 1 (7). Whether or not the rule of thumb holds, the more general condition of proportionality is sufficient to favor the physical map whenever (as is usually the case) it is more accurate than the genetic map. Operationally, the map is preferred that minimizes deviations from the general model.

The locus for HD provides an example. It was mapped to 4p16.3 by linkage with D4S10 (8), but cloning was not achieved until haplotype analysis indicated a 500-kb segment between D4S182 and D4S180 as the most likely site of the disease gene (9). Allelic association played no significant role in localizing HD within that segment because the linkage map was dominated by restriction fragment length polymorphisms with modest heterozygosity and at low resolution, and large populations harbor multiple HD mutations (10). Integration of genetic and physical maps overcomes the first problem (11), and the M parameter of the Malecot model accommodates polyphyletic origin.

We have tried to capture all published data on allelic association with HD (9, 12–16). Results on the same marker with different restriction enzymes have been pooled by weighting each estimate ρ̂ with its information. In proximity to the HD gene, the values for association (Table 1) have a peak at D4S127. A secondary peak at D4S81 has low information. The hypothesis of no association can be rejected (χ²₁₉ = 246.84), and fit of the Malecot model to the physical map is good (χ²₁₅ = 17.71). The genetic map (Table 2) fits less well with χ²₁₅ = 27.38. The model with M = 1, testing monophyletic origin, is rejected by χ²₁ = 24.03 for the physical map. The best model is with L = 0, signifying no spurious association. The estimate of disease location on the physical map (Table 3) lies within its assigned interval (S_D = 3.686), and the information on location (K_D = 111) is higher than with the genetic map which places HD outside its assigned interval. The estimates of M are well under 1, reflecting polyphyletic origin of HD (10). The lod Z₁ for allelic association is enormously significant.

Table 1.

The HD region

Locus	Information, K	Association, ρ	Location		Goodness of fit, χ21		Refs.
			Physical, Mb	Genetic, cM	ρ = 0	ρ = ρ̂
D4S111	9781	0.012	1.100	1.24	19.90	0.52	9, 12–14
D4S115	99	0.224	1.488	1.33	7.36	3.79	9, 12
D4S96	173	0.075	1.500	1.33	2.31	0.37	9, 12, 13, 15
D4S168	46	0.057	2.060	2.56	0.15	0.00	9
D4S113	236	0.003	2.210	2.90	0.00	0.79	9
D4S186	254	0.024	2.281	3.05	0.14	0.45	9
D4S98	1534	0.101	2.360	3.22	19.03	1.37	9, 12, 13
D4S114	132	0.012	2.370	3.24	0.02	0.47	9
D4S43	369	0.140	2.760	3.71	18.28	0.39	9, 12–14, 16
D4S183	77	0.063	2.946	3.79	0.31	0.35	9
D4S182	57	0.237	3.400	3.98	3.21	0.04	9
D4S95	805	0.210	3.524	4.03	85.19	0.62	9, 12–15
D4S127	79	0.445	3.583	4.07	16.85	2.88	9, 16
HD	—	—	3.635–3.804	4.09–4.38	—	—	—
D4S180	206	0.183	3.864	4.54	7.57	0.55	9
D4S125	231	0.173	4.043	5.04	6.92	0.11	9, 14
D4S126	75	0.192	4.308	6.61	2.77	0.14	9
D4S81	14	0.568	4.351	7.57	4.46	2.52	12
D4S10	688	0.162	4.626	7.73	40.09	2.12	9, 12–14, 16
D4S62	12500	0.031	5.679	9.43	12.29	0.22	13
				Total χ2	246.84	17.71

Goodness of fit to the Malecot model (ρ = ρ̂) from the physical map. 

Table 2.

χ² Tests of goodness of fit

Hypothesis	HD			HFE
	df	Physical map	Genetic map	df	Physical map	Genetic map
M = 1, L = 0	17	74.19	72.69	30	101.06	46.15
M = 1	16	41.74	41.80	29	88.68	43.20
L = 0	16	17.71	27.38	29	75.89	28.00
S = S0	16	17.84	33.49	29	98.58	28.13
General	15	17.71	27.38	28	75.89	28.00

S₀, midpoint of disease locus in location database ldb; General, Malecot model with S, ɛ, L, and M estimated. 

Table 3.

Estimates of parameters under the accepted model (L = 0) ± standard error

Estimate	HD		HFE
	Physical map	Genetic map	Physical map	Genetic map
ɛ	1.039  ±  0.124	0.683  ±  0.084	0.284  ±  0.042	1.041  ±  0.130
M	0.282  ±  0.037	0.473  ±  0.104	0.655  ±  0.053	0.703  ±  0.046
SD	3.686  ±  0.095	5.726  ±  0.169	32.379  ±  0.170	53.605  ±  0.045
KD	111	35	34	497
S0	[3.635–3.804]	[4.09–4.38]	30.064	53.570
Z1	47	45	296	307

S_D, location; K_D, information about location; S₀, locus interval on map; Z₁, lod for association. 

For monophyletic genes the estimate of ɛ approximates the number of generations since the founding mutation as 100 ɛ for the genetic map and 100 zɛ for the physical map (2). Table 1 gives z = 0.56, and therefore 68 and 58 generations, respectively. This is close to the reciprocal of the selection coefficient as the expected duration of an HD mutation, despite polyphyletic mutations that have arisen at different times.

Recombinational Heterogeneity in Hemochromatosis (HFE).

When the genetic and physical maps are not proportional over the candidate region, an accurate genetic map should be more reliable than the physical map. This is illustrated by hereditary HFE, one of the commonest recessive diseases in man (17). Its linkage to the HLA complex in 6p21.3 was demonstrated 20 years ago (18). HFE is 4.6 Mb distal to HLA-A but the genetic distance is only 0.75 cM, and for a generation, close linkage was misinterpreted as a small physical distance. Cloning was not achieved until an 8-Mb YAC contig led to dense markers across the region, within which allelic association identified a 600-kb target that was narrowed by haplotype analysis to the interval between D6S2241 and D6S2238 (19). These data have not been published, but other sources give more precise localization when the Malecot model is used with the genetic map (11).

Assuming a gene frequency of 0.05 (17), we estimated association for each source (20–28) and pooled them as above (Table 4). χ² is minimal for the genetic map (61.61 with 28 df), and so we scaled K by γ = 28/61.61 = 0.454. The largest contributions to χ² show no pattern and presumably represent errors in the map or aberrant samples. The physical map is in every respect inferior: larger χ² (Table 2), less information, and the estimated location has an error of nearly 2 Mb, whereas the genetic map gives an accurate location (Table 3). Support for the candidate region from allelic association, measured by lod Z₁ = 307 (Table 3), is overwhelmingly significant and much greater than the evidence from linkage. The parameter M is significantly <1, indicating that alleles for hemochromatosis are polyphyletic. The commonest mutation Cys282Tyr accounts for only approximately three-fourths of all alleles. Other loci cannot be a frequent cause of hereditary hemochromatosis, because the recombination rate is consistent with a single HFE locus, but genetic modifiers may well account for part of the residual heritability (17). The value of ɛ corresponds to 104 generations, or ≈2,080 years since the mutation time traced to a single individual. This mutation coalescence time is included in the 90% confidence interval of 750–3,400 years estimated by a different method (21).

Table 4.

The HFE regions

Locus	Information, K	Association, ρ	Location		Goodness of fit, χ21		Refs.
			Physical Mb	Genetic cM	ρ = 0	ρ = ρ̂
D6S276	5	0.705	28.152	51.59	5.34	1.87	20
D6S1554	130	0.064	28.244	51.68	1.15	0.13	20
D6S1545	504	0.043	28.619	52.10	4.06	5.38	20, 21
D6S1281	48	0.215	28.834	52.32	4.92	0.05	20
GATA	14	0.587	29.312	52.84	10.47	1.01	21
D6S1016	13	0.285	29.604	53.16	2.37	0.33	20
D6S1621	113	0.585	29.708	53.26	85.41	1.00	21
D6S2241	20	0.724	29.856	53.39	22.81	0.52	21
D6S2239	54	0.844	30.054	53.56	84.38	1.62	21
HFE	—	—	30.064	53.57	—	—	—
D6S2238	72	0.752	30.175	53.57	89.77	0.40	21
D6S2231	112	0.559	30.420	53.58	81.25	1.80	21
D6S1558	39	0.451	31.063	53.68	17.55	1.55	20, 21
D6S1260	128	0.608	31.212	53.75	106.85	0.00	20–23
D6S464	130	0.505	31.805	53.86	76.12	0.15	20–24
D6S1002	6	0.851	31.855	53.90	9.80	0.69	24
D6S105	390	0.500	31.855	53.90	218.98	0.11	20, 22, 23, 25, 26
D6S1001	23	0.626	32.152	53.90	19.60	0.27	22
D6S306	110	0.531	32.300	54.01	68.40	0.54	20–23
D6S258	67	0.491	33.929	54.03	35.83	0.10	22, 23
HLA-F	307	0.340	34.279	54.20	79.68	0.45	21–23
HLA-G	33	0.491	34.394	54.20	17.84	0.43	21
D6S128	89	0.429	34.500	54.20	35.98	0.23	26
D6S265	431	0.358	34.622	54.20	123.17	0.18	20–23
HLA-A	664	0.329	34.671	54.32	163.45	0.02	21, 23, 24, 26, 27
Y158	114	0.407	34.819	54.62	41.45	3.00	21
i82	51	0.486	34.836	54.66	26.71	3.25	26, 28
Y129	12	0.367	34.879	54.74	3.72	0.29	21
i97	10	0.185	34.903	54.79	0.73	0.00	28
HLA-E	16	0.265	35.152	55.30	2.45	0.33	21
Y104	57	0.271	35.300	55.60	9.24	1.92	21
P5	49	0.096	35.383	55.77	0.99	0.02	28
				Total χ2	1454.36	28.00

Goodness of fit to the Malecot model (ρ = ρ̂) from the genetic map. 

DISCUSSION

HD illustrates the usual case for allelic association, with little recombinational heterogeneity over the candidate region and the physical map more accurate than the genetic map. The ratio of physical to genetic distance is estimated to be 0.87 distally and 0.38 proximally (Table 1). The difference reflects both recombinational heterogeneity and errors in the physical and genetic maps, especially the latter because markers were restriction length polymorphisms with relatively low heterozygosity and poorly represented in recent maps. The physical map is preferred because of its smaller χ², which leads to more information and more precise localization. Evidently the greater reliability of the physical map outweighs any recombinational heterogeneity.

HFE represents the less common case in which recombinational heterogeneity is so great that the physical map is seriously misleading, reflecting its larger residual χ². The ratio of physical to genetic distance is 0.97 distally and 6.14 proximally (Table 4). The power of allelic association was limited by scarcity of markers until microsatellites were introduced and subsequently by failure to recognize that 1 cM corresponds to several Mb in the region telomeric to HLA-A (29). Finally HFE was shown to lie more distally than earlier researchers had assumed, but the preferred marker D6S105 was still nearly 2 Mb from HFE (25). Allowance for nonuniform recombination would have saved a decade of fruitless search near HLA-A, 4.6 Mb from HFE.

The sine qua non for effective use of linkage or allelic association is an accurate genetic map. At the high resolution required for allelic association, accuracy in the genetic map depends on integration with the physical map, assuming proportionality over distances that ideally would be <1 Mb. The expense in positional cloning of an excessively large and perhaps misleading candidate region exceeds the cost of a reliable integrated map, which has not been attempted at the international level devoted to the mouse and Drosophila, and even the curatorial activity of the Genome database has been abandoned (30, 31). Retrieval of map information is made difficult by several factors including lack of stable symbols for loci. In the face of these obstacles, the location database (11) is a modest and far from complete effort toward map integration, which is indispensable for mapping by allelic association.

Interest in allelic association has passed through three stages. The first was a theoretical treatment of diallelic loci on the assumption of equilibrium between drift and recombination under selection (32). Then real multiallelic loci known to be closely linked were mapped by pairwise kinship under the assumption that recombination dominates selection and mutation, without assuming equilibrium with drift (33). Finally this approach was adapted to mapping of disease loci within a candidate region, stimulated by success in Finland with Luria–Delbruck theory (5), which led to more general methods (7, 2). Xiong and Guo (6) introduced mutation parameters that are generally unknown. Because there is one parameter for each locus, this approach requires replicate samples or a specified location for the disease locus. The more parsimonious Malecot model does not require these conditions and gives simpler models as special cases. It differs from other methods in providing an information weight based on the goodness of fit, allowing data to be combined over studies and with evidence from multipoint linkage.

Experience with the Malecot model has been limited to major genes (Table 5). CAPN3 represents short history in small populations, with absence of one haplotype giving complete association over several loci. The correlation r is less sensitive to a missing class although it makes no allowance for the fact that the frequency of cases is greater than the disease frequency. By using it as the measure of association, localization is much better than by other methods for allelic association (34, 35). All the disease loci except HFE favor the physical map. The accuracy of the genetic map, on which recombination takes place, is the limiting factor in positional cloning unless markers are so close in the neighborhood of the disease locus that the genetic and physical maps are locally proportional.

Table 5.

Mapping errors for the Malecot model (kb)

Disease	Locus	Minimal error	Mean error	Standard error	Refs.
Cystic fibrosis	CFTR	44	44	171	2
Limb-girdle muscular dystrophy 2A	CAPN3	3	23	64	34
Huntington disease	HD	0	33	103	(Table 1)
Hemochromatosis	HFE	35	35	45	(Table 4)

Minimal error, from point estimate to the closer of midpoint or nearest base of locus; mean error, from point estimate to midpoint of locus; Hemochromatosis error, assuming Mb/cM = 1. 

Attempts to identify human genes for common disease (oligogenes) through linkage and mouse homology have been disappointing, and so it is natural to adopt allelic association. Experience with major disease genes is reassuring because it provides greater resolution than linkage and supports a disequilibrium model in which association declines exponentially with recombination and time, with the exponential parameter ɛ corresponding to 100 generations or less. This contrasts with an equilibrium dependent on recombination and population size. However, there is insufficient reason to expect oligogenes to have the short duration characteristic of major genes. If selection on oligogenes is sufficiently weak, and their duration correspondingly long, their allelic association with markers will be less than the upper bound for equilibrium M/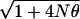, where N is the effective number of founders (36). This bound is much less than for major genes. Even if N were as small as 100, there is presently no evidence that allelic association is more powerful than linkage to localize an oligogene, whether or not isolated populations with small numbers of founders are preferable for studies in allelic association (37). Confronted with uncertainty, we should not accept allelic association as a panacea merely because other approaches have been discouraging, nor should we suppose that in the absence of empirical information either mathematics or computer simulation can credibly represent allelic association for oligogenes in human populations.

ABBREVIATIONS

HD

Huntington disease

HFE

hemochromatosis

df

degrees of freedom

HLA

human leukocyte antigen