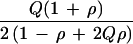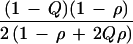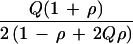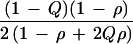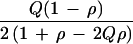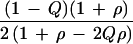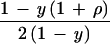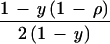Tests and estimates of allelic association in complex inheritance

Abstract

Family-based procedures such as the transmission disequilibrium test (TDT) were motivated by concern that sample-based methods to map disease genes by allelic association are not robust to population stratification, migration, and admixture. Other factors to consider in designing a study of allelic association are specification of gene action in a weakly parametric model, efficiency, diagnostic reliability for hypernormal individuals, interest in linkage and imprinting, and sibship composition. Family-based samples lend themselves to the TDT despite its inefficiency compared with cases and unrelated normal controls. The TDT has an efficiency of 1/2 for parent-offspring pairs and 2/3 for father-mother-child trios. Against cases and hypernormal controls, the efficiency is only 1/6 on the null hypothesis. Although dependent on marker gene frequency and other factors, efficiency for hypernormal controls is always greater than for random controls. Efficiency of the TDT is increased in multiplex families and by inclusion of normal sibs, approaching a case-control design with normal but not hypernormal controls. Isolated cases favor unrelated controls, and only in exceptional populations would avoidance of stratification justify a family-based design to map disease genes by allelic association.

Linkage tests for major loci in human pedigrees were developed by a handful of researchers between 1931 and 1955 (1). In contrast, tests of linkage and allelic association for oligogenes contributing to disease susceptibility have occupied hundreds of workers since 1935 (2), without reaching a consensus. One school favors logarithms of odds (lods) different from the strongly parametric tests for major loci. Lods for oligogenes are weakly parametric, usually with a single parameter that subsumes gene action, frequency, and linkage phase. Recombination is not explicit for single markers, but can be resolved with multiple markers by constraint to a linear genetic map (3). Some methods that do not use lods are strictly nonparametric, and therefore inefficient against a specified alternative to the null hypothesis (4).

Strongly parametric tests distinguish the recombination frequency that applies to all alleles at a pair of loci from allele-specific coupling frequencies for allelic association, which is usually dominated by recombination over many generations. When chance, mutation, and migration are negligible in the sense of being uniform over loci, the greatest allelic association is expected to occur at the same point in the genetic map as the disease locus mappable by linkage, and so the evidence may be combined (5). Then a test for allelic association is an indirect test for linkage, with which it shares closer dependence on the genetic map in centiMorgans (cM) than on the physical map in kilobases (kb). Failure to make that distinction leads to serious error in regions of nonuniform recombination (6). On the other hand, there can be significant allelic association between unlinked loci following recent and extreme population admixture. In short, allelic association and linkage are different phenomena with different parameters that are loosely related and may be confounded in family-based studies (7). For example, fully parametric linkage tests usually assume that coupling and repulsion are equally likely, which is violated by allelic association, but to so small an extent that it has not been a detectable source of error. There is even less scope for confounding of linkage and allelic association in weakly parametric tests.

The unit of observation for major loci wherever located and for oligogenes in mitochondria, the Y chromosome, or the male X chromosome is a two-locus haplotype defined by disease and marker alleles (5). The unit of observation for autosomal oligogenes is a marker genotype classified by disease phenotype, the genotype at the putative disease locus not being inferred. Based on an early success when compared with linkage but not with sample-based tests of association, one of the most popular methods to localize oligogenes is the transmission disequilibrium test (TDT) that “considers parents who are heterozygous for an allele associated with disease and evaluates the frequency with which the allele or its alternate is transmitted to affected offspring” (8). By restriction to heterozygous parents, it differs from other nonparametric tests for association between specific alleles of a polymorphic marker and a disease locus. The parameters of that locus, genotypes of sampled individuals, linkage phase, and recombination frequency are not specified, and the test is not limited to families informative for recombination. Nevertheless, by considering only heterozygous parents, the TDT is specific for association between linked loci. However, it shares the low power of all tests for allelic association unless the parental haplotypes are far from equilibrium. When extended to be weakly parametric, the TDT can estimate association but not linkage except with multiple markers (5). The TDT is often preferred to a more efficient alternative because of its robustness to population stratification, migration, and admixture. This choice has not been based on the structure of real populations or on efficiency, which we examine here under a model of independent parental effects.

The parental contributions are independent if and only if risks are multiplicative; i.e., if the affection probabilities for a marker M with gene frequency Q are in the ratio (1 − ρ)²:(1 − ρ) (1 + ρ):(1 + ρ)² for M*M*, MM*, and MM respectively, where M* is any allele other than M and ρ is the allelic association in the interval ± 1. This ratio may also be expressed as 1:e^ψ:e^2ψ, where ψ = ln[(1 + ρ)/(1 − ρ)]. Correspondence with the β-model for linkage is obvious, the difference being that risks for allelic association are conditional on marker genotype, whereas risks for linkage are conditional on the number of alleles for disease susceptibility identical by descent (9). A corollary is that effects of different disease loci are multiplicative, and therefore additive on a logarithmic scale. Dominance and epistasis are familiar complications with major loci, but unlikely to be important enough for genes of small effect to negate Occam’s razor. The parsimonious β-model gives the greatest power with empirical data on oligogenic linkage (3, 10).

Weakly Parametric TDT Tests

Spielman et al. (8) considered families with s affected children. They assumed all members genotyped for the marker and at least one parent heterozygous for a particular marker allele. This sample raises the problem of heterozygous children in two-allele intercrosses, M¹M² × M¹M². These children may be scored if transmission is inferred from haplotypes or (without assigning the parent) from discordant sibs; e.g., an M¹M¹, M¹M² pair implies that one parent transmitted M¹ to the first child and M² to the second, whereas the other parent transmitted M¹ to both. However an M¹M², M¹M² pair remains unclassifiable.

Transmission depends on the allelic association ρ as in Table 1 (5), where ρ is a proxy for the gene frequency and penetrances of a fully parametric test. In the multiplex case the numbers a, b refer to independent transmissions to s affected children, summed over all MM* parents, and a is the number of times allele M is transmitted. The likelihood is L = (1 + ρ)^a (1 − ρ)^b/2^a+b with maximum likelihood (ML) score U = ∂ ln L/∂ρ and information K = −E {∂² ln L/∂ρ²}. Under H₀ we have ρ = 0, U = a − b, K = a + b, and χ²₁ = U²/K. Each transmission contributes one unit of information. Under the alternative hypothesis H₁ the association parameter is a nonzero function of gene action and frequency at the disease locus, linkage to the marker, and gametic disequilibrium if the two loci are linked. The ML estimate of ρ is (a − b)/(a + b) with information (a + b)/(1 − ρ²).

Table 1.

The TDT test for M transmission from MM^* parents to an affected child, where M^* is any allele other than M

	Transmitted allele		Total
	M	M*
Observed number	a	b	a + b
Expected frequency	(1 + ρ)/2	(1 − ρ)/2	1

Father-mother-child trios can be analyzed as a case-control design without selecting heterozygous parents (Table 2). Under H₀ the score is U = a − b − (a + b)(2Q − 1) with Q = (a + c)/4N, or U = (ad − bc)/2N with K = U²/χ² = 4NQ (1 − Q). This result is the same as for the TDT on N trios with 2N parents of whom a proportion 2Q(1 − Q) are heterozygous, but the case-control design is restrictive to random mating, unrelated families, and one affected child per family. Therefore the TDT is the method of choice for family-based samples.

Table 2.

The family-based case-control design: Transmitted alleles (cases) and nontransmitted alleles (controls) from 2N parents with one affected child

	Marker allele		Total
	M	M*
Cases
Observed number	a	b	a + b = 2N
Expected frequency			1/2
Controls
Observed number	c	d	c + d = 2N
Expected frequency	Q/2	(1 − Q)/2	1/2
Observed number	a + c	b + d	4N

The Sample-Based Case-Control Design: Normal Controls

Epidemiologists often compare affected individuals (cases) and normal persons (controls) who resemble the cases with respect to ethnic group and other relevant attributes but are not affected. Because the individuals are typically independent and therefore unrelated, a sample-based case-control study is fundamentally different from the TDT and other family-based designs. This type of study has both advantages and disadvantages.

We consider first the question of efficiency, defined on ρ as the ratio of variances for a case-control study and a TDT sample with the same number of individuals. Expected frequencies are the same as in Table 2, assuming that the gene frequency is the same for nontransmitted alleles and controls. This assumption neglects bias due to selection of normal controls, which cannot be evaluated except under a fully parametric model. For comparison with N trios, we draw 3N individuals, with equal numbers of cases and controls. Now all alleles are counted, and so a + b = c + d = 3N instead of 2N as in Table 2. Therefore this sample-based design gives 3/2 as much information as the TDT case-control design on the same number of individuals, as is intuitively obvious: each fully informative TDT trio is scored for two transmissions and two nontransmissions, whereas three fully informative individuals in a sample-based design give six informative alleles. Otherwise stated, the TDT efficiency is 2/3 for trios. A fully informative parent-child pair gives one transmission and one nontransmission in the TDT, whereas two fully informative individuals in a sample-based case-control study contribute four alleles, and so the TDT efficiency in this comparison is 1/2.

The Sample-Based Case-Control Design: Hypernormal Controls

Whenever feasible epidemiologists take advantage of the fact that all normal individuals are not equivalent, but may have a phenotype that is the antithesis of affection or be heavily exposed to the causes of disease. They may be said to differ in liability, a continuous latent variable that is truncated to specify affection (11). Individuals with highest liability are affected, and individuals with the lowest liability are hypernormal. If there is a phenotype score highly correlated with liability, then observations in the hypernormal tail are informative about alleles for disease resistance. Even in the absence of a phenotype score, it is still possible to capture much of the advantage of discordant samples by one of several selective case-control strategies (Table 3). Extreme discordance (type 1) was proposed for linkage (12) but is more feasible for association, which in the sample-based case-control design is not dependent on uncommon occurrence of hypernormals in relatives of multiplex cases. The second type looks for genes causing early onset and is efficient when early onset is rarely caused by major genes, or the objective is to detect such genes. Type 3 works best for genes of large or moderate effect. Type 4 suggested human leukocyte antigen (HLA) determinants of resistance to venereal disease in prostitutes (13) and has been brilliantly successful is localizing the CCR5 receptor for HIV-1 in long-term partners of seroconverted patients (14). Type 5 is specific for genes promoting longevity. Type 6 is applicable when the covariate is an important predisposing factor, either environmental or phenotypic. For example, intrinsic asthma might be contrasted with atopic controls without asthma. This list is not exhaustive, but it serves to remind us of the power of sample-based case-control designs, which family-based studies cannot achieve except through selection from a much larger sample.

Table 3.

Selective case-control studies

Type	Case	Control
1	Severely affected	Extremely normal
2	Affected, early onset	Normal, elderly
3	Positive family history	Negative family history
4	Affected	Normal, heavy environmental exposure
5	Elderly survivor	Young
6	Affected, favorable covariate	Normal, unfavorable covariate

Table 4 gives the expected frequencies under a multiplicative model in a sample of 3N individuals equally divided between cases and controls drawn from equally probable tails of the liability distribution. For allele M the cases and controls sum to Q if ρ = 0 or Q = 0.5. The ML score under H₀ is U₁ = a − b − (a + b)(2Q − 1) for cases and U₂ = d − c + (c + d)(2Q − 1) for controls, with U₁ = U₂ = (ad − bc)/3N and U²/χ² = 6NQ(1 − Q). Then U = 2U₁ and K = 24NQ(1 − Q), which is 4 times as great as when normal controls are used and 6 times as much as a family-based test with N trios. The TDT design cannot be enhanced in this way because a subsample of parent-hypernormal child pairs contributes no more information than the same number of parent-affected child pairs.

Table 4.

The sample-based case-control design: Alleles from 3N/2 affected cases and 3N/2 hypernormal controls

	Marker allele		Total
	M	M*
Cases
Observed number	a	b	a + b = 3N
Expected frequency			1/2
Controls
Observed number	c	d	c + d = 3N
Expected frequency			1/2
Observed number	a + c	b + d	6N

Estimation of ρ

Information K is based on the error in sampling from the current population and does not include stochastic variation over time due to finite population size. Because this makes K unreliable, evaluation at ρ̂ may be a fastidious refinement, especially if (as is usual) polyphyletic origin and long history depress ρ under complex inheritance. However, we need assurance that the efficiencies calculated under H₀ are not degraded when ρ > 0.

Estimates of ρ and Q for a case-control design are correlated under H₁, since −E{∂² ln L/∂ρ∂Q} ≠ 0. To evade inversion of an information matrix, we consider the logarithm of a ratio of frequencies as a function of ψ = ln[(1 + ρ)/(1 − ρ)], and so ρ = (e^ψ − 1)/(e^ψ + 1) (15). Then K = I (∂ψ/∂ρ)², where I is the information about ψ and ∂ψ/∂ρ = 2/(1 − ρ²). For the TDT design ln[E(a)/E(b)] = ψ. However, there is a nonzero probability for either observed number to be zero, and so the mean and variance of a/b do not exist. Haldane (16) gave an amended estimator with negligible bias, ψ̂ = ln[(a + 0.5)/(b + 0.5)]. The corresponding amount of information is 1/[1/E(a) + 1/E(b)] = E(a) E(b)/(a + b), or very nearly (a + 1) (b + 1)/(a + b + 2). The error of the latter expression is of order (a + b)⁻³. Here we use the predicted information to confirm that K = (a + b)/(1 − ρ²) for Table 1.

Haldane (16) applied his result to the difference between two logarithms of a frequency ratio. Table 2 gives ψ̂ = ln[(a + 0.5)(d + 0.5)/(b + 0.5)(c + 0.5)] with predicted information 1/[1/E(a) + 1/E(b) + 1/E(c) + 1/E(d)], where E(n) may be approximated by n + 1. We obtain K = 4NQ(1 − Q)/(1 − ρ²) (1 − ρ + 2Qρ − 2Qρ² + 2Q²ρ²). Under H₀ this gives K = 4NQ(1 − Q) as above. Samples of affected cases and normal controls replace N by 3N/2. Samples of affected cases and hypernormal controls (Table 4) give information about 2ψ, and therefore K = 24NQ(1 − Q)/(1 − ρ²) (1 − ρ + Qρ − Qρ² + 2Q²ρ²), which under H₀ is 24NQ(1 − Q).

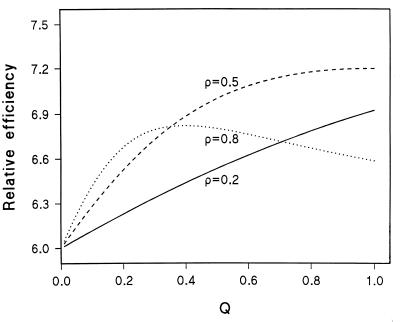
Relative efficiency for ρ > 0 depends on marker gene frequency Q as well as on ρ and the sampling design. The ratio of K for Table 4 and Table 2 gives efficiency of hypernormal controls relative to a family-based design as 6 (1 − ρ + 2Qρ − 2Qρ² + 2Q²ρ²)/(1 − ρ + Qρ − Qρ² + 2Q²ρ²), which has a minimum of 6 under H₀ and a maximum of 7.2 for ρ = 0.5 (Fig. 1). The advantage of sample-based designs is retained for ρ > 0, and the advantage of hypernormal controls is enhanced relative to ρ = 0.

Figure 1.

Efficiency of the sample-based design with hypernormal controls relative to mother-father-child trios with the same number of individuals.

Discussion

We conclude that efficiency of TDT trios under our assumptions is substantially less than for sample-based designs, or 2/3 when compared with normal controls and 1/6 when compared with hypernormal controls. However, efficiency depends on the model and is not the only consideration in choice of sampling strategy. Gene action, validity of the phenotype score, sibship composition, interest in linkage and imprinting, age of probands, and population structure are a few of the factors that influence this choice. Genes for disease susceptibility imply alleles for disease resistance, but not necessarily with the same frequencies as for disease susceptibility. Genotypes with disease resistance may be easier or harder to detect, and more or less likely to give insight into etiology and intervention. The efficiency of hypernormal controls is always as great as normal controls, and usually much greater.

We have assumed multiplicative gene action leading to additivity of effect on a logarithmic scale, the only model that makes maternal and paternal transmission equal and independent. Other authors prefer more complicated models such as additive × additive epistasis (17), under which the efficiency of TDT may be greater or less. While mathematically possible, there is no proven example of such extreme interaction. Estimation of ρ depends only on a odds ratio that is robust to choice of a model. Absent evidence to the contrary, we prefer the parsimonious assumption that small effects behave in a simple way. Once an association is detected, validity of the model should be tested.

Hypernormal controls are easily provided for diseases defined by one extreme of a unimodal continuum, such as obesity and hyperlipidemia. However, phenotype scores are sometimes insensitive to hypernormal liability, and individuals with no evidence of disease susceptibility are common for asthma, atopy, and insulin-dependent diabetes. It may not be feasible to identify extreme hypernormal controls, but some differentiation between random and hypernormal individuals as in Table 3 remains a practicable goal that cannot be efficiently exploited by the TDT.

Sibship composition with respect to affection status and phenotype scores has a considerable impact on efficiency. Normal sibs give some information, most easily recovered under H₀ (Table 5). The parameter y is the frequency of affected children after allowance for the ascertainment scheme. An accurate estimate of y requires segregation analysis. However, under H₀ the ML score for normal is U = z (d − c) with information K = z² (c + d), where z = y/(1 − y). Then χ₁² = U²/K is independent of y, and so a rough estimate is acceptable. This supplements transmission to affected children. For example, in one sample (8) transmission to normal children increases information about allelic association by 25% (Table 6). A generalization to phenotype scores replaces ρ by (e^λχ − 1)/(e^λχ + 1), where λ is a constant similar to ψ and χ is a score with mean 0 in the general population and 1 for affected individuals. A similar extension has been proposed for linkage (9).

Table 5.

The TDT test for M transmission from MM^* parents to a normal child

	Transmitted allele		Total
	M	M*
Observed number	c	d	c + d
Expected frequency			1

Table 6.

Transmission of INS alleles in IDDM (8)

	Number of alleles transmitted		ML scores under H0
	M	M*	U	K	U2/K
Affected	78	46	32.00	124.00	8.26
Normal	42	62	10.88	30.76	3.85
Total	120	108	42.88	154.76	11.88

Multiplex sibships are analyzed efficiently by the TDT. Relative to the sample-based case control study with normal controls the efficiency with s affected sibs is 1 − 1/(2 + s), which approaches but never reaches 1. Efficiency relative to a sample-based case-control study with hypernormal controls approaches 1/4 as s increases. Although consideration of efficiency would never lead to choice of the TDT, sometimes family-based studies are dictated by other concerns. Imprinting cannot be investigated or distinguished from maternal effects without typing the parents. Linkage testing is inefficient unless parents are typed and sibships are selected for affected or hypernormal children. The TDT design uses such sibships well when parental markers are known, and in that case it remains valid if pedigrees are partitioned into nuclear families. Diseases with early onset favor family-based designs, because parents are usually alive and the nuclear family is often intact. Children need not be typed if both parents are homozygous, or if neither carries an allele postulated to be disease-associated. For such confirmatory tests the parents may initially be pooled to screen for informative matings if the candidate allele is seldom homozygous. The cost of studying a nuclear family with s affected children and their parents is often less than the cost of studying s independent cases, although the latter are more informative.

Other considerations may make family studies more costly that a case-control study, even if hypernormal control are not used. Adult diseases and especially diseases of late onset are unfavorable to family-based designs, because the nuclear family is usually dispersed and the parents often dead or unreachable. Sometimes phenotypes are known for a cohort, and then affected and hypernormal samples are easily collected, whereas family members are less accessible and may be less informative. Isolated cases may be much more frequent than familial cases, and the latter be enriched for major loci or homozygosity. Although interesting, this may not be the object of study.

The argument most often used in favor of the TDT is population stratification (7), which has several effects. First, it creates an inbreeding coefficient α > 0. Then with probability α an allele transmitted by a parent is identical by descent to the nontransmitted allele. This event reduces the efficiency of a family-based case-control study that assumes α = 0 relative to the TDT that makes no assumption about α. However, the effect corresponds to multiplication of ψ by 1 − α, and therefore reduces information by a factor (1 − α)². Extensive studies of large populations within an ethnic group give values of α near 0.001, which is negligible (18).

Second, stratification creates allelic association between genes on different chromosomes. For example, the A² allele in the ABO blood group and the rh allele in the Rhesus blood group are characteristic of Europe and Africa, and therefore correlated if race is ignored. In the worst case an investigator might mix ethnic groups with different disease prevalence and marker frequencies, perhaps taking cases and controls from different populations. However this would be extremely careless. Unless genetic epidemiologists are prone to an error that other epidemiologists manage to avoid, the greater cost of the TDT is a deterrent. In rebuttal, a TDT advocate might cite examples where significant association with sample-based controls was not supported by a subsequent TDT. However, alternative explanations weaken this argument in the absence of a compelling example (19). The first result might be a classical type I error, or the second result with an inefficient family-based test might be a classical type II error. If the first sample used inappropriate controls, this should be demonstrated and the investigators reproved, but the adequacy of a case-control design is not in question. TDT efficiency is too low to accept its cost as partial insurance against ineptitude, which unfortunately is not limited to choice of controls.

The issue of population stratification was passionately debated several years ago in relation to DNA testing. The “product rule” assumes that the effect of stratification is negligible within an ethnic group, even if defined vaguely as Caucasian, Black, Asian, or Hispanic. The product rule has withstood controversy (20). However, the stratification argument for the TDT is not based on genetic evidence but on mathematical theory. With random mating the association between unlinked loci declines by 1/2 each generation, and so ρ becomes negligible in a few generations. The situation most favorable to the TDT is a small population with interracial founders, short history, and racially assortative mating (7). This special case should be viewed in context. Allelic association is rarely detected beyond 2 cM, and a candidate region is seldom claimed unless ρ > 0.2. This outcome is more than two orders of magnitude greater than the likely effect of stratification in most populations, which is exceeded when alleles are selected and pooled on the basis of a significance test. The L parameter in the Malecot model makes specific allowance for this background association, which is dominated by the peak in a candidate region (5). Analysis of allelic association should aim to localize that peak, not respond to isolated type I errors.

Since introduction of the TDT there have been three major developments in mapping by allelic association. (i) The number of polymorphic markers has greatly increased, and it is now customary to use multiple markers in a small region, generally less than 10 megabases, that contains a candidate locus recognized by function or suggested by linkage in a genome scan. (ii) The value of phenotype scores to identify hypernormal individuals has been appreciated (12). (iii) The Malecot model is specific for peak association and protects against type I errors due to departures from the model (5). These developments alter the perceived advantages and disadvantages of the TDT. All the factors discussed here should be considered in designing a study of allelic association. Whether or not the cost of a family-based test can be justified, estimates from different samples may be efficiently combined and tested for heterogeneity simply by weighting with the information K.

ABBREVIATIONS

TDT

transmission disequilibrium test

ML

maximum likelihood

H₀

the null hypothesis of no association