Spines and neurite branches function as geometric attractors that enhance protein kinase C action

Abstract

Ca²⁺ and diacylglycerol-regulated protein kinase Cs (PKCs; conventional PKC isoforms, such as PKCγ) are multifunctional signaling molecules that undergo reversible plasma membrane translocation as part of their mechanism of activation. In this article, we investigate PKCγ translocation in hippocampal neurons and show that electrical or glutamate stimulation leads to a striking enrichment of PKCγ in synaptic spines and dendritic branches. Translocation into spines and branches was delayed when compared with the soma plasma membrane, and PKCγ remained in these structures for a prolonged period after the response in the soma ceased. We have developed a quantitative model for the translocation process by measuring the rate at which PKCγ crossed the neck of spines, as well as cytosolic and membrane diffusion coefficients of PKCγ. Our study suggests that neurons make use of a high surface-to-volume ratio of spines and branches to create a geometric attraction process for PKC that imposes a delayed enhancement of PKC action at synapses and in peripheral processes.

Introduction

The development of fluorescently conjugated proteins has allowed investigators to gain new insights into the way proteins behave in living cells. Most cytosolic signaling proteins are able to diffuse very rapidly within the cell (∼10 μm²/s), and the time courses observed are often consistent with a process of random diffusion (Teruel and Meyer, 2000). Random diffusion is a major component of many signaling processes because proteins must be able to move rapidly throughout the cell to locate binding partners and targets. Cell stimulation often creates such local binding sites, and many families of signaling proteins undergo a diffusion-mediated reversible movement, or translocation, from one cellular compartment to another after stimulation.

Conventional PKC isoforms (cPKCs; PKCα, -βI, -βII, and -γ) are one family of signaling proteins that make use of a translocation to bind to plasma membrane lipids. cPKCs are an interesting example of cellular coincidence detectors, meaning that they are jointly activated by the two second messengers Ca²⁺ and diacylglycerol (for reviews see Nishizuka, 1984; Newton, 1995) and are further regulated by phosphorylation (for review see Newton, 2001). A critical step in the activation of cPKCs is the stimulus-induced, rapid translocation from the cytosol to the plasma membrane, a cooperative process that has been shown to be primarily driven by the binding of two or three Ca²⁺ ions that triggers an interaction of cPKCs with lipids in the plasma membrane (Nalefski and Falke, 1996; Sakai et al., 1997; Oancea and Meyer, 1998; Rodriguez-Alfaro et al., 2004). The C2 domain, which is a Ca²⁺-binding module, mediates this translocation, and the subsequent interaction with diacylglycerol is mediated by two C1 domains (Oancea and Meyer, 1998; Shirai and Saito, 2002; Newton, 2004).

Studies over recent years have shown that this type of second messenger–triggered translocation from the cytosol to the plasma membrane occurs not only for cPKCs but also for several other proteins that have lipid interaction domains (Teruel and Meyer, 2000). The human genome (available from GenBank/EMBL/DDBJ under accession no. 11181995; Venter et al., 2001) is thought to have 117 proteins with C2 domains, 63 with C1 domains, and 237 with pleckstrin homology (PH) domains (Fruman et al., 1999; Lemmon, 2003), many of which have been shown to be present in neurons and to be regulated by reversible plasma membrane translocation (Fig. 1 A). cPKCs are arguably the most prominent members in this group of reversible membrane-translocating signaling proteins and are also among the most abundant signaling proteins in the brain. We have therefore focused our study on PKCγ, the neuron-specific cPKC (Saito and Shirai, 2002).

Figure 1.

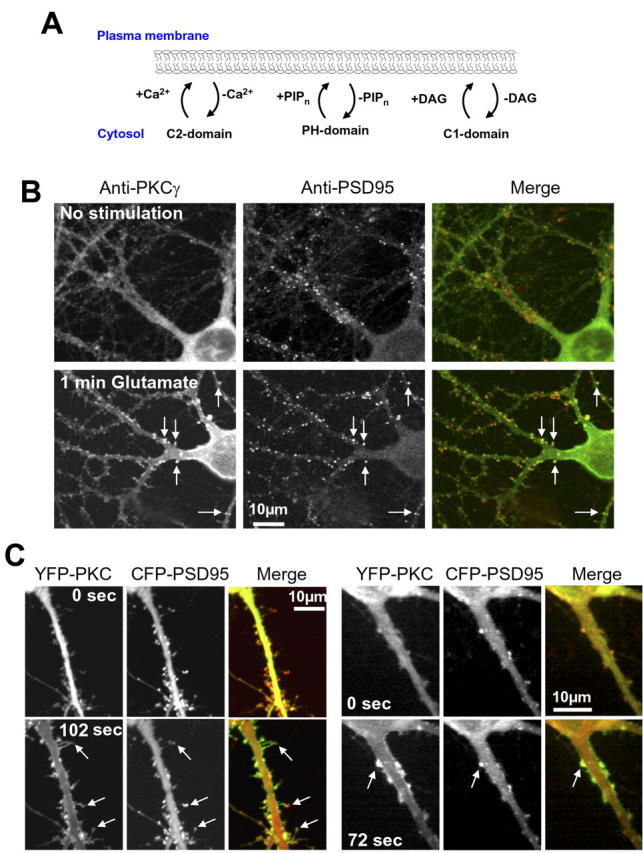
Glutamate-triggered translocation of PKCγ into spines of hippocampal neurons. (A) Schematic view of the reversible plasma membrane–translocation process of signaling proteins. C2, C1, and PH domains are the main classes of known lipid interaction domains that can reversibly translocate signaling proteins to the plasma membrane in response to increases in Ca²⁺, diacylglycerol, and PIP_n lipids, respectively. PIP_n refers to PIP₂ or PIP₃. (B) Confocal microscope images showing the translocation of endogenous PKC (green in the merged image) into spiny structures that also correspond to sites stained with the postsynaptic marker PSD95 (red). A control cell is shown in the top panel, whereas the bottom panels show a different cell that was fixed and stained for 1 min after the application of glutamate. Arrows show examples of sites containing endogenous PSD95, to which PKCγ translocates after stimulation. (C) YFP-PKCγ also translocates to local sites that partially overlap with the postsynaptic marker CFP-PSD95. After stimulation, the fluorescence intensity of YFP-PKCγ was markedly enriched in spines as well as in other dendritic processes compared with nearby plasma membrane sites. Images are shown for two different cells. The left panel shows the magnified image of a dendrite of a neuron transfected with YFP-PKCγ before (top) and 102 s after stimulation with 30 μM glutamate (bottom). Images of CFP-conjugated PSD95 from corresponding time points are shown in the middle panel. In the third panel, the images of YFP-PKCγ (green) and CFP-PSD95 (red) before and after stimulation were overlaid to show the translocation of PKC into spiny structures that protrude from the main dendrite that also contain the PSD95 protein (arrows). Another cell is shown in the series of panels on the right.

Neurons have a distinctive, complex morphology, possessing numerous dendritic branches and spines, which raises the question of whether these unique neuronal membrane structures are involved in neuronal signal integration after the translocation of a protein to the plasma membrane. One factor that may have a significant impact on protein translocation in neurons is the ratio of the surface area of the plasma membrane to the cytosolic volume (surface-to-volume ratio [SVR]). The SVR of thin branches and spines will be larger than that of thicker branches and the cell soma. The importance of the dendritic branch structure for intracellular signaling was implicated in a study looking at inositol 1,4,5-trisphosphate–triggered Ca²⁺ release, in which the localization and intensity of cytosolic signals was shown to depend on the morphology of neurite-like membrane extensions (Fink et al., 1999). Here, we show that glutamate triggers a delayed enhancement of PKC translocation from the soma and thick branches into thin branches, and across spine necks into postsynaptic terminals. This translocation process markedly increases PKC availability in spines beyond that caused by the initiating stimulus and may provide a new type of molecular memory that does not require posttranslational modification. Furthermore, the measured delay times for translocation are consistent with a much lower translocation into spines and branches in response to brief stimuli. This occurs on a time scale of 1 s or less and indicates that the translocation process can integrate activity from receptor stimuli over time periods of a few seconds to tens of seconds.

By using fluorescence photobleaching recovery measurements of local PKC diffusion in the cytosol and at the plasma membrane and by measuring the rate at which proteins can cross the neck of spines, we developed a diffusion-based model that explains the amplitude of the translocation as well as the delay and the persistence in PKC translocation. Our study shows that spines and dendritic thin branches function as attractors that provide cells with a morphology-based timing device that first delays and then prolongs maximal PKC action.

Results

Neuronal stimulation triggers PKCγ translocation into spines and branches

We investigated the localization of endogenous PKCγ in primary cultured rat hippocampal neurons at rest and after stimulation with glutamate using an anti-PKCγ antibody and imaged the fluorescent staining with a laser scanning confocal microscope. In resting cells, the PKCγ staining was distributed throughout the cytosol in the cell soma and in dendritic branches (Fig. 1 B, top). Neurons stimulated for 1 min with glutamate showed a robust translocation of endogenous PKCγ to the plasma membrane of the soma and dendritic branches (Fig. 1 B, bottom). In addition, it was apparent that PKC accumulated in many spine structures and often colocalized with the postsynaptic protein PSD95. The correlation between local spots of PKC and PSD95 puncta can be best seen by direct comparison of the monochrome images (Fig. 1 B, left) or in the merged images (Fig. 1 B, right). We also noticed that in some cases, PKCγ levels were partially elevated in some of the spines of the resting cells, which may be explained by low-level spontaneous activity in the culture.

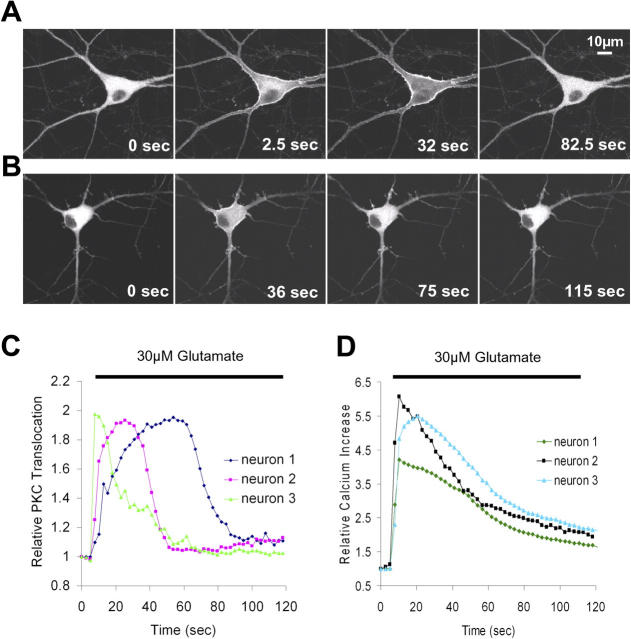
We then investigated the kinetics of the translocation process by expressing YFP-conjugated PKCγ (Sakai et al., 1997; Oancea and Meyer, 1998; Oancea et al., 1998) and monitoring glutamate-triggered translocation in live cells using time-lapse confocal microscopy. In agreement with the antibody experiments, glutamate-induced translocation of YFP-PKCγ to the plasma membrane led, in many cells, to a significant enhancement of PKCγ concentration in synaptic spines. Fig. 1 C shows examples of confocal images from two cells before and after glutamate stimulation, where the postsynaptic marker CFP-PSD95 was used as a spine reference. As apparent in this figure, the resulting PKCγ concentration in the synaptic spines often exceeded increases in nearby plasma membrane regions and was maintained for tens of seconds.

The same translocation of PKCγ into thin branches and spines could also be observed when neurons were stimulated using field stimulation (50 Hz for 1 s, repeated every 2 s; Jacobs and Meyer, 1997). Fig. 2 A shows an example of the dynamics of PKCγ translocation in neurons stimulated with glutamate, whereas Fig. 2 B shows a cell that was stimulated electrically (Video 1, available at http://www.jcb.org/cgi/content/full/jcb.200503118/DC1). It is interesting to note that although glutamate stimulation always triggered PKC translocation in the soma as well as in dendrites, field stimulation often resulted in a more selective PKC translocation in dendrites and spines, with little or no translocation observed in the soma (in 11 out of 22 experiments using electrical stimulation; Fig. S1 and Video 2). This effect is possibly attributable to lower amplitude Ca²⁺ signals triggered by field stimulation in the soma compared with dendrites and spines.

Figure 2.

Translocation of GFP-PKCγ to the plasma membrane in response to glutamate application and electrical field stimulation. (A) Series of confocal images showing the reversible glutamate-triggered (30 μM) plasma membrane translocation of GFP-PKCγ. Glutamate was added after the first image. (B) A train of electrical pulses (50 Hz, lasting 1 s, applied every 2 s, from t = 24 s in the time series) induced translocation of GFP-PKCγ to the plasma membrane (see also Video 1 and Fig. S1, available at http://www.jcb.org/cgi/content/full/jcb.200503118/DC1). (C) The glutamate-induced change in relative fluorescence intensity, corresponding to the relative GFP-PKCγ concentration at the soma plasma membrane, is shown as a function of time for three cells from separate experiments. (D) The same glutamate stimulation (30 μM) that was used to evoke GFP-PKCγ translocation in the experiment shown in C was applied to different, nontransfected cells loaded with the Ca²⁺ indicator Fluo-3 AM. This stimulation generates Ca²⁺ signals that have similar kinetics to GFP-PKCγ translocation (three representative traces from one experiment are shown; n = 10 experiments).

In the soma and in thick dendritic processes, the translocation of PKCγ from the cytosol to the plasma membrane after the application of glutamate occurred in <5 s (Fig. 2 C). Consistent with previous results of PKC translocation in cell lines, the rapid and transient translocation kinetics can be explained by transient Ca²⁺ signals triggered by these two protocols (Fig. 2 D) when also considering the cooperative nature of the Ca²⁺-triggered translocation process (cooperativity of 2–3; Sutton and Sprang, 1998; see Introduction).

In contrast to the translocation to the plasma membrane of the soma and in thick branches, PKCγ translocation into and out of spines was often markedly slower. Fig. 3 A shows time courses of spine translocation triggered after glutamate stimulation (see Video 3, available at http://www.jcb.org/cgi/content/full/jcb.200503118/DC1, for another example of glutamate-triggered PKC accumulation in spines). PKCγ translocation profiles to spines upon electrical stimulation are shown in Fig. S2 C. Note that even though fluorescence was monitored from spines in the same cell, there is considerable variability in the delay time required to reach peak fluorescence and the degree of enrichment of PKC from spine to spine.

Figure 3.

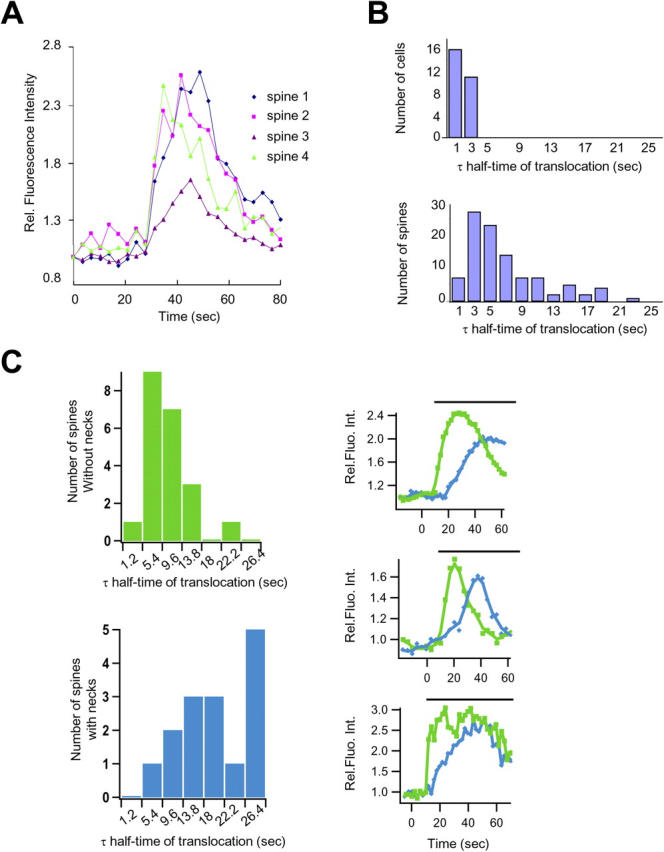
Kinetics of PKCγ translocation into spines are delayed and depend on spine morphology. (A) Time courses showing kinetics of translocation of GFP-conjugated PKCγ in four dendritic spines of the same neuron (Fig. S2, available at http://www.jcb.org/cgi/content/full/jcb.200503118/DC1). (B) Histograms depicting the observed delay for PKCγ translocation into dendritic spines (bottom) compared with the translocation of PKCγ to the plasma membrane of the cell soma (top). The time required for individual spines (n = 100 spines from 11 cells) and soma plasma membranes (n = 27 cells) to attain half-maximal PKCγ accumulation was measured from the point of stimulus addition. (C) Histograms showing the distribution of translocation half-times for spines with or without necks. The translocation of GFP-PKCγ to spines that have a neck (scored only if the spine showed a well-defined narrow neck joining a mushroom-shaped spine (see Fig. S2) is significantly delayed compared with spines with no neck. The half-time of translocation was derived from an exponential fit of these traces (see Materials and methods). 21 spines without a neck and 15 spines with a neck from five different neurons were examined. Individual translocation traces in spines without a neck (green) and with a neck (blue) are also shown from three different neurons.

The kinetics of the delay between the stimulus and the time to reach 50% of maximal translocation in spines is plotted in a histogram in Fig. 3 B (bottom). For comparison, the same kinetic analysis was also performed for the much faster kinetics of plasma membrane translocation in the soma in Fig. 3 B (top). Translocation to the soma plasma membrane typically occurred in <3 s after glutamate addition, whereas the majority of spines accumulated PKCγ after 5–10 s, with some spines requiring even longer.

The different kinetics of accumulation among spines suggests that there might be different populations of spines within the same neuron, whose morphology may influence the rate of PKCγ enhancement. We tested this hypothesis by grouping spines by visual inspection into those with short or no necks and those with necks of ∼0.5 μm or longer. Consistent with the hypothesis that the delay is a result of spine morphology, our findings showed a markedly slower translocation of PKC in those spines with longer necks (Fig. 3 C). The mean translocation half-time (derived from the histogram in Fig. 3 C) is 16.8 ± 2.2 s (standard error) for spines with necks and 6.3 ± 0.8 s for spines without necks (t test, P < 0.0001).

Translocation of PKCγ into thin branches is delayed and remains localized in these structures after PKCγ dissociates from the plasma membrane

In addition to observing a delayed PKCγ translocation into spines, we found that PKCγ showed a marked and delayed translocation into thin branches. When focusing on thin branches and filopodia-type structures that emanate from the dendritic main branches, we found that PKCγ first translocated rapidly to the nearest plasma membrane in the main branch within 2 s of stimulus addition (Fig. 4 A). In the second step, PKCγ translocated over a period of 10 s or longer from the main branches and soma into thin branches and filopodia-type extensions (n = 25 cells). In many cases, PKCγ translocation was prolonged in thin branches and remained there after the response in the soma was over (Fig. 4 A, bottom, t = 82 s). The delayed translocation into thin branches can be shown by comparing the relative intensity increase of GFP-PKCγ at three locations along a thin branch of a neuron. For reference purposes, two additional locations were selected to monitor the plasma membrane of the soma as well as the cytosolic PKC concentration (Fig. 4 B). The regions of interest used for the graph were 3, 7, and 11 μm into the fine branch (Fig. 4 B, schematic diagram). Note that the fluorescence intensity continues to increase along the branch even as the response in the soma is recovering. This data suggests that the translocation into spines and branches is markedly delayed and that PKCγ can remain in these structures for a prolonged period after response to the stimulus has ceased in other parts of the cell.

Figure 4.

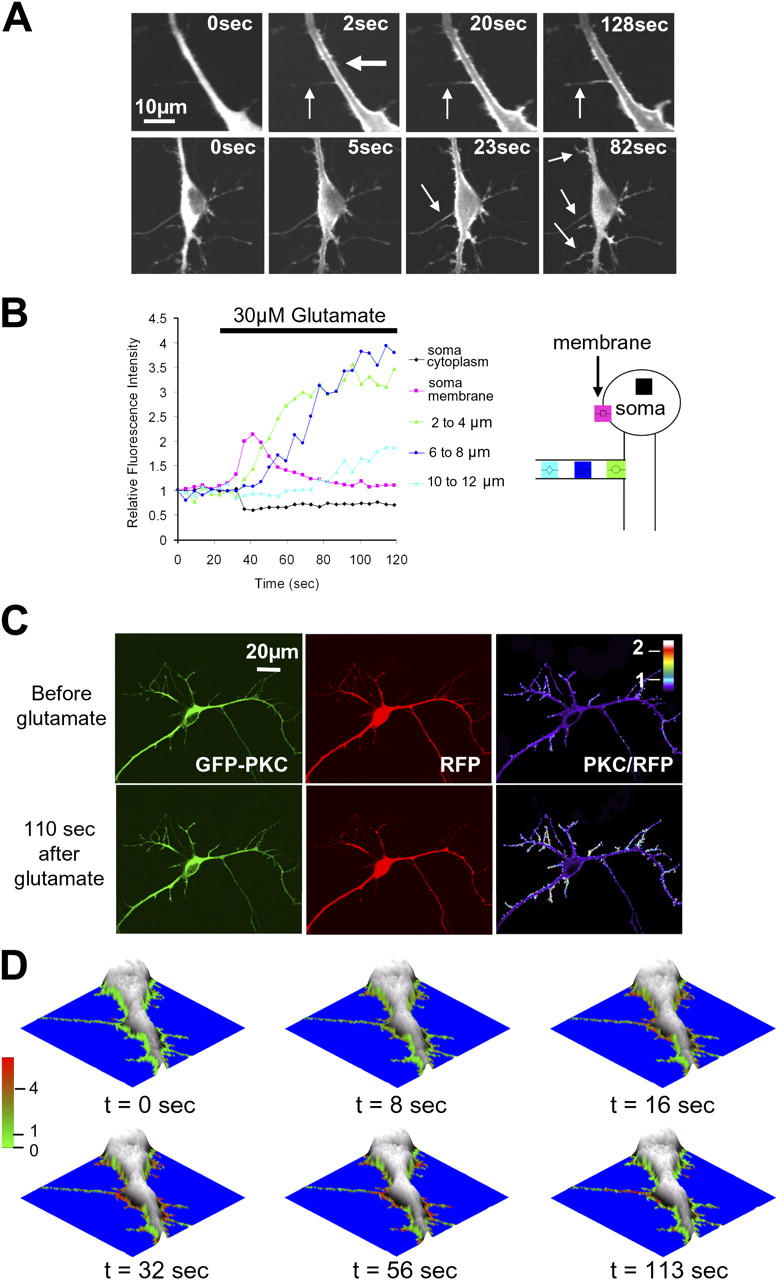
Quantitative analysis of the stimulus-induced relative increase in PKCγ concentration in thin branches. Elevated PKCγ concentration in these branches persists even after PKCγ dissociates from the membrane of main branches and soma. (A) Images from two time series show that glutamate triggers a delayed translocation of PKCγ from thicker into thinner dendritic processes. The thick and thin arrows in the top panel mark thick and thin dendritic processes, respectively. The arrows on the bottom panel indicate thinner branches into which PKCγ translocates after the stimulus. The final image shows retention of PKCγ in many of the thin branches emanating from the thick branches and soma. (B) Comparison of the relative time course of GFP-PKC translocation measured at three locations along a thin branch versus the time course measured in the cytosol and at the plasma membrane of the cell soma. Each region of interest was 2 μm wide, and regions were positioned at 2-μm intervals along the thin branch. (right) The diagram demonstrates the position of each region placed in the soma and along the thin branch. The color of the region and the symbols drawn inside the regions of interest mirror those in the traces in the graph on the left. (C) Ratio imaging comparing GFP-PKCγ in branches to an RFP cytosolic marker before (top) and after (bottom) stimulation. The original GFP and RFP images (left), as well as the pseudocolored ratio images, are shown (right). (D) Series of topographical images showing the overlaid color-coded ratio of PKC/RFP generated using a perimeter mask to highlight changes occurring in thin branches and processes at the edge of the cell. Areas that appear red indicate an enrichment of PKCγ relative to the cytosolic marker, whereas green depicts regions of low PKCγ concentration.

Although this time-course analysis provided useful insights into this delayed translocation mechanism, a true quantitative measure of the PKCγ translocation into spines and thin branches also requires a volume reference marker to measure if, and by how much, PKCγ is locally enriched. A volume marker can also control for potential glutamate-triggered changes in the volume of these structures that could not be detected by light microscopy. We therefore compared the distribution of PKCγ with that of a cytosolic reference protein, DsRed (red fluorescent protein [RFP]), by ratio imaging. The ratio images created show the translocation of PKCγ to the membrane as well as into spines and thin branches as local increases in the ratio intensity (Fig. 4 C and Video 4, available at http://www.jcb.org/cgi/content/full/jcb.200503118/DC1). Using this calibration method, the glutamate-triggered enrichment of PKCγ in most synapses and thin branches was found to be between 2- and 10-fold. Because the ratio representation in Fig. 4 C lacks the information about the cell volume (absolute RFP intensity), we also developed an image representation that combines a surface plot of the fluorescence intensity of the volume marker with a color code that corresponds to the PKC/RFP ratio. This analysis, which generates a topographical display, was based on two binary masks. The first binary mask was the “neuron volume mask,” which uses a minimal fluorescence intensity threshold from the RFP volume marker and identifies where the neuron and its processes are (the area outside of this mask was selected to be blue). The same RFP fluorescence intensity can then be used to create a surface plot within this mask. The second binary mask was a “region of interest mask” that selects the cell periphery and was used to overlay in a color code the relative enrichment of PKCγ over the volume marker (the PKC/RFP ratio).

In Fig. 4 D, a series of topographical plots shows more clearly that PKCγ translocates with a delay from thick branches into thin branches, becomes highly enriched there, and remains elevated for a prolonged time period, even after PKCγ has dissociated from the plasma membrane sites in the rest of the cell.

PKC translocation is likely to be a result of passive diffusion in the cytosol and along the plasma membrane

We investigated whether an active transport process was needed or whether a passive diffusion process would be sufficient to explain the observed translocation into spines and branches. In experiments checking for the involvement of cytoskeletal transport proteases, we found that the translocation of PKC was not delayed when cells were preincubated with latrunculin, an inhibitor of actin polymerization, or nocodazole, an inhibitor of microtubules (unpublished data), suggesting that active transport processes may not contribute to the observed translocation. We then focused on the possibility that diffusion is involved in mediating translocation, by measuring if and how fast YFP-conjugated PKCγ can diffuse in dendritic branches in the absence and presence of glutamate stimulation. For these photobleaching experiments, we used a local bleach pulse with a Gaussian intensity profile that had a 3-μm-diameter. The recovery of this Gaussian profile can be used to measure the diffusion coefficient, D (in μm²/s), by measuring the widening of the Gaussian-shaped bleached area and the parallel reduction in the bleached peak amplitude. This analysis has previously been performed in two dimensions for round cells (Oancea et al., 1998). The geometry of branches allows the use of a one-dimensional version of the analysis in dendrites: I_o− I(x,t) = γ(4πDt)^−1/2 × exp(−x²/4Dt), where γ is a normalization constant, x is the length coordinate, and t is time (Crank, 1975).

As shown in Fig. 5 A, the locally depleted YFP-PKCγ recovered in ∼1 s, suggesting that the cytosolic enzyme can diffuse rapidly in unstimulated neurons. In contrast, in the presence of glutamate, the recovery time of PKCγ was approximately four times slower (Fig. 5 B). By fitting a one-dimensional curve through these series of images, one obtains a best fit for a diffusion coefficient of 5.45 μm²/s in the absence of glutamate and 0.33 μm²/s in the presence of glutamate (Fig. 5 C). As a reference, we also measured the diffusion coefficient of a protein with a different membrane interaction mechanism by expressing a farnesylated YFP-CAAX construct in the neurons (D = 0.52 μm²/s).

Figure 5.

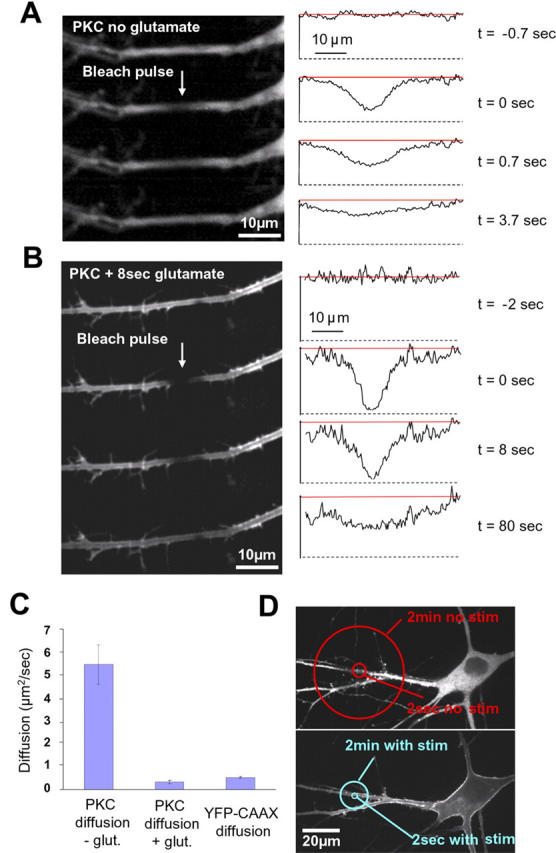
Measurement of the diffusion coefficient of dendritic PKCγ in the presence and absence of stimulation is sufficiently fast to explain the observed translocation behavior. (A, left) Four images taken from a time series of 20 used for the measurement of the PKCγ diffusion coefficients. The Gaussian bleach pulse was applied between the first and second image. (right) Linescan analysis of the recovery of the bleach profile from the series of images shown on the left. (B) The same experiment as in A performed 8 s after stimulation with glutamate and with a longer time course to account for the slower recovery of PKCγ (a total of 70 images were acquired during this experiment). Arrows point to the site of photobleaching within the branch. (C) Bar representation of the dendritic PKCγ diffusion coefficients measured in the absence (n = 15) and presence (n = 9) of glutamate stimulation. In the presence of glutamate, the diffusion of PKC was ∼16 times slower than the diffusion of PKC in the cytosol in the absence of stimulation (0.33 ± 0.07 SEM and 5.45 ± 0.85 SEM, respectively), and it was also slower than the diffusion of membrane-associated YFP-CAAX (diffusion coefficient 0.52 ± 0.04 SEM; n = 13). Error bars represent the SEM for these experiments. (D) The diffusion coefficients from C were used to produce a schematic view illustrating the range of action of PKCγ in the absence (top) and in the presence (bottom) of a stimulus.

The measured diffusion coefficient of PKC in unstimulated dendritic branches is slightly slower than that expected for a protein of the size of PKCγ fused to YFP, whereas the measured diffusion coefficient in the presence of glutamate is similar to that of the farnesylated control construct and other known membrane-interacting proteins (Yokoe and Meyer, 1996; Niv et al., 1999; Teruel and Meyer, 2000). It is useful to point out that the added size of the YFP tag likely only reduces the diffusion coefficient by a small factor because diffusion coefficients are proportional to the inverse of the third root of the mass as well as a shape factor that is generally on the order of 30% or less for the diffusion of many in vitro measured proteins (Cantor and Schimmel, 1980).

The concept of a range of action of a diffusing protein can be used to address the question of whether a diffusive process can explain the translocation of PKC. In the case of a linear dendritic branch, the range of action is simply the average absolute distance from the origin after a time, t (range = [4 × Dt/π]^1/2; Teruel and Meyer, 2000). Over time scales of 2 s and 2 min, PKCγ will diffuse in the absence of a stimulus over a region with a mean diameter of 6 and 46 μm, respectively (Fig. 5 D, top), whereas the same regions will shrink to 2 and 14 μm (Fig. 5 D, bottom) in the presence of a stimulus. Given these outer boundaries for the range of action of PKCγ, it is likely that the observed delay in the translocation into thin branches is consistent with a diffusion process. In the case of spines, diffusion could drive a much faster translocation process than is observed experimentally. This raises the possibility that many spines have neck structures that slow the translocation of PKC into spines and retain PKC in spines after a stimulus is terminated.

Although these considerations address the question of whether diffusion could be responsible for the observed translocation, they do not address the more fundamental question of why an actual enrichment occurs in thin branches and spines and what mechanism defines the amplitude of this enrichment. In the next section, we present a model where the enrichment is primarily a result of an increased SVR of thin branches and spines compared with the main branches and soma.

A surface-to-volume model predicts the local enrichment and the delay times for PKC translocation into thin branches

We tested whether the dendritic branch geometry and surface-to-volume effects can be modeled in computer simulations to predict the measured translocation time course. In the performed simulations, the higher SVR in thin branches is responsible for the relative concentration increase after PKC translocation. We used the diffusion equation (dc/dt = Dδ²c/δx²; Crank, 1975), the measured PKCγ diffusion coefficient (0.3 μm²/s), and typical geometries of main branches (2–5 μm) and smaller, side branches (<1 μm) to model the translocation into thin branches (Fig. 6 A). The model had a starting condition of c(x,0) = 0 (if x > 0) and assumed a large reservoir in the main branch so that the boundary condition at the main branch was c(0,t) = C₀ (if t ≥ 0). The main branch was assumed to have a diameter that was five times larger than that of the thin branch. The model also had a boundary condition after a length (L) into the branch so that dC/dx|_{x = L} = 0. The simulations were based on a fixed length of a thin branch with a uniform tubular shape and assumed that the concentration of PKCγ remained constant in the thick branch (assuming there was a large reserve volume; for details see Materials and methods).

Figure 6.

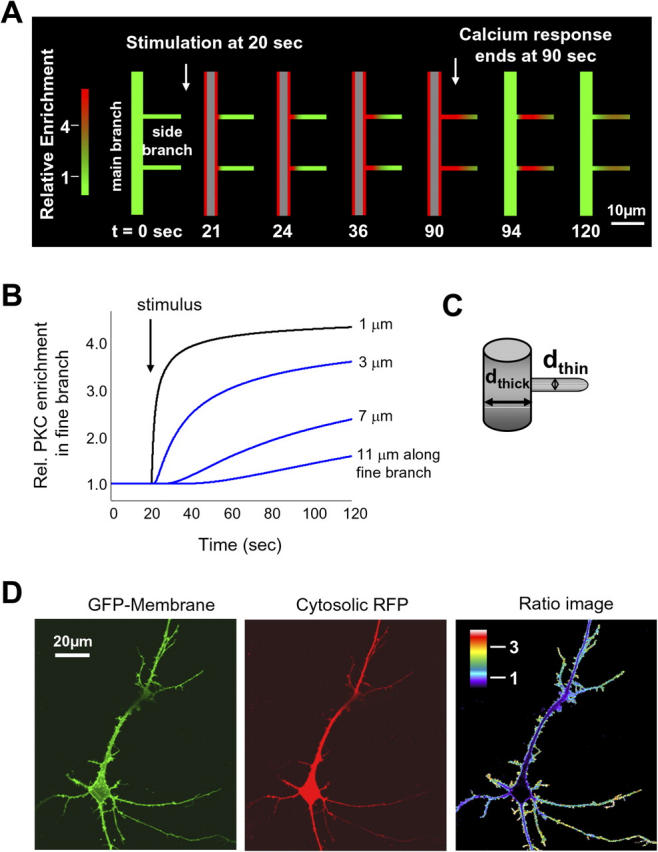
Simulation and modeling of the translocation process into thin branches reveals a geometric attraction process that can suppress subthreshold stimuli, integrate activity, and create molecular memory. (A) Simulation of the PKCγ translocation in a dendritic arbor during transient stimulation. The schematic images were drawn by an analysis program based on data generated from simulating the diffusion of PKCγ in the dendritic arbor after stimulation. In these schematic images, regions of elevated PKCγ concentration are shown in red. After the stimulus has been applied, a rapid translocation of PKCγ to the plasma membrane of the thick branch is observed. These simulations suggest that delayed translocation of PKCγ into thin branches and the prolonged localization in branches after the response to the stimulus has ceased can be explained by surface-to-volume arguments and the measured diffusion coefficient of PKCγ. (B) Simulated concentration profiles of PKCγ at different points along a thin dendritic branch as a function of time (for a 120-s period after the application of the stimulus). The points were chosen according to the experimental results in Fig. 4 B. (C) Schematic illustration of the parameters used for the construction of the thin branch attraction simulation. (D) Measuring the relative SVR (surface-to-volume parameter) in the dendritic arbor. The membrane marker GFP-Lyn, consisting of the myristoylation/palmitoylation motif from Lyn kinase, was coexpressed with a cytosolic RFP. The original images, in addition to the pseudocolored ratio image, are shown.

The resulting simulations are plotted in Fig. 6 A in a color-coded representation that shows PKCγ translocation into two thin branches that emanate from a main branch. Red marks a threefold or larger increase in local PKC concentration, whereas green reflects basal PKC concentration. Fig. 6 B shows the simulated concentration time course of the increase in PKCγ concentration at different locations into the thin branch. The time courses shown reflect increases in PKCγ concentration at positions similar to those measured experimentally in Fig. 4 B, suggesting that the model provides a good match to the experimentally measured PKC translocation. This suggests that the diffusion of PKCγ, the stimulus-induced plasma membrane translocation, and the dendritic geometry are sufficient to explain the measured translocation of PKC into thin branches.

An important parameter in these simulations is the ratio of the surface membrane area to the volume that is lower in the main branch than in the thin branch (surface-to-volume parameter; Fig. 6 C). This local SVR in the dendritic arbor can be directly measured in neurons by comparing the distribution of a plasma membrane–targeted GFP (myristoylated/palmitoylated GFP) to a cytosolic RFP. As shown in Fig. 6 D, the SVR is markedly higher in peripheral dendrites and thin branches with SVRs that were more than three times higher than those of thick branches. The SVRs progressively increased toward the outer peripheral fine branches (n = 6). To exclude the possibility that this was a result of peripheral enrichment of myristoylated/palmitoylated GFP, we also made the same ratio measurements with a farnesylated/polybasic YFP construct (YFP-CAAX) and found the same relative distribution (unpublished data). This suggests that SVR is key to understanding not only the dendritic geometry but also the control of the localization of PKCγ and other membrane-translocating signaling proteins.

The importance of this surface-to-volume parameter makes it useful to derive a quantitative expression for the PKC enrichment that can result from a particular geometry. Assuming the dendritic branches have a tube-like geometry, SV_branch = (π × d_branch × l₀)/(π × d_branch ² × l₀/4) = 4/d_branch, where d_branch is the diameter of the branch and l₀ is the length of the branch (Fig. 6 C). Thus, the maximal amplitude of the translocation from a thick to a thin branch, the maximal enrichment factor (E), simply becomes the ratio of the respective surface-to-volume parameters of the thick and thin branch: E = d_branch/d_thin.

Translocation of PKCγ into spines is delayed by its access across the neck of spines

Although the delay of PKCγ translocation into branches can be explained as a diffusion process, unrestricted diffusion into spines would be expected to lead to a much faster translocation. If there were free access, spines would be loaded with PKCγ in >1 s. On the other hand, if the neck of the spines served as a tight barrier, translocation of PKC into spines would not occur. Thus, the observed 5- to 20-s delay for translocation (Fig. 3, A and B) suggests that the neck of spines is not a diffusion barrier but instead imposes a diffusion constraint and delays diffusion access of PKCγ into spines.

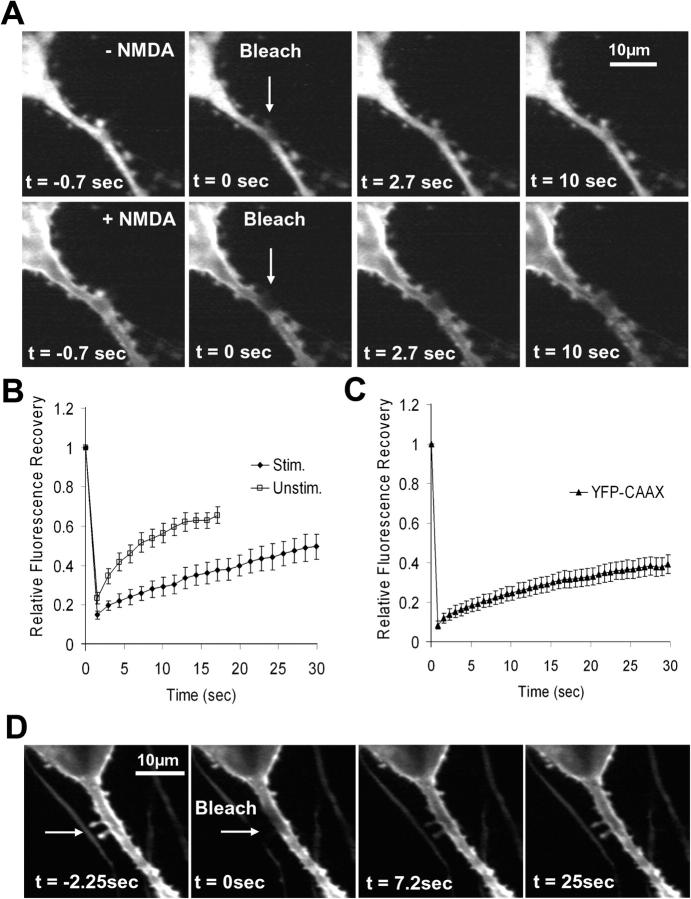
We used photobleaching recovery to directly measure the PKCγ exchange rates across the spine neck by photobleaching the YFP tag of PKCγ locally in the spine and by monitoring how the nonfluorescent protein in the spine exchanged with the fluorescent protein in the branch. Fig. 7 A shows an example of an individual photobleached spine. Time constants for half-maximal recovery ranged from 3 to 15 s in the absence of a stimulus, with spines that had longer necks typically recovering more slowly (Fig. 7, A [top] and B; the values were fit to the initial recovery rate). The mean half-maximal recovery was 12.8 s, with a standard error interval of 11.2–15.0 s (n = 17). We also measured the exchange time at elevated Ca²⁺ concentrations because this more closely matches the situation in which the PKCγ translocation response is observed after stimulation. Photobleaching the same spine after the addition of the glutamate receptor agonist N-methyl-d-aspartic acid (NMDA) resulted in a significantly slower recovery rate of fluorescence in the spine (Fig. 7, A [bottom] and B). The exchange ranged from 10 to >30 s and had a mean half-maximal recovery of 22.7 s, with a standard error of 17.9–31.1 s (n = 6). As a control, the exchange rate of a farnesylated and membrane-inserted K-Ras tail (YFP-CAAX; Fig. 7, C and D) was 53.8 s, with a standard error of 46.6–64 s (n = 12).

Figure 7.

Spine necks delay the translocation of PKCγ and reduce the accessibility of a membrane-bound marker protein. This suggests that spine necks isolate spines against short stimuli while still enabling enrichment of PKCγ as a result of prolonged responses or integrated receptor and electrical activity. (A) Photobleaching of YFP-PKCγ in individual spines is used to measure the rate of PKCγ exchange across the spine neck before (top) and after (bottom) stimulation with 30 μM of the glutamate agonist NMDA. Arrows indicate the spine that was photobleached. (B) Comparison of the average photobleaching recovery rates in unstimulated spines (n = 17) and in spines after glutamate addition (n = 6). (C) Test for potential membrane-diffusion barriers in the neck of dendritic spines. Photobleaching measurements of a membrane-inserted YFP-CAAX protein showed recovery rates comparable to that of PKCγ in the presence of glutamate (n = 12 spines), suggesting that the neck of spines delays diffusion access within the membrane but that there is no actual physical barrier to membrane diffusion.Error bars show SEM. (D) Example of a cell used in the measurements for C. Four confocal images showing the slow recovery of YFP-CAAX fluorescence after photobleaching of two spines (arrows) situated near each other on a thick dendrite.

This experiment shows that the spine neck functions as a diffusion constriction that imposes a delay for diffusion access for cytosolic proteins as well as for membrane-bound PKCγ and membrane-inserted prenylated proteins. Together, these measurements suggest that the delay in the translocation of PKCγ to spines (Fig. 3, A and B) can be explained by a constriction at the neck that reduces the available diffusion space and delays access to the spine.

Spines can function as geometric delay modules

Similar to the enrichment of PKCγ in thin branches depicted in Fig. 4, the enrichment factor for idealized spines, E_spine, can be determined from the different SVRs in spines versus main branches: SVR_spine = (π × d_spine ²)/(π × d_spine ³/6) = 6/d_spine and E_spine = 1.5 × d_branch/d_spine.

Because of the spherical versus tubular geometry, the enrichment factor is 50% higher than that of a fine branch with the same diameter. A comparison of the measured photobleaching recovery of spine PKC in unstimulated cells and the calculated access time can be used to make an estimation of the constriction imposed by the neck on PKC diffusion. For cytosolic diffusion access into spines, access time (ɛ) is calculated as follows: ɛ = 2/3 × d_spine ³ × l_neck/(D × d_neck ²), where l_neck and d_neck are the length and diameter, respectively, of the spine neck and d_spine is the diameter of the spine (Fig. 8 A).

Figure 8.

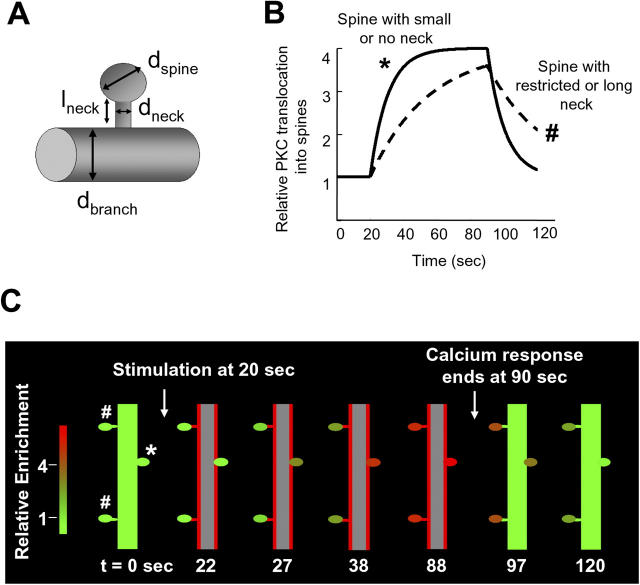
A model of the spine translocation process shows that spine necks provide a means to suppress subthreshold stimuli, integrate activity, and create local memory of past activity. (A) Diagram illustrating the parameters used to simulate translocation of PKCγ into dendritic spines. (B) Simulation of PKCγ translocation curves for two spines with different morphologies. Translocation was compared between a spine that only has a small neck or no neck at all and one that has a restricted neck. The spine with the small neck (*) is a fast-loading synapse and filled rapidly with PKC, unlike the spine with the restriction (#), which loaded much more slowly. (C) Schematic images were drawn by a MatLab program based on simulations of PKCγ translocation from a main branch into three different synaptic spines. One spine had no neck constriction, and two spines had neck constrictions because of long or narrow necks (see Materials and methods for model descriptions). Translocation into the spine without a neck was rapid and reversible, whereas the spines with restricted necks underwent a slow PKCγ recruitment behavior, and the protein remained in the spine for a much longer time than the spine with no neck. Red indicates a high concentration of PKCγ at the plasma membrane or in spines, whereas green shows a low concentration of PKCγ.

Using plausible estimates for typical lengths of necks of 0.5–1 μm (based on light and electron microscopy images and Fig. 3 A) and spine diameters of 0.5–1 μm, one can estimate from the photobleaching measurements that the boundaries for neck diameters may range from 15 to 120 nm (for a description and analysis of different shapes that contribute to this variability see Koh et al., 2002).

Given that spines with long necks have slower access times than those with short or no necks, we show in Fig. 8 B two calculated PKC translocation time courses. These calculations show that the surface-to-volume enrichment factor and the spine neck constriction can delay access to and retention of PKC in spines, leading to amplitude and time courses similar to those observed experimentally in Fig. 3 (A and B). This geometric attraction model is also plotted as a series of panels in Fig. 8 C, in which we depicted the translocation of PKC into two spines with a neck and one without a neck. In these calculations, PKCγ concentration only becomes significantly elevated within spines after a delay of several seconds and remains elevated in spines for a similar period after the response to the stimulus has ceased elsewhere in the cell. During this period, PKCγ remains in a position to be rapidly activated in response to Ca²⁺ signals.

In addition to a mode of operation in which Ca²⁺ signals are triggered across the dendritic arbor, it is likely that spine attraction can be used by cells when Ca²⁺ signals are local in the spine, so that PKCγ becomes trapped in the spine and achieves concentrations even higher than predicted by the enrichment factor. A higher than expected enrichment of PKCγ was in fact observed for several synapses in which the concentration increased threefold (Fig. 3 C), which is higher than that expected from the SVRs alone. Such a role for local synaptic Ca²⁺ signaling and local PKCγ attraction to individual spines is consistent with the earlier finding of NMDA receptor–mediated spine Ca²⁺ signals that can remain locally within the spine and only cause a minimal Ca²⁺ increase in the branch (Wickens, 1988; Sabatini et al., 2002). It is also interesting to note that the shape of the spine is plastic and has been shown to be regulated by electrical activity (Matsuzaki et al., 2004), suggesting that not only the amplitude of translocation but also the delay time of PKCγ access into spines can be regulated by electrical activity.

Discussion

Our study shows that glutamate and electrically triggered Ca²⁺ signals induce a translocation of PKCγ from the soma and thick branches into thin branches and across spine necks into postsynaptic terminals. This translocation process markedly increases PKC availability in spines and may provide a new type of molecular memory. We investigated the mechanisms that generate the delay in the translocation processes and found that the measured kinetics can be explained by a reduced PKCγ diffusion coefficient at elevated Ca²⁺ concentration and a diffusion constriction at the spine neck. The measured delay times suggest that PKCγ translocation is minimal in response to brief stimuli on a time scale of 1 s or less and that the translocation process integrates activity from electrical and receptor stimuli over time periods of seconds. The marked spread in the measured delay times of individual synapses is consistent with the notion that the shape of the constricting spine neck sets an integration or delay time constant for individual synapses. Because PKCγ is capable of regulating many targets within spines, it is plausible that the enrichment leads to a critical concentration of PKCγ that enables significant reorganization/regulation of synaptic proteins and channels.

In addition to functioning as an integration mechanism that increases PKCγ concentration, the delayed translocation out of branches and spines could also provide for a type of molecular memory process that enables individual synapses or branches to remain responsive to subsequent electrical and receptor stimuli. If a signal occurs within that time window, an elevated concentration of PKCγ may still exist in the synapse or branch and higher signaling responses can be triggered.

Roles of PKC in dendritic branches and postsynaptic spines

Our observation that PKC is drawn into thin branches may have important implications for the structure and function of the cell. PKC has been linked to the regulation of axonal as well as dendritic growth, based on the observation that inhibition of PKC blocks growth cone formation after neuronal injury (Geddis and Rehder, 2003) and prevents differentiation and neurite outgrowth in PC12 cells (Das et al., 2004). Many of the effects of PKC on neurites occur by phosphorylation of various cytoskeletal and structural proteins, such as the phosphorylation of the myristoylated alanine-rich C kinase substrate–related domain of adducin, the myosin heavy chain, and many others (Keenan and Kelleher, 1998). For example, spectrin and adducin are both components of dendritic spines and their regulation is likely to be critical in changing the morphology and reorganization of cytoskeletal structures (Matsuoka et al., 1998).

Within spines at the postsynaptic density, cPKCs have major roles in synaptic plasticity and are involved in both long-term potentiation and depression. Several groups have shown that inhibition of postsynaptic PKC prevents the induction of long-term potentiation (Malinow et al., 1989), whereas activation of PKC with phorbol esters results in the increased amplitude of excitatory postsynaptic currents (Carroll et al., 1998). Activation of PKC has also been found to cause rapid changes in the density and distribution of NMDA receptors at the synaptic membrane (Lan et al., 2001; Fong et al., 2002), and phosphorylation of the AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) receptor GluR2 subunit by PKC is believed to be a critical event in the removal of AMPA receptors from the membrane and induction of cerebellar long-term depression (McDonald et al., 2001; Chung et al., 2003).

Studies involving PKCγ-deficient mice further demonstrated the importance of PKC in neuronal development and plasticity. PKCγ is a neuron-specific isoform of PKC, and mice lacking this isoform exhibit mild deficits in spatial and contextual learning (Abeliovich et al., 1993), impaired motor coordination (Chen et al., 1995), and altered dendritic development (Schrenk et al., 2002). The large number of functional targets of PKC in neurons and the deficits seen in knockout mice imply that the conversion of Ca²⁺ signaling activity into an increased PKC concentration in spines and branches described in our study is likely to be a key part of the regulation of many of these PKC substrates.

Dendritic branches and spines as geometric attractors

Based on our study, we propose a more general model for plasma membrane–translocating signaling proteins that may contribute to shaping the neuronal signaling response. In the quantitative model that we developed, the thickness of branches and the constriction of spine necks serve as structural elements that regulate signal integration and enable a short-term molecular memory process. The key parameters in our model are the SVR that defines how much PKC enrichment can occur at a particular structure, the diffusion coefficients of PKC at the plasma membrane and in the cytosol, and the diffusion constriction of the spine neck. We derived equations that approximate the enrichment factors and the delay times and showed that a simulation of this geometric attraction model matches the observed translocation kinetics.

Because this geometric attraction process only depends on the translocation from the cytosol to the plasma membrane and back into the cytosol, it is plausible that the geometric attraction mechanism that applies to PKCγ also applies to other translocating proteins. Given the large number of signaling proteins with similar regulation by receptor-triggered plasma membrane translocation (C2, C1, and PH domains), it is likely that thin processes that extend from main branches or the soma are devoid of many of these signaling proteins in their basal state and that they are selectively loaded with signaling proteins by persistent or frequent, but not by short or infrequent, Ca²⁺, diacylglycerol, and/or phosphoinositide signals.

Finally, it is likely that the same type of geometric attraction process of proteins also occurs in other membrane-rich, elongated structures (such as filopodia and lamillipodia) and thus may take place in a variety of cell types that exhibit related morphological and geometric features (such as fibroblasts and astrocytes).

Materials and methods

Cell culture and transfection

Hippocampal neurons were cultured from 1-d-old postnatal Sprague-Dawley rats. The cells were dissociated by trypsinization and trituration and plated on 4-well chambered cover glasses (Lab-Tek; Nunc) coated with 1 mg/ml of poly-l-lysine (Sigma-Aldrich). The cell culture media consisted of MEM (Invitrogen) supplemented with 5% FCS (Invitrogen), 20 mM glucose, 10 mM Hepes, 0.5 mM sodium pyruvate, 2% B-27 supplement (Invitrogen), and 1 μl/ml of serum extender (Becton Dickinson). Cultures were maintained at 37°C in an atmosphere of 5% CO₂ and were transfected after 7–10 d in vitro. Each well of neurons was treated for 30 min at 37°C with a mixture of 2 μg DNA and 3 μl Lipofectamine 2000 in Opti-MEM buffer (50-μl transfection vol/well; Invitrogen). Neurons were subsequently returned to their original media and imaged 3–7 d after transfection.

DNA constructs

The GFP-PKCγ construct used in this study has been described previously (Oancea and Meyer, 1998; Oancea et al., 1998). YFP-PSD-95 was provided by D. Bredt (Stanford University, Stanford, CA), and the color was replaced with CFP (CFP-C1 vector; CLONTECH Laboratories, Inc.). M. Fivaz (Stanford University School of Medicine, Stanford, CA) cloned the YFP-CAAX construct, and T. Galvez (University of California, San Francisco, San Francisco, CA) made the YFP-PKCγ construct from the original GFP-PKCγ construct.

Live cell microscopy

Fluorescence confocal microscopy was used to monitor the translocation of GFP/YFP PKC fusion constructs in response to global bath application of glutamate or NMDA (typically 10–30 μM with 1–3 μM glycine), or electrical field stimulation. For experiments where PKC translocation was monitored in the presence of agents that disrupt the cytoskeleton, cells were incubated with either 100 nM latrunculin A (Invitrogen) or 5 μg/ml nocodazole (Sigma-Aldrich) for 1 h before the start of the time series.

In the case of electrical stimulation, neurons were grown in glass-bottomed plastic Petri dishes (World Precision Instruments) and stimulated using a plastic chamber insert containing parallel electrodes (Warner Instruments) attached to a stimulator unit (Astro-Med, Inc.) via a stimulus isolator (Warner Instruments). After the fifth image in each time course, transfected cells were stimulated using a train of pulses (50 Hz, 100 mA) every 2 s until the end of the time course. All experiments were performed at RT (22–25°C) in an extracellular buffer containing 5 mM KCl, 125 mM NaCl, 25 mM Hepes, 2 mM CaCl₂, and 30 mM glucose, but lacking magnesium to alleviate the Mg²⁺ block of the NMDA receptor.

Fluorescence images of GFP and RFP constructs were obtained using the 488-nm excitation line of a laser scanning confocal microscope (model Pascal; Carl Zeiss MicroImaging, Inc.) using the manufacturer's acquisition software, and emission was collected through a 505- to 550-nm band-pass filter and a 585 long-pass filter for the GFP and RFP fluorescence, respectively. Cells were imaged on the stage of an inverted microscope (Axiovert 100M; Carl Zeiss MicroImaging, Inc.) using a 40× plan-apo oil immersion objective (1.3 NA; Carl Zeiss MicroImaging, Inc.) or a 63× water objective (1.2 NA). To monitor the typical calcium responses generated by the application of glutamate or NMDA, neurons were incubated at 37°C in a solution containing 5 μM Fluo-3 AM (Invitrogen) for 20 min, washed, and imaged in the extracellular buffer mentioned in the preceding paragraph.

A spinning disk confocal microscope (model Nipkow; PerkinElmer) was used for dual color imaging using CFP- and YFP-labeled constructs. Cells were viewed using an inverted microscope (IX70; Olympus) with a 60× oil immersion objective (1.4 NA; Olympus), and images were acquired with a charge-coupled device camera (Orca II; Hamamatsu) and Metamorph acquisition software. CFP was excited with the 442-nm laser line of a helium-cadmium laser (Kimmon), whereas YFP was imaged with the 514-nm line of an argon ion laser (Melles-Griot). For FRAP experiments, the 514-nm line of a laser (model Enterprise; Coherent) at maximal power (∼35 mW) was used. By placing a 100-μm pinhole in the beam path, it was possible to bleach 80% of the YFP fluorescence in 50 ms in an area of the cytosol with a 6-μm diam.

Immunocytochemistry

After 1 min of treatment with 10 μM glutamate, cells were fixed for 10 min at RT with 4% PFA (Polysciences, Inc.). Slides were subsequently washed twice with PBS and kept in water at 4°C until used. Slides were then blocked with PBS and 0.1% Triton X-100 containing 1% normal goat serum (PBS/Triton; Jackson ImmunoResearch Laboratories), and incubated with the primary antibodies anti-PKCγ (2 μg/ml; Santa Cruz Biotechnology, Inc.) and anti-PSD95 (diluted 1:100 from the original stock; Sigma-Aldrich) overnight at 4°C in PBS/Triton. After three washes with PBS/Triton, cells were incubated with rhodamine-labeled goat anti–mouse IgG and fluorescein-labeled goat anti–rabbit IgG (Invitrogen) in PBS/Triton for 30 min at RT and washed three times with PBS/Triton.

Image analysis

Images were exported as 12- or16-bit tag image files, and fluorescence quantification was performed using Metamorph analysis software (Universal Imaging Corp.). After background subtraction, regions of interest were selected in the cytosolic area and plasma membrane of the soma or along the dendrites of each cell, and the average intensity was measured. In addition, the average intensity of the whole cell was measured, and these values were used to correct for general photobleaching or quenching of the dye after stimulation. For the measurement of PKC refilling after photobleaching in dendrites, we performed a linescan measurement, for which we recorded the fluorescence intensity from each pixel in a line selected along the length of the branch.

To monitor PKC recruitment into thin branches, thresholding and masking were performed on the RFP images and a ratio stack was generated for PKC/RFP. We measured the bleed through of the GFP signal into the RFP channel and found that it was negligible (2.6% on average; n = 12). Bleed through of RFP into the GFP channel was slightly more pronounced and was mainly attributable to the high expression of the fluorophore in the nucleus and cell soma rather than thin branches (7% average bleed through; n = 14).

To determine half-times of translocation, the ascending and plateau phases of the traces were fitted to the following exponential equation: y = a{1 − exp[−(x − 11)/τ]} + 1, where y is the normalized fluorescence intensity and x is the time. The time τ that corresponds to 50% of the translocation response was then derived from the fit.

Model calculations and simulation of diffusion into branches and spines

Diffusion models used for plotting Figs. 6 and 8 were based on Fick's law of diffusion and calculated using a Matlab program. The specific assumptions of the model are described in the main text and figure legends. In short, both simulations made the assumption that PKC translocates initially to the closest plasma membrane and then diffuses with a mixed coefficient in between the measured diffusion coefficients in the cytosol and at the plasma membrane. A conversion of the relative PKC concentration to a green-to-red color code was used by a Matlab program to paint the different thin branches and spines in the shown figures.

In the case of the diffusion into spines, the constriction at the spine neck was derived as follows:

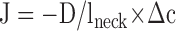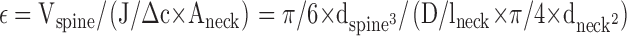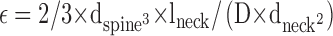See main text for details; ɛ is the time constant for PKC equilibration between the spine head and the branch; J is the flux of PKC into the spine; D is the apparent PKC diffusion coefficient; Δc is the PKC concentration difference between spine head and branch; V_spine and d_spine are the spine volume and diameter, respectively; and l_neck and d_neck are the length and diameter of the spine neck, respectively.

Online supplemental material

Video 1 shows the translocation of GFP-PKCγ to the plasma membrane of the soma and dendrites after electrical field stimulation. Video 2 shows electrical stimulation inducing translocation of GFP-PKCγ to the membrane of thick dendrites without affecting PKC in the soma. Video 3 shows glutamate-induced translocation of GFP-PKCγ into spines. Video 4 shows glutamate stimulation inducing GFP-PKCγ translocation along fine branches protruding from the main dendrites of the cell. Fig. S1 shows electrical stimulation resulted in translocation of PKC to the plasma membrane of dendrites, whereas levels of PKC in the soma cytosol remained unchanged in 50% of the cells examined. Fig. S2 shows the translocation of PKC into dendritic spines upon glutamate or electrical stimulation. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200503118/DC1.