Two modes of exocytosis at hippocampal synapses revealed by rate of FM1-43 efflux from individual vesicles

Abstract

We have examined the kinetics by which FM1-43 escapes from individual synaptic vesicles during exocytosis at hippocampal boutons. Two populations of exocytic events were observed; small amplitude events that lose dye slowly, which made up more than half of all events, and faster, larger amplitude events with a fluorescence intensity equivalent to single stained synaptic vesicles. These populations of destaining events are distinct in both brightness and kinetics, suggesting that they result from two distinct modes of exocytosis. Small amplitude events show tightly clustered rate constants of dye release, whereas larger events have a more scattered distribution. Kinetic analysis of the association and dissociation of FM1-43 with membranes, in combination with a simple pore permeation model, indicates that the small, slowly destaining events may be mediated by a narrow ∼1-nm fusion pore.

Introduction

Vesicular exocytosis is an intricate process with multiple steps leading to the fusion of vesicle and plasma membranes and consequent release of transmitter (for review see Jahn and Sudhof, 1999). Increasing evidence indicates that exocytosis can proceed through distinct mechanisms (Neher and Marty, 1982; Klingauf et al., 1998; Ales et al., 1999; Stevens and Williams, 2000; Klyachko and Jackson, 2002; Wang et al., 2003); full fusion involving the collapse of the vesicle or granule membrane into the plasmalemma and “kiss-and-run” exocytosis where a transient fusion pore connects the lumen of the vesicle to the extracellular space and vesicular contents are released without the vesicle fully collapsing into the plasma membrane. In neuroendocrine cells, both mechanisms contribute to exocytosis, but until recently technical limitations have prevented the investigation of these processes in the fusion of small synaptic vesicles (SVs).

In addition to providing a model for efficient exocytosis, kiss-and-run also provides a mechanism for very rapid recycling of vesicles (Pyle et al., 2000; Aravanis et al., 2003b). An important conceptual advance in this area comes from recent work indicating that blockade of clathrin-mediated endocytosis via an endophilin mutant (Verstreken et al., 2002) reduced release at the Drosophila melanogaster neuromuscular junction, leaving one component of release intact. This finding indicates that a significant fraction of vesicles recycle via a clathrin-independent mechanism—probably kiss-and-run exocytosis. At the same time, this work confirms the importance of clathrin- and dynamin-dependent mechanisms reported previously (Koenig and Ikeda, 1989; Takei et al., 1996), indicating that both recycling routes operate in parallel. This finding is consistent with work from many preparations indicating that at least two distinct mechanisms contribute to endocytosis, which can coexist in the same nerve terminals (Koenig and Ikeda, 1996, 1999; Richards et al., 2000, 2003; Gandhi and Stevens, 2003).

The study of small SV exo- and endocytosis in nerve terminals has been extended by the development of optical techniques to track vesicle cycling (Betz et al., 1992; Ryan et al., 1993; Sankaranarayanan and Ryan, 2000; Gandhi and Stevens, 2003; Aravanis et al., 2003b). In particular, FM dyes have been used to demonstrate that in some cases exocytosis terminates before the complete escape of FM1-43 from labeled vesicles, an observation most compatible with kiss-and-run exocytosis (Aravanis et al., 2003a,b).

In the present work, we build on the advances of Aravanis et al. (2003b). Using a slightly different approach, we have extended this type of analysis and derive a statistical distribution of both subquantal destaining events and putative full fusion events and show that they consist of largely nonoverlapping populations, indicating that two distinct modes of exocytosis operate at hippocampal synapses. The destaining kinetics of each population were also analyzed, revealing that they differed markedly, which is again consistent with distinct exocytic modes. To place our results in a biophysical context, we characterize the interaction between FM1-43 and SV membranes and interpret our results in terms of a vesicular fusion pore. The fastest, putative full fusion events lose their fluorescence rapidly, with kinetics sufficiently fast to be equally consistent with unhindered membrane departitioning or diffusion in the plane of the bilayer (Zenisek et al., 2002). The slower kiss-and-run class of events, which complete before all the dye is lost, are incompatible with either model. These putative kiss-and-run events are tightly clustered in their rate constants, and so support a model in which exocytosis occurs through a fusion pore that prevents lipid mixing. This small conductance pore might then either dilate via intercalation of lipids (Lindau and Almers, 1995), leading to full fusion of the vesicle and plasma membranes, or reverse to close the pore.

Results

Characterization of FM1-43 uptake

FM1-43 staining and destaining has become an important technique for studying vesicle turnover in nerve terminals. To extend this approach to individual vesicles, it is necessary to determine the approximate fluorescence of single vesicles labeled with FM1-43. Electron microscopy with photoconverted FM1-43 has demonstrated that there are ∼30 recycling vesicles within hippocampal boutons (Schikorski and Stevens, 1997, 2001; Harata et al., 2001). Although the change in fluorescence due to the destaining of individual vesicles is below signal to noise in experiments where most cycling vesicles are labeled, it follows that if only a very few vesicles per nerve terminal contain FM1-43, the change in signal due to individual exocytic events will become resolvable (i.e., the signal to noise ratio becomes more favorable). It is well established that the brightness of FM1-43 fluorescence saturates with increasing stimulation. As a result, it becomes possible to calculate an approximate calibration curve for the amount of stimulation that gives rise to the labeling of only a handful of SVs (<8 per bouton).

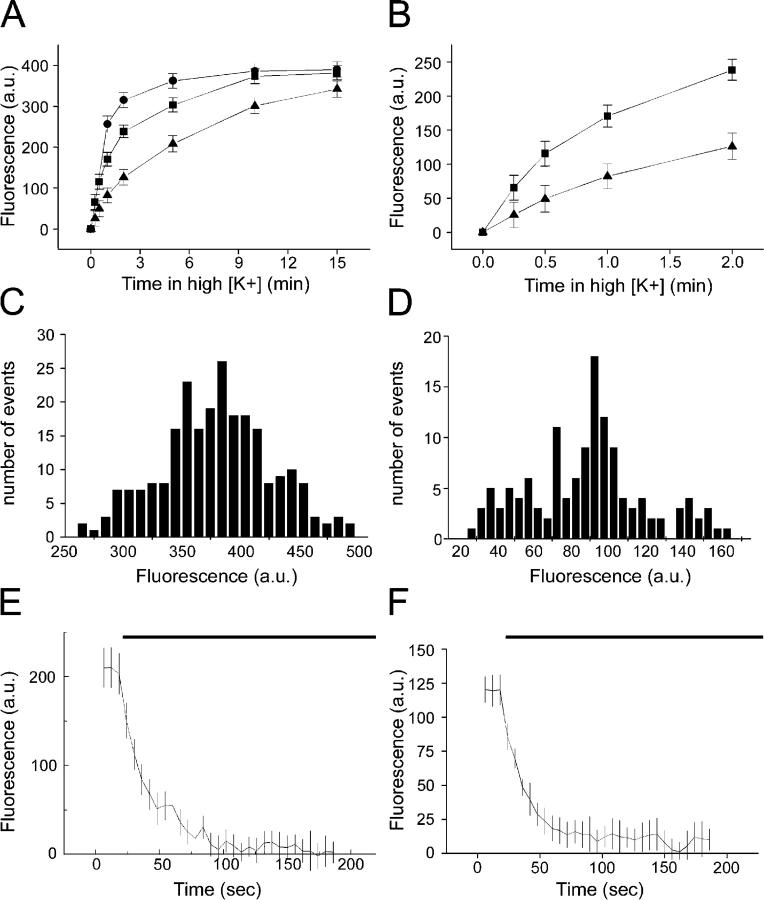
In Fig. 1 A, we show the relationship between length of time in elevated K⁺ concentration and FM1-43 fluorescence in synaptic boutons. The final saturating level of fluorescence was the same for three separate concentrations of K⁺ (25, 40, and 70 mM), although the length of stimulation required to reach that level differed. Fig. 1 B shows an expanded portion of this plot, focusing on the first 2 min in 25 and 40 mM potassium. If ∼400 fluorescence units correspond to an average of 25 vesicles, then one would predict that incubation for 1 min in 25 mM K⁺ would lead to the labeling of approximately five vesicles per nerve terminal. In Fig. 1 (C and D), we compare histograms of bouton intensity from individual coverslips labeled with either 70 mM K⁺ for 10 min or 25 mM K⁺ for 1 min. No pattern underlying the distribution of fluorescence intensities from the strong loading conditions was seen. However, the fluorescence intensities of boutons labeled with a weak protocol might have been expected to show quantal fluctuations in fluorescence intensity. This was not the case, for reasons described in the Discussion. Finally, we compared the rates of destaining of these two groups of boutons in response to a 70-mM K⁺ challenge (Fig. 1, E and F), which revealed similar destaining kinetics, suggesting that the vesicles labeled with the weak protocol were randomly mixed within the overall cycling vesicle pool.

Figure 1.

Loading different fractions of the cycling vesicle pool at hippocampal boutons. Data are from four to six coverslips per treatment, and >100 boutons were analyzed. (A) Comparison of the uptake of 4 μM FM1-43 by boutons when stimulated for varying lengths of time in either 25 (triangles), 40 (squares), or 70 mM K⁺ (circles). (B) Expansion of the first 2 min of A. (C) Distribution of fluorescence intensities of maximally loaded boutons. (D) Distribution of fluorescence intensities of boutons containing only three to eight labeled vesicles (25 mM K⁺ for 1 min). Note the absence of clear quantal peaks. (E) Destaining kinetics of maximally loaded boutons stimulated with 70 mM K⁺ during the time indicated by the bar. (F) Destaining kinetics of weakly loaded boutons stimulated with 70 mM K⁺ during the time indicated by the bar. Note that E and F were obtained using different settings, so the y-axes are not comparable.

Minimally loaded boutons destain with discontinuous steps

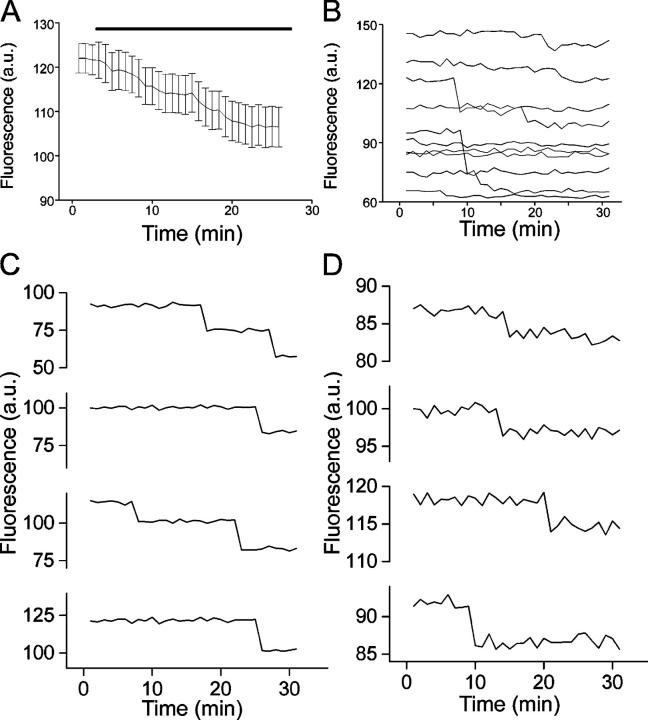
To maximize the resolution of destaining events, we monitored bouton destaining during mild (12 mM) depolarization with long acquisition periods (2 s). Fig. 2 A shows that this level of depolarization gives rise to a modest decrease in fluorescence intensity when averaged across boutons. When we examined the destaining profiles of individual boutons a different picture emerged. As illustrated in Fig. 2 B, the fluorescence in individual boutons remained flat for lengthy periods interspersed with abrupt drops in intensity. Although some of these abrupt drops in brightness matched our estimates for the fluorescence intensity of single vesicles (Fig. 2 C), other events were clearly of smaller amplitude (Fig. 2 D). A complete distribution of events (signal + noise) is provided in Fig. S4 B (available at http://www.jcb.org/cgi/content/full/jcb.200407148/DC1). The analysis procedure is described in detail in the online supplemental material.

Figure 2.

Destaining of weakly labeled boutons is discontinuous during mild depolarization. (A) Ensemble average of boutons labeled as in Fig. 1 D with destaining stimulated by 12 mM K⁺. Data from 115 boutons from four coverslips. (B) Fluorescence traces from individual boutons reveal stepwise drops in fluorescence intensity. (C) A gallery of large (>14 fluorescence units) stepwise destaining events. (D) A gallery of small (<10 fluorescence units) stepwise destaining events.

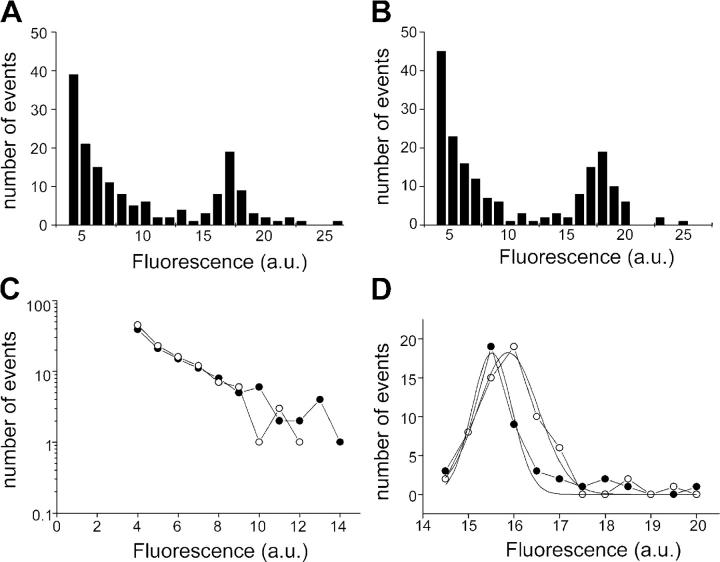
To provide an illustration of the lack of variability between preparations, we plotted frequency histograms of step amplitudes from two separate batches of cultures in Fig. 3 (A and B). In each case there are many events declining exponentially in frequency as they increase in amplitude. In addition to these small events, there is an additional component of larger events with amplitudes corresponding to the estimated single vesicle fluorescence.

Figure 3.

The distribution of fluorescence steps reveals two populations of events. (A and B) Two separate sets (batches of cultures, four to six coverslips each) of pooled events analyzed for the extent of fluorescence decline in individual steps. A similar distribution is seen in each case. (C) The events of smaller amplitude (<14 units) are linear on a semi-log plot, indicating that they can be described by a single exponential distribution. Closed circles are data from A, open circles are data from B. (D) Larger amplitude events (>14 units) show a normal distribution with a peak around 16 units. Closed circles are data from A, open circles are data from B.

By combining the data from Figs. 1–3 we can estimate the size of the recycling pool in these experiments and the number of vesicles labeled. Maximum bouton fluorescence in these experiments was ∼400 units. If single vesicle fluorescence is 16 units, then this would correspond to ∼25 recycling vesicles per bouton, which is in line with previous measurements of the recycling pool in the hippocampus (Schikorski and Stevens, 1997, 2001; Harata et al., 2001), and indicates approximately seven labeled per bouton in the minimal labeling experiments.

If different mechanisms contribute to the two populations of destaining events, this might be revealed by the shape of their amplitude distributions. In Fig. 3 C, we plotted the distribution of small events on a semi-log scale. The good linear relationship suggests that the distribution of small events is governed by a single exponential, comparable to an ion channel with a single open state. In contrast to the exponential distribution seen in small events, the putative quantal events displayed a normal distribution, which is well fitted by a Gaussian curve (Fig. 3 D). The different types of distribution seen for small and large events lead us to conclude that they are governed by distinct mechanisms.

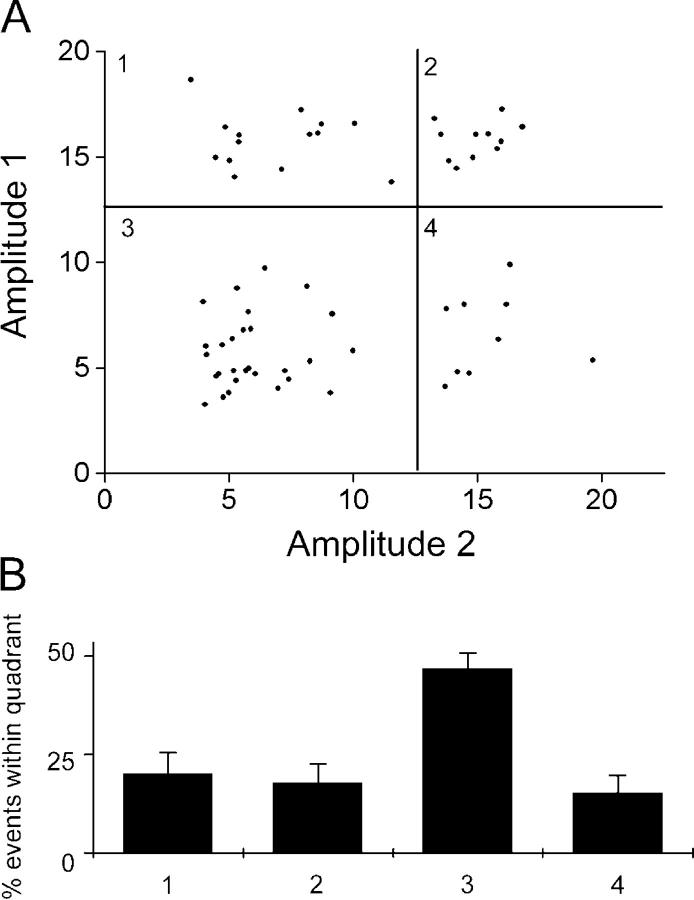
Because GABAergic and glutamatergic nerve terminals differ in their exocytic apparatus (Rosenmund et al., 2002), different kinds of boutons might underlie the two populations of release events seen in our experiments. We investigated this possibility by asking whether or not individual boutons showed both small and large exocytic events. We looked at the first two events from boutons, which showed at least two destaining steps, and plotted the amplitude of the first event against that of the second event (Fig. 4 A). All four possibilities were observed, as quantified on a quadrant basis in Fig. 4 B. No clear trends were evident, although individual boutons may have a different overall balance of small and large events. This finding indicates that the two populations of destaining events are not due to heterogeneity of bouton type. It should be noted that, in contrast to the work by Aravanis et al. (2003b), this likely reflects exocytosis of separate vesicles, not repeated exocytosis of a single vesicle.

Figure 4.

Traces from individual boutons show both large and small events. (A) 62 boutons showing at least two events were analyzed. The amplitude of the first stepwise destaining event was plotted against that of the second. Large and small events were distinguished by a threshold of 14 fluorescence units, indicated by the bold lines; this separated events into four quadrants, numbered 1 through 4, which were then quantified in B. (B) Events were seen in all four quadrants from A. Quadrant 3, small events followed by a second small event, was the most prominent, but occurred in line with the greater proportion of small events seen under these conditions. Overall, the expected distribution would be Q3 > Q1 = Q4 > Q2, and it is not significantly different from this, although the difference between Q3 and the other quadrants is the only one that is significantly different. Error bars are SEM.

Small destaining events lose dye with slower kinetics than large events

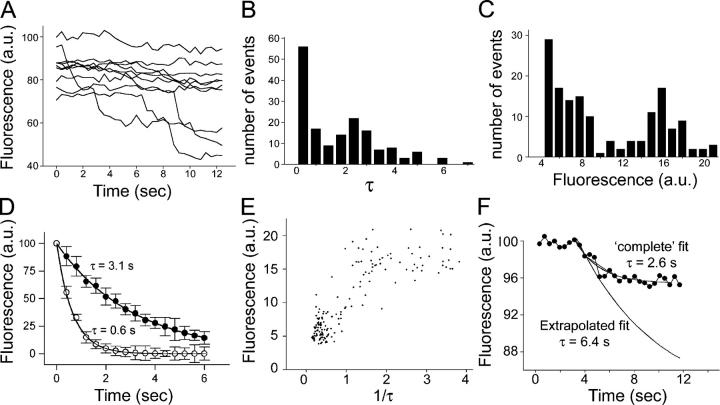
If vesicles undergo full collapse into the plasma membrane they would be expected to lose their dye at a rate limited only by the lateral diffusion within the membrane and the departitioning kinetics of the dye, whereas permeation through a narrow fusion pore might be expected to significantly slow the rate of efflux of the dye. To follow the dye efflux rate, we increased the pixel binning and imaged at 400 ms per time point. We also increased the depolarizing stimulus to 25 mM K⁺, which provided a sufficient number of destaining events while still not causing temporally overlapping events at individual boutons. As we show in Fig. 5 A, although some boutons did not release dye during the stimulus period, others showed clear and abrupt diminutions in brightness. When examined closely, these could be seen to no longer have the step function seen in previous experiments; rather, they showed a more gradual reduction in intensity. These individual destaining events were fitted to single exponentials. The distribution of τ values obtained from such fits are plotted in Fig. 5 B, and the distribution of amplitudes is plotted in Fig. 5 C. In the case of both τ and amplitude, the results fell into two groups, suggesting that two exocytic modes underlie release at these synapses. We were able to separate them with a threshold of 14 fluorescence units, and measure the time course of averaged events (Fig. 5 D), providing average values of τ = 0.65 ± 0.04 s for large amplitude events and τ = 3.11 ± 0.12 s for small events, indicating that they are kinetically distinct.

Figure 5.

Small and large events lose their dye contents with different kinetics. (A) Example traces of boutons labeled with 25 mM K⁺ for 1 min, and then subsequently stimulated with 25 mM K⁺. Imaging frequency was 2.5 frames per second. The abrupt drops in fluorescence intensity no longer occur in a strictly stepwise fashion. 162 events from ∼300 boutons were analyzed in B–E. (B) The exocytic events were fit with single exponentials. τ values are plotted against frequency, and once more exhibit two apparent populations. (C) The amplitude of the drops in fluorescence are plotted against frequency as in Fig. 3 (A and B), and provide a similar pattern. (D) Large (>14 units; open circles) and small amplitude (<14 units; closed circles) events were time aligned and averaged, providing group mean time constants of 0.65 ± 0.04 and 3.11 ± 0.12 s, respectively. (E) The rate constant (1/τ) is plotted against the amplitude of the fluorescence drop. Small events are tightly clustered in both rate constant and amplitude, whereas large events are more variable especially in rate constant. (F) If considered more rigorously, small amplitude events would be expected, according to our hypothesis, to show a behavior where they initially present an exponential decline, which is truncated before completion (by fusion pore closure, in our model). To demonstrate the effect of this on our simple exponential fits (D and E), we have plotted a small amplitude event with an average time course (2.6 s). When we make the assumption that had destaining continued to completion it would have reached a net fluorescence drop of 16 units, and conducted the fit assuming it was interrupted (i.e., by progressive truncation of the trace), we find that the new value for τ is 6.4 s. When performed for all events in this category, we find the mean τ of dye efflux to be 7.16 ± 0.97 s. Error bars are SEM.

To illuminate the relationship between amplitude (amount of FM1-43 lost during single events) and the rate of dye loss (expressed as 1/τ), these parameters are plotted against each other in Fig. 5 E. The data form two clusters: a tight cluster of small events that lose their dye slowly and a diffuse cluster of larger events that lose their dye more rapidly. This is consistent with a model where the amount of dye and the rate of efflux are both limited in parallel by the fusion pore.

Events where FM1-43 destaining was incomplete would be expected to show truncated kinetics (i.e., dye loss will proceed at a certain rate until the presumed fusion pore closes, at which point dye loss would be expected to cease). Consequently, we further analyzed small amplitude events using a truncated exponential model, consisting of a single exponential decline, followed by an abrupt flat line. The fits were constrained by assuming that the “true” amplitude of vesicle fluorescence was 16 units. A representative example is shown in Fig. 5 F. As this example shows, the effect of this truncation is to reduce the apparent τ of destaining; consequently, the τ values for small amplitude events in Fig. 5 (B, D, and E) are probably underestimates, and consequently represent a lower limit for the true τ of destaining. Using this alternative approach, we determined the mean τ of destaining during all small events to be 7.16 ± 0.97 s.

Kinetics of FM1-43 binding to membranes

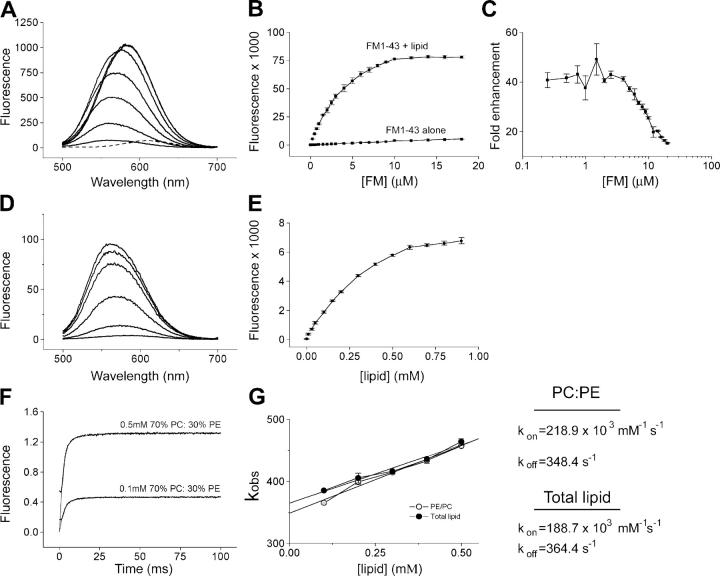
To further interpret our data on vesicle destaining, we performed a detailed analysis of FM1-43 binding and unbinding to and from model membranes. Equilibrium measurements (Fig. 6, A–E) revealed that FM1-43 fluorescence increases ∼40-fold on binding to liposomes (compared with the ∼350-fold enhancement seen on addition of detergent; Henkel et al., 1996), whereas at concentrations above ∼4 μM, the enhancement seen on addition of lipid diminishes sharply. Next, we examined the kinetics of this reaction using a rapid mixing stopped-flow method. FM1-43 concentration was kept constant (4 μM), whereas the liposome concentration was varied from 0.1–0.5 mM. Liposomes composed of synthetic lipids (70% 1,2-dioleoyl-sn-glycero-3-phosphocholine [PC]/30% 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine [PE]) and liposomes formed from purified total brain lipid were compared, and lipid composition was found to have a minimal influence on the k _on and k _off (Fig. 6, F and G).

Figure 6.

Characterization of FM1-43–membrane interactions. (A) Titration of liposomes (0.2 mM lipid composed of 70% PC/30% PE) with FM1-43. Thin lines are fluorescence spectra of FM1-43 with increasing concentrations of FM1-43 (0.25, 1.0, 2.5, 5.0, 8.0, 14.0, and 18.0 μM), and the dashed line is 18 μM FM1-43 without liposomes. (B) Quantification of spectra from A expressed as integrated fluorescence (500–700 nm). Data are the mean of three separate experiments plus SEM. (C) The ratio of fluorescence intensity of FM1-43 with and without liposomes, expressed as fold enhancement. (D) Titration of 4 μM FM1-43 with liposomes. From bottom to top the lipid concentrations are 0.01, 0.1, 0.3, 0.6, 0.8, and 0.9 mM. (E) Quantification of D with error bars showing SEM. (F) Two representative traces from stopped-flow experiments where FM1-43 and liposomes are mixed rapidly (∼1 ms dead time). In each case both the data and single exponential fits are shown. (G) Exponential fits from stopped-flow data provide k _obs, which is plotted against lipid concentration for both synthetic liposomes (70% PC/30% PE) and liposomes formed from purified total brain lipid. Assuming pseudo first order kinetics, k _on and k _off were calculated as detailed in Materials and methods.

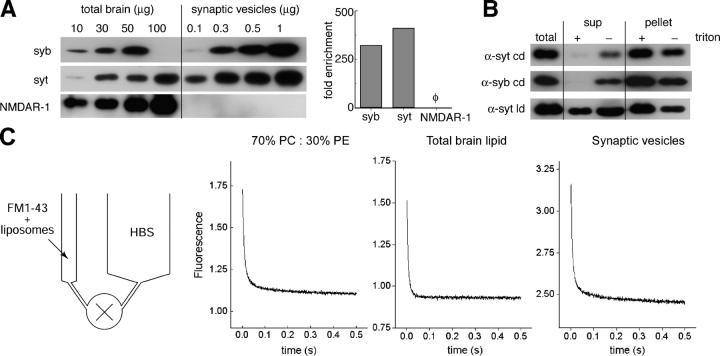
Finally, we assayed the rate of FM1-43 departitioning from three different model membranes, once again using a rapid mixing stopped-flow system (Fig. 7, A–C). FM1-43 (4 μM) was allowed to equilibrate with liposomes (0.1 mM) or SVs; then, samples were rapidly mixed with buffer. Syringes of different volumes were used to provide a 1:11 dilution in the mixing chamber. Again, mixing itself was rapid (∼1 ms dead time). Fig. 7 C shows dilution curves for synthetic lipids (70% PC/30% PE), total purified brain lipids, and SVs, respectively. In each case, the reactions are rapid, reaching completion in well under 500 ms. The resulting curves were best fitted with two exponentials: a fast component of <10 ms and a slow component of ∼100 ms (see Table I for values). If the two leaflets of SVs differed radically in the rate with which FM1-43 departitioned from them, we would have seen additional kinetic components because the SVs are ∼20% in reversed orientation (Fig. 7 B). Although there are differences between the conditions, the data suggest that lipid composition and protein complement make only modest contributions to the departitioning kinetics of FM1-43. Armed with this information, we were able to further interpret the SV destaining data presented in Figs. 1–4.

Figure 7.

FM1-43 rapidly disassociates from liposomes and SVs. (A) Purity of the SV preparation. (left) SVs were blotted for the SV proteins synaptobrevin (syb) and synaptotagmin (syt), as well as the postsynaptic NMDA receptor (NMDAR-1), and visualized by enhanced chemiluminescence. mAbs against synaptobrevin (69.1) and NMDAR-1 (54.1) and a polyclonal antibody against the C2B domain of synaptotagmin were used. Total rat brain homogenate served as a reference to calculate the fold enrichment of synaptotagmin, synaptobrevin, and NMDAR-1 after purification and concentration procedures. (right) Blots shown in the left panel were quantified by densitometry and plotted as fold of enrichment of total protein from rat brains. SV markers, synaptotagmin and synaptobrevin, were enriched ∼300–400-fold, whereas the postsynaptic NMDA receptor was not detected in the SV preparation. (B) A significant fraction (∼20%) of SVs are flipped inside-out during purification. mAbs against the cytoplasmic domain (cd) of synaptotagmin (41.1) and synaptobrevin (69.1), as well as the luminal domain (ld) of synaptotagmin (604.1), were used for immunoprecipitation as described in Materials and methods. In the presence of Triton X-100, 41.1 and 69.1 completely immunoprecipitated synaptotagmin and synaptobrevin. However, in the absence of detergent, a small fraction (∼15–20% of total protein) of synaptotagmin and synaptobrevin were protected from immunoprecipitation by the antibodies. When antibodies against the luminal domain of synaptotagmin (604.1) were used, a small but significant fraction of synaptotagmin was immunoprecipitated in the absence of Triton X-100. (C) Departitioning kinetics of FM1-43 from membranes. 4 μM FM1-43 was mixed with model liposomes composed of 30% PE/70% PC (0.2 mM lipids), total brain lipids (0.2 mM lipids), or purified SVs, as indicated, and then loaded into a small syringe (see schematic, left). HBS was loaded into a separate, larger syringe. Rapid mixing of the contents of the two syringes resulted in a 1:11 dilution of the FM1-43 and the liposomes. Dilution led to a rapid dissociation between FM1-43 and the liposome membranes or SVs and a consequent decrease in fluorescence intensity.

Table I. Kinetics of FM1-43 departitioning from membranes.

Liposomes	Fast τ	Fast amplitude	Slow τ	Slow amplitude
	ms	%	ms	%
70% PC/30% PE	7.9	88	96.3	12
Total brain lipid	5.7	92	31.1	8
Synaptic vesicles	7.4	88	121.3	12

Setting limits on vesicle destaining

Multiple modes can be considered for the escape of FM1-43 from SVs. The simplest case is that the dye rapidly diffuses out in the plane of the membrane once the bilayers fuse, as recently described by Zenisek et al. (2002) in experiments using goldfish retinal bipolar neurons. Equally simple in kinetic terms is the situation where departitioning of the dye from the membrane dominates. In contrast, a mode of exocytosis mediated solely by a lipid impermeant fusion pore relies on two kinetic steps: unbinding of FM1-43 from the membrane balanced by the flux of aqueous FM dye through the fusion pore. All three modes are illustrated in Fig. 8 A.

Figure 8.

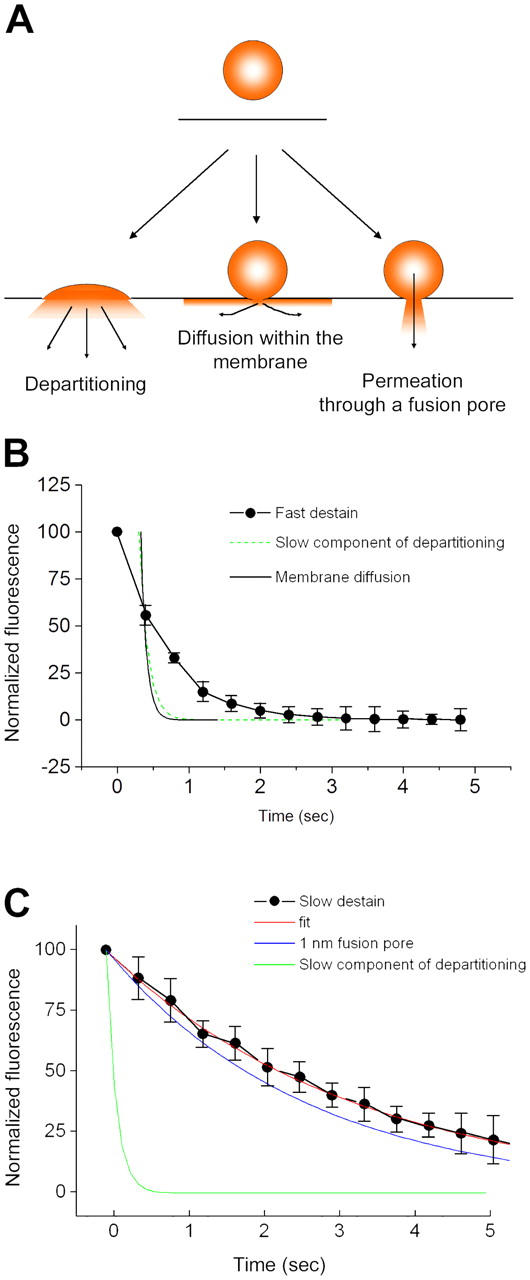
Mechanisms of FM1-43 efflux from exocytosing SVs. (A) Schematic diagram illustrating possible modes by which FM1-43 might leave SVs during exocytosis. If vesicles fully collapse into the plasma membrane, FM1-43 could escape by direct departitioning into the bulk solution. Alternatively, dye could escape through even a tiny fusion pore if the pore was lipidic and allowed mixing of vesicular and plasma membrane components, as a result of diffusion within the bilayer. The final possibility is that a small aqueous pore opens, the constituents of which form a barrier to diffusion of FM1-43 within the membrane. (B) Examination of the kinetics of fast destaining events, using the averaged values from Fig. 5 D. Because the fastest events occur at a rate similar to the sampling frequency, we cannot be certain when the drop in fluorescence actually begins. Consequently, the data do not fall all that far from a τ of ∼120 ms, which is the rate of the slow component of departitioning we observed in our stopped-flow experiments. As a result of the limitations of the imaging frequency, we cannot readily distinguish between FM1-43 leaving vesicles by diffusion within the membrane and leaving by direct departitioning. (C) Examination of the kinetics of slow destaining events. The averaged curves are replotted from Fig. 5 D. The slow component of membrane departitioning is much too slow to account for the kinetics by which FM1-43 escapes from vesicles. Instead, we have compared the rate of efflux of FM1-43 with simple diffusion-limited permeation through an aqueous pore with an opening of 1 nm. There is a fairly close agreement between this and the experimental data, although this model does not take into account any electrostatic interactions or geometric constraints, which might tend to slow the dye efflux. Error bars are SEM.

In Fig. 8 B, we plotted the rate of destaining during a fast event (from Fig. 5 D). Sampling limitations mean that we cannot be certain of the time of the beginning of the destaining event. As a result, the kinetic tail we observed is all that can be fitted. This residual portion of the kinetic does not agree very well with the rate predicted by FM1-43 departitioning from membranes, but it is not very far away. For comparison, we also superimposed the faster rate of membrane diffusion of FM1-43. This rate was calculated via the equation τ = ω²/4D, where ω is the radius of the regions of interest (∼200 nm). The value of D, 1.2 μm²/s, is taken from direct measurement of this property by Zenisek et al. (2002). Although the rate of diffusion within the membrane is faster than the residual kinetics of dye loss (Fig. 8 B), we cannot readily distinguish between the two. Interestingly, the faster edge of the population of large amplitude events does agree well with these two theoretical modes (unpublished data). As a result, the speed of either membrane departitioning or diffusion within the bilayer away from the bouton is reasonably consistent with our data. A possible interpretation of this would be a rapidly expanding fusion pore that results in the complete collapse of the vesicle into the plasma membrane.

If large destaining events lose dye through an expanding fusion pore, what might be the mechanism underlying the small, slower events? In Fig. 8 C, we plotted the rate of destaining during slow events (using the overall group average obtained in Fig. 5 D). In this case, the kinetics of dye loss are much slower than can be explained by unhindered departitioning. A simple explanation would be that the FM1-43 is escaping through a constricted fusion pore that does not permit the molecule to diffuse within the outer leaflet of the bilayer.

If this is the case, the size of the pore can be estimated using a simple pore permeation model. Because k _on and k _off are significantly faster than the measured k _efflux, permeation through the pore, a first order reaction, must be the rate-determining step. If the rate of dye efflux is driven by diffusion, then the relationship between efflux rate, diffusion coefficient D, pore radius r, pore length l, and concentration c is: efflux rate = πr² DcN_A/(l + πr/2) (Hille, 1992). If the pore is 1 nm (Klyachko and Jackson, 2002), the τ is 2.5 s within the range seen in these experiments for slow destaining events. This value is similar to the ensemble average (3.11 s) but faster than revealed by the truncation analysis, suggesting that exocytosis may proceed through a subnanometer pore.

An in vitro model of FM1-43 efflux from vesicles

To better understand the kinetics of dye flux through fusion pores, we examined the influence of a small pore on the rate of FM1-43 efflux from the inside of vesicles in a model system. We chose melittin, a small toxin peptide that can spontaneously form 1.3–2.4-nm pores in membranes (Matsuzaki et al., 1997). To measure the rate of dye efflux from within liposomes, synthetic liposomes (70% PC/30% PE) were formed in the presence of FM1-43. Under control conditions (i.e., no toxin), these retained their fluorescence. However, on the addition of toxin, the liposomes lost their dye with a τ of ∼16 s (Fig. S1, available at http://www.jcb.org/cgi/content/full/jcb.200407148/DC1), and this effect was independent of toxin concentration (unpublished data). This approach gave us a rate of dye loss due to both pore formation and dye permeation through the resulting pores.

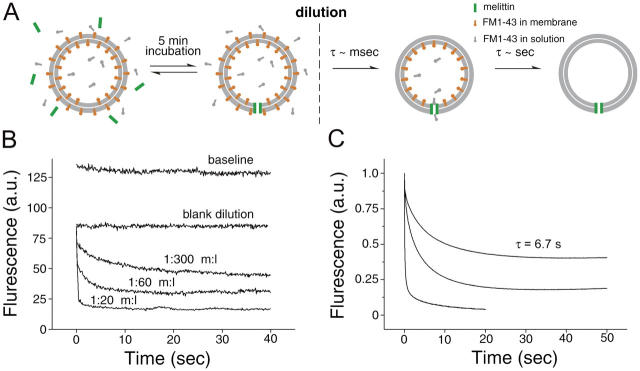
To determine the influence of the pore on dye efflux, we allowed the pores to fully assemble, and then observed the loss of FM1-43 after rapid dilution. Liposomes harboring FM1-43 in both internal and external leaflets were incubated with melittin for 5 min to allow pore formation. The resultant liposomes with melittin pores contained FM1-43 in equilibrium with the external solution (4 μM FM1-43). Liposomes were then rapidly diluted into buffer within a cuvette and the fluorescence was monitored (the experimental procedure is outlined in Fig. 9 A). The loss in fluorescence has two components: a rapid phase of ∼8 ms (i.e., the time course of dye departitioning from the outer leaflet of membranes; Fig. 7), which is too fast for observation in these experiments, and a slower phase that reflects the rate of dye leaving the liposomes via a small pore. After dilution, a slow phase of fluorescence decline was observed (Fig. 9 B), which reflects the rate of dye efflux through fully assembled melittin pores. As the ratio of melittin to lipid was increased from 1:300 to 1:60 and 1:20, the rate of dye loss also increased. This increase in rate is due to an increase in the total number of pores and/or an increase in the diameter of the pores.

Figure 9.

Melittin as a model for efflux of FM1-43 though nanometer size pores. We investigated the rate of FM1-43 efflux through pores by preforming the pores in the presence of 4 μM FM1-43 for 5 min, so that inner and outer leaflets were in equilibrium. (A) An outline of the experimental procedure. Rapid dilution caused the departitioning of FM1-43 from both leaflets—rapidly from the outer leaflet (τ = ∼8 ms; see Fig. 7) and with a slower rate from the inner leaflet that was dependent on the pore density. (B) Hand-mixing experiments. The baseline trace shows the fluorescence from liposomes diluted into buffer that contained 4 μM FM1-43; this trace provides a reference for the maximum signal from these samples. The blank dilution sample was diluted with buffer alone (i.e., no FM1-43 or melittin); the drop in fluorescence compared with the baseline is due to departitioning of the dye from outer leaflet and provides the reference for the fluorescence from FM1-43 in the inner leaflet of the liposomes. In samples preincubated with melittin, a slow phase of fluorescence decline was observed (B), reflecting the rate of dye efflux through fully assembled melittin pores. (C) Rapid mixing stopped-flow measurements of FM1-43 efflux though pores. The destaining kinetics mediated by melittin at 1:300, 1:60, and 1:20 peptide/lipid ratios are plotted from top to bottom. The time course of dye loss from liposomes with multiple pores require multi-exponential fits, and so for simplicity we provide τ values for 1:300 only. When melittin/lipid is 1:20, liposomes contain many pores on average, resulting in rapid destaining kinetics (t _1/2 = 0.1 s). At a melittin to lipid ratio of 1:60, a large proportion of liposomes still possess greater than 1 pore per vesicle. At 1:300 almost half the liposomes have no pores (and therefore do not destain), and the remaining ones have approximately one pore per vesicle. This last case is most equivalent to the situation in SVs where exocytosis proceeds through a single fusion pore. Under these conditions, a single exponential fit is adequate and has a τ of 6.7 s (after bleach correction), a value that is similar to the rate of dye loss from slow destaining events from synaptic boutons (τ = 3–7 s; see Fig. 5).

In Fig. 9 C, we show the destaining kinetics mediated by melittin at 1:300, 1:60, and 1:20 peptide/lipid ratios obtained with a stopped-flow rapid mixing approach. At melittin/lipid ratios of 1:20 and 1:60, liposomes contain multiple pores, resulting in rapid destaining kinetics. At 1:300, almost half the liposomes have no pores (Fig. 9 B), and the remainder will have approximately one pore per vesicle. This last case is most equivalent to the situation in SVs where exocytosis proceeds through a single fusion pore. Under these conditions, the τ of dye release was 6.7 s, which is comparable to the rates of destaining seen in the smaller events (τ = 3.1 to 7.2 s from Fig. 5 [D and F] depending on the analysis used).

Discussion

In the present work, the efflux of FM1-43 from individual vesicles during exocytosis was examined. We report that there are two populations of exocytic events: small events, which lose their dye with slow kinetics, and larger events, apparently equal in intensity to single stained SVs, which lose their dye with much faster kinetics. Because these groups are distinct in both fluorescence intensity and kinetics, they strongly suggest that two modes of exocytosis occur at hippocampal synapses. Consideration of the kinetics with which FM1-43 associates and disassociates from membranes leads to the conclusion that the small, slowly destaining events are mediated by a fusion pore that prevents lipid mixing, whereas the larger, faster destaining events appear mechanistically different and may be mediated by full collapse of vesicles into the plasma membrane.

Almost immediately after the first demonstration of activity-dependent loading and unloading of SVs with FM1-43 (Betz et al., 1992), the technique was applied to hippocampal boutons in culture (Ryan et al., 1993). Over the following decade, there were several studies demonstrating quantal uptake of FM1-43 (Ryan et al., 1997, Murthy et al., 1997; Murthy and Stevens, 1998). More recently, Aravanis et al. (2003b) demonstrated that at least some exocytic events result in incomplete release of the dye contained within a vesicle. Exocytosis through a small pore of short duration might be expected to impose limits on both the rate at which FM1-43 leaves labeled vesicles and the amount of dye that can escape. By measuring these parameters, and directly measuring the association and disassociation of FM1-43 with membranes, we sought to interpret our results in a biophysical context.

Loading conditions that might have been expected to produce a quantized distribution with well resolved peaks of FM1-43 fluorescence did not do so (Fig. 1 D). Examination of the loss of FM1-43 from individual boutons during stimulation revealed why—many of the individual exocytic downsteps were much smaller in amplitude than the predicted fluorescence of a single SV. Therefore, it is likely that during the prolonged washing of the preparation after loading, many boutons would have already undergone several “subquantal” release events, thus smearing the overall distribution. The subquantal release of even a few vesicles will result in a significant blurring of quantal fluorescence peaks. Importantly, we were able to see correlated groupings of both the amplitude and rate of efflux of FM1-43 from vesicles, indicating that in most cases the vesicles were homogeneously labeled. This observation might suggest that individual vesicles engaged in multiple exocytic cycles while FM1-43 was present, thus tending toward equilibrium with the external dye concentration. Other studies, which confined stimulation to brief bursts of action potentials followed by very limited washing, were able to resolve quantized loading of boutons (Ryan et al., 1997; Murthy et al., 1997; Murthy and Stevens, 1998), which may be consistent with relatively homogeneous vesicle loading or may indicate that multiple exocytic rounds occurred.

Previous work on the loading and unloading of FM1-43 in SV preparations have established three broad positions: dye uptake and release is not limited during exocytosis (Ryan et al., 1997; Zenisek et al., 2002), release is limited but not uptake (Klingauf et al., 1998; Pyle et al., 2000; Aravanis et al., 2003b), and both can be limited during exocytosis (Stevens and Williams, 2000; Verstreken et al., 2002). These positions become more consistent when multiple modes of exocytosis are considered; e.g., if two modes of exocytosis exist, as proposed in this work, then one mode might exhibit unhindered access to and from the interior of a SV, whereas the other might show asymmetric or symmetric restriction of FM uptake. The results presented in this paper appear to show homogenous loading, as evidenced by the well separated peaks seen in Fig. 3 (A and B). This is equally consistent with both restricted and unrestricted FM1-43 uptake; if multiple cycles of exocytosis occur, even if only 1/3 of the full amount of FM1-43 is taken up during one round of exocytosis, multiple rounds will produce vesicles that tend toward the “full” state. Consequently, we can only speculate on loading/unloading asymmetry. If the fusion pore operates as a simple cylindrical hole connecting the vesicle lumen with the extracellular space, then one would predict that loading would be obstructed equally with unloading. However, other factors such as charge effects or net membrane flow could skew this, and consequently this should be the subject of further investigation.

A possible alternative explanation for the presence of large and small events is that endocytic splitting occurs; i.e., retrieved SVs fuse together in an endosome and are then separated once more, effectively diluting the FM in some vesicles and giving rise to “partial” destaining steps by an alternative route. However, this interpretation does not fit with the observation that the destaining kinetics for large and small events differ because the rate at which FM1-43 escapes from an exocytosing vesicle is solely determined by the extent of access to the extracellular space.

Other interpretations of our data are possible. The constrained morphology of the synaptic cleft is unlikely to influence the rates of dye loss because FM1-43 will rapidly partition into exposed membranes and can diffuse away in the membrane within milliseconds (Zenisek et al., 2002). However, the synaptic cleft is filled with extracellular matrix, and it is possible that under certain conditions FM1-43 can be released directly onto immobile material that might then impede the efflux of FM1-43 from the synaptic cleft. However, it seems unlikely that this would lead to the tight kinetic groupings seen in these experiments (Fig. 5 E).

The application of our results to models of fusion pore function requires accurate knowledge of the manner in which FM1-43 interacts with membranes. For this reason, we have characterized the kinetics of FM1-43–membrane interactions. Previous studies measured the off-rate of FM1-43 from membranes by puffing it onto the outside of a cell and watching the fluorescence decline during continuous perfusion (Ryan et al., 1996; Klingauf et al., 1998; Richards et al., 2000). Such an approach is strongly influenced by the effectiveness of the perfusion and by access issues (i.e., in regions where cells come against one another in close proximity, wash out is impeded). We avoided these difficulties by using a rapid mixing stopped-flow approach. Under these conditions, lipid and protein composition made little difference to the rates of dye departitioning, but dissociation was surprisingly fast, with even the slow component of unbinding (∼120 ms) being much quicker than previously reported (Ryan et al., 1996; Klingauf et al., 1998; Richards et al., 2000).

The speed with which FM1-43 departitions from membranes has implications for the properties of the fusion pore. To slow the loss of FM1-43 from a process that occurs over tens of milliseconds to one which takes seconds, we have to consider the different ways by which FM1-43 can leave a vesicle. A recent paper by Zenisek et al. (2002) demonstrated that in goldfish retinal bipolar neurons FM1-43 escapes during exocytosis by diffusion in the plane of the lipid bilayer. In contrast, studies in hippocampal boutons have consistently suggested that a significant component of FM1-43 destaining occurs via a fusion pore of limited permeability to dye (Klingauf et al., 1998; Stevens and Williams, 2000; Aravanis et al., 2003b). Because lipid diffusion can be ruled out as a route of FM1-43 destaining during small amplitude events on kinetic grounds, it seems that the fusion pore incorporates a barrier to lipid mixing. We obtained similar results when investigating the rate of efflux of FM1-43 through melittin pores, which are thought to have a diameter of 1.3–2.4 nm (Matsuzaki et al., 1997). The rates of efflux we see in the synthetic situation (τ = 6.7 s) are comparable to the values derived from the truncated exponentials (τ = 7.2 s), indicating that a nanometer scale pore can impede the loss of FM1-43 from the inner leaflet of vesicles to a similar extent to that observed in synaptic boutons.

Three mechanisms for the recycling of SV membrane are currently proposed (Ryan, 2003): full collapse of SVs followed by clathrin-dependent retrieval, dynamin-dependent but clathrin-independent fission of the SV membrane from the plasma membrane, and kiss-and-run exocytosis where reversal of the opening of the fusion pore separates the two bilayers. Although the essential role of dynamin in membrane cycling is well established (Koenig and Ikeda, 1989; Takei et al., 1996), it is not clear that all vesicles use this pathway all of the time. In fact, at the D. melanogaster neuromuscular junction, an apparently kiss-and-run–mediated component of release was recently unmasked in an endophilin mutant (Verstreken et al., 2002), and recent work indicates that clathrin-dependent and -independent mechanisms coexist in hippocampal boutons (Mueller et al., 2004). However, in other preparations, clathrin-independent but dynamin-dependent endocytosis may be important (Holroyd et al., 2002). The data presented here, together with that of Aravanis et al. (2003b), indicate that one route of exocytosis might not involve membrane fusion (based on the absence of lipid exchange), and is therefore likely to operate independently of clathrin and dynamin, although definitive proof of this is lacking. Thus, a consensus can be seen to emerge in which both classical clathrin-dependent endocytosis and fusion pore reversal operate in parallel at hippocampal boutons.

A recent paper provides a candidate for one component of the fusion pore: the transmembrane domain of syntaxin has been shown to line the fusion pores of dense core vesicles in PC12 cells (Han et al., 2004), suggesting that the exocytic machinery may be incorporated in a proteinaceous fusion pore that mediates at least the initial phase of release. However, it is also possible that the bilayer itself may be involved in the formation of a diffusion barrier, via distinct lipid microdomains with hindered diffusional escape, or the tightly curved surface formed when vesicle and plasma membranes merge.

In the present work, we provide evidence that two mechanistically different forms of exocytosis operate at hippocampal boutons. Although FM1-43 escapes readily from vesicles in one subset of events, in more than half of events in this work dye efflux is greatly hindered, suggesting that it occurs through a small (∼1–2 nm) fusion pore. A small fixed fusion pore has important implications for neurotransmitter release. Using the same permeation equation as used in the section Setting limits on vesicle destaining, one can calculate the τ of glutamate release through a 1-nm pore to be ∼1 ms, which contrasts with optimized values at reliable synapses of <100 μs (Bruns and Jahn, 1995; Stiles et al., 1996). Glutamate release over such a slow time course would greatly increase the time to peak glutamate concentration, together with a reduction in the peak itself. As has been discussed previously (Choi et al., 2000, 2003; Klyachko and Jackson, 2002), this would have the result of greatly reducing the AMPA component of synaptic responses, potentially giving rise to a partially desensitized population of receptors and promoting glutamate spillover and metabotropic receptor activation. If kiss-and-run exocytosis results in little or no postsynaptic current (Choi et al., 2000, 2003), then the preponderance of kiss-and-run exocytosis reported in the present work could explain the very low apparent probability of release at hippocampal synapses.

Materials and methods

FM imaging

Hippocampal cultures were prepared from p0-3 rats, plated on poly-l-lysine, and cultured in neurobasal medium with B27 supplement (GIBCO BRL). Cultures were maintained for 12–16 d before use. For imaging, coverslips were placed in an imaging chamber (Warner Instruments) at RT and viewed directly through the coverslip via a 100× 1.4 NA objective on a microscope (model TE300; Nikon). Images were acquired using a Micromax cooled CCD camera (Roper Scientific) interfaced to a computer running Metamorph (Universal Imaging Corp.). Subsequent analysis was performed using ImageJ. For the experiments in Figs. 2 and 3, 2 × 2 binning was used, together with 2-s image integration times. For rapid imaging (Fig. 5), binning was increased to 4 × 4 and the acquisition time cut to 300 ms to give an overall frame rate of 2.5/s. The bathing saline had the following composition: 140 mM NaCl, 5 mM KCl, 2 mM CaCl₂, 2 mM MgCl₂, 5.5 mM glucose, and 20 mM Hepes buffered to pH 7.3 using NaOH. Bleaching corresponded to ∼0.1% frame and was not corrected. Events were detected using a threshold of 3.5 fluorescence units, and then subject to the additional criterion that they must not reverse. A full description of the analysis procedure is available in the online supplemental material.

Liposomes

Total lipids extracted from bovine brain and synthetic PE and PC were obtained from Avanti Polar Lipids. Lipids dried under nitrogen were suspended in Hepes buffer. Liposomes (100 nm) composed of 30% PE/70% PC were prepared by extrusion filter (Davis et al., 1999), whereas liposomes containing total brain lipids were prepared by sonication (∼50 nm) using a Microson ultrasonic cell disruptor (Misonix).

To prepare FM1-43–containing liposomes, 10 mM of dried lipids (30% PE/70% PC) were suspended in Hepes buffer plus FM1-43, with a lipid/FM1-43 ratio of 1:50. The mixtures were passed through 100-nm filters 20 times to obtain unilamellar liposomes.

Preparation of SVs

Crude synaptosomes were prepared from homogenized rat brains using differential centrifugation (Huttner et al., 1983). SVs were released from synaptosomes by hypo-osmotic lysis and were purified as described previously (Hu et al., 2002) with modifications. In brief, lysed samples were centrifuged for 28 min at 28,000 g in a Type 70.Ti rotor to remove heavy membranes. Supernatant was collected, mixed with Optiprep (Sigma-Aldrich) at a 1:1 (vol/vol) ratio, and used as a bottom layer for discontinuous gradient centrifugation. A middle layer of 2 ml of 40% Optiprep containing HBS buffer (50 mM Hepes-NaOH, pH 7.4, and 0.1 M NaCl) and a top layer of 1 ml HBS was added. Centrifugation was at 28,000 rpm for 17 h in an SW-28 rotor. SVs were collected from the interface between the top and the middle layer. To concentrate SVs, samples were mixed 1:1 with 80% Accudenz, overlaid with 0.75 ml HBS, and centrifuged at 41,000 rpm for 8 h in an SW-41 rotor. SVs were collected and dialyzed against 4 liters of HBS overnight to remove the residual Accudenz. SV concentration was determined by comparing light scattering with standard curves obtained from known concentrations of liposomes.

Stopped-flow rapid mixing experiments

Kinetic experiments were performed using a stopped-flow spectrometer (model Photophysics SX 18 MV; Applied Biosystems) at 25°C. FM1-43 was excited at 470 nm, and emission >530 nm was recorded. In experiments studying the on-rate, FM1-43 was loaded into one syringe, and liposomes were loaded into another. Samples were rapidly mixed (dead time ∼1 ms) yielding final concentrations of 4 μM FM1-43 and liposome concentration as indicated in Fig. 6 C. The on- (k _on) and off-rates (k _off) were calculated, assuming pseudo first-order kinetics, according to the following equation: k _obs = (liposome concentration) k _on + k _off. Dissociation of FM1-43–liposome complexes was achieved by rapid 1:11 dilution of 4 μM FM1-43 bound to liposomes (0.2 mM lipids) with HBS.

Steady-state fluorescence measurements

Steady-state fluorescence measurements were made at 24°C using a spectrophotometer (model F-4500 FL; Hitachi). FM1-43 was mixed with liposomes in a cuvette using a castle-style stir bar and samples were excited at 470 nm. Emission spectra were collected from 500 to 700 nm (5-nm slits) and were corrected for blank, dilution, and instrument response.

Antibodies and immunoprecipitation

Mouse mAbs directed against the rat NMDA receptor NMDAR-1 subunit (54.1), synaptobrevin (69.1), the cytoplasmic domain of synaptotagmin (41.1), and the lumenal domain of synaptotagmin (604.1) were provided by R. Jahn (Max-Planck-Institute for Biophysical Chemistry, Göttingen, Germany). Polyclonal rabbit antibodies against the C2B domain of synaptotagmin were provided by T.F.J. Martin (University of Wisconsin, Madison, WI). 50 μl SVs were incubated with 2 μl of 69.1, 2 μl of 41.1, or 10 μl of 604.1, respectively, for 1 h, in HBS with or without 1% Triton X-100. 50 μl of protein G–Sepharose Fast-flow beads (Amersham Biosciences) were mixed with the samples for 1 h. Beads were washed (3×) in binding buffer and collected by centrifugation at 15,000 g for 50 s. 10% of total, supernatant, and pellet were loaded onto SDS-PAGE. Proteins were visualized with HRP-conjugated secondary antibodies and ECL.

Measurement of FM1-43 flux through a melittin pore

FM1-43–containing liposomes were added to Hepes buffer to reach a final lipid concentration of 20 μM. Melittin, dissolved in Hepes buffer, was added to reach melittin/lipid ratios of 1:300, 1:60, and 1:20. FM1-43 fluorescence was excited at 470 nm, and the leakage of FM1-43 from liposomes was followed by the decrease in fluorescence at 570 nm. Formation of the melittin pore was complete within ∼1 min at all melittin concentrations tested.

Liposomes containing FM1-43 were incubated with melittin at melittin/lipid ratios of 1:20, 1:60, and 1:300 for 5 min in the presence of 4 μM FM1-43. This allowed the melittin pores to form without loss of dye from the liposomes. The liposomes, with FM1-43 in equilibrium inside and out, were rapidly diluted by hand-mixing or stopped-flow rapid mixing. The resultant change in fluorescence was followed using either an F-4500 FL spectrophotometer (Hitachi) or an SX.18MV stopped-flow spectrometer (Applied Photophysics).

Online supplemental material

Fig. S1 shows the rate of formation of a melittin pore. Fig. S2 shows regions of interest for analysis. Fig. S3 shows the rates of photobleaching. Fig. S4 is a comparison of noise to evoked destaining events. Fig. S5 shows the measurement of stepwise and decaying fluorescence drops. Online supplemental material is available at http://www.jcb.org.cgi/content/full/jcb.200407148/DC1.