Abstract
Microtubules are long filamentous protein structures that randomly alternate between periods of elongation and shortening in a process termed dynamic instability. The average time a microtubule spends in an elongation phase, known as the catastrophe time, is regulated by the biochemical machinery of the cell throughout the cell cycle. In this light, observed changes in the catastrophe time near cellular boundaries (Brunner, D., and P. Nurse. 2000. Cell. 102:695–704; Komarova, Y.A., I.A. Vorobjev, and G.G. Borisy. 2002. J. Cell Sci. 115:3527–3539) may be attributed to regulatory effects of localized proteins. Here, we argue that the pushing force generated by a microtubule when growing against a cellular object may itself provide a regulatory mechanism of the catastrophe time. We observed an up to 20-fold, force-dependent decrease in the catastrophe time when microtubules grown from purified tubulin were polymerizing against microfabricated barriers. Comparison with catastrophe times for microtubules growing freely at different tubulin concentrations leads us to conclude that force reduces the catastrophe time only by limiting the rate of tubulin addition.
Keywords: microtubules; dynamic instability; force generation; catastrophe time; polymerization
Introduction
During microtubule (MT)* assembly, hydrolysis of tubulin-bound GTP destabilizes the internal structure of a MT, eventually leading to a transition to shortening, termed a catastrophe. This switching between a growing and shortening state, which is referred to as dynamic instability, is important for a wide variety of cellular processes (Desai and Mitchison, 1997). During their lifetime, dynamic MTs often interact with cellular structures like the cell cortex or chromosomes thereby becoming subject to mechanical forces exerted via polymerization (Inoue and Salmon, 1995) or by motor proteins that are connected to these structures (Dujardin and Vallee, 2002). Despite the wealth of knowledge about dynamic instability and its dependence on tubulin concentration and other regulatory factors (Walker et al., 1988, 1991; Fygenson et al., 1994; Desai and Mitchison, 1997; Kinoshita et al., 2001), very little is known about how mechanical forces interfere with dynamic instability, even though recent in vivo work suggests that a growth-opposing force may induce catastrophes (Tran et al., 2001).
We previously developed an in vitro assay to study how an opposing force reduces the growth velocity of MTs (Dogterom and Yurke, 1997; Dogterom et al., 2002). In this assay, single growing MTs strike a microfabricated glass barrier, and forces and growth velocities are derived from analysis of their subsequent elastic response. Here, we use this assay to study the effect of force on dynamic instability. We quantify the catastrophe time under force as a function of the reduced growth velocity. This enables us to compare the results with catastrophe times of MTs growing at similar velocities under nonforce-generating conditions.
Results and discussion
2-μm high barriers of siliconmonoxide were vapor deposited onto glass coverslips using photolithographic techniques in between which small MT seeds grown from biotin-labeled tubulin and GMPCPP (a slowly hydrolyzable GTP analogue) were attached (Fig. 1 A). These seeds did not exhibit catastrophes and served as nucleation sites for dynamic GTP-MTs. The methods used were largely based on previously published procedures (Dogterom and Yurke, 1997) with small but significant modifications that improved the reliability of the assay, allowing us to obtain reasonable statistics on catastrophe events (see Materials and methods). We only analyzed MT plus ends, which are the faster growing ends of the seeds (Walker et al., 1988). MTs that grew in a perpendicular direction toward the barriers were selected for observation and were initially investigated at tubulin concentrations (C T) of 20 and 28 μM, for which the average growth velocity (v 0) during free growth was respectively 1.88 ± 0.03 and 2.40 ± 0.01 μm/min (± SEM). After these MTs reached the barriers, we first analyzed how the growth velocity changed in response to the forces that were generated.
Figure 1.
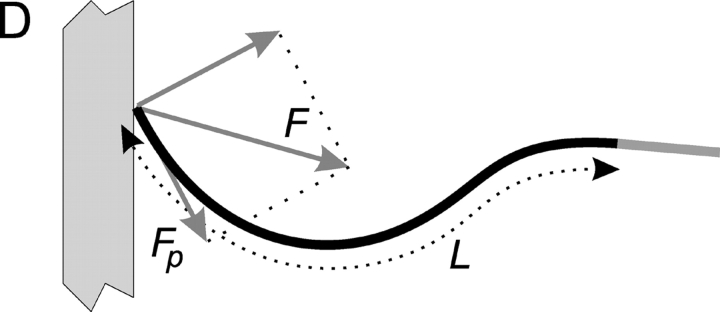
DIC microscopy images of MTs undergoing catastrophes under the influence of force. (A) Schematic side view of the experiment. Seeds attached to the surface (dark regions) nucleate free dynamic MTs in between barriers. A 0.5-μm-deep etched overhang prevents MTs from creeping up the 2-μm-high barrier. Barrier spacing is 60 μm, and barrier width is 15 μm. Picture is not to scale. (B) Microscopy images of a growing and subsequently buckling MT (C T = 28 μM), showing the initiation of growth (t = 0 s), establishment of barrier-contact (194 s), buckling (237 s), relaxation of the buckled MT after a catastrophe (240 s), and the continuation of shortening (252 s). Bar, 5 μm. (C) Microscopy images of a stalled MT (C T = 28 μM), showing growth initiation (t = 0 s), the moment just before a catastrophe while contacting the barrier (117 s), shortening (122 s and 128 s), and regrowth (169 s). The lateral motion of the segment in the box is analyzed in Fig. S1. (D) Parameters derived from the shape analysis. The buckling MT (black) generates a force, F, in contact with the barrier. The parallel component, F p, is responsible for the reduction in MT growth velocity. The length, L, of the MT is given by the distance between the point of barrier contact and the clamped seed (gray area of the MT). See also Video 2 and Fig. S1 available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1.
MTs seeded more than ∼5 μm away from the barrier were seen to continue elongation after they encountered the barrier (Fig. 1 B; Video 1, available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1) and were observed to bend in two ways to facilitate growth: sliding or buckling. During sliding of a MT tip along the barrier, only small compressive forces were applied to the tip. Often, however, the tip started pivoting around a local barrier irregularity, and the point of barrier interaction remained constant for a while. In these cases, MTs built up a relatively large compressive force and started to buckle. For each buckling event, the force component along the growth direction of the MT tip, F p, and the length changes of the MT were determined by analyzing the shape of the buckling MT (Fig. 1 D) every 2 s. The result of such an analysis is shown in Fig. 2 A: after the initial fast establishment of the force, F p slowly goes down as the amplitude of buckling increases, and the force can thus be considered constant during buckling. The growth velocity resulting from this force was derived from a linear fit to the MT length data (Fig. 2 A, inset). This procedure was repeated for all observed buckling events. The average value of F p varied between 0.3 and 10 pN, where higher forces correspond to MTs that had their seed closer to the barrier. For both tubulin concentrations studied we found that the growth velocity decreased with increasing force, in agreement with earlier results (Dogterom and Yurke, 1997).
Figure 2.
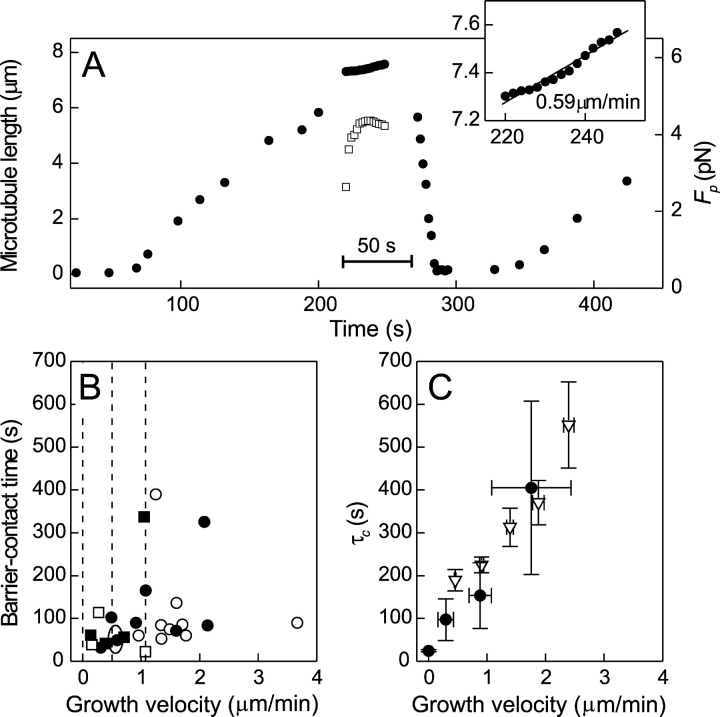
Analysis of MT dynamics. (A) The length (•) of a growing MT before, during, and after buckling together with the force F p (□) as a function of time (C T = 28 μM). Nucleation from a seed (t = 60 s) is followed by growth at an average rate of 2.5 ± 0.1 μm/min. After initiation of barrier-contact (t = 220 s), the average growth velocity equals 0.59 ± 0.03 μm/min (inset). Detailed length information was lost after the MT slipped over a small distance (t = 250 s). A catastrophe (t = 270 s) causes rapid shortening. The barrier-contact time, equal to 270–220 = 50 s is indicated with a horizontal bar. (B) Barrier-contact times for all buckling MTs plotted as a function of the growth velocity during buckling. C T = 20 μM (□ and ▪) or 28 μM (○ and •). Times are shown for MTs that undergo a catastrophe (▪ and •) and for MTs that relax by sliding (□ and ○). The event depicted in A is encircled. (C) Catastrophe time, τc, inferred from various experiments as a function of average growth velocity. The data for free growth were obtained at C T = 7.2, 10, 15.2, 20, and 28 μM (∇). For buckling MTs (•), τc was determined in three growth velocity regimes (0–0.5, 0.50–1.08, and >1.08 μm/min; vertical lines in B) using the data in B. The SD of the averaged velocities and the standard errors on τc are indicated. The average τc for stalled MTs (see Fig. 3) is plotted at zero growth velocity.
To establish the catastrophe behavior of MTs under force-generating conditions, we followed the fate of all buckling MTs. Periods of buckling terminated in two different ways. Sometimes, the MT lost its point of contact, and the MT started sliding along the barrier. In other cases, a buckling MT experienced a catastrophe after which shortening occurred at the same average rate as for MTs under nonforce-generating conditions (unpublished data). In Fig. 2 B, the duration of each buckling event, referred to as barrier-contact time, is plotted against the growth velocity during this time. Both datasets (Fig. 2 B, squares and circles) show the following trend: the more force decreases growth velocity, the shorter the average barrier-contact time becomes. To estimate the average time until catastrophe (the catastrophe time) as a function of growth velocity, the average time between the initiation of barrier-contact and catastrophe (τc) was calculated in three velocity regimes. These regimes are indicated in Fig. 2 B, and all contain four events that end in a catastrophe. In each case, we summed over all barrier-contact times, including the sliding events, and divided this total time by four. The resulting values are plotted in Fig. 2 C as a function of the average growth velocity calculated over all events in a regime (Fig. 2 C, solid symbols). This analysis shows that the catastrophe time decreased as the growth velocity was slowed down by force. Note that we combined two datasets obtained at different tubulin concentrations, for which the initial free growth velocity was slightly different. However, force reduced the velocity of most MTs far below these initial velocities, and therefore, force and not concentration is the main regulator of velocity in Fig. 2 C (solid symbols).
The enhancing effect of an opposing force on the catastrophe rate was most clearly seen for MTs that were seeded at a distance less than ∼5 μm away from the barrier (studied at C T = 15.2, 20, and 28 μM; Fig. 1 C; Video 2, available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1). During their barrier-contact time, buckling was never observed by eye, and these MTs experienced a catastrophe on average 24 ± 1 s (τc ± SEM) after reaching the barrier (Fig. 2 C, solid symbol at zero growth velocity). Using automated tracking of the MT shape, we estimated an upper limit for the growth velocity during barrier-contact of 0.05 μm/min (Fig. S1, available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1). The forces experienced by these short MTs were apparently large enough to stall or nearly stall their growth.
Force and tubulin concentration are independent ways to regulate the growth velocity that a priori do not need to have the same effect on the catastrophe time. Therefore, we compared the relation between τc and growth velocity now established under force to the relation that can be measured for freely growing MTs by tuning the tubulin concentration (Walker et al., 1988; Fygenson et al., 1994). For five concentrations between 7.2 and 28 μM we measured the average growth velocity and the average time between MT nucleation from a seed and a catastrophe (τc) and plotted them in Fig. 2 C as well (open symbols). In making the comparison one needs to keep in mind that the experimental accuracy of the measured τc under load is low because of the limited amount of observed catastrophes. In addition, nonstatistical errors exist especially at the lower growth velocities for both free catastrophes and catastrophes under load: free catastrophes remain undetected when they occur on MTs that only extend very little from their seeds (<0.2 μm), which is not observable and happens more frequently for slowly growing MTs (low C T). Under high load, a slowly growing MT which may have had a catastrophe before buckling could be observed and therefore may have become incorrectly labeled as stalled. Within these limits of our measurements, we find that the velocity-τc relations for free MTs and MTs under load are the same.
The catastrophe time of 24 s found for stalled MTs may be compared with previously reported catastrophe measurements on free MTs that were exposed, in dilution experiments, to a tubulin concentration close to the critical concentration, C T,c. At the critical concentration, there is thermodynamic equilibrium between the C T-dependent rate of tubulin addition given by k onCT,c (s−1) and the C T-independent rate of tubulin removal given by k off (s−1). In this situation, one expects no net growth or shrinkage of the MT as is the case for stalled MTs. In the dilution experiments, a catastrophe time of 10.8 s was observed at a concentration (3.3 μM) slightly below C T,c and at a temperature of 37°C (Walker et al., 1991). Given the slight differences in experimental conditions, this time corresponds reasonably well with our observations for stalled growth.
How can we understand, on a molecular level, the fact that the relation between growth velocity and catastrophe time is the same whether a force is applied or not? Although we lack a detailed understanding of the catastrophe mechanism, we may assume that a catastrophe results from a temporal unbalance between the stabilizing action of the addition of new GTP-bound tubulin subunits (governed by the on-rate) and destabilization by GTP hydrolysis, subunit removal (governed by the off-rate), and possibly other processes (Desai and Mitchison, 1997). All rate constants involved may under force deviate from their zero force values. However, our results suggest that force does not interfere with the catastrophe mechanism other than by changing the rate of tubulin addition (via k on) just as can be achieved by changing C T. This observation supports the Brownian ratchet model that was developed to explain the experimentally measured force-velocity curve for growing MTs and that assumed a force independent k off (Mogilner and Oster, 1999; Doorn et al., 2000).
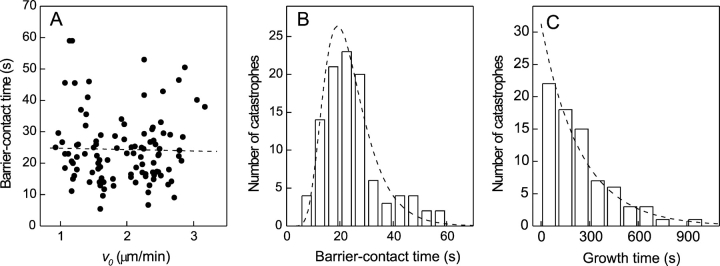
More evidence for the conclusion that force only reduces the on-rate can be obtained from a detailed analysis of the barrier-contact times for stalled MTs. For these MTs it was possible to observe repeated catastrophe events (Video 2) at three different tubulin concentrations leading to much better statistics than could be obtained for buckling MTs. In Fig. 3 A, the barrier-contact time for individual stalled MTs is plotted against the velocity at which each particular MT grew toward the barrier (v 0). There is no significant correlation between these quantities, which indicates that τc for stalled MTs is not a function of v 0 nor of C T. If the on-rate depends on the force, but the off-rate does not, then the force must always reduce the on-rate to the same value for every tubulin concentration to stall the MT. In this case, one would expect the same catastrophe behavior for every tubulin concentration, in agreement with the experimental result. The force that MTs experience when stalled does increase with C T simply because the force needed to stall them is expected to increase with tubulin concentration (Dogterom et al., 2002).
Figure 3.
Comparison of the catastrophe time distribution for stalled and free MTs. (A) Barrier-contact times of 103 stalled, nonbuckling MTs measured at C T = 15.2, 20, and 28 μM as a function of v0, the growth velocity before barrier-contact. A fitted straight line demonstrates the lack of correlation between the two quantities (correlation coefficient R = −0.02, P = 0.82). (B) A histogram of the 103 barrier-contact times together with the prediction of a simple model (dotted line; see Results and Discussion). (C) Distribution of free catastrophe times for 76 events at C T = 10 μM with an average τcvalue of 243 s. The dotted line indicates an exponential distribution with the same average τc. See also Fig. S2 available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1.
The distribution of individual catastrophe times for stalled MTs may contain valuable information about the mechanism that leads to a catastrophe under that particular condition. Since for stalled MTs the barrier-contact time did not seem to depend on v 0, we pooled all 103 events together and plotted them in a single histogram in Fig. 3 B. For comparison, we plotted in Fig. 3 C the histogram of 76 catastrophe events observed for freely growing MTs at C T = 10 μM (Fig. S2, available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1). The distribution in Fig. 3 C is well represented by an exponential, which suggests an underlying random Poisson process, for which the catastrophe probability (or rate) is the same at any time. In other words, the properties of a freely growing MT tip that determine the catastrophe probability seem reasonably stable during growth. The distribution for stalled MTs shown in Fig. 3 B is clearly not an exponential, and the shape implies that the catastrophe probability increases with time after the establishment of barrier-contact. Apparently the MT tip becomes progressively more unstable which may correspond to the accumulation of GDP subunits in its lattice. One may, for example, assume that 13 independent hydrolysis events (one at the end of each protofilament) need to take place before a catastrophe occurs. In that case, the probability of having experienced a catastrophe after a time t is given by (1−exp[−θt])13 where θ is the rate constant for a single hydrolysis event. The corresponding probability density function is plotted in Fig. 3 B for θ = 0.134 s−1. However, other processes may produce similar distributions, and the main conclusion should therefore be that catastrophes for stalled MTs are multistep events, whereas free catastrophes seem to involve only a single step.
Are there any indications that force-induced catastrophes play a role in living cells? Recently reported observations show that catastrophes occur more frequently at the cell periphery than in the cytoplasm in CHO and NRK animal cells (Komarova et al., 2002) and in fission yeast cells (Brunner and Nurse, 2000; Drummond and Cross, 2000; Tran et al., 2001). Given our results, forces generated when polymerizing MT tips impinge on the cellular cytoplasmic membrane are a likely cause for the increased catastrophe rates that are observed. In fission yeast cells, the growth velocity was shown to be reduced from 2.08 μm/min before to 1.30 μm/min after contact with the cell end (Tran et al., 2001). This 40% decrease may, based on our results (Fig. 2 C), be expected to give an ∼40% decrease in catastrophe time. For the measured cytoplasmic τc of 3.2 min, one therefore expects τc = 2 min in contact with the cell end, which given the experimental uncertainties is in good agreement with the 1.5 min reported. Observations of MT buckling in these cells prove that piconewton forces are generated in contact with the cell end, which are large enough to explain the observed reduction in growth velocity. MTs in larger animal cells are longer than those in fission yeast, and they would have to be linked to the rest of the cytoskeleton or form bundles in order to exert significant polymerization forces on the cortex. Other in vivo work suggests that the molecular motor dynein is often bound to the cell cortex where it can bind MTs and influence their dynamics (Dujardin and Vallee, 2002). Possibly, the minus end–directed motion of dynein pulls the growing plus end of the MT against the cortex forcing it to continue growth at a lower rate, making a catastrophe more likely. Finally, polymerization forces are believed to play a role in the buildup of the mitotic spindle, and an accurate description of spindle dynamics (Inoue and Salmon, 1995; Khodjakov et al., 1999; Joglekar and Hunt, 2002) should therefore take force-induced catastrophes into account.
In conclusion, we have shown that a force-induced catastrophe is an intrinsic property of MTs. In vivo, a force-dependent catastrophe rate makes the combination of a high catastrophe rate near cellular boundaries and a negligible catastrophe rate in the cytoplasm possible without the need for localized catastrophe-regulating factors. We have also shown that force affects the catastrophe time primarily by reducing the rate of tubulin addition and does not seem to affect any other process involved in the transition from growing to shrinking. Our data, and in particular the distribution of catastrophe times for stalled MTs, should provide further constraints on the development of models aimed at explaining dynamic instability.
Materials and methods
Microfabrication of barriers
Acid-washed coverslips were used as substrates for microfabrication of barriers (Dogterom and Yurke, 1997). A 7.5-μm-thick layer of photoresist (ma-P 275; Micro Resist Technology) was spin coated, soft baked, exposed to UV light through a photolithographic mask (custom fabricated by Delft Institute of Microelectronics and Submicron Technology), and developed. After creating the photoresist pattern, a 2-μm-thick layer of SiO was vapor deposited under vacuum followed by stripping the remaining photoresist in acetone. Immersion of the samples in buffered hydrofluoric acid created a ridge (or overhang) underneath the deposited lines of SiO. Finally, before use the coverslips were cleaned in chromosulfuric acid and washed five times with deionized water.
Synthesis of nucleation sites
Stable MT seeds were made from a 4:1 mixture of bovine brain tubulin and biotin-labeled tubulin (Cytoskeleton). Remnants of glycerol were removed by dilution in MRB80 (80 mM Pipes, 1 mM EGTA, 4 mM MgCl2, pH 6.8, with KOH) and subsequent concentration using a microconcentrator. Tubulin was then polymerized for 30 min at ∼20 μM in MRB80 plus 0.5 mM GMPCPP (a gift of T.J. Mitchinson, Harvard Medical School, Boston, MA) at 35°C, yielding a few-μm-long stable MTs. These short MTs were diluted 25-fold in MRB80 plus 0.4 mM GMPCPP and 0.62 μM nonlabeled tubulin followed by polymerization for 10 min at 35°C, which extended the seeds with a micron-sized biotin-free region without selfnucleation of new MTs. This region did not bind to a streptavidin-coated surface and served as an efficient MT nucleation site that rapidly nucleates a MT without much delay (Fig. S2).
Sample preparation
A flow cell was created by spacing the microfabricated coverslip and an agarose-coated microscope slide 25 μm apart using two lines of vacuum grease and fine metal wire as spacer. The cell was filled with biotin-labeled BSA (biotin-BSA; Sigma-Aldrich; 2.5 mg/ml in pH 5.2 sodium acetate buffer, 5 min incubation), flushed with MRB80, refilled with streptavidin (1 mg/ml in MRB80, 5-min incubation), flushed again with MRB80, and filled with biotin-labeled nucleation seeds (50-fold diluted in MRB80 from stock, 5-min incubation). Tissue paper was used to blot solutions out of the flow cell while refilling. The method of indirect linkage of streptavidin via an adsorbed layer of biotin-labeled BSA (Gittes et al., 1996) produced a greater reproducibility of seed binding relative to direct binding of streptavidin to the glass as was used previously (Dogterom and Yurke, 1997). Free tubulin (Cytoskeleton) in MRB80 plus 1 mM GTP and 10 mg/ml nonlabeled BSA was flown in at concentrations varying between 7.2 and 28 μM. BSA was used to compete with tubulin for possible nonspecific binding to surfaces. An oxygen scavenging system (Dogterom and Yurke, 1997) was used in the final solution in most but not all experiments to slow down protein deterioration. The addition did not change MT dynamics (unpublished data). After the removal of the metal wires, pressure was applied on the sample while blotting excess fluid. This decreased the sample thickness to the height of the barriers. The glass slide was coated with a thin layer of agarose beforehand (0.4% agarose solution at 70°C), which prevented the sticking of seeds and helped in contacting the barriers with the glass slide, minimizing the chance for a MT to grow over the barrier (Fig. 1 A).
Video microscopy
Samples were observed by video-enhanced DIC microscopy (DMIRB inverted microscope; Leica). The oil immersion objective (100×, NA 1.3) was thermostated yielding a constant sample temperature of 23°C. Background subtraction and contrast enhancement of CCD camera (Kappa) images were performed (Argus 20 image processor; Hamamatsu). The resulting image stream was both recorded on s-VHS videotape and digitized at a rate of 1 frame every 2 s online (SGI visual workstation).
Analysis
The catastrophe time, τc, for freely growing MTs was determined in two different ways. At C T = 20 μM (51 free catastrophes) and 28 μM (30), τc was taken equal to the total observation time of free MT growth (before barrier contact) divided by the number of observed catastrophes. At C T = 7.2 μM (58 free catastrophes), 10 μM (152), and 15.2 μM (49), only MTs were used that grew far away from the barriers and never reached them. In these cases, τc was defined as the average time between MT nucleation and catastrophe. These two methods should give identical results because the catastrophe probability was shown to be independent of MT length (Fig. 3 C and Fig. S2), and MTs only switched from shortening back to growing at the seed.
Barrier-contact time started when a MT found a fixed contact point at the barrier. This event evoked a clearly observable change in the lateral Brownian motion (Fig. S1). Barrier-contact time ended after a catastrophe or after complete relaxation by sliding of a buckled MT along the barrier. Slipping events after which the MT remained buckled were included in the barrier-contact time (Fig. 2 A). For stalled MTs, barrier-contact time always ended with a catastrophe. The error made in the estimation of barrier-contact time by eye is on the order of 1 s (Fig. S1).
The length of a buckled MT was estimated by fitting the theoretical shape of a homogeneous elastic rod to the observed MT shape (Gittes et al., 1996; Dogterom and Yurke, 1997). Shapes of buckling MTs on the digitized images were quantified using computerized image analysis. The images were traced for the typical shadow cast contrast created by the DIC microscopy technique. In most cases, the used routine was able to locate 25 points along the MT. All shapes were inspected by eye, and points were relocated by hand if the routine did not work properly. Shapes were analyzed once every 2 s. During fitting, it was assumed that the seed was perfectly clamped to the glass, which is a proper assumption because due to the improved seed binding protocol, only one further excluded MT was seen to rotate its seed during buckling. Perfect clamping would reduce the fitting problem to a one-parameter fit if both the positions of the seed end and the MT barrier-contact point were known (Landau and Lifshitz, 1986). The point of transition between clamped and free MT is however hard to estimate from the images and only the direction of the seed can be obtained accurately. The barrier-contact point is not visible because it is underneath the barrier. Therefore, in total three additional coordinates, one for the seed's end point and two for the barrier-contact point, needed to be fitted. An initial guess was made for these coordinates. Adjusting these coordinates yielded a final fit for which all MT shapes in a sequence fitted on average best.
Lengths of freely growing MTs were determined by measuring the straight distance between the end of the seed and the MT tip located on digitized images by eye. For every free growing MT the growth velocity was determined using a linear fit to the length data. One single average velocity, v 0, was calculated for each value of C T (weighted with the duration of each growth event).
Online supplemental material
In Fig. S1, an upper limit for the growth velocity during barrier-contact is estimated for the stalled MT that is depicted in Fig. 1 C. In Fig. S2, additional analysis is presented to show that the individual catastrophe times for freely growing MTs are exponentially distributed. Video 1 shows the buckling and subsequent catastrophe of a MT while contacting the barrier. Video 2 corresponds to Fig. 1 C and shows two catastrophes on a stalled MT. Online supplemental material is available at http://www.jcb.org/cgi/content/full/jcb.200301147/DC1.
Supplemental Material
Acknowledgments
We are grateful to D. Brunner, P.T. Tran, E.D. Salmon, R. Bruinsma, and J.W.J. Kerssemakers for helpful discussions; M. Konijnenburg for software development; and A. van Blaaderen, W.J. van der Zande, and B.M. Mulder for critical reading of the manuscript.
This work is part of the research program of the “Stichting voor Fundamenteel Onderzoek der Materie (FOM),” which is financially supported by the “Nederlandse organisatie voor Wetenschappelijk Onderzoek (NWO).”
The online version of this article includes supplemental material.
Footnotes
Abbreviation used in this paper: MT, microtubule.
References
- Brunner, D., and P. Nurse. 2000. CLIP170-like tip1p spatially organizes microtubular dynamics in fission yeast. Cell. 102:695–704. [DOI] [PubMed] [Google Scholar]
- Desai, A., and T.J. Mitchison. 1997. Microtubule polymerization dynamics. Annu. Rev. Cell Dev. Biol. 13:83–117. [DOI] [PubMed] [Google Scholar]
- Dogterom, M., and B. Yurke. 1997. Measurement of the force-velocity relation for growing microtubules. Science. 278:856–860. [DOI] [PubMed] [Google Scholar]
- Dogterom, M., M.E. Janson, C. Faivre-Moskalenko, A. Van der Horst, J.W.J. Kerssemakers, C. Tanase, and B.M. Mulder. 2002. Force generation by polymerizing microtubules. Appl. Physics A-Mater. Sci. Process. 75:331–336. [Google Scholar]
- Doorn, G.S.v., C. Tanase, B.M. Mulder, and M. Dogterom. 2000. On the stall force for growing microtubules. Eur. Biophys. J. Biophys. Lett. 29:2–6. [DOI] [PubMed] [Google Scholar]
- Drummond, D.R., and R.A. Cross. 2000. Dynamics of interphase microtubules in Schizosaccharomyces pombe. Curr. Biol. 10:766–775. [DOI] [PubMed] [Google Scholar]
- Dujardin, D.L., and R.B. Vallee. 2002. Dynein at the cortex. Curr. Opin. Cell Biol. 14:44–49. [DOI] [PubMed] [Google Scholar]
- Fygenson, D.K., E. Braun, and A. Libchaber. 1994. Phase diagram of microtubules. Phys. Rev. E. Stat. Phys. Plasmas. Fluids Relat. Interdiscip. Topics. 50:1579–1588. [DOI] [PubMed] [Google Scholar]
- Gittes, F., E. Meyhofer, S. Baek, and J. Howard. 1996. Directional loading of the kinesin motor molecule as it buckles a microtubule. Biophys. J. 70:418–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inoue, S., and E.D. Salmon. 1995. Force generation by microtubule assembly/disassembly in mitosis and related movements. Mol. Biol. Cell. 6:1619–1640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joglekar, A.P., and A.J. Hunt. 2002. A simple, mechanistic model for directional instability during mitotic chromosome movements. Biophys. J. 83:42–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khodjakov, A., I.S. Gabashvili, and C.L. Rieder. 1999. “Dumb” versus “smart” kinetochore models for chromosome congression during mitosis in vertebrate somatic cells. Cell Motil. Cytoskeleton. 43:179–185. [DOI] [PubMed] [Google Scholar]
- Kinoshita, K., I. Arnal, A. Desai, D.N. Drechsel, and A.A. Hyman. 2001. Reconstitution of physiological microtubule dynamics using purified components. Science. 294:1340–1343. [DOI] [PubMed] [Google Scholar]
- Komarova, Y.A., I.A. Vorobjev, and G.G. Borisy. 2002. Life cycle of MTs: persistent growth in the cell interior, asymmetric transition frequencies and effects of the cell boundary. J. Cell Sci. 115:3527–3539. [DOI] [PubMed] [Google Scholar]
- Landau, L.D., and E.M. Lifshitz. 1986. Theory of Elasticity. Butterworth-Heinemann, Oxford, UK. 187 pp.
- Mogilner, A., and G. Oster. 1999. The polymerization ratchet model explains the force-velocity relation for growing microtubules. Eur. Biophys. J. Biophys. Lett. 28:235–242. [Google Scholar]
- Tran, P.T., L. Marsh, V. Doye, S. Inoue, and F. Chang. 2001. A mechanism for nuclear positioning in fission yeast based on microtubule pushing. J. Cell Biol. 153:397–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, R.A., E.T. Obrien, N.K. Pryer, M.F. Soboeiro, W.A. Voter, H.P. Erickson, and E.D. Salmon. 1988. Dynamic instability of individual microtubules analyzed by video light-microscopy—rate constants and transition frequencies. J. Cell Biol. 107:1437–1448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, R.A., N.K. Pryer, and E.D. Salmon. 1991. Dilution of individual microtubules observed in real-time in vitro—evidence that cap size is small and independent of elongation rate. J. Cell Biol. 114:73–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.