Mg²⁺ Enhances Voltage Sensor/Gate Coupling in BK Channels

Abstract

BK (Slo1) potassium channels are activated by millimolar intracellular Mg²⁺ as well as micromolar Ca²⁺ and membrane depolarization. Mg²⁺ and Ca²⁺ act in an approximately additive manner at different binding sites to shift the conductance–voltage (G_K-V) relation, suggesting that these ligands might work through functionally similar but independent mechanisms. However, we find that the mechanism of Mg²⁺ action is highly dependent on voltage sensor activation and therefore differs fundamentally from that of Ca²⁺. Evidence that Ca²⁺ acts independently of voltage sensor activation includes an ability to increase open probability (P_O) at extreme negative voltages where voltage sensors are in the resting state; 2 μM Ca²⁺ increases P_O more than 15-fold at −120 mV. However 10 mM Mg²⁺, which has an effect on the G_K-V relation similar to 2 μM Ca²⁺, has no detectable effect on P_O when voltage sensors are in the resting state. Gating currents are only slightly altered by Mg²⁺ when channels are closed, indicating that Mg²⁺ does not act merely to promote voltage sensor activation. Indeed, channel opening is facilitated in a voltage-independent manner by Mg²⁺ in a mutant (R210C) whose voltage sensors are constitutively activated. Thus, 10 mM Mg²⁺ increases P_O only when voltage sensors are activated, effectively strengthening the allosteric coupling of voltage sensor activation to channel opening. Increasing Mg²⁺ from 10 to 100 mM, to occupy very low affinity binding sites, has additional effects on gating that more closely resemble those of Ca²⁺. The effects of Mg²⁺ on steady-state activation and I_K kinetics are discussed in terms of an allosteric gating scheme and the state-dependent interactions between Mg²⁺ and voltage sensor that may underlie this mechanism.

INTRODUCTION

The activity of BK-type Ca²⁺-activated K⁺ channels is important for the function of nerve, muscle, and secretory cells (Vergara et al., 1998). BK channels respond to two primary signals, membrane voltage and intracellular Ca²⁺, but are also sensitive to a variety of regulatory ligands, including intracellular Mg²⁺ (Shi and Cui, 2001; Zhang et al., 2001), heme (Tang et al., 2003), and protons (Avdonin et al., 2003), that can influence channel gating under physiological and/or pathophysiological conditions. Therefore, to understand how BK channel activity is regulated it is important to understand how these signaling and regulatory factors affect channel gating and interact with each other. Previous studies suggest that millimolar [Mg²⁺]_i and micromolar [Ca²⁺]_i activate BK channels through similar functional mechanisms (Shi and Cui, 2001; Zhang et al., 2001). Here we show that the action of Mg²⁺ differs from that of Ca²⁺ in its dependence on voltage sensor activation. The results highlight that multiple pathways of communication exist between the transmembrane and cytosolic domains of BK channels.

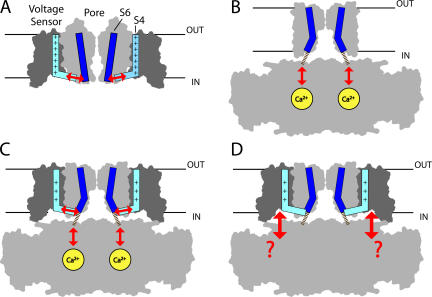
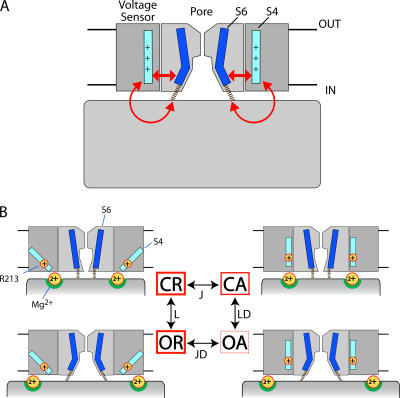
That Ca²⁺ and voltage act independently to regulate opening is evident from BK channel function and consistent with channel structure. BK channels can be fully activated by membrane depolarization in the absence of Ca²⁺ (Cui et al., 1997), and Ca²⁺ facilitates opening in a nearly voltage-independent manner, indicating that Ca²⁺ and voltage sensor activation have energetically additive effects on opening (Cui and Aldrich, 2000; Horrigan and Aldrich, 2002). The transmembrane domain of BK channels, like voltage-gated K⁺ (Kv) channels, includes an S5–S6 pore domain and a charged S1–S4 voltage sensor (Ma et al., 2006). Coupling between the voltage sensor and pore can occur presumably as in Kv channels, via interactions within the transmembrane domain (Fig. 1 A) (Lu et al., 2002; Long et al., 2005b). In addition, BK channels contain a large C-terminal cytosolic domain that interacts with intracellular ligands and is directly attached to the S6 activation gate. The cytosolic domain of each α-subunit contains two putative RCK (regulator of K⁺ conductance) homology domains (RCK1, RCK2), like those in the prokaryotic channel MthK (Jiang et al., 2001). In MthK, RCK domains from different subunits assemble into a gating ring structure that expands upon Ca²⁺ binding to pull open the gate (Fig. 1 B) (Jiang et al., 2002; Ye et al., 2006), suggesting that Ca²⁺ opens BK channels by increasing tension on the RCK1–S6 linker (Niu et al., 2004). Thus models of BK channel structure support that voltage and Ca²⁺ sensors may act independently on the gate (Fig. 1 C) to exert additive effects on steady-state activation.

Figure 1.

Proposed pathways of sensor/gate interaction for different channels. (A) Kv1.2, where the charged S4 segment (light blue) in the voltage sensor is proposed to interact with the S6 activation gate (dark blue) in the pore via the S4–S5 linker (arrows). The outlines of the S1–S4 voltage sensor domain and S5–S6 pore domain for two subunits from the Kv1.2 crystal structure (Long et al., 2005a) are shown in dark and light gray, respectively, and are truncated at S1 (protein data bank code 2A79). (B) MthK, where Ca²⁺ binding to the cytosolic domain is proposed to cause a conformational change that pulls open the gate through short peptide linkers (dashed lines) that are unresolved in the crystal structure (Jiang et al., 2002) (protein data bank code 1LNQ). The attachment points of the linker on the cytosolic domain (in foreground and background) have been altered to better illustrate that linkers are pulled away from the pore axis. (C) A hypothetical BK channel structure formed by appending the Kv1.2 voltage sensors to MthK shows how Ca²⁺ and voltage may both interact with the gate to have independent effects on activation. The position of the voltage sensors was determined by superimposing the pore domains of Kv1.2 (residues 341–406) and MthK (residues 26–91) in PyMol (http://www.pymol.org). (D) The hypothetical BK channel structure also illustrates the possibility that the large cytosolic domain may interact directly with voltage sensors.

Given the example of MthK, one might suppose that any ligand binding to the cytosolic domain of the BK channel must act, like Ca²⁺, to open the gate by pulling on the RCK1–S6 linker. However this is not necessarily the case. Voltage sensors in BK channels, which are absent from MthK, are potentially available to interact with the cytosolic domain, providing an alternative pathway of communication between ligand binding sites and the transmembrane domain. The cytosolic domain of MthK lies close to the transmembrane domain, presents a relatively flat surface toward the membrane, and with a diameter of >70 Å extends laterally far beyond the pore (Fig. 1 B). All of these features, which are presumably necessary to exert lateral force on the gate via short peptide linkers, would also tend to bring the periphery of the gating ring close to the voltage sensor domain in BK channels (Fig. 1 D). Several observations suggest that interactions between cytosolic and voltage sensor domains occur. Ca²⁺ has effects on gating current, consistent with a weak interaction between Ca²⁺ sensors and voltage sensors (Horrigan and Aldrich, 2002). Intracellular heme has a pronounced effect on voltage gating, weakening the allosteric coupling between voltage sensor and gate (Horrigan et al., 2005). Likewise, chemical modification of a native cysteine residue (C430) in the cytosolic domain alters voltage sensor/gate coupling (Zhang and Horrigan, 2005).

Mg²⁺ has effects on BK channel gating that resemble those of Ca²⁺: increasing P_O, slowing I_K deactivation, and shifting the G_K-V relation to more negative voltages with little change in shape (Shi and Cui, 2001; Zhang et al., 2001). Effects of Mg²⁺ and Ca²⁺ on the half-activation voltage (V_0.5) are approximately additive and involve different binding sites (Shi et al., 2002; Xia et al., 2002). Consequently, Mg²⁺ has been proposed to act independently of Ca²⁺ but through a similar functional mechanism. Effects of Mg²⁺ on the G_K-V relation can be reproduced by gating schemes that assume Mg²⁺ acts, like Ca²⁺, to enhance channel opening independent of voltage sensor activation (Shi and Cui, 2001; Zhang et al., 2001; Hu et al., 2006). However, several lines of evidence suggest that Mg²⁺ and Ca²⁺ do not act through identical functional mechanisms. First, high concentrations of Ca²⁺ (>100 μM), which are known to occupy Mg²⁺ binding sites, have effects that differ qualitatively from those of low [Ca²⁺]_i. While 0–100 μM Ca²⁺ produces a nearly voltage-independent increase in log(P_O), 100–1,000 μM Ca²⁺ increases log(P_O) in a voltage-dependent manner (Horrigan and Aldrich, 2002). In addition, mutations in the voltage sensor, including R213Q in S4, disrupt Mg²⁺ sensitivity but not Ca²⁺ sensitivity, suggesting that the voltage sensor plays a critical role in Mg²⁺-dependent activation (Hu et al., 2003). Indeed, recent evidence indicates that Mg²⁺ bound to the cytosolic domain interacts electrostatically with R213 (Yang et al., 2007).

This study examines the functional interaction between Mg²⁺- and voltage-dependent activation of mSlo1 BK channels. Effects of 0–100 mM Mg²⁺ on the steady-state and kinetic properties of ionic and gating currents were examined over a wide voltage range in WT channels and channels where either the voltage sensor or a putative Mg²⁺-binding site in the RCK1 domain were mutated. The results show that Mg²⁺ at the RCK1 site acts primarily to strengthen the allosteric coupling of voltage sensor activation to channel opening. Only at high concentrations (>10 mM), involving an additional very low affinity binding site, does Mg²⁺ have direct effects on opening, like Ca²⁺. Our results together with the proposed electrostatic nature of Mg²⁺/voltage sensor interaction suggest that Mg²⁺ and the voltage sensor must interact in multiple states to account for the effects of Mg²⁺ on voltage sensor/gate coupling.

MATERIALS AND METHODS

Channel Expression and Molecular Biology

Experiments were performed with the mbr5 clone of the mouse Slo1 gene (mSlo1) (Butler et al., 1993) expressed in Xenopus oocytes (for I_K) or HEK 293T cells (for gating current). The clone was propagated and cRNA transcribed as described previously (Cox et al., 1997). Oocytes were injected with ∼0.5–5 ng of cRNA, incubated at 18°C, and studied 3–7 d after injection. HEK cells were transfected with mSlo1 in an SRα vector using Lipofectamine (GIBCO BRL/Life Technologies Inc.) 2–3 d before recording as described previously (Horrigan and Aldrich, 2002). Site-directed mutagenesis was performed with the QuikChange XL Site-Directed Mutagenesis Kit (Stratagene) and confirmed by sequencing.

Electrophysiology and Data Analysis

Currents were recorded using the patch-clamp technique in the inside-out configuration (Hamill et al., 1981) at 20 ± 1°C. For Ca²⁺ experiments, the external solution contained (in mM) 104 KMeSO₃, 6 KCl, 2 MgCl₂, 20 HEPES, and the internal solution contained 110 KMeSO₃, 6 HCl, 20 HEPES, and 2 EGTA (0 Ca²⁺) or 5 HEDTA (Ca²⁺ solution). Ca²⁺ was added as CaCl₂ and [Cl⁻]_i was adjusted to 10 mM with HCl. Free [Ca²⁺] for the 2 μM Ca²⁺ solution was measured (1.8 μM) with a Ca²⁺ electrode (Orion Research Inc.). For Mg²⁺ experiments, the external solution contained (in mM) 225 KOH, 196 HCl, 2 MgCl₂, 10 HEPES, and internal solutions contained 225 KOH, 5 EGTA, 10 HEPES, plus MgCl₂ and HCl to obtain the desired [Mg²⁺] with [Cl⁻]_i = 200 mM. 100 mM Mg²⁺ solution contained a total of 100 mM Mg²⁺ for an estimated free [Mg²⁺] of 96.1 mM. Total Mg²⁺ in other solutions was adjusted to obtain the indicated free [Mg²] (2, 5, 10, 21 mM) as calculated by MaxChelator (http://www.stanford.edu/∼cpatton/maxc.html) (Patton et al., 2004). Since free [Mg²⁺] was not measured, the purity of MgCl₂ and EGTA stocks were assayed by pH-metric titration (Tsien and Pozzan, 1989) against standardized solutions of EDTA and CaCl₂, respectively. For gating currents (I_g) the external solution contained 130 tetraethyl ammonium (TEA)-OH, 100 NMDG, 196 HCl, 2 MgCl₂, 10 HEPES, and internal solution contained 225 NMDG-MES, 10 HEPES, 5 EGTA, plus MgCl₂ and HCl as above. The pH of all solutions was adjusted to 7.2 with MeSO₃. Internal solutions contained 40 μM (+)-18-crown-6-tetracarboxylic acid (18C6TA) to chelate contaminant Ba²⁺ (Diaz et al., 1996; Neyton, 1996).

Data were acquired with an Axopatch 200B amplifier (Molecular Devices Corp.) in patch mode with the Axopatch's filter set at 100 kHz. Currents were filtered by an 8-pole Bessel filter (Frequency Device, Inc.) at 50 kHz (I_K) or 20 kHz (I_g) and sampled at 200 kHz with an 18-bit A/D converter (Instrutech ITC-18). For gating currents, the voltage command was also filtered at 20 kHz. A p/4 protocol was used for leak subtraction (Armstrong and Bezanilla, 1974) with a holding potential of −80 mV. Electrodes were made from thick-walled 1010 glass (World Precision Instruments, Inc.) and their tips coated with wax (KERR Sticky Wax). The electrode's resistance in the bath solution (0.5–1.5 MΩ) was used as an estimate of series of resistance (R_S) for correcting the voltage at which macroscopic I_K was recorded. Series resistance error was <15 mV for all data presented. A Macintosh-based computer system was used in combination with Pulse Control acquisition software (Herrington and Bookman, 1995) and Igor Pro for graphing and data analysis (WaveMetrics, Inc.). A Levenberg-Marquardt algorithm was used to perform nonlinear least-squared fits. Data are presented as mean ± SEM.

Open probability (P_O) was estimated by recording macroscopic I_K when P_O was high (≥0.005–0.05) and unitary currents in the same patch when P_O was low (≤0.01–0.1). Macroscopic conductance (G_K) was determined from tail currents at −80 mV following 50-ms voltage pulses, and was normalized by G_Kmax to estimate P_O. G_Kmax was measured in 5–100 mM Mg²⁺ (0 Ca²⁺) at V > 200 mV from tail currents and was estimated at [Mg²⁺] < 5 mM as G_Kmax (10 Mg²⁺) {γ_K([Mg²⁺])/γ_K(10 Mg²⁺)} where γ_K([Mg²⁺]) is the single channel conductance at −80 mV and is reduced slightly (∼5%) in 10 Mg²⁺ due to Mg²⁺ block. At more negative voltages, NP_O was determined from steady-state recordings of 1–60 s duration that were digitally filtered at 5 kHz. NP_O was determined from all-points amplitude histograms by measuring the fraction of time spent (P_K) at each open level (K) using a half-amplitude criteria and summing their contributions NP_o = ΣkP_k. P_O was then determined by estimating N from G_Kmax (N = G_Kmax/γ_K, where γ_K is the single channel conductance at −80 mV). Mean activation charge displacement (q_a = kT d(ln(P_O)/dV) was measured from the slope of the ln(P_O)-V relation by linear regression over 60-mV intervals and plotted against mean voltage. Fits of the q_a-V relation were similarly determined by linear regression of simulated data (Ma et al., 2006).

Patch-to-patch variation in V_0.5 of the G-V and Q-V relationships are observed for Slo1 channels (Stefani et al., 1997; Horrigan et al., 1999). To compensate for the effect of such variation on mean P_o-V and Q_C-V relations, V_0.5 was determined for each patch and individual relations were shifted along the voltage axis by ΔV_0.5 = (<V_0.5> − V_0.5) before averaging, where <V_0.5> is the mean for all experiments at the same [Mg²⁺]. Patch to patch variation in P_O at extreme negative voltages is also observed (Horrigan et al., 1999). Therefore, mean log(P_O)-V and τ_K-V relations for 0, 10, and 100 mM Mg²⁺ were constructed using only experiments in which both Mg²⁺ data and matching 0 Mg²⁺ controls exist. In this way, mean relations accurately reflect effects of Mg²⁺ that were observed in individual experiments.

Gating capacitance (C_g) was measured using admittance analysis as previously described (Horrigan and Aldrich, 1999). In brief, gating currents were recorded in response to 0.5-s voltage ramps upon which a sinusoidal voltage command (781 hz, 60 mV peak to peak) was superimposed. Admittance was calculated for each cycle of the sinewave, and capacitance was determined after correcting for phase shifts due to instrumentation.

RESULTS

Mg²⁺ and Ca²⁺ Act through Different Mechanisms

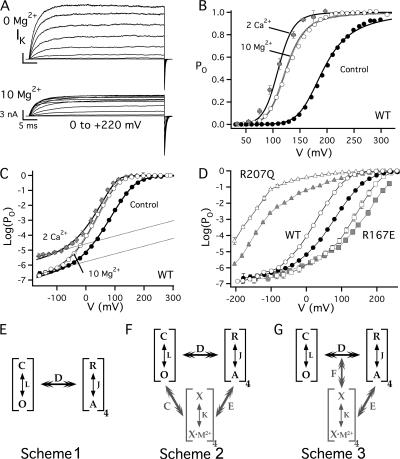
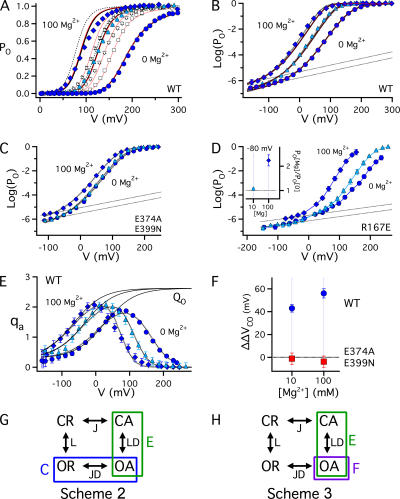
The effects of millimolar [Mg²⁺]_i and micromolar [Ca²⁺]_i on steady-state activation are compared in Fig. 2. In addition to increasing open probability, intracellular Mg²⁺ rapidly blocks the pore in a voltage-dependent manner that effectively reduces single channel conductance at depolarized voltages (Ferguson, 1991). Both of these effects are evident by comparing macroscopic potassium currents (I_K) in the presence and absence of 10 mM Mg²⁺ (Fig. 2 A). I_K was evoked by 50-ms pulses to different voltages in inside-out patches from Xenopus oocytes expressing mSlo1 BK channels. Mg²⁺ decreases outward current at the most positive voltages owing to pore block, but increases tail currents at −80 mV, indicating that P_O is increased. Normalized G_K-V relations, determined from tail currents exhibit a −67.2 ± 4.9 mV shift in half-activation voltage (V_0.5) in response to 10 mM Mg²⁺, with little change in shape, similar to the effect of 2 μM Ca²⁺ (Fig. 2 B).

Figure 2.

Effects of Mg²⁺ on steady-state activation. (A) Effect of 10 mM Mg²⁺ on macroscopic I_K evoked from mSlo1 channels in response to 50-ms pulses to different voltages in 0 Ca²⁺ from a holding potential of −80 mV. Mg²⁺ decreases outward current at high voltages owing to rapid pore block. However tail currents indicate an increase in P_O and slowing of channel deactivation. (B) Mean normalized G_K-V relations (P_o = G_K/G_Kmax) determined from tail currents in 10 mM Mg²⁺(O), 2 μM Ca²⁺(♦) or the absence of divalent cations (control, •). (C) Mean log(P_O)-V relations corresponding to B achieve a weakly voltage-dependent limiting slope at extreme negative voltages, indicating that voltage sensors are in the resting state. Dotted lines are exponential fits to control and Ca²⁺ data with partial charge z_L = 0.3e (Ma et al., 2006). (D) Voltage sensor mutations R207Q (▵, ▴) and R167E (□, ▪) shift both the voltage dependence of activation and Mg²⁺ sensitivity (0 Mg: filled symbols; 10 mM Mg²⁺: open symbols) relative to the WT (O, •), implying that Mg²⁺ action depends on voltage sensor activation and is not intrinsically voltage dependent. (E) Voltage-gating mechanism (Scheme 1). Channels undergo a closed–open (C-O) conformational change that is allosterically regulated by four independent and identical voltage sensors that can undergo a resting-activated (R-A) transition. L and J are voltage-dependent equilibrium constants (L = L₀exp(z_LV/kT), J = J₀exp(z_JV/kT) = exp(z_J[V − V_hC]/kT)) and D is an allosteric factor. (F) Scheme 2 includes a ligand-binding transition (X-X·M²⁺) in each subunit that allosterically regulates channel opening and voltage sensor activation as described by factors C and E, respectively. Solid curves in B and C represent a fit of this model to Ca²⁺-dependent activation in 0–100 μM Ca²⁺ (Horrigan and Aldrich, 2002) (V_hC = 156 mV, z_J = 0.58e, L₀ = 1.06 × 10⁻⁶, z_L = 0.3e, K_D(Ca²⁺) = 11 μM, C = 8, D = 24.4, E = 2.4). The same model with identical values of V_hC, z_J, L₀, z_L, D, and E can fit the Mg²⁺ data (dotted curves) if Mg²⁺ binding is assumed to be voltage dependent (i.e., K_D(Mg²⁺) = K_D(0)exp(−Vγ2e/kT)) (K_D(0) = 9.35 mM, γ = 0.2, C = 1.66) (G) Scheme 3 assumes that ligand binding allosterically regulates voltage/sensor gate coupling and voltage sensor activation as described by allosteric factors F and E, respectively.

Despite similar effects of Mg²⁺ and Ca²⁺ on the G_K-V relation, fundamental differences in the action of these ligands are evident when P_O is plotted on a log-scale versus voltage (Fig. 2 C). P_O was measured to values as low as ∼10⁻⁷ by recording unitary current activity in macropatches containing hundreds of channels. Log(P_O) is increased by 2 μM Ca²⁺ in a nearly voltage-independent manner, shifting the entire log(P_O)-V curve upward by 1.2 log units (a 15-fold increase in P_O) until channels are maximally activated at positive voltages. P_O is increased 15-fold even at extreme negative voltages (≤−100 mV) where voltage sensors are not activated and log(P_O) is weakly voltage dependent (Fig. 2 C, dotted lines) (Horrigan and Aldrich, 2002). By contrast, 10 mM Mg²⁺ has no effect on steady-state activation at extreme negative voltages and increases log(P_o) in a voltage-dependent manner from −80 to +40 mV such that the effects of Mg²⁺ and Ca²⁺ are similar only at more positive voltages.

Why Is the Effect of Mg²⁺ Voltage Dependent?

Two different mechanisms could potentially account for the voltage dependence of Mg²⁺ action; the effect of Mg²⁺ could depend on the activation state of the voltage sensor, or Mg²⁺ binding could be intrinsically voltage dependent. Voltage-dependent binding must be considered because if Mg²⁺ interacts with the voltage sensor it could also lie within the membrane electric field; and a model assuming that Mg²⁺ traverses a fraction of the electric field (γ = 0.2) to reach its binding site can reproduce the effect of 10 mM Mg²⁺ (Fig. 2, B and C, dotted curves, see legend for details). However, the effects of Mg²⁺ on two voltage sensor mutants (R207Q, R167E) in Fig. 2 D indicate that voltage sensor activation is critical to the effect of Mg²⁺ and probably sufficient to account for the voltage dependence of Mg²⁺ action.

R207Q in S4 and R167E in S2 shift voltage sensor activation to more negative and positive voltages, respectively (Ma et al., 2006), such that log(P_O)-V relations for these mutants are shifted along the voltage axis relative to the WT in 0 Mg²⁺ (Fig. 2 D, filled symbols). R207Q also shifts the Q-V relation by more than −250 mV, based on gating current measurements, such that even at −200 mV a significant fraction (∼0.2) of voltage sensors are activated (Ma et al., 2006). Both R207Q and R167E are readily activated by 10 mM Mg²⁺ at depolarized voltages (Fig. 2 D), suggesting these mutations do not disrupt Mg²⁺ binding nor interactions of Mg²⁺ with the voltage sensor (Hu et al., 2003; Yang et al., 2007). However the voltage dependence of Mg²⁺-dependent activation for the mutants is greatly altered relative to the WT, suggesting that Mg²⁺ action depends on the activation state of the voltage sensor. In the case of R167E, Mg²⁺ has no effect on P_O at voltages up to +60 mV where the WT is strongly activated by Mg²⁺. Conversely, R207Q exhibits a robust 30-fold increase in P_O at negative voltages (−120 to −200 mV) where the WT appears insensitive to Mg²⁺. The response of R207Q indicates that Mg²⁺ is capable of occupying its binding site even at extreme negative voltages. Thus, it is unlikely that Mg²⁺ binding is intrinsically voltage dependent; and the inability of the WT to be activated at negative voltages likely reflects that Mg²⁺ is incapable of increasing P_O when voltage sensors are in the resting state. This hypothesis is supported by comparison of the WT and R167E data that show that channels are Mg²⁺ insensitive when P_O is weakly voltage dependent.

Understanding the Action of Mg²⁺ in Terms of Allosteric Mechanisms

To determine how Mg²⁺ and voltage sensors interact mechanistically we interpreted our results in terms of a well-established allosteric gating scheme that accounts for the effects voltage on steady-state activation of BK channels (Fig. 2 E, Scheme 1) (Horrigan and Aldrich, 1999; Horrigan et al., 1999). Scheme 1 asserts that the opening of the gate can be described as a concerted, weakly voltage-dependent transition between an open and closed conformation (C-O) with zero-voltage equilibrium constant L₀ and partial charge z_L. In addition, voltage sensors in each of four independent and identical subunits can undergo a transition between a resting and activated conformation (R-A) characterized by equilibrium constant J₀ and partial charge z_J. The coupling between voltage sensor and gate is described by an allosteric factor D, such that the C-O equilibrium constant increases D-fold for each voltage sensor activated and the voltage sensor equilibrium increases D-fold when the channel opens.

Based on Scheme 1 there are four distinct mechanisms by which a ligand might alter P_o. Ligand binding could (a) influence the intrinsic stability of the gate (L₀), (b) perturb the voltage sensor equilibrium (J₀), (c) alter voltage sensor/gate coupling (D-factor), or (d) alter the gating charge associated with voltage sensor activation (z_J) or channel opening (z_L). The action of Ca²⁺ is mainly accounted for by an effect on the gate (L₀) with a minor impact on voltage sensor activation (J₀). This mechanism can be represented by an allosteric model (Fig. 2 F, Scheme 2) that successfully reproduces the effects of Ca²⁺ (Fig. 2, B and C, solid lines) in terms of a ligand-binding equilibrium (X-X·M²⁺) and allosteric factors C and E that describe the coupling of Ca²⁺ sensors to the gate and to voltage sensors, respectively (Horrigan and Aldrich, 2002). Direct coupling between Ca²⁺ sensors and gate is evident from the ability of Ca²⁺ to increase P_O whether or not voltage sensors are activated. Thus the insensitivity of P_O to 10 mM Mg²⁺ when voltage sensors are in the resting state rules out a similar interaction between Mg²⁺ sensors and gate and indicates that L₀ is unchanged, but leaves open the possibility that Mg²⁺ affects voltage sensor activation or coupling (Fig. 2 G, Scheme 3) or charge.

Mg²⁺ Has Little Effect on Voltage Sensor Activation when Channels Are Closed

To characterize effects of Mg²⁺ on the voltage sensor we recorded gating current from WT and mutant channels (Fig. 3). The results indicate that Mg²⁺ has little effect on the voltage sensor equilibrium (J₀) or gating charge (z_J).

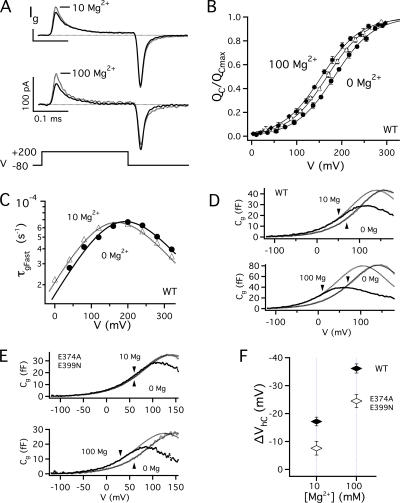
Figure 3.

Effects of Mg²⁺ on gating current were measured in the absence of permeant ions and presence of extracellular tetraethyl ammonium (TEA) to block the pore. (A) I_g evoked by 0.5-ms pulses to +200 mV in the presence (dotted traces) or absence (solid traces) of Mg²⁺, from two different patches testing the effects 10 or 100 mM Mg²⁺. (B) Mean Q_C-V relations in 0 (•), 10 (▵), and 100 (♦) mM Mg²⁺ are fit by Boltzmann functions with identical equivalent charge (z_J = 0.58e) (Horrigan and Aldrich, 2002) and were normalized by the fit amplitude (Q_cMax). Q_C represents the charge distribution for closed channels, determined by fitting the initial 50–100-μs decay of I_gON with an exponential function with time constant τ_gFast and integrating the area under the rising phase and fit (Horrigan and Aldrich, 1999). (C) τ_gFast-V relations for the patch in A are shifted by −21 mV in 10 mM Mg²⁺. Relations are fit by functions of the form τ_gFast = [α(V) + β(V)]⁻¹ where α and β are forward and backward rate constants for voltage sensor activation (0 Mg: α(0) = 58600 s⁻¹, β(0) = 1930 s⁻¹; 10 Mg: α(0) = 45400 s⁻¹, β(0) = 2350 s⁻¹) (z_α = 0.3 e, z_β = −0.2e). Representative C_g-V relations obtained with admittance analysis for (D) WT or (E) E374A/E399N channels in the presence (black curves) and absence (gray curves) of 10 or 100 mM Mg²⁺ are fit by the derivative of a Boltzmann function with respect to voltage (dotted curves) with identical amplitude and charge (z_J = 0.58e). Shifts along the voltage axis indicate the change in V_hC (ΔV_hC). Arrows indicate the upper voltage limit of the fit that was determined over a range where most channels are closed (P_o < 0.1). (F) ΔV_hC = [V_hC(Mg²⁺) − V_hC(0 Mg²⁺)] for WT (♦, n = 6) and E374A/E399N (⋄, n = 4) determined from C_g-V relations.

Voltage sensor activation in BK channels is much faster than channel opening (Stefani et al., 1997; Horrigan and Aldrich, 1999). Therefore ON gating current (I_gON) reflects primarily voltage sensor activation when channels are closed. Fig. 3 A shows the effects of Mg²⁺ on I_gON evoked by brief 0.5-ms depolarizations to +200 mV. 10 mM Mg²⁺ causes an ∼20% increase in peak I_gON with little change in kinetics (Fig. 3 A, top). Application of 100 mM Mg²⁺, to activate very low affinity binding sites (Hu et al., 2006), produces a greater increase in peak current (Fig. 3 A, bottom). Mean charge–voltage relations for closed channels (Q_C-V), determined from I_gON (see Fig. 3 legend) are shifted to more negative voltages by −16.7 ± 2.3 mV (n = 5) or −29.6 ± 2.6 mV (n = 3) in 10 or 100 mM Mg²⁺, respectively (Fig. 3 B). This shift in half-activation voltage (V_hC) occurs without appreciable change in the shape of the Q_C-V relation, suggesting that Mg²⁺ does not alter gating charge. Similarly, effects of 10 mM Mg²⁺ on the time constant of I_gON (τ_gFast) for a single experiment (Fig. 3 C) reflect a small −21 mV shift in the τ_gFast-V relation to more negative voltages.

To better quantify small changes in V_hC (ΔV_hC) by Mg²⁺ we examined gating capacitance (C_g) (Fig. 3, D–F). C_g is the voltage-dependent component of membrane capacitance and reflects the derivative of gating charge with respect to voltage. The C_g-V relation was determined from admittance analysis by measuring I_g evoked by a sinusoidal voltage command superimposed on a 500-ms voltage ramp from −200 to +200 mV (see Materials and methods) (Horrigan and Aldrich, 1999, 2002). At voltages where steady-state P_O is low (<0.1), the C_g-V relation approximates the derivative of Q_C-V (Horrigan and Aldrich, 1999). Thus ΔV_hC can be determined directly from shifts in the foot of C_g-V relation (Fig. 3 D). Because C_g-V is determined rapidly and with high voltage resolution, small V_hC shifts are detectable, the effects of applying and washing out Mg²⁺ can be assessed rapidly, and errors in ΔV_hC due to slow changes in V_hC from channel oxidation or electrode potential drift are minimized. C_g-V analysis for the WT (Fig. 3 D) yielded ΔV_hC values (10 Mg: 17.2 ± 1.5 mV [n = 6], 100 Mg: 36.1 ± 1.6 mV [n = 6]) similar to those determined from Q_C-V relations.

The effect of Mg²⁺ on V_hC is comparable to that of micromolar Ca²⁺ (Horrigan and Aldrich, 2002), consistent with a weak interaction between Mg²⁺ binding and voltage sensor activation in closed channels that increases the voltage sensor equilibrium constant J₀ (e.g., E-factor in Schemes 2 and 3, Fig. 2, F and G). However, millimolar Mg²⁺ may also shift voltage-dependent parameters by nonspecific mechanisms such as screening of membrane surface charge (Hu et al., 2006). Therefore, to assess the impact of the RCK1 Mg²⁺ site on J₀ we compared effects of Mg²⁺ on the WT channel to those of a mutant (E374A/E399N) whose RCK1 site is disrupted (Shi et al., 2002; Hu et al., 2006). This mutation of putative Mg²⁺-coordinating residues, which reduces the G_K-V shift in 10 mM Mg²⁺ by 80% to −14.0 ± 2.0 mV, also reduces effects of 10 or 100 mM Mg²⁺ on the C_g-V relation (Fig. 3, E and F). The difference in ΔV_hC between the WT and mutant (ΔΔV_hC = ΔV_hC(E374A/E399N) − ΔV_hC(WT)) was −9.5 ± 2.8 mV and −11.6 ± 2.8 mV for 10 and 100 Mg²⁺, respectively, likely representing the effect of RCK1 site occupancy on J₀. The similar impact of mutation in 10 and 100 mM Mg²⁺ is consistent with the expectation that the RCK1 site is nearly saturated in 10 mM Mg²⁺(Hu et al., 2006).

The small effect of Mg²⁺ on gating current suggests that Mg²⁺ enhances voltage sensor/gate coupling (D). The −17.2 mV ΔV_hC by 10 mM Mg²⁺ (Fig. 3 F) can account for a similar G_K-V shift but is much too small to explain the observed −67-mV shift (Fig. 2 B). By contrast, an increase in the coupling factor D can shift V_0.5 without affecting V_hC. In addition, enhanced coupling should facilitate channel opening when voltage sensors are fully activated and facilitate voltage sensor activation when channels are open. These predictions are confirmed below by results in Figs. 4 and 5.

Figure 4.

Mg²⁺ facilitates opening in a voltage-independent manner when voltage sensors are constitutively activated. (A) Mean log(P_O)-V relations for WT (•), R207Q (▴), and R210C (▾) in 0 Mg²⁺. Arrows indicate the voltage range where voltage sensors of WT, R207Q, and R210C are fully activated (see text). Dotted curve represents a Boltzmann fit to R210C with partial charge z = 0.46e that describes the weak voltage dependence of channel opening in both mutants when voltage sensors are fully activated (Ma et al., 2006). (B) Mean log(P_O)-V relations for R207Q show that 10 mM Mg²⁺ (▵) increases P_O even when voltage sensors are fully activated. Dotted Boltzmann fits from −20 to +240 mV have identical charge (0.46e) but V_0.5 is shifted by −91.6 mV in Mg²⁺, consistent with a 8.2-fold increase in the C-O equilibrium constant. (C) Mean log(P_O)-V relations for R210C show that 10 mM Mg²⁺(▿) increases the C-O equilibrium constant in a voltage-independent manner when voltage sensors are constitutively activated. Boltzmann fits have identical charge (0.46e) but V_0.5 is shifted by −122 mV in Mg²⁺, consistent with a 16.6-fold increase in the C-O equilibrium constant and a twofold increase in the allosteric coupling factor D.

Figure 5.

Effects of Mg²⁺ on different binding sites were determined by measuring P_O for WT and mutant channels in 0–100 mM Mg²⁺ (0, blue circle; 2, □; 5, ▿; 10, blue triangle; 21, ; 100, blue diamond, mM Mg²⁺). (A) Normalized mean G_K-V relations for the WT in 0–100 mM Mg²⁺. (B) Mean log(P_O)-V relations for WT in 0, 10, and 100 mM Mg²⁺ reveal that 100 Mg²⁺ increases P_O at extreme negative voltages. These plots represent the same data as in A but were averaged in 20 mV rather than 10-mV bins to match the voltage interval for low P_O measurements. Dotted lines are exponential fits to P_O at extreme negative voltages in 0 and 100 Mg²⁺ with partial charge z_L = 0.3e. (C) Mean log(P_O)-V relations in 0, 10, and 100 mM Mg²⁺ for E374A/E399N show that mutation of the putative Mg²⁺ site in RCK1 almost abolishes effects of 10 mM Mg²⁺ but leaves the P_O increase by 100 Mg²⁺ (dotted lines) intact. (D) Mean log(P_O)-V relations in 0, 10, and 100 mM Mg²⁺ for R167E achieve a limiting slope at more positive voltages than the WT, confirming that P_O is increased by 100 Mg²⁺ when voltage sensors are in the resting state (dotted lines). Inset graph plots the ratio of NP_O in the presence and absence of Mg²⁺ at −80 mV from a larger set of experiments. (E) Mean q_a-V relations for the WT in 0, 10, and 100 mM Mg²⁺ were derived from the slope of log(P_O)-V in B (see text). Solid curves are estimates of the Q_O-V relation determined by fitting the foot of the q_a-V relation (to ∼80% of peak q_a) with a function q_a = z_L + 4z_J [1 + exp([V_hO − V]z_J/kT)]⁻¹ where z_L = 0.3e, z_J = 0.58e, and V_hO = 26.5 ± 2.1, −33.6 ± 2.4, −65.6 ± 3.7 mV in 0, 10, and 100 mM Mg²⁺, respectively. (F) Plot of ΔΔV_CO = ΔV_hC − ΔV_hO for 10 and 100 mM Mg²⁺ in WT (blue circle) and E374A/E399N (red square) channels where ΔV_hO = [V_hO(Mg²⁺) − V_hO(0 Mg²⁺)] was estimated from the q_a-V relation as in E and ΔV_hC was determined from gating current (Fig. 3 F). Nonzero values of ΔΔV_CO indicate that Mg²⁺ alters voltage sensor/gate coupling in the WT. However, effects on coupling are abolished by the E374A/E399N mutation. (G) Alternative representation of Scheme 2 (Fig. 2 F) shows the four states defined by the voltage sensor and gate conformation in each subunit and the equilibrium constants defined by Scheme 1 (Fig. 2 E). Boxes denote the states stabilized by ligand binding, as defined by allosteric factors C and E. (H) In Scheme 3, the allosteric factor F defines a stabilization of the OA state that alters voltage sensor/gate coupling (allosteric factor D). Dotted curves in A–E represent simultaneous fits to the P_o-V, log(P_O)-V, and q_a-V relations in 0, 10, and 100 mM Mg²⁺ using Scheme 1 (Fig. 2 E) (Table I parameters WT_A, E374A/E399N). Solid black curves in A and B represent an alternative fit to the WT data (WT_B parameters). Red curves in A represent fits to a two-site model (Eq. 2) that assumes each subunit in the WT contains a very low affinity and an RCK1 binding site described by Schemes 2 and 3, respectively (Table II parameters).

Mg²⁺ Facilitates Opening When Voltage Sensors Are Constitutively Activated

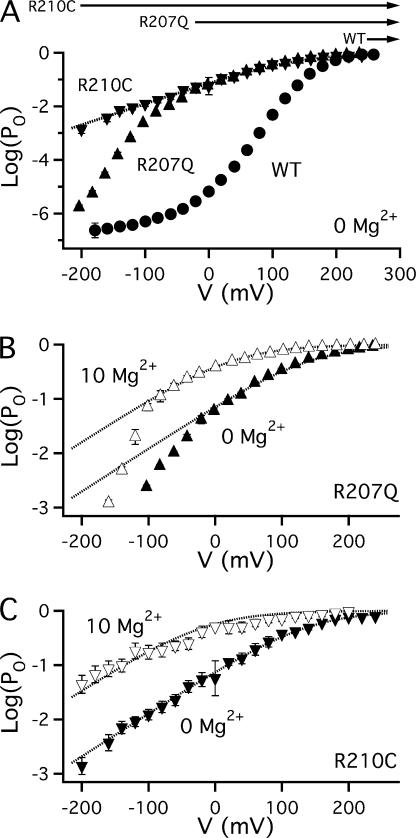
Voltage sensor/gate coupling defines the extent to which P_O is increased by voltage sensor activation. According to Scheme 1, the C-O equilibrium constant increases from L₀ when voltage sensors are in the resting state to L₀D⁴ when all four voltage sensors are activated. If 10 mM Mg²⁺ enhances coupling (D) without affecting L₀, then the C-O equilibrium constant when voltage sensors are fully activated should increase by a factor of δD⁴ where δD = D(Mg²⁺)/D(control). This predicted facilitation of opening cannot be tested for the WT channel because in 0 Mg²⁺ P_O is already nearly saturated (∼1) at potentials >250 mV where voltage sensors are fully activated (compare G_K-V in Fig. 2 B and Q_c-V in Fig. 3 B). However, facilitated opening by Mg²⁺ can be observed in mutants with enhanced voltage sensor activation (R207Q, R210C; Fig. 4).

Fig. 4 A compares the log(P_O)-V relations for WT, R207Q, and R210C channels in 0 Mg²⁺. R207Q shifts Q_C-V, as noted above, such that this relation is saturated and voltage sensors are fully activated at V ≥ −20 mV (Ma et al., 2006) (Fig. 4 A, labeled arrow). Over this voltage range, P_O is weakly voltage dependent and well described by a Boltzmann function (dotted curve) as expected for channels with fully activated voltage sensors undergoing a two-state C-O transition with equilibrium constant L₀D⁴ (Horrigan and Aldrich, 2002). Importantly, the weak voltage dependence of L₀ reduces P_O to nonsaturating levels at potentials where the mutant voltage sensors are still fully activated (e.g., P_O = 0.04 at −20 mV). The P_O-V relation for R210C is indistinguishable from that of R207Q at V ≥ −20 but extends the weakly voltage-dependent phase of P_O to less than −200 mV, suggesting that R210C voltage sensors are constitutively activated (Ma et al., 2006). The difference between WT and R207Q in Fig. 4 A is consistent with a 100-fold change in the voltage sensor equilibrium constant J₀ (Horrigan and Aldrich, 1999; Ma et al., 2006) and illustrates qualitatively the effect expected if Mg²⁺ acts merely to promote voltage sensor activation. That is, an increase in J₀ can shift the steepest part of the log(P_O)-V relation to more negative voltages but cannot increase P_O above the limiting relation defined by L₀D⁴ (Fig. 4 A, dotted curve). By contrast, 10 mM Mg²⁺ markedly increases P_O for R207Q (Fig. 4 B) and R210C channels (Fig. 4 C) when voltage sensors are fully activated, indicating that L₀D⁴ is increased. This increase presumably reflects enhanced voltage sensor/gate coupling (increased D) because L₀, although it cannot be measured directly for R207Q or R210C channels, is insensitive to 10 mM Mg²⁺ in WT and R167E (Fig. 2 D).

Analysis of the mutant data indicate that 10 mM Mg²⁺ produces an approximate twofold increase in the coupling factor D. Fig. 4 C shows that R210C channels are activated by 10 mM Mg²⁺ in a voltage-independent manner, consistent with the assumption that voltage sensors are constitutively activated. Mean log(P₀)-V relations in the presence and absence of Mg²⁺ were fit by Boltzmann functions with identical charge (Fig. 4 C, dotted curves), as expected if Mg²⁺ increases the C-O equilibrium constant by a voltage-independent factor (δD⁴) and Mg²⁺ binding is not voltage dependent. A similar response is observed for R207Q at V ≥ −20 mV (Fig. 4 B, dotted curves). The fits to R207Q and R210C yield δD⁴ values of 8.2 and 16.6, respectively, implying a 1.7–2.0-fold increase in D. A more direct estimate of δD⁴ is obtained from the Mg²⁺-dependent increase in P_O for R210C at extreme negative voltage. Over a range of voltages (−200 to −140 mV) where P_O is small (<0.1) and therefore approximates the C-O equilibrium constant, Mg²⁺ increases P_O by an average of 21.6 ± 6.0-fold (δD⁴), indicating a 2.16 ± 0.13-fold increase in D, consistent with the Boltzmann fits.

Different Mg²⁺ Sites Have Distinct Effects on Gating

To further characterize the action of Mg²⁺ at both RCK1 and very low affinity binding sites we examined the effects on P_O of different [Mg²⁺]_i, up to 100 mM, in WT and mutant channels (Fig. 5). The RCK1 site with an estimated K_D of 2.2–5.5 mM should be nearly saturated at 10 mM Mg²⁺, whereas a putative very low affinity site (K_D: 40–136 mM) is not significantly affected until concentrations >10 mM (Hu et al., 2006). The effects of high and low concentrations of Mg²⁺ appear similar in that G_K-V relations are progressively shifted to more negative voltages with little change in shape (Fig. 5 A) (Shi and Cui, 2001; Zhang et al., 2001; Hu et al., 2006). Increasing Mg²⁺ from 10 to 100 mM shifted the G-V by an additional −34 mV (Fig. 5 A). However, log(P_O)-V relations reveal that 100 mM Mg²⁺ also increases P_O significantly at extreme negative voltages (Fig. 5 B). Thus it appears that occupancy of very low affinity Mg²⁺ sites, unlike the RCK1 site, influence the gate (L₀) to increase P_O when voltage sensors are not activated.

The log(P_O)-V relation in 100 mM Mg²⁺ appears to achieve a limiting slope between −160 and −140 mV, where P_O is increased 2.9-fold relative to the control (Fig. 5 B, dotted lines), implying a 2.9-fold increase in L₀. However measurements below −140 mV were difficult to obtain. Therefore, to confirm that 100 mM Mg²⁺ increases L₀ we also compared log(P_O)-V relations in 0, 10, and 100 mM Mg²⁺ for two mutant channels (Fig. 5, C and D).

Mutation of the RCK1 site (E374A/E399N) largely eliminates the response to 10 mM Mg²⁺ but leaves the P_O increase by 100 mM Mg²⁺ intact (Fig. 5 C). The mutation reduces the G_K-V shift (ΔV_0.5) by 10 and 100 Mg²⁺ to −14.0 ± 2.0 mV and −34.6 ± 1.8 mV, respectively, similar to previous reports (Shi and Cui, 2001; Hu et al., 2006). The reduced shift allows log(P_O)-V to achieve a limiting slope at more positive voltages than the WT (Fig. 5 C, dotted lines), indicating a 2.9-fold increase in L₀ with 100 mM Mg²⁺, like the WT.

The response of E374A/E399N is important not only in verifying that L₀ is increased by 100 mM Mg²⁺ but also in ruling out that Mg²⁺ occupancy of either the RCK1 site or Ca²⁺-binding sites contribute to L₀. The insensitivity of L₀ to 10 mM Mg²⁺ in the WT could conceivably reflect an ability of Mg²⁺ at the RCK1 site to decrease L₀ that is masked by the action of Mg²⁺ at other sites. However, this possibility is unlikely since L₀ is also insensitive to 10 mM Mg²⁺ in E374A/E399N. In addition this result indicates that high affinity Ca²⁺-binding sites, which are known to bind Mg²⁺ at millimolar concentrations, are not responsible for the L₀ increase in 100 mM Mg²⁺ because such sites should already be nearly saturated in 10 mM Mg²⁺ (Shi and Cui, 2001; Zhang et al., 2001; Hu et al., 2006). Thus the E374A/E399N results confirm that occupancy of a very low affinity Mg²⁺ site is required to increase L₀.

The R167E mutant was used to better quantify the effects of Mg²⁺ on L₀ (Fig. 5, D and E). R167E is activated strongly by 100 mM Mg²⁺ but achieves a limiting slope at voltages ∼100 mV more positive than the WT (Fig. 5 D, dotted lines). Thus L₀ can be determined at voltages that are sufficiently negative to achieve a limiting slope but not too extreme to prevent steady-state recording. The effects on L₀ of 10 and 100 mM Mg²⁺ were determined from the change in NP_O at −80 mV in patches where Mg²⁺ was repeatedly applied and washed out. The results confirm that 10 mM Mg²⁺ has little or no effect on L₀ (1.06 ± 0.05-fold change, n = 10), whereas 100 mM Mg²⁺ increased L₀ by a factor of 2.24 ± 0.23 (n = 5)(Fig. 5 D, inset).

Mg²⁺ Enhances Voltage Sensor Activation when Channels Are Open

The voltage dependence of P_O in the WT channel provides further evidence that Mg²⁺ enhances voltage sensor/gate coupling. According to Scheme 1, the equilibrium constant for voltage sensor activation when channels are open (J₀D) is directly proportional to D. Therefore the charge–voltage relation for open channels (Q_o-V), should be shifted to more negative voltages by Mg²⁺ if coupling is enhanced. Although BK channel voltage sensors can move when channels are open, determination of Q_o from gating currents is difficult because channels close rapidly (Horrigan and Aldrich, 1999). However, Q_o can be assessed in a model-independent fashion from the logarithmic slope of the P_o-V relation (Horrigan and Aldrich, 2002). The mean activation charge displacement (q_a = kTd(ln[P_o])/dV) exhibits a bell-shaped dependence on voltage that is plotted in Fig. 5 E for 0, 10, and 100 mM Mg²⁺. q_a is expected to approximate Q_o at voltages where both P_O and Q_c are small (Horrigan and Aldrich, 2002; Ma et al., 2006). Thus the Q_o-V relation is approximated by the foot of the q_a-V relation at negative voltages, and is markedly left-shifted by Mg²⁺, indicating that voltage sensor activation is enhanced when channels are open.

To estimate the increase in voltage sensor/gate coupling by Mg²⁺ we fit the foot of the mean q_a-V relations with a function predicted by Scheme 1 to describe Q_o: Q_o = z_l + 4z_JB(V), where B(V) is a Boltzmann function with charge z_J and half activation voltage V_hO (Fig. 5 E, solid curves). The fits indicate that V_hO is shifted by −60 ± 3 mV and −92 ± 4 mV in 10 Mg²⁺ and 100 Mg²⁺, respectively. Changes in the coupling factor D can be determined by comparing the shift in Q_O (ΔV_hO) to that in Q_C (ΔV_hC). Q_O depends on both D and J₀, whereas Q_C depends only on J₀. Therefore the quantity ΔΔV_CO = [ΔV_hC − ΔV_hO], plotted in Fig. 5 F for WT and E374A/E399N channels, should depend only on D (i.e., δD = exp(z_JΔΔV_CO/kT), based on Scheme 1). Fig. 5 F indicates ΔΔV_CO = 43 ± 3 mV in 10 mM Mg²⁺, corresponding to a 2.7-fold increase in D. 100 mM Mg²⁺ produces a larger ΔΔV_CO (56 ± 4 mV), corresponding to a 3.6-fold increase in D, that probably represents the effect of saturating the RCK1 site. ΔΔV_CO for the E374A/E399N mutant is not significantly different from 0 (P < 0.05, t test) in 10 or 100 Mg²⁺ (Fig. 5 F), implying that all changes in voltage sensor/gate coupling can be attributed to the RCK1 site.

Modeling the Effects of Mg²⁺ on Steady-State Activation

The above results suggest that 10 mM Mg²⁺ acts primarily at the RCK1 binding site to enhance voltage sensor/gate coupling (D) with a minor effect on the voltage equilibrium (J₀), and that 100 mM Mg²⁺ causes additional increases in D, J₀, and L₀ that reflect action at both RCK1 and very low affinity binding sites. To confirm that these parameter changes are sufficient to describe the effects of Mg²⁺ on steady-state activation and to better quantify the changes in D we fit simultaneously the log(P_O)-V, q_a-V, and P_O-V relations for 0, 10, and 100 mM Mg²⁺ using Scheme 1, as defined by Eq. 1:

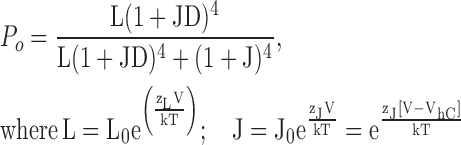(1)

The 0 Mg²⁺ data were fit by setting charge parameters to values determined previously (z_J = 0.58 e, z_L = 0.3 e) (Horrigan and Aldrich, 2002) and allowing all other parameters (J₀, L₀, D) to vary, yielding results (Table I, WT 0 Mg²⁺) similar to previous reports (Horrigan and Aldrich, 2002; Ma et al., 2006). To fit the Mg²⁺ data, the change in J₀ relative to 0 Mg²⁺ was set by gating current measurements (ΔV_hC, Fig. 3 F), while L₀ and D were allowed to vary. Excellent fits to the log(P_O)-V and q_a-V relations were obtained in this way (Fig. 5, B and E, dotted curves), with 10 Mg²⁺ increasing D by a factor of 2.14, and 100 Mg²⁺ causing a greater increase in D (2.83-fold) together with a 2.43-fold increase in L₀ (Table I, WT_A parameters). A similar procedure was used to fit the E374A/E399N data (Fig. 5 C, dotted curves), yielding values of D (Table I, E374A/E399N parameters) that vary by <15% relative to the control, which is within the resolution of our measurement (Ma et al., 2006). Thus, shifts in V_hc determined from gating currents together with an increase in L₀ in 100 Mg²⁺ appear sufficient to account for the changes in log(P_O)-V when the RCK1 site is disrupted.

TABLE I.

Scheme 1 Parameters

	WT	WTA		WTB		E374A/E399N
[Mg2+] (mM)	0	10	100	10	100	0	10	100
VhC (mV)	156.2	139.1	120.1	139.1	120.1	142.9	135.3	118.4
J0 × 102	2.77	4.10	6.34	4.10	6.34	3.76	4.47	6.60
L0 × 106	1.06	1.08	2.57	1.08	2.57	1.66	1.31	4.16
D	24.4	52.2	68.8	48	55	25.9	27.7	23.0

Parameters for Eq. 1 that were varied to fit WT and E374A/E399N data in 0–100 mM Mg²⁺ (Fig. 5, A, B, C, and E). V_hC in 10 and 100 mM were determined as V_hC(0) + ΔV_hC(Mg²⁺) where V_hC(0) was determined from the 0 Mg²⁺ fit and ΔV_hC(Mg²⁺) from gating current (Fig. 3 F). J₀ is determined from V_hC (J₀ = exp(−V_hCz_J/kT)). Charge parameters were fixed (z_J = 0.58 e, z_J = 0.30 e).

Although the fits from Scheme 1 reproduced the effects of Mg²⁺ on log(P_O) and q_a, they overestimated the shift in V_0.5 especially in 100 Mg²⁺ (Fig. 5 A, dotted curves). V_0.5 can be fit at the expense of underestimating the shift in the log(P_O)-V relation by reducing the Mg²⁺-dependent change in D as illustrated by alternative fits in Fig. 5 (A and B, thick solid curves) where D was increased by factors of 1.97 and 2.26 in 10 and 100 mM Mg²⁺, respectively (Table I, WT_B parameters). These parameters reasonably approximate the 10 Mg²⁺ P_O-V and log(P_O)-V relations but overestimate the steepness of P_O-V in 100 Mg²⁺ (Fig. 5 A). This discrepancy reflects a decrease in the slope of P_O-V as Mg²⁺ is increased from 10 to 100 mM Mg², a feature of the data that is not reproduced by Scheme 1.

To account explicitly for the effects of Mg²⁺ binding on the parameters in Scheme 1 we modeled the effects of very low affinity and RCK1 binding sites in terms of Schemes 2 and 3, respectively (Fig. 2, F and G). These allosteric mechanisms assume that Mg²⁺ can bind to any state of the channel defined by Scheme 1 and that effects of Mg²⁺ on the relative stability of different states therefore reflect the relative affinity of Mg²⁺ for these states. This principal is illustrated in Fig. 5 (G and H) by alternative representations of Schemes 2 and 3 that include the four states (CR, OR, CA, OA) and equilibrium constants defined by Scheme 1 for a single subunit, where boxes and associated allosteric factors indicate the states that are stabilized relative to the CR state by ligand binding. In Scheme 2, the action of Mg²⁺ is defined by its dissociation constant for the CR state (K_D) and two allosteric factors (C and E). C defines the increase in affinity associated with channel opening, such that K_D is reduced C-fold for the OR and OA states (Fig. 5 G, labeled box). Likewise, E defines the change in K_D associated with voltage sensor activation (Fig. 5 G, CA and OA states). These changes in affinity can account for effects of Mg²⁺ on the equilibria for channel opening (L₀) and voltage sensor activation (J₀). However, voltage sensor/gate coupling (D) is unchanged in Scheme 2 because the effects of C and E are independent and neither alters binding in a manner that depends on the state of both the voltage sensor and gate. By contrast, in Scheme 3, D is increased F-fold upon ligand binding by assuming that the affinity of the open-activated state (OA) is increased relative to all other states by an allosteric factor F. Scheme 3 also includes an independent effect of voltage sensor activation on Mg²⁺ affinity (E-factor) as in Scheme 2, to account for effects on J₀.

The data in Fig. 5 (A and B) were fit (red curves, Table II parameters) by a two-site model that assumes the channel contains a single RCK1 (site 1, Scheme 3) and a very low affinity (site 2, Scheme 2) binding site in each of four identical subunits, yielding Eq. 2 (see below), where L, J, and D are defined as in Eq. 1; E₁, F₁ and C₂, E₂ are allosteric factors for sites 1 and 2, respectively; and K_i = [Mg²⁺]/K_Di (i = 1,2), where K_Di is dissociation constant for each binding site in the CR state.

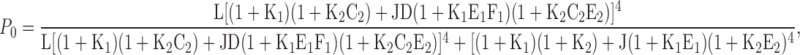(2)

TABLE II.

Two-Site Model Parameters

Site (i)	KDi	Ci	Ei	Fi	KD(CR)	KD(OR)	KD(CA)	KD(OA)
1	5.0		1.35	2.0	5.0	5.0	3.70	1.85
2	70	1.6	2.3		70	43.8	30.4	19.0

Parameters that were varied to fit Mg²⁺ data (Fig. 5, A and B) for WT (Eq. 2) and E374A/E399N (Eq. 2 with K₁ = 0). Remaining parameters (z_J, z_L, J₀, L₀, D) were identical to those for 0 Mg²⁺ in Table I. These parameters predict ΔV_hC values of −15.7 mV (WT, 10 Mg), −36.9 mV (WT, 100 Mg), −6.5 mV (E374A/E399N, 10 Mg), −24.4 mV (E374A/E399N, 100 Mg); similar to those measured in Fig. 3 F.

The fits of Eq. 2 to P_O-V and log(P_O)-V relations in 0, 10, and 100 mM Mg²⁺ were almost identical to those obtained with Scheme 1 (Fig. 5, A and B) and predict shifts in V_hC for both WT and E374A/E399N (Table II) similar to those measured from gating current (Fig. 3 F). Parameters for site 1 (RCK1) were well constrained by fitting P_O-V relations in 2, 5, 10, and 21 mM Mg²⁺ (Fig. 5 A) and yielded a K_D for the CR state of 5.0 mM (the K_D of other states are indicated in Table II). A small E₁-factor (1.35) was sufficient to explain the ΔV_hC attributed to the RCK1 site, whereas a larger F₁-factor of 2.0 was required to explain the enhancement of voltage sensor/gate coupling. The site 2 (very low affinity) parameters were not as well constrained because few concentrations >10 mM were tested and the effect of saturating this site was not determined.

Effects of Mg²⁺ on I_g Kinetics and the Deactivation Pathway

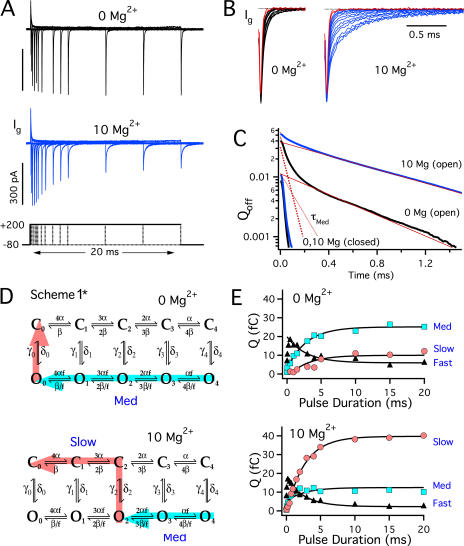
Although gating current is relatively insensitive to Mg²⁺ when channels are closed (Fig. 3), the ability of Mg²⁺ to shift the Q_o-V relation implies that I_g kinetics must be altered when channels are open. Such an effect is evident from OFF gating currents (I_gOFF) following pulses of different duration (0.05–20 ms, +200 mV) in 0 and 10 mM Mg²⁺ (Fig. 6 A). Normalized I_gOFF traces (Fig. 6 B) show that OFF kinetics following brief pulses (≤0.1 ms, red traces), that are comparable to the delay in I_K activation (Horrigan et al., 1999) and open few channels, are similar in 0 or 10 Mg²⁺. However, as pulse duration increases and channels open, voltage sensor deactivation is slowed, reflecting that Q_o-V is shifted to more negative voltages than Q_c-V (Horrigan and Aldrich, 1999). The slowing of I_gOFF occurs in 0 Mg²⁺ but is more prominent in 10 Mg²⁺ (Fig. 6 B) because Mg²⁺ increases the difference between Q_O and Q_C (Fig. 5 F) and the fraction of channels that open at +200 mV (Fig. 2 B).

Figure 6.

Mg²⁺ affects voltage sensor deactivation when channels are open. (A) I_g evoked by pulses to +200 mV of different duration (0.05–20 ms) in 0 and 10 mM Mg²⁺. (B) Normalized OFF currents from A decay more slowly as pulse duration increases, especially in the presence of Mg²⁺. Red traces represent 0.05 and 0.1-ms pulses. (C) OFF kinetics at −80 mV following brief (closed) or prolonged (open) pulses are compared by plotting the quantity Q = Q_OFF(t) − Q_OFFSS on a log scale vs. time where Q_OFF is the integral of I_gOFF and Q_OFFSS is the steady-state value of Q_OFF(t). The “closed” traces, representing the average of 0.05 and 0.1-ms records, have an exponential time course with almost identical kinetics (τ_Fast) in 0 Mg²⁺ (15.5 μs) or 10 mM Mg²⁺ (16.3 μs). The “open” traces, representing the average of 10, 15, and 20-ms records, were fit by triple exponential functions (0 Mg²⁺: q_Fast = 6.2 fC, τ_Fast = 15.5 μs, q_MED = 24.9 fC, τ_MED= 54.1 μs, q_SLOW = 11.2 fC, τ_SLOW = 500 μs; 10 Mg²⁺: q_Fast = 2.6 fC, τ_Fast = 16.3 μs, q_MED = 10.6 fC, τ_MED = 127 μs, q_SLOW = 39.1 fC, τ_SLOW = 756 μs). The Med and Slow components of the fits are shown as dotted and solid lines respectively. (D) Scheme 1* depicts the five closed (C_i) and open (O_i) states defined by Scheme 1, where i represents the number of activated voltage sensors (i = 0–4). δ_i and γ_i are forward and reverse rate constants for channel opening while α and β are rates for voltage sensor activation when channels are closed, and f = . Colored arrows represent different pathways of deactivation and Q_OFF components for open channels in 0 Mg²⁺ (top) or 10 mM Mg²⁺ (bottom) at −80 mV. In 10 mM Mg²⁺, channels can close from open states other than O₀ because Mg²⁺ allows voltage sensors in open channels to remain activated at −80 mV (Q_O, Fig. 5 E). The figure illustrates one possible pathway, through the O₂ state. After channels close, voltage sensors can completely deactivate in 10 mM Mg²⁺ (Q_C, Fig. 3 B). This charge movement is limited by the closing rate and therefore contributes to the Slow component of Q_OFF. (E) The amplitude of the three OFF components (Fast, ▴; Med, light blue square; Slow, pink circle) for the experiment in A are plotted vs. pulse duration and fit by exponential functions (0 Mg²⁺, τ = 2.8 ms; 10 Mg²⁺, τ = 2.6 ms).

To distinguish effects of Mg²⁺ on voltage sensor deactivation kinetics and P_O, OFF kinetics were analyzed by plotting the time course of OFF charge movement (Q_OFF) on a semi-log scale (Fig. 6 C) and comparing the effect of brief (“closed”) and prolonged (“open”) depolarizations. The decay of Q_OFF can be described by three exponential components (τ_Fast, τ_Med, τ_Slow) reflecting the predicted pathways of voltage sensor deactivation (Horrigan and Aldrich, 1999). Scheme 1* (Fig. 6 D) is a kinetic scheme that depicts the 10 states and transitions defined by Scheme 1, representing the O and C conformation with zero to four activated voltage sensors. Q_OFF following a brief depolarization is well described by a single exponential function (τ_Fast) representing the deactivation of voltage sensors in closed channels (C₄ to C₀ transitions in Scheme 1*). Q_OFF for open channels is characterized by a component representing the deactivation of voltage sensors when channels are open (Fig. 6 D, Med) and another that is rate limited by channel closing (Fig. 6 D, Slow). Therefore, Q_OFF following prolonged depolarizations to +200 mV (0, 10 Mg [open], Fig. 6 C) are well fit by triple exponential functions where the fast component is small because most channels are open. This analysis confirms that voltage sensor deactivation in open channels (τ_Med, Fig. 6 C, dotted red lines) is slowed (2.3-fold) by 10 mM Mg²⁺. In addition τ_Slow (Fig. 6 C, solid red lines) is increased 1.5-fold, consistent with a slowing of channel closing by Mg²⁺.

Further insight into the mechanism of Mg²⁺ action is provided by plotting the amplitude of the three OFF components (Q_Fast, Q_Med, Q_Slow) versus pulse duration (Fig. 6 E). As pulse duration increases, Q_Fast is reduced while Q_Med and Q_Slow increase, following the exponential time course of channel opening (solid curves Fig. 6 E) (Horrigan and Aldrich, 1999, 2002). These kinetics are similar in the presence and absence of Mg²⁺ because 10 mM Mg²⁺ has little effect on activation kinetics (Shi and Cui, 2001; Zhang et al., 2001). However the relative amplitudes of Q_Med and Q_Slow are reversed by Mg²⁺. The change in relative amplitude of Q_Med and Q_Slow by Mg²⁺ is qualitatively similar to the effect of recording I_gOFF at a more positive voltage in 0 Mg²⁺ (Horrigan and Aldrich, 1999), supporting that Mg²⁺ shifts Q_o to more negative voltages. In the absence of Mg²⁺, Q_Med is greater than Q_Slow because voltage sensors can completely deactivate at −80 before channels close (Fig. 6 D, 0 Mg²⁺ light blue arrow). That is, the Q_o-V relation in 0 Mg²⁺ indicates that voltage sensors equilibrate to the resting state at −80 mV (Fig. 5 E). By contrast, in 10 Mg²⁺ more than 25% of voltage sensors should remain activated at −80 mV when channels are open (10 Mg²⁺ Q_o-V, Fig. 5 E). Consequently, channels can close from open states other than O₀ (e.g., O₂ in Fig. 6 D, 10 Mg²⁺), and voltage sensor deactivation becomes rate limited by closing (Fig. 6 D, 10 Mg²⁺ pink arrow) such that the ratio of Q_Slow to Q_Med is increased.

Effects of Mg²⁺ on I_K Kinetics

The ability to slow channel closing is a characteristic of Mg²⁺ action at the RCK1 site that is evident by comparing I_K tail currents at −80 mV in 0 and 10 mM Mg²⁺ (Fig. 2 A). Time constants of I_K relaxation (τ_K) plotted versus voltage in Fig. 7 A for 0, 10, and 100 mM Mg²⁺ indicate that 10 mM Mg²⁺ slows I_K deactivation approximately twofold over a wide voltage range (−380 to +100 mV) with little impact on activation kinetics at very positive voltages (+160 to +280 mV). By contrast, increasing Mg²⁺ from 10 to 100 mM to occupy very low affinity sites speeds activation with no additional effect on deactivation at extreme negative voltages (Fig. 7 A) (Zhang et al., 2001; Hu et al., 2006).

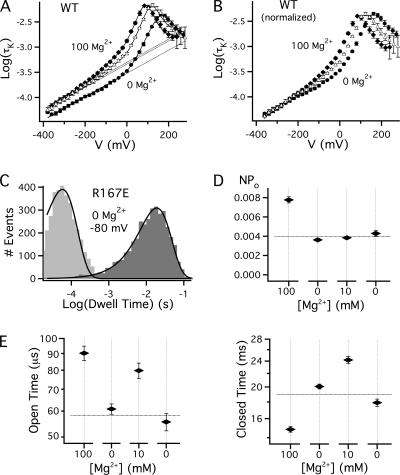
Figure 7.

Effects of Mg²⁺ on I_K kinetics. (A) Mean log(τ_K)-V relations in 0 (•), 10 (▵), and 100 (♦) mM Mg²⁺. Dotted lines are fits to the limiting slope of τ_K between −380 and −240 mV with an exponential function with partial charge −0.135e. Solid curves are fits to Scheme 1* (Fig. 6 D) using parameters in Table III. (B) τ_K-V relations from A were normalized to the 0 Mg²⁺ relation based on the exponential fits. (C) Open and closed dwell-time histograms for R167E at −80 mV in 0 Mg²⁺ from a patch containing ∼10,000 channels. Dwell time histograms were log-binned and are fit by single exponential functions, consistent with a two-state closed–open transition when voltage sensors are in the resting state. (D) NP_O at −80 mV measured from steady-state recordings of 20-30 s total duration in the same patch as C as [Mg²⁺] was changed in sequence from 100 mM to 0, 10 mM, and back to 0 Mg²⁺. The data were acquired in 5-s traces and error bars represent the standard error of measurements from individual traces. (E) Mean open and closed times corresponding to D. Dotted lines in D and E indicate the mean value in 0 Mg²⁺.

That 10 and 100 mM Mg²⁺ have distinct effects on τ_K is not surprising given their action at different binding sites. However, the effects of Mg²⁺ on deactivation kinetics are remarkable in comparison to the effects on steady-state activation. Macroscopic I_K kinetics are rate limited by the C-O transition (Horrigan and Aldrich, 1999) and at sufficiently negative voltages by the O₀ to C₀ rate constant (Fig. 6 D, top). Thus, the ability of 10 Mg²⁺ to slow deactivation at extreme negative voltages is surprising given that 10 mM Mg²⁺ has no detectable effect on the equilibrium constant for the C₀-O₀ transition (L₀). Similarly, the failure of 100 Mg²⁺ to slow deactivation relative to 10 Mg²⁺ is notable because 100 Mg²⁺ increases L₀.

Although previous studies have shown that Mg²⁺ slows deactivation at voltages as low as −200 mV, measurements at more negative voltage were required to confirm that the O₀ to C₀ transition rate is altered. Because Mg²⁺ shifts the Q_o-V relation, channels can close by pathways involving different C-O transitions in the presence and absence of Mg²⁺ (e.g., Fig. 6 D). This difference contributes to the slowing of tail currents in Mg²⁺ at −80 mV. However at sufficiently negative voltages, τ_K should be limited only by the O₀ to C₀ transition whether or not Mg²⁺ is present. Consistent with this prediction, at voltages less than −240 mV the difference in τ_K between 10 and 100 mM Mg²⁺ is almost eliminated and τ_K achieves a limiting voltage dependence that is identical in the presence or absence of Mg²⁺ (Fig. 7 A, dotted lines). Normalized τ_K-V relations (Fig. 7 B) illustrate that a major effect of Mg²⁺ is to shift the τ_K-V relation along the voltage axis, consistent with effects on Q_o. However, the ability of 10 mM Mg²⁺ to increase τ_K 1.53-fold at V < −240 mV confirms that the O₀ to C₀ rate is also reduced.

That the kinetics of the C₀-O₀ transition are affected by 10 mM Mg²⁺ without altering the equilibrium constant suggests that both the forward and reverse rate constants for this transition must be slowed. To test this hypothesis we analyzed unitary current kinetics from a macropatch containing R167E channels at −80 mV where voltage sensors should be in the resting state. Although the patch contained an estimated 10,000 channels, >99% of openings were to the single channel level because P_O at this voltage is low (4 × 10⁻⁷ in 0 Mg²⁺, Fig. 5 D). Both open and closed dwell times histograms were reasonably fit by single exponential components as illustrated for 0 Mg²⁺ in Fig. 7 C, consistent with a two-state C₀-O₀ transition. Changes in NP_O (Fig. 7 D) and mean open and closed times (Fig. 7 E) are plotted as [Mg²⁺] was changed in sequence from 100 mM to 0, 10, and back to 0 Mg²⁺. The results show that the change from 0 to 10 mM Mg²⁺ increases both open and closed times, consistent with a similar slowing of both forward and backward rates of channel opening that leaves NP_O unchanged. Open times were brief but comparable to the ∼100-μs time constant of macroscopic I_K measured for this patch at −80 mV in 0 Mg²⁺. The frequency of channel openings was reversibly reduced by 10 mM Mg²⁺ as expected from the effect on mean closed times. In a patch with N independent channels and brief openings the mean closed time should equal N/(opening rate), implying that the mean closed time of individual channels was ∼3–4 min. Increasing Mg²⁺ from 10 to 100 mM only slightly increased open times but markedly decreased closed times, consistent with the ability of 100 Mg²⁺ to increase NP_O without changing τ_K relative to 10 mM Mg²⁺ at negative voltages. These conclusions about the C₀-O₀ transition from single-channel analysis are consistent with effects of Mg²⁺ on rate constants in Scheme 1* (δ₀, γ₀) derived by fitting the macroscopic data (Fig. 7 A, solid curves, Table III parameters).

TABLE III.

Scheme 1* Parameters

	Rate Constants (s−1)
[Mg2+](mM)	γ0	δ0	δ1	δ2	δ3	δ4
0	3330	.0035	.091	1.9	22.6	101
10	2140	.0023	.061	4.9	163	71
100	1980	.0051	.098	8.6	265	94

Rate constants for the C_i-O_i transitions in Scheme 1* (Fig. 6 D) determined from fits to WT τ_K-V relations in 0-100 mM Mg²⁺ (Fig. 7 A), using equilibrium parameters from Table I (WT, WT_B). Since voltage sensor activation equilibrates rapidly, τ_K was fit by 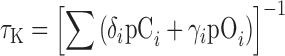, where i represents the number of activated voltage sensors, δ_i and γ_i are forward and backward rate constants for the C_i-O_i transitions and pC_i, pO_i are conditional occupancies of the open and closed states (pC_i = p(C_i|C), pO_i = p(O_i|O)) (Horrigan et al., 1999). Forward rates (δ_i) were varied while backward rates were γ_i = δ_i/L₀Dⁱ and partial charges associated with these rate constants were z_δ = 0.165e and z_γ = −0.135e (Horrigan and Aldrich, 2002).

The effect of Mg²⁺ on the kinetics of the C₀-O₀ transition is important in providing mechanistic information that is not evident from the steady-state data. In particular, the ability of 10 mM Mg²⁺ to slow opening and closing rates demonstrates that Mg²⁺ remains bound to the RCK1 site and can influence channel gating when voltage sensors are in the resting state even though P_O is insensitive to Mg²⁺ under these conditions.

DISCUSSION

Our results show that intracellular Mg²⁺ activates Slo1 BK channels through a fundamentally different mechanism from Ca²⁺. While micromolar [Ca²⁺]_i promotes channel opening independent of voltage sensor activation, millimolar [Mg²⁺]_i acting at a putative binding site in the cytosolic RCK1 domain has effects on opening and voltage sensor activation that are highly interdependent. Mg²⁺ promotes opening only when voltage sensors are activated and facilitates voltage sensor activation mainly when channels are open. Because Mg²⁺ action depends on the conformation of both voltage sensor and gate, the primary effect on gating is to enhance voltage sensor/gate coupling such that open-activated states are stabilized. A two-site allosteric model that incorporates this mechanism reproduces the major effects of Mg²⁺ on steady-state activation. As discussed below, these results support that multiple pathways of communication exist between the cytosolic and transmembrane domains of BK channels. Our data also constrain the possible physical mechanisms that underlie Mg²⁺-dependent activation and voltage sensor/gate coupling, and suggest that the physiological impact of Mg²⁺ could differ qualitatively from that of Ca²⁺.

Communication between Cytosolic and Transmembrane Domains

Ca²⁺ has no effect on voltage sensor/gate coupling (Horrigan and Aldrich, 2002) and is thought to promote channel opening by pulling on the RCK1–S6 linker (Niu et al., 2004). Therefore, the ability of Mg²⁺ to enhance coupling suggests that the cytosolic domain can communicate with the transmembrane domain through pathways other than the RCK1–S6 linker, presumably involving direct or indirect interactions with the voltage sensor (e.g., Fig. 1 D). A similar conclusion was drawn from the effects of intracellular heme (Horrigan et al., 2005). However, the action of Mg²⁺ is remarkable in its simplicity and specificity relative to heme. While heme weakens voltage sensor/gate coupling, it also reduces the efficacy of Ca²⁺ and increases P_O at extreme negative voltages (i.e., increases L₀). These diverse effects on gating, together with a slow onset of action (minutes), suggest that heme binding may perturb the normal conformation of the cytosolic domain such that tension in the RCK1–S6 linker is increased while multiple allosteric interactions are also disrupted (Horrigan et al., 2005). In contrast, 10 mM Mg²⁺ does not alter Ca²⁺ sensitivity (Shi and Cui, 2001; Zhang et al., 2001) and acts rapidly (<1 s) at the RCK1 binding site to enhance voltage sensor/gate coupling without affecting the intrinsic stability of the gate (L₀). The effect of Mg²⁺ is complimentary to that of Ca²⁺, which increases L₀ with no effect on coupling (Horrigan and Aldrich, 2002). Thus Mg²⁺ and Ca²⁺ appear to independently regulate two different pathways of communication, consistent with their additive effects on channel activation. Unlike heme, the effects of Mg²⁺ do not suggest a widespread structural perturbation, and can be understood in terms of stabilizing particular channel states.

The Energetic Effects of Mg²⁺

Mg²⁺ at the RCK1 site acts primarily to stabilize the open-activated (OA) state relative to the other three states (CR, CA, and OR) defined by the voltage sensor and gate conformation in each subunit (Fig. 5 H; Table II). We reached this conclusion by measuring independently each of the equilibrium constants between these states, in effect determining their relative free energies in the presence and absence of Mg²⁺, as specified by three independent parameters (L₀, J₀, and D). The CR-OR equilibrium constant (L₀) is not altered. The CR-CA equilibrium constant (J₀) is only increased slightly. However, the CA-OA and OR-OA equilibria are substantially altered, consistent with an approximate twofold increase in the voltage sensor/gate coupling factor D. By comparing the effects of Mg²⁺ on WT and mutant (E374A/E399N) channels, we showed that all changes in voltage sensor/gate coupling and a fraction of the changes in J₀ can be attributed to the RCK1 site. Modeling the effects of Mg²⁺ in terms of a two-site allosteric scheme (Table II) suggests that saturating the RKC1 site (site 1) stabilizes the OA state relative to CR by 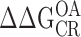= kTln(E₁F₁) = 0.60 kcal mol⁻¹, while stabilizing the CA state by 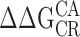= kTln(E₁) = 0.18 kcal mol⁻¹. Thus the energetic effect of Mg²⁺ is weak compared with that of Ca²⁺ binding or voltage sensor activation (1.25 or 1.91 kcal mol⁻¹ per subunit) (Horrigan and Aldrich, 2002).

Parallel Pathways of Voltage Sensor/Gate Coupling

While the interactions that couple voltage sensor activation to channel opening are well defined energetically, they could reflect many different physical mechanisms. The coupling represents a differential effect of voltage sensor conformation on the free energy of closed and open states. Therefore voltage sensor and gate must interact in a state-dependent manner that depends on the conformation of both domains. Such interactions could represent a stabilizing interaction (e.g., bond formation) between voltage sensor and gate that occurs only in the OA state, or destabilizing interactions (e.g., steric or repulsive) that occur in every state but OA. Alternatively, sensor and gate could be coupled in all states by a spring-like connection whose tension varies with both voltage sensor activation and channel opening.

Any of the above or similar mechanisms, alone or in combination, could contribute to the allosteric coupling factor D. Thus the ability of Mg²⁺ to increase D does not require that interactions that normally mediate coupling in the absence of Mg²⁺ are enhanced. Indeed, two lines of evidence suggest that the effect of Mg²⁺ represents a parallel pathway of coupling, independent of that in the transmembrane domain (Fig. 8 A). First, Mg²⁺ in the RCK1 binding site appears to interact with a part of the voltage sensor that is not important for voltage sensor/gate coupling in the absence of Mg²⁺. Interactions of the S4–S5 linker near S5 with S6 are proposed to mediate coupling in Kv channels (Lu et al., 2002; Long et al., 2005b). Although mutations in the S4–S5 linker of Slo1 influence Mg²⁺ sensitivity (Hu et al., 2003), they are at sites near S4 (E219, Q222) that are unlikely to interact directly with S6. In addition, mutations of R213 in S4 virtually abolish Mg²⁺ sensitivity (Hu et al., 2003; Yang et al., 2007), but have no effect on voltage sensor/gate coupling in 0 Mg²⁺ (Ma et al., 2006). Second, interactions between the voltage sensor and Mg²⁺-binding site should be sufficient to influence voltage sensor/gate coupling, because the binding site is in a cytosolic domain attached to S6 and therefore is connected to the gate.

Figure 8.

Voltage sensor/gate coupling and the mechanism of Mg²⁺ action. (A) Multiple pathways of voltage sensor/gate coupling may exist in BK channels. Because the cytosolic domain is connected to the gate via the RCK1–S6 linker (dashed line), interactions between cytosolic and voltage sensor domains could provide a coupling pathway (curved arrow) that is independent of that within the transmembrane domain (straight arrow). (B) A speculative model of Mg²⁺-dependent activation, based on an electrostatic mechanism of interaction between Mg²⁺ in the putative RCK1 binding site and R213 in S4 (Yang et al., 2007). The BK channel is shown in the four states defined in each subunit by the movement of the voltage sensor from resting (R) to activated (A) and by the closed (C) to open (O) conformational change. Channel opening is accompanied by an expansion of the cytosolic domain that alters the position of Mg²⁺ (in its binding site) relative to the transmembrane domain. The Mg²⁺ binding site (green semicircle) in the RCK1 domain includes coordinating residues E374 and E399 and nearby Q397 (Yang et al., 2006). Voltage sensor activation moves R213 relative to the cytosolic domain. In this way the distance and therefore electrostatic repulsion between Mg²⁺ and R213 (indicated qualitatively by the thickness of red boxes surrounding each state) depends on the conformation of both voltage sensor and gate, such that voltage sensor/gate coupling is enhanced. To account for the observed effects of Mg²⁺ on both opening and voltage sensor activation requires that the OA state be stabilized (see text). This is accomplished in the model by maintaining a similar distance between Mg²⁺ and R213 in all states except OA, such that all states are destabilized relative to OA. To account for a small effect of Mg²⁺ on voltage sensor activation when channels are closed we also assume interaction in the CA state is slightly weaker than the CR state, owing to a small outward movement of R213 upon voltage sensor activation, consistent with the small contribution of R213 to gating charge (Ma et al., 2006).

Physical Mechanism of Mg²⁺ Action

Since Mg²⁺ stabilizes primarily the OA state, thermodynamics require that Mg²⁺ affinity is greatest in the OA state, as in Scheme 3. However, the conclusion that Mg²⁺ binding is favored in a particular state does not fully describe how and when Mg²⁺ interacts with its binding site and the voltage sensor. If we suppose that the interactions of Mg²⁺ with its binding site are purely stabilizing, then interactions must exist in the OA state that are stronger or more numerous than in other conformations. Such a situation could arise if both the cytosolic and voltage sensor domains contribute to the Mg²⁺ binding site, but are favorably aligned with each other only when the voltage sensor is activated and the channel is open. However, this hypothesis appears too simple given recent evidence that a destabilizing electrostatic interaction exists between Mg²⁺ and the voltage sensor (Yang et al., 2007); and physical models that take this into account are necessarily more complex, as discussed below.

The effects on Mg²⁺ sensitivity and gating of charge-altering mutations in the voltage sensor and RCK1 domain strongly suggest that Mg²⁺ activates the channel through a long-range electrostatic interaction with R213 in S4 (Yang et al., 2007). Addition of positive charge at position 397 near the RCK1 site (Yang et al., 2006), by either mutation (Q397K, Q397R) or chemical modification, mimics the major effects of Mg²⁺ on channel gating; whereas negative charge at this position (Q397E, Q397D) inhibits activation. Conversely a positive charge at position 213 appears necessary for sensing either Mg²⁺ or charge at position 397. Finally, the effects on gating of Mg²⁺ or Q397K but not Ca²⁺ are strongly inhibited in high ionic strength solutions (1 M KCl), consistent with a long-range electrostatic interaction between Mg²⁺ and the voltage sensor. Based on these results, Yang et al. propose that Mg²⁺ bound to the RCK1 domain alters the local electric field sensed by R213 in S4 and thereby promotes voltage sensor activation. That is, electrostatic repulsion between Mg²⁺ and R213 destabilizes the resting conformation of the voltage sensor. This interaction is presumably state dependent since voltage sensor activation is enhanced by Mg²⁺ primarily when the channel is open.

The observations of Yang et al. (2007) together with our functional analysis place important constraints on the physical nature and state dependence of the interactions underlying Mg²⁺-dependent activation. Most importantly, the ability of R213 mutants to virtually eliminate Mg²⁺ sensitivity suggests that the electrostatic interaction between R213 and Mg²⁺ accounts for the major effects of Mg²⁺ on gating, and therefore must act on balance to stabilize the OA state. This conclusion has two key implications. First, the coordination of Mg²⁺ at its binding site cannot be strongly state dependent. If it were, then the channel's Mg²⁺ affinity should change in a state-dependent manner even in the absence of electrostatic interaction with S4; and gating should therefore remain Mg²⁺ sensitive when R213 is mutated. Although subtle effects of this sort cannot be ruled out, R213 mutations largely eliminate the G_K-V shift and slowing of I_K deactivation by Mg²⁺ (Hu et al., 2003; Yang et al., 2007). Thus it appears unlikely that conformational changes in the binding site associated with channel opening favor Mg²⁺ binding and contribute to Mg²⁺-dependent activation. This conclusion is supported by the observation that a permanent positive charge at position 397 mimics the effects of Mg²⁺ (Yang et al., 2007). Second, if Mg²⁺ stabilizes the OA state via a destabilizing electrostatic interaction, then the interaction must be weakest in the OA state and of similar strength in all other states (CR, CA, OR). That is, Mg²⁺ must destabilize all states relative to OA.

That Mg²⁺ interacts with the voltage sensor in multiple states including closed states may seem counterintuitive since Mg²⁺ has little effect on voltage sensor activation when channels are closed. Indeed, interaction in a single state, open resting (OR), would be sufficient to account for the ability of Mg²⁺ to promote voltage sensor activation when channels are open, by destabilizing OR relative to OA. However, this simple model cannot account for the effects of Mg²⁺ on channel opening. If the OR state is destabilized without also destabilizing the CR state then channel opening should be inhibited when voltage sensors are in the resting state, inconsistent with our finding that L₀ is unaffected by 10 mM Mg²⁺. Conversely, a lack of interaction between Mg²⁺ and the activated voltage sensor would be inconsistent with the ability of Mg²⁺ to facilitate opening of R210C channels when voltage sensors are constitutively activated. Thus accounting for effects of Mg²⁺ on both channel opening and voltage sensor activation requires that multiple states are destabilized.

The conformational changes that allow Mg²⁺ to interact with the voltage sensor in a state-dependent manner are not known in detail. However, a speculative model consistent with our results is illustrated in Fig. 8 B. The model assumes that Mg²⁺ and the voltage sensor interact electrostatically in all states but that the interaction is weakest in the OA state (as indicated by red boxes). Consequently, the OA state has the highest affinity for Mg²⁺ because the voltage sensor repels Mg²⁺ the least. For illustration purposes, interaction strength is assumed to vary with changes in the distance between Mg²⁺ and the charged R213 sidechain, although changes in local dielectric environment could also be involved. Fig. 8 B shows how the distance between Mg²⁺ and R213 could remain relatively constant in all states other than OA if the position of the Mg²⁺-binding site moves with channel opening and R213 moves with voltage sensor activation.

The insensitivity of P_O to Mg²⁺ at extreme negative voltages is accounted for in Fig. 8 B by assuming the Mg²⁺ binding site in the closed and open conformation occupies two different locations that are equidistant from R213 in the resting state. In this way the CR and OR states are equally destabilized. Interestingly, this mechanism is also consistent with our finding that Mg²⁺ slows both opening and closing rates when voltage sensors are in the resting state. This kinetic effect implies that Mg²⁺ destabilizes a transition state between CR and OR. In Fig. 8 B, movement of the Mg²⁺ binding site between closed and open positions would allow Mg²⁺ to approach R213 more closely in a transition state than in either the CR or OR states, thereby destabilizing the transition state.

Although the details of Fig. 8 B are speculative, they are consistent with known features of BK and related channels. The location and movement of the Mg²⁺-binding site relative to R213 is based on the crystal structures of MthK and Kv1.2. Residues in MthK (E138, N158), corresponding to E374 and E399 in the putative Mg²⁺ binding site of Slo1, are on the surface of the gating ring facing the membrane at a distance from the central axis of the channel (∼31 Å) that roughly matches the radial position of the S4 segment in Kv1.2 (Yang et al., 2007). The Mg²⁺-binding site is shown to move away from the central axis upon channel opening, consistent with an expansion of the cytosolic domain as in MthK (Jiang et al., 1999; Ye et al., 2006). Voltage sensor activation is depicted as a tilt and outward translation of S4 that is qualitatively consistent with recent models of Kv channel activation (Ruta et al., 2005; Campos et al., 2007; Pathak et al., 2007). We have assumed that movement of R213 perpendicular to the membrane is small such that interaction with Mg²⁺ in the CA state is not disrupted. This assumption is consistent with the fact that Slo1 is weakly voltage dependent and neutralization of R213 reduces the gating charge associated with voltage sensor activation (z_J) by only 0.3 e (Ma et al., 2006).

One possibility that was not incorporated into Fig. 8 B is that the position of R213 in the transmembrane domain may change with channel opening. Previous results suggest that R213 moves relative to the membrane electric field during opening because mutations at this position reduce the charge associated with opening (z_L) (Ma et al., 2006). If the position of R213 depends on the conformation of both voltage sensor and gate then the requirement that the Mg²⁺-binding site move during channel opening may be reduced. Therefore, Fig. 8 B does not represent a unique solution, but it does illustrate the constraints that must be satisfied to account for the experimental data in terms of electrostatic interactions.

Very Low Affinity Mg²⁺ Binding Sites

Divalent cation binding sites with lower affinity for Mg²⁺ than the RCK1 site are proposed to exist in BK channels because G_K-V shifts produced by increasing [Mg²⁺] or [Ca²⁺] from 10 to 100 mM appear too large to represent surface charge screening (Zhang et al., 2001) and are nearly independent of mutations that eliminate responses to lower concentrations of Mg²⁺ or Ca²⁺ (Hu et al., 2006). The location, number, and physiological significance of these very low affinity sites are unknown. However, our results provide new information about their mechanism of action.

We find that 100 mM Mg²⁺, unlike 10 mM Mg²⁺, increases L₀ and causes a shift in V_hC that is only partially eliminated by mutating the RCK1 site. These effects can be reproduced by an allosteric mechanism (Scheme 2) similar to that used to describe effects of micromolar Ca²⁺. However, very low affinity sites and Ca²⁺ sites differ greatly in the relative magnitude of their effects on the gate and voltage sensor represented by allosteric factors C and E, respectively. The G_K-V shift by Ca²⁺ is dominated by a C-factor of 8, which results in a 4,000-fold increase in P_O at −120 mV (Horrigan and Aldrich, 2002). By contrast the very low affinity site (C = 1.6) increases P_O (−120 mV) approximately threefold in 100 mM Mg²⁺, sufficient to account for only one third of the G-V shift from 10 to 100 mM Mg²⁺. The majority of the G-V shift in high [Mg²⁺] reflects a change in V_hC, which was attributed to an E-factor of 2.3.

The ability of 100 mM Mg²⁺ to increase L₀ supports that the effects of high [Mg²⁺] reflect mechanisms other than surface charge screening. However, the possibility remains that surface charge screening contributes to V_hC. Hu et al. (2006) estimated, based on surface potential calculations, that such a mechanism could shift V_hC by ∼−9 mV from 10 to 100 mM Mg²⁺, which is roughly half of the observed ΔV_hC (−19 mV) for the WT over this concentration range. Therefore, although we were able to model the effects of Mg²⁺ in terms of a single very low affinity site per subunit this is likely an oversimplification. The E-factor in our model could represent a combination of allosteric and surface charge effects. In addition, we observed a decrease in G_K-V slope from 10 to 100 Mg²⁺ that was not accounted for by our model.

Relation to Previous Studies and Physiological Implications

Since Mg²⁺ and Ca²⁺ act through distinct mechanisms, it seems surprising that previous studies were able to model effects of Mg²⁺ on the G_K-V relation, in the presence and absence of Ca²⁺, by assuming Mg²⁺ and Ca²⁺ act through the same mechanism (Shi and Cui, 2001; Zhang et al., 2001; Hu et al., 2006). This comparison raises several questions addressed below. First, can our model account for previous observations that the G_K-V shift by Mg²⁺ is similar in the presence or absence or presence of Ca²⁺? Second, were conclusions of previous studies affected by the use of a Ca²⁺-like model of Mg²⁺ action? Third, is the difference in mechanism of Mg²⁺ and Ca²⁺ action physiologically significant?

Although our experiments were performed in 0 Ca²⁺, we simulated the effect of saturating Ca²⁺ on our two-site model of Mg²⁺-dependent activation (Eq. 2) by increasing the values of L₀ (4096-fold) and J₀ (2.4-fold) as predicted from previous work on Ca²⁺-dependent activation (Horrigan and Aldrich, 2002). This simulation predicts that an increase in [Mg²⁺] from 0 to 100 mM will shift V_0.5 by −105 mV and −78 mV in 0 and saturating Ca²⁺, respectively, similar to the experimental results measured from Zhang et al. (2001) in 0 Ca²⁺ (−104 mV) and 300 μM Ca²⁺ (−72 mV). Thus our model appears to reproduce the combined effects of Mg²⁺ and Ca²⁺ on steady-state activation.

Conclusions about the Mg²⁺ affinity of the RCK1 site should be relatively unaffected by the incorrect assumption that Mg²⁺ acts through a Ca²⁺-like mechanism. Previous studies assumed that Mg²⁺ increases the C-O equilibrium constant L₀ by binding with higher affinity to the open rather than closed conformation (Shi and Cui, 2001; Zhang et al., 2001; Hu et al., 2006). Similarly, our model of the RCK1 site (Scheme 3) assumes the Mg²⁺ affinity of the open-activated (OA) state is greater than any other state. That is, Mg²⁺ does bind better to the open conformation than the closed, so long as the probability that an open channel is in the OA state is high. This probability is indicated by the Q_o-V relation, which is saturated at voltages where the G-V is usually measured (Fig. 5, compare A and E). Therefore, Scheme 3 affects the G-V relation similar to models that assume Mg²⁺ binds equally well to all open states. Consistent with this similarity a previous study using a two-site Ca²⁺-like model of Mg²⁺ action estimated K_D values for the RCK1 site of 5.46 mM (closed) and 2.25 mM (open) (Hu et al., 2006), comparable to our estimates based on Eq. 2 (K_D(CR) = 5 mM, K_D(CA) = 3.7 mM, K_D(OA) = 1.85 mM).

The physiological impact of Mg²⁺-dependent BK channel activation has yet to be defined. However, our results raise the possibility that Mg²⁺ could have a differential impact on BK-dependent processes such as action potential shaping in neurons and the control of vascular smooth muscle tone. Both these processes require an increase in [Ca²⁺]_i to open BK channels that are poorly activated by resting [Ca²⁺]_i at physiological voltages. During an action potential, Ca²⁺ influx through voltage-dependent Ca²⁺ channels together with membrane depolarization activates BK channels to regulate spike duration and the fast afterhyperpolarization (Faber and Sah, 2003). By contrast, BK channels in vascular smooth muscle can contribute to resting membrane potential and myogenic tone by activating at hyperpolarized voltages, near −40 mV, in response to local Ca²⁺ release from internal stores (Ca²⁺ sparks) (Brayden and Nelson, 1992; Wellman and Nelson, 2003). Since physiological concentrations of free Mg²⁺ (0.4–3 mM) (Gupta et al., 1984; Romani and Scarpa, 1992) are sufficient to shift the G_K-V relation (Hu et al., 2006) and the effects of Mg²⁺ and Ca²⁺ on V_0.5 are approximately additive, one might suppose that Mg²⁺ simply increases P_o during any Ca²⁺ transient; enhancing apparent Ca²⁺ sensitivity. However, our results suggest this is not the case. The effect of Mg²⁺, unlike Ca²⁺, depends on voltage sensor activation and is greatly diminished at hyperpolarized potentials (Fig. 2 C). Therefore, Mg²⁺ might be expected to have a smaller impact on vascular smooth muscle tone than on action potential shaping. Of course determining the magnitude of such differences and the overall contribution of Mg²⁺ to BK channel physiology must await further investigation.