Osmotic Pressure and Packaging Structure of Caged DNA

Abstract

We present a theoretical model for aqueous solutions of double-stranded (ds) DNA with explicit consideration of electrostatic interactions, excluded-volume effects, van der Waals attractions, and salt ions. With reasonable parameters estimated from the DNA structure and experimental data for electrolytes, we are able to reproduce the DNA osmotic pressure in the bulk in good agreement with experiment. The predicted DNA osmotic pressure in λ-bacteriophages is found to coincide with that of the PEG8000 solution that inhibits DNA ejection as reported in recent experiments. Based on the radial distributions of DNA segments and of counterions at different degrees of packaging, we find that in the presence of Mg²⁺, DNA forms a multilayer structure near the inner surface of a fully loaded bacteriophage, but at low packing density the DNA segments are depleted from the surface owing to the local condensation of DNA induced by the divalent counterions. By contrast, the multilayer DNA structure is less distinctive in the presence of Na⁺ despite the increase of the DNA density at contact, and the depletion near the capsid surface is not found at low packing density.

Introduction

In the normal form, a native DNA has a double helical structure with two sugar-phosphate chains on the outside joined by complementary basepairs projected into the interior. The cross-section diameter of the double helix is ∼2 nm, and the separation between the equally spaced basepairs is 0.34 nm (1). Because of its large size and high charge density relative to the surrounding solvent molecules and salt ions, understanding DNA packaging from a molecular perspective remains an outstanding problem in cell biology, virology, as well as in biomedical engineering for understanding DNA functionality and for devising efficient gene-delivery vehicles. Recent experiments (2–9) and theoretical investigations (10–16) have revealed highly organized DNA structures within fully loaded bacteriophages and quantified the ejection forces and osmotic pressures of the confined DNA in the viral particles. Built on these investigations, this work aims to develop a quantitative description of the microscopic structure and thermodynamic properties of DNA in bacteriophages from a molecular perspective.

The x-ray diffraction (17) and cryoelectron microscopy (cryo-EM) experiments (2,3) suggest that in bacteriophages such as P22 and lambda, a long sequence of double-strand (ds) DNA is wound tightly into the icosahedral capsid with a layer-by-layer structure approximately concentric to the protein shell. The DNA volume fraction inside a fully packaged viral capsid is in the range of 0.32–0.49, depending on the genome length (12). Under bulk conditions, such high packing density of DNA would lead to a fluid-solid-like transition (18,19). According to recent single-molecule (20–22) and controlled-ejection experiments (4,23–25), the osmotic pressure inside the capsid of an intact bacteriophage is on the order of 50 atm. The high packing density and strong electrostatic repulsion have been recognized as two key factors responsible for the enormous osmotic stress of the DNA inside fully packaged bacteriophages.

Previous theoretical investigations of DNA packaging in bacteriophages are based on a priori assumption of the DNA structure and with an input of the properties of DNA under bulk conditions. For example, the “inverse-spool” model represents a popular hypothesis of DNA packaging in a confined space (15,17,26). It presumes that the packaging starts from the outer bound of the “spool” and winds progressively inwards in an ordered fashion until a critical packing density is sensed by the portal complex. Although the “inverse-spool” model is intuitively appealing and the ring-like structure appears consistent with recent cryo-EM images, the low-resolution experiments (∼2 nm) yield no quantitative information on the ordered structure of the confined DNA. Besides, no experiment has yet provided direct evidence of the ring-like structure at the early stage of packaging. Recent simulation work of Forrey et al. emphasizes the qualitative features of DNA packaging and also indicates that the results are “fundamentally different” from that suggested by the “inverse-spool” model (10). Several theoretical interpretations of the DNA osmotic pressure in bacteriophages were proposed in the framework of the “inverse-spool” model. With the inputs of the DNA persistence length and bulk osmotic pressure from independent experiments, the theoretical predictions were found in good agreement with experimental results for DNA in bacteriophages. Because both the DNA persistence length and bulk osmotic pressure depend on the solution environment and a theoretical description of these properties is yet to be established, the existing theoretical methods provide no connection of DNA packaging with the intermolecular interactions.

Packaging a long sequence of dsDNA in a small viral capsid must overcome the strong electrostatic repulsion due to the backbone charges and the ultimate packing density is restricted by the free volume available to the colossal DNA molecule. Because of the multiple length scales affiliated with the DNA persistence length, capsid radius, and screening small ions, it is a formidable task to describe the structure and thermodynamic properties of caged DNA from a molecular perspective. The nonnegligible size of DNA molecules defies conventional electrostatic theories based on the Poisson-Boltzmann equation and the classical polymer theories based on the Gaussian-chain approximations. The situation becomes worse in the presence of multivalent ions, as multivalent counterions are known to induce effective attractions between the DNA strands, a feature that a simple mean-field theory, such as the Poisson-Boltzmann equation fails to capture. Within the coarse-grained models for the DNA and a continuous representation of the aqueous medium, the packaging structure of DNA is probably amenable to direct simulations but due to the long-range electrostatic interactions and high packing density, the computer simulations will be extremely time-consuming. Direct simulation becomes more challenging with explicit consideration of ions, which is essential to capture the electrostatic correlations. To avoid these difficulties, in this work we apply a density functional theory (DFT) to DNA packaging in viral capsids. In comparison with simulation methods, DFT has the advantage of numerical efficiency and provides direct information on thermodynamic properties of the system under consideration. Unlike conventional methods from statistical mechanics, DFT is able to capture the precise architecture of the molecular backbones and various nonbonded intersegment interactions, particularly the excluded volume interactions and electrostatic interactions, beyond mean-field approximations.

In our previous work, we have developed several density functional methods for quantitative representation of the excluded-volume effects, van der Waals attractions, electrostatic interactions, and hydrogen bonding (see (32,33)). These new versions of DFT have been successfully used to describe the microscopic structures and the thermodynamic properties of a variety of complex systems including polyelectrolytes in confined geometry. With a proper coarse-grained model that captures the size and charge of DNA molecules as well as of the small ions, we expect that the DFT will provide a quantitative representation of the DNA properties in bulk and under confinement.

Molecular model

Because the electrostatic interactions and excluded-volume effects play dominant roles in DNA packaging, we expect that DNA and key components of the surrounding aqueous environment can be described by coarse-grained models. Simpler (cruder) models have been extensively used in the literature for describing the structural and thermodynamic properties of biomacromolecular systems including DNA/RNA packaging, protein folding, and assembly of viral capsids. Although our coarse-grained model neglects specific short-range interactions among biomacromolecules (e.g., hydrogen bonding and basepairing) and therefore they provide no information on atomic details, it represents a major improvement over existing coarse-grained models in that it captures the exact size and charge of all species important for DNA packaging. In addition, our model accounts for the small co- and counterions explicitly.

Specifically, we assume that a long sequence of dsDNA can be represented by a tangentially connected chain of identical charged spheres that each has a diameter the same as the cross-section diameter of a DNA double helix (σ_s = 2 nm). Because the separation between two neighboring DNA basepairs is 0.34 nm, each segment corresponds to 5.9 basepairs (bp) and carries Z_s = −11.8 negative charges. The bonding potential V_b(R) among coarse-grained DNA segments is represented by

$$\text{exp}[-\beta V_{\text{b}}(\text{R})]=\prod _{\text{i}=1}^{\text{M}-1}\frac{\delta (|{\text{r}}_{\text{i}+1}-{\text{r}}_{\text{i}}|-{\sigma }_{\text{s}})}{4\pi {\sigma }_{\text{s}}^2},$$ (1)

where β = 1/k_BT with k_Bbeing the Boltzmann constant and T the absolute temperature, M stands for the degree of polymerization or the number of coarse-grained DNA segments, $\text{R}\equiv ({\text{r}}_1,{\text{r}}_2,\cdots ,{\text{r}}_{\text{M}})$ is a set of coordinates specifying the segmental positions, and δ is the Dirac δ-function. The bonding potential imposes only a connectivity of the coarse-grained DNA segments; it has no direct connection to the glycosidic and phosphodiester bonds that hold the nucleotides together.

As in the standard primitive model of electrolyte solutions, the salt ions are represented by charged spheres, and water is considered as a dielectric continuum. The solvent-mediated pair potential between two spherical particles (DNA segments and ions) consists of a hard-sphere repulsion, Coulomb interaction, and van der Waals attraction:

$$\beta u_{\text{ij}}(r)=\left\{\begin{array}{cc}\hfill \infty \hfill & \hfill r<{\sigma }_{\text{ij}}\equiv ({\sigma }_{\text{i}}+{\sigma }_{\text{j}})/2\hfill \\ \hfill Z_{\text{i}}{Z}_{\text{j}}{l}_{\text{B}}/r-{\epsilon }_{\text{ij}}^{\ast }{({\sigma }_{\text{ij}}/r)}^6\hfill & \hfill r\ge {\sigma }_{\text{ij}}\hfill \end{array}\right),$$ (2)

where r is the center-to-center distance, Z_i and σ_i are the valence and diameter of particle i, respectively, and l_B stands for the Bjerrum length. The van der Waals energy parameter between DNA segments (at T = 298 K, ${\epsilon }_{\text{ss}}^{\ast }={\epsilon }_{\text{ss}}/k_{\text{B}}T=8.835$) is estimated from its chemical composition (27,28). The van der Waals attraction between salt ions is neglected.

Fig. 1 schematically illustrates the model system considered in this work, highlighting the salt ions (small spheres) and connectivity of coarse-grained DNA segments (thin lines). As in previous investigations (15,16), we assume that the interior space of a viral capsid can be represented by an uncharged spherical cavity. In accordance with the neutral cavity model, a hard-wall potential is used to describe the interaction of DNA segments and small ions with the capsid surface. Although the simplified model for the viral capsid is insufficient to distinguish between different hypotheses for the three-dimensional arrangement of a confined DNA, it enables us to quantify the DNA structure by using a one-dimensional radial density profile for the DNA segments and to predict the thermodynamic properties of the DNA without an a priori assumption of the final packaging structure.

Figure 1.

A schematic view of the DNA and small ions packaged in a bacteriophage. The double-stranded DNA is represented by a tangent charged sphere chain where each bead corresponds to 5.9 basepairs and carries Z_s = −11.8 charges. Salt ions, represented by small spheres, are explicitly considered in this work. The thin lines stand for connectivity of the DNA segments and highlight the coshell structure near the capsid surface but amorphous structure at the center.

Density functional theory

The properties of dsDNA in a viral capsid are difficult to calculate because on the one hand, the system entails a large number of ionic species that would be extremely time-consuming for direct molecular simulation and on the other hand, a typical mean-field theory is insufficient to account for both the short- and long-range correlations arising from the excluded-volume effects and strong Coulomb interactions. In this work, we use a nonlocal density functional theory, which has been shown previously to provide an accurate description of the structure and thermodynamic properties of polyelectrolytes (29–31).

In essence, DFT asserts that the microstructure of an equilibrium system, represented by the spatial distributions of the molecules, minimizes the grand potential provided that the chemical potentials of all species are fixed. A central task in the application of DFT is, therefore, to formulate the Helmholtz energy as a functional of the underlying molecular density profiles (32,33). Within the simplified model for DNA, the Helmholtz energy functional (F) is related to the grand potential (Ω) via the Legend transformation

$$\begin{array}{l}\Omega [{\rho }_{\text{M}}(\text{R}),\{{\rho }_{\alpha }(\text{r})\}]=F[{\rho }_{\text{M}}(\text{R}),\{{\rho }_{\alpha }(\text{r})\}]\\ +\int [{\Psi }_{\text{M}}(\text{R})-{\mu }_{\text{M}}]{\rho }_{\text{M}}(\text{R})d\text{R}\\ +\sum _{\alpha =+,-}\int d\text{r}{\rho }_{\alpha }(\text{r})[{\Psi }_{\alpha }(\text{r})-{\mu }_{\alpha }]\text{.}\end{array}$$ (3)

In Eq. 3, the subscripts “M”, “+”, and “−” denote DNA molecule, cations, and anions, respectively; ρ_M(R) stands for a multidimensional density profile depending on the DNA configuration $\text{R}\equiv ({\text{r}}_1,{\text{r}}_2,\cdots ,{\text{r}}_{\text{M}})$ and ρ_α(r) is the density profiles of the salt ions; μ_M and μ_α are the chemical potentials of the DNA and salt ions; Ψ_M(R) and Ψ_α(r) are the capsid confining potentials (i.e., the hard-wall potentials) for the DNA and for the salt ions, respectively. The external potential for the DNA can be decomposed into that for individual segments, i.e., ${\Psi }_{\text{M}}(\text{R})={\sum }_{\text{i}=1}^{\text{M}}{\Psi }_{\text{s}}({\text{r}}_{\text{i}})\text{.}$

The Helmholtz energy functional is closely related to intermolecular interactions. In general, it includes an ideal term F^id that depends on the bond potentials and molecular architecture, and an excess F^ex that accounts for various contributions due to the nonbonded inter- and intramolecular interactions. Within the framework of our simplified model for DNA, the Helmholtz energy functional can be decomposed into five contributions, corresponding to that for an ideal chain (F^id), hard-sphere repulsion or the excluded-volume effects $(F_{\text{hs}}^{\text{ex}})$, direct electrostatic potential and electrostatic correlations $(F_{\text{ele}}^{\text{ex}})$, intrachain correlations $(F_{\text{ch}}^{\text{ex}})$, and van der Waals attraction $(F_{\text{att}}^{\text{ex}})$:

$$F[{\rho }_{\text{M}}(\text{R}),{\rho }_{\alpha }(\text{r})]=F^{\text{id}}+F_{\text{hs}}^{\text{ex}}+F_{\text{ch}}^{\text{ex}}+F_{\text{ele}}^{\text{ex}}+F_{\text{att}}^{\text{ex}}\text{.}$$ (4)

The ideal-gas term F^id is known exactly; it depends on the position and configuration of DNA, the bond potential V_b(R), and the density profiles of salt ions:

$$\begin{array}{l}\beta F^{\text{id}}=\int d\text{R}{\rho }_{\text{M}}(\text{R})[\text{ln}{\rho }_{\text{M}}(\text{R})-1]+\beta \int d\text{R}{\rho }_{\text{M}}(\text{R})V_{\text{b}}(\text{R})\\ +\sum _{\alpha =+,-}\int d\text{r}{\rho }_{\alpha }(\text{r})[\text{ln}{\rho }_{\alpha }(\text{r})-1]\text{.}\end{array}$$ (5)

Because Eq. 5 depends on DNA configurations, direct evaluation of the ideal-gas Helmholtz energy requires multidimensional integrations or computer simulation. The excess Helmholtz energy functional accounts for the thermodynamic nonideality due to various nonbonded inter- and intramolecular interactions.

The excess Helmholtz energy functional due to the hard-sphere repulsion can be accurately described by a modified fundamental measure theory (MFMT) or the “White Bear” version of fundamental measure theory (FMT) (34,35). Unlike alternative versions of DFT for hard spheres that require correlation functions of a uniform state as input and invoke empirical approximations, such as weighted-density approximations, the FMT of Rosenfeld is built upon firm physical and mathematical foundations. It is a coherent theory for uniform as well as inhomogeneous hard spheres, applicable to one component and polydisperse mixtures, fluid and solid phases, and systems consisting of nonspherical convex particles including liquid crystals. Intuitively, MFMT can be understood as an extension of FMT to inhomogeneous systems by using the Boublik-Mansoori-Carnahan-Starling-Leland (BMCSL) equation of state (36,37)

$$\beta F_{\text{hs}}^{\text{ex}}=\int {\Phi }^{\text{hs}}[n_{\alpha }(\text{r})]d\text{r},$$ (6)

in which the reduced excess Helmholtz energy density Φ^hs is a function of six weighted densities n_α(r) (α = 0; 1; 2; 3; V1; V2) (38–40)

$$\begin{array}{l}{\Phi }^{\text{hs}}=-n_0\text{ln}(1-n_3)+\frac{n_1{n}_2-{\text{n}}_{\text{V}1}{\text{n}}_{\text{V}2}}{1-n_3}\\ +\frac{1}{36\pi }\left[n_3\text{ln}(1-n_3)+\frac{n_3^2}{{(1-n_3)}^2}\right]\frac{(n_2^3-3n_2{\text{n}}_{\text{V}2}{\text{n}}_{\text{V}2})}{n_3^3}\text{.}\end{array}$$ (7)

In Eq. 7, the weighted densities are defined as

$$n_{\alpha }(\text{r})=\sum _{\text{i}}{n}_{\alpha ,\text{i}}=\sum _{\text{i}}\int {\rho }_{\text{i}}({\text{r}}^{\prime }){\omega }_{\alpha ,\text{i}}(\text{r}-{\text{r}}^{\prime })d{\text{r}}^{\prime },$$ (7a)

where the sum is over all spherical species, and the weight functions ω_α,I(r) are related to the geometry of a hard sphere, i.e., four scalar functions related to the center-of-mass position, the spherical surface, and the spherical volume, and two vector functions related to the radial variance across the surface. For a uniform fluid, the vector-weighted densities disappear and Eqs. 6 and 7 reduce to the excess Helmholtz energy from the BMCSL equation of state. Although MFMT preserves the advantages of the original theory, it improves the numerical performance, in particular, for highly asymmetric systems as considered in this work.

The third term in Eq. 4 takes into account the correction due to chain connectivity of the coarse-grained DNA segments. Note that this term accounts for the intrachain correlation effects beyond the ideal chain connectivity as imposed by the bond energies. Without this term, for neutral polymers, the treatment reduces essentially to a Flory approach where connectivity is included only at the ideal chain level and is neglected in describing the interactions between disconnected monomers. We include this excess intrachain correlation contribution using an extended first-order thermodynamic perturbation theory (TPT1) (41,42), according to which $F_{\text{ch}}^{\text{ex}}$ can be written as

$$\beta F_{\text{ch}}^{\text{ex}}=\frac{1-M}{M}\int n_{0\text{s}}{\zeta }_{\text{s}}\text{ln}y({\sigma }_{\text{s}},n_{\alpha })d\text{r},$$ (8)

where y(σ_s, n_α) stands for the inhomogeneous contact value of the cavity correlation function (CCF) for the monomeric charged system (i.e., DNA segments and ions). Following our previous work for neutral polymers (41), we have formulated a semiempirical expression for CCF in a mixture of charged spheres on the basis of the mean-spherical approximation (MSA) (43,44)

$$y({\sigma }_{\text{s}},n_{\gamma })=\left[\frac{1}{1-n_3}+\frac{n_2{\sigma }_{\text{s}}\zeta }{4(1-n_3{)}^2}\right]\text{exp}\left(-\frac{{\Gamma }^2{a}_{\text{s}}^2}{4{\pi }^2{l}_{\text{B}}{\sigma }_{\text{s}}}+\frac{l_{\text{B}}{Z}_{\text{s}}^2}{{\sigma }_{\text{s}}}\right)\text{.}$$ (9)

In Eqs. 8 and 9, ${\zeta }_{\text{s}}=1-{\text{n}}_{\text{V}2\text{s}}{\text{n}}_{\text{V}2\text{s}}/n_{2\text{s}}^2$ and $\zeta =1-{\text{n}}_{\text{V}2}{\text{n}}_{\text{V}2}/n_2^2$ are the inhomogeneous factors owing to the nonuniform distributions of DNA segments and all the charged particles, respectively. In Eq. 9, the parameter Γ can be understood as an extension of the Debye screening parameter (to include the effects of ion size and charge correlations):

$$\Gamma =\sqrt{\pi l_{\text{B}}\sum _{\text{i}}{n}_{0,\text{i}}{\left(\frac{1}{1+\Gamma {\sigma }_{\text{i}}}\right)}^2{\left(Z_{\text{i}}-\frac{\pi P_{\text{n}}{\sigma }_{\text{i}}^2}{2(1-n_3)}\right)}^2}\text{.}$$ (10)

The parameters a_s and P_n are two intermediate results introduced in the MSA

$$a_{\text{s}}=\frac{2\pi l_{\text{B}}\left(Z_{\text{ps}}-\frac{\pi P_{\text{n}}{\sigma }_{\text{s}}^2}{2(1-n_3)}\right)}{\Gamma (1+\Gamma {\sigma }_{\text{s}})}$$ (11)

$$P_{\text{n}}=\frac{\sum _{\text{i}}\frac{2n_{1,\text{i}}{Z}_{\text{i}}}{1+\Gamma {\sigma }_{\text{i}}}}{1+\frac{3}{(1-n_3)}\sum _{\text{i}}\frac{n_{3,\text{i}}}{1+\Gamma {\sigma }_{\text{i}}}}\text{.}$$ (12)

As in MSA, the parameter Γ is solved from Eqs. 10–12 by an iterative method.

Equation 9 is obtained from the EXP modification of the radial distribution function (RDF) from MSA. The expression within the square bracket represents the contact value of the RDF for a hard-sphere reference system, which is obtained from the Percus-Yevick theory; the exponential term accounts for the charge correlation and direct Coulomb interaction between two DNA segments. The EXP approximation avoids unphysical solutions of RDF from MSA at conditions of high electrostatic coupling and low ionic density. The EXP approximation gives the contact value of the radial distribution function for monomeric ionic systems that agrees well with simulation results. In comparison with traditional approaches for representing the structures and thermodynamic properties of polymeric systems such as the polymer integral-equation theory and polymer self-consistent field theory, the polymer DFT has the advantage of versatility for polymeric systems with complex intermolecular interactions.

The Helmholtz energy due to the electrostatic interactions $F_{\text{ele}}^{\text{ex}}$ includes two parts: one is due to the direct Coulomb interaction as appearing in the Poisson-Boltzmann equation, and the other accounts for the correlation of charge distributions. The direct Coulomb term $F_{\text{C}}^{\text{ex}}$ is expressed as

$$\beta F_{\text{C}}^{\text{ex}}=\frac{l_{\text{B}}}{2}\sum _{\text{i},\text{j}=\text{s},+,-}\int \int d\text{r}d{\text{r}}^{\prime }\frac{Z_{\text{i}}{Z}_{\text{j}}{\rho }_{\text{i}}(\text{r}){\rho }_{\text{j}}({\text{r}}^{\prime })}{|\text{r}-{\text{r}}^{\prime }|}\text{.}$$ (13)

The Helmholtz energy functional due to the electrostatic correlations $F_{\text{el}}^{\text{ex}}$ can be approximated by a quadratic functional Taylor expansion relative to that for a monomeric bulk fluid of densities $\left\{{\rho }_{\text{i}}^{\text{b}}\right\}$

$$\begin{array}{l}\beta F_{\text{el}}^{\text{ex}}=\beta F_{\text{el}}^{\text{ex}}[\{{\rho }_{\text{i}}^{\text{b}}\}]-\int d\text{r}\sum _{\text{i}=\text{s},+,-}\Delta C_{\text{i}}^{(1)\text{el}}({\rho }_{\text{i}}(\text{r})-{\rho }_{\text{i}}^{\text{b}})\\ -\frac{1}{2}\int \int d\text{r}d{\text{r}}^{\prime }\sum _{\text{i},\text{j}=\text{s},+,-}\Delta C_{\text{ij}}^{(2)\text{el}}(|\text{r}-{\text{r}}^{\prime }|)\\ \times ({\rho }_{\text{i}}(\text{r})-{\rho }_{\text{i}}^{\text{b}})({\rho }_{\text{j}}({\text{r}}^{\prime })-{\rho }_{\text{j}}^{\text{b}}),\end{array}$$ (14)

where the residual first-order and second-order direct correlation functions (DCF) are defined as, respectively,

$$\Delta C_{\text{i}}^{(1)\text{el}}=-\beta {\mu }_{\text{i}}^{\text{el}}=-{\left(\frac{\delta \beta F_{\text{el}}^{\text{ex}}}{\delta {\rho }_{\text{i}}(\text{r})}\right|}_{{\rho }_{\text{i}}(\text{r})={\rho }_{\text{i}}^{\text{b}}}$$ (15)

$$\Delta C_{\text{ij}}^{(2)\text{el}}(|\text{r}-{\text{r}}^{\prime }|)=-{\left(\frac{{\delta }^2\beta F_{\text{el}}^{\text{ex}}}{\delta {\rho }_{\text{i}}(\text{r})\delta {\rho }_{\text{j}}({\text{r}}^{\prime })}\right|}_{{\rho }_{\text{i}}(\text{r})={\rho }_{\text{i}}^{\text{b}},{\rho }_{\text{j}}({\text{r}}^{\prime })={\rho }_{\text{j}}^{\text{b}}}\text{.}$$ (16)

In writing Eq. 14, we assumed that the effect of chain connectivity and van der Waals attractions on the electrostatic part of the direct correlation functions can be neglected. With this assumption, $\Delta C_{\text{ij}}^{(2)\text{el}}(r)$ can be obtained from MSA for simple electrolytes (45,46).

Because the van der Waals interaction is relatively small in comparison with the Coulomb interactions, we represent this part of the Helmholtz energy functional simply by the mean-field approximation (47)

$$\beta F_{\text{att}}^{\text{ex}}=\frac{1}{2}\sum _{\text{i},\text{j}=\text{s},+,-}\int \int d\text{r}d{\text{r}}^{\prime }\left[-{\epsilon }_{\text{ij}}^{\ast }{\left(\frac{{\sigma }_{\text{ij}}}{|\text{r}-{\text{r}}^{\prime }|}\right)}^6\right]{\rho }_{\text{i}}(\text{r}){\rho }_{\text{j}}({\text{r}}^{\prime })\text{.}$$ (17)

Improvement is possible by using the direct or pair correlation function of a charged reference system.

In the bulk phase, the DNA and the ionic density profiles are uniform and Eq. 3 reduces to an equation of state. For the DNA in bacteriophages, the grand potential reaches a minimum at equilibrium, i.e., the first-order functional derivatives of grand potential with respect to the density profiles are equal to zero. The density profiles for the DNA and the salt ions are then calculated from the Euler-Lagrange equations:

$${\rho }_{\text{M}}(\text{R})=\text{exp}\left\{\beta {\mu }_{\text{M}}-\beta V_{\text{b}}(\text{R})-\beta {\Psi }_{\text{M}}(\text{R})-\frac{\delta \beta F^{\text{ex}}}{\delta {\rho }_{\text{M}}(\text{R})}\right\}$$ (18)

$${\rho }_{\alpha }(\text{r})=\text{exp}\left[\beta {\mu }_{\alpha }-\beta {\Psi }_{\alpha }(\text{r})-\frac{\delta \beta F^{\text{ex}}}{\delta {\rho }_{\alpha }(\text{r})}\right]\text{.}$$ (19)

Because the excess Helmholtz energy functional depends only on the densities of DNA segments and salt ions, Eq. 18 can be simplified as

$${\rho }_{\text{M}}(\text{R})=\text{exp}\left\{\beta {\mu }_{\text{M}}-\beta V_{\text{b}}(\text{R})-\sum _{\text{i}=1}^{\text{M}}\left[\beta {\Psi }_{\text{s}}({\text{r}}_{\text{i}})+\frac{\delta \beta F^{\text{ex}}}{\delta {\rho }_{\text{s}}({\text{r}}_{\text{i}})}\right]\right\}\text{.}$$ (20)

The overall segment density profile of DNA is calculated from a summation of the individual segment densities

$${\rho }_{\text{s}}(\text{r})=\sum _{\text{i}=1}^{\text{M}}{\rho }_{\text{s},\text{i}}(\text{r})=\sum _{\text{i}=1}^{\text{M}}\int d\text{R}\delta (\text{r}-{\text{r}}_{\text{i}}){\rho }_{\text{M}}(\text{R})\text{.}$$ (21)

Equations 19 and 21 can be solved iteratively by using the Picard iteration method. In the calculations, the initial density profiles are assumed uniform and given by the bulk densities for salt ions and by 0.01 nm⁻³ for DNA segments. For the small ions, the chemical potentials are fixed at their bulk values during the iteration, and for the DNA segments, the chemical potential is determined from the overall normalization of the segmental density. Iteration stops when the average difference between normalized densities of input and output is <0.1% at all positions.

Results and discussion

We first test the numerical performance of the theoretical model by comparison with experimental results for simple electrolytes and for DNA in a bulk solution. Fig. 2 shows the theoretical predictions for the bulk osmotic pressure of dsDNA in a 2-mM NaCl solution at 25°C. The inset shows predictions from the same theory for the aqueous solutions of NaCl and MgSO₄ relevant to the DNA solutions considered in this work. In these calculations, the coarse-grained chain has M = 25.5 segments, corresponding to 150 bp DNA used in the experiments (48). The diameters of Na⁺, Cl⁻, Mg²⁺, and $\text{S}{\text{O}}_4^{2-}$ are 0.387, 0.362, 0.671, and 0.44 nm, respectively (49,50). At 25°C, the Bjerrum length in water is 0.714 nm. Within a unified thermodynamic model for the DNA solution and for the simple electrolytes, the theoretical predictions are in good agreement with experiments (48,51).

Figure 2.

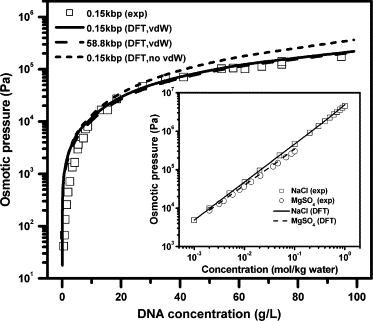
Osmotic pressures for dsDNA in a NaCl solution (2 mM) and for aqueous solutions of NaCl and MgSO₄ at 25°C (inset). Experimental data (symbols) are from Raspaud et al. (48) for DNA and from Lobo and Quaresma (51) for NaCl and MgSO₄. Lines are theoretical predictions.

The generic nature of our model also allows us to examine various effects on the osmotic pressure of the DNA solution. The dashed line in Fig. 2 gives the predicted osmotic pressure in the same aqueous solution but for the chain length M = 10,000, corresponding to 58.8 kbp DNA. At the same weight density, the DNA chain length has only a negligible effect on the osmotic pressure, particularly at high concentration with the relative difference <5%. As suggested in our earlier publications for polyelectrolytes (30,31), when the polyion length is sufficiently long (e.g., M > 20), the structural and thermodynamic properties of a polyelectrolye are insensitive to the chain length for concentrations beyond the overlap concentration. The dotted line in Fig. 2 shows the predictions without considering the van der Waals attraction between DNA segments. Clearly, the van der Waals attraction has noticeable effect on the osmotic pressure and it becomes more important at high DNA concentration. We find that in the DNA concentration considered in this work, the calculated results are not sensitive to small changes in the model parameters.

A key property of interest is the osmotic pressure of DNA inside the capsid of bacteriophages as a function of the packing fraction. Fig. 3 shows the osmotic pressure of DNA in three mutants of λ-bacteriophages as recently investigated by Evilevitch and co-workers (4,23–25). These authors studied the controlled ejection of the phage DNA in PEG8000 solutions in the presence of 10 mM MgSO₄ and 50 mM TrisHCl, a receptor protein (LamB) that opens the phage virus, and an endonuclease (DNase I) that digests the ejected DNA fragments. Ejection is stopped when the ejection force due to the internal osmotic pressure of DNA in the capsid is counterbalanced by that due to the osmotic pressure of the PEG solution. The experimental data correspond to the osmotic pressures of the PEG8000 solution at which the ejection stops. Because the capsid surface is permeable to salt ions but not to DNA segments, in our calculation we treat the system as semiopen with the chemical potentials for salt ions determined from their bulk concentrations. For a given DNA length inside the capsid and the chemical potentials of Mg²⁺ and $\text{S}{\text{O}}_4^{2-}$ determined by the bulk solution, we calculate the DNA osmotic pressure from the contact-value theorem (52)

$${\pi }_{\text{DNA}}={\left(\frac{R_{\text{C}}-0.5{\sigma }_{\text{s}}}{R_{\text{C}}}\right)}^2{\rho }_{\text{s},\text{c}}{k}_{\text{B}}T,$$ (22)

Figure 3.

Osmotic pressure and capsid radius (inset) versus the genome length in three mutants of λ-phages. Experimental data (symbols) are from the literature (4,23–25) for the osmotic pressure of inhibiting polymer solution measured at 37°C and from Earnshaw et al. (17,53) for the capsid radius measured in a monovalent electrolyte solution. The solid line is the total pressure calculated from our work and the dashed line shows the pressure due to the DNA stiffness estimated from the spool-like model.

where R_C is the inner radius of the viral capsid, and ρ_s,c is the DNA contact density, i.e., the number density of DNA segments at the inner surface of the viral capsid predicted by the DFT.

According to Earnshaw et al. (17,53), the inner radius of λ-bacteriophages is 24.6 nm for the empty proheads and 29.5 nm for mutants loaded with >78% (37.83 kbp) of the genome. Beyond 37.83 kbp, the capsid size remains essentially constant. In between 0 DNA content and 37.83 kpb loading, neither experimental measurements nor theoretical predictions are available to describe the relationship between DNA length and capsid size for λ-phages. An earlier experimental work of Eiserling et al. suggested that the reduction in DNA length is proportional to the reduction in capsid volume for bacteriophage T4 (54). We thus assume a linear relationship between λ-capsid radius and genome length when the genome length is shorter than 37.83 kbp. Although the capsid radius was measured in a monovalent electrolyte solution, the same radius is used in our theoretical calculations.

Solving the density profile of the DNA segments from Eq. 21 requires repeated multidimensional integrations with the dimensionality proportional to the DNA degree of polymerization. To accelerate the convergence of numerical iterations in solving the DFT equations, we treat the DNA inside the capsid as being made up of multiples of shorter chains with M = 20 (which is approximately equal to the DNA persistence length in a bulk solution). We have calculated several data points using M = 50; the results are nearly indistinguishable. We believe this insensitivity to the chain length reflects the dominance of the structural and thermodynamic properties of DNA at high densities by the excluded volume, electrostatic, and van der Waals interactions when the chain length is sufficiently long, and is consistent with the behavior of polymer solutions beyond the overlap concentration. Although this behavior is to be expected for bulk solutions, as demonstrated in the results and analysis in Fig. 2 and in our earlier publications (30,31), the current calculation shows that the same is true for DNA in confined environment. This suggests that in many cases, the behavior of a long DNA molecule can be mimicked by many shorter fragments.

The solid line in Fig. 3 shows that the theoretical predictions coincide remarkably well with the experimental data. Based on an earlier analysis (23), there is not an obvious reason why the osmotic pressure inside the capsid should equal the osmotic pressure that stops the ejection at a given DNA length inside the capsid. However, given that our model contains no adjustable parameters and that it accurately predicts the bulk osmotic pressure of DNA solutions, the agreement between the theoretical curve and the experimental data in Fig. 3 is unlikely to be a pure numerical coincidence.

The buffer solution consists of 50 mM TrisHCl, which is not accounted for in our calculations. The ionic species from the buffer (i.e., TrisH⁺ and Cl⁻) were not considered in previous studies (12,15,22,23,25) either. Because of the high charge density of the DNA, its properties are primarily affected by the magnesium ions in the bacteriophages. To a good approximation, the influence of the TrisHCl on the DNA structural and thermodynamic properties are negligible, even though the ionic concentration from the buffer (∼6 mM at pH = 7.4) is comparable with the concentration of MgSO₄ (10 mM).

Although our model does not describe the DNA bending energy explicitly, we may estimate the contribution of the DNA bending energy to the osmotic pressure on the basis of the inverse-spool-like structure of the packaged DNA (12,15,16,26,55,56). According to this model, the DNA bending energy is given by

$$\beta F_{\text{bend}}=\frac{{\xi }_{\text{p}}}{2}\int \frac{ds}{R{(s)}^2}\approx \pi {\xi }_{\text{p}}\sum _{\text{i}}\frac{N(R_{\text{i}})}{R_{\text{i}}},$$ (23)

where ξ_p = 50 nm is the persistence length, R(s) is the local radius of curvature at s, N(R_i) is the number of hoops of radius R_i To estimate the bending energy, we select 10 DNA lengths ranging from 5 kbp (1700 nm) to 50 kbp (17,000 nm). For each DNA length, the number of hoops and radii are estimated from the “inverse spool” model, with the assumption that the separation between neighboring strands is fixed at 2.5 nm. The osmotic pressure due to the DNA bending energy is calculated from ${\pi }_{\text{bend}}=-{(\partial F_{\text{bend}}/\partial V_{\text{C}})}_{\text{T},\text{L}}$ with V_C being the capsid volume. As shown by the dashed line in Fig. 3, we find that in fully packaged bacteriophages, the pressure induced by the DNA stiffness is <3% of the total pressure. As suggested by Evilevitch and co-workers (23), the DNA stiffness makes only a minor contribution to the total pressure under the conditions of significant pressure buildup.

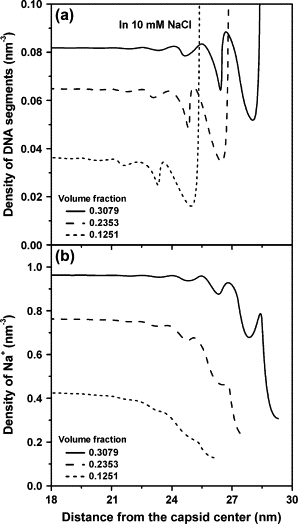
Fig. 4, a and b, present the theoretical predictions for the distributions of DNA segments and Mg²⁺ counterions, respectively. At all conditions, the $\text{S}{\text{O}}_4^{2-}$ concentration inside the bacteriophage is about six orders of magnitude lower than that of Mg²⁺. When the capsid is loaded with a small amount of DNA (volume fraction 0.1378), the DNA segments are depleted from the surface at a length scale comparable to the capsid size. The depletion is caused by the effective attraction due to neutralization of the DNA backbone by Mg²⁺, as evidenced by the close match between the density distribution of Mg²⁺ and that of the DNA segments. The attraction between DNA segments causes the DNA segments to clump in the center of the viral capsid. At higher packing densities, the effective intersegment attraction induced by the divalent counterions is dominated by excluded-volume repulsions. As a result, the DNA segments are oriented by the inner surface of the capsid and form an ordered layer-by-layer structure in consistency with experimental observations. We note that in experiments, the layer spacing is ∼2.5 ∼ 3.0 nm, which is significantly larger than our prediction of ∼1.7 nm (6,17,56,57). This difference can be attributed to our representing the DNA molecule as a chain of tangentially connected spheres with the radius that is the same as the cross-section radius of an effective cylinder (1.0 nm). The space between two adjacent spheres allows closer approach between two such chains than between two cylinders. We could alternatively choose the radius of the DNA segments such that the interstrand spacing is closer to the experimental observations. Because the thermodynamic properties of a DNA solution are mainly determined by the properties of counterions (48), we expect that a small change of the DNA segment radius has only negligible effect on the osmotic pressure. For example, we calculated the bulk osmotic pressure by using DNA segments with a diameter of 2.31 nm, each corresponding to 6.79 basepairs. The osmotic pressure varies no more than a few percent from those shown in Fig. 2 but the increased DNA segment diameter gives much larger layering spacing near the capsid surface.

Figure 4.

The radial distributions of DNA segments (a) and of Mg²⁺ (b) in partially packaged viral capsids in the presence of 10 mM MgSO₄ solution.

To compare the effect of counterions, Fig. 5 shows the results in the presence of 10 mM NaCl under similar volume fractions. Again, the concentration of Cl⁻ ions inside the capsid is nearly zero. Because the electrostatic neutralization by Na⁺ ions is significantly weaker and cannot introduce an effective attraction between DNA segments, a strong DNA accumulation layer appears at the surface even at a very low packing density (volume fraction 0.1251) due to the Coulomb repulsion between the DNA segments. In a highly packaged capsid, DNA forms a few layers in the vicinity of the surface but the density oscillation is less pronounced in comparison with that in the MgSO₄ solution. It appears that the effective attraction induced by the divalent counterions can enhance the localization of DNA at the surface and thereby promotes ordering at high packing density.

Figure 5.

The same as that in Fig. 4 but in the presence of 10 mM NaCl solution.

Fig. 6 compares the dependence of the DNA osmotic pressure on the packing density in a λ-bacteriophage and that in the bulk. Recent experiments (22) show that for MgSO₄ the ejection force is essentially zero up to 30% of packaging, whereas for NaCl there is a significant positive force; this is consistent with our predictions. When the salt is NaCl, the confinement has only minor effect on the DNA osmotic pressure, which is in agreement with an argument proposed by Gelbart and co-workers for the prediction of the DNA ejection force (25). Because the monovalent counterions cannot induce effective attraction between DNA segments, the pressure is always positive and monotonically increases with the volume fraction. When the salt is MgSO₄, we do not observe strong effect of confinement on the pressure at high packing densities. However, at low densities, the DNA osmotic pressure in the bulk has a negative and nonmonotonic regime, reflecting a thermodynamic instability induced by the effective attraction between DNA segments in the presence of Mg²⁺ ions (the pressure remains negative even without the van der Waals attraction). On the other hand, the DNA osmotic pressure inside the capsid remains positive and monotonic at all concentrations. It appears that the confinement breaks the spatial uniformity of the system and hence destroys the instability for phase separation; this instability is now manifested as a strong depletion of the DNA segments from the capsid surface and enrichment near the center (Fig. 4 a). In Fig. 6, we also calculate the DNA osmotic pressure in bulk when each chain contains 10,000 segments. In consistency with Fig. 2, the effect of chain length on DNA osmotic pressure is negligible over all the volume fractions in MgSO₄ or NaCl solution.

Figure 6.

DNA pressure in bacteriophages and in bulk solutions as a function of the packing fraction. In MgSO₄ solution, the small linear rise in the bulk osmotic pressure with density near the origin (the van’t Hoff limit) is not discernible on the scale of the plot.

Conclusions

In summary, we present a coarse-grained model for aqueous solutions of dsDNA that is able to describe the osmotic pressure and radial distribution of DNA in the bulk and in bacteriophages. All the model parameters are obtained from independent experimental results. For example, the DNA diameter is taken from the crystallographic data, the DNA van der Waals attraction is estimated on the basis of its atomic composition, and the diameters for the small ions are from properties of salt solutions not containing DNA. Despite its simplicity, the coarse-grained DNA model retains the exact number of backbone charges and approximate size of dsDNA. More important, it accounts for the solution conditions, in particular for the ion size and valence explicitly.

In contrast to the “worm-like chain” model (14), our model does not describe the DNA bending energy explicitly. Instead, the DNA stiffness is reflected by the excluded volume and more importantly by the strong electrostatic repulsion among neighboring coarse-grained segments. It has been previously argued that in fully packaged bacteriophages the effect of bending energy on DNA packing is relatively small (23).

Unlike previous theoretical investigations that employ empirical fitting parameters valid only in certain DNA concentrations and/or a priori assumptions of packaged structure, our model uses no adjustable parameters and faithfully accounts for the ion-explicit electrostatic interactions and excluded-volume effects. The density functional theory provides a coherent description of the excluded-volume effects, van der Waals attractions, intrachain correlations, and most importantly electrostatic correlations that may result in qualitatively different effects: monovalent counterions can only provide screening but do not induce attraction, while di- and trivalent counterions can lead to attraction between DNA segments. These effects are not captured in any previous models for DNA packaging. The theoretical model presented here is potentially important in understanding the biological function of DNA and in biomedical engineering such as design of effective gene delivery vehicles and prevention of virus infection.