Folding Pathway of the B1 Domain of Protein G Explored by Multiscale Modeling

Abstract

The understanding of the folding mechanisms of single-domain proteins is an essential step in the understanding of protein folding in general. Recently, we developed a mesoscopic CA–CB side-chain protein model, which was successfully applied in protein structure prediction, studies of protein thermodynamics, and modeling of protein complexes. In this research, this model is employed in a detailed characterization of the folding process of a simple globular protein, the B1 domain of IgG-binding protein G (GB1). There is a vast body of experimental facts and theoretical findings for this protein. Performing unbiased, ab initio simulations, we demonstrated that the GB1 folding proceeds via the formation of an extended folding nucleus, followed by slow structure fine-tuning. Remarkably, a subset of native interactions drives the folding from the very beginning. The emerging comprehensive picture of GB1 folding perfectly matches and extends the previous experimental and theoretical studies.

Introduction

Significant theoretical and experimental research efforts are devoted to understanding how proteins fold into their native structures. Determination of the folded structure is a priority for complete biochemical protein characterization. However, a detailed understanding of the folding process requires characterization of all alternative protein conformations that emerge along the folding pathway, including the unfolded state and partially folded intermediates. Elucidation of the principles governing the folding mechanism will have broad implications for predicting structure from sequence, protein design, and an understanding of the formation and propagation of prions and amyloids.

Theoretical studies lead to better understanding of experimental results providing easy-to-interpret structural models. Molecular mechanics is a powerful method for studying complex molecular systems. However, there is a gap between the time scales of classical molecular dynamics (MD) simulation and the time scales of protein folding. Only small and ultrafast folding (in a range of microseconds) proteins are now tractable by means of classical MD simulations (1). An average protein folds orders of magnitude slower. Perhaps, the largest protein folded using the all-atom potential and electrostatic-driven Monte Carlo (MC) procedure was the 46-residue staphylococcal protein A (2). The same protein direct folding simulations were performed by the use of an implicit solvent model combined with high-temperature all-atom MD (3). Energy landscape study of a protein of similar size (40 –residues) was also carried out by an all-atom free energy force field (4).

So far, for larger proteins, all-atom simulations of the entire folding process, from a random coil to the native state, are possible only for Go models. There have been a number of Go potential-based studies of protein G using the simplified model (5), the all-atom model (6), or with a weak Go-like contribution to the applied force field (7). In Go models, only native interactions are taken into account. Consequently, the lowest energy of the native conformation is guaranteed. The obvious weak point of such an approach is that the knowledge of the native structure is needed to construct the Go potential. A significant shortcoming also results from neglecting nonnative interactions, thereby ignoring their sometimes important role in the folding mechanisms (8).

Because of the time scale limitations of the all-atom molecular mechanics, reduced models offer the most promising possibilities to study large-scale protein rearrangements, as recently demonstrated by Liwo et al. (9). Langevin dynamics with the physics-based united-residue force field was applied successfully to the folding of real proteins. Minimalist protein models with potentials biased only on native secondary structure in combination with a sequence design strategy enabled folding kinetics studies of proteins G and L (10), the two proteins with similar folds but different folding mechanisms.

We have used a reduced protein lattice model and MC dynamics to perform equilibrium folding simulations at various folding stages, beginning from the denatured state. The use of a reduced representation of polypeptide chains led to a significant reduction of the conformational space (11), thereby enabling the search for the native state at a reasonable time scale. Compared with the experimental results, we have obtained a similar sequence of folding events and have identified the interactions critical for the folding process.

Our simulations show that the folding of the B1 domain of IgG-binding protein G (GB1) domain is initiated by the formation of a specific nucleus involving the hydrophobic core residues. These residues were previously found by Shakhnovich and co-workers to participate in the specific nucleation event. The study employed all-atom MC simulations with the Go potential (6) and φ values derived from protein engineering as restraints (12). Moreover, they have shown that the nucleus residues are evolutionarily conserved among proteins that share a similar fold but have very little sequence similarity (12). This finding strongly suggests that the native fold topology is a main factor determining the character of the transition state. In this article we present ab initio folding studies that are not driven by any restraints or by structure-specific potentials. This study confirms the specific nucleation process and provides a detailed description of the sequence of nucleation and folding events, from the highly denatured state to the formation of the native-like globule.

The CA–CB side-chain (CABS) model (13) used in this work was successfully employed by the Kolinski-Bujnicki group in edition 6 of Critical Assessment of Protein Structure Prediction, a community-wide testing experiment of protein structure prediction methods (14). The approach ranked second best overall, and more importantly, in the new fold category after Rosetta, the recombination of short fragments extracted from known protein structures (15). Both methods employed a MC search of the conformational space. In comparative modeling cases, the CABS force field has been supplemented with weak spatial restraints derived from homologous templates. Based on the previous denatured state simulations, it was postulated that the CABS model can be used not only for protein structure prediction, but also to study the folding mechanism (16,17). In this study, we employ knowledge-based statistical potentials only, the same as in the ab initio protein structure prediction. The only way for the evolutionary information to enter the force field is the predicted secondary structure (in the commonly used three-letter code), providing a weak bias toward protein-like local interactions.

This is the only structure-specific input in the CABS ab initio modeling procedure, introduced to take advantage of a relatively high level of accuracy of the contemporary secondary structure prediction methods.

Methods

CABS model description

The CABS protein representation and the model force field have been described in detail recently (13). In the reduced representation of the CABS protein chains, each residue is represented by four united groups: Cα, Cβ, the center of mass of the side group, and the center of the peptide bond. Positions of the Cα atoms are restricted to a simple cubic lattice with the lattice grid equal to 0.61 Å. A large number (800) of possible orientations of the virtual Cα-Cα bonds ensure lack of lattice anisotropy effects. On the other hand, the lattice representation facilitates very fast computation of interactions and local conformational transitions. The Cα trace provides a convenient reference frame for the definition of the position of the remaining interaction centers, which are located off-lattice. In the studies of protein dynamics, the simulation process is controlled by the asymmetric Metropolis MC scheme with a long random sequence of local conformational updates. A single step of the MC algorithm consists of several attempts to execute various local conformational transitions for each residue of the model chain. The sequence of the attempts at particular transitions is generated in a random fashion. The MC process simulates the long-time stochastic dynamics of a polypeptide chain.

The force field consists of several potentials of the mean force derived from a statistical analysis of the structural correlations seen in the known protein structures. The short-range interactions include generic protein-like conformational biases and statistical potentials describing local conformational propensities. A model of the main chain network of hydrogen bonds controls mutual packing of β-strands and a proper cooperative assembly of helices. The sequence and geometric context-dependent statistical potentials describe side-group interactions with a cooperative (multibody) component built in an implicit fashion. The CABS model has been tested extensively in numerous applications, including protein structure prediction, protein docking, and studies of long-time dynamics and thermodynamics of proteins and protein assemblies.

CABS simulations and data analysis

During the simulations analyzed in this work, multiple 10,000,000-MC-step isothermal trajectories were collected at different temperatures. The BioShell package (18) for protein modeling computation was used for managing and analyzing the large volume of simulation data.

The side-chain contact patterns were derived from the distributions of the distances between the centers of gravity of the side chains, present in the CABS model, so side-chain reconstruction was not necessary. The values of the contact cutoff distances depend on the identity and mutual orientation of the amino acids involved: two amino acids were assumed to be “in contact” when the distance between any pair of their heavy atoms was smaller than 4.5 Å.

The estimations of the density of states (Fig. 1, a, b, and d, and Fig. 2) were computed using T-pile (19) from 10,000,000-MC-step isothermal trajectories. Simulations were performed independently twice at all temperatures from 1.90 to 2.10 with 0.01 increments. Each simulation produced 100,000 structures and required ∼2 d using a standard machine (3 GHz CPU, Linux box).

Figure 1.

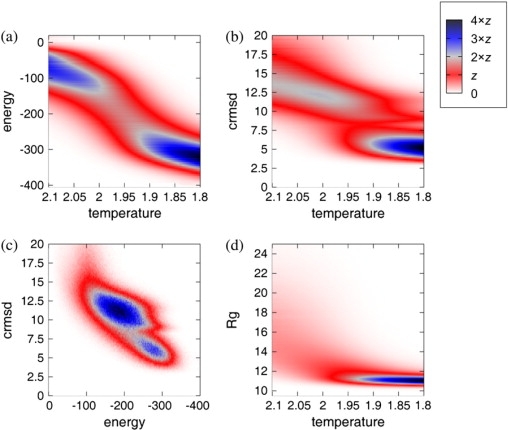
Estimation of the density of states for the various observables: (a) CABS energy as a function of reduced temperature; (b) cRMSD as a function of temperature; (c) cRMSD as a function of CABS energy at the transition temperature (T_t) (T = 1.955); (d) radius of gyration (in Ångstroms) as a function of temperature. Color indicates density of states in arbitrary units, depending on the kinds of data presented in particular plots.

Figure 2.

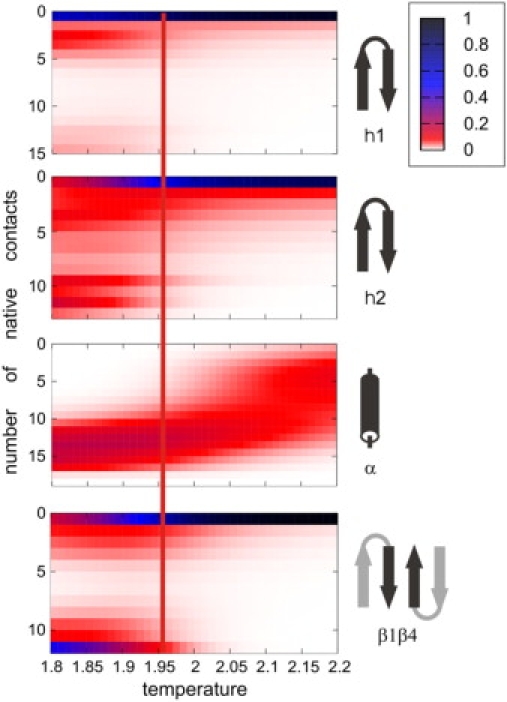
Temperature dependence of the content of native secondary structure elements measured in the simulations. Each panel represents temperature dependence of the number of native contacts within the particular secondary structure elements (right side of the figure). Beginning from the top, the data for the first hairpin, the second hairpin, the helix, and for the pair of the terminal strands are illustrated, respectively. The T_t is marked by a vertical line throughout all panels. The color scale (right of the drawing) denotes probability of the particular number of the contacts.

The software used for the analysis of the simulation data as well as the execution of CABS can be downloaded from our website (20). The movie illustrating the evolution of the density of states (and other system properties) with changing temperature can also be viewed at our homepage ((20), in the Files/Movies section).

Multiscale modeling

The multiscale modeling procedure for the data presented (see Fig. 5) consisted of the following steps. First, the missing backbone atoms were reconstructed using the BBQ algorithm (21). Subsequently, the side-chain rotamers were added using SCWRL (22). Because BBQ and SCWRL use libraries from known structures, an implicit underlying assumption is that the local conformational characteristics seen in folded structures are not far from the related protein chain characteristics in the denatured state. As discussed in the context of short-range statistical potentials, this is a legitimate working hypothesis (13). The resulting all-atom models were subjected to a short refinement procedure. We run the all-atom minimization with frozen α-carbons using Amber7 ff99 force field (23), Amber charges, dielectric constant equal to 1.0, and Powell minimization method implemented in Sybyl (Tripos, St. Louis, MO), without initial optimization. The refinement procedure was iterated 1000 times to improve arrangement of the side-chain rotamers. Side-chain positions sometimes changed significantly, but longer iterations did not bring meaningful changes. Recently a very similar procedure has been effectively used in a hierarchical approach to the model refinement and final structure selection after a coarse-grained modeling with CABS (24). Such multiscale methodology leads to a very good approximation of a model's energy (and free energy). Thus, it may be very useful in comprehensive studies of protein-folding energetics, which is now being pursued in our laboratory.

Figure 5.

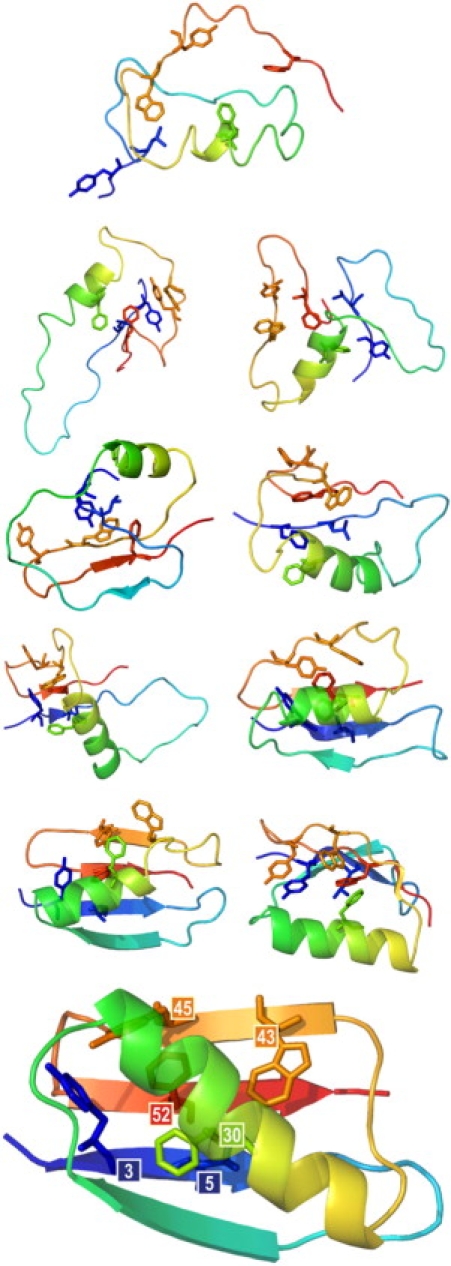
Multiscale modeling: example snapshots from a simulation presenting interactions of the nucleus side chains at various folding stages. Heavy atom bonds of the nucleus residues are marked with colored sticks; the secondary structure is depicted using transparent ribbons. Models were reconstructed from the reduced representation and refined by the procedure described in the Methods section. Afterward, the secondary structure was assigned by the DSSP algorithm (55). At the bottom, the experimental structure of protein G is drawn for comparison with the nucleus residues labeled by their position in the sequence. Pictures of models were drawn using PyMOL (56).

Results and discussion

Key role of the second hairpin in GB1 folding

The B1 domain of streptococcal protein G is a small, very regular α/β structure composed of 56 amino acids. The fold (25) consists of a four-stranded β-sheet and an α-helix tightly packed against the sheet. The sheet can be described as consisting of two symmetrically spaced hairpins: the first one, formed by N-terminal strands and the first β turn (β1-turn1-β2), and the second one, formed by C-terminal strands and the second β turn (β3-turn2-β4). Numerous experimental and theoretical studies highlight the early formation of the second hairpin and its key role in the GB1 folding. The second hairpin was found to be stable in isolation (26) and protected from hydrogen/deuterium exchange early during the folding of the entire protein (27). The isolated second β-hairpin folds on the 10-μs time scale, which is two orders of magnitude faster than the intact protein folding (28). The second hairpin fragment became a model short peptide, and its folding was extensively studied by MD and MC simulations (29). The importance of the second hairpin was also confirmed by φ value analysis (30), which suggested the presence of the well-formed second β-turn in the transition state ensemble.

The role of the supersecondary structural elements in GB1 folding was investigated by coarse-grained MC folding and unfolding MD simulations, which indicated that the helix-second hairpin fragment can stabilize itself to some extent independently of the rest of the protein, whereas the first hairpin cannot (31).

Hydrogen-deuterium exchange and NMR studies suggested that three regions of GB1 may correspond to nucleation sites: the second β-hairpin, the middle of the α-helix, and the N-terminus of the α-helix (27,32). These findings were also found to be consistent with MD unfolding studies (33). Full atom MD in specific solvents suggested that the β-sheet is more mobile and might be expected to unfold earlier than the helix (34). According to protein engineering studies of protein G, complex consequences of the folding kinetics of single point mutations in the helix may suggest its structural diversity during the folding (30). However, effects of several mutations suggested that the helix's C-terminus is better defined than the rest of the helix at the folding transition state ensemble (30).

Protein G unfolding dynamics was also investigated by the older version of the CABS force field with a different chain representation (SICHO model) (35). The first β-hairpin was found to unfold first and to be significantly less stable than the second β-hairpin. Here, we present a much more detailed study. Extensive isothermal simulations from a highly denatured state to the folding temperature were performed, providing a detailed overview of the entire folding process. Changes of the protein properties with the system temperature (T) measured by CABS energy, similarly to the native structure, coordinate root mean-square deviation (cRMSD) and radius of gyration, are shown in Fig. 1. Temperature dependence of the folding progress, with respect to the particular secondary structure elements, measured by the number of native contacts within the given substructure, is illustrated in Fig. 2. According to Fig. 2, the second hairpin and the terminal strands fold in a cooperative two-state fashion, whereas the helix folds in a continuous manner. Furthermore, the native arrangement of the terminal strands seems to have the largest contribution to the overall folding cooperativity. The first hairpin is definitely the least-ordered substructure after the folding transition.

The early formation of the helix and the second β-hairpin is also apparent in residue-specific analysis of the MC trajectories. A native-like arrangement of the side-chain contacts in the transition structures at the transition temperature (T_t) can clearly be seen in Fig. 3 d. Definitely, the helix is the most-ordered residual structure at T_t. It is stabilized by a number of short-range contacts between the side chains separated in the sequence by 3 or 4 positions. Another noteworthy fragment of the local structure at T_t is the second β-hairpin (Fig. 3 d). However, with respect to the long-range interactions, the second hairpin is the main nucleation site, responsible for the early structure formation.

Figure 3.

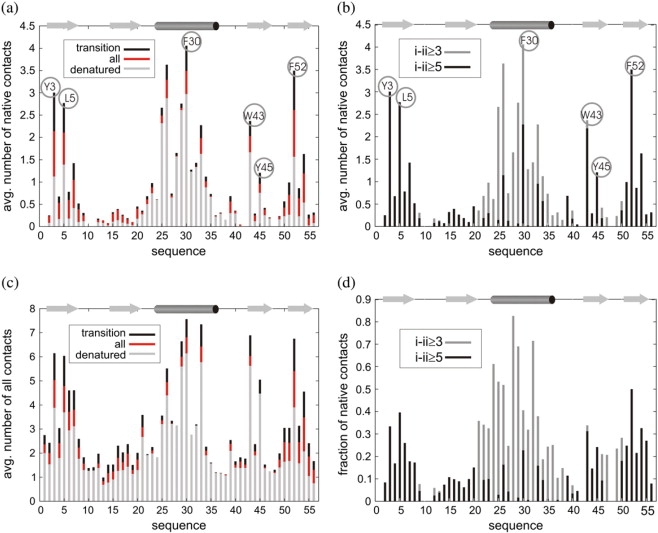
Acquisition of the side-chain contacts at the T_t. Average number of (a) native and (c) all side-chain contacts formed by a single residue is shown. The numbers of contacts are calculated for all the structures from the trajectory at the T_t (red color) and separately for two classes of structures extracted from the trajectory: denatured structures characterized by high cRMSD and high energy values (gray color) and transition structures (placed between the basin of native-like states and broad basin of denatured conformations, see also Fig. 1 c) characterized by medium cRMSD and energy values (black color). For the transition structures the distributions of (b) the average number of contacts and (d) the fraction of the native contacts are illustrated in terms of the distances along the sequence. All i-ii ≥ 3 interactions (gray color) and only nonlocal i-ii ≥ 5 interactions (black color) are displayed in both panels.

Nucleus residues: Y3, L5, F30, W43, Y45, F52

Changes of the protein properties with the system temperature (Fig. 1) suggest a two-state folding kinetics. Two main assemblies are present along the temperature coordinate that correspond to the denatured and more native-like conformations (definitely less heterogeneous than denatured). Transient conformations between these two assemblies were characterized at T_t by residue-specific contact studies (Fig. 3) and by an average side-chain contact map (Fig. 4 b). This analysis and side-chain contact studies presented below show that the folding transition is associated with a specific nucleation event.

Figure 4.

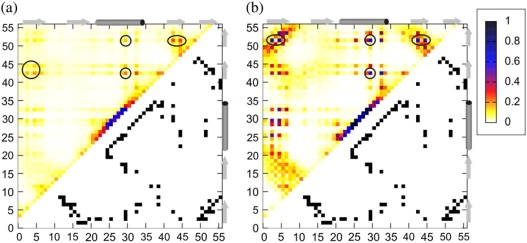
Average contact maps (above the diagonals) compared with the native contact maps (below the diagonals) for (a) the denatured state and (b) the transition structures. Colors indicate frequency of contacts. The average contact map for the denatured state was calculated from the entire isothermal trajectory at T = 2.1. The average contact map for the transition structures is the contact map from isothermal simulation at the T_t for the structures with the transient energy and cRMSD values (the same defined in the Fig. 3 caption). The most persistent contacts between the nucleus residues are circled.

Six residues (Y3, L5, F30, W43, Y45, F52) were found to form the folding nucleus during the MC dynamics simulations described here. The nucleus geometry is shown in Fig. 5 (bottom). The composition of the nucleus is in agreement with the all-atom MC simulations using φ-values as restraints performed by Shakhnovich and co-workers (12). Moreover, the same set of residues was identified by these authors via an inspection of residue conservation in proteins that share fold but not sequence similarity to protein G. The analysis of conservation has shown that all six nucleus residues are among the 10 most frequently conserved in the protein G-like folds. The remaining four of the 10 most conserved ones are T18, A23, A26, and V54. Interestingly, in their secondary structure, subunits A26 and V54 are the second most frequently long-range interacting residues (at T_t): A26 after F30 in the helix, and V54 after F52 in the second hairpin (Fig. 3, b and d). As the authors noted, the nucleus residues are conserved with a high statistical significance in respect to the rest of the sequence, which is consistent with similar observations for other fold families (36). These findings support the idea that the transition state structures and folding mechanisms are determined by the fold topology of native proteins (37). There is a very valuable confirmation of this idea in folding/denaturation studies of ubiquitin (38), which identified a quite similar folding nucleus to that observed by us in GB1. Both proteins are sequentially completely different, although they share the same overall fold, and therefore it is very likely that their folding mechanisms are similar.

Folding mechanism

Native contact clusters analysis (in the long-range interactions terms, Table 1) reveals a well-defined sequence of folding events. The folding process can be described as the sequential assembly of the elements of the supersecondary structure, with the key residues attaching successively to the folding nucleus:

• 1.The first folding event is the formation of the second β-hairpin (strongly stabilized by three hydrophobic residues: W43, Y45, F52).
• 2.With the decrease of T, contacts between the α-helix (F30) and the second β-hairpin (W43, Y45, F52) are increasingly stronger, and finally, at the T_t, they become more persistent than the key contacts within the second hairpin.
• 3.The next folding event is the nucleation of the β-sheet residues between β1- and β4-strands beginning from L5 (β1) and F52 (β4), at the beginning assisted by W43 (β3).
• 4.The involvement of the last nucleus residue in the nucleation process, Y3, results in the formation of the central part of the β-sheet (β1–β4) and the correct fold topology. A fluctuating native-like globule is formed.

Table 1.

Temperature-dependent evolution of the most persistent native long-range side-chain contacts and their clusters

T	1	%1	2		%2		3		%3		4			%4
2.10	45-52	25.7	43-52	45-52	15.0	43-52	43-54	45-52	6.9	30-43	30-52	43-52	45-52	3.1
	43-52	25.0	43-52	43-54	9.6	30-43	30-52	43-52	4.6	5-43	5-52	43-52	45-52	2.2
	30-43	20.7	43-54	45-52	9.2	30-43	43-52	45-52	4.5	30-43	43-52	43-52	43-54	2.1
	5-43	17.8	30-43	45-52	6.9	30-52	43-52	45-52	4.3	30-52	43-52	43-54	54-52	2.0
	30-52	14.3	30-52	43-52	6.9	30-43	30-52	45-52	4.0	30-43	30-52	43-52	43-54	1.8
2.04	45-52	32.0	43-52	45-52	19.8	43-52	43-54	45-52	9.9	30-43	30-52	43-52	45-52	5.8
	43-52	31.7	43-52	45-52	12.9	30-43	30-52	43-52	8.6	5-43	5-52	43-52	45-52	4.3
	30-43	28.3	43-54	45-52	12.7	30-43	43-52	45-52	8.0	30-43	43-52	43-54	45-52	4.1
	5-43	26.5	30-43	45-52	12.4	30-52	43-52	45-52	7.8	30-52	43-52	43-54	45-52	4.0
	30-52	22.4	30-52	43-52	11.9	30-43	30-52	45-52	7.3	26-52	30-43	30-52	43-52	3.6
2.01	43-52	38.5	43-52	45-52	24.4	43-52	43-54	45-52	13.3	30-43	30-52	43-52	45-52	8.4
	45-52	37.2	30-52	43-52	17.7	30-43	30-52	43-52	12.4	30-43	43-52	43-54	45-52	6.5
	30-43	33.2	43-54	45-52	17.1	30-43	43-52	45-52	11.4	3-52	5-52	5-54	7-54	6.4
	5-43	30.6	30-43	43-52	16.6	30-52	43-52	45-52	11.2	30-52	43-52	43-54	45-52	6.3
	30-52	29.4	43-52	43-54	16.3	30-43	30-52	45-52	10.4	5-43	5-52	43-52	45-52	6.1
1.98	43-52	46.9	43-52	45-52	28.9	30-43	30-52	43-52	19.3	30-43	30-52	43-52	45-52	12.2
	45-52	42.1	30-52	43-52	26.5	43-52	43-54	45-52	16.7	3-52	5-52	5-54	7-54	11.9
	30-43	41.3	30-43	43-52	24.8	30-43	43-52	45-52	16.3	5-52	30-43	30-52	43-52	11.3
	30-52	39.8	30-43	30-52	23.3	5-52	30-52	43-52	15.7	4-51	5-52	6-53	7-54	11.0
	5-43	37.2	30-43	45-52	21.7	30-52	43-52	45-52	15.6	3-52	5-52	7-54	30-52	10.7
1.96	43-52	52.4	30-52	43-52	32.6	30-43	30-52	43-52	20.8	3-52	5-52	5-54	7-54	15.8
	30-52	47.2	43-52	45-52	32.0	3-52	5-52	30-52	18.3	4-51	5-52	6-53	7-54	14.7
	30-43	46.4	30-43	43-52	30.6	3-52	5-52	5-54	18.2	3-52	5-52	7-54	30-52	14.4
	45-52	45.0	30-43	30-52	28.9	5-52	30-52	43-52	18.1	3-52	5-52	5-54	30-52	14.2
	5-52	44.0	30-43	45-52	25.6	3-52	5-52	7-54	18.0	3-52	5-52	6-53	7-54	14.0
	3-52	39.9

For each temperature five most frequently appearing native contacts (1), doublets (2), triplets (3), and quadruplets of native contacts (4) are shown. Their frequencies, expressed as the percentages of the snapshots in corresponding trajectories, are also presented. At T = 1.96, near the folding T_t, the sixth contact (in the order of the frequency of occurrence) is additionally shown. Data were collected from isothermal trajectories of 10,000,000 MC steps.

Temperature dependence of the native contact clustering and the sequential acquisition of the native-like secondary structure (Fig. 2) are consistent with protein engineering studies of the β-sheet formation. Mutations in β1-, β3-, and β4-strands have intermediate φ-values, suggesting partial formation of a three-stranded β-sheet composed of these strands in the folding transition state ensemble, whereas the first hairpin and the helix have relatively low φ-values (30). A similar picture of the transition state can also be inferred from the observed subsets of long-range (i-ii ≥ 5) native-like side-chain contacts seen in the transition structures at T_t (Fig. 3 d). Strands β1, β3, and β4 are the most native-like. The internal ordering of the helix is stabilized mainly by local (short-range) interactions, and therefore, single mutations within the helix should not have much impact on the whole GB1 folding mechanism.

It should be emphasized that the description presented here of the protein G folding nucleus growth (Table 1), to our knowledge, is the first in-depth, residue-level report of the nucleation process from the very beginning of a protein of comparable or larger size. In previously mentioned work describing all-atom Go simulations of protein G (6), particularly early folding stages are reported less thoroughly, in terms of secondary structure element acquisition. Namely, three folding pathways were observed, each involving formation of its own assembly: helix-first hairpin, helix-second hairpin, and β1–β4. All pathways appeared to converge to the same folding nucleus, which perfectly agrees with what we found in our simulations, although it is difficult to compare the earlier folding stages.

Although descriptions of the folding nucleus on the level of individual residues match perfectly the above all-atom Go simulations and evolutionary studies, it seems justified to conclude that the resolution of protein features representation in the CABS model is high enough. The minimalist model used in folding kinetic studies of proteins G and L (10) seems to be an example of an insufficient protein representation. As authors admit, their model inadequately describes β-sheet structure (it forms a β-strand bundle instead of a β-sheet for protein G). Their protein G folding studies emphasize the role of assembly of β3-strand with β2 and β1, especially in an intermediate formation (nonnative interactions, not reported before), and, for example, completely neglects the role of β1–β4 formation in the fold assembly, so important in these studies.

Highly denatured state exhibits native-like long-range interactions

At T = 2.1 GB1 is highly unfolded with the average radius of gyration, R_g = 16.4 Å, and the chain expands occasionally to an R_g range of 35 Å (for R_g distribution at different temperatures see Fig. 1 d). At this highly swollen state, the protein begins to form first native-like, long-range interactions (for the side-chain contact map see Fig. 4 a). The average size at T = 2.1 is smaller than the GB1 random coil size (23 Å) (39), mostly because of the partial formation of the helix. As can be seen in Fig. 4 a, the center of the helix is the most persistent fragment of the residual structure, present in more than half of snapshots. The rest of the structure, especially in respect to the nonlocal interactions, remains highly disordered. Remarkably, the most frequently occurring long-range side-chain contacts and their fluctuating clusters involve native contacts between the residues found to participate in the folding nucleus (Table 1, T = 2.1). The most frequent nonnative long-range (i-ii ≥ 5) contacts are also observed for the residues participating in the nucleus: Y33–W43 (present in 25% of snapshots), T25–F30 (17%), Y45–K50 (16%), Y45–T51 (15%), and Y3–W43 (15%). The frequent contacts of Y33 may indicate an important role of this residue in the tight packing of a slightly deformed helix against the sheet. This issue has also been discussed by others (34,40).

Recently, there have been an increasing number of reports suggesting a significant presence of the secondary structure and hydrophobic clustering, even under highly denaturing conditions (41,42). Moreover, it was found that a highly denatured protein can exhibit long-range ordering loosely resembling the native-like topology (43). Therefore, the folding process can be directed from the very beginning, and the search for the conformational space could be more efficient when not starting from an accidental structure. Current assumptions are that understanding of the folding process may be possible after more complete structural studies of the denatured state.

Clearly, from the very beginning of the folding process, the residual structure is initiated by hydrophobic interactions. The major role of the hydrophobic interactions in determining the folding route was also found in a reduced modeling study of protein G, whereby the hydrophobic interactions excised from physical energy terms critically affected the folding route (7). The MC simulations presented here confirm the crucial role of the hydrophobic interactions in the initiation and propagation of protein folding (44).

It should be pointed out that although the simulations started from the native structure, the relaxation of the system is so fast that any effects of memory of the initial conformation are completely eliminated.

Structural characteristics of the native-like globule

The formation of the folding nucleus is followed by the assembly of a native-like loosely packed globular structure with the average cRMSD above 5 Å from the native at the T_t (see Fig. 1 c). To investigate structural properties of this globular state, we extracted a large number of snapshots from the isothermal MC trajectory at T_t of 100,000 structures. Over 14,000 structures (the structures from the low-energy basin having CABS energy values between −240 and −320 and cRMSD from native between 4 and 8 Å) were extracted and clustered using a single-link clustering algorithm (45). In the single-link clustering, the distance between the clusters is defined as the distance between their closest members. With the cutoff distance of 2.2 Å, the largest cluster (representing the lowest free-energy basin) consists of 2557 structures. The structures in this cluster have the correct native topology, although with highly variable structural details. The remaining clusters are smaller by two orders of magnitude and represent incorrect folds (incorrect arrangements of the stands in the β-sheet or the C-terminal and the N-terminal strands shifted in the register by two residues). The schematic drawing of the centroid of the largest cluster and the comparison of the sizes of the top 10 clusters are given in Fig. 6. Clearly, relatively well-defined native-like structures dominate the simulation trajectory.

Figure 6.

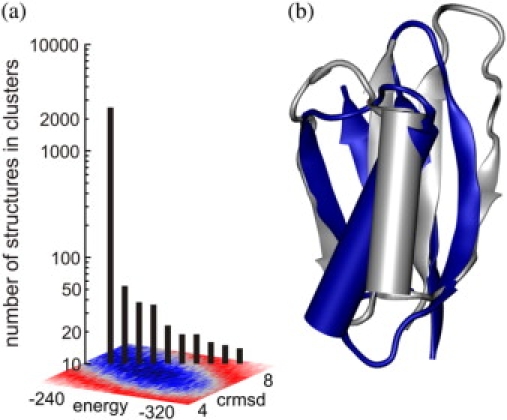
Classification of the structurally related low-energy conformations at T_t. (a) The left-side plot displays in a logarithmic scale the relative sizes (number of members of a cluster) of structural classes obtained from the clustering of all the structures from the low-energy basin at T_t (structures having CABS energy value between −240 and −320 and cRMSD from native between 4 and 8 Å). (b) The right side shows the structure of the centroid of the largest cluster (gray), exhibiting loosely defined conformation (albeit in the correct topology), 5 Å from the native structure, superimposed on the native structure (blue). The image was created using VMD (57).

Is there an intermediate state?

GB1 was initially thought to fold by a two-state process, as do many other small proteins (46). However, continuous-flow fluorescence measurements of GB1 kinetics demonstrated clear deviations from the kinetics expected for a simple two-state process and indicated the presence of an intermediate (47). The time course of the refolding revealed a prominent exponential phase with a time constant of 600–700 μs followed by a second, rate-limiting process with a time constant of 2 ms or longer, depending on denaturant concentration. According to Park et al. (47), the biphasic kinetics of the folding can be modeled quantitatively on the basis of a three-state folding mechanism (folding through an intermediate). An ensemble of intermediate states represents native-like fluorescence properties: W43 becomes largely buried during the initial phase of folding. Additionally, the denaturant-dependent rate constant studies provided insight into the solvent-accessible surface area associated with each transition (47). According to this analysis, the initial barrier, the first transition state TS1, represents a well-solvated ensemble of states with α = 0.29 (the α values indicate a change in the solvent-accessible surface area relative to the unfolded state, for the unfolded state, α = 0; for the native, α = 1), whereas both the intermediate and the second transition state, TS2, are nearly as desolvated as the native state (α = 0.85). The high α value for the intermediate state, α_Intermediate = 0.85, implies that it represents a compact set of conformations with the solvent-exposed surface area only slightly larger than that of the native state, which is consistent with its native-like fluorescence properties. A comparison with other proteins for which α_Intermediate values have been determined on the basis of stopped-flow data shows that the intermediate in the GB1 folding is unusually compact (48). According to Park et al. (47), this is probably a consequence of the fact that the hydrophobic core of GB1 is relatively large for a protein of its size.

The plots shown in Fig. 1 suggest a two-state behavior, although a closer inspection of the structures at the temperatures just below the region of the steepest changes of structural properties clearly indicates that this cooperative chain collapse leads to the molten globule state (Fig. 2), consistent with that described by Park et al. (47).

The molten globule is known as a stable, collapsed state with a partial native-like ordering that proteins can adopt under certain conditions (49,50). The molten globule exhibits a somewhat native secondary and tertiary structure, although with a high mobility of slightly exposed side chains. Interestingly, in our earlier simulation studies (S. Kmiecik and A. Kolinski, unpublished results) of small single-domain proteins, structures significantly more compact and closer to the native structures were usually observed. This is another indication of the three-state folding of GB1. In some simulations of GB1 we observed that long relaxation of the molten globule-like structures, after the initial fast collapse to the proper topology, leads to more closely packed structures with much smaller overall fluctuations near the native state. Because of the coarse-grained character of the CABS model, these compact structures exhibit only partially native-like packing (the best structures were ∼2.5 Å from the native). The backbone geometry and the main-chain hydrogen bond network were native-like, although only a fraction of the side chains became fully fixed (compare the work by Hubner, Shimada, et al. (12)).

Interestingly, the presence of an intermediate is still under debate. Krantz et al. (51) questioned the validity of the analysis by Roder and co-workers (47), suggesting a folding without accumulation of an intermediate, which was later refuted by Roder et al. (52).

Our GB1 simulations support the folding scenario starting from the formation of a loosely packed ensemble of relatively compact states with a native-like overall fold, followed by a rate-limiting formation of the unique native structure with its tightly packed core. Whether the two folding stages can be observed experimentally depends on the stability of the compact intermediates (47). Such accumulation of compact states with the native-like features during the GB1 folding was also observed in MD simulations (53).

Distinct mechanisms of GB1 and CI2 folding

Very interesting is the comparison of the GB1 folding mechanism with the folding mechanism of another small protein, CI2, which is also a paradigm for kinetics studies. Results of CABS modeling of the CI2 folding pathway have been published recently (16). We observed that GB1 and CI2 fold by somewhat different mechanisms. This is in slight disagreement with the interpretation of the experimental data suggested by Daggett and Fersht (54). According to them, CI2 folds via nucleation-collapse around an extended nucleus, similarly to what has been observed in this work for GB1. Indeed, in the case of GB1, all nucleus residues take part in the nucleation event at very early stages of folding. On the contrary, CI2 folds via the assembly of distinct cooperative subunits (16). At the folding transition, the only native tertiary interactions are observed between the two central strands, β3β4. Consolidation of the helix and β3β4 takes place at lower temperatures. In other words, in our simulations CI2 folding can be described as a sequential formation of secondary structure modules, whereas protein G folds as a single structural module (exactly as interpreted by Daggett and Fersht in the case of CI2). Interestingly, when the CABS energy (or radius of gyration) is studied as a function of temperature during the CI2 folding, the stepwise formation of cooperative subunits does not affect its exponential thermal characteristics. It appears that the differences observed in simulations in the folding pathways of GB1 and CI2 are actually in agreement with the available experimental data; the mechanistic picture the simulations provide is easier for comprehensive analysis and interpretation.

Conclusions

The theoretical model of protein G folding resulting from these computer studies is consistent with the experimental observations (30,47) as well as with previous theoretical studies performed by the all-atom Go model, revealing the existence of a well-defined folding nucleus (6,12) and providing a comprehensive picture of the folding mechanism.

This approach may be a very useful tool for qualitative studies of entire folding pathways of large proteins and macromolecular assemblies. Because a procedure exists for fast and accurate protein chain rebuilding (21) with subsequent all-atom refinement and model assessment (24), the proposed method should be applicable to detailed computational studies of long-time dynamics of biomolecular systems. An example of such multiscale modeling is schematically illustrated in Fig. 5, where the rebuilding of the atomic details enabled precise identification of the interaction of the side chains forming the folding nucleus.

The physical folding mechanism observed in the CABS simulations strongly suggests that the interactions in the denatured state are very similar to those in the native structures. Consequently, the knowledge-based potentials derived from native structures are a good approximation of the interactions in the denatured state (16).

Simulations described here provide a detailed insight into the folding mechanism at the level of individual residues. The results consistent with the experimental and theoretical findings prove that the proposed MC dynamics and a sampling scheme mimic qualitative features of the continuous long-time protein dynamics. This opens up a possibility of efficient multiscale computational studies of protein dynamics, folding mechanisms, and protein docking mechanisms.