Numerical simulation of incompressible viscous flow in deforming domains

Abstract

We present a second-order accurate finite difference method for numerical solution of the incompressible Navier-Stokes equations in deforming domains. Our approach is a generalization of the Bell-Colella-Glaz predictor–corrector method for incompressible flow. In order to treat the time-dependence and inhomogeneities in the incompressibility constraint introduced by presence of deforming boundaries, we introduce a nontrivial splitting of the velocity field into vortical and potential components to eliminate the inhomogeneous terms in the constraint and a generalization of the Bell-Colella-Glaz algorithm to treat time-dependent constraints. The method is second-order accurate in space and time, has a time step constraint determined by the advective Colella-Friedrichs-Lewy condition, and requires the solution of well behaved linear systems amenable to the use of fast iterative methods. We demonstrate the method on the specific example of viscous incompressible flow in an axisymmetric deforming tube.

The incompressible Navier-Stokes equations are a combination of evolution equations and constraints caused by the incompressibility condition. As such, the formulation of appropriate time-discretization methods is more subtle than that for evolution equations. To address this issue, Chorin (1) introduced projection methods based on the Hodge decomposition of any vector field into a divergence-free part and a gradient of a scalar field. Projection methods are fractional step methods for which an intermediate velocity is computed that does not necessarily satisfy the incompressibility constraint. This velocity then is corrected so that it satisfies the constraint. More recently, Bell, Colella, and Glaz (BCG) (2) introduced a predictor–corrector method based on Chorin’s ideas. Some of the key advantages of their method are that the advective terms can be treated by using explicit high-resolution finite difference methods for hyperbolic partial differential equations and that only linear systems coming from standard discretizations of second-order elliptic and parabolic partial differential equations, which are amenable to solution using fast iterative methods such as multigrid, must be solved. This leads to a method that is second-order accurate in space and time, a stability constraint on the time step due only to the Courant-Friedrichs-Lewy condition for the advection terms, and a robust treatment of underresolved gradients in the Euler limit. This method has been the basis for the extensive development of new algorithms for the treatment of a variety of low-Mach number flow problems (3–11).

The purpose of this paper is to present the extension of the BCG algorithm to the case of moving deformable boundaries. The principal difference is that the boundary conditions for the divergence-free constraint become both inhomogeneous and time-dependent. There have been a number of previous methods that model deformable boundaries (12–14), but none combine the accuracy, efficiency, and robustness of the BCG approach. We attack this problem by using two ideas. First, we eliminate the inhomogeneity in the constraint equation by performing a nontrivial Hodge splitting of the velocity field into a potential component that carries the inhomogeneities in the boundary conditions for the divergence constraint and a vortical component that satisfies an evolution equation with time-dependent, but homogeneous, constraints. The second idea is a generalization of the BCG time discretization for the solenoidal component that properly accounts for the temporal variation in the constraint. The end result is a method that retains the advantages of the BCG algorithm but for the more general case of flows in deforming domains.

Physical Problem

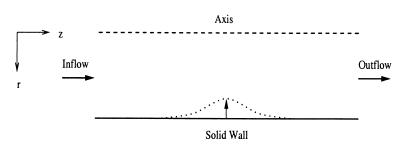
We consider the problem of flow in an axisymmetric, flexible tube (see Fig. 1). The dashed upper boundary of the figure is the centerline, or axis of symmetry, of the tube where r = 0. There is flow into the tube at the left boundary where the classic Poiseuille velocity profile for viscous flow in pipes is prescribed. The wall of the tube is the bottom boundary, r = R(z, t). This infinitely thin solid wall boundary is allowed to move in the middle section of the tube with a prescribed velocity. The inlet and outlet remain fixed.

Figure 1.

Flow through an axisymmetric deforming tube.

Split-Velocity Formulation.

We alleviate the problem of inhomogeneous boundary conditions with a split-velocity formulation on a moving, mapped grid. We first define a continuous mapping from an abstract fixed coordinate system, ξ = (ξ, η), to real axisymmetric coordinates which are time-dependent, x(t) = (r(t), z(t)):

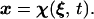1

We then define divergence, gradient and Laplacian operators:

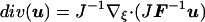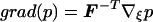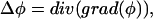2

where u and p are velocity and pressure, respectively, and J is the determinant of F = ∂x/∂ξ. The incompressible Navier-Stokes equations in mapped coordinates are

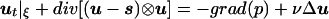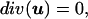3

where s = ∂χ/∂t is the velocity of the moving coordinate system and ν is the kinematic viscosity. The boundary conditions for viscous incompressible flow in an axisymmetric deforming tube are as follows: (i) axis of symmetry (no-flow) u⋅n = 0; (ii) solid wall (prescribed boundary motion) u = u_b; (iii) inflow (prescribed Poiseuille flow) u = 0, v = 2(1 − r²); and (iv) outflow ∂u/∂z = 0. In addition, we need a boundary condition on p at outflow and will defer discussion for later.

We use the Hodge decomposition (15) to split the velocity field into its divergence-free and potential components, u_d and u_p, respectively:

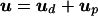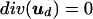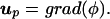4

Here, φ is the solution to Laplace’s equation, Δφ = 0, with normal boundary conditions (see Fig. 1 for geometry): (i) axis of symmetry (no-flow) u_p⋅n = 0; (ii) solid wall (prescribed boundary motion) u_p⋅n = u_b⋅n; (iii) inflow (constant mean flow) u_p⋅n = v_in; and (iv) outflow (conservation of mass, one-dimensional mean flow) u_p⋅n = v_out, where v_out is the one-dimensional solution obtained from conservation of mass for flow in a flexible tube with fixed inlet and outlet (see ref. 16 for details).

This leads to the following equation of motion for u_d:

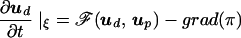5

where

6

A Bernoulli pressure, π, has been defined to absorb all gradients in the split, transformed equations. If the flow is frictionless and purely potential (u = ∇φ), the equation of motion (Eq. 5) reduces to Bernoulli’s equation.

The boundary conditions on u_d are as follows: (i) axis of symmetry, u_d⋅n = 0; (ii) solid wall, u_d⋅n = 0, u_d⋅t = (u_b − u_p)⋅t; (iii) inflow, u_d = 0, v_d = 1 − 2r²; and (iv) outflow, ∂u_d/∂z = 0. The boundary condition on p at outflow is π = 0 at outflow. This is required for the potential flow solution, u_p, to satisfy the Euler equations.

These boundary conditions lead to div and grad operators appearing in Eq. 5 that are formally adjoints to each other:

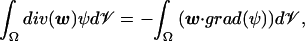7

if w and ψ satisfy the boundary conditions. The reason this is the case is that the boundary conditions for u_d and π are set so that the boundary terms coming from application of the divergence theorem to ∫_Ω∇⋅(wψ)d𝒱 vanish.

Model Problem

A model problem is discussed to address the issue of a time-dependent incompressibility constraint. The model problem is a general form of the equation of motion (Eq. 5). Let f, u ∈ ℛⁿ, π ∈ ℛ^m, A = n × m matrix where u, A, f = u(t), f(t), A(t) are smooth functions in time. The constrained system is comprised of an equation of motion and a homogeneous constraint:

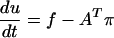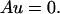8

u corresponds to the fluid velocity in Eq. 5, and f corresponds to the advection and viscosity terms. A and A^T are adjoint matrix operators that correspond to div and grad and include boundary conditions.

The constraint can be used to obtain an equation for π in order to evolve the system exactly. To obtain a “pressure-Poisson” type of equation, we differentiate the constraint (d/dt(Au) = 0) and compare to the divergence of the equation of motion Eq. 8:

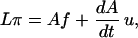9

where L ≡ AA^T. Solvability is assumed for Eq. 9. In the case of an incompressible fluid, either L is invertible, or it has a null-space that is independent of time.

One can express the constraint condition in Eq. 8 in terms of projection operators. We define Q = A^TL⁻¹A and P = I − Q. The operators P and Q are projections onto the subspace of vectors that satisfy the constraint and onto the orthogonal complement of that subspace: If Au = 0, then Pu = u and Qu = 0. Note that these projection operators are functions of time if A, A^T are functions of time.

First, we consider the case in which A is independent of time. The projection operator can be used to eliminate the constraint and reduce the problem to a system of ordinary differential equations:

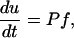10

where we use the fact that PA^Tπ = 0. This system is equivalent to the original one, provided the initial data satisfy the constraint, i.e. (Au)(0) = 0. In that case, the BCG discretization reduces to

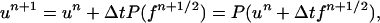11

where Δt is the discrete time step and u⁰ = u(0). This discretization is inherently second-order because of the use of the midpoint rule for f. Also, P(uⁿ⁺¹) = uⁿ⁺¹ if P(uⁿ) = uⁿ.

The BCG discretization can be written in predictor-corrector form:

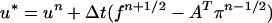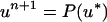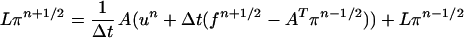12

where uⁿ ≈ u(tⁿ), π^n−1/2 ≈ π(tⁿ − Δt/2).

Next, we generalize the BCG discretization for the model problem with time-dependent A. The difficulty is that, in the time-independent case, we obtained a second-order accurate method by eliminating the constraint and applying the midpoint rule to the resulting system of ordinary differential equations. A reduction corresponding to Eq. 10 does not exist when the constraint is time-dependent, and we must construct a second-order accurate discretization directly for the original constrained system. Such a discretization is given as follows:

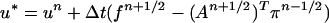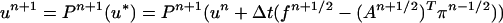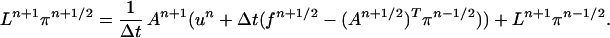13

Let w^new, q^new be solutions approximated by the predictor-corrector scheme:

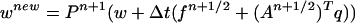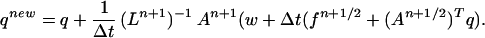14

Define u_eⁿ = u(tⁿ), π_e^n+1/2 = π(t^n+1/2) where u, π are solutions to the model problem (Eq. 8). If w = u_eⁿ and q = π_e^n−1/2 + O(Δt), then

(i) the method is second-order accurate:

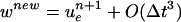and

(ii)

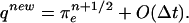Proof of i. In order to prove the consistency of the predictor–corrector discretization, the solution w^new is compared to the standard of a Crank-Nicolson solution, which uses the midpoint rule. It is noted that the midpoint rule for ordinary differential equations yields global second-order accuracy.

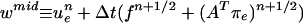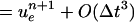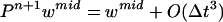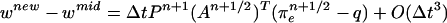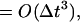because Pⁿ⁺¹(A^n+1/2)^T is O(Δt).

Proof of ii.

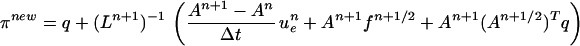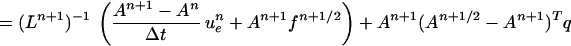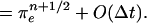Note that ii depends only on q being bounded independent of time; i.e., the proof begins with a statement of the truncation error and ends with the same statement.

There are several points to be made regarding this method. The first is that it requires only the application of a succession of fixed time operators, rather than a solution to problems resulting from differentiation of the constraint with respect to time, such as Eq. 9. In particular, this leads to a solution that satisfies the constraint at the end of each time step. The second point is that, although we obtain a second-order accurate method for the solution u, the approximation for π is only first-order accurate in time, which is, in fact, all that is required. Finally, although we will apply this method to a very specific approach to discretizing the spatial derivatives, the time discretization presented here is itself quite general and could be applied equally well to other discretization strategies.

Discretization for Incompressible Flow

We apply the new time discretization to the split-velocity formulation for incompressible flow. Finite difference approximations are used to discretize the derivatives in the equations of motion. Any time step in the algorithm begins with the knowledge of a cell-centered discrete velocity, U_d,i,jⁿ, at time tⁿ, and a discrete cell-centered Bernoulli pressure, π_i,j^n−1/2, at the lagged time, t^n−1/2 = tⁿ − Δt/2. Also, the discrete potential velocity, U_p, is known at all times from the discrete Dirichlet problem that it satisfies; it is known at both edges and cell centers through averaging operators. The discrete vortical velocity and pressure are evolved by the predictor–corrector scheme discovered in the model problem. Evolution of the dependent variables is predicated on a known initial solution that satisfies the boundary conditions and the incompressibility constraint. Dⁿ, G^n+1/2, Lⁿ, and L_νⁿ are the discrete representations of the operators div, grad, Δ, and Δ_ν, respectively, including boundary conditions.

We now apply the time-discretization in the previous section to the system of equations (Eq. 5) describing the time evolution of u_d. We do this in two steps. First, we compute a time-centered estimate of the right-hand side corresponding to f^n+1/2. Following ref. 2, we solve the system of equations

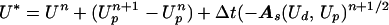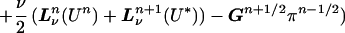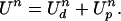15

Here, A_s(U_d, U_p)^n+1/2 is an estimate of the advective terms at time tⁿ + Δt/2, computed by using a second-order accurate Godunov method. If π^n−1/2 were replaced by π^n+1/2, this would be a Crank-Nicolson discretization for the diffusion terms. As is, it is sufficient to obtain an O(Δt²) estimate of ν(L_νⁿ(Uⁿ) + L_νⁿ⁺¹(U*))/2.

In the second step, we apply the discrete evolution. We form

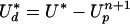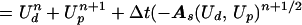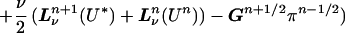16

and obtain the updated solution:

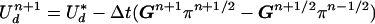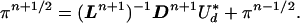17

Results

We present the convergence results of two flow regimes for incompressible viscous flow in an axisymmetric deforming tube. The flow is characterized by Reynolds number, Re = v̄d/ν, where v̄ is the mean velocity, d is the diameter of the tube (d = 2 in all cases), and ν is the kinematic viscosity. The following grid motion is used:

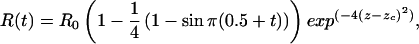18

where R₀ is a radius of unity for an initially rectangular grid and z_c is the axial location of the extremum for a Gaussian movement.

The first case is a low Reynolds number calculation, Re = 8, where v̄ = 1 and ν = 0.25. The convergence results for this case are shown in Table 1 at a time t = 0.5 when the inward boundary velocity is at a maximum where the tube has moved to a position that is 0.875 of the original radius. The second case is a high Reynolds number calculation, Re = 200, where v̄ = 1 and ν = 0.01. The convergence results for this case are shown in Table 2 at a time t = 1 when the boundary has stopped moving at a fully pinched tube position, or 0.75 of the original radius. (See ref. 16 for details on convergence analysis.)

Table 1.

Error for flow in deforming tube (Re = 8)

Case	e1/16	Rate	e1/32	Rate	e1/64
u	4.01  ×  10−3	1.69	1.24  ×  10−3	1.75	3.68  ×  10−4
v	8.25  ×  10−3	2.04	2.01  ×  10−3	2.01	4.99  ×  10−4

Table 2.

Error for flow in deforming tube (Re = 200)

Case	e1/16	Rate	e1/32	Rate	e1/64
u	2.71  ×  10−2	2.34	5.36  ×  10−3	1.94	1.40  ×  10−3
v	7.50  ×  10−2	2.39	1.43  ×  10−2	2.22	3.06  ×  10−3

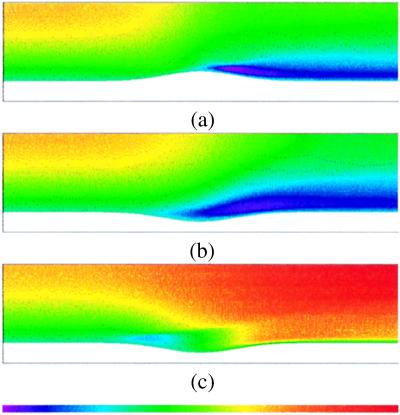
We also present the salient flow features for a complete cycle of the inward and outward movement of the tube wall. Fig. 2 depicts snapshots of the axial velocity for Re = 200 at times when the wall velocity is at a maximum (see Fig. 1 for geometry). A notable feature in this flow scenario is a very sharp gradient that is captured in the axial component of the velocity at time t = 3.5, when the hump is moving back inward from its fully expanded outward position. The strong gradient, which indicates the presence of a shear layer, exists in the axial direction as well as the radial direction. Another observation is movement of the point of separation, which is indicated in the axial component of velocity by a change in sign from positive to negative. As the hump expands outward, the separation point marches from a location just before the midpoint of the hump toward the inlet.

Figure 2.

Axial velocity in tube with inward/outward-moving hump (inlet Re = 200). (a) Time t = 1.5 when the wall is moving outward to the flat position. (b) Time t = 2.5 when wall is moving outward from flat position. (c) Time t = 3.5 when the wall is moving inward to the flat position. (Scale = −1.703–3.773.)

ABBREVIATION

BCG

Bell-Colella-Glaz