Abstract
One of the most recurring questions in protein folding refers to the interplay between formation of secondary structure and hydrophobic collapse. In contrast with secondary structure, it is hard to isolate hydrophobic collapse from other folding events. We have directly measured the dynamics of protein hydrophobic collapse in the absence of competing processes. Collapse was triggered with laser-induced temperature jumps in the acid-denatured form of a simple protein and monitored by fluorescence resonance energy transfer between probes placed at the protein ends. The relaxation time for hydrophobic collapse is only ≈60 ns at 305 K, even faster than secondary structure formation. At higher temperatures, as the protein becomes increasingly compact by a stronger hydrophobic force, we observe a slowdown of the dynamics of collapse. This dynamic hydrophobic effect is a high-temperature analogue of the dynamic glass transition predicted by theory. Our results indicate that in physiological conditions many proteins will initiate folding by collapsing to an unstructured globule. Local motions will presumably drive the following search for native structure in the collapsed globule.
During the folding reaction a protein must form its native secondary structure and collapse into a globular state. But, how do these two dynamic processes interlace with each other (1)? The intrinsic time scales for α-helix (2) and β-hairpin (3) formation have been measured in short peptides that form these secondary structure elements without the protein context. The dynamics of homopolymer collapse has been the subject of intensive theoretical (4–6) and computational analysis (7). In proteins, hydrophobic collapse has been studied by using a variety of computer simulations in different simplified protein models (8–13). However, the experimental investigation of hydrophobic collapse has proven difficult. Most of what we know experimentally about protein reconfiguration dynamics arises from detection of early phases in folding or from measurement of rates of contact formation in unfolded polypeptides (14). How these observations relate to the dynamics of hydrophobic collapse is unclear, because such experiments are either performed in competition with other folding events (15–21) or with no driving force for collapse because of the presence of chemical denaturants (22). The “ideal” experiment to measure directly the dynamics of hydrophobic collapse could be summarized in four requirements: (i) an archetypal protein that can be fully denatured with no chemical denaturants, (ii) a spectroscopic probe to monitor molecular dimensions, (iii) a simple strategy for tuning the degree of collapse, and (iv) a technique to trigger changes in collapse with sufficient time resolution.
Here we study a small acid-denatured protein that collapses as temperature increases. We trigger collapse in nanoseconds by using a laser-induced temperature jump (T jump) instrument. The subsequent relaxation dynamics are inferred from the time-dependent changes in the efficiency of fluorescence resonance energy transfer (FRET) between two terminal fluorophores.
Materials and Methods
NMR Experiments. NMR experiments were carried out in a Bruker 500-MHz instrument as described (23).
Equilibrium FRET Experiments. Equilibrium FRET experiments were performed at 25 μM concentration in citrate buffer at pH 3.0 in an Applied Photophysics (Surrey, U.K.) PiStar instrument. Efficiency of energy transfer between naphtyl-alanine (donor) and dansyl-lysine (acceptor) was determined from the fluorescence quantum yield of the donor by using the equation:
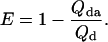 |
[1] |
The intrinsic quantum yield of the donor (Qd) was measured by exciting at 288 nm in the protein labeled at the N terminus with naphtyl-alanine and nonlabeled at the C terminus and using N-acetyl-trytophanamide (Q = 0.13 at pH 7.0 and 298 K) as reference. The quantum yield in the presence of acceptor (Qda) was measured in doubly labeled variant of the protein following the same procedure. Protein concentration was determined by absorbance. To minimize possible errors in concentration caused by the large pH sensitivity of dansyl's absorbance, we determined the concentration of both proteins at the maximum for naphthylalanine (280 nm) and at the isosbestic point for the changes in absorbance of dansyl as a function of pH (266 nm). The molar extinction coefficients of the two fluorophores at pH 3.0 at the two wavelengths (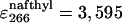 M-1· cm-1,
M-1· cm-1, 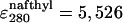 M-1· cm-1,
M-1· cm-1, 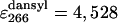 M-1· cm-1,
M-1· cm-1, 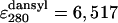 M-1· cm-1) were determined in our laboratory from the absorbance values of standard solutions of the free fluorophores. We used the average of the values obtained with the two procedures, which agreed within 5%. The discrepancy between the FRET efficiency for BBL at pH 3.0 obtained here and that reported previously (23) is caused by a previous slight overestimation of the molar extinction coefficient of dansyl at pH 3.0. This does not affect the previous data at pH 7.0. FRET efficiency as a function of temperature was fitted to a Gaussian chain model by adjusting the effective bond length at each temperature to reproduce the observed FRET. In these calculations we used an experimentally determined R0 of 1.7 nm for the naphthyl–dansyl pair at pH 3.0. The low R0 at this pH is caused by the shift of the dansyl absorption band to the blue, which results in smaller spectral overlap with naphthyl's fluorescence. The quantum yield of naphthyl is almost temperature independent, so R0 can be assumed constant with temperature. To calculate the end-to-end distance from FRET efficiency we have used an orientation factor (κ2) of 2/3, assuming conditions of isotropic dynamic averaging. These conditions are typically met when at least one of the two fluorophores is freely rotating at rates faster than the fluorescence lifetime. This is probably the case for both fluorophores at pH 3.0, as indicated by their invariant quantum yield upon incorporation to the protein. Furthermore, κ2 = 2/3 is a reasonable assumption even for fixed fluorophores if the acceptor has multiple absorption transition dipoles, and therefore mixed polarizations, such as the dansyl moiety. The spectrum and quantum yield of dansyl are very sensitive to the polarizability of its chemical environment (23). The fact that at pH 3.0 these properties remain unchanged at all temperatures for the dansyl group attached to the protein indicates that there are no interactions between the two fluorophores or between dansyl and other hydrophobic residues of the denatured protein.
M-1· cm-1) were determined in our laboratory from the absorbance values of standard solutions of the free fluorophores. We used the average of the values obtained with the two procedures, which agreed within 5%. The discrepancy between the FRET efficiency for BBL at pH 3.0 obtained here and that reported previously (23) is caused by a previous slight overestimation of the molar extinction coefficient of dansyl at pH 3.0. This does not affect the previous data at pH 7.0. FRET efficiency as a function of temperature was fitted to a Gaussian chain model by adjusting the effective bond length at each temperature to reproduce the observed FRET. In these calculations we used an experimentally determined R0 of 1.7 nm for the naphthyl–dansyl pair at pH 3.0. The low R0 at this pH is caused by the shift of the dansyl absorption band to the blue, which results in smaller spectral overlap with naphthyl's fluorescence. The quantum yield of naphthyl is almost temperature independent, so R0 can be assumed constant with temperature. To calculate the end-to-end distance from FRET efficiency we have used an orientation factor (κ2) of 2/3, assuming conditions of isotropic dynamic averaging. These conditions are typically met when at least one of the two fluorophores is freely rotating at rates faster than the fluorescence lifetime. This is probably the case for both fluorophores at pH 3.0, as indicated by their invariant quantum yield upon incorporation to the protein. Furthermore, κ2 = 2/3 is a reasonable assumption even for fixed fluorophores if the acceptor has multiple absorption transition dipoles, and therefore mixed polarizations, such as the dansyl moiety. The spectrum and quantum yield of dansyl are very sensitive to the polarizability of its chemical environment (23). The fact that at pH 3.0 these properties remain unchanged at all temperatures for the dansyl group attached to the protein indicates that there are no interactions between the two fluorophores or between dansyl and other hydrophobic residues of the denatured protein.
Laser-Induced T-Jump Experiments. The laser-induced T-jump instrument used here is based on the general principles as described (24). There are two major differences between our instrument and previous ones. The first one is the use of an optical parametric oscillator to shift the fundamental of the heating Q-switched Nd-YAG laser to a frequency that overlaps with the first vibrational overtone of water (i.e., 1,570 nm). The second difference is that our instrument uses another Q-switched Nd-YAG laser to excite the donor. The fundamental of this laser is frequency quadrupled to 266 nm, and then shifted to 288 nm by first Stokes stimulated Raman emission in a methane containing Raman cell. Excitation with light of 288 nm minimizes the photodamage of the fluorophores. Total fluorescence is collected at 90° and then imaged into a spectrograph and a charge-coupled device camera, providing complete fluorescence spectra with nanosecond resolution. The spectral resolution of this instrument is extremely useful to check for transient spectral changes in the fluorophores, which would indicate the presence of transient interactions occurring during the time scale of the kinetic experiment. No spectral changes were observed in any of the T-jump experiments of acid-denatured BBL. A complete layout of the instrument and a more detailed description of its features are available in Supporting Text and Figs. 5–7, which are published as supporting information on the PNAS web site, www.pnas.org.
Analysis with a 1D Diffusion Model. Kinetic analysis of the laser T-jump experiments was done by using the rate-matrix implementation of the Szabo–Schulten–Schulten 1D model (25). All calculations were performed by using a single diffusion coefficient of 1.1 × 10–7·cm2·s–1 at 1 centipoise. FRET efficiency as a function of time was calculated from the time-dependent end-to-end distance by using R0 = 1.7 nm.
Results and Discussion
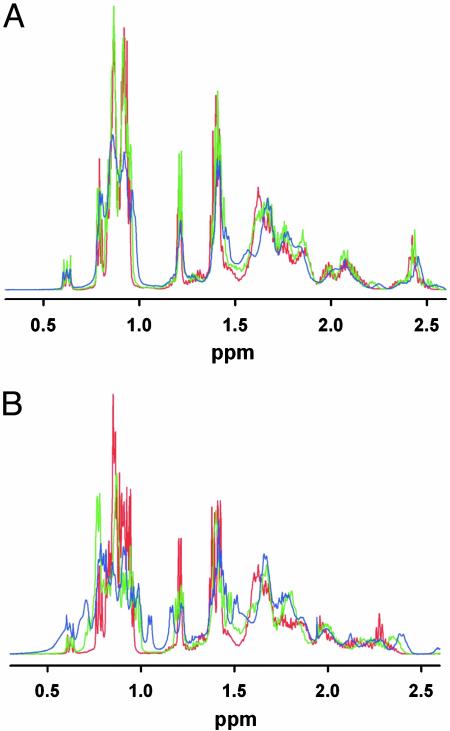
As a model of a protein denatured in the absence of chemical denaturants we use the acid-denatured form of the 40-residue protein BBL. BBL is a simple protein with no cofactors or disulfide bonds (26). In acidic conditions (i.e., pH 3.0) it is fully denatured at all temperatures, as judged by circular dichroism, fluorescence, and differential scanning calorimetry (23). Furthermore, 1D NMR experiments of BBL at pH 3.0 reveal that the chemical environment of the aliphatic protons comprising the core does not significantly change with temperature (Fig. 1A). In contrast, the same experiments at pH 5.3 [pH used for the NMR determination of its 3D structure (26)] show clear temperature-induced changes in the chemical shifts of the aliphatic protons, signaling the breakage of the core upon thermal unfolding (Fig. 1B).
Fig. 1.
1D proton NMR in BBL. (A) Detail of the aliphatic region of the NMR spectra of BBL at pH 3.0 and three temperatures: 273 K (blue), 303 K (green), and 333 K (red). (B) Detail of the aliphatic region of BBL at pH 5.3 and the same three temperatures: 273 K (blue), 303 K (green), and 333 K (red). The 3D structure of BBL was originally determined at pH 5.3 and 293 K (26). The absence of ring-current effects because of the lack of aromatic residues in the core of BBL results in a less spread out aliphatic region of the proton NMR spectrum. Nevertheless, at pH 5.3 significant changes in the chemical shifts of the aliphatic protons of BBL can be observed upon thermal unfolding.
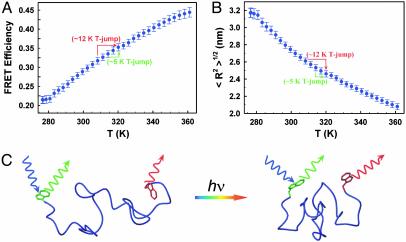
To probe the overall dimensions of the protein we have labeled BBL with naphthyl-alanine at its N terminus and dansyl-lysine at its C terminus, as an effective donor–acceptor pair for FRET experiments. Addition of these fluorescent labels does not change the conformational properties of BBL (23). FRET efficiency between the naphthyl–dansyl pair in acid-denatured BBL indicates that there is significant energy transfer at all temperatures explored (Fig. 2A). The characteristic distance (R0) for this pair is only 1.7 nm at pH 3.0 (see Materials and Methods), indicating that acid-denatured BBL is much more compact than expected for a fully unfolded polypeptide. Furthermore, the FRET efficiency increases steadily with temperature, revealing further contraction of the chain. This finding is not surprising because the hydrophobic effect becomes stronger at higher temperatures. The transfer of hydrophobic residues from a nonpolar environment to water has a maximum free energy at ≈385 K (27) and an inversion of the enthalpy from negative to positive values, signaling a minimum in the partition coefficient, at ≈353 K (28). If the hydrophobic effect overrides the loss in conformational entropy, the denatured protein collapses at higher temperature to diminish the average solvent exposure of its hydrophobic residues.
Fig. 2.
Equilibrium FRET experiments in acid-denatured BBL. (A) FRET efficiency between the N-terminal nafthyl-alanine and the C-terminal dansyl-lysine of BBL in its acid-denatured form (pH 3.0) as a function of temperature. The average and standard deviation of three experiments are shown. The labels illustrate the change in FRET efficiency expected for exemplary T jumps from 308 to 320 K (red) and from 315 to 320 K (green). (B) Mean root square of the end-to-end distance in acid-denatured BBL as a function of temperature. The curve was obtained by fitting the effective bond length of a Gaussian chain model to reproduce the FRET efficiency data of A. The labels illustrate the expected change in end-to-end distance for exemplary T jumps from 308 to 320 K (red) and from 315 to 320 K (green). (C) Schematic representation of an experiment starting from a moderately collapsed state of acid-denatured BBL at low temperature to a more collapsed state at a higher temperature. The degree of collapse is inferred from the end-to-end distance determined from the FRET efficiency (A). The denatured collapsed structures of BBL were calculated with the program x-plor by adding loose distance constraints to represent the experimentally determined degree of collapse of BBL at the lowest and highest temperatures studied in this work.
For a more quantitative analysis of the equilibrium FRET data we have used a simple Gaussian chain model. Fitting the experimental data to a Gaussian distribution of end-to-end distances renders a <R2>1/2 that ranges from ≈3.2 nm at 276 K to ≈2.0 nm at 363 K (Fig. 2B). To translate these values into a size-independent parameter we use the effective bond length, defined as b = (<R2>/N)1/2. N is 40 residues for BBL, resulting in effective bond lengths between ≈0.5 and ≈0.32 nm, compared with a value of ≈1 nm expected for a Gaussian chain in theta conditions (29). As temperature increases the effective bond length decreases, resulting in narrower distributions of end-to-end distances that are shifted to lower values. These simplistic calculations suggest that at high temperature the denatured protein reaches contraction levels close to the native structure [Rg = (<R2>/6)1/2 < 1.0 nm versus Rg ≈ 0.9 nm for native BBL]. However, even in such highly collapsed conditions the Gaussian model predicts an almost negligible probability for end-to-end contacts.
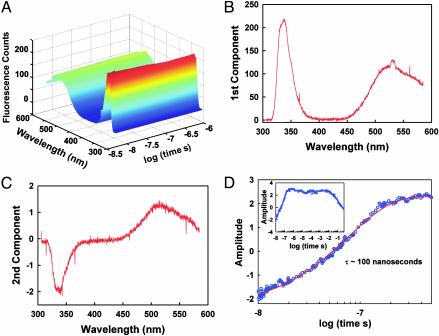
The equilibrium FRET experiments show that it is possible to trigger an increased contraction of acid-denatured BBL with a rapid jump to higher temperatures. The experiment is shown schematically in Fig. 2C. To perform these studies we have used a laser T-jump instrument with fluorescence spectral resolution (see Materials and Methods and Supporting Text). Fig. 3 shows the results obtained after a T jump from 277 to 290 K. The matrix of time-resolved spectra recorded after an ≈8-ns T jump (Fig. 3A) is analyzed by using singular value decomposition (SVD), which produces two non-noise components. The first one is the average fluorescence spectrum. It displays the characteristic spectrum of the donor (maximum at ≈345 nm) and acceptor (maximum at ≈540 nm) (Fig. 3B), and its amplitude is constant. The second component is a spectrum with a negative peak for the donor and a positive peak for the acceptor, as expected for a change in FRET efficiency. Its amplitude shows a very fast exponential relaxation with a relaxation time of ≈100 ns (Fig. 3D) and a signal that accounts for ≈4% of the total fluorescence (see legend to Fig. 3). This change in fluorescence corresponds to an ≈3% increase in FRET efficiency, in agreement with the total FRET change measured in equilibrium (Fig. 2 A). No other changes are observed at longer times, until the sample starts to cool down by diffusion at ≈10 ms (Fig. 3D Inset). There are no spectral shifts in either donor or acceptor, indicating that the relaxation is not produced by a transient interaction between the N- and C-terminal aromatic fluorophores (see Materials and Methods). Control experiments using acid-denatured BBL labeled with only the donor probe showed an invariable donor fluorescence spectrum at all accessible time scales. Therefore, the ≈100-ns relaxation corresponds to the reconfiguration dynamics of acid-denatured BBL, leading to a more collapsed state at higher temperature.
Fig. 3.
Laser T-jump experiments in acid-denatured BBL. (A) Data matrix showing the time-dependent fluorescence spectra of acid-denatured BBL after a T jump from 277 to 290 K. Three hundred spectra obtained at times ranging from 10 ns to 1 μs after the T jump are displayed after noise reduction by SVD. (B) Fluorescence spectrum corresponding to the first component of the SVD procedure shown in absolute fluorescence counts. The amplitude of this component was invariable with time. (C) The second component of the SVD procedure, showing an anticorrelation between the relative intensity of donor and acceptor, as expected for a change in FRET efficiency. (D) Changes in amplitude of the second SVD component as a function of time. Shown are the changes in amplitude at times <500 ns and a fit of the data to a single exponential time course with a relaxation time of ≈100 ns. (Inset) The amplitude of the second component in the whole range of times accessible to this instrument. The decrease in FRET efficiency starting at ≈10 ms is caused by cooling down of the T jump by diffusion of nonheated sample into the illuminated volume. The total changes in fluorescence intensity as a function of time are simply obtained by multiplying the spectrum in C by the amplitudes in D (i.e., ≈4% of the total fluorescence signal for this experiment).
These results show that the hydrophobic collapse of acid-denatured BBL is very fast. Laser-induced T-jump experiments performed at higher pH values, i.e., 3.5–7.0, reveal that the collapse rate in BBL is not sensitive to changes in pH within this range (data not shown), indicating that our observations are relevant to physiological conditions. Interestingly, the time scale obtained here for hydrophobic collapse is in striking agreement with theoretical calculations of the time for the early phase of homopolymer collapse (6) and predictions of the collapse time in polypeptides (30). Nanosecond time scales for nonspecific collapse have also been observed in full-atom molecular dynamics simulations of folding (31, 32). It follows that the much slower time scales found in folding burst-phase experiments must be limited by crossing free energy barriers. For proteins with no heme groups the barrier might result from the formation of partially structured folding intermediates (16, 17). In cytochrome c, the combination of recent time-resolved small angle x-ray scattering measurements (19) with laser T-jump experiments in nonfolding fragments (33) suggests that the burst-phase barrier is produced by the formation breaking of a structured cluster around the heme moiety of denatured cytochrome c.
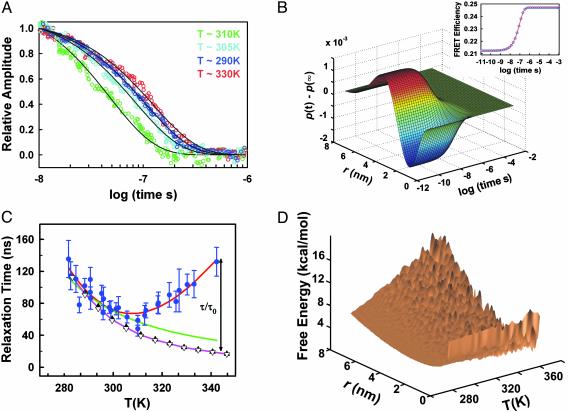
T jumps of ≈14 K starting at temperatures in the range of 270 to 300 K show a weak acceleration of the rate of collapse with temperature (Fig. 4A). In this temperature range, the observed increase of the collapse rate tracks precisely the changes in solvent viscosity with temperature (Fig. 4C Left), indicating the lack of activation energy. This finding suggests that hydrophobic collapse is a diffusive process. The observed relaxation for all experiments, however, is well described by a simple exponential time course (Fig. 4A). Furthermore, the same relaxation times are observed in T jumps of ≈14 K and ≈5 K to the same final temperature, indicating that there is no “memory” of the initial conditions (data not shown). To better understand these results we have analyzed our T-jump experiments assuming that the dynamics of collapse can be described as 1D diffusion on the mean-force potential obtained from the equilibrium end-to-end distance distribution (34). Fig. 4B shows the results for a simulation of the 277–290 K T-jump experiment of Fig. 3. The model produces exponential time courses for the changes in FRET efficiency after a T jump (Fig. 4B Inset). Moreover, it displays no memory effects and reproduces the temperature dependence of the relaxation time in the range of 270–300 K (Fig. 4C) by using a diffusion coefficient (Fig. 4D) of 1.1 × 10–7 cm2·s–1 at 1 centipoise.
Fig. 4.
(A) Normalized amplitude of the second component of the SVD procedure for T jumps of ≈12 K to different final temperatures. The data are shown as color-coded open circles, whereas the fits to single exponential time courses are shown as continuous black lines. (B) Simulation of the relaxation kinetics for the redistribution of end-to-end distances in acid-denatured BBL after a T jump from 277 to 290 K. To define the initial and final conditions for the T-jump experiment we used end-to-end distance distributions calculated with the Gaussian chain model and effective bond lengths in accordance to the data in Fig. 2. Shown is the redistribution of end-to-end distances to the new equilibrium distribution after the T jump [p(r,t) – p(r,∞)]. (Inset) The changes in FRET efficiency as a function of time calculated from the time-dependent end-to-end distance distribution (blue open circles) and an exponential fit to the FRET time course (red line). (C) Temperature dependence of the relaxation time for hydrophobic collapse. Blue circles indicate relaxation times obtained from exponential fits to the amplitude of the second SVD component of 5–14 K T-jump experiments. The error bars correspond to the fitting error. The red line shows a polynomial fit to the data to guide the eye. The green line indicates temperature dependence of the collapse relaxation time (referenced to the experimental value at ≈295 K), as expected from only the change in water viscosity. The magenta line indicates temperature dependence of the collapse relaxation time predicted by the 1D diffusion model. The model predicts slightly stronger temperature dependence because the end-to-end distribution becomes progressively narrower at higher temperature. The relaxation time obtained from the model is essentially independent of the size of the T jump. Black triangles indicate theoretical relaxation times calculated for T jumps of ≈14 K. Open inverted triangles indicate theoretical relaxation times calculated for T jumps of ≈5 K. The black arrow illustrates the ratio between the experimental and theoretical relaxation times that is used to calculate the roughness of the energy landscape. (D) Representation of the energy landscape for collapse of acid-denatured BBL. The surface is calculated as a potential of mean force from the Gaussian distribution of end-to-end distances at different temperatures. The roughness of the surface was obtained by randomly adding to each point in the surface an energy term according to a Gaussian distribution with variance ΔE2 = (kBT)2 ln(τ/τ0), where τ and τ0 are the experimental and theoretical relaxation times for collapse, respectively. A simple rescaling of the temperature axis using the data in Fig. 2B indicates that the estimated roughness corresponds to effective bond lengths ranging from ≈0.5 nm at 283 K to ≈0.36 nm at 333 K.
This diffusion coefficient is ≈15 times slower than one obtained previously for loop formation in peptides (25), probably because the dynamics in the collapsed protein involve transient hydrophobic interactions. It has been argued that the “speed limit” to protein folding is determined by how fast a protein can collapse, which should be no faster than the time it takes to form a short loop (22). Therefore, the collapse diffusion coefficient provides a new upper bound for the folding speed limit. For a 40-residue protein the speed limit is ≈60 ns at 305 K. Assuming a Gaussian chain model, the reconfiguration time for larger proteins can be estimated from τ = <R2>/3D. This approximation results in a speed limit of ≈150 ns for a protein of 100 residues at 305 K (using 0.42 nm as effective bond length for this temperature, as we see in BBL). The actual speed limit could be significantly slower because of friction between different folding segments, producing a rougher energy landscape. Based on kinetic experiments in a very fast-folding mutant of the lambda repressor a speed limit of ≈2 μs has been recently proposed for an ≈80-residue-long protein (21). Combined with our results, these experiments suggest that the folding energy landscape of lambda repressor is, indeed, quite rough. To investigate friction effects in more detail is critical to measure the dynamics of global downhill folding (23, 35).
At ≈308 K the time for collapse reaches a minimum, increasing steadily at higher temperatures (Fig. 4 A and C). A “rollover” of the rate with temperature is typically observed for the folding reaction of two-state proteins and is assigned to a thermodynamic difference in the heat capacities of the denatured and transition states (ΔCpTS) (36). Non-Arrhenius kinetics can also signal the emergence of a dynamic glass transition in a rough energy landscape (35). A simple transition state analysis indicates that a ΔCpTS of –780 Jmol–1·K–1 [i.e., 60% of the ΔCp for global unfolding of BBL at neutral pH (23)] would be required to reproduce the observed “rollover.” Because the collapse reaction of denatured BBL is not two-state and does not involve any measurable changes in heat capacity (23), we conclude that the rollover must have a dynamic rather than thermodynamic origin. A protein collapsing nonspecifically is predicted to undergo a dynamic glass transition at low temperatures, when the thermal energy is low and the local barriers become noticeable (a recent discussion about this topic can be found in ref. 37). The phenomenon that we observe is analogous, but it appears at high temperature because is caused by the hydrophobic effect. At higher temperature the protein is more collapsed, and the transient nonspecific hydrophobic interactions become more frequent and stronger. These interactions must be broken before the protein can reconfigure, resulting in a progressively rougher energy landscape. In acid-denatured BBL the switch from diffusive to nondiffusive dynamics occurs at an effective bond length of ≈0.4 nm. It remains to be seen whether this is a general property of polypeptide chains or depends on their sequence composition and length. The roughness of an energy landscape, defined as the variance in energy, can be obtained directly from equation ΔE2 = (kBT)2 ln(τ/τ0) (35, 38). Fig. 4D shows a representation of the roughness of the landscape for collapse of BBL calculated from the ratio between the relaxation times determined experimentally (τ) and predicted by the diffusion model (τ0). Dynamic glass transitions are commonly observed in computer simulations of folding in simplified protein models (9, 11). However, no low-temperature dynamic glass transition has been reported in protein folding experiments. In fact, previous efforts to find a glass transition have been unsuccessful (40).
What are the implications for protein folding? One issue that has aroused great interest is whether folding is initiated by formation of secondary structure or hydrophobic collapse (1). Addressing this question requires knowing the intrinsic time scales and driving forces for all of these processes. In absence of chemical denaturants there is a strong force to collapse proteins. Equilibrium FRET experiments in BBL (Fig. 2) and in two other small proteins (unpublished results) indicate that nonchemically denatured proteins are collapsed. Quite significant degrees of collapse have been measured by small angle x-ray scattering in larger nonchemically denatured proteins (41) and have been estimated by extrapolation to water of single-molecule FRET experiments in chemically denatured cold-shock protein B (42). The time for collapse measured in this work is much faster than formation of stable β-hairpins (3) and slightly faster than formation of the fastest polyalanine α-helices (2, 14). In initiating folding, only very stable α-helices could compete with collapse. This would result in a stiffer chain and the relatively slower formation of a partially structured state, as seen in engrailed homeodomain (20). However, the driving force toward α-helix formation is weak in natural proteins, as indicated by the marginal stability of their isolated α-helices (43). Therefore, for many proteins, the first step in folding under physiological conditions will be the collapse of the chain leading to a compact unstructured globule, from which native secondary structure and topology will be formed. The subsequent conformational search in the collapsed globule will be primarily guided by local motions, because long-range topological rearrangements involve visiting very improbable expanded conformations. Local dynamics should predominate even more clearly at later stages of folding, where the protein is searching for the native structure in an increasingly compact ensemble of conformations. Interestingly, this scenario favors a view in which folding starts by local nucleation events from which native structure propagates, perhaps explaining the remarkable success of simple Ising-like models in predicting many of the features of protein folding (44) and of contact order in predicting folding rates (39).
Supplementary Material
Acknowledgments
We thank Eva de Alba for encouragement, useful comments on the manuscript, and help with producing Fig. 2C. We are also indebted to Devarajan Thirumalai, Steven Hagen, Jose Manuel Sanchez-Ruiz, and George Lorimer for discussions on the topic and comments on the manuscript. V.M. is a recipient of a Dreyfus New Faculty Award, a Packard Fellowship for Science and Engineering, and a Searle Scholarship.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: FRET, fluorescence resonance energy transfer; T jump, temperature jump; SVD, singular value decomposition.
References
- 1.Baldwin, R. L. (2002) Science 295, 1657–1658. [DOI] [PubMed] [Google Scholar]
- 2.Williams, S., Causgrove, T. P., Gilmanshin, R., Fang, K. S., Callender, R. H., Woodruff, W. H. & Dyer, R. B. (1996) Biochemistry 35, 691–697. [DOI] [PubMed] [Google Scholar]
- 3.Muñoz, V., Thompson, P. A., Hofrichter, J. & Eaton, W. A. (1997) Nature 390, 196–199. [DOI] [PubMed] [Google Scholar]
- 4.de Gennes, P. G. (1985) J. Phys. Lett. 46, L639–L642. [Google Scholar]
- 5.Grosberg, A. Y., Nechaev, S. K. & Shakhnovich, E. I. (1988) J. Phys. 49, 2095–2100. [Google Scholar]
- 6.Pitard, E. & Orland, H. (1998) Europhys. Lett. 41, 467–472. [Google Scholar]
- 7.Kutnetsov, Y. A., Timoschenko, E. G. & Dawson, K. A. (1995) J. Chem. Phys. 103, 3338–3347. [Google Scholar]
- 8.Bryngelson, J. D. & Wolynes, P. G. (1987) Proc. Natl. Acad. Sci. USA 84, 7524–7528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Camacho, C. J. & Thirumalai, D. (1993) Proc. Natl. Acad. Sci. USA 90, 6369–6372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Gutin, A. M., Abkevich, V. I. & Shakhnovich, E. I. (1995) Biochemistry 34, 3066–3076. [DOI] [PubMed] [Google Scholar]
- 11.Onuchic, J., Luthey-Schulten, Z. & Wolynes, P. G. (1997) Annu. Rev. Phys. Chem. 48, 545–600. [DOI] [PubMed] [Google Scholar]
- 12.Dill, K. A. & Chan, H. S. (1997) Nat. Struct. Biol. 4, 10–19. [DOI] [PubMed] [Google Scholar]
- 13.Dobson, C. M., Sali, A. & Karplus, M. (1998) Angew. Chem. Int. Ed. 37, 868–893. [DOI] [PubMed] [Google Scholar]
- 14.Eaton, W. A., Muñoz, V., Hagen, S. J., Jas, G. S., Lapidus, L. J., Henry, E. R. & Hofrichter, J. (2000) Annu. Rev. Biophys. Biomol. Struct. 29, 327–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ballew, R. M., Sabelko, J. & Gruebele, M. (1996) Proc. Natl. Acad. Sci. USA 93, 5759–5764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sabelko, J., Ervin, J. & Gruebele, M. (1999) Proc. Natl. Acad. Sci. USA 96, 6031–6036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Roder, H. & Shastry, M. C. (1999) Curr. Opin. Struct. Biol. 9, 620–626. [DOI] [PubMed] [Google Scholar]
- 18.Hagen, S. J. & Eaton, W. A. (2000) J. Mol. Biol. 301, 1019–1027. [DOI] [PubMed] [Google Scholar]
- 19.Akiyama, S., Takahashi, S., Kimura, T., Ishimori, K., Morishima, I., Nishikawa, Y. & Fujisawa, T. (2002) Proc. Natl. Acad. Sci. USA 99, 1329–1334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mayor, U., Guydosh, N. R., Johnson, C. M., Grossmann, J. G., Sato, S., Jas, G. S., Freund, S. M., Alonso, D. O., Daggett, V. & Fersht, A. R. (2003) Nature 421, 863–867. [DOI] [PubMed] [Google Scholar]
- 21.Yang, W. Y. & Gruebele, M. (2003) Nature 423, 193–197. [DOI] [PubMed] [Google Scholar]
- 22.Hagen, S. J., Hofrichter, J., Szabo, A. & Eaton, W. A. (1996) Proc. Natl. Acad. Sci. USA 93, 11615–11617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Garcia-Mira, M. M., Sadqi, M., Fisher, N., Sanchez-Ruiz, J. M. & Muñoz, V. (2002) Science 298, 2191–2195. [DOI] [PubMed] [Google Scholar]
- 24.Callender, R. & Dyer, R. B. (2002) Curr. Opin. Struct. Biol. 12, 628–633. [DOI] [PubMed] [Google Scholar]
- 25.Lapidus, L. J., Steinbach, P. J., Eaton, W. A., Szabo, A. & Hofrichter, J. (2002) J. Phys. Chem. B 106, 11628–11640. [Google Scholar]
- 26.Robien, M. A., Clore, M., Omichinski, J. G., Perham, R. N., Appella, E., Sakaguchi, K. & Gronenborn, A. M. (1992) Biochemistry 31, 3463–3471. [DOI] [PubMed] [Google Scholar]
- 27.Murphy, K. P., Privalov, P. L. & Gill, S. J. (1990) Science 247, 559–561. [DOI] [PubMed] [Google Scholar]
- 28.Guzman-Casado, M., Parody-Morreale, A., Robic, S., Marqusee, S. & Sanchez-Ruiz, J. M. (2003) J. Mol. Biol. 329, 731–743. [DOI] [PubMed] [Google Scholar]
- 29.Flory, P. J. (1969) Statistical Mechanics of Chain Molecules (Interscience, New York).
- 30.Thirumalai, D. (1995) J. Phys. I France 5, 1457–1467. [Google Scholar]
- 31.Duan, Y. & Kollman, P. A. (1998) Science 282, 740–744. [DOI] [PubMed] [Google Scholar]
- 32.Zagrovic, B., Snow, C. D., Shirts, M. R. & Pande, V. S. (2002) J. Mol. Biol. 323, 927–937. [DOI] [PubMed] [Google Scholar]
- 33.Qiu, L., Zachariah, C. & Hagen, S. J. (2003) Phys. Rev. Lett. 90, 168103. [DOI] [PubMed] [Google Scholar]
- 34.Szabo, A., Schulten, K. & Schulten, Z. J. (1980) J. Chem. Phys. 72, 4350–4357. [Google Scholar]
- 35.Bryngelson, J. D., Onuchic, J. N., Socci, N. D. & Wolynes, P. G. (1995) Proteins Struct. Funct. Genet. 21, 167–195. [DOI] [PubMed] [Google Scholar]
- 36.Scalley, M. L. & Baker, D. (1997) Proc. Natl. Acad. Sci. USA 94, 10636–10640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chahine, J., Nymeyer, H., Leite, V. B., Socci, N. D. & Onuchic, J. N. (2002) Phys. Rev. Lett. 88, 168101. [DOI] [PubMed] [Google Scholar]
- 38.Zwanzig, R. (1988) Proc. Natl. Acad. Sci. USA 85, 2029–2030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Plaxco, K. W., Simons, K. T. & Baker, D. (1998) J. Mol. Biol. 277, 985–994. [DOI] [PubMed] [Google Scholar]
- 40.Gillespie, B. & Plaxco, K. W. (2000) Proc. Natl. Acad. Sci. USA 97, 12014–12019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Millet, I. S., Doniach, S. & Plaxco, K. W. (2002) Adv. Protein Chem. 62, 241–262. [DOI] [PubMed] [Google Scholar]
- 42.Schuler, B., Lipman, E. A. & Eaton, W. A. (2002) Nature 419, 743–747. [DOI] [PubMed] [Google Scholar]
- 43.Muñoz, V. & Serrano, L. (1994) Nat. Struct. Biol. 1, 399–409. [DOI] [PubMed] [Google Scholar]
- 44.Muñoz, V. (2001) Curr. Opin. Struct. Biol. 11, 212–216. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.