Abstract
The post-genomic era is marked by huge amounts of data generated by large-scale functional genomic and proteomic experiments. A major challenge is to integrate the various types of genome-scale information in order to reveal the intra- and inter- relationships between genes and proteins that constitute a living cell. Here we present a novel application of classical graph algorithms to integrate the cellular networks of protein–protein interactions and transcription regulation. We demonstrate how integration of these two networks enables the discovery of simple as well as complex regulatory circuits that involve both protein–protein and protein–DNA interactions. These circuits may serve for positive or negative feedback mechanisms. By applying our approach to data from the yeast Saccharomyces cerevisiae, we were able to identify known simple and complex regulatory circuits and to discover many putative circuits, whose biological relevance has been assessed using various types of experimental data. The newly identified relations provide new insight into the processes that take place in the cell, insight that could not be gained by analyzing each type of data independently. The computational scheme that we propose may be used to integrate additional functional genomic and proteomic data and to reveal other types of relations, in yeast as well as in higher organisms.
INTRODUCTION
The sequencing of whole genomes has paved the way to large-scale experiments that provide vast amounts of valuable data. These include profiling of mRNA and protein expression at a whole-genome scale, locating the binding sites of given transcription factors along the genome, and proteome-wide identification of interacting proteins. While each data set by itself calls for the application of appropriate computational tools for data processing, even more so does the integration of different types of information. Yet, despite the wide recognition of the importance of integrative analyses, only a few such studies have been reported, most of which regard the integration of mRNA profiling data in the yeast Saccharomyces cerevisiae with other types of data (1–10). These integrative analyses provide new molecular insights that could not be revealed using each type of information alone. In the present report, we integrate genome-wide data of protein–protein interaction with data of regulatory proteins and their target genes. Integration of these two types of data is especially important for the investigation of regulatory pathways, as it is widely accepted that many of the pathways in the cell are regulated both at the transcriptional and at the proteomic levels. One common type of molecular pathway that involves both protein–protein and protein–DNA interactions is the regulatory circuit, and the integration scheme presented here is aimed at its discovery.
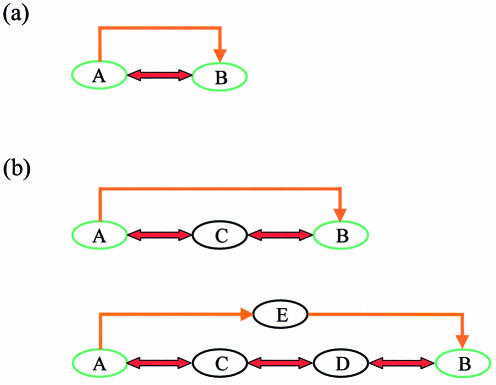
In general, we define a multi-level regulatory circuit between two proteins when they are related both by protein–protein interaction and as regulator–target (Fig. 1a). Feedback loops where a regulatory protein activates the transcription of a target gene, whose product, in turn, inhibits or activates the regulatory protein, provide an example of such multi-level regulatory circuits. The relation between the two proteins defining a circuit is not necessarily direct: proteins can either be related by intermediate interactions or by intermediate regulators (Fig. 1b). Such circuits can be used for complex regulatory tasks, e.g. as signal transducers. For example, in Figure 1b, protein B may transmit a signal to protein C, which, in turn, transmits a signal to protein A.
Figure 1.
Regulatory circuits defined by proteins A and B. A red bi-directional arrow marks protein–protein interaction, and an orange arrow marks transcription regulation. (a) A direct regulatory circuit consists of two proteins, where protein A regulates gene b, and the product of gene b, protein B, interacts with A. Such a circuit can be used for feedback regulation or for switching on a new pathway. In the former, the interaction between A and B prevents A from activating the transcription of the gene encoding protein B, and by this maintains the required level of B. In the latter, the complex AB can be used to activate a new set of genes. In both cases, the circuit serves as the switch that controls the activity of A. (b) Higher order regulatory circuits can be identified between proteins that are indirectly related. These circuits contain intermediate proteins between A and B that either form a series of protein–protein interactions, or a series of regulator–target interactions. In the upper circuit, proteins A and B are related via protein C that interacts with both A and B. In the lower circuit, proteins A and B are related via proteins C and D, and via transcription factor E that is regulated by A and in turn regulates the gene encoding protein B.
Here we present a rigorous integration of large-scale data of protein–DNA and protein–protein interactions. By using a novel approach based on classical graph algorithms (11), these two types of data are efficiently integrated, enabling the discovery of simple and higher order multi-level regulatory circuits. We applied our approach to data of protein–protein and protein–DNA interactions in the yeast S.cerevisiae and discovered all possible regulatory circuits based on these data. The biologically relevant circuits were determined by using the assignments of the circuit proteins to cellular compartments and cellular processes based on experimental data, and by their consistency with results of deletion experiments (12). We illustrate the validity of this computational approach by the already known simple and higher order circuits that it identifies, and report many putative regulatory circuits that can be tested experimentally. The newly identified relations provide new insight into the processes that take place in the cell, insight that could not be gained by analyzing each type of data independently.
MATERIALS AND METHODS
Data sources
Data of transcription factors and their target genes in yeast were extracted from the SCPD database (http://cgsigma.cshl.org/jian) (13), from the YPD database (http://www.proteome.com) (14), and from recent publications on genome-wide experiments that locate binding sites of given transcription factors (15–18). For data extraction from the latter, we used the same experimental thresholds used in the original papers.
Protein–protein interaction data in yeast were extracted from the DIP database (http://dip.doe-mbi.ucla.edu) (19), from the BIND database (http://binddb.org) (20), and from the MIPS database (http://mips.gsf.de/proj/yeast/tables/interaction/) (21). In total, our data set consisted of 5976 protein pairs connected as regulator–target and 8184 protein pairs connected by protein–protein interactions. For interpretation of the results, we used extensively the information in the YPD database and references therein.
Detection of regulatory circuits
The regulator–target relationship is viewed as a transcription regulation graph GR, where there is a directed edge from node i to node j if protein i regulates gene j (we refer to a gene and the protein it encodes interchangeably). Similarly, protein–protein interaction data are viewed as a graph GP, where a bi-directed edge connects nodes i and j if proteins i and j interact.
To detect regulatory circuits we look for protein pairs such that the two pair-mates are connected to each other by a directed path in GR and by a path in GP: (i) for both graphs GR and GP, compute the graph distance between any two proteins that are at most four edges distant from each other; (ii) postulate a kth order circuit for those pairs of proteins for which the larger of the two distances equals k; (iii) define the corresponding circuit as the union of the shortest paths in both graphs, revealed by the BFS algorithm (11). We chose at this stage to concentrate on the shortest paths connecting a protein pair for the sake of simplicity. Apart from its computational aspect, choosing the shortest path has a biological rational, as shorter paths of interactions should allow a more efficient response to external or internal stimuli. If GP and/or GR contain several shortest paths between the pair of proteins that define the circuit, all combinations of these paths are initially considered as potential circuits. In later phases of the analysis, additional assessments are performed to select the most promising circuit(s).
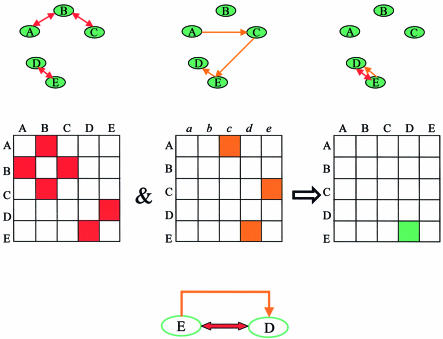
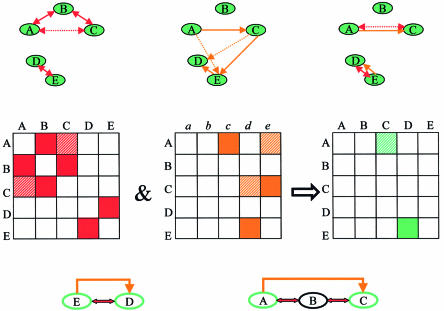
The graphs are represented by their adjacency matrices, and protein pairs that define circuits are detected via simple matrix manipulations (Figs 2 and 3). In brief, the protein–protein interaction data are represented by a symmetric matrix of 6315 × 6315 (the number of yeast protein-encoding genes), with occupied entries for pairs of proteins that are known to interact and empty entries for pairs of proteins for which such data are unavailable. The regulator–target data are represented by a non-symmetric matrix of 6315 × 6315, with occupied entries for proteins and genes that are known to be related as regulator and target, respectively, and empty entries when such a relation is not known. By intersecting the two matrices co-occupied entries can be identified. Each such entry defines a pair of proteins that are related to each other both by protein interaction and as regulator–target, defining a direct regulatory circuit (Fig. 2). Higher order relations between proteins may be detected by multiplication of each matrix by itself: proteins that are either related by intermediate interactions or by intermediate regulators. Intersection of the higher order matrices enables the detection of pairs of proteins that define higher order regulatory circuits (Fig. 3). The circuits themselves are revealed using a graph search method.
Figure 2.
The computational approach for integration of protein–protein and protein–DNA interaction data. (Top) From left to right, the protein–protein interaction graph, the regulator–target relationship graph and the intersection graph. The intersection graph contains a regulatory circuit between E and D. (Middle) The same information using matrix representation is depicted. The protein–protein interaction data are represented by the left-most symmetric adjacency matrix, where red-filled entries mark pairs of interacting proteins [(A,B), (B,C) and (D,E)]. The regulator–target interaction data are represented in the middle adjacency matrix, where orange-filled entries mark regulator–target relationships [(A,c), (C,e) and (E,d)]. Co-occupied entries in the two matrices correspond to protein pairs that are related to each other both by protein–protein interaction and regulator–target relationship, and are revealed by intersecting the two matrices. These co-occupied entries determine the circuits. The resulting intersection matrix is shown on the right, where the green-filled entry marks the pair (E,D) that defines a regulatory circuit (bottom).
Figure 3.
Detection of regulatory circuits of order 2. (Top) From left to right, the protein–protein interaction graph, the regulator–target relationship graph and the intersection graph. In each graph a directed solid edge connects two nodes if the corresponding proteins interact. A directed dotted edge from one node to another exists if a path composed of two solid edges leads from the first node to the other. For example, in the protein–protein interaction graph a dotted edge connects A and C since they are connected by a path A–B–C of length 2. (We ignore paths of the form A–B–A that use the same edge twice in the protein–protein interaction graph.) The intersection graph contains two regulatory circuits, between E and D, and between A and C. (Middle) The graphs as adjacency matrices. As in Figure 2, filled entries mark protein pairs that are connected by a solid edge in the original graphs. By multiplication of each matrix by itself, higher order relations between proteins may be detected. These relations are noted as striped entries in the red and orange matrices (and represent the dotted edges in the corresponding graphs). Entries that are co-occupied in the red and orange matrices are colored green in the intersection matrix: the entries are filled if both corresponding entries are filled, and striped if at least one entry is striped. (Bottom) The resulting regulatory circuits. The regulatory circuits between E and D and between A and C are of orders 1 and 2, respectively.
Statistical significance of circuit abundance
We assess whether the number of protein pairs that define circuits is significantly higher in the integrated network in comparison with their number in integrated randomized networks. To keep the randomized networks as close as possible to the real networks in terms of their network properties, we preserve the topology of each network and permute over the network nodes, generating 1000 random isomorphic networks. Our analysis is conducted in three ways: (i) the protein–protein network is kept as is and the protein–DNA network is randomized; (ii) the protein–DNA network is kept as is and the protein–protein network is randomized; (iii) both networks are randomized. The statistical significance per order is obtained by counting in how many of the integrated random networks the number of protein pairs that define circuits is at least as high as in the real integrated network.
Biological assessment of circuits
Analysis based on proteins’ assignments to cellular processes. Proteins can be annotated based on the cellular processes they participate in (e.g. the transcription factor Ime1 is assigned to the cellular processes meiosis and recombination). Assignments of proteins to cellular processes are provided by the YPD database (14), based on experimental information. For our analysis, we used the documentation in the YPD May 2002 version (14), according to which each protein may be assigned to one or a few out of 43 possible cellular processes. A protein assignment is zero if its biological process is undefined. A circuit score kp is the maximal number (k) of circuit proteins that are assigned to a common cellular process, where p denotes this specific process. We quantify the significance of a circuit’s score by comparing it with the scores of 10 000 random circuits (except for order 1, where we use all available data). Each random circuit is composed of a series of proteins, where every two adjacent proteins interact by our data, and the order of these connections is as in the tested circuit. This ensures that the random circuits pertain to the defined circuitry of the tested one. The significance (P-value) of the original circuit with score kp is computed as the fraction of random circuits where at least k members are assigned to cellular process p. In case k is associated with more than one specific process, the significance is computed per process, and the highest fraction is considered as the significance value. A circuit is considered significant if its P-value is at most 0.05. When more than one shortest path exists between a pair of proteins that define a circuit, all possible circuits are assessed, and the one(s) with the lowest probability is selected (given that the probability is at most 0.05). The circuits that were selected through the cellular process assessment are now subjected to two additional assessments.
Analysis based on the annotation of protein localization. We consider an interaction between two proteins as feasible if the two interacting proteins are localized to the same cellular compartment, or if they are documented as co-participating in a complex. A circuit is considered as biologically feasible if all its interactions are feasible. In this step of the analysis we select among the circuits that passed the first assessment those that are biologically feasible.
To evaluate whether the number of biologically feasible circuits deviates significantly from that expected at random, we perform a binomial test. The expected probability for circuits composed of ℓ physical interactions, ℓ > 1, is obtained by generating 10 000 random circuits, each composed of a series of ℓ + 1 proteins, where every two adjacent proteins physically interact by our data, and computing the fraction of feasible circuits. For ℓ = 1 we use all available data. The protein localization data were taken from Kumar et al. (22) and from YPD (14), where each protein may be localized to one or a few out of 29 possible cellular compartments. In addition, we used protein complex data from MIPS (21) and YPD, to record whether two proteins participate in the same complex.
Note that the two circuit properties, the fraction of proteins that participate in a common cellular process and the fraction of feasible physical interactions, are not completely independent. Nonetheless, correlation analysis indicates that only 10% of their variance is shared (r2).
Analysis based on results of knockout experiments. The data for this assessment were extracted from the Rosetta Compendium of knockout results (12), a data set that contains gene expression profiles of S.cerevisiae genes corresponding to individual deletions of 276 genes. For a circuit that is defined by a regulatory protein A and a target gene B (Fig. 1), we expect that the knockout of B will affect the activity of A, if indeed the circuit functions as a feedback loop. This effect can be experimentally detected by following the changes in the expression levels of other gene targets of A. We define a change in expression only when it is at least 2-fold change. We limit our analysis to genes B that do not themselves encode for transcription factors, to avoid misinterpretation of the knockout results. In cases where we find that genes affected by the knockout of B correspond with gene targets of A, we evaluate the significance of this relationship by a χ2 test.
RESULTS
The computational approach used to integrate the protein–protein interaction and regulator–target data is depicted in Figures 2 and 3 and is described in the Materials and Methods. Intuitively, we represent each type of data as a graph, integrate the two types of data by intersecting the two graphs, and identify pairs of proteins that define a circuit from the intersection graph (we refer to a gene and the protein it encodes interchangeably). The circuits themselves are revealed using an algorithm for finding the shortest paths between two nodes in a graph (11). Application of this algorithm to corresponding pairs of nodes in the two graphs enables the detection of circuits that include both protein–protein and protein–DNA interactions. The order of a circuit is determined to be the maximal number of interactions (protein–protein or regulator–target) that connect the pair-mates. Since one cannot cope manually with the huge amount of genome-scale data, we have automated this process by representing the graphs by their adjacency matrices and employing matrix manipulations (Figs 2 and 3). This computational procedure is guaranteed to detect all circuits in the data that comply with our definition.
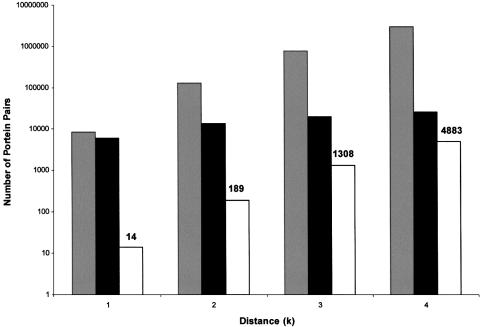
In this study, we extracted regulatory circuits of orders 1–4, based on yeast experimental data of protein–protein and protein–DNA interactions (see Materials and Methods for data sources). In total, our procedure revealed 6394 pairs of proteins that may define regulatory circuits of orders 1–4 (Fig. 4). For each order, the number of protein pairs that define circuits is significantly higher than in integrated random networks (P ≤ 0.05, see Materials and Methods).
Figure 4.
Number of connected protein pairs. Gray bars, protein pairs whose distance in the graph of physical interactions ≤k; black bars, protein pairs whose distance in the regulator–target graph ≤k; white bars, protein pairs defining circuits of order k (based on the intersection graphs). The numbers on the y-axis are presented on a logarithmic scale.
By taking all possible shortest path combinations into account, 18 149 putative circuits were generated. Since the yeast experimental data sets are noisy and may include false interactions, it is essential to narrow down the predicted circuits to the ones that are biologically most promising. To this end, we apply a hierarchical assessment protocol: first, we apply the cellular process assessment to the entire circuit population, as this assessment relies on all proteins in the circuit. Only circuits that are determined to be statistically significant by this analysis are kept. In cases where several circuits are defined for a protein pair, we select the circuit(s) that is most statistically significant. Secondly, the reduced population of circuits that passed this assessment is subjected to two additional assessments, based on cellular localization and knockout data. Only circuits that pass at least one of these additional assessments are considered as potentially biologically relevant circuits. Below we describe these assessments in detail, demonstrate the validity of our approach by examining already known circuits that were reconstructed and verified, and discuss new insights gained by our analysis.
Assessment of circuits
Cellular process assessment. To select the biological meaningful circuits we evaluated the consistency of the proteins participating in a circuit according to their assignments into cellular processes. We expect that within a biologically meaningful circuit, the fraction of proteins participating in a common cellular process, e.g. mitosis, will be significantly higher than that expected at random. Indeed, comparison between the fractions of molecules that participate in the same process in actual and randomly generated circuits revealed that for 3183 out of the 18 149 circuits, the circuit fraction is significantly higher than that of the corresponding random circuits (P ≤ 0.05).
Assessment by protein localizations annotation. To assess the biological feasibility of the circuits we examined the cellular localization of the proteins participating in the protein–protein interaction path within a circuit (14,22). An interaction is feasible if the two interacting proteins are localized to a common cellular compartment or co-participate in a documented complex. Since a protein may be localized to more than one compartment, it may interact with different pair-mates in different cellular compartments, and the protein–protein interaction path of a circuit may span several cellular compartments. We expect that biologically feasible circuits will be entirely composed of feasible protein–protein interactions. Indeed, 729 of the circuits that passed the cellular process assessment are biologically feasible. Notably, the fraction of feasible circuits among the putative circuits is significantly higher than in the corresponding random circuits (see Materials and Methods). For orders 1–4, we obtain statistical significance values ranging from P = 0.0051 to P < 0.0001.
Assessing the circuits by knockout data. To assess the regulatory relevance of the extracted circuits we used a data set that contains gene expression profiles of S.cerevisiae genes corresponding to individual deletions of 276 genes (12). Specifically, changes in expression levels of all the yeast genes were measured in response to the deletion of each one of those 276 genes. For a circuit that is defined by a regulatory protein A and a target gene B (Fig. 1), we expect that the knockout of B will affect the activity of A, if indeed the circuit functions as a feedback loop. This effect could be detected by following the changes in the expression levels of other gene targets of A. To be confident that this effect is not random, we required that the number of the gene targets of A that changed their expression levels upon the knockout of gene B would be statistically significant (see Materials and Methods). It should be noted that the interpretation of knockout results is somewhat problematic, because alternative regulations may mask the effect of the deleted gene, even though such an effect exists. Nevertheless, this approach should be valuable where such effects can be detected.
Apparently, only a small number of circuits could be subjected to this evaluation, as only 62 of the 276 deleted genes coincided with genes B in the circuits. These 62 genes participated in 145 regulatory circuits that were statistically significant by the cellular process assessment. For 25 of these circuits, the relationships between the affected genes and gene targets of the relevant transcription factor were statistically significant (P ≤ 0.05), providing additional supportive evidence for these putative circuits.
In total, 746 circuits were statistically significant by the cellular process assessment, and by either the cellular localization assessment or the knockout results assessment (or by both). A summary of our results is presented in Table 1. The circuits themselves are listed in the Supplementary Material, where for each circuit we report its performance in the three assessments and provide information about the putative cellular process it participates in and on the cellular localizations where the protein–protein interactions occur. For those circuits where we have supportive knockout data we list the potential gene targets of the circuits, based on the knockout results (12).
Table 1. Summary of detected circuits.
| Circuit order | No. of protein pairs that define circuits | No. of circuits | No. of statistically significant circuits by the cellular process assessmenta | No. of feasible circuits according to the localization assessmentb | No. of circuits validated by the knockout resultsc | No. of potential biologically relevant circuitsd |
|---|---|---|---|---|---|---|
| 1 | 14 | 14 | 11 | 8 (10) | 0 (0) | 8 |
| 2 | 189 | 219 | 76 | 41 (58) | 3 (4) | 42 |
| 3 | 1308 | 1993 | 447 | 170 (313) | 6 (21) | 173 |
| 4 | 4883 | 15 923 | 2649 | 510 (1459) | 16 (120) | 523 |
| Total | 6394 | 18 149 | 3183 | 729 (1840) | 25 (145) | 746 |
aCircuits with fractions of proteins assigned to the same cellular process that deviated significantly from random are reported. This assessment was performed for all detected circuits.
bCircuits where all protein–protein interactions are feasible are reported. The cellular localization assessment was performed only for circuits that are statistically significant according to the cellular process assessment, and for which protein localization annotation was available for all proteins in the protein–protein interaction path (this number appears in parentheses).
cCircuits where the relationships between the affected genes and gene targets of the relevant transcription factor were statistically significant are reported. This assessment was performed only for circuits that are statistically significant according to the cellular process annotation. For each circuit order, the total number of circuits that could be tested by the knockout data is shown in parentheses.
dCircuits supported by the cellular process assessment and by at least one other assessment.
Potential biologically relevant circuits
The best way to validate the potential biologically relevant circuits would have been to compare them with a data set of known circuits. We expect that if our approach is valid, it will report all known circuits as biologically relevant. Unfortunately, such a database of known circuits does not exist. To test our approach, we examined 15 examples of known circuits described in the literature. These include the circuits defined by the protein pairs Swi6–Swi4 (23,24), Gal4–Gal80, Gal4–Gal3 and Gal4–Gal1 (25), Ime1–Rim11 and Ume6–Ime1 (26), Ste12–Fus3 (which define two circuits) (27), Ste12–Far1 (28), Cbf1–Met28 and Met4–Met28 (29), Swi4–Clb2 (30), Mbp1–Clb5 (31), and Stb1–Cln1 and Stb1–Cln2 (32). Thirteen of these circuits were considered by the analysis as biologically relevant (87%), lending support to the biological essence of our computational procedure. The two remaining known circuits were verified by only one assessment, indicating that the annotation used to assess the data is incomplete. This suggests that there are more than 746 potential biologically relevant circuits among the detected circuits, which will be revealed when the annotation improves.
Examples of known circuits revealed by our approach
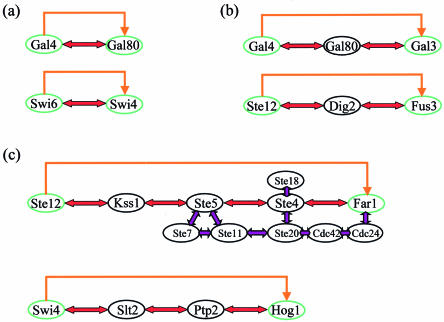
Among the potential biologically relevant circuits, we detected eight direct (first order) regulatory circuits (Table 1), five of which are known. For example, Gal4 and Gal80 that are involved in galactose catabolism define one of these direct regulatory circuits. Gal4 is a transcription factor that activates genes participating in galactose catabolism, including GAL80. Gal80 binds to Gal4, and in the absence of galactose represses its activity (Fig. 5a). Thus, this circuit provides an example for negative feedback regulation. Other examples of direct regulatory circuits involve also positive feedback loops, such as the circuit defined by the pair of transcription factors Swi6–Swi4 (Fig. 5a).
Figure 5.
Detected regulatory circuits. (a) Known direct regulatory circuits. Gal4–Gal80 comprises a negative feedback circuit (see text). The Swi6–Swi4 circuit functions to switch on a new pathway: the transcription of SWI4 depends on Swi6. The complex Swi4–Swi6 (called SBF) is responsible for the transcription of SWI4 as well as for the synthesis of other genes that function in late G1, thus enabling the progression of the cell cycle (23,24). (b) Known regulatory circuits of order 2 (see text). (c) Regulatory circuits of higher orders. Ste12 and Far1 define a known regulatory circuit of order 4 that is part of the mating pheromone response pathway (28) and Swi4 and Hog1 define a putative regulatory circuit of order 3. In the Ste12–Far1 circuit, purple arrows mark protein–protein interactions that are part of the known circuit, but are not detected by our method since we are looking for the shortest path between Ste12 and Far1. A complex of Ste4–Ste18 released from activated pheromone receptors recruits three essential regulators to the plasma membrane, and tethers them in close juxtaposition: a scaffold protein, Far1, that carries the guanine nucleotide exchange factor (Cdc24) for the Cdc42 small GTPase; a Cdc42-activated protein kinase Ste20; and a scaffold protein, Ste5, that carries the three-tiered module of protein kinases (Ste11, Ste7, Fus3). The close juxtaposition enables the following interaction series, Cdc24–Cdc42–Ste20–Ste11–Ste7–Kss1–Ste12, which results in the activation of Ste12. The activated Ste12 is a transcription factor of FAR1, as well as of many other genes involved in the pheromone response pathway. (Conventionally, the pathway is described by the interactions of proteins Fus3 and Dig1/Dig2 with Ste12 instead of Kss1, and we would have detected it if we did not look for the shortest path.) For the Swi4–Hog1 circuit, see text.
Examples of reconstructed known circuits of higher orders could also be found. The pair Gal4–Gal3 that defines a regulatory circuit within the galactose pathway provides an example for a known regulatory circuit of order 2 (Fig. 5b). Gal4 is a transcription factor of GAL3, and the two proteins interact via Gal80. As mentioned above, Gal4 and Gal80 form a complex that inhibits Gal4 from acting as a transcription factor. However, in the presence of galactose, Gal3 interacts with Gal80, releasing the Gal4 inhibition. This enables Gal4 to transcribe genes, specifically GAL3, therefore constituting a positive feedback regulation circuit (25). The same pattern is identified for Ste12–(Dig1 or Dig2)–Fus3 (Fig. 5b), a well known regulatory circuit within the mating pheromone response pathway (28). Ste12 and Dig1/Dig2 form a complex that inhibits Ste12. When Fus3 interacts with Dig1/Dig2 the inhibition is released and Ste12 acts as a transcription factor of FUS3, as well as of other genes related to this pathway. An example of a known circuit of order 4 is demonstrated in Figure 5c. Ste12 and Far1 define the circuit that is part of the mating pheromone response pathway. Since we are searching for the shortest path between the two proteins defining a circuit, our method detected the scaffold proteins that constitute the circuit, but not the auxiliary proteins that interact with them.
An example of a known circuit that was reconstructed but was not included in the list of biologically relevant circuits, is the circuit defined by Gal4–Gal1. This circuit is similar to the Gal4–Gal3 circuit (Gal1 replaces Gal3), both in composition and in function (25). However, although the circuit is known, the annotation regarding the localization of Gal1 in the cell is missing. Gal1 is also not included in the knockout data. Therefore, this circuit was only supported by the cellular process assessment. When the annotation improves, such cases where known circuits are missed would be eliminated.
New relationships between genes and proteins
Our analysis sheds light on possible regulatory relationships between genes and proteins that could not be revealed by independent analyses of each data set. The circuit defined between the proteins Swi4 and Hog1, which was supported by all three assessments, provides an intriguing example (Fig. 5c). In this circuit the interaction path is Swi4–Slt2–(Ptp2 or Ptp3)–Hog1. It was suggested in the literature that an activated form of Hog1, a MAP kinase protein, is able to activate the Hog1 phosphatases Ptp2 and Ptp3 (33). It was also shown that activated Ptp2 and Ptp3 inactivate Slt2, another MAP kinase (34), Slt2 activates Swi4 by phosphorylating it (35) and this activation results in increased overall expression of Swi4 target genes (35). Based on this information, we suggest that the circuit defined by Swi4–Hog1 is a negative feedback loop. Swi4 activates Hog1, and the latter can inactivate Swi4 through the circuit. The three assessments do not only support this circuit’s validity but also provide important insight. From the cellular process assessment we can infer that this negative feedback loop possibly plays a role in the response of the cell to high osmolarity. The protein localization assessment shows that the circuit spans different cellular compartments, where the signal is transferred from the cytoplasm to the nucleus. The gene targets of Swi4 that are affected by the deletion of the HOG1 gene are most likely involved in the response to high osmolarity.
DISCUSSION
A major challenge of the post-genomic research is to understand how cellular phenomena arise from the connectivity of genes and proteins. The network of interactions that connects genes and proteins generates complex molecular circuitry that resembles complex electrical circuits (36). In this report, we present a novel application of classical graph algorithms for the integration of protein–protein and protein–DNA interaction data, to systematically reveal components of the cellular circuitry. Specifically, we focus on the detection of well defined direct and higher order regulatory circuits that involve both protein–protein and regulator–target interactions. By combining the two levels of interaction, a regulatory circuit may function as an efficient positive or negative feedback loop, a key component of various control systems (36–38). We address this question at a genomic scale, and rigorously analyze the available information of protein–protein interaction and gene regulation in the yeast S.cerevisiae. While our computational procedure is applicable to any size of data, its strength is in its ability to efficiently process large amounts of the two types of data. This is of great importance in view of the extensive data sets that have accumulated from the various functional genomic and proteomic studies.
The method we present guarantees the detection of every circuit that complies with our definition based on the available experimental data. Here we based our analysis primarily on genome-wide experimental data. On the one hand, by integrating data from different types of genome-wide experiments we are able to identify novel functional pathways involving both proteins and DNA. On the other hand, genome-wide experiments are susceptible to errors: large-scale protein–protein interaction experiments may produce false-positive results (39,40) and genome-wide location analyses reveal binding of regulatory proteins to DNA, but do not guarantee that the binding has a regulatory effect. Therefore, the validity of the derived circuits depends on the quality of the experimental data, and is expected to improve as the data improve. Nevertheless, regulatory circuit detection is based upon the intersection of two independent data sets, providing cross-validation of the information sources and reducing the amount of false positives contained in each data set.
The integration of the available data of protein–protein and protein–DNA interaction in the yeast S.cerevisiae yielded approximately 6400 protein pairs that define putative multi-level regulatory circuits of orders 1–4. The three assessments that we performed per circuit, testing its biological meaning by the cellular process assessment, its biological feasibility by the protein localization assessment, and its regulatory relevance by its consistency with knockout data, provide an integrative scheme for assessing the circuit’s biological relevance. Applying the three assessments hierarchically to the detected circuits—first the assessment that relies on the entire circuit composition, and secondly, the two assessments which relate to circuit fragments—resulted in the identification of 746 potential biologically relevant circuits. The successful identification of known circuits as biologically relevant supports the rationale of our scheme.
In addition to their confirmatory nature, the three assessments provide intriguing insights. The first assessment may suggest the cellular process in which the regulatory circuit plays a role: if a significant fraction of the circuit proteins participate in a common cellular process, then the circuit is predicted to function as part of this process. Furthermore, the cellular process of a circuit can be used for the annotation of circuit proteins that lack such an assignment. Specifically, we managed to assign biological process annotations to 271 such proteins. As for the localization assessment, it enables mapping up the pathway of a circuit in the cell by tracing the cellular localization annotations attached to the edges. For example, the protein–protein interactions composing the circuit defined by Ste12–Far1 (Fig. 5c) can be traced to several cellular compartments, describing how the mating pheromone signal is carried from the plasma membrane to the nucleus, similarly to other signal transduction pathways. The third assessment, using the knockout data, provides a link to the potential gene targets of the putative circuits.
Our integration method may be extended to different types of analyses. First, we can refine the current analysis by distinguishing between transcription activators and repressors in the regulator–target graph. Secondly, we intend to use our integrated data set to reveal other types of pathways. Such pathways may be composed of alternating regulator–target and protein–protein interactions of the form that underlies, for example, the cell cycle progression (16). Finally, in the current study we relied only on experimental data, but our scheme may utilize putative data as well. When accurate algorithms for prediction of the various gene attributes from sequence data are available (e.g. protein–protein interaction or transcription factor binding sites), they can be used to predict the input data that will be further processed by our approach. One can envision that in the future such approaches may enable extracting knowledge on the regulatory networks in the cell based on genomic sequence data alone.
SUPPLEMENTARY MATERIAL
Supplementary Material is available at NAR Online.
Acknowledgments
ACKNOWLEDGEMENTS
We are grateful to Y. Altuvia, G. Lithwick, E. Sprinzak, R. Hershberg, S. Sattath, T. Kaplan, N. Friedman, B. Chor, R. Pinter, A. Lotem, I. Pilpel, I. Simon, O. Furman, A. Jaimovich and N. Grover for their helpful comments and suggestions. This study was supported by a strategic grant from the Israeli Ministry of Science and by a grant from the Israel Science Foundation, administered by the Israel Academy of Sciences and Humanities (granted to H.M.). E.Y.-L. is supported by the Hurvitz Foundation.
REFERENCES
- 1.DeRisi J.L., Iyer,V.R. and Brown,P.O. (1997) Exploring the metabolic and genetic control of gene expression on a genomic scale. Science, 278, 680–686. [DOI] [PubMed] [Google Scholar]
- 2.Roth F.P., Hughes,J.D., Estep,P.W. and Church,G.M. (1998) Finding DNA regulatory motifs within unaligned noncoding sequences clustered by whole-genome mRNA quantitation. Nat. Biotechnol., 16, 939–945. [DOI] [PubMed] [Google Scholar]
- 3.Marcotte E.M., Pellegrini,M., Thompson,M.J., Yeates,T.O. and Eisenberg,D. (1999) A combined algorithm for genome-wide prediction of protein function. Nature, 402, 83–86. [DOI] [PubMed] [Google Scholar]
- 4.Drawid A., Jansen,R. and Gerstein,M. (2000) Genome-wide analysis relating expression level with protein subcellular localization. Trends Genet., 16, 426–430. [DOI] [PubMed] [Google Scholar]
- 5.Ge H., Liu,Z., Church,G.M. and Vidal,M. (2001) Correlation between transcriptome and interactome mapping data from Saccharomyces cerevisiae.Nature Genet., 29, 482–486. [DOI] [PubMed] [Google Scholar]
- 6.Grigoriev A. (2001) A relationship between gene expression and protein interactions on the proteome scale: analysis of the bacteriophage T7 and the yeast Saccharomyces cerevisiae.Nucleic Acids Res., 29, 3513–3519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ideker T., Thorsson,V., Ranish,J.A., Christmas,R., Buhler,J., Eng,J.K., Bumgarner,R., Goodlett,D.R., Aebersold,R. and Hood,L. (2001) Integrated genomic and proteomic analyses of a systematically perturbed metabolic network. Science, 292, 929–934. [DOI] [PubMed] [Google Scholar]
- 8.Pilpel Y., Sudarsanam,P. and Church,G.M. (2001) Identifying regulatory networks by combinatorial analysis of promoter elements. Nature Genet., 29, 153–159. [DOI] [PubMed] [Google Scholar]
- 9.Kemmeren P., van Berkum,N.L., Vilo,J., Bijma,T., Donders,R., Brazma,A. and Holstege,F.C. (2002) Protein interaction verification and functional annotation by integrated analysis of genome-scale data. Mol. Cell, 9, 1133–1143. [DOI] [PubMed] [Google Scholar]
- 10.Steffen M.A., Petti,A.A., Aach,J., D’Haeseleer,P. and Church,G.M. (2002) Automated modeling of signal transduction networks. BMC Bioinformatics, 3, 34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cormen T.H., Leiserson C.E. and Rivest,R.L. (1990) Introduction to Algorithms. MIT Press, Cambridge. [Google Scholar]
- 12.Hughes T.R., Marton,M.J., Jones,A.R., Roberts,C.J., Stoughton,R., Armour,C.D., Bennett,H.A., Coffey,E., Dai,H., He,Y.D. et al. (2000) Functional discovery via a compendium of expression profiles. Cell, 102, 109–126. [DOI] [PubMed] [Google Scholar]
- 13.Zhu J. and Zhang,M.Q. (1999) SCPD: a promoter database of the yeast Saccharomyces cerevisiae.Bioinformatics, 15, 607–611. [DOI] [PubMed] [Google Scholar]
- 14.Costanzo M.C., Crawford,M.E., Hirschman,J.E., Kranz,J.E., Olsen,P., Robertson,L.S., Skrzypek,M.S., Braun,B.R., Hopkins,K.L., Kondu,P. et al. (2001) YPD, PombePD and WormPD: model organism volumes of the BioKnowledge library, an integrated resource for protein information. Nucleic Acids Res., 29, 75–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ren B., Robert,F., Wyrick,J.J., Aparicio,O., Jennings,E.G., Simon,I., Zeitlinger,J., Schreiber,J., Hannett,N., Kanin,E. et al. (2000) Genome-wide location and function of DNA binding proteins. Science, 290, 2306–2309. [DOI] [PubMed] [Google Scholar]
- 16.Simon I., Barnett,J., Hannett,N., Harbison,C.T., Rinaldi,N.J., Volkert,T.L., Wyrick,J.J., Zeitlinger,J., Gifford,D.K., Jaakkola,T.S. et al. (2001) Serial regulation of transcriptional regulators in the yeast cell cycle. Cell, 106, 697–708. [DOI] [PubMed] [Google Scholar]
- 17.Iyer V.R., Horak,C.E., Scafe,C.S., Botstein,D., Snyder,M. and Brown,P.O. (2001) Genomic binding sites of the yeast cell-cycle transcription factors SBF and MBF. Nature, 409, 533–538. [DOI] [PubMed] [Google Scholar]
- 18.Lee T.I., Rinaldi,N.J., Robert,F., Odom,D.T., Bar-Joseph,Z., Gerber,G.K., Hannett,N.M., Harbison,C.T., Thompson,C.M., Simon,I. et al. (2002) Transcriptional regulatory networks in Saccharomyces cerevisiae.Science, 298, 799–804. [DOI] [PubMed] [Google Scholar]
- 19.Xenarios I., Fernandez,E., Salwinski,L., Duan,X.J., Thompson,M.J., Marcotte,E.M. and Eisenberg,D. (2001) DIP: the Database of Interacting Proteins: 2001 update. Nucleic Acids Res., 29, 239–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bader G.D., Donaldson,I., Wolting,C., Ouellette,B.F., Pawson,T. and Hogue,C.W. (2001) BIND—the Biomolecular Interaction Network Database. Nucleic Acids Res., 29, 242–245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mewes H.W., Frishman,D., Guldener,U., Mannhaupt,G., Mayer,K., Mokrejs,M., Morgenstern,B., Munsterkotter,M., Rudd,S. and Weil,B. (2002) MIPS: a database for genomes and protein sequences. Nucleic Acids Res., 30, 31–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kumar A., Agarwal,S., Heyman,J.A., Matson,S., Heidtman,M., Piccirillo,S., Umansky,L., Drawid,A., Jansen,R., Liu,Y. et al. (2002) Subcellular localization of the yeast proteome. Genes Dev., 16, 707–719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Foster R., Mikesell,G.E. and Breeden,L. (1993) Multiple SWI6-dependent cis-acting elements control SWI4 transcription through the cell cycle. Mol. Cell. Biol., 13, 3792–3801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baetz K. and Andrews,B. (1999) Regulation of cell cycle transcription factor Swi4 through auto-inhibition of DNA binding. Mol. Cell. Biol., 19, 6729–6741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lohr D., Venkov,P. and Zlatanova,J. (1995) Transcriptional regulation in the yeast GAL gene family: a complex genetic network. FASEB J., 9, 777–787. [DOI] [PubMed] [Google Scholar]
- 26.Rubin-Bejerano I., Mandel,S., Robzyk,K. and Kassir,Y. (1996) Induction of meiosis in Saccharomyces cerevisiae depends on conversion of the transcriptional repressor Ume6 to a positive regulator by its regulated association with the transcriptional activator Ime1. Mol. Cell. Biol., 16, 2518–2526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bardwell L., Cook,J.G., Zhu-Shimoni,J.X., Voora,D. and Thorner,J. (1998) Differential regulation of transcription: repression by unactivated mitogen-activated protein kinase Kss1 requires the Dig1 and Dig2 proteins. Proc. Natl Acad. Sci. USA, 95, 15400–15405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dohlman H.G. and Thorner,J.W. (2001) Regulation of G protein-initiated signal transduction in yeast: paradigms and principles. Annu. Rev. Biochem., 70, 703–754. [DOI] [PubMed] [Google Scholar]
- 29.Kuras L., Barbey,R. and Thomas,D. (1997) Assembly of a bZIP-bHLH transcription activation complex: formation of the yeast Cbf1-Met4-Met28 complex is regulated through Met28 stimulation of Cbf1 DNA binding. EMBO J., 16, 2441–2451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Siegmund R.F. and Nasmyth,K.A. (1996) The Saccharomyces cerevisiae start-specific transcription factor Swi4 interacts through the ankyrin repeats with the mitotic Clb2/Cdc28 kinase and through its conserved carboxy terminus with Swi6. Mol. Cell. Biol., 16, 2647–2655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Chen K.C., Csikasz-Nagy,A., Gyorffy,B., Val,J., Novak,B. and Tyson,J.J. (2000) Kinetic analysis of a molecular model of the budding yeast cell cycle. Mol. Biol. Cell, 11, 369–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ho Y., Costanzo,M., Moore,L., Kobayashi,R. and Andrews,B.J. (1999) Regulation of transcription at the Saccharomyces cerevisiae start transition by Stb1, a Swi6-binding protein. Mol. Cell. Biol., 19, 5267–5278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wurgler-Murphy S.M., Maeda,T., Witten,E.A. and Saito,H. (1997) Regulation of the Saccharomyces cerevisiae HOG1 mitogen-activated protein kinase by the PTP2 and PTP3 protein tyrosine phosphatases. Mol. Cell. Biol., 17, 1289–1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mattison C.P., Spencer,S.S., Kresge,K.A., Lee,J. and Ota,I.M. (1999) Differential regulation of the cell wall integrity mitogen-activated protein kinase pathway in budding yeast by the protein tyrosine phosphatases Ptp2 and Ptp3. Mol. Cell. Biol., 19, 7651–7660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Madden K., Sheu,Y.J., Baetz,K., Andrews,B. and Snyder,M. (1997) SBF cell cycle regulator as a target of the yeast PKC-MAP kinase pathway. Science, 275, 1781–1784. [DOI] [PubMed] [Google Scholar]
- 36.Hasty J., McMillen,D. and Collins,J.J. (2002) Engineered gene circuits. Nature, 420, 224–230. [DOI] [PubMed] [Google Scholar]
- 37.Hartwell L.H., Hopfield,J.J., Leibler,S. and Murray,A.W. (1999) From molecular to modular cell biology. Nature, 402, C47–C52. [DOI] [PubMed] [Google Scholar]
- 38.Ferrell J.E. Jr (2002) Self-perpetuating states in signal transduction: positive feedback, double-negative feedback and bistability. Curr. Opin. Cell Biol., 14, 140–148. [DOI] [PubMed] [Google Scholar]
- 39.Legrain P., Wojcik,J. and Gauthier,J.M. (2001) Protein–protein interaction maps: a lead towards cellular functions. Trends Genet., 17, 346–352. [DOI] [PubMed] [Google Scholar]
- 40.Sprinzak E., Sattath,S. and Margalit,H. (2003) How reliable are experimental protein–protein interaction data? J. Mol. Biol., 327, 919–923. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.