Abstract
We explored distance preferences in the arrangement of binding motifs for five transcription factors (Bicoid, Krüppel, Hunchback, Knirps and Caudal) in a large set of Drosophila cis-regulatory modules (CRMs). Analysis of non-overlapping binding motifs revealed the presence of periodic signals specific to particular combinations of binding motifs. The most striking periodic signals (10 bp for Bicoid and 11 bp for Hunchback) suggest preferential positioning of some binding site combinations on the same side of the DNA helix. We also analyzed distance preferences in arrangements of highly correlated overlapping binding motifs, such as Bicoid and Krüppel. Based on the distance analysis, we extracted preferential binding site arrangements and proposed models for potential composite elements (CEs) and antagonistic motif pairs involved in the function of developmental CRMs. Our results suggest that there are distinct hierarchical levels in the organization of transcription regulatory information. We discuss the role of the hierarchy in understanding transcriptional regulation and in detection of transcription regulatory regions in genomes.
INTRODUCTION
Initiation of tissue-specific or spatio-specific transcription in multicellular organisms requires binding of multiple transcription factor molecules to transcription regulatory regions, such as promoters and enhancers (cis-regulatory modules; CRMs). Multiple binding motifs and even multiple binding sites for the same motif presented in the regulatory regions are often described as ‘regulatory clusters’ (1–6). Statistical models, based on motif clustering, are helpful for finding novel CRMs in the genome, but very often they consider only site density (cluster significance) and relative site affinity (such as a weighted matrix score) (6). However, it is known that specific arrangements of binding motifs within the regulatory regions (regulatory clusters) are necessary to achieve proper biological function. Incorporating such architectural features into formal clustering models might facilitate computational recognition of CRMs and interpretation of their biological function (7).
Specific arrangements between binding sites are known from many examples in biology. For instance, recent quantitative studies of basal transcription (8) revealed a striking dependence of basal promoter activity on both the distance and the orientation of an artificial activator binding site (Gal4) and the TATA box. An optimal spacing between binding sites (NF-Y and SRE motifs) has also been demonstrated in the human SREBP-2 promoter (sterol regulatory element-binding protein) (9). In vitro analysis of binding site arrangements in the rat collagenase-3 promoter (10) has revealed that a 10 bp (‘helical’) phasing in binding site distribution provides maximal transcriptional activity. The importance of the ‘helical phasing’ and specific binding site arrangement was also demonstrated in vivo for the murine CD4 promoter (11). In some cases, even a very small difference in the distance between binding motifs results in dramatically different transcriptional outcomes. One of the most striking examples of this kind is the binding of the POU domain transcription factor Pit-1 to its target sites, differentially spaced (2 bp difference) in growth hormone and prolactin gene promoters (12). The ‘helical phasing’ (10 bp) has also been demonstrated computationally (13) using a large number of proximal eukaryotic promoters (14) and the list of binding motifs available from the TRANSFAC database (15). In many of the described quantitative experimental studies, the disruption of specific spacing (phasing) between binding sites resulted in reduction, but not abolishment, of transcription. This fact, together with some known cases of successful promoter reconstruction (16–18), also supports the presence of a certain flexibility in site arrangement.
The biological reasons leading to a specific arrangement of sites in promoters are clear: the transcription factors, bound to promoter DNA, are also involved in specific protein–protein interactions (19,20); therefore, the binding motifs must be distributed in the promoter in a non-random fashion. In other words, the arrangement of binding motifs can control the formation of 3D protein complexes involved in initiation of specific transcription.
Attempts to reveal and describe specific site arrangements resulted in a very interesting concept of composite elements (CEs) (21). In the simplest case, a CE corresponds to a pair of individual binding motifs located at a particular distance and involved in formation of specific tertiary (DNA–protein–protein–DNA) complexes. Identical CEs may perform related functions in different genes. Further development of this concept resulted in construction of a dedicated database TRANSCompel (22), combining sequences for 256 (Release 6.0) CEs from different organisms. Currently, the CE concept is widely used for finding co-localized, synergistic (antagonistic) binding motif pairs (23,24) or combinatorial arrays of motifs responsible for the formation of similar gene expression profiles (25–27).
In the current work, we explored preferential site distances in CRMs of Drosophila developmental genes. CRMs are transcription regulatory units (∼1 kb range), often located far from the transcription start site and responsible for spatio-temporal expression of their cognate developmental genes (3). We recently built a database containing known functional Drosophila CRMs (see our web resource: http://homepages.nyu.edu/~dap5/PCL/appendix2.htm) together with a list of matrices for a number of transcription factors and known transcriptional interactions (6,28). Selection of relevant binding motifs in a particular functionally related group of transcription regulatory regions minimizes the risk of false positives, which is known to be a problem for large-scale analysis of highly diverse data sets.
In this work, we have shown that the binding sites in CRMs of Drosophila are arranged in particular ways, indicating the presence of specific developmental CEs. We also discuss a general model describing hierarchical levels in organization of transcriptional information and the role of CEs in understanding the responses of developmental genes to transcriptional signals.
METHODS
In order to identify binding site cores, we calculated information content I (bits) in the ith column of a binding motif alignment as the Shannon entropy for this alignment column (29):
In this equation, qiα represents the frequency of the letter α (α∈{A,C,G,T}) in the ith position of the alignment. To calculate the score of a binding motif match, we constructed position weighted matrices (PWMs) for each motif using the equation with a pseudocount parameter:
Siα is the score of letter α in position i, niα is the number of letters α in column i of the motif alignment, qα is the frequency of letter α in the Drosophila genome, and a is the pseudocount parameter, which we set as equal to 1. In our previous publications, we discussed how to select the PWM cutoff for the binding motifs in this particular system (28). For each PWM cutoff value, we estimated the site frequency ES as the total number of motif matches above the PWM cutoff in the entire Drosophila genome normalized to the length of the genome.
To estimate randomness of binding site distribution in the CRMs, we have found all distances between neighboring sites and compared the observed distance distribution with the expected distance distribution in a random Bernoulli sequence (see also equation 7). For each jth interval of 10 distances (j = 5, 15…225), we calculated Z-scores (see Fig. 1):
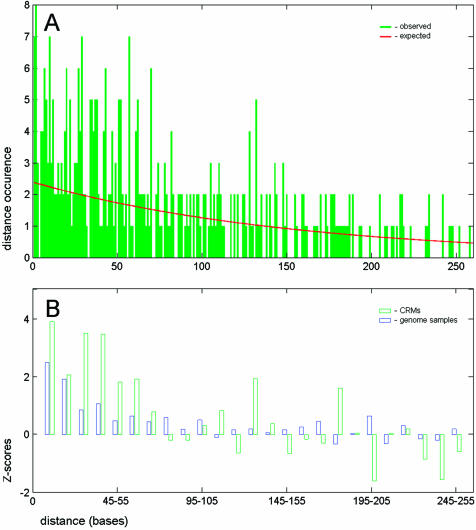
Figure 1.
Distribution of distances built for the neighboring binding sites. (A) The histogram of distances between the neighboring sites for five binding motifs in developmental CRMs. The red line shows the random (geometric) distribution calculated for sites with the same frequency in CRMs. (B) Normalized deviations (Z-scores; see equation 3) between the observed and the expected number of distances. The Z-scores were calculated for distance intervals of 10 bp. The binding sites in CRMs (green bars) are closer than expected from the random distribution and the distribution detected in the genome (blue bars).
In this equation, the expected number of distances Nexpj for each distance interval j in genomic samples was calculated taking into account the site frequency in the genome (EGs = 5E-4). The corresponding PWM cutoff values for Bicoid (Bcd) and Krüppel (Kr) are shown in Table 1. In the case of the CRM data set, we calculated ES from the number of sites having the same frequency in the genome (the same PWM cutoff), but actually found in the CRM data set (ESCRM = the total number of sites in CRMs/total CRM length). Due to the limited size of CRMs, we calculated the total number of distances between the neighboring sites N300CRM only in the range of 1–300 bp. With correction for the maximal possible number of distances (conservative estimation), we calculated the expected number of sites in the jth distance interval as:
Table 1. Site affinity and motif interdependence.
| PWM score | 5 | 5.4 | 5.8 | 6.2 | 6.6 | 7 | 7.4 | 7.8 |
|---|---|---|---|---|---|---|---|---|
| Site E(genome) | 0.002 | 0.001 | 8E-04 | 5.2E-04 | 3.3E-04 | 2E-04 | 1.2E-04 | 1E-04 |
| CRMs | ||||||||
| No. of Bcd sites | 324 | 240 | 172 | 118 | 88 | 67 | 38 | 16 |
| No. of Kr sites | 264 | 207 | 160 | 109 | 87 | 70 | 37 | 29 |
| No. of overlaps | 92 | 72 | 45 | 30 | 22 | 12 | 5 | 0 |
| PECRM (KRi+2|BCDi) | 0.28 | 0.30 | 0.26 | 0.25 | 0.25 | 0.18 | 0.13 | 0.00 |
| PECRM (BCDi–1|KRi) | 0.35 | 0.35 | 0.28 | 0.28 | 0.25 | 0.17 | 0.14 | 0.00 |
| Genome | ||||||||
| PEG (KRi+2|BCDi) | 0.32 | 0.28 | 0.20 | 0.18 | 0.14 | 0.08 | 0.02 | 0.00 |
| PEG (BCDi–1|KRi) | 0.31 | 0.29 | 0.22 | 0.21 | 0.20 | 0.09 | 0.03 | 0.00 |
The table shows changes in the motif interdependence with increasing site probability (PWM cutoff). The number of sites detected in the CRM data set is given for Bcd and Kr motifs for a range of considered site frequency [site E(genome)]. Motif interdependence in the CRM data set was estimated from these numbers with respect to Bcd: PECRM (BCDi–1|KRi) and Kr: PECRM (KRi+2|BCDi). The motif interdependence in CRMs is compared with the motif interdependence in the genome (see the bottom two rows). The interdependence between Bcd and Kr is much higher in CRMs for high-affinity sites.
To obtain comparable statistical values, the Z-scores for genomic sequences were calculated for the sample size of CRMs (NG = N300CRM) using the same equatiion. Statistical noise caused by the small sample size prevented further reduction of the selected distance intervals (see Fig. 1A). Larger intervals would result in lower resolution by distance.
Spectra of distance distributions in the frequency domain were built using the Matlab® (Mathworks, Inc.) signal processing module. We used a filtered fast Fourier transform (FFT) algorithm, implemented in the multiple signal classification method (MUSIC). The order of FFT was set to the maximal, as well as the signal dimension (149 for 300 input points, analyzed range of distances), thus keeping all putative signals without noise reduction. Input signals (Z-scores) for periodic analysis were generated from distance distributions (histograms smoothed by three distance points) using equation 3, taking into account the site frequency observed in the CRM data set (total number of sites in CRMs/total CRM length, see above).
To extract Bcd/Kr functional elements, we calculated PWM scores for Bcd and Kr, respectively, for each position (with the +2 bp shift) of CRM sequences and large genomic samples (1 Mb total). Then, for each jth PWM score zone (i.e. Bcd 5.4–5.8, Kr 7.4–7.8, see Table 2), we found the number of matches in the CRM data set Njobs and compared this number with the number obtained from genome samples Njexp. Notice that in the described test, Njobs and Njexp were different (j here is a PWM score zone) from those given above.
Table 2. Extraction of Bcd/Kr overlaps overrepresented in CRMs.
| Kr\Bcd | 5 | 5.4 | 5.8 | 6.2 | 6.6 | 7 | 7.4 | 7.8 |
| 8.2 | 4/5 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
| 7.8 | 0/0 | 0/0 | 1/2 | 1/4 | 4/7 | 4/4 | 5/2 | 0/0 |
| 7.4 | 0/1 | 4/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 |
| 7 | 2/5 | 5/9 | 6/2 | 1/2 | 5/2 | 1/2 | 1/1 | 1/1 |
| 6.6 | 0/0 | 1/0 | 0/2 | 1/5 | 0/3 | 1/2 | 0/1 | 0/0 |
| 6.2 | 1/3 | 1/3 | 0/3 | 0/1 | 1/2 | 0/0 | 2/1 | 2/1 |
| 5.8 | 1/5 | 2/3 | 0/1 | 1/3 | 0/2 | 5/2 | 1/2 | 1/0 |
| 5.4 | 3/7 | 2/3 | 2/6 | 2/4 | 2/3 | 4/5 | 2/3 | 0/2 |
| 5 | 1/4 | 1/6 | 2/1 | 0/2 | 0/2 | 0/3 | 2/1 | 3/2 |
Comparison between observed and expected numbers of Bcd/Kr overlaps found for the CRM data set. The conservative estimation for the expected number of overlaps was calculated from the number of overlap occurrences in the genome sequences (see Methods). The first row and the first column contain the PWM score cutoff for the Bcd and Kr motifs, respectively. Only in certain score zones is the number of overlapping sites found in CRMs higher than expected (numbers are in bold). Presumably, these score zones contain functional Bcd/Kr overlaps.
To minimize errors caused by the small size of the sample (the number of overlaps in CRM sequences), we calculated a conservative estimator for the number of overlaps, Njexp. To find this number, we evaluated separately the conditional probability of observing a Kr match given a Bcd match PjG (KRi+2|BCDi) and the conditional probability of observing a Bcd match given a Kr match PjG (BCDi–2|KRi). Both conditional probabilities were estimated from the entire genome. To obtain the conservative estimation, we took the maximum over the two expectations for each jth PWM score zone:
Njexp = Max[NjBcdCRM PjG (KRi+2|BCDi); NjKrCRM PjG (BCDi–2|KRi)] 5
Here NjBcdCRN, NjKrCRM are the numbers of Bcd and Kr matches, respectively, found in CRMs for the jth PWM score zone. Notice that the conditional probabilities can also be calculated for any PWM score zone, e.g. for sites having site probability above a selected cutoff E (shown in Table 1):
RESULTS
Mapping binding sites and defining distances
To perform an analysis of distances between binding sites, it is necessary (i) to select and map binding motifs; (ii) to delineate a relevant sequence data set; and (iii) to formulate a working definition of distances between the binding site matches.
We limited our choice to the five best binding motifs for the transcriptional regulators Bcd, Caudal (Cad), Hunchback (Hb), Kr and Knirps (Kni), having a relatively large number of occurrences in our CRM database. To map these binding motifs, we employed a PWM search with parameters described earlier (6,28). In general, we considered only high-affinity sites with probabilities not exceeding 10–3, as estimated from the Drosophila genome (see Methods).
To generate a representative sequence data set, we considered only CRMs regulated by any of the selected transcription factors and containing multiple high-affinity binding sites for these proteins. The positions of binding site clusters previously identified in the context of these CRMs (6) provided a formal criterion for establishing boundaries of the selected early developmental CRMs. The total size of analyzed CRMs after the described pre-screening procedure combined >68 kb of sequence data in 33 non-overlapping contigs. The sequence data can be obtained from our web resource (see New York University website: http://homepages.nyu.edu/~dap5/PCL/pseudoobscura/train_plus_contigs.zip).
Since the binding motifs for selected transcription factors have different widths, we measured the distances between the centers of binding site cores made by site alignment columns with a high informational content (see Methods). Table 3 illustrates the procedure of distance measurement. Notice that distances even for the same binding motif may require coordinate adjustment due to the asymmetry of the motif.
Table 3. Definition of the distance between two binding sites.
| Motif/orientation | Shift | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bicoid > | 1 | 0.08 | 0.08 | 0.98 | 1.36 | 1.48 | 0.96 | 1.48 | 0.78 | 0.09 | |||
| Bicoid < | 0 | 0.09 | 0.78 | 1.48 | 0.96 | 1.48 | 1.36 | 0.98 | 0.08 | 0.08 | |||
| Caudal > | 2 | 0.17 | 0.20 | 0.96 | 0.96 | 0.62 | 0.62 | 0.62 | 0.96 | 0.33 | 0.20 | 0.07 | 0.11 |
| Caudal < | 2 | 0.11 | 0.07 | 0.20 | 0.33 | 0.96 | 0.62 | 0.62 | 0.62 | 0.96 | 0.96 | 0.20 | 0.17 |
| Hunchback > | 1 | 0.15 | 1.10 | 1.59 | 1.66 | 1.34 | 1.32 | 0.57 | 0.54 | 1.33 | 0.07 | ||
| Hunchback < | 1 | 0.07 | 1.33 | 0.54 | 0.57 | 1.32 | 1.34 | 1.66 | 1.59 | 1.10 | 0.15 | ||
| Knirps > | 1 | 0.62 | 0.87 | 0.37 | 0.54 | 0.39 | 0.60 | 1.21 | 1.36 | 1.36 | 0.74 | 0.21 | |
| Knirps < | 2 | 0.21 | 0.74 | 1.36 | 1.36 | 1.21 | 0.60 | 0.39 | 0.54 | 0.37 | 0.87 | 0.62 | |
| Krüppel > | 1 | 0.24 | 0.76 | 0.85 | 0.63 | 0.97 | 0.97 | 0.25 | 0.56 | 0.48 | |||
| Krüppel < | 0 | 0.48 | 0.56 | 0.25 | 0.97 | 0.97 | 0.63 | 0.85 | 0.76 | 0.24 |
The first column contains the names of motifs and the motif orientation. The second column shows the difference between the actual and the adjusted coordinate of the first position of the motif. Coordinates were adjusted to compensate for different motif length and motif asymmetry. Rows contain the informational content of site alignment columns. Motif cores with a high information content are in bold.
With the described rules, the distances can be measured between sites that belong to the same binding motif or between sites belonging to different binding motifs; between sites located on the same DNA strand (in tandem) or sites on the opposite strands (in palindrome).
Non-random arrangement of binding motifs in CRMs
To test whether the binding site arrangement in the Drosophila CRMs is non-random, we calculated all distances between neighboring binding sites for the five motifs, and compared the obtained distance distribution with the random expectation. In a random sequence, the probability of observing distance n between two neighboring PWM matches can be calculated from the geometric distribution (30):
P(n) = ES(1 – ES)n – 17
where ES is the site occurrence in the selected data set and n (bases) is the distance between the neighboring motif matches. In this test, PWM cutoff values (site likelihood ratio values) were set to achieve the same site occurrence for each binding motif in the Drosophila genome, equal to E = 5 × 10–4 (6). We excluded close distances from this consideration (see ‘Overlapping and correlated motifs’ below).
This statistical test (see Fig. 1 and Methods) demonstrated that the distances between sites in CRMs are smaller than expected from the described random model. We also analyzed the distribution of distances between the neighboring binding sites in Drosophila genome samples (1% of genome total). In fact, a similar distance distribution was observed (see Fig. 1B), although the significance of the short distances in genome samples was much smaller. The existence of microsatellites, repetitive sequences and other correlations in DNA (31) can explain the deviation of the observed from the expected distance distribution in genome samples.
The described analysis demonstrated that binding sites in Drosophila CRMs are distributed in a non-random fashion and the fraction of sites having spacing in the range 50–60 bp is larger than expected. This distance range might correspond to CEs containing several closely spaced binding sites. Notice also that even ‘stand alone’ sites may represent parts of CEs, which were not detected in our search using five binding motifs.
Periodic signals in arrangement of a single binding motif
To explore whether binding sites are distributed periodically in CRMs, we calculated distances between any two binding sites (all possible binding site pairs in a CRM) belonging to the same binding motif or to a binding motif combination. In this case, the distance expectation in a random sequence is independent of the distance itself and has a uniform distribution (30). Therefore, we compared the empirical (observed) distribution of distances for any binding site pair with the uniform distribution.
To minimize interference between periodic signals, specific to different binding motifs (or binding motif combinations), we focused our attention on analysis of distances between sites belonging to one or two binding motifs. Periodic signals present in the resulting distance distributions were assessed using Fourier analysis (see Methods).
First, we built distance distributions and the corresponding Fourier spectra for the three most frequent binding motifs from our data set, Bcd, Hb and Kr. The most striking result, confirming the hypothesis of ‘helical phasing’ (see Introduction), was obtained for Bcd (see Figs 2A and B, 3A and B, and 5A). The vast majority of high-affinity Bcd sites are positioned at distances close to 10, 20, 30 etc. bp. The periodicity in the arrangement of Bcd sites drops rapidly with decreasing site affinity, supporting the biological importance of this specific signal. A similar, but not identical periodic signal was observed in the distribution of distances between binding sites for Hb (Figs 2C and 3D). In this case, however, the period was equal not to 10 but to 11 bp. This difference in periodicity might be explained by a slightly different DNA conformation (twist) of the two binding motifs (compare CCTAATCCC, the consensus for Bcd, and TTTTTTTG, the consensus for Hb). Surprisingly, the distribution of another binding motif, Kr, showed no periodic signal corresponding to the ‘helical phasing’ (see Fig. 3E). The different structure of the Kr DNA-binding domain together with the different mechanism of Kr binding might explain the absence of the ‘helical phasing’ in the distribution of Kr sites. Bcd is known to be involved in cooperative DNA binding (32), which typically requires several closely spaced binding sites. Instead, Kr seems to be involved in competitive rather then cooperative DNA binding (see ‘Overlapping and correlated motifs’ below) (33).
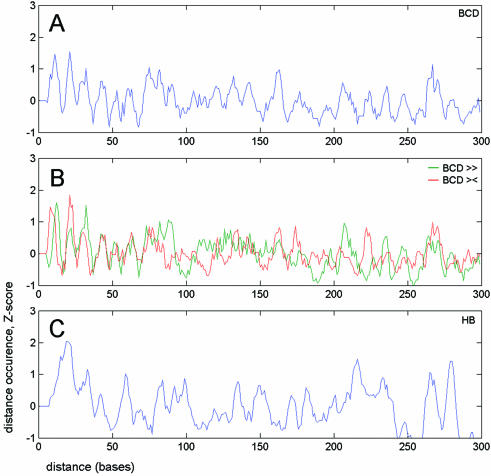
Figure 2.
Distribution of distances built for all binding site pairs. Normalized deviations (Z-scores) calculated for the number of distances between any pair of binding sites. (A) All Bcd site pairs. (B) The same signal is split for Bcd matches found in a tandem (green line) or a palindrome (red line) orientation. (C) All Hb site pairs. In all cases, peaks have a periodic distribution.
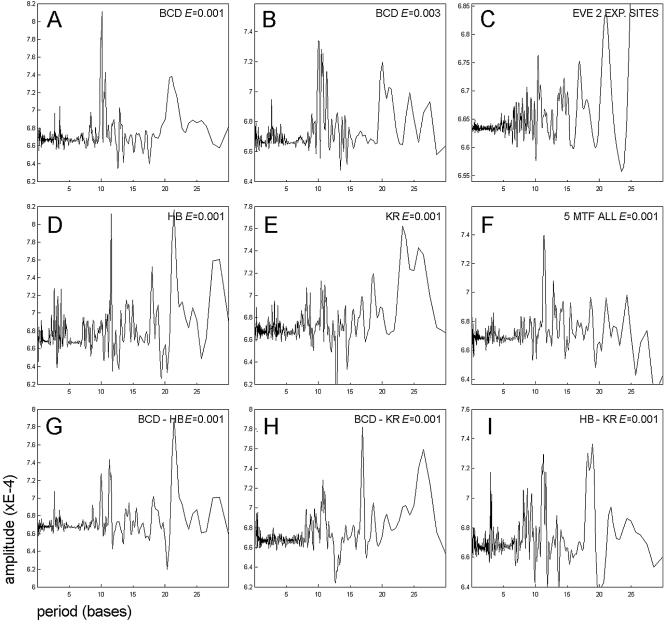
Figure 3.
Periodic signal detected in distance distributions. The spectral amplitude of the Fourier transform for signals such as shown in Figure 2 (all binding site pairs). (A and B) Spectra built for the distribution of Bcd sites with different site probability ES (site affinity). (A) ES = 0.001; (B) ES = 0.003. Note the decrease in the amplitude of the ‘helical’ signal (10 bp) with the increasing ES. (C) Periodicity of site distribution in the even-skipped stripe 2 enhancer. The spectrum built using eve stripe 2 sequences from six Drosophila species. In this case, only experimentally verified sites (not the PWM matches) for Bcd, Hb and Kr were taken into consideration. Together with the main periodic signal (10.5 bp) and its second harmonic (21 bp), one can observe an ‘opposite phase’ signal (17 bp). (D–I) Spectra built for different motif combinations, all having site probability ES = 0.001. (D) Hb motif; (E) Kr motif; (G) Bcd–Hb motif combination; (H) Bcd–Kr motif combination; (I) Hb–Kr motif combination. The spectrum of distance distributions built for the Bcd–Hb motif combination has no additional signals besides those found in the distributions of Bcd and Hb taken separately. A new signal (17 bp) is present in the spectrum built for the combination of Bcd and Kr motifs. This signal is also present in the spectrum built for the even-skipped stripe 2 region (C). (F) Combination of all five binding motifs displays a low-amplitude periodic signal corresponding to the ‘helical phasing’ (11 bp).
Figure 5.
Structure of Bcd–Bcd and Bcd–Kr elements. (A) The alignment of sequences containing specifically spaced Bcd-binding sites (10 bp peak in Fig. 2A). (B) Antagonistic Bcd/Kr element, built from sequences over-represented in CRMs. The list contains some functional Bcd/Kr overlaps found previously in the even-skipped stripe 2 enhancer. The names of CRMs containing the sequences are given at the right side of the alignments.
The arrangement of binding motifs for another transcriptional activator, Cad, also displayed ‘helical phasing’ (data not shown). The Kni motif has a low number of occurrences in our data set and was not considered in this type of analysis.
Periodic signals in arrangement of a binding motif combination
To extract periodic signals corresponding to a specific combination of binding motifs (potential synergistic pairs or CEs), we analyzed distance preferences for pairs (any two matches) of the most frequent motifs from our database, Bcd–Hb, Bcd–Kr and Kr–Hb, and the corresponding Fourier spectra. Expression patterns of Bcd, Hb and Kr in the early embryo have substantial overlaps and the transcription factors are expected to be involved in direct synergistic or antagonistic interactions (33).
Analysis of the Bcd–Hb pair revealed two phasing signals (10 and 11 bp), corresponding to Bcd–Bcd and Hb–Hb combinations (Fig. 3G). The high amplitude of the signal corresponding to the double ‘helical’ period (22 bp) is the result of signal interference from Bcd–Bcd and Hb–Hb pairs (compare positions of peaks corresponding to 2× period in Fig. 3A and D). We also generated the differential Bcd–Hb spectrum (data not shown) by removing distances for Bcd–Bcd and Hb–Hb pairs from our consideration, but detected no high-amplitude periodic signals. Given the periodicity detected in distributions of Bcd and Hb motifs separately, even the presence of a single specific distance for the Bcd–Hb pair would result in a periodic signal. The absence of specific distances between Bcd and Hb suggests that they perform their functions rather independently and perhaps their binding motifs never belong to the same CE, or the potential Bcd–Hb CEs have a flexible structure and are difficult to detect using our type of analysis.
We also explored distance preferences in the distribution of another interesting motif pair, Bcd–Kr. These motifs are very similar (CCTAATCCC, the Bcd consensus, and TAACC CTTT, the Kr consensus) and the corresponding transcription factors are involved in antagonistic interactions by competing for the same binding sequences in regulatory regions (34). We analyzed both the short- (<5 bp, see ‘Overlapping and correlated motifs’, below) and the long-range Bcd–Kr distances. Periodic analysis of the Bcd–Kr distribution (long-range distances) revealed the presence of a new signal, having a period rather opposite to the ‘helical’ (17 bp, see Fig. 3H). The signal was absent in Fourier spectra, built for either Bcd or Kr motif distribution (Fig. 3A and E). The differential Fourier spectrum, generated for Bcd–Kr distances only (data not shown), confirmed the presence of the 17 bp periodic signal and of an additional signal, with a period close to that of the ‘helical’ (11 bp). This second signal is expected, as Bcd and Kr motifs are highly correlated (2 bp shift) and the Bcd sites are distributed periodically (10 bp). However, the signal corresponding to 17 bp is new and its presence suggests that the non-overlapping Bcd and Kr sites have a tendency to be placed on the opposite sides of the DNA helix (bound proteins are facing in opposite directions). In this case, the non-overlapping Bcd and Kr sites may belong to distinct CEs, performing independent functions (see Discussion).
We also extracted periodic signals specific to some other motif combinations (Hb–Kr, no new signals) as well as signals presented in the combination of all five binding motifs (Bcd, Hb, Kr, Kni and Cad). In the latter case, we detected the same ‘helical’ signal (11 bp), although with somewhat lower amplitude. In addition, we measured periodicity in the distribution of experimental sites (not PWM matches) in one of the best studied enhancer regions, even-skipped stripe 2, from six Drosophila species (35). In this case, we also detected the major signal with a period close to 10 bp and the ‘opposite phase’ signal (17 bp), presumably corresponding to the Bcd–Kr motif combination (see Fig. 3C). Table 4 summarizes data for detected periodicities in distributions of the considered binding motif combinations.
Table 4. Periodic signals detected in binding motif distributions.
| Motif | Bcd | Hb | Kr |
|---|---|---|---|
| Bcd | 10, 21 | ||
| Hb | 22 (10, 11) | 11, 22 (18, 19, 28) | |
| Kr | 17 (11, 26) | (11, 18, 19) | 23, 26 (19) |
The signal corresponding to the ‘helical phasing’ (10–11 bp) is present in the distance distribution for Bcd–Bcd and Hb–Hb motif combinations, but absent in the distribution of distances for Kr–Kr. The Bcd–Kr combination displays the signal opposite to the ‘helical phasing’ (17 bp). Low-amplitude signals are shown in parentheses.
These data clearly demonstrate that the arrangement of non-overlapping binding motifs in regulatory regions cannot be described by the simple ‘helical phasing’ formula. Instead, each binding motif as well as each binding motif combination exhibits its own periodicity, sometimes quite different from the major ‘helical’ signal (10–11 bp).
Overlapping and correlated motifs
In the analysis described above, we considered only non-overlapping sites separated by distances exceeding the binding motif lengths. Nevertheless, the overlapping sites are of interest, especially when the binding motifs correlate and the transcription factors compete for the same binding sequences. As described above, the Bcd–Kr (activator–repressor) motif combination is a characteristic example of this quite common biological situation. Bcd (consensus CCTAATCCC) and Kr (consensus TAACCCTTT) motifs may overlap by chance (consensus CCTAAYCCYTTT), but some of the overlaps do correspond to functional antagonistic elements (composite sites) and some do not. We calculated the possible fraction of the functional Bcd/Kr overlaps and extracted these putative antagonistic elements from our database of developmental CRMs.
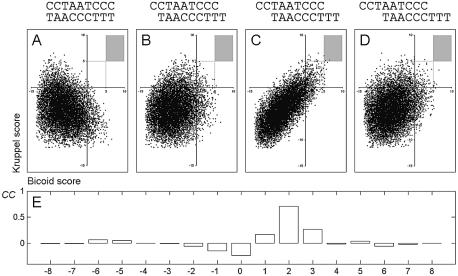
In the first step, we estimated what distance (shift) between Bcd and Kr matches causes maximal motif correlation. For each possible shift, we calculated PWM scores for the Bcd and Kr motifs in every position of a test DNA sequence. Figure 4 shows that the maximal correlation value (CC = 0.7) between the two motifs is observed if they are placed on the same DNA strand (according to the orientations shown) and shifted by two bases. Correlation values obtained for other Bcd/Kr motif shifts were low (no overlapping high-scoring matches). In the second step, we compared the frequency of words containing overlapping Bcd and Kr sites (with the 2 bp shift) in the Drosophila genome with the frequency of the same words in the developmental CRMs (see Methods). Table 2 shows a comparison of the numbers of Bcd/Kr overlaps found in the CRM data set and the corresponding numbers found in the genome and normalized to the sample size (number of sites) of the CRM data set. Words corresponding to Bcd/Kr overlaps and overrepresented in CRM sequences (see numbers in bold in Table 2) were extracted and aligned as shown in Figure 5B. The alignment contains many of the known functional Bcd–Kr elements, for instance those found previously in the even-skipped stripe 2 region.
Figure 4.
Correlation between occurrences of Bcd and Kr motifs. (A–D) Scatter plots show the PWM scores calculated for each position of a test sequence to Bcd (x-axis) and Kr (y-axis). Different shifts between positions of the Bcd and Kr matches (shown on the top of each panel) result in different correlation between the motifs. (A) No shift; (B) +1 bp shift; (C) +2 bp shift; (D) +3 bp shift. Dots in the shaded area correspond to overlapping high-affinity Bcd/Kr sites. (E) Values of the correlation coefficient calculated with different motif shifts. The maximal correlation is observed for a +2 bp shift (CC = 0.7).
The described analysis demonstrates how the test for motif interdependence might help in extraction of antagonistic elements, such as the Bcd/Kr composite binding site. Given a set of transcription regulatory sequences and a list of binding motifs, it seems to be possible to reveal the presence of potential antagonistic relationships among the motifs (competitive binding) without any additional information.
DISCUSSION
Preferred site arrangement in developmental enhancers
The preferential arrangement of binding sites for transcription factors in regulatory modules might be considered as a specific type of functional information encoded in regulatory DNA. In the current work, we demonstrated how to extract preferential site arrangements and potential CEs from large data sets using periodic analysis and a test for motif interdependence.
We have shown that the distribution of Bcd and Hb motifs, considered alone, fits well to the known ‘helical phasing’ rule (10–11 bp), and so the bound transcription factors are placed on the same surface of DNA. According to existing models (10), this preferential binding site arrangement facilitates protein–protein interactions and promotes formation of specific tertiary complexes (DNA–protein–protein–DNA), involved in activation of specific transcription. The phenomenon of ‘helical phasing’ is also known from the distribution of nucleosome positional signals (13), and thus it is very likely that multiple DNA–protein contacts, caused by any large protein complex, have a good chance of following the ‘helical phasing’ rule. The example in Figure 5A represents actual sequences, containing periodically distributed binding sites for Bcd. Alignment of these sequences reveals a common element, containing at least 2–3 high-scoring Bcd matches, which are present in many developmental CRMs.
It is more important, however, that the ‘helical phasing’ rule is not sufficient to describe arrangement of any binding motif or binding motif combination in any regulatory sequence. This fact is demonstrated by periodic signals detected in the distribution of the Kr motif and of the Bcd–Kr binding motif combination (17 bp, see Fig. 3E and H).
Hierarchical levels in the organization of transcription regulatory information
CRMs represent independent functional units, responsible for the formation of specific expression patterns in developing fly embryo. This functional independence of CRMs suggests that they constitute one of the upper levels in the informational hierarchy. Conversely, binding motifs for transcription factors represent the bottom level, as they cannot be divided further, e.g. into smaller functional ‘subwords’. Combinatorial arrangements of binding motifs such as CEs and antagonistic pairs of overlapping motifs (e.g Bcd/Kr) might represent yet another, ‘middle’ level in the informational hierarchy.
In this work, we demonstrated that binding motifs are distributed in Drosophila CRMs in a non-random fashion, with a large fraction of sites belonging to small closely spaced groups (50–70 bp range). Moreover, within these small groups (putative CEs), the distances between the binding sites are far from random and comply with some specific spacing requirements. We believe that these two findings confirm the presence of the ‘middle’ hierarchical level, defining (i) order, (ii) orientation and (iii) spacing in small groups of binding sites. If so, then the ‘upper’ informational level, represented by entire promoters and CRMs, combines several such small functional groups or several CEs, acting independently in their response to the spectrum of native transcriptional signals. For example, repression of the same promoter (CRM) by two transcription factors might be achieved through an independent response of two or more corresponding CEs to the concentrations of these proteins.
One can see that maximal spatial independence of adjacent CEs might be achieved through positioning of corresponding protein complexes on opposite sides of the DNA helix. In this respect, our finding of the 17 bp phasing (opposite to the ‘helical’) in the distribution of the Bcd–Kr motif combination (see Fig. 3C and H) fits the proposed model (see Fig. 6). Three hierarchical levels, binding motifs, CEs and CRMs (as well as proximal promoters), appear to describe the distribution of binding motifs and explain the biological function of motif combinations.
Figure 6.
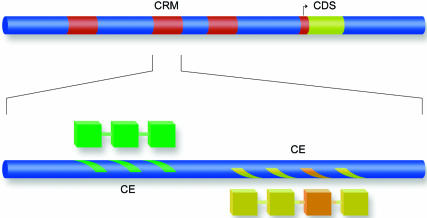
Hierarchy of transcriptional signals. Periodically spaced groups of binding sites (marks on the blue bar) comprise composite elements. Each composite element is responsible for the formation of a cognate protein–protein complex (the connected blocks). A set of independent composite elements bound by different protein complexes (shown by color) comprises a functional cis-regulatory module (CRM).
Genomics approaches and promoter analysis
Specific signals, detected in the distribution of binding motifs at the ‘middle’ level, could be helpful in finding similar CEs in the genome and improving promoter recognition algorithms. On the basis of our periodic analysis and analysis of overlapping motifs, we generated models (alignments) for two putative CEs, containing Bcd–Bcd (synergistic) and Bcd–Kr (antagonistic) motif combinations (see Fig. 5). The motifs corresponding to the CEs are wider, and they provide better grounds for a specific search than the binding motifs for transcription factors themselves. Pre-screening with CEs might also facilitate identification of functional binding motif clusters and functional CRMs in the genome. Periodic arrangement (e.g. ‘helical phasing’) of binding motifs may also help in finding unknown binding motifs in regulatory sequences. This idea can be implemented in motif-extracting software, such as Gibbs Sampler.
CEs can become indispensable for understanding the transcription regulatory code and for reconstructing entire CRMs and promoters. In this respect, identification of CEs in promoters and CRMs and consequent analysis of these CEs both in vivo and in silico represents a high priority goal, as important as identification of promoters themselves. We believe that in future the CE concept will prove to be a powerful tool in analysis of transcription regulatory regions and promoter reconstruction. For instance, the existence of structurally different CEs (together with the different site affinity) might explain the differential gene response to concentrations of transcriptional regulators. Identical CEs found in promoters of different genes may suggest involvement of the genes in the same regulatory cascades and might help in analysis of their function.
Future progress in computational identification of developmental CEs in Drosophila CRMs will depend on the amount and the quality of available binding motifs as well as on the number of available functional CRMs, regulated by the corresponding transcription factors.
Acknowledgments
ACKNOWLEDGEMENTS
We thank Stephen Small for discussion, valuable remarks and help with manuscript preparation. We would also like to thank our reviewers for their careful work and helpful comments. This work was supported by a grant from National Institutes of Health (EM064864) to Claude Desplan. V.J.M. and A.P.L. were also supported in part by grants from the Ludwig Institute for Cancer Research, HHMI East Europe (55000309) and RFBR (02-04-49111). The CRM annotation and related resources are available at the following address: http://homepages.nyu.edu/~dap5/PCL/appendix2.htm.
REFERENCES
- 1.Wagner A. (1999) Genes regulated cooperatively by one or more transcription factors and their identification in whole eukaryotic genomes. Bioinformatics, 15, 776–784. [DOI] [PubMed] [Google Scholar]
- 2.Pickert L., Reuter,I., Klawonn,F. and Wingender,E. (1998) Transcription regulatory region analysis using signal detection and fuzzy clustering. Bioinformatics, 14, 244–251. [DOI] [PubMed] [Google Scholar]
- 3.Berman B.P., Nibu,Y., Pfeiffer,B.D., Tomancak,P., Celniker,S.E., Levine,M., Rubin,G.M. and Eisen,M.B. (2002) Exploiting transcription factor binding site clustering to identify cis-regulatory modules involved in pattern formation in the Drosophila genome. Proc. Natl Acad. Sci. USA, 99, 757–762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Markstein M., Markstein,P., Markstein,V. and Levine,M.S. (2002) Genome-wide analysis of clustered Dorsal binding sites identifies putative target genes in the Drosophila embryo. Proc. Natl Acad. Sci. USA, 99, 763–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rajewsky N., Vergassola,M., Gaul,U. and Siggia,E.D. (2002) Computational detection of genomic cis-regulatory modules applied to body patterning in the early Drosophila embryo. BMC Bioinformatics, 3, 30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lifanov A.P., Makeev,V.J., Nazina,A.G. and Papatsenko,D.A. (2003) Homotypic regulatory clusters in Drosophila. Genome Res., 13, 579–588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stathopoulos A., Van Drenth,M., Erives,A., Markstein,M. and Levine,M. (2002) Whole-genome analysis of dorsal–ventral patterning in the Drosophila embryo. Cell, 111, 687–701. [DOI] [PubMed] [Google Scholar]
- 8.Dion V. and Coulombe,B. (2003) Interactions of a DNA-bound transcriptional activator with the TBP–TFIIA–TFIIB–promoter quaternary complex. J. Biol. Chem., 278, 11495–11501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Inoue J., Sato,R. and Maeda,M. (1998) Multiple DNA elements for sterol regulatory element-binding protein and NF-Y are responsible for sterol-regulated transcription of the genes for human 3-hydroxy-3-methylglutaryl coenzyme A synthase and squalene synthase. J. Biochem., 123, 1191–1198. [DOI] [PubMed] [Google Scholar]
- 10.D'Alonzo R.C., Selvamurugan,N., Karsenty,G. and Partridge,N.C. (2002) Physical interaction of the activator protein-1 factors c-Fos and c-Jun with Cbfa1 for collagenase-3 promoter activation. J. Biol. Chem., 277, 816–822. [DOI] [PubMed] [Google Scholar]
- 11.Sarafova S. and Siu,G. (2000) Precise arrangement of factor-binding sites is required for murine CD4 promoter function. Nucleic Acids Res., 28, 2664–2671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Scully K.M., Jacobson,E.M., Jepsen,K., Lunyak,V., Viadiu,H., Carriere,C., Rose,D.W., Hooshmand,F., Aggarwal,A.K. and Rosenfeld,M.G. (2000) Allosteric effects of Pit-1 DNA sites on long-term repression in cell type specification. Science, 290, 1127–1131. [DOI] [PubMed] [Google Scholar]
- 13.Ioshikhes I., Trifonov,E.N. and Zhang,M.Q. (1999) Periodical distribution of transcription factor sites in promoter regions and connection with chromatin structure. Proc. Natl Acad. Sci. USA, 96, 2891–2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Praz V., Perier,R., Bonnard,C. and Bucher,P. (2002) The Eukaryotic Promoter Database, EPD: new entry types and links to gene expression data. Nucleic Acids Res., 30, 322–324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Matys V., Fricke,E., Geffers,R., Gossling,E., Haubrock,M., Hehl,R., Hornischer,K., Karas,D., Kel,A.E., Kel-Margoulis,O.V., Kloos,D.U., Land,S., Lewicki-Potapov,B., Michael,H., Munch,R., Reuter,I., Rotert,S., Saxel,H., Scheer,M., Thiele,S. and Wingender,E. (2003) TRANSFAC: transcriptional regulation, from patterns to profiles. Nucleic Acids Res., 31, 374–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Guss K.A., Nelson,C.E., Hudson,A., Kraus,M.E. and Carroll,S.B. (2001) Control of a genetic regulatory network by a selector gene. Science, 292, 1164–1167. [DOI] [PubMed] [Google Scholar]
- 17.Szymanski P. and Levine,M. (1995) Multiple modes of dorsal–bHLH transcriptional synergy in the Drosophila embryo. EMBO J., 14, 2229–2238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Arnosti D.N. (2003) Analysis and function of transcriptional regulatory elements: insights from Drosophila. Annu. Rev. Entomol., 48, 579–602. [DOI] [PubMed] [Google Scholar]
- 19.Chytil M., Peterson,B.R., Erlanson,D.A. and Verdine,G.L. (1998) The orientation of the AP-1 heterodimer on DNA strongly affects transcriptional potency. Proc. Natl Acad. Sci. USA, 95, 14076–14081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Remenyi A., Tomilin,A., Scholer,H.R. and Wilmanns,M. (2002) Differential activity by DNA-induced quarternary structures of POU transcription factors. Biochem. Pharmacol., 64, 979–984. [DOI] [PubMed] [Google Scholar]
- 21.Diamond M.I., Miner,J.N., Yoshinaga,S.K. and Yamamoto,K.R. (1990) Transcription factor interactions: selectors of positive or negative regulation from a single DNA element. Science, 249, 1266–1272. [DOI] [PubMed] [Google Scholar]
- 22.Kel-Margoulis O.V., Kel,A.E., Reuter,I., Deineko,I.V. and Wingender,E. (2002) TRANSCompel: a database on composite regulatory elements in eukaryotic genes. Nucleic Acids Res., 30, 332–334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hannenhalli S. and Levy,S. (2002) Predicting transcription factor synergism. Nucleic Acids Res., 30, 4278–4284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Qiu P., Ding,W., Jiang,Y., Greene,J.R. and Wang,L. (2002) Computational analysis of composite regulatory elements. Mamm. Genome, 13, 327–332. [DOI] [PubMed] [Google Scholar]
- 25.Wasserman W.W. and Fickett,J.W. (1998) Identification of regulatory regions which confer muscle-specific gene expression. J. Mol. Biol., 278, 167–181. [DOI] [PubMed] [Google Scholar]
- 26.Krivan W. and Wasserman,W.W. (2001) A predictive model for regulatory sequences directing liver-specific transcription. Genome Res., 11, 1559–1566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pilpel Y., Sudarsanam,P. and Church,G.M. (2001) Identifying regulatory networks by combinatorial analysis of promoter elements. Nature Genet., 29, 153–159. [DOI] [PubMed] [Google Scholar]
- 28.Papatsenko D.A., Makeev,V.J., Lifanov,A.P., Regnier,M., Nazina,A.G. and Desplan,C. (2002) Extraction of functional binding sites from unique regulatory regions: the Drosophila early developmental enhancers. Genome Res., 12, 470–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Waterman M.S. (1995) Introduction to Computational Biology. Chapman & Hall London, UK. [Google Scholar]
- 30.Feller W. (1970) An Introduction to Probability Theory and its Applications, 3rd edn. John Wiley & Sons, New York. [Google Scholar]
- 31.Peng C.K., Buldyrev,S.V., Goldberger,A.L., Havlin,S., Sciortino,F., Simons,M. and Stanley,H.E. (1992) Long-range correlations in nucleotide sequences. Nature, 356, 168–170. [DOI] [PubMed] [Google Scholar]
- 32.Burz D.S., Rivera-Pomar,R., Jackle,H. and Hanes,S.D. (1998) Cooperative DNA binding by Bicoid provides a mechanism for threshold-dependent gene activation in the Drosophila embryo. EMBO J., 17, 5998–6009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Rivera-Pomar R. and Jackle,H. (1996) From gradients to stripes in Drosophila embryogenesis: filling in the gaps. Trends Genet., 12, 478–483. [DOI] [PubMed] [Google Scholar]
- 34.Small S., Blair,A. and Levine,M. (1992) Regulation of even-skipped stripe 2 in the Drosophila embryo. EMBO J., 11, 4047–4057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Ludwig M.Z., Patel,N.H. and Kreitman,M. (1998) Functional analysis of eve stripe 2 enhancer evolution in Drosophila: rules governing conservation and change. Development, 125, 949–958. [DOI] [PubMed] [Google Scholar]