Abstract
The basic differences between the 20 natural amino acid residues are due to differences in their side-chain structures. This characteristic design of protein building blocks implies that side-chain–side-chain interactions play an important, even dominant role in 3D-structural realization of amino acid codes. Here we present the results of a comparative analysis of the contributions of side-chain–side-chain (s-s) and side-chain–backbone (s-b) interactions to the stabilization of folded protein structures within the framework of the CHARMm molecular data model. Contrary to intuition, our results suggest that side-chain–backbone interactions play the major role in side-chain packing, in stabilizing the folded structures, and in differentiating the folded structures from the unfolded or misfolded structures, while the interactions between side chains have a secondary effect. An additional analysis of electrostatic energies suggests that combinatorial dominance of the interactions between opposite charges makes the electrostatic interactions act as an unspecific folding force that stabilizes not only native structure, but also compact random conformations. This observation is in agreement with experimental findings that, in the denatured state, the charge–charge interactions stabilize more compact conformations. Taking advantage of the dominant role of side-chain–backbone interactions in side-chain packing to reduce the combinatorial problem, we developed a new algorithm, ChiRotor, for rapid prediction of side-chain conformations. We present the results of a validation study of the method based on a set of high resolution X-ray structures.
Keywords: protein structure, protein folding, amino acid code, side-chain prediction, electrostatic interactions, van der Waals interactions
An important feature of natural amino acid residues in respect to their role as the basic building blocks of proteins, is that they are assembled from two distinct units—the chemically nonvariable peptide backbone and the highly variable side-chain groups. This characteristic design suggests that interactions between amino acid side chains are important intramolecular interactions in the structural realization of amino acid code. Based on this premise, many knowledge-based potentials used in protein modeling are derived from the frequencies of atomic contacts only between side-chain atoms (Tanaka and Sheraga 1976; Miyazawa and Jernigan 1985; Skolnick et al. 1997). Similarly, many side-chain-predicting algorithms focus their search strategies on intensive sampling of the mutual side-chain–side-chain orientations, some of them based on powerful dead-end elimination theory (Desmet et al. 1992). On the other hand, simpler predictive methods (Eisenmenger et al. 1993; Xiang and Honig 2001) have shown that the sampling of mutual side-chain orientations is relatively unimportant to the prediction of side-chain packing. This suggests that other forces involving side chains may play the dominant role in amino acid side-chain packing and consequently in stabilizing protein native conformation. A few studies have analyzed how the relative contributions of side-chain–side-chain and side-chain–backbone interactions to the stabilization of protein structures extend beyond the well-recognized restrictive role of backbone environment on side-chain conformation (Gelin and Karplus 1979; Desmet et al. 1992). Eisenmenger et al. were among the first to address this question (Eisenmenger et al. 1993). Based on the results of side-chain predictions and the statistics of short-range contacts in a small set of protein structures, the authors concluded that the main chain has the dominant effect on the optimization of side-chain geometry. A more recent statistical analysis (Buchete et al. 2004) of short-range intramolecular contacts in globular proteins demonstrates that side-chain–backbone contacts represent a substantial fraction of all side-chain contacts. From this observation, the authors developed novel, orientation-dependent statistical potentials by including a virtual backbone center as a 21st interacting site. In a study on determinants of side- chain packing (Tanimura et al. 1994) the authors concluded that the average “discriminating power” of side-chain–side-chain and side-chain–backbone interactions are almost equal.
In order to understand the side-chain packing forces better, we undertook a comparative analysis of different intramolecular energy contributions involving amino acid side chains. In agreement with several previous studies, but somewhat contradictory to conventional thinking, our results indicate that among intramolecular side-chain interactions, the side-chain–backbone interaction is the dominant force for side-chain packing and for stabilizing the folded structure. This observation suggests two possible improvements to protein modeling approaches. First, if the mutual interactions between amino acid side chains are of secondary importance, it is possible to reduce the combinatorial search in many side-chain predicting algorithms. Second, side-chain–backbone interaction should be considered when constructing knowledge-based potentials for protein modeling. The calculated electrostatic contribution to s-s interactions showed some interesting but counterintuitive results for misfolded structures. This led us to undertake an additional theoretical analysis of charge–charge interactions involving acidic and basic residues. The results suggest that charge–charge interactions stabilize compact protein conformations in a nonspecific way.
During the past decade, a large number of side-chain optimization algorithms have been described in the literature that use different search strategies and computational methods (De Mayer et al. 1997; Looger and Hellinga 2001), including dead-end elimination theory (Desmet et al. 1992), Monte Carlo methods (Liang and Grishin 2002; Peterson et al. 2004), iterative search (Xiang and Honig 2001), Gaussian evolutionary method (Yang et al. 2002), and graph theory (Canutescu et al. 2003). Most of these methods are based on combinatorial sampling using different types of rotamer libraries, such as backbone-independent (Ponder and Richards 1987), backbone-dependent (Dunbrack Jr. and Karplus 1993), and even libraries including dihedral angles, bond lengths, and bond angles (Xiang and Honig 2001). On the other hand, it has been demonstrated (Eisenmenger et al. 1993) that combinatorial searches can be reduced to a search of side-chain conformers with optimal interactions with backbone only without significant lost of accuracy.
Based on the observation of the dominant role of side-chain–backbone interactions, we developed a new CHARMm (Brooks et al. 1983) based algorithm, ChiRotor, for rapid side-chain modeling by using a limited sampling procedure in combination with energy minimization. Initially ChiRotor places each side chain in absence of other side chains to reduce the combinatorial problem. However, a principle difference between ChiRotor and other similar methods (Eisenmenger et al. 1993) in general is that we limited the combinatorial search to a possible minimum, sampling only three initial conformers per residue. In other words, our working hypothesis was that the steering effect of side-chain–backbone interactions is strong enough that the use of energy minimization makes more exhaustive conformational sampling unnecessary.
Theory
Our analysis focuses on interactions involving side-chain and backbone atoms as variable and nonvariable components of amino acid residues. We used two united atom force fields: CHARMm polar hydrogens (Momany and Rone 1993) and charmm19 (Neria et al. 1996). The Cβ atom is generally treated as part of the backbone since it is present in most amino acid residues and its position is determined from main-chain conformation. However, in the CHARMm force field, a few residues, such as Asp and Ser, have a part of the total side-chain electrostatic charge delocalized on the Cβ atom. To minimize noise in the results from charging backbone groups with a part of side-chain charge, in electrostatic calculations only, the Cβ atom's contribution to the electrostatic energy is treated as part of the side-chain energy.
In empirical molecular models with implicit solvation terms, the total energy of a conformational state can be expressed by the potential of mean-force E:
The potential E is formed from the energies of intramolecular interactions between protein atoms, Fintra, and the interactions of protein atoms with the solvent, ΔGslv. Because the interactions between atoms inside the same residue as well as the interactions between backbone atoms were beyond the scope of this study, the corresponding contributions were omitted. The energies of s-s and s-b intramolecular interactions, Fintra, were calculated as sum of van der Waals and electrostatic terms:
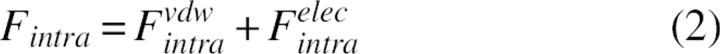 |
Some implicit solvent models, such as Generalized Born (GB) (Still et al. 1990), allow us to combine the electrostatic interactions between charged atoms easily with the screening effect of the solvent polarization. In this study we used the Genborn module in CHARMm (Dominy and Brooks III 1999) as the implicit solvent model. GB allows the polar contribution to be referenced to an environment with the dielectric properties of the protein interior and, consequently, the second term in Equation 2 is calculated as (Bashford and Case 2000):
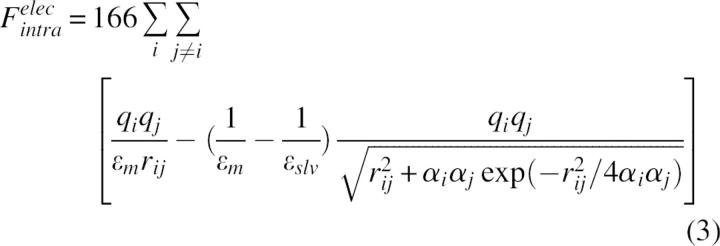 |
where qi are the atomic partial charges, αi are the atomic Born radii, and ɛm and ɛslv are the dielectric constants of the molecule and solvent, respectively.
The additivity of pairwise atomic contributions in Equation 3 allows all terms forming Equation 2 to be decomposed into group–group terms and makes it possible to evaluate and compare the net effect of different types of interactions between variable and nonvariable parts of amino acid residues:
where Fb-b is the energy of intramolecular interactions between backbone atoms, Fs-b is the contribution of the interactions of side chains with backbone, and Fs-s is the interaction energy between amino acid side chains. Taking into account the capability of backbone atoms to form intensive networks of hydrogen bonds, the Fb-b term should have a considerable, even the major contribution to Fintra. However, the value of Fb-b does not reflect directly the differences in amino acid sequence, if excluding some effects of Gly and Pro residues. Hence, the selection of native structure should be going mainly through the optimization of the interactions forming Fs-b, Fs-s, and, of course, ΔGslv between a number of possible backbone folds with relatively low Fb-b energies.
Fs-b and Fs-s can be decomposed additionally as sums of intraresidue and interresidue terms:
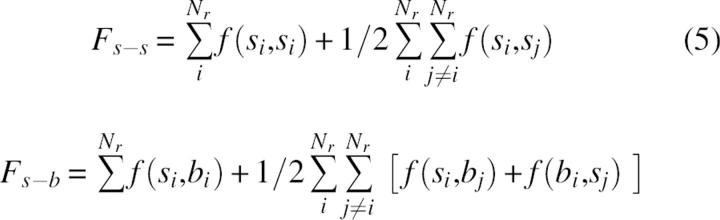 |
where si and bi denote the group of side-chain atoms and backbone atoms of residue i, respectively, and Nr is the number of residues. In contrast to side-chain–side-chain interaction terms, the self terms, f(si,si) and f(bi,si) include some covalent 1–2 and 1–3 interaction types. In the folding process the optimization of f self terms can be important for the selection of the possible backbone or side-chain conformations, but does not contribute directly to the forces that keep protein structures folded. To avoid the noise of a possible artificial coupling between covalent and noncovalent terms, we limited the analysis to the interresidue parts of intramolecular energy, given by
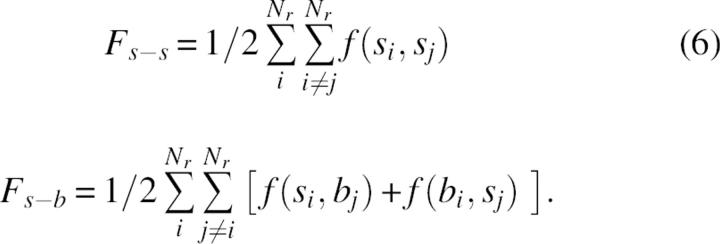 |
Note, that according to Equation 6, any residue i can contribute to side-chain–backbone energy not only through its side-chain atoms, but also through interactions of the backbone group with other side chains. This means that in a random protein structure, the formation of up to two s-b contacts versus no more than one s-s contact will be possible for any two residues in close contact.
Results and Discussion
Side-chain determinants of intramolecular interactions
Most of the results in this article were obtained using a set of 24 nonhomologous proteins with high resolution structures (S24, see Materials and Methods). The atomic composition of the S24 set shows that the average number of side-chain heavy atoms varies from 2.5 to 3 atoms in different proteins, while backbone atoms are consistently ∼4.9 atoms per residue, when the Cβ atom is considered as a part of the backbone. The ratio above suggests that the optimization of s-b interactions might be important for the stabilization of native structure, even taking into account that some backbone atoms are involved in short-range interactions with other backbone atoms. A similar, unbalanced atomic composition has been reported before (Eisenmenger et al. 1993) as well as an unexpectedly large number of short-range s-b contacts compared to s-s interactions.
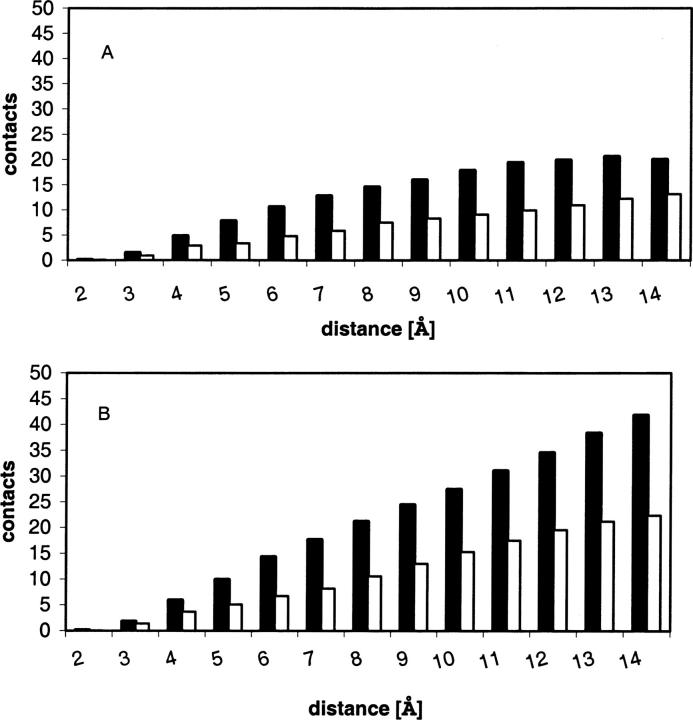
Considering the importance of atomic distributions around the side-chain atoms as determinant of intramolecular forces, we undertook a further analysis. For each structure in the S24 set we calculated the distribution of the heavy atoms around any side-chain atom as a function of distance. The results presented in Figure 1 show the average numbers of side-chain and backbone atoms, respectively, within a 1-Å spherical layer around any given side-chain atom. Figure 1A shows the distribution of a 64-residue protein, 1aho, which is typical for small proteins in the S24 set, and Figure 1B shows the distribution of a 321-residue protein, 1ixh, typical for the large proteins. The most important feature seen in Figure 1 is that side-chain atoms are surrounded mainly by backbone atoms, and the average number of s-b contacts dominates the number of s-s contacts at a ratio of ∼2:1 at almost all distances, including the most important range, ∼3 to ∼6 Å, for stabilizing van der Waals and some polar contacts. Consequently, for the attractive van der Waals interactions, the cumulative stabilizing effect of optimizing the s-b term is expected to be significantly larger than of s-s terms. For the electrostatic terms, however, the distributions on Figure 1 are not directly informative, because of the significant contribution of a small number of charged side chains of acidic and basic residues. However, at least for the “dipole–dipole” type of interactions between side-chain and backbone groups, the results indicate that the optimization of the s-b interaction might have more potential than the s-s optimization to stabilize native structure.
Figure 1.
The average number of side-chain atomic contacts with backbone atoms (black bars) and with side-chain atoms (white bars) as a function of distance. The data are averaged for spherical layers of 1 Å thickness. (A) 1AHO structure (64 residues); (B) 1IXH structure (321 residues).
The striking difference in densities of the surrounding backbone and side-chain atoms was an additional motivation to study the relative contribution of s-b and s-s interactions to the protein folding mechanism. The rigorous approach to study the role of a given interaction type in the folding process is to compare the differences in corresponding free energy terms between native and unfolded states. However, the modeling and evaluation of the average properties of the unfolded state is an extremely difficult problem, because it is related to the sampling of an enormous number of possible conformers. Therefore, following other examples in the literature (Shaefer et al. 1997; Warwicker 1999), we referenced the energy terms of native (ntv) structures not to the energies derived from an ensemble of unfolded structures, but to the energy of a single conformation, modeled as a relaxed β-strand. In other words, the modeled intramolecular energy of folding will be referenced to a “totally unfolded structure” β:
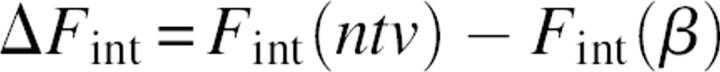 |
and, correspondingly,
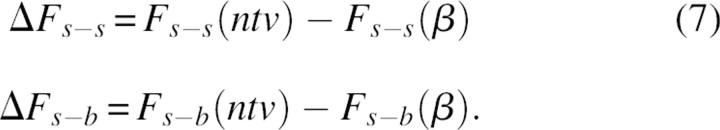 |
Although the extended conformational state might not be the best approximation of the denaturated state (Elcock 1999), we believe that the model results are informative. Equation 7 gives an estimation that is close to the upper limit of the folding energy as well as to the upper limit of the differences in intramolecular energy terms between a folded state and a conformational state with minimum long-range noncovalent interactions.
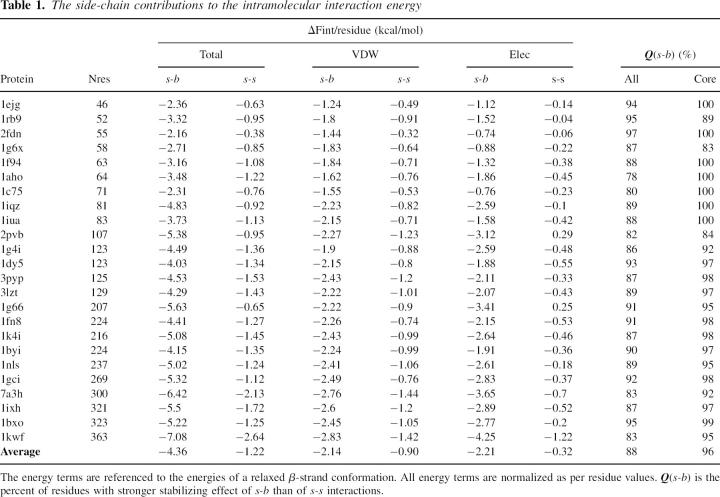
Table 1 compares the s-b and s-s contributions to ΔFint calculated for all proteins from the S24 set. The energy terms are derived from the minimized X-ray structure assuming a minimized reference state.
Table 1.
The side-chain contributions to the intramolecular interaction energy
All energy terms in Table 1 correspond to the normalized per residue values of intramolecular contribution to the folding energy ΔF.
As expected, the transition from an extended state to the native conformation results in a considerable gain in the total side-chain interaction energy, about 5.6 kcal/mol per residue on average. For all studied proteins, the side-chain interactions provide a stabilizing effect on native structure, and this effect becomes stronger with the increasing size of the protein. The most striking result is that, for all studied structures, the stabilizing effect of side-chain–backbone interactions is more than three times stronger than that of the interactions between side chains. Surprisingly this result comes not only from the van der Waals contributions, but also in almost the same proportion from the electrostatic interaction. The last column of Table 1 gives the percentages, Q, of the residues that have lower s-b energies than s-s energies. The significantly lower s-b energies than s-s energies, as well as the high Q values, suggest that the interactions of the side chains with the backbone are effectively the real intramolecular glue that prevents the structure from unfolding, while the interactions between side chains have a secondary effect. The above feature is more strongly expressed in the interactions of the residues from the protein core, because the atoms of surface residues are less involved in intramolecular interactions.
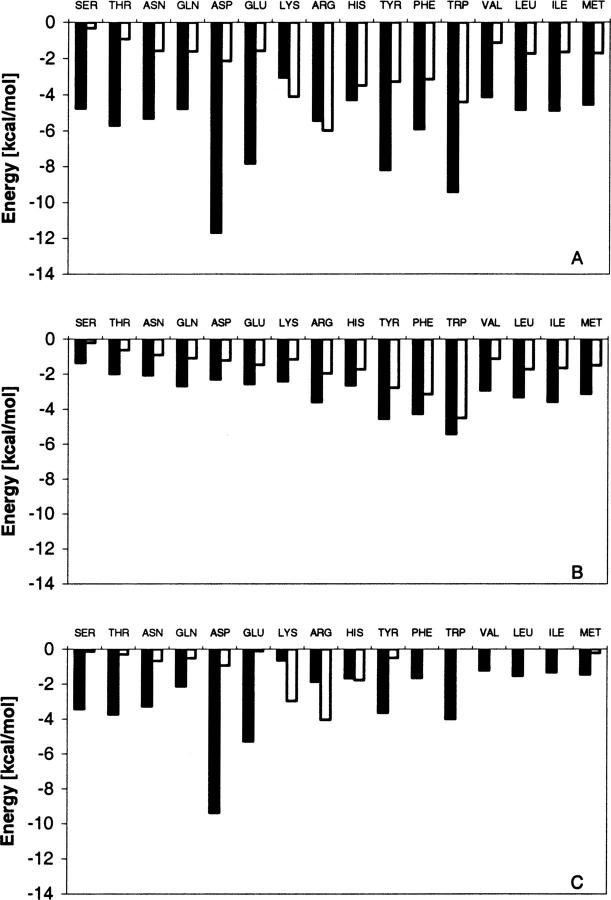
For a more detailed look at the factors influencing the difference between the net s-b and s-s interaction energies, we calculated the contributions of the different types of amino acid residues to ΔFintra. The data shown in Figure 2 represent the mean values of residue contributions averaged over all residues in proteins from the S24 set. A general conclusion that can be drawn from Figure 2 is that both types of interaction terms, s-s and s-b, show stabilizing van der Waals and electrostatic contributions to intramolecular energy of folding for all amino acid residues. In other words, none of the amino acid side chains have evolved a destabilizing role in respect to intramolecular energy of folding. For electrostatic interactions the above result is not exactly trivial, since if there is a difference between the numbers of negatively and positively charged groups, the electrostatic s-s interactions may not favor the folded states, even being optimized almost always in native conformation (Spassov and Atanasov 1994; Spassov et al. 1994; Petrey and Honig 2000). In summary, the stabilizing effect is larger from s-b interactions than from s-s interactions for almost all amino acid residues. This result is in agreement with the results shown in Table 1 and is valid for almost all types of side chains and for both van der Waals and electrostatic interactions, except for the electrostatic terms involving charged Lys and Arg residues. A large electrostatic term of s-s interactions reflects the involvenemt of Lys and Arg residues in salt bridges or networks of charged groups. Similar results should be expected for Asp and Glu; however, not taking into account the metal ions or positively charged ligands in the analysis, the results are affected by uncompensated interactions between anionic side-chain groups involved in ion-binding clusters. Therefore the results of the electrostatic contribution to s-s interaction should be generalized with caution for charged side chains.
Figure 2.
Average contributions of different amino acid residues to intramolecular energy of folding. (Black bars) The energy of s-b interactions; (white bars) s-s interactions. (A) Total interaction terms; (B) van der Waals contributions; (C) electrostatic contributions.
The results in Figure 2 also show a striking difference in the stabilizing effect of s-b interactions involving Asp and Glu relative to all other residues. This feature is consistent with the results of a previous statistical analysis (Spassov et al. 1997) that the interactions between ionogenic side chains and the peptide backbone show a considerably higher level of structural optimization compared to the charge–charge interactions between side chains. However, the effect is only observed for negatively charged Asp and Glu, and not for the positive Lys and Arg residues. A possible explanation of this charge “asymmetry” follows from the asymmetry in the distribution of the electrostatic potential generated from backbone permanent dipoles in the interior of native proteins. It has been found (Spassov et al. 1997; Gunner et al. 2000) that the protein side-chain atoms are immersed dominantly in a space of positive potential generated by the peptide backbone.
The results in Table 1 and Figure 2 demonstrate a major stabilization role of s-b interactions in protein native structure. In addition, it is important to know if the s-b interactions play a dominant role in differentiating the true native fold from alternative folded conformations. One way to study this is to compare energies of native structures with energies of the alternative folds of the same sequence. Similar to the approach used in the study of free energy determinants of tertiary structure (Petrey and Honig 2000), we used the same EMBL set (Holm and Sander 1992) of deliberately misfolded protein structures as structural models to evaluate the discriminative role of the different interaction terms to protein intramolecular energy.
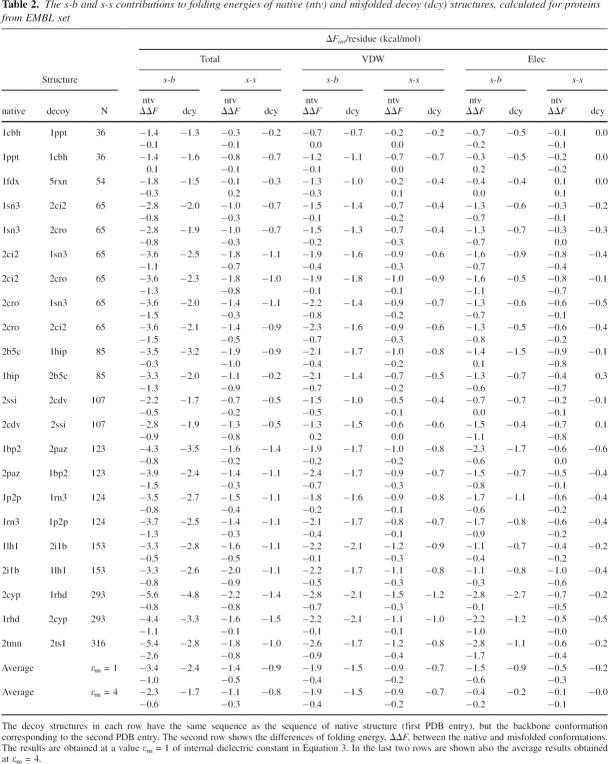
Table 2 compares the energies of s-b and s-s interactions calculated for pairs of native and decoy structures from the EMBL collection of misfolded proteins. Each decoy structure has the same sequence as the native one, but belongs to a completely different fold. The decoy structures are modeled based on the atomic coordinates of protein main chain taken from the second PDB entry in Table 2. As expected, Table 2 shows that the average contributions to ΔF of the native structures of the EMBL set are similar to those of the S24 set and that the two data sets have almost the same ratio between s-b and s-s contributions. The decoy structures also have considerable stabilizing negative ΔF energies for almost all s-b and s-s interactions. This result indicates that the amino acid side chains have many stabilizing intramolecular contacts even in the nonnative folds. Interestingly, both native and decoy conformations show similar ratios between the average values of s-b and s-s interaction terms. For each pair of PDB entries in Table 2, the second row shows the differences, ΔΔF, between the intramolecular energy terms calculated for native and misfolded structures:
Table 2.
The s-b and s-s contributions to folding energies of native (ntv) and misfolded decoy (dcy) structures, calculated for proteins from EMBL set
For almost all types of s-s and s-b interactions, the native structures have lower energies than the decoy structures. On average, the intramolecular interaction energy of an amino acid side chain is lower by 1.4 kcal/mol in the native structures than in the decoy structures. This implies that for a relatively small protein of 100 residues, the native conformation will be differentiated from a misfolded structure by a significant amount, 140 kcal/mol, of intramolecular energy.
Similar to the transition from extended to native conformation, on average, the s-b interactions have about twice as strong an effect on discriminating the decoy structures than s-s interactions, and this is valid for both van der Waals and electrostatic contributions. As a test for a possible effect on the results of the value of molecular dielectric constant, in Table 2 we present also the average results obtained at a value of ɛm in Equation 3 equal to 4. It is seen that in increasing the ɛm value, the absolute values of the electrostatic contributions decrease, but the ratios between s-b and s-s interaction terms remain almost the same in all cases.
An unexpected result from the calculations on the EMBL decoy structures can be seen in the last column of Table 2, where the contributions of side-chain–side-chain electrostatic interactions to folding energy systematically show stabilizing negative values. The energy of s-s electrostatic interactions is formed mainly from the interactions between charged groups, and because the charged groups in decoy structures are distributed in an arbitrary way, one would expect the stabilizing and destabilizing s-s electrostatic contributions to appear in an arbitrary way as well. In an attempt to explain the origin of the stabilizing effect of s-s electrostatic terms seen in all decoy structures, we carried out a novel simple analysis of charge–charge interactions.
Charge–charge interactions in proteins
As an initial model consider a virtual charge multipole or polymer chain containing N+ positively charged groups and N− negatively charged groups approximated as point charges Qi+ = 1 and Qj− = −1 e.u. unit charges with coordinates Xi+ and Xj−, respectively. The total energy of electrostatic interactions Eel can be expressed as:
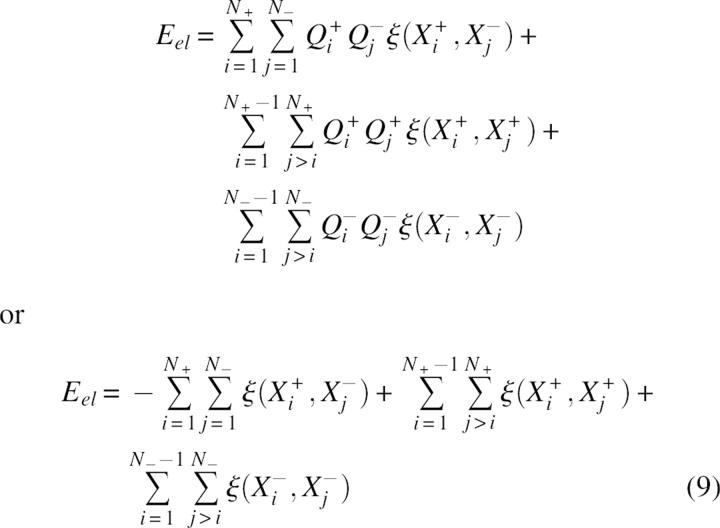 |
where ξ(X, Y) is the energy of interaction of two positive unit charges with coordinates X and Y. In the absence of structure information the pairwise terms in Equation 9 are approximated by a mean interaction energy <ξ> and, using Coulomb's law, <ξ> ≅ C/ ɛ Reff where Reff corresponds to a mean effective distance and C = 332 kcal/mol. Consequently, after some simple transformations, the electrostatic energy can be expressed as:
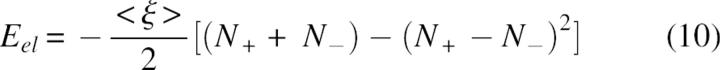 |
or expressed in Coulomb's law
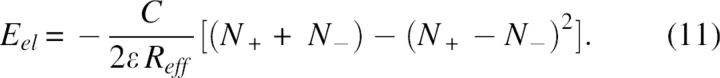 |
The main result, from Equations 9–11, is that the energy of an arbitrary charge constellation will most probably have a negative value, if the numbers of positively and negatively charged groups are the same or not highly unbalanced. For example, the expected electrostatic energy of an arbitrary multipole of 10 positive and 10 negative charges, according to Equation 11, will be a considerably negative value, Eel =−10C/ɛReff and the energy of a small ion-pair cluster of two cations and one anion on a triangle of equal distances will have a negative value, Eel =−C/ɛReff etc.
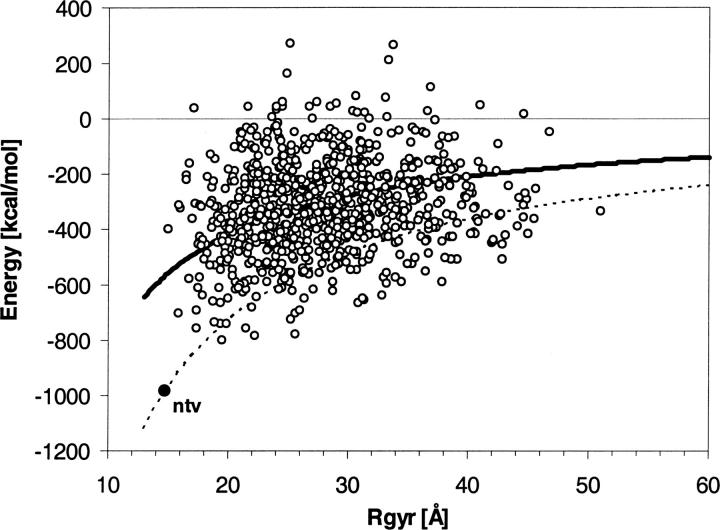
To illustrate the average stabilizing effect of charge–charge interactions following from Equation 11, we calculated the Coulomb contribution to electrostatic energy for an ensemble of 1000 randomly folded structures. The results are shown in Figure 3. The structure of 2i1b in the PDB database is selected for illustrative purposes, as a structure with a balanced number of 18 cationic and 19 anionic side-chain groups. Each of the 1000 arbitrarily folded structures was generated by CHARMm using random combinations of paired values of ϕ and ψ main-chain dihedral angles of amino acid residues. The initial values of ϕ, ψ pairs, (ϕ = −120, ψ = 120°) and (ϕ = −65, ψ = −40°) correspond to the most populated “β strand” and “right α helix” areas on Ramachandran plots. The random structures are relaxed using optimization protocols as explained in Materials and Methods. It is important to note that the structural optimization is carried out without an electrostatic term in the CHARMm energy function. In electrostatic energy calculations the model was idealized by removing all partial charges and modeling the charged groups of ionic residues as point charges, centered on CG, CD, NZ, and CZ atoms of Asp, Glu, Lys, and Arg, respectively. The electrostatic energy for each random structure was calculated as a Coulomb term without any cutoffs. In this analysis the effect of the solvent was not considered and calculation assumed done in vacuum with dielectric constant, ɛ = 1. Considering that the more compact structures correspond to shorter effective distances Reff, in turn, lower electrostatic energy, the computed electrostatic energy term for the random structures is presented in Figure 3 as a function of the radius of gyration, Rgyr.
Figure 3.
The energy of charge–charge interactions in native structure and 1000 random conformation of 2i1b calculated as a function of the radius of gyration of the protein.
The majority of the randomly folded structures show large negative values of the Coulomb electrostatic term, in full agreement with Equation 11. The average energies of the random structures can be approximated by Equation 11 with Reff ≈ 0.7 Rgy and are represented by the bold line in Figure 3. Reflecting the evolutionary optimization of electrostatic interactions, the effective distance between charge centers in native structure shows a lower Reff ≈ 0.4 Rgyr. The dashed line represents Eel calculated using Equation 11 but with Reff ≈ 0.4 Rgyr, i.e., a rough approximation of what energy would be if the structural optimization of charge–charge interactions in a random structure were similar to native structure of 2i1b. Figure 3 shows that the energy values of many random structures are below the dashed line, which implies a relatively low level of spatial optimization of charge–charge interactions in 2i1b native structure, a feature that is not unusual in proteins (Spassov et al. 1994).
Based on the combinatorial dominance of counterion interactions, expressed by Equations 10 and 11, as well as observed in Figure 3, we suggest a novel role of electrostatic interactions as an unspecific folding force that stabilizes not only native structure, but also compact random structures.
An interesting conclusion from Equations 10 and 11 is that, in vacuum or other low dielectric media, proportionally increasing the numbers of positively and negatively charged residues can be used to stabilize structures with more compact shape. In water solvent, however, the situation is more complex, since any gain in intramolecular electrostatic stabilization of the more compact states will be offset by the reduction of the polar interactions between charged groups and solvent molecules. Interestingly, if desolvation effects are neglected, our simple model gives a reasonable explanation of the experimental data reported recently by Pace et al. (2000). Based on the pH-dependent denaturation and mutation experiments, the authors suggested that if not too far from iso-electric point, the unfolded polypeptide chains are rearranged to compact conformations favored by long-range electrostatic interactions. The same conclusion can be drawn from Equation 10; i.e., in more compact structures the charge centers, on average, will be at closer distances, the absolute value of pairwise electrostatic interaction term <ξ> will increase, and, consequently, the electrostatic energy will have more negative values than in more extended structures. Note that, according to Equation 10, the average stabilization effect of charge interactions depends on the difference between positively and negatively charged groups in a nonlinear way, and a highly unbalanced charge multipole will change the sign of the electrostatic energy and will favor extended structures. In other words, the structural characterstics of the denaturated state will be strongly dependent on pH, which could be important in modeling protein stability. An indirect evidence of the above can be found in the profiles of protein stability reported by Elcock (1999). The author finds that if the denaturated state is modeled as a series of compact nativelike states, it is in better agreement with experimental data in general. However, further analysis of the data shows that at very low pH, where the balance is strongly shifted to positive charges, the extended conformation might be a better approximation of the denatured state. The combinatorial dominance of attractive interactions expressed by Equation 10, we believe, is a good basis to explain also the effective sampling of compact denatured states in Monte Carlo experiments (Kundrotas and Karshikoff 2003) at a zero net charge of ionized groups.
ChiRotor—A program for rapid side-chain prediction
The observed dominant role of side-chain–backbone interactions in stabilizing the native structures suggests possible ways to reduce the combinatorial search of side-chain conformers in structure prediction algorithms. Following this idea we developed a new algorithm, ChiRotor, for fast prediction of side-chain conformation using CHARMm. Similar to most side-chain prediction algorithms, ChiRotor constructs side-chain structures of amino acid residues onto a fixed, known backbone framework. On the other hand, in contrast to most existing algorithms, ChiRotor does not use rotamer libraries or any other exhaustive conformational sampling. In ChiRotor the combinatorial search is maximally reduced by ignoring the interaction between side chains from different residues. It also only samples three initial conformations of any amino acid side chains for optimal interactions with peptide backbone. The guiding principle in all steps of the ChiRotor algorithm is to maximally replace the work spent performing a discrete conformational search by CHARMm energy minimization.
We chose to develop ChiRotor as a CHARMm script so that it can be easily incorporated as an integral part in any CHARMm protocol, as well as to produce energy minimized output structures that are consistent with the standard CHARMm parameterization. In particular, it makes ChiRotor useful for preliminary optimization of side-chain conformations before molecular dynamics simulations of homology models or computation models of mutated proteins. An important difference between ChiRotor and many of the known methods for side-chain optimization is that it does not use special energy potentials or scoring functions, but it is designed to work with any standard CHARMm force fields. Written as an open CHARMm script, ChiRotor allows the energy function to be easily extended to a large number of possible potentials of mean force that can be constructed based on the CHARMm routines.
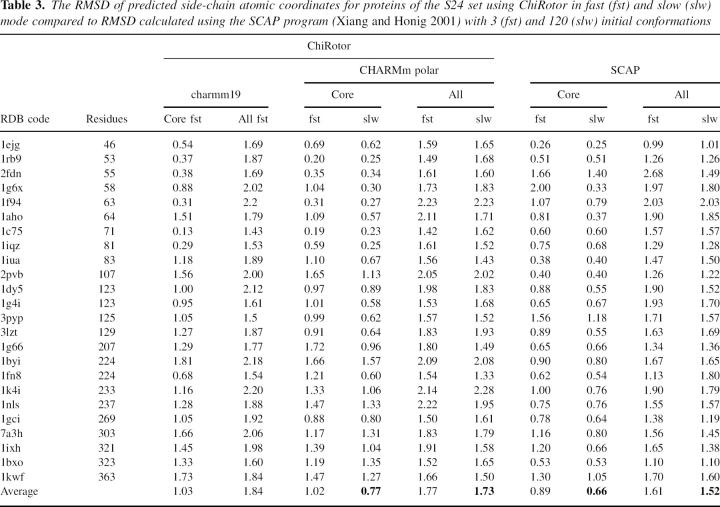
Table 3 reports the testing results of the ChiRotor algorithm on the structures of the S24 set of high-resolution proteins. The complete test was carried out using the CHARMm polar hydrogen force field (Momany and Rone 1993), but the calculations for the fast mode were also repeated using charmm19 (Neria et al. 1996). The results are compared to the results obtained by us for the same set of structures using the SCAP program (Xiang and Honig 2001), one of the best side-chain prediction programs described in the literature. Usually the results of side-chain predictions are presented both in terms of root mean squared deviation (RMSD) of predicted atomic coordinates from native structure and in the percent of correctly predicted dihedral angles. Here, to avoid redundancy, we presented the results as RMSD values only, because the two measures are coupled and, as can be seen in the literature, low RMSD values almost always correspond to high percentages of correctly predicted χ angles.
Table 3.
The RMSD of predicted side-chain atomic coordinates for proteins of the S24 set using ChiRotor in fast (fst) and slow (slw) mode compared to RMSD calculated using the SCAP program (Xiang and Honig 2001) with 3 (fst) and 120 (slw) initial conformations
The results presented in Table 3 demonstrate that despite the highly reduced combinatorial sampling, the ChiRotor algorithm is able to achieve an average RMSD of 0.77 Å for core residues and 1.73 Å for all residues. This level of accuracy is very close to the SCAP algorithm, where calculations carried out in both slow and fast modes corresponded to 3 and 120 initial conformers, respectively. Table 3 and Figure 4 show that the computational cost of the slow mode of ChiRotor is comparable to the fast mode of SCAP, while the accuracy of the two methods is similar. ChiRotor performs slightly better for core residues, but SCAP is slightly more accurate for all residues. At the expense of a considerably increased CPU time (20–30 times), the slow mode of SCAP reduces RMSD for ∼0.1–0.2 Å on average: i.e., 0.67 Å and 1.50 Å on the S24 set and 0.74 Å and 1.66 Å on a set of 18 proteins (Xiang and Honig 2001) for core and all residues, respectively. The accuracy of three of the most recent programs (Xiang and Honig 2001; Liang and Grishin 2002; Peterson et al. 2004) for side-chain optimization has been compared on a set of 65 proteins (Peterson et al. 2004). After multiplying the RMSD data in the Peterson et al. study by a factor of 1.2 to take into account the fact that they included the Cβ atom as part of the side chain in their calculations, all three methods tested show RMSD in a very close range of ∼1.5–1.7 Å for all residues and 0.7–0.9 Å for core residues. Although there are significant differences between the approaches, the overall accuracies of all three methods are very similar. In addition, similar accuracies were reported by the same predicting programs, but using different test sets (Xiang and Honig 2001; Liang and Grishin 2002; Peterson et al. 2004).
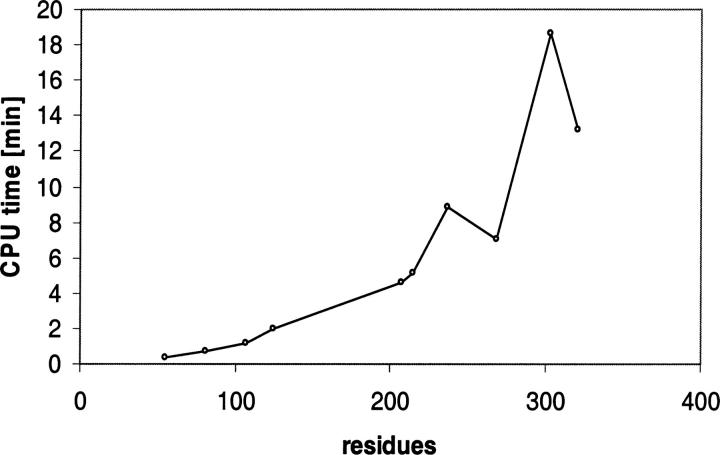
Figure 4.
The CPU time used to predict the side-chain conformation of all residues in proteins of different chain lengths.
The fast mode of ChiRotor shows slightly increased RMSD values for core residues. However, the average RMSD of ∼1 Å is still relatively small, making the fast mode useful in many modeling protocols, including side-chain optimization in homology modeling, loop optimization, and optimization of docked protein complexes. Figure 4 shows the performance of ChiRotor in slow mode on an Intel Pentium 4, 3.0-GHz machine.
The data in Table 3 and Figure 4 demonstrate that in slow mode ChiRotor gives accurate predictions at a low computational cost. In fast mode, ChiRotor shows an almost fivefold increase in calculation speed at the expense of slightly decreased accuracy, thus making it useful for protocols requiring extensive modeling of multiple structures.
Conclusions
While it is obvious that the peptide backbone must have an effect on side-chain conformation, many studies have assumed implicitly that the side-chain–side-chain interactions are the most important intramolecular determinants in stabilizing native structures. The results of a limited set of studies (as discussed in the introduction) suggest a possible dominant role of side-chain–backbone interactions. However most of these conclusions are based on indirect data and do not clarify whether such a feature follows from some restrictive constraints or from the ability of side chains to form stabilizing noncovalent contacts with backbones. In this study we have undertaken a novel comparative analysis of side-chain–side-chain and side-chain–backbone interactions in terms of intramolecular free energies in proteins.
The main result from the comparison of energy differences between completely unfolded and folded structures is that the stabilizing effect of side-chain–backbone interactions is considerably more important than side-chain–side-chain interactions. In addition, the side-chain–backbone interactions outperform side-chain–side-chain interactions in differentiating native structure from the misfolded structures. The side-chain–backbone interactions show about a twice stronger effect on discriminating the decoy structures from the native states than s-s interactions and this is valid for both van der Waals and electrostatic contributions. Interestingly, the results imply a higher capability for amino acid side chains to create stabilizing intramolecular contacts, even in misfolded structures, but the interactions are optimal in native states.
Our analysis leads to the conclusion that the side-chain–backbone interactions are the dominant intramolecular factor in the structural realization of amino acid code. The data in Tables 1 and 2 show quite similar ratios between s-s and s-b terms for almost all structures in the S24 and EMBL protein sets and suggest that the dominance of s-b interactions may be an intrinsic property of protein structures. This is important not only for a better understanding of the protein folding mechanism, but also in choosing the strategies of structure-predicting algorithms. In many knowledge-based potentials used in protein folding models, the effect of s-b interactions is either completely neglected or absorbed in common interaction centers. The identification of a dominant role of s-b interactions can be used to improve the potentials by including the peptide backbone as an additional 20 first interaction center as shown recently (Buchete et al. 2004). It is also possible to develop efficient predicting algorithms where the conformational searching will be focused on the optimization of s-b, instead of s-s interactions, as demonstrated by the ChiRotor approach.
The systematic occurrence of stabilizing electrostatic energy calculated in misfolded structures motivated us to carry out a novel analysis of charge–charge interactions between ionized groups. The effect of combinatorial dominance of interactions between opposite charges, as expressed by Equations 10 and 11, as well as by the analysis of electrostatic energies of a set of random model structures, suggest that charge–charge interactions can act as an unspecific folding force that stabilizes not only the native conformation, but also ensembles of relatively compact random structures. Our analysis, we believe, gives a convincing explanation of the experimental data of Pace et al. (2000), who also suggested that the charge–charge interaction stabilizes the relatively compact unfolded states. It is tempting to speculate that this effect plays a role in the evolution of native protein structures.
Based on the hypothesis of a dominant role of side-chain–backbone interactions, we developed a new algorithm, ChiRotor, for side-chain optimization with minimal combinatorial search. The results of the tests show that at a low computational cost ChiRotor achieves an accuracy of side-chain predictions that is comparable to the most accurate algorithms described in the literature.
Materials and methods
Data sets
S24 is a representative set of 24 nonhomologous proteins with high resolution X-ray structures. All PDB structures included in the set have a resolution better than 1.0 Å and a pairwise sequence identity <20%. The PDB entries in the S24 set were selected based on a culled PDB list obtained using the Protein Sequence Culling Server: http://dunbrack.fccc.edu/Guoli/PISCES.php (Wang and Dunbrack Jr. 2003). For the set of misfolded structures, we used the well-known EMBL set of deliberately misfolded proteins (Holm and Sander 1992). The corresponding PDB files with atomic coordinates were downloaded from the Web site at http://dd.compbio.washington.edu.
Calculations of interaction energy terms
All calculations on proteins from the S24 and EMBL sets are carried out using CHARMm (Momany and Rone 1993) and charmm19 (Neria et al. 1996) parameter sets. The energy values are obtained after preliminary relaxation of the structures using the ABNR (Adopted Basis Newton-Raphson) CHARMm routine for energy minimization and harmonic constraints applied to heavy atoms. The initial structures of the reference unfolded states are constructed from amino acid sequences using CHARMm BUILD routines with, β−strand conformation, ϕ = −120, ψ = 120°, for the main chain and all-trans conformation for all side chains. The electrostatic contributions to s-s and s-b interaction energy terms were calculated according to Equation 3 using the CHARMm Coulombic electrostatic function CDIEL in combination with the GBORN (Dominy and Brooks III 1999) solvation term. To estimate the van der Waals contributions to s-b and s-s interaction terms shown in Tables 1 and 2, we took advantage of the CHARMm routine INTERE to calculate the different contributions to the energy of interactions between the two selected sets of atoms. In most calculations, a value ɛm = 1 was used for the molecular dielectric constant and 80 for the water environment, but the calculations shown in Table 2 are repeated at ɛm = 4. All the nonbonded energy terms are calculated without any distance cutoffs.
The ChiRotor program
ChiRotor is a program for side-chain construction and energy optimization written as a single CHARMm script. ChiRotor can work with any CHARMm force field, but the minimization protocols discussed in this article are optimized for charmm19 and CHARMm polar hydrogen force fields. It is based on a two-stage algorithm that can work in either a fast or slower mode. The latter mode is more accurate.
-
1. In the first stage, the side-chain atomic coordinates of each residue are constructed using CHARMm build routines. The structure of each residue is constructed in three basic initial conformations corresponding to χx = −60°, 60°, and 180° and the rest of the side-chain torsion angles in extended, all-trans conformation. Each of the three conformers is subject to energy minimization in the absence of all other side chains at fixed coordinates of all backbone atoms. All other atoms in the system that do not belong to the set of selected side chains are treated as backbone. The optimization is carried out using ABNR minimization for all residues one by one from N-terminal to C-terminal.
In the fast mode the atomic coordinates of each side chain with the minimum CHARMm energy are saved, while in the slow mode the first two lowest energy conformers are saved. The side chain of proline is constructed in a single initial conformation with, χ1 = 108°, and although it is not subject to the conformational search, it is also energy minimized. The side chains of Cys residues involved in disulfide bridges are regarded as part of the protein backbone, as well as Ala and Gly residues. In the case of partial predictions, the side-chain atoms with known coordinates are considered as part of the template.
2. In the second stage, the side chains of all residues are put together based on the coordinates of the lowest energy conformer of each residue obtained in the first step. The protein structure is minimized again, but now with all side chains included, while the template atoms remain fixed. For the fast mode the above minimization is the final step, while the slow mode includes an additional cycle over all amino acid residues. During this cycle the initial structure of each residue is replaced with the second low-energy conformer from the first stage. The entire structure is again subject to minimization and, if after the optimization the second conformer has a lower energy than the first one, the second conformer is accepted. For some residues with nonsymmetric planar end groups, such as Trp, His, Asn, and Gln, the second cycle includes also an additional rotation corresponding to a change of 180° of terminal χ angle.
In all calculations in the first stage, a short cutoff distance of 10 Å was used and the electrostatic term was not included. During the second stage, the cutoff distance was increased to 14 Å and the electrostatic term was included using the most simple but the fastest model of screened electrostatic interactions using CHARMm RDIEL electrostatic function with “distant dependent dielectric constant” parameter, EPS = 4.
Accuracy evaluation
The side-chain RMSD was calculated relative to X-ray structures, with the protein overlayed based on backbone atoms N, CA, C, and O. Similar to Xiang and Honig (2001), the Cβ atom is excluded from RMSD calculations, because, even subject to minimization, the Cβ coordinates change insignificantly at a fixed main chain. The definition of core residues is exactly the same as in Xiang and Honig (2001) and corresponds to a value of maximum 10% normalized side-chain solvent accessibility. The solvent-accessible surface of individual residues is calculated by CHARMm according to Lee and Richards’ definition (Lee and Richards 1971) using a 1.4-Å solvent probe radius. For SCAP calculations (Table 3; Fig. 4) we used a SGI IRIX64 compilation of SCAP program that corresponds to the method proposed by Xiang and Honig (2001). The SCAP program was downloaded from http://honiglab.cpmc.columbia.edu. All SCAP calculations were based on a large rotamer library and were carried out at both fast and slow modes of 3 and 120 initial conformers, respectively. All other parameters are set to be the same as in the examples given in SCAP documentation. The performance data shown in Figure 4 are obtained using a recent implementation of ChiRotor program on an Intel Pentium 4, 3.0-GHz machine.
Acknowledgments
We thank Dr. Sandor Szalma and Dr. Hugues-Olivier Bertrand for the helpful scientific discussion.
Footnotes
Reprint requests to: Velin Z. Spassov, Accelrys, Inc., 10188 Telesis Court, Suite 100, San Diego, CA 92121, USA; e-mail: vss@accelrys.com; fax: (858) 799-5100.
Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.062447107.
References
- Bashford D. and Case, D.A. 2000. Generalized Born models of macromolecular solvation effects. Annu. Rev. Phys. Chem. 51: 129–152. [DOI] [PubMed] [Google Scholar]
- Brooks B., Bruccoleri, R.E., Olafson, B.D., States, D.J., Swaminathan, S., and Karplus, M. 1983. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4: 187–217. [Google Scholar]
- Buchete N.-V., Straub, J.E., and Thirumalai, D. 2004. Orientational potentials extracted from protein structures improve native fold recognition. Protein Sci. 13: 862–874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canutescu A.A., Shelenkov, A.A., and Dunbrack Jr, R.L. 2003. A graph-theory algorithm for rapid protein side-chain prediction. Protein Sci. 12: 2001–2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Mayer M., Desmet, J., and Lasters, I. 1997. All in one: A highly detailed rotamer library improves both accuracy and speed in modeling of side-chains by dead-end elimination. Fold. Des. 2: 53–66. [DOI] [PubMed] [Google Scholar]
- Desmet J., De Maeyer, M., Hazes, B., and Lasters, I. 1992. The dead-end elimination theorem and its use in protein side-chain positioning. Nature 356: 539–542. [DOI] [PubMed] [Google Scholar]
- Dominy B.N. and Brooks III, C.L. 1999. Development of a Generalized Born model parametrization for proteins and nucleic acids. J. Phys. Chem. B 103: 3765–3773. [Google Scholar]
- Dunbrack R.L. and Karplus, M. 1993. Backbone-dependent rotamer library for proteins. Application to side-chain prediction. J. Mol. Biol. 230: 543–574. [DOI] [PubMed] [Google Scholar]
- Eisenmenger F., Argos, P., and Abagyan, R. 1993. A method to configure protein side-chains from the main-chain trace in homology modelling. J. Mol. Biol. 231: 849–860. [DOI] [PubMed] [Google Scholar]
- Elcock A.H.. 1999. Realistic model of the denaturated states of proteins allows accurate calculations of the pH-dependence of protein stability. J. Mol. Biol. 294: 1051–1062. [DOI] [PubMed] [Google Scholar]
- Gelin B.R. and Karplus, M. 1979. Side-chain torsional potentials: Effect of dipeptide, protein and solvent environment. Biochemistry 18: 1256–1268. [DOI] [PubMed] [Google Scholar]
- Gunner M.R., Saleh, M.A., Cross, E., ud-Doula, A., and Wise, M. 2000. Backbone dipoles generate positive potentials in all proteins: Origins and implications of the effect. Biophys. J. 78: 1126–1144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm L. and Sander, C. 1992. Evaluation of protein models by atomic solvation preference. J. Mol. Biol. 225: 93–105. [DOI] [PubMed] [Google Scholar]
- Kundrotas P.J. and Karshikoff, A. 2003. Effects of charge–charge interactions on dimensions of unfolded proteins: A Monte Carlo study. J. Phys. Chem. 119: 3574–3581. [Google Scholar]
- Lee B. and Richards, F.M. 1971. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 55: 379–400. [DOI] [PubMed] [Google Scholar]
- Liang S. and Grishin, N.V. 2002. Side-chain modeling with an optimized scoring function. Protein Sci. 11: 322–331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Looger L.L. and Hellinga, H.W. 2001. Generalized dead-end elimination algorithms make large-scale protein side-chain structure prediction tractable: Implications for protein design and structural genomics. J. Mol. Biol. 307: 429–445. [DOI] [PubMed] [Google Scholar]
- Miyazawa S. and Jernigan, R.L. 1985. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 18: 534–552. [Google Scholar]
- Momany F.A. and Rone, R. 1993. Validation of the general purpose QUANTA 3.2/CHARMm force field. J. Comput. Chem. 13: 888–900. [Google Scholar]
- Neria E., Fischer, S., and Karplus, M. 1996. Simulation of activation free energies in molecular systems. J. Chem. Phys. 105: 1902–1921. [Google Scholar]
- Pace C.N., Alston, R.W., and Shaw, K.L. 2000. Charge–charge interactions influence the denatured state ensemble and contribute to protein stability. Protein Sci. 9: 1395–1398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peterson R.W., Dutton, P.L., and Wand, A.J. 2004. Improved side-chain prediction accuracy using an ab initio potential energy function and a very large rotamer library. Protein Sci. 13: 735–751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrey D. and Honig, B. 2000. Free energy determinants of tertiary structure and the evaluation of protein models. Protein Sci. 9: 2181–2191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponder J.W. and Richards, F.M. 1987. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J. Mol. Biol. 193: 775–791. [DOI] [PubMed] [Google Scholar]
- Shaefer M., Sommer, M., and Karplus, M. 1997. pH-dependence of protein stability: Absolute electrostatic free energy difference between conformations. J. Phys. Chem. B 101: 1663–1683. [Google Scholar]
- Skolnick J., Jaroszewski, L., Kolinski, A., and Godzik, A. 1997. Derivation and testing of pair potentials for protein folding. When is the quasichemical approximation correct? Protein Sci. 6: 676–688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spassov V.Z. and Atanasov, B.P. 1994. Spatial optimization of electrostatic interactions between the ionized groups in globular proteins. Proteins 19: 222–229. [DOI] [PubMed] [Google Scholar]
- Spassov V.Z., Karshikoff, A.D., and Ladenstein, R. 1994. Optimization of the electrostatic interactions in proteins of different functional and folding type. Protein Sci. 3: 1556–1569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spassov V.Z., Ladenstein, R., and Karshikoff, A.D. 1997. Optimization of the electrostatic interactions between ionized groups and peptide dipoles in proteins. Protein Sci. 6: 1190–1196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Still W.C., Tempczyk, A., Hawley, R.C., and Hendrickson, T. 1990. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 112: 6127–6129. [Google Scholar]
- Tanaka S. and Sheraga, H.A. 1976. Medium- and long-range interaction parameters between amino acids for predicting three dimensional structures of proteins. Macromolecules 9: 945–950. [DOI] [PubMed] [Google Scholar]
- Tanimura R., Kidera, A., and Nakamura, H. 1994. Determinants of protein side-chain packing. Protein Sci. 3: 2358–2365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G. and Dunbrack Jr, R.L. 2003. PISCES: A protein sequence culling server. Bioinformatics 19: 1589–1591. [DOI] [PubMed] [Google Scholar]
- Warwicker J.. 1999. Simplified methods for pK a and acid pH-dependent stability estimations in proteins: Removing dielectric and counterion boundaries. Protein Sci. 8: 418–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang Z. and Honig, B. 2001. Extending the accuracy limits of prediction for side-chain conformations. J. Mol. Biol. 311: 421–430. [DOI] [PubMed] [Google Scholar]
- Yang J.M., Tsai, C.H., Hwang, M.J., Tsai, H.K., Hwang, J.K., and Kao, C.Y. 2002. GEM: A Gaussian evolutionary method for predicting protein side-chain conformations. Protein Sci. 11: 1897–1907. [DOI] [PMC free article] [PubMed] [Google Scholar]