Scope and utility of hydrogen exchange as a tool for mapping landscapes

Abstract

The ability to determine conformational parameters of protein-folding landscapes is critical for understanding the link between conformation, function, and disease. Monitoring hydrogen exchange (HX) of labile protons at equilibrium enables direct extraction of thermodynamic or kinetic landscape parameters in two limiting extremes. Here, we establish a quantitative framework for relating HX behavior to landscape. We use this framework to demonstrate that the range of predicted global HX behavior for the majority of a set of characterized two-state proteins under near-native conditions does not readily span between both extremes. For most, stability may be quantitatively determined under physiological conditions, with semiquantitative boundaries on kinetics additionally determined using modest experimental perturbations to shift HX behavior. The framework and relationships derived in the simple context of two-state global folding highlight the importance of understanding HX across the entire continuum of behavior, in order to apply HX to map landscapes.

Folded proteins sample an ensemble of conformations in addition to the native state (Hvidt and Nielsen 1966; Karplus and McCammon 1983; Dill and Chan 1997). These alternative conformations may be involved in normal protein function, regulation, and degradation, as well as in diseases related to misfolding and aggregation (Kelly 1996; Dobson 1999). The distribution and transit of molecules among the different states is governed by the free-energy differences and barriers between them. This collection of states and barriers make up the folding landscape for a given protein. One approach to collecting information about a protein's landscape involves making measurements as a function of a controllable perturbant such as temperature or denaturant. These progressively unfold the protein, permitting estimation of landscape parameters by extrapolation to physiological conditions (Matthews and Hurle 1987). However, for the majority of proteins that depend on the assistance of chaperone networks to fold in the cell, such methods lead to aggregation (Clark 2004). Therefore, investigating the interplay between folding, function, and disease requires a method with the potential to extract landscape parameters for the protein of interest under near-native solution conditions.

Hydrogen-exchange detection of landscape

Hydrogen-deuterium exchange (HX) is a powerful method that has the capacity to measure directly landscape parameters of conformations sampled under physiological conditions (Englander et al. 1997). In recent years, the utility of hydrogen exchange has been greatly broadened by detection methods using mass spectrometry (MS) (Katta and Chait 1991; Hoofnagle et al. 2003; Eyles and Kaltashov 2004; Wales and Engen 2006). For example, the ability of HXMS to distinguish populations has been invaluable in resolving controversies of parallel protein-folding pathways (Miranker et al. 1993; Heidary et al. 1997; Tsui et al. 1999). The extreme sensitivity enabling investigations at low concentrations has enabled HXMS to probe amyloidogenic processes (Nettleton et al. 1998; Yao et al. 2005). In addition, dynamics of chaperone allostery (Rist et al. 2006), as well as assembly of complexes as large as the HIV capsid protein (Lanman and Prevelige Jr. 2004), have been investigated through HXMS. Changes in surface accessibility mapped by HXMS protection have been used to identify protein–protein interaction sites (Mandell et al. 1998; Woods Jr. and Hamuro 2001; Lee et al. 2004). The ability to monitor HXMS of individual proteins in complexes has provided new insights into substrates bound to chaperones (Robinson et al. 1994; Gross et al. 1996; Weber-Ban et al. 1999). Finally, HXMS has shown great promise for the possibility of monitoring protein stability and dynamics in vivo (Ghaemmaghami and Oas 2001; Engen et al. 2002).

HX is an established tool for mapping conformational landscapes of native proteins (Chamberlain and Marqusee 1997; Arrington and Robertson 2000b; Englander 2000; Woodward et al. 2004; Bai 2006; Bai et al. 2007). The transient sampling of alternative conformations by native proteins at equilibrium leads to an alteration of hydrogen-bonded and solvent-exposed structure. HX capitalizes on a subset of labile protein protons that can exchange with those of water when they are solvent accessible. At pH values above ∼4, this process is initiated by OH⁻ abstraction of a protein proton, notably the amide NH (Eigen 1964). The rate of this process (k_int) is governed predominantly by chemical considerations such as pH, temperature, and protein sequence. However, k_int is only observed in short model peptides (as well as surface exposed amides), as protein structure protects the amide NH through burial and hydrogen bonding, slowing the rate of its exchange (Englander et al. 1997). The exchange of an amide site in a native protein occurs, therefore, with an observed rate constant (k_HX), which is governed in part by chemistry and in part by the sampling of landscape features that result in exposure of the site.

Two regions of a landscape separated by a barrier can be distinguished if they have distinct HX properties. This was first modeled for a single amide site in terms of an equilibrium between two states with the sites inaccessible and accessible to solvent, respectively (Hvidt 1964). This equilibrium is governed by the rate constants for opening (k_u) and closing (k_f) linked to an exchange reaction occurring with k_int only from the open state (Equation 1) (Hvidt 1964):

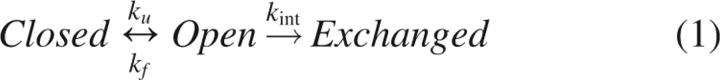The closed and open states represent two points on a landscape, with the stability difference and heights of the barriers separating the closed and open states given by:

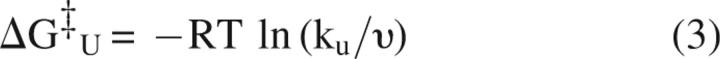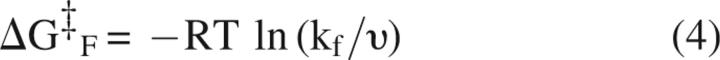respectively, where R = the universal gas constant, T = temperature, υ = k_bT/h, the rate of molecular vibration, k_b = Boltzmann's constant, and h = Planck's constant (Matthews and Hurle 1987).

The landscape is effectively encoded into the apparent hydrogen-exchange rate k_HX. k_HX for a protected site is slowed relative to k_int to an extent determined by k_u and k_f of the opening reaction exposing the site to solvent (Hvidt and Nielsen 1966):

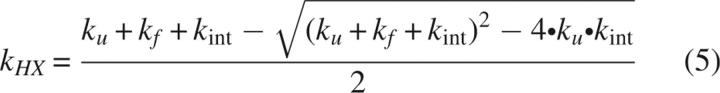For a stable protein (k_f >> k_u), Equation 5 simplifies to (Hvidt and Nielsen 1966):

Here, we focus on HX behavior arising from sites exposed only during the global unfolding equilibrium (N <-> U), with the long-term aim of extending our framework to exploit the broad range of equilibria detected by HX, including breathing from the native state, local unfolding of particular regions, transient population of intermediates, and intermolecular interfaces.

HX in limiting regimes directly extracts conformational parameters

Landscape parameters are readily decoded from k_HX in two limiting extremes, where Equation 6 simplifies to allow direct extraction of either kinetics or thermodynamics. When k_f << k_int, Equation 6 reduces to:

becoming first order, in what as known as the EX1 regime (Hvidt and Nielsen 1966). Measurements of k_HX in EX1 have extracted the global k_u for Protein L (Yi and Baker 1996), ubiquitin (Sivaraman et al. 2001), turkey ovomucoid third domain (Arrington and Robertson 1997), cytochrome c (Hoang et al. 2002), CD2.d1 (Cliff et al. 2004), and OspA (Yan et al. 2002). In the EX2 regime, k_f >> k_int, and Equation 6 reduces to a second order form (Hvidt and Nielsen 1966):

Host—guest peptide studies have permitted calculation of k_int for any amino acid sequence under a broad range of solution conditions (Bai et al. 1993). Global stability calculations for nearly a dozen proteins using k_u/k_f extracted from k_HX measurements under EX2 conditions of residues, which exchange only through global unfolding yield ΔG_U values that closely match those measured through calorimetry or chemical denaturation (Bai et al. 1994; Huyghues-Despointes et al. 1999). Furthermore, the powerful native-state HX approach has also identified and determined the stability of intermediates in many cases (Bai 2006). Thus, features of landscapes can be quantitatively mapped by HX in limiting regimes (Arrington and Robertson 2000b).

EX2 and EX1 behavior are distinguished experimentally through the profile in hydrogen exchange mass spectrometry or the pH dependence of k_HX (Ferraro and Robertson 2004). The evolution of the mass profile as amide protons exchange with heavier solvent deuterons is exceptionally distinct in EX1 vs. EX2 (Miranker et al. 1993; Chung et al. 1997). HX approximated by EX1 gives a two (or more) peak mass profile, whereas EX2 yields only one. This distinction is trivially made, provided the number of sites exposed lead to a resolved separation in position between the unexchanged and exchanged peaks. For situations in which peaks are unresolved, statistical considerations of peak width can be used to distinguish regime (Arrington and Robertson 2000a; Weis et al. 2006). Regimes can additionally be distinguished by making multiple measurements as a function of pH, which changes k_int in a defined manner (Hvidt 1964). In EX2, k_HX scales linearly with changes in k_int (Equation 8), while in EX1, k_HX is independent of changes to k_int (Equation 7) (Ferraro and Robertson 2004). Thus, either HXMS, or multiple measurements of k_HX as a function of pH can be used to identify the HX regime.

Mapping full landscapes (i.e., k_u and k_f for a two-state protein) using HX requires shifting between both limiting regimes (Ferraro and Robertson 2004). Experimentally, solution conditions are altered to shift HX from EX2 toward EX1 by increasing k_int and/or decreasing k_f (Englander et al. 1972; Loh et al. 1996). The most common strategy is to affect k_int using pH (Loh et al. 1996; Swint-Kruse and Robertson 1996; Arrington and Robertson 2000c; Simmons et al. 2003). Intrinsic exchange is base catalyzed above ∼pH 3, resulting in a log-linear dependence of k_int on pH (Hvidt 1964; Englander et al. 1972). For several proteins, this has been exploited to successfully map both thermodynamics and kinetics by measuring k_HX as a function of pH (Arrington and Robertson 1997, 2000c; Sivaraman et al. 2001; Rodriguez et al. 2002; Yan et al. 2002).

Alternatively, HX is shifted toward EX1 by slowing k_f through adding denaturant (Equation 9) (Clarke and Fersht 1996; Loh et al. 1996; Deng and Smith 1998; Sivaraman et al. 2001; Simmons et al. 2003) or increasing temperature (Equation 10) (Loh et al. 1996; Swint-Kruse and Robertson 1996; Kim et al. 2002). These affect k_u as well (Chen et al. 1989):

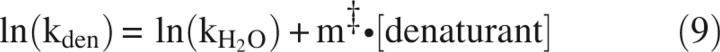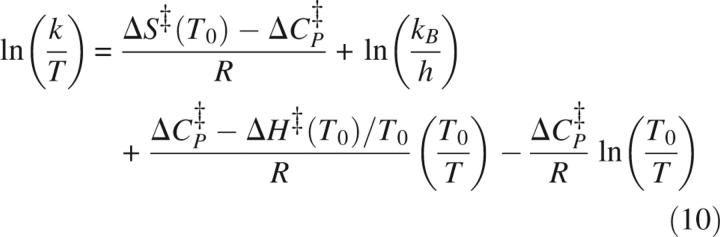where k_den and k_H2O are k_u or k_f in the presence and absence of denaturant, respectively, m^‡ is the slope of denaturant dependence of ln(k_u) or ln(k_f), k is k_u or k_f, T is temperature, and T₀ is the reference temperature. ΔS^‡ (T₀) and ΔH^‡(T₀) are the activation entropy and enthalpy at T₀, and ΔC_p ^‡ is heat-capacity change associated with reaching the transition state. In addition to affecting k_u and k_f, temperature influences k_int: A 10-fold increase in k_int is observed for every increase of ∼22°C (Englander et al. 1997). While there may be some effect of denaturant on k_int, these effects are not large. This is evident in the observation that ΔG_U calculated with Equations 2 and 8 using k_HX values measured in denaturant and calculated values of k_int yields values very close to ΔG_U determined through other means (Huyghues-Despointes et al. 1999).

Perturbation of the landscape to shift HX behavior has important limitations. Multiple measurements as a function of denaturant or temperature are required to extrapolate k_HX to native conditions. The growing recognition that landscapes affect in vivo function and disease makes landscape mapping an essential tool for cell biology and molecular medicine (Kelly 1996; Dobson 1999). However, the majority of proteins cannot be relied upon to fold correctly from a denatured state (Clark 2004). To fully exploit the potential of HX to characterize landscapes, it is necessary to investigate the extent to which landscape parameters may be extracted when solution conditions are limited to the near native. This requires a more quantitative understanding of the intersection between the influence of experimental tools on HX behavior and their impact on the landscape.

In this work, we assess the feasibility of using HX for measuring landscape parameters of proteins. While most proteins are large, with complex landscape topologies, small two-state proteins serve as models of protein domains. Because landscapes of many such model proteins are already well defined, we can assess the type of HX behavior experimentally accessible to them and determine the feasibility and difficulties with regard to using this technique on more complex proteins. We have therefore exploited an existing collection of thermodynamic and kinetic parameters for two-state proteins to evaluate the solution requirements for reaching both limiting regimes to extract both thermodynamics and kinetics from HX measurements. This is done by establishing a generalized framework for examining the interplay of the requirements for reaching the limiting regimes and the underlying conformational landscape. We then use the framework to probe the range of global HX behavior accessible under near-native conditions. Based on this analysis, we determine the extent to which the landscape of an uncharacterized two-state protein may be mapped through native-state HX.

Results

Quantitative framework for relating HX behavior to landscape

To quantitatively investigate the relationship between HX and conformational landscape, we first focused on a single two-state protein. The landscape of PWT spectrin SH3 has been extensively characterized, allowing us to model its global HX behavior and determine under which conditions k_HX simplifies to reveal its thermodynamics or kinetics. k_u and k_f as a function of both denaturant and temperature have been measured for the PWT variant of spectrin SH3, which has a single Gly replacing the second and third residues of the wild-type protein (Martinez et al. 1999). Therefore, k_HX for global HX may be calculated for a given condition using Equation 6 and the average k_int calculated from its sequence at the matched pH and temperature.

k_HX is readily interpreted in two limiting extremes where k_f is either much larger than, or much smaller than k_int. For PWT spectrin SH3 under physiological conditions (pH 6.5, 25°C), the reported k_f is 4.6 s⁻¹, (Martinez et al. 1999) and k_int is 8.5 s⁻¹. Obviously these are too close in value to fulfill either limiting condition. Instead, the global k_HX that would be observed, (1.8 × 10⁻³ s⁻¹ calculated using Equation 6) would lead to 15% error relative to the EX2 approximation (k_HX,EX2 = 2.1 × 10⁻³ s⁻¹), and 85% error relative to the EX1 approximation (k_HX,EX1 = 1.2 × 10⁻² s⁻¹). Thus, to measure the landscape parameters accurately, it is necessary to shift PWT spectrin SH3′s HX from what has been termed the EXX regime (Xiao et al. 2005) into either limiting regime through changing k_int or k_f through experimental manipulations.

To determine and compare the extent of manipulations required to shift HX behavior between limiting regimes in a quantitative and general way, we define a parameter ρ:

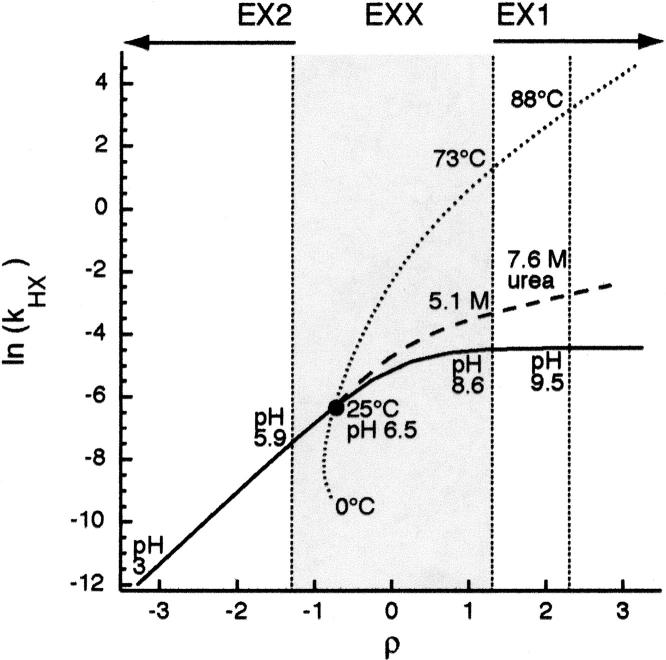
As the transition between the limiting regimes is governed by the relative rates of refolding (k_f) and the intrinsic exchange rate (k_int), ρ quantifies HX behavior relative to the extremes. By systematically comparing k_HX calculated with Equation 6 relative to the limiting approximations of EX1 (Equation 7) and EX2 (Equation 8) for a variety of k_u, k_f, and k_int values over a broad range of ρ, we determined that for a stable protein (k_u/k_f < 0.01) k_HX is within 5% of the EX2 approximation when ρ ≤ −1.3 (k_f > 20•k_int), and within 5% of the EX1 approximation when ρ ≥ 1.3 (k_f < k_int/20). PWT spectrin SH3′s physiological ρ calculated with Equation 11 is –0.7 (Fig. 1), indicating that ρ must be decreased by 0.6 to reach EX2, and increased by 2.0 to reach EX1.

Figure 1.

Global HX behavior for PWT spectrin SH3. Dependence of the apparent HX rate on ρ as a function of pH (solid), denaturant (dashed), or temperature (dotted). Gray shading specifies EXX regime. Black circle indicates HX under physiological conditions (23°C, pH 7). Changes in solution conditions, i.e., pH, T, or [denaturant] are indicated at the EXX boundaries and strongly EX1 (ρ = −1.3, 1.3, and 3.3, respectively).

Together, ρ and k_HX setup a quantitative framework with which to effectively describe the HX behavior of unfolding events leading to exchange. ρ establishes a coordinate along which HX behavior may be characterized relative to the limiting extremes where k_HX reports directly on landscape. As ρ increases from EX2 to EX1, the shift in relative landscape contributions (Equation 6) drives k_HX along a coordinate between a minimum of (k_u/k_f)•k_int to a maximum of k_u. Thus, (ρ, k_HX) may be used to characterize and compare the HX behavior of a given protein under different conditions (Fig. 1) or a set of proteins under the same conditions (Fig. 3A, below).

Figure 3.

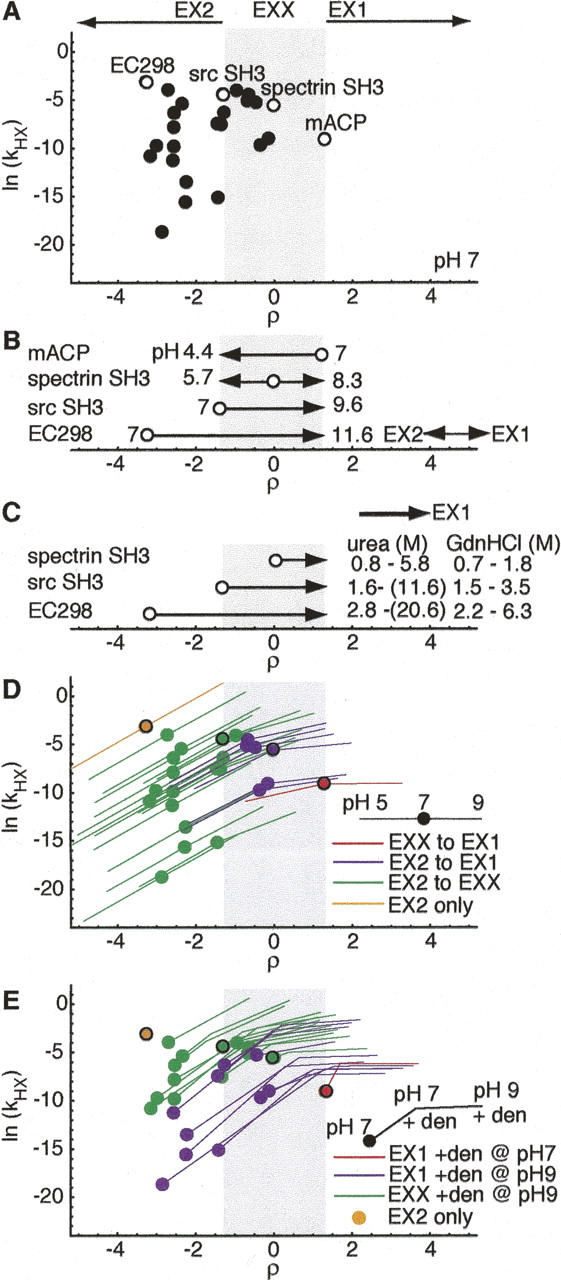
Global HX behavior for two-state proteins. (A) Distribution of HX behavior expected for stable two-state proteins with k_u and k_f characterized under standard conditions of 50 mM ionic strength, pH 7, 25°C (Maxwell et al. 2005). Circles denote global exchange of proteins from analysis set. Open circles indicate representative proteins spanning the range of observed HX behavior (ρ = −3.3, Eco298; ρ = 1.3, srcSH3; ρ = 0, specSH3; ρ = 1.3, mACP). (B) Calculated change in pH required to reach limiting regimes, relative to ρ positions at pH 7 (open circles) of representative proteins. (C) Calculated denaturant concentration required to shift HX from physiological ρ value to EX1. Concentration ranges calculated using maximum and minimum urea and GdnHCl m^‡ _f values reported for proteins in analysis set. (D) HX behavior accessible between pH 5 and pH 9. Circles indicate HX sampled at pH 7. Red indicates mACP, which samples only EX1, purple indicates proteins, which sample both EX2 and EX1, green indicates proteins, which sample EX2 and EXX, and orange indicates EC298, which samples only EX2 between pH 5 and pH 9. (E) HX behavior accessible upon addition of denaturant at modest levels (maintaining k_u/k_f = 0.01: ΔG_U = 11.4 kJ/mol), at pH 7 and pH 9. Red indicates proteins that sample HX far enough into EX1 with denaturant addition at pH 7 to allow k_u extrapolation, purple indicates proteins that sample HX far enough into EX1 with denaturant added at pH 9 to allow k_u extrapolation, green indicates those that shift only to EXX with denaturant addition at pH 9, and orange indicates EC298, which is only 11.4 kJ/mol stable without denaturant.

The relationship between HX and landscape was first investigated for an individual protein by exploiting the known dependence of k_u and k_f for PWT spectrin SH3 on solution conditions. k_HX can be calculated as a function of ρ using alterations to pH (affects k_int), temperature (affects k_int and k_f), or denaturant (affects k_f) (Fig. 1). pH has the greatest ability to shift ρ, in terms of range and direction, as seen by the magnitude of the X-axis change. We calculated the pH curve assuming that only k_int, and neither k_u nor k_f, is affected by side-chain ionization. Given this assumption and the fact that both pH and ρ are based on a log₁₀ scale, a one-unit pH change corresponds to a one-unit change in ρ. Thus, for PWT spectrin SH3, shifting between pH 3 and pH 11 covers seven ρ units. While the assumption that pH has no effect on landscape is unlikely to hold over such a wide range, it is reasonable to expect only minor perturbations over the range required to switch between EX2 and EX1 (pH 5.9–8.6). As such, the calculated change in k_HX when using pH to shift ρ ranges from the limiting EX2 approximation (k_u/k_f)•k_int to the limiting EX1 approximation (k_u).

In contrast to pH, the primary effect of alterations in temperature and addition of denaturant is on landscape and not ρ. Increases in these two perturbants typically slow k_f, resulting in a shift to larger values of ρ (i.e., toward EX1). For PWT spectrin SH3, addition of up to 9 M urea or increasing the temperature between 10°C and 100°C covers just over half of the ρ range accessible through pH (3.6 and 3.9 ρ units, respectively). Importantly, using these to shift HX behavior along the ρ axis changes k_u and k_f to such an extent (determined by Equations 9 or 10), that the protein is destabilized. This is reflected in the greater slopes of the ln k_HX dependence on ρ for the temperature and denaturant curves, relative to the pH curve. Thus, while adding 5.1 M urea, or increasing temperature to 73°C is sufficient to reach the EX1 regime (where k_HX = k_u), still further measurements with increasing temperature or denaturant are needed to extrapolate k_u back to physiological conditions.

The differential effects on PWT spectrin SH3′s landscape from shifting ρ to the same extent using either pH, temperature, or denaturant are illustrated in reaction coordinate form in Figure 2. For pH, ΔG_U is maintained at –15 kJ/mol compared with ΔG_U = 0 at standard state from EX2 to EX1 (Fig. 2B). Increasing temperature or denaturant to simply reach the EX1 boundary, however, leads to a completely destabilized protein (Fig. 2C,D). The ΔG_U at 73°C = +1.4 kJ/mol, and ΔG_U at 5.1 M urea = −0.4 kJ/mol. Continuing into EX1 to enable fitting of the dependence of k_u on temperature or denaturant further destabilizes the protein (ΔG_U at 88°C = +10.7 kJ/mol, and ΔG_U at 7.6 M urea = +6.6 kJ/mol for ρ = 2.3). Thus, applying the (ρ, k_HX) framework using the known landscape parameters of PWT spectrin SH3 illustrates both the relative effectiveness of the common methods for shifting HX (through the magnitude of the ρ change) and the relative consequences on landscape (through the magnitude and slope of the changes to ln[k_HX]).

Figure 2.

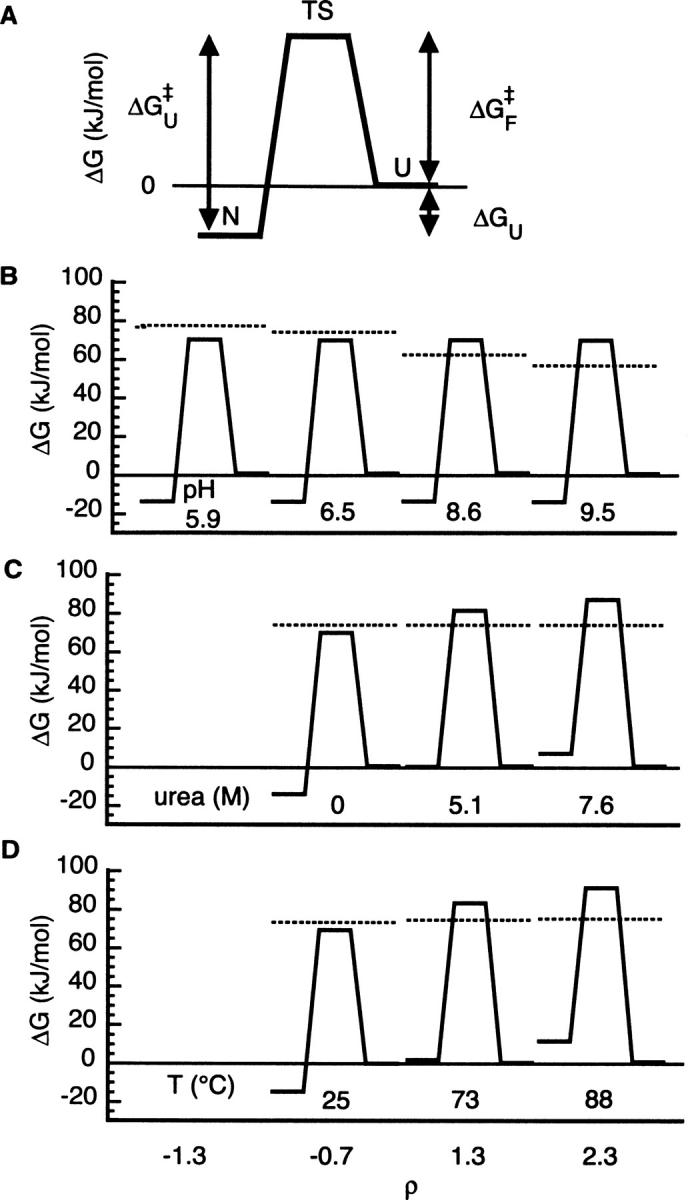
Landscape consequences of shifting PWT spectrin SH3 HX. (A) The conformational parameters of a two-state protein can be expressed in terms of the free energy landscape for unfolding from the native state (N) to the unfolded state (U) via a transition state ensemble (TS). The stability (ΔG_U) and activation free energy barriers to unfolding (ΔG^‡ _U) and folding (ΔG^‡ _F) are calculated from k_u, k_f, and k_u/k_f using Equations 2, 3, and 4, respectively. Free energies are relative to U, arbitrarily set to 0. (B–D) Free energy landscape for PWT spectrin SH3 global unfolding calculated for ρ at the EX2 cutoff (ρ = −1.3), physiological (ρ = −0.5), EX1 cutoff (ρ = 1.3), and strongly EX1 (ρ = 3.3) conditions achieved using pH (B), denaturant (C), or temperature (D). Horizontal line across each landscape indicates apparent free energy barrier to intrinsic chemical exchange under matched conditions calculated from Equation 3 with k_int in place of k_u.

Distribution of HX for characterized two-state landscapes

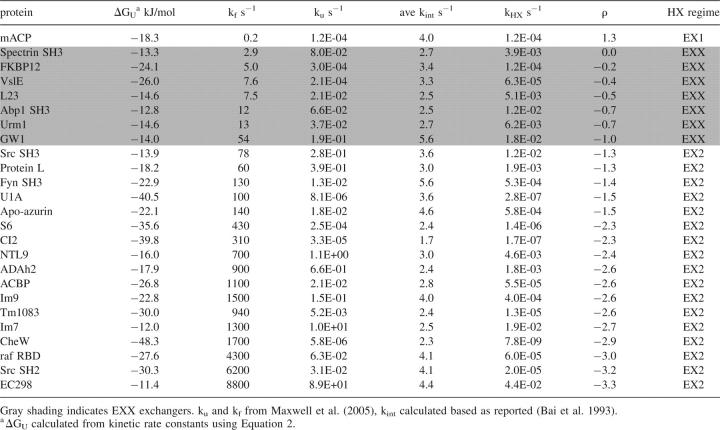
We then applied this framework to a set of two-state proteins whose landscapes have been measured as a function of denaturant and extrapolated to standard conditions (25°C at pH 7, 50 mM buffer). We calculated the HX behavior for those 25 proteins from the 30 in the Maxwell collection (Maxwell et al. 2005), whose measurements were performed at pH 7, and that met our requirement of k_u/k_f ≥ 0.01, above which k_HX vs. ρ is unchanging with stability. For each protein, the intrinsic exchange rate (from the unfolded conformation), k_int, was calculated for each residue in the sequence at pH 7 (Bai et al. 1993), and the average k_int was used in the calculations. The ρ values at pH 7 for global HX calculated using Equation 11 and the k_HX values calculated and averaged using Equation 6 are listed in Table 1.

Table 1.

Expected HX behavior of two-state proteins under physiological conditions (pH 7, 25°C, 50 mM ionic strength)

Global HX under physiological conditions for characterized two-state proteins range from strongly EX2 up to, but not exceeding, the EX1 cutoff (Table 1; Fig. 3A). k_int ranges between 1.7 and 4.1 s⁻¹ for the set, while k_f spans 8800 s⁻¹ to 0.2 s⁻¹. This corresponds to a total range of four ρ units (−3.3 to 1.3). The majority of the proteins (17 of 25) may be classified as EX2 exchangers. They range from EC298 as the most extreme EX2 exchanger (ρ = −3.3), with the fastest folding rate (8800 s⁻¹), to Src SH3, at the EX2 cutoff (ρ = −1.3) with a folding rate of 78 s⁻¹. The remaining characterized proteins fold too slowly to sample EX2. Only one, mACP, folds slowly enough to result in EX1 HX (k_f = 0.2 s⁻¹, ρ = 1.3). Strikingly, seven undergo HX in EXX (k_f = 63–2.9 s⁻¹). Thus, HX under physiological conditions can only readily extract quantitative landscape parameters for 2/3 of characterized proteins.

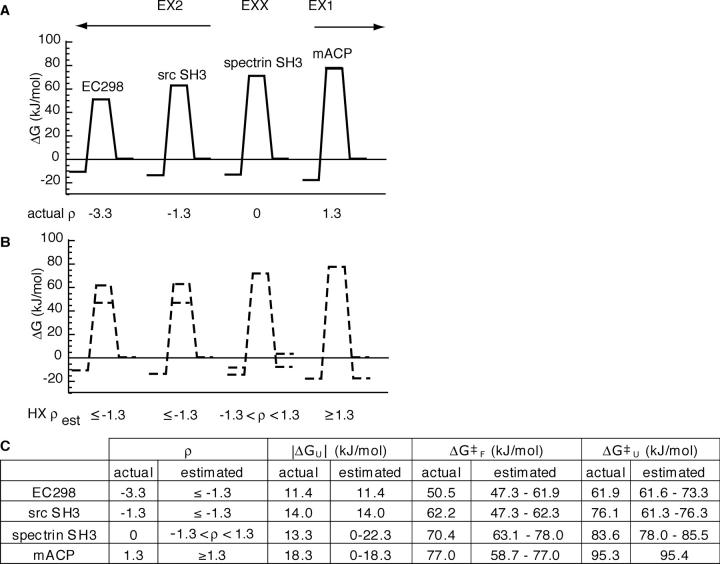
Figure 4.

Theoretical accessibility of two-state landscapes to HXMS mapping. (A) Calculated landscapes (solid lines) based on reported k_u and k_f for proteins spanning the spectrum of observed HX behavior under physiological conditions. (B) Landscape estimates (dashed lines) derived solely from k_HX, ρ_est, and k_int. Maximum and minimum estimates shown by double lines for semiquantitatively determined parameters. (C) Comparison of calculated and HX-derived parameters.

In EX2, the distribution in ln(k_HX) directly reflects the variation in stability (|ΔG_U| = 11.4–50 kJ/mol). The most stable protein of the set, CheW (ΔG_U = −48 kJ/mol) has the slowest k_HX. Notably, its ρ (−2.9) is very close to one of the least stable proteins of the set, Im7 (ρ = –2.7, ΔG_U = −12 kJ/mol), whose k_HX is four orders of magnitude faster. In EX1, the range in ln(k_HX) values reflects the range in unfolding barrier heights, while in EXX, ln(k_HX) values are a complex function of both stability and the unfolding barrier.

Shifting global HX behavior to reach limiting regimes

To determine the requirements for mapping landscapes, we calculated the theoretical range of experimental manipulation required to shift between the EX2 and EX1 regimes for proteins undergoing HX at representative ρ values. (Fig. 3B). Because it affects k_int, pH shifts ρ uniformly (one unit pH change/one ρ unit) for all proteins. Therefore, an EXX exchanger exactly midway between the two limiting regimes at neutral pH like spectrin SH3 can span the 2.6 unit difference between the EX2 and EX1 cutoffs within the most reasonable pH range (5.7–8.3). (Note: In contrast to the PWT spectrin SH3 variant at pH 6.5 above, spectrin SH3 here refers to the wild-type protein at pH 7 in the standardized collection [Maxwell et al. 2005].) However, for those proteins undergoing global HX in a limiting regime at neutral pH, 2.6 reflects the minimum pH change required to reach the other limiting regime. The maximum required in our set is for the strongly EX2 protein, EC298, which nominally samples EX2 up to pH 9, and does not reach the EX1 cutoff until pH 11.6. Thus, for strongly EX2 proteins, increasing pH is effectively insufficient to shift HX into EX1.

Denaturant is always less effective than pH at shifting HX behavior. As demonstrated for PWT spectrin SH3 in Figure 2, denaturant affects all landscape parameters in a protein-specific matter. Using the reported m^‡ _f values for characterized two-state proteins, the denaturant concentration required to increase ρ by one unit ranges from 0.6 to 4.5 M urea and 0.6 to 1.4 M GdnHCl. Thus, modest concentrations are theoretically sufficient to shift ρ of an EXX exchanger to the EX1 cutoff (Fig. 3C). However, for proteins with m^‡ _f values from the lower end of the reported range, shifting ρ from EX2 to the EX1 cutoff would require urea in excess of the solubility limit. In addition, because denaturant affects the k_u as well as k_f, simply reaching the cutoff is not enough. The change in ρ must be yet larger to enable denaturant-dependent measurements of k_u to the standard state. Thus, using denaturant alone to shift HX behavior is unlikely to enable extraction of k_u except for a small subset of EXX exchangers.

Range of global HX behavior accessed under near-native conditions

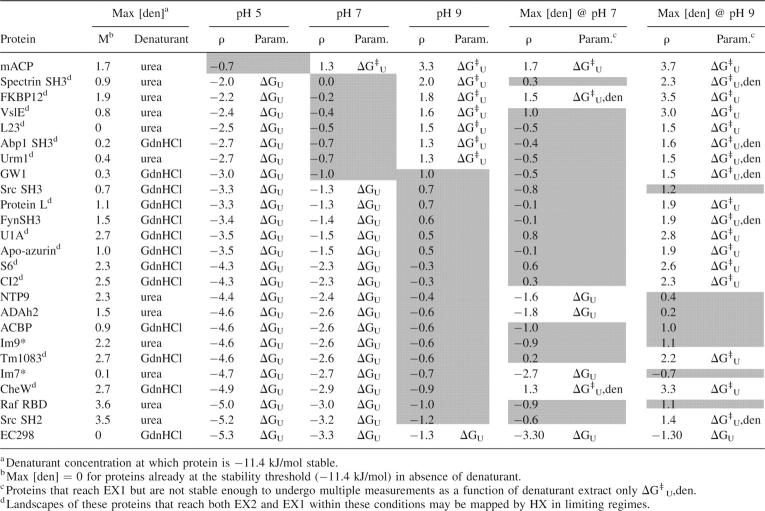
An important advantage of HX is its potential to extract landscape parameters at equilibrium under conditions specifically related to function or disease and from aggregation-prone proteins whose landscapes are not accessible through traditional methods. We therefore investigated the extent to which parameters could be extracted from global HX if a more limited and native range of pH (pH 7 ± 2 units) and denaturant (k_u/k_f ≤ 0.01) are used to perturb the landscape (Table 2).

Table 2.

Range of HX behavior and landscape parameters extracted with mild experimental manipulations

Less than one-quarter of characterized proteins could sample both EX2 and EX1 for extraction of both thermodynamic and kinetic parameters within this pH range (Fig. 3D). Lowering pH to 5, the seven proteins in Table 1 exchanging in EXX at pH 7 can be switched into EX2, theoretically enabling the equilibrium constant to be measured. Six could be shifted into EX1 by adjusting pH to 9, additionally enabling extraction of the kinetic unfolding rate constant to completely characterize the landscape (purple symbols). On the other hand, the range of HX behavior for one EXX exchanger (GW1), and all except one of the EX2 exchangers at neutral pH, would only span EX2 and EXX with pH (green symbols), while mACP (red symbol), which samples EX1 HX at pH 7, would also only shift into EXX through pH manipulation. Furthermore, EC298, which samples the most extreme EX2 HX at pH 7 (orange), still samples EX2 at pH 9. Thus, for the majority of proteins, manipulating pH within a reasonable range from neutral shifts HX into EXX.

Denaturant alone is not effective in shifting HX to enable EX1 measurements, even for EXX exchangers, when restricted to amounts that only mildly destabilize the native protein. We determined the maximum denaturant concentration that could be added to each protein without destabilizing it beyond –11.4 kJ/mol, i.e., k_u/k_f ≤ 0.01, using Equation 9 (Table 2). We then calculated the change in ρ and k_HX at that maximum denaturant concentration (Fig. 3E). HX must be shifted to ρ > 1.3 in order to make multiple EX1 measurements as a function of denaturant and extrapolate k_u to 0 denaturant. Therefore, to classify HX as EX1 in the presence of denaturant, we required a minimum fivefold change in k_u to be induced by the addition of denaturant between the concentration required to shift HX to ρ = 1.3 and the maximum concentration allowed without destabilizing the protein. Hence, even though addition of denaturant at pH 7 shifts HX of FKBP12, an EXX exchanger, and CheW, an EX2 exchanger, to ρ = 1.5 and 1.3, respectively (Table 2), only mACP HX is shifted far enough to enable the necessary measurements to qualify as EX1 under these conditions (Fig. 3E, red symbol).

Plainly, modest amounts of denaturant can theoretically enable k_u measurements in combination with increased pH. By increasing pH from 7 to 9, k_u measurements for 10 additional proteins could be extrapolated from EX1 HX measurements as a function of denaturant (Table 2; Fig. 3E, purple symbols). However, for those proteins exchanging in EXX at pH 7, the addition of denaturant at pH 9 is not an advantage over pH alone, as all except GW1 sample EX1 at pH 9 in the absence of denaturant (Fig. 3B). (Even with denaturant at pH 9, extrapolation of k_u is not possible for GW1.) In contrast, addition of denaturant does shift HX to allow EX1 measurements at pH 9 for seven of the 17 proteins that still sample EX2 at pH 9. Thus, pH and denaturant in combination would enable measurement of k_u for fewer than half of EX2 exchangers, assuming they are pH stable and would not be an advantage over pH alone for EXX exchangers.

Extracting landscape parameters from HX for uncharacterized two-state proteins

We next asked how closely the landscape of an uncharacterized protein (with only k_int known from the sequence) would be determined from HX measurements in EX2, EXX, or EX1 regimes. Since HX regime can be classified through the HXMS profile (Miranker et al. 1993) or the pH dependence of k_HX (Ferraro and Robertson 2004), ρ for any protein undergoing HX can be reasonably estimated as either ρ_est ≤ −1.3 (EX2), −1.3 < ρ_est < 1.3 (EXX), or ρ_est ≥ 1.3 (EX1). Obviously, for EX2 and EX1 HX, identification of the regime allows direct determination of either k_u/k_f or k_u from the measured k_HX.

In addition, assignment of the HX regime enables semiquantitative boundaries to be placed on k_f and k_u, regardless of regime. Because of the relationship between k_int and k_f in determining ρ, estimation of ρ_est enables calculation of the minimum and/or maximum possible value of k_f using the known k_int for the sequence. For EX2, k_f ≥ 20•k_int, in EXX 20•k_int > k_f > k_int/20, and in EX1, k_f ≤ k_int/20. In addition, in EX2 and EXX, these k_f limits may be used to determine boundaries on the possible value of k_u relative to the measured k_HX. In EX2, k_u ≥ 20•k_HX, and EXX, 20•k_HX > k_u > k_HX. These limits on k_f and k_u can in turn be expressed in landscape terms using Equations 2–4, leading to semiquantitative estimates of ΔG_U, ΔG^‡ _U, and ΔG^‡ _F.

To determine how fully the landscape of an unknown protein could be mapped, we compared the landscape information that would theoretically be gained from measurements of HX for four known proteins ranging in ρ from EX2 to the EX1 cutoff. For these proteins, we used only ρ_est, k_HX, and the average k_int calculated from the amino acid sequence to generate HX-derived landscape estimates. These are shown relative to the actual landscape calculated from the reported k_u and k_f values (Fig. 5).

Observation of global EX2 HX under physiological conditions would identify ρ_est ≤ −1.3 for EC298 and src SH3. Therefore, their stability (ΔG_U = −11.4 and −14.0 kJ/mol, respectively) would be quantitatively extracted from their measured k_HX (Fig. 5). In addition, this would set the upper limit for their folding barriers as ΔG^‡ _{F, est} ≤ 61.9 for Eco298 and ΔG^‡ _{F, est} ≤ 62.3 kJ/mol for src SH3. The upper estimate for the folding barriers also places an upper limit for the unfolding barriers, as ΔG^‡ _U = |ΔG_U| + ΔG^‡ _F: ΔG^‡ _{U, est} ≤ 73.3 for Eco298 and ΔG^‡ _U,est ≤ 76.3 kJ/mol for src SH3. These estimates are reasonable for src SH3 (ΔG^‡ _F = 62.2 kJ/mol, ΔG^‡ _U = 76.1 kJ/mol), as its HX is right on the EX2 boundary, but that would not be known for an uncharacterized EX2 protein without further information to pinpoint ρ. As EC298 is the most extreme EX2 exchanger in the standardized set, its actual ΔG^‡ _F (50.5 kJ/mol) roughly sets the lower bound on the possible folding barrier for a protein with ρ_est ≤ −1.3, although some faster folding proteins, such as λ repressor (ΔG^‡ _F = 47.3 kJ/mol) (Maxwell et al. 2005) have been observed. Therefore, the range in folding and unfolding barrier estimates for an uncharacterized protein in EX2 is practically set at ∼15 kJ/mol.

On the other hand, an estimate of ρ_est ≥ 1.3 by observation of EX1, as for mACP (Fig. 5) would quantitatively determine the barrier to unfolding (ΔG^‡ _U = 95.3 kJ/mol), yield an estimate of the minimum possible folding barrier (ΔG^‡ _F,est ≥ 77 kJ/mol) and, therefore, the maximum possible stability (|ΔG_U,est | ≤ 18.3 kJ/mol). For a protein with an actual ρ = 1.3, like mACP, these estimates are accurate (ΔG^‡ _F = 77 kJ/mol, ΔG_U = −18.4 kJ/mol). Without knowing ρ, 0 is the effective boundary for minimum stability. Therefore, for an uncharacterized protein, the uncertainty range for the EX1 folding barrier and stability estimates is set by ΔG_U,est.

For EXX proteins, while no parameter is exactly determined, upper and lower bounds for all of the parameters are obtained based on limits on k_u and k_f set by −1.3 ≤ ρ_est ≤ 1.3. Thus, for spectrin SH3, reasonable ranges for all of the parameters would be obtained from observing its HX in EXX: ΔG^‡ _F = 63.1–78.0 kJ/mol, ΔG^‡ _U = 78–84.3 kJ/mol, and ΔG_U = 0 to −22.3 kJ/mol. The magnitude of those ranges hold for any protein with EXX exchange. Therefore, the uncertainty ranges for parameters estimated for an uncharacterized protein in EXX are 14.8, 7.5, and 22.4 kJ/mol for ΔG^‡ _F, ΔG^‡ _U, and ΔG_U, respectively.

Limited pH changes can be used to refine the ρ estimate, greatly narrowing the uncertainty in landscape parameter determination. While only the EXX exchangers in our analysis would reach both limiting regimes within two units of pH 7, all of the proteins, except the extreme EX2 exchanger EC298, do switch into EXX (Fig. 3D). The EX2 to EXX transition could be identified, for example, by the change in width at the 50% exchange point (Miranker et al. 1996). By titrating pH until such a regime is observed, the average k_int at that pH could be calculated from the sequence and used to estimate k_f from the boundary ρ. Such a procedure could give estimates of k_f within 10-fold, which would give ΔG^‡ _F and ΔG^‡ _U estimates accurate to within 6 kJ.

Discussion

We have developed a general theoretical framework to interrogate the landscape of proteins through HX. The approach capitalizes on qualitative use of HXMS to establish a semiquantitative localization of regime to a defined axis, ρ. Experimental manipulations shift HX into the regimes necessary to enable direct extraction of global landscape parameters. Using this approach, we can extrapolate that under physiological conditions, HX would not allow direct extraction of accurate landscape parameters for nearly one-third of globular proteins. However, it is only this group of proteins that can be manipulated by mild alteration of solution conditions to sample both limiting regimes, and thereby fully map their landscapes.

The optimal tool for shifting HX to limiting regimes is pH. This enables shifts across the broadest range of ρ, and does not rely on changing the landscape. Indeed, monitoring k_HX as a function of pH by NMR has been applied successfully to extract both k_u and k_f through fitting the dependence to Equation 6 (Sivaraman et al. 2001) and through exploiting the range in k_int values in the amino acid sequence to cover the range from EX2 to EX1 (Yan et al. 2002). Denaturant and temperature are far less effective at shifting ρ into EX1. This is consistent with observations that HX rates measured in 2 M denaturant experiments may be used to accurately determine ΔG_U using the EX2 approximation (Equation 8) (Dai and Fitzgerald 2006). Only very stable proteins with steep dependencies of ln(k_f) on denaturant and temperature (large m^‡ _f and ΔC_p ^‡ _F), indicating very native-like transition states (Jackson 1998) sample EX1 without significant destabilization. In addition, multiple measurements of k_HX beyond the EX1 boundary are required to extrapolate landscape parameters to a physiological standard state from added denaturant or increased temperature. Where possible, however, this approach provides additional structural information about the landscape, such as ΔC_p ^‡ _U and m^‡ _U, which correlate with the relative solvent exposure of the transition state (Myers et al. 1995).

In this work, we have assumed that qualitative assessment of exchange regime can be performed by inspection of a hydrogen-exchange mass profile and/or the dependence of hydrogen exchange on pH. Given this, we have shown that simply knowing the sequence and the approximate value of ρ enables a reasonable estimate of global-folding landscape parameters even between the limiting regimes. While two-state behavior cannot be presumed for an uncharacterized system, it is reasonable to presume that a core of residues will exchange at the slowest rates and reflect only the global transition (Li and Woodward 1999; Ferraro and Robertson 2004). Thus, it is our expectation that at least a portion of the landscape of any globular protein can be readily characterized, even for biologically important systems that are particularly challenging experimentally.

HXMS on representative two-state proteins from the published set bear out our assumptions and conclusions. For example, the protein CI2 (ρ = −2.6 at pH 7), gives a characteristic EX2 mass profile with two phases in experiments at pH 6.8 (Xiao et al. 2005). Calculation of ΔG_U from the k_HX for the slow phase (corresponding to exchange of 36/65 residues) measured at 23°C is very close to that reported in Table 1 (ΔG_U [HX] = −32.2 kJ/mol vs. ΔG_U [calc.] = −39.8 kJ/mol). Furthermore, the solution pH must be raised above 10 in order to observe the EX1 profile. This is precisely what is predicted by the ρ framework, as CI2 HX is predicted to just reach the EX1 boundary (i.e., ρ = 1.3) at pH 10.

For protein L, an EX2 exchanger just on the cutoff at neutral pH (ρ = −1.3), a bimodal (i.e., EX1) HXMS profile corresponding to HX of 21/62 residues was observed at 60°C and pH 11 (Yi and Baker 1996). The reported k_HX of 0.06 s⁻¹ corresponds to k_u, and the k_f was estimated to be ∼0.3 s⁻¹ based on the equilibrium constant from other experiments. Here, we calculate the average k_int for protein L under those conditions to be k_int = 5.9 × 10⁵ s⁻¹. These constants therefore correspond to ρ = 6.3, fully five ρ units above the EX1 cutoff. Importantly, the extreme pH used appears to have destabilized the landscape. k_u and k_f extrapolated from measurements in GdnHCl at 58°C, pH 7 (k_u = 2.7 s⁻¹, k_f = 150 s⁻¹) (Scalley and Baker 1997) differ significantly from those reported at pH 11, indicating that the four-unit increase in pH destabilizes the protein by 6.6 kJ/mol.

For most biologically relevant proteins, it is reasonable to assume that solution conditions will not be found that will allow for adequate sampling of both EX1 and EX2 regimes. Strong alteration of the landscape can be expected. We have shown here, for example, that even a model system like PWT spectrin SH3 appears strongly subject to landscape perturbation at denaturant and temperatures required to sample EX1, while high pH appears to destabilize protein L. Plainly, much milder perturbations are desirable to avoid landscape perturbation as well as aggregation. As we have shown, such limited experimental manipulations will primarily enable proteins to sample EXX.

In this work, we presumed a requirement for sampling at several points in the limiting regimes to extract full landscape information. However, landscape information is present, albeit convoluted, in the EXX regime. Recognition of this has driven the development of tools such as numerical simulation of protein HXMS (Arrington and Robertson 2000a; Xiao et al. 2005). The further development and refinement of such tools will ultimately be essential to unlocking the landscape information that is present in EXX. Coupling regime-independent extraction of landscape parameters from native HX with the applicability of MS to virtually any protein promises to greatly expand the range of protein landscapes accessible to experimental investigation.

Materials and Methods

Calculation of expected HX behavior

Our large analysis set (Table 1) consisted of 25/30 proteins from the previously published data set of Maxwell et al. (2005), whose k_u and k_f had been monitored as a function of denaturant exactly at pH 7, and which met the minimum stability requirement of k_u/k_f > 0.01. For all proteins analyzed, k_int was calculated as described (Bai et al. 1993) at the appropriate pH and temperature for each residue and averaged over the sequence. k_HX and ρ were calculated under physiological conditions (pH 6.5, 25°C for PWT spectrin SH3, and pH 7, 25°C, 50 mM ionic strength for Table 1 proteins) with Equations 6 and 11, using the appropriate k_int and the reported k_u and k_f (Martinez et al. 1999; Maxwell et al. 2005) for PWT spectrin SH3 and Table 1 proteins, respectively.

Limiting values of ρ that define EX1 and EX2 were calculated as follows: k_HX was calculated using Equation 6 and compared with the limiting approximations calculated with Equations 7 and 8 as a function of ρ. For stable proteins (k_u/k_f > 0.01), regardless of the individual values of k_u, k_f, or k_int, k_HX is within 5% of the EX1 approximation when ρ ≤ −1.3, and within 5% of the EX2 approximation when ρ ≥ −1.3.

Calculation of effect of solution conditions on ρ and k_HX

Changes in k_int with pH or temperature were calculated based on Bai et al. (1993). Changes in k_f and k_u based on denaturant were calculated with Equation 9 using the m^‡ _f and m^‡ _u reported (Maxwell et al. 2005). For PWT spectrin SH3, changes in k_f and k_u based on temperature were calculated using the reported ΔC_p ^‡ _F and ΔC_p ^‡ _U (Martinez et al. 1999). The corresponding changes in ρ and k_HX were calculated as above using the calculated k_u, k_f, and k_int values.