Precise Measurement of Diffusion Coefficients using Scanning Fluorescence Correlation Spectroscopy

Abstract

We have implemented scanning fluorescence correlation spectroscopy (sFCS) for precise determination of diffusion coefficients of fluorescent molecules in solution. The measurement volume where the molecules are excited, and from which the fluorescence is detected, was scanned in a circle with radius comparable to its size at frequencies 0.5–2 kHz. The scan radius R, determined with high accuracy by careful calibration, provides the spatial measure required for the determination of the diffusion coefficient D, without the need to know the exact size of the measurement volume. The difficulties in the determination of the measurement volume size have limited the application of standard FCS with fixed measurement volume to relative measurements, where the diffusion coefficient is determined by comparison with a standard. We demonstrate, on examples of several common fluorescent dyes, that sFCS can be used to measure D with high precision without a need for a standard. The correct value of D can be determined in the presence of weak photobleaching, and when the measurement volume size is modified, indicating the robustness of the method. The applicability of the presented implementation of sFCS to biological systems in demonstrated on the measurement of the diffusion coefficient of eGFP in the cytoplasm of HeLa cells. With the help of simulations, we find the optimal value of the scan radius R for the experiment.

INTRODUCTION

Fluorescence correlation spectroscopy (FCS) was introduced as a method for the measurement of diffusion coefficients and concentrations of fluorescent molecules in dilute solutions (1). Although FCS and its modifications have since been applied to the investigation of a range of phenomena giving rise to fluorescence fluctuations (e.g., molecular photophysics, intramolecular dynamics, conformational changes, intermolecular interactions, etc. (2–4)), characterization of diffusion remains one of its most common applications.

The principle of FCS lies in the quantification of the magnitude and duration of fluorescence fluctuations caused by molecules freely diffusing in and out of the measurement volume. While the magnitude of the fluctuations yields the number of particles in the measurement volume, and the duration of fluctuations the characteristic time the particles take to cross the volume, the geometry of the measurement volume has to be known to convert these quantities to concentration and diffusion coefficient. The complex shape of the diffraction-limited measurement volume, and the difficulty of its accurate parameterization, have been a limiting factor in the determination of absolute diffusion coefficients with FCS.

The measurement volume is most often approximated by a three-dimensional Gaussian with two parameters describing its lateral and axial extent (5). Since these parameters are difficult to determine independently, FCS is usually employed as a comparative method, where the diffusion coefficient of the investigated compound is related to that of a known standard by a comparison of the diffusion times of the two compounds. However, because of absence of suitable standards (2) and the often encountered difficulty to measure the standard and the investigated sample under the same conditions (e.g., in intracellular applications), alternative methods are sought.

Several FCS variations have been proposed recently to address this problem. Dertinger et al. (6) suggested the use of spatial cross-correlation of fluorescence signals between two overlapping volumes created by two laser beams and fixed at known distance. Jaffiol et al. (7) used a similar configuration, but a single expanded laser beam was used for illumination, and the measurement volumes were defined by two laterally displaced optical fiber apertures. Additionally, thresholding was applied to the fluorescence signal before correlation to enhance the contrast in the resulting cross-correlation function. Blancquaert et al. (8) cross-correlated signals from two volumes of different shapes created by circular and ring pinholes: an inner elongated volume surrounded by an outer annular volume. Ries and Schwille (9) used a line-scanning microscope to measure fluorescence from two lines separated by a defined distance. Cross-correlation of the two signals allows determination of diffusion coefficients of slowly diffusing molecules in biomembranes, or on any flat surface.

Scanning FCS (sFCS) is a common name for a group of FCS methods where the measurement volume is in some way moved relative to the sample (10). It has been implemented for various reasons: to improve the statistical accuracy by measuring the signal from a large number of statistically independent volumes in systems with slow diffusion (11–13); to study binding in immobile samples (14); to avoid photobleaching of slowly diffusing molecules (15); to perform measurements at many locations quasi-simultaneously (16,17); to measure diffusion coefficients over a broad temporal range with a standard laser scanning microscope (18); or to measure diffusion, flow, and immobilization simultaneously (19).

We have implemented circular-scanning FCS in a way most similar to that of Skinner et al. (19), but without the position sensitivity. The motivation was to take advantage of the known scan radius R, and use it as a spatial measure, equivalent to the distance between the measurement volumes in the cross-correlation techniques mentioned above. In this way, determination of the diffusion coefficient is possible without the exact knowledge of the parameters of the measurement volume.

The described implementation of sFCS, rather than being an alternative to the existing sFCS techniques mentioned above, represents a new approach to the measurement of diffusion coefficients providing two significant enhancements over a standard FCS: the calibration of the size of the measurement volume is not necessary, and, consequently, the method becomes robust with respect to disturbances affecting the measurement volume size.

In the following, we describe the procedure to accurately measure the scan radius, and present the results of sFCS measurements on an example of several fluorescence dyes at different scan radii and frequencies. Further, we discuss the choice of the optimal scan radius and frequency, and based on simulations and theoretical considerations, suggest the best values. The lower sensitivity of sFCS to photobleaching, a common limitation in two-photon FCS, compared to FCS with a fixed measurement volume, is demonstrated. The sFCS is shown to be able to detect changes in the size of the measurement volume and yield a correct value of the diffusion coefficient, both in the same measurement, without a need for repeated calibration of the volume size. Finally, it is shown that the technique is capable of measuring diffusion coefficients in living cells without any a priori knowledge about the measurement volume size, and that the sensitivity to the changes in the volume size is also preserved in vivo. An alternative implementation for sFCS is proposed, with less complex illumination optics and a possibility of addition to existing FCS setups based on a two-axis piezo scanner. The sFCS, as implemented in this work, is shown to be a precise and robust technique for the measurement of diffusion coefficients with strong potential for applications in complex heterogeneous systems, such as living cells.

MATERIALS AND METHODS

Experimental setup

The measurements were performed on a home-built two-photon laser scanning microscope (10) using a model UPLAPO 60× W3/IR objective (Olympus, Center Valley, PA). The excitation was provided by a tunable Ti:Sapphire laser (Mira 900-F; Coherent, Santa Clara, CA) whose wavelength was chosen depending on the investigated dye: 790 nm (Alexa 488), 820 nm (Alexa 546, fluorescein, rhodamine 6G), or 920 nm (eGFP). The programmable galvanometer scanners steering the beam allow the system to operate in two modes: a conventional imaging laser scanning microscope mode, and a sFCS mode where the beam is scanned in a circle with a user-defined radius and frequency. The fluorescence, collected by the objective and transmitted through an appropriate emission filter, was detected by an avalanche photodiode (SPCM-CD2801; PerkinElmer, Wellesley, MA). The detected photocount sequence was processed by a SPC-830 module (Becker & Hickl, Berlin, Germany) and stored for further analysis. The SPC-830 module provides timing information of every detected photon with the resolution corresponding to the repetition frequency of the laser (in our case, 13.1 ns).

The scan radii used in this work were in the range 0–1 μm, and the scan frequencies 0.5, 1.0, and 2.0 kHz. Laser excitation intensities between 2 and 5 mW were used in all measurements with the exception of the photobleaching experiments, where up to four times higher intensities were employed. The measurements lasted ∼100 s.

Sample

The fluorescent dyes were dissolved in the following solvents: Alexa 546, Alexa 488 (succinimidyl ester; Molecular Probes, Eugene, OR) and rhodamine 6G in water, eGFP (Clontech, Mountain View, CA) and (5(6)-carboxy-)fluorescein (Sigma-Aldrich, St. Louis, MO) in 100 mM phosphate-citrate buffer, pH = 7.5. The solutions at nanomolar concentrations were placed in a 1-mm-deep well with the bottom and the top formed by a #1.5 coverslip, to prevent evaporation of the solvent during the measurement. The measurement volume was positioned at a distance of ∼100 μm from the coverslip within the well. The experiments were performed at room temperature of 22.5 ± 0.5°C.

Cell culture

HeLa SS6 cells were grown in DMEM including sodium pyruvate (Gibco, Invitrogen, Carlsbad, CA) and 10% Fetal Bovine Serum (Cambrex, East Rutherford, NJ). They were seeded on LabTek chambered cover glasses (Nalge-Nunc, Rochester, NY) 24 h before the transfection with 100,000 cells/ml, leading to 50% confluency on the following day. Transfection of pEGFP-N1 DNA (Clontech) into the cells was mediated by Lipofectamine 2000 (Invitrogen) and followed by a media change after 3 h. The measurements were performed 5–7 h after transfection.

Theory and data analysis

The profile of the measurement volume, reflecting the two-photon excitation, is approximated by three-dimensional Gaussian function W(r),

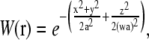(1)

where a is a parameter describing the width of the measurement volume in the lateral (xy) plane, and w is the relative extension of the measurement volume along the optical axis. The model autocorrelation function for simple diffusion, when the measurement volume is scanned in a circle of radius R at a constant frequency f, is the product of the commonly used diffusion model (5) and an exponential scan factor (13,19):

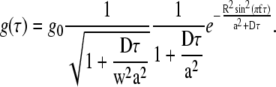(2)

In standard FCS with a fixed measurement volume the exponential factor is equal to 1 because R = 0. In this case the autocorrelation g(τ) depends on the diffusion coefficient D and volume size a via the diffusion time τ_D = a²/D, therefore a has to be known if D is to be obtained from the fit (both cannot be determined at the same time). Scanning the measurement volume is mathematically described by multiplying the model function by the exponential scan factor, which effectively decouples a and D, making it possible for both to be obtained from a single fit. Introducing two additional parameters, R and f, in the sFCS model does not make the fitting analysis less stable due to too many variable parameters, since both R and f can be determined beforehand with sufficient accuracy and then fixed in the fitting process.

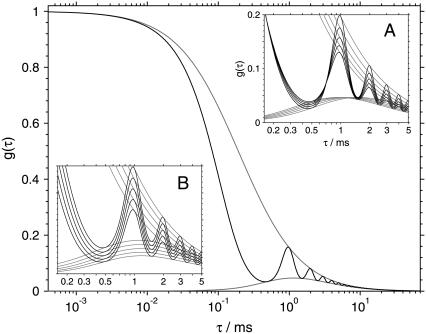
The theoretical autocorrelation (Eq. 2) is shown in Fig. 1. The autocorrelation curve (solid line) exhibits oscillations due to the periodic motion of the scanned measurement volume. The upper envelope of the curve is the autocorrelation function corresponding to a fixed measurement volume (R = 0). The lower envelope corresponds to a cross-correlation between two fixed volumes positioned at a distance equal to the diameter of the scanned circle.

FIGURE 1.

The theoretical autocorrelation function (Eq. 2) when scanning the measurement volume at frequency f = 1 kHz along a circular path of radius R = 0.38 μm (solid line). The upper envelope of the curve (shaded) is the autocorrelation function corresponding to a fixed measurement volume. The lower envelope (shaded) corresponds to a cross-correlation between two fixed volumes positioned at a distance equal to the diameter of the scanned circle. The insets show the variation of the autocorrelation with the diffusion coefficient D (A), and with the size of the measurement volume a (B). The other parameters are: D = 100 μm² s⁻¹, a = 0.14 μm, and w = 6.5.

The insets in Fig. 1 demonstrate decoupling of D and a. While in the standard FCS the increase of diffusion coefficient D produces the same effect on the autocorrelation curve as the decrease of the measurement volume size a, this is clearly not the case in sFCS. Fig. 1 (inset A) shows that the increase of the diffusion coefficient produces a decrease of correlation at time τ = 1/f, but an increase at time τ = 1/(2f), for a suitably chosen scan radius R. However, the decrease of the measurement volume a results in decrease of correlation at all times (Fig. 1, inset B). Thus, D and a influence the autocorrelation in different ways and can therefore be determined independently at the same time (see also Supplementary Material).

An exponential component describing triplet kinetics has not been included in the model autocorrelation, because the triplet component is usually not observed with two-photon excitation (20–22). All experimental data in this work, where no photobleaching occurs, can be fitted well with the model without a triplet component (Eq. 2).

The fluorescence autocorrelations were calculated off-line from the detected stream of photocounts using the timing information of every photocount. We have applied the multiple-τ approach (23), with the lag channel width being doubled every m = 64 channels, rather than the more-often-used doubling every eight channels (24). The first 2m = 128 channels have a width equal to the temporal resolution of 13.1 ns. The calculation algorithm is similar to that published by Magatti and Ferri (25). Using m = 64 results in finer sampling of the autocorrelation curve needed to resolve the oscillations caused by scanning, and prevents distortions due to the finite channel width. This was tested by calculating autocorrelations with m = 128, 64, 32, 16, and 8, and noting that only the diffusion coefficients obtained with m = 8 and 16 were slightly higher than those with m > 16. The value of m can be easily increased within the software, if finer sampling of the autocorrelation is required. The experimental autocorrelation curves were analyzed by weighed nonlinear least-squares method with weights estimated from the data, and using a model function described by Eq. 2. The parameters D, a, w, and g₀ were optimized in the fit, while the parameters R and f were kept fixed at their known values.

Simulations

The autocorrelation curves were calculated according to Eq. 2 with the time channels of width and spacing identical with the experimental curves. Gaussian noise was added to every channel, with the standard deviation σ similar to that of experimental data. This was estimated from the autocorrelation curves of Alexa 546 as 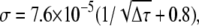where Δτ is the channel width in milliseconds. The parameters in the simulated curves were: D = 100 and 300 μm² s⁻¹, f = 0.5, 1.0, and 2.0 kHz, R = 0–1 μm, g₀ = 1, a = 0.14 μm, and w = 6.5. The simulated autocorrelation curves were analyzed in the same way as the experimental data, and the recovered parameters were processed as described in Results.

RESULTS

Radius calibration

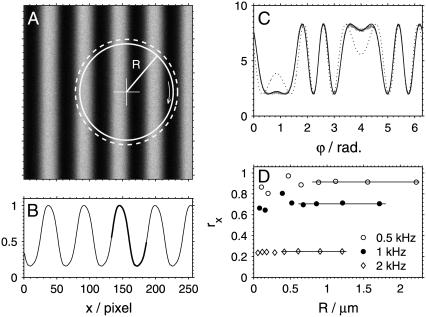
The determination of the diffusion coefficient using sFCS relies on accurate knowledge of the scan radius R. The position of the measurement volume within the xy plane is determined by the driving signal supplied to the galvanometer scanners. The exact relationship between the driving signal and the actual position of the focused laser beam (spatial calibration) was performed by imaging a Ronchi ruling (Edmund Optics, Karlsruhe, Germany) with 600 linepairs per mm, corresponding to a period of 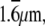in reflection mode (Fig. 2 A). Although the image of the lines is not sharp due to the diffraction-limited resolution, the period along the x direction can be determined with accuracy >0.2% from the intensity profile. The intensity profile p_x(x) averaged over all rows and over the several periods shown in Fig. 2 A is displayed in Fig. 2 B.

FIGURE 2.

Illustration of the calibration of the scan radius R. (A) Image of the Ronchi ruling with 600 linepairs per mm; image size: 8 μm. The solid circle represents the real scanned path with radius R = 2.217 μm, the dashed circle is the nominal path (R_n = 2.418 μm). (B) The intensity profile p_x(x) along the x direction. (C) The experimental temporal profile P(ϕ = 2πft) measured when scanning along the solid circle drawn in panel A (shaded line), the fit using the spatial profile p_x(x) shown in panel B (solid line), and the profile that corresponds to the nominal path shown dashed in panel A (dotted line). (D) The radius reduction factors r_x obtained at different radii R and frequencies f; the solid lines represent the average of the values at four largest radii.

This calibration is sufficient in a standard imaging mode of the microscope used, where the scanning frequencies do not exceed ∼100 Hz. At higher frequencies used in this work (0.5–2 kHz), the scanners are not able to follow the driving signal accurately, resulting in reduced amplitudes and therefore smaller scan radii R than intended. A dynamic calibration is required to determine the real scan radius R in such case. This was performed by scanning the beam at a desired frequency f and nominal radius R_n, and detecting the signal reflected from the Ronchi ruling. The measured signal was averaged over its period 1/(2πf) yielding a temporal profile P(t), t ∈ (0, 1/(2πf)). The profile P(t) was then fitted to the equation P(t) = ap_x(x(t)), where the position x(t) of the laser focus is described by x(t) = x₀ + R cos(2πft + ϕ₀). The fit parameters were: the scaling factor a, the spatial offset x₀, the true scan radius R, and the initial phase ϕ₀. In some cases the specimen moved slightly along the optical axis (z direction) between the measurements of the spatial ruling profile p_x(x) and the temporal profile P(t). This was taken into account in the fitting procedure by convoluting p_x(x) with a Gaussian of width σ (an additional fit parameter; typically 0–4 pixels), thus simulating the blurring due to defocusing. Although this procedure improved the fits, it had negligible effect on the recovered values of R, indicating that this experimental instability is not critical for the calibration.

An example of the experimental profile P(t) for f = 0.5 kHz and R_n = 2.418 μm, and a fit (R = 2.217 μm) is shown in Fig. 2 C. Also shown is a profile that would result from motion along a circle with the nominal radius R_n, if no radius reduction occurred (dashed circle in Fig. 2 A). The large difference between the two profiles for R and R_n indicates the high sensitivity of the calibration method.

The frequency-dependent radius reduction factor r_x ≡ R/R_n was independent of the radius R_n. However, the precision of its determination was rather low at low radii, mainly because of the small spatial variation of p_x(x) limited by light diffraction. Therefore, a reduction factor r_x for every used frequency value was obtained by averaging the values of r_x for the four largest radii measured (Fig. 2 D).

The dynamic calibration was performed for both x and y directions. At the frequency 2 kHz, the highest frequency used, the resulting r_x and r_y values varied by 16%, reflecting the fact that the scanned paths are slightly elliptical. This is likely to be caused by mirrors of different sizes being mounted on the x and y scanners, and therefore different resonant frequencies of the two scanners. The difference between r_x and r_y at lower frequencies was <0.5%. The average r of the r_x and r_y values was used in further data analysis. The values are: r = 0.917 ± 0.005 at 0.5 kHz, r = 0.704 ± 0.006 at 1.0 kHz, and r = 0.23 ± 0.02 at 2.0 kHz.

Measurements of diffusion coefficients D

To determine the diffusion coefficients of Alexa 546, Alexa 488, and eGFP, we measured their fluorescence autocorrelation curves at three scan frequencies (0.5, 1.0, and 2.0 kHz) and a range of scan radii R between 0 and 1 μm. Fluorescein and rhodamine 6G were measured at 0.5 and 1.0 kHz and radii 1.0 and 0.7 μm. The excitation intensities were chosen to achieve high photon count rate per molecule to maximize the signal/noise ratio (5), but were kept below the limit where photobleaching artifacts appear. The photon count rates per molecule ranged from 1.9 kHz (eGFP) to 6.5 kHz (Alexa 546).

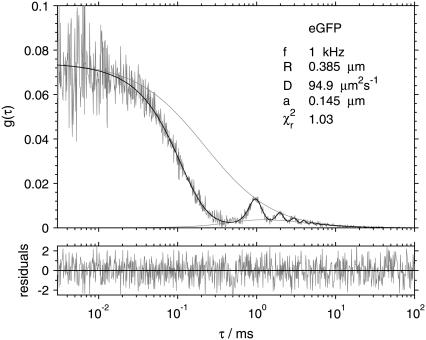
A typical experimental autocorrelation curve with a fit, in this case that of eGFP measured at frequency 1 kHz and radius 0.385 μm, is shown in Fig. 3. Also shown are the upper and lower envelopes, corresponding to the fixed-volume autocorrelation and the cross-correlation between two locations spaced by a distance 2R, respectively. The plot of fit residues indicates the good quality of the fit.

FIGURE 3.

Fluorescence autocorrelation of eGFP measured while scanning at frequency 1 kHz with radius 0.385 μm. The fit to Eq. 2 (solid), upper and lower envelopes (shaded), and fit residuals (bottom graph) are shown.

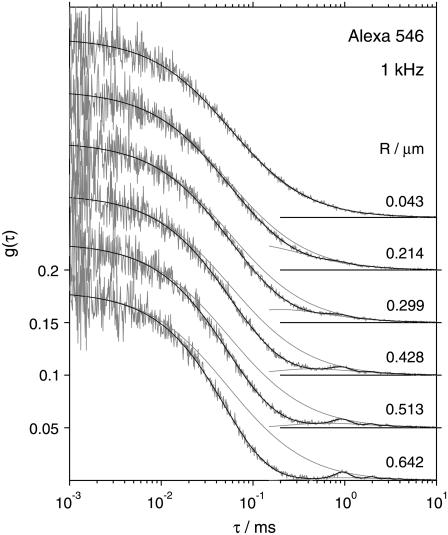
Fig. 4 demonstrates the change of the temporal profile of the fluorescence autocorrelation with varying scan radius R on the example of several experimental curves of Alexa 546 recorded at 1 kHz. Due to the faster diffusion of Alexa 546 than eGFP (higher diffusion coefficient D) the oscillations in the autocorrelation curve are less pronounced than in the curves of eGFP (Fig. 3). The amplitudes of the autocorrelation curves (g(τ) as τ → 0) were independent of the scan radius and frequency in all cases, as expected (also demonstrated in Fig. 4).

FIGURE 4.

Fluorescence autocorrelation curves of Alexa 546 measured at 1 kHz with different radii R. The fits to Eq. 2 (solid) and the upper and a part of the lower envelopes (shaded) are shown. The curves are offset for clarity. Note that the autocorrelation amplitude is independent of the scan radius R.

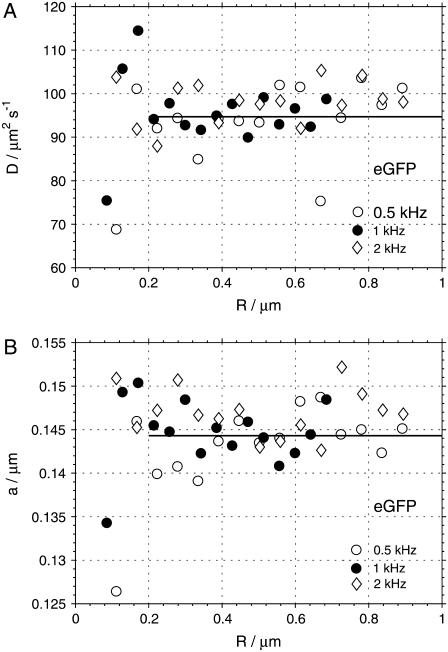
The autocorrelations were analyzed by fitting them to the model function as expressed by Eq. 2. The fits produced random uncorrelated residues with 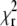values typically in the range 1.00–1.15. Fig. 5 shows the values of the diffusion coefficients D and measurement volume sizes a obtained from the fits of the autocorrelation curves of eGFP measured at three different scan frequencies f and a range of scan radii R. We observe, that at small scan radii (R ≲ 0.2 μm for eGFP, and R ≲ 0.4 μm for the Alexa dyes), the spread of the recovered parameters is much larger than at higher scan radii. This is related to the fact that at small radii the parameters D and a are strongly correlated, and in the limit of zero scan radius (fixed measurement volume) the autocorrelation is a function of the ratio of the two parameters a²/D, as described in Theory and Data Analysis. The change of one parameter can be compensated by an opposite change in the other, and consequently both of them cannot be determined simultaneously. To obtain a more precise value of D and a, we averaged the values obtained from the fits at larger radii (R > 0.2 μm for eGFP, and R > 0.4 μm for the Alexa dyes) and frequencies 0.5 and 1.0 kHz. The data from the measurements at 2 kHz were excluded from the averaging because of far less accurate determination of the radius reduction factor r at this high frequency (see Radius Calibration). In the case of fluorescein and rhodamine 6G, we averaged the values obtained at 0.5 and 1.0 kHz separately, because systematically higher D at higher scan frequencies were obtained: 422 and 450 μm² s⁻¹ for fluorescein, and 422 and 430 μm² s⁻¹ for rhodamine 6G at 0.5 and 1.0 kHz, respectively.

FIGURE 5.

Diffusion coefficients D (A) and measurement volume sizes a (B) obtained from the fits of the autocorrelation curves of eGFP measured at three different scan frequencies f and a range of scan radii R. The lines indicate the mean values calculated as averages over the fit results at frequencies 0.5 and 1 kHz and radii larger than 0.2 μm.

The final values of the diffusion coefficients D are summarized in Table 1. The errors, estimated from the standard deviations of the mean, and the errors in the calibration of the scan radius R, are ∼2%. The difference between the measured diffusion coefficients of Alexa 488 and Alexa 546, for which no literature value is available, is consistent with the difference between their molecular weights (M(Alexa 488) = 643 g mol⁻¹, M(Alexa 546) = 1079 g mol⁻¹) and the Stokes-Einstein relationship between the molecular size and the diffusion coefficient.

TABLE 1.

The diffusion coefficients D determined in this work (T = 22.5 ± 0.5°C) and comparison with literature values

	This work	Literature values
Dye	D [μm2 s−1]	D [μm2 s−1]	T [°C]	Ref.
Alexa 488	435	414	25	(2)
Alexa 546	341	—
eGFP	95	93 ± 4*	25	(2,36)
Fluorescein	436†	422–437	25	(37,38)
Rhodamine 6G	426†	414 ± 1	25	(38)

Note that the diffusion coefficients in water solutions are expected to increase with temperature by ∼2% for every degree in the temperature range used, mainly due to decrease of water viscosity with temperature.

^*The value was corrected for the wrong diffusion coefficient of the reference standard used in Schenk et al. (36).

^†Average of the values obtained at frequencies 0.5 and 1.0 kHz.

Choice of optimal scan radius R and frequency f

When performing sFSC we are free to select the scan radius R and the frequency f within the limits imposed by the hardware. A question remains as to what role the choice of scan radius and frequency plays in the precision and accuracy of the determined parameters (D, a), and what the optimal ranges of their values are.

Two conditions have to be fulfilled for the values of R and f to be suitable: first, the autocorrelation has to be sufficiently sensitive to changes in the diffusion coefficient, so that the noise on the experimental curve does not result in large spread of the values recovered from the fit; and second, the parameters D and a have to be sufficiently uncorrelated, so that D can be obtained without any additional knowledge of the value of a. The second condition is clearly not fulfilled in standard FCS with a fixed measurement volume, and decoupling of D and a is the reason for introducing scanning into FCS, when this is used for the determination of diffusion coefficients.

To understand how R and f influence the values of D and a obtained from the fit, we simulated autocorrelation curves by calculating the values in the time channels according to Eq. 2 and adding noise to the individual data points. We then fitted the curves in the same way as the experimental data, and determined the mean (expectation) values and standard deviations of the two parameters, D and a, obtained from a fit to a single curve. The simulations were performed for the diffusion coefficients 100 and 300 μm² s⁻¹, the same three values of frequencies used in the experiments (0.5, 1.0, and 2.0 kHz), and a range of scan radii R between 0 and 1 μm. For every combination of parameters, 1800 curves were simulated and analyzed.

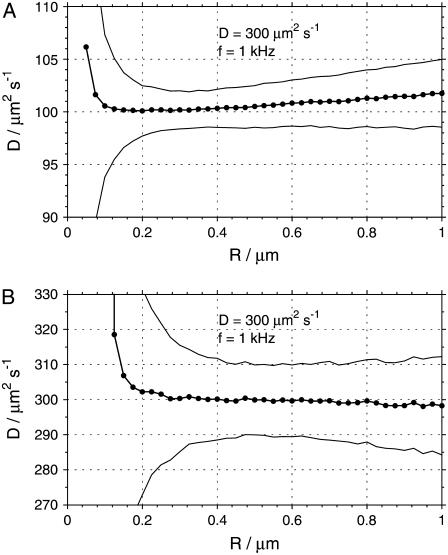
Fig. 6 shows the mean values of diffusion coefficients and their standard deviations σ_D, as obtained from the fits to the simulated data. The standard deviations diverge at low radii, an effect caused by the above-mentioned correlation between D and a and the inability to determine both parameters simultaneously at small or zero radii. At a certain radius, a minimum standard deviation is reached, and at larger radii σ_D slightly increases again. At the same time, the mean value of D exhibits a bias increasing with the scan radius. The optimal value of radius R with the smallest σ_D and no bias in the diffusion coefficient D varied with both D and frequency f, being larger at larger D and smaller f. The standard deviation σ_D at best R was smaller with smaller diffusion coefficient D = 100 μm² s⁻¹ (∼2%) and larger at D = 300 μm² s⁻¹ (∼3%), regardless of the frequency f. Simulations with lower and higher noise level, emulating higher and lower molecular brightness, respectively, provided qualitatively similar results, with the same optimal radius R₀, and lower standard deviations at lower noise levels and vice versa.

FIGURE 6.

The dependence of the diffusion coefficient D recovered from the fits of simulated autocorrelation curves on the scan radius R, displayed for two values of diffusion coefficient: 100 μm² s⁻¹ (A) and 300 μm² s⁻¹ (B). The thick line corresponds to the mean recovered values of D, and the thin lines indicate the ±σ_D widths of the distributions of D (standard deviation). The optimal scan radii R₀ with no bias in D and minimum σ_D are ∼0.35 μm (A) and 0.55 μm (B). Every data point is a result of analysis of 1800 curves.

Similar results were obtained for the measurement volume size a, with the exception that no bias was observed at high radii, and the standard deviations σ_a were smaller than those of D: 1–2%.

To assess the relevance of the results of the simulations for real experiments, the same analysis should be performed on experimental data. This is impractical, however, due to the prohibitively long times needed to acquire a sufficient amount of data. Therefore, we looked for an alternative way to relate the simulation results to practical experiments.

The fitting algorithm used in the analysis of the autocorrelation curves tries to find a minimum of 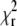by optimizing the variable parameters of the model function. The depth of the minimum, i.e., how strongly 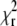changes by varying the fit parameters (or a selected fit parameter) around their optimal value, determines the stability of the fit with respect to noise, and can therefore be expected to be related to the standard deviation of the parameter in question.

We mapped the 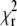minimum by calculating 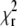for a range of D values centered around the value of D determined by the fit. The obtained curve was then fitted to a quadratic dependence 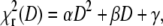with the parameter α being a measure of the depth of the 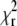minimum. This calculation can be easily performed on both the simulated and the experimental data, since one curve is sufficient to obtain an estimate of α.

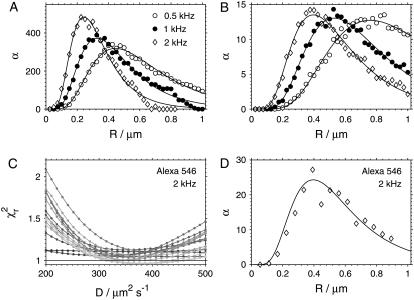
Fig. 7, A and B, show the dependence of the parameter α calculated from the simulated decays on the scan radius R for the same values of diffusion coefficient and frequency as those used in the simulations described above. The datapoints were matched to arbitrary smooth curves (lognormal distributions) to facilitate the estimation of the position of the maximum α. The results show that when the maximum of α is reached, the radius coincides with the optimal R value established on the basis of minimum standard deviation of D (Fig. 6).

FIGURE 7.

Choosing the optimal scan radius R. (A and B) The parameter α from the fits 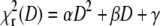obtained from simulated autocorrelation curves at different scan radii R with diffusion coefficient D = 100 μm² s⁻¹ (A) and D = 300 μm² s⁻¹ (B). (C) The dependence of 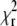on diffusion coefficient D for fits of Alexa 546 autocorrelation curves recorded at radii R = 0.06–0.9 μm (lighter plots → higher R) at frequency f = 2 kHz. (D) The parameter α obtained from the fits to the curves shown in panel C (diamonds) compared to the curve from simulations with D = 300 μm² s⁻¹ and f = 2 kHz (solid line) as shown in panel B (diamonds).

The same calculations were performed with the experimental autocorrelation data. Fig. 7 C shows the dependencies 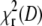for Alexa 546 autocorrelations measured at 2 kHz and a range of scan radius values. The α-values from the fits to these curves are shown in Fig. 7 D, together with a scaled smooth curve corresponding to α-dependence of simulated data with f = 2 kHz and D = 300 μm² s⁻¹ taken from Fig. 7 B. Clearly, the position of maximal α for experimental and simulated data coincides, as is the case for all other combinations of frequencies and investigated dyes (not shown).

These findings indicate that the optimal values of scan radius obtained from simulations can be considered applicable for real measurements, despite the idealization of uncorrelated Gaussian noise in the simulated curves (23), and despite the fact that additional disturbances can be present in real experiments. It is therefore possible, in principle, to perform the simulations described above for all relevant combinations of diffusion coefficients, scan frequencies and radii, and to derive from these results the optimal scan radius and frequency for any diffusion coefficient.

Instead, we attempted to obtain a more general semiempirical formula for the optimal scan radius R from considerations concerning the variations of the autocorrelation curve with the diffusion coefficient. We assume that the measurement of D will be most precise when the autocorrelation is most sensitive to changes in D, i.e., when the changes of g(τ) with D are the largest. At the same time we require that the changes of g(τ) with D are distinguishable from the changes caused by variations in a, to keep the two parameters uncorrelated, as discussed in Theory and Data Analysis, and demonstrated in Fig. 1.

Considering the autocorrelation curves shown in Fig. 1 A, a possible criterion for optimal scan radius R₀ can be formulated: at the optimal scan radius, the changes of g(τ) at times τ = 1/(2f) and τ = 1/f with the diffusion coefficient D are the largest, but with opposite sign (see Supplementary Material for details). Mathematically, the radius R₀ has to be found where the following maximum is reached:

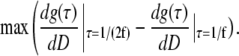(3)

The minus sign indicates that the changes of g(τ) at the two different times occur in opposite directions. A straightforward calculation, simplified by the fact that the second term in Eq. 3 is independent of R, yields the following formula for R₀, together with a useful approximation:

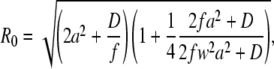(4)

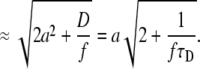(5)

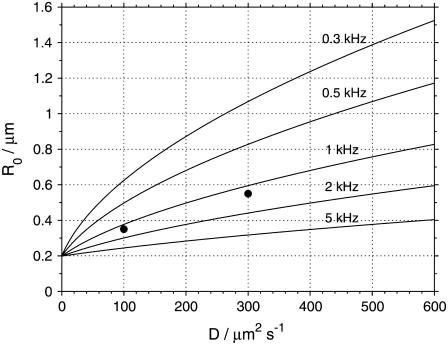
The value of R₀, as a function of the diffusion coefficient D for several scan frequencies and assuming a = 0.140 μm, is displayed in Fig. 8. The R₀ values given by Eq. 4 agree well with the optimal scan radii determined from the simulations, as can be seen from comparison of plots in Fig. 6 with Fig. 8, where the R₀ values obtained from simulations are marked. Equation 4 (or Eq. 5) therefore provides the optimal scan radius at any given frequency. An approximate knowledge of the diffusion coefficient or the diffusion time τ_D of the investigated compound is thus required; this can be determined from a preliminary measurement.

FIGURE 8.

The optimal scan radius R₀ determined from Eq. 4, assuming a = 0.140 μm, plotted for several scan frequencies f. The points at diffusion coefficients 100 and 300 μm² s⁻¹ show the optimal scan radius R₀ for the frequency 1 kHz obtained from simulations as described in the text, and also shown in Fig. 6.

Regarding the choice of the best frequency, there is a clear lower limit since, at frequencies that are too low, the correlation decays to values that are too low, before the measurement volume performs one rotation, and the modifications to the autocorrelation curve due to scanning will be lost in noise.

It may appear that using much higher frequencies than those employed in this work would introduce more oscillations in the autocorrelation curve and so increase the sensitivity. However, the oscillations at times much shorter than the diffusion time are determined mainly by the scanning motion and therefore carry little or no information about the diffusion process. It is therefore not clear whether the use of higher scan frequencies would be beneficial.

The data and simulations presented here do not clearly suggest a certain frequency, apart from the fact that 2 kHz is too high due to the slow response of the scanners, this being a problem of instrumental nature. Due to these facts and the limited range of useful frequencies available, we have not attempted to search for the optimal frequency value in more detail.

We conclude this section by pointing out that the optimal scan radius R is such that the loss of correlation, as expressed by the decay of the autocorrelation curve, should be in the same way due to scanning (which is known: R, f) and due to diffusion (to be determined: D, a). The scanning motion thus acts as an internal reference for the unknown diffusional motion.

Robustness of sFCS measurements

Since the determination of the diffusion coefficient with sFCS does not require any accurate prior knowledge about the size of the measurement volume a, it can be expected that the sFCS measurements will be more robust with respect to disturbances and nonidealities affecting the value of a and thus disqualifying a standard FCS experiment.

It is known that at high excitation intensities, particularly with two-photon excitation, photobleaching of the dye molecules distorts FCS autocorrelation curves and leads to apparently shorter diffusion times τ_D, therefore overestimated diffusion coefficients D (20,26). Scanning the measurement volume, either in a raster (15) or in a circle (19), was shown to alleviate the distortions due to photobleaching.

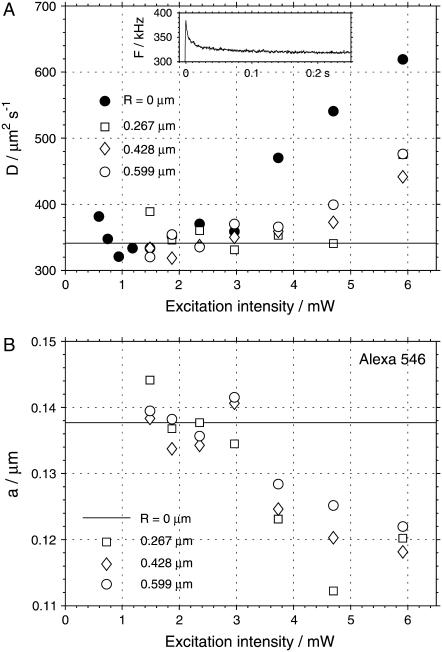
The same reduction of distortions due to photobleaching is observed in sFCS described here, as shown in Fig. 9. The autocorrelation curves of Alexa 546 were measured with a fixed measurement volume and while scanning at 1 kHz and three different scan radii, at a range of excitation intensities. When analyzing the data recorded without scanning, the parameter a had to be fixed at a = 0.138, the value determined from previous sFCS measurements. As expected, photobleaching at higher excitation intensities caused the diffusion coefficient obtained from the experiments with a fixed measurement volume to be increasingly overestimated (Fig. 9 A). On the other hand, the diffusion coefficients from the scanning measurements start to deviate from the correct value at higher intensities than in the absence of scanning. This fact is important, since higher excitation intensities can be applied, thus increasing the molecular brightness and therefore the signal/noise ratio. Similar results were obtained for eGFP and Alexa 488.

FIGURE 9.

The effect of photobleaching on the values of the diffusion coefficient D (A) and the measurement volume size a (B) obtained from the fits of the autocorrelation curves of Alexa 546. The results of measurements with fixed measurement volume (solid circles, R = 0 μm) and measurements at three different scan radii R (open symbols) are shown. The solid line in A indicates the diffusion coefficient measured in the absence of photobleaching. The value of a was fixed to 0.138 μm in the analysis of the data recorded with R = 0 (solid line in B). The scan frequency was 1 kHz. (Inset) Fluorescence decrease due to equilibration between photobleaching and influx of nonbleached molecules to the measurement volume observed upon opening a shutter (excitation power 6 mW, average of 1000 runs).

In situations where there is no possibility to measure the whole intensity series (as shown in Fig. 9 A), but only measurements with limited intensity range are possible, as is often the case in biological applications, we may have no indication whether the value of D obtained from the fit is affected by photobleaching or not. Scanning FCS provides such an indicator: the measurement volume size a. As shown in Fig. 9 B, the volume size a becomes progressively smaller with increasing photobleaching. Since the measurement volume sizes in FCS are usually diffraction-limited, decrease of a can hardly indicate physically smaller measurement volumes, but is more likely a manifestation of distortions in the measurement. The unexpectedly low value of a can therefore be taken as a warning that the recovered diffusion coefficient may not be reliable.

Of course, the quality of the fit remains a universal criterion to reject low-quality data. The autocorrelation curves measured at high bleaching levels did not produce good fits; the 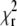values reached up to 2.5. In biological applications, the experimental conditions are often far from ideal, and the requirements on 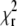and randomness of residuals have to be relaxed, making an additional criterion for acceptance/rejection of parameters obtained from analysis extremely useful.

The fact that the effects observed at high powers are indeed due to photobleaching is demonstrated in the inset in Fig. 9 A. The plot shows an initial decrease of fluorescence intensity after the opening of a shutter. We interpret this behavior as an equilibration between photobleaching and influx of nonbleached molecules into the measurement volume. This equilibration occurs on the scale of ∼30 ms. The triplet state is expected to become populated on a much faster timescale (∼μs), therefore it cannot be the reason for the observations. The stationary concentration of nonbleached molecules in the measurement volume decreases with increasing excitation power, leading to the observed less-than-quadratic dependence of fluorescence (not shown).

Another possible distortion of a FCS measurement is an effective increase of the measurement volume size due to nonideal focusing caused by optical properties of the sample, such as refractive index mismatch or heterogeneity. Such effects are likely to be encountered in biological samples, especially when the measurement is performed deeper within the specimen.

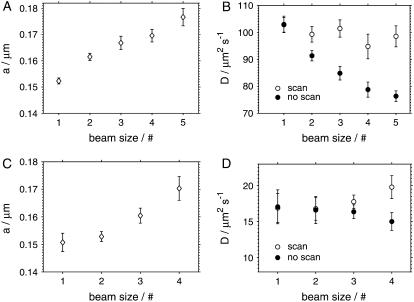
To simulate the increase of the volume size, we decreased the diameter of the excitation beam before entering the scanning unit, thus underfilling the back aperture of the objective and increasing the measurement volume size in the focal plane. The beam diameter was decreased in five steps (five data points in Fig. 10), leading to a progressively larger volume size a. The increase of the measurement volume was confirmed by a lower fluorescence signal and a lower autocorrelation amplitude due to more molecules being present in the measurement volume.

FIGURE 10.

The effect of the size of the measurement volume on the parameters obtained from the analysis of eGFP autocorrelations in TRIS buffer (A and B) and in cells (C and D). The measurement volume size was increased by decreasing the beam diameter in five steps (four steps in case of cell measurements), as indicated by the numbers 1–5 on the x axis. The plots A and C show that the increase of the measurement volume can be detected from the fit by the increasing values of the volume parameter a, both in solution and in the cells. The plots B and D show the diffusion coefficients obtained from sFCS measurements (open circles), and from FCS measurements with a fixed measurement volume (solid circles), where a was fixed at its minimum value (at beam size #1).

Fig. 10, A and B, shows the results of the measurements on eGFP in solution performed both with and without scanning. The analysis of the measurements with scanning yields increasing values of a with a decreasing excitation beam size, without using the information about the beam size in the analysis, as expected. The value of the diffusion coefficient remains independent of the beam size, within the error limits.

To determine the diffusion coefficient from measurements with a fixed measurement volume, the volume size a has to be known. Ignoring the fact that the volume size a increases, and using the value of a from the sFCS measurement with the largest beam size (#1) leads to a progressively smaller apparent diffusion coefficient D, as shown by solid symbols in Fig. 10 B. Thus, while an incorrect assumption about the size of the measurement volume a leads to a wrong value of the diffusion coefficient D in a standard FCS measurement (no scanning), scanning FCS allows us to determine D without accounting for any changes of the volume size a.

We have performed similar measurements with varying the beam size in the cytoplasm of HeLa cells expressing eGFP. Scanning FCS measurements allows us to determine the volume size a and the diffusion coefficient D independently, from a single measurement, as in the solution studies. Decreasing the excitation beam size yields an increasing volume size a from the fits to the sFCS data, as with eGFP in the buffer (Fig. 10 C). FCS measurements without scanning, assuming again the smallest volume size a (beam size #1), produce smaller apparent diffusion coefficients D with larger beam sizes (#3 and #4) where the volume size a deviates significantly from its smallest value (Fig. 10 D). The values of the diffusion coefficient D obtained with sFCS are in agreement with the literature data (16). The larger relative errors of D in cells compared to the buffer measurements are caused by the variability of D among different cells.

These results demonstrate that it is possible to perform in vivo measurements of the diffusion coefficients by sFCS without any knowledge about the size of the measurement volume a. This method is able to detect uncontrolled changes of a, and thus prevent an incorrect determination of D, as would be the case in a standard FCS if assuming a wrong value of a.

FCS is known to be sensitive to nonidealities other than photobleaching or unaccounted changes of the volume size a; for example, optical saturation, the quality of the illuminating laser beam, wrong coverslip thickness, etc. (27,28). We have not attempted to systematically investigate robustness of sFCS to all these effects so far, although such a study will be important for determining the limits of possible applications. We note only that according to our preliminary data, using coverslips of wrong thickness (wrong setting of the correction collar on the microscope objective) results in significantly larger values of a recovered from the fits to sFCS data (up to 17%), with no apparent effect on the value of D.

DISCUSSION AND CONCLUSION

Comparison of the diffusion coefficients measured in this work with the literature data shows a relatively good agreement (Table 1), although the diffusion coefficients of the smaller molecules appear to be systematically biased toward larger values.

The precision of the determination of D is influenced by both the calibration of the scan radius R and the noise on the experimental autocorrelation curves. The precision of the radius reduction factor r determined by calibration is rather high, and is not the limiting factor in our measurements at frequencies 0.5 and 1 kHz. Moreover, we believe that it can be further increased, should the need arise, by elaborating on the calibration procedure described.

The noise on the autocorrelation curves is known to be influenced mainly by the molecular brightness of the investigated fluorochromes (29). Increasing the excitation intensity increases the molecular brightness up to a limit where various artifacts, mainly due to photobleaching and optical saturation, appear (30,31). This limit is considerably lower when two-photon rather than one-photon excitation is used (5,20). We therefore expect that implementing sFCS as described here, with one-photon excitation, would lead to improved signal/noise ratio, and consequently higher precision of the determination of D. Longer acquisition times also reduce the noise in the data, but extensive measurement periods may not always be practical or possible.

The accuracy of the determination of diffusion coefficient with sFCS, i.e., the presence or absence of bias in the measured value, is considerably more difficult to determine, and can be reliably assessed only by comparison with a known standard. We do not know the reason for larger values of D obtained in this work compared to the literature values. The results of the simulations indicate that the diffusion coefficients obtained from fits can be biased, if the scan radius is inappropriately chosen, this being an inherent feature of the fitting algorithm (Fig. 6). However, the deviations predicted by the simulations are too small to explain the differences from the previously published data. Heating in the focus of the objective is also unlikely to be the cause (32).

A small contribution of fast kinetics (triplet) can lead to higher diffusion coefficients if the triplet term is not included in the model function, as confirmed by simulations. For example, 10% contribution of a component with τ_T = 0.003 ms yields D ∼ 2–3% higher. The bias is larger with higher τ_T and larger contribution of the exponential component. However, this hypothesis could not be verified, since we could not resolve any triplet contributions in our data, in agreement with previous observations (20–22).

Another potential source of bias is the approximation of the shape of the measurement volume, as expressed by Eq. 1. Although this approximation is accepted as sufficiently good in standard FCS measurements, its limitations have been shown to appear in certain situations (27,33). We assume this to be the most probable explanation for the observed discrepancies. Implementation of a more accurate description of the measurement volume may help clarify this point (34).

The photobleaching measurements described above, and the demonstrated ability of sFCS to yield constant diffusion coefficients and increasing volume sizes upon decreasing the excitation beam diameter, indicate the robustness of sFCS to experimental conditions that directly or effectively influence the value of a. In a standard FCS, the volume size a has to be known to correctly determine D. For example, it has been shown that when measuring diffusion coefficients of molecules in planar membranes, the vertical position of the laser focus determines the size of the measurement area, and if this is not taken into account, wrong values of D can be obtained (35). Conversely, in sFCS, the recovered value of D is independent of a, therefore the volume size a does not have to be determined independently, as demonstrated here by varying the beam size, or previously with line-scanning FCS on two-dimensional surfaces (9).

The robustness of sFCS is particularly relevant for biological applications, where the samples are often heterogeneous with uncontrollable optical properties. The experiments with cells expressing eGFP show that the essential features of sFCS established in solution measurements are preserved in the in vivo experiments: diffusion coefficients can be obtained without any assumptions about the size of the measurement volume a, and an artificially induced increase of a (by varying the beam size) can be reliably detected in the fits, without any a priori assumptions.

Although we have used the excitation beam diameter to modify the measurement volume size, the volume size in complex samples can increase due to other effects, such as nonideal focusing caused by optical heterogeneity of the sample (refractive index variations).

Since the scan radii are small, typically of a size similar to that of the measurement volume, the presented implementation of sFCS does not require a large homogeneous area within the sample (for example, cytoplasm) or corrections for background pattern, as in other scanning FCS implementations (18).

We see several advantages of circular sFCS compared to the alternative FCS methods for the measurement of diffusion coefficients mentioned in the Introduction: In sFCS the portions of the scanned circular path are illuminated continuously by the rotating beam, but not simultaneously, which is somewhat equivalent to alternating excitation of overlapping volumes in Dertinger et al. (6). Because of this continuous motion, there is no need for interleaved excitation and consequently, both the excitation and detection parts of the experimental setup are relatively simple. Related to this is the straightforward data processing: the stream of photocounts is simply autocorrelated, and no sorting of photocounts into detection channels (6), or the removing of parts of the data due to the laser beam reaching the end of the scan lines and alignment of scan data (9), is necessary. Furthermore, the calibration of the scan radius is relatively simple and highly accurate, and there is no need for complex measurement volume engineering, as in Blancquaert et al. (8).

On the other hand, the need for moving parts (galvanometer scanners) and illumination optics needed for scanning can be seen as a drawback. We suggest that an experimental configuration considerably less complex than a laser scanning microscope as used here, is adequate for the implementation of sFCS. The scan radii employed in sFCS are ∼1 μm, meaning that the angles at which the laser beam has to enter the objective are ∼0.3 mrad, if the objective focal length of 3 mm is assumed. Then, the scanning mirror can be positioned directly in front of the objective, without any scan or relaying lenses, since the displacement of the beam at the back-objective aperture will be a negligible 0.1 mm, if a realistic distance of 30 cm from the objective is assumed. Thus, a common FCS setup can be converted into sFCS by replacing a mirror with a commercially available two-axis piezo scanner. We are currently developing such a system.

We conclude that scanning FCS, as described here, appears to be a promising variation of FCS tailored for the measurement of diffusion coefficients, be it accurate determination of D without any a priori knowledge about the size of the measurement volume in solutions and in vitro experiments, or robust measurements in complex environments, such as living cells and tissues, where possible experimental disturbances affecting the volume size are implicitly taken into account.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.