Decoding of Calcium Oscillations by Phosphorylation Cycles: Analytic Results

Abstract

Experimental studies have demonstrated that Ca²⁺-regulated proteins are sensitive to the frequency of Ca²⁺ oscillations, and several mathematical models for specific proteins have provided insight into the mechanisms involved. Because of the large number of Ca²⁺-regulated proteins in signal transduction, metabolism and gene expression, it is desirable to establish in general terms which molecular properties shape the response to oscillatory Ca²⁺ signals. Here we address this question by analyzing in detail a model of a prototypical Ca²⁺-decoding module, consisting of a target protein whose activity is controlled by a Ca²⁺-activated kinase and the counteracting phosphatase. We show that this module can decode the frequency of Ca²⁺ oscillations, at constant average Ca²⁺ signal, provided that the Ca²⁺ spikes are narrow and the oscillation frequency is sufficiently low—of the order of the phosphatase rate constant or below. Moreover, Ca²⁺ oscillations activate the target more efficiently than a constant signal when Ca²⁺ is bound cooperatively and with low affinity. Thus, the rate constants and the Ca²⁺ affinities of the target-modifying enzymes can be tuned in such a way that the module responds optimally to Ca²⁺ spikes of a certain amplitude and frequency. Frequency sensitivity is further enhanced when the limited duration of the external stimulus driving Ca²⁺ signaling is accounted for. Thus, our study identifies molecular parameters that may be involved in establishing the specificity of cellular responses downstream of Ca²⁺ oscillations.

INTRODUCTION

Cell signaling induced by extracellular stimuli is often accompanied by an increase in the cytosolic calcium concentration [Ca²⁺]_c that, ultimately, regulates a plethora of cellular processes, including secretion, contraction, learning, and proliferation (1–4). Such regulation is mediated by Ca²⁺-dependent enzymes that, in turn, modify downstream targets commonly by phosphorylation. In many cell types, changes in [Ca²⁺]_c occur as repetitive spikes that increase their frequency with the strength of the stimulus (5,6). Information can also be encoded in the amplitude of Ca²⁺ oscillations, which may change with the extracellular stimulus (7–9) and may also depend on the subcellular localization of the target (10,11). Understanding how an extracellular stimulus, encoded in the frequency and amplitude of Ca²⁺ oscillations, is interpreted by different physiological processes is one of the major challenges in the study of Ca²⁺ signaling.

Various experiments have suggested that Ca²⁺ oscillations may be advantageous compared to a constant rise in [Ca²⁺]_c because they increase the efficiency of gene expression at low levels of stimulation (12,13). A long-standing question is how a ubiquitous messenger like Ca²⁺ achieves specificity in its action. Recent data indicate the ability of calmodulin and protein kinase C (PKC) to decode the amplitude of Ca²⁺ oscillatory signal into an appropriate cellular response (14,15). It has been shown that the sensitivity to Ca²⁺ oscillations of different transcription factors such as the nuclear factor of activated T cells (NFAT), nuclear factor kappa B (NFκB) (12,13,16), Ca²⁺-dependent enzymes such as calmodulin (CaM) kinase II (17), and mitochondria (18,19), can depend on the oscillation frequency. Moreover, when the stimulus is transient, the effect of Ca²⁺ oscillations can be maximized within a certain range of frequencies (13,16,20). In Ca²⁺ oscillations, higher frequency implies a higher density of practically uniformly shaped Ca²⁺ spikes and thus also a higher average [Ca²⁺]_c. Thus, the question arises whether the observed increases in target response with rising oscillation frequency are simply due to an increase in the average Ca²⁺ signal or present a true frequency decoding.

Previous theoretical work has focused on how frequency-encoded information is processed by Ca²⁺-regulated proteins (21–23). Frequency decoding is characterized by higher average levels of phosphorylated protein when the frequency of Ca²⁺ oscillations is increased. Detailed models of protein phosphorylation driven by regular Ca²⁺ oscillations have been developed for CaM kinase II (14,24,25), glycogen phosphorylase (26,27), and mitogen-activated protein kinase cascades (28,29). Decoding of Ca²⁺ signals more complex than periodic spiking (e.g., bursting oscillations) has been recently theoretically explored (30,31). Numerical simulations have shown that Ca²⁺ oscillations can be more efficient for protein phosphorylation compared to constant Ca²⁺ signals of equal average [Ca²⁺]_c. The nonlinear dependence of protein activation on Ca²⁺ stimulation, arising from diverse mechanisms, such as cooperative Ca²⁺ binding or zero-order ultrasensitivity, turns out to be of major importance for an efficient processing of oscillatory signals. Furthermore, these models predict that the Ca²⁺ oscillation frequency can discriminate among different signaling pathways.

Although these theoretical studies have provided insight into the mechanisms involved in calcium decoding, their conclusions are based on numerical simulations of detailed models for specific proteins (reviewed in (32)). Because of the large numbers of Ca²⁺-regulated proteins in signal transduction and gene transcription, it is desirable to establish in general terms which molecular properties shape the response to Ca²⁺ oscillations. Investigating Ca²⁺ decoding in an analytically tractable model may provide more insight into the following issues:

• How sensitively can a target protein respond to changes in the frequency of calcium oscillations?

• Under which conditions are Ca²⁺ oscillations more potent than a constant signal in activating a target protein?

• Which properties determine the existence of an optimal activating signal for a particular target?

• Under which conditions can target proteins be differentially activated by Ca²⁺ signals?

Some challenges for such analysis are the nonstationarity of the Ca²⁺ signal and the nonlinearity of the Ca²⁺ dependent processes. The description of Ca²⁺ oscillations using a piecewise constant function can facilitate an analytical solution of the kinetic equations (31,33,34). Indeed, such square-shaped pulses have been used in several experiments (12,13,17) and for numerical simulations (20,35).

In this article, we attempt to establish in general terms which molecular properties determine the target response to oscillatory Ca²⁺ signals. To this aim, we employed an analytically tractable model of a prototypical Ca²⁺-decoding module, consisting of a target protein controlled by a Ca²⁺-activated kinase and the counteracting phosphatase. The modeling of Ca²⁺ oscillations by square-shaped pulses allowed the derivation of a general formula for the target activity as a function of three dimensionless parameters.

Using this formula, we first asked whether a true frequency decoding, at constant average Ca²⁺ signal, is possible. We then examined the conditions under which oscillatory signals are more potent in activating the target protein than constant signals with the same average calcium. To assess the kinetics of the target, we defined an activation time that quantifies the time necessary to reach the maximal target activity. The expressions for the activation time and target activity were used to analyze signaling specificity. In particular, we investigated which molecular parameters determine the optimal signal shape for a limited amount of calcium. Collectively, our results demonstrate that the nonlinear activation of a protein by a Ca²⁺-dependent kinase represents a core system for decoding Ca²⁺ oscillations, and rationalize why oscillatory stimuli increase the efficiency and specificity of cell signaling.

MATHEMATICAL MODEL

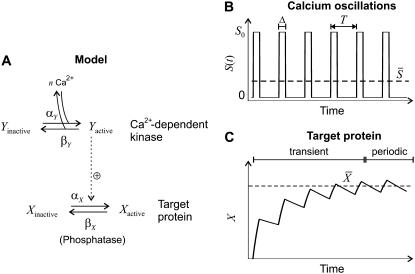
We consider an activation-inactivation cycle of a target protein X (Fig. 1 A). Its activation is induced by phosphorylation through a Ca²⁺-dependent kinase Y, and it is inactivated by dephosphorylation. Cooperative activation of the kinase by Ca²⁺, as observed, for example, for Ca²⁺/CaM-dependent kinases (36,37), is described by the binding of n ions of Ca²⁺. The fractions of active kinase Y and phosphorylated (active) target protein X obey, in the simplest model,

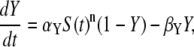(1)

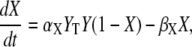(2)

where Y_T represents the total concentration of kinase, S(t) describes the time course of the Ca²⁺ signal, α_Y and β_Y are the rate constants of Ca²⁺ binding and release, and the rate constants of phosphorylation and dephosphorylation are denoted by α_X and β_X, respectively.

FIGURE 1.

Model for the decoding of Ca²⁺ oscillations by a target protein. (A) Model scheme. (B) Oscillations in the Ca²⁺ concentration S(t) have period T, amplitude S₀, spike width Δ, and average 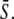(C) The calcium signal induces oscillations in the phosphorylated (active) target protein. After an initial transient, the time-average target activity reaches the steady value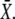

In many cases, Ca²⁺ binding will be much faster than (de)phosphorylation reactions, so that we can assume the binding equilibrium, dY/dt ≈ 0. Equation 2 then becomes

(3)

where, for simplicity, β = β_X. Between calcium spikes, the kinase activity is negligible so that the response time of the target protein is β⁻¹.

The dependence of the phosphorylation rate constant on Ca²⁺ concentration takes the form of the Hill equation

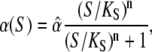(4)

with the maximal value 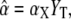the half-saturation constant 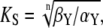and the Hill-coefficient n. Hill equations provide good fits for more realistic Ca²⁺ binding mechanisms, in which case n can take noninteger values (20,30).

Cytosolic Ca²⁺ oscillations consist of a series of spikes separated by intervals of resting Ca²⁺ concentration (38). To enable analytic treatments, Ca²⁺ oscillations are described by a piecewise constant function

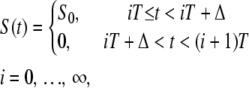(5)

characterized by period T, amplitude S₀, and spike width Δ (Fig. 1 B). For simplicity, the basal Ca²⁺ concentration has been set to zero.

RESULTS

The mean activity of the target protein depends on three dimensionless parameters

Let us assume that before the onset of calcium oscillations, the target protein is completely inactive (i.e., unphosphorylated). The target's response to the oscillations goes through an initial transient to reach an (approximately) periodic state (Fig. 1 C). The mean target activity 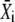during the i^th oscillation cycle is

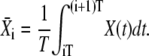(6)

The average is a good measure of the target protein's response if the amplitude of the protein activity oscillations is not too large, that is, when the system integrates the oscillations. This has been seen in the responses of gene expression rates and of mitochondrial metabolism to calcium oscillations (12,16,18,19). However, even if the target amplitudes were large, the average is a useful diagnostic of how sensitively the system responds to the oscillatory signal.

The approximation for the Ca²⁺ spikes (see Eq. 5) allows the derivation of an analytic expression for the average 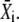After some algebra, one finds for its stationary value 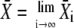(see Appendix A):

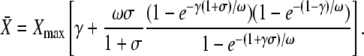(7)

This equation shows how the original parameters combine into three dimensionless parameters that govern the response of the system, as follows here.

The effective activation rate σ during the calcium spike

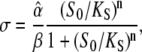(8)

measures how the calcium amplitude S₀ is sensed by the kinase with respect to binding affinity (1/K_S) and cooperativity of kinase activation (Hill coefficient n), and how fast phosphorylation of the target is compared to its dephosphorylation ().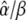

The relative oscillation frequency ω,

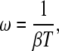(9)

expresses how fast the oscillations are compared with the basal response time of the protein β⁻¹ (see Eq. 3). Thus, the parameter combines the two timescales in the problem. Large ω means fast calcium oscillations and/or a slow response time of the phosphorylation cycle, in which case the phosphorylation cycle will integrate over the oscillations and the amplitude of the oscillations in target activity is small. Conversely, if ω is small, the target activity will closely follow each cycle of the calcium oscillations.

The duty ratio of the oscillations γ,

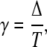(10)

gives the part of the oscillation period during which calcium is elevated and the kinase is active. Hence, the average calcium concentration in the oscillations is

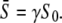(11)

The maximal activity of the target protein X_max is a function of σ,

(12)

Target activity is sensitive to the frequency of narrow calcium spikes

It turns out that the mean target activity 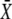is a monotonically increasing function of all three parameters on their natural intervals σ ∈[0,∞), ω ∈[0,∞), and γ ∈[0,1). Increases in the activation rate, oscillation frequency, or duty ratio would therefore all raise the target activity. As experiments on many cell types show that the dose of the external stimuli (e.g., hormones and local mediators) controls primarily the frequency of calcium oscillations and leaves the amplitude unchanged, we asked how sensitively the target protein can respond to variations in frequency. In the limit of slow oscillations (or a rapidly responding protein), we obtained the target activity as

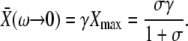(13)

For fast oscillations (or a slowly responding protein), we found

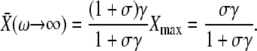(14)

The frequency sensitivity of the target's response to calcium oscillations with constant amplitude becomes maximal,

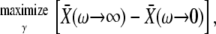(15a)

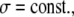(15b)

when the duty ratio obeys

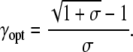(16)

The optimal duty ratio γ_opt lies between 0.5 (for σ = 0) and 0 (for σ → ∞). Hence, calcium oscillations whose frequency can efficiently drive changes in target activity have duty ratios below 0.5, i.e., the spikes occupy less than half of the oscillation. Interestingly, the observed calcium oscillations, for example in liver cells, have duty ratios between 0.05 and 0.5 (39).

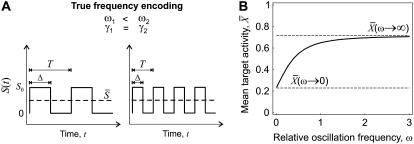
Importantly, when activation rate σ and duty ratio γ are constant and only the relative oscillation frequency ω is varied, the average calcium concentration 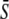remains constant (Fig. 2 A). Therefore, the system can respond purely to changes in the frequency of the calcium signal if the calcium spikes are sufficiently narrow compared to the period of the oscillations. An example of this true frequency decoding is shown in Fig. 2 B. Note that the asymptotic value 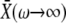is practically reached already for ω ≥ 1. This implies that the target protein activity becomes frequency-insensitive when the oscillation period gets in the range of the basal response time of the target protein (see Eq. 9). We have found this to be the typical behavior for a wide range of parameter values.

FIGURE 2.

Target activity is sensitive to the frequency of narrow calcium spikes. (A) True frequency encoding occurs when the relative frequency ω changes while both amplitude S₀ and average 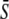stay constant. (B) An example of true frequency decoding is shown here. The mean target activity 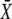is plotted against ω using Eq. 7. The values of 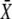in the limit of very slow and very fast oscillations (Eqs. 13 and 14, respectively) are indicated by dashed lines. Parameters: σ = 10, γ = 0.25.

These results demonstrate that true frequency decoding, at constant average Ca²⁺ signal, can occur provided that the Ca²⁺ spikes are narrow and the oscillation frequency is of the order of the target inactivation rate or below.

Oscillations are more potent than constant signals when the kinase binds calcium cooperatively and with low affinity

Given a certain amount of calcium per unit time, what is the signal shape that best activates the target protein? For the piecewise constant oscillatory signal (Eq. 5), the shape at a given calcium average 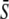is uniquely defined by fixing period T and duty ratio γ, where the latter automatically defines the amplitude Setting the frequency, the optimal signal shape is therefore the solution of

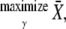(17a)

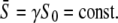(17b)

Using Eq. 14, for high-frequency oscillations, one obtains the maximal target response for

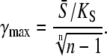(18)

If calcium activation of the kinase is noncooperative or negatively cooperative, n ≤ 1, there is no γ_max. Indeed, for n ≤ 1, 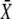is a monotonically increasing function of γ when the average calcium signal is constrained (Eq. 17b). Therefore, the maximal response will be obtained at γ = 1 (that is, the constant calcium signal).

However, when calcium activation of the kinase displays positive cooperativity, n > 1, γ_max can be below 1. Therefore, an oscillatory signal can be more potent in activating the target than a constant signal. The critical case occurs obviously when the maximum is attained for γ = 1 (constant signal). From Eq. 18, we then found that if the condition

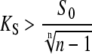(19)

holds, the maximum of 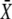occurs for 0 < γ < 1, and hence oscillations with the duty ratio given by Eq. 18 activate the target most strongly. In particular, this oscillatory signal is more potent than a constant signal of the same average calcium.

The function 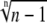lies between 1 and 1.321 for a cooperative calcium decoder with 2 < n < ∞ (the maximum is attained at n = 4.5911). Therefore, an efficient decoder must have comparatively weak calcium affinity, with dissociation constant K_S lying around the peak concentration of the calcium spike S₀ or above.

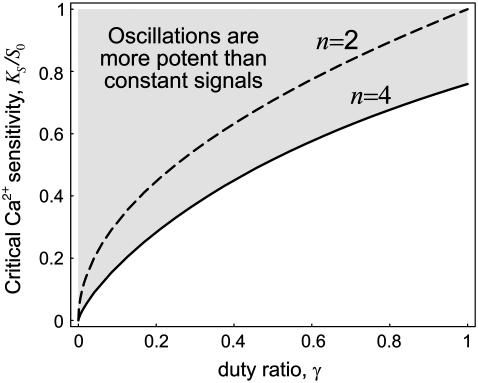
Equation 19, for the superiority of oscillations over constant calcium signals, holds for any duty ratio. However, calcium oscillations typically have rather low duty ratios (γ < 0.5). In this case, the requirement for calcium affinity becomes less stringent. At a given duty ratio γ, oscillations are superior over constant signals if the calcium sensitivity of the kinase, relative to the spike amplitude, satisfies (see Appendix B):

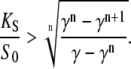(20)

The decrease of the critical dissociation constant with decreasing duty ratio is shown in Fig. 3 for two distinct values of n. So far, all expressions were derived for the case of high-frequency oscillations. We obtained very similar expressions for the general case (Appendix B).

FIGURE 3.

Critical Ca²⁺ sensitivity for an efficient decoding by oscillations. The critical Ca²⁺ dissociation constant K_S (relative to the spike amplitude S₀), above which Ca²⁺ oscillations are more potent than a constant Ca²⁺ signal, is plotted as a function of the duty ratio γ. Curves were obtained using Eq. 20. Parameters: n = 2 (dashed line), n = 4 (solid line).

In summary, our theory shows that Ca²⁺ oscillations activate the target of a Ca²⁺-dependent kinase more efficiently than a constant signal if 1), Ca²⁺ acts cooperatively on the kinase (n > 1); and 2), the Ca²⁺ affinity of the kinase is rather low. As an example, we consider typical cytoplasmic Ca²⁺ spikes with S₀ = 800 nM and γ = 0.3, yielding a critical K_S of 300–440 nM for Hill coefficient of 2–4. Indeed, a range of prominent calcium-activated enzymes appears to satisfy the conditions as an efficient oscillation decoder (Table 1).

TABLE 1.

Examples of calcium-regulated proteins

Protein	Hill coefficient, n	Dissociation constant, KS	Localization	References
Phospholipase Cδ	2–3	0.4–2 μM	Cytoplasm, plasma membrane	(50,51)
Protein kinase Cβ*	2.3	35 μM	Cytoplasm, plasma membrane	(52)
Calmodulin†	1.8	25 μM	Cytoplasm	(53)
Ca2+/Calmodulin-dependent protein kinase II‡	4.4	1.6–5.8 μM	Dendritic spines	(54)
Calcineurin‡	2.8–3	0.6–1.3 μM	Cytoplasm	(55)
Troponin C§	2.8	4.3 μM	Muscle	(56)
Mitochondrial Ca2+ uniporter	2	10–70 μM	Mitochondria	(57)

^*Ca²⁺ binding to the C2 domain of PKC was measured in vitro in the absence of phospholipids (52).

^†Calmodulin contains four Ca²⁺ binding sites. In vitro experiments by Linse et al. (53) suggest dissociation constants of 20, 0.6, 40, and 5 μM at physiological salt concentrations. The values shown in the table correspond to the effective Hill coefficient and dissociation constant assuming a sequential binding of Ca²⁺ (58).

^‡Effective dissociation constant and Hill coefficient for calcineurin bound to calmodulin.

^§Troponin C has two low-affinity and two high-affinity Ca²⁺ binding sites. The reported dissociation constants range from 0.2 to 1 μM for the low-affinity sites and from 15.6 to 40 μM for the high-affinity sites (56). The value shown in the table corresponds to the contraction of a reconstituted muscle.

Target responses to modulations of Ca²⁺ frequency and amplitude

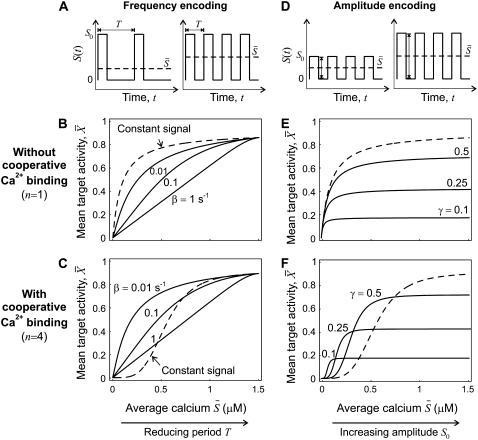
The case of true frequency decoding, in which the shape of Ca²⁺ oscillations is varied but the average Ca²⁺ concentration seen by the protein remains unchanged, has been experimentally studied by means of an engineered control of calcium oscillations. However, in biological reality this case does not seem characteristic. Calcium spikes have a typical width, which is independent of the oscillation period (39). Therefore, an increase in the spike frequency at constant spike amplitude will be accompanied by an increase in the duty ratio γ and hence the average calcium level 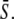We have designated this case as biological frequency encoding. Changes in oscillation period T affect ω as well as γ (since Δ = const.) while σ = const. (Fig. 4 A).

FIGURE 4.

Encoding and decoding of Ca²⁺ frequency and amplitude. (A) Biological frequency encoding: Oscillation period T changes, and therewith the calcium average 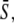while amplitude S₀ remains constant. (B and C) Frequency decoding: Target activity in response to oscillatory (solid lines) or constant (dashed line) Ca²⁺ signals. For the oscillatory signal, the average Ca²⁺ concentration 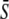is increased by reducing the oscillation period T. (B and C) Correspond to noncooperative (n = 1) and cooperative (n = 4) calcium binding, respectively. (D) Biological amplitude encoding: Oscillation amplitude S₀ changes, and therewith the calcium average 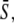while the period T remains constant. (E and F) Amplitude decoding: Target activity 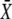in response to oscillatory (solid lines) or constant (dashed line) Ca²⁺ signals. For the oscillatory signal, 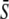is changed by increasing the oscillation amplitude S₀. Panels E and F correspond to noncooperative (n = 1) and cooperative (n = 4) calcium binding, respectively. Parameters: 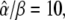K_S = 1 μM, S₀ = 1.5 μM, Δ = 10 s; in panels B and C, β = 0.01, 0.1, 1/s; in panels E and F, β = 0.1/s, and γ = 0.1, 0.25, 0.5.

We compared the target activity achieved with constant signals and frequency-encoded oscillatory signals of the same average calcium 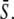In the absence of cooperativity in Ca²⁺ binding (n = 1), a constant signal (Fig. 4 B, dashed line) is always more efficient in activating the target protein than an oscillatory signal (solid lines). On the contrary, when the kinase is activated cooperatively by Ca²⁺ (shown for n = 4), the detection of Ca²⁺ oscillations with lower average concentration is considerably enhanced compared to the constant signal (Fig. 4 C, solid and dashed lines, respectively). In particular, targets with slow activation-inactivation cycles are more efficiently activated than rapidly responding targets (compare the solid lines in Fig. 4, B and C).

Differences in spike amplitudes are particularly relevant in the context of subcellular localization of the target, because in restricted spaces such as between the ER and nearby mitochondria the calcium amplitude can be much higher than in the bulk cytoplasm. Thus, we have defined this second strategy to activate the target protein as biological amplitude encoding. The calcium amplitude S₀ (and hence σ) varies, while ω = const., γ = const. This has the consequence that average calcium also varies (Fig. 4 D). In the absence of cooperativity (n = 1), as for frequency encoding, a constant signal (Fig. 4 E, dashed line) is more efficient in activating the target protein than an oscillatory signal (solid lines). In the presence of cooperativity (n = 4, Fig. 4 F), oscillations enhance signaling efficiency by shifting the activation threshold of the target protein to weaker Ca²⁺ stimuli (lower values of 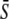). However, the maximal value of the mean target activity 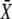is then also reduced.

Thus, at low levels of stimulation, Ca²⁺ oscillations can be more potent in activating a target than constant signals of the same average calcium irrespective of whether the information is transmitted by the amplitude or by the frequency of oscillations. However, this requires cooperativity in the calcium binding.

Calcium oscillations increase the specificity of target activation by sensing its response kinetics

So far, we have examined the activation of a single target protein. A long-standing question is how a ubiquitous messenger like Ca²⁺, with a large number of downstream targets, can elicit selective responses. Experiments suggest that such specificity may arise from differences in Ca²⁺ sensitivity and response kinetics among the downstream targets. Therefore, we compared a slow, insensitive phosphorylation cycle 1 with a fast, sensitive cycle 2 (β₁ < β₂, K_S1 > K_S2).

When the Ca²⁺ concentration remains constant, the more sensitive protein 2 will be preferentially activated (Fig. 5 A). If both phosphorylation cycles differ only in their response kinetics, their target proteins would be equally activated. The question arises whether oscillations can sense the response kinetics of phosphorylation cycles and so increase target specificity compared to a constant signal. Can oscillatory signals upregulate one target protein and downregulate another and vice versa? We demonstrated above that, at a given calcium average, a maximal target activity is obtained for an oscillatory signal of amplitude 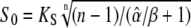(see Appendix B). This optimal amplitude depends not only on Ca²⁺ sensitivity but also on the response kinetics of the cycle. The activities of proteins 1 and 2 become maximal at distinct signal amplitudes and thus they are selectively activated by Ca²⁺ oscillations (Fig. 5 B).

FIGURE 5.

Specificity of target activation. Protein 1 is less Ca²⁺-sensitive and responds slower than protein 2. (A) A constant Ca²⁺ signal preferentially activates protein 2. (B) When the average is kept constant, an optimal oscillatory signal exists for each target protein. (C) Amplitude-encoded oscillatory signals activate primarily protein 2 at low amplitudes and protein 1 at high amplitudes. (D) Frequency-encoded signals preferentially activate protein 2 at low amplitudes and protein 1 at high amplitudes, irrespective of the oscillation period. Protein parameters: 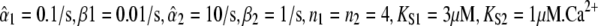signal parameters: Spike width Δ = 20 s; in panel C, γ = 0.5; in panel D, S₀ = 1,2,4 μM.

In the case of amplitude-encoded signals, protein 2 prevails at low levels of stimulation due to its stronger Ca²⁺ sensitivity, whereas the slowly responding protein 1 predominates at higher Ca²⁺ concentrations (Fig. 5 C). On the other hand, frequency encoding provides three different scenarios, depending on the oscillation amplitude. At sufficiently low or sufficiently high amplitudes, one of the two proteins prevails irrespective of the oscillation period. For middle amplitudes, however, protein 1 and protein 2 will be preferentially activated at low and high oscillation frequencies, respectively (Fig. 5 D). Thus, Ca²⁺ oscillations ensure a more specific regulation of target proteins because they can also sense the response kinetics of phosphorylation cycles.

Phosphorylation cycle integrates Ca²⁺ oscillations when their frequency is larger than the target inactivation rate

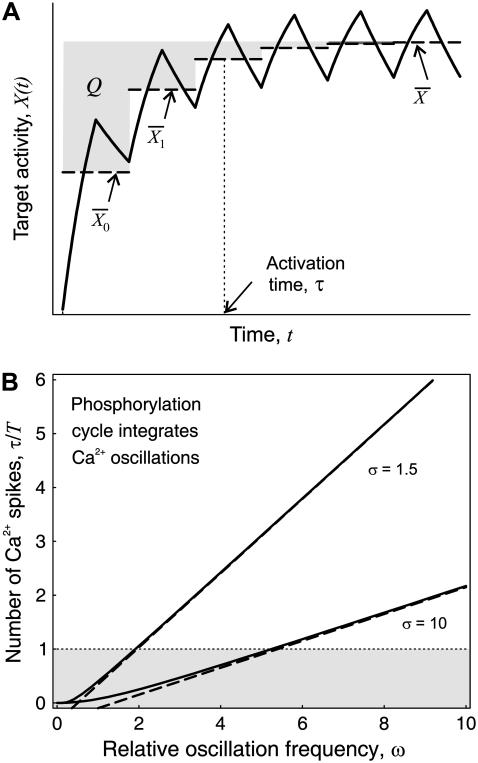
Phosphorylation cycles can either closely follow each cycle of the Ca²⁺ oscillations or rather integrate over the oscillations. The phosphorylation cycle integrates the Ca²⁺ signal if the target activity continuously increases after each Ca²⁺ oscillation. To investigate under which conditions a phosphorylation cycle behaves as an integrator of Ca²⁺ oscillations, we need to evaluate how fast the target protein responds to the Ca²⁺ stimulus. Therefore, we defined the characteristic time τ (see Fig. 6 A)

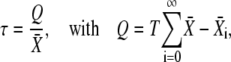(21)

which describes the mean time needed to attain the stationary target activity 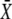in response to an oscillatory signal. Equation 21 resembles the characteristic time previously defined for a constant signal (40). A general expression for τ has been derived in Appendix A (Eq. 35). For fast oscillations, or a slowly responding protein, one obtains

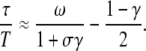(22)

As shown in Fig. 6 B, for a large range of periods, Eq. 22 (dashed lines) is a good approximation of the exact solution (solid lines). The ratio τ/T gives the mean number of Ca²⁺ spikes needed to attain the stationary activity 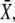and thus is a measure of whether the phosphorylation cycles integrates over the oscillations. When τ/T < 1, the stationary activity 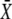will be reached during the first oscillation; this is always the case when ω = 1/βT < 1. Thus, when the oscillation period is larger than the characteristic time 1/β of target inactivation, the Ca²⁺ signal is not integrated by the system. Moreover, large signal amplitudes (large σ) can also reduce the number of spikes necessary to attain 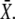Together, our results show that phosphorylation cycles integrate Ca²⁺ oscillations if their amplitude is low and their frequency is larger than the inactivation rate of the target.

FIGURE 6.

Kinetics of target activation by Ca²⁺ oscillations. (A) Shown is the time course of the active target X in response to an oscillatory signal (solid line). The activation time τ (Eq. 21) measures how fast the target protein becomes activated. Depicted also are the mean target activity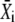 during each oscillation i (dashed line) and the equivalent of the numerator Q in Eq. 21 (shadowed area). (B) The ratio τ/T is plotted against the relative frequency ω using the general expression (solid line) given in Eq. 35, and the simplified solution (dashed line) in Eq. 22. Parameters: γ = 0.3, σ = 2, 10.

Target kinetics and stimulus duration determine the optimal signal shape when calcium amount is limited

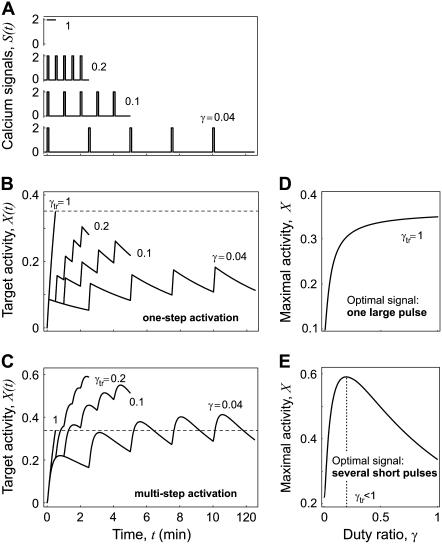
Generally the amount of Ca²⁺ elicited by cell stimulation is limited. Experiments show that in such a case the activation of Ca²⁺-dependent transcription factors like NFAT may be optimized by releasing Ca²⁺ in the form of pulses at short-time intervals (13,16). This raises the question under which conditions Ca²⁺ release as pulses can be more effective than a single continuous signal. Which molecular features determine the optimal signal shape when Ca²⁺ amount is limited? To this end, we compared the target activity in response to Ca²⁺ signals with the same Ca²⁺ amount released either at once or as uniformly-shaped pulses at regular time intervals. The amount of calcium released is given by the total time during which [Ca²⁺]_c remains elevated (Fig. 7 A). The efficiency of decoding such signals can be evaluated by the maximal target activity reached during the last oscillation period.

FIGURE 7.

Decoding of signals with limited amount of calcium. (A) Transient calcium signals: Ca²⁺ stimulation is a single continuous 0.5 min pulse (γ = 1) or 5 pulses of 0.1 min durations at 0.5 min (γ = 0.2), 1 min (γ = 0.1), and 2.5 min (γ = 0.04) intervals. (B) When the kinase responds fast to Ca²⁺ changes (Eq. 3 holds), the optimal signal is a single continuous Ca²⁺ pulse (γ_tr = 1). Shown are the time-courses of the target activity X in response to the Ca²⁺ signals depicted in panel A. (C) When the kinase is slowly activated (Eqs. 1 and 2 hold), the target activity becomes maximal by applying Ca²⁺ pulses at intervals of 0.5 min (γ_tr = 0.2). (D and E) Mean target protein activity for the last oscillation versus the duty ratio γ. A maximal activity is obtained for the optimal duty ratio γ_tr. Parameters: n = 1, S₀ = 2 μM, Δ = 0.1 min, m = 5 spikes; in panels B and D, 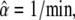β = 0.2/min, K_S = 0.2 μM; in panels C and E, α_X = 1/(μM min), β_X = 0.2/min, α_Y = 20/(μM min), β_Y = 4/min, Y_T = 1 μM .

We found that the optimal form of Ca²⁺ release is primarily determined by the rate of Ca²⁺ binding to the kinase. When Ca²⁺ binding occurs much faster than target kinetics, its activity becomes maximal by releasing Ca²⁺ at once, i.e., optimal duty ratio γ_tr = 1 (Fig. 7, B and D). On the contrary, when the kinase is slowly activated, the target activity is maximized by releasing Ca²⁺ in the form of repetitive short pulses, γ_tr < 1 (Fig. 7, C and E). While the first situation can be considered as a single-step activation (Eq. 3 holds), in the second case the target protein is activated by a two-step kinetics (Eqs. 1 and 2 hold).

To elucidate which processes control this optimal signal, we tried to simplify the full system (Eqs. 1 and 2) when Ca²⁺ binds slowly to the kinase. In such a case, a tractable approximation for the kinase activation is

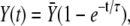(23)

where 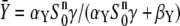is the stationary kinase activity and its activation time. For the target protein, one obtains

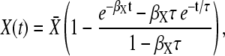(24)

where 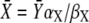is the stationary target activity. The term in brackets gives the fraction of 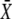attained after time t. Changes in the duty ratio γ exert opposite effects on these two terms. On the one hand, the kinase activity 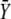increases with γ leading to a higher value of 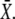On the other hand, because the total signal duration t_tot = mΔ/γ (being m the number of spikes) decreases with γ, a lower fraction of 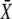will be reached. The optimal signal shape arises from the tradeoff between both opposing effects.

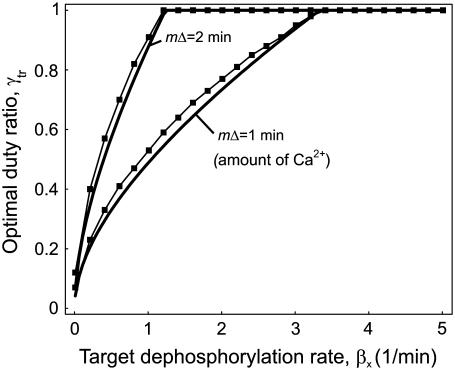
Using Eq. 24, we determined how this optimal signal shape depends on the kinetics of the phosphorylation cycle and on the time during which [Ca²⁺]_c remains elevated. If the target protein is rapidly dephosphorylated (β_X ≫ 1), the optimal signal shape will then be characterized by a rapid succession of spikes and a short total duration (Fig. 8). Conversely, for slowly responding targets, the optimal signal shape has a slow spiking frequency and lasts for longer. This optimal signal is also affected by the time mΔ during which [Ca²⁺]_c remains elevated. We found that the larger this time, the higher the optimal duty ratio will be (Fig. 8). These analytical results were confirmed by numerical simulation of the full system (compare in the solid squares with the solid lines in Fig. 8).

FIGURE 8.

Effect of kinetic parameters on the optimal transient signal. Optimal duty ratio γ_tr of a transient Ca²⁺ signal as a function of the dephosphorylation rate constant β_X of the target protein. The ratio α_X/β_X is kept constant. If the target protein is rapidly inactivated (β_X ≫ 1), the optimal Ca²⁺ signal is characterized by a high duty ratio. The optimal duty ratio will also increase by increasing the total duration of the Ca²⁺ spikes (upper line). The solid lines are calculated with the analytical approximation (Eq. 24); the solid squares are obtained after numerically solving the full system (Eqs. 2 and 3). Parameters: n = 1, S₀ = 2 μM, Δ = 0.2 and 0.4 min (lower and upper line, respectively), m = 5 spikes; α_X/β_X/μM, α_Y = 1/(μM min), β_Y = 1/min, Y_T = 1 μM.

In summary, when Ca²⁺ amount is limited, calcium release in the form of spikes is more effective than a single continuous release if target activation occurs in a two-step kinetics. This condition is fulfilled when Ca²⁺ binds slowly to the kinase. The optimal signal shape is determined by the amount of calcium and the kinetics of the phosphorylation cycle.

DISCUSSION

In this article, the decoding of Ca²⁺ oscillations has been theoretically analyzed in a minimal model of protein activation. Such a model comprises the activation-inactivation cycle of a target protein controlled by a Ca²⁺-dependent kinase and the counteracting phosphatase. The mimicking of Ca²⁺ oscillations by square-shaped pulses allowed for an analytical solution of the kinetic equations. To quantify how sensitively the target protein responds to an oscillatory calcium signal, we derived expressions for the mean target activity and for the activation time. Both depend on three dimensionless quantities that govern the response of the system. Two of these dimensionless quantities (the effective activation rate and the relative oscillation frequency) combine kinetic properties of the target activation with characteristics of the Ca²⁺ signal. This fact indicates that the timescales of Ca²⁺ oscillations and target response are coupled through the decoding mechanism and should not be analyzed separately.

With our model we aimed to answer several questions concerning the decoding of Ca²⁺ oscillations:

• How does a protein respond to changes in the oscillation frequency and when does it function as a signal integrator?

• What are the advantages of having an oscillatory signal?

• Under which conditions is the system response maximized?

• To what extent do Ca²⁺ oscillations confer target specificity?

These four issues will be discussed below.

Frequency sensitivity

Although an increase in the oscillation frequency, leaving the amplitude and average unchanged, always causes an increase in the mean target activity, the magnitude of these changes depends on the inactivation rate of the target and on the duty ratio of oscillations. In case target inactivation is faster than the oscillation frequency, the target activity would simply oscillate along with the Ca²⁺ oscillation and the target does not integrate the signal. By increasing the oscillation frequency, such that Ca²⁺ oscillations are faster than target inactivation, the target protein would not fully inactivate between each Ca²⁺ oscillation and behaves as a signal integrator. In this case, one observes a continuous increase in the target activity at each oscillation cycle. The critical point, over which the target response becomes frequency-insensitive, appears when the oscillation frequency gets in the range of the target inactivation rate. Our analysis demonstrates that true frequency decoding, at constant average Ca²⁺ signal, can indeed occur provided that Ca²⁺ spikes are narrow and the oscillation frequency is of the order of the target inactivation rate or below.

Oscillations versus constant signals

We compared the target response to a constant signal and to a sustained oscillatory signal of the same average Ca²⁺ concentration. Our analysis demonstrates that Ca²⁺ oscillations are more potent in activating the target protein than a constant signal if 1), Ca²⁺ acts cooperatively on the kinase; and 2), the Ca²⁺ sensitivity of the kinase (expressed by the dissociation constant) lies around the peak concentration of the calcium spike or above. Under these conditions, Ca²⁺ oscillations reduce the effective threshold for the target activation. Taking into account the typical values for amplitude and duty ratio of Ca²⁺ oscillations, the predicted critical affinity values lie in the range of the experimentally measured Ca²⁺ sensitivities. Furthermore, we found that target proteins are more efficiently activated by oscillatory signals at low levels of stimulation irrespective of whether the information has been encoded in the amplitude or in the frequency of oscillations. This study provides a theoretical support to the experimental findings on Ca²⁺-dependent gene expression by Dolmetsch et al. (12) and on Ca²⁺-dependent enzyme activation by Eshete and Fields (41), Kupzig et al. (42), and to the numerical simulations by Gall et al. (26).

Optimal signals and target specificity

We also asked, what is the calcium signal shape that best activates a particular target protein? Our analysis demonstrates the existence of an optimal shape, which is determined by the Ca²⁺ sensitivity and kinetics of target response. Thus, by varying the characteristics of Ca²⁺ oscillations, target proteins can be differentially activated. To investigate this issue, we compared two phosphorylation cycles with distinct Ca²⁺ sensitivities and (in)activation kinetics. We found that under specific conditions, Ca²⁺ oscillations can upregulate one protein and downregulate the other one and vice versa. If the cycles only differ in their (in)activation kinetics, the slowly responding protein would be always stronger-activated by Ca²⁺ oscillations than the rapidly responding protein. Such a behavior has been observed experimentally for genes regulated by the two calcium-dependent transcription factors NFAT and NFκB, where the latter factor responds slower to changes in calcium concentration (12).

Cellular responses depend not only on the frequency and amplitude of Ca²⁺ oscillations but also on the duration and number of Ca²⁺ spikes (43). Hence, we examined the specificity of target activation using time-limited Ca²⁺ oscillations. Specifically, we compared the target response when Ca²⁺ stimulation of the same total duration, i.e., the time during which calcium concentration remains elevated, is applied as either a single continuous stimulation or as pulses of short duration at distinct time intervals. Releasing Ca²⁺ at once maximizes the target response when kinase (in)activation or target (de)phosphorylation is fast compared to the duration of the Ca²⁺ transient. However, when the proteins respond slowly, the target activity becomes maximal by releasing Ca²⁺ in the form of pulses with an optimal frequency. We demonstrated analytically that this optimal oscillation frequency arises from the tradeoff between two opposing effects. On the one hand, the kinase activity increases with the oscillation frequency leading to a higher stationary target activity. On the other hand, the total signal duration decreases with the frequency so that a lower fraction of the stationary target activity will be reached. Similar conclusions were arrived at by Marhl et al. on the basis of numerical simulations (28,34).

Our theoretical analysis of target activation by transient Ca²⁺ oscillations is also consistent with the experiments of Li et al. (16) and Tomida et al. (13), who found that the nuclear localization of the transcription factor NFAT is optimized when the Ca²⁺ pulses are applied at short-time intervals. A determinant factor to achieve this effect is the temporal dissociation between Ca²⁺ signals and nuclear translocation of NFAT. Ca²⁺-dependent dephosphorylation of NFAT proceeds faster than its nuclear translocation and rephosphorylation (44). Consequently, Ca²⁺ oscillations can induce a buildup of dephosphorylated NFAT in the cytoplasm, allowing nuclear translocation of NFAT even during the interspike interval, provided that this interval is shorter than the lifetime of dephosphorylated NFAT (13). These experiments point out to the existence of a molecular Ca²⁺ memory in the mechanism of NFAT activation, where an oscillatory input is transformed into a nearly stationary output.

Molecular sensors of calcium signals

Diverse experiments on Ca²⁺ decoding have suggested the existence of molecular sensors capable of interpreting complex temporal Ca²⁺ signals into the correct physiological response. A classic example of such decoders is the small molecule calmodulin, which activates several kinases as well as the phosphatase calcineurin (14,17). More recently, the kinase PKC (15,45) and the small GTPase Ras (46,47) have been also proposed as potential Ca²⁺ decoders. These sensors contain specialized Ca²⁺-binding domains such as the C2 domain with a high structural diversity, allowing the binding of multiple targets with distinct Ca²⁺ sensitivities and activation kinetics. Other elements to consider are the compartmentalization and cross-interactions among signaling molecules. So the question arises: what is the ideal processor for decoding complex Ca²⁺ signals, and what minimal features should it have?

Our study demonstrates that a system consisting of the nonlinear regulation of a target protein by a Ca²⁺-activated kinase and the counteracting phosphatase contains the minimal features required for deciphering temporal Ca²⁺ signals. Autophosphorylation of the target protein (e.g., CaM kinase II) can be considered as a special case of this model, where the Ca²⁺-dependent kinase is itself the target protein. Yet despite its simplicity, this minimal model is able to reproduce all features of Ca²⁺ signaling decoding that have been observed in detailed models (25,26,30). In our model, nonlinear activation of the target protein arises from the cooperative Ca²⁺ binding to the kinase. Other mechanisms that can generate nonlinear responses, such as multiple phosphorylation and feedback regulatory loops, may also be implicated in the decoding of Ca²⁺ signals and should be considered in future studies (48,49). Deciphering of complex Ca²⁺ signals presumably involves activation of multiple Ca²⁺ sensors instead of a central decoder. Complex decoding patterns such as signal integration and summation might emerge from combining single properties of the individual decoders. Therefore, it would be worth extending this approach to a system consisting of multiple Ca²⁺ decoders.

APPENDIX A: TARGET ACTIVITY AND ACTIVATION TIME

Here, we derive the formulas for the mean target activity 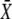and the activation time τ. The linear differential equation (Eq. 3), describing the kinetics of the target protein X, can be separately solved for the spike and interspike intervals (see Eq. 5). The solution of Eq. 3 reads

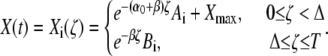(25)

For simplicity, we have introduced the internal time ζ = t − iT within an oscillation cycle ζ∈[0,T]. The target activity during the i^th cycle is denoted by X_i(ζ). The phosphorylation rate α₀ during a Ca²⁺ spike (see Eq. 4) is given by

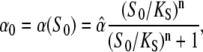(26)

and the maximal target activity is 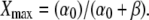The coefficients A_i and B_i are determined from

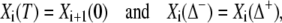(27)

leading to the difference equations

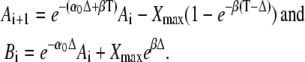(28)

The initial condition X₀(0) = 0 gives A₀ = −X_max. Equation 28 is solved with the Ansatz 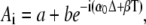where 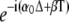is a solution of the homogeneous difference equation. One then obtains

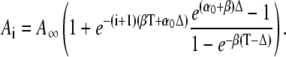(29)

After a sufficiently large number of cycles (i → ∞), the coefficient A_i approaches 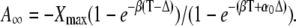Equations 28 and 29 give the second coefficient

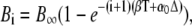(30)

with 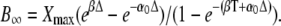The dynamics of the target protein during the i^th cycle is then described by

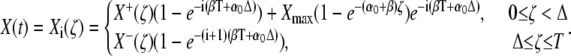(31)

The quantities X⁺(ζ) and X⁻(ζ) denote the stationary target activity during a Ca²⁺ spike (0 ≤ ζ < Δ) and during the interspike interval (Δ ≤ ζ ≤ T), respectively,

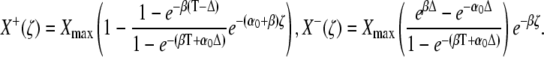(32)

After a sufficiently large number of oscillation cycles (i → ∞), the target activity approaches X⁺(ζ) and X⁻(ζ).

The mean target activity 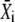during the i^th cycle is defined by 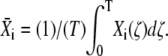Thus, integration of Eq. 31 leads to

(33)

According to Eq. 33, the mean target activity 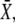i.e., for i → ∞, reads

(34)

Equation 34 is equivalent to Eq. 7, where the dimensionless parameters σ = α₀/β, ω = 1/βT, and γ = Δ/T have been introduced.

The activation time τ of the target protein, defined in Eq. 21, can be calculated using Eqs. 33 and 34. After some algebra, one obtains

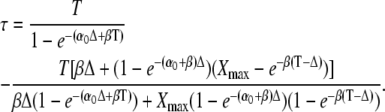(35)

A Taylor expansion of Eq. 35 for T → 0, leaving Δ/T constant, yields

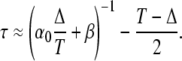(36)

Equation 36 is equivalent to Eq. 22 after introducing the dimensionless parameters.

APPENDIX B: OPTIMAL CA²⁺ SIGNALS

The optimal signal shape at a given average 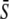is the solution of where the amplitude S₀ has been replaced by 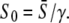Using Eq. 13, for low-frequency oscillations (ω → 0), one obtains the maximal target response for

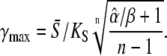(37)

Using Eq. 14, for high-frequency oscillations (ω → ∞), one gets

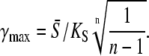(38)

Numerical evaluation of Eq. 7 shows that γ_max is a decreasing function of ω. Thus, Eqs. 37 and 38 give the upper and lower bound for γ_max, respectively.

Oscillations and a constant signal of equal average 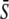have the same efficiency in activating the target protein when 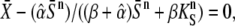where the second term corresponds to the target activity obtained with the constant signal. Solving the above equation yields a critical dissociation constant (K_S/S₀)_crit. When K_S/S₀ > (K_S/S₀)_crit, oscillations are the more potent activating signals. For high frequency oscillations (ω → ∞, Eq. 14 holds), one gets

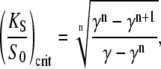(39a)

and

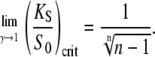(39b)

These formulas correspond to Eqs. 20 and 19, respectively. For low frequencies (ω → 0, Eq. 13 holds) the critical dissociation constant reads

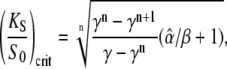(40a)

and

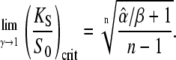(40b)

Since 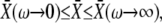Eqs. 39 and 40 give the lower and upper bound for (K_S/S₀)_crit, respectively. Therefore, the condition for the superiority of oscillations over a constant signal is 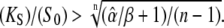This is a more strict condition than Eq. 19, which is valid for any frequency or duty ratio.