Analysis of an SIR Epidemic Model with Pulse Vaccination and Distributed Time Delay

Abstract

Pulse vaccination, the repeated application of vaccine over a defined age range, is gaining prominence as an effective strategy for the elimination of infectious diseases. An SIR epidemic model with pulse vaccination and distributed time delay is proposed in this paper. Using the discrete dynamical system determined by the stroboscopic map, we obtain the exact infection-free periodic solution of the impulsive epidemic system and prove that the infection-free periodic solution is globally attractive if the vaccination rate is larger enough. Moreover, we show that the disease is uniformly persistent if the vaccination rate is less than some critical value. The permanence of the model is investigated analytically. Our results indicate that a large pulse vaccination rate is sufficient for the eradication of the disease.

1. INTRODUCTION

Mathematical models are very useful and frequently used nowadays. For example, in [1], the authors used a novel in vitro pharmacodynamic infection model of tuberculosis by exposing M. tuberculosis to moxifloxacin with a pharmacokinetic half life of decline similar to that encountered in humans. Then the data obtained from this model were mathematically modeled. D'Agata et al. [2] introduced a mathematical model to quantify the contribution of antibiotic exposure and of other modifiable factors to the dissemination of vancomycin-resistant enterococci (VRE) in the hospital setting and provided a framework to assist in targeting necessary interventions aimed at limiting the spread of VRE. An extension of that model that incorporates an environmental reservoir for VRE was developed in [3]. Different models, using fuzzy mathematics, applicable in medicine are reviewed in [4]. Gao et al. [5] developed a model and a pulse vaccination strategy, the repeated application of vaccine over a defined age range. It revealed as an effective strategy for the elimination of infectious diseases.

In the classical epidemiological model [6–13], a population of total size N is divided into S susceptible numbers, I infective numbers, and R recovered numbers. The relation between these three categories leads to the classical SIR model:

$$\begin{array}{ll}\stackrel{.}{S}\left(t\right)& =-\beta S\left(t\right)I\left(t\right),\\ \stackrel{.}{I}\left(t\right)& =-\beta S\left(t\right)I\left(t\right)-\gamma I\left(t\right),\\ \stackrel{.}{R}\left(t\right)& =\gamma I\left(t\right),\end{array}$$ (1)

where $\beta \left(>0\right)$ is the infection parameter or the transmission rate contact, $\gamma \left(>0\right)$ is the removal parameter giving the rate at which infectives become immune, and $1/\gamma$ is the mean infectious period. The initial population are $S\left(0\right),\hspace{0.17em}I\left(0\right)$ positive, and $R\left(0\right)=0$. Obviously, $S\left(0\right)+I\left(0\right)+R\left(0\right)=N$. It is known that $S\left(t\right)+I\left(t\right)+R\left(t\right)=N$ is constant. Dividing $S,\hspace{0.17em}I$, and $R$ by $N$ we may assume that $N=1$ without loss of generality. If death or isolation may occur, $R\left(t\right)$ represents all removals from the population (including immunes, deaths, and isolates). An important parameter is the relative removal rate

$$c=\frac{\gamma }{\beta }.$$ (2)

A major outbreak occurs only if the initial number of susceptibles $S\left(0\right)>c$. This is known as the threshold theorem, $c$ being such a threshold.

Ma et al. [14] formulate an SIR model with time delay effected by assuming that the force of infection at time $t$ is given by

$$\beta e^{-\mu \omega }S\left(t-\omega \right)I\left(t-\omega \right),$$ (3)

where $\mu >0$ is natural death rate and $\omega >0$ is a fixed time during which the infectious agents develop in the vector and it is only after that time that the infected vector can infect a susceptible human. That is, $\omega$ is the infectious period of the disease.

Beretta et al. [15] point out that it is more natural to assume that $\omega$ is a distributed parameter than a fixed time. It is, of course, bounded above by some positive finite time “h,” that is, h is the maximum infectious period. Hence, the force of infection (3) has to be substituted by

$$\beta {\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds,$$ (4)

where f(s), that is the fraction of vector population in which the time taken to become infectious is “s”, is assumed to be a nonnegative function on [0, h]. Mathematically, f : [0, h] → R ₊₀ square integrable on [0, h] and satisfies

$${\int }_0^{h}f\left(s\right)ds=1,\hspace{1em}\hspace{1em}{\int }_0^{h}sf\left(s\right)ds<+\infty ,$$ (5)

where we assume that the parameter ${\omega }^{*}={\int }_0^{h}sf\left(s\right)ds>0$ is the average incubation time in the vector to become infectious.

When natural birth, natural death, and the force of infection (4) are considered, we are yielded to an SIR model with distributed time delay:

$$\begin{array}{ll}\stackrel{.}{S}\left(t\right)& =\mu -\beta {\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-\mu S\left(t\right),\\ \stackrel{.}{I}\left(t\right)& =\beta {\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-\mu I\left(t\right)-\gamma I\left(t\right),\\ \stackrel{.}{R}\left(t\right)& =\gamma I\left(t\right)-\mu R\left(t\right).\end{array}$$ (6)

Here, f(s) satisfies (5). It is assumed that the natural birth rate is equal to the natural death rate and all newborns are susceptible. $\mu \left(>0\right)$ denote the natural birth rate and death rate, $1/\mu$ is the mean life expectancy. The total population size $N\left(t\right)=S\left(t\right)+I\left(t\right)+R\left(t\right)$ satisfies $\stackrel{.}{N}\left(t\right)=\mu \left(1-N\left(t\right)\right)$ and $N\left(t\right)\to 1$ as $t\to \infty$. Hence, model (6) can be regarded as a model with a total constant population. Consequently, we assume that $N\left(t\right)=1$ for all $t\ge 0$. Obviously, $R_0=\beta /\left(\mu +\gamma \right)$ is the reproduction number of the system (6) without time delay. That is, if $R_0>1$, then on average, each infected individual infects more than one other member of the population and a self-sustaining group of infectious individuals will propagate.

For the sake of simplicity, we put in dimensionless form the model equations (6) by redefining a new nondimensional time $\overline{t}=\left(\mu +\gamma \right)t$. This leads to the dimensionable equations

$$\begin{array}{ll}\stackrel{.}{S}\left(\overline{t}\right)& =\overline{\mu }-R_0{\int }_0^{\overline{h}}f\left(s\right)S\left(\overline{t}-s\right)I\left(\overline{t}-s\right)e^{-\overline{\mu }s}ds-\overline{\mu }S\left(\overline{t}\right),\\ \stackrel{.}{I}\left(\overline{t}\right)& =R_0{\int }_0^{\overline{h}}f\left(s\right)S\left(\overline{t}-s\right)I\left(\overline{t}-s\right)e^{-\overline{\mu }s}ds-I\left(\overline{t}\right),\\ \stackrel{.}{R}\left(\overline{t}\right)& =\overline{\gamma }I\left(\overline{t}\right)-\overline{\mu }R\left(\overline{t}\right),\end{array}$$ (7)

where

$$\overline{\mu }=\frac{\mu }{\mu +\gamma },\hspace{1em}{R}_0=\frac{\beta }{\mu +\gamma },\hspace{1em}\overline{h}=\left(\mu +\gamma \right)h,\hspace{1em}\overline{\gamma }=\frac{\gamma }{\mu +\gamma }$$ (8)

are the dimensionless parameters. For convenience, we remove the bars in the following discussion. Thus, the model (7) yields

$$\begin{array}{ll}\stackrel{.}{S}\left(t\right)& =\mu -R_0{\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-\mu S\left(t\right),\\ \stackrel{.}{I}\left(t\right)& =R_0{\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-I\left(t\right),\\ \stackrel{.}{R}\left(t\right)& =\gamma I\left(t\right)-\mu R\left(t\right).\end{array}$$ (9)

Infectious diseases have tremendous influence on human life. Every year millions of human beings suffer or die of various infectious diseases. Controlling infectious diseases has been an increasingly complex issue in recent years. A strategy to control infectious diseases is vaccination. One can investigate under what conditions a given agent can invade a (partially) vaccinated population, that is, how large a fraction of the population we have to keep vaccinated in order to prevent the agent from establishing. However, in practical situations one usually has to start a vaccination campaign when the agent has become endemic. In such a case, will the vaccination effort be sufficient to eliminate? What is the adequate strategy? Constant vaccination is the conventional strategy. Recently, a new strategy denominated pulse vaccination strategy (PVS) has been revealed adequate against poliomyelitis and measles. The effectiveness of constant and pulse vaccination policies are compared theoretically and numerically in [16].

A usual recommendation for measles immunization is to apply a first vaccination dose to all infants of 15 months of age and a second dose at six years. However, it was hypothesized [17] that measles epidemics can be more efficiently controlled when the natural temporal process of the epidemics is antagonized by another temporal process, that is, by a vaccination effort that is pulsed in time rather than uniform and continuous. We call this policy pulse vaccination and it was shown theoretically that if children aged one to seven years are immunized once every five years, that may suffice for preventing the epidemics [18].

The strategy of pulse vaccination (PVS) consists of periodical repetitions of impulsive vaccinations in a population, on all the age cohorts [5, 19–21]. At each vaccination time, a constant fraction of the susceptible population is vaccinated. Some theoretical considerations, practical advantages, and examples of the PVS are presented in [5, 21–23]. For example, some successes against poliomyelitis and measles have been attributed to repeated PVS [24]. As indicated in [25], models have clearly shown the advantages of a mass campaign approach in rapidly achieving high measles population immunity and interrupting measles virus circulation.

Further, we consider PVS in model (9) and assume that τ (>0) denotes the period of pulsing and $\theta \left(0<\theta <1\right)$ is the proportion of those vaccinated successfully. Incorporating pulse vaccination, we propose an SIR model with pulse vaccination and distributed time delay:

$$\begin{gathered} \begin{array}{ll}\stackrel{.}{S}\left(t\right)& =\mu -R_0{\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-\mu S\left(t\right),\\ \stackrel{.}{I}\left(t\right)& =R_0{\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-I\left(t\right),\\ \stackrel{.}{R}\left(t\right)& =\gamma I\left(t\right)-\mu R\left(t\right),\end{array}\hspace{1em}t\ne k\tau , \\ \begin{array}{ll}S\left(t^{+}\right)& =\left(1-\theta \right)S\left(t\right),\\ I\left(t^{+}\right)& =I\left(t\right),\\ R\left(t^{+}\right)& =R\left(t\right)+\theta S\left(t\right),\end{array}\hspace{1em}t=k\tau . \end{gathered}$$ (10)

Note that the variable R do not appear in the first and second equations of system (10). This allows us to attack (10) by studying the subsystem

$$\begin{array}{l}\begin{array}{c}\stackrel{.}{S}\left(t\right)=\mu -R_0{\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-\mu S\left(t\right),\hfill \\ \stackrel{.}{I}\left(t\right)=R_0{\int }_0^{h}f\left(s\right)S\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-I\left(t\right),\end{array}\hspace{1em}t\ne k\tau ,\\ \begin{array}{l}S\left(t^{+}\right)=\left(1-\theta \right)S\left(t\right),\\ I\left(t^{+}\right)=I\left(t\right),\end{array}\hspace{1em}t=k\tau .\end{array}$$ (11)

The initial conditions for (11) are

$$\left({\phi }_1\left(\zeta \right),{\phi }_2\left(\zeta \right)\right)\in C_{+}=C\left(\left[-h,0\right],R_{+}^2\right),\hspace{1em}{\phi }_i\left(0\right)>0, i=1,2.$$ (12)

From biological considerations, we discuss system (11) in the closed set

$$\Omega =\left\{\left(S,I\right)\in R_{+}^2\hspace{0.17em}|\hspace{0.17em}0\le S, I\le 1\right\}.$$ (13)

It can be verified that $\Omega$ is positively invariant with respect to (11), that is, any solution starting in $\Omega$ remains in $\Omega$ in the future.

Most of the research literature on epidemiologic models are established by ODE, delayed ODE, or impulsive ODE [26–28]. However, impulsive equations with distributed time delay have seldom been studied by authors. The main purpose of this paper is to analyze the impulsive model with distributed time delay (11) and establish sufficient condition so that the disease dies out. The second purpose of this paper is to investigate the role of distributed time delay in disease transmission and show that, under appropriate conditions, the disease is uniformly persistent, that is, there is a positive constant q (independent of the choice of the solution) such that $I\left(t\right)\ge q$ for sufficiently large t.

2. DEFINITIONS AND PRELIMINARIES

In the following, we introduce some definitions and state two results which will be useful in subsequent sections.

Definition 1. —

The solution $\left(S\left(t\right),I\left(t\right)\right)$ of system (11) is said to be globally attractive if every solution of system (11) tends to $\left(S\left(t\right),I\left(t\right)\right)$ as $t\to \infty$.

Definition 2. —

System (11) is said to be uniformly persistent if there is an $\eta >0$ (independent of the initial conditions) such that every solution $\left(S\left(t\right),I\left(t\right)\right)$ with initial conditions (12) of system (11) satisfies

$$\underset{t\to \infty }{\text{lim}\text{inf}}S\left(t\right)\ge \eta ,\hspace{1em}\hspace{1em}\underset{t\to \infty }{\text{lim}\text{inf}}I\left(t\right)\ge \eta .$$ (14)

Definition 3. —

System (11) is said to be permanent if there exists a compact region ${\Omega }_0\in \text{int}\Omega$ such that every solution of system (11) with initial conditions (12) will eventually enter and remain in region ${\Omega }_0$.

We now present a technical result.

Lemma 1. —

Consider the following impulsive system:

$$\begin{array}{cc}{u}^{.}\left(t\right)& =a-bu\left(t\right),\hspace{1em}t\ne k\tau ,\\ u\left(t^{+}\right)& =(1-\theta )u\left(t\right),\hspace{1em}t=k\tau ,\end{array}$$ (15)

where $a>0,\hspace{0.17em}b>0,\; and\hspace{0.17em}0<\theta <1$. Then there exists a unique positive periodic solution of system (15):

$${ũ}_e\left(t\right)=\frac{a}{b}+\left(u^{*}-\frac{a}{b}\right)e^{-b\left(t-k\tau \right)},\hspace{1em}k\tau <t\le \left(k+1\right)\tau ,$$ (16)

which is globally asymptotically stable, where $u^{\ast }=\left(a/b\right)\left(\left(1-\theta \right)\left(1-e^{-b\tau }\right)/\left(1-\left(1-\theta \right)e^{-b\tau }\right)\right)$.

Proof. —

Integrate and solve the first equation of system (15) between pulses

$$u\left(t\right)=\frac{a}{b}+\left(u\left(k\tau \right)-\frac{a}{b}\right)e^{-b\left(t-k\tau \right)},\hspace{1em}k\tau <t\le \left(k+1\right)\tau ,$$ (17)

where $u\left(k\tau \right)$ is the initial value at time $k\tau$. Using the second equation of system (15), we deduce the stroboscopic map such that

$$u\left(\left(k+1\right)\tau \right)=\left(1-\theta \right)\left[\frac{a}{b}+\left(u\left(k\tau \right)-\frac{a}{b}\right)e^{-b\tau }\right]\triangleq f\left(u\left(k\tau \right)\right),$$ (18)

where $f\left(u\right)=\left(1-\theta \right)\left[a/b+\left(u-a/b\right)e^{-b\tau }\right]$. It is easy to know that system (18) has unique positive equilibrium $u^{\ast }=\left(a/b\right)\left(\left(1-\theta \right)\left(1-e^{-b\tau }\right)/\left(1-\left(1-\theta \right)e^{-b\tau }\right)\right)$. Since $f\left(u\right)$ is a straight line with slope less than 1, we obtain that $u^{*}$ is globally asymptotically stable. It implies that the corresponding periodic solution of system (15)

$${ũ}_e\left(t\right)=\frac{a}{b}+\left(u^{*}-\frac{a}{b}\right)e^{-b\left(t-k\tau \right)},\hspace{1em}k\tau <t\le \left(k+1\right)\tau ,$$ (19)

is globally asymptotically stable. The proof of Lemma 1 is complete.

Lemma 2 (Beretta and Takeuchi [29]). —

Consider the following equation:

$$\stackrel{.}{y}\left(t\right)=-a_{1}y\left(t\right)+a_2{\int }_0^{h}f\left(s\right)y\left(t-s\right)ds,$$ (20)

where $a_1,a_2,h>0$, and $f\left(s\right)$ satisfies (5). Then the trivial solution $y=0$ of system (20) is globally asymptotically stable if and only if $a_2<a_1$.

3. MAIN RESULTS

In this section, we first demonstrate the existence of the infection-free periodic solution, in which infectious individuals are entirely absent from the population permanently, that is, $I\left(t\right)=0$ for all $t\ge 0$. Under this condition, the growth of susceptible individuals must satisfy

$$\begin{array}{cc}\stackrel{.}{S}\left(t\right)& =\mu -\mu S\left(t\right),\hspace{1em}t\ne k\tau ,\\ S\left(t^{+}\right)& =(1-\theta )S\left(t\right),\hspace{1em}t=k\tau ,\end{array}$$ (21)

We show below that the susceptible population S oscillates with period $\tau$, in synchronization with the periodic pulse vaccination.

According to Lemma 1, we know that periodic solution of system (21)

$${\tilde{S}}_e\left(t\right)=1-\frac{\theta }{1-\left(1-\theta \right)e^{-\mu \tau }}{e}^{-\mu \left(t-k\tau \right)},\hspace{1em}k\tau <t\le \left(k+1\right)\tau ,$$ (22)

is globally asymptotically stable.

Theorem 1. —

The infection- periodic solution $\left({\tilde{S}}_e\left(t\right),0\right)$ of system (11) is globally attractive provided that $R^{*}<1$, where

$$R^{*}\triangleq R_0\frac{1-e^{-\mu \tau }}{1-\left(1-\theta \right)e^{-\mu \tau }}.$$ (23)

The proof will be given in the appendix.

Denote

$${\theta }^{*}=\left(R_0-1\right)\left(e^{\mu \tau }-1\right),\hspace{1em}\hspace{1em}{\tau }_{*}=\frac{1}{\mu }\text{ln}\left(1+\frac{\theta }{R_0-1}\right).$$ (24)

According to Theorem 1, we can easily obtain the following results.

Corollary 1. —

If $R_0\le 1$, then the infection-free periodic solution $\left({\tilde{S}}_e\left(t\right),0\right)$ is globally attractive.

Corollary 2. —

If $R_0>1$, then the infection-free periodic solution $\left({\tilde{S}}_e\left(t\right),0\right)$ is globally attractive provided that $\theta >{\theta }^{*}$ or $\tau <{\tau }_{*}$.

Theorem 1 determines the global attractivity of (11) in $\Omega$ for the case $R^{*}<1$. Its epidemiological implication is that the infectious population vanishes, so the disease will die out.

From Corollaries 1 and 2 we know, in order to successfully prevent disease, the vaccination proportion should be large enough. This would lead to more difficulties and costs to implement vaccination for many people.

In the following, we say the disease is endemic if the infectious population persists above a certain positive level for sufficiently large time.

Theorem 2. —

Suppose that $R_{*}\triangleq \left(1-\theta \right)e^{-\mu h}{R}^{*}>1$. Then there exists a positive constant $q$ such that each positive solution $\left(S\left(t\right),I\left(t\right)\right)$ of system (11) satisfies

$$I\left(t\right)\ge q,\hspace{1em}\text{for }t\text{ large enough.}$$ (25)

The proof will be given in the appendix.

Denote

$$\begin{array}{ll}{\theta }_{*}& =\frac{\left(R_0{e}^{-\mu h}-1\right)\left(e^{\mu \tau }-1\right)}{R_0{e}^{-\mu h}\left(e^{\mu \tau }-1\right)+1},\\ {\tau }^{*}& =\frac{1}{\mu }\text{ln}\left(1+\frac{\theta }{R_0{e}^{-\mu h}\left(1-\theta \right)-1}\right),\\ h_{*}& =\frac{1}{\mu }\text{ln}\left(\frac{R_0\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)}{1-\left(1-\theta \right)e^{-\mu \tau }}\right)\mathrm{.}\end{array}$$ (26)

From Theorem 2, we also easily obtain the following results.

Corollary 3. —

If $R_0{e}^{-\mu h}>1$, the disease will be endemic provided that $\theta <{\theta }_{*}$.

Corollary 4. —

If $R_0{e}^{-\mu h}\left(1-\theta \right)>1$, then the disease will be endemic provided that $\tau >{\tau }^{*}$.

Corollary 5. —

If $R_0\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)>1-\left(1-\theta \right)e^{-\mu \tau }$, then the disease will be endemic provided that $h<h_{*}$.

Theorem 3. —

Suppose $R_{*}>1$. Then system (11) is permanent provided that $\mu >R_0$.

The proof will be given in the appendix.

In the following, we will study the influence of pulse vaccination rate (with $\theta$), period of pulsing (with $\tau$), and so on, on the system (11) by numerical analysis. From Table 1, we can observe that a large pulse vaccination rate or a short period of pulsing is sufficient condition for the global attractivity of infection-free periodic solution $\left({\tilde{S}}_e\left(t\right),0\right)$. From the last line of Table 1, we can also observe that when pulse vaccination rate is very large, although $h=0$, the epidemic disease cannot be permanent yet. This implies that pulse vaccination brings determinant effect on the dynamics behaviors of the model.

Table 1.

The effect of parameters $\theta ,\hspace{0.17em}\tau ,\hspace{0.17em}{R}_0,\hspace{0.17em}\mu$ and h on the global attractivity of the infection-free periodic solution and the permanence of epidemic disease.

$\theta$	$\tau$	$R_0$	$\mu$	$h$	$R^{*}$	$R_{*}$	Attractivity	Permanence
0.6	1	3	0.2	0.5	0.8086	0.2927	Yes	No
0.1	1	3	0.2	0.5	2.067	1.6829	No	Yes
0.6	4	3	0.2	0.5	2.0140	0.7289	Indeterminacy	Indeterminacy
0.6	20	3	0.2	0.5	2.9667	1.0738	No	Yes
0.1	1	3	0.2	4	2.067	0.8357	Indeterminacy	Indeterminacy
0.6	1	3	0.2	0	0.8086	0.3235	Yes	No

4. DISCUSSION

We have analyzed the SIR epidemic model with pulse vaccination and distributed time delay. Two thresholds have been established, one for global stability of the infectious-free solution and one for persistence of the endemic solution.

From Corollaries 2 and 3, we obtain that if $R_0{e}^{-\mu h}>1$, the disease dies out when $\theta >{\theta }^{*}$ whereas the disease persists when $\theta <{\theta }_{*}$. There is a gap between ${\theta }_{*}$ and ${\theta }^{*}$. The reason for this gap is that the thresholds are given in concrete terms in this paper. Does a sharp threshold condition exist? We think the sharp threshold condition exists, but can presumably only be given in abstract terms. Consider the linear DDE

$$\stackrel{.}{I}\left(t\right)=R_0{\int }_0^{h}f\left(s\right){\tilde{S}}_e\left(t-s\right)I\left(t-s\right)e^{-\mu s}ds-I\left(t\right),$$ (27)

where ${\tilde{S}}_e\left(t\right)$ is the $\tau$-periodic disease free state under the vaccination effort $\theta$. The solutions of this linear equation are associated with a compact positive operator on $C\left(\left[-h,0\right]\right)$. Let $r$ be the spectral radius of this operator. The disease dies out if $r<1$ and persists if $r>1$. In terms of the vaccination effort $\theta$ this means that, if $R_0>1$, there is a $\widehat{\theta }\in \left(0,1\right)$ such that the disease dies out if $\theta >\widehat{\theta }$ and the disease persists if $\theta <\widehat{\theta }$. $\widehat{\theta }$ is the unique vaccination proportion $\theta$ for which (27) has a $\tau$-periodic positive solution. ${\theta }_{*}<{\theta }^{*}$ given in the paper are lower and upper estimates of $\widehat{\theta }$. The spectral radius of this operator r and its threshold condition will be considered in our future research.

Moreover, according to Theorems 1 and 2, we can choose the vaccination period (with $\tau$) and increase the proportion (with $\theta$) of those vaccinated successfully such that $R^{*}<1$ in order to prevent the epidemic disease from generating endemic.

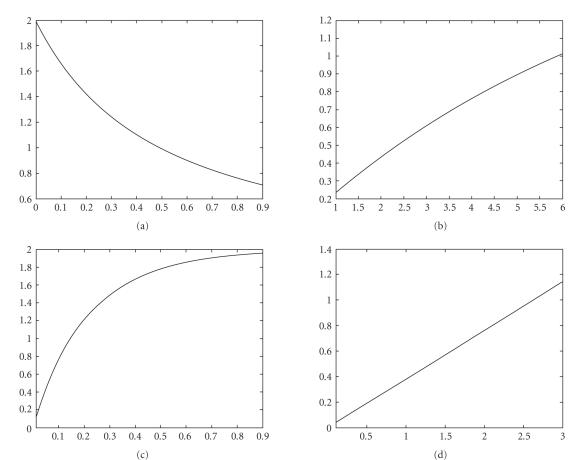
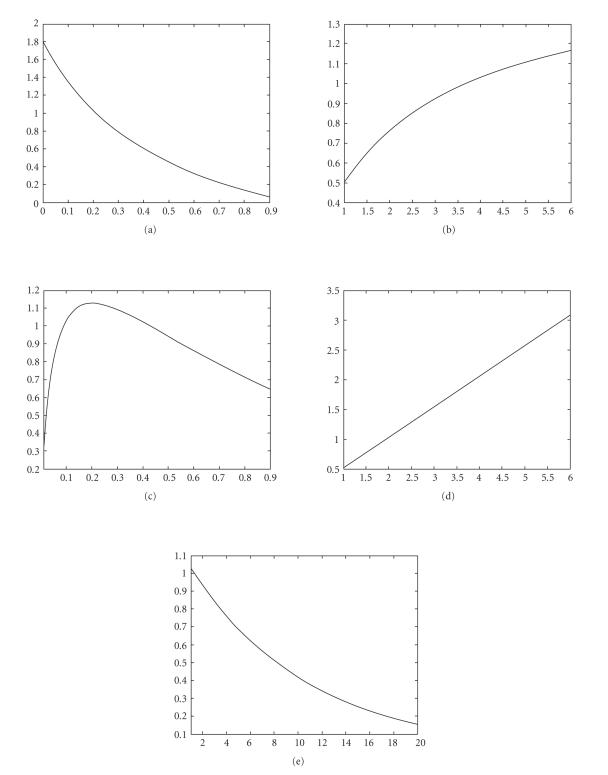
From Figures 1 and 2, we can observe the following.

Figure 1.

The relationship between the parameters and $R^{*}$: (a) “$\theta -R^{*}$,” (b) “$\tau -R^{*}$,” (c) “$\mu -R^{*}$,” (d) “$R_0-R^{*}$.”

Figure 2.

The relationship between the parameters and $R^{*}$: (a) “$\theta -R_{*}$,” (b) “$\tau -R_{*}$,” (c) “$\mu -R_{*}$,” (d) “$R_0-R_{*}$,” (e) “$h-R_{*}$.”

(i) $R^{*}$ and $R_{*}$ are inversely proportional to $\theta$ value and directly proportional to $\tau$ value and $R_0$ value, which implies that pulse vaccination measures the inhibition effect from the behavioral change of the susceptible when they transfer to the infectious class ($I$).

(ii) $R^{*}$ is a directly proportional to $\mu$ value, which implies that the natural birth or death rate measures the inhibition effect from the behavioral change of the susceptible class (with $S$) when it moves into the infectious class ($I$).

(iii) $R_{*}$ is inversely proportional to $h$ value, which implies that the maximum infectious period of the disease measures the inhibition effect from the behavioral change of the susceptible class (with $S$) when it moves into the infectious class ($I$).

(iv) There is a value ${\mu }^{*}$ such that $R_{*}$ is directly proportional to $\mu$ when $\mu <{\mu }^{*}$ and is inversely proportional to $\mu$ when $\mu >{\mu }^{*}$. Therefore the larger death rate is sufficient for the global attractivity of infectionCfree periodic solution $\left({\tilde{S}}_e\left(t\right),0\right)$. It is easy to verify. In fact, we can calculate the derivative of $R_{*}$ with respect to $\mu$

$$\frac{d{R}_{*}}{d\mu }=\frac{\left(1-\theta \right)e^{-\mu h}{R}_0}{{\left[1-\left(1-\theta \right)e^{-\mu \tau }\right]}^2}g\left(\mu \right),$$ (28)

where $g\left(\mu \right)=\theta \tau e^{-\mu \tau }-h\left(1-e^{-\mu \tau }\right)\left(1-\left(1-\theta \right)e^{-\mu \tau }\right).$ Obviously, $g^{\prime }\left(\mu \right)<0$ and $g\left(0\right)>0,{\text{lim}}_{\mu \to +\infty }g\left(\mu \right)<0$. Hence, there exists a ${\mu }^{*}$ such that $d{R}_{*}/d\mu >0$ for $\mu \in \left(0,{\mu }^{*}\right)$, whereas $d{R}_{\ast }/d\mu <0$ for $\mu \in \left({\mu }^{*},+\infty \right)$.

Epidemic models with time delays have received much attention since delays can often cause some complicated dynamical behaviors. Delays in many models can destabilize an equilibrium and thus lead to periodic solutions by Hopf bifurcation [30–32]. It is well known that periodic forcing can drive SIR and SEIR models into a behavior which looks chaotic [33, 34].

The impulsive model with distributed time delay (11) will be analyzed, in particular paying attention to the following points:

(i) the global asymptotic stability for SIR model with pulse vaccination and distributed time delay;

(ii) the behavior of the model when an insufficient level of people undergo the vaccination: bifurcation and chaotic solutions;

(iii) whether periodic or pulse vaccination does a better job than constant vaccination at the same average value.

Appendix

Proof of Theorem 1. —

Since $R^{*}<1$, we can choose ${\epsilon }_0>0$ sufficiently small such that

$$R_0\left(\frac{1-e^{-\mu \tau }}{1-\left(1-\theta \right)e^{-\mu \tau }}+{\epsilon }_0\right)<1.$$ (A.1)

It follows from the first equation of system (11) that $\stackrel{.}{S}\left(t\right)\le \mu -\mu S\left(t\right)$. Thus we consider the comparison impulsive differential system,

$$\begin{array}{cc}\stackrel{.}{X}\left(t\right)& =\mu -\mu x\left(t\right),\hspace{1em}t\ne k\tau ,\\ x\left(t^{+}\right)& =\left(1-\theta \right)x\left(t\right),\hspace{1em}t=k\tau .\end{array}$$ (A.2)

In view of (21), we obtain that the periodic solution of system (A.2), that is, ${\tilde{x}}_e\left(t\right)$ is globally asymptotically stable, and have ${\tilde{x}}_e\left(t\right)={\tilde{S}}_e\left(t\right)$.

Let $\left(S\left(t\right),I\left(t\right)\right)$ be the solution of system (11) with initial values (12) and $S\left(0^{+}\right)=S_0>0$, and let $x\left(t\right)$ be the solution of system (A.2) with initial value $x\left(0^{+}\right)=S_0$. By the comparison theorem for impulsive differential equation [35, 36], there exists an integer $k_1>0$ such that

$$\begin{array}{r}S\left(t\right)<x\left(t\right)<{\tilde{S}}_e\left(t\right)+{\epsilon }_0\le \frac{1-e^{-\mu \tau }}{1-\left(1-\theta \right)e^{-\mu \tau }}+{\epsilon }_0\triangleq \delta ,\\ k\tau <t\le \left(k+1\right)\tau ,k>k_1.\end{array}$$ (A.3)

Further, from the second equation of system (11), we know that (A.3) implies

$$\stackrel{.}{I}\left(t\right)\le R_0\delta {\int }_0^{h}f\left(s\right)I\left(t-s\right)ds-I\left(t\right),\hspace{1em}t>k\tau +h,\hspace{0.17em}k>k_1.$$ (A.4)

Consider the following comparison system:

$$\stackrel{.}{y}\left(t\right)=R_0\delta {\int }_0^{h}f\left(s\right)y\left(t-s\right)ds-y\left(t\right),\hspace{1em}t>k\tau +h,\hspace{0.17em}k>k_1.$$ (A.5)

From (A.1), we have $R_0\delta <1$. According to Lemma 2, we have ${\text{lim}}_{t\to \infty }y\left(t\right)=0$.

Let $\left(S\left(t\right),I\left(t\right)\right)$ be the solution of system (11) with initial values (12) and $I\left(\zeta \right)=\varphi \left(\zeta \right)>0\hspace{0.17em}\left(\zeta \in \left[-h,0\right]\right)$, and let $y\left(t\right)$ be the solution of system (A.5) with initial value $y\left(\zeta \right)=\varphi \left(\zeta \right)>0\hspace{0.17em}\left(\zeta \in \left[-h,0\right]\right)$. By the comparison theorem in differential equation, we have ${\text{lim}}_{t\to \infty }I\left(t\right)\le {\text{lim}}_{t\to \infty }y\left(t\right)=0$. Incorporating into the positivity of $I\left(t\right)$, we know that ${\text{lim}}_{t\to \infty }I\left(t\right)=0.$ Therefore, for any ${\epsilon }_1>0$ (sufficiently small), there exists an integer $k_2>k_1$ (where $k_2\tau >k_1\tau +h$) such that $I\left(t\right)<{\epsilon }_1$ for all $t>k_2\tau$.

From the first equation of system (11), we have

$$\stackrel{.}{S}\left(t\right)\ge \mu -R_0{\epsilon }_1-\mu S\left(t\right),\hspace{1em}\text{for}t>k_2\tau +h.$$ (A.6)

Consider comparison impulsive system for $t>k_2\tau +h$ and $k>k_2$,

$$\begin{array}{cc}ż\left(t\right)& =\mu -R_0{\epsilon }_1-\mu z\left(t\right),\hspace{1em}t\ne k\tau ,\\ z\left(t^{+}\right)& =\left(1-\theta \right)z\left(t\right),\hspace{1em}t=k\tau .\end{array}$$ (A.7)

By Lemma 1, we have the unique periodic solution of system (A.7),

$$\begin{array}{r}{\tilde{z}}_e\left(t\right)=\frac{\mu -R_0{\epsilon }_1}{\mu }+\left(z^{*}-\frac{\mu -R_0{\epsilon }_1}{\mu }\right)e^{-\mu \left(t-k\tau \right)},\\ k\tau <t\le \left(k+1\right)\tau ,\end{array}$$ (A.8)

which is globally asymptotically stable, where $z^{\ast }=\left(\left(\mu -R_0{\epsilon }_1\right)/\mu \right)\left(\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)/\left(1-\left(1-\theta \right)e^{-\mu \tau }\right)\right)$.

Further, in view of the comparison theorem in impulsive differential equation, there exists an integer $k_3>k_2$ such that $k_3\tau >k_2\tau +h$ and

$$S\left(t\right)>\tilde{z}{}_e\left(t\right)-{\epsilon }_1,\hspace{1em}k\tau <t\le \left(k+1\right)\tau ,\hspace{1em}k>k_{3.}$$ (A.9)

Because ${\epsilon }_0$ and ${\epsilon }_1$ are arbitrary small, it follows from (A.3) and (A.9) that ${\text{lim}}_{t\to \infty }S\left(t\right)={\tilde{S}}_e\left(t\right)$. Therefore, the infection-free solution $\left({\tilde{S}}_e\left(t\right),0\right)$ of system (11) is globally attractive. The Proof of Theorem 1 is complete.

Proof of Theorem 2. —

Note that the second equation of (11) can be rewritten as

$$\begin{array}{ll}\stackrel{.}{I}\left(t\right)& =R_0{\int }_0^{h}f\left(s\right)S\left(t\right)I\left(t\right)e^{-\mu s}ds-I\left(t\right)\\ & \hspace{1em}{-R}_0{\int }_0^{h}f\left(s\right)e^{-\mu s}\left[S\left(t\right)I\left(t\right)-S\left(t-s\right)I\left(t-s\right)\right]ds\\ & =I\left(t\right)\left(R_{0}S\left(t\right){\int }_0^{h}f\left(s\right)e^{-\mu s}ds-1\right)\\ & \hspace{1em}-R_0\frac{d}{dt}{\int }_0^{h}f\left(s\right)e^{-\mu s}{\int }_{t-s}^{t}S\left(u\right)I\left(u\right)du\hspace{0.17em}ds.\end{array}$$ (A.10)

Let us consider any positive solution $\left(S\left(t\right),I\left(t\right)\right)$ of system (11). According to this solution, we define

$$V\left(t\right)=I\left(t\right)+R_0{\int }_0^{h}f\left(s\right)e^{-\mu s}{\int }_{t-s}^{t}S\left(u\right)I\left(u\right)du\hspace{0.17em}ds.$$ (A.11)

According to (A.10), we calculate the derivative of $V$ along the solutions of (11),

$$\begin{gathered} \begin{array}{lll}{V}^{.}\left(t\right)& =& I\left(t\right)\left(R_{0}S\left(t\right){\int }_0^{h}f\left(s\right)e^{-\mu s}ds-1\right) \\ \\ & \ge & I\left(t\right)\left(R_0{e}^{-\mu h}S\left(t\right)-1\right).\end{array} \end{gathered}$$ (A.12)

Denote

$$I^{*}\triangleq \frac{\mu }{R_0}\left[1-\frac{e^{\mu h}}{\left(1-\theta \right)R^{*}}\right]=\frac{\mu }{R_0}\left[1-\frac{e^{\mu h}}{R_0}\frac{1-\left(1-\theta \right)e^{-\mu \tau }}{\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)}\right].$$ (A.13)

It is easy to see that $I^{*}>0$ if $R_{*}>1$. Since $R_{*}>1$, we easily see that there exists sufficiently small $\epsilon >0$ such that

$$R_0{e}^{-\mu h}\left(\frac{\mu -R_0{I}^{*}}{\mu }\frac{\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)}{1-\left(1-\theta \right)e^{-\mu \tau }}-\epsilon \right)>1.$$ (A.14)

We claim that for any $t_0>0$, it is impossible that $I\left(t\right)<I^{*}$ for all $t\ge t_0$. Suppose that the claim is not valid. Then there is a $t_0>0$ such that $I\left(t\right)<I^{*}$ for all $t\ge t_0$. It follows from the first equation of (11) that $\stackrel{.}{S}\left(t\right)>\left(\mu -R_0{I}^{*}\right)-\mu S\left(t\right)$, for $t\ge t_0+h$. Consider the following comparison impulsive system for $t\ge t_0+h$:

$$\begin{array}{cc}{v}^{\cdot }\left(t\right)& =\left(\mu -R_0{I}^{*}\right)-\mu v\left(t\right),\hspace{1em}t\ne k\tau ,\\ v\left(t^{+}\right)& =\left(1-\theta \right)v\left(t\right),\hspace{1em}t=k\tau .\end{array}$$ (A.15)

By Lemma 1, we obtain that the unique positive periodic solution of (A.15)

$$\begin{array}{r}{\stackrel{}{\mathrm{v˜}}}_e\left(t\right)=\frac{\mu -R_0{I}^{*}}{\mu }+\left(v^{*}-\frac{\mu -R_0{I}^{*}}{\mu }\right)e^{-\mu \left(t-k\tau \right)},\\ k\tau <t\le \left(k+1\right)\tau ,\end{array}$$ (A.16)

is globally asymptotically stable, where $v^{*}=\left(\left(\mu -R_0{I}^{*}\right)/\mu \right)\left(\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)/\left(1-\left(1-\theta \right)e^{-\mu \tau }\right)\right)$.

In view of comparison theorem for impulsive differential equation, there exists $t_{1\hspace{0.17em}}\left(>t_0+h\right)$ such that the following inequality holds for $t\ge t_1$:

$$S\left(t\right)>{\tilde{v}}_e\left(t\right)-\epsilon >v^{*}-\epsilon \triangleq \sigma .$$ (A.17)

From (A.14), we have $R_0{e}^{-\mu h}\sigma >1$. By (A.12) and (A.17), we have

$$V^{\cdot }\left(t\right)>I\left(t\right)(R_0{e}^{-\mu h}\sigma -1),\hspace{1em}\text{for} t\ge t_1.$$ (A.18)

Set $I_l={\text{min}}_{t\in \left[t_1, t_1+h\right]}I\left(t\right).$ We will show that $I\left(t\right)\ge I_l$ for all $t\ge t_1$. Suppose the contrary. Then there is a $T_0\ge 0$ such that $I\left(t\right)\ge I_l$ for $t_1\le t\le t_1+h+T_0$, $I\left(t_1+h+T_0\right)=I_l$, and $\stackrel{.}{I}\left(t_1+h+T_0\right)\le 0$. However, the second equation of system (11) and (A.17) imply that

$$\begin{array}{cc}\stackrel{.}{I}\left(t_1+h+T_0\right)& \ge \left(R_0{\int }_0^{h}f\left(s\right)e^{-\mu s}S\left(t_1+h+T_0-s\right)ds-1\right)I_l\\ & >\left(R_0{e}^{-\mu h}\sigma -1\right)I_l>0.\end{array}$$ (A.19)

This is a contradiction. Thus, $I\left(t\right)\ge I_l$ for all $t\ge t_1$. As a consequence, (A.18) leads to $V^{\cdot }\left(t\right)>\left(R_0{e}^{-\mu h}\sigma -1\right)I_1\text{for}t\ge t_1,$ which implies that as $t\to \infty$, $V\left(t\right)\to \infty$. This contradicts $V\left(t\right)\le 1+R_{0}h$. Hence, the claim is proved.

Hence, we have to consider two cases. First, $I\left(t\right)\ge I^{*}$ for $t$ large enough. Second, $I\left(t\right)$ oscillates about $I^{*}$ for $t$ large enough. Define

$$q=\text{min}\left\{\frac{I^{*}}{2},I^{*}{e}^{-h}\right\}.$$ (A.20)

We show that $I\left(t\right)\ge q$ for $t$ large enough. The conclusion is evident in the first case. For the second case, let $t^{*}>0$ and $\xi >0$ satisfy

$$\begin{gathered} I\left(t^{*}\right)=I\left(t^{*}+\xi \right)=I^{*}, \\ I\left(t\right)<I^{*},\hspace{1em}\text{for}\hspace{0.33em}{t}^{*}<t<t^{*}+\xi , \end{gathered}$$ (A.21)

where $t^{*}$ is sufficiently large such that

$$S\left(t\right)>\sigma ,\hspace{1em}\text{for}\hspace{0.17em}{t}^{*}<t<t^{*}+\xi .$$ (A.22)

$I\left(t\right)$ is uniformly continuous since the positive solutions of (11) are ultimately bounded and $I\left(t\right)$ is not affected by impulses. Hence, there is a $T\hspace{0.17em}(0<T<h$, and $T$ is independent of the choice of $t^{*}$) such that $I\left(t\right)>I^{*}/2$ for $t^{*}\le t\le t^{*}+T.$ If $\xi \le T$, there is nothing to prove. Let us consider the case where $T<\xi \le h$. Since $\stackrel{.}{I}\left(t\right)>-I\left(t\right)$ and $I\left(t^{*}\right)=I^{*}$, it is obvious that $I\left(t\right)\ge q$ for $t^{*}<t<t^{*}+\xi$. If $\xi >h$, by the second equation of (11), we obtain $I\left(t\right)\ge q$ for $t\in \left[t^{*},t^{*}+h\right]$. Then, proceeding exactly as in the proof for the above, we see that $I\left(t\right)\ge q$ for $t\in \left[t^{*}+h,t^{*}+\xi \right]$. Since this kind of interval $\left[t^{*},t^{*}+\xi \right]$ is chosen in an arbitrary way (we only need $t^{*}$ to be large), we conclude that $I\left(t\right)\ge q$ for $t$ large enough in the second case. In view of our above discussions, the choice of $q$ is independent of the positive solution, and we have proved that any positive solution of (11) satisfies $I\left(t\right)\ge q$ for $t$ large enough. The Proof of Theorem 2 is complete.

Proof of Theorem 3. —

Denote $\left(S\left(t\right),I\left(t\right)\right)$ as any solution of system (11). From the first equation of system (11), we have

$$\stackrel{.}{S}\left(t\right)\ge \mu -R_0-\mu S\left(t\right).$$ (A.23)

By the similar arguments as those in the Proof of Theorem 1, we have that

$$\underset{t\to \infty }{\text{lim}}S\left(t\right)\ge p,$$ (A.24)

where $p=\left(\left(\mu -R_0\right)/\mu \right)\left(\left(1-\theta \right)\left(1-e^{-\mu \tau }\right)/\left(1-\left(1-\theta \right)e^{-\mu \tau }\right)\right)-\epsilon >0$, $\epsilon >0$ is sufficiently small.

We let ${\Omega }_0=\left\{\left(S,I\right)|p\le S\le 1,\hspace{0.17em}q\le I\le 1\right\}$. By Theorem 2 and above discussions, we know that the set ${\Omega }_0$ is a global attractor in $\Omega$, and of course, every solution of system (11) with initial conditions (12) will eventually enter and remain in region ${\Omega }_0$. Therefore, system (11) is permanent. The Proof of Theorem 3 is complete.