Linkage Disequilibrium in Related Breeding Lines of Chickens

Abstract

High-density genotyping of single-nucleotide polymorphisms (SNPs) enables detection of quantitative trait loci (QTL) by linkage disequilibrium (LD) mapping using LD between markers and QTL and the subsequent use of this information for marker-assisted selection (MAS). The success of LD mapping and MAS depends on the extent of LD in the populations of interest and the use of associations across populations requires LD between loci to be consistent across populations. To assess the extent and consistency of LD in commercial broiler breeding populations, we used genotype data for 959 and 398 SNPs on chromosomes 1 and 4 on 179–244 individuals from each of nine commercial broiler chicken breeding lines. Results show that LD measured by r² extends over shorter distances than reported previously in other livestock breeding populations. The LD at short distance (within 1 cM) tended to be consistent across related populations; correlations of LD measured by r for pairs of lines ranged from 0.17 to 0.94 and closely matched the line relationships based on marker allele frequencies. In conclusion, LD-based correlations are good estimates of line relationships and the relationship between a pair of lines a good predictor of LD consistency between the lines.

THERE is widespread interest in exploiting linkage disequilibrium (LD) to map quantitative trait loci (QTL) in human and natural populations and to guide selection in commercial breeding programs in livestock. LD mapping can improve on the mapping resolution of conventional linkage analysis through its use of historical recombinations. The resulting LD markers can be effectively used for marker-assisted selection (MAS) in livestock (Dekkers 2004) because LD markers allow for selection on the marker genotype across the population on the basis of the consistent association between genotype and phenotype.

One requirement for the most effective use of LD mapping and of LD markers in MAS is that marker density is high enough that at least one marker is in sufficiently high LD with any putative QTL. With the availability of whole-genome sequences and large numbers of single-nucleotide polymorphisms (SNPs) in several agricultural species, high-density marker studies have become possible. The cost associated with genotyping, however, leads to an interest in using the smallest required number of markers for LD mapping and MAS. Because the required marker density depends directly on the extent of LD, which varies between populations, an important step prior to any association analysis is to ascertain the extent of LD in the populations of interest.

In practice, it is also of interest to utilize markers whose association has been detected in one population for MAS in other populations or to combine populations for association analyses to increase power. These options rely on consistency of LD across populations, and so it is of interest to ascertain whether the patterns from LD in one population extend to related populations. The extent and consistency of LD for LD mapping and MAS can be assessed by studying marker–marker LD as an estimate for marker–QTL LD in multiple related populations, thereby allowing for the quantification of the required marker density and sample size for association mapping.

Studies on the extent of LD have been conducted in human and several other animal populations. Although initial findings in humans have shown LD to extend over very short distances (Pritchard and Przeworski 2001), subsequent studies in livestock have shown high levels of LD over much longer distances in cattle (Farnir et al. 2000; Vallejo et al. 2003), pigs (Nsengimana et al. 2004), and sheep (McRae et al. 2002). This is thought to be caused by the intensive artificial selection to which commercial animal breeding populations have been subjected for many generations and the ensuing reduction in effective population size, which has been supported by research at least in dairy cattle (Hayes et al. 2003). Studies in commercial layer chicken breeding lines have also found appreciable LD between microsatellite markers as far as 5 cM apart (Heifetz et al. 2005). Heifetz et al. (2005) also looked at the consistency of LD across generations and chromosomal regions and found that LD at shorter distances was conserved across generations but was quite variable between chromosomal regions.

The purpose of this study was to examine the extent of marker-to-marker LD in commercial breeding lines of broiler chickens and to evaluate the consistency of LD across lines. The lines evaluated are representative of populations used in animal breeding programs and may also be representative of closed outbreeding populations of plants and wildlife species in having limited historical effective population size and LD created mostly by drift (Terwilliger et al. 1998). The consistency of LD across lines was related to the genetic distance between lines as estimated from marker allele frequencies.

MATERIALS AND METHODS

Lines:

SNP genotype data from nine commercial broiler chicken pure breeding lines from one major global breeding company (Aviagen), coded line 1 to line 9, were used. The lines evaluated were representative of the lines in a commercial broiler breeding program. A significant proportion of all broilers produced in the world are four-way hybrids derived from combinations of the pure lines examined in this study. In common with all major broiler breeder lines, these pure lines have their origins in the Plymouth Rock and Cornish lines and are closed populations that have undergone multiple generations of selection using genetic evaluations based on multiple-trait best linear unbiased prediction analysis. Traits currently under selection are broadly characterized into broiler traits (e.g., growth rate, feed efficiency), processing traits (e.g., meat yields), breeder traits (e.g., egg production, hatchability, chick output, fertility), and welfare-type traits (e.g., survival, skeletal, and cardiovascular fitness). Selection pressure on the balance of these traits is different for each line to the extent that considerable differences in key traits now exist, enabling a range of hybrid broiler products with different balances of performance to be produced. Effective population size in these lines ranges from 50 to 200, which is representative of most livestock breeding populations and indicates that most LD present in the populations is the result of drift.

A total of 179–244 individuals from each of the nine lines that were representative of males used for breeding within a given time period were used. Although the samples included individuals that were half sibs or full sibs, these relationships are not expected to appreciably bias estimates of LD, in part because sample sizes used were relatively large.

Markers:

We analyzed chromosomes 1 and 4 and used SNPs that were initially identified by the chicken polymorphism consortium on the basis of sequence differences of three domesticated breeds with the wild jungle fowl (International Chicken Polymorphism Map Consortium 2004). None of the lines used in the current study were included in this SNP discovery project. Analysis of SNPs on chromosomes 1 and 4 resulted in sufficient data for analysis of relationships of LD with distance and will be representative of LD on other chromosomes in these populations. Initial SNP assay development was coordinated by H. Cheng, U.S. Department of Agriculture–Agricultural Research Service (USDA–ARS), and resulted in a 3000 SNP (3K) panel with genomewide coverage. A data file titled “Database of SNPs used in the Illumina Corp. chicken genotyping project” (can be downloaded from http://poultry.mph.msu.edu/resources/Resources.htm) describes the original 3K panel developed by a consortium led by H. Cheng (USDA–ARS Avian Disease and Oncology Lab, East Lansing, MI) to genotype a wide variety of chicken populations. This panel was recently used in a QTL mapping study (Abasht and Lamont 2007). To complement the 3K panel, another 3000 SNPs across the genome were chosen from the consortium SNP results to fill in gaps and to increase the density in some candidate gene regions. The total number of SNPs genotyped was 959 for chromosome 1 and 398 for chromosome 4, resulting in ∼1 SNP/200 kb. This study reports on results from the 6000 SNP (6K) panel because it allowed better assessment of LD at short distances because of greater density than the publicly available 3K panel. The 6K panel, however, resulted in levels of LD very similar to those of the publicly available 3K panel, as demonstrated in the supplemental data at http://www.genetics.org/supplemental/. This is as would be expected if most SNPs included are neutral and LD is generated primarily by drift because in that case the extent of LD in a given population will be independent of the specific SNPs included in the panel.

Genotyping and genotype scoring was done by Illumina, utilizing a custom-designed BeadChip (Fan et al. 2003; Gunderson et al. 2004). Genotype calls with a GenCall score <0.25 were excluded, which eliminated <0.5% of SNP genotypes. Over 75% of genotypes had a GenCall score >0.8.

Significance levels for deviations from Hardy–Weinberg equilibrium were computed using an exact test (Wigginton et al. 2005), as implemented in Haploview (Barrett et al. 2005). Although there was limited evidence of deviations from Hardy–Weinberg equilibrium based on the near-uniform distribution of P-values within each line, SNPs with P-values <0.001 were eliminated (0.0–2.3% of SNPs for chromosome 1 and 0.3–2.8% for chromosome 4, for the nine lines). For most analyses, SNPs with minor allele frequencies (MAF) within a line of <0.2 were also eliminated to eliminate potential effects of allele frequencies on LD results. Because of the limited relationships among individuals genotyped, Mendelian segregation errors could not be evaluated accurately in this data set.

Marker positions (in base pairs) were those reported for the second draft of the chicken genome (http://genome.ucsc.edu/cgi-bin/hgGateway?org=Chicken&db=0&hgsid=30948908). Marker positions in centimorgans were estimated by multiplying base pair positions by 2.8, which is the estimate of the average number of centimorgans per megabase for chicken macrochromosomes (International Chicken Polymorphism Map Consortium 2004). Although the relationship between physical and linkage distance is not consistent across the genome (International Chicken Genome Sequencing Consortium 2004), the use of an average relationship is not expected to bias results, apart from increasing variability of relationships between LD and distance.

Linkage disequilibrium measures:

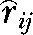Markers with MAF > 0.2 were used to estimate the extent of LD between all pairs of SNPs within each of the two chromosomes on the basis of the correlation between alleles at the two SNPs () and its square () as =D_ij/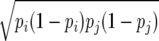 (Hill and Robertson 1968), where D_ij = p_ij − p_ip_j, and p_ij, p_i, and p_j are the frequencies of haplotype ij and allele i at one locus and allele j at the second locus. The programs Haploview (Barrett et al. 2005) and PowerMarker (Liu and Muse 2005) were used to compute LD between markers. We use the notations and for the estimated values of r and r² to differentiate between estimates and true values of these statistics. Compared to other measures of LD such as D′, r² is the preferred measure of LD for biallelic loci because it is related to the amount of information provided by one locus about the other (Ardlie et al. 2002) and is less affected by sample size than D′. The measure r has the added benefit over r² of incorporating the direction of LD, which is important when assessing consistency of LD across lines. The sign (but not the absolute value) of r depends on the (arbitrary) choice of the allele used in the computation of r for each SNP. To ensure consistency of direction, the same alleles were used for each line.

The LD was also computed between all pairs of nonsyntenic markers between chromosomes 1 and 4 to obtain an empirical null distribution for . The frequency distribution of syntenic by distance was compared to the nonsyntenic distribution. We also used the maximum for each SNP with any other SNP to evaluate the distribution of maximum LD, following Spelman and Coppieters (2006) and the distribution of distances at which the maximum value is attained.

Du et al. (2007) reported concerns about possible biases of , especially with small samples and with extreme allele frequencies. Because we did not use SNPs with MAF < 0.2, we were concerned only about potential bias for markers with MAF > 0.45 and for pairs with similar MAFs. A three-dimensional plot of vs. MAF (not presented), however, showed no observable relationships between average and MAF, so we considered correction of for MAF, as suggested by Du et al. (2007), unnecessary.

Decline of LD with distance was estimated by fitting the Sved (1971) equation E(r²) = 1/(1 + 4 × N_e × d) to LD for all pairs of markers, separately for each line and chromosome. The method described in Zhao et al. (2005) to account for heterogeneity of variances of was used to fit this equation.

Comparing lines:

To evaluate consistency of LD at short distances between lines, between pairs of loci from one line were correlated with for the same pairs from each other line. Correlations were computed separately for each chromosome using marker pairs with MAF > 0.2 and that were within 500 kb (∼1.4 cM) of each other. Several possible values for the maximum distance between markers were tried but correlations were rather insensitive to maximum distances in the range of 100–1000 kb. To assess factors contributing to these correlations, correlations were also computed for syntenic marker pairs separated by >4000 kb (∼11.2 cM) and for nonsyntenic marker pairs.

To visualize relationships between lines, the estimated covariances of LD within 500 kb between each pair of lines, j and k (C_jk), were used to create phylogenetic trees, with squared distance between lines j and k (D_jk) given by

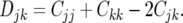Trees based on nonsyntenic LD correlations were created in a similar manner. Resulting trees were compared to phylogenic trees on the basis of marker allele frequencies, which were computed using two algorithms, neighbor joining (Saitou and Nei 1987) and the unweighted pair group method with arithmetic mean (UPGMA) (Sneath and Sokal 1973), as implemented in PowerMarker (Liu and Muse 2005). Trees were graphed using Phylip (Felsenstein 1989). The phylogenetic trees obtained by the different methods and data were compared using the partition metric described in Penny and Hendy (1985) and as implemented in the program Component (Page 1993).

RESULTS

Markers used for analysis:

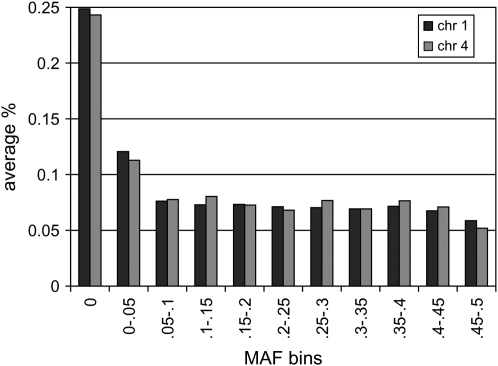
Table 1 shows the number of SNPs that were segregating in each line (MAF > 0) and the number of SNPs that had MAF > 0.05 or 0.2. Numbers of segregating SNPs varied between lines. For all lines and both chromosomes, the distributions of MAF (Figure 1) had the expected half-U shape, although there were differences between lines and chromosomes; e.g., line 4 had a smaller proportion of low MAF markers (<0.05) for both chromosomes, and lines 1 and 3 (for chromosomes 1 and 4, respectively) had a larger proportion than other lines (see Table 1). The large proportion of fixed or low MAF markers (Table 1) may be due to selection of SNPs based on sequence differences of commercial breeds with the wild jungle fowl (International Chicken Polymorphism Map Consortium 2004).

TABLE 1.

Number of markers in each line that have minor allele frequencies (MAF) >0, 0.05, or 0.2 on chromosomes 1 and 4

	Chromosome 1 (958 markers)			Chromosome 4 (392 markers)
Linea	MAF > 0	MAF > 0.05	MAF > 0.2	MAF > 0	MAF > 0.05	MAF > 0.2
1	589	507	348	269	232	146
7	603	526	336	273	241	157
8	693	589	376	276	233	138
6	723	614	386	297	259	159
5	732	649	442	302	272	184
3	745	559	346	301	216	134
2	769	647	405	324	274	172
9	790	673	433	318	279	194
4	812	715	486	336	286	185

^aLines are sorted by number of MAF > 0 on chromosome 1.

Figure 1.—

Frequency distribution of major allele frequencies of markers on chromosomes 1 and 4 across lines. The frequency on the vertical axis is the average of within-line frequencies. Similar distributions were obtained for individual lines.

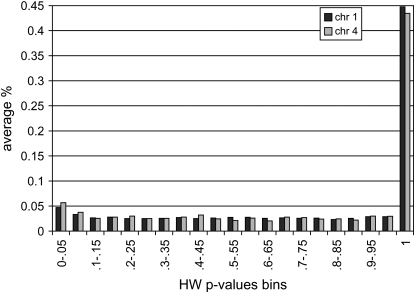
The distribution of P-values for deviations from Hardy–Weinberg equilibrium (computed for all markers) also followed the expected uniform distribution (Figure 2), which is consistent with lack of evidence of deviations from Hardy–Weinberg equilibrium. The large number of SNPs with a P-value of 1.0 results from use of Fisher's exact test for SNPs with extreme allele frequencies. No obvious differences in distributions of P-values were visually identified between lines or chromosomes.

Figure 2.—

Distribution of P-values for deviations from Hardy–Weinberg equilibrium for markers on chromosomes 1 and 4 across lines. The frequency on the vertical axis is the average of within-line frequencies. Similar distributions were obtained for individual lines.

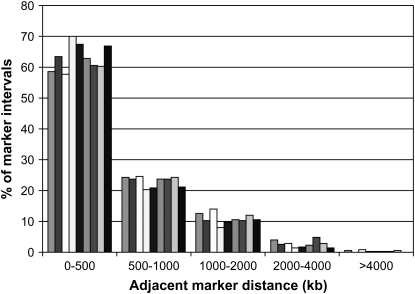
The average distance between adjacent SNPs in the MAF > 0.2 data set was ∼500 kb for chromosomes 1 and 4. A frequency distribution of distances between adjacent SNPs with MAF > 0.2 is in Figure 3 and demonstrates that these two chromosomes were well covered by the 6K panel with a limited number of large gaps. The range of distances obtained with this panel on these two chromosomes makes results from analysis of relationships between LD and distance representative of similar relationships across the genome in these populations.

Figure 3.—

Distribution of the distance between adjacent markers in each line.

Decline of LD with distance:

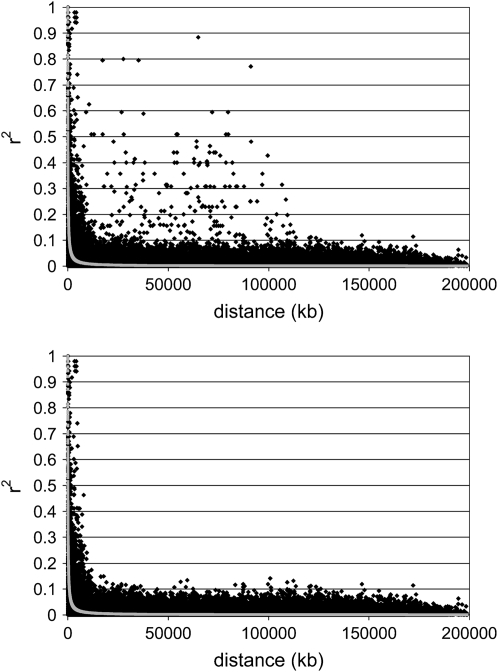
Figure 4 illustrates the decline of LD with distance between markers in a pair for chromosome 1 and line 2, for the MAF > 0.2 data set. The pattern of high LD at short distances that declines steeply as distance increases was common to all lines for both chromosomes and agrees with previous results and theory (Sved 1971). We ignored corrections for sample size as the number of haplotypes was large enough for this to be negligible. When based on the first release of the genome (International Chicken Genome Sequencing Consortium 2004), plots of vs. distance showed nonrandom high LD at large distances for chromosome 1, but these were largely corrected in the second release (Figure 4), although some appreciable deviations remained, most notably in line 2 (Figure 4). To investigate these remaining discrepancies, we looked at all pairs of markers >25,000 kb apart that had > 0.2 for each line and combined the information. A total of 126 markers were involved in the identified high-LD pairs, most of them several times (either in multiple lines or in multiple pairs within the same line), but 2 markers (_rs13920576 and snp-280-14-5024-S-3) contributed to high LD much more than other markers. These 2 markers were eliminated because they are likely misplaced. In the resulting data set, only 10 markers were involved in cases of high LD at large distances, each appearing only once (Figure 4). Chromosome 4 did not show similar problems for either of the two releases of the chicken genome sequence.

Figure 4.—

Decline of linkage disequilibrium (LD) measured by r² against distance in kilobases. Data are for chromosome 1 and line 2, before (left) and after (right) elimination of the two markers most involved in high long-distance LD. Chromosome 4 had a similar pattern of decline but lacked high long-range LD. The graphs combine two different aspects of LD vs. distance: a scatterplot of estimates of r² for pairs of SNPs (solid symbols) and a predicted LD value plot (shaded symbols) based on fitting the equation E(r²) = 1/(1 + 4 × N_e × d), where N_e is the effective population size and d is the distance in morgans (assuming 2.8 cM/Mb). We ignored the sample size correction of +1/n, where n is the number of haplotypes, as it is negligible due to large sample size.

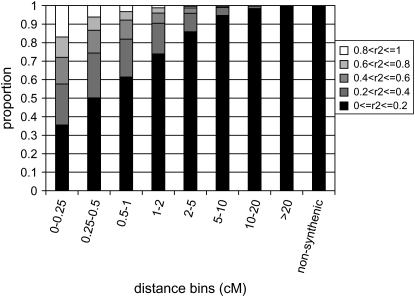
Figure 5 summarizes the frequency distribution of by distance for syntenic and nonsyntenic marker pairs. In general, the amount of LD was less than reported in a previous study on LD in chicken (Heifetz et al. 2005), although this study used microsatellite markers, another measure of LD, and was on layer rather than broiler chicken breeding lines. About 10% of marker pairs within 0.5 cM had > 0.8, and this dropped to 1% for markers >1 cM apart. About 24% of marker pairs within 0.5 cM had > 0.5, and this dropped to 11% for markers 0.5–1 cM apart and to <2% for markers >2 cM apart. The distribution of at distances >20 cM was similar to that of nonsyntenic marker pairs, with 99.99% of values <0.2. Although the amount of LD was limited, the LD observed was nonrandom, since for nonsyntenic markers a very small percentage of values were >0.2. The expected value of between nonsyntenic markers is 1/n, where n is the number of haplotypes, and is very low in our study: ∼0.0025 for any of the nine lines. Differences in LD distributions between lines were limited.

Figure 5.—

Frequency distribution of estimates of LD by r² for syntenic and nonsyntenic marker pairs. The syntenic distribution was computed across chromosomes and lines, within between-marker distance bins. The nonsyntenic distribution was computed across lines. Similar distributions were obtained within lines and chromosomes. Distances, in centimorgans, are computed from the base pair distance by multiplying with the average centimorgan per base pair distance across the chicken genome.

The decline of LD with distance could be adequately modeled on the basis of the Sved (1971) equation: E(r²) = 1/(1 + 4 × N_e × d). Although the magnitude of estimates of N_e based on the decline of LD with distance was sensitive to the choice of smoothing parameter used in the method of Zhao et al. (2005), relative differences in estimates between lines were less sensitive, so resulting estimates are useful mainly for line comparison purposes. Estimates of N_e for the same line but using data from chromosome 1 vs. chromosome 4 were similar, with a correlation of 0.84 and a regression coefficient of 1.02 of the estimate of N_e based on chromosome 1 to N_e based on chromosome 4. The latter coefficient was significantly different from 1.00 at P < 0.01 and is likely caused by a difference in the average base pairs per centimorgan between the two chromosomes. Estimates of N_e were also significantly and negatively correlated with the proportion of fixed markers, with a correlation coefficient of −0.59.

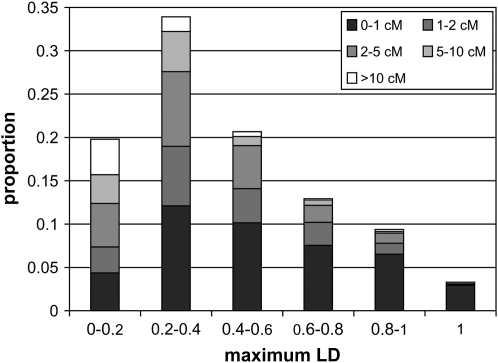
The distribution of maximum of a SNP with all other SNPs (Spelman and Coppieters 2006) suggests that SNPs found to be associated with a trait in LD studies are very likely to be near a relevant QTL. This distribution is graphed in Figure 6, and separated into bins on the basis of the distance between the SNP and its maximum SNP. About 25% of SNPs had a maximum > 0.6 and 80% of SNPs had a maximum > 0.2. For all maximum -value bins >0.2, the shortest-distance bin (<1 cM) was the most frequent and of SNPs with maximum > 0.4, only 5–7% (for the two chromosomes) were >5 cM from their maximum SNP.

Figure 6.—

Frequency of maximum LD of SNPs based on r², across lines and chromosomes. Bins were created on the basis of distance to the SNP for which the maximum LD was registered. A similar distribution was observed for each chromosome separately.

Consistency of LD across lines:

To use QTL information obtained in one population for selection in a different population or to combine association studies across populations, LD patterns must be consistent across lines (Goddard et al. 2006). Otherwise, association studies and selection must be conducted separately within each population. The level of consistency of LD was assessed on the basis of correlations between LD measured by for markers within 500 kb for all pairs of lines (Table 2). Unlike , has directionality and is therefore more appropriate to assess consistency meaningful to the mentioned issues.

TABLE 2.

Correlations of linkage disequilibrium (measured by r) between pairs of lines for markers within 500 kb (above diagonal) and for nonsyntenic markers (below diagonal)

Line	1	2	3	4	5	6	7	8	9
1	—	0.21 (68)a	0.41 (80)	0.45 (133)	0.47 (112)	0.52 (89)	0.94 (200)	0.56 (107)	0.46 (127)
2	0.00	—	0.39 (163)	0.69 (356)	0.36 (241)	0.45 (206)	0.41 (144)	0.47 (157)	0.66 (315)
3	−0.00	0.01	—	0.37 (217)	0.38 (208)	0.64 (217)	0.48 (146)	0.90 (278)	0.41 (197)
4	−0.01	0.02	0.03	—	0.40 (374)	0.46 (308)	0.32 (238)	0.53 (249)	0.76 (504)
5	−0.00	0.01	−0.02	−0.01	—	0.38 (278)	0.39 (219)	0.44 (227)	0.41 (339)
6	−0.01	−0.00	−0.01	0.00	−0.00	—	0.48 (176)	0.70 (223)	0.46 (243)
7	−0.02	−0.01	0.01	−0.00	−0.00	−0.01	—	0.51 (141)	0.46 (226)
8	−0.01	−0.02	0.00	0.00	−0.01	0.00	−0.00	—	0.54 (210)
9	0.01	0.00	0.03	0.01	−0.00	−0.00	−0.00	0.02	—

Only markers with major allele frequencies >0.2 were included.

^aNumber of marker pairs included in computation of the correlation. Correlations for nonsyntenic markers were based on >13,000 marker pairs.

The average correlation over all pairs of lines was 0.52. Correlations did, however differ substantially between pairs of lines, and several lines had very high correlations, >0.9 (pairs 1 and 8, and 3 and 9; see Table 2). For comparison, correlations for LD between nonsyntenic markers was very small, ranging from −0.02 to 0.03 for all pairs of lines (Table 2). To test our conclusion that line correlations are the result of common history, we also computed correlations between LD for syntenic markers that were separated by at least 4000 kb (≈11.2 cM). These correlations ranged from −0.01 to 0.05, with an average of 0.02, i.e., only slightly higher than correlations obtained for nonsyntenic SNPs. The correlations of LD correlations for nonsyntenic SNPs with LD correlations for SNPs at short (<500 kb) and long distances (>4000 kb) were −0.07 and 0.10, respectively. When alternate values were chosen for the minimum distance (results not shown), the correlations rapidly decreased with increased minimum distance for minimum distances <10 cM, but slowly approached the nonsyntenic distribution for minimum distances >10 cM.

Correlations between lines for LD measured by (Table 2) were in general higher than correlations for LD measured by (not shown). Correlations for quantify the extent to which high LD between a pair of markers in one line implies high LD in another; i.e., there is an excess of some haplotype(s) in each line, but not necessarily the same haplotype(s). Correlations between , however, quantify the extent to which there is an excess of the same haplotype(s) in all lines.

A complementary, more explicit measure of consistency of direction is the proportion of marker pairs within 500 kb that had of the same sign for each pair of lines. For LD between markers within 500 kb, this proportion was 66% for the 36 pairs of lines and the pattern of variation was the same as that obtained for LD correlations in Table 2.

Relationships between lines:

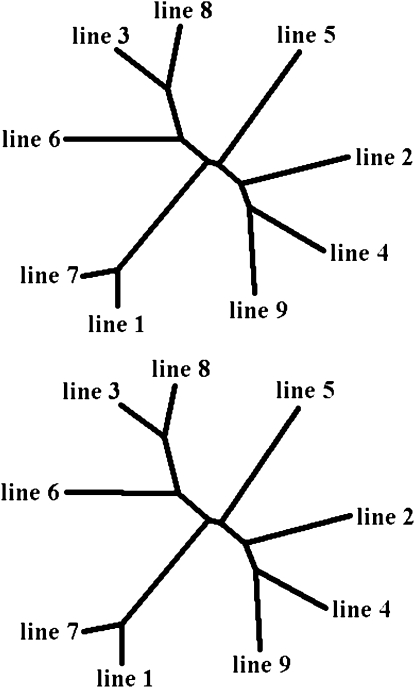
Phylogenetic trees based on allele frequencies (Figure 7) were obtained using two different algorithms, UPGMA and neighbor joining (NJ), separately for chromosomes 1 and 4. The two algorithms gave very similar results (the only difference was in placing line 5 together with lines 1 and 8 by NJ, while placing it separate from all other lines by UPGMA), so only results for the UPGMA algorithm are shown. Trees obtained for the two chromosomes also were nearly identical (Figure 7).

Figure 7.—

Phylogenetic trees based on marker allele frequencies for chromosome 1 (top) and chromosome 4 (bottom). Trees were obtained using the UPGMA algorithm.

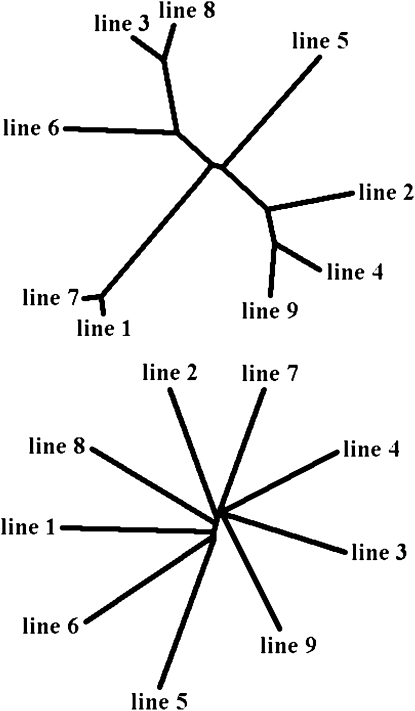
Phylogenetic trees based on LD correlations between lines for pairs of markers within 500 kb (Figure 8, top) had topologies that were very similar to those obtained from allele frequencies. In contrast, trees based on nonsyntenic marker pairs had very different topologies without much apparent structure (Figure 8, bottom). Differences in topology were quantified by the partition metric of Penny and Hendy (1985), a measure that can take values between 0 and 2n − 6, where n is the number of lines; the lower values correspond to more similar topologies. This metric took values between 0 and 4 for pairs of trees based on allele frequencies or short-distance (<500 kb) LD correlations. In general, based on this metric, the syntenic correlation-based trees were as similar to allele-based trees as correlation-based trees from different methods were to each other. For pairs of trees that include at least one nonsyntenic correlation-based tree, however, the metric took values between 9 and 12, close to their maximum value, showing that nonsyntenic trees were very dissimilar to both allele-based and syntenic correlation-based trees and to each other. Also, while nonsyntenic trees held little information on line relationships, all other phylogenetic trees matched the known breeding history of the lines very well.

Figure 8.—

Phylogenetic trees based on covariances of LD estimated by r between lines for pairs of markers within 500 kb (top) and for nonsyntenic pairs (bottom). Trees were obtained using the UPGMA algorithm.

DISCUSSION

We examined patterns of LD in nine commercial breeding lines of broiler chickens of one major breeding organization. Our main findings are that there is widespread nonrandom LD that, however, extends over shorter distances than previously reported in livestock. This LD is consistent across closely related lines and the consistency of LD is directly related to the degree of relationship between lines.

We expect the chicken populations we analyzed to be representative of breeding populations in chickens and other domestic animal species because of similar small effective population sizes and sources of LD (i.e., mainly drift). The lines used for this study may, however, be more related than different breeds of pigs or cattle. Nevertheless, the main conclusions are expected to still apply for these species if the breeds considered have similar allele frequencies. Although results were based on data from two chicken chromosomes, the consistency of results for these two chromosomes suggests that results are representative for other chicken chromosomes in these populations. The results were also found to be consistent between analyses based on the 6K and the 3K panel, indicating that results were independent of the panel used, as expected when SNPs are neutral and most LD is generated by drift.

Previous studies in other animal species (cattle, pigs, sheep) and chicken found LD to extend over large distances, with D′ having an average value of 0.5 for markers <5 cM apart in cattle (Farnir et al. 2000) and χ²′ > 0.5 in 33–34% of marker pairs <5 cM apart and >0.8 in 15–23% of such marker pairs (Heifetz et al. 2005). Both studies mentioned here, however, used microsatellites instead of SNPs and a different statistic (D′ and χ²′ instead of r²) from that in our study. The extent of LD in the populations we studied was much more limited, with only 6% of markers within 5 cM having > 0.5 and only 2% with > 0.8. The lower levels of LD in our study as compared to studies that measured LD by D′ or χ²′ based on multiallelic markers can partially be explained by the known upward bias of D′ (Zhao et al. 2005) and the recently demonstrated upward bias of χ²′ when using multiallelic markers to estimate LD between SNP markers (Zhao et al. 2007). A study of LD between SNPs in Holstein cattle found that 30% of > 0.2 occurred for marker pairs that were >15 cM apart (Spelman and Coppieters 2006), assuming 1.5 cM/Mb for bovine chromosome 1. Correcting for sample size (n = 40), an observed of 0.2 is equivalent to an underlying of 0.175. In the current study, for which sample-size correction was not needed because n > 190, only 5% of > 0.175 occurred when the distance was >15 cM. Thus, the level of LD in the chicken breeding lines we studied appears to be lower than that in Holstein cattle, probably due to differences in historical population structure. The study in cattle also found a larger percentage of markers with high maximum but this difference is largely due to the very high proportion of markers with = 1 (>30%) found in cattle, the probable result of pervasive marker clustering in the SNP panel used in the cattle study (MacLeod et al. 2006). Other sources of disparities could be the differences in average marker densities and in the MAF threshold used.

In conclusion, although we observed lower levels of LD than in other populations, there was sufficient LD at small distances to enable detecting trait associations based on LD mapping, and a large proportion (25%) of markers had maximum LD >0.6. Also, the maximum LD SNP of a marker tended to be in its proximity: only 5–7% of SNPs with maximum LD ≥0.4 were >5 cM from the SNP with which they were in maximum LD. So, the SNP panel used here is suitable for association mapping. The less extensive LD observed in these compared to other livestock breeding populations that have been studied will result in greater ability to fine map QTL in these populations, although a higher density of markers will be required to achieve the same power to detect QTL. The SNPs found to be associated with a trait in LD studies for this SNP panel and these populations are also likely to be in close proximity (within 5 cM) to a relevant QTL. A comparison of the distributions of LD for syntenic and nonsyntenic markers, the latter being an empirical approximation of the null distribution, showed that for distances <20 cM the LD between syntenic markers was nonrandom and, therefore, likely to be conserved across generations.

We also attempted to find signatures of selection on the basis of differences in LD between regions of the chromosome (by fitting a linear model to residual LD after adjusting for distance based on the fitted Sved 1971 equation, i.e., the difference between observed and expected ) and on the basis of differences in F_st estimates at each marker position across the chromosomes. We did find a significant effect of chromosomal region on residual LD but were otherwise unsuccessful in finding patterns of LD that were consistent across methods.

We also studied the relationship between lines on the basis of correlations of LD between marker pairs for each pair of lines, using both and . A previous study on one beef and one dairy cattle breed found that the regression coefficient of in one breed on in the second decreased from 0.99 for markers within 10 kb (∼0.01 cM) to 0.06 for markers separated by 1000–2000 kb (∼1–2 cM) (Goddard et al. 2006), while the proportion of marker pairs for which had a different sign between the two breeds increased from 0.02 to 0.47 for the same intervals (Goddard et al. 2006). For LD at short distance (<500 kb or 1.4 cM), correlations ranged from 0.21 to 0.94 for and were slightly lower (0.13–0.90) when based on . All correlations were positive and several were quite high. The positive correlation suggests that LD created before divergence of the lines was not entirely broken down. However, the fact that the average correlation was substantially less than one also indicates that LD mapping methods fitting a single effect across all lines would have limited power, at least for the marker densities evaluated here. The fact that correlations for were on average higher than correlations for (average correlations were 0.52 for vs. 0.39 for ) shows that, at least in the lines used for this study, there was limited danger of opposite QTL alleles being associated with a given marker allele in different populations, which would be an obvious drawback for a selection program. The correlation between correlations based on and correlations based on was also high, at 0.81. So although the level of LD measured by for a pair of markers in one line was in general not a good predictor of LD in all other lines, for lines that were closely related, the LD tended to be in the same direction. This suggests that LD-based QTL detection methods should be applied across lines only if lines are closely related.

In general, the relationships between pairs of lines as described by correlations based on or were very similar to those derived from differences in allele frequencies between lines. Distance trees based on LD correlations and allele frequencies had similar topologies (Figures 7 and 8). We quantified the similarity of topologies by using partition metrics and found that, in general, correlation-based trees were at least as similar to allele-based trees as correlation-based trees from different methods were to each other. Together with the reduction of correlations with increased distance between markers, this supports the view that correlations are the result of common line history. The fact that LD correlation-based trees closely matched line relationships demonstrates that line history information can be used to assess the benefit of a joint analysis of marker data from different populations for the purpose of LD mapping.