Determination of the rate of the glutamate/glutamine cycle in the human brain by in vivo ¹³C NMR

Abstract

Recent ¹³C NMR studies in rat models have shown that the glutamate/glutamine cycle is highly active in the cerebral cortex and is coupled to incremental glucose oxidation in an ≈1:1 stoichiometry. To determine whether a high level of glutamatergic activity is present in human cortex, the rates of the tricarboxylic acid cycle, glutamine synthesis, and the glutamate/glutamine cycle were determined in the human occipital/parietal lobe at rest. During an infusion of [1-¹³C]-glucose, in vivo ¹³C NMR spectra were obtained of the time courses of label incorporation into [4-¹³C]-glutamate and [4-¹³C]-glutamine. Using a metabolic model we have validated in the rat, we calculated a total tricarboxylic acid cycle rate of 0.77 ± 0.07 μmol/min/g (mean ± SD, n = 6), a glucose oxidation rate of 0.39 ± 0.04 μmol/min/g, and a glutamate/glutamine cycle rate of 0.32 ± 0.05 μmol/min/g (mean ± SD, n = 6). In agreement with studies in rat cerebral cortex, the glutamate/glutamine cycle is a major metabolic flux in the resting human brain with a rate ≈80% of glucose oxidation.

The regulation of the release and re-uptake of the excitatory neurotransmitter glutamate is critical for mammalian brain function (1, 2). Glutamate released from the neuron may be cleared from the synaptic cleft through uptake by neuronal or glial glutamate transporters (3, 4). Recent studies have supported the glia as the major pathway of glutamate clearance (3). Neurons lack the enzymes necessary to perform net glutamate synthesis and depend on the glia to supply precursors. One of the pathways proposed for neuronal glutamate repletion is the glutamate/glutamine cycle (5–8). In this pathway, glutamate taken up by the glia is converted to glutamine by glutamine synthetase (9–11). Glutamine then is released to the extracellular fluid, where it is taken up by neurons and is converted back to glutamate by the action of phosphate-activated glutaminase (12).

The rate of the glutamate/glutamine cycle has been controversial because of difficulties in performing measurements in the living brain. The prevailing belief has been that the glutamate/glutamine cycle is a minor metabolic flux relative to total cellular glutamate metabolism. This view is largely based on the small size of the vesicular glutamate pool compared with other cellular glutamate pools (13, 14). Additional evidence comes from the low flux of isotope from [1-¹³C] glucose into glutamine in studies of brain slices (15).

We have demonstrated that in vivo ¹³C NMR may be used to measure the rate of glutamine labeling (16, 17) from [1-¹³C] glucose in human occipital/parietal cortex. These and subsequent studies (18) demonstrated that, in contrast with results from nonactivated brain slices (15), glutamine labeling is rapid. However, the rate of the glutamate/glutamine cycle was not uniquely determined from these first experiments because of the inability to distinguish the glutamate/glutamine cycle from other sources of glutamine labeling. The major alternate pathway of brain glutamine metabolism is for the removal of cytosolic ammonia (10, 19). In addition to ammonia removal, several other pathways have been proposed as being significant (10, 15) sources of glutamine labeling.

To use in vivo ¹³C NMR to evaluate the glutamate/glutamine cycle rate, we have developed a metabolic model for separating the pathways of glutamine synthesis (20, 21). In this model, the rate of glutamine synthesis for ammonia removal was shown by mass balance to be equal to the rate of anaplerosis at steady state. The model was tested by comparing the rates of the glutamate/glutamine cycle and anaplerotic glutamine synthesis calculated from ¹³C and ¹⁵N NMR experiments under conditions designed to selectively alter the rates of the glutamate/glutamine cycle and ammonia removal (20–23). The important finding of these studies is that, at physiological plasma ammonia, the rate of the glutamate/glutamine cycle far exceeds the rates of other pathways of glutamine synthesis (20, 21).

Label flow from [1-¹³C] glucose to [4-¹³C] glutamate has been shown (17) to measure the in vivo rate of glucose oxidation. Simultaneous measurements from [1-¹³C] glucose into the glutamate and glutamine pools showed that, in the rat, the rate of cortical glucose oxidation increased in a 1:1 molar ratio with the glutamate/glutamine cycle (22, 23). This ratio was consistent with the mechanism proposed by Magistretti and coworkers linking astrocytic glucose uptake stoichiometrically to glutamate neurotransmitter release (24). It extended this model by showing that, in the anaesthetized rat brain, this may be the major mechanism accounting for oxidative glucose consumption (23, 25).

The ability to measure the glutamate/glutamine cycle in human cerebral cortex has important implications in the study of human brain function. In the present study, we used in vivo ¹³C NMR spectroscopy during an infusion of [1-¹³C] glucose to measure glutamate and glutamine labeling in the human occipital/parietal cortex. By improving the sensitivity of ¹³C detection over our first observation of the flux (16) and by using the metabolic model that has been developed and validated in the rat brain (20–23), we have been able to distinguish the anaplerotic pathway of glutamine synthesis from the glutamate/glutamine cycle. These results demonstrate that the glutamate/glutamine cycle is a major metabolic flux in human cortex. Based on the model linking this flux with glucose uptake, this cycle accounts for 80% of glucose oxidation in the resting state.

METHODS

Subjects.

Six healthy subjects (age, 20–28 years old; body weight, 55–91 kg; five female, one male) were studied after written informed consent was obtained from the subjects using forms and procedures approved by the Yale Human Investigations Committee. Subjects were admitted to the Yale University-New Haven Hospital General Clinical Research Center the evening before the study and fasted from 9 p.m. At 6 a.m., an intravenous catheter was placed in an antecubital vein in each arm—one for infusions and the other for measurements of plasma glucose concentration and [1-¹³C] glucose enrichment.

Infusion Protocol.

At the start of the experiment, the plasma glucose concentration was increased to ≈11 mM by a prime continuous infusion of 99% [1-¹³C] glucose (Cambridge Isotope Laboratories, Cambridge, MA) (dextrose 1.1 M) and was kept at this concentration throughout the study with a variable infusion of 60% [1-¹³C] glucose (dextrose 1.1 M). To inhibit endogenous insulin secretion, somatostatin was infused at a rate of 0.1 μg/kg min, and basal insulin concentrations were established by infusing insulin (U-100 Humulin, Eli Lily) at a rate of 24 pmol/m² min. Plasma glucose concentration was measured every 5 min by using a Beckman Glucose Analyzer (Beckman Coulter). Blood samples for determination of plasma insulin, glucagon, and ¹³C enrichment were drawn at 0, 5, 10, and 30 min and thereafter every 30 min for the duration of the study. The plasma glucose fractional enrichments were measured by gas chromatography–mass spectrometry (26).

General in Vivo NMR Protocol.

Subjects were positioned supine on a patient bed in a 2.1 Tesla 1-m bore Oxford Magnet Technology (Oxford, U.K.) magnet with their head positioned in an adjustable holder so that the 8.5-cm ¹³C transceiver coil was subjacent to the occipital and parietal lobes. Spectra were obtained with an extensively modified Biospec AVANCE spectrometer (Bruker, Billerica, MA) with Oxford Magnet Technology shielded gradients and power supplies. The ¹H portion of the radiofrequency coil assembly consisted of two 13-cm circular coil loops arranged spatially to generate a quadrature field (27). Two sets of three-slice gradient echo images were obtained to select a 6- × 4- × 6-cm volume for ¹³C spectroscopy in the occipital and parietal lobes that was centered on the midline between the left and right hemispheres. The y dimension was parallel to the axis of the ¹³C coil. The B₀ field homogeneity in the selected volume was optimized by using the fastermap shimming routine (28) improved from the fastmap method (29). Decoupler power was calibrated based on a stimulated echo sequence, which generated a 1- × 1-cm y column profile through the center of the selected volume.

Localized Adiabatic ¹³C{¹H} Polarization Transfer.

The localization of the NMR signal was based on the three-dimensional ISIS technique (30). Hyperbolic secant pulses (31) (μ = 7) of 7-ms duration with a bandwidth of 3,850 Hz were used to localize a 6- × 4- × 6-cm volume. A spatially selective five-lobe sinc pulse was used to excite a 2-cm y slice followed by a crusher gradient (90%, 10 ms) to enhance surface lipid suppression. For adiabatic polarization transfer, ¹H magnetization first was excited and polarized with a segmented BIR4 90° pulse (32) on ¹H and a simultaneous adiabatic full-passage pulse on ¹³C to allow the formation of ¹H-¹³C one-bond antiphase spin state. An adiabatic half-passage pulse was applied simultaneously with the third segment of the BIR4 90° pulse to obtain heteronuclear polarization transfer. The transferred magnetization (¹H_z¹³C_y) then as rephased by a BIREF-1 pulse (33) on ¹³C and a simultaneous adiabatic full-passage pulse on ¹H. The basic adiabatic half-passage pulses for ¹H and ¹³C are 0.4-ms tanh/tan pulses reoptimized (34, 35) for the radiofrequency coil assembly used in this study. The interpulse delays of the adiabatic polarization transfer sequence were optimized empirically to be 1.35 ms/0.76 ms for the glutamate and glutamine methylene groups. WALTZ-16 decoupling was applied at 2.5 ppm at 15 watts for 187 ms. The recycle delay was set to ≈2 s to generate a 4.5-min block of 128 scans.

Quantitation of [4-¹³C] Glutamate and [4-¹³C] Glutamine.

The time course of the concentrations of [4-¹³C] glutamate and [4-¹³C] glutamine were obtained from the peak amplitudes of these resonances with a 4.5-min time resolution. The steady-state [4-¹³C] glutamate and [4-¹³C] glutamine resonance intensities for each study were obtained by averaging the intensities of the last seven steady-state data points in their time courses. Quantification of the total [4-¹³C] glutamate pool was based on the previously determined steady-state total [4-¹³C]-glutamate concentration corrected by the difference in plasma glucose fractional enrichments (17).

Metabolic Model and Calculations.

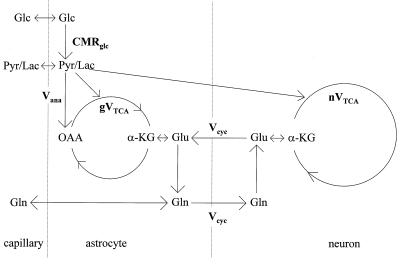
To calculate metabolic fluxes, the in vivo time courses of the [4-¹³C] glutamate and [4-¹³C] glutamine concentrations were fitted simultaneously with a two-compartment metabolic model, which is shown in Fig. 1 (20, 21, 23). As described in the equations below, label will enter the [4-¹³C] glutamine pool from both neuronal [4-¹³C] glutamate, which is transported into the glia, and directly from the glial TCA cycle coupled to the anaplerotic pathway. The anaplerotic flux is the only significant net flux from glial precursors into glutamine under steady-state conditions (20, 21, 23). The ability to distinguish labeling attributable to the glial TCA cycle from labeling attributable to the glutamate/glutamine cycle is based on ¹³C label from neuronal glutamate being delayed by the time required for the large neuronal glutamate pool to isotopically turnover. In contrast, label entering via the glial TCA cycle will rapidly be incorporated into the small glial [4-¹³C]-glutamate pool and will be converted into [4-¹³C]-glutamine without a significant lag.

Figure 1.

Schematic representation of a two-compartment modeling of glutamate/glutamine neurotransmitter cycling between astrocytes and neurons. CMR_glc, cerebral metabolic rate of glucose; V_ana, anaplerosis flux, gV_tca, glial tricarboxylic acid cycle flux, V_cyc, glutamate/glutamine cycling flux, nV_tca, neuronal tricarboxylic acid cycle flux.

Equations.

Glial pool. Based on metabolic steady-state considerations, the only net pathways of glutamine synthesis (V_gln) are the glutamate/glutamine cycle (V_cyc) and de novo glutamine synthesis by the anaplerotic pathway (V_ana):

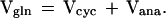1

The enrichment of the glial [4-¹³C] glutamate pool was calculated based on the assumption that the pool size was small enough to be approximated as instantaneously reaching isotopic steady state with the isotopic fluxes passing through the pool. Evidence for this assumption are immunocytochemistry studies (36) and studies that found that the enrichment in glutamine from infused ¹³N and ¹⁵N ammonia is several times greater than glutamate (19). The reversal of the normal product precursor relationship during ammonia fixation has been taken as evidence that the glial glutamate pool is much smaller than the glutamine pool and undergoes rapid isotopic turnover. The steady-state equation for the concentration of glial [4-¹³C]-glutamate ([Glu4^g*]) is given by

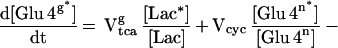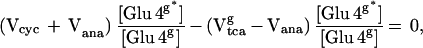2

where V_tca^g is the glial tricarboxylic acid cycle flux, V_cyc is the glutamate/glutamine cycle flux, and V_ana is the anaplerotic flux. The labeling of glial [4-¹³C] glutamine is described by

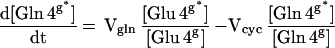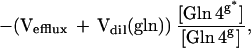3

where V_gln is the total glutamine synthesis rate, V_efflux is the net glutamine efflux rate, and V_dil (gln) is the rate of influx of unlabeled glutamine into the glia.

Neuronal pool.

The labeling of the neuronal [4-¹³C] glutamine pool was described by using the small pool steady-state assumption:

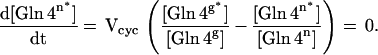4

The ¹³C labeling kinetics of the neuronal glutamate pool was described by

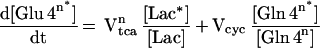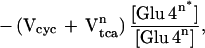5

where V_tcaⁿ is the neuronal tricarboxylic acid cycle flux.

Calculations.

By using the measured plasma glucose concentration and [1-¹³C] glucose fractional enrichment time courses for each study as input, the coupled differential equations [1–5] were solved using input values of V_ana, V_tca^g, V_tcaⁿ V_cyc, V_dil (lac), and V_dil (gln) to minimize the least-square difference between the calculated and measured [Glu4*] and [Gln4*]. The value of V_dil (lac) was determined from the measured fractional enrichment difference between [1-¹³C] glucose and [4-¹³C] glutamate at the end of the study. The value of V_dil (gln) was determined from the measured fractional enrichment difference between [4-¹³C] glutamate and [4-¹³C] glutamine.

A simulated annealing algorithm was used to obtain the values of the metabolic rates that provided the best fit to each data set. The algorithm used arbitrary initial flux rates with the constraint V_tca^g > V_ana as defined in Fig. 1. The total cerebral glutamate and glutamine concentrations in the measured volume were assumed to be 9.1 mM and 4.3 mM, respectively (16). To a first-order approximation, lactate, which has been measured by ¹H NMR to be 0.6 μmol/gm in concentration (37), and all other intermediate metabolites were assumed to have negligible pool sizes. As shown previously by Mason et al. (17), this assumption will have less than a 5% effect on the calculated rate of the neuronal TCA cycle under physiological conditions. For simulation of glucose transport, the Michaelis-Menten kinetic parameters determined by ¹³C NMR of K_m of 4.9 mM and V_max of 3.6 × the cerebral metabolic rate of glucose were used (38). The coupled differential equations were solved numerically by using the Euler method with a digital resolution of 0.1 s per point (39).

RESULTS

Plasma Glucose Concentration and ¹³C Fractional Enrichment.

The concentration and fractional enrichment of plasma [1-¹³C] glucose were rapidly raised by the glucose clamp to ≈11 mM and ≈60% and were held constant throughout the infusion. The constancy of the fractional enrichment simplified the metabolic modeling analysis. The mean and standard deviation of the plasma concentration and fractional enrichment 10 min after the start of the infusion was 11.2 ± 0.3 mM and 62.6% ± 4%, respectively.

In Vivo ¹³C NMR Spectra of Human Occipital/Parietal Cortex.

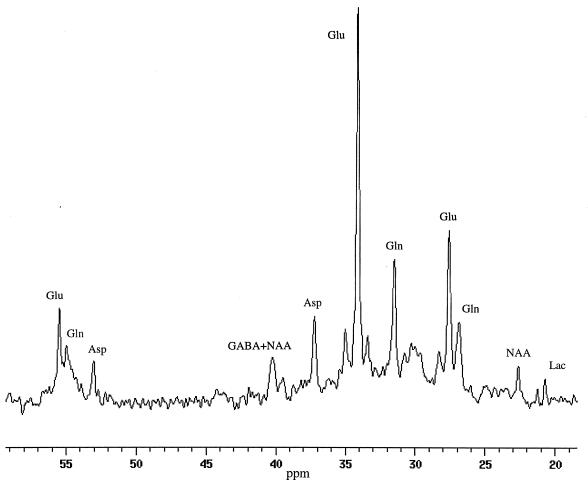
Fig. 2 shows a 67.5-min accumulation of spectra obtained 60 min after the start of the [1-¹³C] glucose infusion. The in vivo ¹³C half-height resonance linewidths from the selected volume were 2–2.5 Hz in the studies. In all subjects, the [4-¹³C]-glutamate at (34.2 ppm) was present in the first spectrum whereas there was an ≈10-min delay before the appearance of the resonance of [4-¹³C] glutamine (31.6 ppm). The time course of the well resolved resonance of [3-¹³C] glutamate at 28.7 ppm also was observed. The resonance of [3-¹³C] glutamine also was observed but was overlapped by the upfield sideband of the isotopomer [3-, 4-¹³C] glutamate. A >3-fold enhancement in sensitivity over our previous study at 2.1 Tesla field was achieved in these experiments because of the use of the adiabatic polarization transfer sequence. The improved sharpness of the localized volume provided by surface suppression eliminated contamination from the intense resonances of scalp lipids. Short TE brain macromolecule resonances (40) were reduced by the spin echo.

Figure 2.

In vivo ¹³C spectrum from the occipital/parietal lobes of a healthy volunteer using ¹H-localized adiabatic polarization transfer technique at 2.1 Tesla. The spectrum was an accumulation of 67.5 min of acquisition 60 min after the start of 1-¹³C-glucose infusion. Homonuclear peaks attributable to [3-, 4-¹³C]-glutamate were clearly resolved from the central [4-¹³C] glutamate and [3-¹³C] glutamate peaks. Labeled resonances are [4-¹³C]-glutamate (Glu4) and [4-¹³C]-glutamine (Gln4), [3-¹³C]-glutamate (Glu3), and [3-¹³C]-glutamine (Gln3), respectively. Other resonances present in the spectrum include [3-¹³C]-lactate at 21 ppm, the sum of the resonance of [2-¹³C]-GABA and the downfield resonance of the ¹³C-¹³C satellite of [4-¹³C]-glutamate at 35 ppm, the sum of the resonance of [4-¹³C]-GABA and N-acetyl aspartate at 41 ppm, and the resonance of [3-¹³C]-aspartate at 37 ppm.

Flux Calculations.

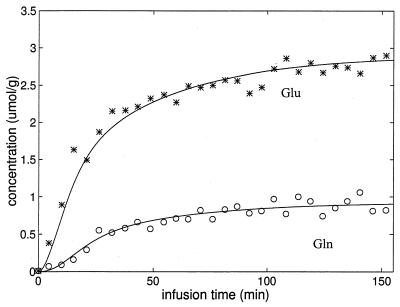
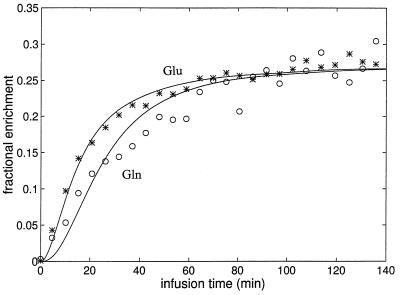
An example of the best fit using the model described above, of the time course of [4-¹³C] glutamate and [4-¹³C] glutamine for an individual study is shown in Fig. 3. The sum data for the six time courses expressed in terms of normalized ¹³C fractional enrichment and the best fit is shown in Fig. 4. In both the individual time course and the summed data, the fractional enrichment of [4-¹³C] glutamine clearly lags the fractional enrichment of [4-¹³C] glutamate, indicative of neuronal [4-¹³C]-glutamate being the main precursor. The best fit to the individual data sets gave a mean total TCA cycle rate of 0.77 ± 0.07 μmol/min/g (mean ± SD, n = 6) (which is a sum of neuronal TCA cycle rate of 0.71 ± 0.08, and the glial TCA cycle rate of 0.06 ± 0.02 μmol/min/g), a glutamate/glutamine cycle rate (V_cyc) of 0.32 ± 0.05 μmol/min/g, and a rate of anaplerotic glutamine synthesis (V_ana) of 0.04 ± 0.02 μmol/min/g. A higher isotopic dilution was required to fit the [4-¹³C]-glutamine time course based on the finding of its steady-state fractional enrichment being ≈26% lower than that of [4-¹³C]-glutamate. The rates obtained from individual studies are listed in Table 1. The rate of glucose oxidation, which was calculated from the total TCA cycle rate and the anaplerotic rate under the assumption that glucose is the only net precursor for brain oxidation, was 0.39 ± 0.04 μmol/min/g.

Figure 3.

A time course of the concentrations of [4-¹³C]-glutamate and [4-¹³C]-glutamine for a single subject. The fit of the two-compartment model shown in Fig. 1 to the data also is shown. Asterisks, glutamate; open circles, glutamine.

Figure 4.

The time course of the summed data of all six subjects for the fractional enrichments of [4-¹³C]-glutamate and [4-¹³C]-glutamine and the best fit of the two-compartment model. The enrichment of [4-¹³C]-glutamine is clearly seen to lag the enrichment of [4-¹³C]-glutamate, consistent with neuronal glutamate being the main precursor for glutamine synthesis via the glutamate/glutamine cycle. All fractional enrichments were normalized to that of [4-¹³C] glutamate. Asterisks, glutamate; open circles, glutamine.

Table 1.

Results of individual fits

Data set	Vtcan, μmol/min/g	Vtcag, μmol/min/g	Vcyc, μmol/min/g	Vana, μmol/min/g
1	0.83	0.02	0.25	0.02
2	0.81	0.05	0.35	0.03
3	0.63	0.06	0.39	0.02
4	0.67	0.09	0.32	0.06
5	0.70	0.06	0.32	0.05
6	0.64	0.06	0.30	0.05

DISCUSSION

The primary limitation in calculating the rate of the glutamate/glutamine cycle in previous isotopic labeling studies was the inability to distinguish between contributions to glutamine labeling from the glutamate/glutamine cycle and the glial TCA cycle. The metabolic model we have developed analyzes the ¹³C NMR data so as to distinguish these contributions based on the shape of the labeling curve of [4-¹³C] glutamine and glutamate. Label entering from the glial TCA cycle (which contains the flux from anaplerosis) will label the small glial glutamate precursor pool rapidly. In contrast, the fractional enrichment of [4-¹³C] glutamine derived from the glutamate/glutamine cycle will initially lag the fractional enrichment of neuronal [4-¹³C] glutamate, which is the label precursor. As shown in Figs. 3 and 4, there is a clear lag in the fractional enrichment of [4-¹³C] glutamine relative to [4-¹³C] glutamate. The model provided a good fit to all of the data sets and showed that the glutamate/glutamine cycle accounted for ≈90% of glutamine synthesis. The rate of the glutamate/glutamine cycle was ≈80% of total glucose oxidation.

The finding of a high rate of label incorporation into [4-¹³C] glutamine from neuronal [4-¹³C] glutamate implies a high rate of uptake and oxidation of [1-¹³C] glucose in the nerve terminal. In agreement with this prediction, there is considerable evidence for high metabolic activity in the nerve terminal, including deoxyglucose autoradiography studies of dorsal root ganglia and the visual cortex of monkeys (41–43). These studies locate the majority of neuronal glucose uptake induced by functional activity to the region of the synapse. It has been shown previously that almost all of the label entering the TCA cycle from [1-¹³C] glucose is incorporated into the neuronal [4-¹³C] glutamate pool through exchange (17).

The low rate of anaplerotic glutamine synthesis is in agreement with previous studies that have measured the uptake of anaplerotic precursors by arteriovenous difference (10, 44, 45). To maintain a steady-state glutamine concentration, one molecule of glutamine must leave the brain for every molecule synthesized by anaplerosis. There also must be a net inflow across the blood–brain barrier of one CO₂ molecule and two NH₄⁺ ions per glutamine molecule synthesized. These steady-state requirements lead to a stoichiometric relationship of anaplerotic glutamine synthesis (V_ana) with the net rates of glutamine efflux (V_efflux), CO₂ fixation (V_CO2), and NH₄⁺ fixation (V_NH4):

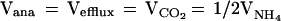6

Based on a review of several studies, the fixation of CO₂ into human brain is ≈0.03 μmol/g/min (44, 45), which is consistent with our rate of V_ana of 0.04 ± 0.02 μmol/g/min. The rate of ammonia influx in human brain under normammonemic conditions is below the accuracy of arteriovenous difference methods (10, 45). For glutamine efflux, the maximum rate is 0.02–0.04 μmol/min/g (45), which, within experimental uncertainties, is in agreement with the V_ana measurement.

The rapid labeling of [4-¹³C] glutamine from [1-¹³C] glucose shown in Figs. 3 and 4 is consistent with previous ¹³C NMR studies in human brain and animal brain (16, 18, 20, 22, 46, 47). The time course of both [4-¹³C] glutamate and [4-¹³C] glutamine are similar to those measured by ¹³C NMR in a previous study (16). The rate of the neuronal TCA cycle is in excellent agreement with previous ¹³C and ¹H-¹³C NMR studies of human brain (17, 46, 48) and measurements using positron-emission tomography and arteriovenous differences (for a comparison of the NMR measurement with other methods, see ref. 17). In combination with the metabolic model, the ≈3× higher sensitivity in the present study allowed the rate of the glutamate/glutamine cycle to be calculated. In a recent 4 Tesla NMR study by Gruetter et al. (18), time courses of [4-¹³C] glutamine and other metabolites were reported in subjects infused with [1-¹³C] glucose. In a preliminary analysis, a similar rate of the glutamate/glutamine cycle was calculated as in the present study. However, a severalfold higher rate of anaplerosis than in the present study was calculated by using the partially overlapped resonances of [2-¹³C] glutamate and glutamine. The discrepancy may reflect the difficulty of accurately deconvoluting these resonances because the high anaplerotic rate is inconsistent with both our present observations and previous arteriovenous balance studies of anaplerotic substrates (43–45).

The in vivo ¹³C NMR measurement may potentially be extended to study the rate of γ-aminobutyric acid (GABA) synthesis and the GABA/glutamine cycle (49, 50). GABA is the main inhibitory neurotransmitter and has been measured by in vivo ¹H and ¹³C NMR in animals and humans (16, 18, 51–53). The partially resolved resonance of [2-¹³C] GABA may be observed at 35 ppm in the summed spectrum of Fig. 2. Because of the entry of GABA into the glial TCA cycle at the succinyl-CoA step, the labeling kinetics of [4-¹³C] glutamine derived from GABA are indistinguishable from label entering through anaplerosis. From our data, the maximum estimate of the rate of the GABA/glutamine cycle, obtained by assuming that V_ana is entirely attributable to GABA, is 11% of the rate of glutamine synthesis. Based on the time course of the combined resonance of [2-¹³C] GABA and the [3-, 4-¹³C] glutamate isotopomer, the turnover time of GABA appears similar to that of [4-¹³C] glutamate, consistent with labeling studies in rat cortex (52).

The ≈80% ratio of the rate of the glutamate/glutamine cycle to glucose oxidation in human cerebral cortex is similar to the ratio found in a ¹³C NMR study of anaesthetized rats (22). In the rat cortex, it was further found that, above isoelectricity (under which V_cyc = 0 and glucose oxidation was reduced to ≈15% of control values), the rate of the glutamate/glutamine cycle increased in a 1:1 ratio with oxidative glucose metabolism at increasing levels of cortical electrical activity (22). These findings are consistent with a model in which glial glutamate uptake and cycling is coupled stoichiometrically to glial nonoxidative glucose uptake and subsequent transfer to the neuron as lactate for oxidation (24, 25). The agreement between the ratio of the glutamate/glutamine cycle to glucose oxidation in human and rat cortex suggests that this mechanism may account for the majority of total glucose oxidation in the human brain.

The measurement of the glutamate/glutamine cycle has implications for models of brain function both at the macroscopic level studied by functional magnetic resonance imaging and at the level of synaptic function and networks of neurons. Despite the lack of stimulation of the occipital and parietal cortices in the present study, the rate of the glutamate/glutamine cycle was close to the rate of glucose oxidation, indicating a high level of recruitment of neurons in these regions by internally generated processes. Some implications of a high level of internally generated neuronal activity on the interpretation of functional imaging studies have been recently discussed (54). On a neural network level, the information carried by glutamate neurotransmission depends on the coordinated time varying patterns of synaptic activity of a multitude of neurons. Because of its low volume and time resolution, the ¹³C NMR measurement is limited to the sum of glutamate release and cycling within a region of cortex. Within these limitations, the ¹³C NMR measurement provides an important boundary condition for the development of realistic neuronal models of excitatory neurotransmitter function in human sensory and cognitive processes.

ABBREVIATIONS

TCA

tricarboxylic acid

GABA

γ-aminobutyric acid