Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2007 Jan;16(1):125–134. doi: 10.1110/ps.062383807

BPPred: A Web-based computational tool for predicting biophysical parameters of proteins

Christian D Geierhaas 1,2, Adrian A Nickson 1,2, Kresten Lindorff-Larsen 2, Jane Clarke 1,2, Michele Vendruscolo 2
PMCID: PMC2222837  PMID: 17123959

Abstract

We exploit the availability of recent experimental data on a variety of proteins to develop a Web-based prediction algorithm (BPPred) to calculate several biophysical parameters commonly used to describe the folding process. These parameters include the equilibrium m-values, the length of proteins, and the changes upon unfolding in the solvent-accessible surface area, in the heat capacity, and in the radius of gyration. We also show that the knowledge of any one of these quantities allows an estimate of the others to be obtained, and describe the confidence limits with which these estimations can be made. Furthermore, we discuss how the kinetic m-values, or the Beta Tanford values, may provide an estimate of the solvent-accessible surface area and the radius of gyration of the transition state for protein folding. Taken together, these results suggest that BPPred should represent a valuable tool for interpreting experimental measurements, as well as the results of molecular dynamics simulations.

Keywords: protein denaturation, urea, guanidine hydrochloride, guanidinium chloride, protein folding, m-values, SASA, radius of gyration, heat capacity, transition state, unfolded state, denatured state

The possibility of interpreting quantities readily measurable experimentally in terms of descriptors of protein strucure has contributed very significantly to our understanding of the folding process. In a seminal work, Myers et al. (1995) considered an earlier suggestion by Schellman (1978) and showed that the change in solvent-accessible surface area (ΔSASA) upon unfolding is related linearly to the experimental m D–N-value (Pace 1986), which describes how the stability ▵G D–N of the native state of a protein decreases linearly with the concentration of denaturant (Tanford 1968, 1970):

graphic file with name 125equ1.jpg

The relationship between m-values and ΔSASA is extremely useful because it gives important insights into the determinants of protein stability and the equilibrium properties of proteins. In order to establish such a relationship, however, one needs an estimate of the value of SASA of the unfolded state. Despite recent advances (Mok et al. 2005), it is still very challenging to measure SASA directly in the denatured state. Myers et al. (1995) derived it from a tripeptide model (Shrake and Rupley 1973; Rose et al. 1985; Miller et al. 1987; Lesser and Rose 1990); later it was shown that this procedure may overestimate it by ∼25% (Creamer et al. 1995, 1997).

In this study, we establish an approximate relationship between the changes in the radius of gyration (ΔR g) upon protein folding and the m-values. Such a relationship is useful as ΔR g is readily measurable experimentally by using small angle X-ray scattering (SAXS) (Lipman et al. 2003) or Förster resonance energy transfer (FRET) (Schuler et al. 2002). Moreover, since we can also show that a relationship exists between ΔR g and ΔSASA, we provide a method that in principle can provide an estimate of the latter independent from any model for the unfolded state.

Furthermore, we use the extensive body of experimental data that has become available since the original work of Myers et al. (1995) on the thermodynamics of protein unfolding to reanalyze a series of relationships between m-values, ΔSASA, ΔC p, and the number N of amino acids in the protein; we also present new relationships between these quantities and ΔR g. We show that knowledge of any of these variables can be used to estimate all the others and present appropriate equations for making these estimates. A Web-based tool that allows users to use the equations that are presented here was developed, BioPhysical PREDictions (BPPred, http://www-clarke.ch.cam.ac.uk). In addition to estimating several biophysical parameters for any given protein, the results are also visualized graphically, as is illustrated below. For example, if two properties are known, for example, the chain length N and the equilibrium m-value, their values can be entered through a Web-based interface and both the predicted and the actual properties are compared graphically against the values available for the other proteins present in the database. The BPPred Web server therefore enables users to verify whether any unusual behavior is displayed by a particular protein upon unfolding, for example, as a consequence of the presence of disulfide bridges.

A further motivation for the present study is given by the current challenge in protein folding to benchmark simulation against experiment (Dinner et al. 2000; Vendruscolo and Paci 2003; Sato et al. 2004). We have been particularly interested in using experimentally derived restraints to determine structures of transition states and other transient species on folding pathways. Transition state structures can be derived from restrained molecular dynamics using experimental Φ-values as restraints (Vendruscolo et al. 2001; Paci et al. 2002, 2003; Geierhaas et al. 2004), or extracted from molecular dynamics unfolding simulations at high temperatures (Daggett 2002; Gsponer and Caflisch 2002; Beck and Daggett 2004). In this case, S- or Φ-values calculated for the resulting structures are compared to experimental Φ-values to validate the results of the simulations (Daggett et al. 1996).

Another experimental parameter that reports on the properties of transition states is the Beta Tanford value (β T), which is the ratio of equilibrium and kinetic m-values:

graphic file with name 125equ2.jpg

β T is commonly used to infer the ΔSASA between the denatured state and the transition state (Vendruscolo and Dobson 2005). We show here that relationships between β T, ΔSASA, and ΔR g can be used to verify the overall structural properties of transition state structures or, alternatively, β T might provide an additional experimental restraint for simulations.

Results and Discussion

Database

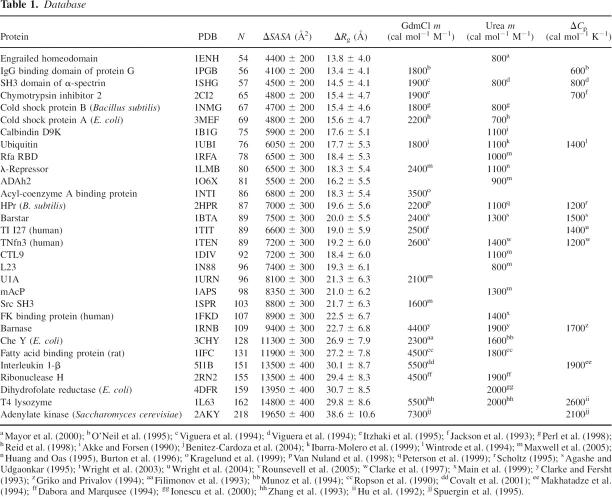
We compiled a database that includes experimental measurements of m-values in GdmCl and urea for a set of 30 disulfide-free, two-state proteins (see Table 1), which included several of the 22 proteins with similar characteristics considered by Myers et al. (1995). We used molecular dynamics (MD) simulations to calculate changes upon unfolding in structural properties (ΔR g and ΔSASA) of these proteins in order to assess their relationship to the corresponding experimental quantities. Simulations were carried out using the CHARMM 19 force field (Brooks et al. 1983) at 573 K and excluded volume interactions, following a procedure similar to that described by Dedmon et al. (2005) and Kristjansdottir et al. (2005), in which only the repulsive part of the Lennard-Jones potential was used in the molecular dynamics simulations. Each protein was simulated for 100 nsec, and usually the protein was already unfolded within the first few nanoseconds. The results of the MD simulations are, within the statistical errors, in agreement with the experimental values of ΔR g (Millett et al. 2002; Kohn et al. 2004) in the cases in which the latter are available (Fig. 1A).

Table 1.

Database

graphic file with name 125tbl1.jpg

Open in a new tab

Figure 1.

Figure 1.

Open in a new tab

(A) Correlation between the change in radius of gyration upon unfolding (ΔR g) and N for the 32 proteins in Table 1. The red line represents the nonlinear fit of ΔR g to N (Flory 1988). For comparison, experimental values of ΔR g are indicated with green circles; data for protein G, ubiquitin, Che Y, mACP, and DHFR (Millett et al. 2002; Kohn et al. 2004). (B) Correlation between the change in solvent-accessible surface area (ΔSASA) and the number of residues N (Myers et al. 1995). Solid lines are the linear fits, and dashed lines represent the statistical deviation, estimated using the jackknife method (Miller 1974).

Reassessment of the relationships between equilibrium m-values, ΔC p, ΔSASA, and N

Equilibrium m-values are related to the changes in heat capacity (ΔC p) upon unfolding (Livingstone et al. 1991; Spolar et al. 1992; Myers et al. 1995). Myers et al. (1995) also showed that the m-values are correlated linearly with ΔSASA, ΔC p, and N. We have reassessed here these relationships by considering the new data that have become available since the work of Myers et al. (1995). In Figure 1B, we present the scatterplot between ΔSASA and N for the database of 30 proteins that we considered. The existence of such a strong correlation enables us to estimate ΔSASA from N:

graphic file with name 125equ3.jpg

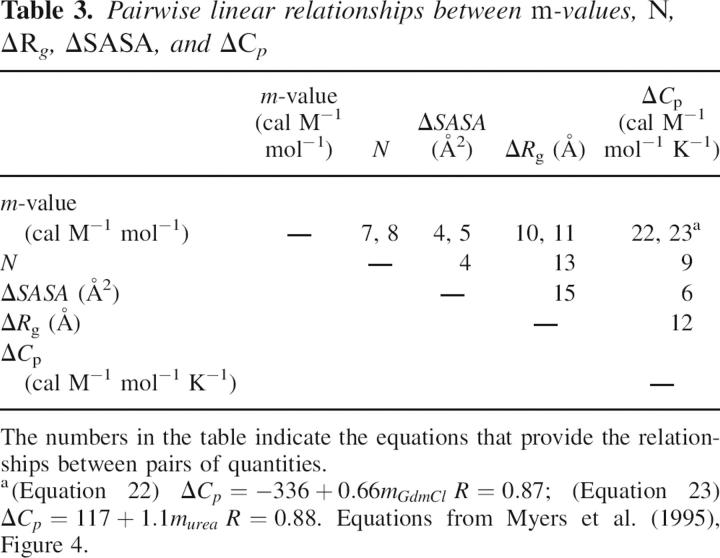
The correlations for GdmCl and urea m-values with ΔSASA (Myers et al. 1995) are shown in Figure 2, A and B, respectively, for our database of 30 proteins. The linear fits are given by, respectively,

Figure 2.

Figure 2.

Open in a new tab

Correlation between ΔSASA and (A) GdmCl equilibrium m-values, (B) urea equilibrium m-values, and (C) ΔC p. The solid line is the linear fit, and the dashed lines represent the statistical deviation, estimated using the jackknife method (Miller 1974).

graphic file with name 125equ4.jpg
graphic file with name 125equ5.jpg

The slope is ∼2.7 times as large for GdmCl as for urea, in agreement with the fact that GdmCl is a stronger denaturant than urea (Myers et al. 1995).

Figure 2C shows the linear fit of the change in heat capacity upon unfolding with ΔSASA:

graphic file with name 125equ6.jpg

This equation can be used to estimate ΔC p from the change in solvent-accessible surface area.

Therefore, all the relationships that Myers et al. (1995) observed for ΔSASA estimated using the glycine-tripeptide model (Shrake and Rupley 1973; Rose et al. 1985; Miller et al. 1987; Lesser and Rose 1990) are also valid if the change in solvent-accessible surface area is calculated from the present molecular dynamics simulations. These equations can be used to quantify, for example, ΔSASA from m-values, and thus determine the SASA of the denatured state of a protein, since the SASA of the native state can be determined from the native structure.

Additional relationships between N, m-value, and ΔC p

In addition to the correlations determined by Myers et al. (1995), we also analyzed the correlations between N, m-values, and ΔC p. We thus defined the following relationships (Fig. 3A, Equation 7; Fig. 3B, Equation 8; Fig. 3C, Equation 9):

Figure 3.

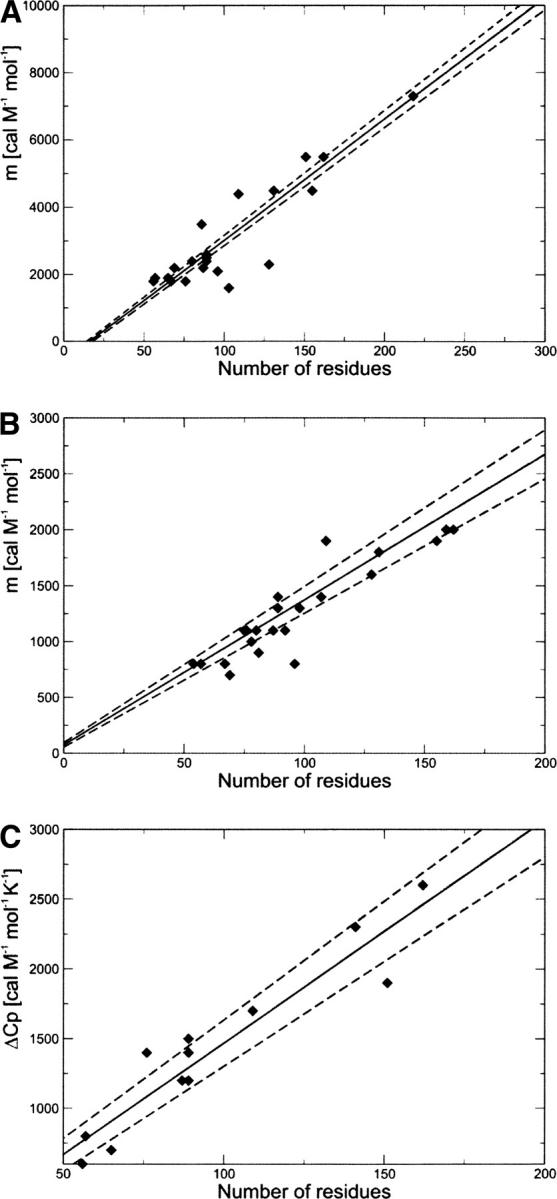
Figure 3.

Open in a new tab

Correlation between the chain length N and (A) GdmCl equilibrium m-values, (B) urea equilibrium m-values, and (C) ΔC p. These relations can be used to estimate m-values and ΔC p from N. The solid line is the linear fit, and the dashed lines represent the statistical deviation, estimated using the jackknife method (Miller 1974).

graphic file with name 125equ7.jpg
graphic file with name 125equ8.jpg
graphic file with name 125equ9.jpg

Relationships involving ΔR g

We investigated whether the correlations provided by Myers et al. (1995) for ΔSASA are also valid for ΔR g. The correlation for the proteins in Table 1 between GdmCl and urea m-values and the change of R g is shown in Figure 4, A and B:

Figure 4.

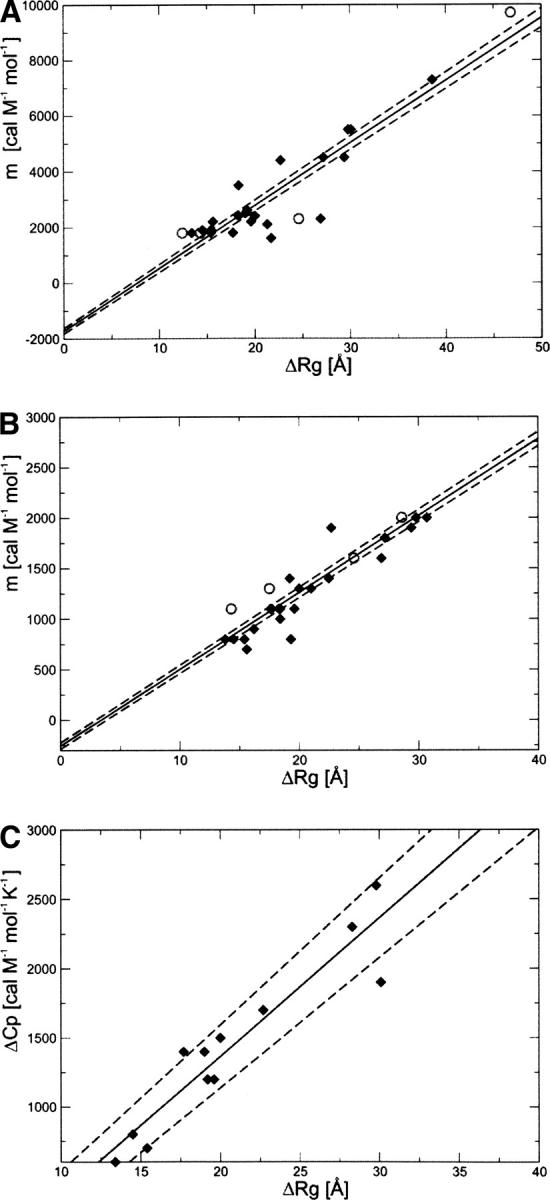
Figure 4.

Open in a new tab

Correlation between ΔR g and (A) GdmCl equilibrium m-values, (B) urea equilibrium m-values, and (C) ΔC p. The solid line is the linear fit, and the dashed lines represent the statistical deviation, estimated using the jackknife method (Miller 1974). For comparison, we have also included the experimental values of ΔR g for protein G, ubiquitin, Che Y, mACP, DHFR, and yPGK (open circles in A and B) (data from Millett et al. 2002).

graphic file with name 125equ10.jpg
graphic file with name 125equ11.jpg

The knowledge of m-values (GdmCl or urea) can thus be used to estimate the values of ΔR g by inverting these relationships. The slope of the linear regression is about three times larger for GdmCl than for urea (225 ± 5 cal mol−1 M−1 Å−1 compared to 76 ± 1 cal mol−1 M−1 Å−1), again reflecting the fact that GdmCl is a stronger denaturant than urea (Myers et al. 1995).

Although the correlation between m-values and ΔR g is statistically significant, there are considerable deviations for proteins with a similar number of residues or a similar ΔR g. The major outliers for GdmCl are src SH3 and CheY (Escherichia coli), and for urea, barnase. These deviations can be attributed to the presence of residual structure in the denatured state. For example, barnase has been shown to exhibit residual structure in the denatured state (Bond et al. 1997). The value of the total charge of the protein can also affect the value of ΔR g. A highly charged protein will be more expanded in the unfolded state, compared to a neutral protein because of electrostatic repulsions. These effects are a likely reason for the observed pH dependence of the m-values for RNase A, RNase T1, and barnase (Pace et al. 1990, 1992). Electrostatic effects can be influenced by GdmCl, which is dissociated in solution (Monera et al. 1994). The comparison of m-values and ΔR g values represents therefore a useful tool for detecting persistent residual structure in the denatured state of proteins.

Furthermore, we find a linear correlation between ΔR g and ΔC p (Fig. 4C):

graphic file with name 125equ12.jpg

Therefore, the change in heat capacity and the m-values does not only correlate to the amount of buried surface that is exposed during unfolding but also to the expansion of the molecule.

We find that N also correlates with ΔR g (Fig. 1A). Therefore, an estimate for ΔR g of a given protein with N residues can be obtained from

graphic file with name 125equ13.jpg

Kohn et al. (2004) and Millett et al. (2002) recently presented an extensive analysis of chemically and thermally unfolded proteins. They showed that the R g of unfolded proteins can be related to N by using a random-coil model (Flory 1988):

graphic file with name 125equ14.jpg

where R 0 is a constant related to the persistence length of the protein and ν is an exponent that describes how R g scales with the length N of the protein. By fitting data from a database of 28 chemically denatured, disulfide-free proteins, Kohn et al. (2004) obtained R 0 = 2.08 ± 0.19 Å and ν = 0.598 ± 0.029, in agreement with both the theoretical values of ν = 0.6 (Flory 1988) and of ν = 0.588 calculated for excluded-volume polymers in a good solvent (LeGuillou and Zinn-Justin 1977). In our case, a similar type of fitting provided values of R 0 = 2.07 and ν = 0.61, both compatible with the results of Kohn et al. The apparent existence of a linear relationship between ΔR g and N (Equation 13) is surprising as R g grows with N 0.6 in the unfolded state and with N 1/3 in the folded state. However, this result can be explained by the small range of values for N considered in our database, for which ΔR g can be approximated by a linear relationship (Fig. 1A).

It has been shown that the R g values of proteins represented by using a repulsive hard-sphere potential should obey the random-coil model (Creamer et al. 1995, 1997; Goldenberg 2003). These results, however, do not necessarily imply the complete absence of residual structure. Fitzkee and Rose (2004) showed that a “rigid-segment model,” in which known protein structures are partitioned alternately into rigid segments linked by individual flexible residues, gives values for R 0 and ν similar to those of Kohn et al. (2004) and Millett et al. (2002), despite the presence of native-like structural elements. The apparent discrepancy between the SAXS experimental results, which are consistent with a random-coil behavior, and other studies that indicate the presence of residual structure can be explained if the proportion of conformers exhibiting residual structure in the unfolded state is rather low (Lindorff-Larsen et al. 2004). These conformers may not affect the result of ensemble-averaged measurements, as the SAXS technique is most sensitive to large values of R g (Kohn et al. 2004). With these considerations in mind, we decided to use molecular dynamics simulations to estimate ΔR g in the cases in which experimental measurements are not yet available. The relations between the number of residues N and either ΔR g or ΔSASA (Equations 13 and 3, respectively) suggest a correlation between the change in radius of gyration and the change in surface-accessible area upon unfolding. Indeed, there is a significant linear correlation between ΔR g and ΔSASA (Fig. 5). As already mentioned, it is very difficult to measure ΔSASA of a protein directly; in contrast, ΔR g can be obtained from experiments (Millett et al. 2002; Kohn et al. 2004). We suggest that ΔSASA can be estimated from R g measurements according to the relationship

Figure 5.

Figure 5.

Open in a new tab

Correlation between ΔSASA and ΔR g. The solid line is the linear fit, and the dashed lines represent the statistical deviation, estimated using the jackknife method (Miller 1974).

graphic file with name 125equ15.jpg

Estimation of R g and SASA of the transition state for folding

One of the motivations for this work was to establish convenient criteria to benchmark the properties of transition states for protein folding obtained from molecular dynamics simulations. A kinetic m-value analysis not only provides information about the R g and SASA of the unfolded state, but also about the R g and SASA of the transition state for folding. The knowledge of equilibrium and kinetic m-values allows the value of RgTS of the transition state of the protein folding reaction to be estimated

graphic file with name 125equ16.jpg

where RgD is the radius of gyration in the denatured state, a r and b r are the constants of the linear correlation between m-values and R g (Equations 10 and 11), where we assumed that the same relationships hold for the transition state, and β T is the ratio of equilibrium and kinetic m-values (Equation 2). Given Equation 16, the radius of gyration of the transition state can be estimated from experimentally derived quantities, that is, if β T is known and RgD is estimated from Equation 10 or Equation 11. Alternatively, RgD can be estimated from molecular dynamics simulations.

The statistical error on the estimate for R g of the transition state can be expressed as

graphic file with name 125equ17.jpg

where δβ T is the experimental error on β T, δ RgN and δ RgD are the statistical deviations of the radius of gyration of the native state and of the denatured state, respectively, and δa r and δb r are the deviations of the constants in Equation 10 or 11.

An analogous relationship can be given for ΔSASA:

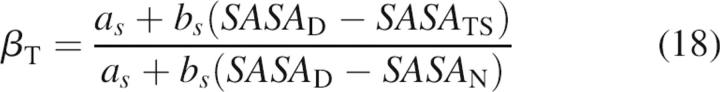graphic file with name 125equ18.jpg

where SASA D is the solvent-accessible surface area in the denatured state, a s and b s are the constants of the linear correlation (Equations 4 and 5), and SASA TS is the solvent-accessible surface area of the transition state for folding. The statistical error for the solvent-accessible surface area of the transition state is

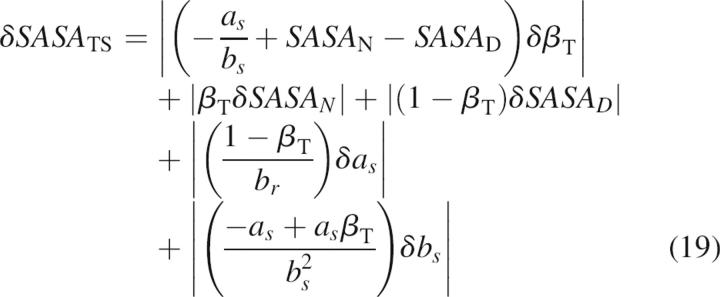graphic file with name 125equ19.jpg

where ΔSASA N and ΔSASA D are the statistical deviations of SASA of the native state and of the denatured state, respectively, and δa s and δa s are the deviations of the constants in Equation 4 or 5.

We have previously determined the structures of the transition states of several proteins using experimental Φ-values as restraints in molecular dynamics simulations (Vendruscolo et al. 2001; Paci et al. 2002, 2003; Geierhaas et al. 2004). We applied the relationships to estimate SASA and R g in the transition states of four proteins, CI2, TNfn3, mACP, and TI I27 (see Table 2). These proteins have been chosen because their β T values range from 0.6 to 0.95. Thus, the transition state structures range from being fairly heterogeneous to being very native-like. It is important to note that, although the values for a and b are different in Equations 16 and 18 depending on the choice of GdmCl or urea as denaturant to measure the m-values, the results for R g and SASA of the transition state are the same within the statistical error (Table 2). We compared the estimated values of R g and SASA of the transition state to those obtained from restrained simulations, finding a good agreement (Table 2) despite the fairly large statistical errors and the potential presence of residual structure in the denatured state, which was not accounted for in our simulations. Deviations from a spherical form might also influence the predictions of RgTS (Geierhaas et al. 2004).

Table 2.

Estimated values for ΔR g and SASA of the transition state for folding

graphic file with name 125tbl2.jpg

Open in a new tab

We also investigated whether it is possible to reduce the fairly large statistical error in the estimate of R g from β T by a simultaneous fitting of m-values, N, and ΔSASA or ΔR g:

graphic file with name 125equ20.jpg
graphic file with name 125equ21.jpg

The statistical errors are, however, too large in this case to allow reliable predictions (data not shown). A more extensive database than the one we used (Table 1), which should become available through future experimental studies, should make this type of prediction possible.

Conclusions

We have presented BPPred, a Web-based tool to predict m-values and several other descriptors of the folding process. These predictions exploit the good accuracy provided by linear relationships between the change in radius of gyration upon unfolding and the m-values from GdmCl and from urea unfolding. Such relationships are analogous to those determined by Myers et al. (1995) between the change in the surface-accessible area upon unfolding and the m-values. The latter result requires a model for the unfolded state, from which the corresponding surface area can be calculated, as its experimental measurement is challenging. Instead, R g can be readily measured experimentally and therefore the new relationships in principle do not depend on any assumption about unfolded states. However, as there is only a very limited number of proteins for which both ΔR g and m-values are known, we used in this study estimates obtained from molecular dynamics simulations. When the comparison is possible, the obtained values for ΔR g are compatible with experimental data within the statistical error. This relationship could be refitted and made completely independent from any particular model used to describe the unfolded state, when more systematic measurements of the R g of unfolded states become available. In addition, we have also reported a linear correlation between the change in radius of gyration and the change in solvent-accessible surface area upon unfolding. This relationship provides an estimate of ΔSASA from the values of ΔR g that can be obtained from experiments.

The linear correlations between m-values, the chain length N, and the change in R g, SASA, and C p upon unfolding that we discussed are summarized in Table 3. Such relationships can be used to estimate any one of these quantities from the knowledge of the other one. These relationships should represent valuable tools for interpreting experimental measurements in terms of the structural properties of the unfolded and of the transition states, as well as providing new ways of enhancing the powerful synergy between experiment and theory in protein folding that has been developed over the last several years.

Table 3.

Pairwise linear relationships between m-values, N, ΔR g, ΔSASA, and ΔC p

graphic file with name 125tbl3.jpg

Open in a new tab

Acknowledgments

C.D.G. and A.A.N. hold a Wellcome Trust Prize Studentship. J.C. is a Wellcome Trust Senior Research Fellow. M.V. is supported by the Royal Society and the Leverhulme Trust.

Footnotes

Reprint requests to: Michele Vendruscolo, Department of Chemistry, University of Cambridge, Lensfield Rd., Cambridge CB2 1EW, UK; e-mail: mv245@cam.ac.uk; fax: 44-1223-763848; or Jane Clarke, MRC Centre for Protein Engineering, Department of Chemistry, University of Cambridge, Lensfield Rd., Cambridge CB2 1EW, UK; e-mail: jc162@cam.ac.uk; fax: 44-1223-336362.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.062383807.

Abbreviations: SASA, Solvent-accessible surface area; ΔSASA, change in solvent-accessible surface area upon unfolding; C p, heat capacity; ΔC p, change in heat capacity upon unfolding; R g, radius of gyration; ΔR g, change in radius of gyration upon unfolding; GdmCl, guanidinium chloride; SAXS, small angle X-Ray scattering; FRET, Förster resonance energy transfer; TS, transition state; N, number of residues; R, Pearson correlation coefficient; β T, Beta Tanford.

References

  1. Agashe, V.R. and Udgaonkar, J.B. 1995. Thermodynamics of denaturation of barstar: Evidence for cold denaturation and evaluation of the interaction with guanidine hydrochloride. Biochemistry 34: 3286–3299. [DOI] [PubMed] [Google Scholar]
  2. Akke, M. and Forsen, S. 1990. Protein stability and electrostatic interactions between solvent exposed charged side chains. Proteins 8: 23–29. [DOI] [PubMed] [Google Scholar]
  3. Beck, D.A. and Daggett, V. 2004. Methods for molecular dynamics simulations of protein folding/unfolding in solution. Methods 34: 112–120. [DOI] [PubMed] [Google Scholar]
  4. Benitez-Cardoza, C.G., Stott, K., Hirshberg, M., Went, H.M., Woolfson, D.N., and Jackson, S.E. 2004. Exploring sequence/folding space: Folding studies on multiple hydrophobic core mutants of ubiquitin. Biochemistry 43: 5195–5203. [DOI] [PubMed] [Google Scholar]
  5. Best, R.B. and Vendruscolo, M. 2006. Structural interpretation of hydrogen exchange protection factors in proteins: Characterization of the native state fluctuations of CI2. Structure 14: 97–106. [DOI] [PubMed] [Google Scholar]
  6. Bond, C.J., Wong, K.B., Clarke, J., Fersht, A.R., and Daggett, V. 1997. Characterization of residual structure in the thermally denatured state of barnase by simulation and experiment: Description of the folding pathway. Proc. Natl. Acad. Sci. 94: 13409–13413. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brooks, B.R., Bruccoleri, R.E., Olafson, B.D., States, D.J., Swaminathan, S., and Karplus, M. 1983. CHARMM—A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4: 187–217. [Google Scholar]
  8. Burton, R.E., Huang, G.S., Daugherty, M.A., Fullbright, P.W., and Oas, T.G. 1996. Microsecond protein folding through a compact transition state. J. Mol. Biol. 263: 311–322. [DOI] [PubMed] [Google Scholar]
  9. Chiti, F., Taddei, N., White, P.M., Bucciantini, M., Magherini, F., Stefani, M., and Dobson, C.M. 1999. Mutational analysis of acylphosphatase suggests the importance of topology and contact order in protein folding. Nat. Struct. Biol. 6: 1005–1009. [DOI] [PubMed] [Google Scholar]
  10. Clarke, J. and Fersht, A.R. 1993. Engineered disulfide bonds as probes of the folding pathway of barnase: Increasing the stability of proteins against the rate of denaturation. Biochemistry 32: 4322–4329. [DOI] [PubMed] [Google Scholar]
  11. Clarke, J., Hamill, S.J., and Johnson, C.M. 1997. Folding and stability of a fibronectin type III domain of human tenascin. J. Mol. Biol. 270: 771–778. [DOI] [PubMed] [Google Scholar]
  12. Covalt Jr., J.C., Roy, M., and Jennings, P.A. 2001. Core and surface mutations affect folding kinetics, stability and cooperativity in IL-1 β: Does alteration in buried water play a role? J. Mol. Biol. 307: 657–669. [DOI] [PubMed] [Google Scholar]
  13. Creamer, T.P., Srinivasan, R., and Rose, G.D. 1995. Modelling unfolded states of peptides and proteins. Biochemistry 34: 16245–16250. [DOI] [PubMed] [Google Scholar]
  14. Creamer, T.P., Srinivasan, R., and Rose, G.D. 1997. Modeling unfolded states of proteins and peptides. II. Backbone solvent accessibility. Biochemistry 36: 2832–2835. [DOI] [PubMed] [Google Scholar]
  15. Dabora, J.M. and Marqusee, S. 1994. Equilibrium unfolding of Escherichia coli ribonuclease H: Characterization of a partially folded state. Protein Sci. 3: 1401–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Daggett, V. 2002. Molecular dynamics simulations of the protein unfolding/folding reaction. Acc. Chem. Res. 35: 422–429. [DOI] [PubMed] [Google Scholar]
  17. Daggett, V., Li, A., Itzhaki, L.S., Otzen, D.E., and Fersht, A.R. 1996. Structure of the transition state for folding of a protein derived from experiment and simulation. J. Mol. Biol. 257: 430–440. [DOI] [PubMed] [Google Scholar]
  18. Dedmon, M.M., Lindorff-Larsen, K., Christodoulou, J., Vendruscolo, M., and Dobson, C.M. 2005. Mapping long-range interactions in α-synuclein using spin-label NMR and ensemble molecular dynamics simulations. J. Am. Chem. Soc. 127: 476–477. [DOI] [PubMed] [Google Scholar]
  19. Dinner, A.R., Sali, A., Smith, L.J., Dobson, C.M., and Karplus, M. 2000. Understanding protein folding via free-energy surfaces from theory and experiment. Trends Biochem. Sci. 25: 331–339. [DOI] [PubMed] [Google Scholar]
  20. Filimonov, V.V., Prieto, J., Martinez, J.C., Bruix, M., Mateo, P.L., and Serrano, L. 1993. Thermodynamic analysis of the chemotactic protein from Escherichia coli, CheY. Biochemistry 32: 12906–12921. [DOI] [PubMed] [Google Scholar]
  21. Fitzkee, N.C. and Rose, G.D. 2004. Reassessing random-coil statistics in unfolded proteins. Proc. Natl. Acad. Sci. 101: 12497–12502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Flory, P.J. 1988. Statistical mechanics of chain molecules. Hanser/Gardner Publications, Inc., Cincinnati, Munich.
  23. Geierhaas, C.D., Paci, E., Vendruscolo, M., and Clarke, J. 2004. Comparison of the transition states for folding of two Ig-like proteins from different superfamilies. J. Mol. Biol. 343: 1111–1123. [DOI] [PubMed] [Google Scholar]
  24. Goldenberg, D.P. 2003. Computational simulation of the statistical properties of unfolded proteins. J. Mol. Biol. 326: 1615–1633. [DOI] [PubMed] [Google Scholar]
  25. Griko, Y.V. and Privalov, P.L. 1994. Thermodynamic puzzle of apomyoglobin unfolding. J. Mol. Biol. 235: 1318–1325. [DOI] [PubMed] [Google Scholar]
  26. Gsponer, J. and Caflisch, A. 2002. Molecular dynamics simulations of protein folding from the transition state. Proc. Natl. Acad. Sci. 99: 6719–6724. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hamill, S.J., Steward, A., and Clarke, J. 2000. The folding of an immunoglobulin-like Greek key protein is defined by a common-core nucleus and regions constrained by topology. J. Mol. Biol. 297: 165–178. [DOI] [PubMed] [Google Scholar]
  28. Hu, C.Q., Kitamura, S., Tanaka, A., and Sturtevant, J.M. 1992. Differential scanning calorimetric study of the thermal unfolding of mutant forms of phage T4 lysozyme. Biochemistry 31: 1643–1647. [DOI] [PubMed] [Google Scholar]
  29. Huang, G.S. and Oas, T.G. 1995. Structure and stability of monomeric λ repressor: NMR evidence for two-state folding. Biochemistry 34: 3884–3892. [DOI] [PubMed] [Google Scholar]
  30. Ibarra-Molero, B., Loladze, V.V., Makhatadze, G.I., and Sanchez-Ruiz, J.M. 1999. Thermal versus guanidine-induced unfolding of ubiquitin. An analysis in terms of the contributions from charge–charge interactions to protein stability. Biochemistry 38: 8138–8149. [DOI] [PubMed] [Google Scholar]
  31. Ionescu, R.M., Smith, V.F., O'Neill Jr., J.C., and Matthews, C.R. 2000. Multistate equilibrium unfolding of Escherichia coli dihydrofolate reductase: Thermodynamic and spectroscopic description of the native, intermediate, and unfolded ensembles. Biochemistry 39: 9540–9550. [DOI] [PubMed] [Google Scholar]
  32. Itzhaki, L.S., Otzen, D.E., and Fersht, A.R. 1995. The structure of the transition state for folding of chymotrypsin inhibitor 2 analysed by protein engineering methods: Evidence for a nucleation-condensation mechanism for protein folding. J. Mol. Biol. 254: 260–288. [DOI] [PubMed] [Google Scholar]
  33. Jackson, S.E., Moracci, M., elMasry, N., Johnson, C.M., and Fersht, A.R. 1993. Effect of cavity-creating mutations in the hydrophobic core of chymotrypsin inhibitor 2. Biochemistry 32: 11259–11269. [DOI] [PubMed] [Google Scholar]
  34. Kohn, J.E., Millett, I.S., Jacob, J., Zagrovic, B., Dillon, T.M., Cingel, N., Dothager, R.S., Seifert, S., Thiyagarajan, P., and Sosnick, T.R., et al. 2004. Random-coil behavior and the dimensions of chemically unfolded proteins. Proc. Natl. Acad. Sci. 101: 12491–12496. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Kragelund, B.B., Osmark, P., Neergaard, T.B., Schiodt, J., Kristiansen, K., Knudsen, J., and Poulsen, F.M. 1999. The formation of a native-like structure containing eight conserved hydrophobic residues is rate limiting in two-state protein folding of ACBP. Nat. Struct. Biol. 6: 594–601. [DOI] [PubMed] [Google Scholar]
  36. Kristjansdottir, A.G., Lindorff-Larsen, K., Fieber, W., Dobson, C.M., Vendruscolo, M., and Poulsen, F.M. 2005. Formation of native and non-native interactions in ensembles of denatured ACBP molecules from paramagnetic relaxation enhancement studies. J. Mol. Biol. 347: 1053–1062. [DOI] [PubMed] [Google Scholar]
  37. LeGuillou, J.C. and Zinn-Justin, J. 1977. Critical exponents for the n-vector model in three dimensions from field theory. Phys. Rev. Lett. 39: 95–98. [Google Scholar]
  38. Lesser, G.J. and Rose, G.D. 1990. Hydrophobicity of amino acid subgroups in proteins. Proteins 8: 6–13. [DOI] [PubMed] [Google Scholar]
  39. Lindorff-Larsen, K., Kristjansdottir, S., Teilum, K., Fieber, W., Dobson, C.M., Poulsen, F.M., and Vendruscolo, M. 2004. Determination of an ensemble of structures representing the denatured state of the bovine acyl-coenzyme a binding protein. J. Am. Chem. Soc. 126: 3291–3299. [DOI] [PubMed] [Google Scholar]
  40. Lipman, E.A., Schuler, B., Bakajin, O., and Eaton, W.A. 2003. Single-molecule measurement of protein folding kinetics. Science 301: 1233–1235. [DOI] [PubMed] [Google Scholar]
  41. Livingstone, J.R., Spolar, R.S., and Record, M.T. 1991. Contribution to the thermodynamics of protein folding from the reduction in water-accessible nonpolar surface-area. Biochemistry 30: 4237–4244. [DOI] [PubMed] [Google Scholar]
  42. Main, E.R.G., Fulton, K.F., and Jackson, S.E. 1999. Folding pathway of FKBP12 and characterisation of the transition state. J. Mol. Biol. 291: 429–444. [DOI] [PubMed] [Google Scholar]
  43. Makhatadze, G.I., Clore, G.M., Gronenborn, A.M., and Privalov, P.L. 1994. Thermodynamics of unfolding of the all β-sheet protein interleukin-1 β. Biochemistry 33: 9327–9332. [DOI] [PubMed] [Google Scholar]
  44. Maxwell, K.L., Wildes, D., Zarrine-Afsar, A., De Los Rios, M.A., Brown, A.G., Friel, C.T., Hedberg, L., Horng, J.C., Bona, D., and Miller, E.J., et al. 2005. Protein folding: Defining a “standard” set of experimental conditions and a preliminary kinetic data set of two-state proteins. Protein Sci. 14: 602–616. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Mayor, U., Johnson, C.M., Daggett, V., and Fersht, A.R. 2000. Protein folding and unfolding in microseconds to nanoseconds by experiment and simulation. Proc. Natl. Acad. Sci. 97: 13518–13522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Miller, R.G. 1974. The jackknife—A review. Biometrica 61: 1–15. [Google Scholar]
  47. Miller, S., Janin, J., Lesk, A.M., and Chothia, C. 1987. Interior and surface of monomeric proteins. J. Mol. Biol. 196: 641–656. [DOI] [PubMed] [Google Scholar]
  48. Millett, I.S., Doniach, S., and Plaxco, K.W. 2002. Toward a taxonomy of the denatured state: Small angle scattering studies of unfolded proteins. Adv. Protein Chem. 62: 241–262. [DOI] [PubMed] [Google Scholar]
  49. Mok, K.H., Nagashima, T., Day, L.J., Hore, P.J., and Dobson, C.M. 2005. Multiple subsets of side-chain packing in partially folded states of α-lactalbumins. Proc. Natl. Acad. Sci. 102: 8899–8904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Monera, O.D., Kay, C.M., and Hodges, R.S. 1994. Protein denaturation with guanidine hydrochloride or urea provides a different estimate of stability depending on the contributions of electrostatic interactions. Protein Sci. 3: 1984–1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Munoz, V., Lopez, E.M., Jager, M., and Serrano, L. 1994. Kinetic characterization of the chemotactic protein from Escherichia coli, CheY. Kinetic analysis of the inverse hydrophobic effect. Biochemistry 33: 5858–5866. [DOI] [PubMed] [Google Scholar]
  52. Myers, J.K., Pace, C.N., and Scholtz, J.M. 1995. Denaturant m values and heat capacity changes: Relation to changes in accessible surface areas of protein unfolding. Protein Sci. 4: 2138–2148. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. O'Neil, K.T., Hoess, R.H., Raleigh, D.P., and DeGrado, W.F. 1995. Thermodynamic genetics of the folding of the B1 immunoglobulin-binding domain from streptococcal protein G. Proteins 21: 11–21. [DOI] [PubMed] [Google Scholar]
  54. Pace, C.N. 1986. Determination and analysis of urea and guanidine hydrochloride denaturation curves. Methods Enzymol. 131: 266–280. [DOI] [PubMed] [Google Scholar]
  55. Pace, C.N., Laurents, D.V., and Thomson, J.A. 1990. pH dependance of the urea and guanidine hydrochloride denaturation of ribonuclease A and ribonuclease T1. Biochemistry 29: 2564–2572. [DOI] [PubMed] [Google Scholar]
  56. Pace, C.N., Laurents, D.V., and Erickson, R.E. 1992. Urea denaturation of barnase: pH dependence and characterization of the unfolded state. Biochemistry 31: 2728–2734. [DOI] [PubMed] [Google Scholar]
  57. Paci, E., Vendruscolo, M., Dobson, C.M., and Karplus, M. 2002. Determination of a transition state at atomic resolution from protein engineering data. J. Mol. Biol. 324: 151–163. [DOI] [PubMed] [Google Scholar]
  58. Paci, E., Clarke, J., Steward, A., Vendruscolo, M., and Karplus, M. 2003. Self-consistent determination of the transition state for protein folding: Application to a fibronectin type III domain. Proc. Natl. Acad. Sci. 100: 394–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Perl, D., Welker, C., Schindler, T., Schroder, K., Marahiel, M.A., Jaenicke, R., and Schmid, F.X. 1998. Conservation of rapid two-state folding in mesophilic, thermophilic and hyperthermophilic cold shock proteins. Nat. Struct. Biol. 5: 229–235. [DOI] [PubMed] [Google Scholar]
  60. Peterson, R.W., Nicholson, E.M., Thapar, R., Klevit, R.E., and Scholtz, J.M. 1999. Increased helix and protein stability through the introduction of a new tertiary hydrogen bond. J. Mol. Biol. 286: 1609–1619. [DOI] [PubMed] [Google Scholar]
  61. Reid, K.L., Rodriguez, H.M., Hillier, B.J., and Gregoret, L.M. 1998. Stability and folding properties of a model β-sheet protein, Escherichia coli CspA. Protein Sci. 7: 470–479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Ropson, I.J., Gordon, J.I., and Frieden, C. 1990. Folding of a predominantly β-structure protein: Rat intestinal fatty acid binding protein. Biochemistry 29: 9591–9599. [DOI] [PubMed] [Google Scholar]
  63. Rose, G.D., Geselowitz, A.R., Lesser, G.J., Lee, R.H., and Zehfus, M.H. 1985. Hydrophobicity of amino acid residues in globular proteins. Science 229: 834–838. [DOI] [PubMed] [Google Scholar]
  64. Rounsevell, R.W., Steward, A., and Clarke, J. 2005. Biophysical investigations of engineered polyproteins: Implications for force data. Biophys J. 88: 2022–2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  65. Sato, S., Religa, T.L., Daggett, V., and Fersht, A.R. 2004. Testing protein-folding simulations by experiment: B domain of protein A. Proc. Natl. Acad. Sci. 101: 6952–6956. [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Schellman, J.A. 1978. Solvent denaturation. Biopolymers 17: 1305–1322. [DOI] [PubMed] [Google Scholar]
  67. Scholtz, J.M. 1995. Conformational stability of HPr: The histidine-containing phosphocarrier protein from Bacillus subtilis . Protein Sci. 4: 35–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Schuler, B., Lipman, E.A., and Eaton, W.A. 2002. Probing the free-energy surface for protein folding with single-molecule fluorescence spectroscopy. Nature 419: 743–747. [DOI] [PubMed] [Google Scholar]
  69. Shrake, A. and Rupley, J.A. 1973. Environment and exposure to solvent of protein atoms. Lysozyme and insulin. J. Mol. Biol. 79: 351–371. [DOI] [PubMed] [Google Scholar]
  70. Spolar, R.S., Livingstone, J.R., and Record, M.T. 1992. Use of liquid-hydrocarbon and amide transfer data to estimate contributions to thermodynamic functions of protein folding from the removal of nonpolar and polar surface from water. Biochemistry 31: 3947–3955. [DOI] [PubMed] [Google Scholar]
  71. Spuergin, P., Abele, U., and Schulz, G.E. 1995. Stability, activity and structure of adenylate kinase mutants. Eur. J. Biochem. 231: 405–413. [DOI] [PubMed] [Google Scholar]
  72. Tanford, C. 1968. Protein denaturation. Adv. Protein Chem. 23: 121–282. [DOI] [PubMed] [Google Scholar]
  73. Tanford, C. 1970. Protein denaturation. C. Theoretical models for the mechanism of denaturation. Adv. Protein Chem. 24: 1–95. [PubMed] [Google Scholar]
  74. Van Nuland, N.A., Meijberg, W., Warner, J., Forge, V., Scheek, R.M., Robillard, G.T., and Dobson, C.M. 1998. Slow cooperative folding of a small globular protein HPr. Biochemistry 37: 622–637. [DOI] [PubMed] [Google Scholar]
  75. Vendruscolo, M. and Dobson, C.M. 2005. Towards complete descriptions of the free-energy landscapes of proteins. Philos. Transact. A Math. Phys. Eng. Sci. 363: 433–450. [DOI] [PubMed] [Google Scholar]
  76. Vendruscolo, M. and Paci, E. 2003. Protein folding: bringing theory and experiment closer together. Curr. Opin. Struct. Biol. 13: 82–87. [DOI] [PubMed] [Google Scholar]
  77. Vendruscolo, M., Paci, E., Dobson, C.M., and Karplus, M. 2001. Three key residues form a critical contact network in a protein folding transition state. Nature 409: 641–645. [DOI] [PubMed] [Google Scholar]
  78. Viguera, A.R., Martinez, J.C., Filimonov, V.V., Mateo, P.L., and Serrano, L. 1994. Thermodynamic and kinetic analysis of the SH3 domain of spectrin shows a two-state folding transition. Biochemistry 33: 2142–2150. [DOI] [PubMed] [Google Scholar]
  79. Wintrode, P.L., Makhatadze, G.I., and Privalov, P.L. 1994. Thermodynamics of ubiquitin unfolding. Proteins 18: 246–253. [DOI] [PubMed] [Google Scholar]
  80. Wright, C.F., Lindorff-Larsen, K., Randles, L.G., and Clarke, J. 2003. Parallel protein-unfolding pathways revealed and mapped. Nat. Struct. Biol. 10: 658–662. [DOI] [PubMed] [Google Scholar]
  81. Wright, C.F., Steward, A., and Clarke, J. 2004. Thermodynamic characterisation of two transition states along parallel protein folding pathways. J. Mol. Biol. 338: 445–451. [DOI] [PubMed] [Google Scholar]
  82. Zhang, T., Bertelsen, E., Benvegnu, D., and Alber, T. 1993. Circular permutation of T4 lysozyme. Biochemistry 32: 12311–12318. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES