Allosteric Voltage Gating of Potassium Channels II

Abstract

Large-conductance Ca²⁺-activated K⁺ channels can be activated by membrane voltage in the absence of Ca²⁺ binding, indicating that these channels contain an intrinsic voltage sensor. The properties of this voltage sensor and its relationship to channel activation were examined by studying gating charge movement from mSlo Ca²⁺-activated K⁺ channels in the virtual absence of Ca²⁺ (<1 nM). Charge movement was measured in response to voltage steps or sinusoidal voltage commands. The charge–voltage relationship (Q–V) is shallower and shifted to more negative voltages than the voltage-dependent open probability (G–V). Both ON and OFF gating currents evoked by brief (0.5-ms) voltage pulses appear to decay rapidly (τ_ON = 60 μs at +200 mV, τ_OFF = 16 μs at −80 mV). However, Q _OFF increases slowly with pulse duration, indicating that a large fraction of ON charge develops with a time course comparable to that of I _K activation. The slow onset of this gating charge prevents its detection as a component of I _gON, although it represents ∼40% of the total charge moved at +140 mV. The decay of I _gOFF is slowed after depolarizations that open mSlo channels. Yet, the majority of open channel charge relaxation is too rapid to be limited by channel closing. These results can be understood in terms of the allosteric voltage-gating scheme developed in the preceding paper (Horrigan, F.T., J. Cui, and R.W. Aldrich. 1999. J. Gen. Physiol. 114:277–304). The model contains five open (O) and five closed (C) states arranged in parallel, and the kinetic and steady-state properties of mSlo gating currents exhibit multiple components associated with C–C, O–O, and C–O transitions.

Introduction

Large-conductance Ca²⁺-activated K⁺ channels (BK channels)¹ are sensitive to membrane potential as well as intracellular calcium. Although the voltage dependence of these channels is weak compared with that of many purely voltage-gated K⁺ (K_v) channels (Barrett et al. 1982; Cui et al. 1997), voltage gating is likely to be of central mechanistic importance to BK channel function. Sequence similarity between the Slo family of BK channels and K_v channels, including the presence of a charged S4 domain, suggests that the basic structure of the BK channel may resemble that of K_v channels, and that Ca²⁺ acts to regulate the function of this voltage-dependent “core” (Cui et al. 1997; Meera et al. 1996; Wei et al. 1994). Consistent with this hypothesis, BK channels can be maximally activated by voltage in the absence of Ca²⁺ (Cox et al. 1997; Cui et al. 1997), gating currents are detected under these conditions (Stefani et al. 1997), and mutations in the S4 region alter the voltage dependence of activation (Diaz et al. 1998; Cui, J., and R.W. Aldrich, manuscript in preparation). Thus, BK channel voltage sensitivity reflects the action of an intrinsic voltage sensor, and Ca²⁺ is not required for channel opening. Ca²⁺ shifts many of the voltage-dependent parameters of BK channel gating to more negative voltages (Barrett et al. 1982; Cox et al. 1997). These results are consistent with a model in which Ca²⁺ binding allosterically regulates voltage-dependent channel activation (Cox et al. 1997; Cui et al. 1997). Such a mechanism implies that voltage-dependent gating plays a critical role in the response of BK channels to both Ca²⁺ and voltage.

In the preceding article (Horrigan et al. 1999), we examined the response of mSlo Ca²⁺-activated K⁺ channels to voltage by recording K⁺ current in the absence of Ca²⁺. The kinetic and steady-state properties of mSlo I _K indicate that the mechanism of voltage gating is complex. In response to a voltage step, I _K activates with an exponential time course after a brief, voltage-dependent delay. The exponential relaxation of I _K suggests that a rate-limiting step dominates channel activation. However, the delay indicates that rapid voltage-dependent transitions also exist in the activation pathway. The time constant of I _K relaxation (τ(I _K)) and steady-state open probability (P _o) both exhibit complex voltage dependencies that are inconsistent with many conventional sequential gating schemes. A particularly important finding is that τ(I _K) and P _o become less voltage dependent at very negative voltages. To account for these results, we proposed a voltage-gating scheme based on an allosteric mechanism.

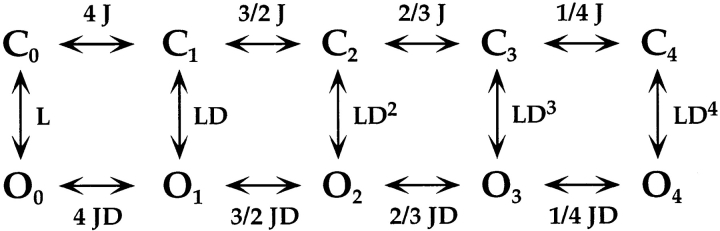
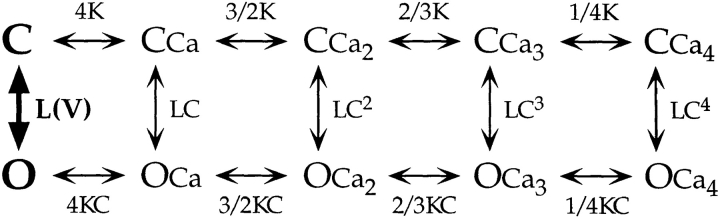
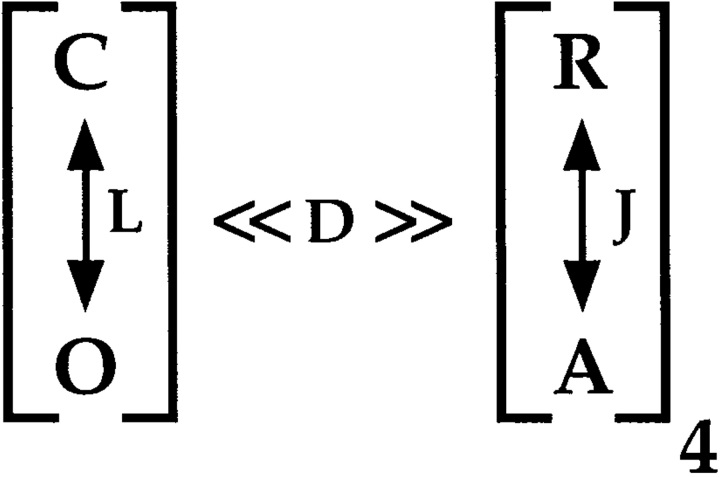
This diagram illustrates the idea that mSlo channels undergo a transition between a closed (C) and open (O) conformation, and that this transition is influenced allosterically by the state of four independent and identical voltage sensors (one for each subunit). We assume each voltage sensor can undergo a transition between a resting (R) and an activated (A) conformation, and the equilibrium constant for the C–O transition (L) increases by a constant factor (D) for each voltage sensor that is activated. Similarly, the equilibrium constant for voltage sensor activation (J) increases D-fold in favor of the activated state, when the channel opens. Therefore, the factor D embodies the allosteric interaction between voltage-sensor activation and channel opening. This mechanism results in a gating scheme (Fig. 1) that contains a parallel arrangement of open and closed states.

Scheme S1.

The horizontal transitions (C–C and O–O) reflect the activation or movement of voltage sensors while vertical (C–O) transitions represent channel opening. The closed and open conformations are each represented by five states, with subscripts (0–4) denoting the number of activated voltage sensors.

For this scheme to reproduce I _K, it is necessary that voltage-sensor activation is fast and accounts for most of the channel's voltage dependence while C–O transitions are slow and weakly voltage dependent (Horrigan et al. 1999). Closed-state transitions (C–C) must be fast and voltage dependent (z _J = 0.55 e per voltage sensor) to describe the delay in I _K activation. C–O transitions must be slow to limit the exponential relaxation of I _K. The weak voltage dependence of τ(I _K) and P _o at negative voltages implies that the charge associated with channel opening is small (z _L = 0.4 e). Finally, the equilibrium constant L is small (∼10⁻⁶) and the allosteric factor large (D = 17), equivalent to an interaction energy of 2.8 kT, to account for the shape of the P _o–V relationship in 0 Ca²⁺.

Such a model provides mechanistic insight and places constraints on the possible molecular events that link voltage-sensor movement and channel opening (Horrigan et al. 1999). The allosteric relationship between voltage-sensor activation and channel opening requires that the channels can open with any number of voltage sensors activated, including none. Furthermore, it requires that the allosteric transitions from closed to open alter the energetics of voltage-sensor movement such that voltage sensors, present in each subunit, are more easily activated when the channel is open. This effect is analogous to the change in ligand affinity that occurs between the T and R states in an allosteric ligand binding model (Monod et al. 1965).

Although the properties of mSlo I _K are consistent with the allosteric model, several aspects of the gating scheme are not tightly constrained by the ionic current data (Horrigan et al. 1999). Transitions among closed and open states (C–C, O–O) do not immediately alter the number of open channels and, therefore, are not observed directly as a change in I _K. Instead, these transitions contribute to the delay in I _K activation and to the complex voltage dependence of I _K kinetics and steady-state activation. However, any voltage-dependent transition must produce a movement of gating charge that can be detected as gating current (I _g). Gating current provides a direct assay of voltage-sensor movement (C–C, O–O transitions) and, therefore, constrains any voltage-dependent gating scheme. The allosteric model makes specific predictions about the kinetic and steady-state properties of gating charge movement and their relationship to I _K. Our experiments examine these predictions and provide a critical test of the model.

Our results are consistent with the assumption that mSlo voltage sensors move rapidly and independently while channels are open or closed. Measurements of the charge associated with voltage-sensor movement are in line with previous estimates based on the ionic current data. Our results also support the prediction that channel opening alters the kinetics of voltage-sensor movement. Finally, we show that some complex kinetic and steady-state properties of mSlo charge movement are reproduced by the proposed gating scheme. These include a large slow component of ON charge that is limited by the speed of channel opening, and three components of OFF charge reflecting C–C, O–O, and C–O transitions. The relationships between these components are consistent with the allosteric model and rule out many alternative schemes.

Materials and Methods

Channel Expression

Experiments were performed with the mbr5 clone of the mouse homologue of the Slo gene (mSlo), kindly provided by Dr. Larry Salkoff (Washington University School of Medicine, St. Louis, MO). The clone was modified to facilitate mutagenesis and was propagated and cRNA transcribed as described previously by Cox et al. 1997. Xenopus oocytes were injected with ∼50 ng of cRNA (50 nl, 1 ng/nl) 3–7 d before recording. mSlo was also subcloned into a mammalian expression vector (SRα; kindly provided by Dr. A.P. Braun, University of Calgary, Calgary, Alberta, Canada) containing the SV40 promoter. HEK 293 cells expressing the large T-antigen of the SV40 virus were cotransfected with mSlo and green fluorescent protein (GFP, as a marker) using LipofectAMINE (GIBCO BRL) 3 d before recording.

Electrophysiology

Currents were recorded using the patch clamp technique in the inside-out configuration (Hamill et al. 1981). Upon excision, patches were transferred to a separate chamber and washed with at least 20 vol of solution. The internal solution contained (in mM) 135 N-methyl-d-glucamine (NMDG)-MeSO₃, 6 NMDG-Cl, 20 HEPES. 40 μM (+)-18-crown-6-tetracarboxylic acid (18C6TA) was added to chelate contaminant Ba²⁺ (Diaz et al. 1996; Neyton 1996; Cox et al. 1997) unless otherwise indicated. In addition, “0 Ca²⁺” solutions contained 2 mM EGTA, reducing free Ca²⁺ to an estimated 0.8 nM in the presence of ∼10 μM contaminant Ca²⁺ (Cox et al. 1997). These solutions are considered Ca²⁺-free for the purposes of this study since [Ca²⁺]_i < 50 nM does not affect Slo channel activation (Cui et al. 1997; Meera et al. 1996). Solutions containing 60 μM Ca²⁺ were buffered with 1 mM HEDTA, and free Ca²⁺ was measured with a Ca²⁺ electrode (Orion Research, Inc.). The external (pipette) solution contained 125 tetraethylammonium (TEA)-MeSO₃, 2 TEA-Cl, 2 MgCl₂, 20 HEPES. pH was adjusted to 7.2. Solutions containing 110 mM K⁺ were as described in the preceding article (Horrigan et al. 1999). Experiments were performed at room temperature (20–22°C).

Measurement of rapid gating current in response to voltage pulses requires accurate subtraction of linear capacitive currents due to the electrode and cell membrane. Electrodes were pulled from thick-walled 1010 glass (World Precision Instruments) and coated with wax (sticky wax; Kerr) to minimize electrode capacitance (∼1 pF). Pipette access resistance (R _s) ranged from 0.7 to 1.5 MV in K-free solutions. Membrane capacitance ranged from 0.25 to 1 pF as determined by the responses to a −10 mV voltage step from −80 mV before and after sealing the electrode tip onto Sylgard (Dow Corning). Data were acquired with an Axopatch 200B amplifier (Axon Instruments, Inc.) in patch mode at a relatively low gain (1–2 mV/pA) to avoid saturation of capacitive transients in response to voltage steps that often exceeded 300 mV. Both the voltage command and current output were filtered at 20 kHz with 8-pole bessel filters (Frequency Devices, Inc.) to limit the speed of fast capacitive transients so that they could be accurately sampled and subtracted. The Axopatch's internal filter was set at 100 kHz. Currents were sampled at 100 kHz with a 16 bit A/D converter (ITC-16; Instrutech). I _g records were typically signal-averaged in response to at least eight voltage pulses, and a P/−4 protocol was used for leak subtraction (Armstrong and Bezanilla 1974) from a holding potential of −80 mV. A Macintosh-based computer system was used in combination with Pulse Control acquisition software (Herrington and Bookman 1995) and Igor Pro for graphing and data analysis (Wavemetrics, Inc.). A Levenberg-Marquardt algorithm was used to perform nonlinear least squares fits.

Simulations

Simulations were calculated at 1-μs intervals using a fifth order Runga-Kutta algorithm with adaptive step size (Press et al. 1992) implemented in Igor Pro (Wavemetrics, Inc.). Voltage commands and simulated currents were convolved with the impulse response of a 20 kHz 8-pole bessel filter to reproduce the experimental condition (see Horrigan et al. 1999).

Admittance Analysis

Admittance (Y) is defined by the expression Y = I/V where V and I represent the amplitude of the sinusoidal voltage command and resultant current at a specific frequency (ƒ). The admittance of a membrane (Y _m) is:

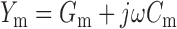1

where G _m and C _m are membrane conductance and capacitance, respectively (j=−1, ω = 2πƒ). G _m and C _m each represent the sum of a contribution from the lipid bilayer (G _b, C _b) and gating charge movement (G _g(V), C _g (V)) (see results):

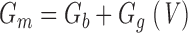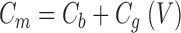The total admittance of the patch equivalent circuit is:

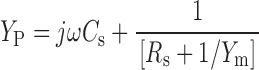2

where C _s is the stray capacitance of the electrode and holder, and R _s is the series resistance. Combining (1) and (2):

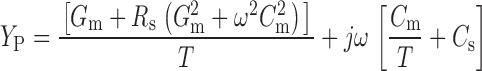3

where

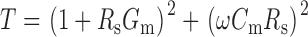Under typical experimental conditions [R _S ≅ 10⁶ , C _m ≅ 1 pF, G _m < 1 nS, ω = 5,451 (ƒ = 868 Hz)], T approaches unity, and this expression can be approximated:

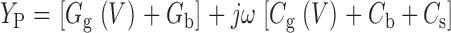4

Therefore, C _g(V) can be determined directly as the voltage-dependent component of Y _p/ω appearing at a phase angle of 90° relative to the command voltage.

For admittance measurements, the membrane was clamped with a sinusoidal voltage command (60 mV peak to peak) generated by the D/A converter of the ITC-16 interface at 18-μs intervals (at least eight samples per cycle of the sinusoid). The voltage command and current signal were both filtered at 20 kHz. Admittance was determined for each cycle of the sinusoid at 0° and 90° after correcting for phase shifts (ΔΦ) due to the filters and amplifier. These were determined at each frequency by measuring the admittance of an electrode in solution (Y = 1/R _S), which should appear at an angle of ΔΦ relative to the command voltage. DC current was determined as the mean current over each cycle of the sinusoid.

results

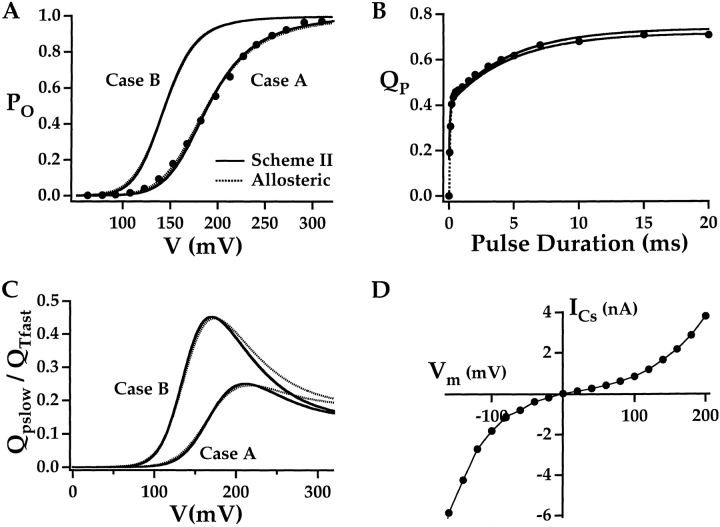
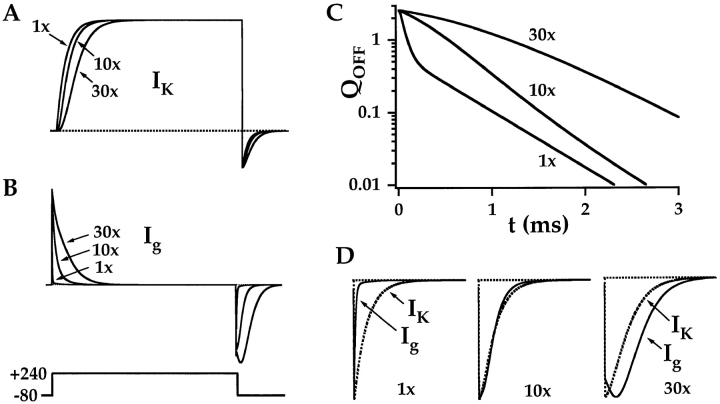
Gating charge movement was examined in excised macropatches from Xenopus oocytes and HEK 293 cells expressing the pore-forming α subunit of mSlo Ca²⁺-activated K channels. Several factors combine to make gating currents more difficult to measure for mSlo than for K_v channels such as Shaker. First, mSlo is less voltage dependent than Shaker, and the gating charge is correspondingly smaller. The steady-state G _K–V relationships for mSlo in 0 Ca²⁺ and Shaker can be approximately fit by Boltzmann functions with equivalent charges of 1 e (Cui et al. 1997) and 5.3e (Zagotta et al. 1994b), respectively. A similar difference is observed based on more sophisticated estimates of total gating charge per channel, ranging from 2.6 to 4.4 e for Slo channels (Horrigan et al. 1999; Stefani et al. 1997) and from 12 to 16e for Shaker (Aggarwal and MacKinnon 1996; Schoppa et al. 1992; Zagotta et al. 1994b). In addition to this 5-fold difference in charge, mSlo exhibits a single channel conductance roughly 10-fold greater than that of Shaker. Thus, the ratio of gating charge to ionic current is almost two orders of magnitude smaller for mSlo than for Shaker. Owing to this relationship, measurement of mSlo gating current (I _g) requires stringent conditions for eliminating I _K. For example, in this study, I _g was recorded in the presence of isotonic (125 mM) external TEA, to block the channel pore, even though internal and external solutions were nominally K⁺-free. Experiments performed in the absence of TEA appear to produce similar results (Stefani et al. 1997) but require extensive washing to assure that residual I _K is eliminated. Even when TEA was present at a concentration almost 1,000-fold higher than the K _i for mSlo block (K _i = 0.14 mM; Butler et al. 1993), I _g could not be recorded in the presence of normal internal K⁺ (110 mM) because I _K was not abolished. Finally, mSlo channels activate only at very positive voltages in 0 Ca²⁺ with a half-activation voltage of +190 mV for G _K (Cui et al. 1997; Horrigan et al. 1999). The high voltages and large voltage steps needed to activate these channels often proved problematic for leak-free recording of small gating currents.

Two approaches were used to measure mSlo gating charge movement. The first involved clamping the membrane with a sinusoidal voltage command and measuring gating charge as a voltage-dependent component of membrane capacitance using admittance analysis (Fernandez et al. 1982). The second involved conventional measurement of gating currents in response to voltage steps. Although the bulk of the analysis was performed using voltage steps, the admittance analysis is presented briefly first (see Fig. 1 and Fig. 2) to provide an initial characterization of mSlo charge movement and to demonstrate several necessary controls.

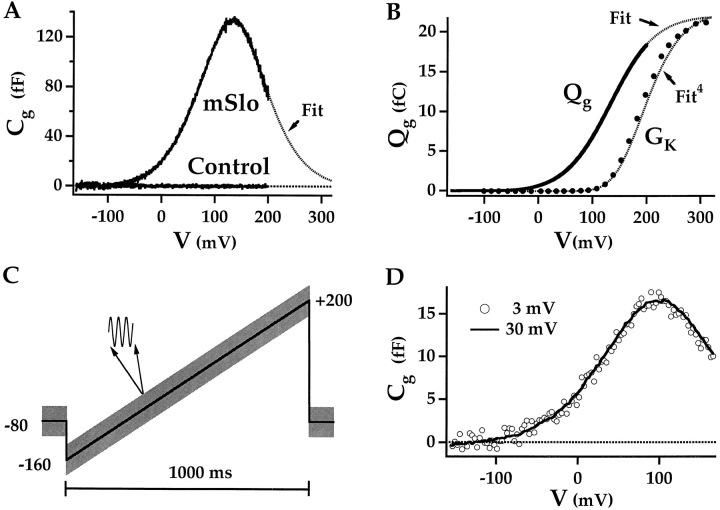
Figure 1.

mSlo gating capacitance. (A) Voltage-dependent membrane capacitance (C _g) is plotted versus voltage for patches excised from HEK 293 cells that expressed mSlo channels (mSlo) or were not transfected (control). Each trace represents the average response to two voltage ramps (see panel C). The baseline (C _g = 0) was set to the mean of C _m between −150 and −100 mV. The C _g–V relationship for mSlo is fit by the derivative of a Boltzmann function with respect to voltage (dashed line) with z = 0.59 e and V_h = 133 mV. (B) The Q_g–V relationship, determined by integrating the C _g–V, is fit by a Boltzmann function. The shape of the average G _K–V relationship (symbols; from Horrigan et al. 1999) can be approximated by raising the Q_g–V fit to the 4th power (Fit⁴). (C) The voltage protocol used to measure C _g in panel A consists of a 1-s voltage ramp from −160 to +200 mV superimposed with a sinusoidal command (30 mV amplitude, 868 Hz). Capacitance was determined for each period of the sinusoid. (D) C _g–V relationships obtained from channels expressed in a Xenopus oocyte using sinusoidal voltage amplitudes of 3 mV (symbols) or 30 mV (solid line) at 1,736 Hz are superimposable, indicating that sinwave amplitude does not effect the measurement. The 3 and 30 mV traces represent the average response to eight and four voltage ramps, respectively. Data are plotted at 3-mV intervals, representing the mean capacitance over eight periods of the sinusoid. The internal solution did not contain crown ether (18C6TA).

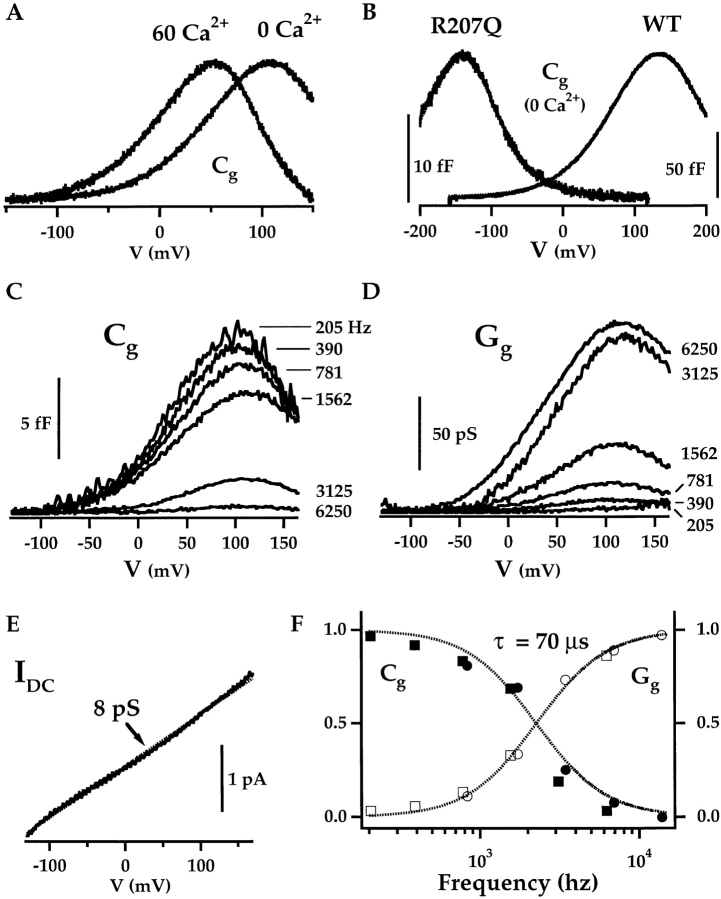
Figure 2.

C _g represents mSlo charge movement. (A) The Ca²⁺ sensitivity of C _g is illustrated by comparing C _g–V relationships obtained in 0 or 60 μM [Ca²⁺]_i from the same patch at 868 Hz. Peak C _g in 0 Ca was 39% larger than in 60 Ca²⁺, but traces were normalized to show the shift in the position of peak C _g along the voltage axis. (B) C _g–V relationships for mSlo wild-type (WT, 1,736 Hz) and mutant (R207Q, 1,500 Hz) channels are similar in shape but are shifted by more than 250 mV relative to each other. Fits, representing the derivative of Boltzmann functions, are superimposed on the data (dashed lines; WT: z = 0.58 e, V_h = 132 mV; R207Q: z = 0.74, V_h = −143 mV). (C) C _g–V relationships for wild-type channels decrease in amplitude as the frequency of the sinusoidal voltage command is increased from 200 to 6,944 Hz. (D) The orthogonal component of the admittance signal (G _g) increases with frequency. (E) DC current measured during the voltage ramp (see Materials and Methods) changes linearly with voltage, demonstrating that the G signal does not represent voltage-dependent changes in G _m and indicating a membrane/seal resistance (125 GV) over the entire voltage range. (F) C _g (solid symbols) and G _g (open symbols) measured at +120 mV are plotted versus frequency for two experiments and are fit by Lorenzian functions, described in the text, with a time constant of 70 μs.

Gating Capacitance Measurements and Admittance Analysis

Membrane capacitance (C _m) represents the ability of charge to redistribute across or within the cell membrane in response to a change in voltage. Therefore, C _m includes a nonlinear voltage-dependent contribution from gating charge movement (C _g) as well as a voltage-independent component due to the lipid bilayer. One of the most sensitive methods for measuring capacitance is admittance analysis. The membrane is driven with a sinusoidal voltage command, and the resulting current is analyzed with a phase-sensitive detector to determine C _m as well as other parameters in the membrane equivalent circuit (Gillis 1995; Lindau and Neher 1988). One advantage of this technique is that residual ionic and “leak” currents can be separated from capacitive (gating) currents based on their phase relative to the command voltage. A related advantage is that measurements can be acquired rapidly without the need for leak-subtraction protocols.

Gating capacitance (C _g) represents the amount of gating charge that moves (ΔQ _g) in response to a small change in voltage (ΔV) and therefore reflects the slope of the Q _g–V relationship (ΔQ _g/ΔV). C _g is also dependent on the kinetics of charge movement and is therefore sensitive to the frequency (ƒ) of the sinusoidal voltage command. Thus, capacitance measurements provide an assay of gating charge mobility reflecting both voltage-dependent and kinetic properties. When measured in response to a small amplitude, low frequency voltage perturbation C _g approximates the derivative of the steady-state Q–V relationship (C _g(V) = dQ _ss/dV) (Fernandez et al. 1982; Fernandez et al. 1983; Taylor and Bezanilla 1979). Thus, if the Q–V can be described by a Boltzmann function Q _ss = [1 + exp(−ze(V − V _h)/kT)]⁻¹ then C _g should exhibit a bell-shaped voltage dependence described by the derivative of a Boltzmann function. This relationship between C _g(V) and Q _ss(V) is strictly valid only when C_g is measured at a frequency approaching zero (C _g0). However, as discussed below, useful information about mSlo charge movement can be obtained using relatively large amplitude (30 mV) sinusoidal voltage commands at frequencies of hundreds or thousands of Hz.

Fig. 1 A shows the C _g–V relationship for mSlo measured at 868 Hz in 0 Ca²⁺ (see Materials and Methods) from channels expressed in an excised macropatch. C _g exhibits a bell-shaped voltage dependence and is well fit by the derivative of a Boltzmann function (Fig. 1 A, Fit). In nontransfected cells, the C–V relationship is flat (Fig. 1 A, Control), representing only the uncompensated linear capacitance of the lipid bilayer and electrode (C _o = C _b + C _s; see ). These contributions to the record in Fig. 1 A were effectively eliminated by setting the baseline equal to zero at negative voltages (less than −100 mV) where C is voltage independent and presumed equal to C _o. The Q _g–V relationship was obtained by integrating the C _g–V trace with respect to voltage, and is plotted in Fig. 1 B together with the normalized conductance–voltage (G _K–V) relationship for mSlo in 0 Ca²⁺ (mean ± SEM, n = 23 [Horrigan et al. 1999]). The Q _g–V relationship is fit by a Boltzmann function (dashed line) characterized by a half-activation voltage (V_h) of 133 mV, corresponding to the peak voltage of the C _g–V curve, and an equivalent charge (z) of 0.59 e. Fits to C _g–V relationships obtained at 868 Hz from many experiments yielded values of V_h = 127.4 ± 3.4 mV and z = 0.61 ± 0.014 e (mean ± SEM, n = 15) in 0 Ca²⁺. These parameters are similar to those estimated in the preceding paper to characterize the charge and voltage dependence of mSlo voltage sensors (V_h(J) = 145 mV and z _J = 0.55 e [Horrigan et al., 1999]). The G _K–V relationship is steeper and shifted to more positive voltages than the Q _g–V, and can be approximated by a Boltzmann function (from the Q _g–V fit) raised to the 4th power as shown in Fig. 1 B.

The C _g–V relationship in Fig. 1 A was measured during a 1-s voltage ramp from −160 to +200 mV. A sinusoidal command (ƒ = 868 Hz) was superimposed on the ramp as indicated in Fig. 1 C, and patch admittance (Y _p) was measured for each cycle of the sinusoid using a phase-sensitive detector implemented in software (Herrington and Bookman 1995). Patch capacitance (C _p) was determined based on the expression:

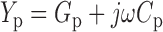5

where the real and imaginary terms represent the components of Y _p appearing at phase angles of 0° and 90°, respectively, relative to the command voltage, and ω = 2πƒ. C _g was then defined as the voltage-dependent component of C _p [C _g(V) = C _p(V) − C _o]. The C _g–V relationship was unaffected by the polarity of the voltage ramp (data not shown), indicating that a pseudo steady-state condition was achieved at each voltage. Because the amount of gating charge detected was small (1–30 fC), admittance was typically measured using a relatively large amplitude 30-mV sinusoidal voltage command (60 mV peak to peak) to increase the signal to noise ratio. We were concerned that such a perturbation might alter the shape of the C _g–V relationship relative to that obtained with a small amplitude command. However, reduction of the sinwave amplitude from 30 to 3 mV had no detectable effect on the C _g–V relationship (Fig. 1 D). This result suggests that the C _g–V was not distorted by the size of the sinusoidal command and is consistent with the weak voltage dependence of mSlo channel gating.

Gating Capacitance Represents mSlo Charge Movement

Although a voltage-dependent component of C _m was not detected in uninjected oocytes, it is important to verify that C _g arises from mSlo channels. High levels of heterologous expression of many membrane proteins in Xenopus oocytes have been shown to upregulate expression of endogenous ion channels (Tzounopoulos et al. 1995). It is conceivable that such endogenous channels could contribute to gating charge movement in cells expressing mSlo. However, several lines of evidence argue against such a contribution. First, similar C _g signals were observed using two different expression systems, Xenopus oocytes (Fig. 1 D and 2 C) and HEK 293 cells (Fig. 1 A and 2 A). Furthermore, C _g is Ca²⁺-sensitive and can be altered by mutating the mSlo channel.

The Ca²⁺ sensitivity of C _g is examined in Fig. 2 A. C _g–V traces obtained in 0 or 60 μM Ca²⁺ from the same patch were normalized to peak capacitance and superimposed. The C _g–V relationships are similar in shape but shift to more negative voltages with increasing [Ca²⁺]_i. The G _K–V relationship for mSlo also exhibits a negative voltage shift upon application of Ca²⁺ in this concentration range (Cui et al. 1997).

The Ca²⁺ sensitivity of C_g suggests that this signal represents mSlo charge movement but does not rule out contributions from endogenous Ca²⁺-sensitive channels. To eliminate this possibility, we examined the properties of an mSlo mutant. Neutralization of a charged residue in the S4 domain of mSlo (R207Q) shifts the G _K–V relationship to more negative voltages and reduces its slope relative to that of the wild-type (Diaz et al. 1998; Horrigan et al. 1999; Cui, J., and R.W. Aldrich, manuscript in preparation). We showed in the preceding paper that these shifts in the G–V can be accounted for by the allosteric voltage-gating scheme if the mutation allows voltage sensors to activate at more negative voltages without altering their charge. Consistent with this hypothesis, the C _g–V relationship for R207Q is approximately the same shape as that for mSlo but is shifted by almost −250 mV (Fig. 2 B). This result also confirms that the C _g signal reflects the gating of mSlo.

The Kinetics of mSlo Gating Charge Movement

To assess the speed of charge movement, we examined the frequency dependence of C _g. In the simplest case, where gating charge movement can be represented by a two-state process, such as voltage-sensor activation from R to A, gating admittance

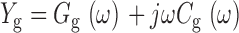6

can be represented by an equivalent circuit consisting of a capacitor C _g0 in series with a resistor R _g0 where τ_g = C _g0 R _g0 is the time constant of gating charge relaxation at a particular voltage (Fernandez et al. 1982; Taylor and Bezanilla 1979). Where

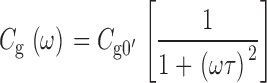7

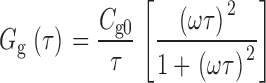8

When the frequency of the sinusoidal voltage command is low (ω << 1/τ), Y _g reduces to a purely capacitive signal (Y _g ≅ jωC _g0), where C _g0 = dQ _ss/dV. As ω increases, C _g should be attenuated, since the gating charge effectively cannot move fast enough to keep up with the voltage command. C _g(ω) is a Lorenzian function that describes the frequency dependence of C _g. At higher frequencies, the gating current should also change phase with respect to the voltage command such that a component of Y _g, described by the function G _g(ω), appears in phase with the membrane voltage.

The frequency dependence of mSlo charge movement is shown in Fig. 2C–F. Consistent with the above predictions, the C _g–V relationship is attenuated as the frequency of the sinusoidal voltage command is increased from 200 to 6,944 Hz (Fig. 2 C). At the same time, a voltage-dependent signal appears in the orthogonal G trace and increases at higher frequencies (Fig. 2 D). The DC current level during the voltage ramp is small and increases in a roughly linear manner with voltage, indicating a constant membrane resistance (R _m) of ∼125 GV (Fig. 2 E). Thus, the G signal in Fig. 2 D represents a component of gating charge movement (G _g) and not a voltage-dependent change in membrane conductance. G _g is almost eliminated at 200 Hz, consistent with the prediction that Y _g will reduce to a purely capacitive signal at low frequencies. Fig. 2 F plots the amplitudes of C _g and G _g measured at +120 mV versus frequency for two experiments. C _g and G _g are well fit by and , respectively, with a time constant (τ) of 70 μs. The relative amplitudes of the admittance components are also consistent with a 70-μs time constant, since C _g and G _g were normalized by C _g0 and C _g0/τ, respectively. Thus, a component of mSlo gating charge appears to move much faster than I _K activation, which is described by a mean time constant of 1.63 ms at +120 mV (Horrigan et al. 1999). We will demonstrate below that an additional component of gating charge moves with the time course of channel activation but is too slow to be detected with admittance analysis.

Conclusions from Capacitance Measurements

Admittance analysis reveals several important properties of mSlo charge movement. Comparison of the Q _g–V and G _K–V relationships (Fig. 1 B) suggests that charge movement can occur at voltages where most channels are closed. The frequency dependence of C _g shows that charge relaxes with a time constant that is much faster than that of I _K activation (Fig. 2 F). Together, these results suggest that admittance analysis detects charge movement associated with rapid closed-state transitions that precede channel opening. In terms of the allosteric voltage-gating scheme, such transitions result from voltage-sensor movement. That the Q _g–V relationship can be fit by a Boltzmann function is consistent with the movement of each voltage sensor being described by a two-state model with a single transition between a resting (R) and an activated state (A). The simple voltage dependence of Q _g also supports the notion that the voltage sensors, in different subunits of the mSlo homotetramer, behave identically and act independently. The approximate 4th power relationship between Q _g–V and G–V is consistent with the assumption that channel opening is linked to the activation of four voltage sensors. However, as discussed below, this relationship may be affected by the different ionic conditions under which I _K and I _g are measured.

Advantages and Limitations of Admittance Analysis

Our results show that admittance analysis provides a sensitive method for detecting and characterizing some aspects of mSlo gating charge movement. By using a large amplitude sinusoidal voltage command in combination with a voltage ramp, we were able to acquire the C _g–V relationship rapidly, and to determine Q _g(V) at submillivolt intervals. The speed of mSlo charge movement is advantageous for admittance analysis because it allows measurements to be performed at hundreds or thousands of Hz where the signal to noise ratio is high (Gillis 1995; Lindau and Neher 1988; Lollike et al. 1995). By the same token, as discussed below, this technique is not well suited to detecting slow components of charge movement and may present difficulties in dissecting complex kinetic behavior.

The charge movement detected with capacitance measurements is much faster than I _K activation. However, any scheme that assumes the C–O conformational change is voltage dependent or that channel opening affects the ability of voltage sensors to move requires that a component of gating charge will relax with the kinetics of I _K activation. The frequency dependence of C _g (Fig. 2 F) can be adequately fit by a single Lorenzian function between 200 and 7,000 Hz and therefore provides no evidence for a slow component of gating charge, which should appear as an additional Lorenzian component at low frequencies. However, the frequency range of our measurements may limit our ability to detect such components. For example, charge that moves with a time constant of 2 ms would produce a C _g component that is attenuated by ∼85% at frequencies >200 Hz.

Admittance analysis is also not an ideal method for dissecting a model as complex as the one we have proposed for mSlo. The allosteric scheme predicts that multiple kinetic components of charge movement will result from C–C, C–O, and O–O transitions. Admittance analysis detects charge movement associated with perturbations about an equilibrium distribution of channel states, and will therefore contain contributions from all of these sources. Slow transitions associated with channel opening should contribute little to C _g at the frequencies used in our experiments. However, fast transitions among closed or open states (C–C, O–O) should be detected. At voltages less than +100 mV, most channels are closed in 0 Ca²⁺, and C _g will mainly reflect C–C transitions. However, at more positive voltages, C _g should represent a combination of open- and closed-state charge movement. For this reason, gating currents measured in response to step depolarizations provide a better method for isolating the various transitions predicted by the model.

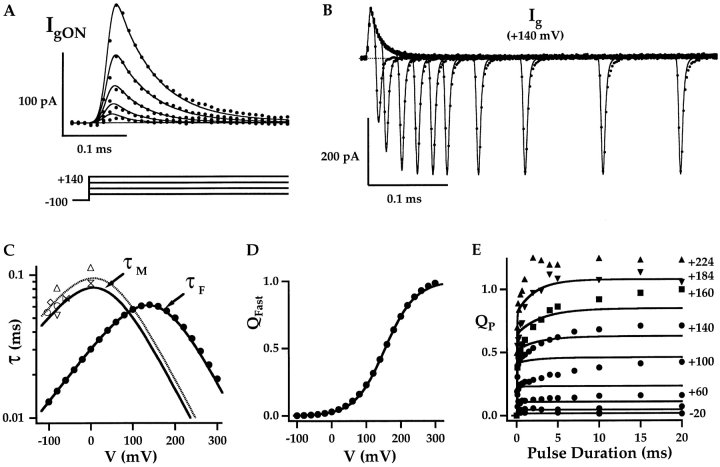
A Fast Component of Gating Current

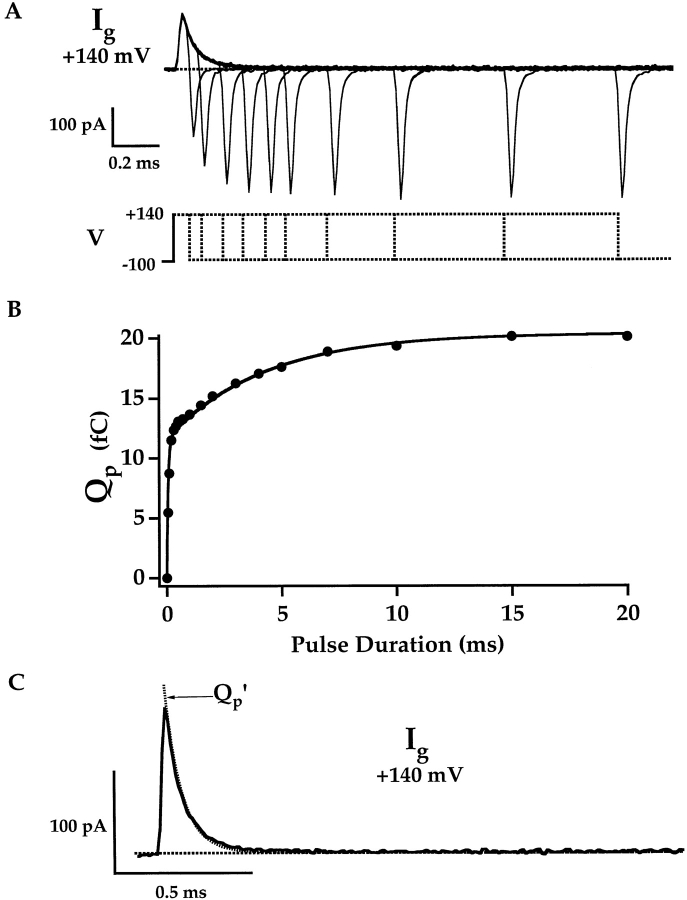
Fig. 3 A shows I _g evoked in response to a 0.5-ms pulse to +160 mV from a holding potential of −80 mV in 0 Ca²⁺. The ON current decays rapidly with a time course that is well fit by an exponential function (dashed line) with a time constant of 59 μs, similar to that determined with admittance analysis at +120 mV (70 μs). The OFF current measured at −80 mV decays more quickly, with a time constant of 17 μs. A family of I _g evoked at different voltages (0 to +160 mV) in response to 1-ms pulses is shown in Fig. 3 B. The Q _ON–V and Q _OFF–V relationships obtained by integrating I _gON and I _gOFF are plotted in Fig. 3 C (open symbols) together with the Q _g–V relationship obtained from capacitance measurements at 868 Hz in the same patch (solid line). At all voltages, Q _ON and Q _OFF are equivalent, as expected for gating charge. The gating current and capacitance measurements superimpose from 0 to +120 mV but diverge at +160 mV.

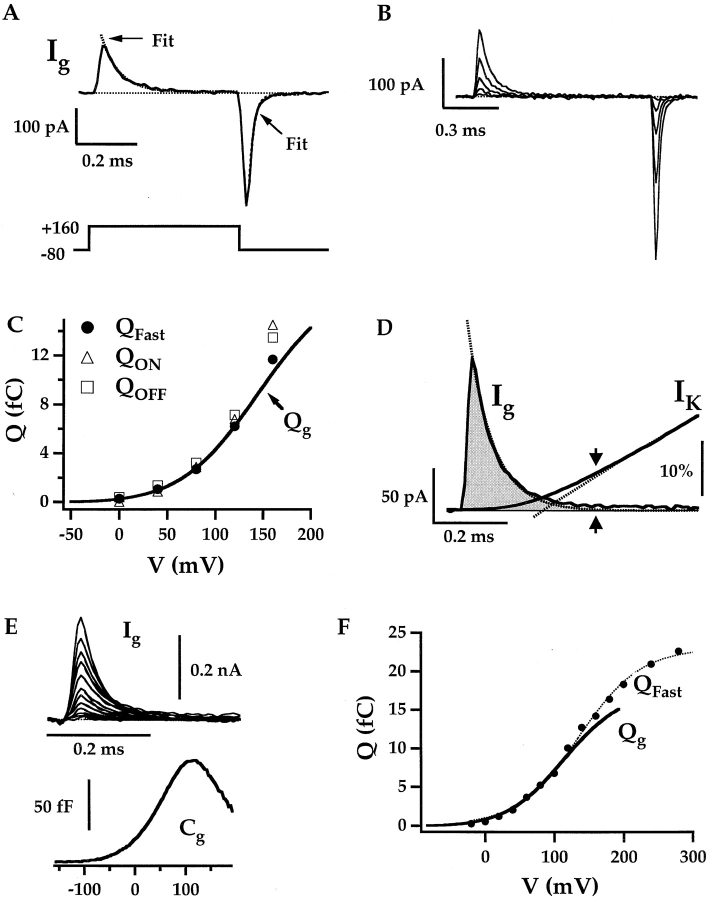
Figure 3.

mSlo gating current. (A) mSlo I _g evoked in response to a 0.5-ms pulse to +160 mV from a holding potential of −80 mV. The trace represents the averaged response to eight pulses. I _gON and I _gOFF are fit by exponential functions (dashed lines). (B) A family of I _g evoked in response to 1-ms pulses to different voltages (0–160 mV in 40-mV steps). (C) Q _ON–V and Q _OFF–V relationships were obtained by integrating I _gON and I _gOFF, respectively (from B) over 1-ms intervals. The Q _g–V relationship was obtained from C _g measurements at 868 Hz in the same patch. Q _fast was determined from an exponential fit to I _gON (see below). (D) I _gON evoked at +160 mV is compared with the initial time course of I _K activation measured at the same voltage from a different experiment. I _K is fit with an exponential function (dashed line) from 0.5 to 20 ms after the start of the pulse. The I _K scale bar represents 10% of the steady-state amplitude. I _gON is also fit with an exponential function, and the shaded area under the fit was used to determine Q _fast. (E) I _gON and C _g measured from a single patch were integrated to determine Q _fast and Q _g, respectively, as plotted in F. The Q _fast–V relationship is fit with a Boltzmann function (z = 0.57 e, V_h = 136 mV).

Similar results were obtained with brief voltage pulses and capacitance measurements because both methods mainly detect fast charge movement. Fig. 3 D compares the time course of I _g evoked at +160 mV to the initial activation of I _K measured at the same voltage from a different experiment. I _g decays, to a large extent, before I _K begins to increase. After 1 ms, I _K increases to 31% of its steady-state amplitude, representing only 7% of maximum P _o. Thus, the channel does not achieve a steady state during a 1-ms pulse, and I _g should reflect little if any slow charge movement that might be associated with channel opening. An important difference between the gating current and capacitance measurements is that the initial decay of I _gON represents charge moved when most channels are closed, while C _g is measured after P _o has reached a steady state and therefore reflects the behavior of both open and closed channels. Thus, I _g measurements allow better isolation of closed-state transitions owing to the large kinetic difference between I _gON and I _K.

Fast I_g: Isolation and Voltage Dependence

According to the allosteric model, the initial decay of I _g represents activation of voltage sensors from a resting (R) to an activated state (A) while channels are closed (i.e., C–C transitions). The exponential decay of I _gON is consistent with such a two-state model. Moreover, in Fig. 3 D, I _K achieves an exponential time course (dashed line) at a time (arrows) when the gating current has almost completely decayed. This correlation between I _g and the delay in I _K activation is consistent with I _g reflecting closed-state transitions in the activation pathway. However, Q _ON measured during a 1-ms pulse is not only an assay of closed-state charge movement, as some channels do open during this time (Fig. 3 D). Q _ON measurements can also be contaminated by outward leak currents that often are observed at voltages greater than +200 mV. To better characterize closed-state transitions, the fast component of ON charge was isolated by fitting an exponential function to the decay of I _g during the first 200 μs of the voltage pulse when most channels are closed. The area under the fit (Q _fast), as indicated by the shaded region in Fig. 3 D, was used as an estimate of closed-state charge movement (Q _C). The Q _fast–V relation in Fig. 3 C (filled symbols) is similar to the Q _g–V relation. When data were acquired over a larger voltage range (Fig. 3 E), Q _g and Q _fast diverge at more positive voltages (Fig. 3 F). The Q _fast–V relationship in Fig. 3 F is well fit by a Boltzmann function (z = 0.57 e, V_h = 136 mV). The difference between Q _g and Q _fast is expected, as it occurs at voltages (>100 mV) where channels begin to open, and Q _g therefore cannot be equivalent to Q _C.

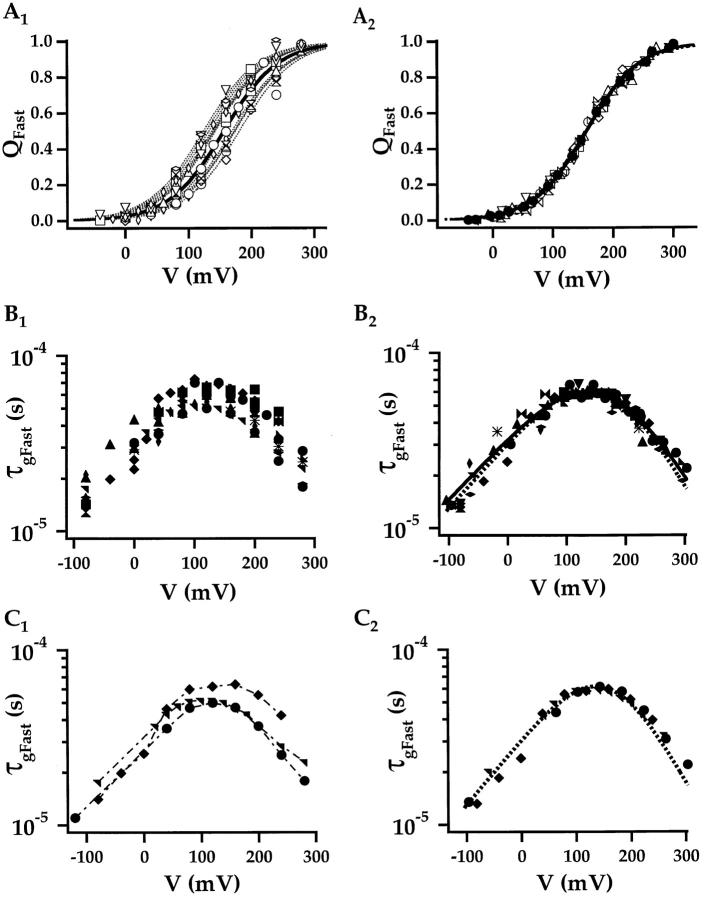
Fig. 4 A₁ plots the normalized Q _fast–V relationships for many experiments. The data were initially fit with Boltzmann functions where all parameters were allowed to vary, yielding a mean equivalent charge <z> = 0.59 ± 0.03 e (mean ± SEM, n = 10). The Q–Vs were then refit with z = <z> and normalized as shown in Fig. 4 A₁. Although the individual plots are reasonably fit using identical values of z, they are scattered in their position along the voltage axis, similar to the mSlo G _K–V relationships (Horrigan et al. 1999). To compare the shapes of the Q–Vs, the individual records were aligned as shown in Fig. 4 A₂ (open symbols) by shifting them along the voltage axis by ΔV = 〈V_h〉 −V_h where V_h is the half-activation voltage of an individual Q–V and 〈V_h〉 is the mean (155 ± 6.5 mV, n = 10) determined from Fig. 4 A₁. These voltage-shifted plots were then used to determine the average Q–V (Fig. 4 A₂, filled symbols). A Boltzmann function with z = 0.59 e and V_h = 155 is superimposed on the data (solid line).

Figure 4.

Voltage dependence and kinetics of fast charge movement. (A₁) The normalized Q _fast–V relationships for many experiments are fit with Boltzmann functions (z = 0.59 e, dashed lines). The solid line is a Boltzmann function indicating the mean half-activation voltage (〈V_h〉 = 155 mV, z = 0.59 e). (A₂) The data from A₁ (open symbols) are aligned by shifting them along the voltage axis by ΔV_h = (〈V_h〉 − V_h). The mean Q _fast–V (filled circles, mean ± SEM) is superimposed on the data together with two Boltzmann fits (V_h = 155 mV; solid line: z = 0.59e, dashed line: z = 0.55 e) and was determined by averaging the shifted data in 15-mV bins. (B₁) Time constants of fast I _g relaxation (τ_gFast) were determined from exponential fits to ON and OFF currents for the experiments in A and are plotted on a log scale versus voltage. (C₁) Three τ_gFast–V relationships from B₁ that cover a large voltage range are compared. (B₂ and C₂) Data from B₁ and C₁ were shifted along the voltage axis by ΔV_h (determined from A) and then normalized to the mean τ_gFast measured from +100 to +180 mV (59 μs). The solid line in B₂ indicates the best fit of a two-state model of voltage-sensor activation where the relationship between the forward (α) and backward (β) rates are constrained such that J = α/β = 1 at +155 mV (z _α = +0.30 e, z _β = −0.21 e, α(0) = 1,310 s⁻¹, β(0) = 30,160 s⁻¹). Dashed lines in A₂, B₂, and C₂ represent the parameters ultimately used in the allosteric model to describe closed-state charge movement (z _α = +0.33 e, z _β = −0.22 e, α(0) = 1,100 s⁻¹, β(0) = 32,120 s⁻¹).

Voltage Dependence of Fast I_g Kinetics

To further characterize the properties of closed-channel charge movement, we examined the voltage dependence of fast I _g kinetics. Time constants of fast I _g relaxation (τ_gFast) were determined from exponential fits to ON and OFF currents for the experiments in Fig. 4 A₁ and are plotted in Fig. 4 B₁. OFF currents, measured at voltages less than +40 mV, were evoked after very brief pulses (0.05–0.25 ms) to +160 or +200 mV and therefore should represent the relaxation of closed channels. τ_gFast exhibits a bell-shaped voltage dependence, consistent with a two-state model of voltage-sensor activation where forward and backward rate constants are voltage dependent. τ_gFast–V relationships from three experiments that covered a large voltage range are compared in Fig. 4 C₁. The individual plots are similar in shape but shifted relative to each other along both axes. The amplitude differences resemble those described previously for the delay in I _K activation (Horrigan et al. 1999) and may reflect temperature variation between experiments conducted at room temperature. To better compare the shape of the τ_gFast–Vs, the plots were first shifted along the voltage axis based on the Q–V shifts determined in Fig. 4 A. The data were then normalized to the mean τ_gFast determined over an interval around the peak of the τ_gFast–V (59.0 ± 2.2 μs, n = 10, from +100 to +180 mV). The resulting records, corresponding to Fig. 4, B₁ and C₁, are plotted in Fig. 4, B₂ and C₂, respectively, and exhibit improved alignment of the τ_gFast–V relationships.

The data in Fig. 4 B₂ were fit with a function τ_gFast = 1/(α+β), representing the predicted τ_gFast–V relationship for a two-state process where the forward (α) and backward (β) rate constants are exponential functions of voltage [α=α₀ e ^z_αekt,β=β₀ e ^z_βekt]. Fits were constrained such that the equilibrium constant J = α/β equals one at the half-activation voltage of the Q_fast–V (V_h(J) = 155 mV). The solid line in Fig. 4 B₂ represents the best fit and is characterized by a total equivalent charge of z _J = 0.51e (z _α = +0.30 e, z _β = −0.21 e).

Estimates of the charge associated with voltage-sensor activation (z _J) based on fits to the Q _fast–V and τ_gFast–V relationships (0.59 and 0.51 e, respectively) apparently differ. However, both relationships can be reasonably fit using the average of these two estimates (0.55 e) (Fig. 4, A₂, B₂, and C₂; dashed lines). This value of z _J was also used in the preceding article to reproduce the ionic current data using the allosteric voltage-gating scheme (Horrigan et al. 1999). One difference is that the value of V_h(J) used to fit the Q _fast–V (155 mV) is 10 mV greater than that previously used to fit I _K. In addition, the values of z _α and z _β used to fit the τ_gFast–V relationship (z _α = +0.33 e, z _β = −0.22 e) indicate that the R–A transition in the allosteric model is not symmetrically voltage dependent as previously assumed.

A Slow Component of ON Charge Movement

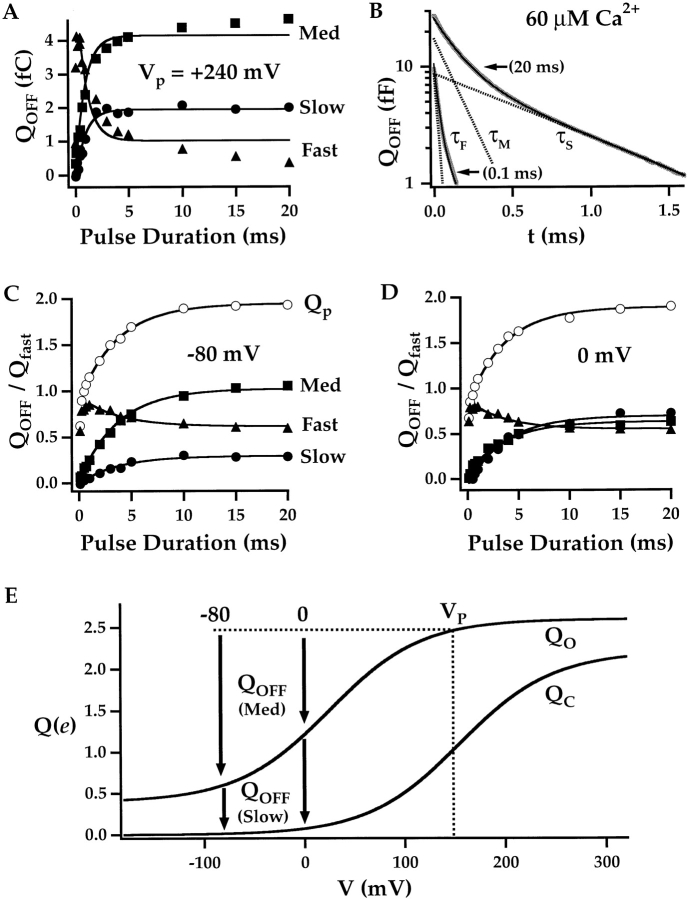
Although the ON currents in Fig. 3 appear to decay with a single-exponential time course, there is a significant slow component of charge movement. Fig. 5 A plots a family of I _g evoked at +140 mV in response to voltage pulses of different duration (see also Fig. 6 A). The peak amplitude of I _gOFF increases rapidly with pulse duration, paralleling the rapid decay of I _gON, and then remains relatively constant for pulses longer than 0.5 ms. The total gating charge moved during the pulse (Q _p) was determined by integrating I _gOFF and is plotted versus pulse duration in Fig. 5 B. Q _p increases with a time course that can be fit by a double-exponential function (solid line) with a fast phase (Q _pFast) corresponding to the rapid decay of I _gON, and an additional phase that is roughly 100-fold slower. The slow component (Q _pSlow) relaxes with a time constant (τ_gSlow) of 4.22 ms and represents a significant fraction of the total gating charge movement at +140 mV (43%) but is too slow to be observed as a component of I _gON. This point is illustrated in Fig. 5 C, which compares I _gON evoked at +140 mV to Q _p′(t) (dashed line). Q _p′(t) is the time derivative of the double-exponential fit to Q _p(t) and should represent the time course of I _gON (Q _p′(t) = dQ _ON/dt = I _gON). These two relationships superimpose, demonstrating that observed I _gON kinetics are consistent with the presence of a large slow component of ON charge movement.

Figure 5.

Slow component of gating-charge movement. A family of I _g was evoked at +140 mV in response to pulses of different duration (0.06–20 ms). (A) Plots the records for 0.06–2-ms pulse duration. The remaining records are shown in Fig. 6 A. (B) Q _OFF was determined by integrating I _gOFF for 3 ms after each voltage pulse and is plotted versus pulse duration (Q _p). Q _p(t) is fit by a double-exponential function with time constants τ_gFast = 63 μs and τ_gSlow = 4.22 ms. τ_gFast was determined by fitting I _gON, and Q _pFast was set equal to Q _fast (11.67 fF) determined as in Fig. 3 D. (C) The time derivative of the fit to Q _p(t) (Q _p′, dashed line) superimposes on the time course of I _gON at +140 mV.

Figure 6.

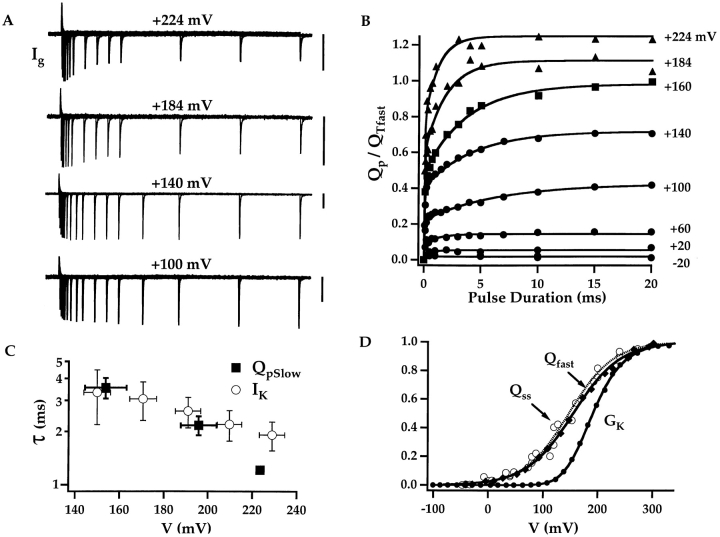
Slow charge movement is limited by channel activation. (A) Families of I _g evoked by pulses of different duration (0.06–20 ms) to the indicated voltages (HP = −80). Records obtained at +184 and +224 mV were from a different patch than those obtained at +100 and +140 mV. Scale bars represent 100 pA. (B) Q _p(t) curves at different voltages from three experiments are fit with double-exponential functions where the time constant and amplitude of the fast component were determined by fitting I _gON with an exponential function. Plots from different experiments (different symbols) were normalized to the total fast charge (Q _Tfast) for each patch (see text). The indicated pulse voltages have been corrected based on the Q–V shifts (ΔV_h) determined in Fig. 4 A for each experiment. (C) The time constants of Q _pSlow relaxation (τ_gSlow) (mean ± SD) are plotted versus voltage and compared with the time constants for I _K relaxation (mean ± SD) from Horrigan et al., 1999. τ_gSlow at +224 mV represents a single measurement. (D) Normalized steady-state Q–Vs (open circles) from four experiments were determined with 20-ms pulses and are fit by a Boltzmann function (dashed line, V_h = 143 mV, z = 0.65 e). Q _ss–V relationships were corrected for ΔV_h determined for these experiments in Fig. 4 A. Averaged Q _fast–V and G _K–V relationships are plotted for comparison (filled symbols) and are fit by the allosteric voltage-gating scheme (solid lines, z _J = 0.55 e, V_h(J) = 155 mV, L = 2 × 10⁻⁶, z _L = 0.4 e, D = 17).

The predicted amplitude of the slow component of I _gON, determined from Q _p′(t), is small (2.1 pA) because it decays slowly. For similar reasons, the slow component of ON charge could not be reliably measured from I _gON. Small sustained outward currents on the order of a few pA were often observed at high voltages, presumably representing residual ionic or leak current. For example, the current trace in Fig. 5 C decays to a steady-state level of 2.2 pA at the end of the pulse. While such small currents have little effect on measurement of Q _fast they can contaminate estimates of slow charge determined by integrating I _gON over a 20-ms pulse. The slow component of Q _p from Fig. 5 B is only 8 fC, equivalent to a 0.4 pA current for 20 ms. Measurements of OFF charge (Q _p) provide a more reliable estimate of slow charge movement because leak is constant at the holding potential.

The voltage dependence of Q _p(t) is examined in Fig. 6. Families of I _g evoked at different voltages in response to pulses of 0.06–20 ms duration are shown in Fig. 6 A. At each voltage, Q _p was plotted versus pulse duration (Fig. 6 B) and fit with a double-exponential function as in Fig. 5 B. The plots represent data from three experiments and were normalized to the total fast charge movement Q _Tfast estimated from the amplitude of a Boltzmann fit to the Q _fast–V relationship for each experiment. The indicated voltages were corrected for shifts in the Q _fast–V relationship as determined in Fig. 4 A.

A slow component of Q _p is observed in Fig. 6 B for V ≥ +100 mV. The time constant of Q _pSlow (τ_gSlow) is comparable to that for I _K activation (τ(I _K)) measured from +140 to +240 mV (Fig. 6 C). The similar magnitude and voltage dependence of τ_gSlow and τ(I _K) suggest that slow charge movement is limited by channel opening. These kinetics also show that gating charge and open probability equilibrate on a similar time scale. Therefore, Q_OFF determined with a 1-ms voltage pulse, as in Fig. 3 C, can underestimate steady-state Q _OFF (Q _ss), determined with a 20-ms pulse, by as much as 40%. Despite this difference, the Q _ss–V and Q _fast–V relationships are similar in shape. Fig. 6 D compares normalized Q _ss–Vs from four experiments to the normalized Q _fast–V and G _K–V relationships. Q _ss–V almost superimposes with Q _fast–V, and the steady-state data were fit with Boltzmann functions with an equivalent charge z = 0.65 ± 0.03 e (mean ± SEM, n = 4), indicating a slightly steeper voltage dependence than Q _fast.

The Relationship between Slow Charge Movement and Channel Activation

The predominantly exponential time course of mSlo I _K suggests that the kinetics of voltage-dependent activation are dominated by a rate-limiting transition (Horrigan et al. 1999). The similar kinetics of Q _pSlow and I _K relaxation implies that slow gating charge movement also reflects this rate-limiting step. It is important to distinguish between two possible sources of slow charge movement. First, the rate-limiting step may represent a voltage-dependent conformational change and therefore contribute directly to Q _pSlow. Second, the rate-limiting step may contribute indirectly to Q _pSlow by limiting the speed of other voltage-dependent transitions in the activation pathway. The data suggest that both of these mechanisms contribute to slow charge movement in mSlo.

We have previously concluded that the transition from a closed to open conformation represents the rate-limiting step in mSlo activation and is weakly voltage dependent (Horrigan et al. 1999). Hence, the rate-limiting step should contribute directly to slow charge movement. However, the charge associated with the C–O transition (z _L = 0.4 e) was estimated to represent only 15% of the total charge per channel. In contrast, slow charge movement in mSlo can represent >40% of the total ON charge (Fig. 6 B). These results are inconsistent with the idea that Q _pSlow merely represents the charge moved during the C–O transition, but they can be understood in terms of the allosteric voltage-gating scheme (Fig. 1).

The allosteric model predicts that the majority of charge movement can be attributed to voltage-sensor activation. Fast I _g is evoked in response to a voltage step as sensors initially equilibrate between resting (R) and activated (A) conformations while the channel is closed. Q _fast is determined by the voltage-dependent equilibrium constant (J) that characterizes the R–A transition. In addition, a slow component of charge movement should be produced as channels open, representing the C–O transition. However, voltage-sensor movement can also contribute to Q _pSlow. When a channel opens, the equilibrium constant for voltage-sensor activation increases by the allosteric factor D, causing sensors to reequilibrate between R and A and produce additional charge movement. This charge movement will be slow because the voltage-sensor reequilibration is limited by the speed of channel opening.

The amplitude of Q _pSlow should depend upon the number of channels that open as well as the fraction of voltage sensors that are initially activated before channels open. For example, at very positive voltages (approximately +300 mV), the model predicts that voltage sensors can be completely activated with channels closed. In this case, channel opening cannot cause additional voltage sensors to be activated so Q _pSlow will represent only the charge associated with the C–O transition (z _L). At less positive voltages, however, Q _pSlow will represent a combination of channel opening and voltage-sensor reequilibration and may therefore be larger than z _L. We will demonstrate later that the magnitude and voltage dependence of Q _pSlow are consistent with the allosteric gating scheme (Fig. 1). The notion that the C–O transition limits slow charge movement is also important in understanding the properties of I _gOFF as discussed below.

Three Components of OFF Gating Charge Movement

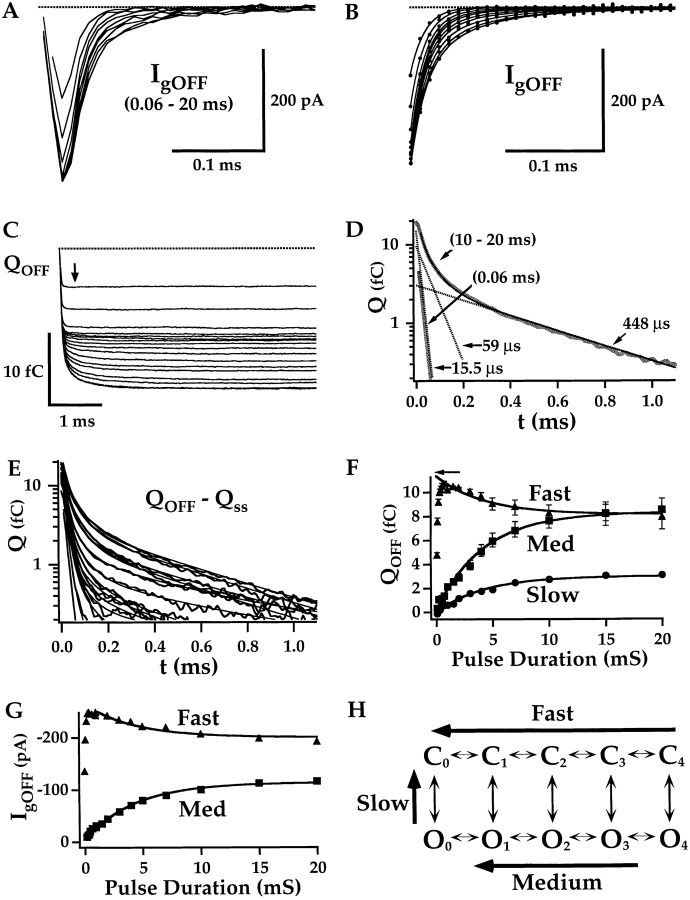
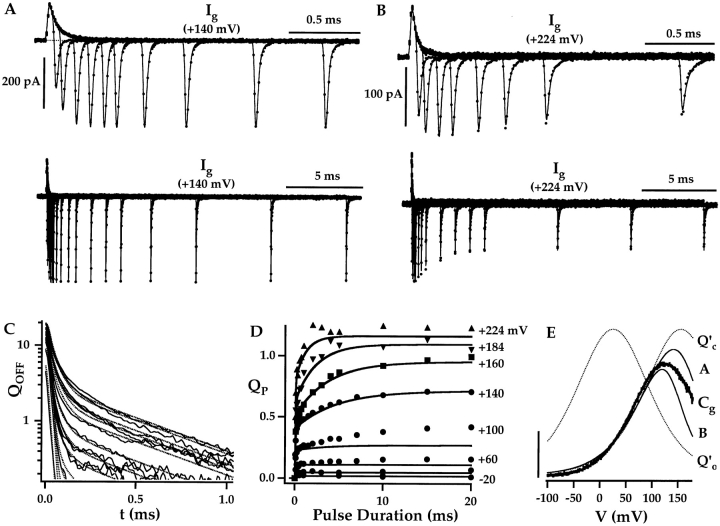
The large slow component of Q _p(t) observed at V ≥ +140 mV in Fig. 6 B indicates that Q _OFF increases with pulse duration. In contrast, the peak amplitude of I _gOFF remains roughly constant or decreases with pulse duration at the same voltages (Fig. 6 A). That I _gOFF can decrease or remain constant while its integral (Q _OFF) increases implies that the kinetics of OFF current change with pulse duration. This change is obvious in Fig. 7 A, which compares OFF currents evoked at −100 mV after pulses to +140 mV of different duration (0.06–20 ms). Two components of I _gOFF are evident from these records. After brief pulses (0.06 or 0.11 ms), OFF current decays with a rapid exponential time course, but an additional slower component appears as pulse duration is increased. The decay of I _gOFF at all pulse durations can be well fit by double-exponential functions with time constants of 15.5 and 59 μs (Fig. 7 B). Both components decay within 300 μs and therefore appear to be fast relative to the time course of channel closing. Potassium tail currents decay with a time constant of 172 ± 15 μs at −80 mV (Horrigan et al. 1999) and therefore require approximately 5τ(I _K) = 900 μs to decay completely. However, a slower component of OFF charge movement can be detected by plotting the integral of I _gOFF (Q _OFF(t); Fig. 7 C). Q _OFF(t) measured after a brief (0.06 ms) voltage pulse achieves a steady state within 300 μs (Fig. 7 C, arrow), consistent with the rapid decay of I _gOFF. In contrast, Q _OFF(t) measured after a 20-ms pulse requires >1 ms to reach a steady state, indicating a slow component of charge relaxation. This component of Q _OFF is not evident in the corresponding I _gOFF trace because it is slow and represents <20% of the total OFF charge.

Figure 7.

Changes in OFF kinetics with channel activation. (A) A family of I _gOFF evoked at 2100 mV after pulses to +140 mV of 0.06–20 ms duration (from Fig. 6 A). Current amplitude is maximal after a 0.5-ms pulse, but I _gOFF decays more slowly as pulse duration increases. The baseline for each record is set to the mean current during an interval 4–5 ms after the pulse. (B) The decay of OFF currents are fit by double-exponential functions with τ_F = 15.5 μs and τ_M = 59 μs. (C) Q _OFF obtained by integrating I _gOFF from A achieves a steady state within 300 μs after a 0.06-ms pulse (arrow) but relaxes more slowly after longer pulses. (D) The kinetics of Q _OFF relaxation after a brief (0.06 ms) or prolonged (10–20 ms) pulses are compared by plotting Q _OFF–Q _ss on a semilog scale. Q _ss is the steady-state value of Q _OFF measured 3 ms after the pulse. The 0.06-ms trace is fit by a single-exponential function (τ_F = 15.5 μs). The 10–20-ms trace, representing an average of 10-, 15-, and 20-ms records, is fit by a triple exponential (solid line, τ_F = 15.5 μs, τ_M = 59 μs, τ_S = 448 μs) where the individual components are indicated by dashed lines. (E) A family of Q _OFF–Q _ss for the data in C. Traces are fit with triple exponential functions with the time constants determined from D. (F) Q _OFF component amplitudes from these fits are plotted versus pulse duration. The relaxation of all three components is fit by exponential functions (solid lines) with a time constant of 4.22 ms. Error bars represent the component amplitudes obtained when τ_M is changed by ±10% (with τ_F and τ_S held constant). The fast component of ON charge (Q _fast) is indicated by an arrow. (G) Fast and Medium I _gOFF component amplitudes determined from B are plotted versus pulse duration. Solid lines represent exponential fits with a time constant of 4.22 ms. (H) The allosteric model predicts three components of Q _OFF relaxation corresponding to the indicated transitions in the gating scheme.

The components of Q _OFF(t) relaxation were further analyzed by plotting the quantity (Q _OFF(t) − Q _OFFss) where Q _OFFss is the steady-state value of Q _OFF(t) measured 3 ms after the voltage pulse (Fig. 7 D). The relaxation of (Q _OFF(t)− Q _OFFss) after a brief pulse (0.06 ms) can be fit by a single-exponential function as indicated by a linear relationship on this semilog plot (τ_F = 15.5 μs). The relaxation of (Q _OFF(t) − Q _OFFss) after a prolonged pulse (average of 10–20-ms records) is more complicated and was best fit by three exponential components (τ_F = 15.5 μs, τ_M = 59 μs, τ_S = 448 μs), indicated by dashed lines in Fig. 7 D, where τ_F was constrained to that used to fit the 0.06-ms record. On average, time constants of 15.7 ± 1.3, 64.7 ± 10.6, and 580 ± 50 μs were measured at −80 mV (mean ± SEM, n = 6).

The time course of development of the OFF charge components were examined by fitting (Q _OFF(t)− Q _OFFss) with triple-exponential functions for all pulse durations (Fig. 7 E). The time constants (termed Fast, Medium, and Slow) were determined from the 0.06- and 10–20-ms traces as in Fig. 7 D, and component amplitudes were varied to fit the other records. The Q _OFF component amplitudes (Q _OFFfast, Q _OFFmed, and Q _OFFslow) are plotted versus pulse duration in Fig. 7 F. The Fast component develops rapidly and then slowly decreases in amplitude as pulse duration is increased. At the same time, a parallel increase in the Medium and Slow components is observed. The slow relaxations in the development of all three components were fit by exponential functions (solid lines) with a time constant of 4.2 ms. This time constant is identical to that used to fit Q _pSlow (Fig. 5 B) and is therefore assumed to represent the time course of channel opening. As discussed below, the results in Fig. 7 F suggest that the Fast component of OFF charge movement represents the relaxation of closed channels, while the Medium and Slow components represent the relaxation of open channels.

Factors Influencing OFF Component Characterization

Accurate separation of Q _OFF components depends on several factors, including the estimation of their time constants. τ_F is most easily determined because the fast component is large and can be examined in isolation using brief voltage pulses. The Slow component can also be effectively isolated because τ_S is almost 10-fold larger than τ_M. However, the small amplitude of the Slow component and its sensitivity to baseline drift make τ_S more difficult to determine than τ_F. The relaxation of Q _OFF(t) to a steady state in Fig. 7 C indicates that I _gOFF decays to the baseline level after ∼1 ms. A small offset or drift in baseline current can prevent Q _OFF(t) from achieving such a steady state and affects determination of τ_S and Q _OFFslow. To minimize such artifacts, the I _g baseline was typically set equal to the mean current measured during an interval 4–5 ms after the end of the pulse. Despite this precaution, drift in Q _OFFss was observed in some experiments (data not shown) and contributes to variability in the estimate of τ_S.

The medium time constant (τ_M) was also difficult to determine because it is only fourfold slower than τ_F and cannot be studied under conditions where the Fast and Slow components are absent. Thus, estimates of τ_M from triple exponential fits to Q _OFF relaxation were sensitive to the estimates of τ_F and τ_S. Error bars in Fig. 7 F indicate the effect of ±10% changes in τ_M on the estimated amplitudes of the different OFF components (with τ_F and τ_S held constant). Such variation still allows reasonable fits to Q _OFF(t) (data not shown); however, an increase in τ_M results in a decrease in the measured Q _OFFmed and a complimentary increase in Q _OFFfast. Larger changes in τ_M produce inadequate fits to Q _OFF(t), and the time course of the Medium component development becomes biphasic as the separation of Fast and Medium components is compromised.

Measurements of Q _OFFmed can be affected by baseline drift or variation in τ_S. Therefore, the development of Fast and Medium components were also studied by fitting I _gOFF with double-exponential functions (Fig. 7 B), a procedure that is less sensitive to the slow component. Fig. 7 G plots the amplitude of the I _gOFF components versus pulse duration, indicating a time course of Fast and Medium component development similar to that determined from Q _OFF (Fig. 7 F). Exponential fits in Fig. 7F and Fig. G, used identical values of τ_gSlow. However, in experiments where baseline drift was a problem, fits to I _gOFF produced more consistent results and were used to determine τ_gSlow.

mSlo Charge Movement and Allosteric Voltage Gating

The presence of three components of OFF gating charge movement, their kinetics, and development with pulse duration can be understood in terms of the allosteric voltage-gating scheme (Fig. 1). As indicated in Fig. 7 H, the allosteric model predicts that OFF charge relaxation will be characterized by Fast, Medium, and Slow components that reflect C–C, O–O, and O–C transitions, respectively. When mSlo channels are closed, OFF currents should represent the relaxation of voltage sensors from an activated to a resting state, corresponding to C–C transitions in the gating scheme. Since brief voltage pulses allow few channels to open, the fast relaxation of I _gOFF after such a pulse (τ_F) mainly reflects the kinetics of this closed-state relaxation pathway. As pulse duration is increased, channels open and their deactivation after the pulse reflects a more complex relaxation pathway involving O–O and O–C transitions. The model predicts that voltage sensors can move even when channels are open. Therefore, the OFF current should exhibit a component that reflects relaxation of voltage sensors from an activated to a resting state, corresponding to O–O transitions in the gating scheme. If these open-state transitions account for the Medium Q _OFF component, to account for the difference between τ_M and τ_F, we must assume that voltage-sensor relaxation is slower when the channel is open than when it is closed. This is a reasonable assumption because the allosteric mechanism requires that channel opening increase the equilibrium constant for voltage-sensor movement D-fold, stabilizing the activated state (A) relative to the resting state (R). Finally, the model predicts that there will be a slow component of OFF charge movement associated with the transition of open channels back to the closed state. Therefore, the slow component should have the same time course as channel deactivation. We will argue later that differences in the observed time course of I _K deactivation and slow charge movement (τ_S) may reflect effects of ionic conditions on channel gating.

If the Fast component of OFF charge movement represents the relaxation of closed channels while Medium and Slow components represent the relaxation of open channels, the effect of pulse duration on the relative amplitude of these components can be understood in terms of the kinetics of channel activation. Q _OFFfast increases initially because voltage sensors can be activated rapidly during brief pulses while channels are closed. As pulse duration increases, the number of closed channels is reduced and Q _OFFfast decreases with the time course of channel activation. At the same time, both Medium and Slow components increase, reflecting an increase in the number of open channels.

Charge Movement Measurements Are Not Contaminated by Ionic Currents

An important conclusion from the above analysis is that the slow components of ON and OFF charge movement are limited by channel opening and closing. Since the kinetics of these components are similar to those of I _K, it is critical to establish that they do not represent contamination of I _g by residual ionic currents. The slow component of ON charge movement was detected as an increase in Q _OFF measured after pulses of different duration, whereas the slow OFF charge was seen as a component of Q _OFF relaxation. Thus, the presence of an inward potassium tail current could potentially contribute to both measurements. This possibility appears unlikely because gating current records that give rise to large slow components of ON charge movement (e.g., Fig. 5 and Fig. 6) do not exhibit appreciable sustained (ionic) current during the voltage pulse. In addition, the slow increase in Q _p with pulse duration involves simultaneous changes in the amplitudes of all three components of Q _OFF relaxation. The Fast component decreases while the Medium and Slow components increase (Fig. 7 F). Although the Slow component relaxes with kinetics similar to that of ionic tail currents, it accounts for only a small fraction of Q _pSlow. Finally, as discussed below, the relative amplitudes and voltage dependence of the different Q _OFF components are consistent with previous estimates of the charge and equilibrium properties of C–C, O–O, and C–O transitions in the allosteric scheme (Fig. 1).

Testing the Allosteric Voltage-gating Scheme

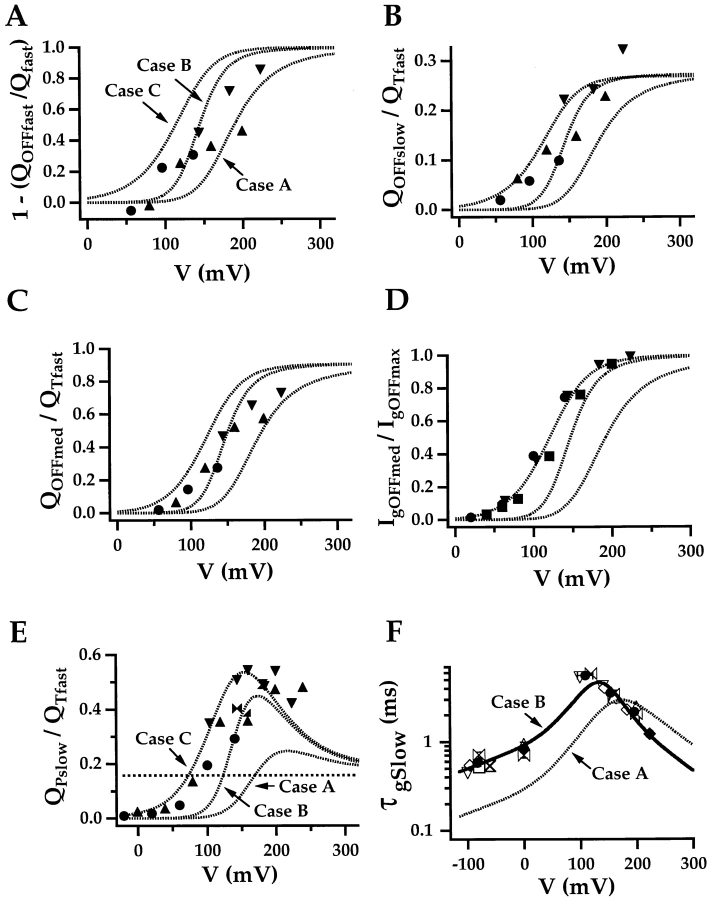
The relationship between P_o and Q _OFFfast.

The allosteric model predicts that the fast component of OFF charge movement should be eliminated after voltage pulses that open all channels. One way to increase P _o is by stepping to more positive voltages. Fig. 8 A plots the time course of Q _OFF component development at +240 mV. The decay of Q _OFFfast is more complete than at +140 mV (Fig. 7 F), consistent with a voltage-dependent increase in P _o. It is likely that the fast component was not eliminated because, in the absence of Ca²⁺, mSlo channels are maximally activated only at very positive voltages (greater than +300 mV) (Horrigan et al. 1999). However, in the presence of 60 μM Ca²⁺, channels can be fully activated at +160 mV. Fig. 8 B compares the relaxation of Q _OFF–Q _OFFss after a 0.1- or 20-ms pulse under these conditions. The 0.1-ms trace decays rapidly and is fit by a triple exponential function (τ_F = 23.8 μs, τ_M = 150 μs, τ_S = 822 μs), with the Fast component representing the majority of OFF charge (91%). However, the 20-ms record is well fit by a double-exponential function using only τ_M and τ_S. This confirms that the Fast component can be eliminated and that the relaxation of open channels back to the closed state contributes only to the Medium and Slow components of Q _OFF.

Figure 8.

Predictions of the allosteric model. (A) Q _OFF component amplitudes determined after pulses to +240 mV in 0 Ca²⁺ are plotted versus pulse duration. The fast component is reduced to <10% of the total OFF charge after a 20-ms pulse. The relaxation of all three components is fit by exponential functions (solid lines) with a τ = 0.91 ms. (B) The decay of Q _OFF–Q _ss is plotted on a semilog scale after 0.1- or 20-ms pulses to +160 mV in 60 μM Ca²⁺ (HP = −80). The 0.1-ms trace is fit by a triple exponential function (solid line, τ_F = 23.8 μs, τ_M = 150 μs, τ_S = 822 μs) and the 20-ms trace is fit with a double-exponential (τ_M = 150 μs, τ_S = 822 μs), indicating that the fast component is eliminated when most channels are opened. Dashed lines represent the two components of the 20-ms fit and the fast component of the 0.1-ms fit. (C) Normalized Q _OFF component amplitudes and total OFF charge (Q _p) are plotted versus pulse duration for pulses to +160 mV in 0 Ca²⁺. OFF components were measured upon repolarization to −80 mV and are normalized to the fast component of ON charge (Q _fast) at +160 mV. (D) When Q _OFF is measured upon repolarization to 0 mV, the Fast component and Q _p are unchanged. However, the Medium component decreases and the Slow component increases in a complementary manner. (E) The charge distributions predicted by the allosteric model for Closed (Q _C) and Open channels (Q _O) are plotted versus voltage (z _J = 0.55 e, V_h(J) = 155 mV, L = 2 × 10⁻⁶, z _L = 0.4 e, D = 17). Arrows indicate the predicted amplitudes of Medium and Slow OFF components at repolarization voltages of −80 and 0 mV after a pulse to +160 mV (V_P).

Voltage dependence of Q_OFF component amplitudes.

To further test the allosteric model, we examined the effect of repolarization voltage on the relative amplitudes of Q _OFF components. I _g was evoked in response to pulses of different duration to +160 mV (0.1–20 ms). After each pulse, the membrane was repolarized to either −80 or 0 mV, and OFF currents were analyzed as in Fig. 7. The amplitudes of the three Q _OFF components are plotted versus pulse duration in Fig. 8C and Fig. D, for −80 and 0 mV, respectively. The component amplitudes were normalized to Q _fast measured in response to a pulse from −80 to +160 mV because a 20% increase in this quantity was observed during the course of the experiment. In the absence of Ca²⁺, steady-state open probability at 0 mV is expected to be small (<10⁻⁴) (Horrigan et al. 1999). Therefore, both repolarization voltages should be sufficiently negative to close most channels. The Q _ss–V relationship (Fig. 6 D) indicates that there is also little change in the steady-state charge distribution between −80 and 0 mV, so total Q _OFF is similar at −80 or 0 mV. Fig. 8C and Fig. D, shows that the time course of total OFF charge development (Q _p(t), open symbols) is also unaffected by repolarization voltage. This is expected, since Q _p(t) represents the time course of ON charge movement and should depend only on the voltage during the pulse (+160 mV). Similarly, the development time course of the three Q _OFF components and the amplitude of the fast component are unaffected by repolarization voltage. However, a change in the relative amplitudes of the Medium and Slow components is observed. Q _OFFslow increased 2.4-fold at 0 mV while Q _OFFmed decreased, such that total Q _OFF remained constant. This complementary change in Q _OFFmed and Q _OFFslow supports the idea that both represent charge movement and are not contaminated by ionic currents.

The effect of voltage on the relative amplitude of Slow and Medium components of Q _OFF can be understood in terms of the allosteric gating scheme (Fig. 1). According to the model, the Medium component represents open state (O–O) transitions while the Slow component is limited by channel closing (O–C). Therefore, Q _OFFmed reflects the voltage-dependent reequilibration of channels among open states. If the membrane is repolarized to a sufficiently negative voltage, Q _OFFmed will be maximal because open channels will rapidly occupy the leftmost open state (O₀) before closing. Under these conditions Q _OFFslow will be small, representing only the charge moved during the transition from O₀ to C₀ (z _L). However, if the membrane is repolarized to a less negative voltage, the open-channel equilibrium may favor occupancy of intermediate open states (O_i) rather than O₀, and Q _OFFmed will be reduced. At the same time, Q _OFFslow will increase to reflect relaxation from O_i to the resting closed state (C₀).

To examine the quantitative predictions of the allosteric scheme (Fig. 1), it is convenient to compare the charge distributions predicted for Closed and Open channels (Fig. 8 E, Q _C(V) and Q _O(V)). Q _C can be expressed in terms of the voltage-sensor equilibrium constant J(V) and charge z _J.

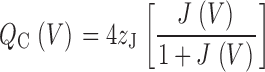9

Therefore, Q _C(V) has the same shape as the Q _fast–V relation, with a maximum amplitude of 2.2 e (4 z _J) when z _J = 0.55 e. Q _O(V) is determined by the open-channel voltage-sensor equilibrium constant (DJ), the voltage-sensor charge z _J, and the charge for the C–O transition (z _L = 0.4 e):

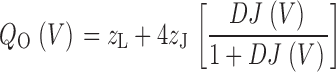10

When D is assigned a value of 17, as in the preceding paper, the half-activation voltage for Q _O(V) is shifted by −130 mV relative to that of Q _C(V), indicating that voltage sensors are easier to activate when channels are open (ΔΔG2.83 kT). The relative amplitudes of Q _OFFmed and Q _OFFslow predicted by the model are indicated by arrows in Fig. 8 E at repolarization voltages of −80 and 0 mV. If voltage sensors equilibrate before channels close, the Medium OFF component evoked from an open channel can be expressed in terms of Q _O:

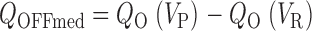11

where V_P is the pulse voltage and V_R is the repolarization voltage. The Slow OFF component is determined by the difference of Q _O and Q _C.

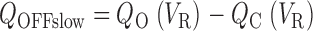12

As illustrated in Fig. 8 E, the model predicts that Q _OFFslow will increase 1.93-fold when OFF charge is measured at 0 mV rather than −80 mV, similar to the 2.38-fold change observed in Fig. 8C and Fig. D.

Simulations of the allosteric model.

The results discussed thus far are qualitatively consistent with the behavior of the allosteric gating scheme (Fig. 1). Simulations based on the model as shown in Fig. 9, Fig. 10, and Fig. 11 also reproduce the major features of the data. However, the parameters that were ultimately used to fit I _g differ from those used to describe ionic currents (Horrigan et al. 1999). Some of these differences are small and may simply reflect a greater accuracy in characterizing fast voltage-sensor movement with gating currents. Other differences, relating to the slow charge movement, suggest that ionic conditions alter mSlo channel gating.

Figure 9.

Simulations of Fast I _g. (A) A family of I _gON evoked at different voltages (0 to +140 mV) is compared with the prediction of the allosteric scheme (solid lines). Data and simulated traces were both evoked in response to filtered voltage pulses (20 kHz) and then filtered at 20 kHz. (B) A family of gating currents evoked at +140 mV in response to pulses of different duration (from Fig. 5 A) is fit by the allosteric model (solid lines). Model parameters for panels A and B are as shown in Table (Case A) with the exception that α and β were decreased by 2% (α(0) = 1,080 s⁻¹, β(0) = 31,681 s⁻¹) to match this experiment. (C) τ_gFast measured from simulated traces at different voltages is plotted versus voltage (filled circles) and compared with the τ_F–V relationship predicted from the parameters assigned to the R–A transition in the model (solid line, τ = 1/(α+β); Case A in Table ). Open symbols indicate the time constant of the Medium OFF component (τ_M) measured from several patches. Lines through these data represent predictions of the allosteric scheme (see text). (D) The Q _fast–V relationship measured from simulated currents (symbols) is compared with the Q _C–V relationship specified by the model (line). (E) The time course of Q _p predicted by the allosteric model (lines) accounts for the fast component of ON charge but underestimates the magnitude of the slow component.

Figure 10.

Estimating open probability from charge movement. The allosteric model predicts a close relationship between P _o and the various Q _OFF components. A, B, and C plot the voltage dependence of these components measured after 20-ms pulses for three experiments. Solid lines indicate predictions of three models (Cases A, B, and C) described in the text. (A) The Fast OFF component should be proportional to the number of closed channels at the end of the pulse. Therefore, [1 − [Q _OFFfast(V_P)/Q _fast(V_P)] is plotted as an estimate of steady-state P _o, where Q _fast is the fast component of ON charge. (B) The Slow OFF component should be directly proportional to P _o. The quantity (Q _OFFslow(V_P)/Q _Tfast) is plotted where Q _Tfast is the total fast charge estimated by fitting the Q _fast–V relationship with a Boltzmann function. (C) The Medium OFF component is normalized by Q _Tfast and plotted versus voltage. (D) The voltage dependence of the Medium OFF component was also examine by fitting I _gOFF with a double-exponential function (τ_F, τ_M) and plotting the normalized amplitude of I _gOFFmed against voltage. I _gOFFmed was normalized by fitting the I _gOFF–V relationship with a Boltzmann function corresponding to Case C (z = 0.98 e). (E) The Slow component of ON charge (Q _pSlow) is expected to exhibit a complex voltage dependence (dashed curves) that is highly sensitive to P _o. The data, normalized by Q _Tfast, indicate that the slow component is too large to be accounted for by the initial allosteric model parameters (Case A) but a shift in the P _o–V relationship (Cases B and C) produces a better fit. A dashed line indicates the charge assigned to the C–O transition (z _L) (F) τ_gSlow determined from the time course of Q _pSlow and Q _OFFslow for many experiments are plotted versus voltage. Solid symbols represent mean ± SEM. Dashed and solid lines represent predictions of Case A and B, respectively (Table ).

Figure 11.

I _g Simulations using modified parameters. (A) I _g evoked at +140 mV in response to pulses of different duration (HP = −100 mV) are plotted on two different time scales and compared with the predictions of the allosteric scheme using modified parameters corresponding to Case B in Fig. 10 (solid lines, Table : Case B). (B) I _g evoked at +224 mV is also fit by the model. (C) Q _OFF–Q _ss corresponding to the records in A are plotted on a semilog scale, demonstrating that the model reproduces all three components of Q _OFF. (D) Q _p(t) from Fig. 6 B is reproduced by the model (Q _ON(t)) for V ≥ +140 mV but the slow component amplitude is underestimated at lower voltages. (E) The C _g–V relationship measured from the same patch as in A at 868 Hz is compared with simulations of the allosteric scheme corresponding to Case A and Case B parameters (solid lines). Dashed lines indicate the derivatives of the Q _c–V and Q _o–V relationships (Q ′_C, Q ′_O). The scale bar represents 50 fF.

In the preceding article, parameters for the allosteric scheme (Fig. 1) were estimated based on fits to the G _K–V relationship, and the voltage dependence of both I _K relaxation kinetics (τ(I _K)−V) and the delay in I _K activation (Δt(I _K)−V). The charge assigned to voltage-sensor movement (z _J = 0.55 e) was identical to that used here to fit the Q _fast–V (Fig. 4 A₂) and τ_gFast–V (Fig. 4 B₂) relationships. However, the half-activation voltage of the Q _fast–V (V_h(J) = 155 mV) determined from gating current measurements is 10 mV more positive than previously estimated. Although this discrepancy is small, it is useful to consider several factors that could potentially contribute to such a difference. First, patch to patch variability is observed for both ionic and gating current data in the position of relationships such as the G _K–V and Q _fast–V along the voltage axis (Fig. 4; see also Horrigan et al. 1999; Stefani et al. 1997). We have attempted to minimize the effects of such shifts by averaging results from many experiments. Nonetheless, such variation could contribute to differences between ionic and gating current data. In addition, the estimate of V_h(J) based on I _K recordings is less direct and therefore likely to be less accurate than that determined from gating currents. The previous estimate of V_h(J) was based, in part, on the ability of the allosteric scheme (Fig. 1) to fit the Δt(I _K)–V relationship. Parameters were assigned to the model with the simplifying assumption that the rate constants for voltage-sensor movement (α, β) are symmetrically voltage dependent (z _α = −z _β). Under this condition, with V_h(J) = 145 mV, the model reproduces the observation that the maximum delay is observed at approximately +153 mV (V_max(Δt)). However, the τ_gFast–V relationship (Fig. 4 B₂) indicates that z _α (0.33 e) is greater than −z _β (0.22 e). Under this condition the predicted relationship between Q–V and Δt(I _K)–V changes such that V_h(J) > V_max(Δt). Thus, V_h(J) is not merely determined by the Δt(I _K)–V relationship but is also influenced by z _α and z _β. Finally, experimental conditions were different for I _K and I _g measurements and might contribute to a real difference in channel gating. For example, Δt(I _K) was measured at a lower temperature (5°C) than I _g (20–22°C). In Shaker K⁺ channels, decreased temperature has been shown to shift the Q–V relationship to more negative voltages (Rodriguez et al. 1998), consistent with the difference in V_h(J) estimated for mSlo from I _K and I _g data. In addition, I _K was recorded in symmetrical 110 mM K⁺ while I _g was recorded with NMDG and TEA replacing internal and external K⁺, respectively. Permeant and blocking ions are known to alter the gating of many K channels (Armstrong 1971; Chen et al. 1997; Fedida et al. 1999; Matteson and Swenson 1986; Sala and Matteson 1991; Swenson and Armstrong 1981; Wang et al. 1999; Yeh and Armstrong 1978), including BK channels (Demo and Yellen 1992; Miller et al. 1987; Neyton and Pelleschi 1991) (see discussion).

Initial I _g simulations (Fig. 9) were generated using parameters determined from a combination of ionic and gating current measurements. The parameters describing the R–A transition for closed channels (z _J = 0.55, V_h(J) = 155 mV, z _α = 0.33, z _β = −0.22) were determined from Q _fast–V and τ_gFast–V relationships as described above. The R–A equilibrium for open channels was assumed to differ from that for closed channels by the allosteric factor D = 17, estimated in the preceding article. The rate constants for this transition were assumed to be symmetrically affected by channel opening such that the forward rate is increased f-fold f=D and the backward rate is decreased by the same factor. Rate constants for the C–O transitions were identical to those used to fit the I _K data at 20°C (Horrigan et al. 1999). Finally, simulated I _g was scaled to experimental records by estimating the number of channels (N) based on the expression N = Q _Tfast/4z _J.

Fig. 9 A plots a family of I _gON evoked at different voltages and compares them to simulations of the allosteric scheme (solid lines). The model reproduces the fast decay and relative amplitudes of these ON currents. The amplitudes of fast gating currents are sensitive to filtering; therefore, the voltage command used in the simulation and the resulting current were filtered at 20 kHz to reproduce experimental conditions (see Materials and Methods). Fig. 9 B plots a family of gating currents evoked at +140 mV in response to pulses of different duration (from Fig. 5 A). The model (solid lines) reproduces the time course and relative amplitudes of ON and OFF currents in response to brief pulses.

The time constants of Fast and Medium charge movement (τ_F and τ_M), predicted by the model, are plotted in Fig. 9 C (solid lines). The τ_F–V relationship is defined (τ_F = [α + β]^-1) by the parameters assigned to the R–A transition when the channel is closed, and is identical to the fit of the τ_gFast data in Fig. 4, B₂ and C₂ (dashed lines). τ_gFast measured from simulated currents (Fig. 9 C, solid symbols) superimposes on τ_F, confirming that exponential fits to fast I _g can be used to estimate the properties of closed-channel voltage-sensor movement. Similarly, the Q _fast–V relationship, determined from these fits, superimposes on the Q _C–V relationship (Fig. 9 D) defined by the model ().

The τ_M–V relationship predicted by the model is the same shape as the τ_F –V but is shifted to more negative voltages owing to the allosteric interaction between channel opening and voltage-sensor movement (τ_M = (αf + βf/D)^-1). Measurements of τ_M from several experiments (Fig. 9 C, open symbols) are similar to those predicted by the model, consistent with the assumption that the forward and backward rate constants for voltage-sensor activation are symmetrically affected by channel opening (i.e., f=D=4.13). A better fit to the data is obtained if f is increased to 4.8 (dashed line) but, given the limited number and voltage range of τ_M measurements, we continue to assume f = 4.13 in the following simulations. The similar voltage dependence of the τ_M and τ_F data supports the conclusion that both Fast and Medium components of OFF charge represent voltage-sensor movement.

In addition to reproducing I _g in response to brief pulses, the model exhibits a slowing of I _gOFF with increased pulse duration (Fig. 9 B). However, this effect is more prominent in the data, suggesting that the model underestimates the amount of slow charge movement. To examine the time course and magnitude of slow charge predicted by the model, I _gON was simulated in response to 20-ms pulses to different voltages and then integrated to obtain Q _ON(t) (Fig. 9 E, solid lines). The time course of Q _ON is biphasic and the fast component matches the data (Q _p(t); Fig. 9 E, symbols), but the slow component is too small, especially at lower voltages. One possible explanation for this underestimate of Q _pSlow is that the model underestimates the number of channels that open at different voltages. In other words, the shape of the P _o–V relationship and/or its position along the voltage axis may not be accurately reproduced. Since the G _K–V relationship was well fit by the allosteric scheme in the preceding paper, this situation could occur if channel opening is enhanced under the ionic conditions where I _g is measured. To test this possibility, we further analyzed the voltage dependence and kinetics of the different charge movement components.

Estimating P_o from charge movement.

The allosteric model predicts that slow changes in both ON and OFF charge movement components are related to channel opening and closing. Therefore, the amplitudes of these components are related to open probability as well the charge distribution for open (Q _O) and closed (Q _C) channels. For example, the fast component of OFF charge depends on Q _C and the number of closed channels at the end of a voltage pulse (1 − P _o):

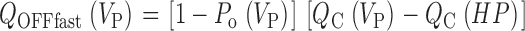13

For a particular pulse voltage (V_P) and holding potential (HP), the second term in this expression can be determined by measuring the fast component of ON charge:

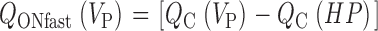14

Therefore, P _o can be estimated by comparing fast components of ON and OFF charge:

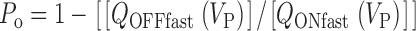15

Fig. 10 A plots the steady-state P _o–V relationship estimated in this way for three experiments where Q _OFFfast(V_P) was measured after a 20-ms pulse and Q _ONfast(V_P) was determined from an exponential fit to I _gON (i.e., Q _fast). Although measurements are scattered, reflecting, in part, the previously noted difficulties in separating Q _OFF components, the data generally follow the shape of the P _o–V relationship predicted by the original model parameters (Fig. 10 A, Case A) but are shifted to more negative voltages. Two additional P _o–V relationships (Cases B and C) are superimposed on the data and will be used throughout this analysis. Case B indicates the prediction of the allosteric scheme (Fig. 1) when the equilibrium constant L is increased 12-fold (equivalent to ΔΔG = 2.5 kT) while leaving the other parameters unchanged. The P _o–V relationship indicated by Case C is roughly the same shape as Case A but is shifted along the voltage axis. Case C was not generated by a gating scheme but can be used in combination with the Q _C and Q _O relationships defined by the original model to make predictions about the voltage dependence of different charge movement components. As discussed below, various aspects of the data are consistent with these altered P _o–V relationships.

The predicted amplitude of the slow component of OFF charge is directly proportional to P _o:

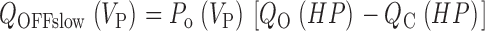16

Fig. 10 B plots normalized Q _OFFslow versus voltage for the same experiments as in Fig. 10 A. Again, the data follow the general shape of the P _o–V relationship predicted by Case A but appear shifted to more negative voltages. The model relationships were generated from the above expression for Q _OFFslow where P _o was specified by Case A, B, or C in Fig. 10 A and Q _O and Q _C were determined from the parameters assigned to the original model as illustrated in Fig. 8 E. The data and model traces were normalized to the total fast charge movement Q _Tfast for each experiment. According to the model Q _Tfast = 4z _J, therefore, the maximum amplitude of the normalized data should be [Q _O(HP) − Q _C(HP)]/4z _J. That the data fall within the amplitude range predicted by the model is therefore consistent with the relative amplitudes of Q _O(HP), Q _C(HP), and z _J specified in the model.

The Medium component of OFF charge is larger and therefore easier to measure than Q _OFFslow but its voltage dependence is determined by Q _O(V) as well as P _o(V):

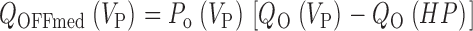17

Fig. 10 C compares the normalized Q _OFFmed–V relationships to the model predictions. Again, the data plots are similar in shape and magnitude to the prediction of Case A but are shifted to more negative voltages. Both data and model predictions were normalized to Q _Tfast as in Fig. 10 B such that the maximum amplitude should be [Q _O(V_P) − Q _O(HP)]/4z _J. Therefore, the magnitude of Q _OFFmed is consistent with Q _O(V) and z _J specified in the model.

The amplitude of the data and model predictions in Fig. 10A, Fig. B, and Fig. C, as noted above, are influenced by several factors in addition to P _o. These include model parameters (Q _O(V), Q _C(V), z _J, z _L) as well as our ability to separate Q _OFF components and determine Q _Tfast. To better examine the voltage dependence of the data, I _gOFFmed–V relationships from several experiments were normalized together with the model predictions to a maximum amplitude of one (Fig. 10 D). I _gOFFmed is proportional to Q _OFFmed, so the model relationships represent normalized versions of those used in Fig. 10 C. I _gOFFmed was normalized based on a Boltzmann fit to the I _gOFFmed–V relationship for each experiment (z = 0.98 e). When scaled in this way, the data from different experiments superimpose. Case C represents a Boltzmann fit to these normalized data (z = 0.98 e, V_h = 121 mV). The P _o–V relationship for Case C (Fig. 10 A) was derived from this fit and the expression for Q _OFFmed ().

The slow component of ON charge movement (Q _pSlow) should exhibit a complex voltage dependence that is determined by P _o(V), Q _C(V), and Q _O(V):

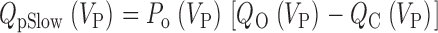18

The Q _pSlow–V relationships plotted in Fig. 10 E were normalized by Q _Tfast and exhibit amplitudes that are larger than predicted by Case A, but are similar to those specified by Cases B and C. The model predicts that Q _pSlow will have a bell-shaped voltage dependence and that Q _pSlow/Q _Tfast approaches a limiting value of z _L/4z _J at positive voltages (Fig. 10 E, dashed line). Our measurements do not extend to high enough voltages to test these predictions. However, the data fall close to the relationships determined by Cases B and C over the voltage range tested, and appear to trend downward at the highest voltages. Importantly, the comparison of Q _pSlow–V relationships for Cases A, B, and C demonstrate that the amount of slow charge movement is highly sensitive to P _o and that Q _pSlow can be considerably larger than the charge associated with the C–O transition.

Finally, we examined the ability of the model to reproduce slow charge movement kinetics. Fig. 10 F plots τ_gSlow over a large voltage range. At positive voltages, τ_gSlow was measured from the time course of development of the Medium component of I _gOFF as in Fig. 7 G. At negative voltages, τ_gSlow was determined from the relaxation of Slow Q _OFF(t) (τ_S). The dashed line in Fig. 10 F represents a fit of the allosteric scheme (Fig. 1) to the time constants of I _K relaxation (τ(I _K)), measured in the preceding paper (equivalent to Case A). τ_gSlow is faster than τ(I _K) for V > ∼+100 mV and is slower than τ(I _K) at negative voltages. However, the voltage dependence of τ_gSlow can be fit (Fig. 10 F, solid line) by adjusting the model parameters as specified for Case B where the equilibrium constant L is increased 12-fold. Both τ_gSlow and τ(I _K) are weakly voltage dependent from −80 to 0 mV, consistent with the idea that the slow relaxation of Q _OFF is limited by channel closing.

Taken together, the data in Fig. 10 support the hypothesis that the properties of slow charge movement can be accounted for by the allosteric voltage-gating scheme (Fig. 1), provided we assume that P _o is increased under the conditions where gating currents are measured. Coordinated changes in all three components of Q _OFF are observed with pulse voltage, consistent with the assumption that their amplitudes depend upon the P _o–V relationship. The relative amplitudes of these components are also consistent with their proposed source in terms of the allosteric scheme and with the charges assigned to various transitions in the model. The voltage dependence of the Medium OFF component suggests that the P _o–V relationship may be similar in shape to that measured with ionic currents (Case A) but is shifted to more negative voltages (Case C). The Fast and Slow component data are consistent with this hypothesis but are inadequate to test the precise voltage dependence of P _o. The data are also insufficient to specify how the model parameters should be altered to account for a change in P _o. Case B, assuming a 12-fold increase in the equilibrium constant L, provides a reasonable first approximation that can account for both a shift in the P _o–V relationship as well as the observed kinetics of slow charge movement.

Simulations of the modified allosteric scheme.

When the C–O transition rates in the allosteric scheme (Fig. 1) are modified, as specified by Case B, improved fits to the gating currents are generated. Fig. 11A and Fig. B, compares simulated currents to I _g evoked at +140 and +224 mV in response to pulses of different duration. The model accurately reproduces the amplitudes of ON and OFF currents, including the decrease in I _gOFF amplitude that occurs with increased pulse duration at +224 mV (Fig. 11 B). The model also fits the time course of I _gOFF and accounts for the slowing of decay kinetics that accompanies increased pulse duration (Fig. 11A and Fig. B). The time course of OFF charge relaxation (Q _OFF–Q _OFFss) after +140 mV pulses are plotted on a semilog scale in Fig. 11 C, and are well fit at all pulse durations. Thus, the model accurately reproduces the kinetics and amplitudes of the three OFF components. The model can account for the slow time constants of both ON and OFF charge movement at all voltages (Fig. 10 F); however, the amplitude of Q _pSlow is underestimated at low voltages (Fig. 10 E, Case B). This point is illustrated in Fig. 11 D, which compares Q _p(t) at different voltages to Q _ON(t) generated by the model. Both the time course and amplitude of Q _p are well fit at V ≥ +140 mV; however, the slow component predicted by the model at lower voltages is reduced in comparison to the data.

Simulation of gating admittance.

To further test the above conclusions, gating currents were simulated in response to a sinusoidal voltage command and compared with admittance analysis results. The C _g –V relationship is compared with the simulations for Cases A and B (solid lines) in Fig. 11 E. Dashed lines indicate the Q _O′–V and Q _C′–V relationships specified by the model. These relationships are the main determinants of C _g–V since they reflect fast voltage-sensor movement. At voltages below +100 mV where channels are closed, C _g approximates Q _C′. At higher voltages, C _g represents an average of Q _C′ and Q _O′ weighted by P _o. Thus, C _g decreases at positive voltages (approaching Q _O′) when P _o is increased (compare Cases A and B). Case A overestimates C _g, suggesting that it underestimates P _o. However, as the P _o–V relationship is shifted (Case B), the model better approximates the peak amplitude and peak voltage of C _g. The effect of P _o on the shape of the C _g–V relationship explains why the mean peak voltage of C _g (+127 mV) is more negative than the half-activation voltage of the Q _fast–V relationship (+155 mV).

Discussion

Examination of gating currents evoked from mSlo Ca²⁺-activated K⁺ channels in the absence of Ca²⁺ has revealed several components of charge movement associated with voltage-dependent gating. We have shown that these results are consistent with an allosteric voltage-gating scheme (Fig. 1) that was proposed in the preceding article to account for the kinetic and steady-state properties of mSlo I _K in 0 Ca²⁺ (Horrigan et al. 1999). Indeed, many of our experiments were designed to test this model. But before discussing these conclusions concerning the allosteric scheme, it is useful to review our results from a more general perspective. The gating current data lead to several model-independent conclusions and allow many alternative gating schemes to be ruled out.

Previous Models of BK Channel Gating

BK channel gating has been extensively studied at the single channel level (Barrett et al. 1982; Magleby and Pallotta 1983a; Magleby and Pallotta 1983b; McManus and Magleby 1991; Moczydlowski and Latorre 1983; Rothberg and Magleby 1998). Kinetic analysis reveals complex dwell-time distributions indicating the presence of multiple open and closed states. Based on such analysis, gating schemes have been proposed that contain a parallel arrangement of open and closed states (McManus and Magleby 1991), superficially resembling the architecture of our allosteric voltage-gating scheme (Fig. 1). However, it is important to recognize that these previous studies were performed in the presence of Ca²⁺, and that the gating schemes used to describe these data therefore contain Ca²⁺-bound states and Ca²⁺-dependent transitions. Thus, the kinetic complexity revealed by the single channel data isn't necessarily related to the mechanism of voltage-dependent gating. Indeed, most schemes derived from single-channel analysis fail to account for the ability of BK channels to open in the absence of Ca²⁺ binding. By examining mSlo channel gating in the absence of Ca²⁺, we have characterized this voltage-dependent pathway, thereby defining a boundary condition that must be satisfied by any complete model of BK channel gating and representing a subset of the states that are accessible in the presence of Ca²⁺.

A model of BK channel gating has been proposed by Cox, Cui, and Aldrich 1997 to account for the effects of voltage and Ca²⁺ on macroscopic mSlo ionic currents, including their ability to activate in the absence of Ca²⁺. The model assumes that mSlo channels undergo a single voltage-dependent transition between a closed and open conformation and that Ca²⁺ binding regulates this transition allosterically. This scheme is essentially a version of the MWC model (Monod et al. 1965; Fig. 2) where channel opening represents an allosteric transition that alters the affinity of Ca²⁺-binding sites and is also voltage dependent.

Scheme S2.

As in the McManus and Magleby model (1991), Fig. 2 contains many states representing different Ca²⁺-bound versions of the closed and open conformation. However, in the absence of Ca²⁺, Fig. 2 reduces to a two-state model with a single voltage-dependent transition between a unliganded closed and open state (highlighted above). By assuming that voltage-dependent activation can be described by a two-state mechanism, Fig. 2 implies that channel opening, voltage-sensor movement, and changes in Ca²⁺ binding-site affinity all occur during a concerted allosteric transition. Our results demonstrate that a more complicated scheme is required to explain voltage-dependent gating and therefore imply that the interaction of Ca²⁺ with the channel may also be more complicated than proposed in Fig. 2 (see Horrigan et al. 1999). In particular, the voltage-dependent C to O transition in Fig. 2 does not consist of a completely cooperative (concerted) step, although considerable cooperativity, as formulated by the allosteric voltage-gating model, is present.

The preceding paper examines several properties of mSlo I _K that are inconsistent with a two-state model of voltage gating (Horrigan et al. 1999). Single channel analysis of mSlo in 0 Ca²⁺ also provides evidence for multiple closed and open states (Talukder and Aldrich 1998). The gating current analysis presented here supports the conclusion that mSlo gating is a multistate process even in the absence of Ca²⁺. A two-state model of voltage-dependent activation requires that charge movement and channel opening occur simultaneously and therefore exhibit identical kinetic and steady-state properties. In other words, I _g should relax with the same near-exponential kinetics of I _K, and the voltage dependence of steady-state charge movement (Q) and open probability (P _o) should be identical. Instead, we observe multiple kinetic components of ON and OFF charge movement with major components of both preceding the relaxation of I _K. In addition, the normalized Q–V and P _o–V relationships are not superimposable (see also Stefani et al. 1997). These results indicate that mSlo channel opening cannot be represented by a concerted transition, and that the MWC model (Fig. 2) is therefore an oversimplification in this regard, although it captures many of the major features of mSlo behavior.

Fast I_g: Evidence for a Two-state Model of Voltage-sensor Movement

Although the overall response of mSlo channels to voltage is complex, gating currents suggest that the movement of individual voltage sensors can be described by a simple two-state model when channels are closed.

I _g evoked during a voltage step exhibits a prominent fast component (I _gFast) representing a majority of ON charge. This fast charge is also detected as a voltage-dependent component of membrane capacitance measured in response to a sinusoidal voltage command, thereby ruling out the possibility that leak subtraction or voltage clamp artifacts contribute to rapid current transients measured in response to large voltage steps. Both admittance analysis and the response to voltage steps indicate that fast gating charge can move at voltages where P _o is normally low, and relaxes roughly 100-fold faster than the time constant of I _K activation. I _gFast decays with exponential kinetics during a time when few channels have opened. The relaxation of OFF current is also fast and single-exponential after brief pulses that open few channels. These results demonstrate that closed unliganded mSlo channels can undergo rapid voltage-dependent transitions.

Because the majority of ON charge moves rapidly, we assume that I _gFast can be attributed to voltage-sensor movement. The exponential kinetics of I _gFast and lack of a rising phase are consistent with a two-state model in which voltage sensors undergo a transition between a resting (R) and activated (A) conformation. The observation that the Q _fast–V relationship is fit by a single Boltzmann function also supports a two-state model. In addition, the time constant of fast I _g relaxation (τ_gFast) exhibits a bell-shaped voltage dependence that can be fit by the inverse sum of two exponential functions, as predicted for a two-state model in which forward and backward rate constants are voltage dependent.

mSlo channels assemble as homotetramers (Shen et al. 1994) and are therefore presumed to contain identical voltage sensors in each subunit. Thus, the simple behavior of I _gFast is consistent not only with a two-state model of voltage-sensor movement but also with the idea that voltage sensors act independently. However, interactions between voltage sensors cannot be ruled out simply based on the kinetic and steady-state properties of fast charge movement. While it is true that such interactions could lead to multiexponential I _gFast kinetics and a non-Boltzmann Q–V, more subtle effects are also possible. For instance, a model that assumes four voltage sensors move in a concerted manner would also predict two-state behavior, the difference being that the Q _fast–V would be fit by a Boltzmann function with equivalent charge (z _Fast) of 4z _J for a concerted model versus z _J for an independent scheme. To distinguish these two possibilities requires an independent estimate of the fast charge per channel (q _fast). Stefani et al. 1997 have reported a total charge (q _T) of 4.4 ± 0.8e per channel (mean ± SD, n = 3) for hSlo based on measurements of I _g and ionic current density in different patches from the same oocyte. Although this estimate is not precise and includes both fast and slow charge, its magnitude argues against a concerted model, since z _Fast = 0.59 e determined for mSlo is much smaller than q _T. An independent model would predict a fast charge of 4z _Fast = 2.36 e, much closer to q _T. The relationship between fast charge movement and channel activation, discussed below, also argues against a concerted model of voltage sensor movement and is consistent with an independent scheme. However, uncertainty in some of these measurements, such as the estimate of q _fast, prevents us from completely ruling out interaction between voltage sensors.

The Coupling of Voltage-sensor Movement to Channel Activation

Since the decay of I _gFast is much faster than the activation of I _K, we considered the possibility that fast charge movement might be unrelated to channel activation. An early component of charge movement has been described in Shaker K channels (Sigg et al. 1999; Stefani and Bezanilla 1996) and squid Na channels (Forster and Greeff 1992) that relaxes rapidly (Shaker: τ < 10 μs, Na channel: τ < 25 μs) and represent <10% of the total gating charge. The speed and small magnitude of this early charge movement suggest it could represent transitions that are not important for channel activation. I _gFast described for mSlo is only severalfold slower than these early components and exhibits a similar equivalent charge. However, in the case of mSlo, several lines of evidence support the idea that fast charge movement is coupled to channel activation.

In contrast to the “early” charge movement in Shaker and Na channels, I _gFast represents a majority of ON charge (Fig. 6 B). In addition, the estimated fast charge per channel Q _fast = 4z _J = 2.36 e (assuming independent voltage sensors) is similar to the equivalent charge that characterizes the maximum voltage dependence of P _o in 0 Ca (z(P _o) = 2.0 e; Horrigan et al., 1999). Thus, the magnitude of I _gFast is consistent with the idea that fast charge movement is important for mSlo channel activation.

The kinetic relationship between I _gFast and I _K also argues that fast charge movement reflects transitions in the activation pathway. Fast charge movement and the delay in I _K activation occur on similar time scales. An example in Fig. 3 D shows that I _gON decays at the same time that I _K achieves an exponential time course. Thus, the achievement of a maximal rate of I _K activation appears correlated with equilibration of fast gating charge. I _K also exhibits a multiexponential rate of increase during the delay (Horrigan et al. 1999), supporting the idea that voltage-sensor transitions are not concerted. If the delay in I _K depends only on the transitions that give rise to I _gFast, then we have previously argued that the delay duration (Δt) should be roughly proportional to τ_gFast (Horrigan et al. 1999). Consistent with this prediction, τ_gFast (Fig. 4) and Δt (Horrigan et al. 1999) exhibit similar bell-shaped voltage dependencies that can be characterized by an equivalent charge of 0.55e and peak voltages of 136 and 153 mV, respectively.

Finally, the Q _fast–V and P _o–V relationships, defining the voltage dependence of fast charge movement and I _K activation, respectively, activate over a similar voltage range, consistent with the idea that these two processes are coupled. We have also shown that the normalized G _K–V relationship can be approximated by raising the Q _g–V relationship to the 4th power (Fig. 1 B). As discussed below, an approximate 4th power relationship between Q _fast–V and P _o–V is predicted by many schemes that assume P _o is enhanced by the activation of four voltage sensors. The relationship between Q–V and G–V is an important test of any voltage-dependent model, but experimental factors limit the interpretation of these data in the case of mSlo. The precise relationship because Q–V and G–V is unclear, owing to the likelihood that gating is altered under the conditions where gating currents are measured.

Sequential Voltage-gating Schemes

Taken together, the above observations indicate that the conformational changes underlying fast charge movement are involved in mSlo channel activation. Therefore, any plausible gating scheme must include a pathway that allows rapid voltage-dependent transitions to occur before channels open. The properties of fast charge movement are consistent with these closed-state transitions, arising from the activation of four independent and identical voltage sensors. Two sequential gating schemes incorporating such a mechanism are considered below (Fig. 1 and Fig. 2) and can reproduce many features of fast charge movement, but can be ruled out based on their failure to account for slow charge movement. These arguments parallel those in the preceding paper based on I _K measurements (Horrigan et al. 1999), and lead to similar conclusions as to the requirement for an allosteric model.

One of the simplest schemes that can account for the properties of I _gFast is the Hodgkin-Huxley (HH) model (Fig. 3).

Scheme S3.

The HH scheme assumes channels are open when all four voltage sensors are activated and predicts a 4th power relationship between the Q–V and G–V relationships:

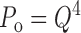19

where Q represents the normalized charge distribution defined by the equilibrium constant for voltage-sensor activation (Q = J/(1 + J)). As noted previously, the observed relationship between Q _g–V and G _K–V appears consistent with this prediction. However, Fig. 3 is inadequate because it cannot account for the presence of both fast and slow components of mSlo charge movement. Similarly, the HH scheme cannot reproduce both the brief delay and slow exponential relaxation that characterize I _K activation kinetics (Horrigan et al. 1999).

Models that assume voltage-sensor activation is followed by a distinct opening transition have proven useful in describing the behavior of channels that deviate from the predictions of the HH scheme (Koren et al. 1990; Perozo et al. 1992; Schoppa and Sigworth 1998; Sigworth 1994; Zagotta and Aldrich 1990; Zagotta et al. 1994a). Such models can account for the presence of fast and slow components of gating current as well as nonsigmoidal I _K activation kinetics (Horrigan et al. 1999; Ledwell and Aldrich 1999; Smith-Maxwell et al. 1998a; Smith-Maxwell et al. 1998b). Fig. 4 (below) assumes that channels can undergo a rate-limiting C–O transition after four independent and identical voltage sensors are activated.

Scheme S4.

Fig. 4 predicts an approximate 4th power relationship between G–V and Q–V described by the expression

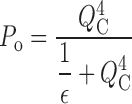20

where Q _C, the closed channel charge distribution, defines the voltage dependence of fast charge movement (Q _C = J/(1 + J)). As illustrated in Fig. 12 A, this model can approximate the observed relationship between the Q _fast–V and G _K–V for mSlo. Fig. 4 can also account for a slow component of ON charge movement (Fig. 12 B) but, as discussed below, cannot reproduce some important aspects of gating current behavior. Similarly, Fig. 4 can approximate the time course of mSlo I _K but does not account for the complex voltage dependence of I _K relaxation kinetics and open probability (Horrigan et al. 1999).

Figure 12.

Predictions of a sequential gating scheme. Predictions of Fig. 4 (dashed lines) are compared with data (symbols) and predictions of the allosteric scheme (solid lines). (A) The G _K–V relationship can be fit by either model (except at very low P _o [Horrigan et al. 1999]), while assigning identical parameters for voltage-sensor movement (z _J = 0.55 e, V_h(J) = 155 mV) and similar charge to the C–O transition (z _∈ = 0.315 e: Scheme IV; z _L = 0.40 e: Allosteric Scheme). Fig. 4 can also approximate the G–V relationship predicted by the allosteric scheme corresponding to Case B by increasing the C–O equilibrium constant (∈(0) = 0.42 Case A; ∈(0) = 4.34 Case B). (B) Both models reproduce the fast and slow components of Q_p(t) at +140 mV (from Fig. 5B). Rate constants for the allosteric model correspond to those used in Fig. 11 (Table , Case B). Fig. 4 used the same rates (α, β) and charge (z _α, z _β) to specify closed-state transitions. The forward and backward rate constants for the C–O transition were δ(0) = 1,392 s⁻¹ and γ(0) = 322 s⁻¹, respectively, and were assumed symmetrically voltage dependent (z _δ = +0.158 e, z _g = 20.158 e). (C) Both models predict similar bell-shaped Q _pSlow–V relationships, implying that a large fraction of slow charge arises from voltage-sensor movement rather than the C–O transitions. (D) The instantaneous I _cs–V relationship for mSlo was measured in symmetrical 110 mM Cs⁺ solutions containing no added K⁺ by activating channels in response to a 50-ms pulse to +200 mV and then stepping to various voltages. I _Cs was measured 100 μs after the pulse to avoid contamination by I _gOFF.

The Slow Component of ON Charge Movement

A slow component of ON charge movement (Q _pSlow) is detected as an increase in Q _OFF after pulses of increasing duration. Q _pSlow develops with the exponential kinetics of I _K activation at depolarized voltages, suggesting that activation and slow charge movement are limited by the same transitions. We have shown that the allosteric voltage-gating scheme (Fig. 1) can reproduce both the kinetics and voltage dependence of Q _pSlow (Fig. 10E and Fig. F). An important conclusion of this analysis is that Q _pSlow represents not only charge moved during the C–O conformational change but a reequilibration of voltage sensors that is limited by channel opening. The allosteric model predicts that transitions among open states (O–O) can contribute to slow charge movement, since voltage sensors reequilibrate after channels have opened. However, a contribution of voltage-sensor activation to slow charge movement does not require a model with multiple open states.

Fig. 4 provides an example of a mechanism by which closed-state transitions contribute to both fast and slow charge movement. Fast I _g is evoked as voltage sensors initially equilibrate between resting (R) and activated (A) while the channel is closed. As channels open, this equilibrium is perturbed because channels can only open when all four voltage sensors are activated. In other words, opening stabilizes the activated voltage sensor, as in the allosteric model. However, in the case of Fig. 4, the establishment of a new voltage-sensor equilibrium can only involve transitions between R and A while the channel is closed.

Fig. 4 can reproduce the time course of Q _p measured at +140 mV, including a large slow component (Fig. 12 B). In addition, Fig. 4 predicts a Q _pSlow–V relationship (Fig. 12 C, solid lines) similar to that produced by the allosteric model (Fig. 12 C, dashed lines). As with the allosteric scheme (Fig. 1), a portion of Q _pSlow represents the charge assigned to the C–O transition (z_∈ = 0.32 e). The bell-shaped voltage dependence of Q _pSlow predicted by Fig. 4 demonstrates that closed-state transitions also contribute to slow charge movement.

In summary, the presence of fast and slow components of ON charge, and their relationship to the time course of I _K activation, suggest that the activation pathway must, at minimum, contain a rate-limiting step that is preceded by one or more rapid voltage-dependent transitions. The kinetics and voltage dependence of I _gFast and the delay in I _K activation, the voltage dependence of Q _fast and G _K together with the tetrameric structure of the channel further suggest that the rapid transitions may be described by the movement of four independent and identical voltage sensors. Therefore, Fig. 4 provides the simplest model that can account for these basic features of the ionic and ON gating current data. However, as discussed below, the properties of OFF charge movement are inconsistent with Fig. 4 and indicate that the activation pathway must include multiple open states.

OFF Charge Movement: Evidence for Multiple Open States

OFF currents, recorded after brief voltage pulses, decay with a single-exponential time course. Such a response is predicted by Fig. 4 and is consistent with activated voltage sensors relaxing rapidly back to a resting state when channels are closed. However, Fig. 4 also predicts that, once channels open, the decay of I _gOFF will be limited by the speed of channel closing (Zagotta et al. 1994b). Therefore, as pulse duration increases, a slow component of OFF charge relaxation should be observed that develops with the time course of I _K activation and decays with the kinetics of I _K deactivation. At the same time that the slow component increases, the fast component of OFF current should decrease as the number of channels that are closed at the end of the pulse is reduced.

Contrary to the prediction of Fig. 4, we observed three components of OFF charge movement. The Fast and Slow components are analogous to those predicted by Fig. 4. However, the Medium component, representing a majority of Q _OFF when channels are maximally activated, provides evidence that channels can undergo transitions among open states. In response to pulses of increasing duration, Q _OFFfast decreases with approximately the same time course as I _K activation while the two slower components, Q _OFFmed and Q _OFFslow, increase in parallel. Q _OFFfast is essentially eliminated under conditions that maximally activate mSlo channels (20 ms at +160 mV in 60 μM Ca²⁺; Fig. 8 B), implying that the Slow and Medium components reflect the relaxation of open channels back to the resting closed state.

We have proposed that the relaxation of the Slow OFF component is limited by the speed of channel closing and, at −80 mV, primarily represents charge moved during the O–C conformational change. Q _OFFslow represents a minority of the total OFF charge (Fig. 10 B), consistent with the notion that the O–C transition is weakly voltage dependent. Similarly, the time constants of slow charge movement (τ_gSlow) and I _K deactivation (τ(I _K)) are weakly voltage dependent at negative voltages (Fig. 10 F). However, the decay of the Slow component is approximately threefold slower than that of potassium tail currents. To account for this difference, we have suggested that channel closing is slowed under the ionic conditions that are used to measure gating currents. The τ_gSlow–V relationship is similar in shape to the τ(I _K)–V relationship and can be fit by the allosteric model if the forward rate constants from C to O are increased while the backward rates are decreased relative to those used to describe I _K. Such a change requires a 12-fold increase in the C–O equilibrium constant (ΔΔG = 2.48 kT), producing a change in the P _o–V relationship that appears consistent with the observed voltage dependence of Q _OFF components and Q _pSlow (Fig. 10, Case B).

The Medium component of OFF charge relaxes ninefold faster than the Slow component and threefold faster than I _K tail currents. Thus, regardless of the effect of ionic conditions on channel gating, the Medium component appears to relax faster than channel closing, implying that voltage sensors can move when channels are open. The similar voltage dependence of τ_M and τ_F (Fig. 4 B₂ and 9 C) supports the idea that the Medium component represents voltage-sensor movement. Thus, any plausible gating scheme must include multiple open states with rapid voltage-dependent transitions between them. The voltage dependence of P _o leads to the same conclusion (Horrigan et al. 1999). The parallel development of Slow and Medium components indicate that once a channel is open, OFF charge relaxation can be described by a constant ratio of Q _OFFmed and Q _OFFslow. This behavior is consistent with the idea that equilibration of channels among different open states is fast relative to the speed of I _K activation.

A Sequential Scheme with Multiple Open States

A sequential scheme, represented in general form below (Fig. 5), could account for Medium and Slow components of OFF charge relaxation, provided transitions among open states are fast compared with the transition from O to C.

Scheme S5.

However, such a model is inconsistent with the voltage dependence of steady-state activation. P _o is weakly voltage dependent at limiting negative voltages, consistent with a charge of 0.4e assigned the C_o–O_o transition in the allosteric scheme (Horrigan et al. 1999). For Fig. 5 to reproduce this limiting voltage dependence, a total charge of 0.4e must be assigned to the transition between C_o and O_o, inconsistent with the assumption that closed-state transitions from C_o to C_m represent the activation of four voltage sensors carrying a total charge of 4z _fast = 2.36 e.

Fig. 5 also appears inconsistent with the relative amplitudes of various ON and OFF charge movement components. For example, we observe that the Medium component of OFF charge is two- to threefold larger than the Slow component measured at −80 mV (Fig. 7 E and 8 A). Thus,

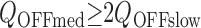21

In addition, the fast component of ON charge is larger than the slow component at all voltages studied:

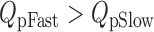22

It can be shown (below) that Fig. 5 cannot account for these observations if and are valid at voltages where P _o ≥ 1/2. This last condition cannot be verified directly, but appears reasonable since and are true at +224 to +240 mV (Fig. 6 B and 8 A), whereas the half-activation voltage of the G _K–V relationship is +190 mV (Horrigan et al. 1999). Moreover, we have argued that P _o may increase under the conditions where gating currents are measured.

The amplitudes of the different charge movement components for either the allosteric model or Fig. 5 can be expressed in terms of Q _C, Q _O, and P _o as specified by . Therefore, by substituting and , can be rewritten:

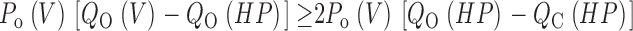23

where V is the pulse voltage and HP is the holding potential (−80 mV). Solving for Q _O(V), we obtain:

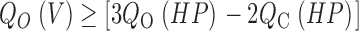24

can also be rewritten by substituting and .

25

Combining and :

26

For a sequential model like Fig. 5, we can further assume:

27

Finally, combining and :

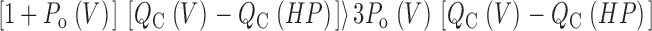28

reduces to P _o(V) < 1/2, indicating that Fig. 5 cannot account for the relative amplitude of ON and OFF charge components while also assuming P _o ≥ 1/2.

The Allosteric Voltage-gating Scheme

Fig. 5 assumes that closed- and open-state transitions occur sequentially and must therefore represent distinct conformational events. An alternative, represented by the allosteric model, is that C–C and O–O transitions represent the same conformational events, i.e., voltage-sensor movement. The kinetics and voltage dependence of the Fast and Medium components of OFF charge movement (Fig. 9 C) are consistent with both C–C and O–O transitions representing voltage-sensor movement, differing only in that the equilibrium constant for voltage-sensor activation is increased when channels open. As demonstrated in this study and in the preceding article, the allosteric model can account for many other properties of mSlo gating in 0 Ca²⁺.

The allosteric model is mechanistically similar to Fig. 4 in that it assumes channels undergo only two types of conformational change: voltage-sensor activation and channel opening. Voltage sensors are assumed to move rapidly and independently in each subunit. Channel opening is relatively slow, weakly voltage dependent, and assumed to represent a concerted transition. Like Fig. 4, the allosteric model assumes channel opening stabilizes the activated voltage sensor. Thus, opening results in a slow component of charge movement that is limited by the speed of channel opening but largely represents voltage-sensor charge movement. Unlike Fig. 4, the coupling of voltage-sensor activation to channel opening is not an obligatory process but rather an allosteric interaction. Therefore, voltage sensors can move when channels are open, accounting for the Medium component of I _gOFF, and channels can open when voltage sensors are not activated, accounting for the weak voltage dependence of P _o measured at negative voltages (Horrigan et al. 1999).

Although the allosteric model allows channels to open when voltage sensors are in a resting state, it predicts that they are most likely to open when all four are activated. Consequently, channels pass through multiple closed states before opening, consistent with the presence of a delay in I _K activation (Horrigan et al. 1999). Similarly, the allosteric scheme can account for an approximate 4th power relationship between Q–V and G–V. The model predicts the following relationship between P _o and Q _C.

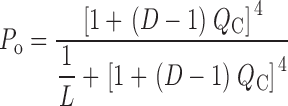29

When L is small and D >> 1, as determined in the preceding article (L = 2 × 10⁻⁶, D = 17, 0 Ca²⁺), this expression can be approximated as:

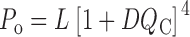30

Finally, the allosteric scheme can account for the presence of three components of OFF charge movement as well as the relative amplitudes of various ON and OFF components. In contrast to Fig. 5, the allosteric model predicts that pathways traversed during channel activation and deactivation are different. Activation involves fast voltage-sensor movement as channels undergo closed-state transitions before opening. Deactivation involves movement of the same voltage sensors as channels undergo open-state transitions before closing. Because the same voltage sensors are moved during open- and closed-state transitions, the rapid components of ON (Q _fast) and OFF charge (Q _OFFfast, Q _OFFmed) are of similar amplitude while the slow components are smaller. Furthermore, the relative amplitudes of Q _OFFmed and Q _OFFslow change with repolarization voltage in a manner specifically predicted by the allosteric scheme (Fig. 8C and Fig. D).

Comparison with Previous Studies of BK Channel Gating

mSlo ionic currents.

The gating current data support the conclusion from the preceding paper that mSlo channel voltage gating in the absence of Ca²⁺ can be described by an allosteric scheme. Indeed, many of the model parameters that were derived to fit I _K data required little or no adjustment to describe the gating currents (e.g., z _J, V_h(J), z _L, D). One feature of the model that could not be determined accurately from I _K measurements was the speed of transitions among open states. The Medium component of I _gOFF provides a direct assay of these transitions and demonstrates that channel opening slows the relaxation of voltage sensors from A to R. The magnitude of this effect is consistent with our previous estimate of the allosteric factor D = 17, provided we assume channel opening almost symmetrically affects the forward and backward rate constants for the R–A transition (Fig. 9 C). However the effect of channel opening on the forward rate was not measured; therefore, the value of D cannot be directly determined from the gating current data.

Single channel studies.

Many of the properties of I _K that implicate a model with multiple open states are observed only at extreme voltages (Horrigan et al. 1999). However, the Medium component of I _gOFF demonstrates that the channels can undergo open-state transitions in response to moderate voltage stimuli, such as repolarization from +160 to 0 mV (Fig. 8 D). This is important because it suggests that complex open-time distributions described previously for single BK channels may to some extent reflect the occupancy of multiple open states in the voltage-dependent activation pathway in addition to different Ca²⁺-bound open states.

Gating currents.

BK channel gating currents have been described previously for hSlo by Stefani et al. 1997, and many of their results, obtained in 0 Ca²⁺, are similar to those presented here for mSlo. For example, the major component of ON current decayed with a rapid exponential time course (τ = 57 ± 10 μs, at +200 mV). A slow component of charge movement was also detected but not examined in detail. The Q–V curve determined with brief 1-ms depolarizations was well fit by a Boltzmann function (z = 0.6 e, V_h = 190 ± 15 mV). In addition, the G–V curve was reported to be steeper than the Q–V, and charge movement was observed at voltages where most channels should be closed.

In addition to these similarities, there are important differences between our results and conclusions and those of Stefani et al. 1997. The normalized G–V and Q–V for hSlo were reported to cross such that the G–V is negative to the Q–V at positive voltages. Such a cross-over, as pointed out by Stefani et al., implies that gating charge can move when channels are open. Although our results lead to a similar conclusion, we do not observe such a relationship between Q–V and G–V in the absence of Ca²⁺. And the allosteric model used to fit our data does not predict a cross-over even though it allows voltage-dependent open-state transitions. In addition, Stefani et al. conclude that only a small fraction of total gating charge must move before channels can open because (a) the Q–V crosses the foot of the G–V where P _o is small, and (b) the Cole-Moore shift is weakly voltage dependent. We disagree with these observations and, for reasons discussed below, conclude that in the absence of Ca²⁺, the majority of gating charge moves before channels open. Stefani et al. also note that the onset of ionic current overlaps the decay of I _g (see Fig. 3) and suggest this provides evidence for open-state charge movement. But most models, including those with a single open state, predict some overlap in the time course of macroscopic I _g and I _K. Finally, Stefani et al. conclude that open-state transitions must be weakly voltage dependent to account for the observation that the major component of charge movement is fast. In contrast, we have shown that the allosteric scheme predicts a small slow component of charge movement even when C–C and O–O transitions are assumed to be equally voltage dependent. And the large Medium component of OFF charge movement provides evidence for significant open-state charge movement.

Some of the discrepancies between our results and those of Stefani et al. 1997 probably reflect real differences in the gating of mSlo and hSlo, but we suggest that the cross-over of Q–V and G–V reported for hSlo may also be affected by the conditions used to measure ionic currents. The Q–Vs for mSlo and hSlo are similar in shape based on Boltzmann fits (z = 0.59 e mSlo; z = 0.6 e hSlo), and the half-activation voltage for the hSlo Q–V is 35 mV more positive than that for mSlo (155 mV mSlo). In line with this difference, the G _K–V for hSlo, measured in symmetrical K⁺ and 0 Ca, is roughly 30 mV more positive than that for mSlo (hSlo: V_h = 220 mV [Diaz et al. 1998; Meera et al. 1996]; mSlo: V_h = 190 mV V [Horrigan et al. 1999). In contrast, the G–V described by Stefani et al. is shifted by −70 mV (V_h = 150 mV) relative to that previously reported for hSlo and is much steeper than that of mSlo based on Boltzmann fits (hSlo: z = 1.3–1.6 e [Stefani et al. 1997]; mSlo: z = 1.0 e [Cui et al., 1997; Horrigan et al. 1999]). These differences may reflect the fact that the G–V reported by Stefani et al. was obtained in symmetrical Cs⁺ rather than K⁺.

Cs⁺ permeates BK channels poorly, allowing Cs⁺ currents to be recorded in patches where I _K would be immeasurably large (Stefani et al. 1997). However, Cs⁺ is also known to alter BK channel gating and is likely to affect the G–V. Demo and Yellen 1992 studied Cs⁺ block of single BK channels and concluded that Cs⁺ occupancy of the pore destabilizes the closed state. This destabilization shifts the P _o–V relationship to more negative voltages and changes its shape because Cs⁺ block is voltage dependent. Similarly the G _Cs–V relationship for hSlo is shifted to negative voltages relative to the G _K–V for hSlo and is steeper than that for mSlo, consistent with an effect of Cs⁺ on channel gating (Demo and Yellen 1992). An increase in steepness of the G–V could occur if Cs⁺ occupancy of the pore is voltage dependent. Consistent with this possibility, the instantaneous I _cs–V relationship recorded for mSlo (Fig. 12 D) is highly nonlinear, indicating that Cs⁺ permeates more readily at very positive or negative voltages. Cs⁺ currents also activate slowly, failing to achieve a steady state during a 25-ms pulse (Stefani et al. 1997). These kinetics differ from those of I _K measured for hSlo (Meera et al. 1996) or mSlo (Horrigan et al. 1999) in 0 Ca²⁺, providing additional evidence for an effect of Cs⁺ on gating and implying that the G _cs–V recorded with 25-ms pulses doesn't represent the steady-state G–V.

hSlo gating currents were also measured in the presence of internal Cs⁺, using isotonic external TEA to block the channel. Therefore, the use of Cs⁺ has the apparent advantage of allowing gating and ionic currents to be recorded with the same internal solution. However, the presence of internal Cs⁺ does not guarantee that channels gate identically when blocked by TEA or conducting Cs⁺. Aside from the possibility that TEA directly affects gating (see below), TEA may inhibit the effect of Cs⁺. Demo and Yellen 1992 found that BK channel block by either internal Cs⁺ or external TEA had no effect on P _o, and they concluded that Cs⁺ could occupy at least two sites in the pore, only one of which affects gating. Thus, it is possible that internal Cs⁺ cannot occupy the critical gating site when the pore is blocked by TEA. This could explain why hSlo gating currents resemble those recorded for mSlo, and may help account for the observed crossing of Q–V and G–V for hSlo.

As discussed previously, mSlo gating may also be affected by the presence of external TEA, internal NMDG, or the absence of K⁺ in experiments measuring gating currents. Several properties of slow charge movement summarized in Fig. 10 suggest that mSlo channels open more readily under the conditions where gating currents were measured. A 10-fold reduction in internal and external K⁺ had no appreciable effect on the G _K–V (data not shown) but we cannot rule out the possibility that gating is altered by the complete removal of K⁺ or its replacement with NMDG. Stefani et al. 1997 found that fast I _g, evoked at voltages where channels do not open, were unaltered by the presence of TEA. We also saw no effect of TEA on fast charge movement measured with admittance analysis in 0 K⁺ (data not shown). However, these experiments do not rule out an effect of TEA on slow charge movement and channel opening.

Another factor that could contribute to an apparent cross-over between Q–V and G–V is the duration of the voltage pulses used to measure gating currents. The Q–V for hSlo was determined using 1-ms pulses and is therefore similar to Q _fast and not a steady-state measurement. Stefani et al. 1997 state that the Q–V determined with longer pulses (10–20 ms) in 0 Ca²⁺ is shifted by −20 mV relative to Q _1ms, an effect that is insufficient to account for the apparent cross-over of Q–V and G–V. We also observed little difference between the normalized Q _ss–V and Q _fast–V curves in 0 Ca²⁺ (Fig. 6 D). However, in the presence of 60 μM Ca²⁺, we observe a large 50 mV shift between Q–Vs determined with 1- or 20-ms pulses (Horrigan, F.T, and R.W. Aldrich, manuscript in preparation). Thus, a cross-over of Q–V and G–V reported by Stefani in 85 μM Ca²⁺ should be strongly influenced by the use of 1-ms voltage pulses.

Despite uncertainties as to the precise relationship between the Q–V and G–V, gating currents recorded for both mSlo and hSlo show that most charge movement in 0 Ca²⁺ is fast, indicating that most charge moves before channels open. The kinetics and voltage dependence of the delay in I _K activation are also consistent with the idea the multiple voltage-dependent closed-state transitions, accounting for the bulk of charge movement, occur before channels open. Finally, the change in delay duration with prepulse voltage (Cole-Moore shift [Cole and Moore 1960]) is, as stated by Stefani et al., less voltage dependent than that observed for Shaker. However, this is consistent with the overall weak voltage dependence and reduced gating charge of BK channels as compared with Shaker and does not imply that a small proportion of total charge moves before Slo channels open. The Cole-Moore shift for mSlo is well described by the allosteric model, which predicts most voltage sensors activate before channels open (Horrigan et al. 1999). The lack of a rising phase in I _g also shows that the earliest closed-state transitions are not weakly voltage dependent.

Detection of Allosteric Voltage Gating

In the preceding article (Horrigan et al. 1999), we discussed the possibility that the behavior of voltage-gated ion channels such as Shaker may be consistent with an allosteric voltage-gating scheme (Fig. 1) like that used to describe mSlo. One reason to consider this possibility is that many, but not all, features of mSlo ionic currents can be adequately described by sequential gating schemes that have been used to describe a variety of other channels. The behaviors of mSlo that deviate from these conventional schemes and implicate the allosteric model are mainly observed under conditions of extreme voltage or low open probability. Therefore, it is possible that other channels operate through an allosteric mechanism but have not been studied under conditions that are necessary to test this model, which may be even more extreme in those channels than for mSlo.

Many of the gating current properties described here for mSlo can also be accounted for by sequential gating schemes containing a single open state such as Fig. 4. However, deviations from the prediction of Fig. 4 are more obvious for gating current than for ionic current. The Medium component of OFF charge movement, in particular, provides a direct indication of open-state transitions. Many voltage-gated K⁺ channels such as Shaker exhibit OFF currents that become slower as pulse duration is increased and channels open (Bezanilla et al. 1991; Bezanilla et al. 1994; Chen et al. 1997; Kanevsky and Aldrich 1999; Zagotta et al. 1994b). However, unlike mSlo, the decay of OFF currents for open Shaker channels appear to be limited by the speed of channel closing as predicted by models like Fig. 4 (Zagotta et al. 1994b). This observation seems to argue against a model with multiple open states. However, as discussed below, the allosteric scheme can account for such results when the speed of voltage-sensor movement or the voltage dependence of open-state transitions is altered.

Two factors allow open-channel charge movement to be detected for mSlo. First, voltage-sensor movement is much faster than channel closing. This difference allows the Medium and Slow components of OFF charge movement to be distinguished and allows open-state transitions to occur before channels close. As discussed below, the relative speed of I _g and I _K in channels such as Shaker might prevent detection of open-state transitions. Another factor that is important for detecting open-state transitions is the open-state charge distribution (Q _O). That is, the voltage dependence of open-state transitions must be such that repolarization to the holding potential causes a redistribution of channels among open states. The effect of repolarization voltage on Q _OFF components in Fig. 8 shows that the Medium component is sensitive to the open-channel charge distribution. Therefore, a change in the voltage dependence of Q _O might alter the ability to detect open-state transitions. For example, if the allosteric factor D is increased, Q _O will be shifted to more negative voltages such that Q _OFFmed measured at −80 mV is reduced.

Fig. 13 shows that a slowing of voltage-sensor kinetics reduces the ability to detect open-channel charge movement. I _K and I _g were simulated in response to a 20-ms pulse to +240 mV as the forward and backward rates for voltage-sensor movement (α, β) were both slowed 10-fold (10×) or 30-fold (30×) relative to those describing mSlo (1×). C–O transition rates and all equilibrium constants were unchanged (relative to Case B parameters). As voltage-sensor movement is slowed, the delay in I _K activation increases (Fig. 13 A) and gating currents are slowed (Fig. 13 B). Under these conditions, I _K and I _g resemble those evoked from a channel such as Shaker where I _K activation kinetics are sigmoidal and ionic and gating currents relax on a similar time scale. Interestingly, a 30-fold slowing of voltage sensor movement also produces a “hook” in I _gOFF, a feature that is also observed in Shaker I _g (Bezanilla et al. 1991; Chen et al. 1997; Perozo et al. 1992). The simulation predicts that P _o approaches unity at the end of a pulse to +240 mV. Therefore, I _gOFF represents the relaxation of open channels. The time course of Q _OFF(t) plotted on a semilog scale in Fig. 13 C is biphasic when voltage-sensor movement is fast (1×) representing the Medium and Slow components of Q _OFF. However, kinetically distinct components of Q _OFF are not evident when voltage-sensor movement is slow (Fig. 13 C, 10× and 30×). Similarly, the decay of I _gOFF is much faster than that of I _K when voltage sensors are fast (Fig. 13 D, 1×). However, I _gOFF and I _K decay with similar kinetics when voltage sensors are slow (Fig. 13 D, 10× and 30×). These results demonstrate that OFF charge movement can be limited by the speed of channel deactivation even when multiple open states are present.

Figure 13.

Voltage-sensor speed and the detection of open-state charge. Ionic and gating currents were simulated in response to a 20-ms pulse to +240 mV (HP = −80 mV) using the allosteric model. Traces labeled 1× were generated using Case B parameters (Table ). 10× and 30× traces indicate the effects of a 10- or 30-fold increase in the time constant of voltage-sensor movement, implemented by decreasing both voltage-sensor rate constants (α, β) and leaving equilibrium constants unchanged. As voltage-sensor movement is slowed (A), the time course of I _K activation becomes more sigmoidal. (B) I _g is slowed and the OFF current becomes ‘hooked.’ Most channels are open at the end of the pulse, and the relaxation of OFF charge plotted as Q _OFF(t)–Q _OFFss in C is biphasic when voltage-sensor movement is fast (1×) representing O–O (Medium) and O–C (Slow) transitions. However, open-channel charge movement is not evident as a kinetically distinct component of Q _OFF when voltage sensors are slowed (10×, 30×). (D) Similarly, the decay of I _gOFF is much faster than I _K deactivation when voltage-sensor movement is fast, but I _gOFF and I _K decay with a similar time constant for 10× and 30× simulations.

Table 1.

Allosteric Scheme Parameters

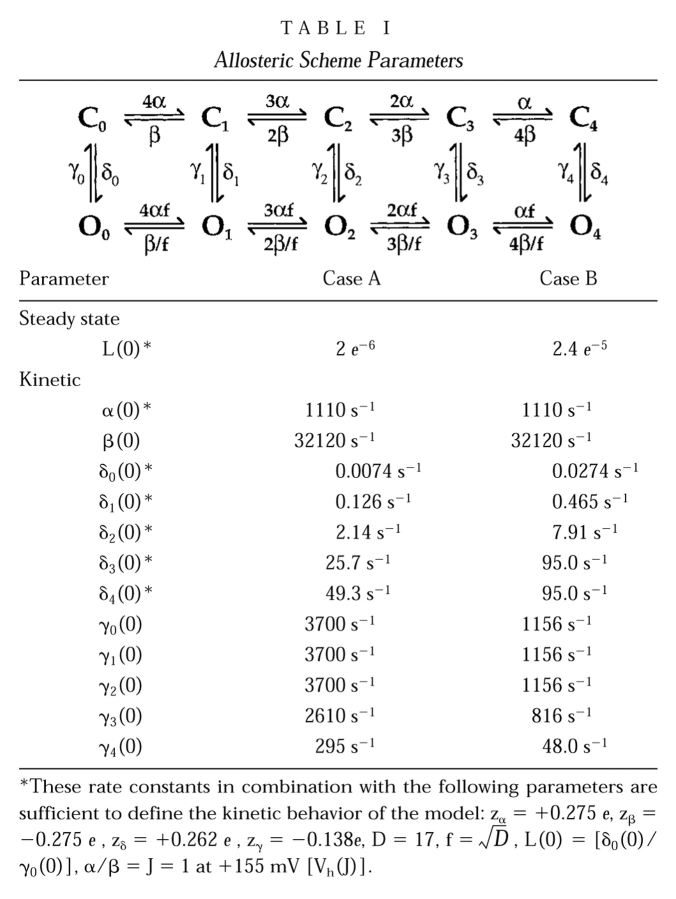
Parameter	Case A	Case B
Steady state
L(0)*	2 e −6	2.4 e −5
Kinetic
α(0)*	1110 s−1	1110 s−1
β(0)	32120 s−1	32120 s−1
δ0(0)*	0.0074 s−1	0.0274 s−1
δ1(0)*	0.126 s−1	0.465 s−1
δ2(0)*	2.14 s−1	7.91 s−1
δ3(0)*	25.7 s−1	95.0 s−1
δ4(0)*	49.3 s−1	95.0 s−1
γ0(0)	3700 s−1	1156 s−1
γ1(0)	3700 s−1	1156 s−1
γ2(0)	3700 s−1	1156 s−1
γ3(0)	2610 s−1	816 s−1
γ4(0)	295 s−1	48.0 s−1

*These rate constants in combination with the following parameters are sufficient to define the kinetic behavior of the model: z_α = +0.275 e, z_β = −0.275 e , z_δ = +0.262 e , z_γ = −0.138e, D = 17, f =D, L(0) = [δ₀(0)/γ₀(0)], α/β = J = 1 at +155 mV [V_h(J)].