Early Intermediates in the Transport Cycle of the Neuronal Excitatory Amino Acid Carrier Eaac1

Abstract

Electrogenic glutamate transport by the excitatory amino acid carrier 1 (EAAC1) is associated with multiple charge movements across the membrane that take place on time scales ranging from microseconds to milliseconds. The molecular nature of these charge movements is poorly understood at present and, therefore, was studied in this report in detail by using the technique of laser-pulse photolysis of caged glutamate providing a 100-μs time resolution. In the inward transport mode, the deactivation of the transient component of the glutamate-induced coupled transport current exhibits two exponential components. Similar results were obtained when restricting EAAC1 to Na⁺ translocation steps by removing potassium, thus, demonstrating (1) that substrate translocation of EAAC1 is coupled to inward movement of positive charge and, therefore, electrogenic; and (2) the existence of at least two distinct intermediates in the Na⁺-binding and glutamate translocation limb of the EAAC1 transport cycle. Together with the determination of the sodium ion concentration and voltage dependence of the two-exponential charge movement and of the steady-state EAAC1 properties, we developed a kinetic model that is based on sequential binding of Na⁺ and glutamate to their extracellular binding sites on EAAC1 explaining our results. In this model, at least one Na⁺ ion and thereafter glutamate rapidly bind to the transporter initiating a slower, electroneutral structural change that makes EAAC1 competent for further, voltage-dependent binding of additional sodium ion(s). Once the fully loaded EAAC1 complex is formed, it can undergo a much slower, electrogenic translocation reaction to expose the substrate and ion binding sites to the cytoplasm.

INTRODUCTION

In the mammalian brain l-glutamate is the major excitatory neurotransmitter (Kandel et al. 1995). It is responsible for rapid chemical signal transmission at excitatory synapses and also involved in excitotoxicity at high concentrations (Choi 1988). Glutamate is removed from the synapse by uptake into neurons and glial cells surrounding the synaptic contacts. This process is mediated by high affinity glutamate transporters and allows the cells to maintain a 10⁶-fold concentration gradient of glutamate across the membrane (Zerangue and Kavanaugh 1996). The glutamate uptake is mediated by the coupled transport of one glutamate molecule to cotransport of three sodium ions and one proton, and countertransport of one potassium ion (Kanner and Sharon 1978; Wadiche et al. 1995a; Zerangue and Kavanaugh 1996).

According to the proposed stoichiometry, a total of two positive charges is moved in the inward direction during a single turnover of the glutamate transporter. Thus, glutamate transport is electrogenic and induces transmembrane currents. At present, only one electrogenic partial reaction of the transporter has been identified that is responsible for <20% of the total charge movement, namely the binding of sodium ions on the extracellular side or conformational changes of the transport protein linked to it (Wadiche et al. 1995b; Wadiche and Kavanaugh 1998; Mennerick et al. 1999). This electrogenic reaction was detected as inhibitor- and Na⁺-sensitive transient charge movements upon applying transmembrane potential jumps. Similar charge movements occurring on a millisecond time scale were characterized in Na⁺-coupled transporters that belong to different families, such as the sugar transporter (Loo et al. 1993), the γ-aminobutyric acid (GABA) transporter (Mager et al. 1993; Lu and Hilgemann 1999), and the phosphate transporters (Forster et al. 1998). Thus, such electrogenic sodium ion–binding reactions appear to be a general feature of Na⁺-driven secondary transporters. However, other investigators and we identified additional charge movements in glutamate transporters that are induced by rapidly applying the amino acid substrate to the extracellular side of the transporter (Otis and Kavanaugh 2000; Bergles and Jahr 1997; Grewer et al. 2000). These reactions most likely carry part of the remaining 80% of the charge moved by the transporter, but they are not characterized well at present.

Closely linked to this issue are questions about the sequence and mechanism of Na⁺ and glutamate binding on the extracellular side of the transporter. In general, such questions can be answered by investigating the dependence of transport currents on the concentration of cotransported ions, as we have recently demonstrated by determining the binding sequence of protons and glutamate to the EAAC1 (Watzke et al. 2000). Although in a number of studies the sodium ion concentration dependence of glutamate transport under stationary conditions was investigated in the past (Kanner and Bendahan 1982; Erecinska et al. 1983; Schwartz and Tachibana 1990; Klockner et al. 1993; Kanai et al. 1995), there are no systematic investigations with regard to the binding sequence of Na⁺ with respect to glutamate.

To elucidate the transporter mechanism in more detail, we determined in this work the influence of the extracellular sodium ion concentration and the transmembrane potential on the steady-state and on the pre–steady-state currents of a neuronal subtype of the glutamate transporter excitatory amino acid carrier 1 (EAAC1) with a time resolution of 100 μs. This time resolution was achieved by applying the method of laser-pulse photolysis of caged glutamate that we introduced recently for studying rapid glutamate transporter reactions (Grewer et al. 2000). To restrict EAAC1 reactions to the Na⁺-translocating half cycle, the charge movements of the transporter were investigated in the Na⁺/glutamate homoexchange mode in the total absence of potassium ions. These conditions allowed us to eliminate K⁺-related EAAC1 reactions and to detect new, short-lived reaction intermediates that are associated with Na⁺-binding and translocation. From the results under stationary conditions, we deduced the binding sequence for glutamate and sodium ions on the extracellular side of EAAC1, in which the glutamate binding process is located in between sodium ion-binding steps.

MATERIALS AND METHODS

Expression of EAAC1 in Mammalian Cells

Rat EAAC1 cloned from rat retina (Rauen et al. 1996; Grewer et al. 2000) was subcloned into the vector pBK-CMV (Stratagene) and used for transient transfection of subconfluent human embryonic kidney cell (HEK293; ATCC No. CGL 1573) cultures with the calcium phosphate–mediated transfection method as described (Chen and Okayama 1987). Electrophysiological recordings were performed 24 h after the transfection for 3 d.

Electrophysiology

Glutamate-induced EAAC1 currents were recorded with an amplifier (model EPC7; Adams and List) under voltage-clamp conditions in the whole-cell current-recording configuration (Hamill et al. 1981). The typical resistance of the recording electrode was 2–3 MΩ. EAAC1-mediated uncoupled anion currents can be increased by using the more permeant anion SCN⁻ instead of chloride (Fairman et al. 1995; Wadiche et al. 1995a; Otis and Jahr 1998). For this reason, two different pipet solutions were used depending on whether mainly the noncoupled anion current (with thiocyanate) or the coupled transport current (with chloride) was investigated (in mM): 130 KSCN or KCl, 2 MgCl₂, 10 TEACl, 10 EGTA, and 10 HEPES, pH 7.4/KOH. The addition of 2.5 mM CaCl₂ (= 0.1 μM free calcium) had no influence on the detected current. For measurements of EAAC1 currents in the Na⁺/glutamate homoexchange mode, the pipet solution contained (in mM): 130 NaCl, 2 MgCl₂, 10 TEACl, 10 EGTA, 10 glutamate, and 10 HEPES, pH 7.4/KOH. The Na⁺ concentration of the external solution was adjusted by mixing a Na⁺-free bath solution of (in mM) 140 choline chloride, 2 MgCl₂, 2 CaCl₂, and 30 HEPES, pH 7.35/NMG, with a Na⁺-rich solution of (in mM) 140 NaCl, 2 MgCl₂, 2 CaCl₂, 15 Tris, and 15 MES, pH 7.35. For the experiments in the absence of chloride, it was replaced by methanesulfonate or gluconate. For inhibiting the leak anion conductance dl-threo-β-benzyloxyaspartate (TBOA; Shimamoto et al. 1998) in concentrations of 6 μM (140 mM Na⁺) to 280 μM (5 mM Na⁺) were applied to the cell according to former determinations of K _i (Grewer et al. 2000) and assuming that the affinity for glutamate and TBOA show the same Na⁺ concentration dependence. For the measurement of the Na⁺- and inhibitor-sensitive transient charge movements upon a voltage jump, the capacitive transient cancellation of the EPC7 amplifier was used. All the experiments were performed at room temperature. Each experiment was repeated at least five times with at least three different cells, and the error bars represent the error of the single measurement (mean ± SD).

Laser-pulse Photolysis and Rapid Solution Exchange

The rapid solution exchange (time resolution ∼100–200 ms) was performed by means of a quartz tube (opening 350 μm) positioned at a distance of ≈0.5 mm to the cell. The linear flow rate of the solutions emerging from the opening of the tube was ∼5–10 cm/s. Laser-pulse photolysis experiments were performed as described previously (Niu et al. 1996). αCNB-caged glutamate (Molecular Probes; Wieboldt et al. 1994) in concentrations of 1 mM (140 mM and 49 mM Na⁺) to 4 mM (18 mM and 10 mM Na⁺) or free glutamate was applied to the cells and photolysis of the caged glutamate was initiated with a light flash (340 nm, 15 ns, excimer laser pumped dye laser; Lambda Physik). The light was coupled into a quartz fiber (diameter 365 μm) that was positioned in front of the cell in a distance of 300 μm. With maximum light intensities of 500–840 mJ/cm² saturating glutamate concentrations could be released, which was tested by comparison of the steady-state current with that generated by rapid perfusion of the same cell with 1 mM (140 mM and 49 mM Na⁺), 2 mM glutamate (18 mM Na⁺), or 4 mM glutamate (10 mM Na⁺; Grewer 1999).

Data were recorded using the pClamp6 software (Axon Instruments), digitized with a sampling rate of 1 kHz (solution exchange) or 25 kHz (laser photolysis and Na⁺ binding transient currents,) and low-pass filtered at 250 Hz or 3–10 kHz, respectively.

Data Evaluation and Terminology

For simplicity, the following terminology was used. The glutamate-induced coupled transport current was termed I ^Glu− _Na+/K+ in the inward transport mode and I ^Glu− _Na+ in the Na⁺/glutamate homoexchange mode. The uncoupled anion current was named I ^Glu− _anionic for the glutamate-dependent component and I _anionic for the glutamate-independent component.

Nonlinear regression fits of experimental data were performed with Origin (Microcal Software) or Clampfit (pClamp8 software; Axon Instruments) by the use of the following equations. The pre–steady-state currents of the anionic current (I ^Glu− _anionic, in the presence of SCN⁻) were fitted with a sum of two exponential functions and a steady-state current component (I _ss): I = I ₁ · exp(−t/τ_rise) + I ₂ · exp(−t/τ_decay) + I _ss. The pre–steady-state transport currents I ^Glu− _Na+/K+ and I ^Glu− _Na+ (in the absence of SCN⁻) were fitted with a sum of three exponential functions and a stationary current component: I = I ₁ · exp(−t/τ_rise) + I ₂ · exp(−t/τ_decay1) + I ₃ · exp(−t/τ_decay2) + I _ss. Under homoexchange conditions, I _ss became zero. The observed time constants of τ_rise of I ^Glu− _anionic were in the range of ≈1 ms and, therefore, were similar to the time constants of τ_decay1 of I ^Glu− _Na+/K+ and I ^Glu− _Na+. For this reason, we named these time constants in the remainder of this article τ_fast. A similar time dependence with τ ≈ 8 ms was found for the time constants τ_decay of I ^Glu− _anionic, and τ_decay2 of I ^Glu− _Na+/K+ and I ^Glu− _Na+. These time constants were named τ_slow.

RESULTS

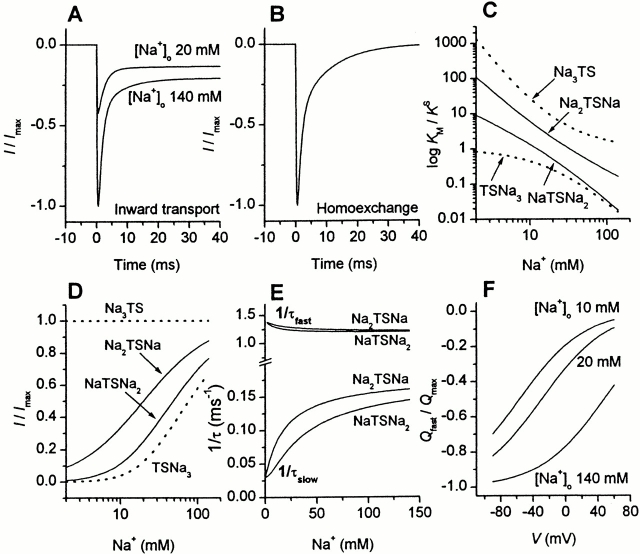
The time course of pre–steady-state kinetics of EAAC1 currents recorded in the anion-conducting mode (I ^Glu− _anionic) after a glutamate concentration jump induced by laser-pulse photolysis of caged glutamate shows a two-exponential behavior (Grewer et al. 2000), which is similar to fast solution exchange experiments on EAAT1 (Wadiche and Kavanaugh 1998) and EAAT4 (Otis and Jahr 1998). A fast phase is associated with the rise of the EAAC1 uncoupled anion current (I ^Glu− _anionic) to a maximum level, and a slow phase is associated with its decay to a steady-state current (Fig. 1 A). When the experiment is conducted at the same concentration of caged glutamate (1 mM), but in the absence of permeant anions, such as SCN⁻, the time dependence of the glutamate-induced current becomes more complex (Fig. 1 B). Under these conditions, the coupled transport component of the current (I ^Glu− _Na+/K+) is observed (Grewer et al. 2000), which is in general about one fourth the size of I ^Glu− _anionic in the inward transport mode (with SCN⁻; data not shown); however, the absolute amplitudes of the current vary up to 10-fold between different cells because of differences in EAAC1 expression levels. The current is inwardly directed (Fig. 1 B), which is consistent with positive charge moving into the cell. As shown in Fig. 1 B, a very rapid rising phase of I ^Glu− _Na+/K+ with a time constant of 0.6 ± 0.2 ms (n = 6) precedes the decay of the current that finally reaches a new steady-state level after ∼50 ms. The kinetics are different from those observed for I ^Glu− _anionic in two ways. First, the maximum of the current is shifted to shorter times; and, second, the decay of the current occurs with two exponentials. Attempts to fit the decay of I ^Glu− _Na+/K+ with only one exponential component yielded significantly inferior fits compared with those with two exponential components, as shown by the analysis of the fitting residuals in Fig. 1 B (top panel). We determined a time constant of τ = 0.9 ± 0.1 ms (n = 6) for the rapidly decaying phase of I ^Glu− _Na+/K+, in the same range as τ = 0.8 ± 0.1 ms (n = 20) for the rising phase of the anionic component of EAAC1 currents (Grewer et al. 2000; Watzke et al. 2000). This result indicates that these phases are associated with the same reaction(s) of EAAC1 (see also Fig. 1 D). The slow phase decayed with an average time constant of τ = 8.8 ± 1.1 ms (n = 6), which is similar to the time constant we found for the decay of I ^Glu− _anionic (τ = 8.7 ± 0.4 ms, n = 20), again suggesting that they represent the same kinetic process. For simplicity, we named the time constants according to their magnitude τ_fast and τ_slow (see materials and methods).

Figure 1.

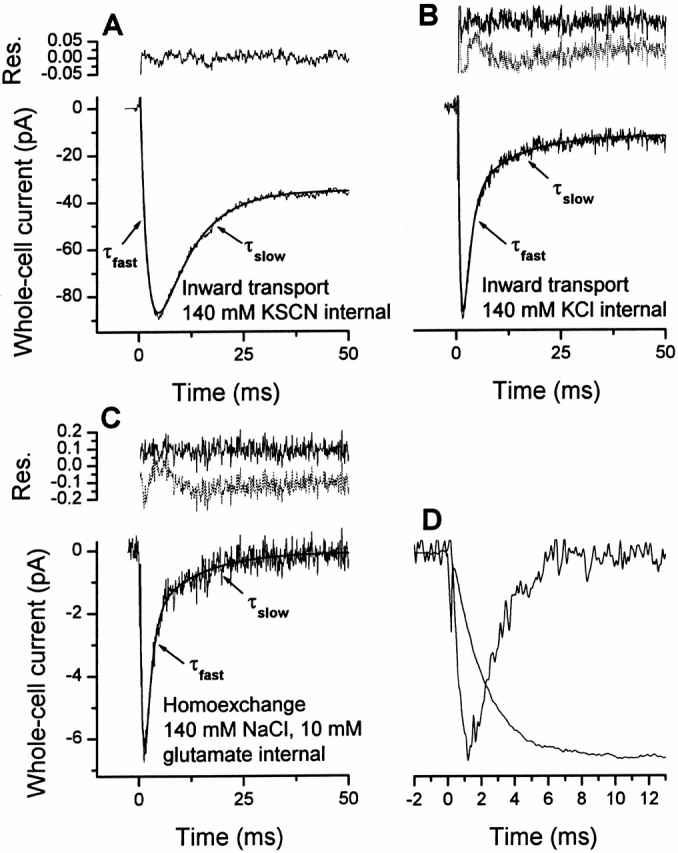
Typical whole-cell current recordings from three different EAAC1-expressing voltage-clamped HEK293 cells. Glutamate was photolytically released from 1 mM of αCNB-caged glutamate with a 340-nm laser flash (400 mJ/cm²) at t = 0. The concentration of photolytically released glutamate was estimated as 150 ± 20 μM. In this, and the following figures, the leak current was subtracted. The solid lines represent the best fits to the data according to a sum of two (A) or three (B and C) exponential functions, respectively (see materials and methods). The residuals of the fits are shown in the top panels ([solid line] two exponentials; [dashed line] three exponentials). The transmembrane potential was 0 mV. (A) The intracellular solution contained 140 mM KSCN. The time constants for the rise and the decay of the current were τ_fast = 1.7 ± 0.1 ms and τ_slow = 8.1 ± 0.1 ms, respectively. (B) The intracellular solution contained 140 mM KCl. The time constants for the current decay were τ_fast = 1.5 ± 0.2 ms and τ_slow = 8.1 ± 0.6 ms. τ_rise was 0.4 ± 0.1 ms. (C) The intracellular solution contained 140 mM NaCl and 10 mM glutamate. The time constants for the current decay were τ_fast = 1.2 ± 0.2 ms and τ_slow = 12 ± 0.5 ms. τ_rise was 0.7 ± 0.1 ms. (D) Comparison of the time course of the current rise of the anionic current component (in the presence of internal Na⁺ and glutamate) and the rapid decay of the transport current component (as shown in C). The latter current was corrected for the slowly decaying phase by subtraction of its exponential contribution that was estimated by the fit. All current traces were normalized to the same maximum amplitude.

Pre–steady-state Currents in the Na⁺/Glutamate Homoexchange Mode

So far, we determined the pre–steady-state kinetics of EAAC1 in the inward transport mode. We then asked the question whether the same charge movements are present when the amino acid substrate and Na⁺ are applied to either side of the membrane and potassium ions are absent (homoexchange mode). Under these conditions, reactions related to the relocation of the K⁺-bound transporter are eliminated, thus, allowing one to isolate the Na⁺/glutamate half cycle of EAAC1. The result of this experiment is shown in Fig. 1 C. The homoexchange current, I ^Glu− _Na+, has a very similar time dependence as I ^Glu− _Na+/K+ in the inward transport mode. However, as expected for electroneutral equilibrium exchange, there is no steady-state current component observed, within experimental error. In analogy to I ^Glu− _Na+/K+ in the inward transport mode, the decay of the transient current is a double exponential process, with a rapidly and a slowly decaying component. As in the inward transport mode, the rate constant of the decay of the rapid phase of I ^Glu− _Na+ is similar to the rise of the anionic current component in the presence of SCN⁻ (I ^Glu− _anionic), as illustrated in Fig. 1 D where both currents were corrected for the contribution of the slow phase and scaled to the same amplitude. These results demonstrate that both, the fast and the slow charge movements are not associated with relocation steps of the K⁺-bound transporter, but rather with the Na⁺/glutamate translocation limb of the transport cycle.

To further characterize the two kinetic phases in the Na⁺/glutamate translocation limb of the transport cycle, we determined their voltage dependence.

Voltage Dependence of Pre–steady-state EAAC1 Currents

Typical glutamate-induced fast EAAC1 currents in the homoexchange mode (I ^Glu− _Na+) as a function of the transmembrane potential (V _m) are shown in Fig. 2 A. Clearly, the transient I ^Glu− _Na+ component increases with decreasing transmembrane potential (Fig. 2 A), is always inwardly directed, and has a tendency to saturate at strongly negative V _m. The rate constant of the decay of the slow current component (1/τ_slow of I ^Glu− _Na+) increases exponentially with decreasing V _m (Fig. 2 B, open circles). This voltage dependence of 1/τ_slow is similar in the inward transport mode (I ^Glu− _Na+/K+, closed circles). In addition, 1/τ_slow for the anionic current component I ^Glu− _anionic in the inward transport mode is shown (open triangles), demonstrating the same voltage dependence, within experimental error. The qualitatively identical voltage dependence of τ_slow determined from I ^Glu− _Na+/K+ and from I ^Glu− _anionic show that they are associated to the same kinetic process in the Na⁺/glutamate translocation limb of the transport cycle. These results further indicate that EAAC1 charge movements are strongly inwardly driven, even in the equilibrium exchange mode. Linear regression of the log(1/τ_slow) versus V _m relationship yields a slope of (−4.7 ± 0.2) × 10⁻³/mV (Fig. 2 B, solid line). This corresponds to a fraction of 0.56 of the transmembrane electric field sensed by this process if one charge was moved.

Figure 2.

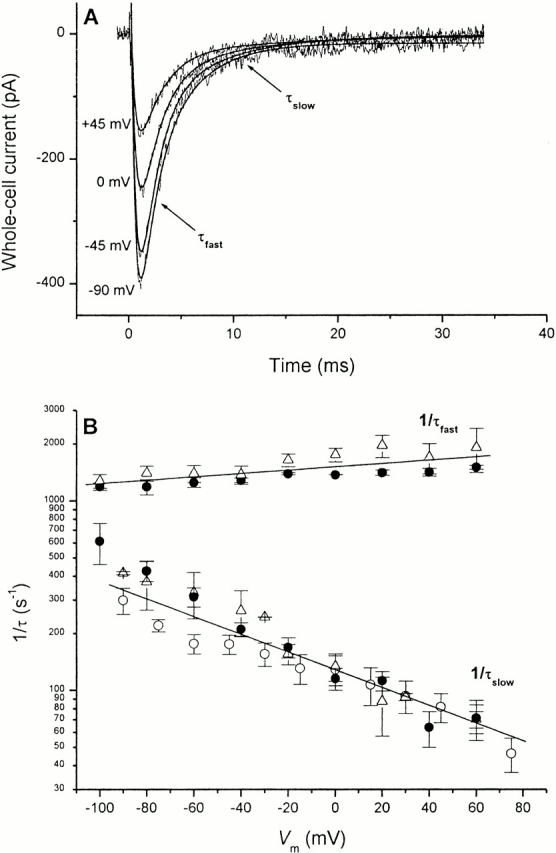
Voltage dependence of EAAC1 transport currents, I ^Glu− _Na+, in the Na⁺/glutamate homoexchange mode. (A) Typical current recording traces. The intracellular solution contained no K⁺, but 140 mM Na⁺ and 10 mM glutamate, the extracellular buffer 140 mM Na⁺. Chloride was replaced with methanesulfonate on both sides of the membrane. The cell was equilibrated with 1 mM αCNB-caged glutamate (∼100 μM released) for 1 s before the laser was fired at time t = 0. The current versus time traces were fit with a sum of three exponentials yielding the following fit parameters: for V _m = +45 mV, τ_rise = 0.42 ± 0.01 ms, τ_fast = 2.0 ± 0.1 ms, and τ_slow = 15.5 ± 0.5 ms; for V _m = 0 mV, τ_rise = 0.49 ± 0.01 ms, τ_fast = 1.8 ± 0.2 ms, and τ_slow = 9.2 ± 0.2 ms; for V _m = −45 mV, τ_rise = 0.53 ± 0.01 ms, τ_fast = 1.5 ± 0.1 ms, and τ _slow = 6.4 ± 0.2 ms; and for V _m = −90 mV, τ_rise = 0.48 ± 0.01 ms, τ_fast = 1.4 ± 0.2 ms, and τ_slow = 4.0 ± 0.2 ms. (B) Relaxation rate constants are shown as a function of the transmembrane potential for different experimental conditions. Open triangles (top trace): 1/τ_fast of I ^Glu− _anionic (KSCN-based pipet solution). Closed circles (top trace): the relaxation rate constant of the rapidly decaying phase 1/τ_fast of I ^Glu− _Na+/K+ (K-methanesulfonate-based pipet solution). Open triangles (bottom trace): 1/τ _slow of I ^Glu− _anionic (KSCN-based pipet solution). Closed circles (bottom trace): the relaxation rate constant of the slowly decaying phase 1/τ_slow of I ^Glu− _Na+/K+ (K-methanesulfonate-based pipet solution). Open circles (bottom trace): the relaxation rate constant of the slowly decaying phase 1/τ_slow of I ^Glu− _Na+ (sodium methanesulfonate/glutamate-based pipet solution). The solid lines represent the results of a linear regression analysis of the log(1/τ) versus V _m relationship with slopes of 8.8 × 10⁻⁴/mV (top line) and −4.7 × 10⁻³/mV (bottom line).

In principle, the voltage dependence of relaxation rate constants and charge movements could be influenced by the distribution of the initial states of the carrier before the glutamate concentration jump. However, in the absence of extracellular K⁺ and glutamate, it is reasonable to assume that EAAC1 is locked in a state (or states) with the glutamate binding site exposed to the external side of the membrane.

In contrast to 1/τ_slow, the rate constant for the fast decaying phase of I ^Glu− _Na+/K+ was only slightly affected by the voltage and increased with increasing the potential (Fig. 2 B, closed circles). The same voltage dependence was found for the time constant of the rising phase of I ^Glu− _anionic (τ_fast see materials and methods) as shown in Fig. 2 B (open triangles), indicating that both rate constants reflect the same reaction process of EAAC1. Comparison of the voltage dependence of τ_slow and τ_fast further show that the slope of (8.8 ± 2.2) × 10⁻⁴/mV of the log(1/τ_fast) versus V _m relationship is only about one fifth of the slope found for the voltage dependence of log(1/τ_slow) and has the opposite sign. Together, these results suggest that the rapidly decaying current component of I ^Glu− _Na+/K+ and I ^Glu− _Na+ (or rapidly rising current component of I ^Glu− _anionic) is associated with an inward charge movement, however, its rate of decay (or rise) is determined by a process that is only weakly and oppositely dependent on the transmembrane potential compared with the slow phase.

In the following paragraphs, we describe the more detailed characterization of these charge movements and their relationship to the binding of extracellular sodium ions and the translocation of substrate across the membrane.

Glutamate-independent Fast Charge Movements Are Inhibited by TBOA

Wadiche and co-workers (Wadiche et al. 1995b) observed kainate-sensitive transient currents in Xenopus oocytes expressing EAAT2 in the absence of glutamate and permeant anions. They suggested that these transient currents result from voltage-dependent binding and unbinding of sodium ions to a site of the transporter, which is located within the electrical field. For EAAC1 expressed in oocytes, however, Kanai and co-workers (Kanai et al. 1994, Kanai et al. 1995) reported, that no significant Na⁺-dependent relaxation currents could be observed. To clarify this controversy and to test if the charge movements observed in the laser-pulse photolysis experiments may be caused by such an electrogenic sodium ion binding process we measured dl-threo-β-benzyloxyaspartate- (TBOA, a nontransportable competitive inhibitor) sensitive charge movements in EAAC1 by applying voltage jumps. As demonstrated in Fig. 3 A (top trace), we observed capacitive transient currents that were abolished in the presence of the competitive inhibitor TBOA. To exclude a change in membrane capacitance during the voltage-jump protocol, the voltage-jump–induced transient currents measured before and after the experiment in the presence of TBOA were subtracted from each other, showing no difference (Fig. 3 A, bottom trace).

Figure 3.

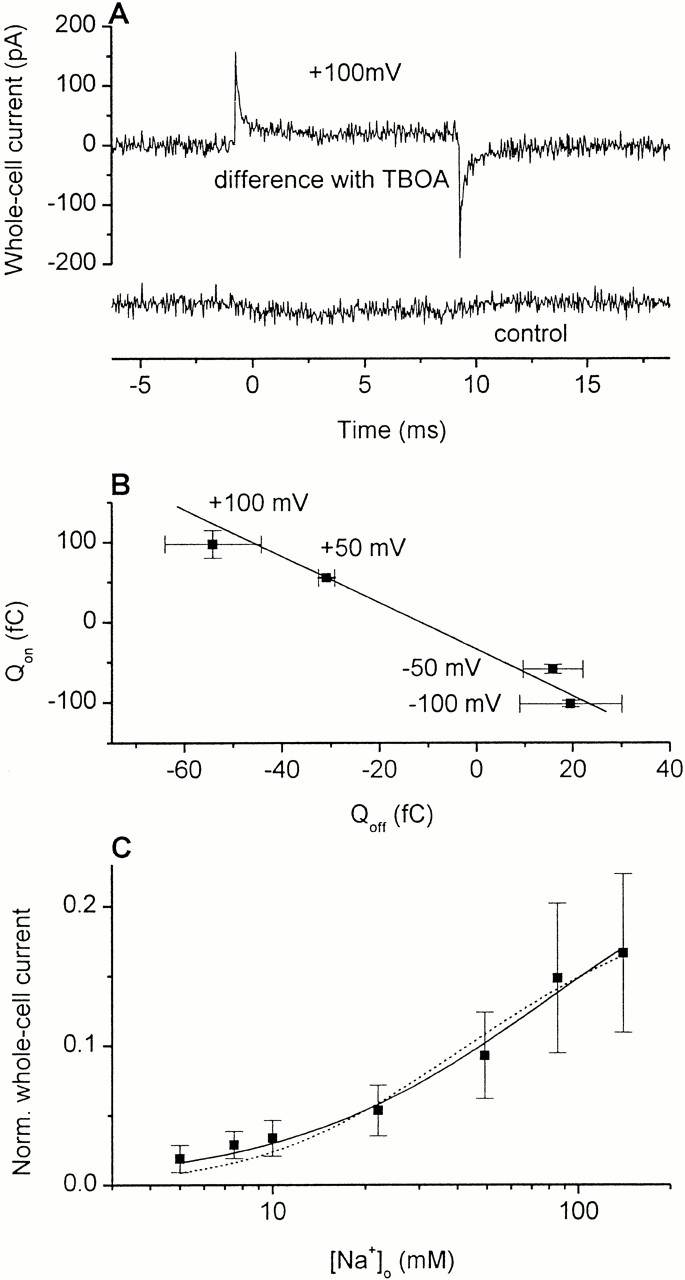
(A) TBOA-sensitive relaxation currents in the presence of 140 mM Na⁺. (top trace) Difference between whole-cell current recordings from a HEK_EAAC1 cell of a 100-mV voltage jump in the absence and presence of TBOA (6 mM) using a KCl-based pipet solution. The time constants for the decay are 0.15 ± 0.02 ms for the on signal and 0.17 ± 0.02 ms for the off signal. (bottom trace) Subtracted current traces in the absence of TBOA recorded before and after a TBOA application to the cell. (B) Integration of three traces as shown in A (top trace) upon the voltage jump (100, 50, −50, and −100 mV) calculating the moved charge for the on and off response. The integration period was limited to 2 ms because of the small stationary offset current that is most likely caused by Cl⁻ permeation of the leak anion conductance. However, after 2 ms, >99.9% of the transient current is decayed. Thus, the error introduced by the limited integration interval should be negligible. (C) Determination of the apparent K _M for Na⁺ in the absence of glutamate by inhibiting the leak anion conductance of EAAC1 with TBOA in concentrations from 6 μM (140 mM Na⁺) to 280 μM (5 mM Na⁺). The whole-cell current recordings were performed with a KSCN-based pipet solution under steady-state conditions and 0-mV transmembrane potential. The leak currents were normalized to the glutamate-induced current (1 mM) at the same cell. The lines represent fits to the Hill equation I = (I _max · [glutamate]ⁿ)/(K _M + [glutamate])ⁿ, with a Hill coefficient of n = 1 and a K _M value of 80 ± 17 mM for the solid line and a Hill coefficient of n = 2 and a K _M value of 20 ± 4 mM for the dotted line.

In line with results obtained by Wadiche and co-workers (Wadiche et al. 1995b), the moved charge for the on and off response was almost the same as shown in Fig. 3 B and as expected for capacitive currents. However, whereas EAAT2 expressed in Xenopus oocytes showed voltage-dependent rate constants for the decay of the transient current in a range of 3–4 ms, τ for EAAC1 in HEK293 cells was voltage independent and at least 20-fold faster with an average time constant of 150 ± 30 μs (n = 12, 2 cells). The voltage independence implies that the determination of this time constant is most likely limited by the time resolution of the voltage clamp (estimated to ∼100 μs from typical series resistance and cell capacitance values, the filter frequency was 3 kHz). Therefore, even though the charge movements are detectable, their time course is distorted by the rate-limiting voltage clamp. However, the existence of these TBOA-sensitive transient charge movements indicate that EAAC1, in analogy to EAAT2, binds sodium ions in a very rapid process before the glutamate binding process occurs (see next paragraphs). For EAAT2, it was found that the inhibitor-sensitive transient charge movements are abolished in the absence of extracellular Na⁺ (Wadiche et al. 1995b), suggesting that the empty transporter does not contribute to these charge movements. The general analogy between EAAC1 and EAAT2 voltage-jump–induced transient currents points toward a similar situation for EAAC1. For the TBOA-sensitive charge movement, we estimated that 25–30% of the transmembrane electric field is traversed by the charge. This is slightly less than what has been reported for EAAT2 by Wadiche et al. (41%; Wadiche et al. 1995b). The extremely rapid time course of the voltage-jump–induced transient current resulting from the first (two) Na⁺-binding reaction(s) to the transporter suggests that these charge movements are distinct from the ones observed after glutamate concentration jumps.

Na⁺ Concentration Dependence of the Leak Anion Conductance

As shown by others (Otis and Jahr 1998) and by us (Grewer et al. 2000), glutamate transporters exhibit a leak anion current (I _anionic), which can be inhibited by transporter-specific nontransported inhibitors, such as kainate (EAAT2) and TBOA (EAAC1). This glutamate-independent current is only detected in the presence of extracellular Na⁺ (Schwartz and Tachibana 1990). We exploited this fact to determine the affinity of EAAC1 for Na⁺ in the absence of glutamate. Voltage-clamped HEK_EAAC1 cells (V _m = 0 mV) were exposed to different Na⁺ concentrations, and the leak anion conductance was inhibited by applying saturating concentrations of TBOA (see materials and methods). As seen in Fig. 3 C, the data could be well fitted by a Hill equation with a Hill coefficient n = 1 and an apparent K _M of 80 ± 17 mM (solid line). This K _M is in good agreement with that reported for EAAT2 (98 mM) obtained by using a different method (Wadiche et al. 1995b). Therefore, these results provide additional and independent evidence that Na⁺ binds to glutamate transporters with relatively low affinity in the absence of glutamate. A fit with n = 2 (dotted line) resulted in a slightly inferior fit, with a χ² twice as high compared with the case of n = 1 (Fig. 3 C). However, within experimental error, it is impossible to differentiate if binding of one or two Na⁺ ions is associated with this process.

Steady-state Currents: [Na⁺] Dependence of K_M

To characterize the [Na⁺] dependence of EAAC1 currents in more detail, we performed experiments under conditions of steady-state inward transport (I ^Glu− _anionic). First, we investigated changes in affinity of EAAC1 for glutamate depending on the extracellular sodium ion concentration. Glutamate in different concentrations was applied to voltage-clamped HEK_EAAC1 cells (V _m = 0 mV) with a rapid solution exchange device. In the whole Na⁺ concentration range (5–140 mM) studied, the glutamate dependencies could be well fitted by Michaelis-Menten–like relationships (Fig. 4 A). From the fits, we determined the apparent glutamate dissociation constants and the current at saturating glutamate concentrations I _max. As seen in Fig. 4 A, reduced extracellular Na⁺ concentrations lead to a pronounced increase of the apparent K _M for glutamate from 7.2 ± 1.1 μM at 140 mM Na⁺ to 380 ± 50 μM at 5 mM external Na⁺. The [Na⁺] dependence of K _M is shown in a logarithmic plot in Fig. 4 B.

Figure 4.

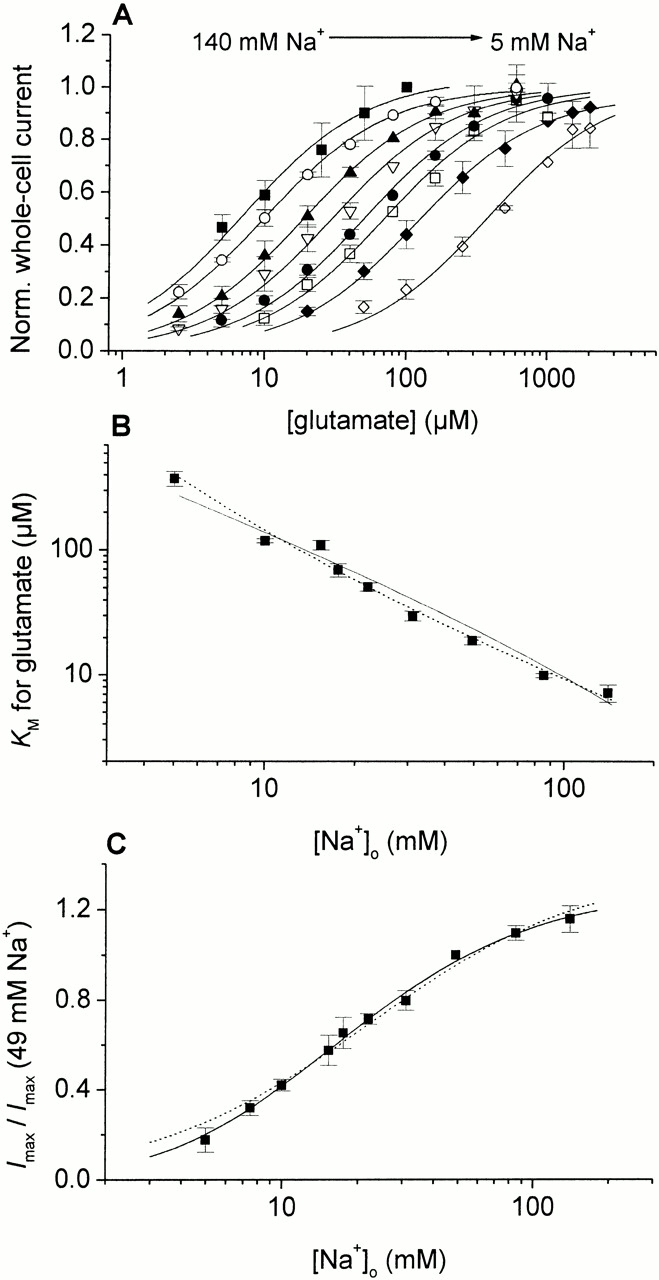
(A) [Na⁺] dependence of the apparent K _M for glutamate from whole-cell current recordings with a KSCN-based pipet solution under steady-state conditions and 0-mV transmembrane potential. With a rapid solution exchange device glutamate was applied to the cell. The solid lines represent fits to the Hill equation I = (I _max · [glutamate]ⁿ)/(K _M + [glutamate])ⁿ with a Hill coefficient of n = 1 to the experimental data at 140 mM (solid squares), 86 mM (open circle), 49 mM (closed up triangle), 31 mM (open down triangle), 23 mM (closed circle), 18 mM (open square), 10 mM (closed diamond), and 5 mM (open diamond) Na⁺. The whole-cell current recordings were normalized to I _max. (B) Double logarithmic plot of the apparent K _M values at different Na⁺ concentrations. The solid line represents the fit to the model NaTSNa₂ (for equation see Table , parameters: K ^S = 18 μM, K ^Na+1 = 80 mM, and K ^Na+2/3 = 120 mM). The dotted line represents the fit to the model Na₂TSNa (for equation see Table , parameters: K ^S = 75 μM, K ^Na+1/2 = 9 mM, and K ^Na+3 = 12 mM). (C) [Na⁺] dependence of I _max from whole-cell current recordings with a KSCN-based pipet solution at 0-mV transmembrane potential. Saturating concentrations of glutamate (10-fold K _M) were applied to the cell with a rapid solution exchange device. The solid and dotted line represent the fits as described in B. Parameters: K ^Na+2/3 = 7.7 ± 0.3 mM, K ^Na+3 = 22 ± 2 mM.

[Na⁺] Dependence of the Glutamate-induced Steady-state Current I_max

By comparing the maximum currents (I _max) induced by saturating glutamate concentrations at different extracellular Na⁺ concentrations, one can investigate the binding order of Na⁺ with respect to glutamate. The equations for the different models are shown in Table . As demonstrated in Fig. 4 C, I _max shows a strong [Na⁺] dependence; lowering the external Na⁺ concentration leads to a significant decrease in the maximum current. If all three sodium ions bind rapidly to the transporter before the glutamate binding process takes place, I _max should be the same in the whole Na⁺ concentration range (see Table and discussion). Thus, we can exclude this model. Therefore, the results suggest a difference in the binding sequence of protons and Na⁺ with respect to glutamate. Whereas protons can bind to the empty transporter before glutamate, at least one Na⁺ must bind to the substrate-loaded carrier. The fits shown in Fig. 4 C represent calculations according to the Hill equations with Hill coefficients of either one or two, indicating that one or two sodium ions bind after glutamate.

Table 1.

Kinetic Models for Glutamate Transport by EAAC1

Model	K M	I max	1/τslow
Na3TS	K S·K Na++Na+Na+ 3	≠fNa+	SK M+S·k f+k b≠fNa+
Na2TSNa	K S·K Na+12+Na+Na+ 2·K Na+3 K Na+3+Na+	Na+ K Na+3+Na+	Na+ K Na+3+Na+·SK M+S·k f+k b=fNa+
NaTSNa2	K S·K Na+1+Na+Na+·K Na+23 K Na+23+Na+ 2	Na+ K Na+23+Na+ 2	Na+ K Na+23+Na+ 2·SK M+S·k f+k b=fNa+
TSNa3	K S·K Na+ K Na++Na+ 3	Na+ K Na++Na+ 3	Na+ K Na++Na+ 3·SK M+S·k f+k b=fNa+
Random	K S	Na+ K Na++Na+ 3	Na+ K Na++Na+ 3·SK M+S·k f+k b=fNa+

Kinetic equations for models of EAAC1 glutamate/Na⁺ cotransport. The following assumptions were made for K _M and I _max and τ_slow: translocation proceeds from the fully loaded carrier, and Na⁺ and glutamate binding is very fast compared to steady-state turnover. Except for the Random model, the derivations are based on ordered and not simultaneous binding of Na⁺ to the transporter.

Na⁺ Concentration Dependence of I^Glu−_anionic Pre–steady-state Kinetics

As shown in Fig. 1, the fast and the slow charge movements are observed for the coupled transport current I ^Glu− _Na+/K+ as well as for homoexchange (I ^Glu− _Na+), indicating that the inwardly directed transient current is not influenced by the intracellular sodium ion concentration. Thus, to test if the pre–steady-state current is associated with binding of extracellular Na⁺, we determined its Na⁺ concentration dependence. Since lowering the extracellular sodium ion concentration leads to a drastic reduction of the I ^Glu− _Na+/K+ current component, the first measurements were done instead with I ^Glu− _anionic, which also contains information about τ_fast and τ_slow. In Fig. 5 A, photolysis experiments at different extracellular Na⁺ concentrations ([Na⁺]_o) are shown. At 140 mM extracellular Na⁺, photolytic release of saturating concentrations of glutamate from αCNB-caged glutamate leads to a rise of the current to a maximum (τ_fast = 0.8 ± 0.1 ms, n = 3) and a decay of the transient current to a steady state (τ_slow = 8.7 ± 0.4 ms, n = 3) that is consistent with previous reports (Grewer et al. 2000; Watzke et al. 2000). When lowering the extracellular Na⁺ concentration to 10 mM, the maximum current amplitude decreased and the ratio between the pre–steady-state current and the stationary current (I _ps/I _ss) changed from 2.7 ± 0.5 to 1.3 ± 0.3 (n = 3; Fig. 5 B, bottom panel). Additionally, τ_slow showed a strong [Na⁺] dependence (Fig. 5 B, top panel). It increases from 14.3 ± 1.4 ms at 49 mM [Na⁺]_o, to 19.9 ± 2.9 ms at 18 mM [Na⁺]_o, to 33.1 ± 5.2 ms at an extracellular Na⁺ concentration of 10 mM. In contrast, the fast time constant for the rising phase of the transient current (τ_fast) is almost [Na⁺] independent as seen in Fig. 5 B (top panel; see , ). This is consistent with the results obtained for the time constant of the fast decaying component of I ^Glu− _Na+/K+, which is also essentially [Na⁺] independent (Fig. 5 B), further supporting the view that these processes are associated with the same reaction of EAAC1.

Figure 5.

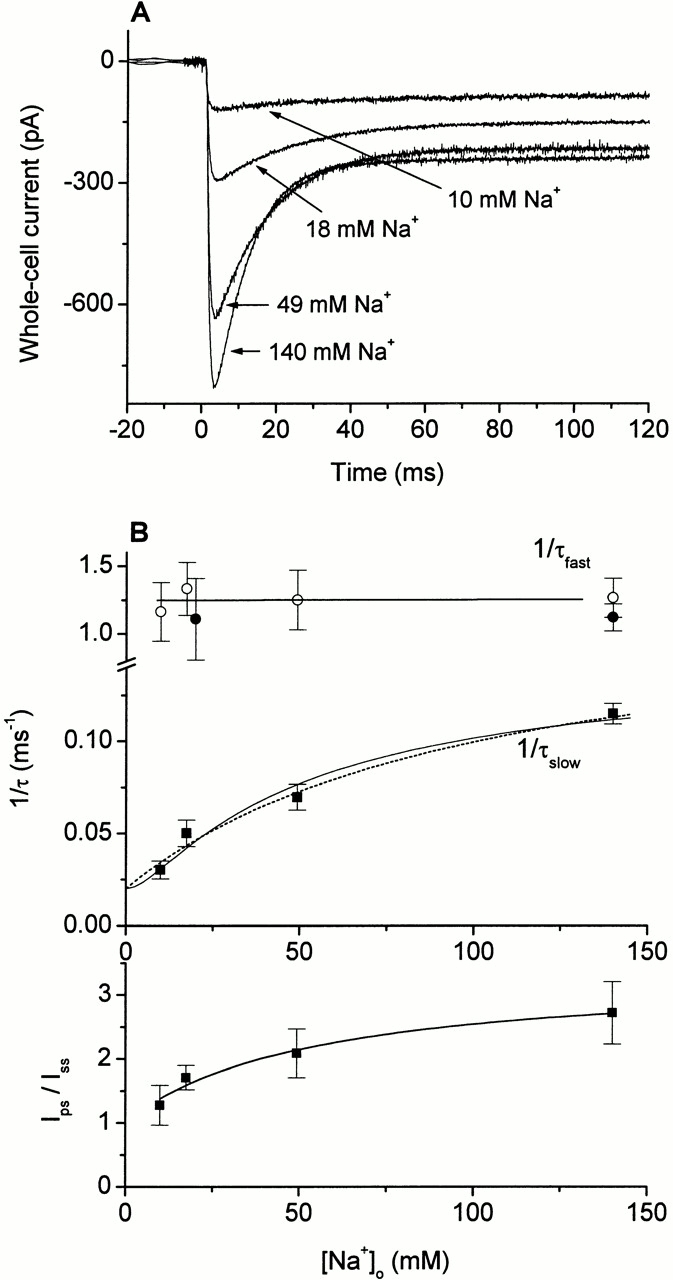
(A) Laser-pulse photolysis experiments of αCNB-caged glutamate on two cells at different Na⁺ concentrations, normalized to the relation in steady-state current obtained from Fig. 4C. The transmembrane potential was 0 mV, a KSCN-based pipet solution was used. The experimental data were fitted to a sum of two exponential functions. The parameters were as follows: 140 mM Na⁺, 150 μM free glutamate (1 mM caged glutamate), τ _slow = 9.5 ± 0.1 ms, and τ_fast = 0.86 ± 0.01 ms; 49 mM Na⁺, 400 μM free glutamate (2 mM caged glutamate), τ_slow = 14.4 ± 0.1 ms, and τ_fast = 0.70 ± 0.01 ms; 18 mM Na⁺, 800 μM free glutamate (4 mM caged glutamate), τ_slow = 21.1 ± 0.1 ms, and τ_fast = 0.83 ± 0.01 ms; 10 mM Na⁺, 1,000 μM free glutamate (4 mM caged glutamate), τ_slow = 34.6 ± 0.9 ms and τ_fast = 0.86 ± 0.03 ms. (B) (top panel, top trace) Averaged values (mean ± SD, n = 3) for 1/τ_fast (open circle) of I ^Glu− _anionic (as shown in A) and 1/τ_fast (closed circles) of I ^Glu− _Na+/K+ (as shown in Fig. 6 A) at different sodium ion concentrations. The solid line was drawn to guide the eye. (bottom trace) Averaged values (mean ± SD, n = 3) for 1/τ_slow (closed square) of I ^Glu− _anionic (as shown in A) at different [Na⁺]. The solid line represents the fit to the model NaTSNa₂ (for equation see Table , parameters: K ^Na+2/3 = 24 ± 7 mM, k _f = 130 ± 20 s⁻¹, and k _b = 20 s⁻¹). The dotted line represents the fit to the model Na₂TSNa (for equation see Table , parameters: K ^Na+3 = 100 ± 40 mM, k _f = 160 ± 30 s⁻¹, and k _b = 20 s⁻¹). (lower panel) Averaged value for the ratio between peak and stationary current (I _ps/I _ss) of I ^Glu− _anionic at different sodium ion concentrations. The ratio decreases from 2.7 ± 0.5 at 140 mM Na⁺, to 2.1 ± 0.4 at 49 mM Na⁺, to 1.7 ± 0.2 at 18 mM Na⁺, and finally to 1.4 ± 0.1 at 10 mM Na⁺. The solid line represents the fit to a modified Hill equation I = ((I _ps/ss (max) − 1) · [glutamate]ⁿ)/(K _app + [glutamate])ⁿ, with I _ps/I _ss (max) = 3.3 ± 0.3, n = 1, and K _app = 52 ± 16 mM.

The Magnitude of the Fast Charge Movement Is Na⁺ Concentration-dependent

To confirm that the Na⁺-binding reaction preceding the glutamate binding step does not cause the fast charge movements, as suggested above, we performed laser-pulse photolysis experiments detecting I ^Glu− _Na+/K+ at low extracellular Na⁺ concentrations. In case of a voltage-dependent Na⁺ preequilibrium preceding glutamate binding, the charge movements should increase with decreasing Na⁺ concentration. The opposite is found experimentally, as demonstrated in Fig. 6 A. The left panel shows the current (I ^Glu− _Na+/K+) recorded in a typical laser-pulse photolysis experiment (1 mM caged glutamate) in the presence of 140 mM extracellular Na⁺. To ensure that the [Na⁺]_o effect is not only caused by a change in the apparent K _M of EAAC1 for glutamate (see previous paragraphs) we raised the glutamate concentration by increasing the concentration of caged glutamate fourfold to 4 mM in the experiments with 20 mM Na⁺. The total charge obtained by integrating the fast component of the current at 140 mM Na⁺ is 47 fC. After decreasing the external Na⁺ concentration to 20 mM, the amplitude of the transient current is reduced by a factor of 3.7 (Fig. 6 A, right trace). The charge of the fast component is 15 fC. In four experiments with two cells, we obtained an average charge ratio Q(20 mM Na⁺)/Q(140 mM Na⁺) of 0.39 ± 0.06 (Fig. 6 B). The time constant for the decay of the fast current component τ_fast was 0.9 ± 0.2 ms (n = 6, 3 cells, 20 mM Na⁺) and, therefore, unchanged when compared with the results obtained at 140 mM extracellular Na⁺.

Figure 6.

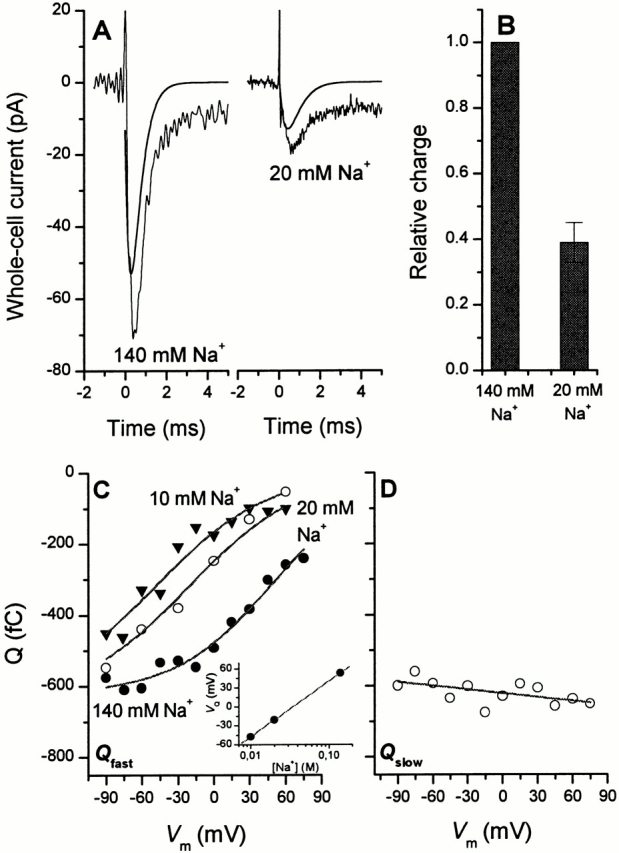
(A) Laser-pulse photolysis experiments with αCNB-caged glutamate at two different extracellular Na⁺ concentrations of 140 mM (left trace) and 20 mM (right trace); the concentration of caged glutamate was 1 mM (140 mM Na⁺) and 4 mM (20 mM Na⁺), respectively. The transmembrane potential was 0 mV and a KCl⁻-based intracellular solution was used. The solid lines represent the current that is generated during the fast phase of the reaction, which was computed by using the fit parameters obtained from a three-exponential fit to the data (see materials and methods) and neglecting the terms for the slowly decaying phase (I ₃) and the steady-state current (I _ss). This current component was integrated to obtain the charge moved in this process, which was 47 fC (140 mM Na⁺) and 15 fC (20 mM Na⁺), respectively. (B) Relative fast charge movement at 140 mM and 20 mM extracellular Na⁺. The charge was calculated according to the procedure shown in A. The data represent the mean (± SD) from four experiments with two cells. (C) Charge movement, Q(V _m), obtained by integrating the rapidly decaying current component at 140 mM (closed circles), 20 mM (open circles) and 10 mM Na⁺ (closed triangles) under homoexchange conditions. The solid lines were calculated according to a Boltzmann function (Q(V _m) = Q _min + Q _max· [1 + exp(z _Q(V _Q-V _m)· F/(RT))]⁻¹) where F is the Faraday constant, R is the molar gas constant, and T is the temperature (see , ). V _Q is the midpoint potential of the charge movement and was set to 53 mV (140 mM Na⁺), −21 mV (20 mM Na⁺) and −48 mV (10 mM Na⁺), and z _Q = 0.55 is the apparent valence. Q _min = 0 fC and Q _max = −630 fC are the minimum and maximum values of the charge movement, respectively. (inset) Dependence of the midpoint potential on the Na⁺ concentration. (D) Charge movement obtained by integrating the slowly decaying current component as a function of the transmembrane potential. The solid line was drawn to guide the eye. The other parameters were as in A. In C and D, the error bars are not shown. However, all data points represent the average of al least four experiments with two cells.

The voltage dependence of the charge carried by the rapid process is shown in Fig. 6 C for I ^Glu− _Na+ in the presence of 140, 20, or 10 mM Na⁺. At high sodium ion concentrations, the moved charge Q integrating the fast current component is invariant at V _m more negative than about −30 mV (Q _max = 620 ± 25 fC) and slightly decreases to 240 ± 28 fC (n = 8, 3 cells) at V _m = +75 mV. When fit to a Boltzmann-like relationship (see , ) a midpoint potential (V _Q) of 53 ± 7 mV and a apparent valence of 0.61 ± 0.08 are obtained (see , and ). At low Na⁺ concentrations (10 and 20 mM), in general, Q demonstrates the same dependence on the transmembrane potential; however, the midpoint potential of the charge movement is shifted to −48 ± 5 mV (10 mM Na⁺) and −21 ± 4 mV (20 mM Na⁺) with an apparent valence of 0.55 ± 0.05, as expected for a shift of the voltage-dependent Na⁺-binding equilibrium to the less-occupied form at low Na⁺ concentrations, according to (see ). From the shift in the midpoint potential, which is shown in Fig. 6 C (inset), the apparent valence is calculated as 0.65, in agreement with the slope factor of the Boltzmann relationships at each Na⁺ concentration. This finding is in agreement with a single voltage-dependent Na⁺-binding reaction of the EAAC1–Na⁺–glutamate complex. It should be noted that at Na⁺ concentrations of 10 and 20 mM, saturation of the charge movements at very negative potentials was not achieved due to the limited accessible range of transmembrane potentials. Therefore, the stated V _Q values at these Na⁺ concentrations represent lower estimates of the true V _Q.

In addition, we determined the charge moved during the slow process that is shown in Fig. 6 D. This charge movement is independent of the transmembrane potential, within experimental error (n = 8, 3 cells). Both charge movements are under saturating conditions of similar magnitude (Fig. 6C and Fig. D). Together, the results imply that charge transfer depends on extracellular Na⁺ and the transmembrane potential, but the rate of the deactivation process of the current does not. Such a Na⁺ concentration dependence can be explained with a two-step mechanism in which a slow and Na⁺- and voltage-independent reaction governs the rate of the current decay, whereas a subsequent rapid and electrogenic Na⁺-binding step is responsible for the inward charge movement.

Voltage Dependence of EAAC1 at Reduced External [Na⁺]

It was previously suggested that sodium ion binding may become rate limiting for the glutamate transporter turnover at low extracellular Na⁺ concentrations (Kanai et al. 1995). We tested this hypothesis by determining the voltage dependence of EAAC1 pre–steady-state currents (I ^Glu− _anionic) at an extracellular Na⁺ concentration of 10 mM in the inward transport mode. Typical results are shown in Fig. 7 A. The decay of the transient current is slowed compared with that observed at 140 mM extracellular Na⁺ at all transmembrane potentials as demonstrated in Fig. 7 B. However, the voltage dependence of 1/τ_slow is essentially unchanged. The slope of the log(1/τ_slow) versus V _m relationship at 10 mM Na⁺ is (−5.6 ± 0.1) × 10⁻³/mV, which is very close to that obtained at a Na⁺ concentration of 140 mM ((−5.5 ± 0.3)× 10⁻³/mV). Consistent with the results obtained at 140 mM extracellular Na⁺, the rate of the current rise is almost voltage independent.

Figure 7.

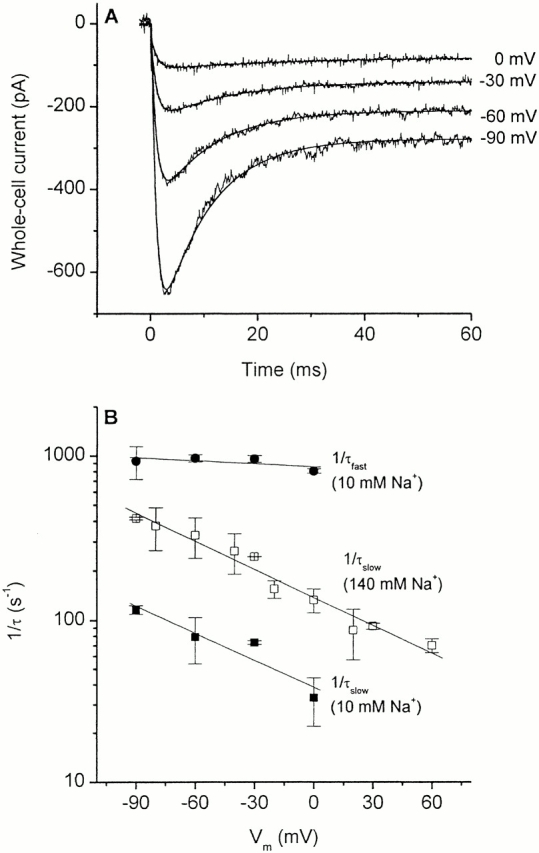
(A) Voltage dependence of the EAAC1 anionic current, I ^Glu− _anionic, in the presence of low concentrations (10 mM) of extracellular Na⁺. Typical current recordings with a KSCN-based pipet solution and the release of ≈850 mM free glutamate (4 mM caged glutamate). Leak currents were subtracted. The solid lines represent the best fits to the data according to the sum of two exponential functions. Parameters: for −90 mV, τ_fast 1.6 ± 0.1 ms, and τ_slow 5.5 ± 0.1 ms; for −60 mV, τ_fast 1.6 ± 0.1 ms, and τ_slow 7.1 ± 0.1 ms; for −30 mV, τ_fast 1.8 ± 0.1 ms, and τ_slow 10.2 ± 0.5 ms; and for 0 mV, τ_fast 1.3 ± 0.1 ms, and τ_slow 31.2 ± 0.2 ms. (B) Averaged values (mean ± SD, n = 5–7, 2 cells) of 1/τ_fast (closed circle) and 1/τ_slow (closed square) of I ^Glu− _anionic in the presence of 10 mM extracellular Na⁺ (as shown in A) and of 1/τ_slow (open square) of I ^Glu− _anionic in the presence of 140 mM extracellular Na⁺ at different holding potentials. The solid lines represent the results of a linear regression analysis of log(1/τ) versus V _m with slopes of −5.6 × 10⁻³/mV (1/τ_slow) and −6.2 × 10⁻⁴/mV (1/τ_fast).

DISCUSSION

Here, we have identified short-lived intermediates of the Na⁺-binding and glutamate translocation reaction of EAAC1 by using a rapid chemical-kinetic technique that we introduced recently to study glutamate transporter function (Grewer et al. 2000; Watzke et al. 2000). The main new findings of this pre–steady-state kinetic study are as follows. First, Na⁺ binding and glutamate translocation are associated with inward movement of positive charge and, thus, electrogenic. Second, binding of Na⁺ and glutamate to the transporter is a sequential, but not a random process. Third, at least three reactions in this sequence of events are voltage-dependent; and fourth, after binding of at least one Na⁺ ion and glutamate to the transporter a structural change of the complex must occur that induces the generation of at least one more Na⁺ binding site on the transporter. These findings lead us to propose a revised and more detailed kinetic model of the Na⁺/glutamate translocating half cycle of EAAC1 and to exclude other possible mechanisms, based on the kinetic data. The model will be discussed in depth in the next paragraphs.

The Nature of the Pre–steady-state Charge Movements

The main characteristic of the pre–steady-state charge movement is that its decay is two-exponential. Thus, the results directly point to the existence of two individual electrogenic reactions that are separated on the time scale. These reactions are also observed in the total absence of intracellular and extracellular K⁺, confirming our previous suggestion that they are related to the translocation of the Na⁺ and glutamate-loaded carrier, but not the relocation of the K⁺-bound form of EAAC1 (Grewer et al. 2000). Interestingly, the onset of the charge movements is not instantaneous. This indicates that another, less voltage-dependent reaction step of EAAC1, most likely glutamate binding, precedes the voltage-dependent reactions leading to the two-exponential charge movement. If glutamate binding was electrogenic, it should result in the generation of an outward current because glutamate binds to and is transported by EAAC1 in its charged, negative form (Nelson et al. 1983; Watzke et al. 2000). Despite a small outwardly directed current spike upon photolysis, which we attribute to an artifact since it was also detected in nontransfected cells, we were not able to consistently detect such glutamate-induced outward currents, strongly supporting previous views that the extracellular glutamate binding site resides in a position on EAAC1 that is located outside of the transmembrane electric field (Vandenberg et al. 1997; Mennerick et al. 1999; Wadiche et al. 1995b).

Which glutamate transporter reactions steps contribute to the inward pre–steady-state I ^Glu− _Na+/K+ current? It has been previously shown that Na⁺ can bind to another transporter subtype (EAAT2) in the absence of glutamate (Wadiche et al. 1995b), and that this binding reaction or a conformational change associated with it is voltage-dependent, based on the analysis of inhibitor-sensitive charge movements induced by voltage jumps. We repeated these experiments with EAAC1. Surprisingly, we estimated an upper limit of 150 μs for the decay time constant of these charge movements, at least 20-fold faster than those observed in EAAT2. These data show that binding of the first sodium ion to EAAC1 is an extremely rapid process. Therefore, the much slower glutamate-induced charge movement cannot be caused by this voltage-jump–induced reaction. Additional evidence for this interpretation was obtained by determining the [Na⁺] dependence of I ^Glu− _Na+/K+. If the pre–steady-state component of I ^Glu− _Na+/K+ was caused by this initial Na⁺-binding step, it should decrease with increasing Na⁺ concentration, however, the opposite effect is found experimentally. The data, however, are consistent with a model that includes two electrogenic steps that follow glutamate binding to EAAC1. This model is described in the next paragraph.

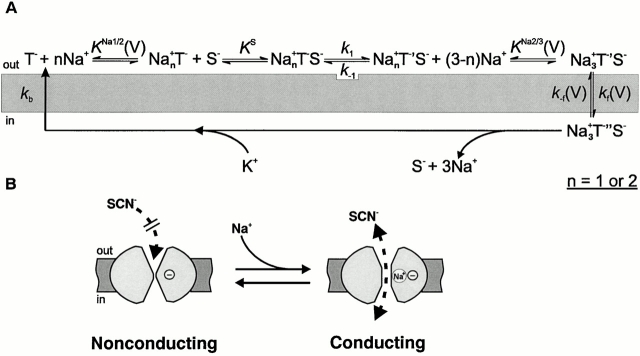
A General Model for the Na⁺/Glutamate Translocating Half Cycle of EAAC1

The kinetic model that we propose for the Na⁺/glutamate translocating half cycle of EAAC1 is shown in Fig. 8 A and is based on sequential, but not random, binding of sodium ions and glutamate to their extracellular binding sites on the transporter protein. In this model, glutamate binds to the Na⁺–EAAC1 complex, and bound glutamate is absolutely necessary for the binding of further sodium ion(s) to EAAC1. In fact, we propose a structural transition of EAAC1 occurring on a millisecond-to-submillisecond time scale that is induced by glutamate binding and renders the transporter competent for binding of one or two more sodium ions. We include such a structural transition in the model based on the following experimental findings that are otherwise difficult to reconcile. First, the fast glutamate-induced charge movement increases with increasing Na⁺ concentration (at saturating [glutamate]), but its rate of decay does not. Second, the fast glutamate-induced charge movement increases with decreasing membrane potential, however, its rate of decay is essentially V _m independent. Third, it is unaffected by intracellular K⁺, Na⁺ and glutamate and, thus, not due to dissociation reactions on the cytoplasmic face of EAAC1. Fourth, the maximum anionic current increases with increasing Na⁺ concentration, but its rate of formation is Na⁺ independent; and fifth, the rate of formation of I ^Glu− _anionic is essentially voltage independent. Together, these observations suggest, independent of a kinetic model, the existence of an electroneutral transporter reaction step that determines the rate of decay of the charge movement and that is unaffected by extracellular Na⁺ and by the transmembrane potential. It is followed by a Na⁺-dependent and electrogenic reaction that is in rapid preequilibrium with respect to the rate-limiting step. This latter step, which we interpret as a voltage-dependent Na⁺ binding reaction (Fig. 8 A) is responsible for the fast phase of the glutamate-induced charge movement that we observe.

Figure 8.

(A) General mechanism for binding of Na⁺ ions and substrate (S) on the extracellular side of the glutamate transporter (T). The conformational state with the amino acid substrate binding sites exposed to the cytoplasm is termed T′′. T′ denotes a state of EAAC1 that is formed with the rate constant k ₁ after initial Na⁺ and amino acid substrate binding and is competent for binding of further sodium ion(s). K ^Na+1/2(V) and K ^Na+2/3(V) are the voltage-dependent dissociation constants of Na⁺ from the transporter, and K ^S is the dissociation constant of the substrate. The voltage-dependent translocation of the fully loaded carrier is characterized by the rate constants k _f for the forward transition and k _−f for the backward reaction. k _b represents the rate constant for the relocation of the empty carrier. Potassium ion dissociation on the extracellular side and proton binding and dissociation steps were neglected for the sake of simplicity. (B) Hypothetical mechanism of the anion conductance of EAAC1. SCN⁻ is shown here as an example of an anion with high permeability. Na⁺ binding to the empty transporter (with a negatively charged binding site) at a site within the transmembrane electric field or to the transporter with negatively charged glutamate bound to it leads to the activation of an anion permeant pathway through the carrier.

Previously, we assigned the slow phase of the glutamate-induced charge movement to the Na⁺/glutamate translocation step across the membrane (Grewer et al. 2000). The data presented here provide further evidence that this assignment is correct. The presence of the slow charge movement under equilibrium exchange conditions proves that it is directly associated with the Na⁺/glutamate translocating half cycle of EAAC1 and not with any K⁺-dependent reactions, such as the relocation of the carrier.

The general model shown in Fig. 8 A can explain all of the results obtained in this study qualitatively. To demonstrate this, we performed analytical calculations based on the equations listed in Table and numerical simulations of the time dependence of transport currents based on (see ). Some of the results of these simulations are shown in Fig. 9 and demonstrate the general good agreement between the experimental data and the predictions of the proposed mechanism regarding the time dependence of transport currents and the effect of the extracellular Na⁺ concentration on the currents.

Figure 9.

Prediction of the time, [Na⁺], and voltage dependence of EAAC1 transporter currents and charge movements based on numerical simulations and the equations shown in Table . (A and B) Transport currents calculated by numerical integration of the differential equations pertaining to the model in Fig. 8 A for inward transport (A) and homoexchange conditions (B) according to (see ). The conditions were chosen to match the experiments shown in Fig. 1 (B and C) and Fig. 6 A. The rate constants for glutamate binding and dissociation were set to 2 × 10⁷ M⁻¹s⁻¹ and 1,000 s⁻¹ and for sodium binding and dissociation to 1 × 10⁵ M⁻¹s⁻¹ and 6 × 10³ s⁻¹, respectively. The other parameters were as follows: k _f = 150 s⁻¹, k _−f = 30 s⁻¹, k _b = 30 s⁻¹, k ₁ = 1,400 s⁻¹, k ₋₁ = 200 s⁻¹, z _Q(fast) = 0.5, z _Q(slow) = 0.7. (C and D) Predicted K _M and I _max as a function of the Na⁺ concentration for the different models calculated according to the equations shown in Table . K ^S was set to 1 and K ^Na+1/2 and K ^Na+2/3 were set to 20 mM. (E) Predictions of the Na⁺ concentration dependence of 1/τ_fast and 1/τ_slow (equations shown in and Table ). The parameters were as in A, except k ₁ = 1,200 s⁻¹. (F) Voltage dependence of the charge moved during the fast phase calculated according to (see ) for a single voltage-dependent Na⁺-binding process. The parameters were the same as before, except that z _Q(fast) was set to 0.65.

Are the Rapid Charge Movements Gating Currents?

Gating currents are generally observed in voltage-gated ion channels (Bezanilla 1985). They precede the activation of ionic currents flowing through the open channel, but are typically much smaller in amplitude. In addition, gating currents are present in the absence of ions that permeate the channel. Therefore, it was proposed that they correspond to the movement of charges that are fixed on the ion channel protein during the gating process. To our knowledge, gating currents have not been observed for ligand-gated ion channels at present. However, glutamate transporters are associated with an anion conductance that is activated by glutamate (Eliasof and Werblin 1993; Fairman et al. 1995; Otis and Jahr 1998). This anion conductance was proposed to be consistent with a channel rather than a transport mechanism (Picaud et al. 1995; Wadiche et al. 1995a), although this point is not totally clarified to date. The rapid charge movements that we observe in EAAC1 closely match the definition of gating charge movement presented above. First, they decay with a similar time constant as that for the activation of the anionic component of the current, I ^Glu− _anionic. Therefore, it appears that inward movement of positive charge is required for the activation of I ^Glu− _anionic. Second, their direction is independent of the anionic gradient across the membrane (Grewer et al. 2000). Third, the charge movement is also observed in the absence of permeant anions. Therefore, it is tempting to speculate that the rapidly deactivating component of I ^Glu− _Na+/K+ represents gating currents of EAAC1. Since this charge movement is Na⁺ dependent, we propose that the gating particle of EAAC1 does not consist of charged residues of the transport protein, but may be a sodium ion moving into its binding site that is located within the membrane electric field. A possible model is graphically illustrated in Fig. 8 B.

Previously, it was speculated that glutamate itself, when bound to the transporter, provides the gating particle and part of the permeation pathway for anions, possibly by contributing its positively charged α-amino group (Wadiche et al. 1995a; Fairman and Amara 1999). In light of our results, such a scenario seems unlikely since the pre–steady-state charge movements are inwardly, and not outwardly directed, implying that initial glutamate binding occurs outside of the transmembrane electric field or within a low field access channel. In addition, the fact that anion current is already observed in the absence of glutamate, but absolutely requires the presence of Na⁺, makes such a scheme appear less likely but supports the Na⁺ hypothesis put forward here.

EAAC1 Properties at Steady-state

The major results from the Na⁺ concentration dependence under conditions of steady-state transport are the following: (1) the apparent affinity of EAAC1 for glutamate (K _M) decreases markedly with decreasing concentration of extracellular Na⁺; and (2) the maximum glutamate-induced current (I _max) decreases with decreasing [Na⁺]. We have derived expressions to quantitatively describe the Na⁺ concentration dependence of K _M and I _max for a number of different models as shown in Table . The expressions are based on the known stoichiometry of EAAC1 (three cotransported Na⁺ ions per glutamate; Zerangue and Kavanaugh 1996) and the assumption that translocation occurs from the fully loaded carrier. The results obtained at steady-state conditions are not consistent with models in which all the cotransported sodium ions bind to EAAC1 either before (model Na₃TS) or after (model TSNa₃) the glutamate molecule or in which Na⁺ and glutamate binding are sequential, but random (Table ). However, the data can be explained by a simple model that incorporates a first Na⁺-binding step before glutamate binding takes place. This EAAC1–Na⁺–glutamate complex can then undergo further binding of Na⁺ ions. Such a mechanism is in good agreement with the pre–steady-state kinetic data and can explain the submillisecond charge movements that we observe in the absence and presence of glutamate. Consistently, nonsaturation of the Na⁺ binding equilibrium with the empty transporter at low concentrations of Na⁺ can be compensated by applying saturating glutamate concentrations. Thus, the apparent rate of the rise of I ^Glu− _anionic and the fast decay of I ^Glu− _Na+/K+ becomes [Na⁺] independent at saturating glutamate concentrations.

Stoichiometry of Na⁺ Binding

Although the data presented here strongly support the sequential Na⁺ and glutamate binding model shown in Fig. 8 A, they do not allow us to differentiate between the models NaTSNa₂ and Na₂TSNa. The voltage dependence of the final Na⁺-binding step is best approximated with a model that involves only one Na⁺ ion (Na₂TSNa). In contrast, the inhibition of the leak anion current by TBOA, which is a measure of the initial Na⁺-binding reaction, is best fit with an apparent Hill coefficient of 1, thus, supporting model NaTSNa₂. The effect of the extracellular Na⁺ concentration on I _max, K _m for glutamate, and the rate constants determined from the pre–steady-state experiments can be equally well described by both models (Fig. 9). Therefore, we conclude that, based on these data, either one of the two Na⁺-binding stoichiometries would be possible. The clarification of this issue will need further, more detailed experiments.

Comparison to Previous Studies

First, our results confirm previous proposals that positive charge is transferred in the Na⁺/glutamate translocation step of the transporter (Kanai et al. 1995; Grewer et al. 2000; Otis and Kavanaugh 2000). However, the results presented here provide the first direct evidence that rapid charge movements are associated with glutamate translocation and not with relocation of the potassium ion bound carrier. The latter reaction most likely determines the steady-state turnover rate of EAAC1 (Grewer et al. 2000).

Second, we present evidence that the glutamate translocation reaction is strongly inwardly driven at negative transmembrane potentials close to the physiologically important range. This result is in good agreement with previous studies on the deactivation of EAAT2 anion currents in the homoexchange mode upon rapid removal of glutamate (Otis and Kavanaugh 2000). Under these conditions, the rate of current deactivation is accelerated at increasingly positive V _m, suggesting that positive charge is moved in the outward direction as would be the case for the relocation of the Na⁺/glutamate bound transporter to expose the binding sites to the extracellular side of the membrane. The rate constant of this process is slower than that for the decay of the initial transient current, which reflects mainly the inwardly directed translocation of the fully loaded carrier. Consistently, the rate constant for the decay of the slow component of I ^Glu− _Na+ did not go through a minimum within the range of V _m of up to 60 mV, suggesting that within this voltage range the equilibrium of the translocation reaction favors exposure of the Na⁺ and glutamate binding sites to the cytoplasm.

Third, we confirmed previous results suggesting that initial binding of sodium ions to the transporter senses part of the transmembrane electric field (Wadiche et al. 1995b). However, in contrast to these studies, the time constant of this binding reaction was more than an order of magnitude faster. The reason for this discrepancy is not known. Possible explanations could be the use of different transporter subtypes; the use of different expression systems; or the inadequacy of the Xenopus oocyte two-electrode voltage clamp system for resolving such fast charge movements.

Finally, it is interesting to note that conformational changes induced by binding of glutamate to the glutamate transporter subtype Glt-1 have been proposed to explain glutamate-induced accessibility changes of specifically introduced cysteine residues that are believed to be not directly part of the glutamate binding site to sulfhydryl-reactive reagents (Zhang and Kanner 1999). Importantly, these accessibility changes are also evoked by inhibitors that are not translocated across the membrane, such as kainate, indicating that they reflect a reaction step that does not involve glutamate translocation. Furthermore, they are not seen in the sole presence of Na⁺ (Zhang and Kanner 1999). Here, we present the first direct evidence for the actual existence of such structural changes.

Comparison to Other Na⁺-coupled Transporters

In general, it is believed that association of Na⁺ with a binding site localized within the transmembrane electric field or conformational changes linked to it is a major source of the electrogenicity of Na⁺-driven transport systems. Our results obtained with EAAC1 confirm such an interpretation. In EAAC1, binding of at least two sodium ions on the extracellular side contribute to the overall charge movement, even though to a relatively minor extent. For many other transporters, however, the substrate translocation steps that follow extracellular substrate and Na⁺-binding are thought to be electroneutral. Such electroneutral behavior was found for the Na⁺ dependent transporters for glucose (Kessler and Semenza 1983; Loo et al. 1993), GABA (Hilgemann and Lu 1999), and inorganic phosphate (Forster et al. 1998). Our results demonstrating that amino acid substrate translocation is electrogenic for EAAC1 contrast these findings and suggest a different transport mechanism.

Another general feature of Na⁺-coupled carriers is that their function is based on a charge balance mechanism. In the sodium glucose transporter, the positive charge of the two cotransported sodium ions is compensated by two negative charges on the transporter that move together with the organic substrate in the electric field (Loo et al. 1993). Similar observations were made for the Na⁺/Ca²+ exchanger in which the translocation of Ca²+ is associated with net movement of negative charge. Thus, the carrier must bear more than two negative charges (Kappl and Hartung 1996). In contrast, the Na⁺/HCO₃ ⁻ transporter translocates the net negative charge that is counterbalanced by positive charges of the ion binding sites (Gross and Hopfer 1998). We proposed a similar mechanism for EAAC1 recently (Grewer et al. 2000). Here, the positive charge that is translocated together with glutamate (three Na⁺ ions and one proton) is compensated by binding of anionic glutamate and by negative charges of the EAAC1 ion binding sites. Therefore, the total charge moved in the translocation step is much less than three, which would be predicted by the stoichiometry of the transporter. This theoretical prediction is in agreement with the relatively weak voltage dependence (relative charge < 0.6) of the glutamate translocation step found experimentally. It can be speculated that the compensation of the positive charge of the cotransported ions by glutamate and the transporter binding sites is required for the function of EAAC1 to ensure that the movement of the ions across the hydrophobic membrane environment is sufficiently fast to rapidly remove glutamate from the synaptic cleft.

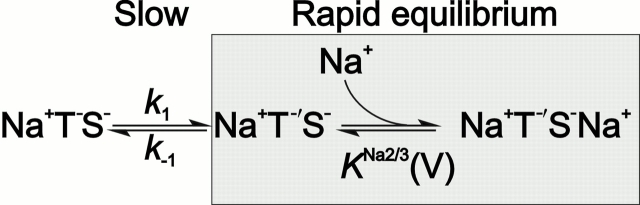
When concentrations of glutamate and Na⁺ are used that saturate their initial binding sites on EAAC1 the model shown in 8 A can be reduced to the following pseudo–two-state model 1:

Scheme S1.

Here, the binding of the final Na⁺ to EAAC1 is thought to be in rapid equilibrium compared with the transition NaTS ↔ NaT′S. Thus, the NaT′S and the NaT′SNa states can be lumped into one state. According to this pseudo–two-state model, the observed relaxation rate constant for the rapid decay of I ^Glu− _Na+/K+, 1/τ_fast, can be expressed as:

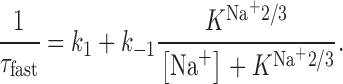1

Here, k ₁ and k ₋₁ are the rate constants for the transitions NaTS → NaT′S and NaT′S → NaTS, respectively, and K ^Na+2/3 is the dissociation constant of the sodium ion from its site on NaT′S. The following assumptions were made: (1) the glutamate concentration is saturating for the initial Na⁺ binding step; (2) binding of glutamate and of the initial Na⁺ ion are in rapid preequilibrium with respect to the transition NaTS ↔ NaT'S. Thus, k ₁ becomes glutamate and Na⁺ independent; and (3) glutamate translocation is comparatively slow and, therefore, can be neglected.

Using the same assumptions, the charge moved during the rapid phase of the current decay can be calculated as:

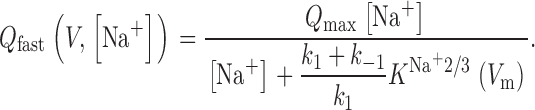2

In this equation, Q _max is a scaling factor and represents the maximum amount of charge movement, which depends on the number of EAAC1 molecules under observation, the elementary charge and the apparent valence of this charge, z _Q. Additionally, it was assumed that the transporter resides fully in the state NaTS until the reaction is initiated. When evaluated in a voltage-dependent manner, resembles a Boltzmann-like relationship. The midpoint potential of the charge movement, V _Q, is [Na⁺] dependent and can be given as:

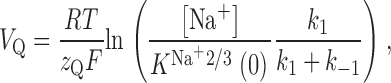3

with R being the gas constant, T being the temperature, and F being the Faraday constant. The voltage dependence of the charge movement is introduced by the voltage dependence of K ^Na+2/3(V _m) = k _−Na/k _+Na, which can be expressed as follows, according to transition-state theory (Läuger 1987):

4

where K ^Na+2/3(0) represents the dissociation constant of Na⁺ from EAAC1 at V _m = 0 mV.

For the simulations of the time dependence of transport currents the following equation was used:

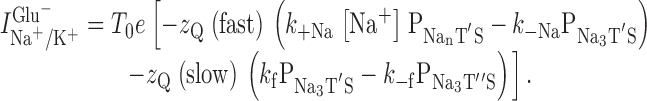5

Here, P denotes the fractional occupancy of the respective state as defined in the model in 8 A. T ₀ is the number of transporters under observation, e is the elementary charge, and k _+Na and k _−Na are the rate constants for binding of the final Na⁺ to EAAC1 and dissociation of this Na⁺ from EAAC1, respectively. The time dependence of the current can be obtained by calculating the time dependencies of the fractional state populations P by numeric integration of the differential equations pertaining to the kinetic scheme shown in 8 A. For simplicity, n (the number of initial Na⁺ binding reactions) was set to 2. Thus, the binding of Na⁺ to the glutamate–EAAC1 complex involves only one Na⁺ ion.