Phase separation and liquid crystallization of complementary sequences in mixtures of nanoDNA oligomers

Abstract

Using optical microscopy, we have studied the phase behavior of mixtures of 12- to 22-bp-long nanoDNA oligomers. The mixtures are chosen such that only a fraction of the sample is composed of mutually complementary sequences, and hence the solutions are effectively mixtures of single-stranded and double-stranded (duplex) oligomers. When the concentrations are large enough, such mixtures phase-separate via the nucleation of duplex-rich liquid crystalline domains from an isotropic background rich in single strands. We find that the phase separation is approximately complete, thus corresponding to a spontaneous purification of duplexes from the single-strand oligos. We interpret this behavior as the combined result of the energy gain from the end-to-end stacking of duplexes and of depletion-type attractive interactions favoring the segregation of the more rigid duplexes from the flexible single strands. This form of spontaneous partitioning of complementary nDNA offers a route to purification of short duplex oligomers and, if in the presence of ligation, could provide a mode of positive feedback for the preferential synthesis of longer complementary oligomers, a mechanism of possible relevance in prebiotic environments.

Molecular crowding of cellular interior is known to play a role in the spontaneous organization of biological macromolecules (1). Several biochemical and physiological processes are found to be influenced by strong packing constraints (2, 3), and complex ordered arrangements, such as liquid-crystalline mesophases, have been shown to arise from highly packed biomolecules (4). Of particular interest is the ordering of highly concentrated DNA in cell nuclei, which can lead to a variety of mesophases in vivo (5). However, whether such ordering caused by packing constraints had represented an evolutionary advantage remains an open question.

Concentrated solutions of fully hybridized nanoDNA (nDNA) exhibit various liquid crystalline forms of supramolecular ordering, promoted by end-to-end adhesion of the paired bases at the terminals of the duplexes. This behavior has been reported recently for a wide set of self-complementary (SC) 6- to 20-bp nDNA sequences and for mutually complementary sequences in the same length range (6). Here we explore the phase behavior of mixtures of nDNA in which only some of the sequences are complementary, thus able to pair in double strands (DSs), and part of the sequences are not, and thus always remain in the solution as single strands (SSs). We have found that in concentrated mixtures of duplex and SS nDNA, the system phase-separates into duplex-rich liquid crystal (LC) domains coexisting with a duplex-poor isotropic phase, leading to the physical segregation of 4- to 6-nm-long complementary chains from noncomplementary ones. This phase separation is a collective effect of the duplex and SS nDNA because the duplexes alone would not form LCs in such solutions, their concentration being well below that required for LC formation. We show that this interesting behavior is effectively described in terms of nucleation and growth of LCs, wherein upon cooling an isotropic solution of SS nDNA, a destabilizing transformation is produced by the hybridization of the complementary oligos as the temperature is lowered below the DSs melting temperature. The phase separation is caused by a combination of duplex formation and end-to-end stacking, leading to depletion-type forces that arise from the entropy gain of depletants (SSs) upon demixing solute particles (duplex aggregates). This manifestation of the depletion interaction is unique in that, above the duplex melting temperature, the depletants and solutes are chemically homogeneous and completely miscible, the difference in molecular size and flexibility enabling a depletion interaction only at temperatures at which duplexes can form. The phase separation described here leads to a spontaneous form of purification of well paired strands from unpaired or badly paired strands. This phenomenon could have provided the basis for a prebiotic molecular selection mechanism and synthesis of extended nucleic polymers by a previously uncharacterized form of LC-promoted autocatalysis.

Phase Separation in nDNA Mixtures.

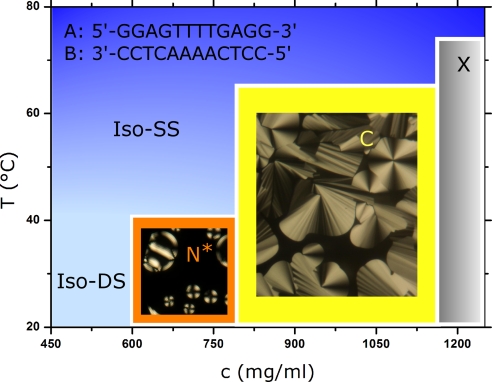
As for the case of SC oligonucleotides (6), solutions of concentrated mutually complementary nDNA self-assemble and organize into LC phases. In Fig. 1, we show depolarized transmitted light microscopy (DTLM) images for the chiral nematic and columnar LC phases found in nDNA-A plus nDNA-B (A–B) 1:1 mixtures, and we sketch the main features of the phase diagram. We find that the nDNA concentration c at the phase boundaries is c(isotropic-nematic) ≈ 600 mg/ml, c(nematic-columnar) ≈ 780 mg/ml, and c(columnar-crystal) ≈ 1,180 mg/ml. The concentration of neat DNA is c ≈ 1,800 mg/ml. When the temperature T is raised, phases melt. At the same time, when T grows above the nDNA melting temperature T_M, duplexes unbind. Previous work (6) indicates that T_M is equal or slightly larger than the temperature at which LC domains melt, both of them showing an increase with nDNA concentration.

Fig. 1.

Phase diagram of aqueous solution of a 1:1 mixture of nDNA-A and nDNA-B. Upon increasing the total DNA concentration c, a chiral nematic (N*), a columnar (C), and a crystalline phase (X) appear whose textures from DTLM are shown. Upon increasing the temperature T, phases melt into an isotropic phase of SSs (Iso-SS). When c < 600 mg/ml and at T below the nDNA duplex unbinding temperature, an isotropic phase of DSs is found (Iso-DS).

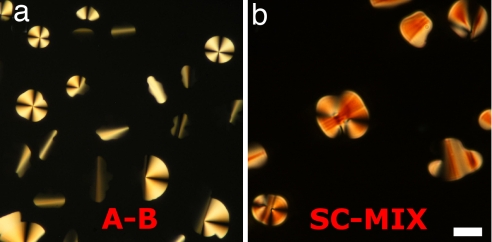
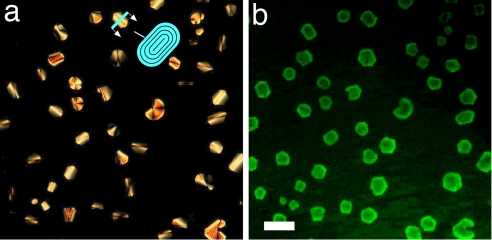
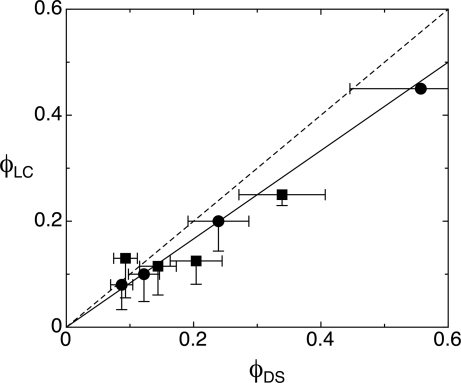
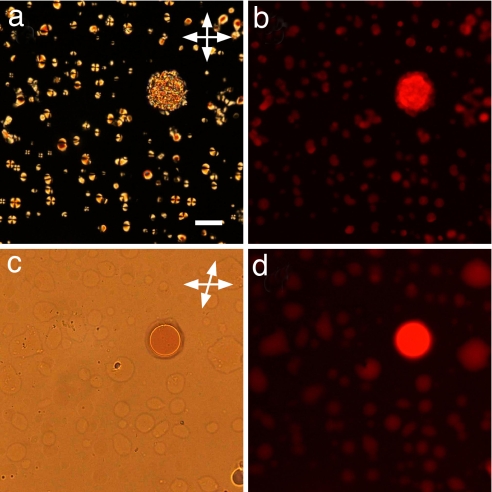
In Fig. 2 a and b, we show DTLM images of cells containing, respectively, an A–B sample with molar ratio [B]/[A] = 3 and a mixture of 16-mer SC nDNA with mixed SSs (MIX) sample with molar ratio [MIX]/[SC] = 4, after equilibration at room temperature. We observe in both cases an isotropic majority phase rich in SS nDNA (black in transmission), coexisting with LC domains rich in nDNA duplexes. Analogously to what was described previously (6), the optical textures of the LC domains observed in the experiments here indicate either chiral nematic or columnar ordering of the duplexes, depending on the nDNA concentration. The emergence of these phases is explained by the presence of attractive interactions between the duplex paired terminal bases, yielding end-to-end stacking. In the majority of our observations of A–B and SC–MIX samples, we could detect domains of columnar phases, as those reported in Fig. 2, whereas the chiral nematic was observed only for values of [B]/[A] and [MIX]/[SC] smaller than 3. The partitioning of the duplex nDNA into the LC domains is confirmed by doping the sample with a small percentage of nDNA-A labeled with a FITC group externally to the duplex. The result of FITC labeling is shown in Fig. 3, where it is apparent that the fluorescence is larger within the LC domains. We cannot extract quantitative information from this measurement because the fluorescent moiety disturbs the LC ordering, and thus FITC-conjugate 12-mers are less concentrated in the domains than the “clean” 12-mers. Quite interestingly, no LC phase was ever detected in mixtures of nDNA-B and FITC-conjugate nDNA-A when the FITC group was on the 5′ terminus, thus destroying end-to-end adhesion. When equilibrium is reached, the LC domains fill a given fraction of the cell, φ_LC, which we find to be approximately equal to the DS volume fraction φ_DS = V_DS/(V_SS + V_DS), where V_DS and V_SS are the total volumes occupied by duplexes and SSs, respectively. The values of φ_DS reported in Fig. 4 are calculated from the mass fraction of the various nDNA sequences by modeling the duplexes as cylinders of diameter 2.4 nm and height 4 nm (12 bp) and 5.5 nm (16 bp) and the SSs as flexible coils whose radius of gyration can be computed according to the Krakty–Porod equation. On this basis, V_SS has been computed by using the “consensus” values of 4.3 Å per base for the SS contour length and 3 nm for the SS persistence length (7). However, these values are not an unambiguous choice, because the contour length could be set to the chemical length of 6 Å per base, and the persistence length could be shorter because of the large concentration of DNA and ions (8). We exploit this difference to quantify the uncertainty in the determination in φ_DS (error bars in Fig. 4). Hence, data contain a rather large uncertainty on which should be added the difficulty in controlling preparations of sub-milligram cells. Furthermore, because there are some LC domains that do not fill the cell gap, the determination of φ_LC also is approximate, the values in Fig. 4 being an upper boundary because they are extracted by assuming a cylindrical shape (across the cell surfaces) of the domains. However, the linear dependence of φ_LC on φ_DS, and the close match in the values of the two volume fractions, indicates that the segregation of the duplexes inside the LC domains is almost complete. Actually, the fact that the slope is smaller than 1 (0.8 according to the linear fit shown by the solid line in Fig. 4) could reflect the better packing of nDNA in the LC than in the isotropic phase.

Fig. 2.

Depolarized transmitted optical microscopy images of LC domains in unbalanced mixtures of nDNA-A and nDNA-B (a) and of nDNA-SC in a solution containing a mixture of SS nDNA sequences (b). The molar ratios are [B]/[A] = 3 and [MIX]/[SC] = 4. (Scale bar: 20 μm.)

Fig. 3.

Depolarized transmitted optical microscopy (a) and fluorescence (b) images of the same columnar domains in an unbalanced A–B mixture ([B]/[A] = 10) in which a small fraction (1/40) of A sequences was labeled with fluorescein bound externally to the double helix. (Scale bar: 50 μm.) (a) Duplex-rich LC domains appear brighter on the coil-rich background because of the LC birefringence. The developable domain textures are consistent with the columnar phase constraint of constant column spacing. The sketch shows the cross-section of the shield-like domains, where the black lines represent the local columnar axis.

Fig. 4.

Volume fraction of LC domains, φ_LC, as a function of φ_DS, the ratio between the total volumes of duplexes and the total volume of nDNA, as computed on the basis of the sample prepartion. Circles and squares represent A-B and SC-MIX mixtures, respectively. Lines represent φ_LC = φ_DS (dashed) and φ_LC = 0.8 φ_DS (solid). Error bars are evaluated as described in the text.

The notion of a nearly complete segregation of duplexes from nDNA mixtures is compatible with the pairing and stacking strengths. If some mechanism, to be described below, acts to condensate the aggregated duplexes, an equilibrium is attained at the domain boundaries between free duplexes (of molar concentration [DS_free]) and duplexes bound by stacking forces to the columnar structure ([DS_LC]). [DS_free] = k_as [DS_LC], where k_as, the equilibrium constant, expresses the free-energy difference ΔG_DS between associated and free DS. Previous analysis of the nDNA phase diagram has led us to determine the DS end-to-end adhesion energy to be approximately E ≈ 6–8 k_BT, a value that constitutes a lower estimate for ΔG_DS, given the presence of additional entropic forces, as described below. Hence, ΔG_DS > 6–8 k_BT implies [DS_free]/[DS_LC] = k_as < exp(−ΔG_DS/k_BT) = 10⁻³, an evaluation supporting the notion of an almost complete segregation of DS into the LC domains. Moreover, to obtain a nearly complete segregation of the nDNA duplexes, it is necessary that nearly all complementary oligomers are associated in DSs. Because the nDNA concentration for a columnar phase for 12-mers is ≈800–1,000 mg/ml (see Fig. 1), from the estimate above we expect [DS_free] ≈ 0.2–0.3 mM. Given the fact that the binding constant for the oligomers under study at T = 35°C is of the order of 10⁷ M⁻¹ (9), we deduce that, even in the MIX SS nDNA-rich phase, the large majority of the SC 16-mers is bound in duplexes. The same is even more true for the A–B mixture, where the large concentration of B strands in the SS nDNA-rich phase strongly favors the binding of the residual A strands. Hence, in both the A–B and SC–MIX mixtures, we can assume the duplex to be fully associated.

Nucleation of LCs.

The association of complementary strands into duplexes drastically alters their statistical physical properties, transforming the highly flexible SSs, whose persistence length is of the order of a few bases, to rigid segments of double helix, whose persistence length is much longer than their length (10). As this association proceeds, the concentration of duplexes increases and the system is brought into a metastable state, a condition that leads to the formation and growth of nuclei of a stable equilibrium phase. As T is raised above the duplex melting temperature, the nuclei dissolve and, if T is lowered again, form again in different positions. The T quench necessary to trigger the onset of the nucleation process is rather mild, enough to ensure the duplex formation, which effectively yields a deep quench from an hypothetical high T state with associated duplexes but melted LC domains, a condition that cannot be achieved upon heating because, as T is raised, the duplexes melt. The almost complete phase separation of duplexes and SSs is a consequence of this effectively deep quench.

Inspection of Figs. 2 and 3 reveals two main geometries for the growing domains: either circular developable domains with four perpendicular brushes or domains with an uniform optical axis and variable birefringence. These latter domains appear to have an elongated shape in DTLM but actually are approximately spherical, as can be observed by fluorescence microscopy (Fig. 3b) or by uncrossing the polarizers in DTLM, indicating that the domain growth is basically isotropic. In both domain geometries, the stacked nDNA columns run parallel to the Iso-C phase interface. In the focal conic domains, they circle the central defect line. In the uniaxial domains, there are regions (black in DTLM) in which the columns run mainly perpendicular to the cell surfaces, the apparently elongated shape in DTLM resulting from the racetrack structure of the columnar director field, as sketched in Fig. 3a. This notion is supported by the fact that in the apparently elongated domains the refractive index is larger for polarization along the long axis of the birefringent part of the uniaxial domains, indicating that the nDNA columns run parallel to its short axis. Domains often have a smoothed polygonal shape, with “corners” normally located in the dark homeotropic regions of the uniaxial domains, probably related to the hexagonal symmetry of the C phase.

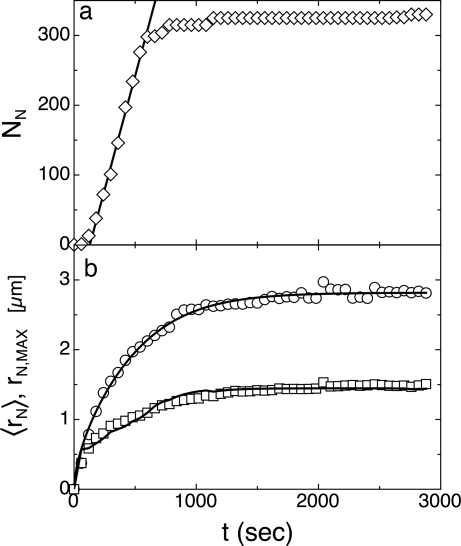
To gain insight into the nucleation process, we performed a detailed analysis of the early stages of the formation and growth of nuclei, extracting the number of nuclei N_N and their average size (radius r_N) as a function of time t. The results are shown in Fig. 5, where N_N and r_N versus t are shown for an A–B mixture for [B]/[A] = 10, with t = 0 the time when the hot stage reaches T = 35°C. Data indicate that both N_N and r_N reach an approximately steady-state value after ≈20 min. On a larger time scale (days), domains undergo an additional growth that we interpret as caused by the aggregation of LC nuclei having a size too small to be optically detected.

Fig. 5.

Time dependence of number and radius of LC nuclei for an A–B mixture. The number of LC nuclei N_N measured after the hot stage reaches T = 35°C (diamond) and calculated from a nucleation rate of 0.8 nuclei per second (line) are reported in a. The radius of the largest (early nucleated) LC domains r_N,MAX (circles), the mean nuclei radius 〈r_N〉 (squares), and the best fits of the Von Smoluchowski model to the data (lines) are shown in b. The noise in the fitting curve for 〈r_N〉 is attributable to the convolution of the model with the derivative of N_N, performed to take into account the time distribution in the first appearance of the nuclei.

Nucleation involves the ordering of nDNA duplexes in a large enough quantity that the free-energy gain associated with the formation of the stable phase overcomes the penalty associated with the surface tension of the interface. As the nuclei grow, the mixture is depleted of monomers, and the nucleation rate decreases and eventually vanishes. We have extracted from the data in Fig. 5a the nucleation rate ρ. In doing so, we have neglected the first data points, as the real onset of the nucleation is rather undetermined because of the ≈0.5-μm microscopy resolution limits, a length much larger than the nucleation critical radius estimated below. However, assuming negligible merging of nuclei in the early stages of nucleation, the value for ρ, even if evaluated at a later stage, is correct. We find a nucleation rate of 0.8 nuclei per s in the observed volume, corresponding to a rate ρ = 4 × 10⁻⁶/μm³·s. To discuss the implications of this value, we need to first discuss the growth mechanism.

Once nuclei of supracritical diameter are formed, their growth is controlled by the diffusion either of single duplexes or of stacked duplexes that contact the nuclei and merge into them. Given the concentration of duplexes in the initially homogeneous isotropic sample and the end-to-end adhesion energy E ≈ 6–8 k_BT, we expect the mean aggregation number N of stacked duplexes $N=(1+\sqrt{1+4\phi \text{exp}(\epsilon +k_I\phi )})/2\approx 3$, where φ is the volume fraction of DS nDNA and k_I ≈ 1.45 is a virial coefficient taking into account the steric repulsion between monomers (11). In the simplest scenario, the merging of DS nDNA into LC nuclei takes place with no activation barrier, i.e., in a diffusion-limited regime. This process is easy to model by using the approach originally proposed by Von Smoluchowski to describe the kinetics of colloidal aggregation (12). Accordingly, we have computed the growth rate of a nucleus on the basis of the following assumptions: (i) the duplexes, insulated or grouped in short stacked chains, have an average diffusion coefficient D, and when they contact the nucleus, they become part of it; (ii) at any time, diffusion of duplexes is a steady-state process determined by their concentration gradient; (iii) the local concentration of duplexes in the proximity of the nuclei is determined by the bound/free-equilibrium k_as and hence is effectively negligible; and (iv) the total concentration of duplexes is conserved within a spherical basin of radius R_B, whose size is experimentally determined from the mean distance of the nuclei. From these ingredients, a growth profile r_N(t) can be determined (see Materials and Methods), with D as the only free parameter, the other ones being set on the basis of the concentration of nuclei in the cell and of the concentrations of duplexes in the cell and nuclei. The growth process is shown in Fig. 5b in two ways: through 〈r_N〉, the average value for r_N calculated on the set of nuclei visible in a picture at a given time, and through r_N,MAX. the size of the largest nuclei, corresponding to those first nucleated in the cell. We have fitted both curves with the calculated r_N(t). To fit 〈r_N(t)〉, we have convoluted the calculated r_N(t) with the nucleation rate extracted from the N_N(t) data. We have determined D = 0.16 μm²/s (fit to r_N,MAX) and D = 0.11 μm²/s (fit to 〈r_N〉). Given the difficulty in determining the (large) viscosity of such a tiny quantity of material, to confirm our picture of the growth process, we determined D for diluted A–B nDNA duplexes in a concentrated solution of B SSs, by making a contact cell with a pure B solution and a B solution doped with FITC-labeled nDNA-A. We acquired fluorescence profiles as a function of time across the contact line, fitted them with the error function spatial dependence expected for the diffusional evolution of a step function in concentration, and extracted D = 0.06 ± 0.01 μm²/s [details are given in supporting information (SI) Materials and Methods; see also SI Figs. 7 and 8]. Although the comparison suffers from various uncertainties, the most severe being the difficulty in determining the basin radius R_B, the rough agreement between the two different determinations of D indicates that the growth of the nuclei is indeed attributable to a diffusion-limited process of single or weakly aggregated duplexes. This analysis also enables us to approximately estimate the viscosity, η = 1.2 ± 0.5 Pa·s, of the concentrated nDNA solutions investigated here. The value obtained is large but not uncommon in concentrated aqueous solutions of polymers (13).

Phase separation through nucleation can be described as an activated process, for which

where ρ_o is a space-time density of homogeneous nucleation “trials” and E* is the maximum in E(r), the work necessary to establish a crystallite of radius r via a reversible thermodynamic path (14). In the case of homogeneous nucleation, the attempt rate ρ_o can be estimated as n/τ, where n ≈ 1/λ³ is the duplex density in the sample just after the quench, λ is the mean spacing between duplexes in the same conditions, and τ ≈ λ²/D is the time for a duplex to diffuse the distance λ. Because in our experiments n ≈ 10⁷ molecules per μm³ and τ ≈ 0.4 ms, we find ρ_o ≈ 3 × 10¹⁰/μm³·s, which with the measured ρ ≈ 4 × 10⁻⁶/μm³·s enables us to extract E* ≈ 36 k_BT from Eq. 1.

Classical nucleation theory (15) provides an estimate for the activation barrier E* in terms of γ, the surface tension at the liquid–liquid crystal interface. Namely E*/k_BT = (16π/3)(γλ_LC²/k_BT)³/s², where λ_LC ≈ 3 nm is the mean (isotropically averaged) duplex spacing in the LC phase. s = Δμ/k_BT = ln([DS]/[DS_free]) expresses the difference Δμ in bulk Gibbs free-energy per particle between the droplet interior and the quenched isotropic phase. [DS] and [DS_free] are the molar concentration of DS in the quenched isotropic phase and in the isotropic phase coexisting with the LC domains. Because [DS_free] ≈ [DS_LC]/1,000 (see above) and [DS] ≈ [DS_LC]/10 (from the [A]/[B] ratio), s ≈ 4.6. From the value of E* extracted from the data, we obtain γλ_LC² = 3.5 k_BT and hence γ ≈ 1.5 mJ/m² for the LC droplet surface tension, which is comparable with that of protein crystals in solution (16). These figures also imply an estimate for the critical radius for nucleation R*. According to classic nucleation theory, R* = 2γλ_LC³/Δμ = 2γλ_LC³/s k_BT ≈ 5 nm, a value well below the resolution of DTLM observations.

Phase Separation in nDNA-PEG Mixtures.

The behavior described so far for nDNA mixtures has interesting analogies with the very well studied mixtures of proteins and flexible polymers such as poly(ethylene glycol) (PEG), where protein crystals nucleate in a PEG-rich isotropic background (17, 18). In both systems, the mixture made of compact molecular structures (proteins, DNA duplexes) and flexible chains (PEG, SS nDNA) is unstable and nucleates domains where the more rigid of the two species develops supramolecular ordering. To further explore the generality of the phenomenon, and to gain clues to interpret the observations, we have studied mixtures of nDNA duplexes and PEG of molecular mass ranging from 200 to 20,000 Da with a corresponding gyration radius between 0.5 and 6 nm (19). The mixtures were handled and observed in the same way as the nDNA mixtures. The DNA to PEG molar ratios are [DNA]/[PEG] ≈ 0.1 and the total DNA concentration is c ≈ 100 mg/ml, well below the value needed to get LC phases in absence of the PEG.

The polarized and fluorescence microscope observations are as follows. (i) At the lowest PEG molecular masses, we could not observe any phase separation. Separation and LC domain formation instead occur with PEG having molecular mass equal to 1,000 Da or larger, leading to a state of the system apparently quite similar to the one observed in nDNA mixtures, as shown in Fig. 6a. (ii) The separated phase is indeed rich in nDNA, as we could check by doping the starting solution with ethidium bromide, which has a strong interaction with the DNA bases and hence marks the nDNA-rich domains with a larger fluorescence as shown in Fig. 6b. (iii) Despite the apparent similarity, a quite relevant difference can be detected by heating the sample above the DS nDNA melting temperature. We find that the phase separation does not depend on the formation of duplexes but on the chemical or physical mismatch between PEG and SS nDNA. Fig. 6 c and d shows, respectively, DTLM and fluorescence microscopy images of the same sample held at T = 75°C for 1 h, a time sufficient to thoroughly disperse nDNA LC domains into the SS nDNA background, especially because highly concentrated PEG solutions typically are less viscous than the nDNA mixtures (13). We found that nDNA domains did not dissolve, so that by cooling again, domains formed in the same locations as they were previously, an occurrence never observed in nDNA mixtures. To further prove this point, we mixed PEG with noncomplementary nDNA, obtaining phase separation even in this case (data not shown). Hence, we understand the formation of LC domains in this case as a consequence of a liquid–liquid phase separation where one of the phases is rich in complementary SS nDNA, which then hybridize, end-to-end couple, and order.

Fig. 6.

Depolarized transmitted optical microscopy (a and c) and fluorescence (b and d) images of droplets of a SC nDNA mixed with PEG (molecular mass 8,000 Da). Birefringent domains are visible at room temperature under crossed polarizers (a), and the segregation of DNA helices is manifested through the fluorescent dye ethidium bromide (b). Sample held for hours at high temperature (75°C), at which LC domains melt, still show DS-rich domains, visible both under slightly decrossed polarizers (c) and in fluorescence image (d). (Scale bar: 50 μm.)

Recent systematic observation of lysozyme and PEG indicate that, quite similarly, the formation of protein crystal is anticipated by a liquid–liquid phase separation where droplets of isotropic concentrated protein solutions are formed, and in which crystals are later formed (18). On the contrary, and despite careful checking, in none of among the many SS plus DS nDNA mixtures we have studied could we recognize phase separation of domains not associated with LC ordering.

Entropy and Energy Combine to Drive the nDNA Phase Separation.

In the A–B and SC–MIX mixtures, the fraction of the nDNA-making duplexes can be as small as 10% of the total nDNA content, in turn, typically in the range of 500–1,000 mg/ml. If we imagine for a moment that the SSs were absent, the duplex concentration would be too small to enable significant end-to-end duplex adhesion, even with the 6-k_BT attractive adhesion energy inferred from the experiments on SC oligomers. In this case, given the phase diagram in Fig. 1, LC phases should not be expected to form. The phase separation of such dilute duplex mixtures, leading to the condensation of duplexes into high concentration domains, indicates the presence of an additional effective attractive interaction between the duplexes that can only be attributable to the SSs. Because DNA is phase-separating from DNA, this interaction is not likely to be enthalpic in nature; however, rather, because of some fundamental incompatibility of the SS and duplex DNA with respect to their mixing behavior, it therefore must be entropic in nature. Given the fact that duplex DNA is much more rigid than SS DNA, one's attention is immediately drawn to the known entropic immiscibility of rigid and flexible polymers in solution (20) and to the entropic depletion interaction forces arising in binary mixtures of particles of different sizes or penetrability (21).

Hence, depletion-type forces provided by SS nDNA are necessary for the DS condensation to take place. At the same time, the enthalpic contribution from the duplex stacking energy is necessary as well, which is demonstrated by the suppression of the phase separation when stacking is impaired as in the case of DS nDNA terminated by a FITC moiety.

A rough estimate of the total force holding the nDNA duplexes in the domains can be obtained by combining the typical intercolumnar distance in the nDNA C phase (6) with the corresponding osmotic pressure Π measured, for the same packing, in long DNA C phases (22), i.e., Π ≈ 10⁶-10⁷ Pa. The energy for detaching an nDNA duplex from the LC domain is of the order Πv_DS ≈ 3–30 k_BT, where v_DS is the volume of a single DS. This energy goes into unstacking the nDNA paired terminal bases (6–8 k_BT) and into winning the entropic force, whose simplest estimate is Π_SS ≈ [SS]RT ≈ 6 × 10⁵ Pa, i.e., the osmotic pressure of the SS. Accordingly, the energy required to overcome the entropic forces is Π_SSv_DS ≈ 2 k_BT.

Entropic Forces.

The depletion attraction between particles first was found theoretically by Asakura and Oosawa in their description of the interaction of hard particles in the presence of non-adsorbing polymers, modeled as penetrable spheres (23). They found an increase of the entropy of the polymer spheres when the hard particles were moved together, leading to an effective attraction between the particles. Depletion forces have been observed and analyzed theoretically in a variety of systems, including mixtures of large and small colloidal particles, both with spheres and rods, mixtures of colloidal particles and polymers, and mixtures of proteins and polymers, inducing either or both particle aggregation and phase separation (21, 24). Depletion forces also are credited as being responsible for the formation of protein crystals in mixtures of proteins and polymers such as PEG (17).

The depletion effect is most easily understood in systems of large and small hard (repulsive) particles wherein the volume available to and thus the entropy of the small particles is increased by aggregation of the large particles. The size difference becomes less relevant when rigid particles are mixed with flexible polymers. In this case, phase separation of a particle-rich phase and a polymer-rich phase is expected at every ratio between particle radius and coil gyration radius R_G. In the nDNA mixtures described here, size of duplexes and R_G of SS nDNA are similar. In this regime, according to depletion models (25), liquid–liquid phase separation should be expected. However, trying to account for our experimental data on the basis of hard sphere and penetrable polymer coil model is obviously an oversimplification. DNA strands are highly charged, and hence the system is in a regime of high repulsion and high osmotic pressure. Moreover, it has been shown that in the so-called “protein limit” of the depletion forces, specific interactions play a major role, yielding, for example, to polymer length dependences not predicted by the simplified theories (26).

Phase separation and orientational ordering in one of coexisting phases in mixtures of rods and polymers first was predicted by Flory (20) on the basis of a lattice model. Accordingly, the entropic gain in aligning long rod-like particles may drive a phase separation in which the random coils are almost completely expelled by the nematic phase. Later models (27, 28) focus on the depletion forces present in polymer and rod-like colloids mixtures and also predict phase coexistence of isotropic and anisotropic phases. These predictions account for part of the behavior observed in mixtures of polymers and bohemite rods (29), cellulose rods (30), and filamentous viruses (24).

Even more generally, entropic forces are expected to play a major role in concentrated solutions of mixed solutes, in which the solutes differ not only in size or penetrability, as in the case of depletion forces, but also in flexibility and tendency to self-assemble, giving rise to rich phase diagrams, which includes nematic LC ordering (31). These forces are considered to be responsible for various mechanisms of self-assembly and spatial organization in living cells (1). Indeed, mismatch in flexibility and tendency to aggregate into elongated chains are exactly the key properties of the nDNA system. Unfortunately, the range of the ratio persistence/contour lengths is in the case of SSs too small with respect to the range explored in these models, whereas its width, comparable to duplexes, its limited flexibility, and the electrostatic repulsion make the penetrable sphere description of Asakura–Oosawa's depletion interaction also hard to apply. However, despite the fact that the theoretical models summarized here do not fit the range of statistical physical properties of duplex and SS nDNA, their combination strongly supports the notion that entropic forces act to segregate duplexes from SS nDNA.

Conclusions

The phase separation of nDNA mixtures described here can be understood as a combination of depletion-type entropic forces, attributable to flexibility mismatch, and energy gained upon stacking the paired terminals of DS nDNA. The subtle combination of elements appears finely tuned in nDNA because neither LC ordering nor liquid–liquid phase separation occurs if end-to-end adhesion of duplexes is suppressed, by introduction of steric hindrance at the duplex ends, for example. This DNA behavior is in contrast to other depletants, such as short-chain PEG polymers, that we find can induce liquid–liquid phase separation without LC ordering. Indeed, interesting analogies emerge between PEG-promoted protein crystallization and PEG-promoted liquid crystallization of nDNA duplexes because in both cases a liquid–liquid phase separation appears to precede crystal or LC ordering, an effect probably attributable to the strong mismatch in molecular properties between the chemically heterogeneous PEG and DNA solutes. By contrast, the homogeneity of nDNA mixtures makes the chemical forces tenuous enough not to be sufficient to provide phase separation by themselves, in which case duplexing, stacking, or some combination of these is needed to create a mismatch in solute flexibility strong enough to drive phase separation.

Such a delicate balance may be related to molecular selection processes in the first emergence of polynucleic acids. The phase separation described here, leading to a spontaneous form of purification of well paired strands from unpaired or badly paired strands, could have provided the basis for a prebiotic molecular selection mechanism. Should the partitioning of complementary nDNA duplexes shown here combine with conditions favoring ligation, a previously uncharacterized form of LC-promoted autocatalysis would be established. This process would favor the preferential growth of the oligomers well aligned inside the liquid crystallites and thus promote the polymerization of complementary oligos.

At the same time, duplex segregation and liquid crystallization driven by SS nDNA appear as a test bench for the exploration and understanding of entropic forces in the low nanoscale size range. This system is particularly attractive because its chemical homogeneity reduces the complexity and variability of intermolecular forces, typically relevant in the case of concentrated heterogeneous solutions of macromolecules (26), hence simplifying interpretation.

Materials and Methods

We studied two classes of nDNA mixtures: (i) mixtures of two mutually complementary 12-mers, GGAGTTTTGAGG (nDNA-A) and CCTCAAAACTCC (nDNA-B), hereafter called the A–B samples, and (ii) mixtures of SC 16-mers, ACGCAGAATTCTGCGT (nDNA-SC) with a selection of random SS 20- and 22-mers, hereafter called the SC–MIX samples. Aqueous nDNA solutions were introduced in homemade glass sandwich cells (gap 7 μm) by capillary action, then dried to the desired concentration, and sealed with glue or fluorinated oil. Phase separation and LC formation were observed to take place at constant room temperature T = 25°C within minutes to hours after cooling, depending on the concentration and the volume ratio (see SI Figs. 9 and 10 for images of LC formation during a typical cooling sequence). Further experiments were performed by using nDNA-A labeled with fluorescein (FITC) groups chemically bonded through a short linker either on the sixth nucleotide of the A sequence externally to the duplex or on the 5′ terminal. All oligos, purified by HPLC, have been purchased from Primm s.r.l. (Milano, Italy).

In the experiments, we also used PEG chains with molecular masses of 200, 400, 600, 1,000, 8,000, and 20,000 Daltons purchased from Sigma–Aldrich. Finally, the fluorophore ethidium bromide (Sigma–Aldrich) also was used.

Cells were analyzed with a Nikon TE200 inverted microscope either in transmission between crossed polarizers (depolarized transmission optical microscopy, DTLM) or via fluorescence with filter sets appropriate to the observation of FITC or ethidium bromide. Images were acquired on a Nikon DS-5M camera. The temperature of the cells was controlled with an Instec (Boulder, CO) hot stage having stability better than 0.1°C. Image analysis was performed with ImageJ and Matlab software on black-and-white 2,560 × 1,920-pixel images, thresholded to exclude camera noise. During growth experiments, images were taken every minute. Density measurements on the A–B 1:1 mixture were performed by analyzing the spectrum of light reflected from cells especially made with high-refractive index glasses and extracting the refractive index of the solution from the Fabry–Perot interference fringes, as described in ref. 6.

Experiments on nucleation and growth were performed on samples that had been kept at T = 70 > T_M for tens of minutes, to ensure spatial uniformity of the concentration, and then quenched to T = 35°C, a temperature well below T_M. As the samples cool, LC domains appear and gradually grow in area to fill a fraction of the cell that ultimately saturates.

To extract the average diffusion coefficient D of the nDNA duplexes from the measured growth of the LC area fraction, a first-order differential equation is derived from a Von Smoluchowski-type model in which the duplexes diffuse in a spherical basin of radius R_B and join, through a diffusion-limited process, the spherical nucleus of radius r_N located at the center of the basin. The volume of the nucleus is proportional, through the number density n_in, to the number of contained duplexes. In this frame, the dimensionless quantity Y(t) = r_N(t)/R_B is given by the solution of the differential equation:

where D₀ = D/R_B², Y₀ = n₀/n_in and n₀ is the number density of nDNA duplexes in the basin of radius R_B before the nucleation. The value of the parameter R_B is determined from the average distance between the nuclei at equilibrium. The parameters D₀ and Y₀ are obtained from the fitting of Y(t) to the experimental data by means of two kind of analysis: (i) Y(t) is directly fitted to the measured size of the five largest domains r_N,MAX(t)/R_B; and (ii) the calculated Y(t) is convoluted with the measured number of nuclei that appeared in each time interval, and the resulting curve is fitted to the measured value of 〈r_N(t)〉/R_B.