Efficient coupling of catalysis and dynamics in the E1 component of Escherichia coli pyruvate dehydrogenase multienzyme complex

Abstract

Protein motions are ubiquitous and are intrinsically coupled to catalysis. Their specific roles, however, remain largely elusive. Dynamic loops at the active center of the E1 component of Escherichia coli pyruvate dehydrogenase multienzyme complex are essential for several catalytic functions starting from a predecarboxylation event and culminating in transfer of the acetyl moiety to the E2 component. Monitoring the kinetics of E1 and its loop variants at various solution viscosities, we show that the rate of a chemical step is modulated by loop dynamics. A cysteine-free E1 construct was site-specifically labeled on the inner loop (residues 401–413), and the EPR nitroxide label revealed ligand-induced conformational dynamics of the loop and a slow “open ↔ close” conformational equilibrium in the unliganded state. An ¹⁹F NMR label placed at the same residue revealed motion on the millisecond-second time scale and suggested a quantitative correlation of E1 catalysis and loop dynamics for the 200,000-Da protein. Thermodynamic studies revealed that these motions may promote covalent addition of substrate to the enzyme-bound thiamin diphosphate by reducing the free energy of activation. Furthermore, the global dynamics of E1 presumably regulate and streamline the catalytic steps of the overall complex by inducing an entirely entropic (nonmechanical) negative cooperativity with respect to substrate binding at higher temperatures. Our results are consistent with, and reinforce the hypothesis of, coupling of catalysis and regulation with enzyme dynamics and suggest the mechanism by which it is achieved in a key branchpoint enzyme in sugar metabolism.

The pyruvate dehydrogenase multienzyme complex (PDHc) is an exquisite machine that catalyzes the oxidative decarboxylation of pyruvate to acetyl CoA (1).

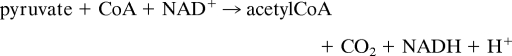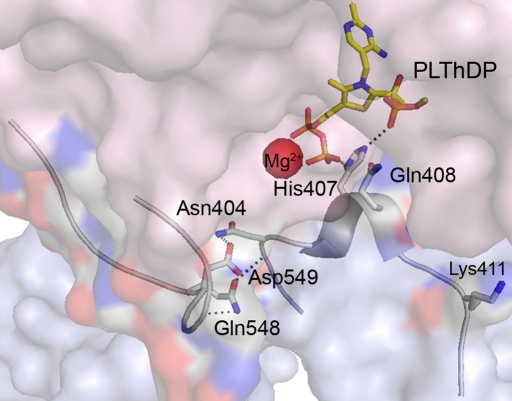
In Escherichia coli, the PDHc is composed of multiple copies of three components: E1ec, E2ec, and E3ec, which consecutively catalyze part(s) of the above overall reaction. E1ec is a thiamin diphosphate (ThDP)-dependent α₂ homodimer with mass 198,948 Da and catalyzes the reactions shown in supporting information (SI) Scheme I. The crystal structure of E1ec complexed with ThDP revealed two disordered regions near the active site with no discernible electron density (2), spanning residues 401–413 (inner loop) and 541–557 (outer loop), which become ordered in the presence of C2α-phosphonolactylThDP (PLThDP), a stable analogue of the first ThDP-bound predecarboxylation covalent intermediate C2α-lactylThDP (LThDP) (3) (Fig. 1). The enzyme could also catalyze very efficiently the formation of PLThDP from methyl acetylphosphonate (MAP), an excellent electrostatic analogue of pyruvate (SI Scheme II). The dynamic behavior of these active center loops in E1ec is critical for catalytic functions starting from a predecarboxylation event and culminating in transfer of the acetyl moiety to the E2ec component (i.e., intercomponent communication; ref. 4).

Fig. 1.

Position of the dynamic active-center loops over the active center formed at the interface of the E1ec dimer. The inner (residues 401–413) and outer loops (residues 541–557) are seen ordered over the intermediate analogue PLThDP (yellow-blue-orange sticks), an analogue of the first covalent intermediate LThDP.

The disorder–order transformation in E1ec modulated by the interaction of H407 with PLThDP acts as a “feed-forward” switch by preparing the active site for the next step, receiving the lipoamide group of the E2ec component (3). These observations suggested that in E1ec, the dynamics of active-center loops may be correlated to substrate turnover. Correlated biological processes of considerable interest, such as ligand binding, catalysis, and conformational transitions, occur on time scales ranging from picoseconds to days, and the conformational transition is often coupled to ligand binding and catalysis (5–7). The relationship between the time scale of such motions and their specific roles in catalysis is an important current issue in enzymology.

We here use a site-specifically labeled cysteine-free variant of E1ec to monitor dynamics of the inner loop. Using stopped-flow circular dichroism (SF-CD), viscosity-dependent kinetics, EPR, and ¹⁹F NMR, we show that the inner loop exists in a thermal equilibrium of open and closed conformers in the unliganded state. This equilibrium responds strongly to the addition of substrate analogue producing a stable predecarboxylation intermediate and shifts to a single species corresponding to the closed conformation. The rate of thermal fluctuations in the unliganded state was on the same order of magnitude as the k_cat and was consistent with SF-CD kinetic data. Our results are consistent with the notion that loop dynamics and catalysis in E1ec are correlated and represent the rate-limiting step for the E1ec catalysis. The data also suggest that overall dynamics of E1ec creates a regulatory switch to streamline the catalytic steps in the complex.

Results

Loop Dynamics Influences Covalent Addition of the Substrate to ThDP.

To identify which microscopic step(s) in SI Scheme I respond to loop dynamics, we present the following. Interpretation of our results is aided by our assignment of a negative CD band centered near 320–330 nm to (i) the 4′-aminopyrimidine tautomer of ThDP (AP form in SI Scheme I; ref. 8) or (ii) the Michaelis complex (MC) formed with either substrate (9) or substrate analogue MAP (9, 10). We have shown that on E1ec, it is difficult to observe the AP form. However, addition of pyruvate to the E401K loop variant under a variety of conditions produced the negative CD band corresponding to MC, stabilized as a result of very slow catalysis caused by impaired loop dynamics (4). It could be shown that the MC is fully formed in E1ec and E401K, as measured with SF-CD, within the dead time of the instrument (1 ms) (SI Fig. 7). However, formation of PLThDP from MAP (SI Scheme II) on E1ec (k₁^obs = 3.6 ± 0.2 s⁻¹ and k₂^obs = 0.35 ± 0.06 s⁻¹) was slower than MC formation and significantly slower in E401K (k₁^obs = 0.37 ± 0.05 s⁻¹and k₂^obs = 0.04 ± 0.01 s⁻¹) (Fig. 2). Clearly, formation of PLThDP, hence formation of C–C covalent bond (k₂ in SI Scheme I), and not formation of MC (k_MM), is the rate-limiting predecarboxylation step. Because C–C bond formation, but not MC formation, is dramatically slowed down (10-fold compared with E1ec) in E401K, loop dynamics apparently greatly influence covalent addition of substrate to the enzyme-bound ThDP.

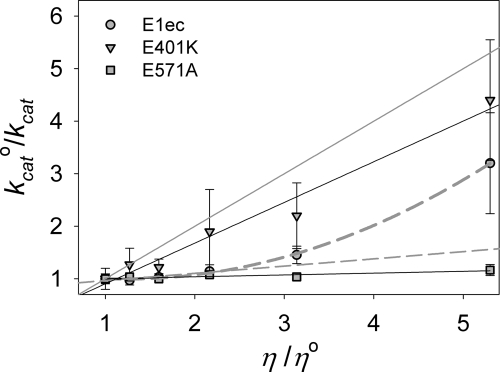
Fig. 2.

Rate of formation of PLThDP in E1ec and E401K. Fifty-micromolar active sites in 50 mM KH₂PO₄ (pH 7.0) containing 0.2 mM ThDP and 1.0 mM MgCl₂ in one syringe were mixed with 50 μM MAP in the same buffer. (A and B) E1ec at η = 1.0 and 5.3, respectively. (C and D) E401K at η = 1.0 and 5.3, respectively.

Viscocity-Dependent Kinetics Supports Correlation of Catalysis and Loop Dynamics.

Variation of k_cat⁰/k_cat [the ratio of the k_cat⁰ measured in buffer to that measured in the presence of the viscogen (k_cat)] with viscosity (η) in E1ec gave a linear plot (slope = 0.06 ± 0.04) at low viscosity (Fig. 3, linear dashed gray line), but at higher viscosity the plot deviates from linearity (Fig. 3, nonlinear dashed gray line). In contrast, such a plot for E401K was linear and displayed a much larger slope (0.8 ± 0.1). Our earlier studies signaled that the rate-limiting transition state in E1ec catalysis involves steps through formation of LThDP (i.e., predecarboxylation steps) (11). Consistent with this observation, similar values are observed for k_cat for pyruvate (3.2 ± 0.3 s⁻¹) and the rate of formation of PLThDP (k₁^obs = 3.6 ± 0.2 s⁻¹) at η = 1.0 in E1ec (SI Table 2 and Fig. 2). Because formation of MC (k_MM), a step preceding LThDP formation, is not rate-limiting for either E1ec or E401K (ref. 11 and SI Fig. 7), lower catalytic rates (i.e., higher slopes) in the variants strongly suggest impaired catalysis due to loop disorder (i.e., impaired loop dynamics). The nonlinear plot observed with E1ec might simply reflect changes in loop dynamics as a result of increasing medium resistance or alternatively a change in rate-determining step.

Fig. 3.

Effect of viscosity on the k_cat for E1ec, E401K, and E571A. The solid gray line has a unit slope and represents the diffusion-controlled limit. The nonlinear dashed gray line is a nonlinear fit to the E1ec data, whereas linear dashes gray line is a linear fit to the initial E1ec data points.

We resolved this dilemma by directly measuring the rate of predecarboxylation steps in E1ec at η = 5.3. The MC was again fully formed within the mixing time of instrument (1 ms, unchanged at higherη) (SI Fig. 7); however, the rate of formation of PLThDP (k₁^obs = 0.96 ± 0.23 s⁻¹) was similar to k_cat (1.0 ± 0.3 s⁻¹) measured at η = 5.3 (Fig. 2 and SI Table 2). With E401K, the k₁^obs = 0.067 ± 0.01 s⁻¹ was again similar to k_cat = 0.07 ± 0.01 at η = 5.3 (Fig. 2 and SI Table 2). We conclude that the rate-determining step is unchanged as a result of increasing viscosity, and the nonlinear kinetics with increasing viscosity in E1ec reflect progressive impairment of loop dynamics and associated catalysis.

To ascertain that these observations in the presence of viscogens are indeed due to changes in viscosity and to rule out nonspecific effects due to the presence of glycerol, we used the E571A variant. The highly conserved residue E571 is located within hydrogen-bonding distance of the N1′ atom of ThDP, and the Rutgers group has proposed that it is responsible for catalyzing the tautomeric equilibration leading to formation of the 1′,4′-iminopyrimidine tautomer of ThDP. We have shown that in E571A, chemical steps are rate-limiting (unpublished work); thus, this variant serves as an ideal control for all nonviscosity effects. A plot of k_cat⁰/k_cat against η/η⁰ for the E571A variant (Fig. 3) yields a straight line with a very small slope (0.03 ± 0.01). Thus, the magnitude of nonviscosity effects is very small, and hence the observed effects of viscosity on catalysis of E1ec and its variants could be attributed to the dynamic modulation of catalysis.

Construction, Characterization, and Covalent Labeling of a Cysteine-Free E1ec.

To quantify inner-loop dynamics, we used site-specific labeling (SSL) of a cysteine-free E1ec variant (E1ec_−C6; replacing six cysteines per monomer). Earlier studies with single cysteine substitutions indicated that such an approach had good chances of success on E1ec (12). Construction, characterization, and covalent labeling of E1ec_−C6 are given in the SI Text. The cumulative effect of the six substitutions, reintroduction of a single cysteine, and covalent labeling led to only modest reduction in activities and structural stability (SI Table 3 and SI Fig. 8), nor was binding of ThDP and MAP affected in variants (SI Table 4). Moreover, the dynamic behavior of the SSL variants was shown to be present in E1ec as well (see below). These observations affirm that our construct is valid for characterization of E1ec loop dynamics.

EPR Studies Reveal a Dynamic Equilibrium of Conformations of the Inner Active-Site Loop.

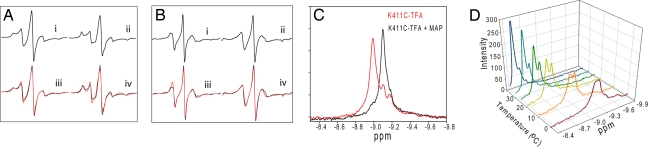
The EPR spectrum of the nitroxide radical inserted at position Q408C (Q408C-MTSL) revealed the presence of two components in the unliganded enzyme at room temperature: an intrinsic component that is mobile with a rotational correlation time (τ_R) of 1.3 ns comprising 25% and an immobile component (τ_R = 5.4 ns) of 75% (Fig. 4 and Table 1). Upon addition of MAP to form PLThDP, the τ_R for the mobile component remained the same but increased dramatically to 8.3 ns for the immobile component. Similar results were obtained for K411C-MTSL (K411C derivatized with MTSL), but the contribution from the mobile component was very small, and the spectra did not require simulation with a two-component model. A single-component simulation of the K411C-MTSL spectra showed an ≈214% increase in the τ_R, indicating a dramatic reduction in the mobility of the probe on MAP addition. Compared with Q408C-MTSL, the τ_Rs for K411C-MTSL are fast; presumably, the mobility of the probe in the presence and absence of MAP is faster in K411C-MTSL. Because K411 is located at the hinge of the loop, the probe could move more freely than at Q408. However, for the same reason, the probe may also be less sensitive to changes in its vicinity, perhaps accounting for the smaller contribution of the mobile component in the K411C-MTSL spectra. Nevertheless, addition of substrate analogue gave a measurable change.

Fig. 4.

EPR and ¹⁹F NMR analysis of conformational dynamics of inner loop in response to MAP and temperature. (A) Spectra of Q408C-MTSL (350 μM) before (i) and after addition (ii) of MAP (1.0 mM) (iii) and (iv) are the simulations (red line) of i and ii, respectively. (B) Spectra of K411C-MTSL (350 μM) before (i) and after addition (ii) of MAP (1.0 mM); iii and iv are simulations (red line) of i and ii, respectively. (C) Effect of MAP addition on the spectra of K411C-TFA. The red line is a spectrum of K411C-TFA and shows three resonances at −8.993, −9.106, and −9.193 ppm. The resonance at −9.193 ppm is due to oxidized free label, did not show any ligand-induced changes, and could be removed by extended washing (D). The black trace is a K411C-TFA (250 μM) after addition of saturating amount (500 μM) of MAP. Spectra were acquired at 30°C and referenced to the external standard trifluoroacetate. The data represent 2,048 transients processed with 5 Hz line broadening and a spectral window of 34,617 Hz. (D) Effect of temperature on the ¹⁹F NMR spectra of unliganded K411C-TFA (250 μM). Sample conditions were the same as above.

Table 1.

Effect of addition of substrate analogue (MAP) on the EPR parameters of MTSL-labeled K411C and Q408C

Sites	Q408C-MTSL		Q408C-MTSL + MAP		K411C-MTSL		K411C-MTSL + MAP
	τR, ns	Percent	τR, ns	Percent	τR, ns	Percent	τR, ns	Percent
1	1.3 ± 0.001	25	1.4 ± 0.004	18	0.11 ± 0.02	100	0.35 ± 0.004	100
2	5.4 ± 0.02	75	8.3 ± 0.04	82	NA	NA	NA	NA

Spectral simulations in Fig. 4 A and B were used to derive the parameters. NA, not applicable, because simulations were done assuming the presence of a single component. Protein and MAP concentrations were 350 μM and 1.0 mM, respectively.

We have now shown on E1ec and the E571A that the disordered active-center loops become ordered on formation of PLThDP from MAP (3). This ordered conformation could be associated with a closed one, because it protects the active site from solvent, in contrast to a disordered (or open) conformation, in which the enamine reacts with excess pyruvate in the “carboligation” side reaction (4). Also, because the fraction of immobile component increased with concomitant decrease in the fraction of mobile component (their respective τ_R values showing reciprocal changes), we hypothesize that these components might represent two environments encountered by the probe reflecting different conformations. Consequently, we assign changes in the EPR spectra resulting from addition of MAP to a change in the ratio of open to closed states of the mobile loops. We conclude that the loops exist in an equilibrium of open and closed states in the unliganded state and the population shifts to a preponderance of the closed state on binding of the substrate analogue to produce PLThDP. We further hypothesize that similar changes would occur on binding of the substrate pyruvate in place of MAP.

Unlike in the NMR experiments (below and Fig. 4), the EPR experiments did not suggest total conversion of the mobile component to the immobile one. Approximately 18% of mobile component was still present in Q408C-MTSL after addition of excess MAP, perhaps due to the presence of free label in solution, present even after total conversion of the mobile component to immobile one.

¹⁹F NMR Studies Provide a Quantitative Estimate of the Rate of Active-Site Loop Fluctuations.

Given the time regime of the X-band EPR experiments, we turned to ¹⁹F NMR. The initial ¹⁹F NMR studies confirmed the conclusions from EPR studies. The ¹⁹F spectra of K411C-TFA (K411C derivatized with Br-TFA) showed two distinct and unequally populated resonances at −8.993 and −9.106 ppm, respectively. On addition of MAP, the resonance at −8.993 disappeared and the one at −9.106 became more intense (Fig. 4C). Using the reasoning we used for interpreting the EPR results, we assigned the −8.993- and −9.106-ppm resonances to the open and closed conformations of the loop, respectively. As the same resonances are also present in the unliganded state (see below), the ligand-induced changes in chemical shift can be attributed to environmental changes around the probe rather than directly to the presence of ligand. As with the EPR results, the two resonances corresponding to open and closed conformations in K411C-TFA are not very well resolved, because of the position of the probe. Nevertheless, two distinct states of a singly labeled enzyme could still be detected.

In the unliganded population, the conformational equilibria exhibited strong temperature dependence (Fig. 4D) and resemble chemical exchange type effects (13), therefore exchange rates (k_ex = k_AB + k_BA) could be extracted by line shape simulations. At all accessible temperatures, within error range, the line shape simulations (SI Fig. 9I) yielded an exchange rate constant of <1.0 s⁻¹. In order of magnitude, this value is similar to the observed k_cat of the K411C-TFA (k_cat = 0.38 s⁻¹ according to E1-component-specific assay at 30°C), suggesting a quantitative correlation of loop dynamics and catalysis in E1ec. This is consistent with the variation of k_cat values for K411C-TFA with temperature (SI Fig. 9II) and strongly supports the quantitative correlation. Therefore, we conclude that the dynamics of the active center loops may represent a rate-limiting catalytic step consistent with stopped-flow CD and viscosity-dependent kinetics data.

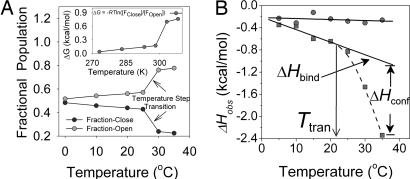
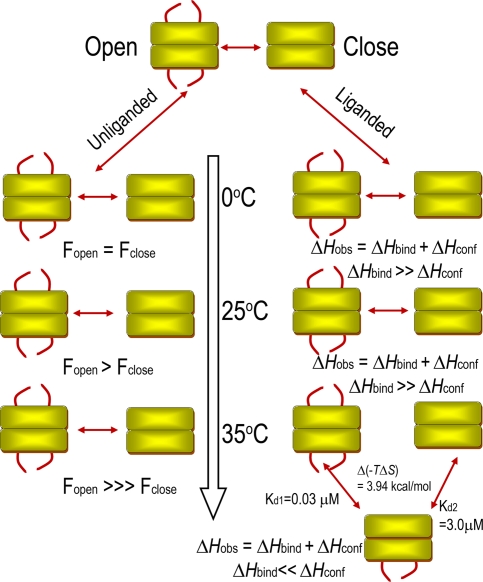
The ratio of open to closed populations exhibited remarkable temperature dependence. Although low temperatures favor equal populations of the open and closed conformations, the open conformation predominates at higher temperatures. A Lorentzian deconvolution of the K411C-TFA ¹⁹F spectra at different temperatures revealed that the population transition is not linear; instead, there is a step transition in population equilibrium in favor of the open conformation >25°C (Fig. 5A).

Fig. 5.

Effect of temperature on conformational equilibrium of loop and ligand binding. (A) Temperature-dependent dynamic equilibrium in inner-loop populations of K411C-TFA (250 μM). (Inset) Effect of temperature on the energetics of the population equilibrium. (B) Effect of temperature on the molar heat of binding (ΔH_obs) of MAP to E1ec (squares). The solid line represents the linear fit to low-temperature data (5–25°C), whereas the broken line is a fit to higher-temperature data (25–35°C). The transition temperature (T_tran) is a temperature at which step transition (close/open) takes place, and ΔH_conf starts to become appreciable and contributes strongly to the observed molar heat of binding (ΔH_obs = ΔH_bind + ΔH_conf). Circles represent the effect of temperature on the molar heat of binding (ΔH_obs) of MAP to H407A. A solid line through these points is a linear fit to data.

Temperature-Dependent Conformational Equilibrium Is Also Present in E1ec.

To demonstrate that the conformational equilibrium of the inner loop observed with EPR and NMR studies is not an artifact of cysteine substitution, reintroduction of a cysteine or introduction of covalent probes, we measured changes in enthalpy (ΔH_obs) on MAP binding as a function of temperature. We used isothermal titration calorimetry (ITC) to characterize the conformational changes that accompany a binding event (14). At lower temperatures, the ΔH_obs varied linearly with temperature, resulting in very low value of ΔCp_obs; however, at >25°C, there was a marked deviation from linearity (Fig. 5B). This temperature dependence of ΔH_obs and the resultant increase in negative ΔCp_obs is a hallmark of a process in which ligand binding is coupled to a conformational change (14) and is a thermodynamic signature of a preexisting conformational equilibrium in the unliganded enzyme (15–18). Thus, the conformational equilibrium observed by EPR and NMR, and the step transition in population ratio in favor of the open (disordered) conformation at higher temperature (according to deconvolution of the NMR signal and reflected here by the ΔH_conf term), are also present in the E1ec.

The mechanism of this process can be interpreted (see Fig. 6 legend) by using the following reasonable assumptions typical of ligand-binding processes: (i) the association of MAP and E1ec comprises a rigid-body-binding interaction and an intramolecular conformational change; (ii) the enthalpy and heat capacity of binding are negative (ΔH_bind < 0 and ΔCp_bind < 0); (iii) the enthalpy and heat capacity for the conformational transition are also negative (ΔH_conf < 0 and ΔCp_conf < 0), as if the binding induced conformational change caused burial of a hydrophobic binding pocket. The observed free energy of binding (ΔG_obs) was found to be entropically driven (SI Table 5) over the entire temperature range, presumably due to changes in solvation (19) and is consistent with the above observations and assumptions.

Fig. 6.

Schematic of the effect of temperature on the dynamics of the unliganded and liganded E1ec. In unliganded E1ec (no MAP), the loops exist as a conformational equilibrium of open and closed states (Fig. 4). This equilibrium gradually shifts in favor of the open conformation up to 25°C; there is a step transition in favor of the open conformation at 25°C (T_tran, Fig. 5B). During ligand binding >25°C, the step “close ↔ open” transition gives rise to a configurational enthalpic term (ΔH_conf) of a much higher magnitude, resulting from a ligand-induced disorder-to-order transition, which causes progressive reinforcement of observed enthalpy (ΔH_obs). However, at 35°C, where the rate of conformational fluctuations of the loop (k_ex) and hence the coupled rate of covalent substrate addition (k₂) increases, the catalytic rate is regulated by temperature induced anticooperative binding of ligand. At this temperature, binding of the second ligand incurs an entropic penalty, which results in 100-fold weaker affinity for the second molecule of ligand giving rise to the observed negative cooperativity.

Entropy of Binding Differentiates Two Identical Substrate-Binding Sites at Elevated Temperature.

Binding of MAP to E1ec gave rise to striking isotherms. Although at temperatures <30°C the binding isotherm suggested two identical binding sites for the dimer, the affinities at the two sites differ sharply >30°C (SI Fig. 10). The two distinct sites generated at elevated temperatures bind MAP with 100-fold difference in affinity (K_d1 = 0.03 μM and K_d2 = 3.0 μM), as a result of difference in free energy of binding (ΔG₁^obs − ΔG₂^obs = −2.84 kcal/mol). This difference emanates entirely from the entropy change (TΔS₂^obs − TΔS₁^obs = 3.94 kcal/mol) and opposes the enthalpically favored binding of the second ligand. Therefore, the apparent negative cooperativity induced at a higher temperature is entropically driven in its entirety.

Discussion

Accumulating data for a wide variety of enzymes indicate that conformational dynamics play an important role in catalysis and in some cases may be rate-determining. Our earlier study on the inner loop over the E1ec active site (4) revealed that the loop residues have multiple important roles including formation of the predecarboxylation intermediate through the later stages, where the intermediate is channeled to the E2ec component. In this investigation, we probe the potential correlation of dynamics with catalysis.

The EPR studies provided the first assessment of loop dynamics and revealed a dynamic equilibrium in the unliganded state, also confirmed by the ¹⁹F NMR and thermodynamic studies. What is the explanation for a preexisting conformational equilibrium in E1ec? One school of thought suggests that conformational equilibria allow proteins to adopt new conformations, which in turn help them to bind distinct ligands without undergoing evolutionary changes (20). Manipulation of conformational equilibrium was successfully used to “tune” ligand-binding affinities (21). Such a conformational equilibrium has also been suggested as the mechanism of recognition of unlimited numbers of antigens by a limited repertoire of antibodies (22). In E1ec this is manifested in its ability to use diverse substrates (23), and the inability of loop variants in which the conformational equilibrium was disrupted, to do so (data not shown). Also consistent with this notion is the high sequence homology found among homodimeric 2-oxo acid dehydrogenases of which E1ec is a member (data not shown).

A second explanation, and probably more relevant to our results, suggests that reaction-correlated conformational preequilibria represent “promoting motions” (millisecond-to second time scales) that influence the catalysis by reducing the free energy of activation (24). Consistent with this suggestion, our data imply that preexisting conformational equilibria in E1ec may provide an entropic and enthalpic (ΔH_conf) driving force for covalent addition of substrate to the enzyme-bound coenzyme (Fig. 5B and SI Table 5). In variants where this equilibrium is disrupted [as evidenced from a temperature-independent ΔH_obs (Fig. 5B and ref. 4) and crystal structure (3, 4)], the K_{d PLThDP} significantly increased, whereas the rate of PLThDP formation (in E401K) significantly decreased. This suggests that preequilibrium may “be harvested for catalytic turnover” (25). However, this hypothesis is controversial (ref. 26 and refs. therein). Some researchers question (i) whether in the absence of information for a reference state (in the absence of enzyme), contributions of dynamics to catalysis could be assessed and (ii) coupling of a slow preexisting conformational equilibrium (with concomitant preexisting reaction barrier) with catalysis. Although the possibility of electrostatic catalysis in E1ec [facilitated by interaction between H407 and PLThDP (Fig. 1)] mediated via loop motion has been proposed (3, 4, 27), the effect of disruption of this interaction is modest [H407A and E401K reduce k_cat (E1ec specific) by ≈10-fold (4, 27)]. Further, it is difficult to model an E1ec reference reaction, because there simply is no reaction in the absence of ThDP, whereas the protein supplies a 10¹²-fold rate acceleration over and above that by ThDP itself (28). Our results and conclusions are consistent with the generalized hypothesis in ref. 25 and suggest that energetics via conformational dynamics play a significant role in catalysis.

Strikingly, E1ec exhibited negative cooperativity with respect to MAP binding that was apparent only >30°C; <30°C, the two sites are essentially identical. The binding of a second molecule of MAP in E1ec incurs a large entropic penalty resulting in negative cooperativity (SI Fig. 10). As mentioned earlier and suggested by this study, the formation of LThDP (k₂ in SI Scheme I) is the rate-limiting step in E1ec catalysis due to its control by loop dynamics. Presumably, at higher temperatures, due to an increase in the rate of loop fluctuations (sharpening of NMR peak at 35°C; see Fig. 4D), k₂ increases and, as a result the downstream chemical steps, particularly reductive acetylation of E2ec, could become rate-limiting. Our results regarding loop movement refer to isolated E1ec component. For the overall reaction of the complex, reductive acetylation is probably rate limiting (11). In pyruvate decarboxylase (catalyzing the sequence of reactions as E1ec through decarboxylation) from both Zymomonas mobilis and Saccharomyces cerevisiae, product release is the rate-limiting step (29). Because cooperativity is a mechanism to sharpen or dampen the responsiveness of a system in response to a stimulus (30), we speculate that the negative cooperativity induced in E1ec at higher temperature might act as a regulatory switch to down-regulate the covalent substrate addition (k₂) and help to streamline all catalytic steps in the complex.

The fact that the negative cooperativity is entropic in nature is not unprecedented. The possibility of allosteric regulation through entropic mechanisms has long been recognized and studied (31–34) and undermines the exclusivity of mechanical view of signal propagation (35). Although a ligand-induced conformational transition in E1ec might suggest “freezing out” of dynamics (loss of configurational entropy), the compensating increases in entropy contained in motions with other modes or timescales (in the backbone or the side chains of the protein, ligand and solvent) have been shown to drive the binding with negative cooperativity (33, 36–38). Because negative cooperativity is induced at higher temperature, our results suggest that similar processes may be responsible for, and could explain the observed-binding behavior in E1ec at higher temperature.

In the crystal structures of E1ec loop variants studied to date, both loops are seen disordered even when the only stabilizing interactions that are disrupted by the substitutions are between the inner loop and the protein (E401K and K403E) (4) or between the inner loop and intermediate analogue (H407A) (3) rather than between two loops. Therefore, the dynamics of the two active-center loops appear to be concerted, they work in tandem. Hence, we speculate that our observations on inner loop dynamics would apply to the outer loop as well.

In conclusion, our observations suggest efficient coupling of catalysis with dynamics in a key branch point enzyme in sugar metabolism. This coupling appears to lower the transition state of covalent addition of substrate to ThDP by a combination of enthalpic and entropic components. As with many dimeric enzymes that use allosteric communication to regulate catalysis, E1ec uses negative cooperativity to regulate catalysis in the entire complex, but unusually, this regulation is entirely entropically driven. Our results share many similarities with recent studies in which conformational equilibrium was observed in the unliganded state of enzymes, indicating that our observations and conclusions might be of more general applicability for enzymes that use dynamics to “fine tune” catalysis.

Methods

Site-Directed Mutagenesis, Protein Purification, and Activity Measurements.

The methods for plasmid isolation, site-directed mutagenesis, protein expression, and purification are described elsewhere (12, 39). The subunit specific (DCPIP) and overall activities were determined as described elsewhere (40). Determination of K_{d PLThDP} was essentially similar to the CD method described elsewhere (4). The thermal unfolding of the E1ec_−C6 and E1ec was monitored at 222 nm. The temperature was increased from 25°C to 80°C in 1°C increments with 0.16-min equilibration time and 5-s collection time. K_{d ThDP} was measured by quenching of the intrinsic protein fluorescence by the ThDP as described in ref. 40.

¹⁹F NMR Spectroscopy.

The ¹⁹F NMR spectra of trifluoroacetonylated samples were recorded on a Varian INOVA 500-MHz spectrometer. The spectral simulations used WINDNMR-Pro (41).

EPR Measurements and Spectral Analysis.

All EPR spectra were recorded at room temperature (293 K) on a Brüker ELEXYS E500 EPR spectrometer and simulated by using the nonlinear least-squares analysis (42). The rotational correlation time, τ_R, was calculated by using τ_R = (6R)⁻¹, where R, the average rotational diffusion rate constant, is defined as R = (R_⊥R_‖)^1/2 (43).

Isothermal Titration Calorimetry.

A 0.5-mM ligand solution in an injection syringe was titrated with 0.01 mM E1ec or H407A in a 1.35 ml of sample cell for determination of enthalpy (ΔH_obs), entropy (ΔS_obs) and heat capacity (ΔCp_obs).

Additional Details.

Detailed descriptions of all methods and data analyses are included in SI Text.