Transient regulation of transport by pericytes in venular microvessels via trapped microdomains

Abstract

A phenomenon that has defied explanation for two decades is the time scale for transient reabsorption in the classic experiments of Michel and Phillips on individually perfused frog mesentery microvessels. One finds that transient reabsorption lasts <2 min before a new steady state of low filtration is established when the lumen pressure is abruptly dropped from a high to a low value. Our experiments in frog and rat venular microvessels under a variety of conditions revealed the same time trend for new steady states to be established as in Michel and Phillips' experiments. In contrast, one theoretically predicts herein that the time required for the tissue albumin concentration to increase to values for a new steady state to be achieved through reabsorption is in the order of several hours. In this paper we propose a new hypothesis and theoretical model for this rapid regulation, namely that pericytes covering the interendothelial cleft exits create small trapped microdomains outside the cleft exits which regulate this transient behavior. Our electron microscopy studies on rat mesenteric venular microvessels reveal an average pericyte coverage of ≈85%. The theoretical model based on this ultrastructural study predicts an equilibration time on the order of 1 min when the lumen pressure is abruptly lowered. The basic concept of a trapped microdomain can also be extended to microdomains in the interstitial space surrounding skeletal muscle capillaries.

In the pioneering study of transvascular fluid exchange on individually perfused frog mesentery microvessels, Michel and Phillips (1) concluded that, at steady state, no reabsorption (fluid flows from tissue to lumen) was possible at low pressure under the conditions of their experiments. They observed that transient reabsorption lasts <2 min before a new steady state of low filtration (fluid flows from lumen to tissue) is reestablished when the lumen pressure (P_L) is abruptly dropped from a high to a low value. These observations form the starting point for the model of dynamic fluid exchange in venular microvessels (VMs) described in this paper. Theoretically, one predicts herein using the model in ref. 2 that the time required for the albumin concentration in the tissue (large continuous interstitial space outside microvessels containing the lymphatic system) to increase to values necessary to establish the new low filtration steady state is in the order of several hours if the tissue concentration (C_T) is to rise to its filtration steady state value through reabsorption. We propose that pericytes (PCs) surrounding the endothelial cells (ECs) in these VMs create a previously overlooked trapped microdomain (TM) at the cleft exit which regulates the temporal response of these VMs to changes in P_L. This regulation can explain the huge discrepancy between the experimentally observed and the theoretically predicted equilibration times when P_L is abruptly lowered. The TM allows one to achieve quasi-steady equilibration on a time scale that is 2–3 orders of magnitude shorter than the much larger tissue space. These questions are important because, as we show, the model describes the conditions in mammalian VMs where new steady states favoring filtration may be established within a few minutes. This result, in turn, forms the basis for further understanding of mechanisms in tissue that would enable reabsorption of 0.5–1 liter of fluid from human interstitium after hemorrhage as described further in Discussion.

Although Eberth (3) and Rouget (4, 5) initially reported perivascular cells on the surface of microvessels among a variety of species, Zimmermann (6) first introduced the term “pericyte” to describe these cells in 1923. Subsequent researchers demonstrated that PCs are highly ramified and in close association with microvessels, including arterioles, capillaries and venules, in virtually every organ and tissue over a wide range of species. Electron microscopy (EM) has demonstrated that PCs have single prominent nuclei and long processes extending circumferentially as well as longitudinally around microvessels and are anchored to the neighboring ECs by adhesion plaques (7, 8). PC coverage varies among the types of tissues and microvessels, with overall coverage ranging between 11% in cardiac muscle capillaries to ≈50% in the retinal capillaries in rat with more extensive coverage on VMs than capillaries (9).

The variation in PC coverage is believed to reflect the different roles PCs play within various tissues. PCs have been associated with stabilization and vasoregulation of microvessels. More recently, evidence has emerged that PCs are essential for vessel formation, maturation, and maintenance and capable of guiding vessel sprouting processes during angiogenesis (10).

In this paper, we propose a previously unrecognized function of PCs, namely the transient control of water and albumin transport in VMs due to the thin TM that results from the close apposition of the PCs and the ECs. Over 90% of water that passes across the VM wall goes through the EC cleft. The albumin transport across the VM wall is by diffusive and convective fluxes through the interendothelial clefts and by flux through intraendothelial vesicles distributed along the entire EC. Therefore, we examine the PC coverage of the VM wall focusing on the spatial relationship between PCs and the EC cleft and the geometry of the TM between PCs and ECs. Schulze and Firth (8) found that PC processes are preferentially located close to interendothelial junctions in rat myocardial capillaries. In the EM experiments on rat mesenteric VMs reported herein we found that average PC coverage is 84%, average cleft exit coverage by PCs is 83%, and the typical separation between ECs and the surrounding PCs is nearly uniform and of the order of a few hundred nanometers.

Based on this EM study, we establish a theoretical model to describe the transient transport behavior, induced by abrupt changes in P_L, within the TM in combination with the entire endothelial layer which is described by the simplified 1-D model developed in ref. 2.

Theoretical Background

Michel (11) and Weinbaum (12) independently proposed a revision to the classic Starling principle which states that the Starling forces due to hydrostatic and oncotic pressures should be applied just locally across the endothelial glycocalyx layer (EGL), instead of globally between lumen and tissue as previously assumed. To describe this hypothesis, sophisticated 3D theoretical models for the revised Starling principle have been constructed based on the detailed ultrastructural measurements on mesenteric VMs of frog and rat (13–15). More recently, the key ideas in these 3D models have been made more convenient to apply by developing a simpler 1D model which closely represents its much more complex 3D counterpart for the revised Starling principle. This simplified 1D model closely approximates the effective hydraulic and diffusional resistance of the EGL and the EC cleft with its tight junction (TJ) strand and provides accurate solutions for the water velocity, v, and solute flux per unit cleft length, J_S/A, at the cleft exit if the lumen and tissue pressure and concentration are prescribed.

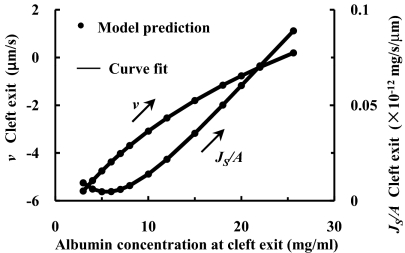
Michel and Phillips assumed in their experiments (1) that in the new steady state after P_L has been changed, the new C_T is given by the ratio of the total albumin to water flux, J_S/J_V, and that the cleft exit concentration, C, is equal to C_T. The assumption is that there is no loss of albumin from the tissue near the VM and C_T is uniform. In the experiments of Michel and Phillips, and in experiments on rat mesenteric VMs (15), this is most likely the case when the mesothelium is not damaged and loss of albumin into the lymphatics is negligible. In a typical experiment carried out in rat mesenteric VMs, measurements of J_V/A are first taken in a high filtration state, e.g., P_L = 60 cm H₂O, and then P_L rapidly reduced to 15 cm H₂O. Initially there is transient reabsorption that satisfies the classical Starling principle. However, according to the assumptions in Michel and Philips, after a short time (≈2 min), C_T rises and a new steady state of low filtration is achieved in which C_T = C = J_S/J_V. The characteristic time for diffusional equilibration in the cleft, t_C, is given by L²/D where D is the diffusion coefficient of albumin in the cleft and L is the cleft depth. If D = 2 × 10⁻⁷ cm²/s and L = 411 nm (15), t_C ≈ 0.01 s. This rapid equilibration of albumin in the cleft strongly suggests that the transition to the new steady state occurs in a quasi-steady manner in which the steady state 1-D model in (2) can be applied at each time interval. The solutions for v and J_S/A follow a path shown by the arrows in Fig. 1 in which it is assumed that P_T = 0 as C_T rises from 3 to 25.6 mg/ml.

Fig. 1.

One-dimensional steady state solutions (2) for velocity (Left) and albumin flux per μm cleft length (Right) at cleft exit when albumin concentration at cleft exit is specified. P_L = 15 cm H₂O, C_L = 50 mg/ml, albumin permeability of the entire endothelial layer P_D = 0.5 × 10⁻⁷ cm/s, and hydraulic permeability of the entire endothelial layer L_P = 1.3 × 10⁻⁷ cm/s/cm H₂O.

The interpretation described above has been widely accepted for the past two decades. However, a closer examination of the solution trajectory in Fig. 1 reveals a fundamental paradox. One notes that v at the cleft exit increases from −5.6 μm/s to 0.2 μm/s (left scale) as C_T increases to the new steady state of low filtration. Because there is a ≈500 fold expansion in area at the cleft exit (18 nm cleft height to 10 μm average spacing between clefts), J_V/A in the tissue space is only on average ≈3 μm/s/500 or ≈6 nm/s. If the half spacing between VMs was 100 μm it would take 1.7 × 10⁴ s or nearly 5 h to turn over the water in this tissue space. A related estimate can be made for the time it would take for the albumin flux at the cleft exit to increase C_T from 3 to 25.6 mg/ml (right scale). In this case J_S/A increases from 0.01 to 0.1 × 10⁻¹² mg/s/μm per unit cleft length with an average value of ≈0.04 × 10⁻¹² mg/s/μm cleft length. The volume of the tissue half space between venules per unit cleft length is 100 μm (average half spacing between VMs or half tissue space) × 10 μm (average spacing between clefts) or 1,000 μm³. The change in C_T is (25.6–3.0 mg/ml) or 22.6 mg/ml. Thus, to add enough albumin to this tissue volume to achieve the new steady state equilibrium would take ≈ 5 × 10⁵ s or ≈6 days, if the tissue volume did not change.

The above estimations indicate that, whether viewed from a water or albumin flux stand point, the measured time to achieve the new steady state is at least 2–3 orders of magnitude too short. These calculations indicate that a new paradigm is needed to explain the classic experiments in ref. 1 on frog VMs and the rat experiments on VMs in ref. 15. This conclusion is further supported by the experiments in (15) wherein the tissue is backloaded at 50 mg/ml and made isotonic relative to the albumin concentration in the lumen (C_L). In these experiments, confocal measurements were made 5 μm from the vessel wall after tissue loading at both high and low P_L. No change in C_T was observed up to 20 min after P_L was raised from 20 to 60 cm H₂O, indicating that even at a high filtration rate the water flux into the tissue was too small to wash out the albumin even near the wall. Combined these observations suggest the existence of a TM whose dimensions are significantly less than the tissue space, but significantly more than the cleft depth because equilibration in the latter is only 0.01 s and, thus, much too rapid to explain Michel and Phillips' observations or those in the VMs of rat mesentery (15).

Experimental Results

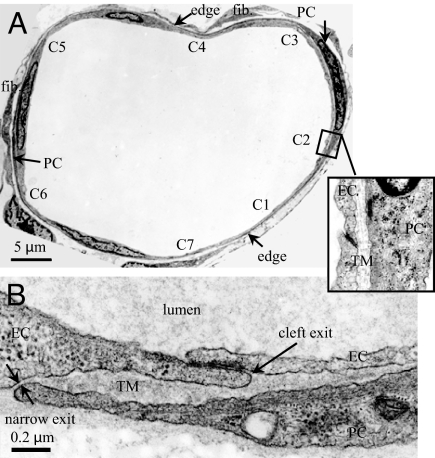
The EM in Fig. 2A illustrates the distribution of PCs around VMs in rat mesentery. PCs are closely apposed to the ECs, typically with a 100 to 200 nm separation between the two cells forming the TM (Fig. 2A Inset). The PC at the right of the figure covers ≈40% of the circumference of the vessel (“edge” to “edge” in the figure) and blocks direct pathways to the interstitium from four EC clefts (C1–C4). Other segments of the endothelial surface and EC clefts are covered by different PC processes in this VM cross-section. In the rat mesentery VMs on average, 0.84 ± 0.03 of the endothelial surface is covered and 0.83 ± 0.03 of the EC clefts are covered by PCs (mean ± sem, n = 10 sections). At the edges of PC images in the cross-sections there often appears a highly narrowed separation between the EC and PC (Fig. 2B) as described in refs. 7 and 8. Such occlusion of the pathway to the interstitium would provide further isolation of the TM.

Fig. 2.

Electron microscope images of a rat venular microvessel (VM). (A) Cross-section of a VM in rat mesentery. There are seven endothelial cell (EC) clefts, C1-C7, with all of the cleft exits covered by neighboring pericytes (PCs). PCs are immediately underneath ECs. There are two fibroblasts (fib.) outside PCs. The blowout shows C2 covered by a PC with a trapped microdomain (TM) of uniform thickness in between. (B) An enlarged view showing a cleft exit covered by a PC, creating a TM of roughly uniform thickness except at the narrow exit.

We have described experiments to measure both transient fluid filtration and reabsorption after rapid changes in P_L, and fluid exchange after establishing pseudo steady state conditions in the rat mesentery VMs. For example, in experiments such as those in figures 4 and 5 of ref. 15, the vessel perfusates contained albumin with an effective osmotic pressure of 27 cm H₂O. The initial steady-state filtration conditions for all experiments were established with P_L of 60 cm H₂O. When P_L was reduced rapidly (within 0.5 s) to 15–20 cm H₂O and there was no albumin in the tissue surrounding the VMs, reabsorption was always measured. In most of these experiments in VMs the hydraulic conductivities were 3- to 5-fold lower than in similar frog VMs studied in ref. 1, and we were unable to follow the transient for more than 20–30 s. In particular, we could not measure a time at which reabsorption was converted to filtration because, at the low reabsorption rates measured in these mammalian vessels, the tendency of the red cells in the perfusates to settle under gravity rendered them unreliable flow markers for longer periods. Nevertheless, in steady state experiments in which we carefully maintained P_L in the range of 15–20 cm H₂O for periods of 1–2 min after reducing from 60 cm H₂O, we confirmed the observations in ref. 1 that the forces governing net fluid exchange approached those expected in a new pseudo steady state within 1–2 min, see figure 5 of ref. 15. Previously, similar measurements of transient and steady state fluid exchange were made in VMs of frog mesentery (14). For example, in figure 4 of ref. 14, transient reabsorption was measured after steady filtration was first established at 35 cm H₂O and P_L was rapidly reduced to 10 cm H₂O. However, slow filtration was measured in the same vessel when P_L of 10 cm H₂O was maintained for ≈2 min after lowering P_L. Although our experiments in frog and rat VMs were not designed to reproduce precisely the conditions of ref. 1, they clearly show, under a variety of conditions, the same trend for new steady states to be established in periods of a few min as in ref. 1 rather than periods of hours or days.

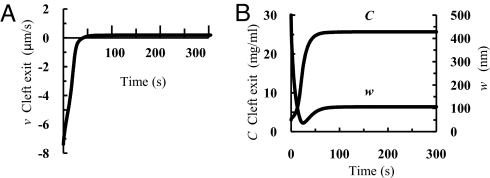
Fig. 4.

Time-dependent change in v, C, and w at the cleft exit. Velocity v (A) and concentration C (B Left) and thickness w of region TM (B Right) as functions of time after P_L is dropped from 60 to 15 cm H₂O. K = 0 and P_D = 0.5 × 10⁻⁷ cm/s.

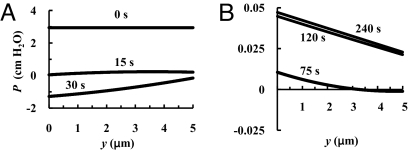
Fig. 5.

Pressure distribution in region TM 0, 15 and 30 s (A), and 75, 120, and 240 s (B) after P_L is abruptly dropped from 60 to 15 cm H₂O. K = 0 and P_D = 0.5 × 10⁻⁷ cm/s.

Theoretical Model

Fig. 3A is a sketch of the ultrastructure shown in Fig. 2, and Fig. 3B is its idealized mathematical model showing that a PC covers an EC cleft exit creating a small TM with an exit region E. The thickness of region TM, w, is time varying but uniform except for the narrow region E at the PC edge whose thickness is fixed by cross-bridging fibers. Based on this idealized ultrastructure, we develop a time dependent model to describe the transition in pressure, P, thickness, w, and concentration, C, of the TM between the initial and new steady state when P_L is abruptly changed. For each instant in time, we treat the flow in the cleft as quasisteady and assume that C is only time varying and, therefore, nearly uniform because of the small dimensions of this space. The structural parameters for the EGL and the cleft are the same as those summarized in Table 1 of ref. 2. The sketch in Fig. 3A is a modified version of figure 1A in ref. 16.

Fig. 3.

Sketch (A) and idealized 1D model (B) of PC and EC arrangement that forms region TM covering EC cleft exit and idealized 1D cleft geometry with TJ adapted from refs. 2 and 16. π_L and P_L, hydrostatic and oncotic pressures in the vessel lumen; π_T and P_T, hydrostatic and oncotic pressures in the interstitium; L_F, thickness of the glycocalyx; L₁, depth of the TJ strand from luminal cleft entrance; L, mean value of total cleft depth. Region F is the EGL of thickness L_F. Region A is the cleft region of depth L₁ in front of the TJ strand. Region TJ is the tight junction of depth L_TJ. Region B is the cleft region of depth L- L₁-L_TJ behind the TJ strand. Region TM is the trapped microdomain of thickness w. Region E is the exit of region TM at PC edge. Region E is of thickness w_E and length L_E. Region T is the tissue space of depth L_T and width 2H, the average spacing between clefts.

Table 1.

Transport parameters

Parameter	JSt
		Constant		Doubled
PD (×10−7 cm/s)	0.50	0.26	0.08	0.50
K (×10−7 cm/s)	0	0.19	0.45	0.41
JSV/JSt (at PL = 15 cm H2O)	0	50%	80%	50%

Water and albumin transport in region TM are determined by net water and albumin fluxes into region TM and the relative resistance of regions TM and E. Overall mass conservation for water requires that the time dependent change in volume of region TM be related to the instantaneous change in thickness, dw/dt, of this region.

Here u(y,t) is the local velocity in the y direction in the TM, H is the half spacing between clefts and u_H(t) is the velocity at y = H. The momentum equation in the TM satisfies Darcy's law, i.e.,

where P is the hydrostatic pressure and K_TM is the Darcy permeability of region TM. Mass conservation for albumin requires that the time dependent change in albumin concentration in region TM, C, be related to the net albumin flux entering or leaving region TM and the volume change of this region,

where J_S/A and J_SH/A are the albumin fluxes per unit area at the cleft exit and at y = H, K is the coefficient describing the vesicular albumin flux, J_SV, given by the second term on the right of Eq. 3, and P_D in Table 1 is the diffusive permeability of the entire endothelial layer including the EGL and the cleft. The values of K are chosen in combination with P_D (Table 1) such that (i) J_SV/J_St is 0, 0.5, and 0.8 when the total albumin flux, J_St, is held constant, and (ii) J_SV/J_St is 0.5 and J_St is doubled.

K_TM varies with the compression of the TM and is described by the theoretical model in ref. 17 for the compression of the thin subendothelial intima beneath rat aortic endothelium due to pressure loading. This thin intimal layer is of comparable thickness and similar matrix structure to our region TM. The theoretical model in ref. 17 predicts that a 5-fold compaction of the thin intimal layer in rat aorta at physiological P_L leads to a 10-fold decrease in the Darcy permeability of the intimal layer. Huang et al. (18) subsequently confirmed in situ the 5-fold compaction in rat aortic intima when transmural pressure increased from 0 to 150 mm Hg.

To determine u_H(t), the velocity of the water leaving region TM through region E, one needs to know the relative resistance of regions TM and E. w_N is the neutral position of the PC membrane when there is no flow. Both the EC and the PC are attached by integrins to extracellular matrix fibers in the TM. The elastic restoring force of this layer is proportional to the displacement [w₀(t) − w_N], i.e.

where the subscript 0 denotes values at y = 0 (entrance to region TM) and k_TM is the elastic constant for the matrix layer. The method to determine the value of k_TM is described in supporting information (SI) Appendix A.

Conservation of mass, momentum and albumin in region E requires that

and

where the subscripts E and T denote region E and the tissue space, and P_T = 0 (19). For w_E = 50 nm and L_E = 200 nm (present study and refs. 7 and 8), K_PE = 2.15 nm² based on the theoretical model in ref. 17. Eqs. 5 specify the exit conditions for region TM. Eq. 5c assumes that the albumin flux in region TM is convection dominated because diffusion gradients are small except in the junctional region E where these gradients can be significant.

At each step in the forward integration on time, one calculates v and J_S/A using quasisteady solutions for the EC cleft and EGL developed in ref. 2, where C and P₀ are obtained from the previous step of the integration. The integration of the momentum equation, Eq. 2, using Eq. 1, gives the pressure distribution, P(y,t), in the TM. The integration constant is determined by applying the boundary condition at y = H and treating u_H(t) as a time-dependent parameter. The solutions for P(y, t) and u_H(t) are given in SI Appendix B. One then solves Eqs. 1–4 to obtain u, w, and C, and updates K_TM and k_TM based on the value of w(t) using the relations developed in refs. 17 and 18. The initial conditions for C and P₀ are obtained using the same steady state solutions for the endothelial layer as in (2) at the initial P_L. If P_L = 60 cm H₂O before P_L is dropped to 15 cm H₂O, C(t = 0) = 3 mg/ml and P₀(t = 0) = 2.9 cm H₂O; and if P_L = 15 cm H₂O before P_L is increased to 60 cm H₂O, C(t = 0) = 25.6 mg/ml and P₀(t = 0) = 0.05 cm H₂O. The integration on time describes the time course of the transition from the initial to the new steady state after P_L is abruptly changed.

Results

Fig. 4 shows the changes in velocity, v, concentration, C, at the cleft exit, and the thickness, w, of region TM with time after P_L is dropped from 60 to 15 cm H₂O. The curves shown are for K = 0 and P_D = 0.5 × 10⁻⁷ cm/s. However, the results for different combinations of K and P_D in Table 1 are nearly indistinguishable on the scale shown in Fig. 4. For all cases, the abrupt change in P_L creates a large initial reabsorption of water from region TM, −7.4 μm/s at the cleft exit. However, the reabsorption is short-lived and the velocity approaches a new equilibrium of low filtration, 0.2 μm/s (0.4 μm/s when J_St is doubled) at the cleft exit, within 1 min after P_L drops. Cleft exit concentration rises from 3 to 25.6 mg/ml (27.1 mg/ml when J_St is doubled) and follows a similar time course. However, w experiences a more complex path dropping from 500 nm to 40 nm (55 nm when J_St is doubled) and then rising to an equilibrium value of 106 nm (112 nm when J_St is doubled) in ≈2 min.

Fig. 5 shows pressure distribution profiles in region TM at different times after P_L is lowered to 15 cm H₂O for K = 0 and P_D = 0.5 × 10⁻⁷ cm/s. The initial P₀, 2.9 cm H₂O, counterbalances the elastic restoring force of the matrix and initiates draining of region TM. P₀ decreases rapidly to ≈0 within 15 s, and then becomes negative reaching its lowest value at ≈30 s after reabsorption started, which coincides with the moment when w reaches its lowest value, 40 nm, Fig. 4B. P₀ increases back to ≈0 at ≈75 s, and P₀ achieves its final equilibrium value, ≈0.05 cm H₂O, in ≈2 min. This small pressure balances the restoring force of the matrix in the new low filtration steady state.

Although the pressure gradients are negligible when the fiber matrix in the TM is in tension and P > 0, the pressure gradients are significant when the fiber matrix is in compression and P < 0. The nonnegligible pressure gradients cause w to vary with y for 15<t<45 s for K = 0 and P_D = 0.5 × 10⁻⁷ cm/s as shown in Fig. C1 SI Appendix C. The results (not shown) for P are insensitive to the differences in relative contribution of albumin fluxes listed in Table 1.

Solutions were also obtained for C and w as functions of time if P_L is increased from 15 to 60 cm H₂O, the reverse transient process to that described in Figs. 4 and 5 for K = 0 and P_D = 0.5 × 10⁻⁷ cm/s. w increases monotonically from 106 nm to 500 nm, C decreases from 25.6 to 3 mg/ml and the equilibration time is ≈45 s. These solutions are shown in Fig. D1 in SI Appendix D.

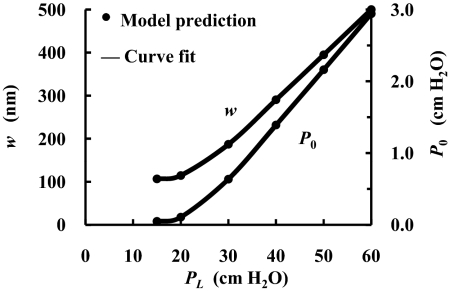
Fig. 6 examines a wider range of pressure changes for K = 0 and P_D = 0.5 × 10⁻⁷ cm/s. w is the steady state thickness of the TM as a function of P_L between 15 and 60 cm H₂O (left scale), and P₀ is the steady state pressure at the cleft exit as a function of P_L (right scale). P₀ decreases from 2.9 cm H₂O at P_L = 60 cm H₂O to ≈0 when P_L<20 cm H₂O. Approximately 95% of the total hydraulic resistance resides in the EGL and the cleft, whereas the remaining ≈5% resides in the regions TM + E. Thus the TM does not contribute significantly to the overall hydraulic resistance even as w varies. These results are insensitive to the values of K and P_D in Table 1.

Fig. 6.

Steady-state thickness of the TM (Left) and pressure at the cleft exit (Right) as functions of P_L. K = 0 and P_D = 0.5 × 10⁻⁷ cm/s.

Discussion

In this paper, we advance a hypothesis for the regulatory function of PCs to explain the large discrepancy between the experimentally observed and theoretically predicted equilibration time for the transient transport behavior observed when P_L is abruptly lowered from a high filtration state in VMs. Our ultrastructural measurements in rat mesentery reveal that there is a TM at 80–90% of the cleft exits created by the close apposition of the ECs and PCs. Although it has not been possible to fix tissue for EM in a high filtration state in which the subendothelial matrix is in a state of tension, related studies on the subendothelial intima of healthy rat aorta (17, 18) reveal a matrix layer of similar composition and thickness which compresses ≈5-fold under pressure loading. The present theoretical model predicts that if an equivalent expansion of this space occurs during a state of high filtration, the draining of this space due to transient reabsorption will lead to a rise in concentration in the TM and a rapid establishment of a new steady state when P_L is suddenly lowered. This result closely mirrors the observations in refs. 1 and 15 for frog and rat mesentery, which show that a new steady state is established within 1–2 min after a rapid decrease in P_L. We do not have the detailed ultrastucture of the PC coverage in these frog mesenteric vessels, but we suggest that the effective PC coverage in the region of cleft exits must approach that described in rat VMs presented herein.

The existence of this TM explains a fundamental paradox, namely that if the entire tissue space were to come to equilibrium it would take ≈5 h to drain enough water for the concentration to rise to the new steady state value. Moreover, the albumin flux through the cleft and/or vesicles is so small that it would take several days for enough albumin to enter and achieve the final steady state value if the tissue volume did not change.

In the high filtration limit, the albumin transport at steady state is dominated by the convective flux through the clefts, whereas in the low filtration limit, the albumin transport at steady state is dominated by the diffusive flux through the clefts and/or the vesicles. However, because J_St is always small, the rapid concentration increase at the cleft exit and behind the EGL after P_L is abruptly altered is due primarily to the volume change resulting from the net water flux out of the TM. Therefore, the transient behaviors following P_L change are relatively insensitive to the source of the albumin flux, whether it be through the cleft or vesicles.

In contrast to previous ultrastructural studies, which have mainly elaborated on the differences in PC coverage in different species and tissues, our ultrastructural studies using EM on rat mesenteric VMs focus on the spatial relationship between the EC clefts and the surrounding PCs and the geometry of the TM between the ECs and the PCs. The geometry of this region determines not only the water and albumin flux through the cleft but also the distribution of the vesicular flux into the TM or directly into the tissue. Previous studies show that PC coverage is much lower in rat and human skeletal muscle and rat myocardial capillaries, 11–24%, and ≈50% in rat retinal capillaries (9). We do not have the corresponding measurements for rat mesenteric capillaries, but the discrepancy conforms to the observation that there is much more extensive coverage of VMs than capillaries (9).

Our EM study, as well as that in ref. 7, show that except at the exit region E, region TM has a nearly uniform thickness of the order of a few hundred nm, the same as the compressible subendothelial arterial intima examined in refs. 17 and 18. The similarity would occur because both are a subendothelial matrix secreted by the ECs. The intima undergoes a very substantial compression when the lumen is pressurized, as shown in ref. 18 for rat aorta. The subendothelial arterial intimal thickness at P_L = 150 mmHg is only 20% that at 0 mm Hg. Region TM is not only able to sustain compression due to the porous nature of its fiber matrix, but also to resist stretching due to focal adhesion plaques of integrin origin (7, 8) to extracellular matrix fibers between the ECs and the surrounding PCs. EMs shown in ref. 7 suggest that in a fully hydrated state the thickness of region TM is ≈500 nm and there is evidence of stretched focal adhesions. As shown in Fig. 4B, we assume that in the transition from the initial to the new steady state when P_L is lowered from 60 to 15 cm H₂O, the initial thickness of region TM is 500 nm, a 5-fold expansion beyond its neutral position, w_N, of 100 nm at zero pressure. During reabsorption, it first compresses to 40 nm, a 2.5-fold compression from w_N, and finally equilibrates at 106 nm with a tiny stretch beyond w_N due to low steady state filtration. An elastic restoring force is needed that prevents region TM from infinite expansion at high filtration and also slow swelling due to slow filtration at low P_L. There are no measurements of the spring constant, k_TM, describing this elastic restoring force. In the present model for the TM we have estimated k_TM = 7.35 × 10⁻³ cm H₂O/nm by requiring that the matrix stretch from 100 to 500 nm in the high filtration state at P_L = 60 cm H₂O. For this value of k_TM one finds that the initial pressure P₀ in the TM is 2.9 cm H₂O (Fig. 5A).

When the pressure gradient in the TM is positive in the +y direction, water is flowing toward the cleft exit and the thickness, w, of the TM is decreasing toward its minimum value, w = 40 nm at t = 30 s (Fig. 4B). Albumin concentration in the TM, C, increases monotonically as water is being reabsorbed (Fig. 4B). For t >75 s the pressure gradient becomes negative in the +y direction and water is slowly exiting from region E of the TM. For these longer times the TM gradually expands due to the slow filtration that develops after the concentration reaches its new steady state value. This slow expansion is nearly complete at t ≈ 2 min, when the elastic restoring force just balances the pressure in region TM. The net albumin flux into the TM and water drainage from the TM rapidly increase the concentration at the cleft exit, leading to an elevation in oncotic pressure behind the EGL that arrests reabsorption. The water velocity at the cleft exit turns positive at t≈45 s, and establishes its equilibrium value at t≈2 min (Fig. 4A) which is in close agreement with the observations in refs. 1 and 15.

Fig. 4B shows that when P_L is abruptly dropped from 60 to 15 cm H₂O, C rises from 3 to 25.6 mg/ml in <1 min. The albumin concentration behind the EGL rises correspondingly at the same pace to arrest the short-lived reabsorption. However, the albumin concentration at the exit of region E in the much larger tissue space barely rises within this 1-min equilibration time. The dense matrix structure in region E maintains a large concentration difference between region TM and the much larger tissue space until the albumin concentration in the tissue eventually rises. The same occurs for the reverse case when P_L is abruptly increased from low to high value, except that the concentration gradient across region E is in the opposite direction.

When w>w_N, and the elastic restoring force is present, the hydrostatic pressure in region TM is nearly independent of y except for 15< t <75 s, Fig. 5. K_TM varies between 22 and 220 nm², at least one order of magnitude >K_PE, which we have estimated as 2.15 nm² based on the observed thickness of this region. Therefore, the hydraulic resistance and the pressure gradient in region TM is much lower than those in region E. When w<w_N, the elastic restoring force follows a nonlinear elastic law derived from the experiments in ref. 18. For the maximum compaction of the TM, w≈40 nm, the elastic constant is 2.7 times that when w ≥ w_N.

The PCs are stiffer than the fibrous matrix layer in region TM, due to their prominent nuclei and dense bands of actin filaments both near nuclei and in the peripheral processes (20). However, the distributed pressure loading, Eq. B6 in SI Appendix B, acts transverse to the PC cell membrane causing it to deflect along its length when the pressure gradient in the y direction is significant. This occurs only for 15 < t < 75 s and for other times w is nearly uniform (Fig. C1 in SI Appendix C). The pressure in region TM has its maximum value of 2.9 cm H₂O when P_L is initially lowered (Fig. 5A). In all previous models for filtration this small initial pressure is neglected and the cleft exit pressure is assumed to be the same as the tissue pressure P_T. However, once the new steady state of slow filtration is achieved, t > 2 min, the difference between P₀ and P_T is negligible (Fig. 5).

In the experiments of refs. 14 and 15, where the tissue is isotonically backloaded, the leakage of albumin through the mesothelium overwhelms the albumin flux from the lumen. The presence of a TM allows one to establish a cleft exit concentration that differs greatly from the much larger tissue space. This enables the VMs to rapidly establish a new steady state equilibrium after P_L is dropped that is close to the behavior of Michel and Phillips experiments where there is no tissue loading. The concentration in region TM, because of its small dimensions, can be regulated by the transport through the EC clefts and vesicles largely uncoupled from the tissue space except for the small fraction of clefts whose exit region is not covered by PCs. Because the PC coverage is not complete in VMs of rat mesentery, the new steady state equilibrium a few minutes after P_L is dropped will be either low filtration or significantly reduced reabsorption, depending on the relative magnitude of the water flux through the exposed and PC covered clefts.

The present model applies to tissues where the primary filtration occurs through VMs where a large fraction of the EC clefts are covered by PCs. The same concept can be applied to tissues, such as skeletal muscle, with small PC coverage, if there are small regions in the interstitium where water can accumulate. In these tissues it is well recognized that reabsorption can continue for 20–30 min after a sudden drop in P_L as would occur after hemorrhage (21). Muscle filtration coefficients in the range of 0.01–0.02 ml/min/ mmHg per 100 g of tissue would account for 15–30 ml of fluid reabsorbed per kg of skeletal muscle in 30 min when P_L was reduced by 5 mmHg. Thus, reabsorption of between 0.3–0.6 liters is expected from 20 kg of such tissue. Removal of this volume from an estimated 2.5–3 liters of interstitial fluid would increase the average interstitial protein concentration by 15–20%, enough to slow but not stop further reabsorption. Thus, observed time constants for reabsorption of 20–30 min are shorter than values of an hour or more that would be expected if the time course were determined by the average protein concentration in the total interstitial fluid volume. These calculations suggest that the observed behavior can be explained if there are small regions in the interstitial space close to the microvessel walls which function as larger TM in a manner analogous to the TM formed by PC coverage. These microdomains would function on a time scale of tens of minutes in contrast to regions deeper in the interstitial space, which would take a much longer time to regulate.

Experimental Methods

The micrographs of rat VMs analyzed for PC coverage are taken from a previous study by our group (15). The data are from 10 sections taken from five VMs. The sections represent randomly distributed sites (i.e., sites not less than 50 μm distant from one another). The details of animal preparation, tissue processing for EM, and measurements for L_P are summarized in SI Appendix E.