Folding domain B of protein A on a dynamically partitioned free energy landscape

Abstract

The B domain of staphylococcal protein A (BdpA) is a small helical protein that has been studied intensively in kinetics experiments and detailed computer simulations that include explicit water. The simulations indicate that BdpA needs to reorganize in crossing the transition barrier to facilitate folding its C-terminal helix (H3) onto the nucleus formed from helices H1 and H2. This process suggests frustration between two partially ordered forms of the protein, but recent φ value measurements indicate that the transition structure is relatively constant over a broad range of temperatures. Here we develop a simplistic model to investigate the folding transition in which properties of the free energy landscape can be quantitatively compared with experimental data. The model is a continuation of the Muñoz–Eaton model to include the intermittency of contacts between structured parts of the protein, and the results compare variations in the landscape with denaturant and temperature to φ value measurements and chevron plots of the kinetic rates. The topography of the model landscape (in particular, the feature of frustration) is consistent with detailed simulations even though variations in the φ values are close to measured values. The transition barrier is smaller than indicated by the chevron data, but it agrees in order of magnitude with a similar α-carbon type of model. Discrepancies with the chevron plots are investigated from the point of view of solvent effects, and an approach is suggested to account for solvent participation in the model.

The routes a protein travels on the way to its native ensemble are the result of a sensitive exchange between energy and entropy coupling the protein to its solvent environment. Often the basic topography of the folding landscape (1) can be understood just from what would be necessary kinetically for a protein-like molecule to organize itself into a particular native shape (2–4), but the detailed way in which a protein interacts with solvent can qualitatively affect the way it folds (5, 6). The conformation of a protein is coupled to large-scale fluctuations in solvent density (7–9), and for small globular proteins investigated in kinetics experiments, most of the change in solvent exposure (10) can occur before the protein is half folded. The rate at which a protein explores its conformational space is slaved to local solvent motions (11, 12), and together these effects can have a significant influence on the time scale for folding.

Recently methods have become available to simulate proteins with explicit solvent on a time scale long enough to explore folding (13–15). These simulations provide the most precise picture of protein kinetics, but are as a result less wieldy to describe variations that occur across different experiments and solvent conditions (16–18). Typically, much more simplistic α-carbon type models have been used to address these problems, and when guided by experiment they can provide an accurate description of the interplay among protein folding routes (3, 4). A parallel approach established by Muñoz and Eaton (19–21) is to partition the free energy landscape of the protein into a network of small ensembles that can be described by polymer physics methods. This approach has the advantage that solvent effects might be included on a practical time scale, but it is usually less accurate than explicit chain models because the partitioning methods introduce dynamical constraints that conflict with, or oversimplify, the kinetics of the protein (22, 23). Here we develop a method to solve this problem.

In the Muñoz–Eaton model, the configuration space of a protein is in effect partitioned in terms of a local order parameter describing the proximity of chemical bond angles in the residues to their native values. The partitioning is accomplished by labeling the residues in a protein configuration as folded (native like) or unfolded (free, or ensemble like) depending on their order parameter values, and then grouping together configurations that have the same pattern of labels. Configurations with unfolded loops (24, 25) are neglected in the model so that folded segments always represent independent nuclei, and consequently the ensemble free energies are simple to describe. The model can be solved exactly by special techniques (26, 27), and it provides a convenient way to construct basic inferences from experiments (28, 29). Nevertheless, the terms that are being neglected (unfolded loops and intermittency of native contacts between folded segments (30, 31)) are precisely those that coordinate the expulsion of solvent from the protein (2, 13, 32), and it is of interest to describe these terms from the point of view of the original model.

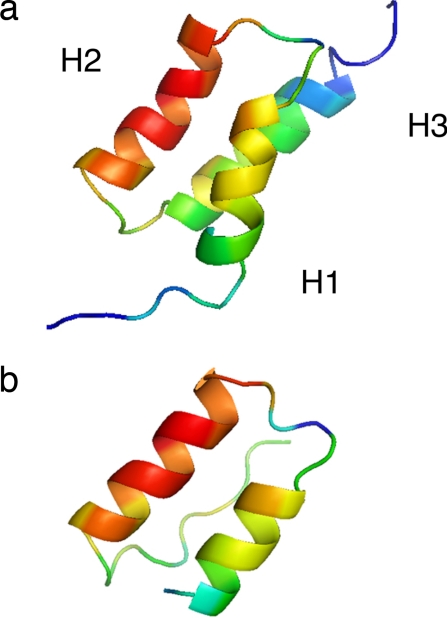
We accomplish this here by continuing the geometric approach of Muñoz and Eaton, including separate order variables to describe the state of contact between the folded segments. The resulting system of constraints resembles the local-order coupling model for explicit chains (33). To test the model, we use it to describe the folding landscape of the B domain of staphylococcal protein A (BdpA), which allows an extensive comparison to thermodynamics and kinetics measurements. BdpA (Fig. 1) is one of the most widely studied proteins of the past decade (34). Folding kinetics and single-molecule FRET measurements indicate that BdpA folds cooperatively over a broad range of solvent conditions (18), yet the system is still small enough to simulate by first principles methods on a computer (13–15). The folding nucleus (16), which forms around the first two helices, includes most of the binding interface from the complex with an IgG Fc fragment (35); H3 is unstructured in the complex, but structured in the transition state in all-atom simulations; however, in crossing the transition barrier, further rearrangement of the helices is required to consolidate contacts with H3 before the protein can fold. These features suggest that BdpA is weakly frustrated by extra “functional” requirements (binding preferences) of Staphylococcus aureus (34). But recent measurements to detect temperature changes in the transition structure (17) indicate that whatever frustration exists, it is not strong enough to divide the landscape into kinetically separate routes (29). By fitting our model to thermodynamic stability data (17, 29) we are able to bridge between the kinetics measurements and the detailed simulations to describe the folding landscape under various solvent conditions.

Fig. 1.

Native structures of BdpA. (a) NMR structure of wild-type BdpA colored according to φ values calculated later in this work. φ values in the range 0 ≤ φ ≤ 0.8 correspond to blue, green, yellow, orange, and red. (b) Crystal structure from the complex of BdpA with the IgG Fc fragment colored as in a.

Model

We consider systems that can be described by a Gō (native only) interaction model in which nonnative contact is repulsive at short distances just to exclude the volume occupied by the protein (3, 4). Let q_i = 0, 1 label the local structure of a residue i (folded or unfolded) in a partially unfolded protein as in the Muñoz–Eaton model. Each pattern of labels {q_i} describes an ensemble of protein configurations Γ with structurally similar folded segments α_k. To describe the intermittency of contacts between the α_k, we partition Γ into smaller ensembles Γ_n ∈ Γ according to whether the degree of native organization between pairs of folded segments α_k and α_l exceeds some threshold value. This is accomplished by providing the folded segments with separate labels (superscripts), α_k → α_k^a, so that native contact between two segments α_k^a and α_l^b is established only if a = b. Leaving to later the question of what actually decides the threshold values for native order, the ensembles Γ_n can each be depicted by a Feynman-like diagram (36) formed by the following procedure [see supporting information (SI) Fig. 5]: First a line is drawn to represent the unfolded protein and labeled circles are placed at points along its length to represent the α_k^a. Circles with the same label are then joined together into nuclei by bending the unfolded lines to form the diagram (note that two circles can have the same label only if contacts exist between them in the native state). Each Γ contains an ensemble Γ₁ corresponding to the fully collapsed (natively connected) configuration of the α_k^a, and each partially collapsed diagram Γ_n≠1 corresponds to a topologically different way of “pulling apart” the folded segments in Γ₁. For small proteins like BdpA, there is no need to consider diagrams with more than four folded segments, so the number of diagrams in Γ is always ≤15.

To describe the free energy of a diagram the energy is then defined as E = −ε Σ_i<j Q_ij(Γ_n), where ε is the energy per contact, Q_ij(Γ_n) = 0 or Q_ij^N, and Q_ij^N is the native contact matrix. Q_ij(Γ_n) = Q_ij^N only if residues i and j are located in the same nucleus.

To describe the entropy, first note that besides Γ₁, each Γ contains an ensemble Γ₀ in which the α_k^a are completely pulled apart (all labels are different). The entropy Δs of unfolded residues in Γ₀ can be estimated from the entropy of unfolded proteins (37), and the entropy cost ΔS(Γ_n) to then sequentially close Γ₀ into any of the diagrams Γ_n ∈ Γ will be estimated in terms of the cost for closing a single loop,

where p(x, x′)Δv is the fraction of unrestricted chain configurations emanating from a point x that terminate at the point x′ within a small volume Δv about the size of a residue (38) and k is Boltzmann's constant. The entropy of a diagram is then S = (N − q)Δs − ΔS, where N is the number of residues, q is the number of folded residues, and ΔS is a sum of terms described by Eq. 1.

Random loop insertions in proteins are well modeled as Gaussian chains with excluded volume (39), and the persistence length appears close to the size of a backbone unit (40, 41). Therefore, we neglect relatively small excluded volume effects here and use the simplest possible Gaussian approximation,

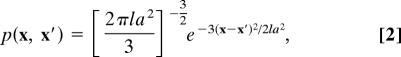giving

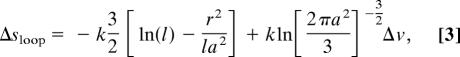where l is the number of links, r is the distance between end residues, a = 3.8 Å, and for simplicity we let $\Delta v=\raisebox{1ex}{$4$}\!\left/ \!\raisebox{-1ex}{$3$}\right.\pi a^3$, which is about the volume of a large branched residue (38).

Typically, the structure of a diagram makes it obvious how to approximate ΔS in terms of Δs_loop(l, r). But we also have to consider situations where, for example, an α_k^a appears along the unfolded part of a loop. This event would lead to a kind of effective loop consisting of two unfolded segments of length l₁ and l₂ joined across a physical distance r′ by the folded segment. To describe this diagram, we first interpret the folded segment as if it were an unfolded part x of a loop of total length l = l₁ + x + l₂, where

and δ ∈ [0, 1]. The variable part of the entropy cost is then multiplied by

to account for the entropy of segment x. The few more complex diagrams that require this approximation contribute minimally to the results (SI Text and SI Fig. 6). The contact matrix and parameters entering into these expressions are described in Methods.

Results

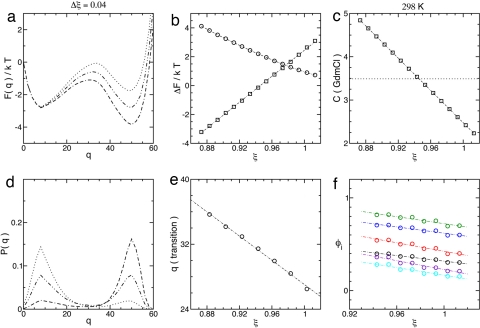
The system can now be depicted as a kind of foam, or network (1) of ensembles with free energy F(Γ_n) = E(Γ_n) − TS(Γ_n), where T is the temperature. To quantitatively compare the model to the data, the melting free energy of the model is mapped to the measured free energy in terms of a stability parameter ξ. To accomplish this, the energy is written as ε/T = ξNΔs/Q^N, where Q^N = Σ_i<j Q_ij^N. The free energy profile is F(q) = −kTlnZ(q) (Fig. 2a), where Z(q) = Σ_Γn^q exp(−F(Γ_n)/kT) and the sum includes ensembles with q folded residues. The ends of the profile balance when ξ = 1.

Fig. 2.

ξ dependence of landscape parameters. (a) Free energy profile across the melting transition, ξ_m ≃ 0.946. (b) Melting free energy ΔF_‡-D (□) and transition state barrier ΔF_‡-D (○). (c) Mapping between stability values and denaturant concentration at 25°C. The dotted line indicates the melting concentration c_m ≃ 3.49 M GdmCl. Data points occur at integer multiples of Δξ = 0.01 (Δc ≃ 0.186) about ξ ≃ 0.943. (d) Distribution of states P(q) corresponding to a. The stability range corresponds to the FRET data in figure 6 of ref. 18. (e) Location of the transition q^‡(ξ). The data points were calculated by fitting the barrier to a quadratic. (f) φ values for the degree of helix formation as in figure 5 of ref. 17 (the color scheme is the same, and the plot describes a similar range of stability). φ_i(ξ) variations for tertiary structure are slightly larger.

The profile can be quantified by its critical points in the denatured (D), transition (‡), and native (N) ensembles: The transition barrier is defined as ΔF_‡-D = F(q^‡) − F(q^D)and the melting free energy is ΔF_D-N = kTlnZ_D/Z_N, where Z_D = Σ_q≤q^‡Z(q) and Z_N = Σ_q>q^‡Z(q) are the partition functions for denatured and native ensembles (Fig. 2b). ξ is mapped to solvent conditions by equating ΔF_D-N(ξ) to the melting free energy measured at T = 25°C (17). Fig. 2c plots this relationship and connects the melting point ξ_m to the melting concentration of denaturant. The predicted melting temperature in 2 M guanidinium chloride (GdmCl) is T_m ≃ 50°C, very close the value T_m ≃ 52°C measured by Sato and Fersht (17), and the melting transition closely resembles single model FRET data (18) (Fig. 2d). The folding barrier (∼2kT at midpoint) has the same order of magnitude as the barrier for an α-carbon model of the protein with Gō interactions (42).

The actual size of the barrier can be estimated from chevron plots of folding/unfolding rates versus denaturant (18). Assuming two-state (exponential) kinetics, the slope of the folding arm of the chevron predicts a change of ∼7kT between 0 M GdmCl and melting, which is not inconsistent with estimates from current kinetic models that include solvent effects explicitly (11, 43). In the kinetic model used by Fersht and coworkers, the slope of the chevron, m_‡-D, is proportional to the change in solvent-accessible surface area (SASA) between denatured and transition states (18). The fractional change in SASA can be calculated as m_‡-D/m_D-N = ∂ΔG_‡-D/∂ΔG_D-N, where m_D-N is the change in SASA between denatured and native states and G is the Gibbs free energy (10). The result is about m_‡-D/m_D-N ∼ 0.7–0.8 for BdpA. Although our model does not include solvent, we can calculate m_‡-D/m_D-N from the ratio of slopes ΔΔF_‡-D/ΔΔF_D-N. The result is m_‡-D/m_D-N ≃ 0.45, which is about equal to the fraction of contacts formed at q^‡. Although the model and measured transitions occur in roughly the same regions of the profile (range of native order), a smaller fraction of the surface area is lost in the transition. Because the model is mapped to ΔF_D-N this value indicates that the slope of ΔF_‡-D is a bit smaller than in the chevron plots. The difference in scale of activation barriers is very similar to what results when small cooperative (three-particle) terms are added to the Gō model (44). These terms can be related to solvent participation in terms of the n-cluster model of phase separation (9, 45), which, along with the results above, suggests that the coupling between the solvent and the structure of the protein (32, 46, 47) is described inaccurately here. It should be possible to account for this coupling better by defining the strength of pair interactions to depend on the amount of local (in space) native order, and the inclusion of these terms already tends to improve protein φ values in explicit chain models (44).

In the Gō model, φ values are usually calculated as φ_i ≃ 〈q_i〉^‡/Q_i^N, where q_i = Σ_j Q_ij(Γ_n) and the angle brackets denote the thermal average at q^‡ (48). Fig. 2f plots φ_i(ξ) for comparison with the φ_i(T) measurements in ref. 17, and Fig. 2e plots the location of the transition, q^‡(ξ). Variations in φ_i(ξ) in Fig. 2f roughly agree with the those in φ_i(T) across the measured temperature range (17), and the uniform increase of curves in Fig. 2f with decreasing ξ reflects the slight shift in the transition state toward the native ensemble. Fig. 3 plots the local order, 〈q_i〉, and the contact order, 〈Q_ij〉/Q_ij^N, along the folding profile, and Fig. 4 describes the landscape and φ values at 2 M GdmCl for different realizations of Q_ij^N described in Methods. The folding pathway described by Fig. 3 is consistent with the replica exchange (all-atom) simulations of Garcia and Onuchic except for H3 helical content [apparently, this is related to the absence of denaturant (17) and high melting temperature (13) of the simulations]. The model pathway appears to describe early formation of the binding interface H1:H2 followed by reorganization across the transition state to consolidate long-range contacts with H3.

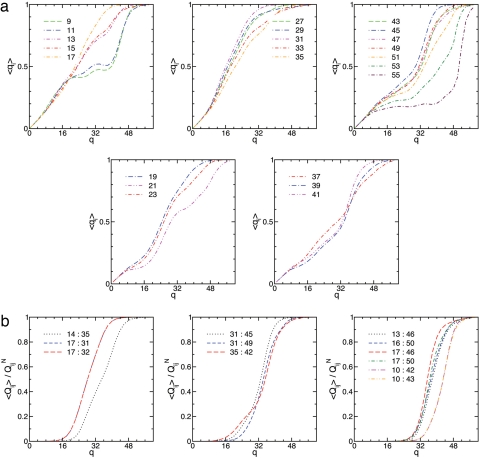
Fig. 3.

Degree of local order, 〈q_i〉, for helix and turn residues (a) and degree of interhelical contact order, 〈Q_ij〉/Q_ij^N, across helices H1:H2, H3:H2, and H1:H3 near the melting transition (b). Keys identify the data for residue index i or index pair i: j. Helix H2 and the C-terminal part of H1 form early, but a indicates that some reorganization occurs in H1 and the turns as the transition is crossed at q^‡ = 32. In b, H1:H2 contacts form early, then H3:H2 and finally H1:H3 contacts form during the reorganization process described in a.

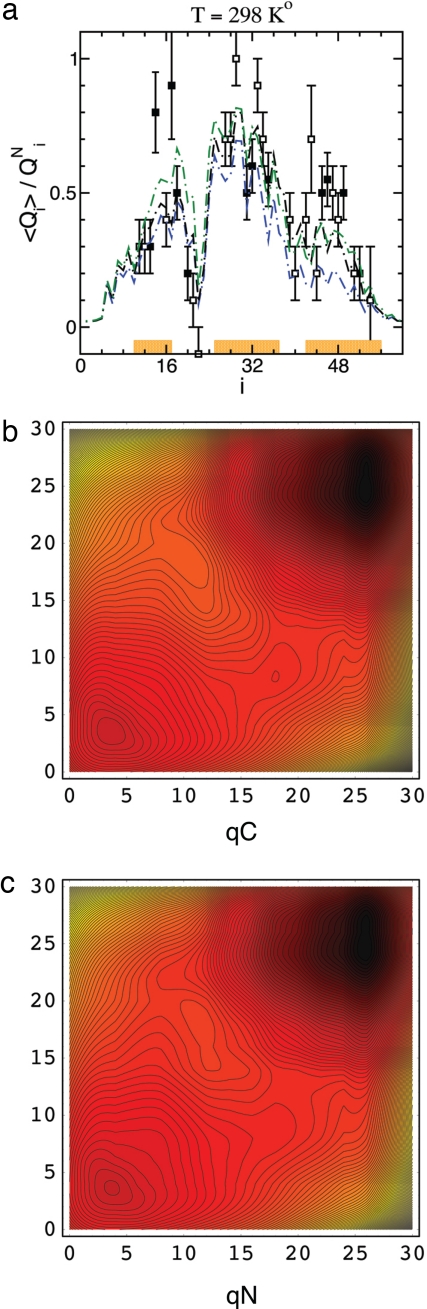
Fig. 4.

Two-dimensional projections of the folding network. (a) Calculated φ values for the wild-type (blue line) and perturbed (black line) contact matrices are shown together with the wild-type melting values (green line). Measured φ values for surface (open symbols) and core (filled symbols) residues are from ref. 16. The level of agreement between the perturbed and measured φ values is about the same as in ref. 29. (b and c) Free energy landscapes for two contact models described in Methods. The landscapes are a projection of the folding network onto the coordinates q_N = Σ_i≤N/2 q_i and q_C = Σ_i>N/2 q_i, where n = 60. (b) The wild-type NMR structure. (c) The same structure weighted by the function (1 + 5/r_ij)/2 for ξ corresponding roughly to 2 M GdmCl at 25°C (levels on the landscapes are separated by ∼0.1kT).

Discussion

Recently, Itoh and Sasai (29) provided a thorough description of BdpA folding by using an exact Muñoz–Eaton model. Here we have followed their approach of fitting ΔF_D-N to stability measurements to allow a clear comparison of results. Their model predicts that the symmetry of the transition state is broken as ξ is brought through the melting point. However, this process is accompanied by large changes in φ values that are not then observed in the φ_i(T) measurements of Sato and Fersht (17). Actually, all of the models above appear to be describing a similar effect, namely weak frustration between two forms of the protein (22, 34). What separates our model is basically that (i) the contact matrix is calculated to reflect the change in exposed surface area (32), and (ii) the largest contribution to φ_i consists of the diagrams Γ_n≠0 that allow unfolded loops.

The discrepancies in ΔF_‡-D seen here and in the α-carbon model (42) seem to indicate missing solvent/cooperative effects; however, the all-atom model folds across a barrier of only ∼1–2kT at midpoint. This situation can be explained somewhat by the conditions of the simulation (13), but it still seems to allow for barrierless folding (28, 49) at high stability, and a calculation of the diffusion constant along the lines of ref. 43 would be helpful here. At the same time, it would be interesting to explore different extensions of the n-cluster model (couplings between Q_ij and space-local order) as a means to fit the system to chevron data, and it seems likely that this approach would improve the level of agreement with other measured properties of the free energy landscape.

Methods

To calibrate the model, we applied it to several small proteins where the landscape had been described by (i) all-atom simulations or (ii) otherwise accurate models where φ values were available (13, 14, 50–52). Figs. 2–4 were calculated by using δ = 0, Δs = 1k (29), and segments of two residues. The results were insensitive to δ and weakly dependent on the ln(l) part of the entropy cost [adjusting this term to account for excluded volume (36) affects mainly the size of the barrier], but neglecting the extension term r²/la² (25) can lead to more qualitative changes in the landscape (see SI Text and SI Fig. 7).

The contact matrix is calculated to reflect the change in exposed surface area on folding (32). A contact is registered in Q_ij^N between a pair of atoms in residues i and j if the atoms are within a distance r_c in the NMR structure of the protein and |i − j| > 1. The contact radii are selected to allow a water molecule between atoms (25): r_c = 6 Å for pairs of heavy atoms, 5 Å for heavy and hydrogen atoms, and 4 Å for hydrogens [including hydrogens (53) leads to more cooperative folding]. The unperturbed contact matrix is calculated from the wild-type NMR structure for comparison with ref. 29. In Fig. 4c we weight Q_ij^N with the function (1 + 5/r_ij)/2 to improve the φ values at 2 M GdmCl. This model is similar in all respects the model in Figs. 2–4b except for the details of the transition. The better resolved NMR structure of the Y15W mutant (16) leads to more of an imbalance between H1 and H3 φ values, but the folded region of the landscape then contains two native-like ensembles similar to what is observed in the all-atom simulations (13). Weighting these contacts by inverse C^α distance did not influence the balance between H1 and H3.