Elimination of the BK_Ca Channel's High-Affinity Ca²⁺ Sensitivity

Abstract

We report here a combination of site-directed mutations that eliminate the high-affinity Ca²⁺ response of the large-conductance Ca²⁺-activated K⁺ channel (BK_Ca), leaving only a low-affinity response blocked by high concentrations of Mg²⁺. Mutations at two sites are required, the “Ca²⁺ bowl,” which has been implicated previously in Ca²⁺ binding, and M513, at the end of the channel's seventh hydrophobic segment. Energetic analyses of mutations at these positions, alone and in combination, argue that the BK_Ca channel contains three types of Ca²⁺ binding sites, one of low affinity that is Mg²⁺ sensitive (as has been suggested previously) and two of higher affinity that have similar binding characteristics and contribute approximately equally to the power of Ca²⁺ to influence channel opening. Estimates of the binding characteristics of the BK_Ca channel's high-affinity Ca²⁺-binding sites are provided.

INTRODUCTION

Large-conductance Ca²⁺-activated K⁺ channels (BK_Ca)* play an important feedback role in a number of physiological processes, most notably smooth-muscle contraction and neurosecretion, which involve changes in both membrane potential and intracellular Ca²⁺ concentration ([Ca²⁺]) (Latorre et al., 1989; McManus, 1991; Robitaille and Charlton, 1992; Robitaille et al., 1993; Nelson and Quayle, 1995). To accomplish this function they have evolved a unique sensitivity to both these signaling modalities that manifests as a Ca²⁺-dependent, leftward shifting of the channel's conductance-voltage (G-V) relation (Barrett et al., 1982; Methfessel and Boheim, 1982; Moczydlowski and Latorre, 1983). Biophysical studies have shed considerable light on the mechanism by which voltage-sensor activation influences channel opening (Cox et al., 1997; Stefani et al., 1997; Diaz et al., 1998; Rothberg and Magleby, 1998; Horrigan and Aldrich, 1999; Horrigan et al., 1999; Talukder and Aldrich, 2000). Less is known, however, about the BK_Ca channel's Ca²⁺-sensing mechanism and it is upon this mechanism that the present work is focused.

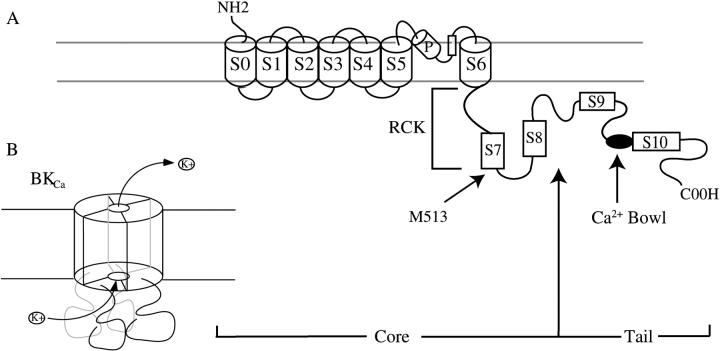
BK_Ca channels (Fig. 1) are structurally similar to K⁺ channels gated only by voltage (K_V). Four identical subunits, known by their gene name slo, form a fully functional channel (Shen et al., 1994), and the amino-terminal third of the Slo protein contains several membrane-spanning regions, including a pore domain and a S4 helix that likely forms the channel's voltage sensors (Adelman et al., 1992; Butler et al., 1993; Diaz et al., 1998; Cui and Aldrich, 2000). Unlike K_V channels, however, the Slo subunit contains a large intracellular domain that confers Ca²⁺ sensitivity on a voltage-gated structure (Wei et al., 1994; Schreiber et al., 1999; Moss and Magleby, 2001). The COOH-terminal part of this intracellular domain is termed the channel's “tail,” while the portion of Slo that precedes the tail is termed the “core” (Fig. 1) (Wei et al., 1994). Neither core nor tail contain canonical Ca²⁺-binding motifs, and so the origin of the BK_Ca channel's Ca²⁺ sensitivity remains unresolved.

Figure 1.

Schematic diagrams of the BK_Ca channel. (A) Diagram of the Slo subunit, four of which form a fully functional BK_Ca channel. Indicated are the core and tail domains, the pore helix (P), hydrophobic regions (S1-S10), the RCK domain, and the Ca²⁺-bowl. (B) Schematic diagram of a Slo tetramer.

There is reason to believe, however, that the tail is involved in Ca²⁺ sensing. Transfer of a large portion of the mouse Slo (mSlo) tail to a Ca²⁺-insensitive Slo homologue (Slo3) confers significant Ca²⁺-sensitivity (Schreiber et al., 1999), and ⁴⁵Ca²⁺ binding to a tail polypeptide is reduced 56% by the mutation of five aspartates (Bian et al., 2001) that are among ten acidic residues in an unusually well-conserved tail domain termed the “Ca²⁺ bowl” (Schreiber and Salkoff, 1997). This domain contains 28 amino acids, and mutations here have been shown to cause rightward G-V shifts at constant [Ca²⁺], shifts similar to those observed with the wild-type channel when [Ca²⁺] is lowered (Schreiber and Salkoff, 1997; Bian et al., 2001; Braun and Sy, 2001). Thus, the Ca²⁺ bowl may form a Ca²⁺-binding site.

Arguing against an exclusive or even dominant role for the Ca²⁺ bowl in Ca²⁺ sensing, however, are the following observations: when the same aspartates were mutated in the full-length channel, the channel remained Ca²⁺ sensitive, its G-V relation still shifting well over 100 mV in response to changes in [Ca²⁺] (Bian et al., 2001); and this has been the case for all Ca²⁺ bowl mutations so far reported (Schreiber and Salkoff, 1997; Bian et al., 2001; Braun and Sy, 2001). No mutation in the Ca²⁺ bowl has been shown to substantially alter the concentration range over which the channel responds to Ca²⁺, and mutations outside the Ca²⁺ bowl have also been shown to cause rightward G-V shifts at constant [Ca²⁺] (Diaz et al., 1998; Cui and Aldrich, 2000; Braun and Sy, 2001). Thus, if there is a Ca²⁺-binding site in the Ca²⁺ bowl, then there are likely to be others outside this region as well (Schreiber and Salkoff, 1997; Schreiber et al., 1999; Bian et al., 2001).

To investigate further the role of the Ca²⁺ bowl in the Ca²⁺-sensing mechanism of the BK_Ca channel, we made a series of mutations in the mSlo Ca²⁺ bowl and analyzed their effects on the energetics of Ca²⁺-dependent gating. Our data argue that Ca²⁺ bowl mutations can eliminate the ability of a high-affinity Ca²⁺-binding site to promote channel opening, and therefore suggest that a Ca²⁺-binding site is present in this region. In addition, however, we have identified another site, at the end of the channel's seventh hydrophobic domain, that when mutated, also impairs Ca²⁺ sensing. And when the two sites are mutated together, all high-affinity Ca²⁺ response is lost. Thus, we propose that the BK_Ca channel contains two types of high-affinity Ca²⁺-binding sites, and in the experiments detailed below we estimate their binding characteristics.

MATERIALS AND METHODS

Channel Expression

The BK_Ca α subunit clone (mbr5) was propagated in the E. coli strains Top 10 or XL1-blue. In vitro transcription was performed with the “mMessage mMachine” kit with T3 RNA polymerase (Ambion). To record macroscopic currents ∼0.5–50 ng of cRNA was injected into Xenopus laevis oocytes (stage IV-V) 2–6 d before recording.

Mutagenesis

All mutations were made with the Quick Change Site–directed mutagenesis kit (Stratagene), and mutations were identified by sequencing around the point of the mutation. Further, the coding regions of the following channels were sequenced in their entirety (wild-type mSlo [mbr5], Δ896–903, M513I, Δ896–903+M513I, Δ899–903+M513I).

Electrophysiology

Electrophysiological recordings were performed essentially as described previously (Cox and Aldrich, 2000). All recordings were done in the inside-out patch-clamp configuration (Hamill et al., 1981). Patch pipettes were made of borosilicate glass (VWR micropipettes), and had resistances of typically 1–2 Mohms in our recording solutions. Their tips were coated with wax (Sticky Wax) and fire polished before use. Data were acquired using an Axopatch 200B patch clamp amplifier (Axon Instruments, Inc.) or a list EPC-7 and a Macintosh-based computer system using “Pulse” acquisition software (HEKA Electronik) and the ITC-16 hardware interface (Instrutech). Records were digitized at 20-μs intervals and low pass filtered at 10 KHz. All experiments were performed at room temperature, 22–24°C. Before current records were analyzed and displayed, capacity and leak currents were subtracted using a P/5 leak subtraction protocol with a holding potential of −120 mV and voltage steps opposite in polarity to those in the experimental protocol.

Solutions

In general, recording solutions were composed of the following (in mM). Pipette solution: 80 KMeSO₃, 60 N-methyl-glucamine-MeSO₃, 20 HEPES, 2 KCl, 2 MgCl₂, pH = 7.20. Internal solution: 80 KMeSO₃, 60 N-methyl-glucamine-MeSO₃, 20 HEPES, 2 KCl, 1 HEDTA or 1 EGTA, and CaCl₂ sufficient to give the appropriate free Ca²⁺ concentration; pH, 7.20. EGTA (Sigma-Aldrich) was used as the Ca²⁺ buffer for solutions containing <0.8 μM free [Ca²⁺]. HEDTA (Sigma-Aldrich) was used as the Ca²⁺ buffer for solutions containing between 0.8 and 10 μM free [Ca²⁺], and no Ca²⁺ chelator was used in solutions containing 100 μM free [Ca²⁺]. 50 μM (+)-18-crown-6-tetracarboxylic acid (18C6TA) was added to all internal solutions to prevent Ba²⁺ block at high voltages.

The appropriate amount of total Ca²⁺ (100 mM CaCl₂ standard solution; Orion Research, Inc.) to add to the base internal solution containing 1 mM HEDTA or 1 mM EGTA to yield the desired free Ca²⁺ concentration was calculated using the program Max Chelator (Bers et al., 1994), which was downloaded from www.stanford.edu/~cpatton/maxc.html, and the proton and Ca²⁺-binding constants of Bers (supplied with the program) for pH = 7.20, T = 23°C, and ionic strength = 0.15. The ability of 18C6TA to chelate Ca²⁺, as well as K⁺ and Ba²⁺, was also considered in these calculations using the following dissociation constants: Ca²⁺ 10⁻⁸ M (Dietrich, 1985), K⁺ 3.3 × 10⁻⁶ M (Dietrich, 1985), Ba²⁺ 1.6 × 10⁻¹⁰ M (Diaz et al., 1996). Free [Ca²⁺] was measured with a Ca-sensitive electrode (Orion Research, Inc.) and the measured value was reported. Free [Ca²⁺] measurements were precise to within ∼8%. Standard Ca²⁺ solutions for calibration of the Ca-sensitive electrode were purchased from World Precision Instruments (10⁻⁸–10⁻² M). Endogenous [Ca²⁺] in our internal solution before addition of Ca²⁺ chelator was estimated from the deviation from linearity of the Ca-sensitive electrode's response at 10 μM added [Ca²⁺], and was 16–20 μM. Endogenous [Ca²⁺] was then compensated for when making Ca²⁺-buffered solutions.

During our experiments, the solution bathing the cytoplasmic face of the patch was exchanged using a sewer pipe flow system (DAD 12) purchased from Adams and List Assoc. Ltd.

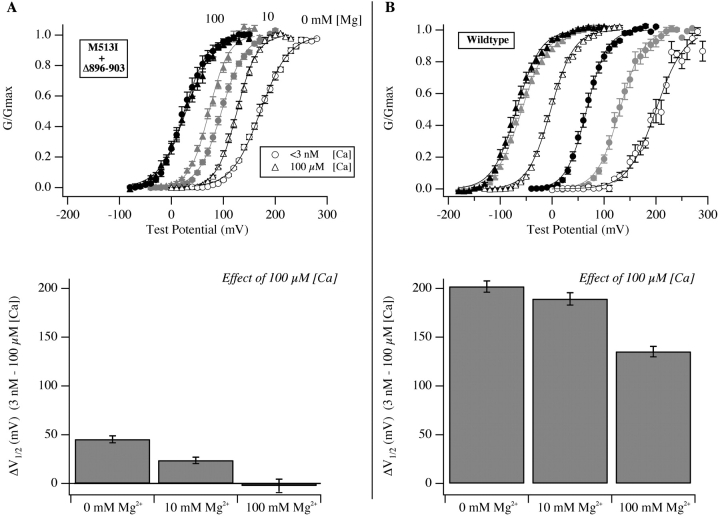
In the experiments of Fig. 5 , Mg²⁺ was often added to the internal solution. When this was the case, the following solutions were used. For the solution containing nominally 0 [Ca²⁺] and 10 mM [Mg²⁺], our base internal solution described above was used with the addition of 5 mM rather than 1 mM EGTA, and 12.1 mM MgCl₂ (Sigma-Aldrich 4.9 M stock). For the solution containing 100 μM [Ca²⁺] and 10 mM [Mg²⁺] our base internal solution was used without added chelator, and 90 μM CaCl₂ and 10 mM MgCl₂ were added. For solutions containing 100 mM [Mg²⁺] our base internal was also used, except N-methyl-glucamine was not included, and then either 15 mM EGTA and 112 mM MgCl₂ were added to create a solution containing nominally 0 [Ca²⁺] and 100 mM free [Mg²⁺], or 0 EGTA, 100 mM MgCl₂, and 90 μM CaCl₂ were added to create a solution containing 100 μM free [Ca²⁺] and 100 mM free [Mg²⁺].

Figure 5.

The remaining Ca²⁺ response of M513I+Δ896–903 is blocked by Mg²⁺. (A) Top, G-V curves for the double mutant M513I+Δ896–903. Circles represent <3 nM [Ca²⁺]. Triangles represent 100 μM [Ca²⁺]. Open symbols indicate the absence of Mg²⁺. Grayed symbols indicate the presence of 10 mM [Mg²⁺]. Darkened symbols indicate the presence of 100 mM [Mg²⁺]. Each curve has been fitted with a Boltzmann function. Bottom, plots of the change in V_1/2 as [Ca²⁺] is increased from <3 nM to 100 μM in the presence of either 0, 10, or 100 mM [Mg²⁺]. (B) Same experiment as in A except the wild-type channel was used. Mean V_1/2 values were determined from Boltzmann fits to the data from each experiment individually.

Determination of G-V Curves and Fitting

Conductance-voltage (G-V) relations were determined from the amplitude of tail currents measured 200 μs after repolarization to a fixed membrane potential (−80 mV) after voltage steps to the indicated test voltages. Each G-V relation was fitted with a Boltzmann function (G = G_max/[1 + e^{−zF{V − V1/2}/RT}]) and normalized to the peak of the fit. All curve fitting was done with “Igor Pro” graphing and curve fitting software (WaveMetrics, Inc.) using the Levenberg-Marquardt algorithm to perform nonlinear least squares fits. Values in the text are given ± the standard error of the mean.

RESULTS

Mutations at the Ca²⁺ Bowl Alter Ca²⁺ Binding

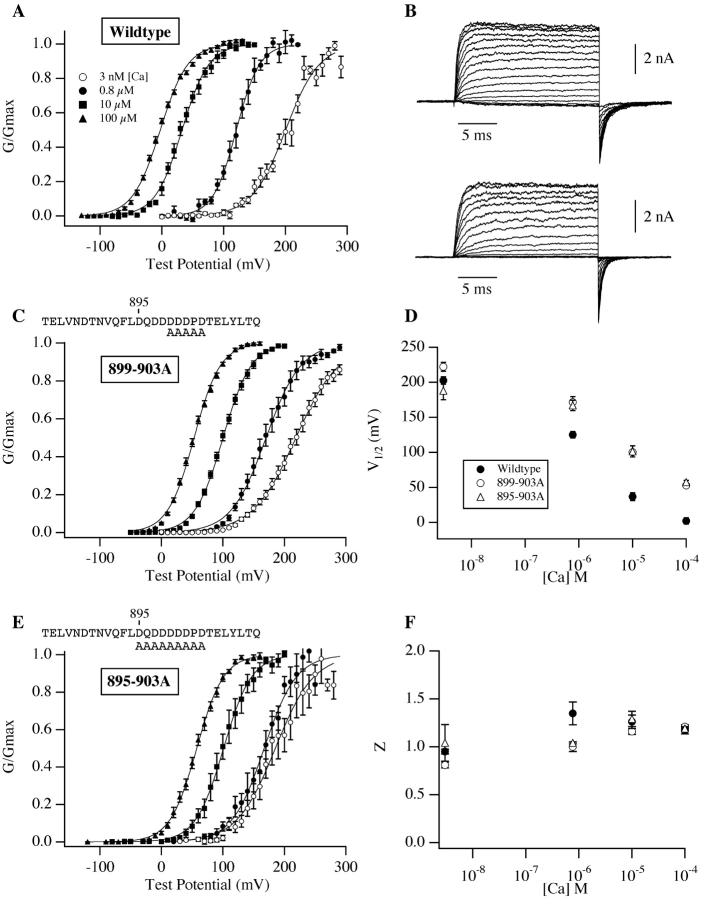
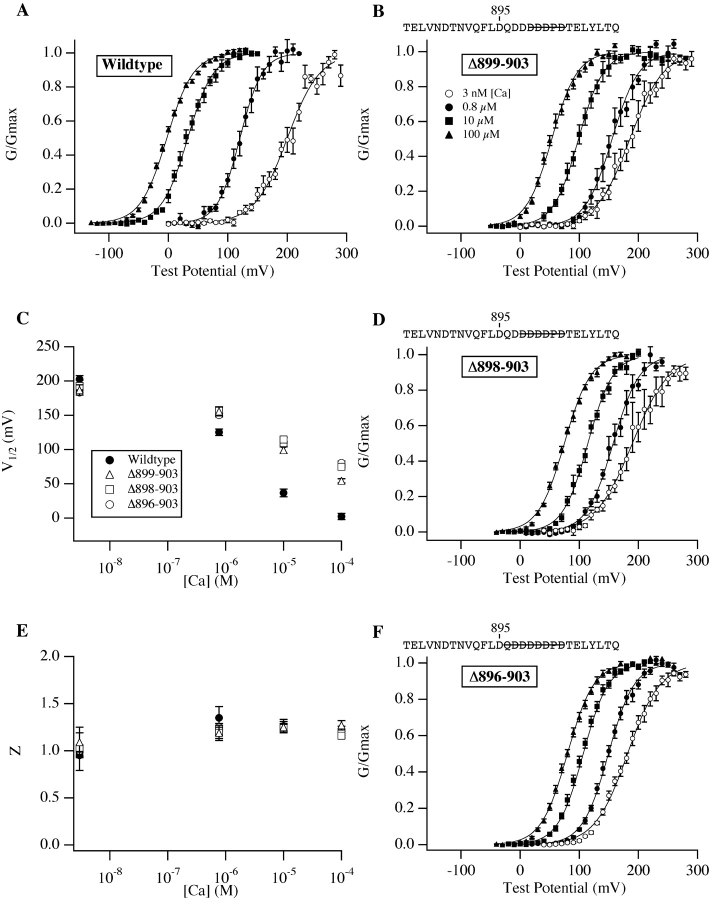
We began our investigation by mutating to alanine five contiguous residues (899–903) in the mSlo Ca²⁺ bowl, four potentially Ca²⁺-coordinating aspartates, and a proline (commonly a helix-breaking residue that might reasonably be important for maintaining the secondary structure of the surrounding region). Despite this fairly dramatic manipulation, however, the 899–903A mutant shares many functional characteristics with the wild-type channel (Fig. 2) . Except at 0.8 μM where the mutant's G-V curve is somewhat shallower, at most [Ca²⁺] the shapes of the wild-type and mutant curves are indistinguishable (Fig. 2 F and Table I) . The mutant and wild-type G-V curves are also in similar positions at 3 nM [Ca²⁺] (although the mutant's curve is somewhat right-shifted; Fig. 2 D and Table I). And perhaps most importantly, the mutant channel is still quite Ca²⁺ sensitive. Its G-V relation shifts over 150 mV as [Ca²⁺] is increased from 3 nM, a concentration too low to be sensed by the channel (Meera et al., 1996; Cui et al., 1997; Cox and Aldrich, 2000), to 100 μM, near saturating for the channel's high-affinity Ca²⁺-binding sites (Cox et al., 1997; Shi and Cui, 2001; Zhang et al., 2001). Thus, the 899–903A mutation does not eliminate the Ca²⁺ sensitivity of the mSlo channel, but it does reduce the power of Ca²⁺ to shift the mSlo G-V curve leftward along the voltage axis such that by 100 μM the mutant's G-V curve stands 52 mV to the right of the corresponding wild-type curve (Fig. 2, A, C, and D; Table I).

Figure 2.

Ca²⁺ bowl mutations reduce mSlo's Ca²⁺ response. (A) G-V relations determined from inside-out Xenopus oocyte macropatches expressing the mSlo protein. [Ca²⁺] are as indicated on the figure. (B) Wild-type (top) and mutant (895–903A; bottom) mSlo current families recorded with voltage steps to between −40 and 130 mV with 100 μM internal [Ca²⁺]. Tail potentials are −80 mV; holding potentials are −120 mV (top) and −100 mV (bottom). (C) G-V relations determined from patches expressing the Ca²⁺ bowl mutant 899–903A. The residues mutated to alanine are indicated above the plot. (D) Half maximal activation voltage (V_1/2) vs. [Ca²⁺] plots for the data in panels A, C, and E. The points plotted are average parameter values determined from experiments fitted individually with a Boltzmann function (see Table I for values). Symbols represent channel type as indicated on the figure. (E) G-V relations determined from patches expressing the Ca²⁺ bowl mutant 895–903A. (F) Apparent gating valence (z), determined from Boltzmann fits, plotted as a function of [Ca²⁺] (see Table I for values). Symbols represent channel type as in D. Error bars in this and subsequent figures represent standard error of the mean.

TABLE I.

Boltzmann-Fit Parameters for Wild-type and Mutant mSlo G-V Curves^a

[Ca]	Channel Type	V1/2	z	n
		mV
3 nM	Wild-type	203 ± 5.3	0.95 ± 0.03	4
	899-903A	222 ± 6.3	0.81 ± 0.03	14
	895-903A	188 ± 12.7	1.04 ± 0.19	5
	Δ899-903	183 ± 3.4	1.02 ± 0.05	19
	Δ898-903	193 ± 8.8	1.02 ± 0.23	5
	Δ896-903	183 ± 3.5	1.00 ± 0.06	19
	M513I	193 ± 2.8	0.97 ± 0.04	14
	M513I+Δ899-903	162 ± 3.9	1.01 ± 0.07	7
	M513I+Δ896-903	172 ± 2.8	0.95 ± 0.02	11
71 nM	Wild-type	197 ± 2.8	0.90 ± 0.05	6
	Δ899-903	178 ± 2.6	0.97 ± 0.03	11
	Δ896-903	180 ± 4.6	1.03 ± 0.04	19
	M513I	196 ± 3.0	0.93 ± 0.04	8
	M513I+Δ896-903	170 ± 2.2	0.93 ± 0.02	7
130 nM	Wild-type	186 ± 2.5	0.96 ± 0.04	8
	Δ899-903	174 ± 3.3	0.96 ± 0.02	11
	Δ896-903	169 ± 2.4	1.13 ± 0.04	20
	M513I	189 ± 3.8	0.95 ± 0.04	8
	M513I+Δ896-903	172 ± 3.0	0.89 ± 0.03	4
360 nM	Wild-type	156 ± 3.0	1.12 ± 0.05	7
	Δ899-903	161 ± 3.4	1.11 ± 0.04	11
	Δ896-903	160 ± 2.7	1.14 ± 0.05	8
	M513I	168 ± 3.9	1.12 ± 0.04	8
	M513I+Δ896-903	160 ± 2.2	1.13 ± 0.04	4
0.8 μM	Wild-type	125 ± 4.7	1.35 ± 0.12	7
	899-903A	172 ± 8.0	1.00 ± 0.05	10
	895-903A	167 ± 7.4	1.04 ± 0.01	5
	Δ899-903	150 ± 4.4	1.14 ± 0.05	9
	Δ898-903	158 ± 4.6	1.19 ± 0.06	6
	Δ896-903	150 ± 2.9	1.25 ± 0.05	18
	M513I	140 ± 3.2	1.28 ± 0.07	15
	M513I+Δ899–903	159 ± 4.5	1.11 ± 0.07	8
	M513I+Δ896–903	165 ± 4.5	1.08 ± 0.07	7
10 μM	Wild-type	37 ± 5.6	1.26 ± 0.07	8
	899-903A	100 ± 2.7	1.16 ± 0.03	16
	895-903A	101 ± 7.9	1.29 ± 0.08	6
	Δ899-903	96 ± 3.2	1.17 ± 0.05	9
	Δ898-903	115 ± 3.9	1.24 ± 0.05	5
	Δ896-903	107 ± 3.4	1.25 ± 0.03	12
	M513I	106 ± 2.4	1.17 ± 0.03	16
	M513I+Δ899–903	149 ± 3.2	1.18 ± 0.04	7
	M513I+Δ896–903	158 ± 4.6	1.11 ± 0.10	7
100 μM	Wild-type	1 ± 2.4	1.17 ± 0.03	22
	899-903A	53 ± 1.7	1.21 ± 0.02	21
	895-903A	57 ± 2.7	1.19 ± 0.02	8
	Δ899-903	54 ± 2.4	1.18 ± 0.05	17
	Δ898-903	80 ± 2.3	1.21 ± 0.04	24
	Δ896-903	75 ± 2.2	1.16 ± 0.02	5
	M513I	85 ± 2.6	1.24 ± 0.05	21
	M513I+Δ899–903	114 ± 2.1	1.43 ± 0.04	10
	M513I+Δ896–903	127 ± 2.3	1.35 ± 0.04	11

Data is ± SEM. n, number of observations.

^a =

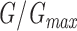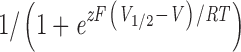
These data indicate that the 899–903A mutant is similar to a class of Ca²⁺-bowl mutants termed by Schreiber and Salkoff (1997) to be “(+)-shifted,” as at 100 μM, 10 μM, and 0.8 μM [Ca²⁺], the mutant's G-V relation is between 45 and 65 mV right or (+)-shifted relative to wild-type (see Fig. 2 D and Table I). However, because of the similarity of the mutant and wild-type curves at very low [Ca²⁺] (something also described for the [+]-shifted deletion mutant Δ897–899 by Schreiber and Salkoff [1997]), one might also consider the 899–903A channel's G-V curves, examined over a series of [Ca²⁺], as compressed along the voltage axis.

Because G-V compression can be attributed to an alteration in the voltage-sensing aspect of gating (Cox et al., 1997; Cox and Aldrich, 2000; Cui and Aldrich, 2000), it is reasonable to question whether the Ca²⁺-binding properties of the mSlo channel have been altered at all by the 899–903A mutation. However, the mutation's relatively small effects on G-V steepness and position at very low [Ca²⁺] and its large effect on G-V position at high [Ca²⁺] make a compelling case for a true change in the channel's Ca²⁺-binding properties. This can be evaluated quantitatively by interpreting these data in terms of the voltage-dependent Monod-Wyman-Changeaux model (VD-MWC), which supposes a central voltage-dependent closed-to-open conformational change that is allosterically regulated by Ca²⁺ binding (Cox et al., 1997; Cox and Aldrich, 2000) (see diagram in Fig. 6 B). According to this model, the position of the channel's G-V relation as indexed by its half-activation voltage (V_1/2) is given by the following function of [Ca²⁺]

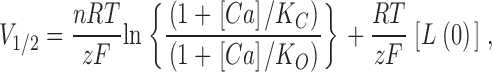where K _O and K _C represent the model's Ca²⁺ dissociation constants when the channel is open or closed, respectively, L(0) represents the equilibrium constant of the central closed-to-open conformational change in the absence of an applied voltage, z represents the gating charge associated with this conformational change, n represents the number of Ca²⁺-binding sites that influence opening, and R, T, and F have their usual meanings. The amount that V_1/2 will change with a given increase in [Ca²⁺] (ΔV_1/2) is then

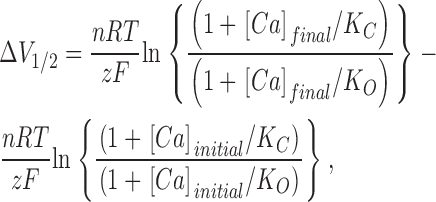and the change in the product zFV_1/2 is given by

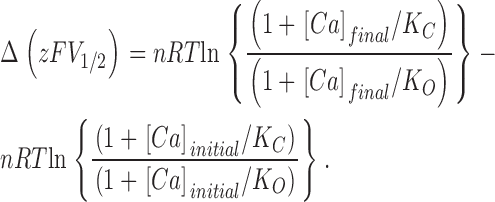(1)

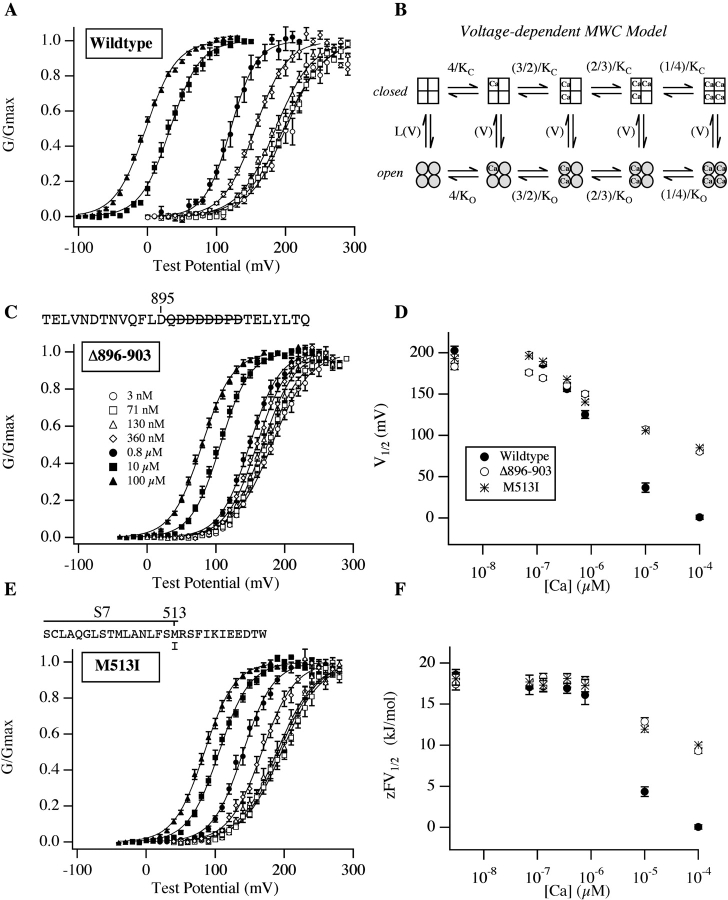
Figure 6.

Estimating ΔG(0)_o-c based on the VD-MWC model. (A, C, and E) Wild-type and mutant G-V curves for the indicated mutants determined over an expanded series of [Ca²⁺] as indicated in C. (B) Diagram of the voltage-dependent MWC model (Cox et al., 1997). Horizontal transitions represent Ca²⁺ binding. Vertical transitions represent the conformational change by which the channel opens. K _C and K _O represent the model's closed and open-state Ca²⁺ dissociation constants, respectively. (D) V_1/2 vs. [Ca²⁺] plots for the data in A, C, and E (see Table I for values). (F) zFV_1/2 vs. [Ca²⁺] plots for the data in A, C, and E. Mean values of z and V_1/2 were determined from fits to individual experiments separately and are listed in Table I. For the VD-MWC model, zFV_1/2 = ΔG(0)_o-c. Symbols indicate channel type as in D.

Eq. 1 is important here because for the VD-MWC and related models (see for example Cox et al., 1997), zFV_1/2 is equal to the free energy difference between open and closed at 0 mV (ΔG(0)_o-c) (Cui and Aldrich, 2000), and thus ΔzFV_1/2 is equal to the change in this free-energy difference (ΔΔG(0)_o-c) as [Ca²⁺] is increased, a quantity, unlike ΔV_1/2, that depends only on the Ca²⁺-binding properties of the model (Cox et al., 1997; Cox and Aldrich, 2000; Cui and Aldrich, 2000). For wild-type mSlo, ΔzFV_1/2,(3 nM to 100 μM), evaluated from Boltzmann fits (see Table I), is 18.5 ± 0.66 kJ/mol, whereas for the 899–903A mutant it is 11.1 ± 0.60 kJ/mol. Thus, the 899–903A mutation appears to reduce the degree to which 100 μM [Ca²⁺] alters the channel's free energy difference between open and closed by 7.4 kJ/mol or 40%, and Eq. 1 suggests it must do so by reducing either the change in affinity that occurs at each Ca²⁺-binding site as the channel opens (that is the ratio K _C/K _O), or the number of binding sites the channel contains (n). This latter possibility is particularly interesting, as it would suggest that the 899–903A mutation knocks out a subset of the channels Ca²⁺ binding sites. Indeed, based on similar findings, Schreiber and Salkoff (1997) have argued that “(+)-shifted” mutants represent a complete loss of Ca²⁺-bowl function and that the channel's remaining Ca²⁺ sensitivity arises from Ca²⁺ binding elsewhere.

If this idea is correct, then mutations in the Ca²⁺ bowl more severe than 899–903A would not be expected to display a more severe phenotype, as under this hypothesis Ca²⁺ binding at the Ca²⁺ bowl is completely lost with 899–903A. To test this prediction, we mutated to alanine four additional residues in the heart of the Ca²⁺ bowl (895–903), three aspartates and one glutamine. Remarkably, despite the loss of 7 of 10 Ca²⁺ bowl acidic side chains, the 895–903A channel's equilibrium gating behavior is still appreciably Ca²⁺ sensitive, and very similar to that of the less severe 899–903A mutant (Fig. 2 E and Table I). Other than a small leftward (rather than rightward) G-V shift at 3 nM [Ca²⁺], neutralizing an additional three acidic and therefore potentially Ca²⁺-coordinating side chains had no further effect on G-V position as a function of [Ca²⁺] (Fig. 2 D and Table I). Thus, the smaller 899–903A mutation appears to be sufficient to completely eliminate Ca²⁺ binding at the Ca²⁺ bowl.

To examine, however, whether deleting rather than altering Ca²⁺-bowl residues might create a more severe phenotype, we also made the following deletion mutants: Δ895–903, Δ896–903, Δ898–903, and Δ899–903 deletions of 9, 8, 6, and 5 residues, respectively. Unfortunately, the Δ895–903 mutant did not produce stable currents. The others, however, did express well and displayed phenotypes that are similar to that of the alanine-substitution mutants described above: little effect at 3 nM and a fairly large reduction in the power of 100 μM [Ca²⁺] to shift the mSlo G-V relation leftward (Fig. 3) . In fact, the phenotype of the smaller deletion (Δ899–903) is virtually identical to that of 895–903A, and that of the larger deletions differs primarily at 100 μM [Ca²⁺], where the G-V curves for Δ896–903 and Δ898–903 are 74 and 79 mV right-shifted relative to wild-type, rather than 56 mV as is observed for 895–903A (Fig. 3 C and Table I). Despite this difference, the similar phenotypes of the five Ca²⁺-bowl mutants described above suggest the disruption of a common function, and we might tentatively conclude that the alanine-substitution mutants (899–903A, 895–903A) and the smaller deletion (Δ899–903) cause a near complete loss of function at the Ca²⁺ bowl, whereas the larger deletions (Δ896–903, Δ898–903) eliminate Ca²⁺-bowl function.

Figure 3.

Many Ca²⁺ bowl mutants behave similarly. (A) Wild-type G-V relations determined at a series of [Ca²⁺] as in Fig. 2. (B) G-V relations for the mutant Δ899–903. The residues deleted are indicated above the plot with a line drawn through them. (C) V_1/2 vs. [Ca²⁺] plots for the channels in A, B, D, and F (see Table I for values). (D) G-V relations for the mutant Δ898–903. (E) z vs. [Ca²⁺] plots for the channels in A, B, D, and F (see Table I for values). Symbols represent mutants as indicated in C. (F) G-V relations for the mutant Δ896–903. In A, B, D, and F symbols represent [Ca²⁺] as indicated in B.

Another Ca²⁺-binding Site

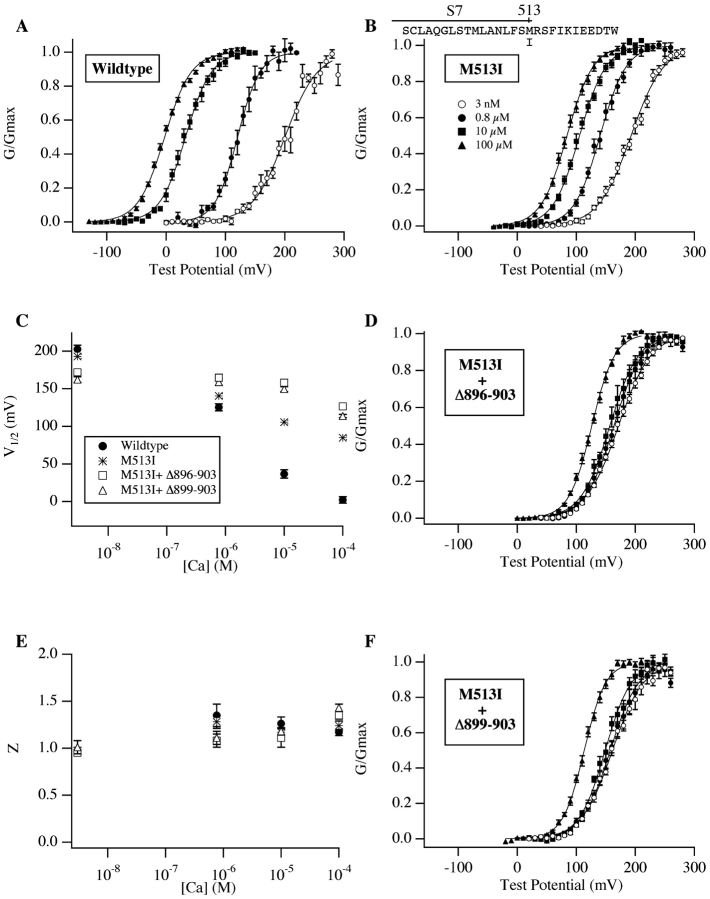
The above conclusion implies, as has been suggested (Schreiber and Salkoff, 1997; Bian et al., 2001), that high-affinity Ca²⁺-binding sites, not associated with the Ca²⁺ bowl, are responsible for the remaining Ca²⁺ sensitivity of the mutants described above. To search for these sites we examined a string of three acidic residues (EED 520–522) just past the channel's seventh hydrophobic segment (S7) in the intracellular part of the core (Wei et al., 1994; Jiang et al., 2001). We mutated all three to alanine, but the resulting mutant showed little deviation from wild-type behavior (unpublished data). However, when we mutated a nearby residue, M513, as shown in Fig. 4 B, the mutation created a channel with a reduced Ca²⁺ sensitivity similar to that of the Ca²⁺-bowl mutants described above (compare Fig. 4 B to Fig. 3 B, D, and F). Interestingly, M513 is at the end of S7, which places it 370 amino acids away from the Ca²⁺ bowl in the channel's primary sequence. Thus, it could be that this mutation affects a different Ca²⁺ binding site from that affected by mutations in the Ca²⁺ bowl but with perhaps similar binding characteristics. As we know little, however, about the tertiary structure of the BK_Ca channel, it could also be that mutations at the two sites alter the same binding site.

Figure 4.

Double mutants that eliminate mSlo's high-affinity Ca²⁺ response. (A) Wild-type G-V relations. (B) G-V relations over a series of [Ca²⁺] for the mutant M513I. (C) V_1/2 vs. [Ca²⁺] plots for the channels in A, B, D, F (see Table I for values). Symbols represent mutants as indicated on the figure. (D) G-V relations for the double mutant M513I+Δ896–903. (E) z vs. [Ca²⁺] plots (see Table I for values). Symbols represent mutants as indicated in C. (F) G-V relations for the double mutant M513I+Δ899–903. In A, B, D, and F symbols represent [Ca²⁺] as indicated in B.

To distinguish between these possibilities we made the double mutant M513I+Δ896–903. If each mutation acts independently, then their effects should be additive; if they act on the same process, this would not be expected (Goldstein et al., 1994; Stocker and Miller, 1994; Hidalgo and MacKinnon, 1995). G-V curves from the double mutant are shown in Fig. 4 D, and, as is evident, to a first approximation the mutations are additive. The two mutations reduce the mSlo channel's Ca²⁺ sensitivity considerably more than either mutation alone. In fact, the mutant channel shows almost no response to [Ca²⁺] below 10 μM, and it shows only a 45 ± 3.6 mV leftward G-V shift as [Ca²⁺] is increased from 3 nM to 100 μM (as compared with the 202 ± 5.8 mV shift of the wild-type channel, Table I). Thus, the two mutations together create a channel with only a low-affinity Ca²⁺ response, and interestingly the double mutant M513I+Δ899–903, which involves the smaller Ca²⁺-bowl deletion, displays an identical phenotype (Fig. 4 F).

Mg²⁺ Eliminates the Double Mutant's Ca²⁺ Sensitivity

BK_Ca channel gating can be modulated by intracellular Mg²⁺ (Golowasch et al., 1986) and millimolar concentrations of Mg²⁺ have recently been shown to activate the mSlo channel via a site in its core domain that also has a low affinity for Ca²⁺ (Shi and Cui, 2001; Zhang et al., 2001). As the double mutants described above show only a low-affinity Ca²⁺ response, we tested whether the remaining Ca²⁺ sensitivity of the M513I+Δ896–903 mutant is due to Ca²⁺ binding at this low-affinity, Mg²⁺-sensitive site. We examined the shift of the double mutant's G-V relation in response to 100 μM [Ca²⁺] in the absence and presence of 10 and 100 mM [Mg²⁺]. If Ca²⁺ binding at the Mg²⁺-sensitive site is responsible for the double mutant's low-affinity Ca²⁺ response, then 100 mM [Mg²⁺] would be expected to occupy this site and eliminate the effect of Ca²⁺, whereas 10 mM [Mg²⁺] would be expected to inhibit but not eliminate the effect of Ca²⁺ (Shi and Cui, 2001; Zhang et al., 2001).

As shown in Fig. 5 A, these predictions were born out in our data. In the presence of 10 mM [Mg²⁺] the Δ896–903+M513I channel's G-V shift, when exposed to 100 μM [Ca²⁺], is reduced from 45 ± 3.6 mV to 24 ± 3.4 mV, and in the presence of 100 mM [Mg²⁺] it is completely eliminated (ΔV_1/2 = −2 ± 6.8 mV, see Fig. 5 A, bottom). Furthermore, when the same experiment is performed with the wild-type channel (Fig. 5 B), 100 mM [Mg²⁺] does not completely eliminate the effect of 100 μM [Ca²⁺], but rather reduces ΔV_1/2 by an amount similar to its effect on the double mutant (Fig. 5 B bottom). These results argue that Mg²⁺ only effectively blocks the channel's low-affinity Ca²⁺ binding sites (as has been reported, Shi and Cui, 2001; Zhang et al., 2001), and that the weak Ca²⁺ response of the double mutant is due to low-affinity Ca²⁺ binding at Mg²⁺-sensitive sites. Furthermore, the high-affinity response of the wild-type channel must therefore arise from Ca²⁺ binding at sites whose functional effects are completely eliminated by the double mutant. This is remarkable, because it suggests the presence of three types of Ca²⁺-binding sites on the mSlo channel, one of low affinity whose effects can be blocked by high concentrations of Mg²⁺, and two of higher affinity, one whose effects are eliminated by mutations in the Ca²⁺ bowl, and another whose effects are eliminated by mutation at M513.

Estimating the Ca²⁺-binding Characteristics of the Channel's High-Affinity Sites

The mutations described above must cause complete loss of function at their respective sites; otherwise, the double mutant would respond to Ca²⁺ even after its low-affinity sites are occupied by Mg²⁺. Thus, they provide an opportunity to estimate the binding characteristics of the sites they disrupt. To do this, however, requires extracting from the wild-type and mutant G-V data the degree to which Ca²⁺ binding is affecting ΔG(0)_o-c, the free energy difference between open and closed in the absence of an applied voltage. That is, we would like to plot ΔG(0)_o-c rather than V_1/2 as a function of [Ca²⁺], so as to examine a physically meaningful Ca²⁺-dependent quantity that is independent of the mechanism by which the channel responds to voltage, and yet readily interpretable in terms of the binding properties of the channel's Ca²⁺-binding sites.

A strategy which has been used to do this in the past is to fit each G-V relation with a Boltzmann function and from the parameters of the fit estimate ΔG(0)_o-c as ΔG(0)_o-c = zFV_1/2 (Cox and Aldrich, 2000; Cui and Aldrich, 2000; Jiang et al., 2001; Shi and Cui, 2001), and in fact this was the strategy we used above in examining the 899–903A mutant. In effect, it assumes a two-state model for the channel's voltage-sensing mechanism, and then on the basis of this model estimates the effect of Ca²⁺ binding on the free energy difference that the applied voltage must overcome to open the channel. As discussed above, for the voltage-dependent MWC model (Fig. 6 B) this strategy is strictly correct (Cox et al., 1997; Cox and Aldrich, 2000; Cui and Aldrich, 2000).

Results of such an analysis for the wild-type channel and the Δ896–903 and M513I mutants are plotted in Fig. 6 F, together with standard V_1/2 vs. [Ca²⁺] plots (Fig. 6 D). New data have been added for each channel at 71, 130, and 360 nM [Ca²⁺] so as to get a better sense of the shapes of the resulting ΔG(0)_o-c vs. [Ca²⁺] relations. Upon examining these relations, we see that the zFV_1/2 values, or equivalently the ΔG(0)_o-c values, of the three channels are very similar at 3 nM [Ca²⁺], indicating that the intrinsic free energy difference between open and closed is unaltered by the mutations. Also, 100 μM [Ca²⁺] causes a smaller change in the ΔG(0)_o-c values of the two mutants than it does that of the wild-type channel, reflecting a weaker influence of Ca²⁺ binding on the channel's closed-to-open conformational change. More interesting, however, are the shapes of the three ΔG(0)_o-c vs. [Ca²⁺] curves. Over the [Ca²⁺] range 3 nM to 0.8 μM, where V_1/2 for all three channels is changing appreciably (see Fig. 6 D), ΔG(0)_o-c for all three channels remains nearly constant (Fig. 6 F). This is unexpected, because, according to the current view, it is only through altering ΔG(0)_o-c that Ca²⁺ binding alters V_1/2. That is, Ca²⁺ binding is thought to shift the mSlo G-V relation, not because it alters the channel's voltage-sensing mechanism, but because it decreases the energy barrier this mechanism must work against. Thus, V_1/2 is not expected to change without a concomitant change in ΔG(0)_o-c, and the incongruity we observe between Fig. 6, D and F, suggests that either this view is not correct, or the method we have used to estimate ΔG(0)_o-c is inaccurate, at least at [Ca²⁺] less than ∼1 μM.

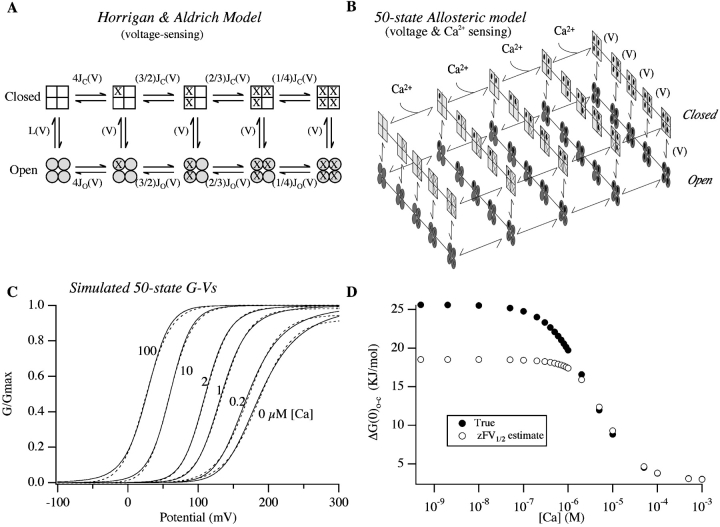
To test the latter possibility, we used a model of BK_Ca channel gating developed by Horrigan et al. (1999) that is more sophisticated in its voltage-sensing mechanism than the VD-MWC model. It supposes four voltage sensors, one in each subunit, that move independently to promote channel opening. Voltage-sensor movement is not required for channel opening, however, but rather promotes opening in a manner similar to Ca²⁺ binding in an MWC system. It also supposes a weak voltage dependence associated with its central closed-to-open conformational change, and not including Ca²⁺ binding, it consists of the 10 states illustrated in Fig. 7 A. Adding then four identical Ca²⁺-binding sites that also allosterically promote opening leads to the 50-state model depicted in Fig. 7 B (Cox and Aldrich, 2000; Rothberg and Magleby, 2000). Although apparently complex, this model contains only seven free parameters, and yet it has been shown to account for mSlo macroscopic currents over wide ranges of [Ca²⁺] and voltage both with and without the BK_Ca β1 subunit (Cox and Aldrich, 2000) and, as well, gating currents at nominally 0 [Ca²⁺] (Horrigan and Aldrich, 1999; Horrigan et al., 1999). Furthermore, a scheme of the same form was developed simultaneously to account for mSlo's single-channel gating behavior (Rothberg and Magleby, 2000). Thus, the model illustrated in Fig. 7 B, although overly simple in its Ca²⁺-sensing mechanism, represents the latest view of the relationship between Ca²⁺ binding and voltage sensing in BK_Ca-channel activation.

Figure 7.

A more complex model of mSlo gating suggests errors in our ΔG(0)_o-c estimates at low [Ca²⁺]. (A). Diagram of the model Horrigan et al. (1999) used to described the voltage-dependent gating of the mSlo channel. Horizontal transitions represent voltage sensor activation. Vertical transitions represent the conformational change by which the channel opens. J _C(V) and J _O(V) are the equilibrium constants for voltage-sensor activation when the channel is either closed or open where: J _C(V) = J _C(0)exp(zFV/RT) and J_O(V) = J _O(0)exp(zFV/RT); and L(V) is the equilibrium constant between open and closed when no voltage sensors are active and no Ca²⁺ is bound where: L(V) = L(0)exp(qFV/RT). (B) 50-state mSlo model. Here Ca²⁺ binding occurs along the long horizontal axis, voltage sensor movement along the short horizontal axis, and transitions from the upper to the lower tier indicate channel opening. The front face of this scheme corresponds to the model in A. (C) Simulated G-V curves from the model in B at the [Ca²⁺] indicated on the figure. For more discussion of this model see (Cox and Aldrich, 2000; Cui and Aldrich, 2000; Rothberg and Magleby, 2000). Parameters were as follows: J _C(0) = 0.066; J _O(0) = 1.10; z = 0.51; L(0) = 2e-6; q = 0.4; K _C = 10 μM, K _O = 1 μM. Each curve is fitted with a Boltzmann function (dashed lines). (D) Plots of ΔG(0)_o-c as a function of [Ca²⁺] for the model in C. Darkened circles indicate the true ΔG(0)_o-c of the model calculated as 4RTln[(1+ [Ca]/K _C)/(1 + [Ca]/K _O)] + 4RTln[(1 + J _C(0))/(1 + J _O(0))] − RTln[L(0)], while the open circles represent estimates obtained from Boltzmann-fit parameters as zFV_1/2.

Fig. 7 C shows simulated G-V curves from this model. The parameters used to generate these curves were similar to those used recently to fit wild-type mSlo data (Cox and Aldrich, 2000). Adjacent to these curves (Fig. 7 D) the true ΔG(0)_o-c of the model is plotted as a function of [Ca²⁺] (closed circles). These values were determined mathematically from the probability of open-conformation occupancy at 0 mV. Also plotted (open circles) are estimates of ΔG(0)_o-c obtained by fitting each simulated curve with a Boltzmann function and calculating ΔG(0)_o-c from the fit parameters.

Interestingly, although the 50-state model assumes no direct effect of Ca²⁺ binding on voltage sensing, the Boltzmann method of estimating ΔG(0)_o-c severely underestimates the model's true ΔG(0)_o-c at [Ca²⁺] below ∼1 μM, where its G-V curves become both increasingly shallower and poorly fitted by a Boltzmann function, characteristics also observed in the data (see Figs. 2–4). Furthermore, the underestimation occurs in such a way that the estimated ΔG(0)_o-c vs. [Ca²⁺] relation is almost constant between 0 and 1 μM [Ca²⁺], when the true relation is changing by ∼23%. Thus, the unexpected, flat characteristic we observed in our analysis of the data in Fig. 6 is also observed here, and it thus seems likely that in Fig. 6 F we are indeed underestimating ΔG(0)_o-c at low [Ca²⁺] when using zFV_1/2 as an estimator.

To attempt to better estimate ΔG(0)_o-c, we took advantage of the understanding of the voltage-dependent mechanism of mSlo gating developed by Horrigan et al. (1999). Instead of using a Boltzmann function, we fit each G-V curve with the following function, which describes the G-V relation of the scheme diagramed in Fig. 7 A (Horrigan and Aldrich, 1999; Horrigan et al., 1999).

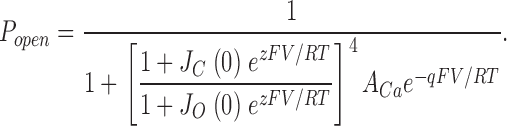(2)

Here, J _O(0) and J _C(0) represent the equilibrium constants for voltage-sensor movement in each subunit at 0 mV when the channel is open or closed, respectively, z represents the gating charge associated with each voltage sensor, q represents the gating charge associated with the model's central conformational change, and A _Ca is a Ca²⁺-dependent factor that is logarithmically related to ΔG(0)_o-c. That is, assuming only that Ca²⁺ binding promotes opening, and the voltage-dependent gating mechanism described by the scheme in Fig. 7 A, for any [Ca²⁺], we may write:

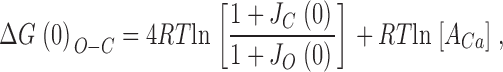(3)

where the first term in Eq. 3 does not vary with [Ca²⁺] and the second one does.

Thus, we fit the wild-type and mutant G-V curves with Eq. 2, fixing the voltage-dependent gating parameters to values we have used previously to describe mSlo gating (Cox and Aldrich, 2000), and from the A _Ca parameter and Eq. 3 calculated ΔG(0)_o-c. This method of estimating ΔG(0)_o-c is precisely accurate for the 50-state model, and precisely accurate as well for any model with a voltage-sensing mechanism described by the scheme in Fig. 7 A, regardless of the number and type of Ca²⁺-binding sites it contains, as long as those sites do not directly interact with the channel's voltage sensors.

Estimates of ΔG(0)_o-c as a function of [Ca²⁺] for the wild-type channel and three of the mutants described above are plotted in Fig. 8 A. Supporting the idea that we have improved our estimates of ΔG(0)_o-c at low [Ca²⁺], the ΔG(0)_o-c vs. [Ca²⁺] relations for all four channels are no longer flat in the 3 nM to 0.8 μM [Ca²⁺] range, but now better follow changes in V_1/2. In Fig. 8 B we have shifted each curve in A vertically so as to have a value of zero at 3 nM [Ca²⁺], and thereby created plots of ΔΔG(0)_o-c, the change in ΔG(0)_o-c as a function of [Ca²⁺], a measure of the influence of [Ca²⁺] on the energetics of channel opening. And in Fig. 8 C we have plotted difference curves obtained by subtracting each mutant's curve in Fig. 8 B from the wild-type curve. These curves measure the Ca²⁺ influence lost by each mutation and thus are reflective of the properties of the binding site each mutation disrupts.

Figure 8.

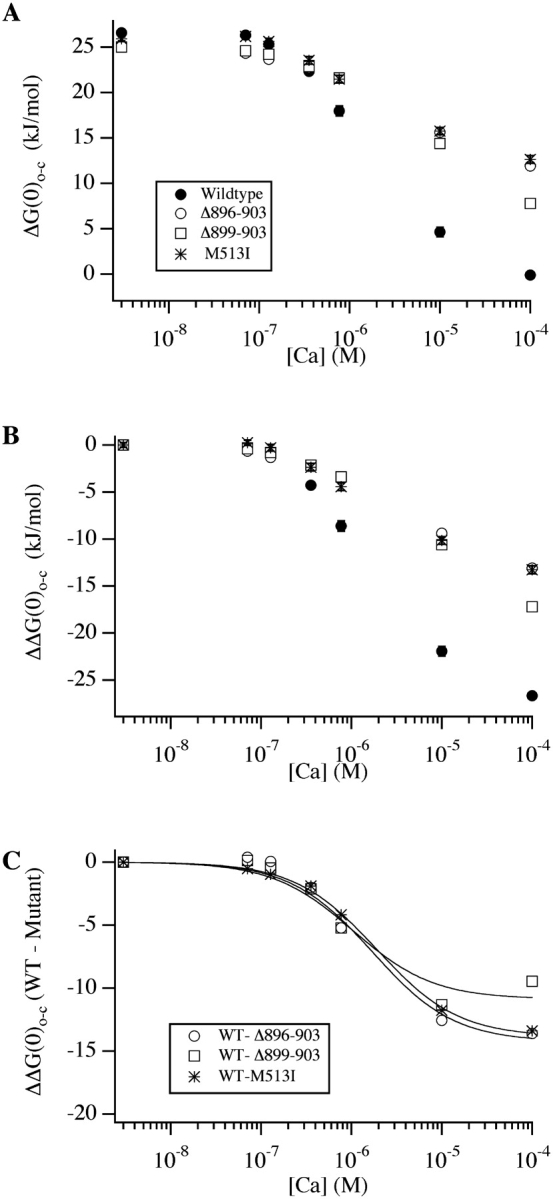
Energetics of Ca²⁺ binding to mutant and wild-type mSlo channels. (A) Estimates of ΔG(0)_o-c as a function of [Ca²⁺] obtained by fitting each experiment with Eq. 2 and then calculating ΔG(0)_o-c from Eq. 3. Constant parameters were: J _C(0) = 0.059, J _O(0) = 1.020, z = 0.51, q = 0.4. Symbols indicate channel type as indicated on the plot. (B) The curves in A have been shifted so each curve has a value of 0 at 3 nM [Ca²⁺]. (C) WT-mutant difference curves. Each mutant's curve in B has been subtracted from the wild-type curve in B to create difference curves that indicate the properties of the site disrupted by each mutation. Error bars, which represent standard error of the mean, are included in A and B; they are often smaller than the plot symbols.

To estimate the Ca²⁺-binding parameters of each site we then fit each curve in Fig. 8 C with the following function, which describes the allosteric effect of four independent ligands influencing a central conformational change (Cui and Aldrich, 2000).

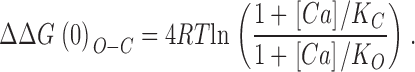(4)

This relation has two free parameters, K _C and K _O, and listed in Table II are estimates of these parameters for the sites disrupted by each mutation. Examining the results from the Δ896–903 and M513I mutations, we see that both types of high-affinity Ca²⁺-binding site appear to function similarly, each having an affinity for Ca²⁺ of 3.5–3.8 μM when the channel is closed and 0.80–0.94 μM when the channel is open, and each maximally altering ΔG(0)_o-c by approximately −3.4 kJ/mol as Ca²⁺ binds, for a total of approximately −13.5 kJ/mol for each type of site. Also listed under site 1 in Table II, however, are affinity-constant estimates derived from the WT Δ899–903 difference curve in Fig. 8 C, because, as discussed below, it is not clear which mutant, Δ896–903 or Δ899–903, represents elimination of just Ca²⁺ bowl function. The values derived from the WT-Δ899–903 difference curve suggest a somewhat higher Ca²⁺ affinity for site 1, both in the closed and open conformation (K_C = 1.8 μM, K_O = 0.6 μM), with a maximum ΔΔG_Ca(0)_o-c per site of −2.4 kJ/mol for a total of −9.5 kJ/mol.

TABLE II.

Estimates of the Binding Characteristics of mSlo's High-Affinity Ca²⁺-binding Sites

Site	Mutant that disrupts	ΔΔG(0)o-c a total	Number of binding sites assumed	ΔΔG(0)o-c a per site	KC b	KO b	KC/KO
		kJ/mol		kJ/mol	μM	μM
1	Δ896-903	−13.6 ± 0.6	4	−3.4	3.5 ± 0.9	0.8 ± 0.2	4.4
	Δ899-903	−9.5 ± 0.6	4	−2.4	1.8 ± 0.7	0.6 ± 0.2	3.0
2	M513I	−13.4 ± 0.6	4	−3.3	3.8 ± 0.2	0.94 ± 0.06	4.0

^aΔΔG_o-c(0) contributed by the given site n response to a change in [Ca²⁺] from 3 nM to 100 μM.

bk_C = closed-state dissociation constant; K_O = open state dissociation constant. Estimates were derived from fits of Eq. 4 to the difference curves in Fig. 8 C.

Are the Mutants Quantitatively Additive?

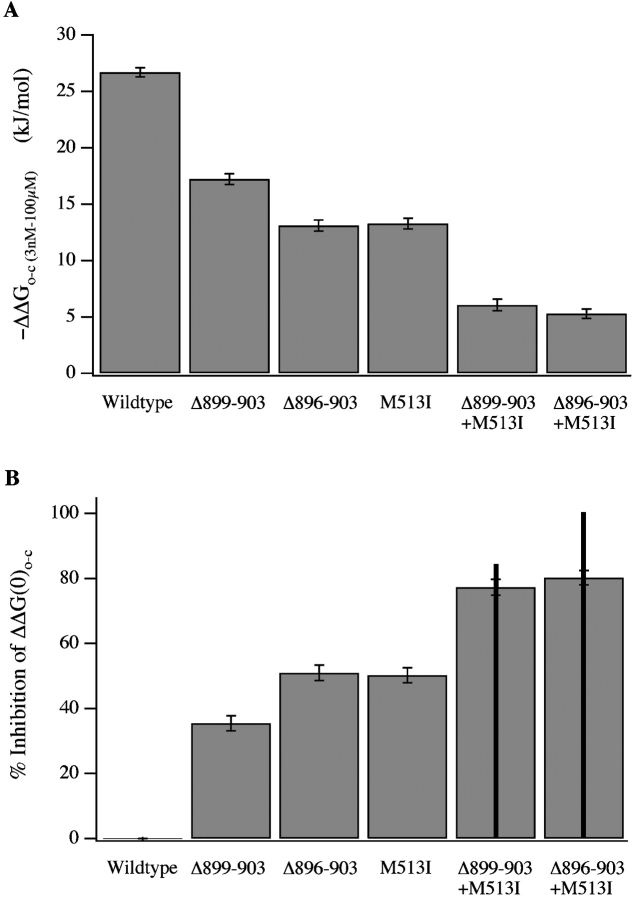
The data in Fig. 8, A and B, also allow us to determine if mutations in the Ca²⁺-bowl and M513I act truly independently, as is expected if each affects a distinct binding site, and binding at one site does not influence binding at the other. To test this we plotted, in Fig. 9 A, the effects of 100 μM [Ca²⁺] on ΔG(0)_o-c for the mutant and wild-type channels, and, in Fig. 9 B, the degree to which each mutation inhibits the wild-type channel's response to 100 μM [Ca²⁺]. Consistent with Fig. 3, the Δ899–903 mutant is somewhat more responsive to [Ca²⁺] than Δ896–903 (Fig. 9 A), and thus it reduces the channel's response to 100 μM [Ca²⁺] (ΔΔG(0)_o-c; 3 nM to 100 μM) somewhat less (Fig. 9 B). Perhaps surprisingly, however, the double mutants involving M513I and either Δ899–903 or Δ896–903 behave almost identically. Thus, the extra effect of the larger deletion is not evident when combined with M513I, suggesting one pair of mutations is not completely additive. Indeed, the predictions of strict additivity are indicated on Fig. 9 B (solid black lines), and consistent with this observation, the effects of M513I and Δ899–903 are truly additive, whereas those of M513I and Δ896–903 are less than quantitatively additive by 20%.

Figure 9.

Additivity of mutations. (A) −ΔΔG(0)_o-c (3 nM to 100 μM [Ca²⁺]) is plotted for each channel type. (B) For each channel type is plotted (ΔΔG(0)_o-c (3 nM to 100 μM [Ca²⁺])_wild-type − ΔΔG(0)_o-c (3 nM to 100 μM [Ca²⁺])_mutant)/ΔΔG(0)_o-c (3 nM to 100 μM [Ca²⁺])_wild-type,, which is the percent reduction in response to 100 μM [Ca²⁺] caused by each mutation. Vertical black lines indicate the predictions of strict additivity, and are thus the sums of the bars for each individual mutant that contributes to a double mutant.

The meaning of this result is open to a number of interpretations. One possibility is that the two binding sites do not behave independently, in which case mutations that knockout each site separately would not be expected to be quantitatively additive when combined. Alternatively, it could be that the M513I and Δ896–903 mutations have partially overlapping spheres of influence. This would also be expected to produce a less than additive effect. Thus, we cannot be certain which mutation Δ896–903 or Δ899–903 best represents loss of Ca²⁺-bowl function, and therefore in Fig. 8 C we have analyzed both.

DISCUSSION

We have described mutations at two positions in the mSlo channel's intracellular COOH-terminal domain, the Ca²⁺ bowl and M513, that when mutated individually decrease the channels response to Ca²⁺ by approximately half, as judged by G-V shifts in response to 100 μM [Ca²⁺]. Furthermore, the effects of mutations at each site are largely Ca²⁺ dependent, suggesting they are primarily altering Ca²⁺ binding, rather than other aspects of gating such as voltage sensing or the intrinsic energetics of channel opening. Reinforcing this conclusion, we have analyzed the behavior of mutants at both sites in terms of allosteric models that provide a means of estimating the degree to which a given mutation alters the power of Ca²⁺ to influence the energetics of channel opening (ΔΔG(0)_o-c), a property that depends solely on the Ca²⁺-binding characteristics of the channel. Results of such analyses suggest that mutations at each site decrease the energy that 100 μM [Ca²⁺] imparts to the channel's closed-to-open conformational change also by approximately half, as if each site were responsible for approximately half of the channel's Ca²⁺ sensitivity.

Are There Two High-Affinity Sites?

It is natural to question whether mutations that create similar phenotypes alter the same or different processes. One could imagine that although separated by 370 amino acids in the channel's primary sequence, the Ca²⁺ bowl and M513 are oriented such that mutations at both sites alter the same process by which Ca²⁺ binding promotes opening. The observation that the combined effect of mutations at both sites is considerably stronger than mutations at either site alone, however, argues against this hypothesis. In fact, the double mutants, Δ896–903+M513I and Δ899–903+M513I, do not respond appreciably to [Ca²⁺] below ∼10 μM, whereas the single mutants, Δ896–903, Δ899–903, and M513I, each start to respond to [Ca²⁺] (as does the wild-type channel) at ∼0.1 μM. Thus, mutations at the two sites are qualitatively additive, and likely alter separate binding sites. Indeed, we find that the energetic effects of Δ899–903 and M513I, as shown in Fig. 9 B, are very close to quantitatively additive. The difference between the measured ΔΔG_o-c value (3 nM to 100 μM) of the double mutant M513I+Δ899–903 and the value predicted by strict additivity is 2.25 kJ/mol, a value that is <10% of the ΔΔG_o-c (3 nM to 100 μM) of the wild-type channel, and less than is typically taken to indicate nonindependence in studies of interactions between mutations (1.5 kT or 3.69 kJ/mol; Schreiber and Fersht, 1995; Naranjo and Miller, 1996; Ranganathan et al., 1996). Thus, it would appear that the Δ899–903 and the M513I mutations are acting independently and on separate Ca²⁺-binding sites.

We cannot rigorously exclude the possibility, however, that the Δ899–903 and M513I mutations affect a single binding site in such a way that they happen to behave additively. In fact, the combined effects of the Δ896–903 and M513I mutations are less than additive by 5.47 kJ/mol, or 20% of the of the wild-type channel's ΔΔG_o-C value (3 nM to 100 μM). Here, one mutation partially obscures the effects of the other, suggesting a common process is altered. This result could also be explained, however, by supposing that the binding of Ca²⁺ at one site influences binding at the other, or more simply that in addition to disrupting the Ca²⁺ bowl, the Δ896–903 mutation has a partial effect at the second site, a conclusion that also requires the presence of two types of high-affinity sites. Thus, we think two distinct high-affinity Ca²⁺-binding sites are likely.

Supporting this conclusion, Bian et al. (2001) have found that the Ca²⁺-bowl mutation 897–901N reduces the dSlo channel's Hill coefficient for Ca²⁺ activation by a factor of ∼2 at many voltages, a result consistent with the idea that the Ca²⁺-bowl mutation disrupts one type of high-affinity Ca²⁺-binding site while leaving another intact. This same mutation also reduces Ca²⁺ binding to a fusion protein consisting of the last 280 amino acids of dSlo by approximately half. Furthermore, Schreiber and Salkoff (1997) have argued for a second type of mSlo Ca²⁺-binding site based on the observation that mutations at the Ca²⁺ bowl alter the effects of Ca²⁺, but leave the activating effects of Cd²⁺ unaltered. And in another series of experiments they divided the mSlo tail domain into four regions (A–D) and found that both region B, which contains the Ca²⁺ bowl, and region C which does not, can each confer partial Ca²⁺ sensitivity upon an insensitive mSlo_core–mSlo3_tail chimeric channel. Thus, the two high-affinity site interpretation we have given our results is not at odds with previous work.

Do the Mutations Create Complete Loss of Function?

Does each mutation completely eliminate the effect of Ca²⁺ binding at the site it disrupts? The answer to this question appears to be yes, at least for the Δ896–903 and the M513I mutations, as when both mutations are made together all high-affinity Ca²⁺ response is lost, leaving only a low-affinity response blocked by high concentrations of Mg²⁺. Indeed, Shi and Cui (2001) and Zhang et al. (2001) have extensively examined the ability of Mg²⁺ to activate the mSlo channel. Both groups concluded that Mg²⁺ activates the channel via a site separate from the channel's high-affinity Ca²⁺-binding sites. This site was estimated to have an affinity for Ca²⁺ of 0.6–1 mM when the channel is open and 2–3 mM when the channel is closed, and an affinity for Mg²⁺ of 2–6 mM when the channel is open and 10–20 mM when the channel is closed (Zhang et al., 2001). For a channel with four such sites, a simple VD-MWC type model predicts that this low-affinity site would start to influence the position of the mSlo G-V relation at just above 10 μM [Ca²⁺], just as we observed with our double mutants (simulations not shown). And it would be ∼90% occupied by 100 mM [Mg²⁺] and therefore almost fully activated. Thus, our double mutant Δ896–903+M513I acts exactly as one would predict if it creates a channel whose high-affinity Ca²⁺-binding sites have lost their function, but whose low-affinity Mg²⁺-sensitive, Ca²⁺-binding sites are still intact (Figs. 4 and 5). These results therefore lend further credence to the notion that the BK_Ca channel has low-affinity, Mg²⁺-sensitive Ca²⁺-binding sites that are separate from its high-affinity sites, and they pave the way for the study of these low-affinity sites in isolation.

No Other Binding Sites

The results of our double mutant experiments also argue that the mSlo channel contains no other high-affinity Ca²⁺-binding sites besides those disrupted by mutations at the Ca²⁺ bowl and M513 and no low-affinity sites that are not Mg²⁺sensitive. If either of these suppositions were not correct, then the Δ896–903+M513I channel would be expected to respond to increases in [Ca²⁺] in the presence high concentrations of Mg²⁺ via these as yet unaccounted for sites. Generally, no such response is observed. It should be mentioned, however, that although we saw no significant change in the G-V position of the Δ896–903+M513I channel as [Ca²⁺] was increased from <3 nM to 100 μM in the presence of 100 mM [Mg²⁺], we did see a small but consistent change in the shape of the channel's G-V relation. The relation became more shallow by 27% (Fig. 5) as [Ca²⁺] was raised. Whether this is due to weaker binding of Mg²⁺ at low voltages, or some real remaining Ca²⁺ effect will require further investigation.

Estimates of Ca²⁺-binding Characteristics

Identifying mutations that cause a complete loss of function at mSlo's high-affinity Ca²⁺-binding sites affords a unique opportunity to estimate the binding characteristics of these sites. Results of our analysis suggest that the site disrupted by M513I, which we refer as site 2, accounts for ∼50% of the −26.7 kJ/mol that 100 μM [Ca²⁺] imparts to the channel closed-to-open conformational change, whereas the Ca²⁺ bowl site (site 1) imparts 35–50%, depending on which mutation (Δ899–90 or Δ896–903) is analyzed. Thus, type 1 and 2 sites appear to contribute roughly equally to the high-affinity effects of Ca²⁺. Assuming one binding site of each type per subunit (four per channel), and taking our estimates from the Δ896–903 mutant, we estimate K_O for both sites to be 0.8–0.9 μM and K_C to be 3.5–3.8 μM. Thus, both sites appear to have very similar binding characteristics. If, however, the channel has an unequal number of sites of each type, as might arise if one type of site is formed at the interface between subunits while the other is not, this may not be the case. But our estimates of the energetic contributions of each type of site (−9.5 to −13.6 kJ/mol for site 1 and −13.4 kJ/mol for site 2) would remain valid.

How Do the Mutations Create a Loss of Function?

How do the mutations we have described exert their effects? Must they act directly at the binding site? Indeed, one might suppose that mutations at either position affect Ca²⁺ sensitivity, not because they affect Ca²⁺ binding, but because they affect the ability of Ca²⁺ binding to influence opening. Suppose, as suggested by Schreiber et al. (1999), that there is a Ca²⁺-binding domain that swings as if on a hinge after Ca²⁺ binds, and in so doing promotes opening. One might then suppose that a given mutation breaks the hinge without affecting Ca²⁺ binding. Thermodynamic constraints dictate, however, that in order for Ca²⁺ binding to promote opening, the affinity of the binding site must increase as the channel opens, and conversely, if a binding site's affinity increases as the channel opens, binding must promote opening. Thus, for a mutation to eliminate the effectiveness of a binding site, it must either prevent binding altogether, or prevent the change in affinity that occurs at the binding site as the channel opens. Thus, binding and the transduction of binding to opening are inextricably linked, and the mutations we have described must therefore affect Ca²⁺ binding.

One might still ask, however, whether the mutations we have studied disrupt residues that actually make contact with Ca²⁺? Our data do not rule out the possibility that some protein endogenous to the oocyte associates with mSlo to form its Ca²⁺ sensors, as is the case for the small-conductance Ca²⁺-activated K⁺ channel, which uses constitutively associated calmodulin as its Ca²⁺ sensor (Xia et al., 1998; Wissmann et al., 2002). It is conceivable, then, that mutations at the Ca²⁺ bowl or M513 disrupt such an association. For the Ca²⁺ bowl mutations, however, there are good reasons to think this is not the case. First, these mutations remove acidic side chains that could provide the negative charge density normally associated with Ca²⁺ coordination. Second, two laboratories have found that Ca²⁺ will bind to recombinant Slo fusion proteins overexpressed and purified from bacteria, and will do so in gel overlay assays where auxiliary proteins would not likely remain associated (Bian et al., 2001; Braun and Sy, 2001). And third, as mentioned above, the Ca²⁺-bowl mutation 897–901N inhibits this binding by approximately half (Bian et al., 2001). Thus, it seems likely that the Ca²⁺ bowl does in fact form a Ca²⁺-binding site, although this is not directly demonstrated by our data.

The situation for the M513I mutation is less clear. Methionines are not commonly Ca²⁺ coordinators, so it may be that M513I interferes with the linkage between binding and opening (by linkage we mean that which causes the binding site to increase its affinity as the channel opens). This could be the movement of a key atom closer to the Ca²⁺ ion in its site, as is the case with cGMP when the cyclic nucleotide–gated channel opens (Varnum et al., 1995). Or perhaps the M513I mutation inhibits an intersubunit association of intracellular domains that may occur after Ca²⁺ binds. Such an association has been shown to occur after Ca²⁺ binds to the SK channel (Schumacher et al., 2001), and M513 lies at the very end of mSlo's seventh hydrophobic domain (S7), a region that might reasonably bury its hydrophobic side chains by dimerization, perhaps with its counterpart on a neighboring subunit, when prodded by Ca²⁺ binding.

Pursuing this idea further, M513 also lies at the very end of mSlo's RCK domain, which spans from just after S6 to the end of S7 (Jiang et al., 2001). In the recent crystal structure of the E. coli K⁺ channel's RCK domain (Jiang et al., 2001), the αG helix, where M513 would be predicted to lie, participates in a dimer interface. Thus, although the homology in this region between the E. coli K⁺ channel and mSlo is low, and the E. coli channel does not contain a methionine at the position corresponding to mSlo's 513, by structural analogy we might still speculate that M513 is important for the formation of dimers between mSlo's intracellular domains.

Alternatively, it could also be that M513I disrupts a Ca²⁺-binding site formed by the RCK domain itself, since much of this domain has a structure commonly associated with ligand-binding proteins known as a Rossman fold (Branden and Tooze, 1991) and Rossman folds have been shown to form binding sites for a variety of small molecules, including ions (Lee et al., 1995). So, although M513 is not in mSlo's predicted Rossman fold, its close proximity suggests its mutation may destabilize a Ca²⁺-binding site formed therein (Jiang et al., 2001).

It is interesting to note that the mSlo3 channel, a Ca²⁺-insensitive mSlo homologue, contains neither a Ca²⁺ bowl nor a methionine at position 513 (Schreiber et al., 1998) and thus its lack of Ca²⁺ sensitivity is easily explained in terms of our results. Less easy to explain, however, is the observation that a channel containing the mSlo core and the mSlo3 tail, and thus one that has lost its Ca²⁺ bowl but retains M513, is in large-part Ca²⁺ insensitive (Schreiber et al., 1999; Moss and Magleby, 2001). This result could mean that there are elements of the mSlo tail besides those we have mutated that are required for the proper functioning of a binding site in the core of the channel, or conversely, that M513 interacts with a Ca²⁺-binding site in the mSlo tail, besides the Ca²⁺ bowl, that is not present in the mSlo3 tail. Clearly, confirmation of any of these hypotheses must await new physiological and structural data.