Horizontal gene transfer among genomes: The complexity hypothesis

Abstract

Increasingly, studies of genes and genomes are indicating that considerable horizontal transfer has occurred between prokaryotes. Extensive horizontal transfer has occurred for operational genes (those involved in housekeeping), whereas informational genes (those involved in transcription, translation, and related processes) are seldomly horizontally transferred. Through phylogenetic analysis of six complete prokaryotic genomes and the identification of 312 sets of orthologous genes present in all six genomes, we tested two theories describing the temporal flow of horizontal transfer. We show that operational genes have been horizontally transferred continuously since the divergence of the prokaryotes, rather than having been exchanged in one, or a few, massive events that occurred early in the evolution of prokaryotes. In agreement with earlier studies, we found that differences in rates of evolution between operational and informational genes are minimal, suggesting that factors other than rate of evolution are responsible for the observed differences in horizontal transfer. We propose that a major factor in the more frequent horizontal transfer of operational genes is that informational genes are typically members of large, complex systems, whereas operational genes are not, thereby making horizontal transfer of informational gene products less probable (the complexity hypothesis).

It is becoming increasingly apparent that many genes within eukaryotes and prokaryotes have been acquired by horizontal transfer, but not all genes are equally likely to be transferred (1–9). The preferential horizontal transfer of genes in both eukaryotes and prokaryotes is strongly correlated with gene function. Specifically, genes participating in transcription, translation, and related processes (informational genes) are far less likely to be horizontally transferred than genes participating in housekeeping functions (operational genes) (9). Furthermore, the frequency of horizontal transfer in prokaryotes is not related to evolutionary rates (nucleotide substitution rates) because evolutionary rates for operational and informational genes have not differed significantly since the cyanobacteria and proteobacteria diverged (9).

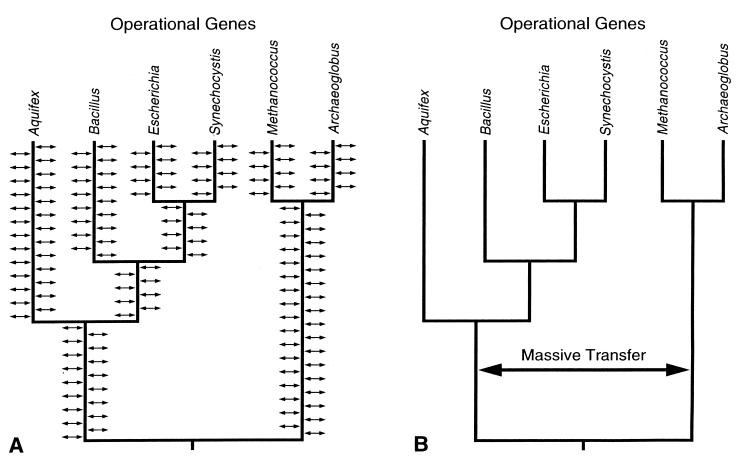
Two alternative hypotheses (9) have been proposed to explain the previously observed patterns of horizontal transfer. The first, the continual horizontal transfer hypothesis, is shown in Fig. 1A and proposes that horizontal transfer of operational genes is a continual process in prokaryotes. This hypothesis implies that horizontal gene transfer of operational genes is a far more important factor in prokaryotic evolution than previously thought.

Figure 1.

A comparison of the early and the continual horizontal transfer hypotheses. In the continual hypothesis (A), the horizontal arrows indicate that the transfer of operational genes has been occurring since the last common ancestor of prokaryotes. In the early massive hypothesis (B), the single large arrow indicates that one or a few massive horizontal transfer events preceded the diversification of the eubacteria.

The second, or early massive horizontal transfer hypothesis, is shown in Fig. 1B. It proposes that one, or a few, massive ancient exchanges of (operational) genes occurred early in prokaryotic evolution, before the diversification of modern prokaryotes. This hypothesis explains the observed similarity of evolutionary rates for operational and informational genes since cyanobacteria and proteobacteria diverged. It supports the idea that massive horizontal exchanges could have created modern prokaryotes.

Both hypotheses are illustrated in Fig. 1, with the protein synthesis elongation factor (EF) 1α gene tree for reference (10). In the continual hypothesis (Fig. 1A), operational genes are continually being transferred among various prokaryotic lineages so that operational gene trees are predicted to differ from each other and also differ from informational trees. In contrast, in the early massive hypothesis (Fig. 1B), the creation of modern prokaryotes preceded their diversification, so that operational and informational gene trees are predicted to have similar topologies. Three separate lines of evidence supporting the continual hypothesis are presented in Results.

METHODS

Identification of Orthologs.

Orthologs were required to satisfy a symmetrical (distance-like) selection procedure (9) and also to have been identified in the published descriptions of the genomes. Orthologs were accepted only if the genomic descriptions matched for all six proteins or if five of the six descriptions matched and one of the six was not classified. Of the 1,735 genes within the Methanococcus genome, 628 protein sequences were identified and classified by function (11). Of these, 312 satisfied the symmetrical selection procedure (203 operational and 109 informational), and 144 of these satisfied our ortholog criteria (88 operational and 56 informational genes). Informational genes included the following categories: transcription, translation, tRNA synthetases, and GTPases/vacuolar ATPase homologs. Operational genes included the following categories: amino acid biosynthesis, biosynthesis of cofactors, cell envelope proteins, intermediary metabolism, fatty acid and phospholipid biosynthesis, nucleotide biosynthesis, and regulatory genes. Energy metabolism, transport proteins, cell processes, “other,” and replication categories were not included.

Star Sequence Alignments.

To reduce alignment biases, protein sequences were aligned as amino acids, because these provide the most reliable alignment (12). Each prokaryotic sequence was globally aligned with respect to the Aquifex guide sequence (13) by using parameters identical to those described elsewhere (9).

Paralog Rooting.

To root the trees, Escherichia and Methanococcus gene paralogs were identified (9) among the set of 628 classified ORFs. To separate paralogs derived from ancient duplications, which can be used to root trees (but see ref. 14), from paralogs derived from more recent duplications, we calculated four taxon trees containing both the Escherichia and the Methanococcus orthologs and paralogs. Only genes that produced trees in which the Methanococcus and Escherichia orthologs were sister taxa were accepted (28 sets of operational genes and their paralogs, and 12 sets of informational genes and their paralogs). Using the methanogen paralog as the guide sequence, we constructed alignments for the six prokaryotes plus the methanogen paralog and analyzed them as described above.

Phylogenetic Analyses.

Three methods of phylogenetic analysis, Jukes-Cantor distances (15), maximum parsimony (15), and paralinear (logdet) distances (16, 17) were used to analyze both the ortholog sets and the set containing the paralog root. Maximum parsimony and Jukes-Cantor (not shown) gave results essentially identical with those from paralinear distances. For phylogenetic analysis only amino acid replacement positions were converted to nucleotides to reduce reconstruction artifacts.

Branch Lengths.

To ascertain whether our results for ortholog trees were attributable to horizontal transfer or to artifacts of phylogenetic reconstruction (15), we calculated branch lengths for the informational and operational trees. Horizontal transfer not only can alter the topologies of phylogenetic trees but it also can reduce the lengths of their internal branches. With the alignments used for Figs. 2 and 3, we calculated the branch lengths of the four taxon trees relating Escherichia, Synechocystis, Methanococcus, and Archaeoglobus with paralinear distances. The mean central branch length for operational (0.071 ± 0.05 substitutions per position) was significantly shorter than that for informational trees (0.237 ± 0.05 substitutions per position), consistent with the operational genes experiencing significant horizontal transfer. In contrast, the mean peripheral branch lengths differed little between the operational trees (0.201 ± 0.05 substitutions per position) and the informational trees (0.164 ± 0.05 substitutions per position). The central branch lengths support extensive horizontal transfer in the operational lineage and the peripheral branch lengths indicate only minor substitution rate differences between operational and informational genes, consistent with previous findings (9).

Figure 2.

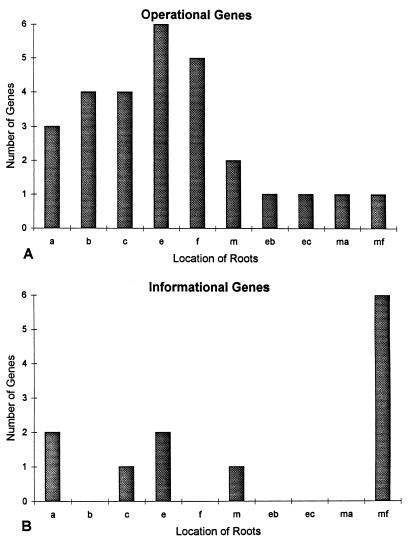
Paralog rooting of the operational and informational trees. Roots of trees calculated from operational (A) and informational (B) genes are shown. A one-letter code indicates that the paralog root is found in a terminal branch of the tree, as follows: a, Aquifex; b, Bacillus; c, Synechocystis; e, Escherichia; f, Archaeoglobus; and m, Methanococcus. A double-letter code indicates that the paralog root is found in the internal branch that defines a clade as follows: eb, Escherichia–Bacillus clade; ec, Escherichia–Synechocystis clade; ma, Methanococcus–Aquifex clade; and mf, Methanococcus–Archaeoglobus clade. A χ² test (see Methods) indicates that the distribution of roots is significantly different (P < 0.0039) for the two lineages.

Figure 3.

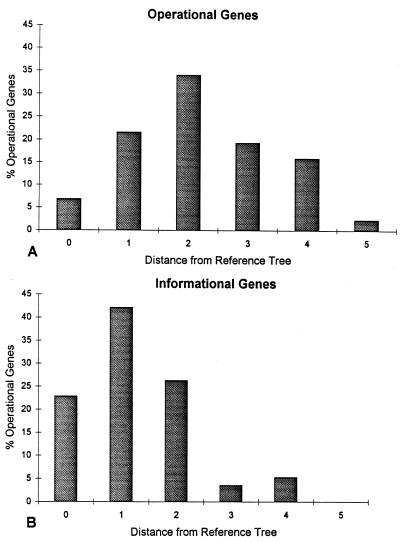
The distribution of peripheral branch–transfer distances of operational and informational trees from the EF-1α reference tree. The mean distance of operational trees (A) is 2.3 steps, whereas the mean distance of the informational trees (B) is 1.2 steps. By the χ² test the two distributions are significantly different (P < 0.0003).

Calculating Distances Between Trees.

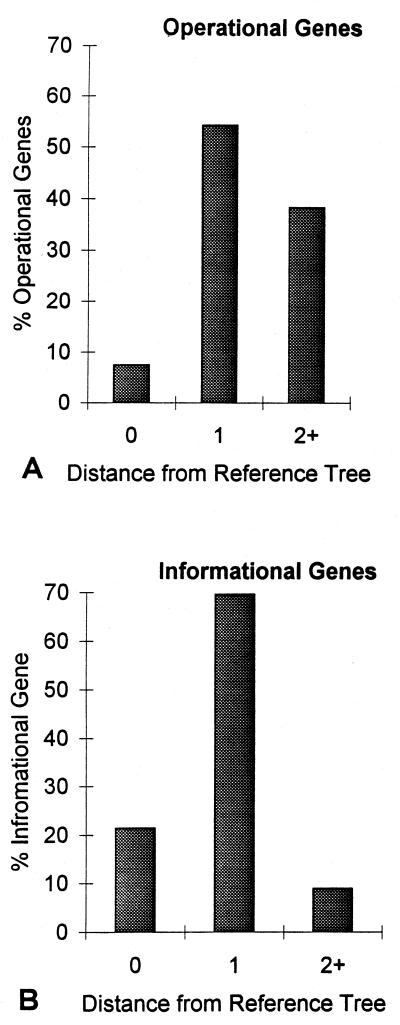
We defined the peripheral branch–transfer distance between a tree and a reference tree as the minimum number of times that peripheral branches of the tree must be moved through a node to transform it into the reference tree [J.A.L., unpublished data; see Robinson and Foulds (18) for a related measure]. With a six-taxon “caterpillar-shaped” tree (19) as the reference, the maximum distance between it and any other six-taxon tree is five steps. Of the 105 possible six-taxon trees, 1 will be zero steps from the reference tree, 6 will be one step away, 20 will be two steps away, 36 will be three steps away, 36 will be four steps away, and 6 will be five steps away. Prune-and-regraft distances (d) have been described by Allen and Steel (20). For six taxa, 1 tree corresponds to the reference tree (d = 0), 30 trees are one step from the reference tree (d = 1) and 74 trees are two or more steps away (d = 2+).

Conventions for Describing Internal Branch Bootstraps.

The alternative topologies detailed in Fig. 5 were defined as follows. The taxa from left to right (Fig. 5, either A or B) were labeled 1 through 6, and the four groups that surround each internal branch were labeled a, b, c, and d. For the topmost quartet a = {1, 5, 6}, b = {2}, c = {3}, and d = {4}; for the middle quartet, a = {1}, b = {5, 6}, c = {2}, and d = {3, 4}; and for the bottom quartet, a = {1}, b = {2, 3, 4}, c = {5}, and d = {6}. The bootstrap probabilities shown for each internal branch, labeled from top to bottom, correspond to the three possible topologies, e = [(a, b),(c, d)], f = [(a, c),(b, d)], and g = [(a, d),(b, c)], respectively.

Figure 5.

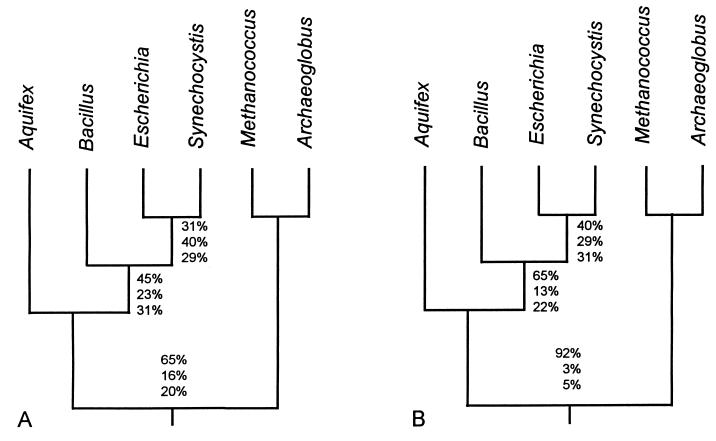
Phylogenetic trees indicating the local deviations of operational and informational trees from the reference tree. The average percentages of support for the alternative local topologies of the operational genes (A) and the informational genes (B) are indicated. The top number associated with each internal branch is the average support for the quartet shown and the bottom two values are for the two alternative topologies (see Methods).

Statistics.

χ² values were calculated from pooled data to reduce artifacts caused by low counting statistics. For comparing the distributions of distances (from a reference tree) observed for operational and informational genes (Fig. 3), bins corresponding to four and five distance steps were combined, because only two counts corresponded to five distance steps. For comparing the locations of paralog roots (Fig. 2), data were combined into three bins. All trees rooted in peripheral branches leading to eubacteria were combined, those rooted in peripheral branches leading to Methanococcus or to Archaeoglobus were combined, those rooted in interior branches leading to Methanococcus and to another organism were combined, and one root in the interior branch of an operational tree leading to Synechocystis, Methanococcus, and Archaeoglobus was not scored because of the small number of counts (one count).

RESULTS

The continual and the early massive horizontal transfer hypotheses can be formally tested by the reconstruction of informational and operational trees and their analyses. For these tests, 312 orthologous genes (203 operational and 109 informational genes, see Methods) were identified, aligned, and analyzed by using the complete proteomes of Aquifex aeolicus (21), an early branching extremely thermophilic eubacterium, Escherichia coli (22), a proteobacterium, Synechocystis 6803 (23), a cyanobacterium, Bacillus subtilis (24), a Gram-positive bacterium, Methanococcus jannaschii (11), a methanogen, and Archaeoglobus fulgidus (25), an extremely thermophilic sulfate-reducing methanogen relative. With a subset of the 312 orthologous genes (the 144 most reliable orthologs, see Methods), three tests of the competing theories were performed. All three tests yielded consistent results and supported the continual horizontal transfer hypothesis to the exclusion of the early horizontal transfer hypothesis.

A Gene Paralog Test of the Continual vs. the Massive Early Horizontal Transfer Hypotheses.

Paralog rooting can potentially discriminate between the two horizontal transfer hypotheses. A tree calculated from a set of ancient gene orthologs and paralogs contains the root of the tree of life at the point where the paralog branch joins the orthologs (26–28).

We identified 40 sets of paralogous operational and informational genes that could be reliably identified. These were aligned and trees were calculated with paralinear (logdet) distances (see Methods). The locations of roots for the operational and informational trees are shown on the horizontal axes in Fig. 2. The distributions of roots for operational and informational genes are strikingly different and statistically significant at the 1% level (P < 0.0039, χ² = 13.35, df = 3, see Methods).

Recently, Philippe and Forterre (29) proposed that paralog rooting is not reliable to identify the root of the tree of life. Penny et al. (14) suggested that failure to account for covariation when calculating deep phylogenies can cause such long branch attraction. Because the roots of the operational trees were the most variable, we looked for biases that could cause erratic rooting. If long branch attraction affects the rooted operational trees, then the long branch, which defines the root of the tree, would be expected to join to the longest peripheral branch in the ortholog gene tree. Thus, branch lengths were calculated for operational trees. In five trees, the paralog root and the ortholog branch containing the root were longest, suggesting that long branch attraction may have caused incorrect rooting. When we reanalyzed the data and omitted the five suspect trees, significant but reduced χ² support remained (P < 0.0098, χ² = 11.38, df = 3, see Methods), suggesting that long branch attraction had slightly biased our results.

The relative uniformity of the root for the informational genes is consistent with their undergoing little lateral transfer, whereas the lack of a prominent single root for operational genes indicates that they have undergone substantial horizontal transfer, consistent with the continual horizontal transfer hypothesis.

A Topological Test of the Horizontal Transfer Hypotheses.

Because of the danger of long branch effects in rooted paralog trees, analyses of unrooted ortholog trees were undertaken. If extensive horizontal change were limited to times before the divergence of the eubacteria (the Massive hypothesis), then the topologies of operational and informational trees should be identical, because horizontal transfer will have predated the divergence of individual taxa. However, if operational genes were continuously transferred (the Continual hypothesis), then operational trees should be more distant from the reference tree than informational trees.

Hence, we calculated the peripheral branch–transfer distances (see Methods) between the most probable paralinear distance tree and the EF-1α reference tree for operational and informational genes. Fig. 3 shows that the mean distance of operational trees (2.3 steps) is significantly greater than for informational trees (1.2 steps). By the χ² test the distributions also differ significantly (P < 0.0003, χ² = 23.0, df = 5). Among the informational trees, 23% match the reference tree and 47% are one step away. In contrast, only 6% of the operational trees match the reference tree. This indicates that far more transfers of single branches are required for operational trees than for informational trees. Although peripheral branch–transfer distances discriminate between a large range of distances, they do not model the process of horizontal gene transfer accurately. Thus, we also used a distance metric designed to count horizontal transfers.

Recently, Allen and Steel (20) formulated a prune-and-regraft distance metric (see Methods) to model horizontal gene transfer. Their distance corresponds to the minimum number of multiple, or single, branches that must be cut and regrafted to match a tree with the reference. The distributions of prune-and-regraft distances for informational and operational trees are shown in Fig. 4. More than 40% of the operational trees require two or more horizontal transfer events, whereas less than 10% of the informational trees require two or more. By the χ² test, the distributions differ at the 0.01% significance level (P < 0.00007, χ² = 19.08, df = 2). This strongly indicates that operational genes experience significantly more horizontal transfers than informational genes, decisively ruling in favor of the continual horizontal transfer hypothesis.

Figure 4.

The distribution of prune-and-regraft distances of operational and informational trees from the reference tree. By the χ² test the two distributions are significantly different (P < 0.00007).

The Course of Horizontal Transfer.

To estimate the percentage of genes exchanged during the intervals represented by internal branches in the reference tree, we performed quartet calculations (Fig. 5). These calculations estimate the local variation within operational and informational trees. Each internal branch relates four groups of taxa and represents the bootstrap support averaged over the 144 genes. The upper number of each group of three is the average percentage bootstrap support for the reference topology shown, and the next two numbers indicate the average support for the two possible alternatives (see Methods). Thus, if the numbers for a branch of the informational tree were 100%, 0%, 0%, from top to bottom, this would indicate that every tree calculated from an informational gene had the same local structure as the reference tree. Results obtained with the paralinear (logdet) distance algorithm (16, 17) are listed in Fig. 5 [similar results were obtained with the parsimony and Jukes-Cantor methods (15), not shown].

For informational genes, one finds a mean bootstrap support of 92% for the Aquifex + Bacillus + Escherichia + Synechocystis clade, whereas for operational genes one finds bootstrap support of only 65% for this clade, consistent with more operational gene exchange. In the informational tree, Aquifex has 65% support as being the deepest branching member of the eubacterial clade, whereas among the operational genes, it has only 45% support, again consistent with greater operational gene exchange. The branch relating Escherichia + Synechocystis is also better supported by informational genes (40%) than by operational genes (31%); however, this “bushy” part of the eubacterial tree has long been problematic and ambiguous (30). The patterns that emerge are the following: informational genes more consistently produce a single tree (the reference tree) than do operational genes, consistent with the continual hypothesis; deepest tree branchings more frequently mirror the reference tree than do recent branchings.

DISCUSSION

Given such strong support for the continual horizontal transfer hypothesis, there seems little doubt that horizontal transfer is and has been an important factor in prokaryotic genome evolution. To understand factors responsible for the frequency of horizontal transfer, within the framework of the continual theory, one needs to consider differences between operational and informational genes.

Horizontal gene transfer is not an abstract theoretical process. The probability that a specific gene will be successfully transferred to a new host depends on the specific mechanistic details of transformation, transfection, and conjugation (31), on the relationships of these mechanisms to the types of nucleic acids that are being transferred (single-stranded, double-stranded, linear, circular, etc.) (32), and even on such factors as the distribution of integrases in organisms (33). It is not our goal to propose a theory that explains in detail the probabilities that a specific gene will be transferred. Rather, it is our goal to understand why operational genes are on average more successfully transferred than informational genes, even when rates of evolution are similar for both types.

The Complexity Hypothesis.

We propose a solution that we call the complexity hypothesis. An obvious distinction between both gene types is that informational genes, particularly the translational and transcriptional apparatuses, are large, complex systems. In contrast, most operational genes are members of small assemblies of a few gene products. We propose that the complexity of informational gene interactions is a significant factor that restricts their successful horizontal transfer rates relative to the high horizontal transfer rates observed for operational genes. Two examples will help to illustrate our point.

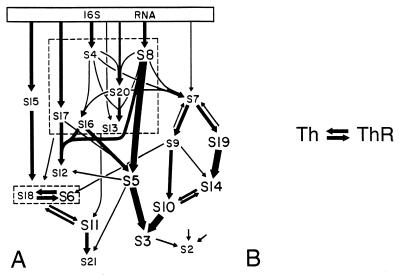
Translation in Escherichia requires the coordinated and complex interactions of at least 100 gene products. The assembly map shown (34) in Fig. 5A helps illustrate this point. It summarizes the principal assembly interactions observed for the Escherichia small ribosomal subunit. In practice this represents only part of the interactions of this complex [other small subunit interactions, not shown, include those with initiation factors 1, 2, and 3, EF-Tu, EF-Ts, and EF-G, termination factors RF1, RF2, and RF3, 86 tRNAs, numerous mRNAs, and large ribosomal subunit components (approximately 31 proteins, 23S rRNA and 5S rRNA)]. They also interact with nongene products such as ions, small molecules such as GTP, GDP, etc., and membranes, all of which are presumed to be present in a potential host. According to the assembly map, on average, a subunit protein interacts during assembly with four to five other ribosomal gene products.

In contrast, many operational proteins interact with fewer gene products. In the thioredoxin-thioredoxin reductase complex (Fig. 5B), for example, each protein interacts with just one other gene product.

To understand how complexity can influence the probability of successful horizontal transfer, consider the fate of a foreign gene that has been integrated into a host chromosome. For simplicity, assume that the gene product will function provided that it can make the necessary bonding interactions with its neighbors. Furthermore, assume that genes for thioredoxin and ribosomal protein S5 have been horizontally transferred to separate Escherichia hosts, that both share a similar percentage of protein identity, and that the probability of each protein successfully making a required interaction with another gene product is 0.25. According to this simplified model, the probability that a transferred thioredoxin could successfully interact with thioredoxin reductase would be 0.25, whereas the probability that a transferred S5 could be assembled into a small subunit is 0.25⁶ (= 0.00024) or about 1,000 times less. Thus, the probability of a successful horizontal transfer will be strongly affected by the number of interactions that a protein must make with its neighbors.

We think many of the observed differences between the horizontal transfer of informational and operational genes can be explained by complexity. This does not exclude the potential roles of operons in facilitating the transfer of protein complexes. Indeed, this is an appealing aspect of the “selfish operon” proposal (35). Although ribosomal proteins are in operons, this is unlikely to permit horizontal transfer of the translation apparatus, because that would require many independent transfers of noncontiguous operons.

The extensive amount of horizontal transfer between prokaryotes observed in this study makes it clear that horizontal transfer must be a major contributor to the evolution of genomes. The taxonomic breadth and extent of transfer has been so vast that one can think of the operational gene component of prokaryotes as a single global organism. This concept refers to a subset of the genome and hence differs from previous notions of global organisms such as those inspired by the discovery of transferable drug resistance. The effective population size for the worldwide collection of operational genes is enormous and the potential for the creation of innovations is, and has been, correspondingly great.

Figure 6.

Examples of the complexity of gene product interactions in informational genes (A) and operational genes (B). The assembly map (34) of the Escherichia, small ribosomal subunit is shown in A as an illustration of the high complexity that is frequently present in the translational apparatus. The thioredoxin (Th) and thioredoxin reductase (ThR) complex is shown in B as an example of the reduced complexity present in some operational genes.

ABBREVIATION

EF

elongation factor