Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2006 Nov;15(11):2568–2578. doi: 10.1110/ps.062255806

Backbone dynamics of SDF-1α determined by NMR: Interpretation in the presence of monomer–dimer equilibrium

Olga K Baryshnikova 1, Brian D Sykes 1
PMCID: PMC2242403  PMID: 17075134

Abstract

SDF-1α is a member of the chemokine family implicated in various reactions in the immune system. The interaction of SDF-1α with its receptor, CXCR4, is responsible for metastasis of a variety of cancers. SDF-1α is also known to play a role in HIV-1 pathogenesis. The structures of SDF-1α determined by NMR spectroscopy have been shown to be monomeric while X-ray structures are dimeric. Biochemical data and in vivo studies suggest that dimerization is likely to be important for the function of chemokines. We report here the dynamics of SDF-1α determined through measurement of main chain 15N NMR relaxation data. The data were obtained at several concentrations of SDF-1α and used to determine a dimerization constant of ∼5 mM for a monomer–dimer equilibrium. The dimerization constant was subsequently used to extrapolate values for the relaxation data corresponding to monomeric SDF-1α. The experimental relaxation data and the extrapolated data for monomeric SDF-1α were analyzed using the model free approach. The model free analysis indicated that SDF-1α is rigid on the nano- to picosecond timescale with flexible termini. Several residues involved in the dimer interface display slow micro- to millisecond timescale motions attributable to chemical exchange such as monomer–dimer equilibrium. NMR relaxation measurements are shown to be applicable for studying oligomerization processes such as the dimerization of SDF-1α.

Keywords: backbone dynamics, NMR, chemokine, SDF-1α, monomer–dimer equilibrium

SDF-1α is a member of the chemokine family, which is responsible for the trafficking of lymphocytes and numerous reactions in the immune system (Baggiolini 1998; Kunkel and Godessart 2002). SDF-1α is particularly interesting due to its involvement in HIV pathogenesis (Berson et al. 1996) and in a variety of cancers (Muller et al. 2001; Murphy 2001; Cooper et al. 2003; Phillips et al. 2003; Rubin et al. 2003). It is generally expected that inhibition of the interaction of SDF-1α with its receptor CXCR4 will be an important therapeutic breakthrough that will reduce the propagation rate of a variety of cancers and HIV-1 (Epstein 2004). SDF-1α exerts its biological function through interaction with the G-protein coupled receptor, CXCR4, in two steps. The first step includes the recruitment of a chemokine from solution, and the second step involves the insertion of the SDF-1α N terminus into the seven-helix bundle of the receptor and the initiation of a signaling cascade (Crump et al. 1997).

The interaction of a chemokine with its receptor can be modulated in several ways. One of them is by the interaction of the chemokine with components of extracellular matrix such as glycosaminoglycans. These have a noticeable affinity for chemokines and thus help to bring the chemokines from bulk solution and concentrate them in proximity to the membrane surface (Kuschert et al. 1999). Another way to modulate chemokine signaling is through multivalency, which is a well-known strategy employed by nature (Mammen et al. 1998). Multivalency allows for an increase in the local concentration of a ligand on a surface and hence increases the observed affinity for its receptor. Several chemokines are known to exist as oligomers in concentrated solutions (Fernandez and Lolis 2002). If chemokines are oligomeric in vivo at physiological concentrations, this might enhance the efficiency of recruitment and bring an additional level of regulation of signaling. Some in vivo studies suggested that dimerization is not required for the activation of a receptor (for example, IL-8) (Rajarathnam et al. 1994). Other studies demonstrated that at least in certain cases the ability of chemokines to dimerize influences the magnitude of signaling efficiency (for example, CCL2, CCL4, and CCL5) (Proudfoot et al. 2003).

The oligomerization behavior of SDF-1α in vitro in terms of monomer–dimer equilibrium is controversial. The first NMR structure reported by Crump and coworkers characterized SDF-1α as a monomer under experimental conditions based on the following observations: No NOE contacts corresponding to a dimer interface were found, no slowly exchanging protons at the dimer interface were observed, and the molecular weights obtained with sedimentation equilibrium centrifugation were consistent with that expected for the monomeric species (Crump et al. 1997). In the two reported crystal structures, SDF-1α was dimeric, with the dimer interface similar to the interface formed by IL-8 (Dealwis et al. 1998; Ohnishi et al. 2000). The original NMR structure of SDF-1α determined by Crump et al. (1997) was slightly different from the structures of individual SDF-1α subunits determined by crystallography, especially in the position of the C-helix. The most recent NMR structure of SDF-1α (Gozansky et al. 2005) under different experimental conditions was closer to the individual subunits of SDF-1α in the crystal structures. Monomer–dimer equilibrium has been characterized by several biophysical methods, including solution state NMR, with Kd values in the range of ∼150 μM to ∼3 mM (Holmes et al. 2001; Veldkamp et al. 2005). In the study by Veldkamp et al. (2005), special emphasis was drawn to the role of experimental conditions, e.g., pH and buffer content, on the monomer–dimer equilibrium.

In the present report, we describe detailed backbone 15N relaxation measurements for SDF-1α at several concentrations. Relaxation data obtained from heteronuclear NMR experiments are typically interpreted with respect to fast pico- to nanosecond local internal motions within a protein, the overall global rotational tumbling of a protein, and slow micro- to millisecond timescale motions that may be indicative of an underlying chemical exchange phenomenon such as monomer–dimer equilibrium (Ishima and Torchia 2000). Using the dependence of the NMR parameters on SDF-1α concentration, we have determined the dimerization constant Kd to be ∼5 mM. While the Kd indicates weak dimerization, proper analysis of the relaxation data obtained at various SDF-1α concentrations requires that the monomer–dimer equilibrium be taken into account. The dimerization of SDF-1α can account for slight differences between solution state structures determined by NMR (Crump et al. 1997; Gozansky et al. 2005). Importantly, we have found that regions from SDF-1α that are involved in the dimer interface in crystallographically determined structures are involved in slow timescale motions. Given that oligomerization of chemokines may be crucial for enhancement of signaling by increasing the affinity of the chemokine–receptor interaction, a thorough investigation of the nature of SDF-1α oligomerization is important.

Results

15N-T1, T2, and NOE data

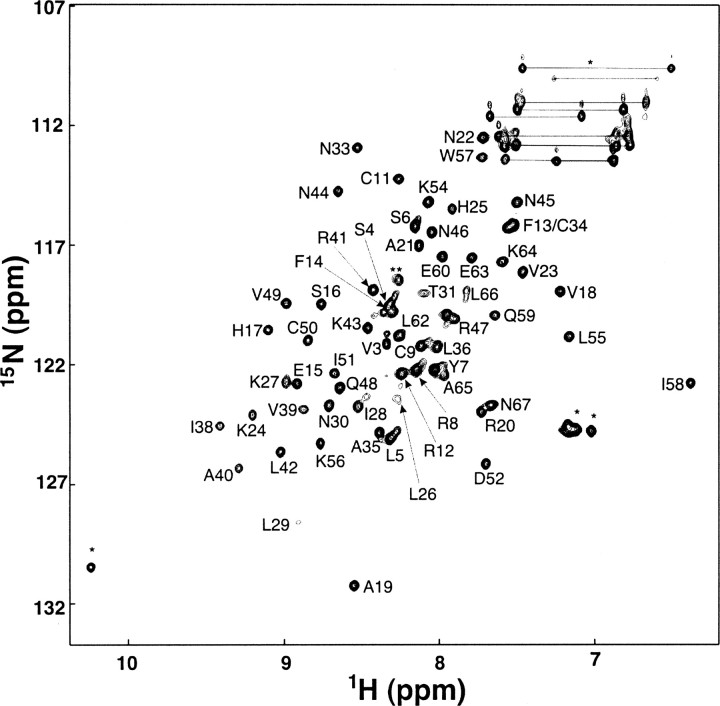
Backbone amide 15N relaxation parameters were obtained using 2D 1H–15N correlation NMR spectroscopy with a typical spectrum of 1.5 mM SDF-1α shown in ▶. Backbone 15N and 1H chemical shifts for SDF-1α were assigned using 3D NOESY-HSQC and 3D TOCSY-HSQC spectra (Zhang et al. 1994) and were in good agreement with 1H chemical shifts obtained previously using homonuclear 2D NMR spectroscopy (Crump et al. 1997). However, as described below, the 1H chemical shifts were found to be dependent on protein concentration. Relaxation properties were determined for 56 of the 67 backbone amide 1HN-15N pairs. Residues that could not be analyzed include: Lys1, due to exchange with solvent; Phe13 and Cys34, whose chemical shifts overlap; Pro2, Pro10, Pro32, and Pro53, lacking backbone amide protons; Leu26, due to line broadening; and Gln37, whose chemical shifts are not assigned. In several cases, residues Tyr61, Leu62, Phe14, and Val4 were excluded due to peak overlap. In the cases of very diluted samples, the resonances for Phe13 and Cys34 could be discriminated and were therefore included in the analysis.

Figure 1.

Figure 1.

Open in a new tab

2D 1H–15N HSQC correlation spectrum of 1.5 mM SDF-1α. Assigned residues are indicated on the spectrum with labels. Arginine and glutamate side chain amide protons as well as the indole NH of Trp57 are indicated with an asterisk. The resonance marked with a double asterisk was not assigned.

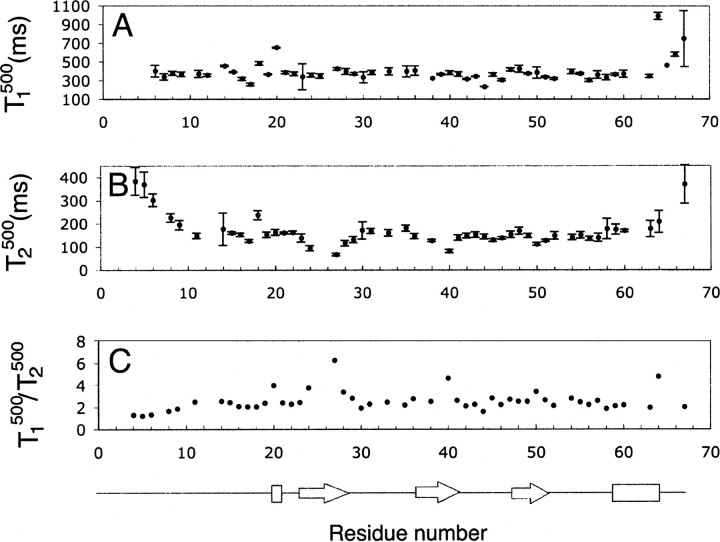
15N-T1, T2, and NOE data for a sample containing 1.5 mM of recombinant 15N-labeled SDF-1α were obtained at proton frequencies of 500 and 600 MHz, and 30°C. 15N-T1, T2, and NOE data are summarized in ▶ and depicted in ▶. The average NOE600/NOE500 ratio was 1.04 ± 0.20 (▶). T1500 and T1600 followed similar per residue patterns with an average T1600/T1500 ratio equal to 1.29 ± 0.07 (▶). T2500 and T2600 also showed similar per residue patterns with an average T2600/T2500 ratio equal to 0.87 ± 0.06 (▶). The T1/T2 ratios at 500 and 600 MHz are shown in ▶.

Table 1.

NMR relaxation measurements obtained for 1.5 mM SDF-1α

graphic file with name 2568tbl1.jpg

Open in a new tab

aThe excluded residues were the following: 3–14, 17, 23–25, 27, 29, 31, 38, 45, 48, and 66–67 for the data set acquired at 500 MHz and 3–9, 12, 18, 29–31, 35–36, and 64–67 for the data set acquired at 600 MHz. Residues were excluded if NOE500 < 0.60 and NOE600 < 0.65.

bAverage error of fitting is 15 msec.

cAverage error of fitting is 32 msec.

dAverage error of fitting is 3 msec.

eAverage error of fitting is 6 msec.

fAverage error of fitting is 12 msec.

gAverage error of fitting is 25 msec.

hAverage error of fitting is 2 msec.

iAverage error of fitting is 4 msec.

Figure 2.

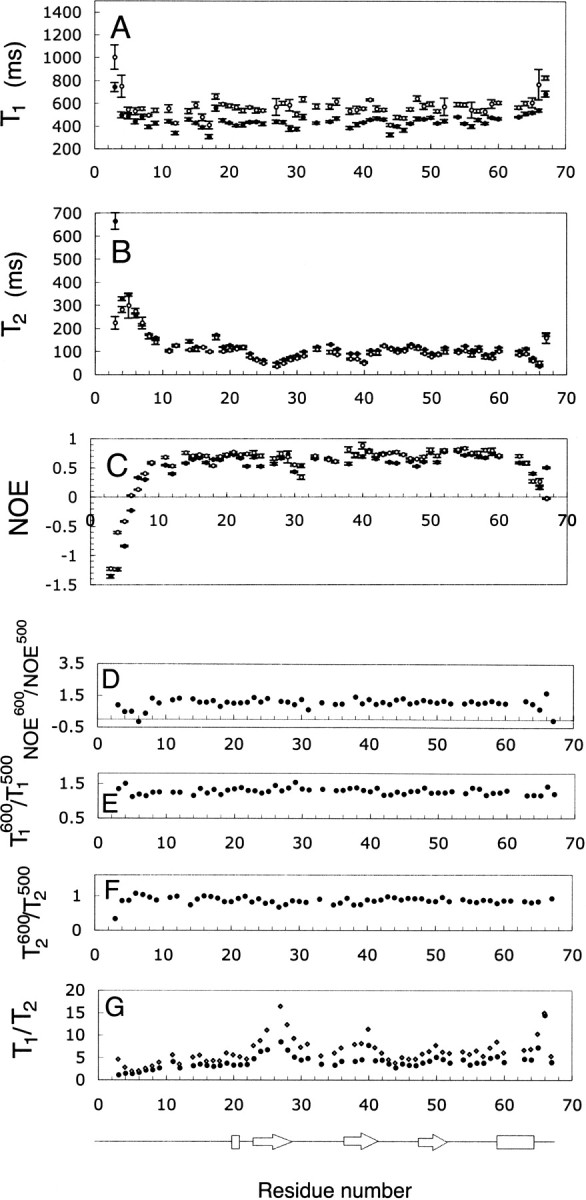
Figure 2.

Open in a new tab

(A–G) Relaxation data obtained at two magnetic fields for 1.5 mM SDF-1α. (A) T1600 (○) and T1500 (•); (B) T2600 (○) and T2500(•); (C) NOE600 (○) and NOE500 (•); (D) NOE600/NOE500 ratio; (E) T1600/T1500 ratio; (F) T2600/T2500 ratio; and (G) T1600/T2600 ratio (Inline graphic) and T1500/T2500 ratio (•). Elements of secondary structure were determined from the coordinates of the crystal structure (Dealwis et al. 1998).

The N- and C-terminal regions (residues 3–8 and 62–67) of SDF-1α were more flexible than the core of the protein (▶). These regions were identified on the basis of low NOE values and larger values of T1 and T2, in comparison to regions within the structured core of the protein. This observation is in agreement with structural information obtained by solution state NMR and X-ray crystallography, which indicate that the N terminus was unstructured in the case of NMR or lacked electron density in the case of crystallography (Crump et al. 1997; Dealwis et al. 1998). Residues 23–27 and 30–31 also have NOE and T2 values lower than average and may be more flexible than the structured core of the protein. However, the per residue profile for T1/T2 ratios (▶) shows an increase in the region spanning residues 23–31, suggesting that these residues may be involved in chemical exchange. The regions from residues 36–42, 49–51, and 65–67 may also be involved in chemical exchange based on high T1/T2 and low T2 values.

Concentration dependence of 15N-T2 values

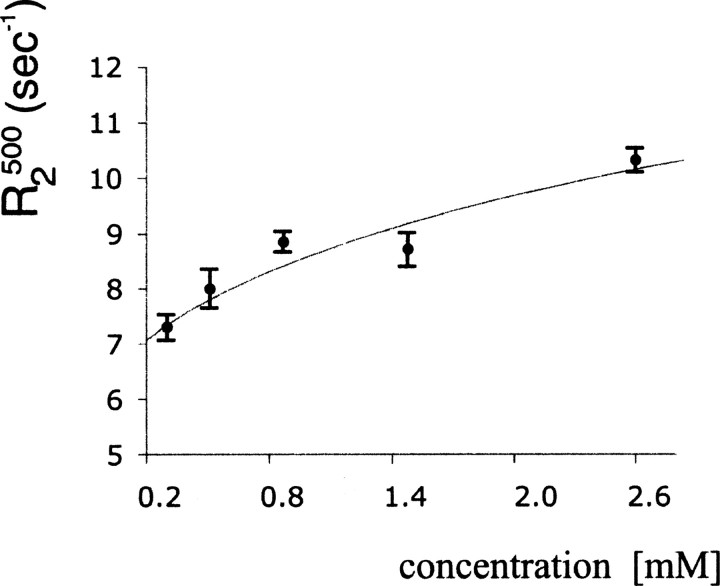
The theoretical T2 values for monomeric SDF-1α were calculated to be 176 and 181 msec at 500 and 600 MHz, respectively (Lipari and Szabo 1982a; in-house script written by Stéphane Gagné). These values were obtained by assuming that S2 = 0.85 (Goodman et al. 2000), and τm = 3.9 nsec. The theoretical values were significantly larger than the experimental values of 109 and 130 msec determined at 500 and 600 MHz, respectively. However, for dimeric SDF-1α, the theoretical T2 values were equal to 102 msec for T2600 and 107 msec for T2500. Thus, in the limit of fast exchange between monomer and dimer, it is likely that SDF-1α was partially dimeric in solution, leading to a decrease in the experimental T2 values. In order to explore this phenomenon further, we measured T2500 values for a range of concentrations, including 2.6, 1.5, 0.9, 0.5, and 0.3 mM. As shown in ▶, T2500 data show a clear dependence on concentration, with the lowest T2500 values observed for the most concentrated sample. This dependence is also highlighted in a plot of the average value of R2500 (1/T2500) for the core residues as a function of SDF-1α concentration (▶). The core residues included 15, 16, 18–22, 33, 35, 39, 41–43, 46, 50, 52, 54–60.

Figure 3.

Figure 3.

Open in a new tab

15N-T2500 relaxation data for SDF-1α samples containing different concentrations. 15N-T2500 relaxation data is shown for 2.6 mM (•), 0.9 mM (○), and 0.3 mM (▴) SDF-1α. Only three T2500 data sets from a total of five are shown for clarity.

Figure 4.

Figure 4.

Open in a new tab

15N-R2500 relaxation data obtained for residues in the structured core of SDF-1α. R2 values were averaged and plotted as a function of the concentration of SDF-1α. The best fit to Equation 8 yielded Kd = 9 ± 24 mM, R2m = 7 ± 1 sec−1, and R2d = 18 ± 15 sec−1.

To describe the concentration dependence of R2500 in the presence of SDF-1α dimerization, the value of the observed transverse relaxation rate R2obs can be written as

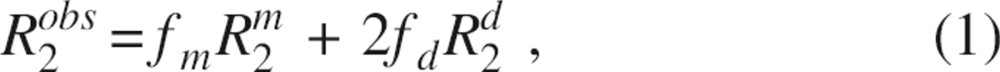graphic file with name 2568equ1.jpg

where R2m and R2d are the transverse relaxation rates for pure monomer and dimer, respectively, and the fractions of monomeric and dimeric species are denoted as

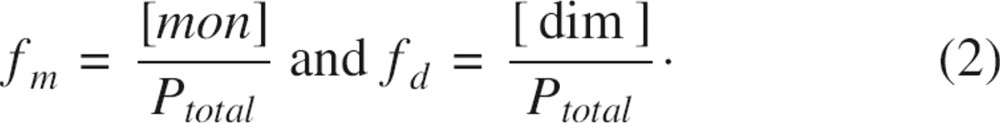graphic file with name 2568equ2.jpg

The total concentration of the protein is given by the expression

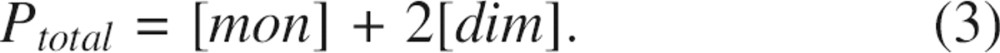graphic file with name 2568equ3.jpg

Substitution of Equations 2 and 3 into 1 yields

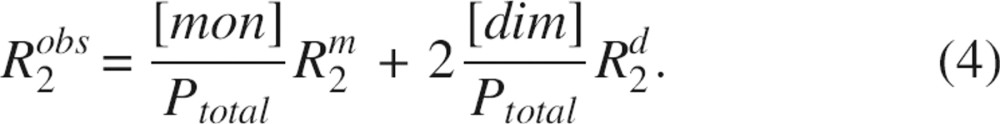graphic file with name 2568equ4.jpg

The concentration of monomeric and dimeric protein can be derived by solving Equation 3 and the following equation for the dissociation constant:

graphic file with name 2568equ5.jpg

with respect to protein concentration to yield:

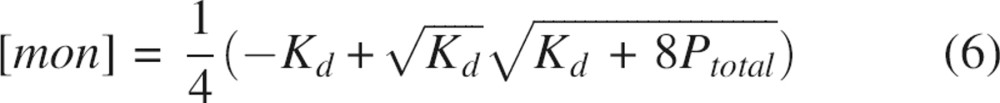graphic file with name 2568equ6.jpg

and

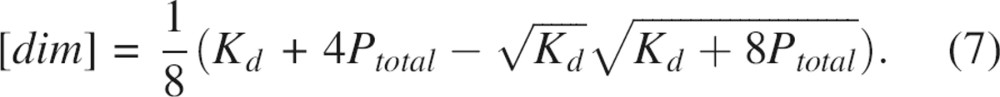graphic file with name 2568equ7.jpg

Substitution of Equations 6 and 7 into Equation 4 and subsequent simplification yields:

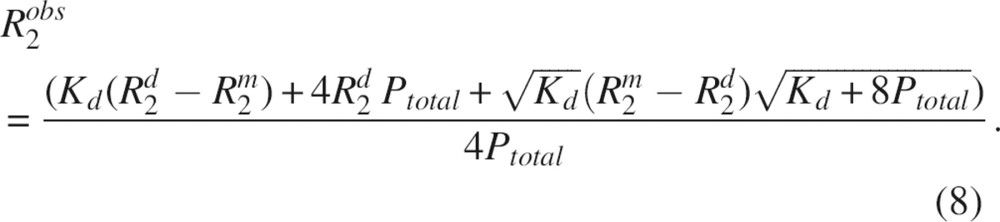graphic file with name 2568equ8.jpg

Equation 8 was implemented into the program xcrvfit to conduct nonlinear least squares fitting (www.pence.ca/~software). Experimental R2 data were fit to Equation 8 to yield the following best fit parameters: Kd = 9 mM, R2m = 7 sec−1, and R2d = 18 sec−1 (▶). The quality of the fit at lower concentrations was significantly better than that at higher concentrations. Thus, the extrapolation of the R2 value to the lowest concentration where the protein is predominantly monomeric is more reliable than the extrapolation to concentrations where the protein is expected to oligomerize. The value of the dimerization constant was evaluated with several other methods as described below for the purposes of verifying the fitted Kd and obtaining a reliable error estimate.

Dimerization constant calculated using 1D 1H NMR spectroscopy

Chemical shifts are sensitive to changes in molecular structure and local environment. The chemical shifts obtained from 1D 1H spectra offer advantages of being very accurate, since the resolution of 1D 1H spectra acquired at 500 MHz were normally <1 Hz. However, due to peak overlap, only a few resonances can be easily traced in the spectra. Changes in chemical shifts for the clearly distinguishable peaks from the indole NH of Trp57, the aromatic 2,6H and 3,5H of Tyr7, and 2,6H of Phe13 and Phe14 as a function of SDF-1α concentration were fit to the following equation, which was derived in a fashion similar to that of Equation 8:

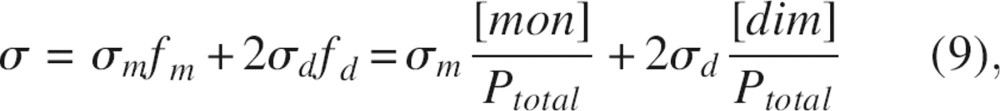graphic file with name 2568equ9.jpg

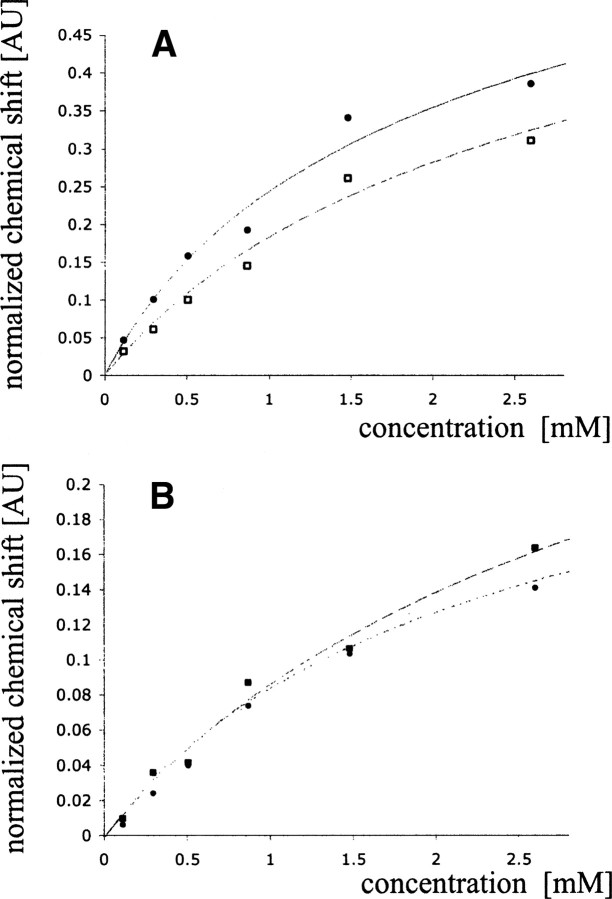
where σm and σd are chemical shifts for a monomer and a dimer respectively. Kd was calculated for every individual proton (▶), and the representative fits of chemical shift data to Equation 9 are shown in ▶. The average value for Kd was 5 ± 1 mM.

Table 2.

Values of the dimerization constant determined using chemical shift changes in 1D 1H and 2D 1H–15N HSQC spectroscopy

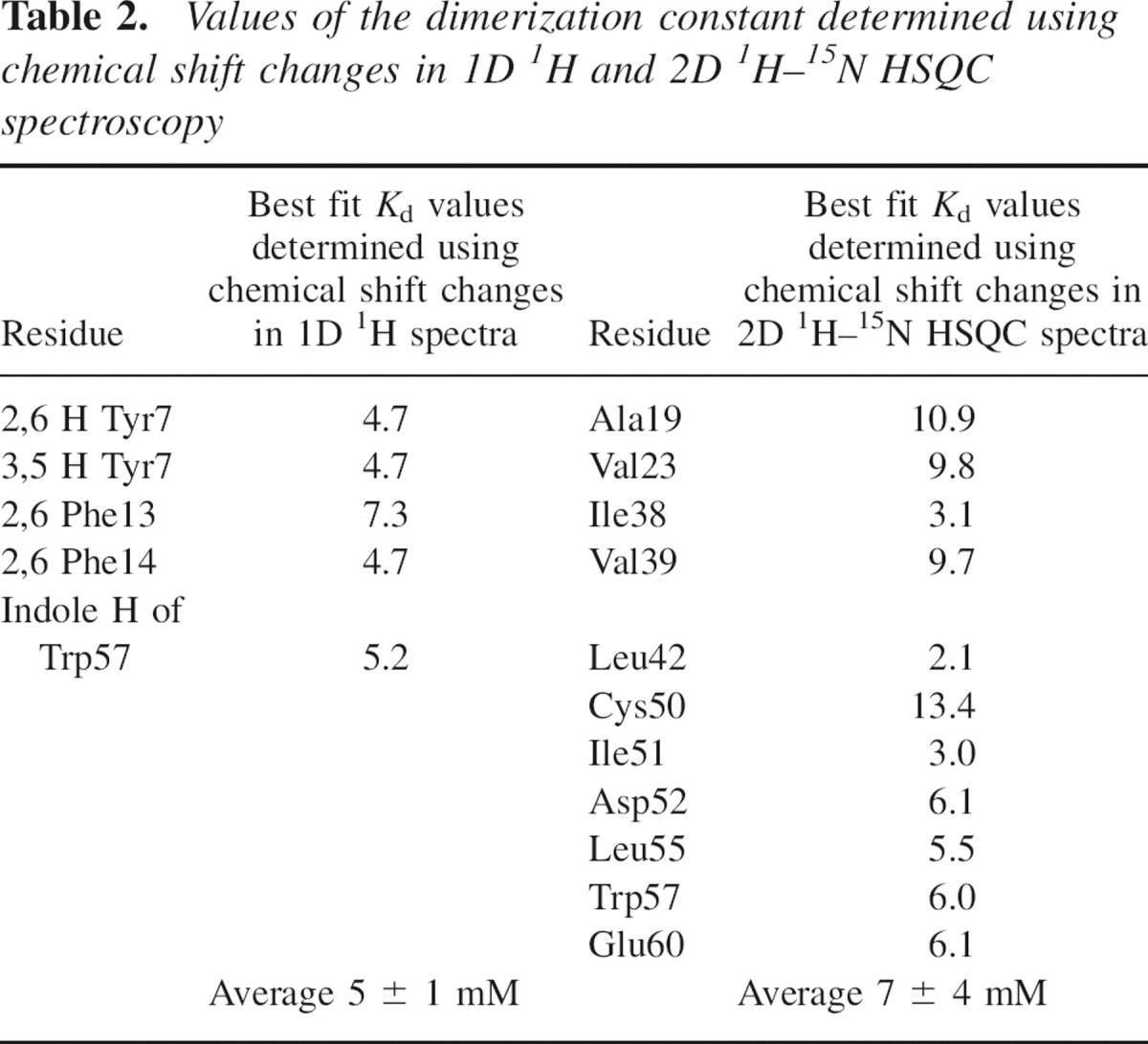
graphic file with name 2568tbl2.jpg

Open in a new tab

Figure 5.

Figure 5.

Open in a new tab

Chemical shift changes obtained using 1D 1H and 2D 1H–15N NMR spectroscopy plotted as a function of SDF-1α concentration. (A) Normalized proton chemical shift changes determined using 1D NMR spectroscopy as a function of SDF-1α concentration for 3,5H of Tyr7 (•) and 2,6H of Phe14 (□). (B) Normalized proton chemical shift changes determined using 2D 1H–15N NMR spectroscopy as a function of SDF-1α concentration for Val39 (▪) and Trp57 (•).

Dimerization constant calculated using 2D 1H–15N HSQC NMR spectroscopy

Chemical shift changes upon dilution of SDF-1α were followed using 2D 1H–15N HSQC NMR spectra. The resolution for the 1H dimension from these spectra in our experiment was ∼20 Hz, significantly less than that from the corresponding 1D 1H spectra. However, in contrast to 1D spectra, chemical shifts for a larger number of peaks could be monitored as a function of SDF-1α concentration. Data from residues showing the largest proton chemical shift changes were fit to Equation 9 with the program xcrvfit to extract per residue Kds (▶; ▶). The average Kd value for SDF-1α dimerization was determined to be 7 ± 4 mM.

Extrapolation of per residue T1500 and T2500 values to infinite dilution

Per residue T2500 and T1500 values at infinite dilution were obtained using Equation 8 and Kd = 5 mM, determined using the most accurate method (1D 1H spectrometry). The data set used for extrapolation included T2500 data obtained experimentally for the concentrations of 2.6, 1.5, 0.9, 0.5, and 0.3 mM and T1500 data obtained for the concentrations of 2.6, 1.5, 0.9, and 0.3 mM. The average value for the extrapolated T2500 for the protein core was 158 ± 24 msec with an average error of 12 msec (▶), and the average value for extrapolated T1500 for the protein core was 364 ± 40 msec with an average error of 20 msec (▶). The values of T1500 and T2500 extrapolated to infinite dilution are close within the determined errors to the theoretical values for monomeric SDF-1α, which are 388 msec for T1 and 181 msec for T2 at 500 MHz. Extrapolated T2 and T1 followed the same per residue trend as the experimentally obtained T2500 and T1500 (▶).

Figure 6.

Figure 6.

Open in a new tab

Relaxation parameters, T1500 (A), T2500 (B), and T1500/T2500 (C), extrapolated to infinite dilution. Elements of secondary structure were determined from the coordinates of the crystal structure (Dealwis et al. 1998).

Model free analysis of backbone dynamics

Backbone amide 15N-T1, T2, and NOE data sets acquired at 500 and 600 MHz for samples containing 1.5 mM and 0.3 mM of SDF-1α were examined by model free analysis. This approach affords the interpretation of relaxation measurements in terms of the overall correlation time, generalized order parameters, and local motions (Lipari and Szabo 1982a,b). The overall rotational tumbling of SDF-1α was assumed to be isotropic, given that rotational diffusion anisotropy was found to be negligible in previous backbone 15N relaxation studies of monomeric chemokines (Crump et al. 1999; Mizoue et al. 1999) and the dimeric chemokine, IL-8 (Grasberger et al. 1993). The overall correlation times determined as previously described using T1, T2, and NOE data (Spyracopoulos et al. 2001) were τm500 = 6.79 nsec and τm600 = 7.24 nsec for a sample containing 1.5 mM of SDF-1α, and τm500 = 5.04 nsec and τm600 = 7.17 nsec for a sample containing 0.3 mM of SDF-1α. The rotational correlation times for these two concentrations appeared to be overestimated in comparison to the expected values for monomeric SDF-1α (7.8 kDa). Interestingly, the rotational correlation time is overestimated for the most diluted sample, for which the fraction of dimer is ∼5% based on our measurements of Kd. This observation is consistent with previous studies, which have shown that slight dimerization and/or higher order aggregation can influence the interpretation of relaxation data (Schurr et al. 1994). The overall correlation time was also determined using the per residue T1500 and T2500 values extrapolated to infinite dilution and NOE500 data for 1.5 mM SDF-1α, because NOE500 did not change during dilution and this data set had the smallest error. The correlation time obtained in this manner was 4.42 nsec.

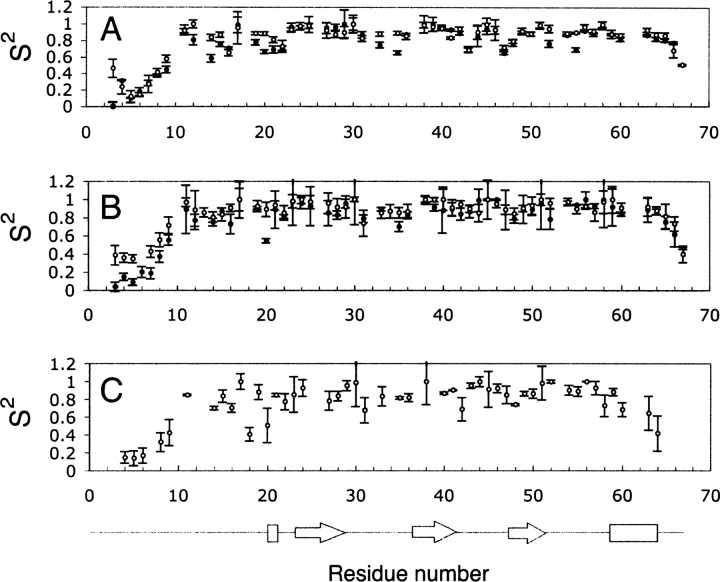
In typical implementations of the model free approach, five different dynamic models (Lipari and Szabo 1982a; Clore et al. 1990) can be utilized to obtain the generalized order parameters (S2), chemical exchange terms (Rex), and internal correlation times (τm and τs). The average S2 for all residues was equal to 0.77 ± 0.04 and 0.81 ± 0.05 for 1.5 mM SDF-1α for data collected at 500 and 600 MHz, respectively, 0.79 ± 0.09 and 0.86 ± 0.07 for 0.3 mM SDF-1α (500 and 600 MHz, respectively), and 0.77 ± 0.09 for the data set extrapolated to infinite dilution (▶). The values of S2 for the core residues were 0.81 ± 0.03 and 0.87 ± 0.03 for 1.5 mM SDF-1α sample (500 and 600 MHz, respectively), 0.87 ± 0.07 and 0.91 ± 0.06 for 0.3 mM SDF-1α (500 and 600 MHz, respectively), and 0.83 ± 0.07 for the extrapolated data set. Residues in the unstructured regions, the N and C termini and loops, displayed smaller values of S2, indicative of larger amplitudes timescale motions. The experimental error in the relaxation measurements increases with increasing dilution of SDF-1α as a result of decreasing signal-to-noise ratio. Therefore, the model free parameters extracted from T1, T2, and NOE data collected for dilute samples showed greater error. The average S2 value was slightly smaller for the extrapolated data set, but similar within reported errors to the average S2 for data collected at 1.5 and 0.3 mM SDF-1α (▶).

Figure 7.

Figure 7.

Open in a new tab

Generalized order parameters, S2, for samples containing different concentrations of SDF-1α, and relaxation data extrapolated to infinite dilution. (A) Generalized order parameters for 1.5 mM SDF-1α at 500 (•) and 600 (○) MHz. (B) Generalized order parameters for 0.3 mM SDF-1α at 500 (•) and 600 (○) MHz. (C) Generalized order parameters obtained using T1500 and T2500 values extrapolated to infinite dilution.

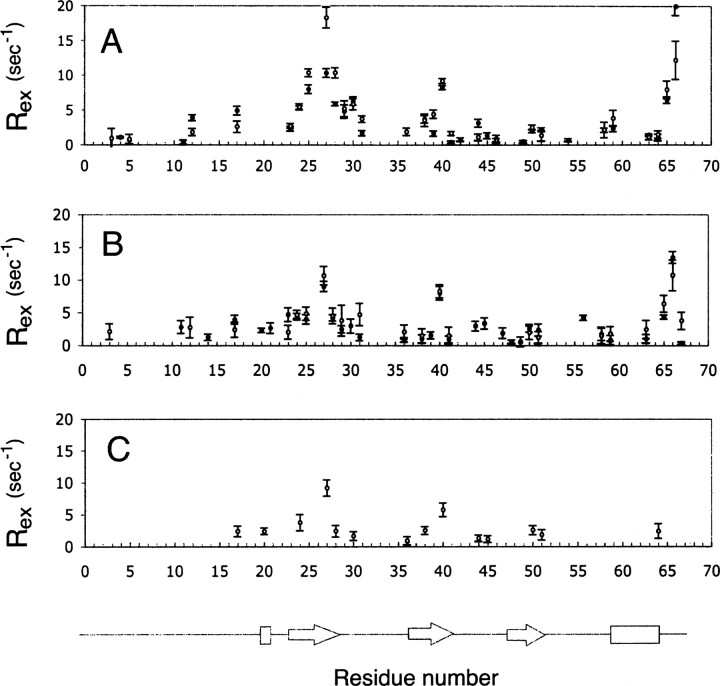
The values for Rex indicating a chemical exchange phenomenon are shown in ▶. The trend for Rex shows the highest values in the regions of residues 23–31, 36–40, 50–51, and at the C terminus. The residues displaying the largest values of Rex are directly involved in the formation of the dimer interface. The value of the Rex terms decrease upon dilution from ∼20 sec−1 for 1.5 mM SDF-1α to ∼10 sec−1 for 0.3 mM SDF-1α. Rex terms remain in the extrapolated data. These include 17, 20 (the N terminus), 24, 27, 28, 30 (the first β strand), 36, 38, 40 (the second β strand), 50–51 (the third β strand), and 64 (the C-terminal helix). If the rate of interconversion of exchanging species is fast relative to the chemical shift difference, the value of Rex600/Rex500 should be equal to 6002/5002, or 1.44. Residues with Rex600/Rex500 values within the range 1.44 ± 0.28 (20% of error) included 23, 25, 27, 28, 50, and 65 for 1.5 mM SDF-1α and 25, 27, 28, 29, 38, 41, and 65 for 0.3 mM SDF-1α.

Figure 8.

Figure 8.

Open in a new tab

Rex parameters obtained for samples containing different concentrations of SDF-1α and for the case where relaxation parameters extrapolated to infinite dilution. (A) Rex parameters for 1.5 mM SDF-1α at 500 (•) and 600 (○) MHz. (B) Rex parameters for 0.3 mM SDF-1α at 500 (•) and 600 (○) MHz. (C) Rex parameters obtained using T1500 and T2500 values extrapolated to infinite dilution.

Discussion

SDF-1α is an important chemokine that plays a critical role during initial phases of development in the immune system, neuronal patterning (Zou et al. 1998), and vascularization (Tachibana et al. 1998). Later in life, SDF-1α remains present at a constant level, unlike other chemokines, which are mostly expressed during inflammation (Godiska et al. 1995). Several malignant tumors take advantage of SDF-1α interaction with its receptor, CXCR4, which allows them to metastasize into tissues producing SDF-1α and form secondary tumors (Murphy 2001). The structure of SDF-1α has been determined independently by several groups using both solution state NMR and X-ray crystallography (Crump et al. 1997; Dealwis et al. 1998; Ohnishi et al. 2000; Gozansky et al. 2005). Here we have used backbone amide 15N relaxation measurements to analyze dimerization of SDF-1α. The importance of dimerization with respect to biological function of SDF-1α is discussed.

SDF-1α exists in monomer–dimer equilibrium

The experimental relaxation data reported herein demonstrates the existence of monomer–dimer equilibrium for SDF-1α. Proton chemical shifts observed in both 1D and 2D NMR experiments and the per residue transverse relaxation rates, R2, demonstrated a dependence on the concentration of SDF-1α. The concentration dependence of chemical shifts and relaxation rates was used to determine a dimerization constant of 5 ± 1 mM. This Kd value indicates a weaker self-association than previously reported (Holmes et al. 2001), but agrees with the dependence of Kd on buffer composition (Veldkamp et al. 2005). In the present study, the buffer was of low ionic strength, containing only 20 mM acetate and negligibly small amounts of azide and chloride. The buffer composition was optimized in the previous study to minimize dimerization (Crump et al. 1997). High ionic strength buffers are expected to neutralize the positively charged residues on the first β-sheet (Lys24, His25, Lys27), reducing repulsion between monomers and favoring dimer formation (Veldkamp et al. 2005). In our experiments, the percentage of dimer was 27.4% in the most concentrated sample (2.6 mM of SDF-1α) and 19.2% and 5.2% in the sample containing 1.5 mM and 0.3 mM SDF-1α, respectively.

Model free analysis

Protein dimerization often complicates the interpretation of relaxation measurements (Korchuganov et al. 2001; Spyracopoulos and Sykes 2001), causing significant overestimations of the generalized order parameter and internal motions, as shown by simulations (Schurr et al. 1994). The model free analysis appropriate for the interpretation of relaxation measurements of purely monomeric or dimeric species is not a desirable method if both species are present in substantial quantities. There are a number of approaches that account for monomer–dimer equilibrium in model free analysis (Fushman et al. 1997; Grzesiek et al. 1997; Gryk et al. 1998; Pfuhl et al. 1999). One of these approaches presents dynamic data qualitatively (Grzesiek et al. 1997), and another requires approximations such as equivalent local motions for both dimeric and monomeric species (Fushman et al. 1997). In the present study, we extrapolated relaxation parameters to infinite dilution to obtain T1 and T2 values for the monomeric species, similarly to the approach of Pfuhl et al. (1999), where relaxation data was extrapolated to infinite dilution and to pure homodimer. Model free analysis was performed on relaxation data sets obtained for two different concentrations of SDF-1α and on a data set with relaxation parameters extrapolated to infinite dilution. The value of the overall correlation time for SDF-1α decreased with decreasing fraction of dimer, as previously observed (Fushman et al. 1997; Pfuhl et al. 1999; Mercier et al. 2001). For relaxation data extrapolated to infinite dilution, a value of 4.42 nsec for τm500 is reasonable for a 7.8-kDa protein containing flexible termini. This is consistent with previous hydrodynamic calculations for the dynamin pleckstrin homology (PH) domain, which indicated that a flexible tail slightly decreased the rate of overall rotational tumbling (Fushman et al. 1997).

The generalized order parameters obtained for 1.5 and 0.3 mM SDF-1α and the data set with relaxation parameters extrapolated to infinite dilution show similar trends with the flexible N terminus (residues 1–9) and C terminus (residues 63–67). Previous simulations predicted that S2 can be substantially overestimated for proteins that self-associate (Schurr et al. 1994). However, the results presented herein were similar to the results of previous experimental studies (Pfuhl et al. 1999), which indicate that increases in S2 in the presence of dimerization are not dramatic.

Interestingly, residues 8–12 have been suggested to interact with the cognate SDF-1α receptor (Ohnishi et al. 2000; Baryshnikova et al. 2005). The N terminus of SDF-1α (residues 1–17) adopts an extended conformation with two cysteines, Cys9 and Cys11, constraining the region 8–12 by two disulfide bonds Cys9–Cys34 and Cys11–Cys50. In the present study, the average S2 values of 0.91 ± 0.09 and 0.87 ± 0.1 for Cys11 and Arg12 correspondingly indicate that the flexibility of this region is restricted on the picosecond timescale. For comparison, the average S2 value for Arg8 was found to be 0.43 ± 0.05. Restriction of flexibility within this region may contribute favorably to the energy of the interaction with a receptor.

The number of residues requiring Rex terms to properly account for relaxation data and the magnitude of the Rex terms displayed a dependence on protein concentration as previously observed (Pfuhl et al. 1999). The dependence of Rex on the fraction of monomeric protein was not linear, as expected from theoretical (Luz and Meiboom 1963) and experimental (Baldo et al. 1975) studies. Given that relaxation data for residues 25, 26, and 29 were missing due to line broadening or due to the poor quality of the extrapolations, it is possible that the entire first β strand may be involved in a conformational exchange. The second set of residues mapped to the second β strand, the third β strand, and the C terminus. Residues belonging to the first β strand and the C-helix directly participate in formation of the dimer interface. Residues in the second and third β strands requiring Rex terms interact with residues found within the interface.

In the absence of monomer–dimer exchange, e.g., in the purely monomeric case, some residues still required Rex terms in the model free analysis. These are generally the same residues involved in dimerization (▶), and must reflect conformational flexibility within the monomer. A mechanism consistent with this data is:

Figure 9.

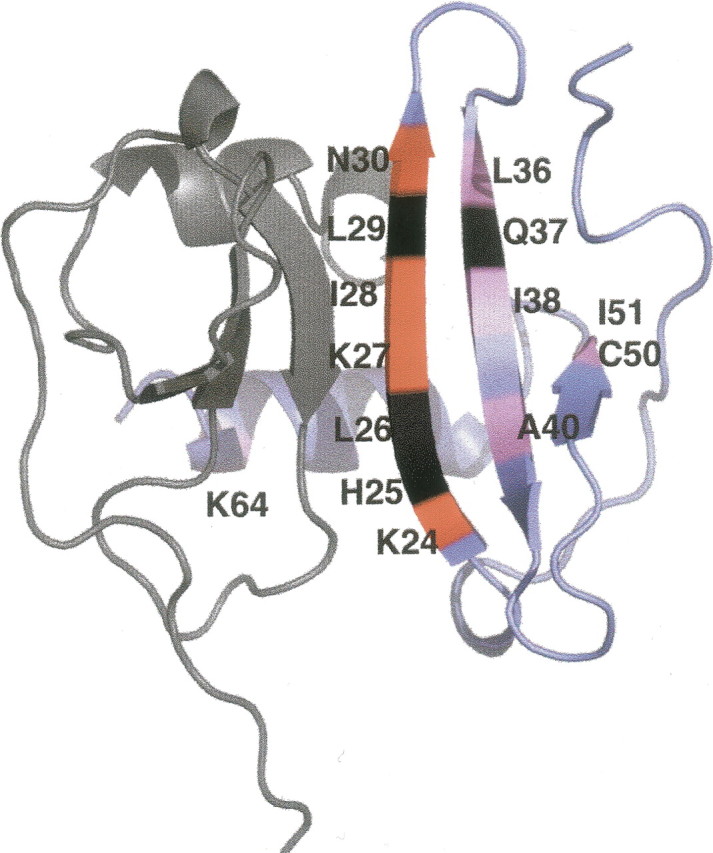
Figure 9.

Open in a new tab

Mapping of the residues requiring Rex terms on the structure of SDF-1α dimer. The structure of dimeric SDF-1α is taken from Ohnishi et al. (2000) (PDB code 1QG7). The two monomers are shown in gray and blue, with the residues suspected to undergo chemical exchange indicated with labels on the blue monomer. Regions colored in red are directly involved in formation of dimer. Regions colored in pink may be indirectly affected by the formation of a dimer. Residues in black are missing from the model free analysis due to line broadening or inadequate quality of the extrapolations.

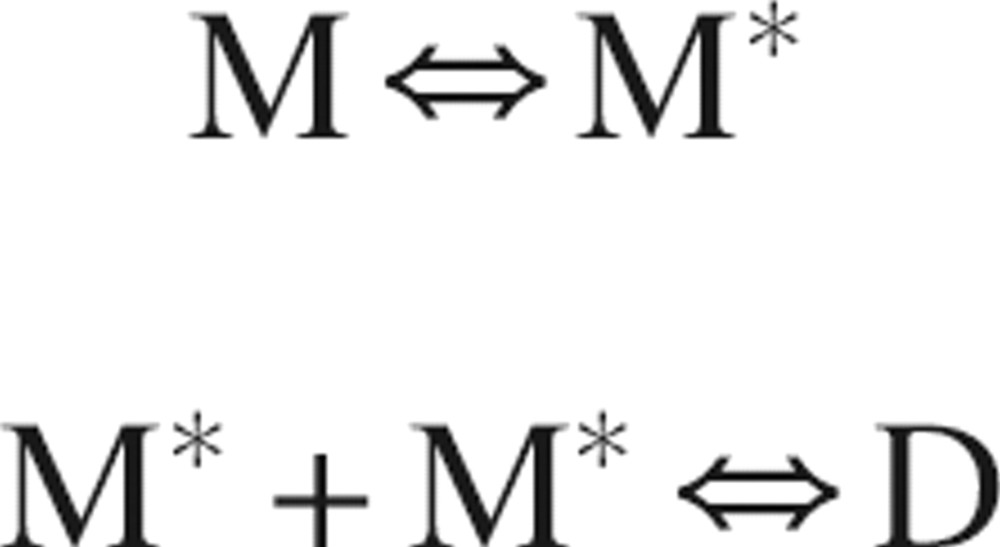graphic file with name 2568equ10.jpg

where M represents a conformation of the monomer less prone to dimerization, M* a conformation more prone to dimerization, and D the dimer. Such a mechanism would help explain the apparent discrepancies in the solution structures of SDF-1α determined by NMR. The NMR structure determined by Gozansky et al. (2005) is similar to dimeric structures determined using X-ray crystallography (Dealwis et al. 1998; Ohnishi et al. 2000) and would represent the species M*, whereas the Crump et al. (1997) structure would represent the species M. The phosphate buffer used by Gozansky et al. (2005) is expected to favor dimerization as compared to the acetate buffer used by Crump et al. (1997) (Veldkamp et al. 2005).

Comparison with other chemokines and implications for receptor interaction

Chemokines were found to undergo dimerization using two major subclasses of binding modes. The first group dimerizes in a fashion similar to IL-8, utilizing residues on the first β strand to establish the dimer interface, and the second group dimerizes similar to vMIP-I, utilizing residues from N-terminal loops (Luz et al. 2005). It would be interesting to compare the parameters obtained from relaxation measurements, especially Rex terms, with respect to the different dimerization modes utilized by chemokines. In the case of IL-8, which exists predominantly in dimeric form, the existence of monomer–dimer equilibrium resulted in line broadening in regions of residues that make intersubunit contacts, even if the concentration of a monomer was negligible (Grasberger et al. 1993). In the case of eotaxin, eotaxin-2, and eotaxin-3 (Crump et al. 1999; Ye et al. 2001; Mayer and Stone 2003), information regarding the dimer interface is lacking, and, therefore, Rex terms cannot be ascribed to self-association. For the chemokine fractalkine, residues involved in crystal packing and those with Rex terms are partially overlapped (Mizoue et al. 1999). These studies suggest a correlation between oligomerization behavior of proteins and the requirement for Rex terms to account for the relaxation data, but thorough studies of the concentration dependence of relaxation measurements are needed.

The biological relevance of chemokine oligomerization may differ among the various members of the chemokine family that includes more than 60 members with a broad range of dissociation constants and oligomerization conditions. The dependence of SDF-1α dimerization on pH and buffer composition was studied recently by Veldkamp et al. (2005). SDF-1α, with a physiological concentration of 25–50 ng/mL (Liao et al. 2005) and a dimerization constant from ∼150 μM in PBS buffer (Holmes et al. 2001) to ∼5 mM in acetate buffer (this study), is unlikely to dimerize under physiological conditions. However, high ionic strength and interactions between SDF-1α and glycosaminoglycans at the cell surface can increase the fraction of dimeric SDF-1α. Therefore, it is reasonable to expect that SDF-1α in vivo can function both as a monomer and as a dimer under certain conditions. The intrinsic ability of SDF-1α to dimerize and the interplay with the cell surface environment may play a role in modulating the interaction of SDF-1α with its cognate receptor.

Conclusions

In this study, we have obtained extensive 15N backbone amide relaxation data for SDF-1α, and the dependence on concentration using solution state NMR spectroscopy. The relaxation measurements identified flexible regions of the protein (the N and C termini) and regions that undergo chemical exchange. The N terminus is flexible up to residue 9, where it is constrained by a disulfide bond. This N-terminal region was previously suggested to be involved in the interaction with the receptor. Thus, motional restriction of this particular area might be biologically relevant by decreasing the entropic cost of receptor binding. The β-sheet region of SDF-1α demonstrated significant line broadening, likely as a result of chemical exchange between monomer and dimer. The relaxation measurements were used to calculate a dimer dissociation constant of 5 ± 1 mM. For the model free analysis, protein dimerization was found to have a negligible effect on the generalized order parameters. Additionally, the number of residues requiring an Rex term to fit relaxation data, and the magnitude of the Rex terms, decreased with a decrease in the fraction of dimer. For the extrapolated case, in the absence of monomer–dimer exchange, residues requiring an Rex term map to the first and second β strands and to the C-terminal helix, which are directly and indirectly involved in formation of the dimer interface. The presence of Rex terms for the extrapolated case indicates the existence of conformational exchange within monomeric species and helps rationalize the apparent discrepancies between NMR structures done under different solution conditions, clearly indicating the importance of knowledge of the degree of oligomerization in the calculation of solution structures.

Materials and methods

Protein expression and purification

The DNA encoding human SDF-1α (residue 1–67) was purchased from InvivoGen and subcloned into the pET-3a expression vector from Novagen. Escherichia coli strain BL21(DE3)pLysS was transformed with the expression vector and incubated at 37°C to an OD600 of 0.6–0.8. Cell cultures were induced with IPTG to a final concentration of 1 mM and harvested after 3 h. Uniformly 15N-labeled SDF-1α was expressed similarly in a minimal media enriched with 15N ammonium sulfate (Li et al. 2002). The cell pellet was lysed using a French press, centrifuged (10,000 rpm, 10 min), homogenized, and solubilized in 8 M urea buffer (50 mM Tris at pH 8.0). The homogenate was centrifuged again to remove cell walls and membrane debris (18,000 rpm, 1 h), and applied to a cation exchange CM-Sepharose column (50 mM Tris at pH 8.0). The protein was refolded by overnight dialysis against 10 mM NH4HCO3, and the first methionine residue was cleaved with CNBr as described earlier (Smith 2003). The protein was purified on a size exclusion column (Superdex 75), dialyzed against 10 mM NH4HCO3, and lyophilized. The molecular weight determined by MALDI mass spectroscopy was equal to the expected value for SDF-1α (7831 ± 1 for reduced species). The amino acid composition of a recombinant protein was confirmed independently by the amino acid analysis. In order to test the biological activity of recombinant SDF-1α, a chemotaxis assay on mice spleenocytes was performed. Recombinant SDF-1α demonstrated chemotactic responses similar to the commercially available control SDF-1α sample (data not shown).

Sample preparation

NMR samples were prepared in 500 μL of buffer containing 20 mM CD3COONa, 1 mM NaN3, and 1 mM DSS in 90% H2O/10% D2O. The pH was adjusted to 4.9. The two most concentrated samples were prepared by dissolving the lyophilized powder of recombinant SDF-1α. The rest of the samples were serially diluted from the sample containing 1.5 mM of SDF-1α, where the concentration was verified by amino acid analysis. The concentrations of recombinant SDF-1α analyzed in this work were equal to 2.6, 1.5, 0.9, 0.5, 0.3, and 0.1 mM.

NMR spectroscopy (data acquisition and processing)

All NMR data were acquired at 30°C on a Varian Inova 500 MHz spectrometer and a Varian Unity 600 MHz spectrometer equipped with Z-axis pulsed field gradient triple resonance probes. In order to assign the backbone and side chain 1H and 15N chemical shifts, 3D NOESY-HSQC, 3D TOCSY-HSQC, and 2D 1H–15N HSQC were acquired at 500 MHz for 1.5 mM SDF-1α. The assigned 1H chemical shifts were in agreement with the previously reported assignments (Crump et al. 1997). The relaxation data were obtained from 15N-T1, 15N-T2, and 1H–15N NOE experiments conducted at 500 and 600 MHz for samples containing 2.6, 1.5, 0.8, 0.5, and 0.3 mM SDF-1α. At 500 and 600 MHz, T1 data were acquired using relaxation delays of 10, 50, 100, 200, 300, and 400 msec, and T2 data were acquired using relaxation delays equal to 10, 30, 50, 70, 90, and 110 msec. The delays between transients in T1 and T2 experiments were set to 3.5 sec for 600 MHz and 2.5 sec and 3.5 sec in T1 and T2 experiments, respectively, for 500 MHz. A sufficiently long delay between transients was necessary to prevent the sample from heating as previously shown (Gagne et al. 1998). 1H–15N NOE experiments were conducted using delays of 5 sec for spectra recorded without proton saturation at both fields and delays of 2 sec for spectra recorded with proton saturation. The proton saturation time was equal to 3 sec and the total time between acquisitions was equal to 5 sec. In addition, to follow the chemical shift changes as a function of SDF-1α concentration, 1D 1H spectra and 2D 1H–15N HSQC spectra were acquired for every sample including the most diluted sample containing 0.1 mM SDF-1α. Processing of NMR data was accomplished with NMRPipe software. Relaxation parameters T1 and T2 were obtained using NMRview and were in agreement with T1 and T2 values calculated using Mathematica scripts provided by Leo Spyracopoulos (Department of Biochemistry, University of Alberta, Canada). The quality of the fits was reflected in the calculated uncertainties. An in-house written script (Pascal Mercier) was used to extract per residue values of 1H–15N NOEs from NMRview.

Acknowledgments

We thank Angela Thiessen and David Corson for valuable help with protein cloning, expression, and purification; Jason Couglin for his kind help with chemotaxis assay; Jeff DeVries for maintenance of spectrometers; Dr. Pascal Mercier for stimulating discussions; and Dr. Brian F. Volkman, Dr. Steffen P. Graether, and especially Dr. Leo Spyracopoulos for critical reading of the manuscript and valuable comments. The scripts for model free analysis were kindly provided by Dr. Leo Spyracopoulos (available at www.bionmr.ualberta.ca/~lspy/index_7.html). This work was supported by the Protein Engineering Network of Centres of Excellence (PENCE) and Alberta Heritage Foundation for Medical Research scholarship.

Footnotes

Reprint requests to: Brian D. Sykes, Department of Biochemistry and Protein Engineering Network of Centres of Excellence, University of Alberta, 713 Heritage Medical Research Centre, Edmonton, Alberta T6G 2S2, Canada; e-mail: brian.sykes@ualberta.ca; fax: (780) 492-0886.

References

  1. Baggiolini, M. 1998. Chemokines and leukocyte traffic. Nature 392 565–568. [DOI] [PubMed] [Google Scholar]
  2. Baldo, J.H., Halford, S.E., Patt, S.L., and Sykes, B.D. 1975. The stepwise binding of small molecules to proteins. Nuclear magnetic resonance and temperature jump studies of the binding of 4-(N-acetylaminoglucosyl)-N-acetylglucosamine to lysozyme. Biochemistry 14 1893–1899. [DOI] [PubMed] [Google Scholar]
  3. Baryshnikova, O.K., Rainey, J.K., and Sykes, B.D. 2005. Nuclear magnetic resonance studies of CXC chemokine receptor 4 allosteric peptide agonists in solution. J. Pept. Res. 66 12–21.16650056 [Google Scholar]
  4. Berson, J.F., Long, D., Doranz, B.J., Rucker, J., Jirik, F.R., and Doms, R.W. 1996. A seven-transmembrane domain receptor involved in fusion and entry of T-cell-tropic human immunodeficiency virus type 1 strains. J. Virol. 70 6288–6295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Clore, G.M., Szabo, A., Bax, A., Kay, L.E., Driscoll, P.C., and Gronenborn, A.M. 1990. Deviations from the simple 2-parameter model-free approach to the interpretation of 15N nuclear magnetic-relaxation of proteins. J. Am. Chem. Soc. 112 4989–4991. [Google Scholar]
  6. Cooper, C.R., Chay, C.H., Gendernalik, J.D., Lee, H.L., Bhatia, J., Taichman, R.S., McCauley, L.K., Keller, E.T., and Pienta, K.J. 2003. Stromal factors involved in prostate carcinoma metastasis to bone. Cancer (3 Suppl): 97 739–747. [DOI] [PubMed] [Google Scholar]
  7. Crump, M.P., Gong, J.H., Loetscher, P., Rajarathnam, K., Amara, A., Arenzana-Seisdedos, F., Virelizier, J.L., Baggiolini, M., Sykes, B.D., and Clark-Lewis, I. 1997. Solution structure and basis for functional activity of stromal cell-derived factor-1; dissociation of CXCR4 activation from binding and inhibition of HIV-1. EMBO J. 16 6996–7007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Crump, M.P., Spyracopoulos, L., Lavigne, P., Kim, K.S., Clark-lewis, I., and Sykes, B.D. 1999. Backbone dynamics of the human CC chemokine eotaxin: Fast motions, slow motions, and implications for receptor binding. Protein Sci. 8 2041–2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Dealwis, C., Fernandez, E.J., Thompson, D.A., Simon, R.J., Siani, M.A., and Lolis, E. 1998. Crystal structure of chemically synthesized [N33A] stromal cell-derived factor 1α, a potent ligand for the HIV-1 “fusin” coreceptor. Proc. Natl. Acad. Sci. 95 6941–6946. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Epstein, R.J. 2004. The CXCL12-CXCR4 chemotactic pathway as a target of adjuvant breast cancer therapies. Nat. Rev. Cancer 4 901–909. [DOI] [PubMed] [Google Scholar]
  11. Fernandez, E.J. and Lolis, E. 2002. Structure, function, and inhibition of chemokines. Annu. Rev. Pharmacol. Toxicol. 42 469–499. [DOI] [PubMed] [Google Scholar]
  12. Fushman, D., Cahill, S., and Cowburn, D. 1997. The main-chain dynamics of the dynamin pleckstrin homology (PH) domain in solution: Analysis of 15N relaxation with monomer/dimer equilibration. J. Mol. Biol. 266 173–194. [DOI] [PubMed] [Google Scholar]
  13. Gagne, S.M., Tsuda, S., Spyracopoulos, L., Kay, L.E., and Sykes, B.D. 1998. Backbone and methyl dynamics of the regulatory domain of troponin C: Anisotropic rotational diffusion and contribution of conformational entropy to calcium affinity. J. Mol. Biol. 278 667–686. [DOI] [PubMed] [Google Scholar]
  14. Godiska, R., Chantry, D., Dietsch, G.N., and Gray, P.W. 1995. Chemokine expression in murine experimental allergic encephalomyelitis. J. Neuroimmunol. 58 167–176. [DOI] [PubMed] [Google Scholar]
  15. Goodman, J.L., Pagel, M.D., and Stone, M.J. 2000. Relationships between protein structure and dynamics from a database of NMR-derived backbone order parameters. J. Mol. Biol. 295 963–978. [DOI] [PubMed] [Google Scholar]
  16. Gozansky, E.K., Louis, J.M., Caffrey, M., and Clore, G.M. 2005. Mapping the binding of the N-terminal extracellular tail of the CXCR4 receptor to stromal cell-derived factor-1α. J. Mol. Biol. 345 651–658. [DOI] [PubMed] [Google Scholar]
  17. Grasberger, B.L., Gronenborn, A.M., and Clore, G.M. 1993. Analysis of the backbone dynamics of interleukin-8 by 15N relaxation measurements. J. Mol. Biol. 230 364–372. [DOI] [PubMed] [Google Scholar]
  18. Gryk, M.R., Abseher, R., Simon, B., Nilges, M., and Oschkinat, H. 1998. Heteronuclear relaxation study of the PH domain of β-spectrin: Restriction of loop motions upon binding inositol trisphosphate. J. Mol. Biol. 280 879–896. [DOI] [PubMed] [Google Scholar]
  19. Grzesiek, S., Bax, A., Hu, J.S., Kaufman, J., Palmer, I., Stahl, S.J., Tjandra, N., and Wingfield, P.T. 1997. Refined solution structure and backbone dynamics of HIV-1 Nef. Protein Sci. 6 1248–1263. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Holmes, W.D., Consler, T.G., Dallas, W.S., Rocque, W.J., and Willard, D.H. 2001. Solution studies of recombinant human stromal-cell-derived factor-1. Protein Expr. Purif. 21 367–377. [DOI] [PubMed] [Google Scholar]
  21. Ishima, R. and Torchia, D.A. 2000. Protein dynamics from NMR. Nat. Struct. Biol. 7 740–743. [DOI] [PubMed] [Google Scholar]
  22. Korchuganov, D.S., Nolde, S.B., Reibarkh, M.Y., Orekhov, V.Y., Schulga, A.A., Ermolyuk, Y.S., Kirpichnikov, M.P., and Arseniev, A.S. 2001. NMR study of monomer–dimer equilibrium of barstar in solution. J. Am. Chem. Soc. 123 2068–2069. [DOI] [PubMed] [Google Scholar]
  23. Kunkel, S.L. and Godessart, N. 2002. Chemokines in autoimmunity: From pathology to therapeutics. Autoimmun. Rev. 1 313–320. [DOI] [PubMed] [Google Scholar]
  24. Kuschert, G.S., Coulin, F., Power, C.A., Proudfoot, A.E., Hubbard, R.E., Hoogewerf, A.J., and Wells, T.N. 1999. Glycosaminoglycans interact selectively with chemokines and modulate receptor binding and cellular responses. Biochemistry 38 12959–12968. [DOI] [PubMed] [Google Scholar]
  25. Li, M.X., Corson, D.C., and Sykes, B.D. 2002. Structure determination by NMR. Isotope labeling. Methods Mol. Biol. 173 255–265. [DOI] [PubMed] [Google Scholar]
  26. Liao, T.S., Yurgelun, M.B., Chang, S.S., Zhang, H.Z., Murakami, K., Blaine, T.A., Parisien, M.V., Kim, W., Winchester, R.J., and Lee, F.Y. 2005. Recruitment of osteoclast precursors by stromal cell derived factor-1 (SDF-1) in giant cell tumor of bone. J. Orthop. Res. 23 203–209. [DOI] [PubMed] [Google Scholar]
  27. Lipari, G. and Szabo, A. 1982a. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 104 4546–4559. [Google Scholar]
  28. Lipari, G. and Szabo, A. 1982b. Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 104 4559–4570. [Google Scholar]
  29. Luz, Z. and Meiboom, S. 1963. Nuclear magnetic resonance study of protolysis of trimethylammonium ion in aqueous solution—Order of reaction with respect to solvent. J. Chem. Phys. 39 366. [Google Scholar]
  30. Luz, J.G., Yu, M., Su, Y., Wu, Z., Zhou, Z., Sun, R., and Wilson, I.A. 2005. Crystal structure of viral macrophage inflammatory protein I encoded by Kaposi's Sarcoma-associated herpesvirus at 1.7 Å. J. Mol. Biol. 352 1019–1028. [DOI] [PubMed] [Google Scholar]
  31. Mammen, M., Choi, S.K., and Whitesides, G.M. 1998. Polyvalent interactions in biological systems: Implications for design and use of multivalent ligands and inhibitors. Angew. Chem. Int. Ed. 37 2754–2794. [DOI] [PubMed] [Google Scholar]
  32. Mayer, K.L. and Stone, M.J. 2003. Backbone dynamics of the CC-chemokine eotaxin-2 and comparison among the eotaxin group chemokines. Proteins 50 184–191. [DOI] [PubMed] [Google Scholar]
  33. Mercier, P., Spyracopoulos, L., and Sykes, B.D. 2001. Structure, dynamics, and thermodynamics of the structural domain of troponin C in complex with the regulatory peptide 1–40 of troponin I. Biochemistry 40 10063–10077. [DOI] [PubMed] [Google Scholar]
  34. Mizoue, L.S., Bazan, J.F., Johnson, E.C., and Handel, T.M. 1999. Solution structure and dynamics of the CX3C chemokine domain of fractalkine and its interaction with an N-terminal fragment of CX3CR1. Biochemistry 38 1402–1414. [DOI] [PubMed] [Google Scholar]
  35. Muller, A., Homey, B., Soto, H., Ge, N., Catron, D., Buchanan, M.E., McClanahan, T., Murphy, E., Yuan, W., and Wagner, S.N., et al. 2001. Involvement of chemokine receptors in breast cancer metastasis. Nature 410 50–56. [DOI] [PubMed] [Google Scholar]
  36. Murphy, P.M. 2001. Chemokines and the molecular basis of cancer metastasis. N. Engl. J. Med. 345 833–835. [DOI] [PubMed] [Google Scholar]
  37. Ohnishi, Y., Senda, T., Nandhagopal, N., Sugimoto, K., Shioda, T., Nagal, Y., and Mitsui, Y. 2000. Crystal structure of recombinant native SDF-1α with additional mutagenesis studies: An attempt at a more comprehensive interpretation of accumulated structure–activity relationship data. J. Interferon Cytokine Res. 20 691–700. [DOI] [PubMed] [Google Scholar]
  38. Pfuhl, M., Chen, H.A., Kristensen, S.M., and Driscoll, P.C. 1999. NMR exchange broadening arising from specific low affinity protein self-association: Analysis of nitrogen-15 nuclear relaxation for rat CD2 domain 1. J. Biomol. NMR 14 307–320. [DOI] [PubMed] [Google Scholar]
  39. Phillips, R.J., Burdick, M.D., Lutz, M., Belperio, J.A., Keane, M.P., and Strieter, R.M. 2003. The stromal derived factor-1/CXCL12-CXC chemokine receptor 4 biological axis in non-small cell lung cancer metastases. Am. J. Respir. Crit. Care Med. 167 1676–1686. [DOI] [PubMed] [Google Scholar]
  40. Proudfoot, A.E., Handel, T.M., Johnson, Z., Lau, E.K., LiWang, P., Clark-Lewis, I., Borlat, F., Wells, T.N., and Kosco-Vilbois, M.H. 2003. Glycosaminoglycan binding and oligomerization are essential for the in vivo activity of certain chemokines. Proc. Natl. Acad. Sci. 100 1885–1890. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Rajarathnam, K., Sykes, B.D., Kay, C.M., Dewald, B., Geiser, T., Baggiolini, M., and Clark-Lewis, I. 1994. Neutrophil activation by monomeric interleukin-8. Science 264 90–92. [DOI] [PubMed] [Google Scholar]
  42. Rubin, J.B., Kung, A.L., Klein, R.S., Chan, J.A., Sun, Y., Schmidt, K., Kieran, M.W., Luster, A.D., and Segal, R.A. 2003. A small-molecule antagonist of CXCR4 inhibits intracranial growth of primary brain tumors. Proc. Natl. Acad. Sci. 100 13513–13518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Schurr, J.M., Babcock, H.P., and Fujimoto, B.S. 1994. A test of the model-free formulas. Effects of anisotropic rotational diffusion and dimerization. J. Magn. Reson. B. 105 211–224. [DOI] [PubMed] [Google Scholar]
  44. Smith, B.J. 2003. Chemical cleavage of polypeptides. Methods Mol. Biol. 211 63–82. [DOI] [PubMed] [Google Scholar]
  45. Spyracopoulos, L. and Sykes, B.D. 2001. Thermodynamic insights into proteins from NMR spin relaxation studies. Curr. Opin. Struct. Biol. 11 555–559. [DOI] [PubMed] [Google Scholar]
  46. Spyracopoulos, L., Lavigne, P., Crump, M.P., Gagne, S.M., Kay, C.M., and Sykes, B.D. 2001. Temperature dependence of dynamics and thermodynamics of the regulatory domain of human cardiac troponin C. Biochemistry 40 12541–12551. [DOI] [PubMed] [Google Scholar]
  47. Tachibana, K., Hirota, S., Iizasa, H., Yoshida, H., Kawabata, K., Kataoka, Y., Kitamura, Y., Matsushima, K., Yoshida, N., and Nishikawa, S., et al. 1998. The chemokine receptor CXCR4 is essential for vascularization of the gastrointestinal tract. Nature 393 591–594. [DOI] [PubMed] [Google Scholar]
  48. Veldkamp, C.T., Peterson, F.C., Pelzek, A.J., and Volkman, B.F. 2005. The monomer–dimer equilibrium of stromal cell-derived factor-1 (CXCL 12) is altered by pH, phosphate, sulfate, and heparin. Protein Sci. 14 1071–1081. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Ye, J., Mayer, K.L., Mayer, M.R., and Stone, M.J. 2001. NMR solution structure and backbone dynamics of the CC chemokine eotaxin-3. Biochemistry 40 7820–7831. [DOI] [PubMed] [Google Scholar]
  50. Zhang, O., Kay, L.E., Olivier, J.P., and Forman-Kay, J.D. 1994. Backbone 1H and 15N resonance assignments of the N-terminal SH3 domain of drk in folded and unfolded states using enhanced-sensitivity pulsed field gradient NMR techniques. J. Biomol. NMR 4 845–858. [DOI] [PubMed] [Google Scholar]
  51. Zou, Y.R., Kottmann, A.H., Kuroda, M., Taniuchi, I., and Littman, D.R. 1998. Function of the chemokine receptor CXCR4 in haematopoiesis and in cerebellar development. Nature 393 595–599. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES