Force field influences in β-hairpin folding simulations

Abstract

All-atom force fields are now routinely used for more detailed understanding of protein folding mechanisms. However, it has been pointed out that use of all-atom force fields does not guarantee more accurate representations of proteins; in fact, sometimes it even leads to biased structural distributions. Indeed, several issues remain to be solved in force field developments, such as accurate treatment of implicit solvation for efficient conformational sampling and proper treatment of backbone interactions for secondary structure propensities. In this study, we first investigate the quality of several recently improved backbone interaction schemes in AMBER for folding simulations of a β-hairpin peptide, and further study their influences on the peptide's folding mechanism. Due to the significant number of simulations needed for a thorough analysis of tested force fields, the implicit Poisson-Boltzmann solvent was used in all simulations. The chosen implicit solvent was found to be reasonable for studies of secondary structures based on a set of simulations of both α-helical and β-hairpin peptides with the TIP3P explicit solvent as benchmark. Replica exchange molecular dynamics was also utilized for further efficient conformational sampling. Among the tested AMBER force fields, ff03 and a revised ff99 force field were found to produce structural and thermodynamic data in comparably good agreement with the experiment. However, detailed folding pathways, such as the order of backbone hydrogen bond zipping and the existence of intermediate states, are different between the two force fields, leading to force field–dependent folding mechanisms.

Classical molecular mechanics energy models, usually termed force fields, are widely used in molecular dynamics simulations of biomolecules. Apparently, the accuracy of such energy models crucially depends on the parameters that are empirically fitted to high-level quantum mechanical (QM) calculations and to experimental data of small organic molecules. While molecular mechanics force fields have been improved over time, there are few issues that remain to be solved. Related to protein folding simulations, these issues include the accurate treatment of implicit solvation that is commonly used for efficient conformational sampling and the accurate modeling of backbone interactions that is crucial for secondary structure propensities. These issues are important if one wishes to obtain insights into the protein folding mechanisms and to predict protein structures. In this study, we focus on proper modeling of secondary structures with force fields distributed in the AMBER 8 release (Case et al. 2004) and study their influences on the structural and thermodynamic properties of a test system. A brief review on AMBER force fields is first presented below.

The first-generation force field in AMBER, ff86, was developed by Weiner et al. (1986), and was intended for simulations of proteins and nucleic acids. While ff86 was found to have considerable success (Hall and Pavitt 1984; Nilsson and Karplus 1986), it was mostly used in a simple-minded distance-dependent dielectric treatment of solvation screening (Seibel et al. 1985; Singh et al. 1985; Tilton et al. 1986; Guenot and Kollman 1992). As computing power increased, so did the need to develop parameters for more realistic simulations of biomolecules in explicit solvents. Cornell et al. (1995) published the second generation AMBER force field, ff94. ff94 is a complete revision to ff86 while mostly maintaining the same functional form, but without explicit hydrogen bonding terms (Cornell et al. 1995). Bond and angle parameters were refitted to reproduce experimental normal mode frequencies. In charge derivation, HF/6–31G* was used instead of HF/STO-3G. Restrained electrostatic potential fit, RESP, was also introduced in the charge fitting process (Bayly et al. 1993). The 1–4 electrostatic scaling factor was also changed from 1/2 to 1/1.2 (Bayly et al. 1993). New van der Waals parameters were optimized to reproduce liquid-state properties. The 1–4 van der Waals scaling factor of 1/2 was retained. Based on the MP2/6–31G* ab initio model, side chain torsion parameters were refitted. ff94 is the first force field in AMBER that contains nonzero backbone torsion (ϕ/ψ) terms. In ff86, these terms were set to zero. While ff94 does a reasonable job in describing intermolecular interactions, it has not been widely parameterized to reproduce the relative conformational energy of a large number of organic systems (Wang et al. 2000).

Therefore, Wang et al. (2000) introduced a partial revision to ff94 (ff99), which was aimed at small organic molecules. New atom types and generic and specific torsion parameters were introduced, based on available experimental data and high-level QM computational data. Backbone torsion terms were also modified again to reduce the error obtained with ff94. This time, torsion refitting was performed with an automatic procedure, PARMSCAN (Wang et al. 2000). A few equilibrium bond angles and bond lengths were also modified. However, ff99 has been reported to give imbalance between the protein backbone secondary structures (Garcia and Sanbonmatsu 2002; Zhou 2003). In deriving ff99, one of the two hypotheses (Wang et al. 2000) was that if one could fit the nonbonded parameters (for example atomic charges) correctly, the need to fit dihedral terms would be reduced. This turns out not to be true; as will be discussed below, that accurate fitting to the dihedral term is a necessary step in force field development. Interestingly, Garcia and Sanbonmatsu (2002) reported that turning off backbone torsion terms in ff94 (i.e., the ff86 approach) dramatically improved the thermodynamic folding properties of alanine-based peptides. Following their approach, we consider turning off the backbone torsion term in ff99 as a separate revision to the ff99 force field and name this approach as ff99off. Using ff99off as a reference, we plan to study whether there is any improvement in applying more elaborate revisions to ff99.

To improve the balance of secondary structure propensities, two modifications to ff99 were developed, namely ff99m1 (Simmerling et al. 2002) and ff99m2 (J. Wang and R. Luo, in prep.). These force fields tried to modify the ϕ/ψ torsion parameters with respect to MP2/cc-pVTZ//HF/6–31G* potential energies of seven low-energy conformations of alanine dipeptide (Wang et al. 2000) and 11 low-energy conformations of alanine tetrapeptide (Beachy et al. 1997). ff99m1 has been documented in literature (Simmerling et al. 2002) and is reported to fold the Trp-cage miniprotein (Simmerling et al. 2002). ff99m2 has been documented in the AMBER 8 release (Case et al. 2004), but no application has been reported. In the development of ff99m2, PARMSCAN (Wang et al. 2000) was used to minimize the root-mean-squared deviation (RMSD) between MP2/cc-pVTZ//HF/6–31G* and ff99m2 potential energies for the seven dipeptide and 11 tetrapeptide conformations mentioned above (Beachy et al. 1997; Wang et al. 2000). After optimization, the best five parameter sets with RMSDs <1.0 kcal/mol were selected for further analysis. The final parameter set was chosen as the one with smallest torsional barriers, based on the principle that the torsional perturbation should be as small as possible. The optimized ff99m2 parameter set agrees with QM excellently: the RMSD of the 18 training potential energies is 0.79 kcal/mol, and the average unsigned deviation is 0.59 kcal/mol (J. Wang and R. Luo, in prep.). ff99ci is the third modification to ff99 in which only the backbone torsion parameters are treated differently from ff99m1 and ff99m2. The parameters are obtained by bicubic spline fitting (Mackerell et al. 2004) to the MP2/cc-pVTZ//HF/6–31G* potential energy surface over ϕ/ψ of alanine dipeptide only.

The third-generation AMBER force field, ff03, was developed by Duan et al. (2003). In ff03, both atomic partial charges and ϕ/ψ torsion parameters were revised. The charge fitting was based on the B3LYP/cc-pVTZ//HF/6–31G** method in an organic solvent to mimic the protein interior dielectric. Backbone torsion parameters were derived using the MP2/cc-pVTZ//HF/6–31G** potential energy surfaces of alanine and glycine dipeptide. Other parameters (bond, bond angle, side chain torsion, and van der Waals) were retained from ff99. ff03 was reported to be able to fold an alanine-based helical peptide, a β-sheet-forming peptide, and Trp-cage (Duan et al. 2003).

In this study, we first investigate the quality of six AMBER force fields, namely, ff94, ff99off, ff99m1, ff99m2, ff99ci, and ff03, for folding simulations of the well-studied β-hairpin peptide from the C-terminal region of protein G (Blanco et al. 1994; Fesinmeyer et al. 2004), and further study their influences on the peptide's folding mechanism. Due to the significant number of simulations needed for a thorough analysis of tested force fields, the implicit Poisson-Boltzmann (PB) solvent was used in all simulations. As shown in the Materials and Methods section below, the implicit Poisson-Boltzmann solvent was found to be reasonable for studies of secondary structures based on a set of simulations of both α-helical and β-hairpin peptides with the TIP3P explicit solvent as benchmark. Replica exchange molecular dynamics was also utilized for further efficient conformational sampling.

Results and Discussion

The trajectories obtained using all six force fields (ff94, ff99off, ff99m1, ff99m2, ff99ci, and ff03) are analyzed and discussed in three different categories: structural distribution, folding thermodynamics, and folding pathway. Simulated peptide structures are discussed in terms of nuclear Overhauser effect (NOE), native contact fraction, backbone RMSD, salt bridge content, and secondary structure propensity. Simulated thermodynamic properties are discussed in terms of temperature-dependent population of native structure and folding transition temperature. Lastly, simulated folding pathways are analyzed in terms of folding free energy landscape and order of backbone hydrogen bond formation. Structural analyses are performed in the 282 K trajectories that are closest to the experimental condition (See Materials and Methods, for the detail of replica exchange molecular dynamics). From this point on, we will refer to each analyzed data from each simulation simply by the name of the force field used in the simulation.

Structural distributions

NOE pairs

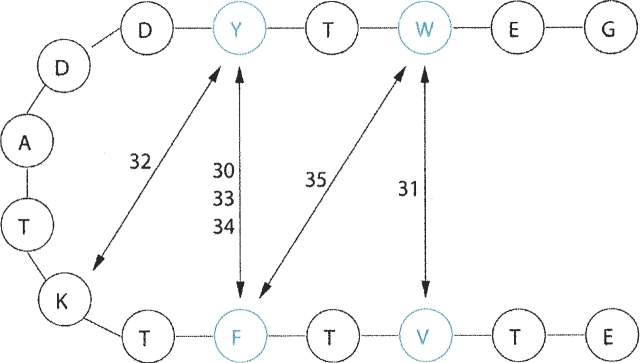
There are 35 NOE pairs reported for this peptide, though its solution structure cannot be resolved at atomic detail (Blanco et al. 1994). These pairs, listed in ▶, can be categorized into four groups, as shown in ▶. The first group (from pair 1 to 10) is for distances between hydrogens (N-H and CA-H) of the same residue. The second group (from pair 11 to 22) is for distances between CA-H of one residue and N-H of its neighboring residues. The third group (from pair 23 to 29) is for distances between N-Hs of two neighboring residues. The last group (pairs 30 to 35) includes various proton–proton couplings between interstrand hydrophobic residues, which describe the overall geometry of the peptide. Specifically, protons of Y45 interact with its hydrophobic counterpart F52 in three different ways (pairs 30, 33, and 34) and to K50 (pair 32). Protons of W43 interact with its hydrophobic counterpart V54 (pair 31) as well as to F52 (pair 35). Therefore pairs 30, 31, 33, 34, and 35 represent interactions between hydrophobic residues that make up the hydrophobic core, as described in ▶. The last group in ▶ is the most important of all for defining the peptide's tertiary structure. This is also the group where most disagreements between simulations and NMR occur.

Table 1.

NOE pairs measured in NMR experiment (Zhou and Berne 2002)

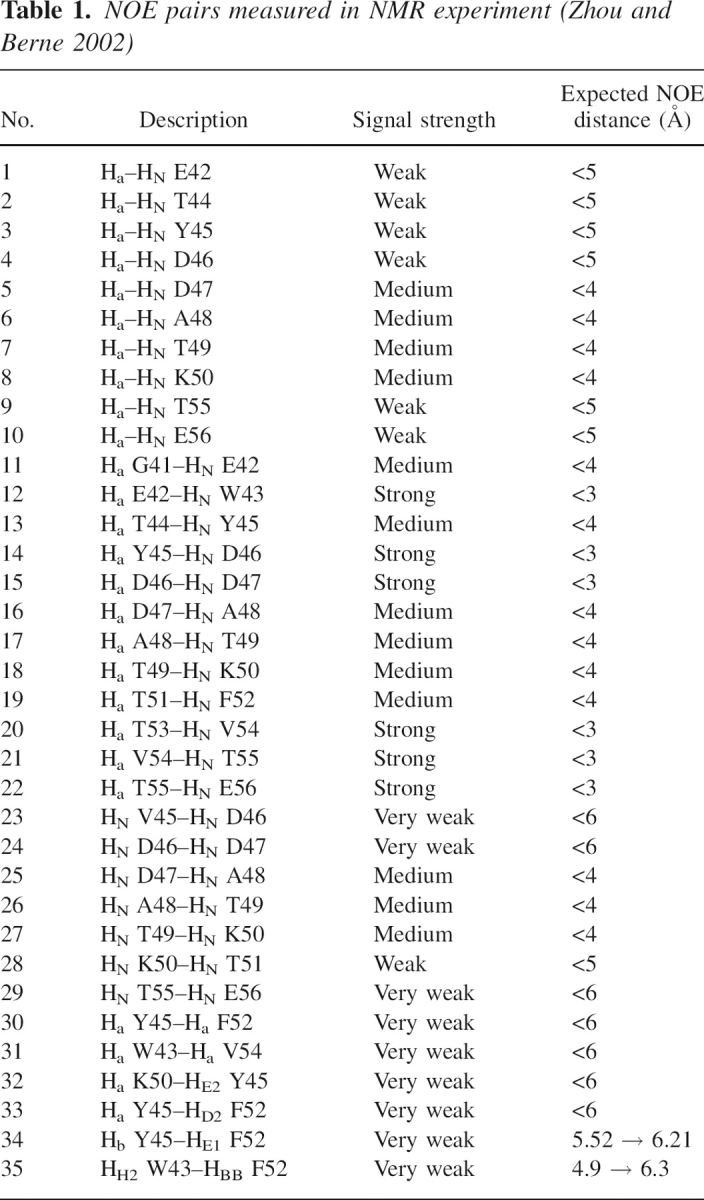
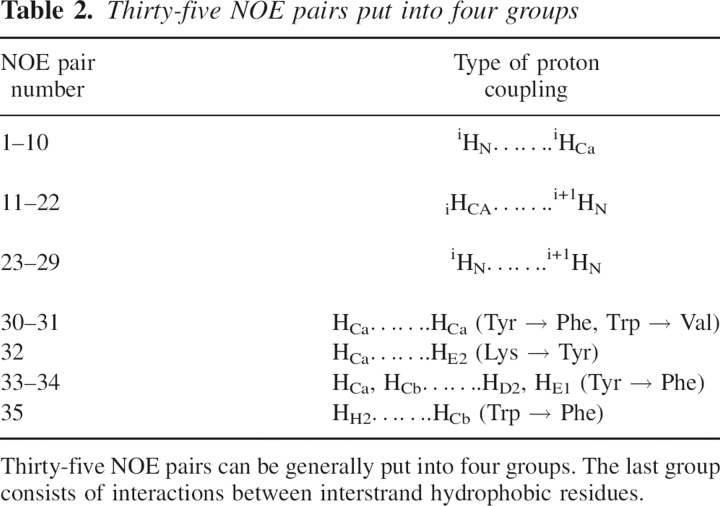
Table 2.

Thirty-five NOE pairs put into four groups

Figure 1.

The five most important NOE pairs in the β-hairpin peptide. Here, residues are shown simply as a string of beads. Hydrophobic residues are labeled in blue. The number close to the double-sided arrow represents the NOE pair number.

▶ shows computed NOEs from all six force fields. The coloring scheme of Pande and coworkers is followed (Zagrovic et al. 2001): green is for agreement with NMR, black for disagreement with NMR, and red for the likelihood of not observing in NMR. Calculated NOEs in ff94, ff99off, and ff99m1 have varying levels of disagreement with NMR. ff99m2 and ff03 agree with NMR all the way up to pair 33, but both suggest that pairs 34 and 35 should not be observed in NMR: in ff03, pair 34 has a distance of 7.06 ± 3.08 Å and pair 35 has a distance of 6.91 ± 3.66 Å; in ff99m2 the distances are 6.73 ± 3.81 Å and 6.47 ± 2.44 Å, respectively. Interestingly, ff99ci agrees with NMR for all pairs including the two last pairs, for which all other force fields fail to agree with NMR: pair 34 has a value of 6.01 ± 1.42 Å and pair 35 has a value of 5.83 ± 1.95 Å. These two pairs are estimated to be in the range of 5.52 to 6.21 Å and 4.9 to 6.3 Å, respectively, in NMR (Blanco et al. 1994).

Figure 2.

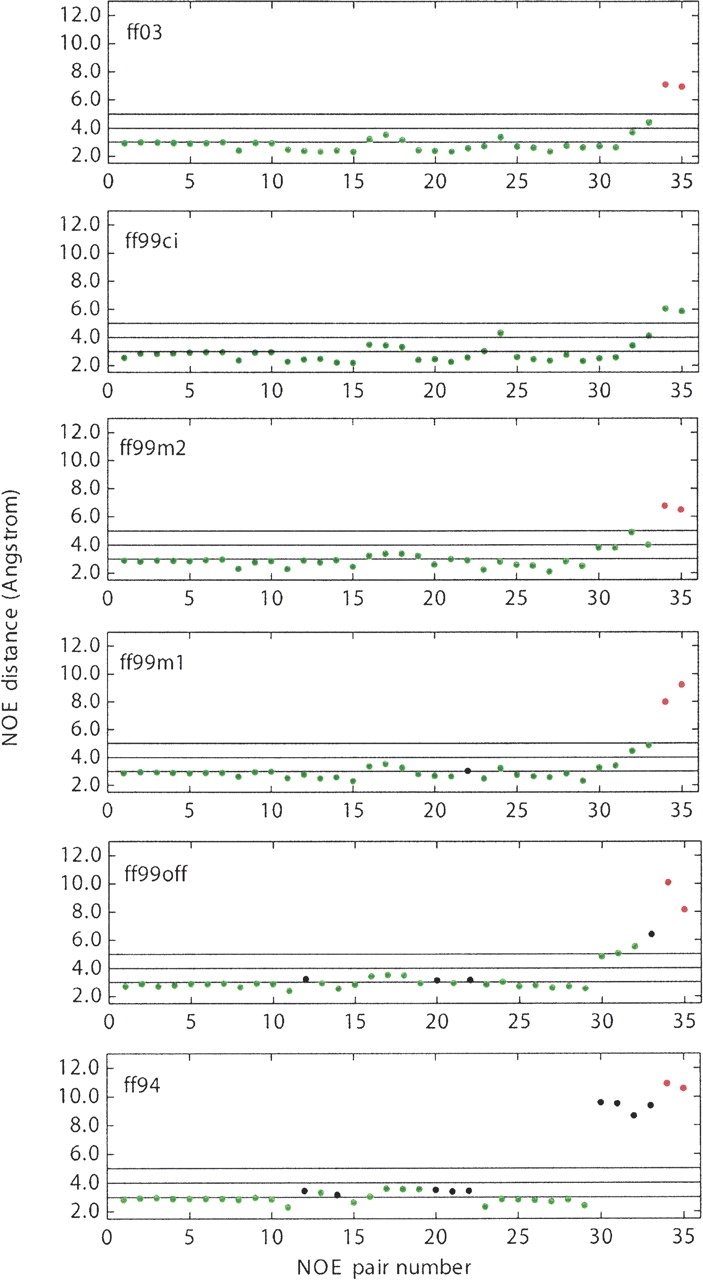
NOE distances for all six force fields at 282 K. (Blue) In agreement with experimentally reported NOE results; (black) not in agreement with reported NOE results; (red) not observable in experiment.

We found one interesting similarity between our PB simulation and Zhou's generalized Born (GB) simulation (Zhou 2003). In both our and Zhou's ff94 simulations, pairs 12, 14, 20, 21, and 22 are in disagreement with NMR. This suggests that the disagreement is more attributable to the force field than the solvation model. Since the difference among ff99ci, ff99m2, ff99m1, and ff99off is only in the backbone torsion parameters, the better agreement in later force fields indicates that backbone torsion parameters are important to obtaining correct secondary structures. Garcia and Sanbonmatsu (2002) also reported a similar effect in the study of a helical peptide using ff94, where the simulation with no backbone ϕ/ψ parameters gave the peptide's transition temperature much closer to experiment than ff94.

However, it should be pointed out that available NOE data are not specific enough to quantitatively define the solution structure in atomic detail. Indeed, it is necessary to combine other analyses together with NOE data to fully describe the influence of a force field on the secondary structure propensity. For example, in ▶, ff03 and ff99m2 show very similar NOEs, but give rise to completely different secondary structures from the following analyses.

Native contacts and backbone RMSD

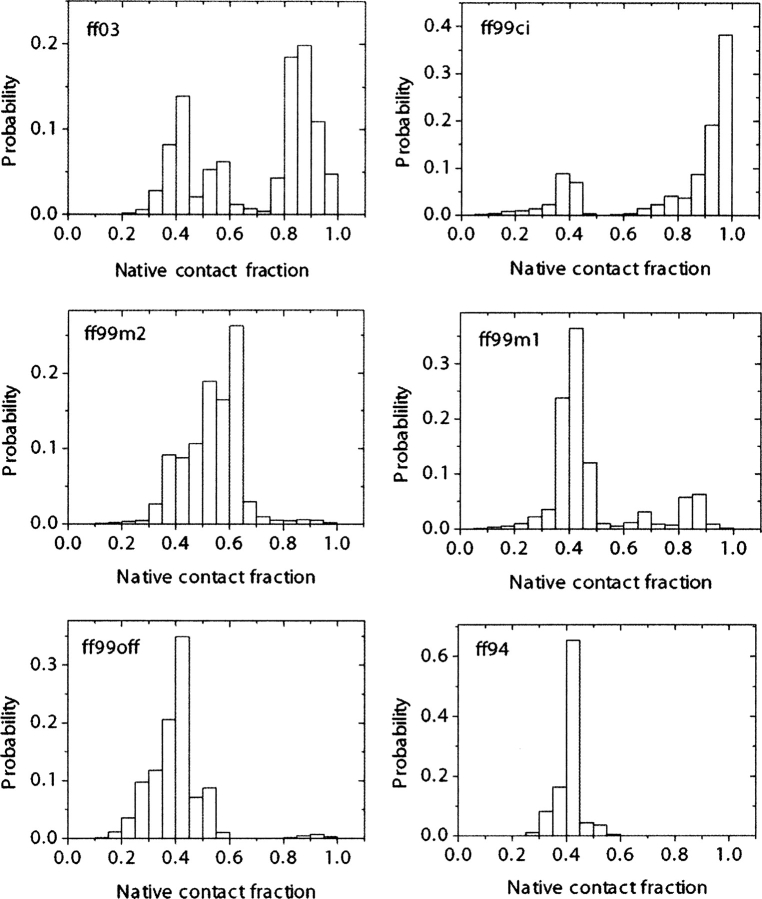
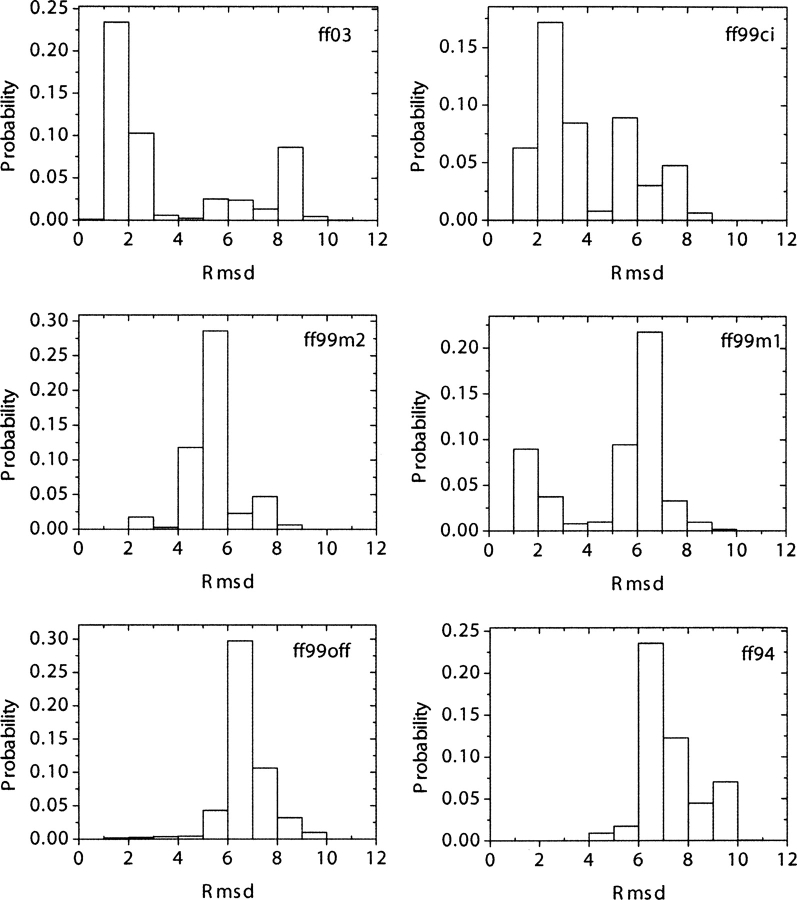
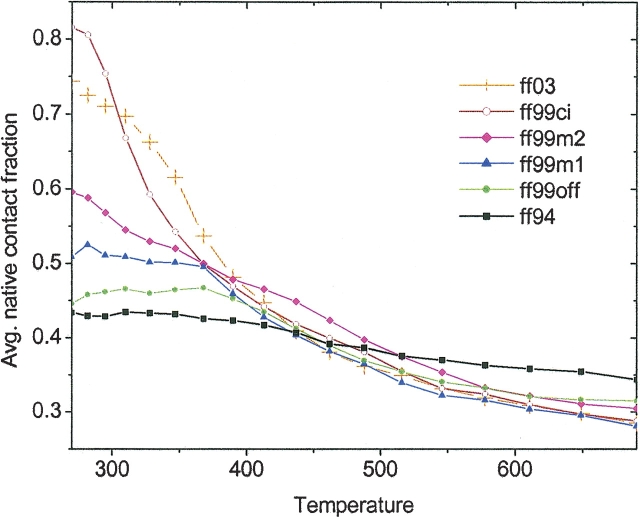
For each force field, native contact fraction and backbone RMSDs were calculated with the crystal structure as reference. As shown in ▶, the most populated state shows native contact fractions of 0.95–1.00 in ff99ci, 0.85–0.90 in ff03, 0.60–0.65 in ff99m2, and 0.40–0.45 in ff99m1, ff99off, and ff94. Simulation in ff99m1 does not show any sign of improvement over ff99off, as they both have a similar native population. Comparison between ff99ci and ff03 becomes more interesting, as both have high native contact fractions in their most populated states. ▶ shows backbone RMSD distributions of all force fields. As in the analysis of native contact fraction, ff99m1, ff99off, and ff94 all result in most conformations having RMSD of 6–7 Å and ff99m2 having 5–6 Å. On the other hand, most conformations in ff99ci have RMSDs of 2–3 Å, and those in ff03 have RMSDs of 1–2 Å. It will be shown later in the free energy landscape analysis that conformations in ff03 are more native-like than those in ff99ci by having slightly more hydrogen bonds (on average 0.5 more). As we have mentioned above, ff03 (Duan et al. 2003) was designed by a systematic fitting to the ϕ/ψ potential energy surface of alanine and glycine dipeptides, and ff99ci by bicubic spline fitting to the ϕ/ψ potential energy surface of alanine dipeptide. In other force fields, only a few important conformers are considered in fitting backbone torsion parameters. Looking at the improvements of native contact fraction and backbone RMSD in ff99ci and ff03, it is apparent that reproducing high-level QM (MP2/cc-pVTZ//HF/6–31G*) energy surface over accessible conformational space of model peptides is absolutely necessary to achieve realistic structures in protein folding with molecular mechanics.

Figure 3.

Distributions of native contact fractions for all six force fields at 282 K.

Figure 4.

Distributions of backbone RMSD (Å) for all six force fields at 282 K.

Secondary structure propensity

Populations of secondary structures were also analyzed following a previous study (Zhou 2003) to obtain more insights into simulated structural data. Earlier studies (Garcia and Sanbonmatsu 2001; Zagrovic et al. 2001) showed significant helical contents in the folding process of the β-hairpin and argued that lack of helical structure in experiments might be due to the limited time resolution. While this may stand the test of time and further experiments, we believe that overpopulation of helical structure in simulation is most likely due to the improper parameters in tested force fields. Our analysis is shown in ▶, where olive-green represents β-sheet and gray represents α-helix. The populations of β-sheet and α-helix are: 56% β and 28% α in ff03; 62% β and 15% α in ff99ci; 1% β and 76% α in ff99m2; 13% β and 76% α in ff99m1; 1% β and 87% α in ff99off; and 0% β and 96% α in ff94. Our data show that helical structures may exist in the process of folding regardless of force fields used, but to a lesser extent than that of β-hairpin, as can be seen from ff99ci and ff03, which show good agreement with experimental structural data. In ff99ci and ff03, β-hairpins interchange with α-helices intermittently, consistent with the condition of thermodynamic equilibrium, where native structure is in equilibrium with non-native ones, which is not the case in the other four force fields. Therefore, the high helical content is attributable to the protein force field as pointed out by Zhou (2003). In ff99ci and ff03, we notice significant improvement of balance in secondary structures simply by fixing the backbone torsion terms. Zhou (2003) speculated that the formation of β-hairpin is mostly due to the solvation terms and the formation of α-helix is due to the backbone torsion terms. Here, it is found that the protein force field is equally important in folding of both β and α secondary structures.

Figure 5.

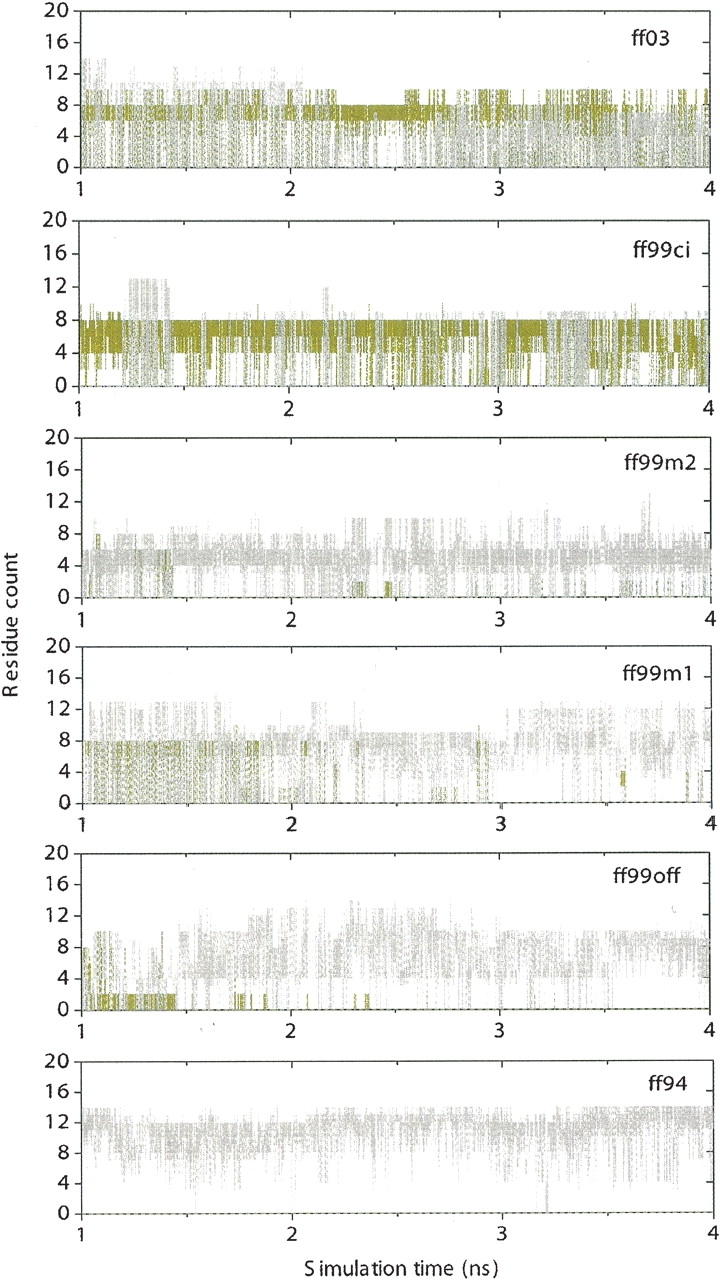
Numbers of residues in β (olive green) and in α (light gray) versus simulation time for all six force fields at 282 K.

Salt bridge populations

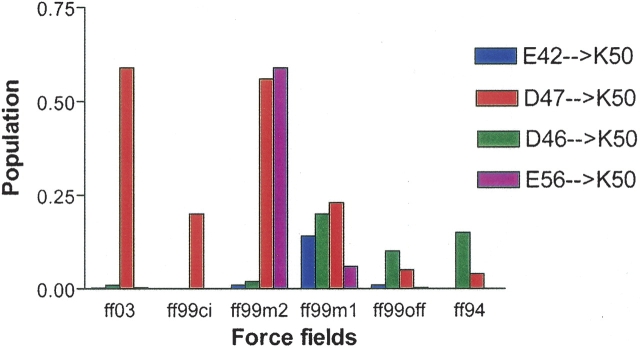
We also analyzed salt bridge populations in the most populated ensemble in each force field. These ensembles have RMSDs of 1–2 Å in ff03, 2–3 Å in ff99ci, 5–6 Å in ff99m2, and 6–7 Å in ff99m1, ff99off, and ff94. A salt bridge is defined to have a maximum distance of 4.0 Å between the centers of mass of two charged side chain groups. The five residues with side chains that can form, salt bridges in the peptide are: E42, D46, D47, K50, and E56. These five residues can form four possible salt bridges: E42/K50, D46/K50, D47/K50, and E56/K50. However, only one salt bridge is found in the crystal structure of the peptide, located near the turn between D47 and K50 with a distance of 3.73 Å. Therefore, three other salt bridges observed in the ensemble are regarded as non-native ones. ▶ shows the populations of the salt bridges in all six force fields. Note that whether a salt bridge is native or not is more important over its population because the presence of salt bridges other than D47/K50 indicates a problem in achieving the proper turn structure to form the native β-hairpin. This means that the existence of salt bridges E42/K50, D46/K50, or E56/K50 is not compatible with the native β-hairpin conformation because the core hydrophobic interaction has to be disrupted for these salt bridges to form. We notice that both native and non-native salt bridges can coexist, as in the case of ff99m2 in ▶, where D47/K50 and E56/K50 occupy >50% of the time in the ensemble, resulting in non-native structures overall.

Figure 6.

Populations of salt bridges in the most populated structural ensemble for all six force fields at 282 K. All force fields except ff99ci show various occupancies of non-native salt bridges that may disrupt the hydrophobic interaction. Note that ff03 only shows very low populations of non-native salt bridges.

Zhou (2003) argued that non-native salt bridges were due to the improper balance between electrostatic and hydrophobic interactions in tested continuum solvent models in his study. Here it seems that backbone torsion parameters also play a crucial role. As we can see from ▶, ff99off has two non-native salt bridges. ff99m1 and ff99m2, developed with the hope of fixing the backbone torsion terms, simply end up with more non-native salt bridges. Only when the backbone torsion terms are fitted systematically can one eliminate the appearance of non-native salt bridges as in ff99ci.

Folding thermodynamics

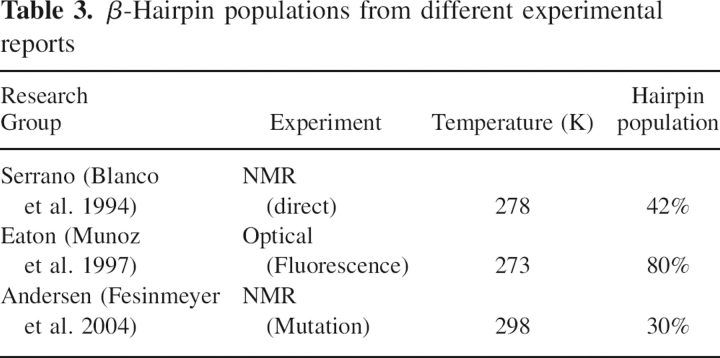
The temperature dependence of β-hairpin population has been in much debate both experimentally (Blanco et al. 1994; Munoz et al. 1997; Fesinmeyer et al. 2004) and theoretically (Dinner et al. 1999; Klimov and Thirumalai 2000; Garcia and Sanbonmatsu 2001; Zhou et al. 2001). ▶ lists measured β-hairpin population from different experiments, which ranges from 30% to 80%. It should be pointed out that the measurements are not contradictory to one another because different experimental probes are used. Further, there is an overall trend of decreasing β-hairpin population with increasing temperature: Studies by the Eaton group (Munoz et al. 1997) suggest 80% at 273 K, which is the lowest temperature in all experiments, and 50% at 300 K; the Serrano group (Blanco et al. 1994) reports 42% at 278 K; and Andersen's group (Fesinmeyer et al. 2004) estimates 30% at 298 K. To compare simulated populations with measurements from different experimental probes, different population analysis should be used as in previous studies (Dinner et al. 1999; Klimov and Thirumalai 2000; Garcia and Sanbonmatsu 2001; Zhou et al. 2001). First, native hydrogen bonding probabilities were calculated to estimate NMR-derived hairpin population (Blanco et al. 1994; Fesinmeyer et al. 2004). Such analysis also gives a hint as to which native hydrogen bond plays an important role in the folding process (Zhou et al. 2001), which will be discussed below. Second, the native C_α-C_α contact population was calculated to compare with the hairpin population from fluorescence experiment (Munoz et al. 1997). The rate of decay on β-hairpin population over a range of temperatures will also be discussed among all six force fields.

Table 3.

β-Hairpin populations from different experimental reports

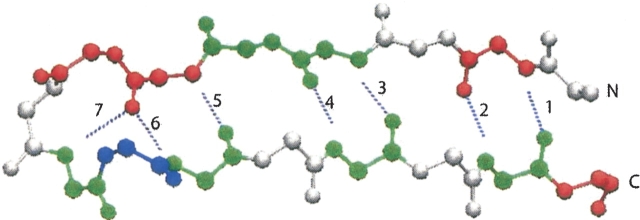
Following previous studies, a hydrogen bond is defined to have a bond distance of <3.5 Å (between the donor and acceptor atoms) and a bond angle of at least 150°. ▶ shows native hydrogen bonds numbered in sequence starting from the open end of the hairpin toward the turn region as proposed by Dinner et al. (1999) and Garcia and Sanbonmatsu (2001). The hydrogen bonding probability of each native hydrogen bond as a function of temperature is shown in ▶ for all six force fields. ff99ci has the average native hydrogen bonding of 31%, which is very close to a recent NMR study (Fesinmeyer et al. 2004) of 30% at 298 K, as well as the first NMR study (Blanco et al. 1994) of 42% at 278 K. The average hydrogen bonding is 27% in ff03, <10% in ff99m1 and ff99m2, and <2% in ff94 and ff99off. The fact that ff99m1, ff99m2, ff94, and ff99off have very low probability accounts for these force fields’ inabilities to balance the secondary structures, as discussed above. These are comparable with previous simulation data in the literature: Garcia and Sanbonmatsu (2001) reported 45%, Dinner et al. (1999) reported 54%, and Zhou et al. (2001) reported 49%. All claimed to reach qualitative agreement with Serrano's (Blanco et al. 1994) NMR measurement.

Figure 7.

Backbone hydrogen bonding in the β-hairpin peptide. They are labeled from the open end of the hairpin toward the turn. Only backbone atoms are shown. Residues are labeled as red for acidic, blue for basic, and green for polar.

Figure 8.

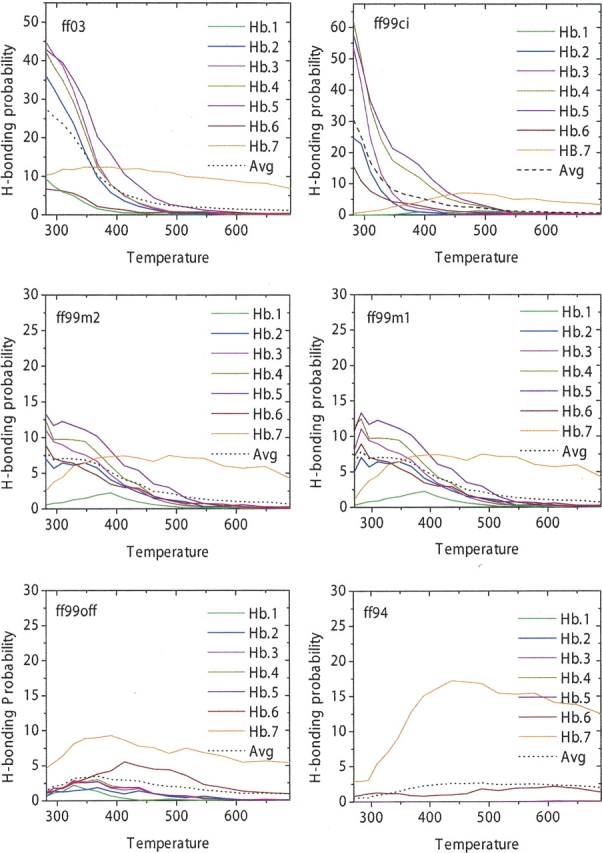
Hydrogen bonding probabilities versus temperature for all six force fields. Dotted line represents the average probability over all seven hydrogen bonds.

The second type of analysis using native contact fraction is shown in ▶. As the native contact fraction is based on the C_α-C_α distances of non-neighboring residues, it generally looks for structures that have β-hairpin-like conformations. The analysis was first proposed by Klimov and Thirumalai (2000) to correlate with florescence measurements. As pointed out by Eaton and colleagues (Munoz et al. 1997), a β-hairpin population can be detected by the presence of a hydrophobic core through fluorescence of a tryptophan residue. While this type of analysis is not directly comparable to NMR measurement, it is useful to understand how the β-hairpin population decreases with increase in temperature. Our simulation shows the β-hairpin population of 82% in ff99ci at 270 K, which is very similar to the fluorescence result of 80% at 270 K. ff99ci maintains the β-hairpin population of 81% at 282 K, and 67% at 310 K. Experimentally, the β-hairpin population is only 40% at 310 K and 0% above 360 K. In ff03, the populations are 74% at 270 K, 72% at 282 K, and 70% at 310 K. Although the simulated decay is not as fast as the experimental decay, ff99ci yielded the transition temperature closest to experimental at 365 K. From the plot of native contact fraction versus temperature, we can obtain the folding transition temperature, T_F, where 50% of the population is native-like. Using an off-lattice Gō model, Klimov and Thirumalai (2000) was able to reproduce the transition temperature predicted from experiment (Munoz et al. 1997). Zhou and Berne (2002) tried to produce the transition temperature using an all-atom model, but T_F was ∼475 K, which was much higher than the experimental T_F of ∼300 K. In our simulations, ff94 and ff99off never reached the 50% level; therefore, T_F is determined only for the other four force fields. ff99m1, ff99m2, and ff99ci produce T_Fs at ∼365 K and ff03 at ∼380 K. However, only the T_Fs of ff99ci and ff03 were both considered as reasonable from our structural analyses, because the other two force fields had very low native populations at 270 K. It is worth noting that the β-hairpin population decays faster in ff99ci than in ff03; this is somewhat related to the better β-hairpin structures in ff03.

Figure 9.

Native contact fractions versus temperature for all six force fields. At transition temperature, T_F, the native contact fraction is theoretically assumed to be 50%.

Folding pathway

Free energy landscape

To understand the β-hairpin's folding mechanism, its free energy landscape was analyzed with two reaction coordinates used previously (Zhou et al. 2001): the radius of gyration of the hydrophobic core (Rg_core) and the number of native backbone hydrogen bonds (N_BBH). The contour lines are drawn in the unit of kT. Its free energy landscape in the OPLSAA force field with SPC explicit solvent can be found in a previous study (Zhou et al. 2001), where four states were observed—unfolded (U) state, hydrophobic collapsed (H) state, partially folded (P) state, and folded (F) state. State U has a high value of Rg_core with no native backbone hydrogen bonding. State H has a decreased Rg_core indicative of the initiation of hydrophobic packing. States P and F have Rg_core at about the same value as H, but with N_BBH from 2 to 3 in state P, and N_BBH from 4 to 5 in state F. Features from this explicit water simulation (Zhou et al. 2001) will be regarded as reference in our analyses.

▶ shows the free energy contour maps of the β-hairpin in all six force fields. In both ff99ci and ff03, the most populated structure is similar to the features of crystal structure as well as the F state of the explicit water simulation. Here, the most populated structure correlates to the structural ensemble with the lowest free energy according to Equation ▶. The four other force fields identify non-native structures as the most populated. Among them, ff94 is the worst of all, with no indication of native hydrogen bonding: neither state P nor state F is present. Zhou (2003) also studied the β-hairpin in ff94 with GBSA (generalized Born/surface area), but state P is present in his free energy plot. This is probably due to the use of surface area (SA) in his simulation. Our previous analysis of solvent models shows that the SA term overstabilizes the hairpin in both GB and PB solvents (Lwin et al. 2006). In ff99off, P and F states are at the same Rg_core value, whereas in ff99m1 they are different. There is no folded state in ff99m2, but three P states are present with one, two, and three N_BBH, one of which is at a higher Rg_core value than the others.

Figure 10.

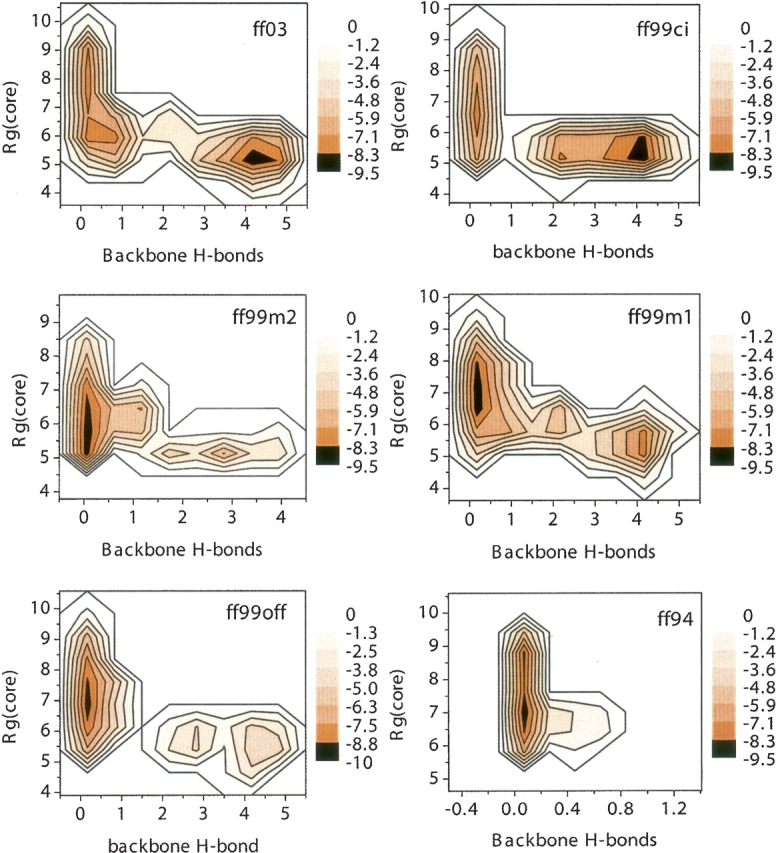
Free energy landscapes for all six force fields at 282 K.

Only ff99ci and ff03 are further analyzed, because the native-like F state is the most populated only in these two force fields. The Rg_core of F state in ff99ci is 5.2 → 5.8 Å and its N_BBH ranges from 3.75 → 4.3. Interestingly, ff03 simulation produces slightly better native-like structures in the F state with Rg_core mostly centered around 5.25 Å and N_BBH from 3.8 to 4.8. The simulated Rg_core values from both ff99ci and ff93 are very close to that (5.41 Å) of the native peptide conformation in the full protein. NMR experiment further shows that the native dimension in the full protein is an upper bound, because more interactions were observed between the aromatic residues in the stand-alone peptide than in the full protein (Blanco et al. 1994). Thus, the Rg_core value in ff03 is in excellent agreement with available experimental data. It is possible that ff03’s slightly higher β propensity in its calibration stage may account for the observed better native hairpin structure.

Free energy barriers between the various states were also analyzed for ff99ci and ff03. In ff99ci, U + H is 0.44 kcal/mol (0.74 kT) lower than P, and F is 1.16 kcal/mol (1.94 kT) lower than P. That means that the P state has a higher free energy than both U + H and F states. Therefore, to reach the folded state, the free energy barrier is between U + H and P. In ff03, U is 0.14 kcal/mol (0.24 kT) lower than H, and F is 1.00 kcal/mol (1.67 kT) lower than H. That means that the H state has a higher free energy than both U and F states. Therefore, to reach to the folded state, the free energy barrier is from U to H. Garcia and Sanbonmatsu (2001)^, Zhou et al. (2001)^, Zagrovic et al. (2001), and Bolhuis (2003) all claim that the H state is not very well populated and has a higher free energy than other states. Our ff03 simulation agrees with their claims. However, in ff99ci the fusion of U and H makes it difficult to assess its agreement or disagreement with previous studies.

Overall, both ff99ci and ff03 simulations suggest the familiar L-shaped folding pathway as in previous studies (Zhou et al. 2001), although the exact locations of the states are different. Thus, consistent with previous studies, our data show that the peptide folding proceeds first with hydrophobic collapse, then with backbone hydrogen bond formation. Interestingly, the partially folded P state does not exist at all in ff03. Thus, whether the peptide proceeds by a three-state folding or by a two-state folding really depends on which force field is used, although there are no major differences observed in simulated structural and thermodynamic properties.

Order of hydrogen bonding

The thermodynamic analyses described above do not directly shed light on the peptide's folding kinetics. However, we can indirectly deduce the sequence of hydrogen bonding from their populations. ▶ shows the probability of forming native backbone hydrogen bonds in each of the six force fields. However, only ff99ci and ff03 are considered for further discussion. ff99ci gives an order of 4, 5, 3, 2, 6, 7, and 1 at 282 K. The fact that hydrogen bonds 4 and 5 are very highly populated indicates that there is a correlation between the hydrophobic core formation (Y45 and F52) and the two hydrogen bonds. This is because interaction Y45/F52 is flanked by these two hydrogen bonds (4 and 5). Their formation is followed by the formation of 3 and 2, but not by 6 and 7. Our observed sequence of hydrogen bonding in ff99ci is similar to the proposed folding mechanism of Dinner et al. (1999): hydrogen bonds propagate outward from Y45 and F52. However, our conclusion in ff99ci is different from two earlier studies where the hairpin folding was found to initiate from the β-turn region (Munoz and Eaton 1999; Klimov and Thirumalai 2000) and moves outward along the β-hairpin. Mousseau and colleagues (Wei et al. 2004) reported yet another type of folding mechanism, that non-native hydrogen bonds form first; then, a creeping motion between the two strands causes the non-native hydrogen bonds to break and the native hydrogen bonds to form.

As there are slight differences in the free energy landscapes of ff99ci and ff03, so are there in the sequence of backbone hydrogen bonds forming. In ff03, the hydrogen bonds form in the order of 3, 5, 4, 2, 7, 1, and 6. Although hydrogen bonds 2 through 5 flank the hydrophobic interactions of the hairpin, a hydrogen bond zipping-up fashion from the hydrophobic core cannot be deduced. It looks more like a simultaneous formation of all four hydrogen bondings. This is consistent with the fact that no intermediate state was observed in the free energy landscape of ff03. Thus, in ff03, the folding mechanism can be summarized as a two-state folding with simultaneous formation of all four internal backbone hydrogen bonds. Bolhuis (2003) has also reported a two-state folding mechanism with a transient intermediate state.

Materials and methods

Molecular system

The peptide used in our study is the 16-residue C-terminal β-hairpin (residues 41–56) of protein G (PDB code 1PGB) with sequence GEWTYDDATKTFTVTE. The peptide in aqueous solution was found to adopt a stable hairpin structure similar to that in the full protein (Blanco et al. 1994; Fesinmeyer et al. 2004). Its folding kinetics were studied, with folding half-time within 6 msec (Munoz et al. 1997). Its simple structure, yet with the characteristics of a full protein, makes it an ideal system for theoretical protein folding studies, both kinetically (Klimov and Thirumalai 2000; Zagrovic et al. 2001; Wei et al. 2004) and thermodynamically (Dinner et al. 1999; Pande and Rokhsar 1999; Garcia and Sanbonmatsu 2001; Zhou et al. 2001; Zhou and Berne 2002; Zhou 2003). Due to the abundance of literature on the peptide, we have chosen it for our analysis on the influence of force field parameters in folding simulations.

Simulation methodology

All simulations were performed with replica exchange molecular dynamics (REMD) as proposed by Sugita and Okamoto (1999). It should be noted that MD was used only to generate new conformations. Therefore, REMD was not intended for kinetic simulations. In fact, the formulism of REMD can be derived from the Metropolis criteria (Metropolis et al. 1953) and the generalized ensemble theory in equilibrium statistical thermodynamics (Sugita and Okamoto 1999). In this study, each REMD (for each tested force field) was simulated with the same 18 target temperatures roughly separated following an exponential distribution: 270 K, 282 K, 295 K, …, 611 K, 649 K, and 690 K, as in a previous study (Zhou 2003). The distribution of temperatures was chosen such that the actual replica exchange probability was ∼40% on average and was the same for all force fields. Exchange was allowed between neighboring replicas so that, except for those at the lowest and the highest temperatures, each replica has the opportunity to exchange with both neighboring replicas alternately. Although exchanges between any two replicas are allowed, the acceptance ratio would be small if their canonical potential energy distributions overlap little with each other.

In each replica, one short MD simulation was run for 1 psec with a 1-fsec time step. Constant temperature was maintained with Berendsen's weak temperature coupling scheme (Berendsen et al. 1984). Velocity rescaling was used when a replica was restarted from a different temperature (Sugita and Okamoto 1999). Conformations were saved every 0.1 psec. Replica exchange was performed at the end of each short MD simulation and a total of 4000 exchanges were performed. Therefore, the total simulation time was 4 nsec with 40,000 conformations saved in each replica. Out of the 4 nsec simulation run, the data from the last 3 nsec was used for analysis, leaving the first 1 nsec as the equilibration period. The equilibrium period was found to be quite sufficient, as the potential energy of each replica reached equilibrium within 1 nsec.

Protein model

The energy model for the protein was the AMBER force field (Case et al. 2004) described as follows:

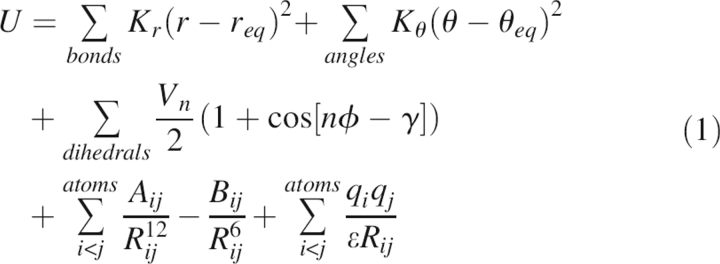Here, K_r and K_θ are force constants for bond length, r, and bond angle, θ, respectively; r_eq and θ_eq are corresponding equilibrium bond length and bond angle, respectively. ϕ is the dihedral angle; V_n is its corresponding force constant; and γ is its phase angle, which takes the values of either 0° or 180°. A_ij and B_ij are van der Waals repulsive and London dispersion force constants, and R_ij is pairwise distance between atoms i and j. q_i and q_j are partial atomic charges, and ɛ is the dielectric constant of the system. Interactions between atoms that are separated by three bonds are considered 1–4 interactions, which consist of both van der Waals part and electrostatic part, in addition to the dihedral terms. The 1–4 van der Waals interaction is scaled down by a factor of 2; the 1–4 electrostatic interaction is also scaled down in some force fields, but left as-is in others. In ff94, ff99m1, ff99m2, and ff03, the 1–4 electrostatic scaling factor is 1.2; and in ff99off and ff99ci it is not scaled. Also considered are nonbonded interactions that are either separated by more than three bonds or not bonded at all.

Solvent model

The solvent model used is an implicit solvent based on the finite-difference Poisson-Boltzmann (PB) method (Luo et al. 2002; Lu and Luo 2003). The parameters necessary to set up PB calculations were adopted from published data (Luo et al. 2002; Lu and Luo 2003). It was found that inclusion of the surface area (SA) term makes the β-hairpin too stable, regardless of the implicit solvent models used in a previous study (Lwin et al. 2006). Also, the most populated ensemble with SA deviates more significantly from the crystal structure than that without SA. This is in part due to the oversimplification in the treatment of nonpolar solvation by the SA term. Indeed, studies by the Levy group (Levy et al. 2003) have shown that the current SA formalism is problematic in estimating the solvation free energy of proteins. However, inclusion of nonpolar solvation interaction is important if significant change occurs along the folding pathway of the tested peptide. Fortunately, this is not the case in the tested system. Thus, the SA term was left out in our current study as a reasonable approximation (Lwin et al. 2006).

Considering the various approximations in the solvation treatment by the PB solvent, we find it necessary to compare the performance of the PB solvent and the explicit solvent on the β-hairpin in this study. A poly-alanine α-helical peptide of 11 residues was also included to rule out any potential bias in secondary structure due to the approximations used. The ff99ci parameter set was used for this comparison. Explicit solvent simulations were run with Jorgensen's TIP3P water model (Jorgensen et al. 1983) in a truncated octahedron water box with a buffer zone of 10 Å. Long-range electrostatic interactions were treated by the Particle Mesh Ewald method (PME) (Darden et al. 1993). Default options for PME as in AMBER8 were used, except that the real space cutoff distance was set at 9 Å. A single MD simulation was performed for each peptide system using either PB or PME. To effectively sample both folded and unfolded conformations of both peptides, a high temperature of 450 K in the NVT ensemble but with the room-temperature water density was used. An independent study in our group has shown that the simulation condition is, in fact, reasonable for studying electrostatic solvation interactions: the electrostatic solvation free energies of tested amino acid side chain analogs are very similar to those at room temperature (C. Tan and R. Luo, unpubl.). A 10-nsec trajectory was run for PME with a 2-fsec time step. Snapshots were saved every 5 psec. A 2-nsec trajectory was run for PB with a 1-fsec time step. Snapshots were saved every 1 psec. Berendsen's weak temperature coupling scheme (Berendsen et al. 1984) was applied with a coupling constant of 1 psec for both simulations. Note that a longer simulation time was used in PME than that in PB to account for the less efficient sampling in PME.

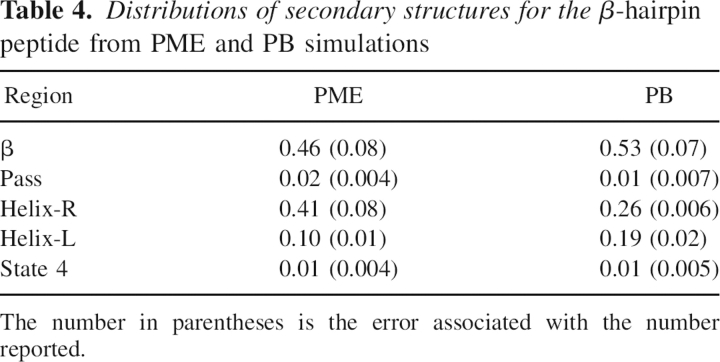
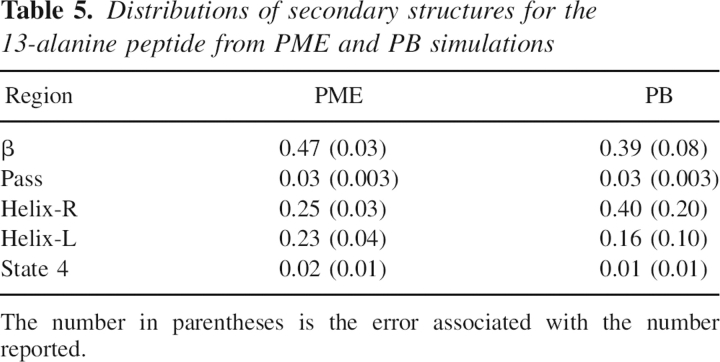
Distributions of backbone torsion angles were then analyzed to ensure that PB is acceptable in our study of folding thermodynamics of secondary structures. For the β-hairpin, 10 residues (E42 to D46 and T51 to T55) in the β strands were considered. ϕ/ψ angles of these residues were computed for the saved snapshots in PB and PME trajectories, respectively. A total of 2000 snapshots in each simulation were considered. ▶ shows the ϕ/ψ distributions of the β-hairpin from PB and PME simulations. The two plots in the figure closely resemble each other. We further partitioned each distribution as reported by Hu et al. (2003) and calculated population distributions in each region. The partitioned populations are shown in ▶. The β structures are populated at 53% in PB and at 46% in PME for the β-hairpin at tested condition. Similarly, as in the β-hairpin, ϕ/ψ angles of the middle seven alanine residues in the poly-alanine peptide from 2000 conformations were considered in the analysis. ▶ shows the ϕ/ψ distributions of the α-helix in PB and PME simulations. As shown in ▶, the α structures are populated at 56% in PB and at 48% in PME for the α-helix at the tested condition. A similar agreement for the α-helix was found between PB and PME as that for the β-hairpin. While differences in sampling are present, the sampling of the different regions is approximately similar, such that it is not expected that the use of the PB solvent would significantly impact the conclusions in the present study. Furthermore, no noticeable bias by PB was found in either structure, considering all of the approximations used. Therefore, the PB implicit solvent is a reasonable choice in the force field analysis of secondary structures.

Figure 11.

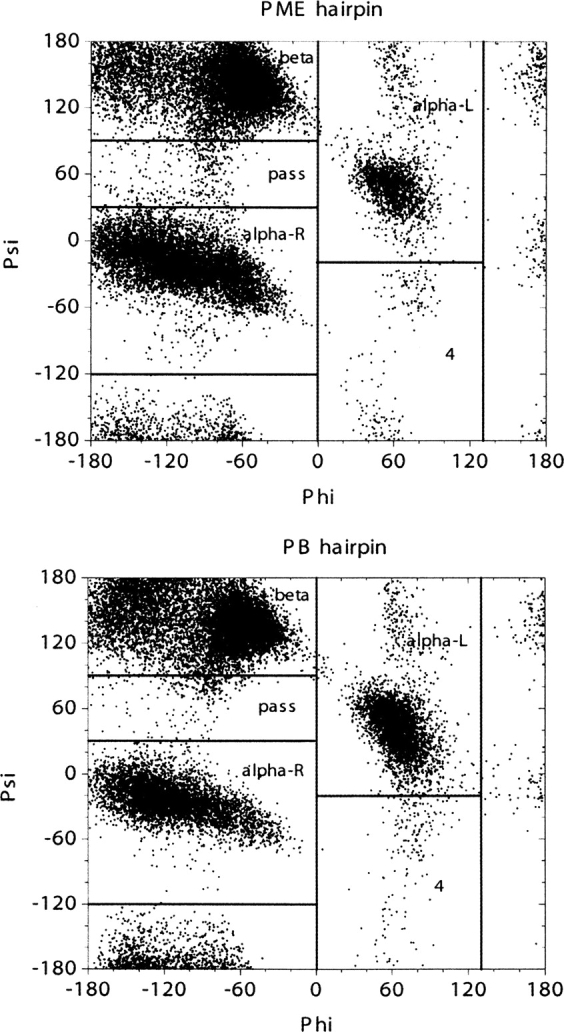
Distributions of ϕ/ψ angles in the β-hairpin peptide from PME and PB simulations at 450 K. ϕ/ψ angles are obtained from the 10 residues that form β-hairpin in the crystal structure.

Table 4.

Distributions of secondary structures for the β-hairpin peptide from PME and PB simulations

Figure 12.

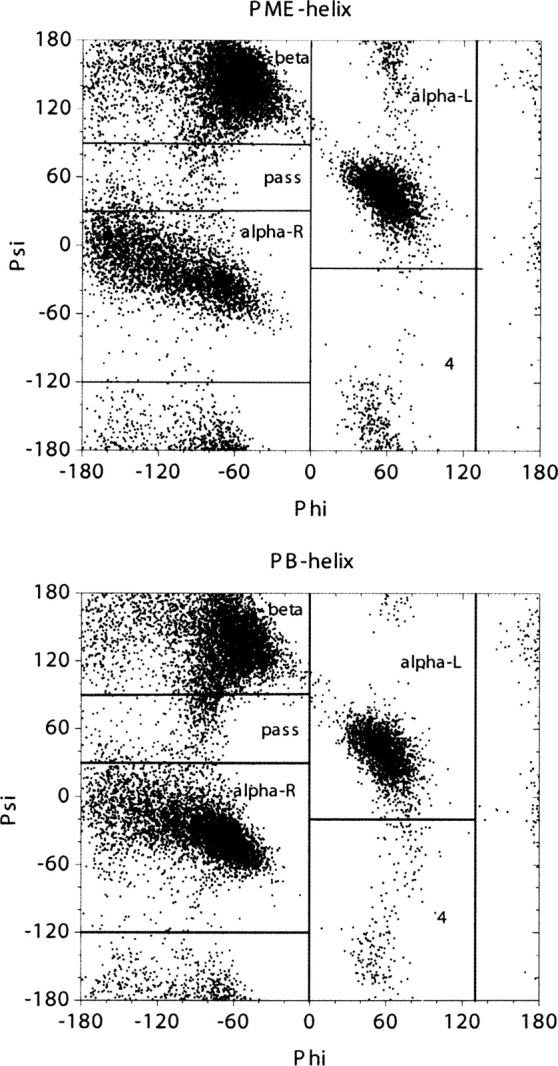
Distributions of ϕ/ψ angles in the 13-alanine peptide from PME and PB simulations at 450 K. ϕ/ψ angles are obtained from the middle seven alanine residues.

Table 5.

Distributions of secondary structures for the 13-alanine peptide from PME and PB simulations

Analysis parameters

Structural analysis was first performed using RMSD and native contact fraction with reference to the crystal structure. RMSD is defined as

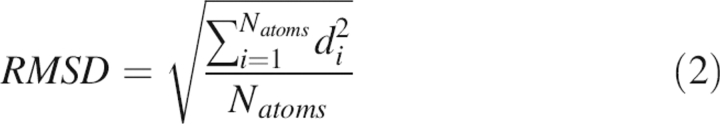where d_i are pairwise atomic distances between the reference structure and a saved snapshot after the two are superimposed and N_atoms is the number of atoms considered in RMSD calculation. PTRAJ in AMBER8 is utilized to calculate RMSD on backbone heavy atoms (C_a, C, N, and O). A native contact is defined as a C_a-C_a distance <6.5 Å between any two nonadjacent residues in the reference structure. All defined native contact C_a-C_a distances are then searched in a saved snapshot to compute its native contacts. Apparently, the number of native contacts in any snapshot would be less than that in the reference structure. The fraction of native contact is then defined as the ratio between the number of native contacts in the saved snapshot and the number of native contacts in the reference structure.

We also compared simulated structures with a previous NMR structural measurement, namely, the nuclear Overhauser effect, or NOE (Blanco et al. 1994). NOE provides information about the distance between a pair of atoms that are close together in space but may be separated by many bonds. The NOE signal strength is inversely proportional to the sixth power of the distance. The average NOE distance between the two atoms is calculated as

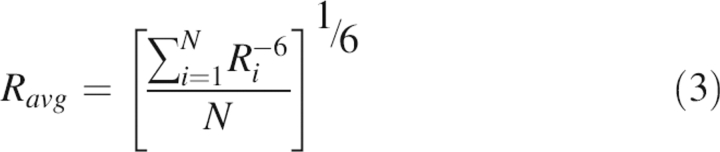where R_i is the distance between the two atoms involved in NOE coupling and N is the number of snapshots.

To understand the peptide's folding mechanism, its free energy landscape, i.e., potential of mean force (PMF) [W(X)], was calculated by histogram analysis (Garcia and Sanbonmatsu 2001; Zhou 2003), where X represents a specified set of reaction coordinates in relation to P(X), the probability distribution function,

with Z being the partition function and β the inverse temperature β = (kT)⁻¹. The change in PMF as a function of the change in reaction coordinates is obtained by the ratio of the corresponding probability distribution functions:

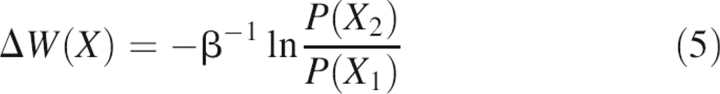The reaction coordinates utilized in the free energy analysis are the core radius of gyration (Rg_core) and the number of backbone hydrogen bonds (N_BBH). Rg_core is obtained from the radius of gyration of the four hydrophobic residues, W43, Y45, F52, and V54. MMTSB Tool Set (Feig et al. 2001) was utilized to calculate the radius of gyration. N_BBH involves five of the seven backbone hydrogen bonds shown in ▶. The two innermost hydrogen bonds close to the loop region are not considered (Pande and Rokhsar 1999; Klimov and Thirumalai 2000; Zhou et al. 2001; Zhou 2003). A backbone hydrogen bond is defined between a pair of backbone atoms, N and O, when they are separated by a distance <3.5 Å and have an angle (N-H…O) >150.0°.