Mapping the phase diagram of the writhe of DNA nanocircles using atomistic molecular dynamics simulations

Abstract

We have investigated the effects of duplex length, sequence, salt concentration and superhelical density on the conformation of DNA nanocircles containing up to 178 base pairs using atomistic molecular dynamics simulation. These calculations reveal that the partitioning of twist and writhe is governed by a delicate balance of competing energetic terms. We have identified conditions which favour circular, positively or negatively writhed and denatured DNA conformations. Our simulations show that AT-rich DNA is more prone to denaturation when subjected to torsional stress than the corresponding GC containing circles. In contrast to the behaviour expected for a simple elastic rod, there is a distinct asymmetry in the behaviour of over and under-wound DNA nanocircles. The most biologically relevant negatively writhed state is more elusive than the corresponding positively writhed conformation, and is only observed for larger circles under conditions of high electrostatic screening. The simulation results have been summarised by plotting a phase diagram describing the various conformational states of nanocircles over the range of circle sizes and experimental conditions explored during the study. The changes in DNA structure that accompany supercoiling suggest a number of mechanisms whereby changes in DNA topology in vivo might be used to influence gene expression.

INTRODUCTION

DNA topology in vivo is extremely diverse. Whilst regions of the genetic material must be accessible during transcription, replication and repair, the bulk must be compacted to fit within the nucleus. In bacteria, circular plasmids are condensed by supercoiling the DNA into highly writhed superhelical structures. The importance of higher order DNA structure is illustrated by the elaborate machinery for the regulation of DNA topology that exists within the cell. Families of topoisomerase and gyrase enzymes alter the level of supercoiling by transiently introducing single or double strand breaks and changing the number of times the two strands of the duplex are wrapped around each other (1). Variation in DNA topology influences promoter activity and is consequently involved in the regulation of gene expression and replication (2). For example, the shock response of bacterial cells placed under environmental pressure (such as starvation or thermal stress) is accompanied by dramatic changes in supercoiling, which enable the cell to rapidly modify transcription rates across the whole genome, whereas adaptation through genetic mutations can only occur over a much longer timescale (3,4).

Closed circular DNA can form superhelical structures whenever the topological quantity known as the linking number Lk (1) deviates from its value in a torsionally relaxed duplex Lk₀. The quantity Lk₀ is simply the number of base pairs (bp) in the circle divided by the helical repeat. The linking number is constrained to be integral in closed circular structures and cannot be altered without cutting either one or both DNA strands. The linking number difference ΔLk = Lk − Lk₀ is commonly normalised to the size of the circle and expressed as the superhelical density σ where:

1

The topological property, the linking number, is related to two geometrical parameters of the duplex; the helical twist (Tw) and the writhe (Wr), where the writhe is a measure of the contortion of the DNA axis.

2

A relaxed DNA circle will have a twist producing around 10.5 bp per helical turn and zero writhe. If Lk ≠ Lk₀, then the system has the possibility of relieving unfavourable torsional stress within the helix by repartitioning it into writhe to form a superhelical structure, in accordance with Equation (2). DNA extracted from cells is generally found to be negatively supercoiled at superhelical densities of around −0.06 (1).

The topological and geometrical properties of small DNA circles may differ significantly from that observed for sequences which are far longer than the persistence length [∼150 bp (5)]. In this regime, the detailed molecular structure of DNA becomes more significant and elastic polymer theories may no longer be valid. The formation of tight DNA loops by proteins bound at distant sites on the DNA plays an important role in gene regulation (6,7). An in vivo analysis of DNA looping in the lac operon repressor system found that the free energy of looping was far more sensitive to the inter-operator distance than would be expected from simple continuum theories (8). In a study of circle formation as a function of DNA length, Cloutier and Widom reported cyclisation probabilities for circles containing between 89 and 105 bp that are greater than those expected from simple models of DNA bending (9), although these experimental results were later disputed by Du et al. (10). A subsequent atomistic MD study showed sharp kinks forming in relaxed and over-wound 94 bp DNA circles (11). These kinks might well be responsible for relaxing some of the elastic energy stored in highly bent DNA and therefore for the unexpectedly high cyclisation probabilities that have been observed experimentally. As well as increased bending rigidity, smaller circles also display a much higher resistance to writhing. Bates and Maxwell showed that gyrase is only able to introduce negative writhe into circles that contain more than 174 bp (12). Later studies of supercoiling in larger DNA circles (>300 bp) observed that underwinding by <1 helical turn induced negative writhing (13); yet it was necessary to underwind a 178 bp duplex by 2 helical turns in a high salt environment before negative writhing would occur (14).

Until recently, theoretical studies of DNA topology have been performed using coarse-grained models that represent the duplex either as a continuous elastic rod or at the level of individual base pair steps. Although these models have provided important new insight into DNA topology (14–18), they are not able to provide information at the atomic level, which may be important in understanding how protein-DNA recognition is affected by changes in topology and ultimately how supercoiling and packing influence transcription. The treatment of sequence-dependent effects is also rather limited within these coarse-grained representations. Furthermore, it is not possible to observe kink formation or base pair separation when high torsional stresses are imposed on the duplex.

Improved computational methods have made it possible to explore ever larger systems at the atomic level. This study uses atomistic molecular dynamics (MD) simulations of DNA nanocircles ranging from 90 to 178 bp in size to provide new insight into the partitioning of twist and writhe in DNA nanocircles as a function of circle size, DNA sequence, salt concentration and superhelical density. By combining the results from these MD simulations with simple physical arguments, we are able to plot the phase diagram describing the conditions required for the formation of writhed DNA nanocircles. These initial studies use simple alternating AT and GC sequences to avoid the complications of sequence-dependent effects occurring within a single nanocircle, which will be the subject of future studies. Despite this simplification, our calculations indicate that a rather detailed description of the duplex is required to correctly describe the behaviour of these systems.

MATERIALS AND METHODS

The calculations were run on the 404 core Opteron Myrinet supercomputer cluster at Leeds and the UK National Grid Service (NGS). All MD simulations used the AMBER 8 suite of programs (19), and the CURVES 5.1 program was used to analyse DNA helical parameters (20). Initial coordinates for linear DNA structures were generated using the NUCGEN module in AMBER 8. Circular DNA configurations with helical twist values corresponding to under-/overwinding from −2 to +3 helical turns were produced from the linear structure using code developed in house (see Supplementary Data). The system was thermalised and equilibrated using a standard multistage protocol (21) as described in Tables 1S and 2S in the Supplementary Data. The DNA was described by the AMBER-99 force field (22). A selection of these simulations were repeated using the PARMBSC0 forcefield for comparison (23), the results using the two forcefields are in good agreement (as described in the Supplementary Data in Figure 1S). The SHAKE algorithm was used to constrain bonds to hydrogen allowing an integration timestep of 2fs during the MD runs. All simulations were performed at constant temperature (300 K) and pressure (1 atm). In explicitly solvated runs, the DNA was surrounded by sufficient K⁺ counterions to neutralise the system and a periodic box of TIP3P solvent molecules that extended 15 Å beyond the limits of the solute in each dimension. The fast particle mesh Ewald method (implemented within the PMEMD module of AMBER 8) was used to calculate long-range electrostatic interactions. In the implicitly solvated simulations, the generalised Born/surface area (GB/SA) method using the Tsui and Case parameters (24) was used with a cutoff of 50 Å. The GB/SA model offers a simple and convenient method for exploring larger DNA nanocircles as a function of salt concentration. As the approximations in the model become unreliable at very high salt, the concentrations used in the study provide only a semi-quantitative estimate of the electrostatic screening and should be interpreted with some caution. Although several MD studies of DNA have been reported at high salt conditions using explicit solvent methods, these frequently suffer from poor equilibration and, in our opinion, further methodological development is required before these seemingly more accurate simulations can be considered reliable. Therefore, we consider the GB/SA methodology to be a sensible compromise between accuracy and computational expense, despite the caveats associated with high-salt conditions. A quantitative comparison between explicitly and implicitly solvent models (hydrogen bond distances and root mean square fluctuations from the uniform circular starting structure) is provided as Supplementary Data (Figures 3S and 5S).

RESULTS

Writhing and denaturation of 90 base pair nanocircles in explicit solvent

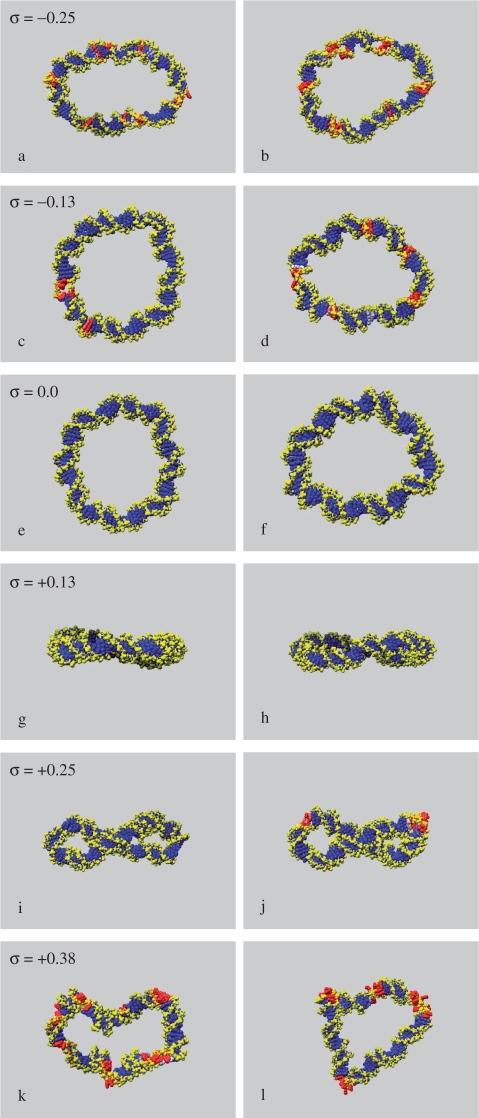
Experimental studies suggest that DNA has an equilibrium average helical twist of around 34.3°. Therefore a 90 base pair sequence will possess about 8.5 helical turns when torsionally relaxed. This value is constrained to be integral when the DNA is bent into a closed loop. The amount of helical stress introduced into the circle will depend on how far each base step is forced to deviate away from the ideal twist value and also upon the magnitude of the associated elastic constant. Both of these vary with sequence, as studies of structural databases and large-scale MD simulations have revealed (25,26). One slight complication is that it is a well-established feature of the AMBER parameterisation of DNA that it tends to predict a smaller value for the relaxed helical twist (c. 32°), compared to the values typically obtained experimentally. To confirm this in the context of circularised DNA where some twist/bend coupling might occur, we performed 4ns simulations on both d(GC)₉₀ and d(AT)₉₀ circles in which one strand was ‘nicked’ so that any torsional strain could be eliminated. As expected, we found that both sequences relaxed to states were the average helical twist oscillated between 31.6 and 32.8°. On this basis, a closed circle with Lk = 8 will be close to perfectly relaxed in simulations. Using explicitly solvated MD, we have investigated intact 90 base pair circles with Lk = 6, 7, 8, 9, 10 and 11, corresponding to situations ranging from considerably under-wound to highly over-wound, and using both d(AT)₉₀ and d(GC)₉₀ for comparison. The simulations start from uniform circular structures and are continued for sufficient time for the nature of any conformational changes to become apparent (Table 1). A representative starting structure is shown in Figure 1, and the resulting structures in Figure 2. To establish whether the double helical structure of the DNA remains intact during each simulation, we have calculated the average hydrogen bond distances between complementary base pairs around each circle. Hydrogen bond distances offer the most simple and convenient descriptor for detecting melted regions of the duplex [although base stacking interactions can be as important as hydrogen bonding in maintaining the stability of duplex DNA (27)]. Denatured regions in each circle are shown in Figure 2, where red indicates average bond distances >3 Å. Graphs showing the hydrogen bond distances plotted as a function of position around the circle are provided as Supplementary Data in Figure 2S.

Table 1.

MD simulations of 90 base pair nanocircles using explicit solvent

Sequence	Linking number	Key in Figure 2	Superhelical density	Simulation length (ns)	Structural change
d(GC)90	6	a	−0.25	2.5	Denaturation
d(AT)90		b		2.5	Denaturation
d(GC)90	7	c	−0.13	10	Partial denaturation
d(GC)90				10	Partial denaturationa
d(AT)90		d		10	Denaturation
d(GC)90	8	e	0.0	9	Little change
d(AT)90		f		9	Little change
d(GC)90	9	g	+0.13	5	Circle bending
d(AT)90		h		5	Circle bending
d(GC)90	10	i	+0.25	18	Positive writhing
d(GC)90a				10	Positive writhinga
d(AT)90b		j		27	Positive writhingb
d(AT)90				5	Denaturation
d(GC)90	11	k	+0.38	3	Denaturation
d(AT)90		l		3	Denaturation

^aThese simulations were performed with the PARMBSC0 forcefield.

^bThis simulation was performed with the hydrogen bonds restrained for the first 17.5 ns.

Figure 1.

Initial structure of a 90-mer circle under-wound by one helical turn. The surrounding solvent box is also shown.

Figure 2.

Representative structures from the ends of MD simulations of d(GC)₉₀ (left) and d(AT)₉₀ simulations (right) with increasing superhelical density (σ). The base pairs are coloured in accordance with average Watson–Crick hydrogen bond distances during the simulations; <2 Å (blue), 2.5 Å (white) and >3 Å (red).

90 base pair circles at zero and low positive superhelical densities

DNA circles that are relaxed or over-wound by one helical turn show little change in conformation during the course of the simulation. The torsional stress in the over-wound circles causes the DNA to bend out of the plane (Figure 2g and h), whereas the relaxed circles remain largely planar when viewed edge-on (Figure 2e and f). There is little disruption to base-pairing within these systems, the exception being a single base pair in over-wound d(AT)₉₀ which breaks early on in the simulation and which does not reform over a timescale of 5 ns. Analysis of this structure in more detail reveals the formation of a ‘Type II kink’ as described by Lankaš et al.

90 base pair circles at high superhelical densities

DNA circles at high levels of over-/underwinding (−2 and +3 helical turns) denature into structures containing a mixture of single- and double-stranded DNA during relatively short MD trajectories. The torsional forces within these circles are sufficiently large to overcome the favourable interactions between complementary base pairs. A clear periodicity is apparent in both the under-wound (Figure 2a and b) and over-wound (Figure 2k and l) circles, which, in the majority, coincides with the helical repeat of the duplex (Figure 2S). Inspection of these unstable circular structures shows that strand separation is most likely to occur whenever the minor groove is located on the inside of the circle. However, there are clear differences in the behaviour of the over- and under-wound nanocircles. The over-wound circles appear considerably writhed, despite denaturation, whereas the under-wound circles do not (Figure 2a and b) compared to (k,l).

90 base pair circles at intermediate superhelical densities

Very different behaviour is observed for negatively and positively wound circles at intermediate superhelical densities, as Figure 2 clearly shows. Bubble-like regions of single-stranded DNA form within both under-wound d(GC)₉₀ and d(AT)₉₀ during the simulation, although the d(GC)₉₀ sequence is more robust (Figures 2c, d and 2S). These single-stranded regions occur predominately where the minor groove is located on the inside of the circle. In contrast, the d(GC)₉₀ circle over-wound by +2 helical turns undergoes a supercoiling instability and buckles over timescales ∼10 ns to form a supercoiled DNA loop (Figure 2i). Analysis of the d(GC)₉₀ structure reveals the formation of ‘Type I’ kinks (in the Lankaš et al. terminology) at CG steps at both apices of the supercoil where the bending stress is greatest. The over-wound d(AT)₉₀ circle is unable to withstand even these moderate levels of torsional stress due to its reduced hydrogen bonding capacity relative to d(GC)₉₀, and overwinding by 2 helical turns leads to local strand separation rather than supercoiling. To demonstrate that differences in hydrogen bonding interactions within AT-rich and GC-rich DNA are responsible for this sequence-dependent behaviour, we performed an additional simulation of d(AT)₉₀ in which the hydrogen bonds were restrained throughout the simulation to prevent local melting. The DNA then buckled to form a supercoiled structure over a timescale ∼18 ns. The restraints were removed and the simulation continued for an additional 9 ns, during which denaturation occurred only at the apices of the supercoil where the DNA bends significantly, as shown in Figure 2j. The observation that the double helical structure of circles under-wound by one helical turn is destabilised relative to circles over-wound by an equivalent amount is consistent with the belief that underwinding promotes cellular processes that require strand separation by weakening the duplex structure of DNA (2,28–30).

Implicitly solvated simulations and the writhing of larger DNA nanocircles

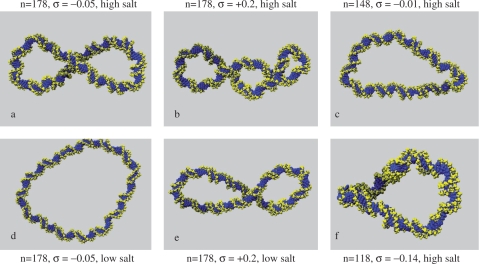
To investigate how the ability of over-/under-wound circles to writhe depends on the salt concentration and the size of the DNA loop, we have run MD simulations of d(GC)₉₀, d(GC)₁₁₈, d(GC)₁₄₈ and d(GC)₁₇₈ at high (1 M), medium (0.25 M), and low (0.01 M) salt concentrations using an implicit solvent model to improve computational efficiency. We also performed a smaller number of GB/SA simulations of AT-containing circles for comparison, the results from these simulations are presented as Supplementary Data in Figure 6S. The effective salt concentration of the explicitly solvated simulations is around 0.25 M, the exact value depends on the precise size of the water box used in each separate MD calculation. As well as reducing the number of atoms which must be considered, structural changes are accelerated when implicit solvent models are used due to reduced friction within the system. We observe that d(GC)₉₀ at a superhelical density of +0.25 equilibrates to a positively writhed structure over timescales of ∼10 ns when explicitly solvated, whereas the same conformational changes occurs in around 500 ps in the absence of a viscous solvent, as can been seen from the convergence of the root mean squared deviation from the circular starting structures shown as Supplementary Data in Figure 5S. It should be noted, however, that a large electrostatic cut-off (50 Å) must be employed to obtain accurate results for highly charged systems of this size. Consequently, even these more approximate computational methods are time consuming. The results of implicitly solvated simulations containing between 90 and 178 bp are summarised in Table 2 and are shown pictorially in Figure 3.

Table 2.

MD simulations of alternating d(GC)_n nanocircles. All simulations use the GB/SA solvent model

No. base pairs	Simulation length (ns)	Superhelical density	GB/SA salt (M)	Structural change
90	6	−0.13	1	Attempts to writhe, circle collapses and partially denatures
90	4	−0.13	0.01	Circle unwinds/expandsa
90	5	−0.13	0.25	Partial denaturation
90	2.5	+0.13	1	Circular
90	9	+0.38	0.25	Positive writhing
118	12	−0.14	1	Fluctuates between circular/writhed
148	5	−0.01	1	Fluctuates between circular/negatively writhed
148	5	−0.09	1	Negative writhing
178	7	−0.05	1	Negative writhing
178	5	−0.05	1	Negative writhingb
178	2	−0.05	0.01	Writhed structure unwindsa
178	5	−0.05	0.25	Fluctuates between circular/negatively writhed
178	5	+0.20	1	Highly positively writhed
178	2	+0.20	0.01	Writhed structure partially unwindsa
178	5	+0.20	0.25	Positive writhing
178	2.5	Linear	1	Linear

^aStarting structures for these MD runs at 0.01 M GB/SA salt were obtained from simulations run at 1 M GB/SA salt to observe the effect of suddenly reducing the electrostatic screening.

^bThis simulation was performed with the PARMBSC0 forcefield.

Figure 3.

Representative structures from MD simulations of d(GC)_n circles showing final DNA conformations in high (1 M) and low (0.01 M) GB/SA salt at various superhelical densities (σ).

Simulations of d(GC)₉₀

The d(GC)₉₀ nanocircle remains circular at a small positive superhelical density of +0.13 (Lk = 9) and at a GB/SA salt concentration of 1 M. At a superhelical density of −0.13 (Lk = 7), the under-wound nanocircle transiently exhibits writhed configurations, but no single highly writhed conformation persists. When the GB/SA salt concentration is suddenly dropped to 0.01 M during the course of the simulation, the DNA is stiffened and remains fixed in a predominantly circular topology. Simulations run at 0.25 M also remain circular, in agreement with the equivalent explicitly solvated simulation previously described. Most importantly, no negative writhing occurs for nanocircles containing only 90 bp using either solvent model, despite the accelerated dynamics expected in implicit solvent (when solvent friction is neglected) and the conditions of high electrostatic screening that can be explored with GB/SA. In contrast, GB/SA simulations of the over-wound circle with Lk = 10 at 0.25 M undergo a buckling transition to form a highly writhed structure containing one crossing point, in agreement with the explicitly solvated simulations. This transition does not occur at very low salt concentrations, consequently the DNA remains circular.

Simulations of d(GC)₁₇₈

The largest circle d(GC)₁₇₈ considered in this study evolves into a negatively writhed structure containing one crossing point at a superhelical density of −0.05 at high salt, as shown in Figure 3a. An experimental study by Bednar and coworkers also observed negative writhe in a 178 bp circle at high concentrations of counterions. Dropping the GB/SA salt concentration to 0.01 M during the simulation causes the superhelix to unwind back into a circular configuration due to the combination of the increased electrostatic repulsion at the crossing point of the negatively charged sugar-phosphate backbone and the reduced bendability of the duplex (Figure 3d). Once again, this is consistent with the experimental study that detected only low values of writhe at a salt concentration not exceeding 0.25 M. Simulations run at 0.25 M fluctuate between negatively writhed and circular conformations To compare the effects of over- and underwinding, we also over-twisted d(GC)₁₇₈ to a superhelical density of +0.2 at a GB/SA salt concentration of 1 M. This over-wound circular structure rapidly writhes. Figure 3b shows a view in which the DNA backbone crosses at two points at this salt concentration. Projections producing two crossings were not observed in structures from any of our earlier simulations, providing qualitative support for higher writhe in this case. When the GB/SA salt concentration was suddenly reduced to 0.01 M, the structure unwound back to a roughly circular configuration before rewinding to form a superhelix in which only one crossing point (Figure 3e) can be detected. This simulation produced the only writhed configurations that we observed at very low salt concentrations. At 0.25 M, the DNA fluctuates between conformations containing either one or two crossing points.

Simulations of d(GC)₁₄₈ and d(GC)₁₁₈

The smaller d(GC)₁₄₈ under-wound circle negatively writhes at high salt and at a critical superhelical density that lies somewhere between −0.01 and −0.09. However, when the circle size is decreased to d(GC)₁₁₈, the system becomes too small to form a writhed superhelix, even at superhelical densities of −0.14. Although highly writhed configurations form transiently due to thermal fluctuations, these structures rapidly unwind, and the nanocircle fluctuates continuously through conformations intermediate between circular and negatively writhed configurations (Figure 3f). Very similar behaviour is observed for d(GC)₁₄₈ but at the lower superhelical density of −0.01 (Figure 3c). We do not think that the absence of writhe in these systems is due to the presence of a free energy barrier that cannot be crossed over the timescale of the simulation. Rather, the large thermal fluctuations between circular and writhed states suggest that the potential energy surface is rather flat. The curious properties of these nanocircles results from the competition between the torsional stress stored by the negative superhelical density within the duplex (which can be relieved by writhing) and the cost of bending the DNA at the apices (which is required for a superhelix to form). Our calculations have identified experimental conditions for which these two opposing terms are almost equal. These nanocircles can be said to be ‘frustrated’, a concept that is well established in the study of protein folding (31).

The phase diagram of writhing and denaturation of DNA nanocircles

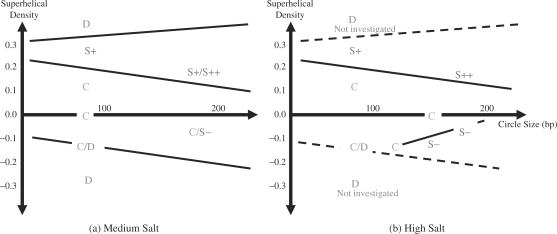
To summarise the series of simulations performed in this study, we have combined our observations with simple physical arguments to sketch a phase diagram of the writhing of DNA nanocircles at medium (Figure 4a) and high (Figure 4b) salt concentration. In general, writhing should always be easier for larger circles. The torsional energy stored in the helix at a given superhelical density is proportional to the length of the DNA, and the bending energy required to form the apices of the superhelix decreases with increasing circle size (as the end loops tend to be larger). Raising the salt concentration improves electrostatic screening and decreases the rigidity of the DNA (32). Therefore, the thermodynamic balance between twist and writhe is tipped in favour of writhe as the salt concentration increases. We observe a variety of DNA conformational phases during this study; namely circular (C), positively writhed containing one or two crossing points (S+/S++), negatively writhed (S−) or denatured (D). These are plotted as a function of circle size and superhelical density in Figure 4a and b using the simulation data reported in Tables 1 and 2. Though writhe can be calculated analytically for simple mathematical closed curves (33,34), applying this to discrete atomistic models of DNA is non-trivial. Therefore, conformational states are assigned based on a simple visual inspection of the final structures obtained from each of the simulations performed, as shown in Figures 2 and 3. The results from the MD simulations define regions on the phase diagram corresponding to a particular conformational state. It is then necessary to deduce the positions of the phase boundary. For simplicity, linear functions have been used to define the phase boundaries in Figure 4a and b, which we feel is appropriate considering the resolution provided by our data obtained to date.

Figure 4.

DNA conformation as a function of circle size and superhelical density at an intermediate GB/SA salt concentration of 0.25 M (a) and a high GB/SA salt concentration of 1M (b). Individual points are plotted for each of the simulations reported in Tables 1 and 2, lines denote the phase boundaries between the regions corresponding to circular (C), positively writhed with either one (S+) or two crossing points (S++), negatively writhed (S−) and denatured (D) DNA.

Phase boundaries for denaturation

The simulations of d(GC)₉₀ at low salt produce the denatured phase at high levels of torsional stress, as in Figure 4a. The denatured state occupies a larger region of the phase diagram for negative superhelical densities because the double-stranded structure is less stable if subjected to underwinding relative to overwinding. Since increasing the size of the nanocircles reduces the bending stress in the duplex, we expect that bigger circles will withstand larger superhelical densities before denaturation occurs. Consequently, we hypothesise that the slopes of the two lines defining the phase boundaries of the denatured states should be positive for overwinding and negative for underwinding, as shown. We do not explore extremely large torsional stresses at high GB/SA salt. Although there is experimental evidence to suggest that DNA is stabilised by increasing salt concentration (35), we assume that this can be neglected to a first approximation. Therefore these phase boundaries are retained in Figure 4b (but are shown as dashed lines).

Phase boundaries for positive writhing

The DNA remains circular at sufficiently small values of overwinding. For larger values, we observe a region of positively writhed DNA at both salt concentrations, which extends toward lower superhelical densities as the circles increase in size. This phase boundary, therefore, has a negative gradient in Figure 4b. At high salt, we observe the highly writhed over-wound structure for d(GC)₁₇₈ (denoted by S++ in Figure 4b to indicate that there is a projection where two crossing points can be detected, as also shown in Figure 3b).

Phase boundaries for negative writhing

In contrast to the over-wound duplexes, no negatively writhed states are observed for under-wound circles at low or medium salt for the small sizes investigated. At high GB/SA salt, we observe the emergence of the negatively writhed phase (Figure 3a) for circles larger than d(GC)₁₁₈. By increasing the size of the circles at a (almost) fixed superhelical density, we see that there is a critical size for the formation of negatively writhed structures that lies between 118 and 148 bp at superhelical densities of between −0.01 and −0.1. The phase boundary, separating circular and writhed states, has a positive slope for under-wound sequences as larger circles writhe more readily for a given amount of torsional stress. Since equivalent size-dependent behaviour is observed for over-wound duplexes, the asymmetry between over- and underwinding observed for small DNA circles will become less pronounced for larger sequences. This is to be expected, as the DNA will behave as a homogeneous elastic rod at low superhelical densities whenever the sequence is much longer than the persistence length.

Observation of a ‘critical point’ in the phase diagram

The emergence of a new phase for a certain critical value of one of the controlling parameters is commonly observed in phase diagrams. This point on the phase diagram is known as the critical point. Similarly, Figure 4b shows that the negatively writhed state does not occur in circles >118 bp for the salt conditions we investigated. Even though we have a finite size system, we refer to this point as a ‘critical point’, making an analogy with phase transitions in bulk systems. Theories of phase transitions predict that particularly large thermal fluctuations will be observed on the approach to the critical point (which makes the precise position of the phase boundary between circular and writhed structures somewhat difficult to define); this is because the free energy surface flattens as the distinction between the two phases disappears (36). Accordingly, we observe that d(GC)₁₁₈ and d(GC)₁₄₈ (constrained at superhelical densities of −0.14 and −0.01, respectively) both undergo particularly large changes in writhe as the nanocircle fluctuates between circular and superhelical configurations.

DISCUSSION

Our simulations show that the writhe of a supercoiled DNA circle is controlled by a delicate balance between opposing energetic terms. The transition from a circular to a writhed conformation reduces the torsional stress, but increases the electrostatic repulsion within the backbone of the DNA. Writhe will be suppressed whenever the twist energy of the DNA is less than the sum of the bending energy at the apices and electrostatic repulsion at points where the two DNA strands are in close proximity (such as the crossing points of the superhelix). Therefore, the formation of writhed superhelical structures occurs at lower superhelical densities for larger circles and at higher salt concentrations.

Although over- and underwinding are equivalent for a homogeneous rod, this is not the case for a real DNA helix, as our simulations clearly show. Over- and underwinding involve very different structural changes within the duplex. We hypothesise that positive writhing occurs more readily because overwinding the DNA reduces the volume of space available to each base within the duplex, whereas untwisting does not. Therefore, positive writhing must occur at a certain critical twist value to relieve van der Waals clashes, regardless of the size of the circle. We also observe that underwinding is more likely to produce melted regions than equivalent levels of overwinding, in agreement with the general idea that negative supercoiling in vivo destablises the duplex and facilitates processes that require strand separation (such as transcription). It is interesting to note that thermophiles possess topoisomerases that are able to introduce positive supercoils into DNA, whereas mesophiles do not (28,37).

Simple homopolymeric sequences were chosen for this study to aid the interpretation of the data. Our calculations show that the formation of circular and higher order DNA structures introduces inhomogeneity into these regular polymeric systems by breaking the helical symmetry of the linear molecule. We observe that the denatured regions formed in under-wound DNA are most likely to occur whenever the minor groove is located on the inside of the nanocircle, in agreement with the results of Lankaš and coworkers. The increased likelihood of melting the DNA through bending into the minor rather than the major groove might very well be exploited by sequence selective DNA-binding proteins that distort the duplex as part of the recognition process. For example, repair proteins often bend the DNA to locally melt the duplex and extract a base into their active site (38,39). Our data also suggests that the hydrogen bonds between complementary base pairs are strained at the apices of supercoils where the bending stress within the duplex large (Figure 4S). The relative accessibility of sequences at the apices of supercoils potentially provides an additional component to DNA recognition events and suggests a possible mechanism whereby writhing and topology can regulate cellular processes. Furthermore, the bending energy required to form the apices of the supercoil is expected to be highly sequence dependent. Therefore, it seems likely that a carefully chosen mixture of relatively stiff and flexible sequence elements could produce very specific superhelical structures under a given set of environmental conditions.

Our data also has the potential to provide quantitative thermodynamic information about the changes in free energy that accompany the formation of higher order DNA structures. The enthalpic term is relatively straightforward to obtain from the simulations. However, entropic changes are also likely to be important, as we have demonstrated in a number of previous theoretical studies of DNA flexibility (40,41). Strand separation, although energetically unfavourable, is able to generate a large amount of entropy. If this favourable entropic contribution is of sufficient magnitude to compensate for the enthalpic penalty associated with under-twisting the DNA, then the torsionally relaxed topoisomer may not be the lowest free energy state for a circle of a given size. The possible role of denaturation bubbles in lowering the free energy of DNA bending has already been studied experimentally (42) and theoretically (43). To calculate this contribution from the MD simulations of nanocircles will require a generalisation of our methodology for calculating entropic changes in oligomers to these far larger systems, which is non-trivial. These calculations are currently underway.