Instability of signaling resolution models of parent–offspring conflict

Abstract

Recent signaling resolution models of parent–offspring conflict have provided an important framework for theoretical and empirical studies of communication and parental care. According to these models, signaling of need is stabilized by its cost. However, our computer simulations of the evolutionary dynamics of chick begging and parental investment show that in Godfray’s model the signaling equilibrium is evolutionarily unstable: populations that start at the signaling equilibrium quickly depart from it. Furthermore, the signaling and nonsignaling equilibria are linked by a continuum of equilibria where chicks above a certain condition do not signal and we show that, contrary to intuition, fitness increases monotonically as the proportion of young that signal decreases. This result forces us to reconsider much of the current literature on signaling of need and highlights the need to investigate the evolutionary stability of signaling equilibria based on the handicap principle.

The study of food solicitation has had a controversial history (1–5). Today, it is commonly believed that begging is a reliable signal, stabilized by its cost, whereby young inform their parents of their need of food. Consider the case of an adult bird rearing young in single-chick broods (1). The optimal parental investment, from the perspective of the chicks and the parents, depends on the condition of the chick. Godfray (1) assumed that chicks beg with intensity x(c) when they are in condition c and parents bring an amount y(x) of food when chicks beg with intensity x (whatever the condition of the chick, assumed to be unknown to the parent). With the assumption that x(c) and y(x) are continuously differentiable, he could derive the functions x*(c) and y*(x) that constitute a Nash equilibrium (6) for the hypothesized fitness functions. At the Nash equilibrium, chicks in lower condition beg at higher intensity and parents provide more food to chicks begging at higher intensity (1), in agreement with the results from most experiments and observations (7). Because at the Nash equilibrium nobody can benefit from a unilateral behavioral modification, it was implicitly assumed that evolution would end up finding this Nash equilibrium: begging, signaling of need, was thus expected to evolve and be stable.

In addition to the signaling equilibrium derived by Godfray (1), the model has a more efficient nonsignaling Nash equilibrium (8, 9), where chicks do not beg and parents provide all chicks with the same amount of food. Our aim was to investigate the evolutionary stability of the signaling and the nonsignaling equilibria. To do this we simulated in the computer the evolutionary dynamics of parent–offspring communication. In the description of these simulations, a function x(c) that assigns a begging intensity x for each condition c will be referred to as an offspring strategy, and a function y(x) that assigns an amount of parental care y for each begging intensity x will be referred to as a parental strategy.

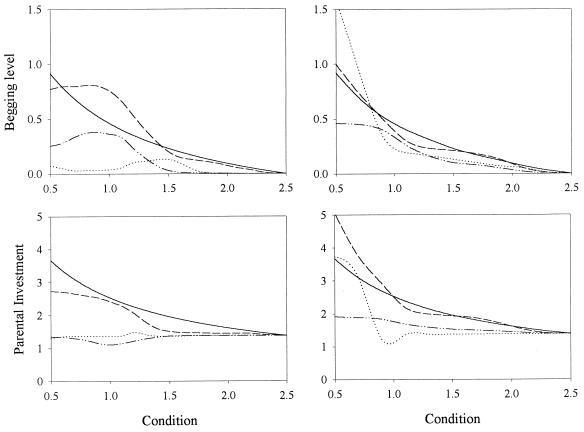
In a first simulation we followed the signaling model (1) as closely as possible. We simulated two populations of N offspring and N parental strategies, competing in a two-round context. In the first round, offspring strategies competed against each other and the payoff of an offspring strategy depended on the strategies present in the parental population at the moment. Each offspring strategy produced 100 (possibly inaccurate) copies of itself. Each copy (the “offspring”) selected at random one parental strategy (the “parent”). The offspring was allocated a random condition c, and the begging level x and parental investment y were determined from c according to the strategies of the offspring and parent. The offspring received a “score” corresponding to its inclusive fitness (1). The second round constituted an analogous competition between the parental strategies, with the pertinent modifications in the calculations of inclusive fitness (1). At the end of each round, the N offspring and N parents with highest scores were selected to constitute the next generation, and the process was iterated. The results of some simulations are shown in Fig. 1, where it can be seen that the signaling equilibrium was not stable. For the parameter values used and small populations (N = 100), the population approached the nonsignaling equilibrium, but for bigger populations (N = 1,000) strong signaling remained at the end of the simulations.

Figure 1.

Two-round contest. Mean begging level (Upper) and parental investment (Lower) plotted as a function of chick’s condition when population size was N = 100 (Left–shows average over five runs) and N = 1,000 (Right–single run). The solid line represents the initial condition and the others values after 1,000, 5,000 (dashed lines) and 10,000 (dotted lines) generations. Young condition c was selected from a rectangular distribution (0.5–2.5) (2). Young and parental inclusive fitness (2) were calculated according to F_ch = (1 − e^−c⋅y) − V⋅x − r⋅γ⋅y and F_p = (1 − e^−c⋅y) − V⋅x − γ⋅y, respectively (V = 0.1, γ = 0.08, r = 0.5). The contest started at the signaling equilibrium. Signaling strategies were coded as interpolation tables which could mutate with probability 0.05. An offspring strategy coded for the begging intensities x(c_i) associated with evenly distributed conditions c_i (i = 0, … nc; c₀ = 0.5, c_nc = 2.5; nc = 20 for N = 100 and nc = 10 for N = 1,000), and a parental strategy coded for the parental investment levels y(x_i) associated with evenly distributed begging intensities x_i (i = 0, … nx; x₀ = 0.0, x_nx = 2.5; nx = 50 for N = 100 and nx = 25 for N = 1,000). The begging strategy for a chick with condition c and the parental response to a begging intensity x were determined from the x(c_i) and y(x_i), respectively, by polynomial interpolation (third order). In case of mutation, a “bump” was added to the table by randomly choosing an integer J (uniform distribution between 0 and nc or nx) and a real z (standard normal distribution) and adding to every entry i in the table the amount 0.2⋅(0.05 + w)⋅z⋅exp[−(8⋅(i − J)/nw)²] where w = x(c_J) and nw = nc for the offspring strategy and w = y(x_J) and nw = nx for the parental strategy. To avoid ending with oscillating strategies, the interpolation tables were smoothed to ensure that they had at most one maximum and one minimum (the highest and lowest values in the table were looked for, and terms were ordered in the three sections: from first term to first extremum, between the two extrema, and between second extremum and end of table).

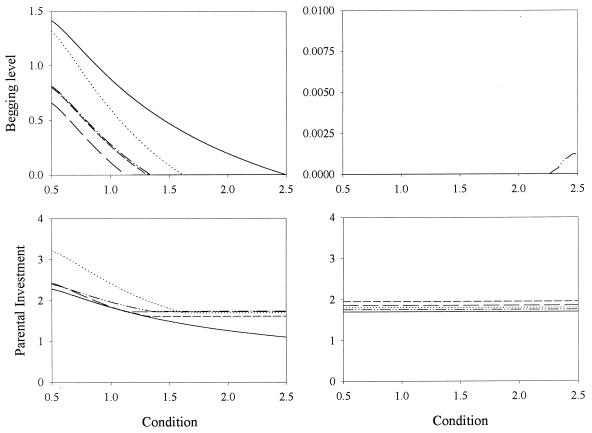
Although the approach used to generate Fig. 1 closely followed the assumptions of Godfray’s signaling model, it failed to incorporate a number of facts that may be important in real populations. In particular, instead of having individuals who used their offspring strategy when young and their parental strategy when breeding, we had a contest between two independent populations of offspring and parental strategies. To overcome this problem we simulated a sexual haploid population living in a set of “territories.” Individuals had a single copy of two genes, coding for an offspring and a parental strategy. In each generation, every adult (the caring parent) reared a young that resulted from mating with a randomly selected individual. Offspring inherited each gene from one of its parents, randomly selected (both genes could be inherited from the same parent, or one gene from each: inheritance of the two genes was independent). The coefficient or relatedness between successive offspring of a caring parent was hence r = 0.5. Each young was randomly assigned a condition c and its begging-strategy gene was used to determine the begging level x. The caring parent used its parental-strategy gene to select an amount of food y that was provided to the young. The quantities c, x, and y were then used to calculate individual fitness (1). At this point young dispersed to randomly selected territories and a new breeding population was selected by choosing, at each territory, a breeder from the previous resident and all the young arriving at that territory. The probability that a given individual was chosen was equal to its fitness relative to the mean fitness at the territory (this constitutes another important difference with respect to the previous simulations, where the globally optimal strategies were selected to form the following generation). By allowing random mutations in the offspring and parental strategies, it was observed that nonsignaling is a stable equilibrium and signaling is not (Fig. 2). Nevertheless, after one million generations begging had not disappeared, and chicks in low condition begged for food as vigorously as ever (although there was a high degree of variability in the strategies of different individuals, not shown in the figure).

Figure 2.

Evolutionary dynamics of begging. Mean begging level (Upper) and parental investment (Lower) are plotted as a function of chick’s condition when the simulation was started at the signaling (Left) and nonsignaling (Right) equilibrium. Note that, because of the specific life history chosen for the simulation, the signaling equilibrium is given by 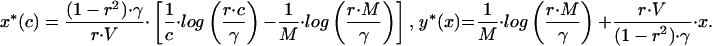The solid line represents the initial condition and the others, values after 250,000, 500,000, 750,000 (dashed lines), and 1,000,000 (dotted lines) generations. The population had 1,225 territories. Young condition c was selected from a rectangular distribution (0.5–2.5) (2). Young and parental fitness (2) were calculated according to F_ch = (1 − e^−c⋅y) − V⋅x and F_p = 1 − γ⋅y, respectively (V = 0.1, γ = 0.08). Young dispersed at random. Signaling strategies could be any linear combination of the signaling equilibrium solution and polynomials of degree up to five. The genes coded for the coefficients of the terms, which could mutate with probability 0.001. In case of mutation, a single coefficient k was selected a random and a value (k + 0.05)⋅0.2⋅z was added to it, where z was a random variate chosen from a standard normal distribution. Mating and dispersal were random, irrespective of “distance” between territories. Qualitatively similar results were obtained with haploid and diploid individuals, when strategies were coded as neural networks or interpolation tables, and when mating and dispersal were restricted to neighboring territories.

Despite their huge differences (asexual vs. sexual reproduction, global and deterministic vs. local and random selection), both simulations produced very similar results. It remains to be investigated whether nonsignaling is a global attractor in big populations and, if it is, the relationship between rate of convergence and population size. If nonsignaling were not a global attractor, or if convergence were very slow, communication could be preserved, despite the lack of stability, essentially forever.

The stability of the signaling and nonsignaling equilibria can be analyzed analytically if discontinuous functions are included in the strategy set. In this case, the model admits partially signaling equilibria where only chicks in low condition signal: chicks with condition c > c₀ do not signal and received an amount of food y₀. Chicks with condition c < c₀ signal at intensity x(c) > x₀ (parents do not respond to signals of intensity below x₀) and receive an amount of food y(x) > y₀. Chicks with condition c = c₀ are indifferent between signaling at intensity x₀ or not signaling. It is shown in the Appendix that although these partially signaling equilibria cannot exist if the strategy set includes only continuous functions, when discontinuous strategies are considered, the set of partially signaling equilibria constitutes a continuum linking the signaling and nonsignaling equilibria in the (c₀, x₀) plane. When the distribution of chick conditions is uniform, and the same fitness functions and parameter values used by Godfray (1) are used, the expected fitness of parents and chicks increases monotonically as c₀ decreases (i.e., as the proportion of chicks that signal decreases) and is maximum for the nonsignaling equilibrium (Fig. 3). It follows that, in a strategy space that includes discontinuous functions, nonsignaling is convergence stable, whereas signaling is not. Because partial equilibria exist for any parameter values and most distributions of chick conditions, and because fitness is higher at the nonsignaling than at the signaling equilibria for a wide range of parameter values and distributions of chick conditions (9), this result is likely to be robust with respect to changes in parameter values.

Figure 3.

Inclusive fitness of parents (solid line) and offspring (dotted line) at the partially signaling equilibria, plotted as a function of the proportion of offspring that signal. Fitness functions and parameter values as in ref. 2.

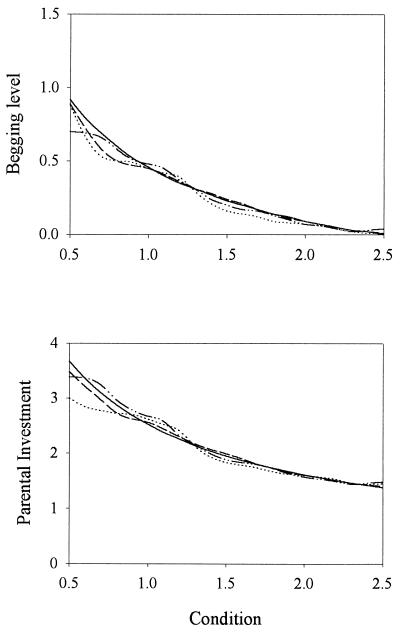
In a strategy space that includes discontinuous strategies, the partially signaling equilibria (together with Fig. 3) would be sufficient explanation for the instability of the signaling equilibrium. In our simulations, however, only continuous strategies were considered. As we proceed to show, the factor responsible for the instability of the signaling equilibrium in the absence of discontinuous strategies seems to be variability in offspring’s condition and its effect on fitness. To a large extent, condition will determine which individuals constitute the next generation: a chick in very good condition with a suboptimal signaling strategy will be more likely to survive than a chick in very bad condition with an optimal strategy. That this factor played a key role in the instability of the signaling equilibrium was demonstrated with a modification of the simulations: for each parent–offspring pair, instead of choosing a random value of c to calculate fitness, parent and offspring fitness were calculated as the average obtained over 25 randomly chosen conditions of the chick. This procedure effectively eliminates variability in chick condition and thus selects the strategies leading to a higher average fitness. With this modification, the population remained at the signaling equilibrium (Fig. 4).

Figure 4.

Importance of stochasticity. Simulations as in Fig. 1 (N = 100), except that the payoff of a strategy was calculated as the average inclusive fitness over 25 random values of c. Similar results were obtained when the simulations were run as in Fig. 2.

Two main conclusions follow from our results. First that our understanding of signaling of need is worse than we thought, and second that the results obtained above seem to contradict empirical observations. There is considerable empirical evidence that begging contains information about need and that parents adjust feeding effort to the level of begging (10–13). This is true both for species with one young and species with several young. Further, there seem to be no examples of species in which begging does not occur.

There are a number of possible causes for this paradox. The most likely possibility is that one or several stabilizing factors present in nature are not included in present analyses of begging. Fig. 4 suggests that an iterated version of the model would be stable. As parents and their offspring interact a large number of times during the rearing period, this might seem a satisfactory solution. There are, however, a number of problems with it. In the long run, (i) the payoffs are not additive and (ii) the fitness functions should be age dependent. These two problems could potentially be solved if the number of iterations is not too large (say, if we consider the parent–offspring interaction during a few hours or a day). If only a short period is considered, however, because the condition of a chick in consecutive visits will be strongly correlated, (iii) the begging strategy will be tested in only a limited range of conditions, instead of being tested in the entire possible range: the situation is then intermediate between that plotted in Figs. 2 and 4 and we have no guarantee that signaling will be stable. As a result, although signaling may well be stable in a dynamic interaction, the full solution of a dynamic model remains to be elucidated. In particular, because of the marked differences between the solutions of static and dynamic games (6), it is possible that the dynamic interaction admits a signaling solution that is both stable and efficient.

An alternative possibility is that what we observe in nature is not evolutionary stability. Begging and feeding strategies may fluctuate within certain ranges over evolutionary time. If so, a positive relationship between need and begging level, and between begging level and parental effort, may nevertheless occur for most (or all) the states of this dynamics, as was the case in our simulation. Similar results have been obtained in recent simulations of signal evolution using artificial neural networks as models of the receiver. In these simulations communication occurs but signaler and receiver constantly change their strategies as biases in the receiver are exploited and the receiver counteradapts (14, 15). The cost of signaling varies over time but is roughly dependent on the degree of conflict between the players involved.

Future studies must address two questions: how signals evolve (10, 16) and how (and whether), once evolved, signaling systems are stabilized or maintained. The existence of a nonsignaling equilibrium where both signalers and receivers have higher expected fitness than at the signaling equilibrium seems to be the norm rather than the exception (8, 17). Most signaling games are likely to admit partially signaling solutions. Whether in sexual selection or in any other context, the “quality” of the signaler will normally have a strong impact on its fitness, whatever its signaling strategy. Furthermore, in many contexts the quality of an individual may be relatively fixed throughout its life, leading to a situation closer to that represented in Figs. 1 and 2 than in Fig. 4. It is therefore possible that our results generalize to other signaling models based on the handicap principle (18, 19). We believe that the evolutionary stability of these models must be critically reexamined.

Partially Signaling Equilibria

We start by introducing some definitions. The expected inclusive fitness of a begging strategy x(c) paired with a parental response y(x), F_ch[x(c); y(x)], is given by (2, 12)

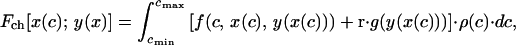A1

where f(c, x, y) is the inclusive fitness of a chick in condition c, begging with intensity x and receiving an amount y of parental provisioning; g(y) is the expected future reproductive success of a parent providing y to its present offspring; r is the coefficient of relatedness between the chick and future offspring; ρ(c) is the probability distribution function for the condition of the young, and c_max and c_min are the maximum and minimum values, respectively, that the condition of the chick may attain. Likewise, the expected inclusive fitness of a parental strategy y(x) paired with a begging strategy x(c), F_p[y(x); x(c)], is given by

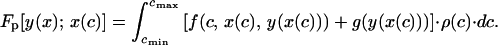A2

For Godfray’s model (2),

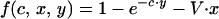A3

and

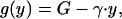A4

where V is the proportional cost of begging, γ is the cost of providing food, and G is a constant.

A partially signaling equilibrium can be defined by c₀ (the condition above which chicks do not signal) and x₀ (the minimum nonzero signal intensity used by chicks). The following conditions must be satisfied at a partially signaling equilibrium. For the parents:

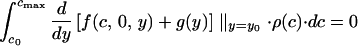A5

and

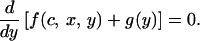A6

Eq. A5 defines the optimal investment level for nonsignaling chicks and Eq. A6, for signaling chicks. In the signaling region, the optimal signaling level is determined by

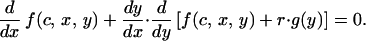A7

Finally, chicks with condition c₀ must be indifferent between signaling (at intensity x₀) or not:

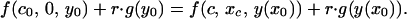A8

Absence of Continuous Solutions.

The conditions that must be satisfied are Eqs. A5–A8 and the continuity conditions x₀ = 0 and y₀ = lim_x→0 y(x). Let us assume that c₀ < c_max. Then we must have

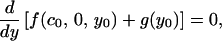A9

which derives from the continuity condition combined with A6. But A5 and A9 cannot be satisfied if c₀ < c_max: because f_yc < 0, if A9 is satisfied the integrand in A5 is always negative, and hence the integral is also negative.

This result shows that we cannot have a partially signaling equilibrium that is continuous in y: if there is a partially signaling equilibrium, one must have y₀ < y(x₀).

Consider now the case where y(x) is discontinuous but x(q) is continuous. In other words, y₀ < y(x₀) (hence discontinuous), and x₀ = x(c₀) = 0 (continuous, because chicks with c > c₀ do not beg). The inclusive fitness of a chick with condition c and begging at intensity x has a maximum at some value y*(c, x) > y_sig(x) (because of the parent–offspring conflict). For y < y*(c, x), F_ch(c, x, y) is an increasing function of y. Suppose now that c₀ < c_max. In this case, y₀ < y(x = 0) and A8 cannot be satisfied. This completes the proof that if a partially signaling equilibrium is to exist, both x(c) and y(x) must be discontinuous.

Discontinuous Solutions.

Consider now the case y₀ < y(x₀) and x₀ = x(c₀) > 0. Parents give a certain amount of food y₀ (defined by A5) if x < x₀ and some increasing amount of food for higher begging levels.

With the fitness functions defined in A3 and A4 it is possible, for every value of c₀, to obtain a value of x₀ such that A5–A8 are all satisfied. The values of x₀ and y₀ increase continuously as c₀ goes from c_max to c_min.