Action-at-a-distance interactions enhance protein binding affinity

Abstract

The identification of protein mutations that enhance binding affinity may be achieved by computational or experimental means, or by a combination of the two. Sources of affinity enhancement may include improvements to the net balance of binding interactions of residues forming intermolecular contacts at the binding interface, such as packing and hydrogen-bonding interactions. Here we identify noncontacting residues that make substantial contributions to binding affinity and that also provide opportunities for mutations that increase binding affinity of the TEM1 β-lactamase (TEM1) to the β-lactamase inhibitor protein (BLIP). A region of BLIP not on the direct TEM1-binding surface was identified for which changes in net charge result in particularly large increases in computed binding affinity. Some mutations to the region have previously been characterized, and our results are in good correspondence with this results of that study. In addition, we propose novel mutations to BLIP that were computed to improve binding significantly without contacting TEM1 directly. This class of noncontacting electrostatic interactions could have general utility in the design and tuning of binding interactions.

The field of protein design has made substantial advances over the last 20 years, based largely on phrasing the appropriate inverse problem and developing methods capable of addressing inverse design (Drexler 1981; Pabo 1983). Much current protein design work involves the construction of stabilizing protein side-chain arrangements by methods such as dead-end elimination (Desmet et al. 1992; Goldstein 1994; Lasters et al. 1995; Gordon and Mayo 1998 Gordon and Mayo 1999; Leach and Lemon 1998; Mendes et al. 1999; De Maeyer et al. 2000; Looger and Hellinga 2001), self-consistent mean-field theory (Koehl and Delarue 1994; Koehl and Levitt 1999a,b; Kono and Saven 2001), simulated annealing (Lee and Subbiah 1991; Hellinga and Richards 1994; Shenkin et al. 1996; Jiang et al. 1997, 2000), genetic algorithms (Tufféry et al. 1991, 1993, 1997; Jones 1994; Desjarlais and Handel 1995), and combinatorial search (Tufféry et al. 1991, 1993, 1997). That is, successful design has been achieved by consideration of detailed atomic interactions and their effect on packing geometry and energetics (Dahiyat and Mayo 1997; Harbury et al. 1998; Calhoun et al. 2003; Kuhlman et al. 2003). The design of protein binding interfaces may be achieved by a similar overall approach, although the additional requirement to treat solvation and electrostatic interactions adds a further layer of complexity (Lee and Tidor 2001a).

An alternative strategy that does not demand the same detailed packing of side chains into an exquisite three-dimensional jigsaw puzzle may be desirable in many cases. One such method involves the enhancement of affinity through relatively long-range electrostatic effects by the mutation of surface residues located somewhat outside of the binding interface. When surface mutations are not located directly at the binding interface, a detailed consideration of packing may be unnecessary. Moreover, when the effects of mutations act over a relatively long range, such as through electrostatic interactions, design attributes should be more tolerant of local imperfections in structural models. Less apparent, however, is how effective these types of mutations can be (since much of the interaction may be screened by solvent), and how particularly favorable mutations of this class can be identified. An important design consideration is the counterplay of favorable intermolecular electrostatic interactions made between the partners in the bound state and unfavorable desolvation costs incurred by each partner due to binding; this balance leads to counterintuitive behavior for the energetics of electrostatic interactions in biological systems (e.g., Hendsch and Tidor 1994 e.g., Hendsch and Tidor 1999^; Lee and Tidor 1997). The lessons learned from detailed analyses of short-range electrostatic interactions, such as salt-bridges and hydrogen-bond networks, may or may not prove to be extendible in a straightforward manner to longer range electrostatic interactions of this nature (termed here “action-at-a-distance” interactions).

We have begun to address these issues by analyzing the affinity of the β-lactamase inhibitor protein (BLIP) for binding the TEM1 β-lactamase, with a focus on electrostatic interactions. Using methods based on a continuum solvation model, we computed the electrostatic contributions to the energetics of TEM1 binding for wild-type BLIP and for a set of BLIP mutants whose changes were focused at surface positions. The degree of electrostatic complementarity between binding partners correlates well with the experimentally determined binding affinities, which suggests that these complementarity tools may be particularly useful both in understanding and in designing surface mutations. To complete the binding analysis, both van der Waals and hydrophobic contributions to the binding energetics were also calculated. Preliminary analysis indicated that change in side-chain entropy was not a significant component of binding energy for the residues examined in this study, and is not considered here.

Our laboratory has previously described a measure of electrostatic complementarity between two binding partners (Kangas and Tidor 1998; Lee and Tidor 2001b). Termed the residual potential and computed from continuum electrostatic calculations, this measure can be expressed numerically as a statistical quantity or viewed graphically overlaid on the structure, which highlights regions of particularly high or low electrostatic complementarity. The consideration of electrostatics in binding involves balancing favorable interactions made between the members of the complex in the bound state with the loss of favorable interactions that each component makes with solvent upon binding. For perfect complementarity, this balance is met such that the interaction potential of the receptor is opposite in sign and equal in magnitude to the ligand desolvation potential. Thus, we may derive a measure, termed the residual potential, that describes the balance:

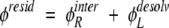(1)

The residual potential is near zero in regions of high complementarity and is larger in magnitude in regions of poorer complementarity. It is important to note that the definition of the residual potential is fundamentally asymmetric, describing the complementarity of the ligand for binding the receptor. A complex for which the ligand is perfectly complementary to its receptor may not be as complementary when the roles of its components are reversed; the receptor may not be perfectly complementary to the ligand (Lee and Tidor 2001b). Also, the definition here applies to binding with no conformational change. While BLIP remains fairly rigid upon binding to TEM1, TEM1 undergoes a subdomain realignment upon binding to BLIP (Strynadka et al. 1992, 1994, 1996). Despite this, BLIP and not TEM1 is mutated in this study, and the thermodynamic cycle of TEM1–BLIP binding may be written such that rearrangement of TEM1 occurs as an energetic constant independent of BLIP. Moreover, it is likely that the energetics of the class of surface mutations pursued here are, for the most part, relatively insensitive to the effects of modest conformational changes upon binding. A numerical statistic for the complementarity of a ligand for its receptor can be obtained from the correlation of the interaction and desolvation potentials, φ_R^inter and φ_L^desolv

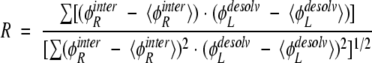(2)

where the summations run over the points of interest (typically sampling the molecular surface of the ligand) and quantities in angle brackets represent averages over the points. For perfect complementarity the correlation coefficient is −1. Negative values smaller in magnitude indicate imperfect complementarity, while positive values indicate anti-complementarity.

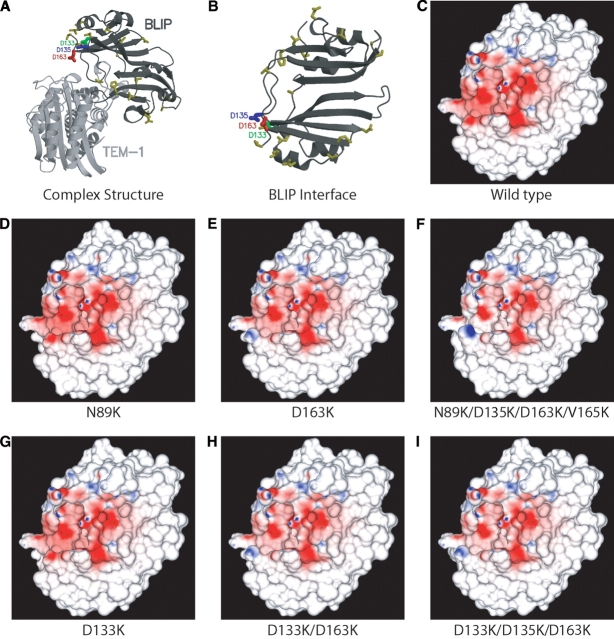
Wild-type BLIP binds to TEM1 with a K_d of 1.25 nM (Selzer et al. 2000), burying 2560 Ų of solvent exposed surface and forming 11 hydrogen bonds and four salt bridges across the binding interface, making it a “large” protein–protein complex by the classification scheme of Janin, Chothia, and Lo Conte (Lo Conte et al. 1999). The residual potential for TEM1 binding on the surface of BLIP was computed and is displayed in Figure 1C ▶, along with an overview of the structure in Figure 1, A and B ▶. The desolvation potential of BLIP is quite complementary to the interaction potential of TEM1 projected onto the BLIP surface; most regions of positive desolvation potential are well matched by regions of negative interaction potential, and vice versa. However, examination of the residual potential makes it clear that BLIP is not perfectly complementary to TEM1. Specifically, the net residual potential is negative over a large area of the binding surface. This can be viewed as either an excess negative interaction potential from TEM1 or as an insufficiently positive desolvation potential from BLIP. Thus, this suggests that the binding affinity of BLIP for TEM1 may be improved by appropriate mutations that increase the relative positive charge on the inhibitor (mutations of acidic residues to neutral or basic residues, and mutations of neutral residues to basic residues) or by mutations that decrease the relative negative charge on the enzyme. However, the asymmetry of the residual potential suggests that such mutations should be targeted to particular regions of the periphery of the interface.

Figure 1.

Structure and residual potential of the TEM1–BLIP complex. (A) Structure of the complex between BLIP and TEM1. Selected mutated side chains are included. Locations of high-activity mutations are labeled individually. Olive-colored residues indicate sites of low-activity mutations. Figure made with Molscript (Kraulis 1991) and Raster3d (Merritt and Bacon 1997). (B) Structure of BLIP at the TEM1–BLIP interface, with residues shown as described in A. (C–I) Residual potentials for TEM1-BLIP binding on the surface of BLIP variants: (C) wild type; (D) N89K; (E) D163K; (F) N89K, D135K, D163K, V165K; (G) D133K; (H) D133K, D163K; (I) D133K, D135K, D163K. Residual potentials are colored on linear scales from 0 to −20 kT/e in red and 0 to 20 kT/e in blue.

To address the question of asymmetry in the effectiveness of mutations, a set of surface residues near, but not at, the binding interface (the “periphery” of the interface) was chosen. The opportunity for improving the electrostatic complementarity of BLIP for TEM1 by mutation of each of these residues to lysine was then evaluated. Mutant structures were built, and their relative electrostatic complementarity and binding affinities were estimated computationally (see Table 1). The results show two classes of single mutants, “low activity” and “high activity.” The low-activity mutations produced little change in ΔG^comput _bind and in R (the residual potential measure of electrostatic complementarity), with estimated enhancements in binding affinity of 1 kcal/mol or less relative to wild type. When the residual potential was examined on a high-resolution computer graphics system, no change could be seen visually (see Fig. 1D ▶). By contrast, high-activity mutations resulted in significant changes in computed electrostatic complementarity and binding affinity. Three of the four BLIP amino acid positions for which high-activity mutations were found, Asp 133, Asp 135, and Gln 161, are a sufficient distance from the TEM1 binding site that no solvent-accessible surface area is buried for these positions upon binding, and negligible changes in van der Waals binding free energy result (less than 0.1 kcal/mol relative to wild type upon mutation to lysine). Nevertheless, computations predict that these mutations improve the binding free energy of the TEM1–BLIP complex by 1.9, 1.4, and 1.2 kcal/mol, respectively. The other, Asp 163, does not contact TEM1 in the wild-type complex structure, but does in the computed model mutation to lysine. To determine whether the contact involving Lys 163 is important for its ability to stabilize the TEM1–BLIP complex, we also studied Lys 163 in an extended conformation that is not significantly buried upon TEM1 binding. In both conformations we find a calculated binding improvement of over 5 kcal/mol, relative to wild type, although the minimized conformation is significantly more favorable than the extended form. Each member of the high-activity class exhibits enhanced electrostatic complementarity as measured by visual examination of the residual potential. Although the strongest patches of noncomplementarity remain, the background of negative residual potential, which fills the TEM1 binding site of BLIP, is reduced. The residual potentials for TEM1 binding of the BLIP mutants D163K and D133K are shown in Figure 1, E and G ▶. When the three highest activity mutations were combined, the computed effects were almost completely additive. This is consistent with the picture that adding just enough positive charge in appropriate locations on the surface of BLIP works to partially cancel the overly negative residual potential, but adding too much positive charge in one region overcancels the negative residual potential and makes it positive. Taken together, these results suggest that changing overall molecular charge alone is insufficient to improve binding affinity in this “electrostatically unbalanced” complex, but that when applied in the appropriate regions, increases in positive charge density can lead to computed enhancements in binding affinity.

Table 1.

Energetic details of mutations to BLIP

BLIP mutations	R	ΔΔGes (kcal/mol)	ΔΔGvdw (kcal/mol)	ΔΔGSASA (kcal/mol)	ΔΔGcalc (kcal/mol)	ΔΔGaexp (kcal/mol)
Wild type	−0.63	0.00	0.00	0.00	0.00	0.00
V3K	−0.64	−0.09	−0.05	0.00	−0.14	N/D
T5K	−0.64	−0.32	−0.02	0.00	−0.35	N/D
E28K	−0.64	−0.02	−0.01	0.00	−0.04	N/D
T32K	−0.64	−0.64	0.05	0.00	−0.59	0.19
H45K	−0.65	−0.41	0.01	0.00	−0.40	N/D
S60K	−0.63	−0.12	−0.01	0.00	−0.12	N/D
A61K	−0.63	−0.21	−0.08	0.00	−0.29	N/D
A77K	−0.64	−0.23	−0.02	0.00	−0.25	N/D
L85K	−0.64	−0.35	−0.01	0.00	−0.35	N/D
N89K	−0.63	−0.14	0.00	0.00	−0.14	−0.47
V93K	−0.64	−0.27	−0.03	0.00	−0.29	−0.49
V134K	−0.64	−0.41	−0.02	0.00	−0.42	N/D
T140K	−0.63	0.37	−0.54	−0.15	−0.32	−0.02
D153K	−0.64	−0.28	−0.01	0.00	−0.29	N/D
Q157K	−0.64	−0.28	0.00	0.00	−0.28	N/D
Q161K	−0.65	−1.15	−0.01	0.00	−1.16	N/D
V165K	−0.64	−0.64	−0.03	0.00	−0.67	N/D
D133K	−0.66	−1.85	−0.04	0.00	−1.88	N/D
D135K	−0.65	−1.32	−0.06	0.00	−1.38	N/D
D163A	−0.69	−5.00	0.93	0.17	−3.90	−1.34
D163K	−0.71	−4.46	−3.22	−0.55	−8.23	−1.99
T140K/Q157K	−0.64	−0.46	−0.54	−0.15	−1.14	−0.41
N89K/D163K/V165K	−0.76	−5.26	−3.12	−0.96	−9.34	−2.40
V134K/D135K/D163K	−0.73	−5.19	−3.29	−0.55	−9.03	−3.06
N89K/D135K/D163K/V165K	−0.77	−5.64	−3.18	−0.96	−9.78	−3.36
D133K/D163K	−0.74	−5.63	−3.21	−0.55	−9.45	N/D
D133K/D135K/D163K	−0.75	−6.15	−3.22	−0.55	−9.87	N/D

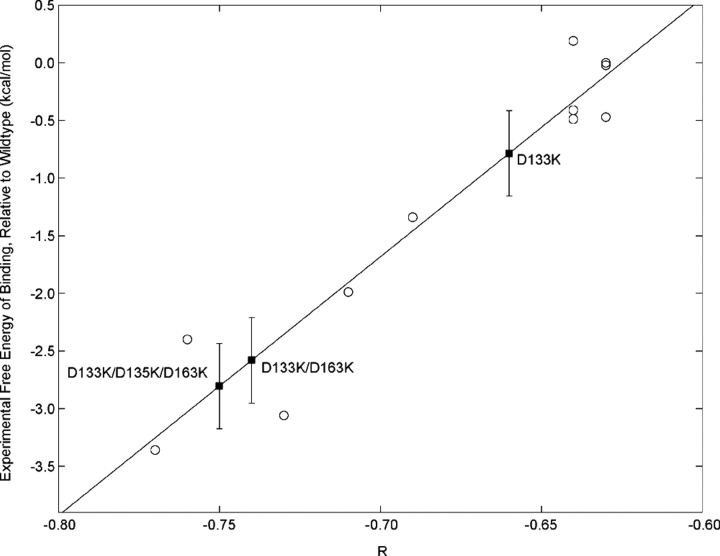
A number of the mutations studied computationally here were also made and studied experimentally and computationally by Schreiber and coworkers (Selzer et al. 2000). For these single mutations the qualitative agreement between experiment and computation is excellent. The low-activity class of mutation, with predicted electrostatic binding enhancements of 0.5 kcal/mol or less, all produced small binding enhancements experimentally (less than 1 kcal/mol, relative to wild type). The only single mutation for which our computations predict high activity that was studied, D163K, was shown experimentally to enhance binding affinity by 2.0 kcal/mol. A D163A mutant was also studied experimentally, and calculations made for this mutant show similar results (see Table 1). Four multiple mutants included in the study by Selzer et al. (2000) were modeled and subjected to the same computational analysis. Again, the computational analysis reproduces the experimental division between a single low-activity mutant and three high-activity mutants. Overall, the calculated results show good agreement with the experimental data. One illustration of this is the strong correlation of the experimental binding free energies to those calculated here. The fact that similarly strong correlation is found between experimentally determined binding free energy and the residual potential statistic, R (Fig. 2 ▶) suggests that electrostatic effects are a primary means by which these mutants act, as reflected in an improvement of overall electrostatic complementarity. Thus, the residual potential and its quantitative analysis show significant promise as tools for understanding, and potentially designing, these types of surface mutations, some of which act via through-solvent interactions, to promote binding.

Figure 2.

Variation of experimental binding free energies with R, the correlation coefficient between the BLIP desolvation potential and the TEM1 interaction potential, calculated on the surface of BLIP. Open circles indicate mutants previously characterized (Selzer et al. 2000). The correlation coefficient of R and the experimental binding free energy is 0.96. The diagonal line indicates the least-squares best fit. Black squares indicate novel mutants characterized computationally, and are placed on the best fit line. Error bars on novel mutants indicate the standard deviation of points for which an experimental binding affinity has been calculated from the best-fit line.

Three of the multiple mutants studied by Selzer et al. (2000) contained the D163K mutation: N89K/D163K/V165K, V134K/D135K/D163K, and N89K/D135K/D163K/V165K. These multiple mutants alter the total charge on BLIP by +4e, +5e, and +6e, respectively, and we calculate for them improvements in binding free energy of −9.3, −9.0, and −9.8 kcal/mol (electrostatic components of −5.3, −5.2, and −5.6 kcal/mol), respectively, relative to wild type. Two of these contain the additional high-activity mutation D135K. The correlation of the interaction and desolvation potentials is improved for these mutants relative to D163K, and a decrease in the excess negative residual potential can be seen (see residual potential for the +6e mutant, Fig. 1F ▶). These results also agree with experiment; N89K/D163K/V165K, V134K/D135K/D163K, and N89K/D135K/D163K/V165K have experimental improvements in binding free energy of 2.4, 3.1, and 3.4 kcal/mol, respectively, all higher affinity than D163K alone. Despite the fact that each of these multiple mutants has a significant steric improvement in computed binding affinity, this improvement is prompted by the D163K mutation in every case. The strong correlation of the residual potential statistic, R, with experimentally determined binding free energies for these multiple mutants leads us to believe that electrostatics is nonetheless the primary cause for improvement with these mutations, and that the high computed steric improvement is the source of most of the discrepancy between experimental and computed values of ΔΔG_bind (see Fig. 2 ▶). It is possible that imbalances between protein–protein and protein–solvent dispersion and steric interactions are responsible for the significant overprediction of binding energies of some mutants. This imbalance would affect only the nonelectrostatic contributions to binding and thus would not change the interpretation of electrostatic action-at-a-distance interactions presented here. Work to address this imbalance is ongoing (S.M. Lippow, K.D. Wittrup, and B. Tidor, unpubl.).

The calculations suggest that the best previously uncharacterized mutant, D133K, could likewise be improved by combination with other favorable mutations. The multiple mutants D133K/D163K and D133K/D135K/D163K alter the net charge on BLIP by +4e and +6e. For these structures, our calculations predict binding free energies of −9.4 and −9.9 kcal/mol relative to wild type, with electrostatic components of −5.6 and −6.2 kcal/mol, respectively. It is noteworthy that the D133K/D135K/D163K triple mutant has a better computed binding free energy than any other mutant considered in this study. The residual potential for this triple mutant is shown as Figure 1I ▶.

We have examined the computed binding free energy and electrostatic complementarity of a series of mutants of the β-lactamase inhibitor protein and analyzed the results with comparison to experimental binding free energies to TEM1 β-lactamase. We find that the correlation coefficient of the BLIP desolvation potential and the TEM1 interaction potential on the surface of BLIP is strongly correlated to the experimental binding free energies. In addition, this increased correlation can be seen visually as a reduced residual potential in many cases. A previously uncharacterized mutation of Asp 133 to Lys is proposed, which calculations suggest would enhance binding affinity both alone and in concert with previously identified mutations. The effects of these mutations are localized to the extent that they act on patches of the surface, somewhat locally improving the residual potential. However, the interactions are not specific; three of the four most effective mutation locations (D133, D135, and Q161) are > 7 Å from TEM1, and the D163K mutation has similar computed effects even in different conformations. This helps to confirm the overall mechanism by which these mutations act; relatively long-range electrostatic interactions act through a region of solvent to improve the overall electrostatic complementarity of the ligand for its target receptor. More generally, favorable action-at-a-distance electrostatic interactions may occur at regions of the protein surface which are close enough to the binding site to allow for a significant charge–charge attraction between ligand and receptor, but far enough away that the desolvation penalty incurred by placement of the charge is small. We expect that the electrostatic action-at-a-distance interaction is used widely in biology, both as a means of improving binding when tight binding is required, and as a more general means of modulating free energy of binding to achieve a desired degree of affinity. Moreover, the general mechanism of long-range projection of electrostatic potential may play a part in other biomolecular functions such as folding and catalysis. Further work investigating more generally the design of surface mutations that permute the residual potentials toward increased complementarity is ongoing (D.F. Green, B.A. Joughin, and B. Tidor, in prep.).

Materials and methods

All calculations were performed using the 1.7 Å crystal structure of the BLIP–TEM1 complex solved by James and coworkers as an initial model (Strynadka et al. 1996). Hydrogen atoms were added using the HBUILD facility (Brünger and Karplus 1988) within the CHARMM computer program (Brooks et al. 1983) with the PARAM22 all-atom parameter set (MacKerell et al. 1998). Visual analysis of the hydrogen-bonding patterns including ionizable groups indicated that all ionizable residues should retain their standard protonation states (structure solved at pH 8.8). This resulted in a net charge of −2e for BLIP and −7e for TEM1. Moreover, all water molecules were removed in the calculations (there was no interfacial solvent).

Residues on BLIP were selected for mutation by visual examination of all residues between 6 Šand 15 Šfrom any atom in TEM1 in the bound complex that also expose > 40 Ų of solvent accessible surface area. From these, proline, cysteine, and glycine residues were discarded, as were any residues that appeared to make structurally significant intramolecular hydrogen bonds. In addition, we chose representative positions to mutate from strings of positions contiguous in sequence space. Finally, we chose to model the mutations to D163 suggested by Selzer et al. (2000) and to D133 based on a continuum electrostatic analysis of the detailed contributions of the individual side chains of BLIP to TEM1 binding (D.F. Green, B.A. Joughin, and B. Tidor, in prep.).

Model structures of single mutants to BLIP were generated by holding all backbone atoms and all nonmutated side chains fixed, while allowing mutated side chains to take the lowest energy conformation achieved by minimizing in CHARMM with a distance-dependent dielectric of 4r from seed locations generated by combinatorially scanning all side-chain dihedral angles in 30° increments in the TEM1-bound state. Multiple mutant model structures were created by combining independently generated single mutant side chains when the mutations were located more than two residues apart in the BLIP sequence. When mutant residues were in closer proximity, the side-chain structures were generated simultaneously in the same manner as single mutants, but with coarser dihedral scanning in 120° increments.

Binding free energies were calculated as the sum of van der Waals, solvent-accessible surface area, and continuum electrostatic terms, using the approximation of rigid-body docking. The van der Waals contribution to binding free energy was calculated with the PARAM22 set of parameters for the program CHARMM. The solvent-accessible surface area contribution was calculated in the manner suggested by Sitkoff et al. (1994), with the surface area contribution to the free energy of a structure calculated as 5.4 calories per square ångstrom of surface area plus a constant of 920 calories. The contribution of burying surface area to binding free energy is then calculated as the difference between the complex free energy and the sum of the free energies contributed by the unbound BLIP and TEM1 surface areas.

Continuum electrostatic calculations were performed by numerical solution of the Poisson-Boltzmann equation, using a locally modified version of the program DELPHI (Gilson et al. 1988; Sharp and Honig 1990a,b) with PARSE atomic radii and partial atomic charges (Sitkoff et al. 1994). A grid of 257 × 257 × 257, with a spacing of 0.29 Å, was used to calculate electrostatic binding free energy. Residual potentials were calculated from a coarser 129 × 129 × 129 grid to decrease the difficulty of storing and plotting surface potentials. For all electrostatic calculations, a protein dielectric constant of 4 and a solvent dielectric of 80 were used, along with an ionic strength of 0.145 M and a 2.0 Å ion exclusion layer. Surface potentials were displayed and numerically analyzed with locally developed software.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.041283105.