Abstract
Success in high-resolution protein–protein docking requires accurate modeling of side-chain conformations at the interface. Most current methods either leave side chains fixed in the conformations observed in the unbound protein structures or allow the side chains to sample a set of discrete rotamer conformations. Here we describe a rapid and efficient method for sampling off-rotamer side-chain conformations by torsion space minimization during protein–protein docking starting from discrete rotamer libraries supplemented with side-chain conformations taken from the unbound structures, and show that the new method improves side-chain modeling and increases the energetic discrimination between good and bad models. Analysis of the distribution of side-chain interaction energies within and between the two protein partners shows that the new method leads to more native-like distributions of interaction energies and that the neglect of side-chain entropy produces a small but measurable increase in the number of residues whose interaction energy cannot compensate for the entropic cost of side-chain freezing at the interface. The power of the method is highlighted by a number of predictions of unprecedented accuracy in the recent CAPRI (Critical Assessment of PRedicted Interactions) blind test of protein–protein docking methods.
Keywords: protein–protein docking, side-chain modeling, rotamer minimization, side-chain entropy
Protein–protein interactions play an essential role in many biological processes because many cellular events involve the formation of protein–protein complexes. Elucidation of the structural details of these complexes will undoubtedly contribute to our understanding of their functional properties, and thus is a major goal of structural biology (Camacho and Vajda 2002; Halperin et al. 2002; Smith and Sternberg 2002; Vajda and Camacho 2004). However, only a small fraction of experimentally determined structures are of protein–protein complexes (Berman et al. 2000). Therefore, it is of substantial interest to develop computational docking methods that, given the structures of the individual component proteins, are able to assemble them into the complex in an accurate and reliable way.
Many early and current methods for protein–protein docking use the rigid-body approximation in which the backbone and side-chain conformations of the protein components are kept fixed throughout the simulation. Search strategies, such as the fast Fourier transform (FFT) (Katchalski-Katzir et al. 1992; Gabb et al. 1997; Chen and Weng 2002), geometrical hashing (Norel et al. 1999), Boolean operations (Palma et al. 2000), and genetic algorithms (Taylor and Burnett 2000; Gardiner et al. 2001), have been used to rapidly search rigid-body orientation space. Not surprisingly, these methods have shown strengths in solving docking problems where there is excellent shape complementarity, for example, to reassemble a protein complex from its co-crystallized components. However, protein interfaces exhibit considerable plasticity, and conformational changes of backbone and/or side chains are often observed at the protein interface upon formation of the complex. This has been addressed in the context of rigid-body docking using a reduced protein model (Vakser et al. 1999; Zacharias 2003) or softened protein surfaces (Gabb et al. 1997; Palma et al. 2000) to allow some tolerance of atomic clashes across protein interfaces. Alternatively, side-chain flexibility has been represented explicitly in some docking methods. Jackson and coworkers (Jackson et al. 1998) used a self-consistent mean field approach to iteratively refine protein side chains in the models generated by their rigid-body docking program, FTDOCK, and found that the refinement of side-chain conformation led to an improvement in interface geometry. In another flexible docking study, Lorber et al. (2002) showed that introducing multiple conformers for each interface residue leads to a better discrimination between near-native and nonnative models. Similarly, Fernandez-Recio et al. (2002) carried out Biased Probability Monte Carlo Minimization to optimize the interface side chains in a large-scale test including 24 protein–protein complexes and concluded that for most of the targets the near-native solution was significantly better ranked after the side-chain refinement step. However, in all these methods, side-chain flexibility is limited to the ligand interface only.
Recently, we developed a new docking program, Rosetta-Dock, to predict protein–protein interactions (Gray et al. 2003). Unlike grid-based rigid-body docking methods, we retain a full atomic representation of the protein partners and allow side-chain conformations of the interface residues on both receptor and ligand to change in the course of optimizing the rigid-body displacement. Side-chain flexibility in RosettaDock was modeled through a protocol initially implemented in protein design, as described by Kuhlman and Baker (2000). It uses a simulated annealing algorithm that searches through backbone-dependent rotamers from the expanded 2002 Dunbrack rotamer library (Dunbrack and Cohen 1997) supplemented with additional rotamers generated by varying χ angles by + and −1 standard deviation. To eliminate the potential bias imposed by optimizing side chains at different interfaces in different models and to save computation time, the side chains of each protein component are rebuilt from rotamers before docking (prepacking) and only side chains of interface residues are subjected to refinement later in docking. Such treatment of modeling side-chain conformations might have two shortcomings: (1) Side-chain conformations are restricted to discrete rotamers which may hinder accurate modeling of the details of interatomic interactions; (2) useful information on the side-chain conformations in the unbound structures is discarded due to the rotamer-based prepacking.
In this paper, we describe our efforts to enhance the performance of RosettaDock by improving its handling of side-chain flexibility by (1) implementing a torsion minimization step in cycling through alternative rotamers to sample the off-rotamer space, and (2) including the side-chain information from the unbound native structures in side-chain packing. We show that the new method increases the accuracy of side-chain modeling and improves the energetic discrimination between native-like and nonnative-like docking models. We also demonstrate that the new treatment creates a distribution of side-chain interaction energies within and between the two component proteins that is more similar to the distribution observed in native protein complexes. Finally, we show results with our improved docking method in the CAPRI experiment (Janin et al. 2003) and illustrate how the accurate modeling of interface side-chain conformational changes contributed to successful predictions.
Results
We begin this section by describing an approach to going beyond the rotamer approximation by introducing continuous minimization of torsion angles into the side-chain optimization process. We first test this approach both in the repacking and redesign of monomeric proteins (Fig. 2 ▶). Next, we combine this approach with the inclusion of side-chain information from the unbound structure, and test the performance of the method in the repacking of protein–protein interfaces (Figs. 3 ▶–5 ▶ ▶). We show that the new method of modeling side-chain conformations improves the recognition of close-to-native complexes in docking calculations (Fig. 6 ▶). Finally, we show examples of the use of the new method in the recent CAPRI protein–protein docking challenge (Fig. 7 ▶).
Figure 2.
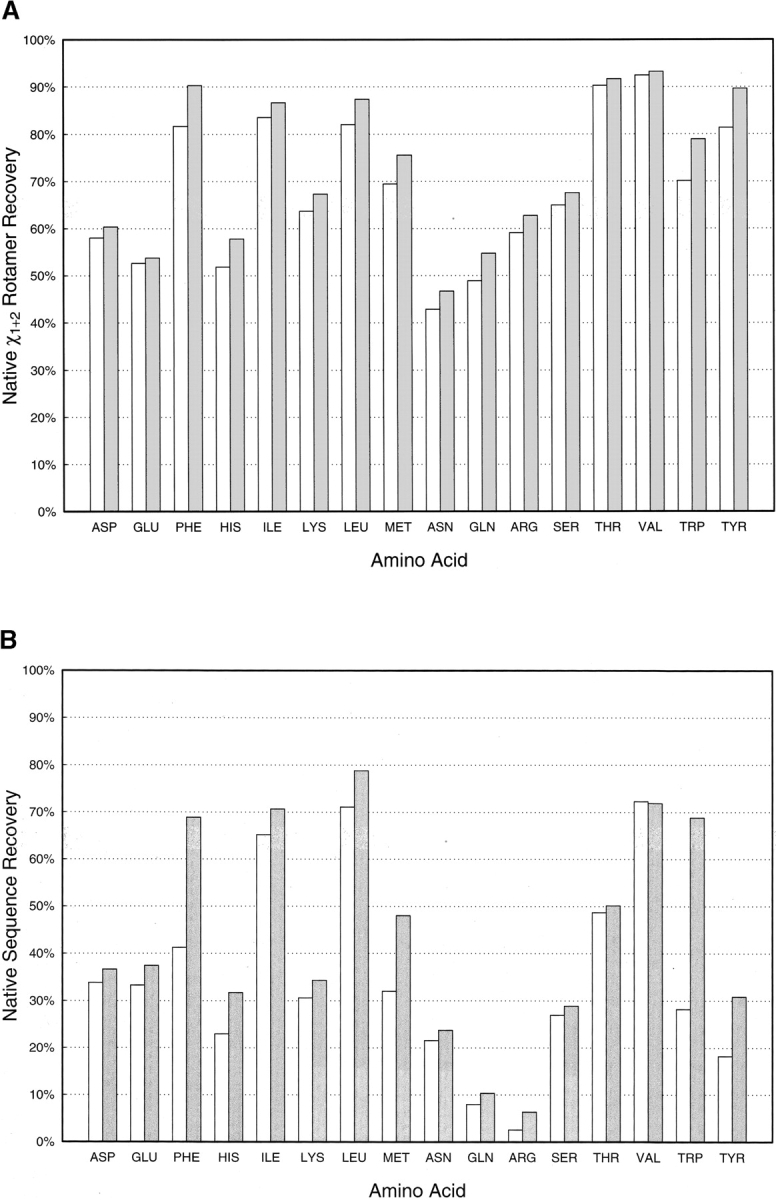
RTMIN improves side-chain repacking and sequence redesign in monomeric proteins. (A) Side-chain repacking test; (B) sequence redesign test. The results are shown in the figure for the standard packing protocol (white) and the standard packing protocol plus RTMIN (gray). In both tests, positions which are ALA, GLY, PRO, and CYS in the native sequence are excluded from the calculation. (ALA and GLY do not have rotamers; PRO has such a restrained side chain that very limited torsion space is accessible to minimization; CYS is often involved in formation of disulfide bonds and may not be modeled properly without a more specialized treatment). In the side-chain repacking test, a side chain is considered to be correctly predicted if its angular deviations are <40° for both χ1 and χ2 angles from the native conformation. In the sequence redesign test, each sequence position is selected one at a time, with the rest of the protein fixed in its native conformation. Twenty amino acids with all their possible rotamers are considered at this position. The rotamer which yields the lowest energy determines the residue chosen for this position. If it matches the native amino acid, this sequence position is considered to be recovered. The first and last five residues in the protein are excluded from the sequence redesign test.
Figure 3.
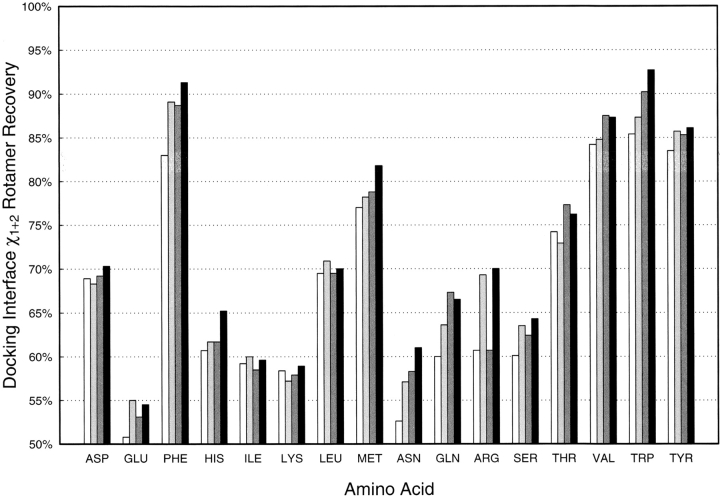
Comparison of results of side-chain repacking of interface residues in native complexes. The side-chain packing results are shown in the figure for the standard side-chain packing protocol (white), the standard side-chain packing protocol plus RTMIN (light gray), the standard side-chain packing protocol including native unbound rotamers (dark gray), and the standard side-chain packing protocol including native unbound rotamers and RTMIN (black).
Figure 4.
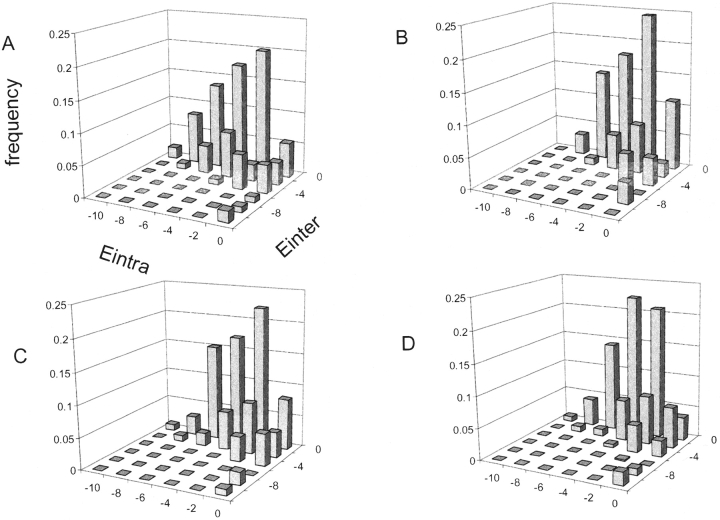
Assessment of side-chain modeling based on residue interaction energy distributions. Distribution of interface residue energies within and between the protein partners (Eintra vs. Einter) for Arginine: (A) native bound protein complexes; (B) native bound protein complexes with repacked interfaces using the standard packing protocol; (C) native bound protein complexes with repacked interfaces using the improved side-chain modeling protocol (the standard packing protocol including unbound native rotamers and RTMIN); (D) true positive models (TP, low-score and low-RMSD models) of the bound docking perturbation runs using the improved side-chain modeling protocol (see Materials and Methods). When native interfaces are repacked, increased similarity to the native distribution is seen with the improved protocol, compared to the original protocol; note that in B, entropically unfavorable combinations (Eintra ~ 0, Einter ~ 0) are enriched, while entropically favorable conformations (Eintra ~ 0, Einter << 0 and Eintra << 0, Einter ~ 0 are less frequent, or even absent. There are 110 and 998 ARG interface residues included in the calculation in the native complexes (A–C) and the true positive models (D), respectively. The figure was created using Microsoft Excel.
Figure 5.
Recapitulation of side-chain conformational changes in docking. Distributions of the number of residues that are conserved in rotamer conformation upon binding are shown for the interface GLU (A); ILE (B); ARG (C). White bars represent the counts for all interface residues. Gray bars represent the counts for those residues that do not change rotamer conformation upon binding. Symbol points represent distributions after repacking the interface of the native complex using different side-chain modeling protocols: standard packing protocol (open circle); standard packing protocol with RTMIN (cross sign); standard packing protocol including native unbound rotamers (plus sign); standard packing including native unbound rotamers and RTMIN (open square). The counts are distributed into bins of residue energy values in the native unbound structures. The white bars represent the extreme level of rotamer conservation assumed by classical rigid-body docking methods with all side chains fixed, while the gray bars show the distribution that a perfect flexible side-chain docking method which accounts for the right degree of side-chain flexibility would achieve. The symbol points indicate how well the different side-chain modeling methods handle the balance between rotamer conservation and side-chain flexibility.
Figure 6.
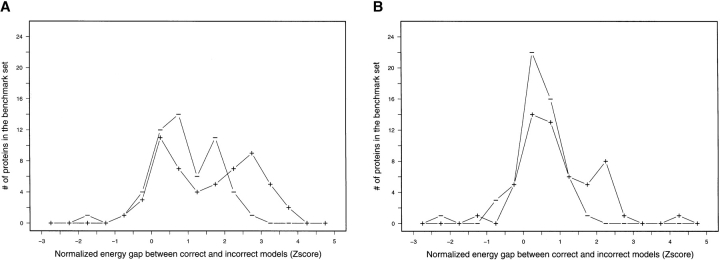
The improved side-chain modeling method significantly improves the energy separation between correct and incorrect models. The normalized energy gap (Z-score) between near-native and nonnative models was computed as described in the Materials and Methods section for docked conformations generated for the 54 protein complexes in the benchmark of Chen et al. (2003). The Z-scores for the 54 protein complexes were binned into intervals of 0.5 Z-score units and the count for each bin is plotted in (A) bound docking perturbation studies with the standard side-chain modeling protocol (“−”) and with the improved side-chain modeling protocol (“+”). (B) Unbound docking perturbation studies with the standard side-chain modeling protocol (“−”) and with the improved side-chain modeling protocol (“+”). For both the bound and unbound cases, there are a significantly larger number of proteins with an energy gap between correct and incorrect docked arrangements >1 standard deviation (Z-score >1) when the new side-chain modeling method is applied.
Figure 7.
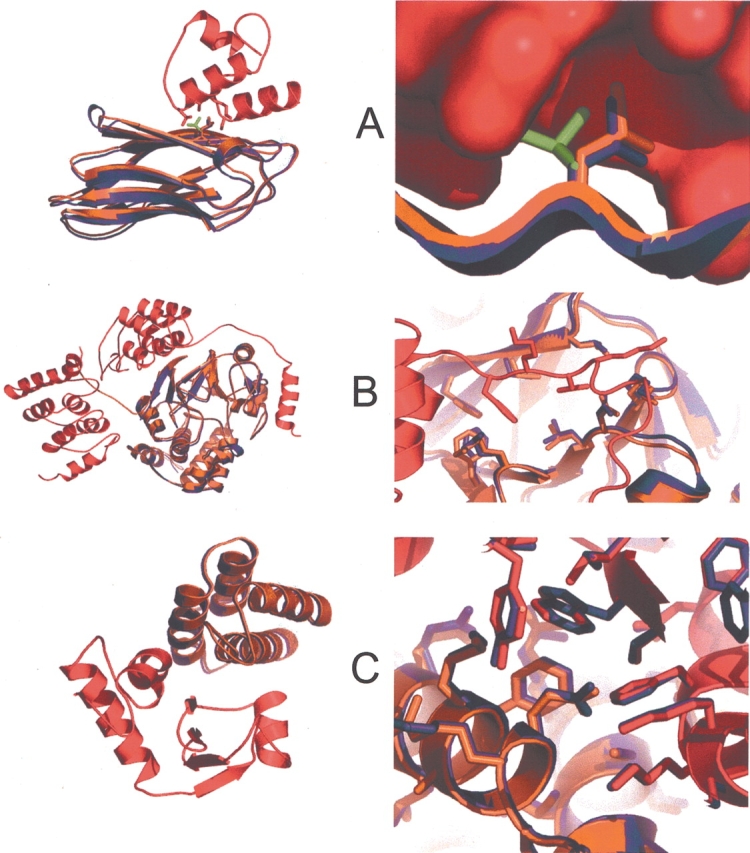
Examples of accurate predictions in the CAPRI experiment. Overview of backbone orientation (left) and zoom-in view of side-chain prediction (right) of our predicted models in the CAPRI experiment are shown for (A) Target 12: Dockerin–Cohesin complex (Shimon et al. 1997; Lytle et al. 2001; Carvalho et al. 2003) (I_RMSD = 0.27 Å), (B) Target 14: MYPT–PP1 complex (Goldberg et al. 1995; Terrak et al. 2004) (I_RMSD = 0.38 Å), (C) Target 15: ImmD–ColD complex (Graille et al. 2004) (I_RMSD = 0.23 Å) (see http://capri.ebi.ac.uk for detailed description of CAPRI targets and evaluation reports). The predicted model is superimposed onto the native complex by the receptor backbone. The receptor and ligand of the native complex are colored red and orange. The ligand of the predicted model is colored blue. In Target 12, the side chain of LEU83 in the unbound conformation (green) clashes with the receptor in the native rigid-body position and it is moved to the native side-chain conformation after docking. This demonstrates the necessity of allowing side-chain flexibility in docking.
Illustration of difficulty with rotamer-based modeling
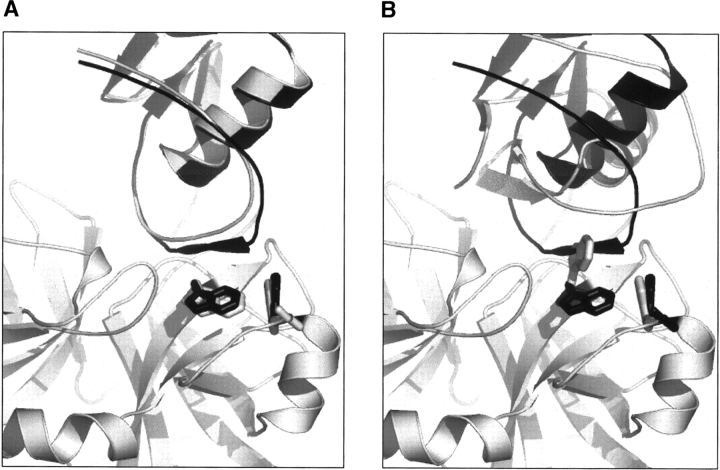
We were motivated to develop our method for going beyond the rotamer approximation by considering the example shown in Figure 1 ▶. In a docking study of the α-Chymotrypsin/Ovomucoid third domain complex (PDB: 1CHO), we found that a near-native model had a higher energy than many nonnative models due to clashes between the side chains of TRP172 and TRP215 (Fig. 1A ▶). In fact, the two side chains are both in rotameric states similar to the native side-chains, with deviations of <25° on χ1 and χ2 angles. But because TRP has a bulky aromatic side chain, relatively small inaccuracies in torsion space can be amplified in terms of displacements of atom positions. In this example, the distance between CZ2 of TRP215 and CE3 of TRP172 decreases from 3.9 Å in the native to 2.9 Å in the model. Since the side-chain packing method used to generate the model is restricted to a discrete set of rotamers from the rotamer library, the only way to avoid such side-chain clashes is to select different rotamers. As illustrated in Figure 1B ▶, the side chain of TRP215 is rebuilt with a nonnative rotamer. Although the clashes between the two TRPs are totally released in this case, the nonnative conformation of TRP215 forces the other protein to shift into a nonnative rigid-body orientation.
Figure 1.
Rotamer approximation of side-chain conformations restricts accurate docking of 1CHO. (A) Low-RMSD model with a high energy due to side-chain clashes between Trp172 and Trp215. (B) High-RMSD model with a low energy with the clashes relieved. The predicted models are superimposed on the native complex structure based on the receptor backbone. The receptor backbone is colored gray. The ligand and the receptor Trp172 and Trp215 side chains in the native complex structure and in the predicted structure are colored black and gray, respectively.
The 1CHO example highlights limitations of rotamer-based side-chain modeling in protein–protein docking. One solution to this problem is to utilize very large, finely sampled rotamer libraries. This is the approach taken by Looger and Hellinga (Looger et al. 2003) in their ground-breaking ligand binding site design, which involved up to 5000 rotamers at each designed position, and by Xiang and Honig (2001), who achieved excellent side-chain packing results with a rotamer library with over 7560 members. For large interfaces, which can involve many tens of residues, such large libraries become intractable, particularly for problems such as flexible backbone design and protein docking, which require iterative repacking/redesign of the interface. An alternative to very finely sampled rotamer libraries is to have an efficient mechanism for exploring side-chain conformational space beyond that defined by a discrete rotamer library. It is important to note that simply minimizing the energy at the end of a rotamer search is not sufficient, as the correct rotamer may be present in the library but not selected by the packing algorithm because it makes clashes that could be relieved by a few degree changes in a χ angle (Fig. 1 ▶; continuous minimization is unlikely to produce large changes in side-chain conformations due to the sizable torsional barriers). Thus, side-chain χ angles must be optimized during or prior to the searching through rotamer combinations, which could potentially be quite expensive computationally. The evolutionary algorithm of Yang et al. (2002) and the genetic algorithm of Desjarlais and Handel (1999) used a stochastic search to explore off-rotamer states, and Havranek and Harbury (2003) used gradient-based minimization methods to optimize side-chain–backbone interactions prior to their mean field combinatorial optimization.
Rotamer trials with side-chain minimization (RTMIN)
To resolve the problem illustrated in the 1CHO example above, we sought to develop a method that combines the advantages of combinatorial rotamer-based searching of side-chain configurational space with continuous minimization. The method, which we call “rotamer trials with side-chain minimization (RTMIN),” is described in detail in the Materials and Methods section, and only a short overview is given here. Starting with the lowest energy conformation obtained in a standard combinatorial simulated annealing rotamer optimization, each side-chain is selected one at a time and allowed to sample each of its possible rotamer conformations. The χ angles for each of these rotamers are then subjected to a torsion space minimization procedure using the Davidon-Fletcher-Powell (DFP) Quasi-Newton algorithm (Press et al. 1992) with the rest of the protein held fixed, and the energy is evaluated. After all possible rotamers of a given residue are minimized, the “minimized” rotamer with the lowest energy is selected and the side-chain coordinates are updated. The procedure is then repeated with a residue randomly chosen from the positions which have not been surveyed. The additional minimization step enables us to go beyond the limitations of a discrete rotamer library and sample a continuous spectrum of side-chain conformations. Related approaches have been described previously (Dunbrack and Karplus 1993; Vasquez 1995).
Side-chain packing and sequence design tests
We first validate the method in side-chain packing and sequence design tests using high-resolution monomeric proteins. Figure 2A ▶ shows the results of repacking side-chains of 129 monomeric proteins with and without RTMIN. For each protein, all the side chains except those of ALA, GLY, PRO, and CYS are removed and rebuilt first with standard rotamers from the Dunbrack rotamer library using the combinatorial packing protocol (see Materials and Methods). Then, the repacked structure is subjected to one cycle of RTMIN. The extent of native side-chain recovery is calculated for both the repacked structures and the minimized structures grouped for each residue type. For all amino acid side chains, the minimized structures exhibit a higher frequency of recovery of native rotamers over the nonminimized structures. The improvements are especially dramatic for amino acids with aromatic side-chains (PHE, TYR, TRP, HIS) and long aliphatic side chains (MET, LEU). In Figure 2B ▶, for each of the same set of monomeric proteins, we design one sequence position at a time in the context of the native structure using standard rotamers with and without RTMIN. Similarly, a higher percentage of native sequence recovery is observed for all 16 residue types when RTMIN is implemented in the design protocol. The most striking examples are TRP and PHE, for which 20% and 15% increases are obtained with RTMIN. These results show that going beyond rotamer limitations can considerably improve the quality of side-chain packing in models, which is critical for structure prediction, design and docking.
Inclusion of native rotamers from unbound structures
While prediction/design of a monomeric protein requires rebuilding side chains from scratch onto a given backbone, in protein–protein docking the core side-chain conformations are unlikely to change, and the side-chain modeling problem in this context becomes modeling the change in conformations at the interface of the complex. In classical rigid-body docking methods, side chains are frozen all the time and the underlined assumption is that side-chains at the interface do not change their rotamers frequently so that they do not have to be remodeled. This assumption appears not unreasonable in many cases, given that approaches lacking side-chain flexibility have been successful in quite a few docking predictions. In a recent survey on a set of known protein complexes and their unbound components, it was found that at least 50% side chains at the interfaces do not switch rotamer conformations upon binding (K. Wiehe and Z. Weng, pers. comm.). Thus, side-chain flexibility in docking should be modeled with care.
In contrast to the classical rigid-body methods, the docking protocol described by Gray et al. (2003) discards the side-chain information completely from the unbound structures, since side chains are always removed and then rebuilt from scratch prior to a docking simulation. In order to overcome this shortcoming, we tested including native rotamer information from the unbound structures as additional context-specific rotamers in the rotamer library used for side-chain modeling in docking. These native unbound rotamers are assigned low internal energies (see Materials and Methods) to favor them during the cycles of side-chain refinement during docking.
The new side-chain modeling method improves packing of native interfaces
Analysis of rotamer recovery
We first tested our new treatment of side-chain flexibility in improving interface rotamer recovery in native protein–protein complexes (Fig. 3 ▶). Native side-chains at the interface (excluding ALA, GLY, CYS, and PRO) are removed from the backbone of the complex structure and regenerated using four different protocols: standard repacking (white), standard repacking with a subsequent cycle of RTMIN (light gray), standard repacking with additional native unbound rotamers in the library (dark gray), and standard repacking with the unbound native rotamers and RTMIN (black). As shown in the figure, combining the inclusion of native unbound rotamers and RTMIN together increases the side-chain recovery for all residues. LEU, ILE, GLU, and ARG benefit more from the off-rotamer search by RTMIN, and the contributions from native unbound rotamers seem to be dominant for GLN, THR, and VAL. Performance for the remaining residues, especially PHE, HIS, MET, and TRP, was improved considerably by the combination of the two approaches.
Analysis of distributions of Eintraand Einter
Side-chains at the protein surface are usually relatively mobile, and rigidifying them at the interface upon association results in reduction in side-chain conformational entropy. Hence, for a residue to contribute favorably to the binding free energy, the gain in favorable interactions across the interface must more than offset the entropy loss, or the residue must already be frozen to some extent due to favorable intraprotein interactions. These considerations have implications for the distribution of interaction energies within (Eintra) and between (Einter) the protein partners at the protein–protein interface. Residues making few intra-protein interactions (Eintra ~ 0) are likely to be mobile in the isolated protein, and hence will pay a high entropic price when frozen at the complex interface, which must be overcome by a large interprotein energy (Einter << 0). Alternatively, residues with very favorable intraprotein energies (Eintra <<0) are probably already fixed in the unbound structure, and do not pay a significant entropic price upon binding. Therefore, we would expect that a properly packed interface will primarily contain residues with quite favorable intraprotein or interprotein interactions (Eintra << 0 or Einter << 0), while a poorly packed interface will contain more residues whose losses of side-chain entropy cannot be compensated (Eintra ~ 0 and Einter ~ 0).
To assess the quality of side-chain packing at protein interfaces, we separate the interaction energy of a given residue (Etotal) into Eintra and Einter, and plot the frequency distribution of Eintra versus Einter for different amino acids (see Materials and Methods). Figure 4A ▶ shows the distribution for ARG interface residues in the native complex structures. As expected, we do observe measurable distributions in the entropically more favorable regions where Eintra ~ 0 and Einter << 0 (right lower corner) or Eintra << 0 and Einter ~ 0 (left upper corner). Figure 4B ▶ shows the Eintra versus Einter frequency distribution after applying the standard repacking protocol to native interfaces. Compared to that of the native complex structures, we see a significant increase in the small energy bin (Eintra ~ 0, Einter ~ 0), and a decrease or disappearing of the entropically more favorable bins described above (Eintra ~ 0, Einter << 0 and Eintra << 0, Einter ~ 0). The new approach that includes unbound rotamers and RTMIN creates a more native-like distribution (Fig. 4C ▶).
Analysis of rotamer conservation at modeled interfaces
An optimal protocol should be able to predict the structure of the interface in the bound conformation from the unbound conformation, by accounting for the right degree of side-chain flexibility: i.e., by moving flexible interface side chains, while keeping rigid interface side chains fixed. As a means of measuring this, we kept the backbone in the bound conformation (to isolate the side-chain component of this problem), modeled the side-chain conformations of interface residues using the different protocols described above and evaluated for each modeled interface the level of rotamer conservation with respect to the unbound conformation. The interface residues are binned based on the residue energy in the unbound structure and the distributions are shown in Figure 5 ▶ for three residue types: GLU, ILE, and ARG. The packing protocol used in our original work, which fully discards the side-chain information from the unbound structure, appears to be a very radical approach because it varies many side-chain rotamers which should be fixed (open circles vs. gray bars). When the new treatments of side-chain flexibility, namely, including unbound rotamers (plus signs), RTMIN (cross signs), or both (open squares) are applied, the distributions become more similar to the experimentally observed one (gray bars), indicating that the new method indeed improves side-chain packing at protein interfaces by accounting for the right degree of side-chain flexibility. Not surprisingly, including unbound rotamers makes a dominant contribution to the improvement while RTMIN also appears very helpful to preserve more native unbound rotamers for ARG, especially in more favorable energy bins (residue energy < −5). As discussed earlier, interactions involving long polar side chains, such as in ARG, are very sensitive to the accuracy of the rotamer approximation and a rotamer-only modeling protocol probably cannot recover many native interactions. Searching the off-rotamer states by RTMIN is likely to correct the errors that result from a rotamer approximation, and therefore a higher fraction of native unbound ARG rotamers will be preserved after repacking. It is also worth noting that although there is no direct correlation between the energy of an interface residue and the probability of rotamer change from unbound to bound (gray bars versus white bars), interface residues which form very favorable interactions (the most favorable energy bins of ARG and GLU) in unbound structures do tend to keep their rotamers unchanged upon binding.
New side-chain modeling methods improve recognition of close-to-native complexes in docking calculations
We used perturbation studies (Gray et al. 2003) to examine the effects of the new side-chain modeling protocol on the free energy landscape surrounding native structures starting from either the bound backbones or the unbound backbones of the 54 benchmark targets (Chen et al. 2003). For each target, 1000 models were generated and Z-scores (see Materials and Methods), which reflect how well the low-RMSD models are distinguished from the rest of the model population, were calculated. The higher the Z-score is, the better the discrimination, and Z = 1 was adopted as a cutoff to define a successful discrimination. In Figure 6 ▶, the distributions of Z-scores of 54 targets in the perturbation studies are plotted, with each curve representing a different protocol. In the bound perturbation studies (Fig. 6A ▶), higher Z-score values are obtained for more targets when the new docking protocol is applied, as shown by the shift of the “plus” curve towards the right with respect to the control run (the “minus” curve). The difference is even more dramatic in the unbound perturbation studies (Fig. 6B ▶). The peak between 0 and 1 in the control (“minus”) curve shrinks and a new distribution around Z = 2 is observed for the protocol using both the inclusion of native unbound rotamers and RTMIN (the “plus” curve). The number of targets with Z > 1 increases from 22 to 32 in the bound small perturbations and from 7 to 21 in the unbound perturbation runs, respectively, when the new protocol is implemented. The improvements in Z-score are paralleled by an increase in the “funnel” character of energy versus RMSD plot. Most low-RMSD (near-native) models were pushed into the bottom of the funnels and the energy difference between the low-RMSD models and the rest of model population were significantly enlarged (data not shown). The perturbation results suggest that the new treatment of side-chain flexibility (preserving native unbound rotamers and searching off-rotamer conformations with RTMIN) improves protein–protein docking, since the probability of recognizing a correct docking model when sampling the neighboring subspace around the native conformation is increased, thus resulting in stronger convergence on the global (native) minimum.
Importance of side-chain flexibility for protein docking: Examples from the CAPRI experiment
CAPRI is a community-wide double-blind experiment aimed at assessing the capacity of protein docking methods to predict protein–protein interactions based on the structures of the protein components (Janin et al. 2003). We used our docking protocol with improved treatment of side-chain flexibility in the recent CAPRI Rounds 4 and 5 and produced predictions with very high accuracy for several targets. The importance of allowing for side-chain flexibility in docking is highlighted by the prediction of CAPRI Target 12, the dockerin–cohesin complex. Our top model is very similar to the actual crystal structure of the complex (the model has the lowest backbone RMSD for interface residues (I_RMSD), 0.27 Å, of all predictions for this target) (Fig. 7A ▶, left). This excellent prediction was made possible due to the ability of side chains to rearrange, as exemplified by LEU83 of the cohesin (Fig. 7A ▶, right). Overall, our docking method was successful for six out of the eight targets in Rounds 4 and 5, five of which ranked the best among all the predictions as assessed using the I_RMSD measure (Fig. 7B,C ▶) (unpublished evaluation reports at http://capri.ebi.ac.uk).
Discussion
We have presented a protein–protein docking protocol with an improved treatment of side-chain flexibility. Compared to our previous “rotamer-based-only” packing algorithm, the new protocol treats side-chain flexibility in docking both more conservatively and more radically. On the one hand, in order to preserve and utilize side-chain information from the native unbound structure, which has been demonstrated to be quite useful by the classical rigid-body methods, we take a conservative approach and add these side-chain conformations into the rotamer library and lower their self-energies so that they are preferentially selected. On the other hand, considering the sampling limitation imposed by the rotamer approximation, we go beyond the rotamer restriction and adopt a continuous side-chain refinement algorithm, “rotamer trials with side-chain minimization,” to cyclically optimize the side-chain conformations beyond rotameric space. The incorporation of these two new approaches increases the accuracy of modeling side chains at interfaces and produces more native-like distributions of intramolecular and intermolecular residue energies when side chains are modeled onto the native complex backbones. Encouragingly, the new treatment improved the energetic discrimination between the native-like and non-native-like models in docking simulations in a benchmark set and has contributed to identifying unambiguously the correct models in the blind docking predictions in the CAPRI experiment.
In addition to correcting errors of selecting wrong rotamers due to the inaccuracy of rotamer approximations (Figs. 2 ▶, 3 ▶), we also find in practice that RTMIN is able to reduce the energy significantly simply by adjusting χ angles by a few degrees. By combining the combinatorial packing method with RTMIN, we take advantage of the rotamer library for the rapid coarse grained search, without limiting side-chain conformations to the original rotamer set. Indeed, the computational efficiency of the method derives from the assumption that at most one residue per set of interacting residues is poorly represented by the rotamer library, which will clearly be false in some situations. However, we find in practice that large reductions in energy and improvements in side-chain conformation are obtained despite this limitation, suggesting that the assumption is not unreasonable. Previously, Vasquez (1995) found that a final round of side-chain torsion refinement on a set of monomeric proteins using a similar algorithm led to decreased side-chain RMSDs.
We have previously shown that “energy funnels” exist for many protein–protein complexes in bound and unbound perturbation studies and that the combination of rigid-body optimization and side-chain refinement at the high-resolution stage is able to guide models towards native-like conformations along the energy landscape once the neighboring space is sampled. However, it was also seen in some cases that the energies of near-native models varied over a broad range despite high structural similarity with each other and some of the models were stuck in higher energy traps. This was probably caused by poor side-chain packing with atomic overlaps or voids within the interface (Fig. 1 ▶). When we incorporated the new side-chain refinement scheme into the docking protocol, although the number of “energy funnels” does not increase significantly in the perturbation runs, we do observe that more near-native models with initially high energies overcome the local barrier to move deep down to the “funnel” bottom, as indicated by the dramatic shift of the Z-score distributions to higher values. This suggests that by improving the treatment of side-chain flexibility, the radius of convergence of the method has been increased.
An important contribution to the thermodynamics of protein folding and protein binding is the loss of entropy that results from restricting the number of accessible side-chain rotamers in the native structure (Doig and Sternberg 1995). However, this contribution to the free energy has been neglected by most of the docking methods including ours. We reasoned that this neglect could lead to an increased number of residues which make weak intermolecular interactions in the predicted complex structures because the modest energy decrease is not offset by the entropy loss associated with side-chain freezing. By analyzing the frequency distributions of residue intraprotein energy (Eintra) and interprotein energy (Einter), we found that the neglect of side-chain entropy produces a small but measurable increase in the number of residues whose interaction energy cannot compensate for the entropic cost of side-chain freezing at the interface when the native interface was repacked (Fig. 4 ▶, cf. A and C) or when docking was performed (Fig. 4 ▶, cf. A and D). Consistent with the relatively small differences, inclusion of a simple side-chain entropy loss term did not significantly improve the discrimination of low and high RMSD docked complexes (data not shown). We concluded that while the neglect of side-chain entropy loss in our model is physically inaccurate, it is probably not contributing to a significant reduction in docking performance, perhaps because the side-chain entropy loss associated with different docked arrangements is roughly comparable.
In this paper we have optimized the treatment of side-chain flexibility in protein–protein docking, in particular in our RosettaDock approach. The next challenge is to incorporate backbone flexibility efficiently yet accurately to allow accurate prediction of protein–protein interactions even in the presence of significant backbone rearrangements.
Materials and methods
Data sets
The monomeric protein test set used in the side-chain repacking and sequence redesign was compiled using the PISCES server (Wang and Dunbrack 2003). It contains 129 high-resolution (<1.3 Å) structures solved by X-ray crystallography with 50–500 residues.
Docking benchmark
The 54 docking benchmark protein complexes used in this paper are the same as those tested by Gray et al. (2003), which were selected from the benchmark set constructed by Chen et al. (2003).
Combinatorial packing
The side-chain placement method described by Kuhlman and Baker (2000) uses a simulated annealing algorithm that searches through backbone-dependent rotamers and can rapidly come close to a globally optimal solution of side-chain conformations for all the residue positions. The method includes the option to expand the standard rotamer library for each residue by including either subrotamers, i.e., the major rotamer angles + and − 1 standard deviation of those angles, or additional rotamers such as side-chain torsion angles existing in a specific structure.
Rotamer trials
Starting from a full-atom structure, each side chain is selected one at a time and allowed to sample each of its possible rotamer conformations with all the other side chains being fixed. After all the possible rotamers of a given residue are surveyed, the rotamer with the lowest energy (including the starting rotamer) is selected, and the procedure is repeated with the next residue in the protein. This fast protocol was employed in addition to the combinatorial packing in the previous version of our docking method to achieve computational efficiency.
Rotamer trials minimization (RTMIN)
RTMIN consists of a combination of rotamer trial and side-chain minimization. During rotamer trials, in addition to trying each rotamer at a given residue position, the χ angles of this rotamer are subjected to torsion space minimization procedure using the Davidon-Fletcher-Powell Quasi-Newton minimization technique (Press et al. 1992), and the energy is evaluated. After all the possible rotamers of this residue are minimized, the “minimized” rotamer with the lowest energy (including the ‘minimized’ starting rotamer) is selected.
Inclusion of unbound rotamers
The χ angles of each side-chain in the unbound component proteins are calculated and appended to the rotamer library in the side-chain modeling procedure in the docking protocol. These χ angles are optimized during the RTMIN process as are the χ angles of standard rotamers. For runs with the bound structure, the sequence of the bound structure does not always match its unbound counterparts, and in this case a sequence alignment map is generated between bound and unbound structures and the native unbound rotamers are included only for those equivalent residue positions with identical amino acids. As described in Kuhlman and Baker (2000), the side-chain packing potential contains a term representing the internal energy of each rotamer. To favor the unbound native rotamer, its internal energy was set to be equal to that of the lowest energy rotamer in the library for that position.
Docking
The docking protocol implemented in this paper and in the CAPRI docking predictions shown in Figure 7 ▶ is an improved version of the method developed by Gray et al. (2003). It employs a low-resolution rigid-body Monte Carlo search followed by simultaneous optimization of backbone displacement and side-chain conformations using Monte Carlo minimization. In the current protocol, the rotamer library is further expanded to include major χ2 angles + and − 1 standard deviation of those angles for PHE, TRP, and TYR. In addition, RTMIN is implemented right after every full, combinatorial side-chain packing step to allow sampling of off-rotamer side-chain conformations. For the docking runs starting from the unbound backbones, two additional changes were added to preserve useful side-chain information in the native unbound crystal structures: First, the step in the previous protocol where the native side-chain conformations were discarded is skipped, and instead, a RTMIN cycle is performed to optimize the starting side-chain conformations. Second, native side-chain torsion angles in the unbound structures are added to the rotamer library for use in the side-chain packing and RTMIN cycles during docking. With the addition of unbound rotamers and minimization steps, the computational cost of RosettaDock generally increases by about 50% to 150%, depending on the size and composition of the modeled interface. For example, with one single 800-MHz CPU, it currently takes 6.6 and 12.2 min on average to produce one full-atom docking model for 1QFU (a 500-residue protein complex) using the standard and improved RosettaDock protocol, respectively.
Z-score
The low-RMSD Z-score (Zlrms) reflects the discrimination of near-native from nonnative conformations. For a given target in the docking small perturbation runs, Zlrms is defined as:
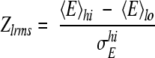 |
where 〈E〉hi and 〈E〉lo are mean values of the energies of models with high RMSD and low RMSD, respectively. σEhi is the standard deviation of the energy scores of models with high RMSD. Low RMSD (near-native) models are defined as the lowest 5% of the RMSD population. RMSD values are computed over all ligand Cαcoordinates from the native structure.
Residue energy distributions
Eintra is the favorable interaction energy (Lennard-Jones attractive energy + hydrogen bond energy) of a residue with other residues in the same protein and Einter is the favorable interaction energy of a residue with the other protein partner. In Figure 4 ▶, Eintra and Einter are binned into square bins of 2 × 2 energy units. The relative occupancy of different square bins is plotted. Residues with Einter > −0.3 were not included in the count, in order to make sure that only interface residues are considered. In Figure 5 ▶, the energy value of each residue in unbound structures was binned into intervals of 2 energy units and the absolute count of each bin was plotted. Here we included only residue positions that are at the native interface (within 8 Å centroid–centroid distance to residues in the other partner), and that have the same amino acid in the bound and unbound structure.
Plots and figures
Unless specified, R software (Ihaka and Gentleman 1996) was used to make plots. PYMOL (http://www.pymol.org) was used to produce figures for protein models.
Software availability
The improved RosettaDock protocol, now in C++, is available free for academic use at http://depts.washington.edu/ventures/UW_Technology/Express_Licenses/Rosetta.
Acknowledgments
We thank the many scientists who have participated in the development of the suite of computational tools used in the Baker laboratory for computations on the structure of proteins. In particular, Jeffrey G. Gray laid the groundwork for RosettaDock, and Brian Kuhlman developed the method of rotamer trials for fast rotamer packing. Keith Laidig of Formix, Inc. built and maintained reliable, state-of-the-art computing resources. We also thank Sandor Vajda for helpful discussions. O.S.-F. carries a Damon-Runyon Fellowship DRG-1704-02 from the Damon Runyon Cancer Research Foundation. This work was supported by a grant from the NIH.
Abbreviations
PDB, Protein Data Bank
RMSD, root-mean-square deviation.
Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.041222905.
References
- Berman, H.M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T.N., Weissig, H., Shindyalov, I.N., and Bourne, P.E. 2000. The Protein Data Bank. Nucleic Acids Res. 28 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camacho, C.J. and Vajda, S. 2002. Protein–protein association kinetics and protein docking. Curr. Opin. Struct. Biol. 12 36–40. [DOI] [PubMed] [Google Scholar]
- Carvalho, A.L., Dias, F.M., Prates, J.A., Nagy, T., Gilbert, H.J., Davies, G.J., Ferreira, L.M., Romao, M.J., and Fontes, C.M. 2003. Cellulosome assembly revealed by the crystal structure of the cohesin–dockerin complex. Proc. Natl. Acad. Sci. 100 13809–13814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, R. and Weng, Z. 2002. Docking unbound proteins using shape complementarity, desolvation, and electrostatics. Proteins 47 281–294. [DOI] [PubMed] [Google Scholar]
- Chen, R., Mintseris, J., Janin, J., and Weng, Z. 2003. A protein–protein docking benchmark. Proteins 52 88–91. [DOI] [PubMed] [Google Scholar]
- Desjarlais, J.R. and Handel, T.M. 1999. Side-chain and backbone flexibility in protein core design. J. Mol. Biol. 290 305–318. [DOI] [PubMed] [Google Scholar]
- Doig, A.J. and Sternberg, M.J. 1995. Side-chain conformational entropy in protein folding. Protein Sci. 4 2247–2251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunbrack Jr., R.L. and Cohen, F.E. 1997. Bayesian statistical analysis of protein side-chain rotamer preferences. Protein Sci. 6 1661–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunbrack Jr., R.L. and Karplus, M. 1993. Backbone-dependent rotamer library for proteins. Application to side-chain prediction. J. Mol. Biol. 230 543–574. [DOI] [PubMed] [Google Scholar]
- Fernandez-Recio, J., Totrov, M., and Abagyan, R. 2002. Soft protein–protein docking in internal coordinates. Protein Sci. 11 280–291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabb, H.A., Jackson, R.M., and Sternberg, M.J. 1997. Modelling protein docking using shape complementarity, electrostatics and biochemical information. J. Mol. Biol. 272 106–120. [DOI] [PubMed] [Google Scholar]
- Gardiner, E.J., Willett, P., and Artymiuk, P.J. 2001. Protein docking using a genetic algorithm. Proteins 44 44–56. [DOI] [PubMed] [Google Scholar]
- Goldberg, J., Huang, H.B., Kwon, Y.G., Greengard, P., Nairn, A.C., and Kuriyan, J. 1995. Three-dimensional structure of the catalytic subunit of protein serine/threonine phosphatase-1. Nature 376 745–753. [DOI] [PubMed] [Google Scholar]
- Graille, M., Mora, L., Buckingham, R.H., Van Tilbeurgh, H., and De Zamaroczy, M. 2004. Structural inhibition of the colicin D tRNase by the tRNA-mimicking immunity protein. EMBO J. 23 1474–1482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray, J.J., Moughon, S., Wang, C., Schueler-Furman, O., Kuhlman, B., Rohl, C.A., and Baker, D. 2003. Protein–protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol. 331 281–299. [DOI] [PubMed] [Google Scholar]
- Halperin, I., Ma, B., Wolfson, H., and Nussinov, R. 2002. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins 47 409–443. [DOI] [PubMed] [Google Scholar]
- Havranek, J.J. and Harbury, P.B. 2003. Automated design of specificity in molecular recognition. Nat. Struct. Biol. 10 45–52. [DOI] [PubMed] [Google Scholar]
- Ihaka, R. and Gentleman, R. 1996. R: A language for data analysis and graphics. J. Comput. Graph. Stat. 5 299–314. [Google Scholar]
- Jackson, R.M., Gabb, H.A., and Sternberg, M.J. 1998. Rapid refinement of protein interfaces incorporating solvation: Application to the docking problem. J. Mol. Biol. 276 265–285. [DOI] [PubMed] [Google Scholar]
- Janin, J., Henrick, K., Moult, J., Eyck, L.T., Sternberg, M.J., Vajda, S., Vakser, I., and Wodak, S.J. 2003. CAPRI: A Critical Assessment of PRedicted Interactions. Proteins 52 2–9. [DOI] [PubMed] [Google Scholar]
- Katchalski-Katzir, E., Shariv, I., Eisenstein, M., Friesem, A.A., Aflalo, C., and Vakser, I.A. 1992. Molecular surface recognition: Determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl. Acad. Sci. 89 2195–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhlman, B. and Baker, D. 2000. Native protein sequences are close to optimal for their structures. Proc. Natl. Acad. Sci. 97 10383–10388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Looger, L.L., Dwyer, M.A., Smith, J.J., and Hellinga, H.W. 2003. Computational design of receptor and sensor proteins with novel functions. Nature 423 185–190. [DOI] [PubMed] [Google Scholar]
- Lorber, D.M., Udo, M.K., and Shoichet, B.K. 2002. Protein–protein docking with multiple residue conformations and residue substitutions. Protein Sci. 11 1393–1408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lytle, B.L., Volkman, B.F., Westler, W.M., Heckman, M.P., and Wu, J.H. 2001. Solution structure of a type I dockerin domain, a novel prokaryotic, extra-cellular calcium-binding domain. J. Mol. Biol. 307 745–753. [DOI] [PubMed] [Google Scholar]
- Norel, R., Petrey, D., Wolfson, H.J., and Nussinov, R. 1999. Examination of shape complementarity in docking of unbound proteins. Proteins 36 307–317. [PubMed] [Google Scholar]
- Palma, P.N., Krippahl, L., Wampler, J.E., and Moura, J.J. 2000. BiGGER: A new (soft) docking algorithm for predicting protein interactions. Proteins 39 372–384. [PubMed] [Google Scholar]
- Press, W.H., Teukolsky, S.A., Vetterling, W.T., and Flannery,B.P. 1992. Numerical recipes in FORTRAN: The art of scientific computing. Cambridge University Press, New York.
- Shimon, L.J., Bayer, E.A., Morag, E., Lamed, R., Yaron, S., Shoham, Y., and Frolow, F. 1997. A cohesin domain from Clostridium thermocellum: The crystal structure provides new insights into cellulosome assembly. Structure 5 381–390. [DOI] [PubMed] [Google Scholar]
- Smith, G.R. and Sternberg, M.J. 2002. Prediction of protein–protein interactions by docking methods. Curr. Opin. Struct. Biol. 12 28–35. [DOI] [PubMed] [Google Scholar]
- Taylor, J.S. and Burnett, R.M. 2000. DARWIN: A program for docking flexible molecules. Proteins 41 173–191. [PubMed] [Google Scholar]
- Terrak, M., Kerff, F., Langsetmo, K., Tao, T., and Dominguez, R. 2004. Structural basis of protein phosphatase 1 regulation. Nature 429 780–784. [DOI] [PubMed] [Google Scholar]
- Vajda, S. and Camacho, C.J. 2004. Protein–protein docking: Is the glass half-full or half-empty? Trends Biotechnol. 22 110–116. [DOI] [PubMed] [Google Scholar]
- Vakser, I.A., Matar, O.G., and Lam, C.F. 1999. A systematic study of low-resolution recognition in protein–protein complexes. Proc. Natl. Acad. Sci. 96 8477–8482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vasquez, M. 1995. An evaluation of discrete and continuum search techniques for conformational analysis of side chains in proteins. Biopolymers 36 53–70. [Google Scholar]
- Wang, G. and Dunbrack Jr., R.L. 2003. PISCES: A protein sequence culling server. Bioinformatics 19 1589–1591. [DOI] [PubMed] [Google Scholar]
- Xiang, Z. and Honig, B. 2001. Extending the accuracy limits of prediction for side-chain conformations. J. Mol. Biol. 311 421–430. [DOI] [PubMed] [Google Scholar]
- Yang, J.M., Tsai, C.H., Hwang, M.J., Tsai, H.K., Hwang, J.K., and Kao, C.Y. 2002. GEM: A Gaussian Evolutionary Method for predicting protein side-chain conformations. Protein Sci. 11 1897–1907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zacharias, M. 2003. Protein–protein docking with a reduced protein model accounting for side-chain flexibility. Protein Sci. 12 1271–1282. [DOI] [PMC free article] [PubMed] [Google Scholar]