Abstract
To better characterize the transition state for folding/unfolding and its sensitivity to environmental changes, we have run multiple molecular dynamics simulations of chymotrypsin inhibitor 2 (CI2) under varying solvent conditions and temperature. The transition state structures agree well with experiment, and are similar under all of the conditions investigated here. Increasing the temperature leads to some movement in the position of the transition state along several reaction coordinates, as measured by changes in properties of the transition state structures. These structural changes are in the direction of a more native-like transition state as denaturation conditions become more severe, as expected for a Hammond effect. These structural changes are not, however, reflected in the global structure as measured by the total number of contacts or the average S-values. These results suggest that the small changes in average Φ-values with temperature seen by experiment may be due to an increase in the sensitivity of the transition state to mutation rather than a change in the average structure of the transition state. A simple analysis of the rates of unfolding indicates that the free energy barrier to unfolding decreases with increasing temperature, but even in our very high temperature simulations there is a small free energy barrier.
Keywords: transition state, Hammond effect, molecular dynamics, chymotrypsin inhibitor 2, unfolding rate
The process of protein folding and unfolding involves the passage from one state to another. The rate of transition between two states is generally defined by the highest free energy ensemble of conformations that must be accessed in passing between these states. These high free energy conformations make up the transition state ensemble. In the case of proteins whose folding is thermodynamically and kinetically two-state, only the folded and unfolded states are significantly populated, and the folding process may be described in terms of a single transition state.
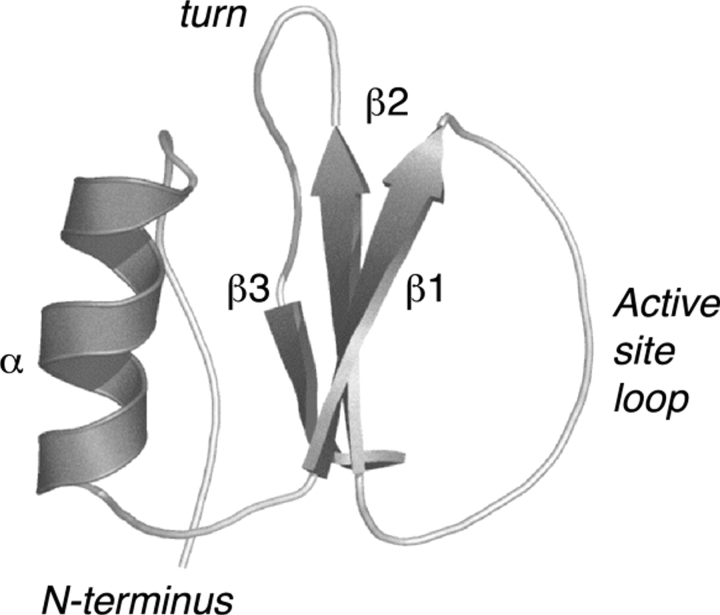
Chymotrypsin inhibitor 2 (CI2) (Fig. 1 ▶) was the first protein whose folding and unfolding were determined to be thermodynamically and kinetically two-state (Jackson and Fersht 1991). The folding/unfolding transition was characterized in detail experimentally by the protein engineering method and by high temperature molecular dynamics (MD) simulations (Li and Daggett 1994; Otzen et al. 1994; Itzhaki et al. 1995). By clustering the conformations observed in the high-temperature MD simulation, a model for the transition state of unfolding was identified that correctly predicted the experimentally determined Φ-values and provided structural explanations for them at the atomic level (Li and Daggett 1994, 1996; Daggett et al. 1996). This transition state model was later verified by MD-guided protein engineering experiments (Ladurner et al. 1998), direct calculation of Φ-values using free energy perturbation methods (Pan and Daggett 2001) and by refolding attempts starting with structures before, at, and after the transition state (De Jong et al. 2002).
Figure 1.
The native structure of CI2. CI2 is composed of a three-stranded β-sheet folded against the N terminus and α-helix, forming a single hydrophobic core (1YPC; Harpaz et al. 1994).
Here we expand our MD model of the transition state to include multiple simulations under varying denaturation conditions. The transition state of CI2 has been shown experimentally to be mildly sensitive to denaturation conditions (Matouschek et al. 1995; Oliveberg et al. 1998). The transition state becomes more native-like under conditions that more strongly favor the denatured state, consistent with a Hammond effect (Hammond 1955; Matouschek and Fersht 1993). This effect was seen as a shift in the relative m-values of the transition state upon mutation and by a shift in the Φ-values of most mutants with temperature (Oliveberg et al. 1998).
Analysis of the shift in the apparent position of the transition state seen by the change in m-values may be complicated by changes in the ground states of the protein upon mutation (Oliveberg et al. 1998; Otzen and Oliveberg 2002; Sánchez and Kiefhaber 2003). The m-value for unfolding increases with increasing destabilization, leading to an effectively lengthened reaction coordinate. There is still a small change in the m-value for folding to or from the transition state that is not accounted for by the change in the length of the reaction coordinate, indicating that the position of the transition state along the reaction coordinate changes for strongly destabilizing mutations. Movement of the position of the transition state along a reaction coordinate monitored by calculating Φ-values at a range of temperatures was of the same magnitude as the movement observed by monitoring the m-values, although the apparent position of the transition state along the reaction coordinate is not the same by the two methods (Oliveberg et al. 1998). The apparent transition state movement also depends on the specific mutation made, as different mutations at a given position can lead to quite different temperature effects.
We have identified and characterized the unfolding transition state of CI2 from 21 independent simulations under denaturing conditions. These include two simulations at 373 K, two simulations at 398 K, three simulations at 448 K, three simulations at 473 K, and six simulations at 498 K in pure water, as well as five simulations at 333 K in 8 M urea. The overall unfolding process under these conditions for most of the simulations has been described elsewhere (Li and Daggett 1994, 1996; Daggett et al. 1996; Day et al. 2002; Bennion and Daggett 2003).
Results
The transition state of unfolding is defined by a conformational clustering method in which conformations generated in the simulation are compared against one another in an all-versus-all fashion (Levitt 1983; Li and Daggett 1994, 1996). Individual conformations are mapped to points in a three-dimensional space such that the distance between any two points corresponds to the root-mean-squared deviation between the α-carbons (Cα-RMSD) of the appropriate structures. Native-like structures cluster into a small portion of this space. The transition state is defined as the point at which the trajectory exits the extended native-like cluster. The time at which this transition occurs varies with changing denaturation conditions (Table 1), with the protein unfolding much more quickly under more extreme denaturing conditions.
Table 1.
Average calculated S-values under different conditions compared with experimental Φ-values
| T (K) | 〈tTS〉 (nsec) | 〈S a〉 | R (298 K)b | R (343 K)c |
| 333d | 1.8 ± 0.2 | 0.47 ± 0.03 | 0.69 | 0.74 |
| 373 | 12.5 ± 10.4 | 0.41 ± 0.05 | 0.74 | 0.75 |
| 398 | 6.1 ± 3.1 | 0.45 ± 0.05 | 0.69 | 0.73 |
| 448 | 1.0 ± 0.5 | 0.43 ± 0.04 | 0.73 | 0.75 |
| 473 | 0.4 ± 0.2 | 0.43 ± 0.04 | 0.72 | 0.72 |
| 498 | 0.2 ± 0.1 | 0.40 ± 0.03 | 0.63 | 0.65 |
| Average | — | 0.43 | 0.71 | 0.73 |
a Average S for the 26 positions considered in Oliveberg et al. (1998). Errors are based on deviations within randomly chosen ensembles from a set of 100 simulations at 498 K (see Materials and Methods).
b Correlation between average S-values and 298 K Φ-values from Oliveberg et al. (1998).
c Correlation between average S-values and extrapolated 343 K Φ-values from Oliveberg et al. (1998).
d 333 K simulations were solvated in 8 M urea.
Structure of the transition state
The transition state of unfolding of CI2 is a relatively homogenous ensemble of conformations with native-like topologies but weakened tertiary and secondary structure (Fig. 2 ▶). The conformations making up the ensemble are all expanded relative to the native state, and the core has begun to open and become exposed to solvent. The native α-helix generally remains intact, whereas the β-sheet is more disrupted. The ensemble is more heterogeneous with respect to the loops, turns, and N and C termini. Contact between the N and the C terminus is not maintained in any of the conformations from the high temperature simulations, but it is maintained in three of five of the chemical denaturation simulations.
Figure 2.
The structure of the transition state from each simulation. Secondary structure was assigned using KSDSSP (Kabsch and Sander 1983).
The range of structures observed under different conditions is similar to the range observed in multiple simulations under the same conditions (Fig. 3 ▶). This heterogeneity can be quantified by considering the average Cα-RMSD between transition state structures from different simulations. The average Cα-RMSD between transition states from all six 498 K simulations is 4.0 ± 0.6 Å. This value is 4.5 ± 0.8 Å when transition states from 100 independent simulations at 498 K are compared (R. Day and V. Daggett, unpubl.). The average Cα-RMSD between transition states from the urea denaturation simulations is similar at 3.8 ± 0.7 Å, while that between transition states from the full range of temperatures is slightly higher at 4.5 ± 0.7 Å. Finally, the average Cα-RMSD between chemically and thermally derived transition states is 4.6 ± 0.8 Å. It appears, then, that any structural changes with changing denaturation conditions will be small against the background of the inherent structural heterogeneity of the transition state.
Figure 3.
Structural heterogeneity of the transition state. Three ensembles of transtion state structures are considered. The first (373–498 K) consists of one structure from each of the five temperatures between 373 K and 498 K. The average Cα-RMSD between thermally derived structures is 4.5 ± 0.7 Å. The second (498 K) consists of structures from five of the 498 K simulations. The average Cα-RMSD between all six 498 K transition states is 4.0 ± 0.6 Å. The third (333 K, 8 M urea) is formed by structures from the five urea simulations (average Cα-RMSD: 3.8 ± 0.7 Å).
S-values and comparison to Φ-values
An S-value is a measure of the amount of structure at a given residue, defined by the amounts of secondary and tertiary structure at each residue (see Materials and Methods). It has been shown to correlate with experimental Φ-values (Daggett et al. 1996). An experimental Φ-value measures the effect of mutation at a given position and is interpreted in terms of structure at that position. Methods that account for mutations directly, such as ΦMD and free energy perturbation (Li and Daggett 1996; Pan and Daggett 2001), model the experimental free energy changes more accurately and can achieve better correlation with experiment, but these methods can be computationally expensive and do not measure structure directly. We wish to look for structural changes directly, so we focus on S-values. As there can be a great deal of variation in the Φ-values for different mutations at a given position (Fig. 4 ▶), we attempted to choose X → Ala or Ala → Gly scanning mutants when possible to minimize possible charge effects. Additionally, negative Φ-values were disregarded as their structural interpretation is generally unclear. The single exception to this is the V19A mutation. The negative Φ-value at this position is interpreted as being due to nonnative contacts in the transition state (Jackson et al. 1993; Li and Daggett 1994; Itzhaki et al. 1995), so its Φ-value is considered to be 1.26 for purposes of comparing with S-values.
Figure 4.
Experimental Φ-values and calculated S-values as a function of residue number. Φ-values (○) are from Itzhaki et al. (1995). Multiple Φ-values at a given position correspond to different mutations at the same position. S-values (•) are averaged over all simulations.
The pattern of S-values across the sequence of CI2 is quite similar to that of the Φ-values. Figure 4 ▶ shows the experimental Φ-values at each position in the sequence and the average S-values from all simulations. The correlation coefficient between the two is 0.71. The pattern of S-values from individual simulations is similar to that of the average, with the exception of one of the 498 K simulations, where the helix is not well formed in the transition state. The correlation coefficients between the experimental Φ-values and S-values for the individual simulations range from 0.36 to 0.71, with an average of 0.62. Averaging over multiple simulations at each temperature generally improves this correlation, with a maximum of 0.76 observed by averaging over a set of 100 simulations (R. Day and V. Daggett, unpubl.). Averaged S-values and their correlation with experiment are given in Table 1. The average S-value does not change significantly across the 125° range explored in the thermal denaturation simulations, and is essentially unchanged by urea, indicating that the position of the transition state along this structural reaction coordinate is relatively insensitive to changing temperature. The S-values for individual residues vary from simulation to simulation, but they do not show clear temperature dependencies. The average S-values for each temperature are mapped onto representative transition state structures in Figure 5 ▶.
Figure 5.
Transition state structures from each temperature colored by S-values. S-values range from 0 (red) to 1 (blue).
While there is no significant change in the S-values with changing temperature, there are small changes in the experimental Φ-values with increasing temperature. Φ-Values at 343 K were extrapolated from their experimentally determined temperature dependence (Oliveberg et al. 1998). The correlation between these extrapolated Φ-values and the S-values from simulation initially is slightly higher than the correlation with the 298 K Φ-values (Table 1). If the extrapolation is carried out linearly beyond 343 K, however, the correlation does not continue to increase. The average of the S-values is 0.4, compared to the experimental values of 0.3 at 298 K and 0.4 at 343 K (Oliveberg et al. 1998).
Other reaction coordinates
By considering the position of the transition state along a variety of simple reaction coordinates, it is possible to obtain a quantitative view of the effects of changing denaturation conditions. As expected based on the structural heterogeneity of the transition state (Fig. 3 ▶), the difference in average properties for the transition state structures from different conditions is generally on the same order as the range of properties seen for the same conditions (Table 2). Some trends and differences are observed in the average values of some of these properties, however, both between different temperatures and between different solvent conditions.
Table 2.
Average properties of TS ensembles as a function of simulation conditions
| Temperature (K) | Total no. of contactsa | No. of main-chain H-bondsb | SASA (Å)b | Radius of gyration (Å) | No. of native contactsa,c |
| Native state | |||||
| 298d | 210 ± 5e | 21 ± 2 | 4538 ± 118 | 10.7 ± 0.1 | 187 ± 5 |
| Transition state | |||||
| 333f | 172 ± 5 | 11 ± 1 | 5670 ± 179 | 12.0 ± 0.2 | 153 ± 6 |
| 373 | 173 ± 9 | 14 ± 2 | 5309 ± 283 | 12.0 ± 0.3 | 136 ± 10 |
| 398 | 172 ± 9 | 14 ± 2 | 5419 ± 283 | 11.9 ± 0.3 | 140 ± 10 |
| 448 | 179 ± 7 | 15 ± 2 | 5248 ± 231 | 11.8 ± 0.3 | 145 ± 8 |
| 473 | 173 ± 7 | 14 ± 1 | 5269 ± 231 | 11.7 ± 0.3 | 146 ± 8 |
| 498 | 170 ± 5 | 13 ± 1 | 5509 ± 163 | 11.8 ± 0.2 | 146 ± 6 |
| Denatured stateg | |||||
| 333 | 130 ± 13 | 8 ± 2 | 6805 ± 431 | 15.7 ± 2.0 | 102 ± 13 |
| 373 | 171 ± 6 | 13 ± 2 | 5350 ± 203 | 12.1 ± 0.7 | 115 ± 3 |
| 398 | 161 ± 7 | 11 ± 2 | 5561 ± 208 | 12.5 ± 0.3 | 102 ± 3 |
| 448 | 161 ± 8 | 8 ± 2 | 5848 ± 229 | 14.6 ± 1.0 | 85 ± 3 |
| 473 | 152 ± 9 | 6 ± 2 | 5806 ± 269 | 13.3 ± 0.7 | 93 ± 4 |
| 498 | 140 ± 11 | 10 ± 4 | 6701 ± 252 | 17.9 ± 1.6 | 85 ± 4 |
a A contact is defined by a 5.4 Å distance between any heavy atom pair other than N-O pairs, which have a 4.6 Å distance cutoff.
b A hydrogen bond is defined by a 2.6 Å distance cutoff between donor and acceptor and a 35° angular cutoff.
c Native contacts are defined as those present in the crystal structure, lYPC (Harpaz et al. 1994).
d 298 K values are averaged over the last 40 nsec of a 50 nsec simulation.
e Errors for the native and denatured states are based on the spread of values within the ensemble. Errors for the transition state are based on deviations within randomly chosen ensembles from a set of 100 simulations at 498 K (see Materials and Methods).
f 333 K simulations were solvated in 8 M urea.
g Denatured state values are averaged over the period of simulation in which all structures are at least 8 Å Cα-RMSD from the crystal structure.
The largest differences between the temperature-derived transition states and those obtained in simulated chemical denaturation are seen in the number of main-chain–main-chain hydrogen bonds and in the solvent-accessible surface area (Table 2). The transition state obtained by chemical denaturation has fewer main-chain hydrogen bonds and an increased degree of solvent exposure. This is consistent with the combination of direct and indirect effects observed in the overall unfolding pathway (Bennion and Daggett 2003). Urea preferentially hydrogen bonds to the protein backbone, leading to a lower number of main-chain hydrogen bonds, and it disrupts water structure, reducing the penalty for exposure of nonpolar groups to the solvent.
While the differences in transition state structures at different temperatures are similar to those between multiple simulations at one temperature, by averaging over multiple simulations it is possible to detect trends with temperature (Fig. 6 ▶). As the temperature is increased, the transition state shifts slightly closer to the native state in terms of the fraction of native contacts, the radius of gyration, and the amount of β-sheet structure. These increases are very slight. The increase in the fraction of native contacts corresponds to about one contact gained per 13° temperature increase, while the increase in β-sheet structure only adds one residue to the sheet every 20°. The radius of gyration decreases by about 0.1 Å per 50° temperature increase.
Figure 6.

Structural properties of the transition state as a function of temperature. The native (crystal structure: 1YPC; Harpaz et al. 1994) values are indicated by • at 298 K, the urea values by ▴ at 333 K, and in pure water at different temperatures values by — at the appropriate temperature. Error bars are based on the standard deviations in multiple ensembles chosen at random from a set of 100 simulations at 498 K (see Materials and Methods). (A) Native contacts: The line is a linear fit with a slope of 8.3 contacts/100 K and a correlation coefficient of 0.91. (B) Radius of gyration: The line is a linear fit with a slope of -0.22 Å/100 K and a correlation coefficient of 0.93. (C) β-strand content: The line is a linear fit with a slope of 2.1%/100 K and a correlation coefficient of 0.86.
The fraction of residues in the α-helix shows no clear trends with changing denaturation conditions (data not shown). The fraction of the helix in the protein is generally between 0.12 and 0.18, although it drops as low as 0.07 in one transition state. This range represents the largest variation of the properties studied here, and it may be that trends would arise with more sampling at the various temperatures.
The relative position of the transition state along a reaction coordinate may be determined as well as the absolute position if the properties of the native and denatured states are known. Native and denatured state values for the various properties under consideration here are given in Table 2. The properties of the native state are expected to be fairly constant under all conditions, so their values are determined by averaging over a 298 K simulation. The denatured state is a much broader ensemble, and the relative populations of different conformations within this ensemble are expected to change with changing conditions, leading to changes in denatured state properties. The denatured state values listed in Table 2 are taken from the ends of the simulations detailed in Day et al. (2002). These simulations, especially those at the lower temperatures, are unlikely to have explored a significant amount of the conformational space available in the denatured state. In particular, given the compact nature of the denatured conformations at the lower temperatures, the TS would be positioned very near the denatured state. This points to a weakness in the use of such simple reaction coordinates, as the transition state is structurally native-like (Fig. 5 ▶). At the highest temperature, 498 K, the protein more fully unfolds, yielding the relative TS position along a SASA-defined reaction coordinate of 0.55, in agreement with the experimental βT value of 0.6.
Unfolding rates
The transition state times may be considered as first passage times and converted to rates and plotted against inverse temperature for direct comparison with experimental rates. Here we consider the unfolding rates from MD simulations compared to the experimental unfolding rates for three proteins: CI2, Engrailed homeodomain (EnHD), and α3D (Fig. 7 ▶). The experimental data are fit to an Arrhenius-like relation:
Figure 7.
Inverse temperature dependence of the unfolding rate and unfolding free energy barrier. Filled points (•) are the experimentally determined unfolding rates. Circled points (⊙) are the inverse of the time taken to reach the transition state in MD simulation. In A–C, the solid lines are fits of Equation 3 (see text) to the experimental data. Dashed lines are fits of Equation 3 with ΔCp‡ = 0 to the high temperature MD data. The dotted line is the activation free energy, ΔG‡(T), from the fit of Equation 3 with ΔCp‡ constant in units of RT. (A) Unfolding data for EnHD from Mayor et al. (2003). (B) Unfolding data for α3D from Zhu et al. (2003). (C,D) Unfolding data for CI2. Experimental data are from Tan et al. (1996). The point at 1/T = 2.8 × 10−3 is the folding rate at the Tm. In D, the solid line is a fit of Equation 3 with ΔCp‡ = 6030 − 16.8T (Tan et al. 1996; see text). The dashed line is an extrapolation of Equation 3 with ΔCp‡ = 0 based on the values of ΔH‡ and ΔS‡ at 360 K (1/T = 2.78 × 10−3).
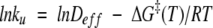 |
(1) |
Deff, the effective rate of diffusion on the folding/unfolding landscape, takes the place of the familiar preexponential factor in the Arrhenius relation. In transition state theory for gas phase reactions, the preexponential factor is essentially the rate of bond vibrations, kBT/h, or about 1012 sec−1. In fitting Equation 1 to the experimental data, we chose a simple heuristic for the estimation of Deff: We took 1010 sec−1 to be a reasonable value of Deff, as the earliest time of exit from the native cluster in many simulations of different proteins at 498 K is ~100 psec. In Figure 7 ▶, A–C, ΔG‡(T) is given by:
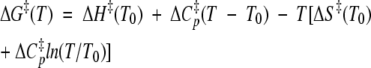 |
(2) |
where ΔH‡(T0) and ΔS‡(T0) are the enthalpy and entropy, respectively, at some reference temperature, T0, and ΔCp‡, the heat capacity change on unfolding from the native to the transition state, is left as a free parameter.
In all three cases considered here, there is a rollover in the rate as a function of 1/T in going from the relatively low temperatures used in experiment to the highest temperatures employed in MD simulation. The high temperature rates are much slower than what would be predicted from the experimental curves. This rollover can be seen most clearly for EnHD. Here, the rates of unfolding at 373 K (1/T = 2.68 × 10−3) and 348 K (1/T = 2.87 × 10−3) from simulation are similar to the rates predicted by experiment, but the rate is relatively unchanged in going from 373 K to 498 K (1/T = 2.01 × 10−3). An explanation for this rollover can be seen when the activation free energies from the fits of Equation 1 to the experimental data are plotted against the inverse temperature (Fig. 7 ▶, dashed line). In all cases the activation free energy becomes small near the rollover from experimental to the highest simulation temperatures. When the activation barrier becomes very small, Equation 1 no longer holds and the rate of unfolding is determined by the presence of local traps and bottlenecks on the energy landscape. There are several confounding factors that may change this rollover temperature. Using different values of Deff will change the point at which the rollover occurs by affecting the activation entropy calculated from Equation 2. The temperature at which the rollover would occur using different values of Deff can be determined by finding the point on the rate curve at which the unfolding rate is equal to Deff. Additionally, an increase in effective pressure is required to maintain liquid water at the higher simulation temperatures. An increased pressure increases the free energy barrier to unfolding by requiring additional pressure-volume work to expand the protein. The solvent excluded volume of the transition state of CI2 is ~350 Å3 greater than that of the crystal structure volume. This corresponds to an increase in the free energy barrier of about 5 cal/mol/atm, or 2.5 kcal/mol at 498 K due to the increased pressure needed to maintain water in the liquid state. A larger assumption is that the heat capacity difference between the native and transition states is constant. This is unlikely to be valid over the entire temperature range considered.
Tan et al. (1996) observed a slight decrease in ΔH‡ with increasing temperature, indicating that ΔCp‡ is not constant for CI2. They fit a quadratic function to this curve, yielding a temperature-dependent heat capacity, ΔCp‡ = 6030 − 16.8T. Integration of this function yields an expression for the free energy of activation that can be used in place of Equation 2:
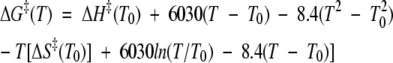 |
(3) |
This expression was used to fit the experimental unfolding rates of CI2 over the temperature range for which ΔCp‡ is positive, yielding the solid line in Figure 7D ▶. At higher temperatures, ΔCp‡ was assumed to be zero and a linear extrapolation was used to determine the expected rates. The temperature at which the free energy barrier is expected to disappear is about 473 K (1/T = 2.1 × 10−3), significantly higher than that predicted assuming a constant heat capacity increment of unfolding.
The linear dependence of ln k on the inverse temperature seen in simulation is consistent with the presence of a free energy barrier and a heat capacity increment of zero going from the native state to the transition state. The rate of EnHD’s unfolding at 348 K by MD simulation is somewhat faster than that predicted by experiment, suggesting that the free energy barrier in our potential function is slightly lower than the actual barrier. The rates of CI2 unfolding at 398 K and 373 K, both of which are below the apparent rollover point, also suggest that the free energy barrier in simulation is not as high as the actual free energy barrier. Experimental values determined at these temperatures would be necessary to truly assess the difference.
Discussion
Position of the transition state
A small shift in the position of the transition state of CI2 along a folding/unfolding reaction coordinate has previously been seen by two experimental measures: (1) The relative solvent-accessible surface exposure of the transition state decreases with increasingly destabilizing mutations (Matouschek et al. 1995; Oliveberg et al. 1998), and (2) the average Φ-value increases with increasing temperature (Oliveberg et al. 1998). By both of these measures, the transition state appears to become more native-like under conditions in which the native state is energetically more similar to the transition state, consistent with the Hammond postulate (Hammond 1955). In other words, more extreme conditions or mutations yield a more native-like transition state.
Protein folding differs from the simple organic reactions for which the Hammond postulate was originally formulated in that it involves the formation and breakage of many weak interactions rather than only one or a few strong covalent bonds. As such, defining a simple reaction coordinate that accurately defines the relative positions of the native, transition, and denatured states is not trivial. Nevertheless, we have observed similar Hammond behavior for several properties in MD simulations of CI2. As the temperature increased, the transition state contained a higher β-sheet content, had a decreased radius of gyration, and had more native contacts. The magnitudes of these changes are all on the order of the uncertainty in the average value, allowing for the possibility that the trends would not hold up in larger ensembles. The presence of such trends in multiple properties, however, suggests that it is a real, though small, effect. For several other properties, including the total number of contacts formed, the number of main-chain hydrogen bonds formed, and the total solvent-accessible surface area, we did not see any trends with temperature.
Another complicating feature of the protein folding/unfolding reaction is the possible movement of the reactant or product states. While the native state is a relatively small ensemble of well-defined structures, the denatured state is a highly heterogeneous ensemble of conformations. Different denaturing or destabilizing conditions may favor different conformations within this ensemble, leading to changes in the position of the denatured state along some reaction coordinates. This effect is seen experimentally with changes in meq for a number of proteins, including CI2 (Sánchez and Kiefhaber 2003). This effect was also observed here, as the denatured values for all properties considered became progressively less native-like as the temperature increased. While there is an apparent trend toward lengthening the reaction coordinate with increasing temperature, the current data set does not allow accurate quantification of this trend. The lower temperature simulations presented here probably only sample a small region of the conformational space available to the denatured state. While temperature is probably having a real effect on the denatured state, we cannot be sure that we have adequately sampled denatured conformations at the lower temperatures without running much longer that our current 100 nsec simulations.
Oliveberg et al. (1998) observed movement of the transition state along a reaction coordinate defined by Φ-values with increasing temperature. The magnitude of this movement is not uniform throughout the protein, or even at a particular site. Different mutations at the same site give different sensitivities to temperature. The average value of Φ increases by ~0.1 per 100° temperature increase. Although the relative degree of structure in the transition state measured by S-values approximates the relative free energy effects of mutation measured by Φ-values, S-values are not strongly affected by simulation conditions. The S-values for individual residues can vary significantly, and the small number of simulations available at the lower temperatures prohibits the determination of accurate S-values and temperature trends for individual residues. Averaging over all residues somewhat mitigates this problem with sampling, although the small number of simulations available at lower temperatures still leaves us with some uncertainty in the average value. The S-values averaged over all experimentally probed residues are essentially constant over the 125° range considered here. The standard deviations may mask a slight temperature effect, but probably not as large as the ~0.l per 100° calculated by Oliveberg et al. (1998).
The S-values correlate slightly better with Φ-values given by Oliveberg et al. (1998) at 343 K than with those at 298 K. When extrapolated to higher temperatures, however, this correlation decreases. A similar increase in the correlation between simulated TS structure and Φ-values with increasing temperature has been observed for the small helical protein E3BD (Ferguson et al. 2005). In both cases, the correlation between simulation and experiment seems to reach a maximum near the protein’s Tm. This is also the temperature range in which the free energy barrier begins decreasing rapidly in a constant ΔCp‡ model. It is possible that there are slight changes in the position of the transition state with large changes in the free energy barrier height that we will not see in our simulations where the changes in barrier height are much smaller.
Rates of unfolding
It is apparent from the experimental unfolding rates of several proteins that the free energy barrier to unfolding decreases with increasing temperature, and that at some point it will become negligible relative to the thermal energy available to the system. The expression for the unfolding rate given in Equation 1 only holds in the presence of a significant free energy barrier, that is, ΔG‡(T) >> RT. For positive values of ΔCp‡, Equation 2 yields a decreasing free energy barrier as T is increased. Thus, at high temperatures, the protein is expected to enter a barrierless unfolding regime in which Equation 1 no longer holds; there is only one significantly populated state, and the rate of unfolding is determined by the local features of the free energy landscape as the protein diffuses toward this unfolded state (Bryngelson et al. 1995). A similar regime has been hypothesized to exist for the folding process. Barrierless folding has been claimed for one protein experimentally (Garcia-Mira et al. 2002), although those results have been called into question (Ferguson et al. 2004). In the barrierless unfolding case, the TS identified by conformational clustering would still be a good indicator of the overall folding mechanism and pathway, but might not correspond to the true location of the free energy barrier at lower temperatures. The results of simulations at lower temperatures (De Jong et al. 2002) indicate that the high temperature transition state corresponds to the location of the folding/unfolding free energy barrier. Additionally, correlation between the simulation transition state and the experimental transition state has been established using multiple metrics (Li and Daggett 1994, 1996; Daggett et al. 1996; Ladurner et al. 1998; Pan and Daggett 2001). There are essentially two adjustable parameters in Equations 1 and 2 that define the temperature at which unfolding becomes barrierless, Deff, the effective diffusion along the folding–unfolding reaction coordinate, and ΔCp‡, the heat capacity change associated with unfolding from the native to the transition state.
Akmal and Muñoz (2004) recently used a viscosity and temperature-dependent correction of Deff estimates based on experimental measurements and a constant ΔCp‡ in order to estimate the free energy barrier heights of several two-state proteins as a function of temperature. They find that the free energy barrier to the unfolding of CI2 drops to zero around 390 K. It is interesting to note that there was a significant free energy barrier to folding at all temperatures for all the proteins considered. Our Deff is significantly faster than that inferred from experiment at 298 K (Kubelka et al. 2004). The effective diffusion can be expected to speed up at higher temperature both due to the increase in available energy and the increase in water diffusion, as modeled by Akmal and Muñoz (2004). As a simple heuristic, we assume that unfolding cannot occur significantly faster than Deff, and set Deff to the fastest unfolding time observed in simulation. Using our faster Deff, we obtain a slightly higher rollover temperature, but if Deff is chosen within certain reasonable limits, its value does not change the rollover temperature significantly. If ΔCp‡ is constant, the fitted curves are quite steep near the rollover temperature for all of the proteins considered, so several orders of magnitude change in Deff only changes the rollover temperature by a small amount. The heat capacity change from the native to transition state can have a much greater effect on the roll-over temperature, as it determines the effect of temperature on the components of the free energy barrier.
ΔCp‡ is generally taken to be constant in experimental studies. Privalov and Makhatadze (1990, 1992) showed, however, that the heat capacity change for unfolding decreases with increasing temperature for several proteins, approaching zero somewhere between 400 K and 450 K. This decrease is due to a decrease in the effects of hydration with increasing temperature. In as much as the heat capacity increment of unfolding to the transition state is due to hydration of groups exposed by partial unfolding, ΔCp‡ can be expected to remain smaller than ΔCpN-D and drop to zero. Tan and coworkers (1996) observed a slight downward curvature in the dependence of ΔH‡ on temperature for CI2, indicating a decrease in ΔCp‡ with temperature. Their quadratic fit to the ΔH‡ temperature dependence goes to zero around 360 K. A more likely trend in ΔCp‡ with temperature would follow ΔCpN-D and asymptotically drop to zero at a higher temperature (Gill et al. 1985; Privalov et al. 1989). This decrease in ΔCp‡ would lead to a slowing of the rate at which the free energy barrier to unfolding decreased. That is, the free energy barrier would be present at higher temperatures than those predicted based on a constant ΔCp‡. Depending on the precise dependence of ΔCp‡ on temperature, this could be a major or minor effect. A more accurate model of the behavior of ΔCp‡ at high temperatures is needed if the temperature at which downhill folding occurs is to be identified.
A linear dependence of the natural logarithm of the unfolding rate on inverse temperature can be explained by Equation 1 and a heat capacity increment of zero. Thus, the essentially linear dependence of ln ku on the inverse temperature for CI2 seen in the MD simulations can be fit with a small free energy barrier. The rate of EnHD’s unfolding at 348 K by MD simulation is somewhat faster than that predicted by experiment, suggesting that the free energy barrier in our simulations is slightly lower than the actual barrier. The fast rates of CI2 unfolding also suggest that the free energy barrier in simulation is not as high as the actual free energy barrier. While a temperature-dependent Deff and a negligible free energy barrier cannot be ruled out, the unfolding rates are consistent with a small free energy barrier.
Conclusions
While the temperatures at which simulations and experiments are performed are nearing one another for individual systems (Mayor et al. 2003; Zhu et al. 2003; Ferguson et al. 2005), long extrapolations are necessary in most other cases. Additionally, the timescales of unfolding at lower temperatures are such that running the large numbers of simulations required for true ensemble averaging is infeasible. The evidence from present simulations and experiment, however, indicates that the structure of the transition state of wild-type CI2 does not change significantly under varying denaturation conditions, and the extrapolations are justified. The overall degree of structure in the transition state, as measured by the average S-values, total contacts, solvent-accessible surface area, and main-chain hydrogen bonds, does not change with temperature. The character of that structure does, however, change with temperature. As the temperature increases, the fraction of native contacts increases and the transition state becomes slightly more compact. This points to the possibility that the sensitivity of the transition state to mutation might change with temperature without large changes in structure. Mutations can change the position of the transition state along the reaction coordinate (Matouschek et al. 1995; Sánchez and Kiefhaber 2003), and the effect of temperature may be to make the transition state more sensitive to mutation, rather than to change its position along the reaction coordinate. This effect may also explain the difference in the degree of change in the Φ-values for different mutations at the same position (Oliveberg et al. 1998).
Materials and methods
All simulations were carried out using ENCAD (M. Levitt, Molecular Applications Group) with previously published potential functions (Levitt et al. 1995, 1997). For high temperature simulations, the initial structure was either the crystal structure of CI2 (1YPC; Harpaz et al. 1994), a structure from the NMR ensemble (3CI2; Ludvigsen et al. 1991), or a structure from a 298 K simulation (Day et al. 2002). These structures were then solvated in water to a depth of at least 8 Å in all directions from the protein. Solvent densities were set to values appropriate for each temperature by expanding this water box. Experimental solvent densities were used: 0.958 g/mL at 373 K, 0.939 g/mL at 398 K, 0.890 g/mL at 448 K, 0.861 g/mL at 473 K, and 0.829 g/mL at 498 K (Haar et al. 1984). The simulation times for the pure water simulations were 94 nsec and 40 nsec at 373 K; 40 nsec and 30 nsec at 398 K; 40 nsec, 10 nsec, and 10 nsec at 448 K; 20 nsec, 5 nsec, and 5 nsec at 473 K; and 20 nsec, 7.8 nsec, 3 nsec, 3 nsec, 3 nsec, and 3 nsec at 498 K. Other simulation details can be found in Day et al. (2002) and Li and Daggett (1996). The urea simulations were performed similarly, except that water molecules were randomly replaced with urea molecules to give a mol fraction of 0.186 for 8 M urea. The density was set to the experimental density of 1.103 g/mL. The urea potentials are described elsewhere (Zou et al. 2002). More simulation details for the urea simulations can be found in Bennion and Daggett (2003). Solvent excluded volumes for the crystal and transition state structures were calculated using the VADAR Web server (Willard et al. 2003; http://redpoll.pharmacy.ualberta.ca/vadar).
S-values are defined as the product of S2° and S3° (Daggett et al. 1996). S2° is the fraction of individual transition state structures in which the backbone configuration is similar to the native backbone. For residues that are in α-helix or β-sheet in the native state, similarity is based on an α-helix definition of −100° < φ < −30°, −80° < ψ < −5°, and a β-sheet definition of −170° < φ < −50°, 80° < ψ < −170°. All other residues are considered similar to the native conformation if they are within 35° of the native backbone torsion angles. S2° values are averaged over three residue windows. S3° values are the ratio of the average number of atom contacts made in the transition state and the number of atom contacts made in the native state. The contacts made in the transition state need not be made in the native state, allowing values >1.
The errors given in Tables 1 and 2 and Figure 6 ▶ are based on a set of 100 simulations of CI2 run at 498 K (R. Day and V. Daggett, unpubl.). Large numbers of randomly chosen transition state ensembles from two, three, five, and six simulated ensembles were generated and the average properties for each set were determined. The error bars for properties at 373 K and 398 K are based on the standard deviation in the average values of the two simulation ensembles. The error bars for properties at 448 K and 473 K are based on the standard deviation in the average values of the three simulation ensembles. The error bars in the 498 K and 333 K (urea) properties are based on the standard deviations in the six and five simulation ensembles, respectively. The errors at the low temperatures may be somewhat smaller than those shown as more conformational space is expected to be available at higher temperatures, but these values should still give a reasonable idea how far the true mean is from the presented average values.
Acknowledgments
We acknowledge helpful suggestions from Dr. Alan R. Fersht. The initial simulations at a range of temperatures were run by Dr. Sihyun Ham and the urea simulations by Dr. Brian J. Bennion. Financial support was provided by the NIH (GM 50789). R.D. was also supported by a Molecular Biophysics Training Grant from the NIH (2 T32 GM008268-17).
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.041226005.
References
- Akmal, A. and Muñoz, V. 2004. The nature of the free energy barriers to two-state folding. Proteins 57 142–152. [DOI] [PubMed] [Google Scholar]
- Bennion, B.J. and Daggett, V. 2003. The molecular basis for the chemical denaturation of proteins by urea. Proc. Natl. Acad. Sci. 100 5142–5147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryngelson, J.D., Onuchic, J.N., Socci, N.D., and Wolynes, P.G. 1995. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 21 167–195. [DOI] [PubMed] [Google Scholar]
- Daggett, V., Li, A., Itzhaki, L.S., Otzen, D.E., and Fersht, A.R. 1996. Structure of the transition state for folding of a protein derived from experiment and simulation. J. Mol. Biol. 257 430–440. [DOI] [PubMed] [Google Scholar]
- Day, R., Bennion, B.J., Ham, S., and Daggett, V. 2002. Increasing temperature accelerates protein unfolding without changing the pathway of unfolding. J. Mol. Biol. 322 189–203. [DOI] [PubMed] [Google Scholar]
- De Jong, D., Riley, R., Alonso, D.O.V., and Daggett, V. 2002. Probing the energy landscape of protein folding/unfolding transition states. J. Mol. Biol. 319 229–242. [DOI] [PubMed] [Google Scholar]
- Ferguson, N., Schartau, P.J., Sharpe, T.D., Sato, S., and Fersht, A.R. 2004. One-state downhill versus conventional folding. J. Mol. Biol. 344 295–301. [DOI] [PubMed] [Google Scholar]
- Ferguson, N., Day, R., Johnson, C.M., Allen, M.D., Daggett, V., and Fersht, A.R. 2005. Simulation and experiment at similar temperatures: Ultrafast folding of a thermophilic protein by nucleation-condensation. J. Mol. Biol. (in press). [DOI] [PubMed]
- Garcia-Mira, M.M., Sadqi, M., Fischer, N., Sanchez-Ruiz, J.M., and Munoz, V. 2002. Experimental identification of downhill protein folding. Science 298 2191–2195. [DOI] [PubMed] [Google Scholar]
- Gill, S.D., Dec, S.F., Olofsson, G., and Wadsö, I. 1985. Anomalous heat capacity of hydrophobic solvation. J. Phys. Chem. 89 3758–3761. [Google Scholar]
- Haar, L., Gallagher, J.S., and Kell, G.S. 1984. NBS/NRC steam tables: Thermodynamic and transport properties and computer programs for vapor and liquid states of water in SI units. Hemisphere Pub. Corp., Washington, DC.
- Hammond, G.S. 1955. A correlation of reaction rates. J. Am. Chem. Soc. 77 334–338. [Google Scholar]
- Harpaz, Y., elMasry, N., Fersht, A.R., and Henrick, K. 1994. Direct observation of a better hydration at the N-terminus of an α-helix with glycine rather than alanine as the N-cap residue. Proc. Natl. Acad. Sci. 91 3–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itzhaki, L.S., Otzen, D.E., and Fersht, A.R. 1995. The structure of the transition state for folding of chymotrypsin inhibitor 2 analysed by protein engineering methods: Evidence for a nucleation-condensation mechanism for protein folding. J. Mol. Biol. 254 260–288. [DOI] [PubMed] [Google Scholar]
- Jackson, S.E. and Fersht, A.R. 1991. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry 30 10428–10435. [DOI] [PubMed] [Google Scholar]
- Jackson, S.E., elMasry, N., and Fersht, A.R. 1993. Structure of the hydrophobic core in the transition state for folding of chymotrypsin inhibitor 2: A critical test of the protein engineering method of analysis. Biochemistry 32 11270–11278. [DOI] [PubMed] [Google Scholar]
- Kabsch, W. and Sander, C. 1983. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22 2577–2637. [DOI] [PubMed] [Google Scholar]
- Kubelka, J., Hofrichter, J., and Eaton, W.A. 2004. The protein folding “speed limit.” Curr. Opin. Struct. Biol. 14 76–88. [DOI] [PubMed] [Google Scholar]
- Ladurner, A.G., Itzhaki, L.S., Daggett, V., and Fersht, A.R. 1998. Synergy between simulation and experiment in describing the energy landscape of protein folding. Proc. Natl. Acad. Sci. 95 8473–8478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt, M. 1983. Molecular dynamics of native protein. II. Analysis and nature of motion. J. Mol. Biol. 168 621–657. [DOI] [PubMed] [Google Scholar]
- Levitt, M., Hirshberg, M., Sharon, R., and Daggett, V. 1995. Potential-energy function and parameters for simulations of the molecular dynamics of proteins and nucleic-acids in solution. Comput. Phys. Commun. 91 215–231. [Google Scholar]
- Levitt, M., Hirshberg, M., Sharon, R., Laidig, K.E., and Daggett, V. 1997. Calibration and testing of a water model for simulation of the molecular dynamics of proteins and nucleic acids in solution. J. Phys. Chem. B 101 5051–5061. [Google Scholar]
- Li, A. and Daggett, V. 1994. Characterization of the transition state of protein unfolding by use of molecular dynamics: Chymotrypsin inhibitor 2. Proc. Natl. Acad. Sci. 91 10430–10434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ———. 1996. Identification and characterization of the unfolding transition state of chymotrypsin inhibitor 2 by molecular dynamics simulations. J. Mol. Biol. 257 412–429. [DOI] [PubMed] [Google Scholar]
- Ludvigsen, S., Shen, H., Kjaer, M., Madsen, J.C., and Poulsen, F.M. 1991. Refinement of the three-dimensional solution structure of barley serine proteinase inhibitor 2 and comparison with the structures in crystals. J. Mol. Biol. 222 621–635. [DOI] [PubMed] [Google Scholar]
- Matouschek, A. and Fersht, A.R. 1993. Application of physical organic chemistry to engineered mutants of proteins: Hammond postulate behavior in the transition state of protein folding. Proc. Natl. Acad. Sci. 90 7814–7818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matouschek, A., Otzen, D.E., Itzhaki, L.S., Jackson, S.E., and Fersht, A.R. 1995. Movement of the position of the transition state in protein folding. Biochemistry 3413656–13662. [DOI] [PubMed] [Google Scholar]
- Mayor, U., Guydosh, N.R., Johnson, C.M., Grossman, J.G., Sato, S., Jas, G.S., Freund, S.M.V., Alonso, D.O.V., Daggett, V., and Fersht, A.R. 2003. The complete folding pathway of a protein from nanoseconds to microseconds. Nature 421 863–867. [DOI] [PubMed] [Google Scholar]
- Oliveberg, M., Tan, Y.J., Silow, M., and Fersht, A.R. 1998. The changing nature of the protein folding transition state: Implications for the shape of the free-energy profile for folding. J. Mol. Biol. 277 933–943. [DOI] [PubMed] [Google Scholar]
- Otzen, D.E. and Oliveberg, M. 2002. Conformational plasticity in folding of the split β-α-β protein S6: Evidence for burst-phase disruption of the native state. J. Mol. Biol. 317 613–627. [DOI] [PubMed] [Google Scholar]
- Otzen, D.E., Itzhaki, L.S., elMasry, N.F., Jackson, S.E., and Fersht, A.R. 1994. Structure of the transition state for the folding/unfolding of the barley chymotrypsin inhibitor 2 and its implications for mechanisms of protein folding. Proc. Natl. Acad. Sci. 91 10422–10425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan, Y. and Daggett, V. 2001. Direct comparison of experimental and calculated folding free energies for hydrophobic deletion mutants of chymotrypsin inhibitor 2: Free energy perturbation calculations using transition and denatured states from molecular dynamics simulations of unfolding. Biochemistry 40 2723–2731. [DOI] [PubMed] [Google Scholar]
- Privalov, P.L. and Makhatadze, G.I. 1990. Heat capacity of proteins. II. Partial molar heat capacity of the unfolded polypeptide chain of proteins: Protein unfolding effects. J. Mol. Biol. 213 385–391. [DOI] [PubMed] [Google Scholar]
- ———. 1992. Contribution of hydration and non-covalent interactions to the heat capacity effect on protein unfolding. J. Mol. Biol. 224 715–723. [DOI] [PubMed] [Google Scholar]
- Privalov, P.L., Tiktopulo, E.I., Venyaminov, S.Y., Griko, Y.V., Makhatadze, G.I., and Khechinashvili, N.N. 1989. Heat capacity and conformation of proteins in the denatured state. J. Mol. Biol. 205 737–750. [DOI] [PubMed] [Google Scholar]
- Sánchez, I.E. and Kiefhaber, T. 2003. Hammond behavior versus ground state effects in protein folding: Evidence for narrow free energy barriers and residual structure in unfolded states. J. Mol. Biol. 327 867–884. [DOI] [PubMed] [Google Scholar]
- Tan, Y.J., Oliveberg, M., and Fersht, A.R. 1996. Titration properties and thermodynamics of the transition state for folding: Comparison of two-state and multi-state folding pathways. J. Mol. Biol. 264 377–389. [DOI] [PubMed] [Google Scholar]
- Willard, L., Ranjan, A., Zhang, H., Monzavi, H., Boyko, R.F., Sykes, B.D., and Wishart, D.S. 2003. VADAR: A web server for quantitative evaluation of protein structure quality. Nucleic Acids Res. 31 3316–3319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu, Y., Alonso, D.O., Maki, K., Huang, C.Y., Lahr, S.J., Daggett, V., Roder, H., DeGrado, W.F., and Gai, F. 2003. Ultrafast folding of α3D: A de novo designed three-helix bundle protein. Proc. Natl. Acad. Sci. 100 15486–15491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou, Q., Bennion, B.J., Daggett, V., and Murphy, K.P. 2002. The molecular mechanism of stabilization of proteins by TMAO and its ability to counteract the effects of urea. J. Am. Chem. Soc. 124 1192–1202. [DOI] [PubMed] [Google Scholar]