Skip to main content
PMC home page
Protein Science : A Publication of the Protein Society logoLink to Protein Science : A Publication of the Protein Society
. 2005 Jul;14(7):1787–1799. doi: 10.1110/ps.051391205

Protein dynamics control proton transfer from bulk solvent to protein interior: A case study with a green fluorescent protein

Anoop M Saxena 1, Jayant B Udgaonkar 2, Guruswamy Krishnamoorthy 1
PMCID: PMC2253357  PMID: 15937281

Abstract

The kinetics of proton transfer in Green Fluorescent Protein (GFP) have been studied as a model system for characterizing the correlation between dynamics and function of proteins in general. The kinetics in EGFP (a variant of GFP) were monitored by using a laser-induced pH jump method. The pH was jumped from 8 to 5 by nanosecond flash photolysis of the “caged proton,” o-nitrobenzaldehyde, and subsequent proton transfer was monitored by following the decrease in fluorescence intensity. The modulation of proton transfer kinetics by external perturbants such as viscosity, pH, and subdenaturing concentrations of GdnHCl as well as of salts was studied. The rate of proton transfer was inversely proportional to solvent viscosity, suggesting that the rate-limiting step is the transfer of protons through the protein matrix. The rate is accelerated at lower pH values, and measurements of the fluorescence properties of tryptophan 57 suggest that the enhancement in rate is associated with an enhancement in protein dynamics. The rate of proton transfer is nearly independent of temperature, unlike the rate of the reverse process. When the stability of the protein was either decreased or increased by the addition of co-solutes, including the salts KCl, KNO3, and K2SO4, a significant decrease in the rate of proton transfer was observed in all cases. The lack of correlation between the rate of proton transfer and the stability of the protein suggests that the structure is tuned to ensure maximum efficiency of the dynamics that control the proton transfer function of the protein.

Keywords: green fluorescent protein, proton transfer, protein dynamics, Kramers’ theory, viscosity dependence, laser-induced pH jump, caged proton

In recent years there has been a gradual shift of paradigm in structural biology, namely a shift from seeking explanation of biomolecular function based on structure to that based on a combination of structure and dynamics (Frauenfelder et al. 1991; Stock 1999; Fenimore et al. 2002; Hammes-Schiffer 2002). For example, the static picture of oxygen carrier myoglobin does not reveal any path for an oxygen molecule to reach its binding site (Frauenfelder et al. 1991). Hence, the movement of the oxygen molecule relies upon specific breathing dynamics of the protein. Such demonstrations of “functional” dynamics, although relatively rare, are strong pointers toward the new paradigm mentioned above (Creveld et al. 1998; Miller and Agard 1999; Feher and Cavanagh 1999; Wolf-Watz et al. 2004). The main limitation in identifying correlations between dynamics and function lies in finding conditions that would alter dynamics with minimum perturbation of the average structure.

Proton transfer through the protein matrix, which is intimately involved in several proteins including proton pumps such as bacteriorhodopsin (Luecke et al. 1999), ATP synthase (Abrahams et al. 1994), and cytochrome oxidase (Iwata et al. 1995), is one of the ideal functions to address the correlation between dynamics and function. This is due to the involvement of a large cross section of the protein (from surface to interior) involved in proton transfer by using a network of H-bonds. Green fluorescent protein (GFP), a very commonly used fluorescent marker in cell biology (Shimomura et al. 1962; Tsien 1998), is an ideal model system to study the correlation of dynamics and proton transfer. The fluorescence intensity of GFP depends on the pH of the medium (Haupts et al. 1998; Kneen et al. 1998), and GFP has been used as an intracellular pH indicator (Wachter et al. 1997; Robey et al. 1998). Since the chromophore of GFP is buried within the protein, its pH sensitivity would rely upon proton transfer from the protein surface to the interior of the protein. Thus, GFP is a unique model system in that it has a very well defined and localized destination for proton transfer and the process can be monitored with ease and reliability.

GFP has a compact barrel-shaped structure made of 11 β-strands with an α-helix running through the central axis of the cylindrical structure. The chromophore of GFP that is responsible for its green fluorescence is formed from residues Ser65-Tyr66-Gly67 in the α-helix and is at the center of the cylindrical structure and almost perpendicular to the cylinder axis. It is highly protected from the bulk solvent by the surrounding β-strands leading to a small Stoke’s shift and a high quantum yield of fluorescence (Brejc et al. 1997). Wild-type GFP shows complex fluorescence properties (Tsien 1998). In contrast, enhanced green fluorescence protein (EGFP), with the mutations F64L and S65T, shows a single excitation peak at 488 nm and emission at 510 nm (Cormack et al. 1996). pH titration of EGFP fluorescence shows a sharp decrease in fluorescence intensity upon going to a low pH value with an apparent pKa of ~5.8 (Kneen et al. 1998). Explanations for the pH dependence include models based on (1) the protonation state of Tyr66 and (2) pH-dependent conformational changes in the protein structure around the chromophore (Dickson et al. 1997; Haupts et al. 1998; Schwille et al. 2000; Hanson et al. 2002; McAnaney et al. 2002) (for details, see Discussion). The structure of the protein, however, remains largely intact in the pH range 8–5 (see below).

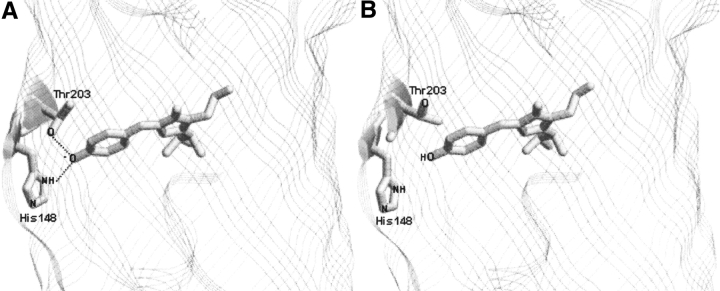
The GFP chromophore is surrounded by a highly complex H-bonding network (Omro et al. 1996; Brejc et al. 1997; Hanson et al. 2002). Hence, proton transfer reactions around the chromophore could be sensitive to the perturbation in local structure. The crystal structures of GFP obtained at low and high pH values (Elsliger et al. 1999; Hanson et al. 2002) show that some of the side chains near the chromophore change their orientation depending on the pH (Fig. 1 ▶). These side chains are likely to play a role in controlling the rate of proton transfer to the chromophore site. Recently, we have established a laser photolysis-induced pH-jump method to monitor fast kinetics of reversible transfer of protons between the bulk solvent and the GFP chromophore (Mallik et al. 2003). Preliminary results (Mallik et al. 2003) from these studies had suggested a correlation between protein dynamics and the rate of protonation of the chromophore.

Figure 1.

Figure 1.

Open in a new tab

Structural changes at the immediate vicinity of the phenoxide ring of the chromophore in S65T GFP (Elsliger et al. 1999) at two different pH levels, 8 (A) and 4.6 (B). Structures at pH 8 and 4.6 were drawn using RASMOL software and the PDB files with accession codes 1EMG and 1C4F, respectively.

In the present work, we have monitored the kinetics of GFP fluorescence change during pH jumps under a variety of conditions with the aim of shedding light on the rate-limiting step of the overall proton transfer process. pH jumps from 8 to 5 (where the protein is in native form) were carried out using the nanosecond laser photolysis method described earlier. Dynamics of EGFP were modulated by using various perturbants such as salts, viscogens, and temperature. These perturbants have either a stabilizing or a destabilizing effect on the protein. It was found that the proton transfer process was inhibited by all the perturbants. Thus, it appears that the proton transfer route is highly coordinated, and any perturbation will lead to its disruption.

Results

Laser-induced pH jump and proton transfer kinetics in EGFP

The kinetics of proton transfer in EGFP were monitored by the laser-induced pH jump technique. Details of the experimental technique can be found in our earlier work (Mallik et al. 2003). Basically, the pH of the medium was jumped from ~8 to ~5 in ~10 nsec by a Q-switched nanosecond pulse of 355 nm radiation. The “caged proton” 2-nitrobenzaldehyde undergoes photolysis to 2-nitrosobenzoic acid (Scheme 1 ▶) liberating protons within a few nanoseconds (George and Scaiano 1980; Abbruzzetti et al. 2000). Although pH jumps obtained are from single-shot experiments, the large amplitude of pH jumps ensures significant levels of signal changes. Figure 2 ▶ shows a typical trace of decrease in fluorescence intensity obtained during the pH jump from 8 to 5 that spans the entire pH titration of fluorescence intensity of EGFP (Fig. 2 ▶, inset A). In these experiments, the change in fluorescence intensity was monitored at ~510 nm by exciting at ~480 nm, which corresponds to a change in the amount of the deprotonated form of the chromophore (Haupts et al. 1998; Elsliger et al. 1999; Hanson et al. 2002). We label the decrease in fluorescence intensity following a pH jump from 8 to 5 as the “protonation process” of the chromophore; the justification for this assertion is provided in Discussion.

Scheme 1.

Scheme 1.

Open in a new tab

Mechanism depicting laser-induced pH jump caused by the photolysis of o-nitrobenzaldehyde to form o-nitrosobenzoate.

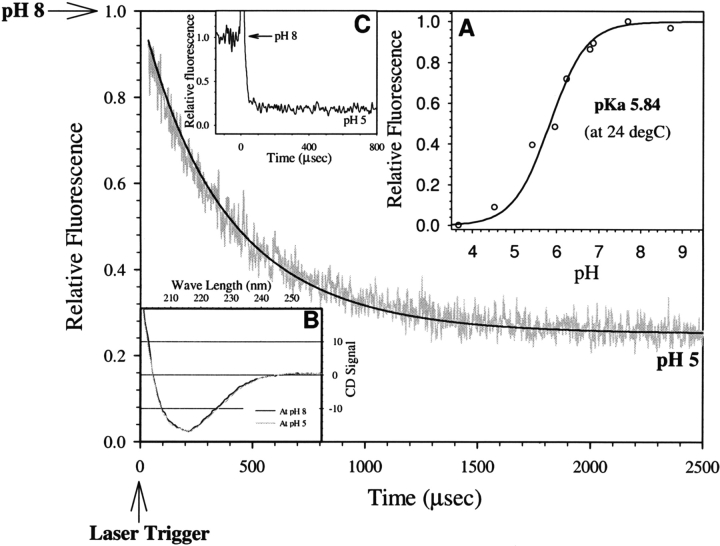
Figure 2.

Figure 2.

Open in a new tab

A typical pH jump trace showing kinetics of protonation of EGFP chromophore upon jumping the pH from 8 to 5. The smooth line was simulated by Equation 5 with rate constants k1 and k−1 as 3.5 × 108 M−1sec−1 and 5.0 × 102 sec−1, respectively. (Inset A) pH titration curve of fluorescence intensity of EGFP. (Inset B) Circular dichroism spectra of EGFP at pH 8 and 5 as shown by black and gray continuous lines, respectively. (Inset C) Result of pH jump in fluoresceinlabeled bovine serum albumin (with experimental conditions same as in EGFP) demonstrating rapid (<10 μsec) protonation of surface-labeled fluorescein.

To effectively use the information obtained from the experiments shown in Figure 2 ▶, the following were confirmed: (1) The entire protonation process was captured in the observation timescale as confirmed by the observation of a similar amplitude change when the reaction was monitored for a longer time in manual pH jump experiments (data not shown); (2) protein secondary structure remained unaffected when the pH was changed from 8 to 5 as confirmed by the CD spectroscopy (Fig. 2 ▶, inset B) and also shown by the crystal structure studies of S65T mutant of GFP at low pH values (Elsliger et al. 1999; Hanson et al. 2002); and (3) fluorescence lifetimes (τF) and rotational correlation times (φ) of the EGFP chromophore were similar in the pH range 8–5 (τF ~3.1 nsec and 1.7 nsec with amplitudes of 0.65 and 0.35, respectively, and φ ~ 9.8 nsec) indicating structural similarity at pH 8 and 5 at least in the vicinity of the chromophore. Moreover, the fluorescence decrease observed during the pH transition of 8–5 was found to be completely reversible. The proton transfer process in EGFP (half time ~ 300 μsec; Fig. 2 ▶) is slower than that of small molecules such as fluorescein or of fluorescein attached covalently to the surface of proteins such as barstar and bovine serum albumin by several orders of magnitude (half time<10 μsec; Fig. 2 ▶, inset C), which suggests that the proton transfer process in EGFP is controlled by the protein matrix (H-bonded network) and its dynamics.

The time profile of fluorescence decrease following the pH jump (Fig. 2 ▶) was fitted to Equation 5 (below). This equation describes the experimental traces in an exact manner when compared to a more simplistic exponential decay analysis. However, the conclusions derived are very similar when either of the two methods is used. The rate constants for the protonation (k1) and deprotonation (k−1) of the EGFP chromophore at pH 5.3, estimated from Equation 5, are 3.5 × 108 M−1 sec−1 and 5.0 × 102 sec−1, respectively. These rate constants should be treated only as operational parameters, as they could represent a combination of various processes such as proton flow through the network and proton transfer to the chromophore (see below). Furthermore, the rate coefficients recovered from our experiments were significantly smaller when compared to those obtained by FCS (k1=1.5 × 109 M−1 sec−1 and k−1=4.5 × 103 sec−1; Haupts et al. 1998). These differences are discussed in detail in the Discussion section.

Viscosity dependence of proton transfer kinetics

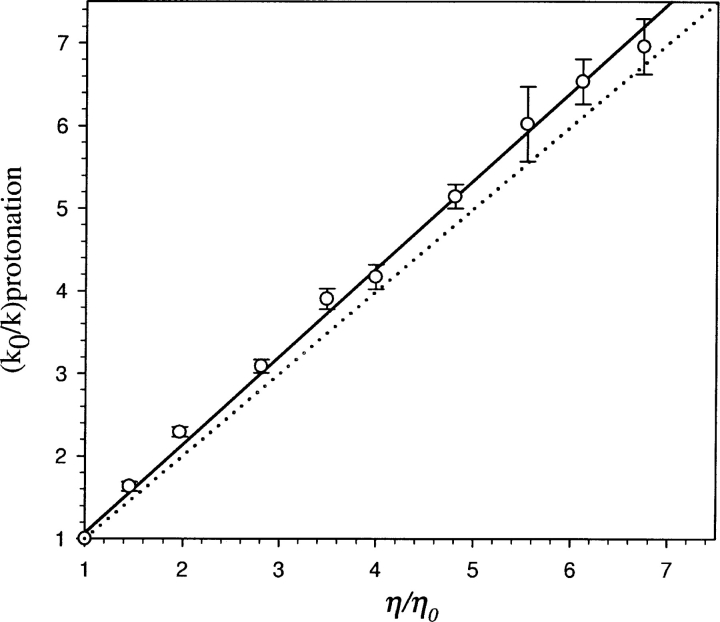
The presumption that proton transfer in EGFP could be modulated by the protein matrix prompted us to look for experimental demonstrations of the influence of protein dynamics. The viscosity dependence of proton transfer kinetics is a major handle in addressing the involvement of protein dynamics. Figure 3 ▶ shows the viscosity dependence of the rate constants when the bulk viscosity was increased by the addition of glycerol. The near linear dependence (with unit slope) of the ratio of rate constants with that of bulk viscosity is in line with the expectation from Kramers’ theory (Kramers 1940; Gavish and Yedgar 1995), which predicts an inverse relationship between the rate constant and viscosity in the high-friction regime as that encountered in condensed media. The dramatic reduction in the rate constants associated with the proton transfer process with an increase in solvent viscosity could indicate reduced accessibility of protons from the protein–water interface to the chromophore.

Figure 3.

Figure 3.

Open in a new tab

Dependence of the protonation rate constant (k) of EGFP chromophore on solvent viscosity (η) (open circles). k and k0 are the protonation rate constants of EGFP at solvent viscosities of η and η0, respectively. k0 and η0 correspond to the situation in the absence of viscogen (glycerol). Continuous line shows the least square fit with slope=1.09 and the dotted line corresponds to Kramers’ relationship (slope=1) between the rate constant and the solvent viscosity (k∝1/η).

Temperature dependence of proton transfer kinetics

With the aim of obtaining more insight into the energetics and mechanism of the proton transfer process, an analysis of the temperature dependence of the proton transfer process was carried out in the temperature range of 7°C–45°C (Fig. 4 ▶). The forward rate (i.e., the protonation process) is nearly temperature independent (ΔE ~ 0.3 kcal mol−1; Fig. 4A ▶), suggesting that it is almost a barrierless process. The apparent energy of activation for the reverse process (i.e., the deprotonation process) was ~14.8 kcal mol−1 (Fig. 4B ▶). Thus the decrease in pKa of the chromophore with increase in temperature, observed in pH titrations (data not shown), is mainly due to an increase in the rate of the deprotonation process.

Figure 4.

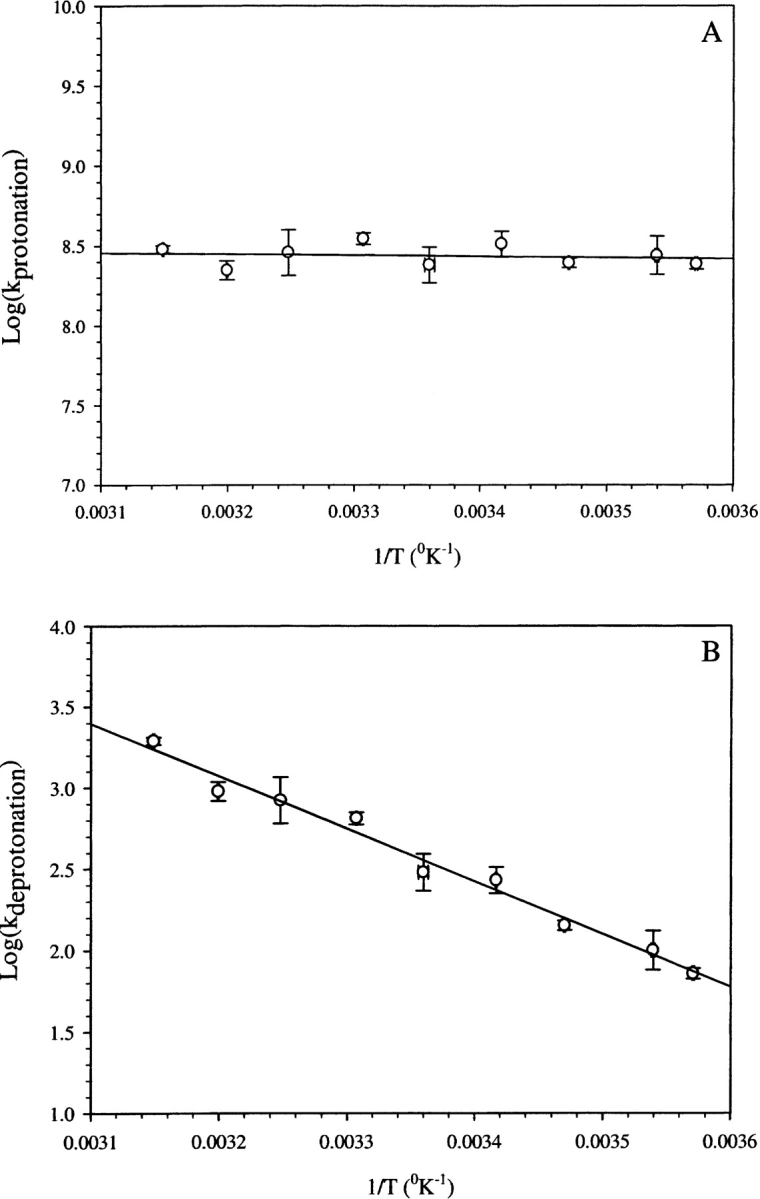
Figure 4.

Open in a new tab

Arrhenius plots showing the variation in the protonation rate constant (A) and deprotonation rate constant (B) as a function of 1/T.

pH dependence of proton transfer kinetics

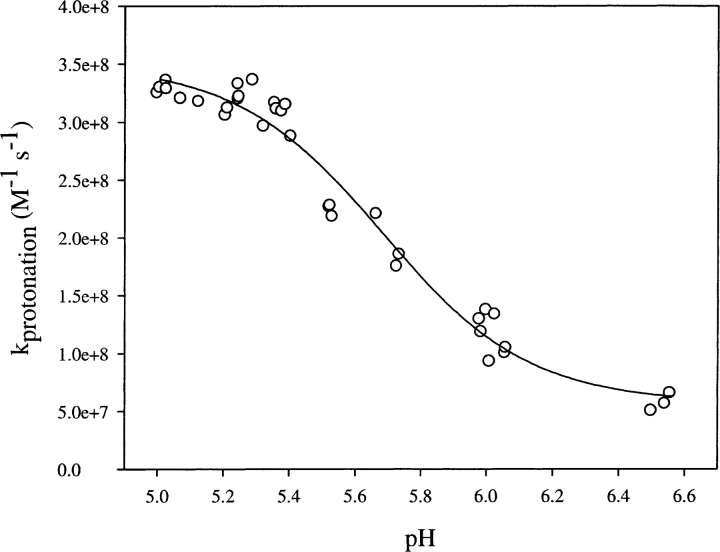
The pH dependence of the rate of proton transfer from bulk solvent to the protein interior was expected to offer extra insights into the mechanism. The overall rate constant for the proton transfer process is decreased significantly with an increase in pH (Fig. 5 ▶). Proton concentration was taken into account via Equation 5 while estimating k1 at various pH values, and hence the observed pH dependence reflects the inherent effect of pH on k1. Thus, this observation indicates the presence of a pH-induced conformational change with an apparent pKa of ~5.6. The gross structure of the protein remained unchanged in the pH range 5–8 as shown by circular dichroism (CD) spectra (Fig. 2 ▶, inset B), and hence structural change(s) responsible for the change in the proton transfer rate appear to be local and subtle.

Figure 5.

Figure 5.

Open in a new tab

pH dependence of protonation rate constant of EGFP. Data were obtained by pH-jump experiments from an initial value of pH 8 to various lower values given in the figure.

Could the pH-dependent conformational change inferred from the proton transfer kinetics be seen through any other window? With the aim of answering this question we monitored the fluorescence of the single tryptophan, Trp57, which is ~14 Å away from the EGFP chromophore. Fluorescence emission spectra of Trp57 in EGFP could be seen with ease unlike in the case of other GFP mutants such as S65T-GFP. (This could be due to an unfavorable orientation between the GFP chromophore and the tryptophan side chain in EGFP, resulting in the absence of energy transfer from Trp to GFP unlike in the case of S65T mutant [Omro et al. 1996].) The pH titration of Trp57 fluorescence showed a continuous decrease in the fluorescence quantum yield without any spectral shift in the pH range 9–5 (Fig. 6A ▶). Also, as shown in Figure 6B ▶, the quenching of Trp57 fluorescence by acrylamide was more efficient at pH 5 than at pH 8. The values of the bimolecular quenching constant at pH 5 and 8 in the absence of any additive, estimated from the Stern–Volmer plot (Fig. 6B ▶), were 1.1 × 1010 M−1sec−1 and 3.8 × 109 M−1sec−1, respectively. This result indicates enhanced conformational dynamics, and hence the altered solvent accessibility at the Trp57 site of the protein, at lower pH values. The observed pH dependence of conformational dynamics can be reconciled with the overall similarity of the structures at pH values of 8 and 5 (Fig. 2 ▶, inset B; Elsliger et al. 1999; Hanson et al. 2002) by noting that while the average structure could remain largely pH independent, structural dynamics could be pH dependent.

Figure 6.

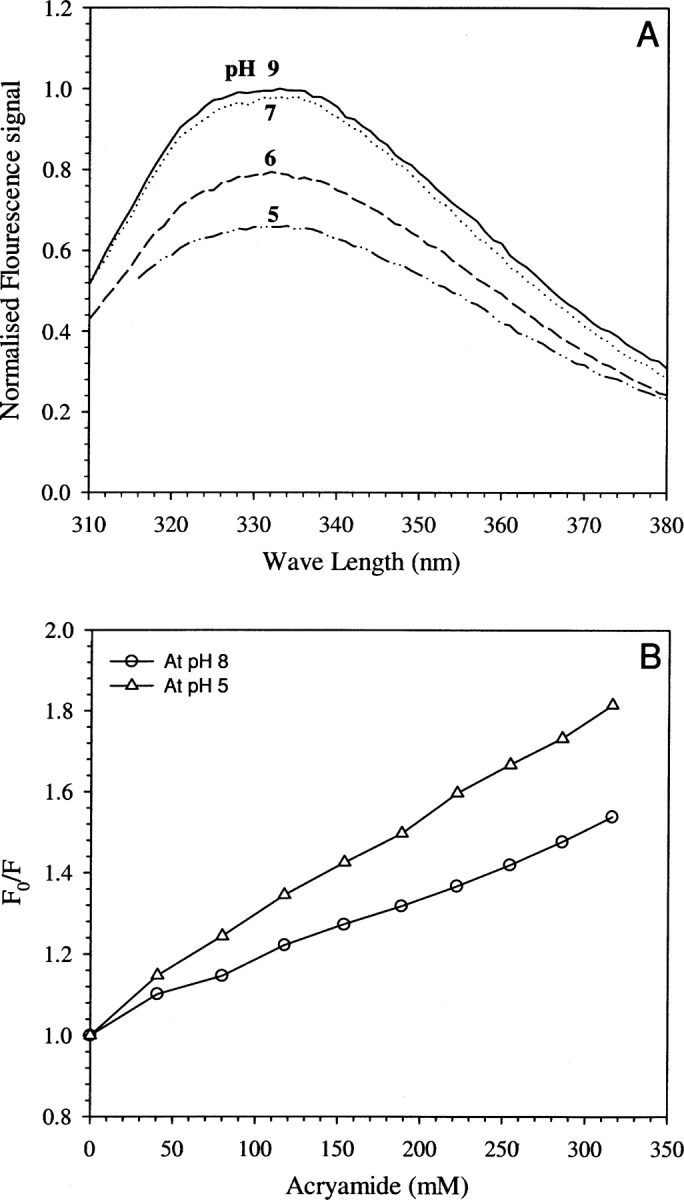
Figure 6.

Open in a new tab

(A) Fluorescence emission spectra of tryptophan in EGFP showing the decrease in fluorescence intensity as a function of pH (9–5). (B) Stern–Volmer plots of steady-state fluorescence intensity showing the quenching of fluorescence by acrylamide at pH 8 (open circles) and at pH 5 (open triangles).

Salt effect on proton transfer kinetics

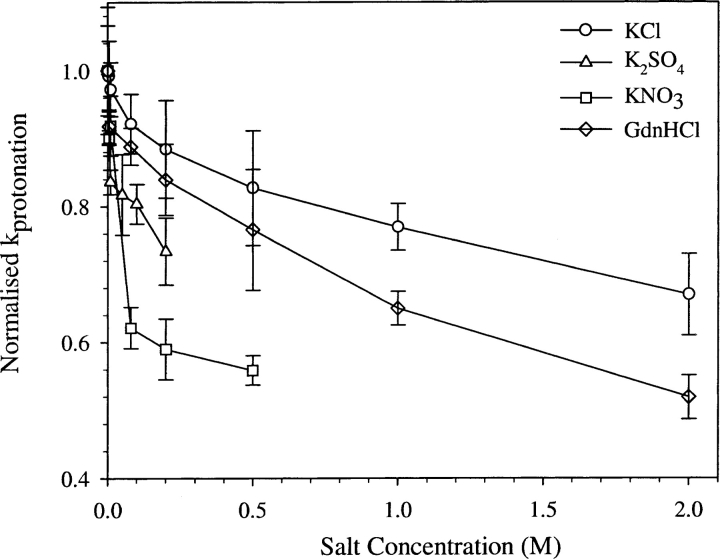
Is the rate of proton transfer sensitive to water structure or solvent dynamics at the protein–water interface? To answer this question, the effects of various chaotropic salts such as KCl, KNO3, and K2SO4 on the proton transfer kinetics were studied. In all the cases studied here (Fig. 7 ▶), the rate constant of proton transfer was found to decrease with the increase in the salt concentration. The effect of salt on the pKa of the chromophore was determined and incorporated into Equation 5 while estimating the value of k1 as in the case of other perturbants. However, in the cases of K2SO4 and KNO3, the magnitude of shifts in the pKa values were quite large at high concentrations of salts, and hence, data collections were restricted to <0.5 M.

Figure 7.

Figure 7.

Open in a new tab

Normalized protonation rate constant of EGFP at various concentrations of salts: KCl (open circles), KNO3 (open squares), K2SO4 (open triangles), and GdnHCl (open diamonds).

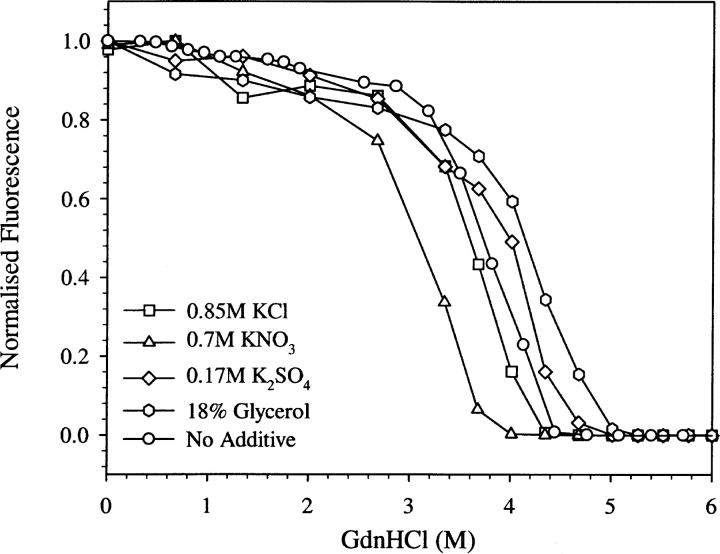
The general decrease in k1 in the presence of salt (albeit to different extents; Fig. 7 ▶) might be the result of an unfavorable perturbation of the dynamics that control the proton transfer process. The concentrations of GdnHCl used were below that corresponding to the beginning of the unfolding transition of EGFP as shown by the denaturation curve (open circles in Fig. 8 ▶). The melting curve shown in Figure 8 ▶ by open circles agrees well with that reported elsewhere (Verkhusha et al. 2003).

Figure 8.

Figure 8.

Open in a new tab

GdnHCl-induced denaturation curves of EGFP at pH 8, in the absence of any additive (open circles) and in the presence of various additives such as 0.85 M KCl (open squares), 0.7 M KNO3 open triangles), 0.17 M K2SO4 (open diamonds), and 18% glycerol of viscosity 1.61 cP (open hexagons), obtained by EGFP fluorescence measurements at 520 nm.

Change in stability of EGFP in presence of various additives

To see the effect of various additives on the stability of EGFP, GdnHCl-induced unfolding of EGFP was monitored (Fig. 8 ▶). The denaturant titration curves show that some perturbants such as glycerol and K2SO4 increased the stability, whereas salts such as KCl and KNO3 decreased the stability. Thus, there is no obvious correlation between the change in the stability and the change in the proton transfer rate constant k1.

Discussion

Proton transfer kinetics in EGFP

As mentioned in the introduction, proton transfer in GFP could be an effective handle to address the correlation between dynamics of proteins with their function, in general. In the case of GFP, proton transfer from bulk solvent to the chromophore, which is located in the interior of the protein, can be thought of as a prototype function.

First, we should address the question as to the identity of the physical process that causes the pH-jump-induced decrease in fluorescence intensity (Fig. 2 ▶). As mentioned earlier, pH sensitivity of GFP fluorescence could have a variety of origins depending on the mutation of side chains and experimental conditions (Dickson et al. 1997; Haupts et al. 1998; Schwille et al. 2000; Hanson et al. 2002; McAnaney et al. 2002). One of the simplest models to explain pH sensitivity is based on pH-controlled reversible transformation between protonated (state A, absorption peak at 390 nm) and deprotonated (state B, absorption peak at ~485 nm) forms of the chromophore (Tsien 1998). However, time-resolved spectroscopic studies (Chattoraj et al. 1996; Lossau et al. 1996; Schwille et al. 2000; McAnaney et al. 2002; Winkler et al. 2002; Kennis et al. 2004) and hole burning spectroscopic studies (Creemers et al. 1999) have indicated that the broad absorption at ~485 nm is due to a combination of two anionic forms, namely B and I. I is the ground state of I*, the product of excited state proton transfer (ESPT) reaction from A* (see below). It has also been suggested that the B state is the product of irreversible decarboxylation of E222 in wild-type GFP and in some mutants having similar photophysics (van Thor et al. 2002). We note that the near perfect agreement between the pKa values estimated from pH titration of either the absorption spectra (at 390 nm or at 490 nm) or the fluorescence emission spectra (Haupts et al. 1998; MacAnaney et al. 2002; our data on EGFP [Fig. 2 ▶, inset A] and absorption titration [data not shown]) seems to support this simpler model of pH-dependent fluorescence change.

A more sophisticated model for explaining pH dependence of fluorescence comes from the exhaustive series of time-resolved spectroscopic studies mentioned above. The basic elements of the model are as follows: Excitation at ~390 nm (state A) results in excited protonated chromophore A*, which undergoes ESPT to form deprotonated I*, which emits in the region ~510 nm generating I. I and I* equilibrate with B and B*, respectively, on slow timescales. At high (~8) pH values, ESPT is efficient owing to favorable H-bonding network geometry around the chromophore leading to strong green fluorescence of I* with a peak at ~510 nm. At low pH (~5) values ESPT is largely inhibited (in S65T mutants but not in wtGFP) due to unfavorable orientation of nearby residues involved in the H-bonding network. Hence A* decays to A by emitting blue fluorescence at ~460 nm (Hanson et al. 2002). Thus according to this mechanism, the pH dependence of green fluorescence arises from pH-dependent structural changes that modulate the efficiency of ESPT.

While the above model based on ESPT could explain the pH dependence of fluorescence when it is excited at the A band (~390 nm), this model is not appropriate when the protein is excited at the ~490-nm band that is associated with the B and I states mentioned above. Both the B and I states are deprotonated forms of the chromophore and emit at ~510 nm. In our experiments, the excitation and emission wavelengths were ~480 nm and 510 nm, respectively. Hence the observed decrease in fluorescence following pH jumps (from 8 to 5; Fig. 2 ▶) is likely to have been caused by a decrease in the population of B (and/or I) and a concomitant increase in the protonated form A.

The presence of two anionic forms, B and I, raises the question of whether both the forms are in a direct protonation equilibrium with the A form. Alternatively, one could think of a sequential process from B to A via I. In this context, pH titrations of optical absorption of EGFP have shown the following (Haupts et al. 1998; our data not shown): (1) There is a well-marked isobestic point indicating the presence of only two forms; (2) there is no pH-independent absorption in both the 390-nm and 490-nm bands unlike for other mutant proteins such as deGFP1 and deGFP2, which showed a pH-independent absorption in an ~400-nm band (Hanson et al. 2002); (3) pH titrations of the two absorption bands are reversible, indicating that the 490-nm band is unlikely to be due to irreversible decarboxylation of E222 as suggested in wild-type GFP (van Thor et al. 2002); and (4) the pKa value estimated from either absorption titration or fluorescence titration are identical (5.80 ± 0.05). These observations indicate that either the absorption spectra of B and I are very similar to each other or the 490-nm band is largely contributed by either B or I. In any case, the observed decrease in fluorescence (Fig. 2 ▶) can be interpreted as due to a decrease in the population of B and I, leading to the protonated A form. An alternative explanation wherein the pH dependence of fluorescence could arise due to pH-dependent rearrangement of protein side chains leading to quenching of fluorescence of the anionic chromophore is not supported by the observed pH-dependent absorption (at ~490 nm; Haupts et al. 1998; our data not shown) of the anionic form. Thus the pH dependence of fluorescence is most likely to come from pH dependence of the population of the anionic form.

The overall proton transfer process that is monitored by the pH-jump-initiated fluorescence changes (Fig. 2 ▶) can be dissected into the following “elementary” processes: (1) diffusion of protons in the bulk solvent, (2) transfer of protons from bulk solvent to the protein–water interface, (3) proton flow from the interface to the chromophore site through a H-bonded network, and (4) rearrangement of side chains around the GFP chromophore, as well as of the chomophore itself, to enable the transfer of proton to the deprotonated chromophore. The last step could also involve possible transformation of B into I. Since these steps could be expected to occur sequentially, the observed process (Fig. 2 ▶) would be dominated by the slowest (rate-determining) of the four steps mentioned above. Process 1 is unlikely to be the rate-determining step since protonation of free fluorescein (wherein the protonation site is exposed) occurs within 10 μsec (Mallik et al. 2003) in contrast to EGFP protonation which occurs in ~300 μsec. Process 2 is also an unlikely candidate since proton transfer at interfaces have been shown to occur without any major kinetic barrier (Gutman et al. 1992; Maity and Krishnamoorthy 1995), and is expected to occur on the submicrosecond timescale. In fact, protonation of fluorescein covalently attached to the surfaces of proteins such as barstar and bovine serum albumin occurred within ~10 μsec in our setup (Fig. 2 ▶, inset C). Thus, either process 3 or process 4 is the most likely candidate for the rate-determining process. However, the involvement of process 2 cannot be summarily ruled out (see below). In this work, one goal has been to resolve between these possibilities by modulating the proton transfer kinetics in a variety of ways.

In the present pH jump experiments on EGFP, the observed time constant for protonation of the EGFP chromophore was ~300 μsec upon changing the pH from 8 to 5, while that for the S65T mutant form of GFP was ~87 μsec (Mallik et al. 2003). EGFP differs from S65T-GFP by the single additional mutation F64L. Being close to the site of the chromophore and the putative H-bond networks involved in proton pathway, the F64L mutation might affect the efficiency of proton transfer from bulk solvent, thereby slowing down the overall process.

Rate constants associated with the protonation (k1) and deprotonation (k−1) processes were obtained by fitting the kinetic traces (Fig. 2 ▶) to Equation 5. Values of k1 and k−1 were 3.5 × 108M−1sec−1 and 5.0 × 102 sec−1, respectively, when the pH transition was from 8 to ~5.3 in buffer at 22°C. These estimates are based on a model of a single-step protonation–deprotonation reaction. In view of our dissection of the overall process into four elementary processes (see above), k1 and k−1 would be dominated largely by the rate-determining step. As mentioned earlier, the rate constants recovered from our pH jump experiments are slower, by a factor of 3–5, than those recovered from FCS experiments (Haupts et al. 1998; Schwille et al. 2000). This is probably due to the basic difference between the perturbative relaxation method used in this work and the near-equilibrium FCS method. In the pH jump relaxation method, the concentration of protons in the bulk solvent is jumped to higher values, and the subsequent proton transfer to the chromophore buried inside the protein is monitored. This entire process occurs in several steps as described above (see Discussion, paragraph 6), and it has been argued above that one of the steps, namely proton transfer through the protein matrix, is slower than the rest. In contrast, the FCS method monitors the fluctuation in the protonation state of the chromophore, and the observed process most likely represents the shuttling of protons between the chromophore and a nearby side chain, a process that could be one of the steps mentioned above. In this connection it is worth noting that a recent study using ultrafast multipulse control spectroscopy has given the timescale of proton transfer to an I-like species to form the A state as 400 psec in a wild-type-like mutant form of GFP (Kennis et al. 2004), which is faster than the timescale in our experiments by six orders of magnitude. Hence, the process observed in our experiments, wherein the initiation is by a pH jump in bulk solvent (Fig. 2 ▶) in contrast to observations on excited state proton transfer (Kennis et al. 2004), could be rate limited by slow transformation of B into I coupled to protein conformational changes.

Solvent viscosity dependence of proton transfer kinetics

It is well known that rates of diffusion-controlled bimolecular chemical reactions are inversely proportional to bulk solvent viscosity as expected from the Smoluchowski theory of diffusion-controlled reactions (Bamford and Tipper 1969; Hasinoff and Chishti 1982). Such a viscosity dependence of rates is not easily comprehensible in complex unimolecular biochemical processes such as protein folding, ligand dissociation from proteins, and so forth. Experimental demonstrations of viscosity dependence in such processes (Alberding et al. 1981; Goldberg and Baldwin 1998; Ladurner and Fersht 1999) have provided impetus in using it as an effective tool for gaining a deeper understanding of protein dynamics–controlled processes. The unfolding and refolding reactions of several proteins have been shown to be controlled by the bulk solvent viscosity (Chrunyk and Matthews 1990; Bhattacharyya and Sosnick 1999; Jacob et al. 1999). In these studies, viscosity dependence has been used to identify the location of transition states in the folding/unfolding pathways. In many situations, diffusion-controlled (and hence, viscosity-dependent) chain collapse has been identified as the rate-determining step in the folding process.

Ligand dissociation from proteins is another unimolecular process that has been shown to be controlled by viscosity (Ansari et al. 1992). In the case of ligand binding processes, viscosity dependence has been shown to arise from conformational fluctuations between sub-states of the protein dictating the rate of entry of ligand, rather than from a diffusion-controlled binding process that invokes static barriers (Beece et al. 1980). One of the key elements in understanding fluctuation between conformational substates is the knowledge of the extent of solvent-controlled flexibility of protein side chains. It has been shown (Lakshmikanth and Krishnamoorthy 1999) that the response to viscosity of the dynamics of solvent-exposed side chains depends upon the structural integrity of the protein. All these observations serve to demonstrate the utility of varying solvent viscosity for gaining a deeper understanding of protein functions.

Theoretical treatment of the dynamic influence of solvent viscosity in unimolecular reactions was first provided by Kramers (Kramers 1940; Gavish 1980; Hynes 1985; Gutfreund 1995). This theory, which is a significant advancement beyond the transition state theory, treats the chemical reaction as a Brownian diffusion over an energy barrier accompanied by friction with solvent molecules. Collision with solvent would lead to several recrossings over the barrier, and in the high friction limit (corresponding to reactions in condensed phase) the rate constant (k) is predicted to vary inversely proportional to the viscosity η (Kramers 1940; Hynes 1985; Gutfreund 1995). However, a phenomenological expression, ɛ=−δ(lnk)/δ(ln η) with ɛ in the range of 0<ɛ≤ 1 (Gavish 1980) is more useful while describing the observations in general.

While Kramers’ prediction (ɛ=1) has been verified in the folding process of a number of proteins (Chrunyk and Matthews 1990; Bhattacharyya and Sosnick 1999; Jacob et al. 1999), there have been observations of 0<ɛ<1 in a number of situations, including the folding reactions of some other proteins (Jacob et al. 1997; Silow and Oliveberg 2003). Such sublinear and nonlinear behavior has also been seen in processes such as unfolding of protein, ligand dissociation (Ansari et al. 1992), side chain dynamics in native proteins (Lakshmikanth and Krishnamoorthy 1999), and quenching of protein fluorescence by acrylamide (Eftink and Hagaman 1986). The nonlinear nature of viscosity dependence on the rate of photodissociation of CO from myoglobin was explained as due to the contribution of internal friction involving protein atoms and the external friction arising from solvent molecules (Ansari et al. 1992). The sublinear viscosity dependence (ɛ<1) of side chain dynamics in native proteins might originate from preferential hydration of protein surfaces by water in water–glycerol mixtures (Lakshmikanth and Krishnamoorthy 1999). Thus, it appears that a variety of processes in native proteins are coupled weakly (ɛ<1) to viscosity (Eftink and Hagaman 1986; Ansari et al. 1992; Lakshmikanth and Krishnamoorthy 1999). In view of this, the linear dependence (ɛ=1) observed in the present situation (Fig. 3 ▶) indicates strong coupling. This suggests that a change in solvent viscosity modulates the rate of proton transfer through the H-bond network connecting the protein–water interface with the chromophore. The alternative model, wherein the proton transfer rate is controlled by the conformational changes involving the buried chromophore, is less likely. This is due to the fact that dynamics in the protein interior are likely to be coupled only weakly to viscosity changes, as observed in the case of quenching of buried chromophores in parvalbumin and ribonuclease T1 (Eftink and Hagaman 1986).

Perturbation of proton transfer kinetics in EGFP

We surmised that the temperature dependence of proton transfer kinetics could be an effective indicator of the rate-limiting process in the chain of events leading to protonation of the chromophore. The near temperature independence of k1 (Fig. 4A ▶), which is rather surprising, might indicate this as a barrierless process. A simple diffusion-limited protonation process could be expected to have an activation barrier. However, if the overall protonation process is rate limited by proton hopping through a H-bonded network, as suggested in this work, we might expect the process to be barrierless, analogous to the Grotthuss mechanism (de Grotthuss 1806) of tunneling of protons through “proton wires” (Agmon 1995). In contrast to such a widely believed model of proton tunneling, direct experiments on the mobility of protons in ice at low temperatures have shown the motion of hydronium ion as an activated process (Cowin et al. 1999). Furthermore, since proton relay would require a H-bonded network connecting the chromophore with the protein surface, the rate of proton flow would be expected to decrease with an increase in temperature due to weakening of the network. Thus, the observed very low temperature dependence of k1 might be the result of a fortuitous combination of activated movement of protons and the temperature-dependent stability of the H-bonded network. The latter could involve an exothermic ionization of side chains (such as a His residue) involved in the internal proton transfer network. In this model, the overall rate constant becomes a product of the temperature-dependent rate constant (which is also viscosity dependent) and the equilibrium constant of the exothermic process.

Furthermore, pH dependence of the overall rate constant with an apparent pKa of ~5.6 (Fig. 5 ▶) suggests the involvement of His (148) and/or Glu (222) side chains in the proton transfer network. The involvement of His148 in the backbone dynamics has been shown recently (Seifert et al. 2003). It is important to note that the apparent pKa of ~5.6 inferred from these studies is unrelated to the pKa (5.8) of the EGFP chromophore (Fig. 2 ▶, inset A). Furthermore, the increase in the bimolecular quenching constant, of Trp57 by acrylamide, at pH 5, when compared to pH 8 (Fig. 6B ▶), along with the pH dependence of its emission spectra (Fig. 6A ▶), are indicators of increased solvent accessibility and increased dynamics at lower pH values. Thus, the role of dynamics in modulating proton transfer is highlighted once again.

Proton transfer from surface to interior is fine-tuned

The arguments given above suggest that proton transfer from the protein–water interface to the GFP chromophore limits the rate of protonation. Validation of this model would have implications in many proteins such as proton pumps (Luecke et al. 1999) and channels (Lear 2003; Starace and Bezanilla 2004) wherein transport of protons through protein matrix is encountered. Apart from providing a direct estimate of the timescale of the proton transfer process, the effect of protein/solvent dynamics on proton transfer efficiency (Lill and Helms 2002; Cui and Karplus 2003) could also be delineated.

Water structure around the protein might significantly influence the kinetics of proton transfer. This expectation was borne out by the observed slowing down of the proton transfer process by salts such as KCl, KNO3, and K2SO4, which are known to perturb water structure by the Hofmeister effect (Hofmeister 1888; Baldwin 1996). Perturbation of H-bonding properties of water by the salts is the most favored model for the Hofmeister effect (Baldwin 1996). The observed stronger effect of KNO3 when compared to the other salts supports the view that disruption of water structure is the cause for the decrease in the rate of protonation. The effect of changes in water structure on the protonation kinetics could occur in two different ways: (1) It could alter the overall dynamics of the protein (Gavish and Yedgar 1995) and hence the dynamics of H-bond network involved in the protonation, and/or (2) interfacial proton transfer from bulk solvent to the protein (process 2 mentioned earlier) could be drastically slowed down by the distruption of water structure. The second possibility can be ruled out because measurements of the protonation of fluorescein attached to the surface of proteins such as barstar or BSA occurs within 10 μsec, both in the absence and presence of chaotropic salts (Fig. 2 ▶, inset C).

In the case of denaturant GdnHCl, the slowing down of the protonation process might have come about by partial denaturation of the protein. Although the concentrations of the denaturants used were subdenaturing concentrations (open circles in Fig. 8 ▶), partial weakening of the protein structure might contribute to the slowing down of the protonation kinetics. These observations also bring out another striking aspect of the structure and function of EGFP, namely, the native structure can undergo subtle changes in its dynamics resulting in significant changes in its function. In the present situation these subtle changes could be alteration, by the denaturants, of the structure and dynamics of theH-bonded network of side chains involved in the proton relay from bulk solvent to the protein interior.

Is there a correlation between the stability of EGFP and the rate of proton transfer? The observed deceleration of the rate by subdenaturing concentrations of the denaturant, GdnHCl (open circles in Fig. 8 ▶) might suggest the presence of such a correlation. However, the observation that the proton transfer process is also decelerated, albeit to different extents, by perturbants that stabilize the protein (Fig. 8 ▶) clearly indicates the absence of any correlation between stability and the rate of proton transfer. Taken together, our observations point out that proton transfer in EGFP, which can be considered as a prototype function of proteins, is indeed finely tuned for maximum efficiency. Any alteration in the structure and dynamics, however subtle it may seem, leads to a decrease in its efficiency. Furthermore, even agents that increase the stability of EGFP (such as glycerol and K2SO4; Fig. 8 ▶) cause only a decline in the efficiency of proton transfer.

In conclusion, the present work has shown that the protonation process of the GFP chromophore in EGFP is rate limited largely by transfer of protons from bulk solvent to the chromophore.

Materials and methods

Chemicals

All the chemicals used were of the highest purity grade available from Sigma Aldrich Inc. In all the pH jump experiments, a very low buffer concentration, ~20–50 μM Tris, was used to ensure the initial pH of 8. For doing the pH titration (pH 3–9) of EGFP under various conditions, 20 mM of NaH2PO4, citric acid, Tris buffer were used.

Protein preparation

EGFP was obtained from MC4100 Escherichia coli cells containing pEGFP (Clontech). The bacterial cells were grown at 28°C for 30 h. The cells isolated by centrifugation were lysed by sonication in 50 mM Tris-HCl, 1 mM EDTA, 0.1 M NaCl (pH 8). The supernatant was collected by centrifugation and 25%–45% ammonium sulphate cut was collected. This ammonium sulphate cut was then dissolved in a minimum volume of 20 mM Tris, 1 mMEDTA, and 1 mM β-mercaptoethanol, and loaded onto a Sephadex G-50 column pre-equilibrated with the same buffer. Collected fractions with the appropriate OD ratio A280/A488 were further purified by DEAE Sepharose-CL-6B, precharged with 2 M NaCl, in a linear gradient of (0–0.1 M NaCl). Purified fractions with OD ratio A280/A488 ~2 were pooled out and purity was further confirmed to be >98% on SDS-PAGE. Protein was characterized by recording the absorption and emission spectra and also by the pKa (5.8) obtained by pH titration.

Bovine serum albumin was labeled with fluorescein by reaction of the protein (150 μM) with a 10-fold excess of fluoceinisothiocyanate in 2 mM Tris-HCl, 250 μM EDTA (pH 8.0) for 30 min at 20°C and passing through a PD10 gel filtration column to remove the unreacted label.

Method of pH jump

Rapid pH jump experiments were carried out on a pH jump setup, details of which can be found elsewhere (Viappiani et al. 1998). A Quantel Brilliant-B Q-switched Nd:YAG laser giving 5-nsec pulses at 1064 nm was frequency-tripled to obtain a 355-nm beam with a pulse energy of ~200 mJ. This UV beam was focused just before the cuvette containing the sample solution with ~1 mM o-nitrobenzaldehyde (o-NBA), which upon photoexcitation becomes a weak acid (o-nitrosobenzoic acid with pKa~4), and rapidly increases proton concentration in a cylindrical volume of 4 mm diameter and 2 mm length in the cuvette (the activated volume). A Xenon arc lamp beam (480 nm) with a diameter of 2 mm was incident at the center of the activated volume, ensuring the florescence excitation volume to be fully contained within the activated region. The fluorescence signal (510 ± 10 nm), after filtering, was detected by a 9-stage model R928 photomultiplier tube (Hamamatsu) and recorded using a 500-MHz digital oscilloscope. Data acquisition was triggered by the UV laser shot through the photodiode. The homogeneity of the pH jump within the excitation volume was confirmed for several seconds after the laser flash pholysis of o-NBA by pH experiments using fluorescein.

Kinetic curves associated with the observed proton transfer process in EGFP under various experimental conditions were analyzed by assuming EGFP chromophore protonation reaction as a two-state process (see, however, Discussion)

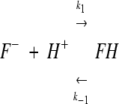graphic file with name M1.gif

where F−and FH are the anionic and protonated form of the fluorophore. k1 and k−1 are the apparent rate constants for the protonation and deprotonation reactions, respectively.

The rate of reaction will be

graphic file with name M2.gif (1)

The displacement of the concentration of the reactant or product from final equilibrium at any time, t, is

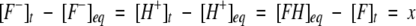graphic file with name M3.gif (2)

Putting the above values in Equation 1, we get

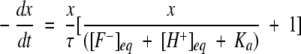graphic file with name M4.gif (3)
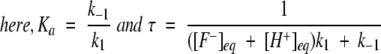graphic file with name M5.gif (4)

Solving Equation 3 for x, we get the kinetic equation to obtain the rate constants for proton transfer process as,

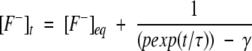graphic file with name M6.gif (5)
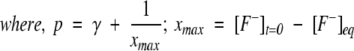graphic file with name M7.gif
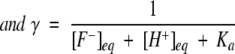graphic file with name M8.gif

[F−]eq and [H+]eq are the final equilibrium concentrations of anionic fluorophore and proton, respectively. [F−]t and [F−]t=0 are the concentrations of anionic fluorophore at times t and 0, respectively.

Kinetic traces following the laser-induced pH jumps were analyzed using Equation 5. The dissociation constant Ka determined from the pH titration of the fluorescence intensity at various solvent conditions (similar to inset A in Fig. 2 ▶) was used in Equation 5 while fitting the kinetic traces. This procedure retains k1 as the only free parameter during nonlinear least square fits of the data (by using Sigma Plot). The final equilibrium concentrations [F−]eq and [H+]eq used in Equation 5 were estimated from the amplitude of the pH jump-induced relaxation traces (Fig. 2 ▶) and the pH titration curve (Fig. 2 ▶, inset A).

Circular dichroism (CD) measurements

CD spectra of EGFP at pH 8 and 5 were collected on a Jasco 810 spectropolarimeter. All measurements were done with a protein concentration of 5 μM in 20 mM NaH2PO4 buffer.

Steady-state and time-resolved fluorescence measurements

All the steady-state fluorescence measurements were carried out using a SPEX fluorolog (T-format) FL111 spectrofluorimeter by exciting EGFP chromophore at 480 nm and monitoring the emission at 520 nm.

Time-resolved fluorescence intensity and anisotropy decay measurements under various pH conditions were carried out using a time-correlated single photon counting setup. One-picosecond pulses of 962 nm radiation from the Ti-sapphire femto/picosecond (Spectra Physics) laser, pumped by an Nd-YLF laser (Millenia X, Spectra Physics), were frequency doubled to 481 nm by using a frequency doubler/tripler (GWU, Spectra Physics). Fluorescence decay curves were obtained at the laser repetition rate of 4MHz by a microchannel plate photomultiplier (Model R2809u, Hamamatsu Corp.) coupled to a time-correlated single-photon counting setup. The instrument response function (IRF) was obtained at 481 nm using a dilute colloidal suspension of dried nondairy coffee whitener. The half width of the IRF was ~40 psec. Fluorescence emission measurements from the samples excited at 481 nm were done at 520 nm using a 515-nm cutoff filter. In fluorescence lifetime measurements, the emission was monitored at the magic angle (54.7°) to eliminate the contribution from the decay of anisotropy. In time-resolved anisotropy measurements, the emission was collected at directions parallel (I||) and perpendicular (I⊥) to the polarization of the excitation beam. The anisotropy was calculated as

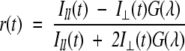graphic file with name M9.gif (6)

where G(λ) is the geometry factor at the wavelength λ of emission. The G factor of the emission collection optics was determined in separate experiments using a standard sample (Fluorescein). The fluorescence decay curves at the magic angle were analyzed by deconvoluting the observed decay with the IRF to obtain the intensity decay function represented as a sum of three or four exponentials

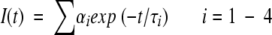graphic file with name M10.gif (7)

where I(t) is the fluorescence intensity at time t and αi is the amplitude of the ith lifetime τi such that ∑iαi=1. The time-resolved anisotropy decay was analyzed based on the model

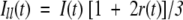graphic file with name M11.gif (8)
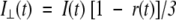graphic file with name M12.gif (9)
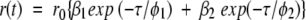graphic file with name M13.gif (10)

where r0 is the initial anisotropy (in case of EGFP, r0=0.35) and βi is the amplitude of the ith rotational correlation time φi such that ∑iβi=1. The shorter component φ1 representing the internal motion of the chromophore could be modeled as a hindered rotation.

Acknowledgments

A.M.S. acknowledges receipt of a Kanwal Rekhi career development fellowship. This work was funded by the Tata Institute of Fundamental Research and by a grant (Swarnajayanti Fellowship to J.B.U.) from the Department of Science and Technology, Government of India.

Article published online ahead of print. Article and publication date are at http://www.proteinscience.org/cgi/doi/10.1110/ps.051391205.

References

  1. Abbruzzetti, S., Crema, E., Masino, L., Veeli, A., Viappiani, C., Small, J.R., Libertini, L.J., and Small, E.W. 2000. Fast events in protein folding: Structural volume changes accompanying the early events in the N→I transition of apomyoglobin induced by ultrafast pH jump. Biophys. J. 78 405–415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Abrahams, J.P., Leslie, A.G., Lutte, R., and Walker, J.E. 1994. Structure at 2.8 Å resolution of F1-ATPase from bovine heart mitochondria. Nature 370 621–628. [DOI] [PubMed] [Google Scholar]
  3. Agmon, N. 1995. The Grotthuss mechanism. Chem. Phys. Lett. 244 456–462. [Google Scholar]
  4. Alberding, N., Lavalette, D., and Austin, R.H. 1981. Hemerythrin’s oxygen-binding reaction studied by laser photolysis. Proc. Natl. Acad. Sci. 78 2307–2309. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Ansari, A., Jones, C.M., Henry, E.R., Hofrichter, J., and Eaton, W.A. 1992. The role of solvent viscosity in the dynamics of protein conformation changes. Science 256 1796–1798. [DOI] [PubMed] [Google Scholar]
  6. Baldwin, R.L. 1996. How Hofmeister ion interactions affect protein stability. Biophys. J. 71 2056–2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Bamford, C.H. and Tipper, C.F.H. 1969. Comprehensive chemical kinetics, Vol. 1: The practice of kinetics. Elsevier, Amsterdam, The Netherlands.
  8. Beece, D., Eisenstein, L., Frauenfelder, H., Good, D., Marden, M.C., Reinisch, L., Reynolds, A.H., Sorensen, L.B., and Yue, K.T. 1980. Solvent viscosity and protein dynamics. Biochemistry 19 5147–5157. [DOI] [PubMed] [Google Scholar]
  9. Bhattacharyya, R.P. and Sosnick, T.R. 1999. Viscosity dependence of the folding kinetics of a dimeric and monomeric coiled coil. Biochemistry 38 2601–2609. [DOI] [PubMed] [Google Scholar]
  10. Brejc, K., Sixma, T.K., Kitts, P.A., Kain, S.R., Tsien, R.Y., Omro, M., and Remington, S.J. 1997. Structural basis for dual excitation and photoisomerization of the Aequorea victoria green fluorescent protein. Proc. Natl. Acad. Sci. 94 2306–2311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chattoraj, M., King, B.A., Bublitz, G.U., and Boxer, S.G. 1996. Ultra-fast excited state dynamics in green fluorescent protein: Multiple states and proton transfer. Proc. Natl. Acad. Sci. 93 8362–8367. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chrunyk, B.A. and Matthews, C.R. 1990. Role of diffusion in the folding of the α subunit of tryptophan synthase from Escherichia coli. Biochemistry 29 2149–2154. [DOI] [PubMed] [Google Scholar]
  13. Cormack, B.P., Valdivia, R.H., and Falkow, S. 1996. FACS-optimized mutants of the green fluorescent protein (GFP). Gene 173 33–38. [DOI] [PubMed] [Google Scholar]
  14. Cowin, J.P., Tsekouras, A.A., Iedema, M.J., Wu, K., and Ellison, G.B. 1999. Immobility of protons in ice from 30 to 190 K. Nature 398 405–407. [Google Scholar]
  15. Creemers, T.M., Lock, A.J., Subramaniam, V.V., Jovin, T.M., and Volker, S. 1999. Three photoconvertible forms of green fluorescent protein identified by spectral hole-burning. Nat. Struct. Biol. 6 706. [DOI] [PubMed] [Google Scholar]
  16. Creveld, L.D., Amadei, A., van Schaik, R.C., Pepermans, H.A., de Vlieg, J., and Berendsen, H.J. 1998. Identification of functional and unfolding motions of cutinase as obtained from molecular dynamics computer simulations. Proteins 33 253–264. [PubMed] [Google Scholar]
  17. Cui, Q. and Karplus, M. 2003. Is a “proton wire” concerted or stepwise? A model study of proton transfer in carbonic anhydrase. J. Phys. Chem. B 107 1071–1078. [Google Scholar]
  18. de Grotthuss, C.J.T. 1806. Sur la dé composition de l’eau et des corps qu’elle tient en dissolution à l’aide de l’électricité galvanique. Ann. Chim. 58 54–74. [Google Scholar]
  19. Dickson, R.M., Cubitt, A.B., Tsien, R.Y., and Moerner, W.E. 1997. On/ off blinking and switching behaviour of single molecules of green fluorescent protein. Nature 388 355–358. [DOI] [PubMed] [Google Scholar]
  20. Eftink, M.R. and Hagaman, K. 1986. Viscosity dependence of the solute quenching of the tryptophanyl fluorescence of proteins. Biophys. Chem. 25 277–282. [DOI] [PubMed] [Google Scholar]
  21. Elsliger, M., Wachter, R.M., Hanson, G.T., Kallio, K., and Remington, S.J. 1999. Structural and spectral response of green fluorescent protein variants to changes in pH. Biochemistry 38 5296–5301. [DOI] [PubMed] [Google Scholar]
  22. Feher, V.A. and Cavanagh, J. 1999. Millisecond-timescale motions contribute to the function of the bacterial response regulator protein Spo0F. Nature 400 289–293. [DOI] [PubMed] [Google Scholar]
  23. Fenimore, P.W., Frauenfelder, H., McMahon, B.H., and Parak, F.G. 2002. Slaving: Solvent fluctuations dominate protein dynamics and functions. Proc. Natl. Acad. Sci. 99 16047–16051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Frauenfelder, H., Sligar, G., and Wolynes, P.G. 1991. The energy landscapes and motions of proteins. Science 254 1598–1603. [DOI] [PubMed] [Google Scholar]
  25. Gavish, B. 1980. Position-dependent viscosity effects on rate coefficients. Phys. Rev. Lett. 44 1160–1163. [Google Scholar]
  26. Gavish, B. and Yedgar, S. 1995. Solvent viscosity effect on protein dynamics: Updating the concepts. In Protein-solvent interactions, 1st ed. (ed.R.B. Gregory), pp. 343–373. Marcel Dekker, Inc., New York, NY.
  27. George, M.V. and Scaiano, J.C. 1980. Photochemistry of o-Nitrobenzaldehyde and related studies. J. Phys. Chem. 84 492–495. [Google Scholar]
  28. Goldberg, J.M. and Baldwin, R.L. 1998. Kinetic mechanism of a partial folding reaction. 2. Nature of the transition state. Biochemistry 37 2556–2563. [DOI] [PubMed] [Google Scholar]
  29. Gutfreund, H. 1995. Kinetics for the life sciences. Cambridge University Press, Cambridge, UK.
  30. Gutman, M., Nachiel, E., and Kiryati, S. 1992. Dynamic studies of proton diffusion in mesoscopic heterogeneous matrix II. The interbilayer space between phospholipids membranes. Biophys. J. 63 281–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hammes-Schiffer, S. 2002. Impact of enzyme motion on activity. Biochemistry 41 13335–13343. [DOI] [PubMed] [Google Scholar]
  32. Hanson,G.T.,McAnaney,T.B., Park,E.S., Rendell, M.E.P.,Yarbrough,D.K., Chu, S., Xi, L., Boxer, S.G., Montrose, M.H., and Remington, S.J. 2002. Green fluorescent protein variants as ratiometric dual emission pH sensors. 1. Structural characterization and preliminary application. Biochemistry 41 15477–15488. [DOI] [PubMed] [Google Scholar]
  33. Hasinoff, B.B. and Chishti, S.B. 1982. Viscosity dependence of the kinetics of the diffusion-controlled reaction of carbon monoxide and myoglobin. Biochemistry 21 4275–4278. [DOI] [PubMed] [Google Scholar]
  34. Haupts, U., Maiti, S., Schwille, P., and Webb, W.W. 1998. Dynamics of fluorescence fluctuations in green fluorescent protein observed by fluorescence correlation spectroscopy. Proc. Natl. Acad. Sci. 95 13573–13578. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Hofmeister, F. 1888. Zur lehre von der wirkung der salze. Zweite mittheilung. Arch. Expt. Pathol. Pharmakol. 24 247–260. [Google Scholar]
  36. Hynes, J.T. 1985. Chemical reaction dynamics in solution. Ann. Rev. Phys. Chem. 36 573–597. [Google Scholar]
  37. Iwata, S., Ostermier, C., Ludwig, B., and Michel, H. 1995. Structure at 2.8 Å resolution of cytochrome c oxidase from Paracoccus denitrificans. Nature 376 660–669. [DOI] [PubMed] [Google Scholar]
  38. Jacob, M., Schindler, T., Balbach, J., and Schmid, F.X. 1997. Diffusion control in an elementary protein folding reaction. Proc. Natl. Acad. Sci. 94 5622–5627. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Jacob, M., Geeves, M., Holtermann, G., and Schmid, F.X. 1999. Diffusional barrier crossing in a two-state protein folding reaction. Nat. Struct. Biol. 6 923–926. [DOI] [PubMed] [Google Scholar]
  40. Kennis, J.T., Larsen, D.S., van Stokkum, I.H., Vengris, M., van Thor, J.J., and van Grondelle, R. 2004. Uncovering the hidden ground state of green fluorescent protein. Proc. Natl. Acad. Sci. 101 17988–17993. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Kneen, M., Farinas, J., Li, Y., and Verkman, A.S. 1998. Green fluorescent protein as a noninvasive intracellular pH indicator. Biophys. J. 74 1591–1599. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Kramers, H.A. 1940. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica (Utrecht) 7 284–304. [Google Scholar]
  43. Ladurner, A.G. and Fersht, A.R. 1999. Upper limit of the time scale for diffusion and chain collapse in chymotrypsin inhibitor 2. Nat. Struct. Biol. 6 28–31. [DOI] [PubMed] [Google Scholar]
  44. Lakshmikanth, G.S., and Krishnamoorthy, G. 1999. Solvent-exposed tryptophans probe the dynamics at protein surfaces. Biophys. J. 77 1100–1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Lear, J.D. 2003. Proton conduction through the M2 protein of the influenza A virus; a quantitative, mechanistic analysis of experimental data. FEBS Lett. 552 17–22. [DOI] [PubMed] [Google Scholar]
  46. Lill, M.A. and Helms, V. 2002. Proton shuttle in green fluorescent protein studied by dynamic simulations. Proc. Natl. Acad. Sci. 99 2778–2781. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Lossau, H., Kummer, A., Heinecke, R., Pöllinger-Dammer, F., Kompa, C., Bieser, G., Jonsson, T., Silva, C.M., Yang, M.M., Youvan, D.C., et al. 1996. Time-resolved spectroscopy of wild-type and mutant Green Fluorescent Proteins reveals excited state deprotonation consistent with fluorophore–protein interactions. Chem. Phys. 213 1–16. [Google Scholar]
  48. Luecke, H., Schobert, B., Richter, H.T., Cartailler, J.P., and Lanyi, J.K. 1999. Structural changes in bacteriorhodopsin during ion transport at 2 Å resolution. Science 286 255–261. [DOI] [PubMed] [Google Scholar]
  49. Maity, H.P. and Krishnamoorthy, G. 1995. Absence of kinetic barrier for transfer of protons from aqueous phase to membrane–water interface. J. Biosci. 20 573–578. [Google Scholar]
  50. Mallik, R., Udgaonkar, J.B., and Krishnamoorthy, G. 2003. Kinetics of proton transfer in a green fluorescence protein: A laser-induced pH jump study. Proc. Indian Acad. Sci. (Chem. Sci.) 115 307–317. [Google Scholar]
  51. McAnaney, T.B., Park, E.S., Hanson, G.T., Remington, S.J., and Boxer, S.J. 2002. Green fluorescent protein variants as ratiometric dual emission pH sensors. 2. Excited-state dynamics. Biochemistry 41 15489–15494. [DOI] [PubMed] [Google Scholar]
  52. Miller, D.W. and Agard, D.A. 1999. Enzyme specificity under dynamic control: A normal mode analysis of α-lytic protease. J. Mol. Biol. 286 267–278. [DOI] [PubMed] [Google Scholar]
  53. Omro, M., Cubitt, A.B., Kallio, K., Gross, L.A., Tsien, R.Y., and Remington, S.J. 1996. Crystal structure of the Aequorea victoria green fluorescent protein. Science 273 1392–1395. [DOI] [PubMed] [Google Scholar]
  54. Robey, R.B., Ruiz, O., Santos, A.V.P., Ma, J., Kear, J., Wang, L., Li, C., Bernardo, A.A., and Arruda, J.A.L. 1998. pH-dependent fluorescence of a heterologously expressed Aequorea green fluorescent protein mutant: In situ spectral characteristics and applicability to intracellular pH estimation. Biochemistry 37 9894–9901. [DOI] [PubMed] [Google Scholar]
  55. Schwille, P., Kummer, S., Heikal, A.A., Moerner, W.E., and Webb, W.W. 2000. Fluorescence correlation spectroscopy reveals fast optical excitation-driven intramolecular dynamics of yellow fluorescent proteins. Proc. Natl. Acad. Sci. 97 151–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Seifert, M.H., Georgescu, J., Ksiazek, D., Smialowski, P., Rehm, T., Steipe, B., and Holak, T.A. 2003. Backbone dynamics of green fluorescent protein and the effect of histidine 148 substitution. Biochemistry 42 2500–2512. [DOI] [PubMed] [Google Scholar]
  57. Shimomura, O., Johnson, F.H., and Saiga, Y. 1962. Extraction, purification and properties of aequorin, a bioluminescent protein from the luminous hydromedusan, Aequorea. J. Cell. Comp. Physiol. 59 223–239. [DOI] [PubMed] [Google Scholar]
  58. Silow, M. and Oliveberg, M. 2003. High concentrations of viscogens decrease the protein folding rate constant by prematurely collapsing the coil. J. Mol. Biol. 326 263–271. [DOI] [PubMed] [Google Scholar]
  59. Starace, D.M. and Bezanilla, F. 2004. A proton pore in a potassium channel voltage sensor reveals a focused electric field. Nature 427 548–553. [DOI] [PubMed] [Google Scholar]
  60. Stock, A. 1999. Biophysics. Relating dynamics to function. Nature 400 221–222. [DOI] [PubMed] [Google Scholar]
  61. Tsien, R.Y. 1998. The green fluorescent protein. Annu. Rev. Biochem. 67 509–544. [DOI] [PubMed] [Google Scholar]
  62. van Thor, J.J., Gensch, T., Hellingwerf, K.J., and Johnson, L.N. 2002. Phototransformation of green fluorescent protein with UV and visible light leads to decarboxylation of glutamate 222. Nat. Struct. Biol. 9 37–41. [DOI] [PubMed] [Google Scholar]
  63. Verkhusha, V.V., Kuznetsova, I.M., Stepanenko, O.V., Zaraisky, A.G., Shavlovsky, M.M., Turoverov, K.K., and Uversky, V.N. 2003. High stability of Discosoma DsRed as compared to Aequorea EGFP. Biochemistry 42 7879–7884. [DOI] [PubMed] [Google Scholar]
  64. Viappiani, C., Bonettu, G., Carcelli, M., Ferrari, F., and Sternieri, A. 1998. Study of proton transfer processes in solution using the laser induced pH-jump: A new experimental setup and an improved data analysis based on genetic algorithms. Rev. Sci. Instrum. 69 270–276. [Google Scholar]
  65. Wachter, R.M., King, R.A., Heim, R., Kallio, K., Tsien, R.Y., Boxer, S.G., and Remington, S.J. 1997. Crystal structure and photodynamic behavior of the blue emission variant Y66H/Y145F of green fluorescent protein. Biochemistry 36 9759–9765. [DOI] [PubMed] [Google Scholar]
  66. Winkler, K., Lindner, J., Subramaniam, V., Jovin, T.M., and Vöhringer, P. 2002. Ultrafast dynamics in the excited state of green fluorescent protein (wt) studied by frequency-resolved femtosecond pump-probe spectroscopy. Phys. Chem. Chem. Phys. 4 1072–1081. [Google Scholar]
  67. Wolf-Watz, M., Thai, V., Henzler-Wildman, K., Hadjipavlou, G., Eisenmesser, E.Z., and Kern, D. 2004. Linkage between dynamics and catalysis in a thermophilic–mesophilic enzyme pair. Nat. Struct. Mol. Biol. 11 945–949. [DOI] [PubMed] [Google Scholar]

Articles from Protein Science : A Publication of the Protein Society are provided here courtesy of The Protein Society

RESOURCES