Abstract
Many protein–protein docking algorithms generate numerous possible complex structures with only a few of them resembling the native structure. The major challenge is choosing the near-native structures from the generated set. Recently it has been observed that the density of conserved residue positions is higher at the interface regions of interacting protein surfaces, except for antibody–antigen complexes, where a very low number of conserved positions is observed at the interface regions. In the present study we have used this observation to identify putative interacting regions on the surface of interacting partners. We studied 59 protein complexes, used previously as a benchmark data set for docking investigations. We computed conservation indices of residue positions on the surfaces of interacting proteins using available homologous sequences and used this information to filter out from 56% to 86% of generated docked models, retaining near-native structures for further evaluation. We used a reverse filter of conservation score to filter out the majority of nonnative antigen–antibody complex structures. For each docked model in the filtered subsets, we relaxed the conformation of the side chains by minimizing the energy with CHARMM, and then calculated the binding free energy using a generalized Born method and solvent-accessible surface area calculations. Using the free energy along with conservation information and other descriptors used in the literature for ranking docking solutions, such as shape complementarity and pair potentials, we developed a global ranking procedure that significantly improves the docking results by giving top ranks to near-native complex structures.
Keywords: protein–protein interaction, docking, conservation index, binding free energy, molecular recognition, computer simulations
Predicting the structure of protein–protein complexes using computational methods has progressed substantially (Cherfils and Janin 1993; Janin 1995; Shoichet and Kuntz 1996; Sternberg et al. 1998; Camacho and Vajda 2002; Halperin et al. 2002; Smith and Sternberg 2002). Numerous docking algorithms have been developed based on shape-complementarity search algorithms (Katchalski-Katzir et al. 1992), such as PUZZLE (Helmer-Citterich and Tramontano 1994), DOCK (Ewing et al. 2001), FTDock (Gabb et al. 1997), DOT (Mandell et al. 2001), and ZDOCK (Chen et al. 2003a). Since protein–protein docking is a hard problem to address due to the large number of degrees of freedom involved, some new techniques were introduced into docking procedures: HEX uses expansion of the molecular surface and electric field in spherical harmonics (Ritchie and Kemp 2000), BIGGER involves surface-implicit methods (Palma et al. 2000), and AutoDock (Morris et al. 1998), DARWIN (Taylor and Burnett 2000; Gardiner et al. 2003), GAPDOCK (Gardiner et al. 2003), and GEMDOCK (Yang and Chen 2004) use genetic algorithms.
In principle, calculation of the free energy change upon binding of two proteins should allow determination of the native structure. Although the enthalpic part of the free energy can be calculated with some accuracy, the entropic contributions are not easy to calculate without resorting to semiempirical and less accurate calculations. Furthermore, the computational load can become too large, especially for unbound docking (starting with individual protein crystal structures), which can potentially involve large protein conformation changes. Heuristic criteria, such as shape-complementarity and coarse-grained residue potentials, have been used with relative success (Camacho et al. 2000a). Still, the main bottleneck is choosing the near-native structures from large sets of generated complexes based on a standard global ranking procedure that will bring the near-native structures at the top of the generated structures data set.
Additional information has been used to better select near-native structures: HADDOCK (Dominguez et al. 2003) and TreeDock (Fahmy and Wagner 2002) use information based on chemical shift perturbation data resulting from NMR titration experiments or mutagenesis, whereas ConsDock (Paul and Rognan 2002) uses consensus analysis for protein–ligand interactions. ProMate (Gottschalk et al. 2004) is based on a statistical analysis of several properties found to distinguish binding regions from nonbinding ones.
Recent studies of protein complexes have tested the importance of factors, such as interface propensity of residues, accessible surface area, planarity, protrusion, packing energies, and binding areas (Jones and Thornton 1996; Tsai et al. 1997; Larsen et al. 1998; Lo Conte et al. 1999). A test using averages of these factors as an indicator of protein-binding sites showed an ~66% success rate for 59 predictions (Jones and Thornton 1997).
There have also been several reports investigating the role of conservation of interfacial residues in naturally occurring protein complexes, using evolutionary tracing of conserved residues in homologous sequences and structures (Lichtarge and Sowa 2002; Ben-Zeev and Eisenstein 2003; Glaser et al. 2003; Lichtarge et al. 2003; Mihalek et al. 2004; Yan et al. 2004). Our recent analysis of well-resolved protein complexes indicated that the density of highly conserved residues is higher in protein–protein interface positions compared to the other positions of the protein surfaces (B.V.B. Reddy and Y.N. Kaznessis, in prep.). We actually find that highly conserved positions in surface regions of proteins involved in non-antibody–antigen complexes tend to be in interacting patches. On the other hand, for antibody–antigen complexes, a very low number of conserved positions is observed in the interface regions. This information can potentially assist in the selection of near-native structures. However, to our knowledge, no attempts have been made to use residue conservation information to filter and rank the docking solutions of protein complexes.
In this paper we describe our docking analysis and ranking of docked complex structures for 59 benchmark complexes (Chen et al. 2003b). In the first stage, we use FTDock (Gabb et al. 1997; Moont et al. 1999) to generate 10,000 docked models for each of the complexes. Our study is focusing on the second stage to refine and rerank the docked structures. We use conserved residue position information as a filter to reduce the number of docked structures. Besides filtering, we use conservation information to rank the remaining docked structures. We evaluate these approaches and report on the results.
In this paper we also report on our efforts to develop a global ranking scheme. For each docked model, we relax the conformation of the side chains by minimizing the energy with CHARMM and then calculate the binding free energy using a generalized Born method and the solvent-accessible surface area. We finally develop a global ranking procedure so that the near-native structures rank at the top, using all available information from docking, free energy calculations, and residue conservation information.
Results and Discussion
In order to test the usefulness of our filter and ranking methods, we applied our algorithms to a benchmark of 59 nonredundant protein complexes first used by Chen et al. (2003b). This benchmark set includes 22 enzyme–inhibitor complexes, 19 antibody–antigen complexes, 11 other complexes, and seven difficult test cases. This benchmark has been used by other groups to test their docking methods (Gray et al. 2003; Li et al. 2003). Gottschalk et al. (2004) also used 21 complexes of this benchmark to test their scoring function of tightness of fit. Since unbound–unbound docking (using single protein crystal structures as input) is more challenging than bound–bound docking (using the structures obtained from protein-complex crystals), we have carried out the unbound–unbound docking and unbound–bound docking as given by the benchmark (Chen et al. 2003b).
Analysis of FTDock performance
Using FTDock (http://www.bmm.icnet.uk/docking) (Gabb et al. 1997; Moont et al. 1999), we obtained 10,000 docked models and their ranks according to the correlation function (equation 3) of shape complementarity and pair potential (see “Docking calculations” below). For these 10,000 models, we calculated the root mean square deviation (RMSD) of Cα atoms of each model structure from the native complex structure. We then defined “hits” as the number of models having RMSD <4.5 Å from the native structure (shown in Table 1). Also shown in Table 1 are the lowest RMSD (LRMSD) complex obtained with FTDock and its corresponding shape-complementarity rank and pair-potential rank. It can be seen in Table 1 that there are 26 complexes with LRMSD <2.5 Å, 15 complexes with LRMSD >2.5 Å but <3.5 Å, and eight complexes with LRMSD >3.5 Å. We are thus confident that FTDock can generate model complexes close to native structures. Nonetheless, for five complexes (1AVW, 1BQL, 1EFU, 1FIN, 1GOT), FTDock failed to generate near-native structures, as the LRMSDs for these complexes are >4.5 Å.
Table 1.
The results of FTDock and filtering for the benchmark complexes
| FTDock results | After filtering and reranking | ||||||||
| Complex | Hits | LRMSD (Å) | SC_rank | PP_rank | NRC | G_rank (other work) | Hits (E_hits) | I_fact (I1, I2) | IOR |
| 1A0O | 13 | 2.62 | 9346 | 371 | 2721 | 31 (284a, 11b) | 12 (4) | 3.39 | 9.07 |
| 1ACB | 29 | 0.31 | 7497 | 2654 | 2485 | 89 (18a, 1b, 11c) | 21 (15) | 2.91 (1.94, 1.96) | 17.75 |
| 1AHW | 9 | 3.33 | 2942 | 2437 | 2875 | 316 (7a, 1b) | 5 (0) | 1.93 | 0 |
| 1ATN | 11 | 0.40 | 2960 | 249 | 4211 | 7 (7a, 1b) | 9 (7) | 1.94 (1.94, 1.65) | 32.75 |
| 1AVW | 0 | 4.69 | 5697 | 958 | 3998 | 2102 (3a, 2b, 1c) | 0 (0) | 1 (1.0, 1.0) | 0 |
| 1AVZ | 25 | 2.64 | 7580 | 2611 | 2210 | 686 (53466a, _b) | 21 (0) | 3.80 (2.86, 1.81) | 0 |
| 1BQL | 0 | 5.30 | 5668 | 1176 | 2615 | 570 (13a, 1b) | 0 (0) | 1 (1.0, 1.0) | 0 |
| 1BRC | 21 | 1.29 | 1022 | 12 | 2825 | 12 (24a, 3b, 106c) | 12 (6) | 2.02 (1.23, 1.79) | 14.1 |
| 1BRS | 36 | 1.66 | 2822 | 21 | 2785 | 13 (65a, 13b, 599c) | 29 (9) | 2.89 | 8.64 |
| 1BTH | 14 | 3.70 | 5851 | 909 | 3110 | 693 | 8 (0) | 1.84 (1.68, 1.16) | 0 |
| 1BVK | 13 | 3.03 | 5974 | 1602 | 2322 | 512 (821a, 1314b) | 13 (1) | 4.31 (3.07, 2.00) | 1.79 |
| 1CGI | 89 | 1.58 | 3143 | 78 | 2753 | 84 (4a, 8b, 16c) | 70 (25) | 2.86 (1.86, 2.08) | 9.83 |
| 1CHO | 60 | 1.25 | 631 | 83 | 3504 | 21 (3a, 1b, 5c) | 44 (19) | 2.09 (1.48, 1.86) | 15.1 |
| 1CSE | 56 | 0.92 | 7556 | 9248 | 2981 | 304 (198a, 1b, 500c) | 43 (5) | 2.58 (1.81, 1.61) | 3.47 |
| 1DFJ | 1 | 3.24 | 5005 | 168 | 2894 | 997 (1a, 1b, 181c) | 1 (0) | 3.46 | 0 |
| 1DQJ | 13 | 2.95 | 4294 | 986 | 3428 | 1306 (9249a, 952b) | 12 (0) | 2.69 (1.55, 1.65) | 0 |
| 1EFU | 0 | 5.71 | 5786 | 550 | 4205 | 898 | 0 (0) | 1 (1.00, 1.00) | 0 |
| 1EO8 | 2 | 3.01 | 8161 | 125 | 1395 | 0 | 0 (0.00, 3.56) | ||
| 2812 | 134 (1497a, _b) | 2 (1) | 3.56 | 14.06 | |||||
| 1FBI | 17 | 2.68 | 730 | 3869 | 2880 | 1381 (642a, 153b) | 14 (0) | 2.86 (2.12, 1.52) | 0 |
| 1FIN | 0 | 5.94 | 9597 | 7502 | 4072 | 389 | 0 (0) | 1 (1.00, 1.00) | 0 |
| 1FQI | 6 | 3.05 | 5230 | 949 | 2810 | 379 | 2 (0) | 1.19 | 0 |
| 1FSS | 70 | 1.80 | 640 | 5758 | 2694 | 7 | 0.37 (0.58, 2.26) | ||
| 2697 | 1086 (50a, 42b, 8c) | 42 (2) | 2.26 | 1.28 | |||||
| 1GLA | 5 | 2.75 | 4405 | 239 | 3846 | 34 (9794a, _b) | 5 (3) | 2.60 (1.56, 2.12) | 23.18 |
| 1GOT | 0 | 5.80 | 9134 | 320 | 3245 | 222 | 0 (0) | 1 (1.00, 1.00) | 0 |
| 1IAI | 5 | 3.27 | 6733 | 473 | 2274 | 29 (997a, _b) | 4 (1) | 3.52 (3.24, 2.03) | 5.68 |
| 1IGC | 92 | 1.03 | 7439 | 8306 | 2628 | 2552 (153a, 21b) | 11 (0) | 0.46 | 0 |
| 1JHL | 19 | 0.74 | 9474 | 482 | 4404 | 1414 (333a, 41b) | 19 (0) | 2.27 (1.15, 1.97) | 0 |
| 1KKL | 5 | 3.26 | 5019 | 2753 | 3076 | 2569 | 4 (0) | 2.60 (2.12, 1.25) | 0 |
| 1KXQ | 9 | 0.46 | 2717 | 344 | 3476 | 1 | 8 (3) | 2.56 (1.16, 1.82) | 13.04 |
| 1KXT | 16 | 0.45 | 184 | 2194 | 3794 | 265 | 8 (0) | 1.32 (1.02, 1.00) | 0 |
| 1KXV | 16 | 1.69 | 2934 | 525 | 3901 | 139 | 9 (0) | 1.44 (1.27, 1.10) | 0 |
| 1L0Y | 1 | 2.93 | 5717 | 1339 | 3004 | 0 | 0 (0.0, 0.0) | ||
| 2799 | 1587 | 0 (0) | 0 | 0 | |||||
| 1MAH | 46 | 1.10 | 8347 | 3904 | 3258 | 2 | 0.13 (0.39, 1.58) | ||
| 2754 | 653 (24a, 1b, 2c) | 20 (2) | 1.58 | 2.75 | |||||
| 1MEL | 10 | 1.26 | 6387 | 460 | 2579 | 7 (3a, 1b) | 6 (3) | 2.33 (1.64, 1.98) | 12.90 |
| 1MLC | 10 | 1.39 | 716 | 1230 | 2544 | 58 (128a, 2b) | 9 (3) | 3.54 (2.30, 1.97) | 8.48 |
| 1NCA | 7 | 0.41 | 3974 | 3226 | 1637 | 0 | 0 (0.00, 2.06) | ||
| 2778 | 600 (1a, 8b) | 4 (0) | 2.06 | 0 | |||||
| 1NMB | 6 | 0.77 | 903 | 677 | 2136 | 148 (135a, 1b) | 3 (0) | 2.34 (2.35, 0.99) | 0 |
| 1PPE | 660 | 0.56 | 966 | 5 | 2695 | 5 (1a, 1b, 9c) | 394 (74) | 2.22 (1.24, 1.57) | 5.00 |
| 1QFU | 5 | 0.69 | 2920 | 997 | 1439 | 0 | 0 (0.60, 3.60) | ||
| 2781 | 190 (388a, 29b) | 5 (3) | 3.60 | 16.6 | |||||
| 1SPB | 40 | 0.95 | 183 | 163 | 2837 | 1 (1a, 1b) | 33 (9) | 2.91 (1.83, 1.59) | 7.73 |
| 1STF | 15 | 0.63 | 60 | 2822 | 2803 | 2 (1a, 1b, 302c) | 15 (10) | 3.57 (2.19, 2.15) | 18.67 |
| 1TAB | 80 | 0.72 | 1359 | 3723 | 3591 | 1318 (79a, 10b, 319c) | 49 (0) | 1.71 (1.32, 1.24) | 0 |
| 1TGS | 25 | 1.64 | 8598 | 293 | 3046 | 54 (3a, 8b, 22c) | 22 (11) | 2.89 (1.89, 1.95) | 15.23 |
| 1UDI | 24 | 2.34 | 4032 | 4754 | 2824 | 18 (5a, 3b, 1c) | 24 (3) | 3.54 | 3.53 |
| 1UGH | 7 | 3.80 | 2481 | 2222 | 2785 | 771 (8a, 1b) | 5 (1) | 2.56 | 5.57 |
| 1WEJ | 10 | 2.74 | 8512 | 295 | 2433 | 451 (183a, 4b) | 10 (0) | 4.11 (2.52, 1.81) | 0 |
| 1WQ1 | 13 | 2.39 | 420 | 7315 | 2833 | 510 (15a, 16b) | 11 (0) | 2.99 | 0 |
| 2BTF | 5 | 1.61 | 2420 | 53 | 3909 | 59 (2a, 1b) | 5 (4) | 2.56 (1.35, 2.07) | 31.27 |
| 2JEL | 8 | 2.86 | 6887 | 1221 | 1955 | 40 (233a, 301b) | 8 (3) | 5.12 (2.18, 1.93) | 7.33 |
| 2KAI | 76 | 1.51 | 1070 | 1032 | 2801 | 154 (388a, 144b, 112c) | 36 (4) | 1.69 (1.24, 1.59) | 3.11 |
| 2MTA | 15 | 2.87 | 32 | 20 | 2676 | 4 | 10 (1) | 2.49 | 2.68 |
| 2PCC | 39 | 2.28 | 8412 | 606 | 3410 | 500 (22338a, _b) | 31 (2) | 2.33 (1.64, 1.62) | 2.20 |
| 2PTC | 59 | 1.42 | 277 | 1067 | 2914 | 71 (193a, 2b, 75c) | 42 (10) | 2.44 (1.70, 1.76) | 6.94 |
| 2SIC | 16 | 1.86 | 162 | 4 | 3690 | 1 (11a, 1b, 674c) | 13 (11) | 2.20 (1.12, 1.68) | 31.22 |
| 2SNI | 23 | 2.52 | 4015 | 1756 | 2928 | 268 (1262a, _b, 2281c) | 18 (5) | 2.67 (1.75, 1.73) | 8.13 |
| 2TEC | 54 | 0.45 | 305 | 9612 | 2943 | 139 (1a, 1b, 324c) | 52 (11) | 3.27 (2.04, 1.90) | 6.22 |
| 2VIR | 5 | 0.80 | 3403 | 3484 | 2035 | 362 (1101a, 80b) | 5 (2) | 4.91 (4.13, 2.01) | 8.14 |
| 3HHR | 1 | 4.50 | 6462 | 2838 | 3125 | 889 | 1 (0) | 3.20 (1.89, 2.04) | 0 |
| 4HTC | 11 | 1.46 | 1912 | 761 | 2813 | 1 (3a, 1b, 6c) | 11 (6) | 3.56 | 15.34 |
| 1FIN_BB | 10 | 0.41 | 15 | 21 | 4035 | 2 | 10 (9) | 2.48 (1.18, 2.22) | 36.32 |
The number of complexes with RMSD <4.5 Å (Hits), shape-complementarity ranks (SC_rank), pair potential ranks (PP_rank) and the lowest RMSD (LRMSD) model in the 10,000 possible docked models for each complex are shown. After applying the filters, the number of complexes remaining (NRC), the sorting global score calculated from equation 12 for the LRMSD (G_rank), the number of hits within the first 100 ranks (E_hits), the improvement over random (IOR), the improvement factor by combining filter I and filter II (I_fact), and the I_fact for performing filter I and II separately (I1, I2) are also given in the right portion. The numbers in italic are obtained by performing only filter II. The ranks obtained in other work are given in parentheses. “_” indicates that no hit was found.
aZDOCK (PSC+DE+ELEC) rank (Chen et al. 2003a).
bZDOCK (PSC)+RDOCK rank (Li et al. 2003).
cRanks of the first near-native complex (Gottschalk et al. 2004) are also shown for comparison with the G_rank.
In order to explore the effect of conformation change on docking procedure, we also carried out a bound–bound dock for 1FIN (listed in Table 1 as 1FIN_BB). Comparing with unbound–unbound docking of 1FIN, we observe that the bound–bound docking gives a model complex with LRMSD = 0.41 Å, with ranks of 15 and 21 for shape complementarity and pair potential, respectively. For unbound–unbound 1FIN docking we could only get a lowest RMSD model of 5.94 Å with very high rank values of 9597 (shape complementarity) and 7502 (pair potential).
The rank based on shape complementarity predicts near-native structures very poorly: the average rank of the LRMSD complexes is 4123, with only three of the 60 complexes registering ranks better than 100. It is thus clear that shape complementarity is not by itself an adequate means for choosing near-native structures.
The pair-potential rank did improve the ranks for 47 complexes out of the 60 cases. From Table 1, it can be observed that there are only 12 complexes with pair-potential ranking worse than shape complementarity. Nonetheless, ranks based on pair potential do not have impressive predictive ability. For example, only five complexes (1BRC, 1BRS, 1PPE, 2MTA, 2SIC) have ranks <20 for the LRMSD model, and another three complexes (1CGI, 1CHO, 2BTF) have ranks of LRMSD complexes <100. The rest have very high rank values.
Filters performance
First, we try to reduce the number of possible docked models from the generated 10,000, without filtering out the lower RMSD models. As described in “Filters” below, we developed two filters based on residue conservation information. In the functionally interacting natural proteins, such as enzyme–inhibitor complexes, we gave higher ranks for the models with a higher number of conserved positions in the interface region. In the case of antigen–antibody interactions, the interacting regions are highly variable, and we gave higher ranks for the models with low numbers of conserved positions. After performing the first filter, we used filter II (see below) to reduce the number of complexes to ~2000–4000 models. These results are also shown in Table 1. It can be seen that combining with the conservation filter and filter II the number of complexes is reduced from 56% to 86%.
In Table 1, there are 11 complexes (1A0O, 1AHW, 1BRS, 1DFJ, 1FQ1, 1IGC, 1UDI, 1UGH, 1WQ1, 2MTA, 4HTC) for which sufficient homolog sequences were not available from nonredundant databases to calculate the conserved residue position information. Therefore, only filter II is applied for these complexes (in this case, filter II only includes three normalized ranks without the conserved residue position information).
When we applied the filters to the model sets, some near-native structures are also filtered out (false negatives), besides nonnative structures. Here we define the improvement factor (I_fact) as:
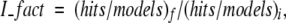 |
where hits/models is the ratio of the number of structures with RMSD < 4.5 Å from the native structure over the number of complex models, before—(hits/models)i—and after—(hits/models)f—applying the filters.
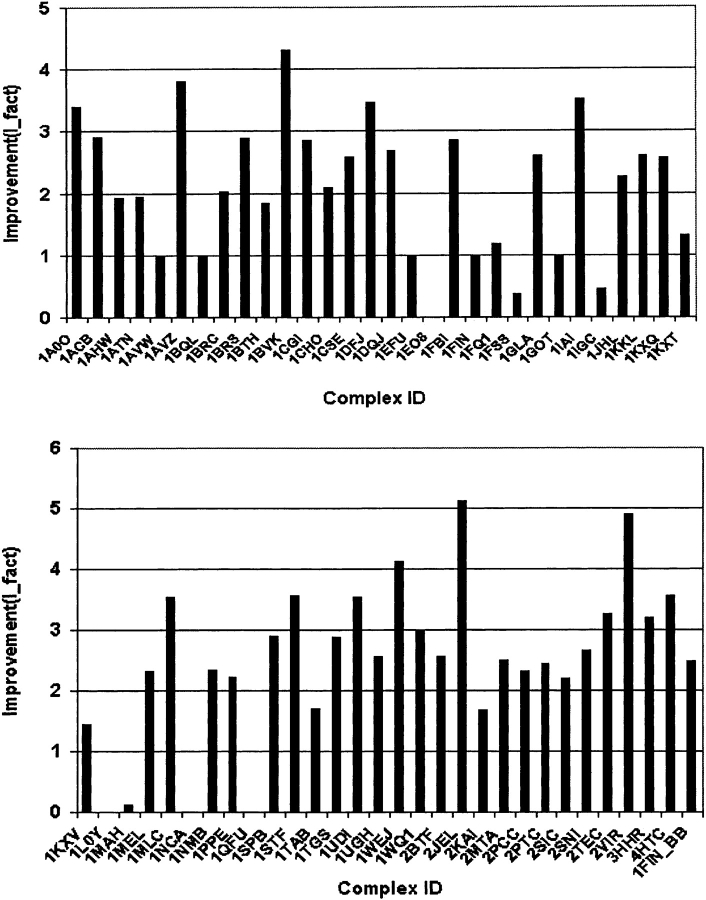
The results are shown in Table 1 and Figure 1 ▶. It is observed that there are 48 out of 60 complexes with I_fact >1.0. Most of them (44) are >2.0, which means the improvement is >100%. For a few complexes, applying the filter resulted in >400% improvement.
Figure 1.
The improvement after filtering. The results are (1) 48 out of 60 complexes have I_fact > 1; (2) there are five complexes (1AVW, 1BQL, 1EFU, 1FIN, 1GOT) with I_fact = 1 because FTDock did not generate hits to begin with; (3) there are three complexes for which our filters worsen the results (1FSS, 1IGC, 1MAH) with 1 > I_fact ≥ 0 after filtering; (4) there are four complexes (1EO8, 1L0Y, 1NCA, 1QFU) for which our combined filter failed with I_fact = 0.0 since all of the near-native structures (2, 1, 7, and 5, respectively) were filtered out. After applying only filter II for these seven complexes, I_facts were improved (I_fact > 1.0) (Table 1).
There are five out of 60 complexes (1AVW, 1BQL, 1EFU, 1FIN, 1GOT) with I_fact = 1.0. From Table 1, it can be observed that for these five complexes (see “Analysis of FTDock performance” above), FTDock did not generate any near-native structure (with RMSD <4.5 Å), that is, no hits are found. When we examined these structures more carefully, we found that except for 1FIN, in which the LRMSD structure was filtered out, the LRMSD structures are still in the filtered subset of these proteins. Moreover, the filters have reduced the number of model structures for these five complexes by a factor of 2.5 to 4. This shows that the filters assist with even these five complexes.
Our filters failed for seven complexes: there are three complexes (1FSS, 1IGC, 1MAH) for which I_fact is <1.0 (Fig. 1 ▶; Table 1). For these structures proportionately more near-native model structures are filtered out than unrelated ones. In Figure 1 ▶, it can also be observed that four complexes (1EO8, 1L0Y, 1NCA, 1QFU) have I_fact = 0. This means that we filtered out all of the near-native structures (two, one, seven, and five hits for the four complexes, respectively). When we examined the number of conserved residue positions at the interface for these four complexes, we found that there is a high number of conserved residue positions for antibody–antigen systems 1EO8 and 1QFU, and a low number of conserved residues for non-antibody 1L0Y and 1NCA, contrary to most of the complexes investigated.
The global rank (see next section) for these four failed complexes (1EO8, 1L0Y, 1NCA, 1QFU) and two of the complexes (1FSS, 1MAH) without improvements are also given in Table 1 without using filter I. It is observed that except for 1L0Y, the I_fact values of the rest of five complexes are >1.0, and the lower RMSD models are still in the subset. 1L0Y only has one hit (see Table 1) and is filtered out by filter II, but other lower RMSD models are still in the subset. Conserved residue position information cannot be calculated for 1IGC, since there are not enough homologous sequences in the database. The result of 1IGC listed in Table 1 is obtained by just using filter II. Its improvement (I_fact) is still <1.0 since lower RMSD models are filtered out.
By comparing the results before and after filtering (Table 1), it becomes clear that only in a few cases (1AHW, 1CHO, 1FIN, 1FQ1, 1IGC, 1KKL, 1WQ1), the LRMSD model structure was filtered out, but even in these cases the second lowest RMSD complex is retained into the remaining subset. For all other complexes the structure closest to the native structure is always in the remaining subset. This demonstrates that our conserved residue information filters work well for the benchmark set.
In order to check the redundancy of filter I and filter II, we tested them separately on those complexes that have enough conserved residue position information. The I_fact values for performing these two filters separately are also listed in Table 1 (columns I1 and I2). Both of them do improve the efficiency with most of I_fact values (I1, I2) being >1.0. After combining them, we observed further significant improvement (I_fact in Table 1). The combined I_fact values are greater than the individual I_fact values (I1, I2). We conclude, thus, that it is necessary to include filters when conserved residue information is available, in order to substantially decrease the number of model structures and improve the prediction.
The efficiency of global ranking
The free energy of binding would in principle suffice to determine the native structure from a large set of complexes. Unfortunately, the free energy we calculated does not rank near-native structures at the top of the list. This could be the result of inaccuracies in the potential force fields used for calculating enthalpic terms or in the empirical entropic terms. Conformational changes upon binding, whether local or global, can also result in significant changes in the free energy of binding (Camacho et al. 2000a). As a result we have to resort to empirical descriptors, and since none can individually predict near-native structures with great accuracy, we decided to combine multiple descriptors in a global ranking scheme.
Empirical rankings based on more than one descriptor have been attempted before: In ZDOCK (Chen et al. 2003a) shape complementarity, electrostatics and desolvation energies were combined to get a final target function, and AutoDock (Morris et al. 1998) involved more energy terms into the score function. A major bottleneck for composite, global scoring functions is that the weights for different quantities are difficult to determine.
As described in “Global normalized ranking” below, we derived a global ranking function by renormalizing the rank of each descriptor used (equation 11), and used weights 1, 1, 2, 4, and 5 for shape complementarity, binding free energy, conservation index, desolvation energy, and pair-potential energy, respectively, in a new global ranking function (equation 12). Using this function we obtained a new global rank for each model complex. Some examples (18 out of 60 complexes) of the global rank versus the RMSD are shown in Figure 2 ▶.
Figure 2.
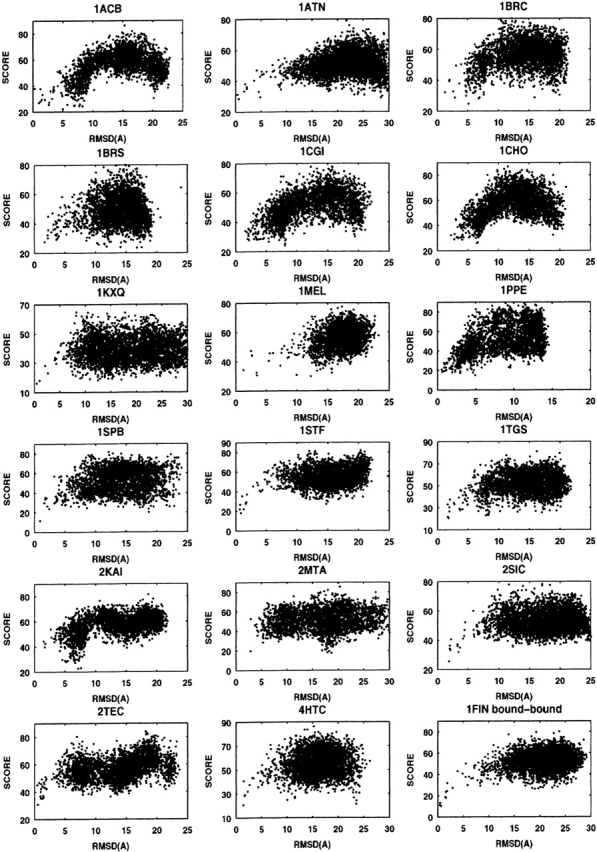
Global ranking for 18 complexes. RMSD vs. rank score (equation 12) for those decoys from FTDock and filtered by our filters.
The rank of the LRMSD structure for each complex is also listed in Table 1 (G_rank). From Figure 2 ▶ and the value of the G_rank, we can see that in most of the model complexes the near-native complexes have lower ranks. Comparing our G_rank with PP_rank in Table 1, there are only four cases (1CGI, 1EO8, 1JHL, 1L0Y) for which our G_rank is higher than the pair-potential rank. For another 56 complexes, our global ranking fairs better than the pair-potential rank. Comparing our results with the results obtained by rigid-body displacement (Gray et al. 2003), Pro-Mate (Gottschalk et al. 2004), ZDOCK (Chen et al. 2003a), and RDOCK (Li et al. 2003) (ranks are also listed in Table 1 for comparison), our ranking scheme produces a similar fraction of accurate predictions, although each method may not produce accurate predictions for the same complexes. Overall, our ranking results compare well with ZDOCK and ProMate results. RDOCK results are better than ours in most cases.
Since the methods for generating the decoy complexes, for evaluating and ranking them are dissimilar in all these studies, the information obtained and reported herein can be considered as complementary to other methods.
In Table 1, we also give the number of hits (E_hits) within the first 100 ranks. For 22 complexes, application of the global rank resulted in no hits in the top 100 ranked structures. We should note that for five of them there were no hits to begin with, because FTDock did not generate any. For the rest of 38 complexes, application of the global ranking improves substantially the predictive ability. Specifically, we calculate the improvement over random (IOR) for these 38 complexes
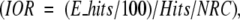 |
where NRC is the number of complexes after filtering, and we find significant IOR values (see Table 1). The average calculated IOR for these 38 complexes is 11.18. Even when the 17 complexes with IOR = 0 are included in the average calculation, the average IOR for the 55 complexes for which FTDock generated hits is 7.72.
Figure 3 ▶ shows model structures of the best predictions superimposed on the native structures for some of the selected targets with rank <10. The complexes 4HTC, 2MTA, 1SPB, 1STF, 1KXQ, and bound–bound 1FIN (1FIN_BB) have given excellent prediction with rank of 1 or 2 for the lowest RMSD structure.
Figure 3.
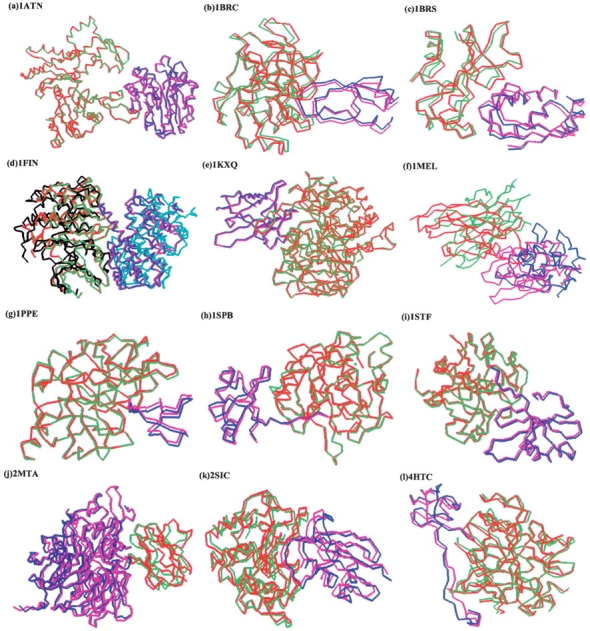
Selected structures from our global predictions. Red and blue indicate the experimental co-crystal. Green and purple indicate the best prediction of rank <10 determined by equation 12. For 1FIN, the bound–bound (green and purple) and unbound–unbound (black and light blue) results are shown in the same figure.
Comparing 1FIN with 1FIN_BB, we can see for bound–bound docking (1FIN_BB) we get better results over the unbound–unbound docking (Fig. 3d ▶). This should be expected since unbound–unbound docking involves a large conformational change. Since we only performed our algorithms on unbound–unbound cases (except for 1FIN, where we did both, and the unbound–bound complexes in the benchmark), it is expected that our docking procedure will give better results for bound–bound docking systems. Moreover, if the initial docking procedure (FTDock) gave more hits, then our ranking procedure could potentially determine the near-native structures.
Concluding remarks
In this work we have demonstrated the usefulness of conserved residue position information in identifying possible near-native complex model structures from docking solutions. We have used this information to develop two filters, reducing the number of docked model structures by 56% to 86% depending on the complex, while keeping near-native complexes in the remaining subset. We applied our method to a benchmark set of 59 complexes. There are 11 complexes for which we didn’t find enough homolog sequence information. Thus, we could not apply our filter at present. Only for four of the remaining complexes did our filter fail to retain the near-native structures, and for another three out of 60 complexes (the 59 benchmark and the FIN bound–bound calculation), our filter did poorly compared to FTDock results.
After filtering, we minimized the side-chain structure of the remaining model structures, and we calculated the binding free energy and desolvation energy. We developed a ranking scheme by renormalizing and weighting a combination of the ranks based on conservation position information, shape complementarity, desolvation energy, pair potential, and binding free energy. Excluding the five complexes for which FTDock did not generate any hits (with RMSD < 4.5 Å), the average improvement over random for the top 100 ranked structures is 7.72. For 17 complexes IOR = 0, but for the majority (38 complexes) we observed significant improvements in predictive ability, in terms of predicting near-native structures in the highest-ranked 100 structures. Generally, our approach can be easily adapted to any other docking algorithms to refine their ranking results.
Materials and methods
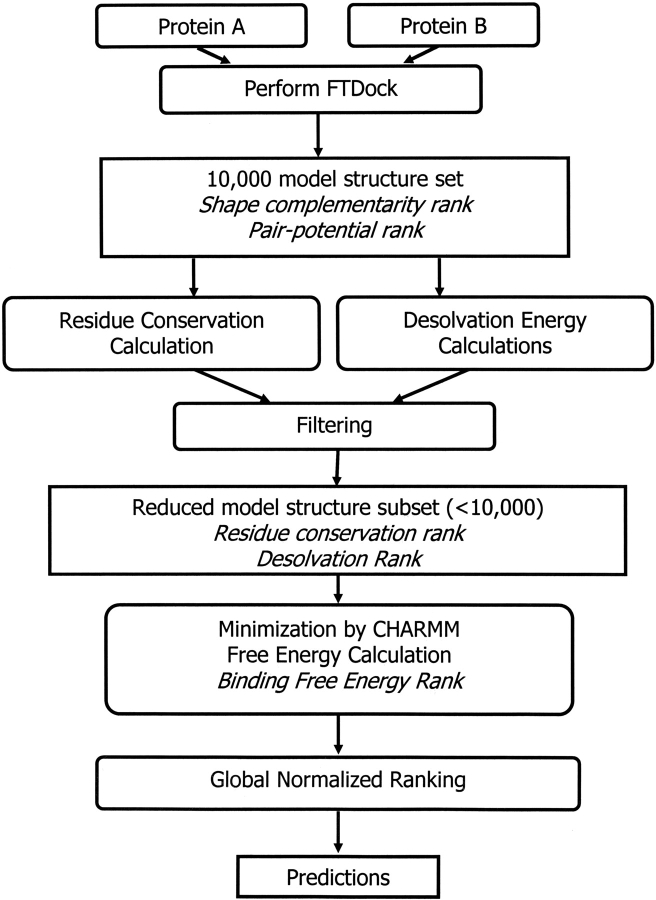
In Figure 4 ▶, we present a diagram with the steps that constitute our method. Briefly, for any two protein molecules A and B, we generate 10,000 structures using FTDock (Gabb et al. 1997; Moont et al. 1999). FTDock also calculates a shape-complementarity value and a pair-potential value for these 10,000 model structures. We then calculate conservation indices for the surface positions of the proteins and also calculate the desolvation energy upon binding. Using these two properties, along with the shape complementarity and the pair potential, we develop two filters to reduce the number of model structures to a number considerably lower than 10,000. We then use CHARMM to minimize the energy of the filtered structures, and we calculate the free energy of binding. Finally, we use the ranks of the model structures for all the properties to generate a global ranking scheme, which improves our ability to pick near-native structures from the set of putative native structures. The methods are detailed as follows.
Figure 4.
Schematic representation of the algorithms used.
Docking calculations
To generate model docked structures, we used the FTDock software package (Gabb et al. 1997; Moont et al. 1999; http://www.bmm.icnet.uk/docking), which uses an efficient geometric recognition algorithm to identify molecular surface complementarity (Katchalski-Katzir et al. 1992). This method is based on a purely geometric approach and takes advantage of techniques applied in the field of pattern recognition. The geometric recognition algorithms include a digital representation of the proteins by 3D discrete functions for the surface and the interior, a correlation function calculation using Fourier transformation that assesses the degree of molecular surface overlap and penetration upon relative shifts of the molecules in 3D, and a scan of the relative orientations of the molecules in 3D. Here we just give a brief summary of the docking procedure we followed.
The calculation of shape complementarity between any two proteins A and B initially projects the two molecules onto a 3D grid of N3 points, represented by discrete functions:
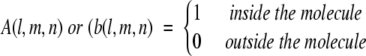 |
(1) |
Then the surface and the interior of each molecule is distinguished by parameters ρ and δ respectively:
 |
(2) |
The correlation function (score) is calculated as:
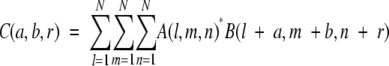 |
(3) |
where
 |
with (a, b, r) the shift vector of molecule B around molecule A. We used ρ = 1, δ= −15 for the empirically chosen parameters to calculate the correlation function C(a, b, r). Using a discrete fast-Fourier transform (FFT), the computation is on the order of N3 ln(N3) instead of the order of N6 of the direct calculation using equation 3. Using this scoring function, we ranked all of the possible generated complex structures (in our case we initially keep 10,000).
Moont et al. (1999) generated empirical residue–residue pair potentials to further screen possible protein–protein docking complexes by FTDock. We also used their 20 × 20 matrix of pairwise interaction potentials. For each docked complex, we calculate the distance between residues of the two proteins. If this distance is <4.5 Å, we obtain the interaction value from the matrix, then sum up all the values and get the final interaction energy for each complex. Using this interaction information, a new rank (pair-potential rank) is generated.
Conservation of residue positions
To evaluate the extent of conservation of interacting positions on the surface of proteins, we calculate conservation indices as follows:
Homologous sequences
The two protein sequences of each investigated complex were used to obtain their homologous sequences from SWALL, an annotated nonredundant protein sequence database (nonredundant SWISS-PROT + TrEMBL + TrEMBLnew), using the FASTA3 (http://www.ebi.ac.uk/fasta33/) sequence similarity search tool at the European Bioinformatics Institute. Homologous sequences with <30% gaps in the sequence and >35% sequence identity to the parent sequence were used for analysis. If the evolutionary distance (described below) between any two sequences is <5%, then we randomly removed one of the sequences from the homolog set. The remaining sequences were used for calculating the residue conservation index (described below).
Evolutionary distance
Evolutionary distance among the sequences is calculated using the structure-based amino acid substitution matrix M(a, b) (Gonnet et al. 1992). A similarity score Sii for sequence i is calculated by summing the identical substitution [diagonal values from M(a, b)]. Similarly, score Sjj is calculated for sequence j. A similarity score Sij between the sequences i and j is calculated using substitution matrix values of corresponding aligned residues between the two sequences. An evolutionary distance (EDij) between the two sequences is calculated using
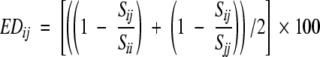 |
(4) |
Conservation index of residue position
Evolutionary distances between the reference sequence and its homologs were used to calculate residue conservation index (CIl) for each position l using the amino acid substitution matrix, similar to the amino acid variability or conservation used by Valdar and Thornton (2001). Conservation Index (CIl) is a weighted sum of all pairwise similarities between all residues present at the position. The CIl value is calculated using equation 5 in a given alignment and takes a value in the range [0, 1].
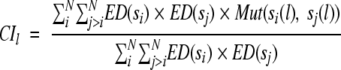 |
(5) |
where N is the number of homologous sequences in the alignment; si(l) and sj(l) are the amino acids at the alignment position l of sequences si and sj, respectively; ED(si) and ED(sj) are the average evolutionary distance of s(i) and s(j) from the remaining homologs. Mut(a, b) measures the similarity between the amino acids a and b as derived from the amino acid substitution matrix M(a, b) defined as:
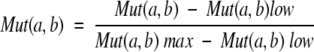 |
(6) |
where a, b are the pairs of amino acids at a given alignment position l. M(a,b)low is the lowest value in the substitution matrix (−5 in the Gonnet matrix; Gonnet et al. 1992) and M(a, b)max is the maximum value among all the possible substitution pairs in that position. Thus Mut(a, b) takes a value in the range [0, 1].
Using PSA (Richmond and Richards 1978; Sali and Blundell 1990), the solvent-accessible surface area (SASA) of amino acids is calculated and used to identify surface residues and buried residues. We have then identified the top 8% and 17% of highly conserved residues, which have solvent accessibility >25% of their total surface area. As an example, in Table 2 we list the highly conserved surface residues of complex 1TAB’s E and I chains.
Table 2.
The top 17% highly conserved positions for 1TAB
| 3G (55.6, 0.85) | 4G (33.9, 0.98) | 6T (33.9, 0.98) | 10N (26.5, 0.46) | |
| 11T (56.6, 0.46) | 21G (85.2, 0.51) | 31N (37.5, 0.52) | 32S (25.5, 0.47) | |
| 40H (37.1, 0.98) | 69K (37.2, 0.49) | 74P (70.8, 0.46) | 77N (42.4, 0.47) | |
| 92S (50.8, 0.44) | 93A (52.5, 0.63) | 97N (58.7, 0.47) | 101A (31.6, 0.45) | |
| 1TAB:E | 102S (32.8, 0.62) | 107T (90.6, 0.44) | 113G (74.8, 0.45) | 139K (46.3, 0.45) |
| 141P (27.2, 0.55) | 144S (37.1, 0.47) | 146S (67.3, 0.57) | 149K (42.9, 0.48) | |
| 158S (78.4, 0.45) | 167E (77.4, 0.45) | 169G (53.4, 0.64) | 170K (42.5, 0.57) | |
| 174Q (61.3, 0.53) | 184S (83.8, 0.46) | 194G (29.4, 0.96) | 196G (59.2, 0.53) | |
| 200K (66.0, 0.46) | 208K (27.7, 0.54) | 214S (63.7, 0.46) | 218Q (75.8, 0.47) | |
| 1TAB:I | 13C (40.5, 1.00) | 15K (104.0, 0.67) | 18P (58.8, 0.89) | 23C (36.7, 0.96) |
| 31C (33.3, 0.68) | 35C (59.1, 0.75) |
Solvent-accessible area and the conservation index (CI in equation 5) are given in parentheses, respectively. The residues shown in bold fall in the top 8% list.
For each complex, we add all conservation indices for each conserved position and use them to rank the complexes after filtering. In this case, two conservation ranks are obtained for groups 1 and 2, respectively. We have observed (B.V.B. Reddy and Y.N. Kaznessis, in prep.) that in the functionally interacting natural proteins, such as enzyme–inhibitor complexes, the surface density of conserved positions is significantly higher in the interface region than in the rest of the protein surface. In Table 3 we demonstrate that this observation is valid for the benchmark set of protein–protein complexes investigated herein with sufficient homolog sequences.
Table 3.
The occurrence and the fraction (shown in parentheses) of residue positions in different classes of conservation indices for the interfacial and noninterfacial surface region of the benchmark structures with sufficient homolog sequences
| Conservation index (CI) of group intervals | ||||
| <0.40 | 0.40–0.60 | 0.60–0.85 | >0.85 | |
| Nonantigen–antibody complexes | ||||
| Noninterfacial surface residues | 3266 (0.42) | 2058 (0.26) | 1497 (0.19) | 1009 (0.13) |
| Interfacial surface residues | 405 (0.35) | 253 (0.22) | 259 (0.23) | 225 (0.20) |
| Ratio | 0.85 | 0.84 | 1.19 | 1.53 |
| Antigen–antibody complexes | ||||
| Noninterfacial surface residues | 1128 (0.16) | 2154 (0.31) | 2169 (0.31) | 1440 (0.21) |
| Interfacial surface residues | 282 (0.49) | 147 (0.25) | 106 (0.18) | 43 (0.07) |
| Ratio | 2.98 | 0.81 | 0.58 | 0.36 |
| Only antibody regions | ||||
| Noninterfacial surface residues | 860 (0.17) | 1729 (0.34) | 1700 (0.34) | 761 (0.15) |
| Interfacial surface residues | 196 (0.61) | 73 (0.23) | 43 (0.13) | 9 (0.03) |
| Ratio | 3.59 | 0.66 | 0.40 | 0.19 |
| Only antigen regions | ||||
| Noninterfacial surface residues | 268 (0.15) | 425 (0.23) | 469 (0.25) | 679 (0.37) |
| Interfacial surface residues | 86 (0.33) | 74 (0.29) | 63 (0.25) | 34 (0.13) |
| Ratio | 2.30 | 1.27 | 0.96 | 0.36 |
Solvent accessibility >10% is used as the cutoff to define a residue as surface residue.
Based on the CI values, calculated with equation 5, we have divided all the available sequence positions into four groups: group 1 positions have CI values ≤0.4, group 2 positions have CI values between 0.4 and 0.6, group 3 positions have values between 0.60 and 0.85, and group 4 positions have values >0.85. In Table 3, the distribution is shown of amino acid positions in each group with different conservation indices. We have used a 10% solvent accessibility cutoff to differentiate surface residues and buried residues and only looked at surface residues. We also present the ratio between the fraction of noninterfacial (noninteracting) and interfacial (on the protein–protein interface) surface residues at all the conservation intervals.
It can be seen from Table 3 that for non-antigen–antibody complexes the ratio increases progressively from 0.85 to 1.53 at higher CI intervals. This is a clear indication that the number of highly conserved positions in the interfacial region is significantly more compared to noninterfacial regions.
This finding is not in agreement with the study of Caffrey et al. (2004), who reported only a slight increase in conservation of interfacial regions. A calculation of average conservation indices for the interacting patches of the benchmark protein–protein complexes explains the discrepancy and verifies the results of our previous study (B.V.B. Reddy and Y.N. Kaznessis, in prep.). This calculation shows that the average conservation indices for all the residues in the interaction sites are indeed only slightly higher as shown by other researchers (Caffrey et al. 2004; B.V.B. Reddy and Y.N. Kaznessis, in prep.). Nonetheless, although the average CI of interacting patches is not a useful measure for the prediction of interacting sites on protein surfaces, the actual number of highly conserved residues in the interfacial region can help in accurately identifying putative interaction sites on given protein structures. Therefore, we have used the number of highly conserved positions per interaction site as our filter to identify the interaction sites. We assigned high ranks to complexes that had a large number of conserved positions at the interacting interface for non-antigen–antibody complexes.
From Table 3 it can be also seen that for antigen–antibody complexes the ratio decreases progressively from 2.98 to 0.36 at higher CI intervals (unlike the non-antigen–antibody complexes). This is a clear indication that the number density of highly conserved positions in the interfacial region is significantly smaller compared to noninterfacial regions. From Table 3 it can be seen that the ratio decreases at higher CI intervals for both antigen and antibody regions. Therefore, we gave higher ranks to the models with low numbers of conserved positions.
That the antigen interface is not conserved in the manner of non-antibody–antigen complexes is perhaps an unexpected finding. At present we do not have any clear explanation for this finding, and to our knowledge there is no study on conservation signals for antigens. Nonetheless, based on the strength of the signal, we have used a reverse conservation filter for both antibodies and antigens.
In principle, it is more difficult to predict the binding site of an antigen, since for antibodies this region is known. Our computations provide a means for identifying the antigen-binding site.
Filters
Conservation position filter
Using homologous sequences we calculated conservation indices for each docked model using equation 5. We have identified the top 8% (defined as group 1) and top 17% (defined as group 2) of highly conserved and well-exposed surface residues, in each polypeptide chain of the interacting complex.
We counted the total number of group 1 and group 2 positions in each modeled complex interface region. Using the group 1 and group 2 conservation positions as a filter, the total number of docked models is reduced. We selected only the models that have at least four of group 1 positions or six of group 2 positions in the interface region of the enzyme–inhibitor model complexes. In the case of antigen–antibody complexes (e.g., 1JHL, 1KXQ), we have reversed the selection, limiting to two or less group 1 positions and four or less group 2 positions. We chose these cutoffs because we maximized the number of filtered docking solutions out of the 10,000 generated structures with the minimum number of near-native structures, as discussed in “Results” above.
Filter II
A second filter was developed to lower the number of model structures further, using the average conservation rank along with other three ranks (shape complementarity, pair potential, and desolvation energy; described in the next section). If the rank of a complex is worse than 1200 in any of the four rankings, then the corresponding model is filtered out of the set of putative near-native structures. Filter II is performed with only three ranks if conservation information is not available as described in “Results” above.
Side-chain relaxation and binding free energy calculation
Since the generated docked complexes have very strong side-chain overlap effects (atoms are very close to each other), we cannot calculate the binding energy correctly. Therefore, for each possible complex we perform energy minimization to reduce the side-chain overlap effects. We used the CHARMM (Brooks et al. 1983) molecular mechanics simulation package for energy minimization. With CHARMM, we built in the missed atoms and all hydrogen atoms, fixed all backbone atoms, and let the side-chain atoms relax to the minimum internal energy. Minimization was stopped if the energy did not change by more than 0.1% of the total energy of the complex. We should note here that this step is particularly computationally intensive. We thus worked on only the filtered structures after using the calculated conservation indices.
Using the relaxed structures, we calculated the binding free energy. With some approximation, the free energy change can be divided into several terms (Camacho et al. 2000b; Dennis et al. 2002):
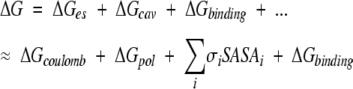 |
(7) |
These terms can be calculated separately: ΔGcoulomb and ΔGpol can be calculated with the Generalized Born model with the Debye-Huckel approximation (Jayaram et al. 1998, 1999):
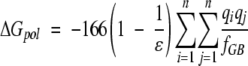 |
(8) |
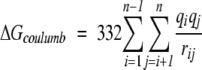 |
(9) |
where fGB = (rij2 + αij2e−D)1/2, αij = (αiαj)1/2, D = rij2/(2αij)2, and αi is the effective Born radius of the atom, which can be obtained by pairwise dielectric descreening procedure (Hawkins et al. 1996). The desolvation energy term ∑σkSASAk can be calculated using the Solvent-Accessible Surface Area for each residue (SASAk). The weights (σk) for each residue are taken from the work of Wang et al. (1995). For the binding interaction, we use van der Waals interaction of the form:
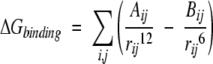 |
(10) |
The summation is for all the atom pairs from the two proteins. The potential parameters Aij and Bij for each atom pair are taken from the CHARMM force field (Brooks et al. 1983) and AutoDock (Morris et al. 1998). From the value of free energy ΔG, we calculated a new rank for all filtered possible complexes.
We also generated a rank based on only the desolvation term of the free energy, which is the only part of the free energy that can be calculated without relaxing the docked structures with minimization.
Global normalized ranking
Our goal is to determine an optimal ranking procedure for identifying near-native structures. We could use a weighted sum of all the calculated descriptors (shape complementarity, pair-potential, CHARMM energy, binding free energy, desolvation energy, conservation indices) to produce a global rank for the filtered subset of docked models, but values of these properties are not in the same units, and the weights are not universal and hard to optimize. In our algorithm, instead of using the real value of each descriptor, we used the rank of each property since they have the same meaning and can be summed together.
For each individual descriptor, a normalized ranking method is applied. The rank was obtained by finding the maximum (Vmax) and minimum (Vmin) of their values and using the following equation:
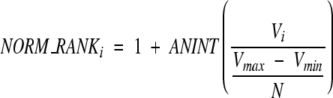 |
(11) |
where Vi is the property value of complex i, and N is the total number of complexes after filtering. There may be some gaps if the difference between complexes is large, and several complexes can have the same rank number if their values are very close to one another. Nonetheless, this normalized method clearly reveals the difference among the complexes. Specifically for the binding free energy descriptor, we set the Vmax equal to zero. If for a complex the binding free energy is greater than zero, we assign the highest rank (in our case is 10,000) to that complex.
The global score is simply obtained by a weighted average of all normalized ranks:
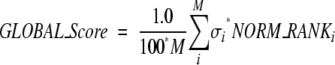 |
(12) |
where M is the number of rank methods (descriptors), and σi is the weights for descriptor i. Factor 100 is a scale factor that reduces the maximum of global_score to 100.
To determine which properties should be included in our global ranking and what their weights should be (σi in equation 12), we calculated Pearson’s correlation coefficients (Devore and Peck 2001) between each of the descriptor ranks and the RMSD of the models from the native structure. From our calculated correlation coefficients, we found the CHARMM energy has a particularly low value of correlation coefficients (<0.10). Therefore we have excluded the CHARMM energy from our ranking procedure and only use M = 5 descriptors (shape complementarity, pair potential, conserved residue, binding free energy, desolvation energy) into our final global rank.
Ideally, for the best possible prediction, the correlation coefficient would be equal to 1 (best ranked having lowest RMSD, second best ranked having second lowest RMSD, etc.). These coefficients provide a measure of the predictive ability of a single descriptor. They also provide a means of comparing the different descriptors.
There is no descriptor that does well, in terms of correlation coefficient values, for all 59 complexes. Specifically, we found that the pair-potential descriptor has a significant correlation coefficient value (>0.10) for 22 complexes, desolvation energy has significant positive correlation in 13 complexes, conserved residue descriptor has significant correlation in 10 complexes, shape-complementarity values correlate well with RMSD in three complexes, and that the binding free energy has significant correlation coefficient values in three complexes. For some complexes more than one descriptor gives significant correlation coefficient values.
We determined the weights for equation 12 using the relative number of complexes for which each descriptor does well, in terms of predictive ability and correlation coefficient values. Taking also into account the fact that for some complexes more than one descriptor does well, we used weights of 1, 1, 2, 4, and 5 for shape complementarity, binding free energy, conservation index, pair-potential energy, and desolvation energy, respectively. Hence, we use these relative coefficients as the weights σ for each descriptor in equation 12.
Acknowledgments
This work was supported in part by the Minnesota Supercomputer Institute (MSI) and the University of Minnesota Biotechnology Institute. This work is also supported by the Army High Performance Computing Research Center (AHPCRC) under the auspices of the Department of the Army, Army Research Laboratory, contract no. DAAD10-01-2-0014. The content does not necessarily reflect the position or the policy of the government and no official endorsement should be inferred. AHPCRC and the MSI provided access to computing facilities. Y.D. expresses his gratitude to Yuke Sham and Shuxia Zhang of MSI for their help in performing computations.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.04941505.
References
- Ben-Zeev, E. and Eisenstein, M. 2003. Weighted geometric docking: Incorporating external information in the rotation-translation scan. Proteins 52 24–27. [DOI] [PubMed] [Google Scholar]
- Brooks, B.R., Bruccoleri, R.E., Olfson, B.D., States, D.J., Swaminathan, S., and Karplus, K. 1983. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comp. Chem. 4 187–217. [Google Scholar]
- Caffrey, D.R., Somaroo, S., Hughes, J.D., Mintseris, J., and Huang, E.S. 2004. Are protein–protein interfaces more conserved in sequence than the rest of the protein surface? Protein Sci. 13 190–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Camacho, C.J. and Vajda, S. 2002. Protein–protein association kinetics and protein docking. Curr. Opin. Struct. Biol. 12 36–40. [DOI] [PubMed] [Google Scholar]
- Camacho, C.J., Gatchell, D.W., Kimura, S.R., and Vajda, S. 2000a. Scoring docked conformations generated by rigid-body protein–protein docking. Proteins 40 525–537. [DOI] [PubMed] [Google Scholar]
- Camacho, C.J., Kimura, S.R., DeLisi, C., and Vajda, S. 2000b. Kinetics of desolvation-mediated protein–protein binding. Biophys. J. 78 1094–1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen, R., Li, L., and Weng, Z. 2003a. ZDOCK: An initial-stage protein-docking algorithm. Proteins 52 80–87. [DOI] [PubMed] [Google Scholar]
- Chen, R., Mintseris, J., Janin, J., and Weng, Z. 2003b. A protein–protein docking benchmark. Proteins 52 88–91. [DOI] [PubMed] [Google Scholar]
- Cherfils, J. and Janin, J. 1993. Protein docking algorithms: Simulating molecular recognition. Curr. Opin. Struct. Biol. 3 265–269. [Google Scholar]
- Dennis, S., Kortvelyesi, T., and Vajda, S. 2002. Computational mapping identifies the binding sites of organic solvents on proteins. Proc. Natl. Acad. Sci. 99 4290–4295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devore, J. and Peck, R. 2001. Statistics: The exploration and analysis of data, 4th ed., p. 136. Duxbury Press, Pacific Grove, CA.
- Dominguez, C., Boelens, R., and Bonvin, A.M. 2003. HADDOCK: A protein–protein docking approach based on biochemical or biophysical information. J. Am. Chem. Soc. 125 1731–1737. [DOI] [PubMed] [Google Scholar]
- Ewing, T.J., Makino, S., Skillman, A.G., and Kuntz, I.D. 2001. DOCK 4.0: Search strategies for automated molecular docking of flexible molecule databases. J. Comput. Aided Mol. Des. 15 411–428. [DOI] [PubMed] [Google Scholar]
- Fahmy, A. and Wagner, G. 2002. TreeDock: A tool for protein docking based on minimizing van der Waals energies. J. Am. Chem. Soc. 124 1241–1250. [DOI] [PubMed] [Google Scholar]
- Gabb, H.A., Jackson, R.M., and Sternberg, M.J. 1997. Modelling protein docking using shape complementarity, electrostatics and biochemical information. J. Mol. Biol. 272 106–120. [DOI] [PubMed] [Google Scholar]
- Gardiner, E.J., Willett, P., and Artymiuk, P.J. 2003. GAPDOCK: A Genetic Algorithm Approach to Protein Docking in CAPRI round 1. Proteins 52 10–14. [DOI] [PubMed] [Google Scholar]
- Glaser, F., Pupko, T., Paz, I., Bell, R.E., Bechor-Shental, D., Martz, E., and Ben-Tal, N. 2003. ConSurf: Identification of functional regions in proteins by surface-mapping of phylogenetic information. Bioinformatics 19 163–164. [DOI] [PubMed] [Google Scholar]
- Gonnet, G.H., Cohen, M.A., and Benner, S.A. 1992. Exhaustive matching of the entire protein sequence database. Science 256 1443–1445. [DOI] [PubMed] [Google Scholar]
- Gottschalk, K.E., Neuvirth, H., and Schreiber, G. 2004. A novel method for scoring of docked protein complexes using predicted protein–protein binding sites. Protein Eng. Des. Sel. 17 183–189. [DOI] [PubMed] [Google Scholar]
- Gray, J.J., Moughon, S., Wang, C., Schueler-Furman, O., Kuhlman, B., Rohl, C.A., and Baker, D. 2003. Protein–protein docking with simultaneous optimization of rigid-body displacement and side-chain conformations. J. Mol. Biol. 331 281–299. [DOI] [PubMed] [Google Scholar]
- Halperin, I., Ma, B., Wolfson, H., and Nussinov, R. 2002. Principles of docking: An overview of search algorithms and a guide to scoring functions. Proteins 47 409–443. [DOI] [PubMed] [Google Scholar]
- Hawkins, G.D., Gramer, C.J., and Truhlar, D.G. 1996. Parametrized models of aqueous free energies of solvation based on pairwise descreening of solute atomic charges from a dielectric medium. J. Phys. Chem. 100 19824–19839. [Google Scholar]
- Helmer-Citterich, M. and Tramontano, A. 1994. PUZZLE: A new method for automated protein docking based on surface shape complementarity. J. Mol. Biol. 235 1021–1031. [DOI] [PubMed] [Google Scholar]
- Janin, J. 1995. Protein–protein recognition. Prog. Biophys. Mol. Biol. 64 145–166. [DOI] [PubMed] [Google Scholar]
- Jayaram, B., Sprous, D., and Beveridge, D.L. 1998. Solvation free energy of biomacromolecules: Parameters for a modified generalized Born model consistent with the AMBER force field. J. Phys. Chem. B 102 9571–9576. [Google Scholar]
- Jayaram, B., McConnell, K.J., Dixit, S.B., and Beveridge, D.L. 1999. Free energy analysis of protein–DNA binding: The EcoRI endonuclease–DNA complex. J. Comput. Phys. 151 333–357. [Google Scholar]
- Jones, S. and Thornton, J.M. 1996. Principles of protein–protein interactions. Proc. Natl. Acad. Sci. 93 13–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ———. 1997. Prediction of protein–protein interaction sites using patch analysis. J. Mol. Biol. 272 133–143. [DOI] [PubMed] [Google Scholar]
- Katchalski-Katzir, E., Shariv, I., Eisenstein, M., Friesem, A.A., Aflalo, C., and Vakser, I.A. 1992. Molecular surface recognition: Determination of geometric fit between proteins and their ligands by correlation techniques. Proc. Natl. Acad. Sci. 89 2195–2199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen, T.A., Olson, A.J., and Goodsell, D.S. 1998. Morphology of protein–protein interfaces. Structure 6 421–427. [DOI] [PubMed] [Google Scholar]
- Li, L., Chen, R., and Weng, Z. 2003. RDOCK: Refinement of rigid-body protein docking predictions. Proteins 53 693–707. [DOI] [PubMed] [Google Scholar]
- Lichtarge, O. and Sowa, M.E. 2002. Evolutionary predictions of binding surfaces and interactions. Curr. Opin. Struct. Biol. 12 21–27. [DOI] [PubMed] [Google Scholar]
- Lichtarge, O., Yao, H., Kristensen, D.M., Madabushi, S., and Mihalek, I. 2003. Accurate and scalable identification of functional sites by evolutionary tracing. J. Struct. Funct. Genomics. 4 159–166. [DOI] [PubMed] [Google Scholar]
- Lo Conte, L., Chothia, C., and Janin, J. 1999. The atomic structure of protein–protein recognition sites. J. Mol. Biol. 285 2177–2198. [DOI] [PubMed] [Google Scholar]
- Mandell, J.G., Roberts, V.A., Pique, M.E., Kotlovyi, V., Mitchell, J.C., Nelson, E., Tsigelny, I., and Ten Eyck, L.F. 2001. Protein docking using continuum electrostatics and geometric fit. Protein Eng. 14 105–113. [DOI] [PubMed] [Google Scholar]
- Mihalek, I., Res, I., and Lichtarge, O. 2004. A family of evolution–entropy hybrid methods for ranking protein residues by importance. J. Mol. Biol. 336 1265–1282. [DOI] [PubMed] [Google Scholar]
- Moont, G., Gabb, H.A., and Sternberg, M.J. 1999. Use of pair potentials across protein interfaces in screening predicted docked complexes. Proteins 35 364–373. [PubMed] [Google Scholar]
- Morris, G.M., Goodsell, D.S., Halliday, R.S., Huey, R., Hart, W.E., Belew, R.K., and Olson, A.J. 1998. Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function. J. Comput. Chem. 19 1639–1662. [Google Scholar]
- Palma, P.N., Krippahl, L., Wampler, J.E., and Moura, J.J. 2000. BiGGER: A new (soft) docking algorithm for predicting protein interactions. Proteins 39 372–384. [PubMed] [Google Scholar]
- Paul, N. and Rognan, D. 2002. ConsDock: A new program for the consensus analysis of protein–ligand interactions. Proteins 47 521–533. [DOI] [PubMed] [Google Scholar]
- Richmond, T.J. and Richards, F.M. 1978. Packing of α-helices: Geometrical constraints and contact areas. J. Mol. Biol. 119 537–555. [DOI] [PubMed] [Google Scholar]
- Ritchie, D.W. and Kemp, G.J. 2000. Protein docking using spherical polar Fourier correlations. Proteins 39 178–194. [PubMed] [Google Scholar]
- Sali, A. and Blundell, T.L. 1990. Definition of general topological equivalence in protein structures. A procedure involving comparison of properties and relationships through simulated annealing and dynamic programming. J. Mol. Biol. 212 403–428. [DOI] [PubMed] [Google Scholar]
- Shoichet, B.K. and Kuntz, I.D. 1996. Predicting the structure of protein complexes: A step in the right direction. Chem. Biol. 3 151–156. [DOI] [PubMed] [Google Scholar]
- Smith, G.R. and Sternberg, M.J. 2002. Prediction of protein–protein interactions by docking methods. Curr. Opin. Struct. Biol. 12 28–35. [DOI] [PubMed] [Google Scholar]
- Sternberg, M.J., Gabb, H.A., and Jackson, R.M. 1998. Predictive docking of protein–protein and protein–DNA complexes. Curr. Opin. Struct. Biol. 8 250–256. [DOI] [PubMed] [Google Scholar]
- Taylor, J.S. and Burnett, R.M. 2000. DARWIN: A program for docking flexible molecules. Proteins 41 173–191. [PubMed] [Google Scholar]
- Tsai, C.J., Lin, S.L., Wolfson, H.J., and Nussinov, R. 1997. Studies of protein–protein interfaces: A statistical analysis of the hydrophobic effect. Protein Sci. 6 53–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdar, W.S. and Thornton, J.M. 2001. Protein–protein interfaces: Analysis of amino acid conservation in homodimers. Proteins 42 108–124. [PubMed] [Google Scholar]
- Wang, Y.H., Zhang, H., and Scott, R.A. 1995. A new computational model for protein-folding based on atomic solvation. Protein Sci. 4 1402–1411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan, C., Dobbs, D., and Honavar, V. 2004. A two-stage classifier for identification of protein–protein interface residues. Bioinformatics 20 i371–i378. [DOI] [PubMed] [Google Scholar]
- Yang, J.M. and Chen, C.C. 2004. GEMDOCK: A generic evolutionary method for molecular docking. Proteins 55 288–304. [DOI] [PubMed] [Google Scholar]