Abstract
Protons are powerful modulators of cardiac function. Their intracellular concentration is regulated by sarcolemmal ion transporters that export or import H+-ions (or their ionic equivalent: 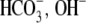 ). One such transporter, which imports H+-equivalents, is a putative Cl−/OH− exchanger (CHE). A strong candidate for CHE is SLC26A6 protein, a product of the SLC26A gene family of anion transporters, which has been detected in murine heart. SLC26A6 protein is suggested to be an electrogenic
). One such transporter, which imports H+-equivalents, is a putative Cl−/OH− exchanger (CHE). A strong candidate for CHE is SLC26A6 protein, a product of the SLC26A gene family of anion transporters, which has been detected in murine heart. SLC26A6 protein is suggested to be an electrogenic 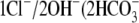 ) exchanger. Unfortunately, there is insufficient characterization of cardiac CHE against which the properties of heterologously expressed SLC26A6 can be matched. We therefore investigated the proton, Cl−, and voltage dependence of CHE activity in guinea-pig ventricular myocytes, using voltage-clamp, intracellular pH fluorescence, and mathematical modeling techniques. We find that CHE activity is tightly regulated by intracellular and extracellular pH, is voltage-insensitive over a wide range (±80 mV), and displays substrate dependence suggestive of electroneutral 1Cl−/1OH− exchange. These properties exclude electrogenic SLC26A6 as sole contributor to CHE. Either the SLC26A6 product in heart is electroneutral, or CHE comprises at least two transporters with oppositely balanced voltage sensitivity. Alternatively, CHE may comprise an H+-Cl− coinflux system, which cannot be distinguished kinetically from an exchanger. Irrespective of ionic mechanism, CHE's pH sensitivity helps to define resting intracellular pH, and hence basal function in the heart.
) exchanger. Unfortunately, there is insufficient characterization of cardiac CHE against which the properties of heterologously expressed SLC26A6 can be matched. We therefore investigated the proton, Cl−, and voltage dependence of CHE activity in guinea-pig ventricular myocytes, using voltage-clamp, intracellular pH fluorescence, and mathematical modeling techniques. We find that CHE activity is tightly regulated by intracellular and extracellular pH, is voltage-insensitive over a wide range (±80 mV), and displays substrate dependence suggestive of electroneutral 1Cl−/1OH− exchange. These properties exclude electrogenic SLC26A6 as sole contributor to CHE. Either the SLC26A6 product in heart is electroneutral, or CHE comprises at least two transporters with oppositely balanced voltage sensitivity. Alternatively, CHE may comprise an H+-Cl− coinflux system, which cannot be distinguished kinetically from an exchanger. Irrespective of ionic mechanism, CHE's pH sensitivity helps to define resting intracellular pH, and hence basal function in the heart.
INTRODUCTION
In the heart, intracellular pH (pHi) exerts a major influence on cellular processes such as 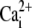 signaling (1), contraction (2) and electrical excitability (3). It is no surprise, therefore, that cardiac myocytes possess a sophisticated pHi regulatory system. This comprises powerful cytoplasmic buffers and sarcolemmal ion-transport proteins. Among the latter, Na+/H+ exchange and
signaling (1), contraction (2) and electrical excitability (3). It is no surprise, therefore, that cardiac myocytes possess a sophisticated pHi regulatory system. This comprises powerful cytoplasmic buffers and sarcolemmal ion-transport proteins. Among the latter, Na+/H+ exchange and 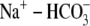 cotransport extrude excess acid from the myocyte, while
cotransport extrude excess acid from the myocyte, while 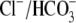 exchange and Cl−/OH− exchange extrude excess base (4). A sarcolemmal lactic acid transporter is also recruited in response to enhanced anaerobic metabolism (5). Under normal physiological conditions, the regulatory system maintains pHi at a steady-state value of ∼7.2.
exchange and Cl−/OH− exchange extrude excess base (4). A sarcolemmal lactic acid transporter is also recruited in response to enhanced anaerobic metabolism (5). Under normal physiological conditions, the regulatory system maintains pHi at a steady-state value of ∼7.2.
Of the various ion transporters involved in cardiac pHi regulation, least is known about Cl−/OH− exchange. It was first identified functionally in guinea-pig myocytes as an H+-equivalent influx transporter that reduces pHi (6,7). Subsequent work has also implicated its presence in rat (unpublished) and rabbit ventricular myocytes (8). Its activity is Cl−-dependent, Na+-independent, and is activated by low extracellular pH (pHo) and high pHi. H+-equivalent transport through the carrier seems to be unaffected by the removal of 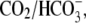 or by the addition of 0.5 mM 4,4′-diisothiocyanatostilbene-2,2′-disulfonic acid (DIDS), a
or by the addition of 0.5 mM 4,4′-diisothiocyanatostilbene-2,2′-disulfonic acid (DIDS), a 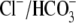 exchange inhibitor (6,7,9). These results appear to rule out known myocardial products of the Anion Exchange (AE) gene family (the SLC4A family) as candidates for CHE, all of which are DIDS-sensitive and transport
exchange inhibitor (6,7,9). These results appear to rule out known myocardial products of the Anion Exchange (AE) gene family (the SLC4A family) as candidates for CHE, all of which are DIDS-sensitive and transport  (10). An independent Cl−/OH− exchanger (CHE) or, alternatively, an H+-Cl− cotransporter, has therefore been proposed. Recently, protein and mRNA products of the SLC26 superfamily, most notably SLC26A6, have been identified in murine myocardium (11). When transfected into HEK293 cells, the protein product mediates both
(10). An independent Cl−/OH− exchanger (CHE) or, alternatively, an H+-Cl− cotransporter, has therefore been proposed. Recently, protein and mRNA products of the SLC26 superfamily, most notably SLC26A6, have been identified in murine myocardium (11). When transfected into HEK293 cells, the protein product mediates both 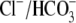 and Cl−/OH− exchange with relatively low sensitivity to DIDS, suggesting it may account for CHE activity in heart.
and Cl−/OH− exchange with relatively low sensitivity to DIDS, suggesting it may account for CHE activity in heart.
There has been no extensive characterization of the kinetic transport properties of cardiac CHE. Without this, a comparison cannot be made with the properties of heterologously expressed candidate transporters. In this work, we have therefore monitored H+-equivalent flux through CHE in guinea-pig ventricular myocytes loaded with the pH-sensitive fluorescent dye, carboxy-seminaphtharhodafluor-1 (carboxy-SNARF-1). We have quantified the dependence of ion transport on extracellular Cl− concentration, and on pHo and pHi. We have also examined the effects of manipulating membrane potential on CHE kinetics, in view of a recent debate on the voltage sensitivity and electrogenicity of some SLC26A gene products, with reports both for (12–14) and against (15) electrogenicity.
Having characterized the kinetic properties of CHE, we have used computational modeling to explore the underlying mechanism. Such an approach, when applied previously to epithelial brush-border membranes, suggested that H+-Cl− cotransport rather than Cl−/OH− exchange was the more likely ionic arrangement (16). We have investigated if such a distinction can be made for the system in heart. We have also analyzed our data for evidence of allosteric regulation of CHE by pHi and pHo. Results of experiments and modeling demonstrate that CHE is specialized to import acid into the cardiac myocyte, in a voltage-insensitive but tightly proton-controlled manner. Candidate transporters that may underpin these properties are considered.
METHODS
Isolation of guinea-pig ventricular myocytes
The procedures used in the isolation process have been described previously (17). Briefly, after cervical dislocation, hearts were excised from female albino guinea-pigs (350–450 g) and perfused via a modified Langendorff method. Single ventricular myocytes were isolated using both enzymatic and mechanical dispersion (for some experiments, we used 0.7 mg/ml collagenase, Type I or II (Worthington Biochemical, Reading, UK) and 0.04 mg/ml protease (Sigma, St. Louis); for others, we used Blendzyme III (Roche Diagnostics, Burgess Hill, UK). The cells were suspended in 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) buffered Dulbecco's modified Eagle's medium and left at room temperature until use. Myocytes that displayed a rod shape and calcium tolerance were used in the study.
pHi measurements
The pHi of single isolated myocytes was measured using carboxy-SNARF-1, a dual-emission, pHi-sensitive fluorophore. Cells were loaded by incubation in a 10–20 μM solution of carboxy-SNARF-1-AM ester at room temperature for 5–10 min. Carboxy-SNARF-1 loaded in individual cells was excited at 540 ± 12 nm and fluorescence emission was measured simultaneously at 590 ± 5 and 640 ± 5 nm using an inverted microscope (Diaphot; Nikon, Kingston upon Thames, UK) adopted for epifluorescence. The signals were digitized at 0.5 kHz (CED 1401+). The SNARF emission ratio (590 nm/640 nm) was calculated and converted to a pHi value using calibration data, obtained by superfusing 145 mM K+-containing solutions at pH 8.5, 7.5, 6.5, and 5.5, containing 10 μM nigericin, as described by Thomas et al. (18).
Solutions
Experiments were performed using nominally 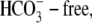 HEPES-buffered Tyrode solutions containing (mM): 140 NaCl, 1.0 MgCl2, 4.5 KCl, 2.0 CaCl2, 11 glucose, and 20 HEPES (pKa = 7.5) for pH values 6.8, 7.4, and 7.8. When required, the solution contained 20 mM 3-[4-(2-Hydroxyethyl)-1-piperazinyl]propanesulfonic acid (HEPPS) (pKa = 8.0) for pH 8.4, or 20 mM 2-(N-morpholino) ethanesulfonic acid (MES) (pKa = 6.1) for pH 6.4 and 6.2. Cl−-free Tyrode solutions contained (mM): 140 Na-gluconate, 4.5 K-gluconate, 4.0 Ca-gluconate, 1.0 Mg-gluconate, 11 glucose, and 20 HEPES, MES, or HEPPS. When acetate was added to solutions, an equimolar amount of anion (either Cl− or gluconate) was omitted. In the experiments performed to determine the
HEPES-buffered Tyrode solutions containing (mM): 140 NaCl, 1.0 MgCl2, 4.5 KCl, 2.0 CaCl2, 11 glucose, and 20 HEPES (pKa = 7.5) for pH values 6.8, 7.4, and 7.8. When required, the solution contained 20 mM 3-[4-(2-Hydroxyethyl)-1-piperazinyl]propanesulfonic acid (HEPPS) (pKa = 8.0) for pH 8.4, or 20 mM 2-(N-morpholino) ethanesulfonic acid (MES) (pKa = 6.1) for pH 6.4 and 6.2. Cl−-free Tyrode solutions contained (mM): 140 Na-gluconate, 4.5 K-gluconate, 4.0 Ca-gluconate, 1.0 Mg-gluconate, 11 glucose, and 20 HEPES, MES, or HEPPS. When acetate was added to solutions, an equimolar amount of anion (either Cl− or gluconate) was omitted. In the experiments performed to determine the 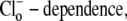 equimolar substitutions were performed to give the required concentration of [Cl−]o (1.4, 14, and 98 mM), while osmolality was maintained at 300 mOsm/kg (measured with a osmometer; Micro Instruments, Witney, UK). In most experiments, when measurements of acid-equivalent influx were made, 30 μM HOE 694 (an NHE inhibitor) was included in the superfusates, except at pHo 8.4, when 300 μM HOE 694 was added, as the drug is only active in the protonated form (pK ∼8.2 base on a derivative, amiloride (19)).
equimolar substitutions were performed to give the required concentration of [Cl−]o (1.4, 14, and 98 mM), while osmolality was maintained at 300 mOsm/kg (measured with a osmometer; Micro Instruments, Witney, UK). In most experiments, when measurements of acid-equivalent influx were made, 30 μM HOE 694 (an NHE inhibitor) was included in the superfusates, except at pHo 8.4, when 300 μM HOE 694 was added, as the drug is only active in the protonated form (pK ∼8.2 base on a derivative, amiloride (19)).
Experimental protocols
The standard experimental protocol for studying CHE activity (as demonstrated in Fig. 1) consisted of baseloading the cell using a 3–4 min acetate prepulse (40–80 mM, depending on the desired magnitude of post-acetate alkalosis). Upon acetate removal, cells were perfused with a Cl−-free solution to maintain the intracellular baseload. Readdition of 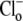 reactivated CHE, resulting in a recovery of pHi back to control levels. Experiments were performed when cells were superfused with air-equilibrated solution (i.e., nominally CO2-free conditions). When perfusates devoid of CO2 were required, they were equilibrated with 100% O2 in loosely stoppered glass flasks, and solution was led to the superfusion chamber through double-sleeved silastic tubing, with 100% O2 flowing through the double-sleeved space. The volume above the superfusion chamber was surrounded by a 10-cm-high Perspex collar, also filled with flowing 100% O2. The ability of the perfusion system to exclude a selected atmospheric gas was initially tested by switching the perfusate to 100% N2-equilibrated Tyrode's, and measuring the fall of PO2 in the solution flowing through the chamber, using a miniature O2-electrode (PreSens, Regensburg, Germany). PO2 was reduced to ∼0.5 Torr in ∼15 min. This implied that atmospheric PCO2 in a superfusate (nominally 0.03% in air-equilibrated solution) would be reduced by nearly 300-fold (to 0.0001%), when 100% O2-equilibrated solutions were flowing through the chamber.
reactivated CHE, resulting in a recovery of pHi back to control levels. Experiments were performed when cells were superfused with air-equilibrated solution (i.e., nominally CO2-free conditions). When perfusates devoid of CO2 were required, they were equilibrated with 100% O2 in loosely stoppered glass flasks, and solution was led to the superfusion chamber through double-sleeved silastic tubing, with 100% O2 flowing through the double-sleeved space. The volume above the superfusion chamber was surrounded by a 10-cm-high Perspex collar, also filled with flowing 100% O2. The ability of the perfusion system to exclude a selected atmospheric gas was initially tested by switching the perfusate to 100% N2-equilibrated Tyrode's, and measuring the fall of PO2 in the solution flowing through the chamber, using a miniature O2-electrode (PreSens, Regensburg, Germany). PO2 was reduced to ∼0.5 Torr in ∼15 min. This implied that atmospheric PCO2 in a superfusate (nominally 0.03% in air-equilibrated solution) would be reduced by nearly 300-fold (to 0.0001%), when 100% O2-equilibrated solutions were flowing through the chamber.
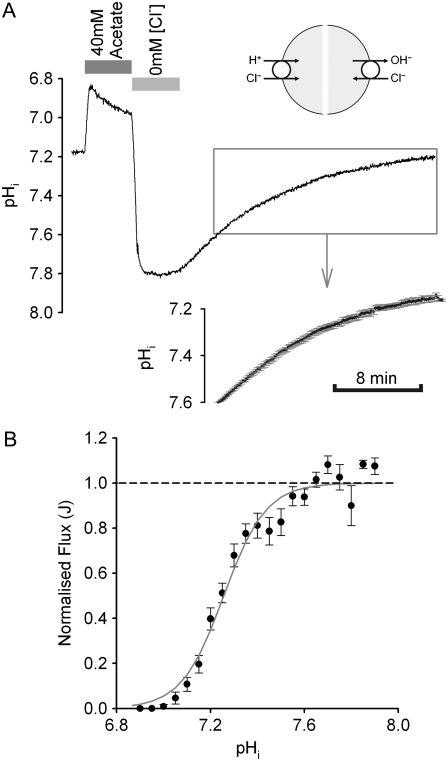
FIGURE 1.
Stimulating CHE: recovery from alkaline pHi. (A) Experimental protocol illustrating the acetate prepulse technique, used to baseload a guinea-pig ventricular myocyte superfused with Cl−-free HEPES-buffered Tyrode's solution. The myocyte is exposed transiently (4 min) to 40 mM sodium acetate. Readmitting 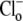 then reactivates CHE, permitting pHi to recover to control levels. The upper inset (cartoon) illustrates possible ionic mechanisms. Whole-cell intracellular pH recorded using intracellular, ratiometric SNARF fluorescence. The lower inset shows a portion of the pHi recovery, averaged over the pHi range 7.6–7.2 (n = 15 experiments). (B) Recovery rates for pHi have been converted to values for H+-equivalent influx (see Methods), and plotted versus pHi in the range 7.8–7.0 (n = 9–15 measurements for each point). H+-equivalent influx has been normalized to the peak flux, estimated by fitting the data with a Hill curve. The best-fit (shaded curve) is described by a Hill coefficient of 4.8 and a pK of 7.25.
then reactivates CHE, permitting pHi to recover to control levels. The upper inset (cartoon) illustrates possible ionic mechanisms. Whole-cell intracellular pH recorded using intracellular, ratiometric SNARF fluorescence. The lower inset shows a portion of the pHi recovery, averaged over the pHi range 7.6–7.2 (n = 15 experiments). (B) Recovery rates for pHi have been converted to values for H+-equivalent influx (see Methods), and plotted versus pHi in the range 7.8–7.0 (n = 9–15 measurements for each point). H+-equivalent influx has been normalized to the peak flux, estimated by fitting the data with a Hill curve. The best-fit (shaded curve) is described by a Hill coefficient of 4.8 and a pK of 7.25.
Calculation of net sarcolemmal H+-equivalent influx
Net H+-equivalent influx through CHE was estimated from the accompanying fall of pHi. Net acid influx (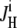 ) was computed using the equation
) was computed using the equation
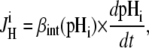 |
(1) |
where βint (intrinsic buffering power) is the H+-ion buffering capacity in the cell, and is a function of pHi, as measured previously (20). In most experiments, as described above, CHE activity was initiated by re-adding 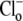 after initially baseloading the cell under
after initially baseloading the cell under 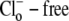 conditions. In some experiments, CHE activity was estimated when
conditions. In some experiments, CHE activity was estimated when 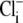 concentration was close to zero (see, e.g., Fig. 4 and Fig. 5 C). In these cases, the value for dpHi/dt was obtained from the initial pHi change (linear regression to first 30s of pHi change) measured after readdition of
concentration was close to zero (see, e.g., Fig. 4 and Fig. 5 C). In these cases, the value for dpHi/dt was obtained from the initial pHi change (linear regression to first 30s of pHi change) measured after readdition of 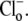 In other experiments, H+-equivalent influx was measured at different times after
In other experiments, H+-equivalent influx was measured at different times after 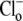 readdition. In these latter cases (see, e.g., Fig. 1 and Fig. 5 B), dpHi/dt was measured at different successive values of pHi during CHE activity. This was done by piecewise fitting of the pHi timecourse, measuring the dpHi/dt gradient every 5 s, and then interpolating the flux to the desired pHi (taken as the midpoint of the pHi change).
readdition. In these latter cases (see, e.g., Fig. 1 and Fig. 5 B), dpHi/dt was measured at different successive values of pHi during CHE activity. This was done by piecewise fitting of the pHi timecourse, measuring the dpHi/dt gradient every 5 s, and then interpolating the flux to the desired pHi (taken as the midpoint of the pHi change).
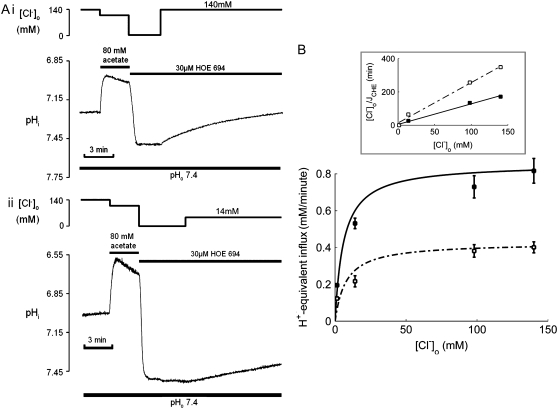
FIGURE 4.
[Cl−]o-dependence of CHE activity. (A) Recovery of pHi was measured after readdition of (i) 140 mM or (ii) 14mM Cl−, after an acetate prepulse performed to baseload a guinea-pig myocyte in a nominally CO2-free HEPES-buffered Tyrode solution. HOE 694 (30 μM) was included to block Na+-H+ exchange during Cl−-activated pHi recovery. Superfusate pHo was maintained at 7.4. (B) The timecourses of pHi recovery were converted to H+-equivalent influx computed at pHi = 7.5–7.55, and plotted as a function of [Cl−]o (1.4, 14, 100, 140 mM). Measurements (n = 6) were performed on experiments at pHo 7.4 (open symbols) or 6.4 (solid symbols). Flux values are derived from the initial rate of recovery of pHi, when [Cl−]i is close to zero. Data were best-fitted with Hill curves with cooperativity 0.76 and 0.85 for pHo 7.4 and 6.4, respectively. (Inset) A Hanes plot demonstrates that changing pHo has a significant effect on Vmax (slope−1) and only a modest effect on Km (intercept) for 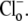
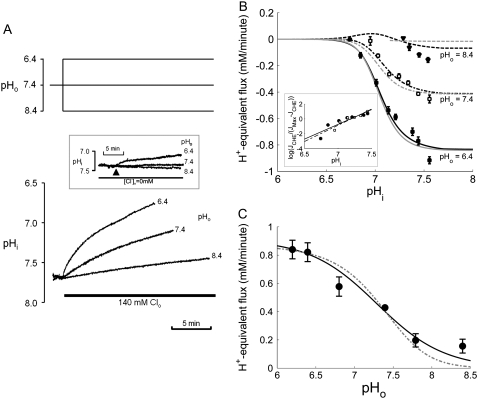
FIGURE 5.
pHi- and pHo-dependence of CHE activity. (A) Recovery of pHi was measured after readdition of 140 mM Cl− at pHo 6.4, 7.4, or 8.4, after an acetate prepulse performed to baseload a guinea-pig myocyte in a nominally CO2-free HEPES-buffered Tyrode's solution. Thirty-micrometers HOE 694 was included to block Na+-H+ exchange during Cl−-activated pHi recovery. (Inset) pHi timecourses measured in the absence of 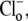 at three pHo values. The arrow indicates the time of the change of pHo. (B) The timecourses of pHi recovery were converted to H+-equivalent flux, calculated over the pHi range 6.8–7.6 for pHo 6.4 (solid squares), 7.4 (open squares), and 8.4 (solid triangles). Cl−-independent flux was subtracted from the data. The data were fitted with models for electroneutral CHE (solid curves) or 1Cl−/2OH− electrogenic CHE (shaded curves). (Inset) a Hill plot of data measured at pHo 7.4 (solid squares) and 6.4 (open squares) fitted with Hill coefficients of 4.37 and 3.97. (C) measurements of H+-equivalent influx plotted as a function of pHo, estimated at a common pHi of 7.69. The data were fitted with model of electroneutral CHE (solid curve) or 1Cl−/2OH− electrogenic CHE (dashed curve).
at three pHo values. The arrow indicates the time of the change of pHo. (B) The timecourses of pHi recovery were converted to H+-equivalent flux, calculated over the pHi range 6.8–7.6 for pHo 6.4 (solid squares), 7.4 (open squares), and 8.4 (solid triangles). Cl−-independent flux was subtracted from the data. The data were fitted with models for electroneutral CHE (solid curves) or 1Cl−/2OH− electrogenic CHE (shaded curves). (Inset) a Hill plot of data measured at pHo 7.4 (solid squares) and 6.4 (open squares) fitted with Hill coefficients of 4.37 and 3.97. (C) measurements of H+-equivalent influx plotted as a function of pHo, estimated at a common pHi of 7.69. The data were fitted with model of electroneutral CHE (solid curve) or 1Cl−/2OH− electrogenic CHE (dashed curve).
Averaged data are presented as mean ± SE, where n = number of observations.
Electrophysiological measurements
Electrophysiological measurements were made with whole-cell, ruptured-patch pipettes, made of borosilicate capillary glass (No. 8250; Dow Corning, Corning, NY) with resistance typically 1.5 MΩ when backfilled. Filling solutions contained 15 mM NaCl, 110 mM K-aspartate, 5 mM KCl, 5 mM MgCl2, 14 mM HEPES (to match the buffering capacity of intracellular mobile buffer (21)), pH-adjusted to 7.15 with 2 M KOH. Voltage-clamp control was provided by a model No. 200B system with a model No. CV203BU cooled headstage (Axopatch, Axon Instruments, Union City, CA). Membrane potential (Vm) and membrane current (Im) were filtered at 5 kHz, digitized at 10–20 kHz with a 16-bit A/D converter (model No. 1322A; Axon Instruments), and analyzed using pCLAMP 8 software (Axon Instruments). The reference electrode was a flowing 3 M KCl bridge for experiments involving changes in bath Cl−, and an Ag-AgCl pellet was used when 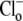 was maintained at a constant concentration. Cells were held initially at −80 mV and then clamped to +80 mV for 2–4 min. Bathing solutions contained 0.5 mM BaCl2 to block inward IK1, and 10 μM nifedipine to reduce Ca2+ entry that may subsequently affect pHi (22). Cell pHi was simultaneously measured using carboxy-SNARF-1, as described above. The reversal potential for electrogenic CHE (ECHE) transporting n H+-equivalent and m Cl− ions across the membrane was calculated using the formula
was maintained at a constant concentration. Cells were held initially at −80 mV and then clamped to +80 mV for 2–4 min. Bathing solutions contained 0.5 mM BaCl2 to block inward IK1, and 10 μM nifedipine to reduce Ca2+ entry that may subsequently affect pHi (22). Cell pHi was simultaneously measured using carboxy-SNARF-1, as described above. The reversal potential for electrogenic CHE (ECHE) transporting n H+-equivalent and m Cl− ions across the membrane was calculated using the formula
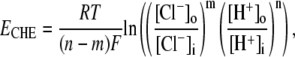 |
(2) |
where R, T, and F are the gas constant, temperature, and Faraday's constant, respectively. In the calculation, we have assumed constant [Cl−]i or allowed [Cl−]i to increase as a result of CHE activity.
Modeling methods
In this study, we derive transporter models to elucidate the currently unknown modality of the cardiac CHE carrier. The model rate constants for a given cycle are constrained via thermodynamic principles, where the products of the forward and backward rates for a given cycle are equal at equilibrium. The steady-state fluxes are calculated using rapid equilibrium assumptions for ion binding and unbinding. The transitions between intracellular and extracellular facing conformations are assumed to take place more slowly than ion binding events, and hence the forward and backward rates are represented explicitly. Voltage variation is assumed to be small during experiments (removal and readdition of 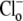 affects membrane potential of cardiac tissue by only a few mV (23)) allowing the voltage dependence of any model parameter to be assumed constant.
affects membrane potential of cardiac tissue by only a few mV (23)) allowing the voltage dependence of any model parameter to be assumed constant.
Starting with simple electroneutral transporter models (six-state models), we proceed to more complex arrangements incorporating, for example, multiple substrate binding sites (eight-state models), an allosteric H+ modifier site, and a putative electrogenic transport stoichiometry (twelve-state models). In each case, we assess the ability of the model to reproduce the experimental results. The models are described in Results, and the governing equations are provided in the Appendix.
RESULTS
Measuring CHE activity
Fig. 1 A illustrates the experimental protocol for activating CHE. An isolated ventricular myocyte was superfused with HEPES-buffered Tyrode's, nominally free of  buffer. Prepulsing the cell with 40 mM extracellular acetate induced an intracellular baseload. In the absence of extracellular Cl− (replaced by gluconate), pHi stabilized at ∼7.8. Readdition of
buffer. Prepulsing the cell with 40 mM extracellular acetate induced an intracellular baseload. In the absence of extracellular Cl− (replaced by gluconate), pHi stabilized at ∼7.8. Readdition of 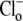 then prompted an intracellular acidification, consistent with Cl−-influx coupled to OH− efflux on a Cl−/OH− exchange transporter (or, alternatively, HCl influx on an H+-Cl− cotransporter). For convenience, we refer to this as an H+-equivalent influx on CHE. Several experimental records from different cells have been averaged in the inset to Fig. 1 A, demonstrating the monotonic intracellular acidification. H+-equivalent influx (
then prompted an intracellular acidification, consistent with Cl−-influx coupled to OH− efflux on a Cl−/OH− exchange transporter (or, alternatively, HCl influx on an H+-Cl− cotransporter). For convenience, we refer to this as an H+-equivalent influx on CHE. Several experimental records from different cells have been averaged in the inset to Fig. 1 A, demonstrating the monotonic intracellular acidification. H+-equivalent influx (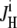 ) was estimated from individual pHi timecourses (see Methods), measured over a range of pHi values. Fig. 1 B shows average H+-equivalent influx, normalized to the maximal flux estimated from the best-fitting Hill curve. The data shows that flux increased steeply at pHi values above 7.0 and saturated at ∼7.6. The stimulation of CHE activity by a rise of pHi is consistent with previous reports (4,7).
) was estimated from individual pHi timecourses (see Methods), measured over a range of pHi values. Fig. 1 B shows average H+-equivalent influx, normalized to the maximal flux estimated from the best-fitting Hill curve. The data shows that flux increased steeply at pHi values above 7.0 and saturated at ∼7.6. The stimulation of CHE activity by a rise of pHi is consistent with previous reports (4,7).
CHE activity is not dependent on HCO3− availability
CHE activity is clearly evident when myocytes are superfused with 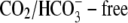 Tyrode's to block
Tyrode's to block 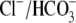 exchange activity ((6,9); see also Fig. 1). Residual
exchange activity ((6,9); see also Fig. 1). Residual 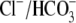 exchange may persist, however, because of
exchange may persist, however, because of 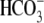 contamination, caused by the hydration of atmospheric or metabolically produced CO2. A previous attempt has been made to remove these sources of CO2 (9), but specific effects on Cl−-dependent H+-equivalent influx were not examined.
contamination, caused by the hydration of atmospheric or metabolically produced CO2. A previous attempt has been made to remove these sources of CO2 (9), but specific effects on Cl−-dependent H+-equivalent influx were not examined.
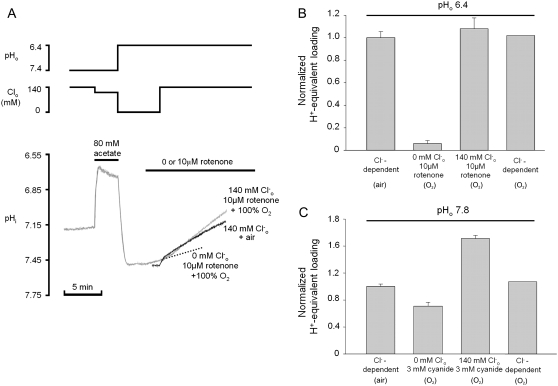
Fig. 2 A illustrates an experiment performed using HEPES-buffered superfusates. A myocyte was baseloaded (acetate prepulse) in Cl−-free solution, while pHo was reduced to 6.4. Re-adding 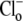 (solid trace) prompted a robust intracellular acidification via CHE. A Cl−-activated acidification occurred (shaded trace, and see Fig. 2 B) even when the superfusate contained 10 μM rotenone (to inhibit metabolic CO2 production) and was saturated with 100% O2 (to remove atmospheric CO2-contamination). Mean Cl−-activated acid influx was also quantified (Fig. 2 C) when 3 mM cyanide was used instead of rotenone (in this case pHo was adjusted to 7.8 rather than 6.4). The cause of the higher background, Cl−-independent acid-loading observed in these latter experiments (Fig. 2 C, column 2) was not established, but it may reflect an ability of HCN to act as a membrane-permeant proton carrier. Cl−-activated acid influx, however, was unaffected by cyanide (Fig. 2 C, column 4), indicating that CHE activity is not reliant on residual
(solid trace) prompted a robust intracellular acidification via CHE. A Cl−-activated acidification occurred (shaded trace, and see Fig. 2 B) even when the superfusate contained 10 μM rotenone (to inhibit metabolic CO2 production) and was saturated with 100% O2 (to remove atmospheric CO2-contamination). Mean Cl−-activated acid influx was also quantified (Fig. 2 C) when 3 mM cyanide was used instead of rotenone (in this case pHo was adjusted to 7.8 rather than 6.4). The cause of the higher background, Cl−-independent acid-loading observed in these latter experiments (Fig. 2 C, column 2) was not established, but it may reflect an ability of HCN to act as a membrane-permeant proton carrier. Cl−-activated acid influx, however, was unaffected by cyanide (Fig. 2 C, column 4), indicating that CHE activity is not reliant on residual 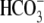 availability and must be caused by OH−-ion efflux or H+-ion influx.
availability and must be caused by OH−-ion efflux or H+-ion influx.
FIGURE 2.
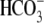 independence of CHE activity. (A) Shaded trace: a guinea-pig myocyte is baseloaded (80 mM acetate prepulse) during superfusion with HEPES-buffered, air-equilibrated solution containing 30 μM HOE 694 (to inhibit NHE). On removal of acetate, cell is exposed to Cl−-free solution of pH 6.4, and then additionally to 100% O2 and 10 μM rotenone (to create CO2-free conditions). The pHi acidifies slowly (dashed trace). Readdition of 140 mM
independence of CHE activity. (A) Shaded trace: a guinea-pig myocyte is baseloaded (80 mM acetate prepulse) during superfusion with HEPES-buffered, air-equilibrated solution containing 30 μM HOE 694 (to inhibit NHE). On removal of acetate, cell is exposed to Cl−-free solution of pH 6.4, and then additionally to 100% O2 and 10 μM rotenone (to create CO2-free conditions). The pHi acidifies slowly (dashed trace). Readdition of 140 mM 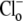 (to reactivate CHE) stimulates a more rapid acidification. (Solid trace) Different experiment, showing
(to reactivate CHE) stimulates a more rapid acidification. (Solid trace) Different experiment, showing 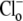 readdition, when superfusates are air-equilibrated, contain 30 μM HOE 694, and lack rotenone. Note that Cl−-dependent acidification is comparable in the two traces. (B) Cl-dependent H+-equivalent loading is similar in air and in CO2-free conditions. (Column 1) Cl−-dependent H+-equivalent loading in air-equilibrated solutions, estimated from pHi-acidification rates; (column 2) H+-equivalent loading in Cl−-free, CO2-free conditions; (column 3) H+-equivalent loading after
readdition, when superfusates are air-equilibrated, contain 30 μM HOE 694, and lack rotenone. Note that Cl−-dependent acidification is comparable in the two traces. (B) Cl-dependent H+-equivalent loading is similar in air and in CO2-free conditions. (Column 1) Cl−-dependent H+-equivalent loading in air-equilibrated solutions, estimated from pHi-acidification rates; (column 2) H+-equivalent loading in Cl−-free, CO2-free conditions; (column 3) H+-equivalent loading after 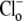 readdition in CO2-free conditions; and (column 4) Cl−-dependent H+-equivalent loading in CO2-free conditions (column 3 minus column 2) (n = 6). H+-equivalent loading in O2 was sampled at pHi 7.4, and normalized to the control Cl−-dependent loading measured in air. (C) Cl−-dependent H-equivalent loading is similar in air and in O2-equilibrated, CN−-containing conditions (30 μM HOE 694 present in superfusates); loading rates sampled at pHi 7.4, and normalized to Cl−-dependent rate measured in CN-free, air-equilibrated conditions. A quantity of 3 mM NaCN was added to a baseloaded myocyte bathed in Cl−-free 100% O2-equilibrated solution of pH 7.8 (column 2);
readdition in CO2-free conditions; and (column 4) Cl−-dependent H+-equivalent loading in CO2-free conditions (column 3 minus column 2) (n = 6). H+-equivalent loading in O2 was sampled at pHi 7.4, and normalized to the control Cl−-dependent loading measured in air. (C) Cl−-dependent H-equivalent loading is similar in air and in O2-equilibrated, CN−-containing conditions (30 μM HOE 694 present in superfusates); loading rates sampled at pHi 7.4, and normalized to Cl−-dependent rate measured in CN-free, air-equilibrated conditions. A quantity of 3 mM NaCN was added to a baseloaded myocyte bathed in Cl−-free 100% O2-equilibrated solution of pH 7.8 (column 2); 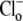 readdition prompted a larger H+-equivalent loading (column 3); Cl−-dependent H+-equivalent loading in 100% O2/CN− (column 4) is comparable to Cl−-dependent loading measured in CN−-free, air-equilibrated conditions (column 1) (n = 6).
readdition prompted a larger H+-equivalent loading (column 3); Cl−-dependent H+-equivalent loading in 100% O2/CN− (column 4) is comparable to Cl−-dependent loading measured in CN−-free, air-equilibrated conditions (column 1) (n = 6).
Electrogenic CHE?
Although protein products of the SLC4A anion exchange gene family (AE) are electroneutral transporters (10), some anion exchange products of another family, SLC26A, are thought to be electrogenic and voltage-sensitive (12–14). Depending on the isoform, they exchange two 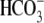 or OH− ions for each Cl− ion (e.g., SLC26A6; (13,14)), or two Cl− ions for each OH− or
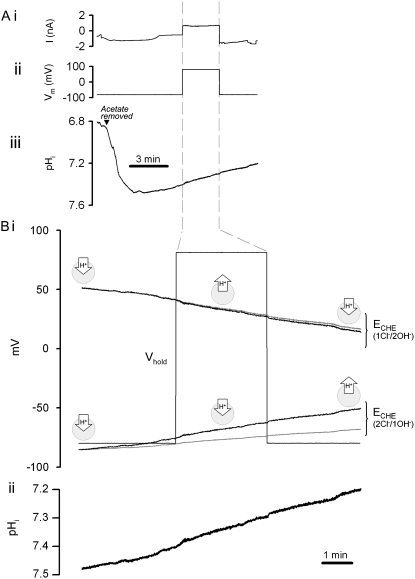
or OH− ions for each Cl− ion (e.g., SLC26A6; (13,14)), or two Cl− ions for each OH− or 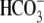 (e.g., SLC26A3; (13,14)). We explored the possible voltage sensitivity of cardiac CHE by manipulating membrane potential under voltage-clamp (ruptured patch) conditions. Fig. 3 shows one such experiment. Membrane potential was clamped initially at −80 mV, while pHi was measured simultaneously. CHE was then stimulated by alkalinizing the cell (by acetate prepulse), whereupon pHi started to recover back to control levels. The membrane potential was then depolarized to +80 mV for 3 min (Fig. 3 Bi). Superimposed on the membrane potential trace are the reversal potentials (ECHE) expected for a 1Cl−/2OH− and a 2Cl−/1OH− exchanger (see Methods). Note that the values for ECHE are predicted to vary over time in accordance with the changes of pHi. Note also that, at different times during the experiment, the electrochemical driving force (Vm–ECHE) acting on each putative electrogenic carrier would have been reversed (i.e., at different times, the holding potential was positive or negative to a transporter's reversal potential), which should terminate or even reverse carrier activity. Despite this, there was no detectable effect on the rate or direction of recovery of pHi (Fig. 3 Bii). Similar results were obtained in four other experiments. We conclude that cardiac CHE behaves functionally as an electroneutral, voltage-insensitive system. CHE activity cannot be described solely by a 1Cl−/2OH− or a 2Cl−/1OH− transporter. We return to this point in the Discussion.
(e.g., SLC26A3; (13,14)). We explored the possible voltage sensitivity of cardiac CHE by manipulating membrane potential under voltage-clamp (ruptured patch) conditions. Fig. 3 shows one such experiment. Membrane potential was clamped initially at −80 mV, while pHi was measured simultaneously. CHE was then stimulated by alkalinizing the cell (by acetate prepulse), whereupon pHi started to recover back to control levels. The membrane potential was then depolarized to +80 mV for 3 min (Fig. 3 Bi). Superimposed on the membrane potential trace are the reversal potentials (ECHE) expected for a 1Cl−/2OH− and a 2Cl−/1OH− exchanger (see Methods). Note that the values for ECHE are predicted to vary over time in accordance with the changes of pHi. Note also that, at different times during the experiment, the electrochemical driving force (Vm–ECHE) acting on each putative electrogenic carrier would have been reversed (i.e., at different times, the holding potential was positive or negative to a transporter's reversal potential), which should terminate or even reverse carrier activity. Despite this, there was no detectable effect on the rate or direction of recovery of pHi (Fig. 3 Bii). Similar results were obtained in four other experiments. We conclude that cardiac CHE behaves functionally as an electroneutral, voltage-insensitive system. CHE activity cannot be described solely by a 1Cl−/2OH− or a 2Cl−/1OH− transporter. We return to this point in the Discussion.
FIGURE 3.
Voltage independence of CHE activity. (A) A guinea-pig myocyte, in a nominally CO2-free HEPES-buffered Tyrode solution, was voltage-clamped in whole-cell, ruptured-patch configuration, while pHi was monitored simultaneously. The myocyte was baseloaded by an 8 min prepulse with 40 mM acetate. During recovery of pHi from the baseload, holding potential (Vhold) was depolarized from −80 mV to +80 mV for a period of 3 min. (i) Current injected into myocyte, (ii) membrane potential, (iii) pHi. (B). (i) Timecourse of holding potential (Vhold) and predicted reversal potentials (ECHE) for two putative forms of electrogenic CHE transport, 2Cl−/1OH− and 1Cl−/2OH−, plotted assuming constant [Cl−]i of 30 mM, equal to pipette-filling solution [Cl−] (shaded trace), or assuming that [Cl−] rises over time from 30 mM, due to CHE activity (solid trace); [Cl−]i rising by 2.6 and 10.6 mM for Cl−/2OH− and 2Cl−/OH−, respectively. Inward and outward H+-flux icons represent thermodynamically predicted direction of carrier activity. (ii) pHi recovery from alkaline pHi, replotted at higher amplification from panel Aiii, showing lack of effect of membrane potential on timecourse of pHi recovery (compare this to the direction of pHi change expected from individual electrogenic transporters, see icons). Similar results were obtained in four other experiments.
[Cl−]o-dependence of CHE activity
Fig. 4 Ai illustrates pHi recovery from a baseload (induced by 80 mM acetate prepulse), after readdition of 140 mM 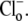 Fig. 4 Aii shows that, in a separate experiment, a slower recovery was induced by readdition of 14 mM
Fig. 4 Aii shows that, in a separate experiment, a slower recovery was induced by readdition of 14 mM 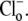 Fig. 4 B pools data from several experiments where various concentrations of
Fig. 4 B pools data from several experiments where various concentrations of 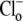 (0–140 mM) were tested. To remove effects of NHE, 30 μM HOE 694 was added to all superfusates. In each case, initial H+-equivalent influx was estimated immediately after the addition of
(0–140 mM) were tested. To remove effects of NHE, 30 μM HOE 694 was added to all superfusates. In each case, initial H+-equivalent influx was estimated immediately after the addition of 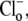 when
when 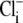 concentration is close to zero (see Methods). Initial Cl−-activated H+-equivalent influx, computed at a common pHi of 7.5–7.55, was a saturating function of [Cl−]o (open squares). In other experiments, pHo was reduced to 6.4 and then
concentration is close to zero (see Methods). Initial Cl−-activated H+-equivalent influx, computed at a common pHi of 7.5–7.55, was a saturating function of [Cl−]o (open squares). In other experiments, pHo was reduced to 6.4 and then 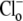 was re-added. In these cases, initial Cl−-activated H+-equivalent influx, again taken at a common pHi of 7.5–7.55, was still a saturating function of [Cl−]o, but maximal flux (Vmax) was significantly larger. A Hanes Plot of the data (Fig. 4 B, inset) demonstrated that reducing pHo from 7.4 to 6.4 had the principal effect of doubling Vmax (1/slope) from 0.43 to 0.86 mM min−1, compared with only a modest shift in Km (y intercept = Km/Vmax) from 6 mM to 8 mM. Hill coefficients for flux activation by
was re-added. In these cases, initial Cl−-activated H+-equivalent influx, again taken at a common pHi of 7.5–7.55, was still a saturating function of [Cl−]o, but maximal flux (Vmax) was significantly larger. A Hanes Plot of the data (Fig. 4 B, inset) demonstrated that reducing pHo from 7.4 to 6.4 had the principal effect of doubling Vmax (1/slope) from 0.43 to 0.86 mM min−1, compared with only a modest shift in Km (y intercept = Km/Vmax) from 6 mM to 8 mM. Hill coefficients for flux activation by 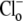 were 0.76 ± 0.2 (pHo 7.4) and 0.85 ± 0.1 (pHo 6.4), suggesting no more than one binding site for Cl− on the transporter.
were 0.76 ± 0.2 (pHo 7.4) and 0.85 ± 0.1 (pHo 6.4), suggesting no more than one binding site for Cl− on the transporter.
Dependence on pHi
Fig. 5 A shows sample traces superimposed from three experiments where CHE activation was recorded by re-adding 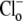 at three different pHo values (6.4, 7.4, and 8.4). The lower the pHo, the faster and larger the Cl−-activated intracellular acidification. Further experiments showed that the changes of pHi were greatly reduced when pHo was altered in the absence of
at three different pHo values (6.4, 7.4, and 8.4). The lower the pHo, the faster and larger the Cl−-activated intracellular acidification. Further experiments showed that the changes of pHi were greatly reduced when pHo was altered in the absence of 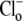 (Fig. 5 A, inset), indicating a Cl−-independent H+-equivalent influx of −0.12, 0.0, and 0.23 mM min−1, at pHo 8.4, 7.4 and 6.4. In contrast, influx measured in the presence of
(Fig. 5 A, inset), indicating a Cl−-independent H+-equivalent influx of −0.12, 0.0, and 0.23 mM min−1, at pHo 8.4, 7.4 and 6.4. In contrast, influx measured in the presence of 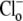 could be as large as 1.2 mM min−1.
could be as large as 1.2 mM min−1.
Data, averaged from several individual experiments, are plotted in Fig. 5 B, after subtracting the Cl−-independent H+-equivalent influx. The Cl−-dependent flux increased steeply with a rise of pHi from 7.0 to 7.5 (compare with Fig. 1 B), displaying an apparent 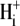 cooperativity of >3.0 (see Fig. 5 B, inset). This is reminiscent of the high cooperativity for
cooperativity of >3.0 (see Fig. 5 B, inset). This is reminiscent of the high cooperativity for  activation of Na+/H+ exchange (NHE 1) (24), with the difference that, for CHE, intracellular H+ ions appear to inhibit rather than stimulate the transporter. High
activation of Na+/H+ exchange (NHE 1) (24), with the difference that, for CHE, intracellular H+ ions appear to inhibit rather than stimulate the transporter. High 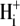 cooperativity for NHE activation has been suggested to be caused by
cooperativity for NHE activation has been suggested to be caused by 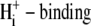 to an allosteric modifier site(s), in addition to the transport site on the carrier protein. The curves drawn through the points in Fig. 5 B (main panel) have been fitted using allosteric models for CHE, described later in the Results. Reducing pHo displaces the pHi dependence of CHE activity to the left along the pHi axis, to lower pHi values (Fig. 5 B). Thus, the sensitivity of CHE to pHi is modulated by pHo. In effect, reducing pHo attenuates the inhibitory effect of intracellular H+ ions on CHE activity.
to an allosteric modifier site(s), in addition to the transport site on the carrier protein. The curves drawn through the points in Fig. 5 B (main panel) have been fitted using allosteric models for CHE, described later in the Results. Reducing pHo displaces the pHi dependence of CHE activity to the left along the pHi axis, to lower pHi values (Fig. 5 B). Thus, the sensitivity of CHE to pHi is modulated by pHo. In effect, reducing pHo attenuates the inhibitory effect of intracellular H+ ions on CHE activity.
Dependence on pHo
Fig. 5 C shows H+-equivalent flux through CHE, plotted as a function of pHo. Measurements of initial acid influx after  readdition were made (see Methods) at a common value of pHi (∼7.7). Reducing pHo increased H+-equivalent influx, consistent with previous reports for CHE activity (6); the effect tended toward saturation at pHo values of 6.2. Sensitivity to pHo can be best described by an H+-binding curve with a Hill coefficient of 0.96 ± 0.11, consistent with a single extracellular H+-binding site. There was no evidence for a high level of
readdition were made (see Methods) at a common value of pHi (∼7.7). Reducing pHo increased H+-equivalent influx, consistent with previous reports for CHE activity (6); the effect tended toward saturation at pHo values of 6.2. Sensitivity to pHo can be best described by an H+-binding curve with a Hill coefficient of 0.96 ± 0.11, consistent with a single extracellular H+-binding site. There was no evidence for a high level of 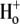 cooperativity, unlike that measured for
cooperativity, unlike that measured for 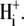 Sensitivity to pHo displayed half-maximal activity at a value of ∼7.25, close to the physiological value of pHo (7.4). Thus, in addition to intracellular pH (see above), extracellular pH will be a key determinant of CHE activity.
Sensitivity to pHo displayed half-maximal activity at a value of ∼7.25, close to the physiological value of pHo (7.4). Thus, in addition to intracellular pH (see above), extracellular pH will be a key determinant of CHE activity.
Kinetic models of CHE: Cl−/OH− exchange or H+-Cl− cotransport?
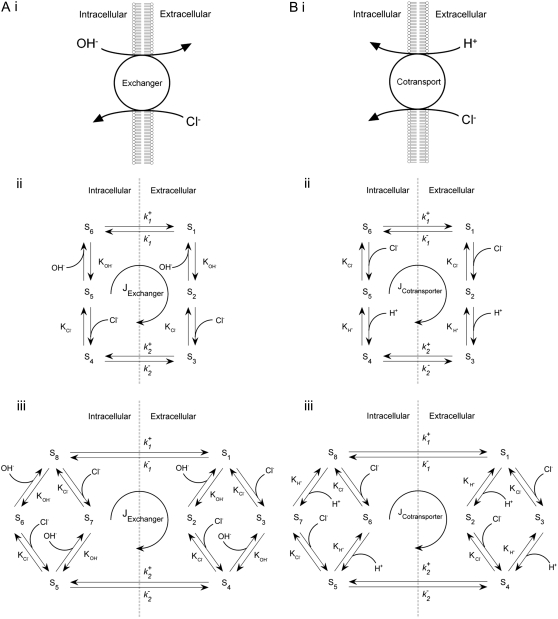
In the following sections, we use computational modeling to assess possible transporters that may underpin cardiac CHE activity. Initially, we ask if the H+-equivalent substrate can be identified unequivocally as an OH− or an H+ ion. To do this, we explore the transport modalities illustrated in Fig. 6. The two modes are either a ping-pong Cl−/OH− exchanger (Fig. 6 Ai) or an H+-Cl− cotransporter (Fig. 6 Bi). For simplicity, we consider the case of an electroneutral system, as this is consistent with the voltage insensitivity of CHE (Fig. 3). The additional complexity of an allosteric 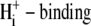 site is dealt with later. A six-state model represents the simplest scheme where, for an exchanger (Fig. 6 Aii), there is a single binding site on the internal or external configuration of the carrier, to which either a Cl− or OH− ion attaches while, for cotransport (Fig. 6 Bii), there is ordered Cl− and H+-ion binding to separate sites. An eight-state model is more flexible: for an exchanger (Fig. 6 Aiii), it allows binding of Cl− and OH− to independent sites in both the inward and outward facing configurations, although translocation of only one ionic species (Cl− or OH−) is permitted at any time. For cotransport (Fig. 6 Biii), the eight-state model allows for random-order binding of H+ and Cl− ions. Details of the derivation of the eight-state model are given in the Appendix.
site is dealt with later. A six-state model represents the simplest scheme where, for an exchanger (Fig. 6 Aii), there is a single binding site on the internal or external configuration of the carrier, to which either a Cl− or OH− ion attaches while, for cotransport (Fig. 6 Bii), there is ordered Cl− and H+-ion binding to separate sites. An eight-state model is more flexible: for an exchanger (Fig. 6 Aiii), it allows binding of Cl− and OH− to independent sites in both the inward and outward facing configurations, although translocation of only one ionic species (Cl− or OH−) is permitted at any time. For cotransport (Fig. 6 Biii), the eight-state model allows for random-order binding of H+ and Cl− ions. Details of the derivation of the eight-state model are given in the Appendix.
FIGURE 6.
Schematic diagrams for six- and eight-state kinetic CHE models. Kinetic diagrams: Cl−/OH− exchanger models (A, left panels) and H+-Cl− cotransporter models (B, right panels). Cartoons for (Ai) Cl−/OH− exchange and (Bi) H+-Cl− cotransport. Schematics of six-state scheme for (Aii) Cl−/OH− exchange and (Bii) H+-Cl− cotransport and eight-state scheme for (Aiii) Cl−/OH− exchange and (Biii) H+-Cl− cotransport. The circular arrows denote direction of net transporter activity. Transition between different conformational states (s1–s6 or s1–s8) of the transporter is indicated by the straight arrows. Ion binding or unbinding to various states is indicated by the curved lines that merge with the transition arrows. The equilibrium constant for each ion binding and unbinding is represented by the parameters KCl, KOH, and KH for the respective ions.
We demonstrate below that the experimental results shown in Fig. 4 B require a model with a minimum of eight states, and that such models cannot distinguish between OH− or H+ ion transport. Fig. 4 B quantified the  dependence of CHE activity. As those measurements were performed at a pHi of ∼7.5, transport inhibition caused by H+ binding to an intracellular allosteric modifier site would have been minimal (∼2% inhibition, calculated from the modifier-site model described below). The six-state Cl−/OH− exchange scheme (Fig. 6 Aii) has a single extracellular/intracellular binding site, and so extracellular Cl− and OH− ions will compete for binding. The Vmax for acid influx, at saturating
dependence of CHE activity. As those measurements were performed at a pHi of ∼7.5, transport inhibition caused by H+ binding to an intracellular allosteric modifier site would have been minimal (∼2% inhibition, calculated from the modifier-site model described below). The six-state Cl−/OH− exchange scheme (Fig. 6 Aii) has a single extracellular/intracellular binding site, and so extracellular Cl− and OH− ions will compete for binding. The Vmax for acid influx, at saturating  concentration, should thus be independent of changes of pHo, as shown by the definition of the maximum flux (Eq. 3) derived from Appendix Eq. 18:
concentration, should thus be independent of changes of pHo, as shown by the definition of the maximum flux (Eq. 3) derived from Appendix Eq. 18:
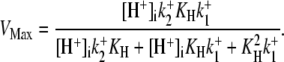 |
(3) |
As the experimental value for Vmax increased upon reduction of pHo (Fig. 4 B), we can reject the six-state exchanger formulation of CHE. The same experimental dataset also permits the rejection of the six-state cotransporter scheme (Fig. 6 Bii). This model has four permutations, each with a different order of binding or unbinding of Cl− and H+ on the extracellular and intracellular configurations of the carrier. Depending on the permutation, the maximum H+-equivalent influx through CHE, with zero  and saturating
and saturating 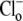 concentration (i.e., the condition immediately after readdition of 140 mM
concentration (i.e., the condition immediately after readdition of 140 mM 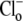 shown in Fig. 4 A), is predicted to respond to changes of pHo in a way that does not match the experimental results.
shown in Fig. 4 A), is predicted to respond to changes of pHo in a way that does not match the experimental results.
For example, two of the four permutations require H+ to bind before Cl− in the extracellular conformation. In these cases, in the presence of saturating levels of 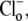 Vmax will be given by Eqs. 4 and 5 (these equations refer respectively to the situation where H+ subsequently unbinds first or second at the intracellular site of the transporter):
Vmax will be given by Eqs. 4 and 5 (these equations refer respectively to the situation where H+ subsequently unbinds first or second at the intracellular site of the transporter):
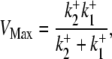 |
(4) |
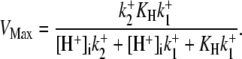 |
(5) |
Neither Eq. 4 nor Eq. 5 contains a pHo dependence. Our experiments, however, have shown that the apparent Vmax under these conditions varies with pHo (see Fig. 4 B), thus ruling out these permutations of the model.
The other two permutations require that H+ should bind after Cl− in the extracellular conformation. The six-state cotransporter model then predicts that changing pHo from 7.4 to 6.4 will result in the ratio of the apparent 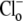 binding affinities at both pHo values (Km|pHo=6.4/Km|pHo=7.4) being 10(7.4–6.4)-fold larger than the ratio of Vmax values at both pHo values (Vmax|pHo=6.4/Vmax|pHo=7.4), i.e., effects of
binding affinities at both pHo values (Km|pHo=6.4/Km|pHo=7.4) being 10(7.4–6.4)-fold larger than the ratio of Vmax values at both pHo values (Vmax|pHo=6.4/Vmax|pHo=7.4), i.e., effects of 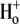 and
and 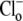 on CHE activity will appear predominantly competitive. Our experimental results fail to validate this constraint, as demonstrated by the data shown in Fig. 4 B. The experiments report that the Km ratio is 0.75 and the Vmax ratio is 2, such that the affinity ratio is in fact 2.67-fold smaller than the Vmax ratio.
on CHE activity will appear predominantly competitive. Our experimental results fail to validate this constraint, as demonstrated by the data shown in Fig. 4 B. The experiments report that the Km ratio is 0.75 and the Vmax ratio is 2, such that the affinity ratio is in fact 2.67-fold smaller than the Vmax ratio.
To test further the viability of the six-state cotransporter scheme, the model parameters were reduced to algebraic functions of the Vmax and Km values derived from the 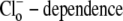 data shown in Fig. 4 B (a similar method is described in Eqs. 22 and 23). This allowed the model to be reduced to one free parameter (in our case
data shown in Fig. 4 B (a similar method is described in Eqs. 22 and 23). This allowed the model to be reduced to one free parameter (in our case 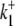 ).
). 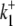 was then varied between 10−4 and 106; all parameter sets within this range were found to be nonviable due to the presence of negative rate constants. Given the above algebraic and numerical evidence, we conclude that a six-state cotransporter does not provide a good description of the data.
was then varied between 10−4 and 106; all parameter sets within this range were found to be nonviable due to the presence of negative rate constants. Given the above algebraic and numerical evidence, we conclude that a six-state cotransporter does not provide a good description of the data.
In contrast to the nonviability of the six-state model, the eight-state model of CHE readily predicts the pHo sensitivity of 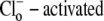 H+-equivalent influx, as shown by the curves fitted to the data in Fig. 4 B. It should be noted, however, that predictions of the exchanger model (Fig. 6 Aiii) are the same as those for the cotransporter (Fig. 6 Biii). We show in the Appendix that the effects of pHi and pHo on H+-equivalent transport are mathematically identical for both model types. Thus, although a simple model of CHE with separate binding sites for Cl− and H+ equivalents successfully predicts the experimental behavior of pHi, it cannot distinguish between H+ and OH− ion transport. For convenience we therefore continue to refer to CHE as a Cl−-coupled H+-equivalent transporter.
H+-equivalent influx, as shown by the curves fitted to the data in Fig. 4 B. It should be noted, however, that predictions of the exchanger model (Fig. 6 Aiii) are the same as those for the cotransporter (Fig. 6 Biii). We show in the Appendix that the effects of pHi and pHo on H+-equivalent transport are mathematically identical for both model types. Thus, although a simple model of CHE with separate binding sites for Cl− and H+ equivalents successfully predicts the experimental behavior of pHi, it cannot distinguish between H+ and OH− ion transport. For convenience we therefore continue to refer to CHE as a Cl−-coupled H+-equivalent transporter.
Modeling the pHi and pHo sensitivity of H+-equivalent transport: electroneutral CHE
Before modeling the pH sensitivity of CHE, two points were considered.
Firstly, we considered whether changes of intracellular Cl− concentration during our experiments may be influencing our quantification of CHE's pH-sensitivity. This is unlikely to be the case for our measurements of extracellular pH (Fig. 5 C) and extracellular Cl− sensitivity (Fig. 4), as these were made immediately after 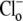 readdition, when
readdition, when 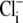 concentration would have been close to zero. In contrast, CHE's intracellular pH sensitivity was assessed experimentally from the whole timecourse of acidification of pHi after
concentration would have been close to zero. In contrast, CHE's intracellular pH sensitivity was assessed experimentally from the whole timecourse of acidification of pHi after 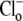 readdition (Fig. 5 B). During this period,
readdition (Fig. 5 B). During this period, 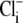 concentration must rise. To allow for the effect of this on the apparent pHi sensitivity of CHE, one must estimate the rise. Assuming a flux-stoichiometry of one Cl−-ion coupled with one H+-equivalent (as described by the eight-state model), we have approximated the increase of
concentration must rise. To allow for the effect of this on the apparent pHi sensitivity of CHE, one must estimate the rise. Assuming a flux-stoichiometry of one Cl−-ion coupled with one H+-equivalent (as described by the eight-state model), we have approximated the increase of 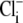 concentration by integrating H+-influx over time, using a numerical procedure. This approach ignores possible contributions to Cl− entry from other transporters such as NKCC (Na+K+2Cl− cotransport) (25,26), but it at least recognizes that
concentration by integrating H+-influx over time, using a numerical procedure. This approach ignores possible contributions to Cl− entry from other transporters such as NKCC (Na+K+2Cl− cotransport) (25,26), but it at least recognizes that 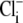 concentration will vary with pHi. A rise of
concentration will vary with pHi. A rise of 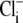 has been measured previously in cardiac tissue during activation of
has been measured previously in cardiac tissue during activation of 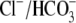 exchange (27,28).
exchange (27,28).
Secondly, the pHi sensitivity of H+ influx exhibits cooperativity, with a Hill coefficient for 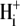 of > 3.0 (see Fig. 5 B, inset), suggesting an allosteric
of > 3.0 (see Fig. 5 B, inset), suggesting an allosteric 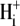 modifier site. This site has been modeled by a scaling factor, representing the proportion of active transporters. An individual CHE transporter is assumed to be dormant when its modifier site is titrated by intracellular H+ ions. A rise of pHi permits dissociation of the H+ ions, allowing the carrier to mediate ion transport. An H+-binding affinity at this site of pKa = 7.0, with a Hill coefficient of 4.0, provides a good description of the transporter's pHi sensitivity.
modifier site. This site has been modeled by a scaling factor, representing the proportion of active transporters. An individual CHE transporter is assumed to be dormant when its modifier site is titrated by intracellular H+ ions. A rise of pHi permits dissociation of the H+ ions, allowing the carrier to mediate ion transport. An H+-binding affinity at this site of pKa = 7.0, with a Hill coefficient of 4.0, provides a good description of the transporter's pHi sensitivity.
Model parameters describing the pHi and pHo sensitivity of CHE were derived for the eight-state electroneutral model, using the experimental dataset shown in Fig. 5 B assuming a fixed pHi of 7.5. The transporter flux equation (Eq. 15) can be rearranged to provide analytic definitions of Vmax and Km for Cl−-activated flux (Eqs. 22 and 23, respectively). Combining these definitions with thermodynamic constraints (Appendix Eq. 11), and including the influence of [Cl−]i accumulation and the intracellular H+-modifier site, leaves a single free parameter (in our case 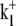 ) to be fit to the data. The full set of fitted model parameters for the eight-state transporter is listed in Table 1. The best fit of the model to the experimental data in the main panel of Fig. 5 B is indicated by the continuous and dashed lines. The pHi-sensitive H+-equivalent influx is well represented, particularly in the pHo range 6.4–7.4. Also reproduced by the model is the pronounced leftward shift of pHi dependence as pHo is reduced.
) to be fit to the data. The full set of fitted model parameters for the eight-state transporter is listed in Table 1. The best fit of the model to the experimental data in the main panel of Fig. 5 B is indicated by the continuous and dashed lines. The pHi-sensitive H+-equivalent influx is well represented, particularly in the pHo range 6.4–7.4. Also reproduced by the model is the pronounced leftward shift of pHi dependence as pHo is reduced.
TABLE 1.
Parameters used in simulations
| Parameter | 8-state electroneutral | 12-state electrogenic |
|---|---|---|
| KCl | 5.64 mM | 6.12 mM |
| KH | 10−4.292 mM | 10−4.558 mM |
| Ka | 10−4.0 mM | 10−4.0 mM |
| na | 4.0 | 4.0 |
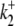 |
0.0165 s−1 | 0.0158 s−1 |
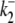 |
0.0424 s−1 | 3.186 × 10−4 s−1 |
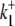 |
1.2782 s−1 | 2.425 s−1 |
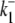 |
0.4983 s−1 | 0.7856 s−1 |
Electrogenic (Cl−-2H+) and electroneutral (1Cl−-1H+) CHE model parameters derived from [Cl−]o and pHi-pHo kinetic data. Ka and na are the allosteric binding site affinity constant and Hill coefficient, respectively.
Because we did not measure 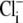 concentration changes directly in our experiments, but only inferred them from CHE-driven changes of pHi, we tested whether the pKi and
concentration changes directly in our experiments, but only inferred them from CHE-driven changes of pHi, we tested whether the pKi and 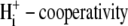 values (derived by fitting the model to the experimental data) were affected by doubling the Cl− influx assumed for each H+-equivalent influx. In experiments like those shown in Fig. 5 A, this would then double the predicted increase of
values (derived by fitting the model to the experimental data) were affected by doubling the Cl− influx assumed for each H+-equivalent influx. In experiments like those shown in Fig. 5 A, this would then double the predicted increase of 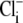 after the readdition of
after the readdition of 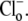 The output of the model was insensitive to this maneuver. There was <0.1 pH unit change in the derived value for pKi, no change in the Hill coefficient for
The output of the model was insensitive to this maneuver. There was <0.1 pH unit change in the derived value for pKi, no change in the Hill coefficient for 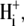 and <2.5% change in the other transporter parameters. It therefore seems unlikely that failure to take adequate account of changes of [Cl−]i will have significantly distorted our derivation of CHE's pHi sensitivity.
and <2.5% change in the other transporter parameters. It therefore seems unlikely that failure to take adequate account of changes of [Cl−]i will have significantly distorted our derivation of CHE's pHi sensitivity.
Modeling the pHi and pHo sensitivity of H+-equivalent transport: electrogenic CHE
As well as exploring the ability of a 1Cl−/1OH− (H+) electroneutral transporter to satisfy the Cl− and pH dependence of CHE activity, we also investigated the predictions of an electrogenic transporter. A recent report proposes that the dominant cause of CHE activity in murine ventricular myocytes is the SLC26A6 gene product (11), which may operate with a 1Cl−/2OH− stoichiometry (12–14). An electrogenic exchanger mandates a more complex computational model, as illustrated in Fig. 7. This has a minimum of 12 states, to account for the additional binding of substrate (OH−) to transport sites on the carrier. By assuming that the membrane potential of a ventricular cell is relatively constant after 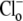 readdition, the electrical driving force acting on the electrogenic carrier will also be constant (replacing
readdition, the electrical driving force acting on the electrogenic carrier will also be constant (replacing 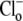 with an impermeant anion induces a change of membrane potential of a few mV only (23,29)). The voltage sensitivity of transport is not therefore coded specifically into the model, and becomes subsumed into the model parameters (see Appendix).
with an impermeant anion induces a change of membrane potential of a few mV only (23,29)). The voltage sensitivity of transport is not therefore coded specifically into the model, and becomes subsumed into the model parameters (see Appendix).
FIGURE 7.
Schematic diagram for the 12-state kinetic CHE model. Twelve-state schematic diagram (left panel) for electrogenic Cl−/2OH− exchange (cartoon in right panel, denoting net direction of transmembrane operation of transporter). The12-state model contains three independent binding sites, two for binding OH− ions and one for Cl−. The binding affinities are independent of the carrier conformation and number of ions bound. The model does not distinguish between the two OH− binding sites, which both have the same binding affinity. Transitions 1–6 occur when binding sites are exposed to the extracellular compartment. Transitions 7–12 occur when binding sites are exposed to the intracellular compartment. Transitions from consecutive odd- to even-numbered states (e.g., S1 to S2) involve Cl− binding/unbinding. Transitions between consecutive even-numbered states (e.g., S2 to S4) or between consecutive odd-numbered (e.g., S1 to S3) states on the same side of the membrane involve OH− binding/unbinding. Rate constants and binding affinities have been omitted for clarity.
As with the electroneutral model of CHE, the H+-equivalent flux predictions of the electrogenic CHE model can be shown to be identical for OH− or H+ ion transport (assuming random-order binding of Cl− and OH− in the cotransport model; see Appendix). For simplicity, in Fig. 7, we show only the exchanger (1Cl−/2OH−) scheme. The effect of [Cl−]i-changes on carrier activity were again incorporated into the model by integrating H+-equivalent flux over time, but adjusted for the new ionic stoichiometry. The model made identical predictions as electroneutral CHE for Cl− activation of acid influx, and its sensitivity to pHo (solid and dashed lines through data shown in Fig. 4 B). As with the electroneutral model, the electrogenic model could be fitted reasonably well to the pHi-dependent data shown in Fig. 5 B, with the notable exception that, contrary to experimental observation, CHE was predicted to remain essentially dormant at pHo 8.4 (note that flux in pHo 8.4 was not estimated at very low pHi, as the kinetics of the 1Cl−/2OH− carrier close to its reversal pH are not readily predicted without a more formal coding for charge movement). Model parameters derived from the fitting procedure are listed in Table 1. The best fit (shaded solid and dashed lines in Fig. 5 B) required incorporation of an allosteric 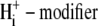 site of pK 7.0 with a Hill coefficient of 4.0 (in the model this particular Hill coefficient was constrained to be an integer number). These allosteric parameters are virtually identical to those derived for the electroneutral model. It is notable that the best-fits for electroneutral and electrogenic models to the data in Fig. 5 B are very similar in the pHo range 6.4–7.4, predicting similar
site of pK 7.0 with a Hill coefficient of 4.0 (in the model this particular Hill coefficient was constrained to be an integer number). These allosteric parameters are virtually identical to those derived for the electroneutral model. It is notable that the best-fits for electroneutral and electrogenic models to the data in Fig. 5 B are very similar in the pHo range 6.4–7.4, predicting similar 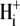 cooperativity values for CHE inhibition of 3–4.
cooperativity values for CHE inhibition of 3–4.
Testing predictions of the eight- and twelve-state models
The electroneutral and electrogenic models were tested in three ways.
Firstly, they were used to predict the pHo sensitivity of H+ influx shown in Fig. 5 C (solid line for electroneutral, and dashed line for electrogenic models). Simulations were performed with initial [Cl−]i = 0 mM, [Cl−]o = 140 mM, pHi = 7.69, and pHo between 6.0 and 8.5. Results of the simulations match the experimental data (solid circles) reasonably well, although the electroneutral model gave the better overall fit (the L2 norm of the error is ‖e‖2 = 0.1463 and ‖e‖2 = 0.2071 for the electroneutral and electrogenic carriers, respectively). Interestingly, despite the fact that the electrogenic model comprises the transport of two OH− ions for each Cl−, the overall 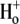 cooperativity predicted by the model was 1.49, much less than 2.0. This is to be compared with the predicted
cooperativity predicted by the model was 1.49, much less than 2.0. This is to be compared with the predicted 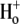 cooperativity of 1.0 for the electroneutral model.
cooperativity of 1.0 for the electroneutral model.
Secondly, both models predict saturation of H+-equivalent influx at pHi values higher than ∼7.5 (Fig. 5 B). Although such high pHi levels were not explored experimentally in Fig. 5 B, there was a tendency toward flux-saturation as pHi increased (compare with data obtained at pHo 8.4 and 7.4). High pHi levels were, however, tested in the experiments summarized in Fig. 1 B, and clear flux-saturation at pHi 7.6 was obtained, thus confirming the model prediction.
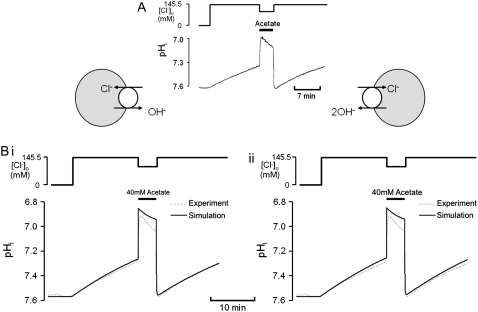
Thirdly, the models were tested by simulating the effect on pHi of activating CHE, and comparing results with published experimental data from Fig. 3 of Leem and Vaughan-Jones (7) (Fig. 8 A). Fig. 8 B superimposes the timecourses of pHi change observed in the experiment (dashed line) with model simulations (continuous lines) for electroneutral (1Cl−/1OH−) (Fig. 8 Bi) and electrogenic (1Cl−/2OH−) (Fig. 8 Bii) carriers. The experimental trace was recorded in nominally 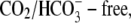 HEPES buffered solution, in a guinea-pig ventricular myocyte. The pHi was initially alkalinized using an 80 mM acetate prepulse in Cl−-free solution. Re-adding 145.5
HEPES buffered solution, in a guinea-pig ventricular myocyte. The pHi was initially alkalinized using an 80 mM acetate prepulse in Cl−-free solution. Re-adding 145.5 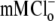 then activated CHE, producing a slow recovery of pHi from the intracellular baseload. The experiment was simulated assuming that, for pHi > 7.1, CHE mediates all H+-equivalent transport, an assumption supported by the stability of high pHi in Cl−-free solution (Fig. 8 A). For pHi < 7.1, NHE is active, and this was simulated as a simple function of pHi (Eq. 6), while a background H+ flux (JBG) was set to 0.025 mM s−1 (30). The simulated timecourses of pHi recovery upon activating CHE are shown in Fig. 8 B, and match well the experimentally recorded timecourse.
then activated CHE, producing a slow recovery of pHi from the intracellular baseload. The experiment was simulated assuming that, for pHi > 7.1, CHE mediates all H+-equivalent transport, an assumption supported by the stability of high pHi in Cl−-free solution (Fig. 8 A). For pHi < 7.1, NHE is active, and this was simulated as a simple function of pHi (Eq. 6), while a background H+ flux (JBG) was set to 0.025 mM s−1 (30). The simulated timecourses of pHi recovery upon activating CHE are shown in Fig. 8 B, and match well the experimentally recorded timecourse.
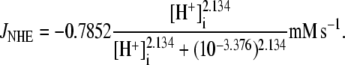 |
(6) |
The timecourse of pHi change during the acetate prepulse was simulated using the approach adopted by Leem et al. (4) and outlined below, where α = exp(−VmF/RT), Vm = −80 mV, PHAc = 6.77 × 10−8 cm s−1, PAc = 0.12 cm s−1, KAc = 10−1.528 mM, and ρ = 2017 cm−1 (7). F, R, and T are Faraday's constant, the gas constant, and temperature, respectively. Extracellular ionized and nonionized acetate concentrations were calculated using HAco = Actoto[H+]o/(KAc+[H+]o) and Aco = Actoto − HAco, respectively:
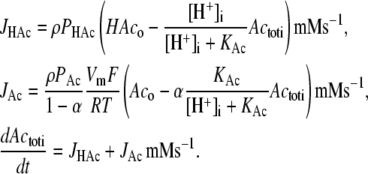 |
(7) |
To compute CHE-mediated H+-equivalent flux, it was necessary to take account of changes of [Cl−]i during CHE activation, assuming all Cl− flux was through CHE and either a 1:1 or 2:1 H+-equivalent: Cl− stoichiometry for CHE. Changes of pHi were modeled using Eq. 8, where βint was defined in mM per pH unit based on Zaniboni et al. (20):
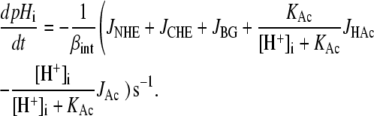 |
(8) |
We conclude that the Cl− and pH dependence of CHE does not permit one to distinguish readily between possible electroneutral and electrogenic configurations; both models predict most pHi changes reasonably accurately. The electroneutral model, however, provides the better overall fit to the data. In particular, at high values of pHo (= 8.4), the electrogenic model predicts little or no pHi-dependent activity, which is clearly contrary to experimental findings. Furthermore, the lack of voltage sensitivity of CHE over a wide range (−80 to +80 mV), although not specifically explored in the models, cannot be reconciled with an exclusive role for the electrogenic transporter.
FIGURE 8.
Modeling pHi changes induced by CHE activity. (A) pHi timecourse measured experimentally, showing pHi recovery from intracellular baseload induced first by readdition of  followed by a subsequent 40 mM acetate prepulse and another pHi recovery from the baseload (trace taken from Fig. 3 of (7)). (B) Model simulations (solid traces) of the experiment shown in panel A, based on (i) electroneutral Cl−/OH− exchange (eight-state model; see Fig. 6 Aiii) or (ii) electrogenic Cl−/2OH− exchange (12-state model; see Fig. 7). The experimental timecourse has been superimposed (dashed trace in Bi and Bii).
followed by a subsequent 40 mM acetate prepulse and another pHi recovery from the baseload (trace taken from Fig. 3 of (7)). (B) Model simulations (solid traces) of the experiment shown in panel A, based on (i) electroneutral Cl−/OH− exchange (eight-state model; see Fig. 6 Aiii) or (ii) electrogenic Cl−/2OH− exchange (12-state model; see Fig. 7). The experimental timecourse has been superimposed (dashed trace in Bi and Bii).
DISCUSSION
Physiological regulation of CHE activity is by pH
In this work, we have experimentally characterized and then mathematically modeled the dependence of cardiac CHE activity on the concentrations of its transported substrates. The system conducts H+ equivalents into the ventricular myocyte in a Cl− and pH-dependent manner (Fig. 5, B, and C). It can do this even under stringent 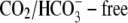 conditions, when the intracellular metabolic generation of
conditions, when the intracellular metabolic generation of 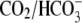 is inhibited with cyanide or rotenone, and atmospheric CO2 has been eliminated (Fig. 2). Acid influx via CHE cannot, therefore, result from the transport of
is inhibited with cyanide or rotenone, and atmospheric CO2 has been eliminated (Fig. 2). Acid influx via CHE cannot, therefore, result from the transport of 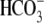 ions out of the cell. This result consolidates other reports for CHE (6,9), although a dependence of
ions out of the cell. This result consolidates other reports for CHE (6,9), although a dependence of 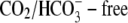 flux on
flux on 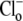 has not previously been demonstrated. We conclude that CHE involves the coupled movement of Cl− and H+ or OH− ions.
has not previously been demonstrated. We conclude that CHE involves the coupled movement of Cl− and H+ or OH− ions.
The activation of CHE by different concentrations of extracellular Cl− (Hill coefficient ∼0.80, Fig. 4 B) suggests a single Cl−-ion binding site on the extracellular facing configuration of the carrier molecule. As the apparent equilibrium constant for 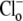 (Kapp,Clo∼7 mM) is >10-fold lower than extracellular Cl− concentration (∼120 mM), the
(Kapp,Clo∼7 mM) is >10-fold lower than extracellular Cl− concentration (∼120 mM), the 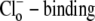 site will normally be close to saturation. Natural variation of plasma [Cl−]o, which can be in the range ±5–10 mM (e.g., (31)), will not significantly change CHE activity, suggesting the transporter is not a physiological sensor of [Cl−]o. In contrast, CHE activity varies greatly with changes of pHi and pHo in the physiological range (see Fig. 5, B and C). Thus, CHE will serve as a physiological pH sensor, its activity being tightly regulated by pH on either side of the sarcolemma.
site will normally be close to saturation. Natural variation of plasma [Cl−]o, which can be in the range ±5–10 mM (e.g., (31)), will not significantly change CHE activity, suggesting the transporter is not a physiological sensor of [Cl−]o. In contrast, CHE activity varies greatly with changes of pHi and pHo in the physiological range (see Fig. 5, B and C). Thus, CHE will serve as a physiological pH sensor, its activity being tightly regulated by pH on either side of the sarcolemma.
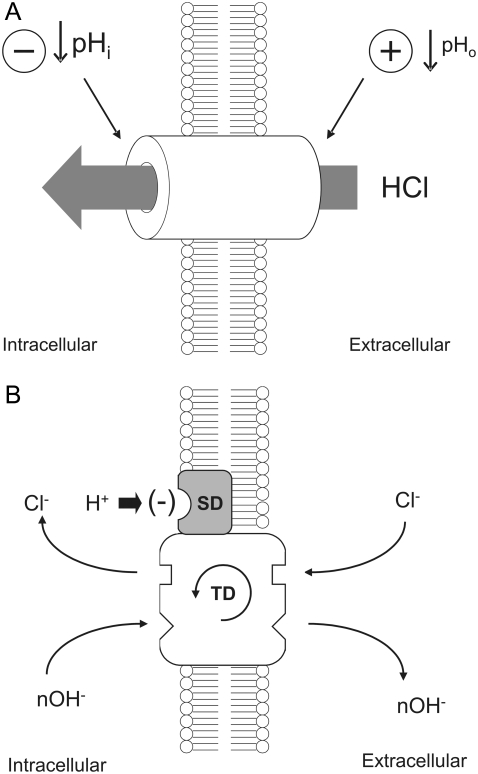
Despite two different possible modes of H+-equivalent transport via CHE (utilizing either OH− or H+ ions), CHE functions, in pH terms, like a proton-gated leak of hydrochloric acid into the cell, as illustrated schematically in Fig. 9 A. The leak is stimulated by extracellular H+ ions, but inhibited by intracellular H+ ions. It is likely to contribute to the dependence of steady-state pHi on pHo in the cardiac cell. On average, resting pHi in ventricular myocytes falls by nearly 40% of a tonic fall in pHo, and much of the acid influx that underpins this is conducted via CHE (6). In the short term, the influx may help to buffer an extracellular acidosis, by transferring the acid onto intracellular buffer sites. The magnitude of the accompanying decline of pHi will eventually be limited by the inhibitory effect of intracellular H+ ions on acid influx, and also by acid extrusion on transporters such as NHE and NBC, which are themselves regulated by pHi and pHo (for review, see (32)). In the presence of 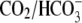 buffer, the acid-influx role of CHE will be supplemented by
buffer, the acid-influx role of CHE will be supplemented by 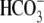 efflux on the cardiac
efflux on the cardiac 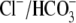 exchanger (7). Thus cardiac CHE appears to be specialized as part of a multitransporter complex that controls pHi. In epithelial tissues, CHE has been proposed, variously, to be a controller of either pHi (rat distal colon; (33)) or
exchanger (7). Thus cardiac CHE appears to be specialized as part of a multitransporter complex that controls pHi. In epithelial tissues, CHE has been proposed, variously, to be a controller of either pHi (rat distal colon; (33)) or 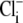 (rat duodenal brush border membrane; (34)). In the latter case,
(rat duodenal brush border membrane; (34)). In the latter case, 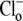 affinity appears much lower than for cardiac CHE, as might be expected for a physiological sensor of extracellular Cl− concentration (16).
affinity appears much lower than for cardiac CHE, as might be expected for a physiological sensor of extracellular Cl− concentration (16).
FIGURE 9.
Schematic diagrams of CHE. (A) CHE acts, in effect, as a leak of hydrochloric acid into the cardiac cell, regulated by pHi (low pH inhibitory) and pHo (low pH excitatory). (B) CHE represented as Cl−/OH− exchange, showing separate transport binding sites for intracellular and extracellular Cl− and OH− (n = 1,2) ions, positioned on the transport domain (TD) of the carrier. Ion transport is also regulated by a proton-binding, allosteric controller (the proton sensor domain, SD) positioned on the intracellular face of the protein. Proton binding to the SD inhibits carrier activity.
H+-Cl− cotransport versus Cl−/OH− exchange
Our modeling of CHE indicates that Cl−/OH− exchange and H+-Cl− cotransport modes of activity would display the same kinetic behavior, with respect to membrane fluxes of Cl− and intracellular changes of pH. This is because the general form of the eight-state or twelve-state exchange and random-order binding cotransport models means they are mathematically equivalent. They cannot therefore be distinguished using flux data alone. A previous analysis of epithelial CHE (16) suggested H+-Cl− cotransport is the more likely configuration. In that report, exchangers were assumed to be unable to form ternary complexes, i.e., they bind only one of the two transported substrates at any moment. For electroneutral Cl−/OH− exchange this meant, in effect, that Cl− and OH− ions compete for binding to a single site on the carrier. This led to the adoption of a six-state model for the exchanger-mode of CHE, while a minimum description of electroneutral H+-Cl− cotransport required an eight-state model (with separate sites for simultaneous H+ and Cl−-ion binding). Such models can, in theory, be distinguished kinetically. The exchanger will show competition between transported substrates while the cotransporter will not. Both epithelial and cardiac CHE display a predominantly noncompetitive interaction between 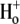 equivalents and
equivalents and 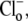 which might be taken to indicate H+-Cl− cotransport, as proposed by Alvarado and Vasseur (16). There is no compelling reason, however, to assume that all exchangers are nonternary. Furthermore, other putative exchangers, like Na+/H+ exchange, display competitive (24), noncompetitive (35), or mixed (36) substrate interactions, a reflection possibly of the different NHE isoforms dominant in different tissues. While exchangers are likely to obey ping-pong kinetics for the transport step, with only one type of substrate moving at any moment across the membrane, this does not preclude the possibility of ternary complexes forming reversibly on the external or internal facing configuration of the carrier, as illustrated for the eight-state (electroneutral) and twelve-state (electrogenic) models shown in this work (e.g., Fig. 6 Aiii and Fig. 7). In these cases the predicted kinetic behavior of the exchanger model does not differ from the similar-state cotransporter model. A distinction between H+ and OH− modes of transport cannot therefore be made. For convenience, however, we continue to use the acronym “CHE” when referring to the cardiac transporter, while recognizing that the mode of transport has yet to be resolved.
which might be taken to indicate H+-Cl− cotransport, as proposed by Alvarado and Vasseur (16). There is no compelling reason, however, to assume that all exchangers are nonternary. Furthermore, other putative exchangers, like Na+/H+ exchange, display competitive (24), noncompetitive (35), or mixed (36) substrate interactions, a reflection possibly of the different NHE isoforms dominant in different tissues. While exchangers are likely to obey ping-pong kinetics for the transport step, with only one type of substrate moving at any moment across the membrane, this does not preclude the possibility of ternary complexes forming reversibly on the external or internal facing configuration of the carrier, as illustrated for the eight-state (electroneutral) and twelve-state (electrogenic) models shown in this work (e.g., Fig. 6 Aiii and Fig. 7). In these cases the predicted kinetic behavior of the exchanger model does not differ from the similar-state cotransporter model. A distinction between H+ and OH− modes of transport cannot therefore be made. For convenience, however, we continue to use the acronym “CHE” when referring to the cardiac transporter, while recognizing that the mode of transport has yet to be resolved.
Conformation-dependent substrate binding affinities?
One assumption in our modeling is that the substrate binding affinities of cardiac CHE are constant throughout different stages of the transport cycle. We made this simplifying assumption as there is no evidence, as yet, to the contrary. Nevertheless, asymmetry in substrate binding affinity has been detected experimentally for extracellular and intracellular facing configurations of the AE1 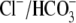 exchanger (37), and for other more complex carriers such as the Na+/K+ ATPase (see (38)). We do not exclude a similar asymmetry for CHE, despite the fact that the carrier is probably not a protein product of the AE gene family. We can only infer the real binding affinities for H+, OH−, or Cl− from our present measurements of apparent binding affinities, taken when the full transport cycle for CHE has been activated. More sophisticated experiments on partial reactions within the cycle will be needed to probe any sidedness of real affinity. We have, however, been able to exclude the possibility that the presence of asymmetry defines the minimum number of transition states (six or eight) required for modeling either Cl−/OH− or H+-Cl− modes of electroneutral transport. When assuming asymmetric extracellular and intracellular substrate affinities, a minimum of eight states is still required for both modes, reinforcing the conclusion that they cannot be distinguished kinetically.
exchanger (37), and for other more complex carriers such as the Na+/K+ ATPase (see (38)). We do not exclude a similar asymmetry for CHE, despite the fact that the carrier is probably not a protein product of the AE gene family. We can only infer the real binding affinities for H+, OH−, or Cl− from our present measurements of apparent binding affinities, taken when the full transport cycle for CHE has been activated. More sophisticated experiments on partial reactions within the cycle will be needed to probe any sidedness of real affinity. We have, however, been able to exclude the possibility that the presence of asymmetry defines the minimum number of transition states (six or eight) required for modeling either Cl−/OH− or H+-Cl− modes of electroneutral transport. When assuming asymmetric extracellular and intracellular substrate affinities, a minimum of eight states is still required for both modes, reinforcing the conclusion that they cannot be distinguished kinetically.
The gene product for CHE: electroneutral versus electrogenic transporters
Armed with the transport properties of cardiac CHE, one may ask which gene product underlies the process. Insensitivity of the carrier to high concentrations of DIDS (0.5 mM) (6,7) and to 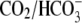 removal (7,9) suggests that it is not a known member of the AE (SLC4A) family of bicarbonate transporters. This conclusion is further supported by recent evidence that SLC4A3 and SLC4A1 in heterologous expression systems appear to support
removal (7,9) suggests that it is not a known member of the AE (SLC4A) family of bicarbonate transporters. This conclusion is further supported by recent evidence that SLC4A3 and SLC4A1 in heterologous expression systems appear to support 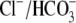 but not Cl−/OH− exchange (11,39); however, counter-results have been reported (13). Casey and co-workers (11) suggest that CHE in guinea-pig heart may, instead, be an SLC26A6 gene product, particularly as the relevant mRNA and protein products are heavily expressed in murine ventricular tissue. While some studies have suggested that the SLC26A6 protein does not support Cl−/OH− exchange (40,41), others have concluded that it does (12–15). SLC26A6 transfected into HEK293 cells results in the functional appearance of Cl−/OH− exchange, as judged from
but not Cl−/OH− exchange (11,39); however, counter-results have been reported (13). Casey and co-workers (11) suggest that CHE in guinea-pig heart may, instead, be an SLC26A6 gene product, particularly as the relevant mRNA and protein products are heavily expressed in murine ventricular tissue. While some studies have suggested that the SLC26A6 protein does not support Cl−/OH− exchange (40,41), others have concluded that it does (12–15). SLC26A6 transfected into HEK293 cells results in the functional appearance of Cl−/OH− exchange, as judged from 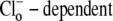 changes of pHi in
changes of pHi in 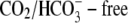 conditions (11). The changes, however, are inhibited by high concentrations of DIDS, as expected for SLC26A6 gene products, and they are enhanced in the presence of
conditions (11). The changes, however, are inhibited by high concentrations of DIDS, as expected for SLC26A6 gene products, and they are enhanced in the presence of 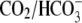 buffer, suggesting
buffer, suggesting 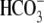 ions are also transported on the carrier, two features that are not evident for cardiac CHE (6,7).
ions are also transported on the carrier, two features that are not evident for cardiac CHE (6,7).
One property of the SLC26A6 anion exchanger that has attracted particular attention recently is its possible electrogenicity. Evidence for the transport stoichiometry is contentious, with reports for both 2OH− (or 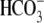 )/1Cl− electrogenic (12–14) and 1OH− (or
)/1Cl− electrogenic (12–14) and 1OH− (or 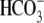 )/1Cl− electroneutral activity ((15). Heterologous expression of SLC26A6 results in a voltage-sensitive membrane current (13,14), proposed to reflect electrogenic OH− (or
)/1Cl− electroneutral activity ((15). Heterologous expression of SLC26A6 results in a voltage-sensitive membrane current (13,14), proposed to reflect electrogenic OH− (or 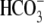 ) transfer through the carrier, although some (15) have suggested the current may not be linked directly to transport stoichiometry. It is notable that H+-equivalent influx through cardiac CHE is insensitive to large excursions of membrane potential from +80 to −80 mV, consistent with a previous report employing smaller voltage jumps of ±40 mV (6). Such voltage insensitivity can be reconciled with an electroneutral (Fig. 6) but not an electrogenic transporter (Fig. 7). The voltage range tested should have terminated or even reversed H+-equivalent flux through a 2OH− (or
) transfer through the carrier, although some (15) have suggested the current may not be linked directly to transport stoichiometry. It is notable that H+-equivalent influx through cardiac CHE is insensitive to large excursions of membrane potential from +80 to −80 mV, consistent with a previous report employing smaller voltage jumps of ±40 mV (6). Such voltage insensitivity can be reconciled with an electroneutral (Fig. 6) but not an electrogenic transporter (Fig. 7). The voltage range tested should have terminated or even reversed H+-equivalent flux through a 2OH− (or 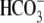 )/1Cl− exchanger, thus excluding it as the sole component of cardiac CHE.
)/1Cl− exchanger, thus excluding it as the sole component of cardiac CHE.
We investigated whether the pHi and pHo dependence of CHE may provide a clue to the carrier's underlying stoichiometry. The movement of two OH− ions per electrogenic carrier cycle (Fig. 7) could conceivably result in a higher level of 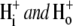 cooperativity for flux activity than for a simple electroneutral carrier (Fig. 6) that exchanged only one OH− ion per cycle. Our computational modeling, however, indicates that using substrate dependence to distinguish transport-stoichiometry may not be straightforward. The models show that the steep
cooperativity for flux activity than for a simple electroneutral carrier (Fig. 6) that exchanged only one OH− ion per cycle. Our computational modeling, however, indicates that using substrate dependence to distinguish transport-stoichiometry may not be straightforward. The models show that the steep 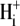 cooperativity measured experimentally for cardiac CHE may be dominated by H+ binding to an allosteric modifier site, and little affected by transport stoichiometry. Furthermore,
cooperativity measured experimentally for cardiac CHE may be dominated by H+ binding to an allosteric modifier site, and little affected by transport stoichiometry. Furthermore, 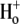 cooperativity, which should be determined largely by extracellular OH− unbinding from the carrier, is predicted in the models to vary from 1.0 for an electroneutral carrier to just under 1.5 for the electrogenic carrier. Such modest differences in cooperativity may be difficult to measure experimentally with a high degree of confidence. Nevertheless, an
cooperativity, which should be determined largely by extracellular OH− unbinding from the carrier, is predicted in the models to vary from 1.0 for an electroneutral carrier to just under 1.5 for the electrogenic carrier. Such modest differences in cooperativity may be difficult to measure experimentally with a high degree of confidence. Nevertheless, an 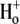 cooperativity of 0.96 was measured experimentally in this work, which would tend to support the electroneutral configuration. The cooperativity of activation of CHE by
cooperativity of 0.96 was measured experimentally in this work, which would tend to support the electroneutral configuration. The cooperativity of activation of CHE by 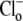 provides no additional clue as, for both types of carrier, it should equal 1.0, given that only one Cl− ion per cycle participates in each scheme. Indeed, experimentally measured
provides no additional clue as, for both types of carrier, it should equal 1.0, given that only one Cl− ion per cycle participates in each scheme. Indeed, experimentally measured 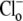 cooperativity was in this range (0.76–0.86, Fig. 4 B).
cooperativity was in this range (0.76–0.86, Fig. 4 B).
The evidence that SLC26A6 underpins CHE activity in heart is therefore equivocal. If one argues that the SLC26A6 carrier is electrogenic with a 1Cl−/2OH− (or 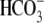 ) stoichiometry, then it should display clear voltage sensitivity, and this has not been observed for CHE in guinea-pig myocytes (Fig. 3). This could indicate either that the SLC26A6 carrier in heart is electroneutral, or that voltage sensitivity is disguised by the presence of another H+-equivalent transporter. It is of interest, therefore, that SLC26A3 gene products have been detected in murine ventricular tissue (11), in addition to SLC26A6. The protein product appears to support
) stoichiometry, then it should display clear voltage sensitivity, and this has not been observed for CHE in guinea-pig myocytes (Fig. 3). This could indicate either that the SLC26A6 carrier in heart is electroneutral, or that voltage sensitivity is disguised by the presence of another H+-equivalent transporter. It is of interest, therefore, that SLC26A3 gene products have been detected in murine ventricular tissue (11), in addition to SLC26A6. The protein product appears to support 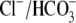 and Cl−/OH− exchange when expressed heterologously in Xenopus oocytes and HEK293 cells (11,13,14), but it is suggested to operate with an opposite transport stoichiometry to that of electrogenic SLC26A6, exchanging 1OH− (or
and Cl−/OH− exchange when expressed heterologously in Xenopus oocytes and HEK293 cells (11,13,14), but it is suggested to operate with an opposite transport stoichiometry to that of electrogenic SLC26A6, exchanging 1OH− (or 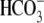 ) ion for two or more Cl− ions (13,14). This carrier cannot, by itself, account for H+-equivalent influx through cardiac CHE as, under resting physiological conditions (membrane potential at ∼–80 mV), it would be energized thermodynamically to promote H+-equivalent efflux (at pHi 7.2, ECHE would be −50 mV, see Fig. 3 B). Furthermore, there is no evidence for Cl−-sensitive acid efflux from the mammalian ventricular myocyte (17). But a 2Cl−/1OH− transporter should be voltage-sensitive and, during depolarization of the membrane potential positive to the transporter's equilibrium potential, it may reverse (see Fig. 3 B) to provide H+-equivalent influx. Thus, while H+-equivalent influx through electrogenic SLC26A6 may decrease with depolarization, influx through SLC26A3 may conceivably increase.
) ion for two or more Cl− ions (13,14). This carrier cannot, by itself, account for H+-equivalent influx through cardiac CHE as, under resting physiological conditions (membrane potential at ∼–80 mV), it would be energized thermodynamically to promote H+-equivalent efflux (at pHi 7.2, ECHE would be −50 mV, see Fig. 3 B). Furthermore, there is no evidence for Cl−-sensitive acid efflux from the mammalian ventricular myocyte (17). But a 2Cl−/1OH− transporter should be voltage-sensitive and, during depolarization of the membrane potential positive to the transporter's equilibrium potential, it may reverse (see Fig. 3 B) to provide H+-equivalent influx. Thus, while H+-equivalent influx through electrogenic SLC26A6 may decrease with depolarization, influx through SLC26A3 may conceivably increase.
As pointed out by Ko et al. (13), coexpression of electrogenic SLC26A6 and SLC26A3 gene products in the same cell membrane could result in a functionally electroneutral Cl−/OH−(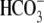 ) system that still mediated a net acid flux. For this to happen in a ventricular cell membrane, the kinetic activity and expression levels of the two opposing H+-equivalent carriers would need to be finely balanced so as to eliminate any voltage sensitivity of H+-equivalent flux. Such a balance would be remarkably fortuitous, unless coexpression and functional activity of the transporters were mechanistically coordinated in some way. Expression of the transporters was not measured in the guinea-pig ventricular myocytes used in this work. Indeed, protein expression has so far only been reported for SLC26A6 in murine ventricular myocytes (11). Nevertheless, in the latter cells, mRNA transcripts for both transporters were readily detected, but SLC26A6 expression was 100-fold greater than for SLC26A3. If sarcolemmal protein expression were to match transcript levels, it would be difficult to see how opposing flux activity in the two transporters could be balanced so precisely, particularly during rapid jumps of membrane potential. Differences, however, in transporter expression between guinea-pig and mouse cannot be excluded, especially as the functional expression of other H+-equivalent transporters, such as Na+-
) system that still mediated a net acid flux. For this to happen in a ventricular cell membrane, the kinetic activity and expression levels of the two opposing H+-equivalent carriers would need to be finely balanced so as to eliminate any voltage sensitivity of H+-equivalent flux. Such a balance would be remarkably fortuitous, unless coexpression and functional activity of the transporters were mechanistically coordinated in some way. Expression of the transporters was not measured in the guinea-pig ventricular myocytes used in this work. Indeed, protein expression has so far only been reported for SLC26A6 in murine ventricular myocytes (11). Nevertheless, in the latter cells, mRNA transcripts for both transporters were readily detected, but SLC26A6 expression was 100-fold greater than for SLC26A3. If sarcolemmal protein expression were to match transcript levels, it would be difficult to see how opposing flux activity in the two transporters could be balanced so precisely, particularly during rapid jumps of membrane potential. Differences, however, in transporter expression between guinea-pig and mouse cannot be excluded, especially as the functional expression of other H+-equivalent transporters, such as Na+-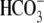 cotransport, can vary dramatically among species (22). The question of the identity of the transporters contributing to cardiac CHE activity must therefore remain open. What can be concluded is that CHE flux conforms well to an electroneutral Cl−/OH− exchanger, controlled by pHi and pHo, and this excludes sole contribution from an electrogenic SLC26A6 transporter. Given that H+-Cl− and Cl−/OH− modes of transport cannot be distinguished kinetically, the possibility must also remain that cardiac CHE in guinea-pig myocytes is mediated via a novel H+-Cl− cotransport protein.
cotransport, can vary dramatically among species (22). The question of the identity of the transporters contributing to cardiac CHE activity must therefore remain open. What can be concluded is that CHE flux conforms well to an electroneutral Cl−/OH− exchanger, controlled by pHi and pHo, and this excludes sole contribution from an electrogenic SLC26A6 transporter. Given that H+-Cl− and Cl−/OH− modes of transport cannot be distinguished kinetically, the possibility must also remain that cardiac CHE in guinea-pig myocytes is mediated via a novel H+-Cl− cotransport protein.
Proton sensor domain
The steep dependence of cardiac CHE activity on pHi (Fig. 1 and Fig. 5 B) is in contrast to the previous linear dependence reported by Leem et al. (4). This difference can be attributed to higher resolution measurements in this work, performed over a broader range of pHi values. Our computational modeling suggests that, irrespective of whether electroneutral (i.e., 1OH−) or electrogenic (i.e., 2OH−) transport is assumed, the high 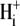 cooperativity measured experimentally for CHE cannot be simulated unless an intracellular modifier site for H+ (or OH−) ions is introduced, of pK ∼7.0 and Hill coefficient 4.0. Thus the transporter may possess two functional domains. One domain, accessed from both the internal and external environment, would mediate substrate binding and transport. Given that one of the substrates is an H+-equivalent ion, this would immediately confer some pH sensitivity on the system. For example, extracellular H+-binding to the transport domain (TD) is the main explanation in our models for the pHo sensitivity of CHE (Fig. 5 C). The other domain, accessed from only the internal environment, would mediate H+-equivalent sensing and subsequent modulation of transporter flux. H+-binding to this sensor domain (SD) in the CHE model accounts for most of the steep inhibitory effect of low pHi on CHE activity. TD and SD regions on the carrier are illustrated schematically for Cl−/OH− exchange mode in Fig. 9 B.
cooperativity measured experimentally for CHE cannot be simulated unless an intracellular modifier site for H+ (or OH−) ions is introduced, of pK ∼7.0 and Hill coefficient 4.0. Thus the transporter may possess two functional domains. One domain, accessed from both the internal and external environment, would mediate substrate binding and transport. Given that one of the substrates is an H+-equivalent ion, this would immediately confer some pH sensitivity on the system. For example, extracellular H+-binding to the transport domain (TD) is the main explanation in our models for the pHo sensitivity of CHE (Fig. 5 C). The other domain, accessed from only the internal environment, would mediate H+-equivalent sensing and subsequent modulation of transporter flux. H+-binding to this sensor domain (SD) in the CHE model accounts for most of the steep inhibitory effect of low pHi on CHE activity. TD and SD regions on the carrier are illustrated schematically for Cl−/OH− exchange mode in Fig. 9 B.
We chose to model the SD by assuming that an individual carrier molecule is inactive until its intracellular SD region is occupied by four OH− ions (or, equivalently, when four H+ ions unbind from the domain). This will occur when pHi rises from its resting value. Such a model would not preclude the siting of SD within a multimeric rather than a monomeric carrier protein. The concept of distinct SD and TD regions for a carrier has previously been proposed to account for high 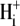 cooperativity in the activation of NHE (24,35,42–44). An alternative NHE model involves oscillating dimers whose subunits have radically different
cooperativity in the activation of NHE (24,35,42–44). An alternative NHE model involves oscillating dimers whose subunits have radically different 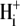 affinities (45). This latter model was not pursued in this work, because it is limited to
affinities (45). This latter model was not pursued in this work, because it is limited to 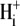 cooperativity values between 1.0 and 2.0—lower than the level of cooperativity observed for CHE.
cooperativity values between 1.0 and 2.0—lower than the level of cooperativity observed for CHE.
A low rather than a high cooperative effect of 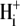 has been reported for enterocyte apical brush-border membrane CHE (16), where the Hill coefficient for
has been reported for enterocyte apical brush-border membrane CHE (16), where the Hill coefficient for 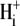 binding is 0.46. This low value was suggested to be caused by slippage of H+ transport through the carrier. The apparent difference in pHi sensitivity of cardiac and epithelial CHE is dramatic and may reflect the expression of different H+-equivalent transport molecules in the two tissues. The difference may also reflect different physiological functions for the two types of transporter, with the greater emphasis on pHi regulation for cardiac CHE. It is notable, however, that direct pHi measurements in intact cells were not made when estimating
binding is 0.46. This low value was suggested to be caused by slippage of H+ transport through the carrier. The apparent difference in pHi sensitivity of cardiac and epithelial CHE is dramatic and may reflect the expression of different H+-equivalent transport molecules in the two tissues. The difference may also reflect different physiological functions for the two types of transporter, with the greater emphasis on pHi regulation for cardiac CHE. It is notable, however, that direct pHi measurements in intact cells were not made when estimating 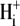 cooperativity of epithelial CHE (16). Instead, experiments were performed on BBM vesicles, where values for intravesicular pH were assumed. The possibility of errors in the estimate of epithelial CHE's pHi sensitivity should not therefore be excluded.
cooperativity of epithelial CHE (16). Instead, experiments were performed on BBM vesicles, where values for intravesicular pH were assumed. The possibility of errors in the estimate of epithelial CHE's pHi sensitivity should not therefore be excluded.
CONCLUSIONS
The transport properties of cardiac CHE are consistent with either Cl−/OH− exchange or H+-Cl− cotransport. The flux activity of CHE can be best fit by an electroneutral, voltage-insensitive mechanism, whose activity is tightly regulated by pHi and pHo. Whether CHE reflects a single type of transporter or a precisely coordinated combination of different transporters remains to be resolved. In effect, the CHE system acts like an H+-gated leak of HCl into the cell (Fig. 9 A). This leak will be particularly important in the regulation of cardiac pHi, not only during acute displacements of extracellular pH, but also during displacements of pHi from its steady state. When pHi is close to its resting value, the magnitude of CHE-mediated acid influx in the intact myocyte (Figs. 1 B and 5 B) is comparable to that through the cell's other acid-loading transporter, 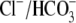 exchange, and comparable to H+-equivalent extrusion through Na+/H+ exchange and Na+-
exchange, and comparable to H+-equivalent extrusion through Na+/H+ exchange and Na+-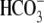 cotransport (4). H+-dependent regulation of CHE is thus an important component of the system that sets resting pHi, and hence basal function in the heart.
cotransport (4). H+-dependent regulation of CHE is thus an important component of the system that sets resting pHi, and hence basal function in the heart.
Acknowledgments
The HOE 694 was a kind gift from Dr. U. Albus, Hoescht Aktengesellschaft, Germany.
S.A.N. thanks the Maurice and Phyllis Paykel Trust and the New Zealand Tertiary Education Commission for providing funding. N.P.S. acknowledges support by the Marsden Fund of the Royal Society of New Zealand through grant No. 04-UOA-177 and the National Institute of Health, through NIH/National Institute of Biomedical Imaging and BioEngineering multiscale grant No. RO1-EB005825-01. R.D.V.-J. thanks the British Heart Foundation for funding (grant No. RG/1998012) and the Wellcome Trust (Human Physiome Program grant).
APPENDIX
Electroneutral carrier models
Here we provide a detailed derivation of the eight-state, electroneutral, independent-binding cotransporter model (Fig. 6 Biii). The remaining three electroneutral models can be derived by applying the same principles over analogous steps.
At equilibrium, the rates of transition between consecutive states in the transport cycle must be equal, resulting in the set of relations described by
 |
(9) |
KAx is the dissociation constant of ion A in compartment x (i = intracellular, o = extracellular). The value Sj is the jth state and  and
and  are the transition rates between the extracellular and intracellular space, in which the plus (+) and minus (−) symbols correspond to the clockwise and anticlockwise directions, respectively, and where j is equal to one or two when the carrier is moving Cl− out of or into the cell, respectively. The eight-state cotransporter contains four possible loops, resulting in the same thermodynamic constraint. For example, the product of the left- and right-hand side steady-state equations (see Eq. 9) for the loop S1, S3, S4, S5, S7, and S8 are equal, resulting in
are the transition rates between the extracellular and intracellular space, in which the plus (+) and minus (−) symbols correspond to the clockwise and anticlockwise directions, respectively, and where j is equal to one or two when the carrier is moving Cl− out of or into the cell, respectively. The eight-state cotransporter contains four possible loops, resulting in the same thermodynamic constraint. For example, the product of the left- and right-hand side steady-state equations (see Eq. 9) for the loop S1, S3, S4, S5, S7, and S8 are equal, resulting in
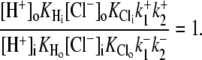 |
(10) |
Assuming that the dissociation constants are the same for both intracellular and extracellular states, and considering balanced intracellular and extracellular ion concentrations, then the thermodynamically consistent constraint is attained:
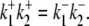 |
(11) |
Using the rapid flux transport assumption to reduce the model to two states, representing the intracellular (Si) and extracellular (So) conformations, leads to
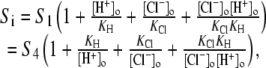 |
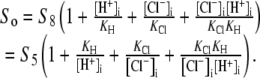 |
(12) |
The rate of transition between the two states can then be described by combining Eqs. 9 and 12 to define the rates 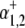 and
and 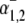 in the anticlockwise and clockwise directions, respectively:
in the anticlockwise and clockwise directions, respectively:
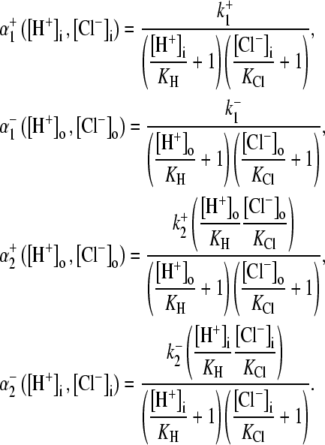 |
(13) |
At steady state,
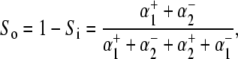 |
(14) |
resulting in a steady-state flux of
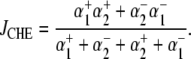 |
(15) |
Allosteric inhibition is characterized by the addition of a Hill scaling factor, such that the flux with allosteric effects is
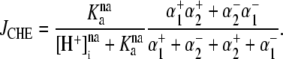 |
(16) |
This allosteric mechanism assumes that when an H+ sensor site, with a binding affinity of Ka and cooperativity of na, is occupied by H+ ions, the transporter is unable to function.
With each of the four models proposed, the transporter is described by Eq. 16 with the definition of the α-values changing with each model. The definition of α for the six-state (with [Cl−]o-[H+]o binding and [H+]i-[Cl−]i unbinding order) state cotransporter and the six- and eight-state exchangers are defined in Eqs. 17–19, respectively. The six-state cotransporter (see Fig. 6 Bii) α-values are
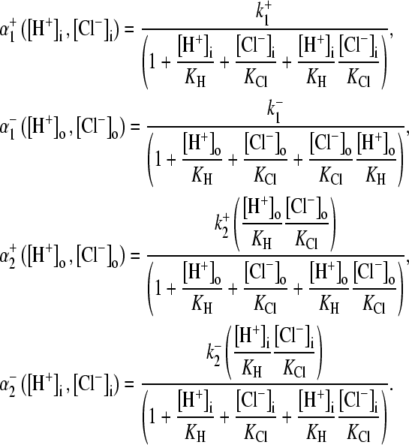 |
(17) |
The six-state exchanger (see Fig. 6 Aii) α-values are
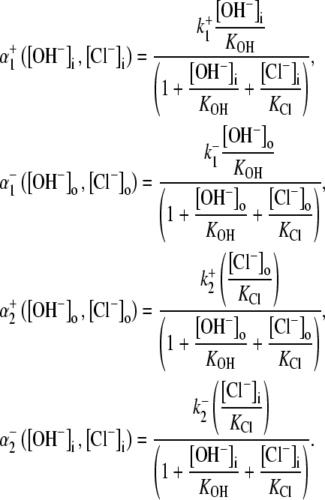 |
(18) |
The eight-state exchanger (see Fig. 6 Aiii) α-values are
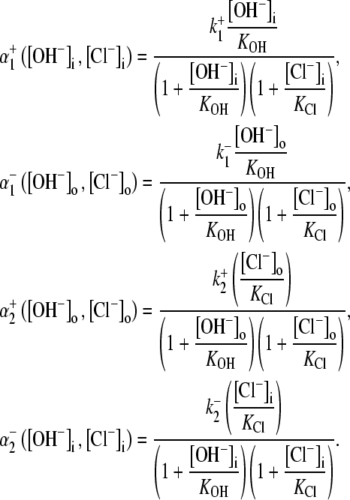 |
(19) |
The eight-state exchanger and the eight-state cotransporter are mathematically identical; this can be shown by making the substitution [OH−]/KOH = KH/[H+] into Eq. 19, which is then equal to Eq. 13.
Electrogenic carrier models
In electrogenic models, two OH− ions are exchanged for one Cl− (see Fig. 8), or two H+ ions are cotransported with one Cl− ion across the membrane. As these carriers are electrogenic, the flux through the carrier will be voltage-dependent. Voltage dependence of cyclical carrier models can be represented by including a voltage-dependent model parameter (46). As the voltage changes experienced during experiments are likely to be nominal, we assumed that any voltage-dependent model parameter will remain constant. Because of this, we were able to simplify the model by removing voltage from the thermodynamic constraints of the system. This is energetically valid, provided ECHE > Vm, as will have been the case for the simulations shown in this work. Inclusion of voltage in the thermodynamics of the model will, however, be required if it is to be extended to a more general case. The electrogenic model equations were derived using the same method as for the electroneutral models, ignoring any charge movement. The α-values for the 12-state exchanger are given in
 |
(20) |
The 12-state cotransporter α-values are
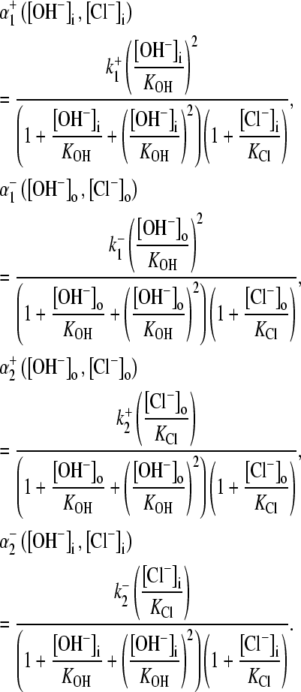 |
(21) |
Fitting the model
The eight-state model parameters were fitted in three phases. First, the Hill equations, with the Hill coefficient rounded to one, were fit to the two [Cl−]o dependent data sets, recorded at two pHo values (see Fig. 4 B). The eight-state model equations were then manipulated to give algebraic definitions of Vmax (Eq. 23) and Km (Eq. 22). Rearranging these equations, and using the thermodynamic consistency equation (Eq. 11), gave algebraic definitions of KH, KCl, 
 and
and 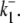 In the third phase, the sole remaining parameter
In the third phase, the sole remaining parameter 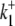 was fit to the pHi/pHo-dependent data (see Fig 5). This method allows us to calculate a unique parameter set for the model:
was fit to the pHi/pHo-dependent data (see Fig 5). This method allows us to calculate a unique parameter set for the model:
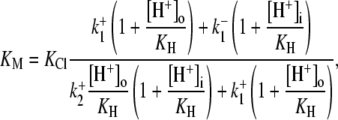 |
(22) |
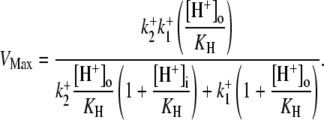 |
(23) |
Editor: David S. Weiss.
References
- 1.Choi, H. S., A. W. Trafford, C. H. Orchard, and D. A. Eisner. 2000. The effect of acidosis on systolic Ca2+ and sarcoplasmic reticulum calcium content in isolated rat ventricular myocytes. J. Physiol. 529:661–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bountra, C., and R. Vaughan-Jones. 1989. Effect of intracellular and extracellular pH on contraction in isolated, mammalian cardiac muscle. J. Physiol. 418:163–187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Komukai, K., F. Brette, C. Pascarel, and C. H. Orchard. 2002. Electrophysiological response of rat ventricular myocytes to acidosis. Am. J. Physiol. Heart Circ. Physiol. 283:H412–H422. [DOI] [PubMed] [Google Scholar]
- 4.Leem, C. H., D. Lagadic-Gossmann, and R. D. Vaughan-Jones. 1999. Characterization of intracellular pH regulation in the guinea-pig ventricular myocyte. J. Physiol. 517:159–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Poole, R. C., and A. P. Halestrap. 1993. Transport of lactate and other monocarboxylates across mammalian plasma membranes. Am. J. Physiol. Cell Physiol. 264:C761–C782. [DOI] [PubMed] [Google Scholar]
- 6.Sun, B., C. H. Leem, and R. D. Vaughan-Jones. 1996. Novel chloride-dependent acid loader in the guinea-pig ventricular myocyte: part of a dual acid-loading mechanism. J. Physiol. 495:65–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Leem, C. H., and R. D. Vaughan-Jones. 1998. Sarcolemmal mechanisms for pHi recovery from alkalosis in the guinea-pig ventricular myocyte. J. Physiol. 509:487–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ryan, K. D., R. L. Skolnick, and K. W. Spitzer. 1998. Endothelin-1 stimulates C1−/OH− exchange in ventricular myocytes. Biophys. J. 74:A160. [Google Scholar]
- 9.Leem, C. H. and R. D. Vaughan-Jones. 1997. Chloride-hydroxyl exchange in the guinea-pig ventricular myocyte: no role for bicarbonate. J. Mol. Cell. Cardiol. 29:2483–2489. [DOI] [PubMed] [Google Scholar]
- 10.Alper, S. L. 2006. Molecular physiology of SLC4 anion exchangers. Exp. Physiol. 91:153–161. [DOI] [PubMed] [Google Scholar]
- 11.Alvarez, B. V., D. M. Kieller, A. L. Quon, D. Markovich, and J. R. Casey. 2004. SLC26A6: a cardiac chloride-hydroxyl exchanger and predominant chloride-bicarbonate exchanger of the mouse heart. J. Physiol. 561:721–734. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xie, Q., R. Welch, A. Mercado, M. F. Romero, and D. B. Mount. 2002. Molecular characterization of the murine SLC26A6 anion exchanger: functional comparison with SLC26A1. Am. J. Physiol. 283:F826–F838. [DOI] [PubMed] [Google Scholar]
-
13.Ko, S. B. H., N. Shcheynikov, J. Y. Choi, X. Luo, K. Ishibashi, P. J. Thomas, J. Y. Kim, K. H. Kim, M. G. Lee, S. Naruse, and S. Muallem. 2002. A molecular mechanism for aberrant CFTR-dependent
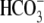 transport in cystic fibrosis. EMBO J. 21:5662–5672. [DOI] [PMC free article] [PubMed] [Google Scholar]
transport in cystic fibrosis. EMBO J. 21:5662–5672. [DOI] [PMC free article] [PubMed] [Google Scholar] -
14.Shcheynikov, N., Y. Wang, M. Park, S. B. H. Ko, M. Dorwart, S. Naruse, P. J. Thomas, and S. Muallem. 2006. Coupling modes and stoichiometry of
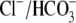 exchange by SLC26A3 and SLC26A6. J. Gen. Physiol. 127:511–524. [DOI] [PMC free article] [PubMed] [Google Scholar]
exchange by SLC26A3 and SLC26A6. J. Gen. Physiol. 127:511–524. [DOI] [PMC free article] [PubMed] [Google Scholar] - 15.Chernova, M. N., L. Jiang, D. J. Friedman, R. B. Darman, H. Lohi, J. Kere, D. H. Vandorpe, and S. L. Alper. 2005. Functional comparison of mouse SLC26A6 anion exchanger with human SLC26A6 polypeptide variants: differences in anion selectivity, regulation, and electrogenicity. J. Biol. Chem. 280:8564–8580. [DOI] [PubMed] [Google Scholar]
- 16.Alvarado, F., and M. Vasseur. 1996. Theoretical and experimental discrimination between Cl−-H+ symporters and Cl−/OH− antiporters. Am. J. Physiol. 40:C1612–C1628. [DOI] [PubMed] [Google Scholar]
- 17.Lagadic-Gossmann, D., K. J. Buckler, and R. D. Vaughan-Jones. 1992. Role of bicarbonate in pH recovery from intracellular acidosis in the guinea-pig ventricular myocyte. J. Physiol. 458:361–384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Thomas, J. A., R. N. Buchsbaum, A. Zimniak, and E. Racker. 1979. Intracellular pH measurements in Ehrlich ascites tumor-cells utilizing spectroscopic probes generated in situ. Biochemistry. 18:2210–2218. [DOI] [PubMed] [Google Scholar]
- 19.Kleyman, T. R., and E. J. Cragoe. 1988. Amiloride and its analogs as tools in the study of ion transport. J. Membr. Biol. 105:1–21. [DOI] [PubMed] [Google Scholar]
- 20.Zaniboni, M., P. Swietach, A. Rossini, T. Yamamoto, K. W. Spitzer, and R. D. Vaughan-Jones. 2003. Intracellular proton mobility and buffering power in cardiac ventricular myocytes from rat, rabbit, and guinea-pig. Am. J. Physiol. 285:H1236–H1246. [DOI] [PubMed] [Google Scholar]
- 21.Swietach, P., and R. D. Vaughan-Jones. 2005. Relationship between intracellular pH and proton mobility in rat and guinea-pig ventricular myocytes. J. Physiol. 566:793–806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yamamoto, T., P. Swietach, A. Rossini, S. H. Loh, R. D. Vaughan-Jones, and K. W. Spitzer. 2005. Functional diversity of electrogenic sodium-bicarbonate cotransport in ventricular myocytes from rat, rabbit and guinea-pig. FASEB J. 19:A1632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fozzard, H. A., and C. O. Lee. 1976. Influence of changes in external potassium and chloride ions on membrane potential and intracellular potassium ion activity in rabbit ventricular muscle. J. Physiol. 256:663–689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Aronson, P. S., J. Nee, and M. A. Suhm. 1982. Modifier role of internal H+ in activating the Na+-H+ exchanger in renal microvillus membrane-vesicles. Nature. 299:161–163. [DOI] [PubMed] [Google Scholar]
- 25.Clemo, H. F., J. J. Feher, and C. M. Baumgarten. 1992. Modulation of rabbit ventricular cell volume and Na+/K+/2Cl− cotransport by cGMP and atrial natriuretic factor. J. Gen. Physiol. 100:89–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Terashima, K., A. Takeuchi, N. Sarai, S. Matsuoka, E. B. Shim, C. H. Leem, and A. Noma. 2006. Modeling Cl− homeostasis and volume regulation of the cardiac cell. Phil. Trans. Roy. Soc. A. Math. Phys. Eng. Sci. 364:1245–1265. [DOI] [PubMed] [Google Scholar]
- 27.Vaughan-Jones, R. D. 1979. Regulation of chloride in quiescent sheep-heart Purkinje fibers studied using intracellular chloride and pH-sensitive micro-electrodes. J. Physiol. 295:111–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vaughan-Jones, R. D. 1986. An investigation of chloride-bicarbonate exchange in the sheep cardiac Purkinje fiber. J. Physiol. 379:377–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Carmeliet, E. E. 1961. Chloride ions and the membrane potential of Purkinje fibers. J. Physiol. 156:375–388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Swietach, P., C. H. Leem, K. W. Spitzer, and R. D. Vaughan-Jones. 2005. Experimental generation and computational modeling of intracellular pH gradients in cardiac myocytes. Biophys. J. 88:3018–3037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.van Beaumont, W., J. C. Strand, J. S. Petrofsky, S. G. Hipskind, and J. E. Greenleaf. 1973. Changes in total plasma content of electrolytes and proteins with maximal exercise. J. Appl. Physiol. 34:102–106. [DOI] [PubMed] [Google Scholar]
- 32.Vaughan-Jones, R., and K. Spitzer. 2002. Role of bicarbonate in the regulation of intracellular pH in the mammalian ventricular myocyte. Biochem. Cell Biol. 80:579–596. [DOI] [PubMed] [Google Scholar]
-
33.Rajendran, V. M., and H. J. Binder. 1993. Cl−-
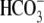 and Cl−-OH− exchanges mediate Cl− uptake in apical membrane-vesicles of rat distal colon. Am. J. Physiol. 264:G874–G879. [DOI] [PubMed] [Google Scholar]
and Cl−-OH− exchanges mediate Cl− uptake in apical membrane-vesicles of rat distal colon. Am. J. Physiol. 264:G874–G879. [DOI] [PubMed] [Google Scholar] - 34.Liedtke, C. M., and U. Hopfer. 1982. Mechanism of Cl− translocation across small intestinal brush-border membrane. 2. Demonstration of Cl−-OH− exchange and Cl− conductance. Am. J. Physiol. 242:G272–G280. [DOI] [PubMed] [Google Scholar]
- 35.Jean, T., C. Frelin, P. Vigne, P. Barbry, and M. Lazdunski. 1985. Biochemical properties of the Na+/H+ exchange system in rat brain synaptosomes. Interdependence of internal and external pH control of the exchange activity. J. Biol. Chem. 260:9678–9684. [PubMed] [Google Scholar]
- 36.Wu, M.-L., and R. D. Vaughan-Jones. 1997. Interaction between Na+ and H+ ions on Na+-H+ exchange in sheep cardiac Purkinje fibers. J. Mol. Cell. Cardiol. 29:1131–1140. [DOI] [PubMed] [Google Scholar]
- 37.Liu, D., S. D. Kennedy, and P. A. Knauf. 1996. Source of transport site asymmetry in the Band 3 anion exchange protein determined by NMR measurements of external Cl− affinity. Biochemistry. 35:15228–15235. [DOI] [PubMed] [Google Scholar]
- 38.Stein, W. D. 1986. Transport and Diffusion Across Cell Membranes. Academic Press, San Diego, CA.
- 39.Papageorgiou, P., B. E. Shmukler, A. K. Stuart-Tilley, L. Jiang, and S. L. Alper. 2001. AE anion exchangers in atrial tumor cells. Am. J. Physiol. 280:H937–H945. [DOI] [PubMed] [Google Scholar]
- 40.Knauf, F., C.-L. Yang, R. B. Thomson, S. A. Mentone, G. Giebisch, and P. S. Aronson. 2001. Identification of a chloride-formate exchanger expressed on the brush border membrane of renal proximal tubule cells. Proc. Natl. Acad. Sci. USA. 98:9425–9430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Waldegger, S., I. Moschen, A. Ramirez, R. J. H. Smith, H. Ayadi, F. Lang, and C. Kubisch. 2001. Cloning and characterization of SLC26A6, a novel member of the solute carrier 26 gene family. Genomics. 72:43–50. [DOI] [PubMed] [Google Scholar]
- 42.Vaughan-Jones, R. D., and M. L. Wu. 1990. Extracellular H+ inactivation of Na+-H+ exchange in the sheep cardiac Purkinje fiber. J. Physiol. 428:441–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Green, J., D. T. Yamaguchi, C. R. Kleeman, and S. Muallem. 1988. Cytosolic pH regulation in osteoblasts. Interaction of Na+ and H+ with the extracellular and intracellular faces of the Na+/H+ exchanger. J. Gen. Physiol. 92:239–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wakabayashi, S., T. Hisamitsu, T. X. Pang, and M. Shigekawa. 2003. Kinetic dissection of two distinct proton binding sites in Na+/H+ exchangers by measurement of reverse mode reaction. J. Biol. Chem. 278:43580–43585. [DOI] [PubMed] [Google Scholar]
- 45.Lacroix, J., M. Poet, C. Maehrel, and L. Counillon. 2004. A mechanism for the activation of the Na+/H+ exchanger NHE-1 by cytoplasmic acidification and mitogens. EMBO Rep. 5:91–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Smith, N. P., and E. J. Crampin. 2004. Development of models of active ion transport for whole-cell modeling: cardiac sodium-potassium pump as a case study. Prog. Biophys. Mol. Biol. 85:387–405. [DOI] [PubMed] [Google Scholar]