Investigations of Vibrational Coherence in the Low-Frequency Region of Ferric Heme Proteins

Abstract

Femtosecond coherence spectroscopy is applied to a series of ferric heme protein samples. The low-frequency vibrational spectra that are revealed show dominant oscillations near 40 cm⁻¹. MbCN is taken as a typical example of a histidine-ligated, six-coordinate, ferric heme and a comprehensive spectroscopic analysis is carried out. The results of this analysis reveal a new heme photoproduct species, absorbing near 418 nm, which is consistent with the photolysis of the His⁹³ axial ligand. The photoproduct undergoes subsequent rebinding/recovery with a time constant of ∼4 ps. The photoproduct lineshapes are consistent with a photolysis quantum yield of 75–100%, although the observation of a relatively strong six-coordinate heme coherence near 252 cm⁻¹ (assigned to ν₉ in the MbCN Raman spectrum) suggests that the 75% lower limit is much more likely. The phase and amplitude excitation profiles of the low-frequency mode at 40 cm⁻¹ suggest that this mode is strongly coupled to the MbCN photoproduct species and it is assigned to the doming mode of the transient penta-coordinated material. The absolute phase of the 40 cm⁻¹ mode is found to be π/2 on the red side of 418 nm and it jumps to 3π/2 as excitation is tuned to the blue side of 418 nm. The absolute phase of the 40 cm⁻¹ signal is not explained by the standard theory for resonant impulsive stimulated Raman scattering. New mechanisms that give a dominant momentum impulse to the resonant wavepacket, rather than a coordinate displacement, are discussed. The possibilities of heme iron atom recoil after photolysis, as well as ultrafast nonradiative decay, are explored as potential ways to generate the strong momentum impulse needed to understand the phase properties of the 40 cm⁻¹ mode.

INTRODUCTION

Heme proteins are involved in a wide variety of biologically important processes such as electron transfer, signaling, catalysis, and transport of small ligands. These proteins are a ubiquitous presence in living organisms and the heme prosthetic group, Fe protoporphyrin IX (FePPIX), found at the active site of this class of biomolecules, is intimately involved in their various functions. In many circumstances, the heme iron atom cycles through a variety of oxidation, spin, and/or coordination states. Depending on the specific protein, the central iron atom explores oxidation states from +2 to +4, while the iron coordination in native proteins is typically 5 or 6, with one or two axial ligands, along with the four porphyrin nitrogens.

Heme systems have been the target of intense research that is traditionally focused on the relationship between structure and function and on the role of dynamics (1–38). Protein dynamics focuses both on the larger-scale evolution between different protein conformations and on the smaller (usually sub-Ångstrom) length-scales that are involved in movement along the chemical reaction coordinate associated with changes in electronic state (e.g., oxidation, reduction, spin reconfiguration, bond cleavage, and bond formation). The aspect of the dynamics that generates electronic state changes generally involves vibrational modes, and the study of such modes allows us determine the reaction coordinates and increases our understanding of how structure relates to function.

Frequency domain vibrational spectroscopies such as infrared and Raman spectroscopy are useful tools in studies of the higher frequencies, but generally are not able to probe vibrational modes of biomolecules in aqueous solution that appear at <200 cm⁻¹. In most cases, protein reactions involve transitions that go over reaction barriers through thermally driven fluctuations. Since k_BT ∼200 cm⁻¹ (at room temperature), we expect that important functionally reactive modes exist within the 0–200 cm⁻¹ range where it is difficult to observe them experimentally. These low-frequency vibrational modes can be delocalized and involve many nuclei. In principle, such modes can be involved in the rapid transfer of energy between distant protein sites (39) (allosteric interactions). In addition, out-of-plane motions of the heme group are also expected to fall within this range (39–47) and the protein-induced distortions of the heme can activate or prime certain key low-frequency modes to tune the reactivity of the protein (19,48–50).

To achieve a better understanding of the reaction mechanisms of heme proteins, we have begun to systematically compare different proteins using femtosecond coherence spectroscopy (FCS), which offers a reliable means to resolve vibrational spectral content at <200 cm⁻¹. In contrast to previous studies (35,51–68) involving diatomic ligands (CO, NO, O₂) bound to ferrous myoglobin (Mb), we report here on studies involving ferric heme proteins, which are equilibrium samples not expected to undergo photon-driven dissociation reactions.

There is a large subset of heme systems that are ferric in their native state (cytochromes, peroxidases, etc.) and this study is motivated by the desire to document the low-frequency dynamics of six coordinated ferric systems. We do this with emphasis on metMb and its cyanide derivative (MbCN) as representatives of typical histidine-ligated hexa-coordinated ferric heme systems. There are a number of prior biophysical studies on these complexes, both experimental (69–72) and theoretical (73). We choose these proteins for more intensive study using FCS because the samples are easily available as homogeneous biochemical preparations, have well-characterized spin and coordination states, and are quite stable.

FCS is an ultrafast pump-probe technique that employs the bandwidth of femtosecond laser pulses to create and subsequently detect coherent vibrational motions in the sample of interest. The theoretical basis of this time-domain spectroscopy can be found elsewhere (74–82), so the details are not discussed here. However, one important theoretical aspect of the experiments is that, in principle, coherences can be created on both the excited- and ground-state potential energy surfaces. In the case of heme π-π* excited states (Soret band), the lifetimes are so short (∼10–20 fs) (83–87) that the excited-state coherences are not sustained or observed. In contrast, for molecules with long-lived excited states, the excited-state coherences are dominant (88,89) as expected theoretically (77). If ultrafast photophysical processes take place in the sample (e.g., ultrafast ligand dissociation), then the resulting product ground state can be considered for many purposes as a long-lived excited state.

The cyanide anion (CN⁻) binds to the high-spin ferric heme of metMb with very high affinity, displacing the water ligand, and forming a low-spin structure. On the other hand, CN⁻ rarely binds to ferrous hemes, although binding is reported for reduced horseradish peroxidase (71). Infrared (IR) measurements on metMbCN provide conclusive evidence for CN binding as metal cyanide (Fe-CN) as opposed to HCN being the ligand (71). These spectroscopic studies suggest a tilted rather than a bent geometry for the bound CN ligand (71) and also indicate the existence of a hydrogen bond between the bound CN and a distal side amino-acid residue, presumably a histidine (71). Temperature dependent polarized Raman measurements have also been used to suggest that the hexacoordinate low-spin heme group is domed (70). More recent time-resolved measurements on MbCN have reported that, on a picosecond timescale, the spectral evolution is very similar to that of ferrous proteins (69). These time-resolved IR and visible absorption measurements suggest that recovery of the fully ligated electronic ground state occurs on a 3–4 ps timescale and either CN photolysis or d-d iron excited states are proposed as the possible intermediates on the path to ground-state recovery (69). Recent numerical simulations have been carried out to help clarify which intermediate is most likely, and the calculations suggest that CN photolysis is an unlikely source of the observed transient spectral changes (73), leaving d-d excited-state decay as the suggested source of the observed 3–4 ps ground-state recovery time.

In this work we first present an overview of the low-frequency heme modes in ferric heme proteins. The main emphasis is placed on metMb, particularly metMbCN, and we report the low-frequency spectra of these species. The phase and amplitude excitation profiles of MbCN reveal surprising structure and the absolute phase of the strong low-frequency mode at 40 cm⁻¹ suggests a novel momentum transfer mechanism for resonant excitation of coherent motion. To explain the 40 cm⁻¹ mode amplitude and phase-excitation profiles, the issue of MbCN ligand photolysis (either CN or His⁹³) is revisited, leading us to suggest that the proximal histidine is the dissociable ligand. This suggestion also helps to explain a variety of other spectroscopic observations (69).

MATERIALS AND METHODS

Sample preparation

Horse heart myoglobin was purchased from Sigma (St. Louis, MO) as lyophilized salt-free powder and used without further purification. For FCS measurements the protein was dissolved in phosphate buffer solution (0.1 M, pH = 7.5). The concentration was adjusted so that the sample's optical density at the pump wavelength was between 0.7 and 1.0 O.D. in a 1-mm pathlength spinning sample cell. Given the large range of the excitation wavelengths employed for excitation profile measurements (from 400 nm to 438 nm), the final protein concentration was between 100 and 150 μM. The CN-ligated complex was prepared by adding small aliquots of concentrated (1 M) potassium cyanide (KCN) to the dissolved protein solution. The formation of the CN complex was monitored by optical absorption measurements in a model No. U-3410 (Hitachi, Tokyo, Japan) spectrophotometer to insure that the process was complete. The final sample was then transferred into the spinning cell, thoroughly insulated, and then moved to the cell holder for ultrafast spectroscopic measurements. Optical absorption spectra were taken before and after FCS experiments to insure that the integrity of the sample was maintained during the experiments.

FCS laser system

The laser system consists of a tunable (750–960 nm) Ti-Sapphire oscillator (MIRA 900; Coherent, Santa Clara, CA) pumped by a diode laser (Verdi 10; Coherent). The oscillator was able to generate 50–100 fs pulses at a repetition rate of 76 MHz with energy of ∼10 nJ/pulse. To resonantly excite the samples in the Soret band, the IR output of the laser was frequency-doubled in a 250 μm β-barium borate crystal and then chirp-compensated by a pair of SF10 prisms to within 10% of the transform-limit time-bandwidth product. Subsequently, the laser light was split into a pump arm and a probe arm, with a power ratio of 2:1 between the two. The pump beam was modulated using an acousto-optic modulator (Neos Technologies, Melbourne, FL) at 1.5 MHz. Before entering the sample, the pump and probe beam polarizations were adjusted to be perpendicular to one another. The time delay between the pump and probe pulse was controlled by a Klinger translation stage (Newport, Irvine, CA) in steps of 1 μm (6.66 fs in time domain). Both beams were focused into the spinning sample cell using a three-inch achromatic lens in a near-parallel geometry. After the sample, the beams were recollimated and the pump light was spatially blocked (using a pinhole) and extinguished by a polarization analyzer that only allowed the probe light to pass. The detection step of the experimental procedure allowed us to focus on different ranges of the coherent signal (77,90,91). In an open-band detection scheme we employed a photodiode to measure the entire spectral bandwidth of the pulse probe. This kind of measurement leads to a better resolution of lower frequency modes in the range 20–100 cm⁻¹. The detuned or dispersed detection scheme used a monochromator to select a portion of the probe bandwidth away from the carrier frequency of the probe pulse. Since the third-order polarization oscillates at the optical carrier frequency ± the vibrational coherence frequency, this configuration selectively detects the higher frequency modes in the coherent signal (77,90,91) with improved reliability in the ∼200–400 cm⁻¹ region. The detuned FCS results allow direct comparison with frequency domain techniques like Raman spectroscopy.

FCS data analysis

The experimental data have components arising from electronic and vibrational population transfer as well as vibrational coherence. In resonance, the population decay is usually the dominant component and it can often be represented by a distribution of exponentials. Although it carries important information regarding various dynamic processes (cooling, lineshape dynamics, ligand rebinding kinetics, etc.), this component is removed to reveal the residual coherence signal. Due to its amplitude (generally approximately two orders-of-magnitude larger than the coherence signal) special precautions have to be taken for the fitting procedure.

The data analysis follows a sequential approach. We first employ a maximum entropy method algorithm to fit the nonoscillatory part of the signal because this method does not make assumptions regarding the number of exponentially decaying processes (92). The residual signal left after the removal of the nonoscillatory decay involves the coherences that arise from the superposition of vibrational states coupled to the resonant electronic excitation. This signal typically damps within a few picoseconds due to dephasing mechanisms and sample inhomogeneities so it is fitted to a sum of damped cosine functions using a linear predictive single-value decomposition (LPSVD) algorithm. There are a few parameters that can be controlled during the LPSVD fitting procedure, such as the number of oscillations or the time-domain range of the data. Given the fact that a small amount of noise is always present in the experimental data, we use the low frequencies observed in the Raman spectrum to help avoid over- or underfitting of the data.

Thus, we first analyze the detuned data (which optimizes the detection of the higher frequencies within the pulse bandwidth) to make sure that the global fitting parameters (such as the number of oscillators, noise level, and time-domain range of the data) optimize the correlation with the frequencies determined independently from the Raman spectrum. The power spectra obtained from the detuned measurements generally extend below 200 cm⁻¹, which represents the lower-limit cutoff for Raman measurements. After analysis of the detuned data, we consider the open-band experiment and compare the frequencies in the overlapping regions. Examination of the data from numerous independent samples has generally produced strong correlations between the frequencies extracted using the three experimental conditions (Raman, detuned FCS, and open-band FCS). However, we have noticed that data from protein samples have better signal/noise than heme model compounds because the damping timescale of the coherence signal is significantly longer in the protein environment. As a result, the correlations of the FCS and Raman spectra are generally better in proteins than for heme model compounds.

Quantum yield and continuum measurements

The transient spectra of MbCN in the Soret band region were generated by employing an amplified Ti:Sapphire laser system (REGA 9000, Coherent) with white-light continuum generation. The system generates 50-fs laser pulses at 800 nm with a repetition rate of 250 kHz and an average power of ∼1 W. The laser light was passed through a beam splitter and one of the beams feeds an optical parametric amplifier (OPA 9400, Coherent) to get pulses centered at 580 nm used for pumping the sample. The other beam was used for generating a probe pulse continuum in a spinning fused silica disk. The OPA pulses were compressed by a pair of SF10 prisms to ∼50 fs and then both pump and probe pulses were focused into the spinning-sample cell using a 2-inch focal length achromatic lens. The time delay between pump and probe pulses was controlled by a motorized translation stage (Melles Griot, Albuquerque, NM). The transient absorption data were collected by an optical multichannel analyzer connected to a diode array (Princeton Instruments, Trenton, NJ) mounted on the axial port of a monochromator. A shutter (Uniblitz, Rochester, NY) alternately blocks and unblocks the pump beam so that a reference spectrum is recorded along with the pump-induced transient spectrum.

Trial absorption spectra of the transient product states of MbCN are constructed by adding scaled amounts of the equilibrium reactant spectrum to the transient difference spectra until the bleaching component is eliminated. The scaling factors are determined by comparison with MbCO, which is known to undergo photolysis with 100% quantum yield (35,93,94). Measurements on the MbCO sample (not shown) were conducted under identical experimental conditions (same sample cell, same excitation conditions). By scaling the difference absorption spectrum between deoxyMb and MbCO to the transient absorption, we find that 6.5% of MbCO molecules in the sample volume undergo pump pulse photolysis. The MbCN sample was excited under the same conditions and, by taking into account the difference in the absorption of the samples across the pump pulse bandwidth (i.e., integrating the absorption cross section over the range where the pump has nonzero intensity), we calculate that 20% more molecules of MbCN are photoexcited when compared to the MbCO sample. Thus, the photoexcited fraction of MbCN in the illuminated volume is 7.8%. For the fitting procedure in Fig. 9, we used the transient data measured at 0.5 ps so the survival fraction of the photoproduct, exp(−0.5 ps/4 ps) ∼0.9, has slightly diminished. This means that a 100% ligand dissociation quantum yield (Y_L) corresponds to summing ∼7% of the equilibrium MbCN spectrum with the 0.5 ps transient difference spectrum to remove the bleaching signal of the equilibrium MbCN that has been photoexcited. Subsequent trial photoproduct absorption curves, corresponding to Y_L<100%, were generated by adding correspondingly smaller amounts of the equilibrium MbCN spectrum to the transient spectrum. The estimated error in this calculation is ∼10–20%.

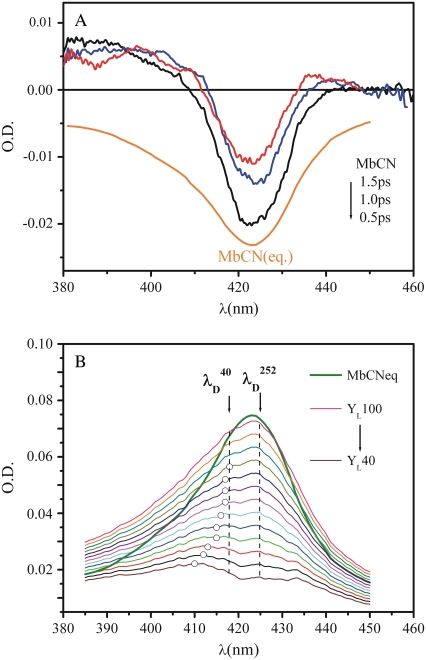
FIGURE 9.

(A) Transient continuum absorption measurements (0.5 ps, 1.0 ps, 1.5 ps) of MbCN taken using a 580 nm pump wavelength. The equilibrium absorption spectra of MbCN is presented for reference because it corresponds to the bleaching component of the transient signal. The continuum spectra were gently smoothed using a Fourier filter to remove high-frequency noise. (B) A series of product state line shapes found by addition of the scaled equilibrium MbCN absorption to the transient difference spectrum at 0.5 ps. Different scaling assumes different amounts of ligand photolysis. The resulting photoproduct line shapes are subsequently fitted with a sum of two Gaussian functions: one, corresponding to the hot six-coordinate MbCN species is allowed to have variable amplitude but the peak wavelength is held fixed at 425 nm with a FWHM = 31 nm. The other, corresponding to the photolyzed material, is allowed to vary all parameters (amplitude, central wavelength, and FWHM). The open circles correspond to the central wavelength of the fitted photoproduct band. The dashed lines at 418 nm and 425 nm correspond to the minima of the 40 cm⁻¹ and the 252 cm⁻¹ coherence amplitudes as obtained from the FCS data. These positions correspond to the peaks of the underlying Soret resonances that couple to the respective modes. The equilibrium spectrum of MbCN is also displayed as a solid green curve for reference.

Resonance Raman measurements

Resonance Raman spectra were generated by employing a standard Raman setup with a 90° light-collection geometry and a single grating monochromator (model No. 1870B; Spex Industries, Edison, NJ). To correctly measure the intensity of the polarized scattered light an optical scrambler was inserted in front of the monochromator. The monochromator output is coupled to a liquid-nitrogen-cooled charge-coupled device (Princeton Instruments). An interferometric notch filter (Kaiser Optical Systems, Ann Arbor, MI) was used to extinguish the laser light and improve the system performance over the low-frequency domain of Raman shifts. Samples were excited with ∼5 mW of the 413.1-nm line generated by a krypton laser (Innova 300, Coherent). A standard quartz cuvette (NSG Precision Cells, Farmingdale, NY) was used for the experimental Raman measurements.

RESULTS

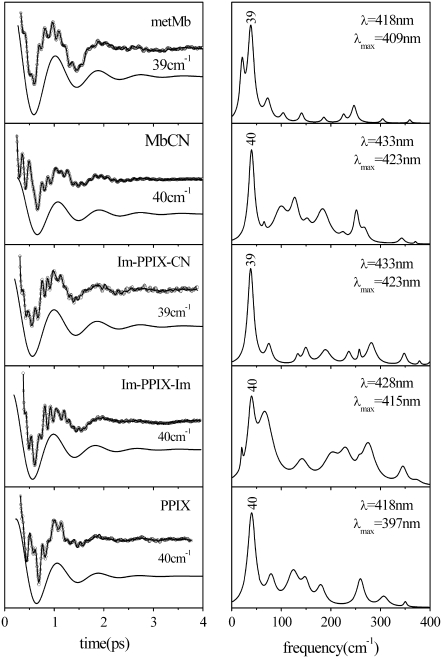
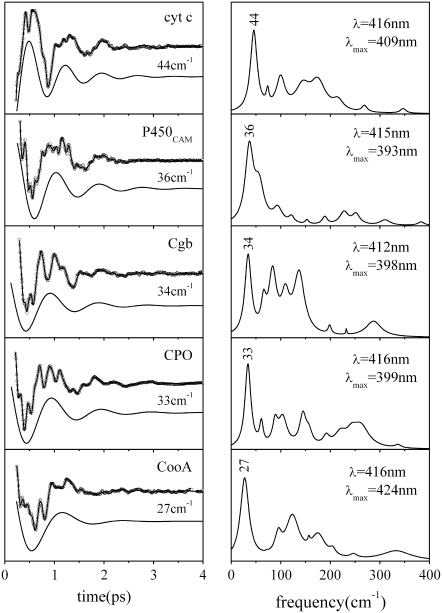
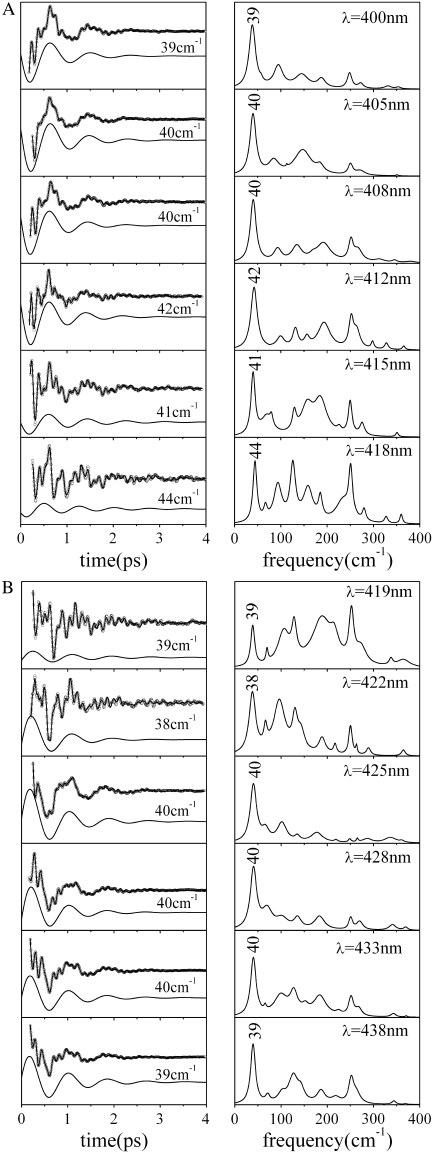
The FCS spectra of most of the ferric systems investigated to date are dominated by a feature that shows up between 25 and 45 cm⁻¹ in the power spectrum. Figs. 1 and 2 display a series of FCS experiments (left panels) and the corresponding LPSVD fit and transform to the frequency domain spectra (right panels). For ferric Mb samples and related model compounds based on Fe³⁺-PPIX (denoted as PPIX in Fig. 1), the principal mode reliably shows up at 40 ± 2 cm⁻¹ and it is easily recognizable even in the raw data due to its large amplitude (the displaced solid curves in the left panels show the LPSVD components for this mode). In other ferric systems the most intense mode appears at frequencies as high as 44 cm⁻¹ (cyt c) or as low as 27 cm⁻¹ (CooA) (Fig. 2). This apparent protein specificity suggests that axial ligation and protein-induced deformation of the heme geometry are the main factors responsible for the variation in frequencies. The underlying source of the frequency sensitivity will be more thoroughly explored in separate investigations. At this point, we simply want to emphasize the motivation for more detailed investigations of low-frequency modes in ferric systems.

FIGURE 1.

The open-band coherence spectra of ferric metMb and Fe³⁺PPIX model systems. The left panels show the oscillatory components and the LPSVD fits (solid curves through data). The LPSVD components corresponding to the dominant mode near 40 cm⁻¹ are displaced below (the phase for this mode is found to be ∼π/2 ± π/8 for all samples). The right panels show the corresponding power spectra. The pump/probe excitation wavelengths and Soret peak (λ_max) of each sample are given in the right panels.

FIGURE 2.

The open-band coherence spectra of five different ferric heme protein systems. The left panels show the oscillatory components and the LPSVD fits (solid curves through data). The LPSVD components corresponding to the dominant modes between 27 and 44 cm⁻¹ are displaced below the data (the phases for these modes are found to be ∼3π/2 ± π/8 for cyt c, ∼π/4 ± π/6 for P450_cam, and ∼0 ± π/6 for Cbg, CPO, and CooA). The right panels show the corresponding power spectra. The excitation wavelengths and the Soret peak (λ_max) of each sample are denoted in the right panels. Note the phase of ferric cyt c is shifted by π relative to the other ferric samples with the well-defined phase shown in Fig. 1. This observation is currently under study and may indicate the presence of a transient photoreduction process.

Frequency domain techniques like Raman spectroscopy cannot reliably access vibrational modes in the sub-200 cm⁻¹ range due to interference from elastic and quasi-scattering phenomena. On the other hand, direct time-domain measurements can excite and probe Raman active frequencies that lie within this low-frequency range. Generally, the time-domain results correlate very well with the Raman data at the higher frequencies where comparisons can be made. Detuned detection is used to access the higher frequency region in the time-domain measurements, while the open-band condition probes the lowest frequencies with the best resolution and fidelity.

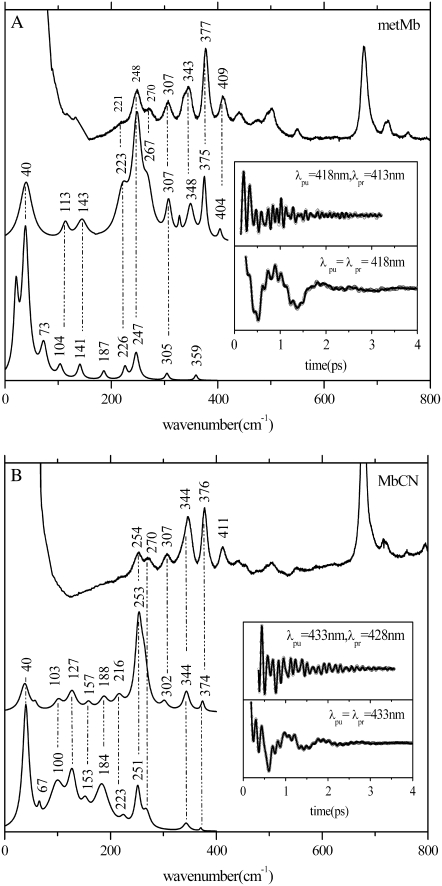
To optimize the time-domain detection of the higher frequencies we employ a detuned (or dispersed) detection scheme, as outlined in Materials and Methods. Fig. 3 shows the FCS-Raman correlation for metMb (Fig. 3 A) and MbCN (Fig. 3 B) samples, where the FCS data were collected in both open-band and detuned detection schemes using pulses with a center (i.e., carrier) wavelengths of 418 nm (Fig. 3 A) and 433 nm (Fig. 3 B). We elected to study the ferricyanide derivatives (e.g., MbCN and ImFePPIXCN) in a variety of protein and solvent conditions to specifically probe the role of the heme environment and to remove any possible ambiguities associated with the iron spin and coordination state that might exist for metMb, which has a weakly-bound water ligand. Because of our interest in the lower frequency modes (≲k_BT), we often employ the open-band detection technique. However, a drawback of the open-band detection scheme is that the higher frequencies appear with lower relative amplitudes and larger frequency errors. (Similarly, the lowest frequencies are less reliable using detuned conditions.) When establishing the final set of frequencies for a particular sample, we generally use the detuned condition to assign the higher frequency modes and the open-band condition for the lower frequencies.

FIGURE 3.

(A) The correlation between the Raman and coherence spectra for metMb. The inset shows the oscillatory components and the LPSVD fits to the open-band (lower) and dispersed (upper) data. The Raman data were measured employing a 413.1-nm excitation wavelength while the open-band FCS data were measured using a 418-nm excitation wavelength. The dispersed data were collected with a 0.5-nm spectral window, detuned 5nm (λ_pr = 413 nm) to the blue of the 418-nm carrier wavelength. (B) The correlation between the Raman and coherence spectra for MbCN. The inset shows the oscillatory components and the LPSVD fits to the open-band (lower) and dispersed (upper) data. The Raman data were measured employing a 413.1-nm excitation wavelength while the open-band FCS data were measured using a 433-nm excitation wavelength. The dispersed data were collected with a 0.5-nm spectral window, detuned 5 nm (λ_pr = 428 nm) to the blue of the 433-nm carrier wavelength.

The time-domain data in Fig. 3 are transformed into the frequency domain, using the LPSVD algorithm as described in Materials and Methods, and then compared against continuous-wave Raman data collected with 413.1-nm wavelength excitation. The insets show the FCS experimental data (detuned upper curve and open-band lower curve) after the removal of the monotonically decaying population signal (which, as expected (77), is significantly diminished in the detuned measurement). There is very good correlation between FCS and Raman measurements, with frequency errors of ∼±4 cm⁻¹ for the weaker modes in the overlapping region and somewhat better precision achieved for the stronger modes.

The metMb data in Fig. 3 A shows a very strong mode at 40 cm⁻¹ and there is excellent agreement between the traditional resonance Raman spectrum and the FCS-determined frequencies above 200 cm⁻¹. For the MbCN sample, shown in Fig.3 B, a strong high-frequency mode appears at ∼253 cm⁻¹ in the detuned measurement, which correlates well with a Raman mode of MbCN at 254 cm⁻¹ that has been assigned (70,95) to ν₉. Even though it weakens in the open-band detection configuration (due to its higher frequency), this mode has a long damping time and strongly modulates the open-band coherence signal as seen from the experimental data in Fig. 3 B (inset). As with metMb, there is a dominant low-frequency mode near 40 cm⁻¹ (with a period of ∼800 fs) in MbCN that can be seen directly in the time-domain data.

Fig. 4 presents the data used to extract the amplitude and phase excitation profiles of MbCN, which is a well-characterized hexa-coordinate ferric heme system with a very strong coherence signal and good stability over the 2–3 h required for the FCS measurements. Measurement of the FCS excitation profiles can help to identify the location(s) of the underlying resonant electronic excitation(s) as well as clarify the mechanisms of resonant enhancement. There are a number of general observations that can be made upon examination of the experimental data presented in Fig. 4. For example, when the excitation wavelength is at its extremes near 400 nm or 438 nm, the open-band FCS signal is dominated by the strong low-frequency mode near 40 cm⁻¹. On the other hand, when the excitation is near 418–419 nm, the open-band 40 cm⁻¹ mode signal diminishes and the higher frequency modes (e.g., the ν₉ mode near 252 cm⁻¹) are much stronger.

FIGURE 4.

FCS spectra of MbCN as a function of excitation wavelength between 400 and 418 nm (A) and between 419 and 43 8nm (B). The left panels show the oscillatory signals and the LPSVD fits, with the component associated with the mode near 40 cm⁻¹ displaced below. The right panels show the corresponding power spectra. The excitation wavelength is shown in the upper-right corner of each panel.

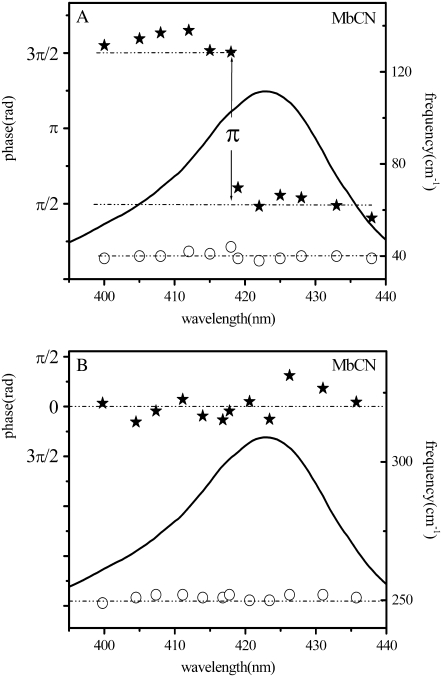
The strong low-frequency mode also can be seen to undergo a phase jump of π on the blue side of the Soret absorption peak, as the excitation wavelength is tuned between 418 and 419nm. The top and bottom panels of Fig. 4 show the wavelength domains over which the 40 cm⁻¹ mode maintains an approximately constant phase. The phase excitation profile of the 40 cm⁻¹ mode, extracted from the data in Fig. 4, is presented in Fig. 5 A. The amplitude of this mode also depends strongly on the laser excitation wavelength. As expected from theoretical considerations (77), its amplitude is much larger for excitation wavelengths on either side of the region where the phase jump takes place.

FIGURE 5.

Plot of the phase (solid stars) and the frequency (open circles) of the 40 cm⁻¹ mode (A) and the ν₉ mode (B) of MbCN as a function of the excitation wavelength. The equilibrium absorption spectrum of MbCN (solid curve) is displayed for reference. The distinct phase jump of π for the 40 cm⁻¹ mode between the two excitation wavelength domains is evident.

As can be seen in Fig. 4, the higher frequency modes dominate the FCS signals collected in the vicinity of the phase jump, where the amplitude of the 40 cm⁻¹ mode is at a minimum. We also extracted the phase excitation profile of the strong high-frequency ν₉ mode (near 252 cm⁻¹) and the results are displayed in Fig. 5 B. It is noteworthy that the phase of this mode does not jump, or drift, and to a good approximation it can be considered to be zero within the noise (a possible phase discontinuity at 425 nm might be discernable near the resonant band maximum, but it has been shown theoretically (49) that the discontinuous phase jump for ground-state coherences depends sensitively on the magnitude of inhomogeneous broadening). On the other hand, the amplitude of this mode also shows a discernable minimum near 425 nm that can be clearly seen in the experimental data and in the corresponding power spectrum of Fig. 4 B.

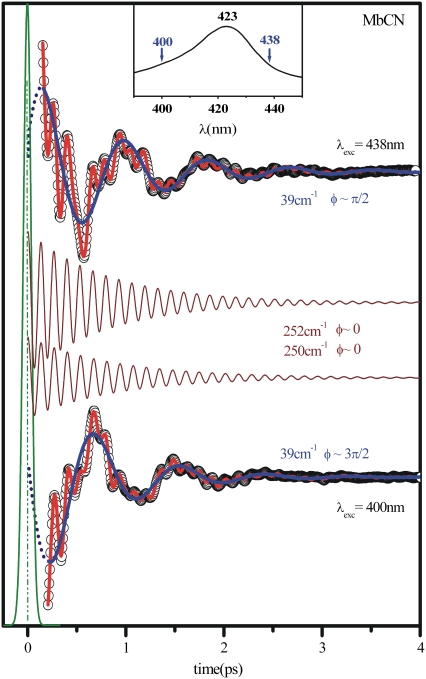
The strikingly different wavelength-dependent behavior of the phases and amplitudes of these two coherent signals is clearly depicted in Fig. 6, where the data at the red and blue side of the Soret maximum are directly compared. The autocorrelation signal that determines time zero is also shown, along with the LPSVD fits for the 40 cm⁻¹ mode (blue curves) and for the mode near 252 cm⁻¹ (displaced maroon curves). It is clear that the phase of the high-frequency mode stays fixed while the phase of the low-frequency mode jumps by π (from π/2 to 3π/2) when the signals at the excitation extremes are compared.

FIGURE 6.

Phase behavior of the 40 cm⁻¹ and the ν₉ modes in MbCN. The phase behavior is contrasted as the excitation wavelength is moved from 400 nm to 438 nm. The 40 cm⁻¹ mode LPSVD component (blue) is plotted on top of the experimental data while the ν₉ mode LPSVD component is plotted in maroon and displaced from the data for a better visualization. The autocorrelation signal (which sets the zero time delay) is displayed in green. The solid red curve through the data is the full LPSVD fit.

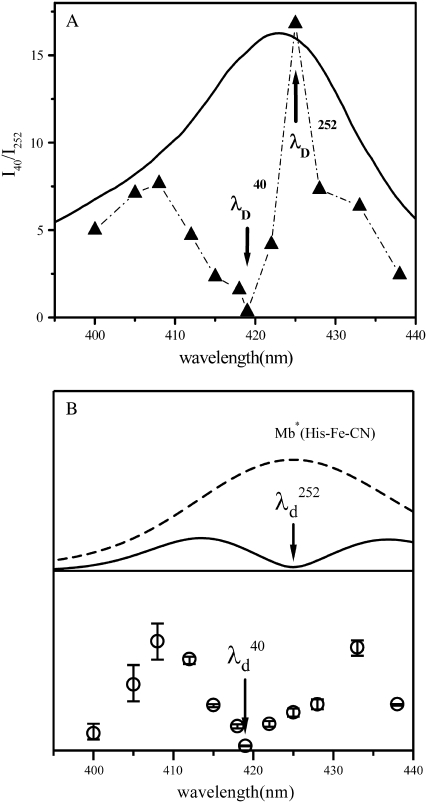
In Fig. 7 A, a plot of the ratio of the relative amplitudes of these two modes, I₄₀/I₂₅₂, strongly suggests that they are coupled to different resonant electronic excitations. The fact that we see a minimum in the 252 cm⁻¹ mode amplitude at 425 nm (where the Soret maximum of the vibrationally hot ground-state species is expected), along with its assignment as ν₉ in the Raman spectrum of MbCN, strongly indicates that this is a ground-state coherence of hot six-coordinate MbCN. Theory predicts that the amplitude of its coherence signal will minimize near the resonant band center, as shown in the upper part of Fig. 7 B at 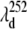∼ 425 nm. In the figure, we use a Gaussian approximation to simulate the hot six-coordinate MbCN absorption band peaking near 425 nm and the theoretical 252 cm⁻¹ mode excitation profile that goes with it. When this theoretical profile is multiplied by the measured ratio I₄₀/I₂₅₂, we can extract the amplitude profile for the 40 cm⁻¹ mode. The excitation profile of the 40 cm⁻¹ mode is shown by the solid data points in the lower portion of Fig. 7 B and a dip in the profile is obvious at 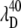∼ 418 nm (see arrows). This provides very strong evidence that the 40 cm⁻¹ mode is coupling to a different electronic transition than the 252 cm⁻¹ mode.

FIGURE 7.

(A) The measured ratio of the amplitudes of the 40 cm⁻¹ mode and the 252 cm⁻¹ mode as a function of the excitation wavelength. The absorption spectrum of MbCN (thick curve) is displayed for reference. The arrows denote the wavelengths, corresponding to the amplitude minima of the two modes (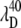 and 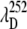). (B) Predicted amplitude of the 40 cm⁻¹ mode as a function of the excitation wavelength (solid circles). The absorption lineshape of hot six-coordinate MbCN (dashed line) and amplitude excitation profile of its 252 cm⁻¹ mode (solid bilobed line) are shown in the upper panel. The Soret peak position and FWHM of the hot six-coordinate species Mb*(His-Fe-CN) were taken to be 425 nm and 31 nm, respectively. Here, the FWHM of the hot MbCN Gaussian lineshape was taken to be 20% broader than that of the equilibrium species. This lineshape was simulated by standard lineshape theory (111) using electronic damping of 300 cm⁻¹, Gaussian inhomogeneity of 110 cm⁻¹, and a low-frequency bath mode (ν_b = 50 cm⁻¹, S_b = 15). The amplitude excitation profile of the 252 cm⁻¹ mode was calculated by the effective linear response theory (77) using S = 0.02, T = 300 K, and a pulse width of 60 fs. The amplitude excitation profile of the 40 cm⁻¹ mode was found as the product of the 252 cm⁻¹ profile and the I₄₀/I₂₅₂ ratio shown in Fig. 7 A. The error bars in the lower panel represent simulations of the hot six-coordinate lineshape that are 20 ± 10% broader than the equilibrium lineshape.

The π-phase flip of the 40 cm⁻¹ mode, and its bilobed amplitude behavior shown in Fig. 7 B are suggestive of wave packet motion on a product state potential energy surface (19,77). However, the absolute values of the 40 cm⁻¹ phase (±π/2) are anomalous. In contrast, the phase and amplitude of the 252 cm⁻¹ mode show the normal behavior expected for coherences evolving on the initial ground-state energy surface, activated by a resonant-stimulated Raman process (77).

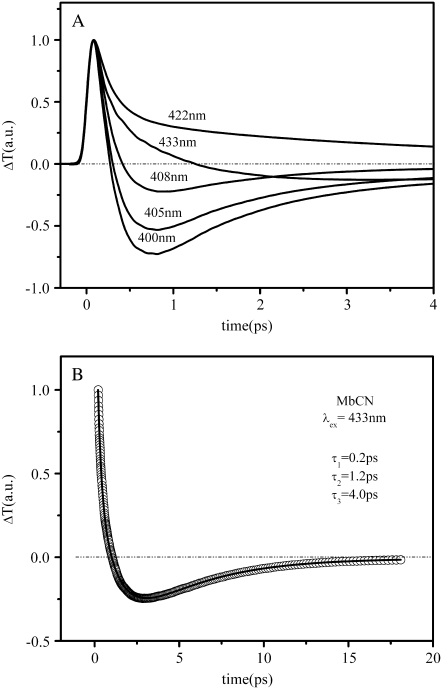
To help understand the excitation profile of the 40 cm⁻¹ mode, we need to consider the signals associated with the monotonic kinetics/population decay. The transient absorption, measured at five different excitation wavelengths in Fig. 8 A, show striking variability. An important observation is that, as we tune the excitation wavelength to the blue of the MbCN Soret band maximum (423 nm), a relatively strong absorbance (ΔT < 0) appears on subpicosecond timescales. The transient absorption obtained with excitation wavelengths on the red side of the MbCN Soret maximum (λ > 422 nm) can be explained by spectral dynamics associated with the hot six-coordinated species (red-shifted and broadened absorption). However, the transient absorption observed at <408 nm, along with the different amplitude minima (λ_D) for the 40 cm⁻¹ and 252 cm⁻¹ modes, suggests the presence of an additional short-lived transient species and we must consider the likelihood that a product state is present. Photolysis of one of the iron ligands of MbCN is an obvious possibility. In Fig. 8 B, we display an extended transient absorbance trace at 433 nm along with the multiexponential fits that extract the time constants (0.2 ps, 1.2 ps, and 4.0 ps).

FIGURE 8.

(A) Series of transient transmission (ΔT) traces of MbCN at five different excitation wavelengths. As the excitation wavelength approaches 400 nm there is a sharp decrease of the transmitted signal on the picosecond scale that corresponds to transient absorption in this region. (B) Longer timescale transient transmission of MbCN recorded at 433 nm. The experimental signal has been normalized and the data corresponding to the first 100 fs have been removed to eliminate contamination from coherent coupling signals. Fitting the remaining data with a sum of three exponentially decaying processes results in time constants of 0.2 ps, 1.2 ps, and 4 ps.

In Fig. 9 A we present the full transient absorption spectra of MbCN, using a pump wavelength of 580 nm and a white-light continuum probe (35,96). In Fig. 9 B we have summed the reactant lineshape (equilibrium MbCN) to the transient difference spectrum at 0.5 ps, to approximate the lineshape of the transient species formed at 0.5 ps. A set of scaling factors, corresponding to adding different amounts of the equilibrium bleach, are shown in Fig. 9 B. The scaling factor is related to the quantum yield for photoproduct formation (denoted as Y_L) as discussed in Materials and Methods. The appearance of the MbCN photoproduct on the subpicosecond timescale suggests that photolysis of either the CN⁻ or the His⁹³ ligand is taking place with a significant (but nonunity) quantum yield, Y_L. The arrows denoting 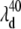and 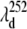depict the wavelengths where the respective modes show amplitude minima and, in the case of the 40 cm⁻¹ mode, a phase jump. These wavelengths are used to constrain the possible transient absorption lineshapes and the allowed values of Y_L (see Discussion).

The issue of the ligand rebinding timescale can be addressed by the kinetic analysis in Fig. 8 B, which results in three exponential time constants (0.2 ps, 1.2 ps, and 4.0 ps) that accompany the equilibration of the MbCN sample. These time constants are consistent with independent infrared studies of the ultrafast photophysics of MbCN, which found time constants of 0.23 ps, 1.3 ps, and 3.6 ps (69). As discussed below, we offer a new interpretation of the longer ∼4 ps relaxation phase, and suggest that it is associated with the dissociation and rapid recombination of the proximal histidine, His⁹³.

DISCUSSION

General observations

The femtosecond coherence spectra of most ferric heme systems investigated to date, with the notable exception of horseradish peroxidase (F. Gruia et al., unpublished), are dominated by a low-frequency mode that appears below 50 cm⁻¹ (Fig. 1). A variety of other low-frequency modes are also active in the region between 50 and 200 cm⁻¹. The fact that these modes are strongly excited by thermal fluctuations (k_BT ∼ 200 cm⁻¹ at 300 K) makes them likely candidates for reaction coordinates connected to protein function. As a consequence, a more detailed analysis of this frequency region is an important goal. Although the low-frequency region is difficult to probe, we can use femtosecond coherence spectroscopy, which reveals the frequency, phase, and amplitude of the normal mode oscillations. The changes in the phase and amplitude of the low-frequency modes as the laser excitation wavelength is tuned across the resonant absorption band yield additional information about the existence of underlying resonant electronic states and about the various mechanisms that are responsible for generating the coherent molecular motions (77,78).

MbCN is a particularly well-characterized ferric system, with exceptionally good stability and an unambiguous spin and coordination state (low-spin, six-coordinate). It also has a strong oscillatory coherent signal over a wide range of excitation wavelengths and a dominant low-frequency mode at 40 ± 2 cm⁻¹. As can be seen in Fig. 2, for both metMb and MbCN, the detuned FCS data correlate very closely with the Raman spectrum in the higher frequency region where the data overlap.

In the discussion below, we focus on MbCN as a prototypical example of six-coordinate, low-spin, ferric heme system and discuss its low-frequency modes, as probed by FCS. We study MbCN based on the position of its Soret peak (423 nm) as well as its stability. Excitation profile measurements need to be run over a relatively wide range, using wavelengths on both the red and blue sides of the absorption band. Experimental constraints limit us to excitation wavelengths between 400 and 450 nm, allowing a thorough investigation of the MbCN excitation profile. An open question for MbCN has to do with the issue of ligand photolysis and the structure of the photoproduct state absorbing near 418 nm. Previously reported experiments and numerical simulations on MbCN suggest that CN⁻ does not undergo photolysis (69,73), although this is not completely excluded by the prior data (69). The appearance of relatively long-lived excited electronic states that perturb the CN vibrator and its IR frequency have been suggested as a more likely explanation of the earlier measurements (69). On the other hand, proximal histidine photolysis has not been considered previously (69,73), and that is the possibility we explore further here.

We have measured the amplitude (Fig. 7) and phase (Fig. 5) excitation profiles of MbCN over the Soret band region, from 400 nm to 438 nm (the equilibrium MbCN Soret peak appears at 423 nm). The FCS data, LPSVD fits, and power spectra are displayed in Fig. 4. An important observation is that the dominant low-frequency mode (near 40 cm⁻¹) undergoes a sharp and easily identifiable phase jump between 3π/2 (−π/2) and π/2 when the laser is near 418–419 nm. It is noteworthy that this wavelength is significantly blue-shifted with respect to the Soret band maximum (423 nm) and that a minima in the amplitude of the 40 cm⁻¹ mode also appears at 418–419 nm (Fig. 7).

Phase jumps have been observed in other experiments on heme proteins, but with a few notable differences (77,90). For MbNO the Soret peak is located at 421 nm and the sample is clearly photolabile so the deoxyMb product state Fe-His coherence (near 220 cm⁻¹) is observed with the heme in a ferrous, five-coordinate, state (Soret peak near 435 nm). This state has many of the attributes of an electronically excited state, but with a relatively long lifetime equal to the inverse of the ligand rebinding rate. The phase jump from 0 to π results from probing the wave-packet motion on the product state potential energy surface and it occurs at 438 nm, near the Soret peak of the deoxyMb product state, which is 3-nm red-shifted with respect to its equilibrium absorption spectrum. The red shift is due to the spectral lineshape dynamics of the hot five-coordinated ferrous heme that appears when photolysis takes place.

This observation contrasts with the MbCN experiments reported here, where the phase jump takes place at a wavelength that is blue-shifted with respect to the Soret peak. It suggests that the 40 cm⁻¹ mode is not coupled (at least not strongly) to the vibrationally hot MbCN Soret band at ∼425 nm, but rather to a product state transition that develops on a very fast (subpicosecond) timescale with an equilibrium absorption spectrum that probably peaks a few nanometers below 418–419 nm, in the 415–416-nm range (this is because the peak of a hot absorption spectrum is often broadened and red-shifted by 2–4 nm with respect to equilibrium). The phase jump (Fig. 5) and the amplitude minimum (Fig. 7) of the 40 cm⁻¹ mode, which both occur near 418 nm, are indicative of the presence of a transient product state that is blue-shifted with respect to equilibrium MbCN. The phase jump of π also suggests that the 40 cm⁻¹ mode coherence is reaction (or nonradiatively) driven. Since this mode is coupled to the five-coordinated photoproduct, we tentatively assign it here as the doming mode enhanced by photolysis. However, the absolute magnitude of the phase of the 40 cm⁻¹ mode also shows some very unusual properties. It is found to be 3π/2 (or −π/2) to the blue of 418 nm and π/2 to the red of 419 nm. Although the π-phase jump can be understood, the absolute values of the phase (±π/2) are not consistent with standard electronically resonant harmonic models (77) as discussed in more detail below. The strong intensity of the 40 cm⁻¹ mode is thought to be due to transient heme displacement along the doming coordinate that is induced by impulsive momentum transfer associated with the photophysical process.

Another strong, and easily discernable, mode is observed at 251–253 cm⁻¹ in the FCS data. This mode also appears in the Raman spectrum of MbCN at 254 cm⁻¹ (the lowest well-resolved Raman mode in Fig. 2 B) and it has been assigned to ν₉ (70,95). This mode has significant resonance Raman coupling (97), so it also appears as a relatively strong mode in the coherence spectra. However, in contrast to the 40 cm⁻¹ mode, the 252 cm⁻¹ mode displays the phase and amplitude behavior that is expected for a ground-state coherence coupled to the MbCN Soret band. The phase is close to zero across the entire tuning range of probe wavelengths, and a minimum in the amplitude profile occurs near 425 nm. If the hot six-coordinate MbCN has normal absorption lineshape dynamics (i.e., a red-shifted and broadened Soret band), the existence of a minima in the coherence amplitude profile near 425-nm excitation is expected. (A typical coherence amplitude excitation profile is bilobed with a minimum at the resonant absorption peak, as shown in Fig. 7 B.) Based upon its excitation profile behavior, and its appearance in the MbCN Raman spectrum, we assign the 252 cm⁻¹ mode to the ground state ν₉ coherence of hot six-coordinate MbCN (λ_max ∼425 nm).

The contrasting behavior of the 40 cm⁻¹ mode and ν₉ is clearly displayed in Fig. 6 where the absolute phase of the cosine function, used to fit the coherent response, is seen to be ±π/2 for the 40 cm⁻¹ mode. This, along with the different amplitude minima found for the two modes (Fig. 7), is strong evidence that they are coupled to separate electronic transitions and that the fundamental mechanism underlying their appearance is quite different.

There are a number of other modes at <300 cm⁻¹ that appear in the coherent signals, although their amplitudes are not as dominant as the 40 cm⁻¹mode or ν₉. The frequencies detected by the LPSVD analysis are presented in Table 1 as a function of the excitation wavelength (open-band detection). There are six modes that consistently appear in all the spectra, regardless of the excitation wavelength, and their average frequency and variance can be found in the last row of the Table: 40, 95, 149, 186, 251, and 269 cm⁻¹. In addition to these modes, there are three other modes that intensify as the excitation wavelength is moved to the red. The average frequencies of these red-enhanced modes are 67, 129, and 221 cm⁻¹. The observation of wavelength dependence in the spectral content once again suggests that the experiment is probing a mixture of electronic species that develop when MbCN is photoexcited.

TABLE 1.

Low-frequency modes of MbCN

λex	γa	γb	γc	γd	γe	ν18	γf	ν9	ν52
400	39(s)		93(m)		143(m)	185(w)		249(m)	272(w)
405	40(s)		86(m)		145(m)	184(w)		251(m)	271(w)
408	40(s)		92(m)	134(m)		190(m)		252(m)	268(w)
412	42(s)		98(m)	132(m)	157(w)	193(m)		252(m)	266(w)
415	41(s)	69(w)	80(m)	129(m)	157(m)	185(s)	224(w)	251(m)	274(w)
418	44(s)	66(w)	92(m)	125(s)	157(m)	186(m)	230(w)	251(s)	278(w)
419	39(m)	69(w)	104(m)	127(s)		185(s)	215(m)	252(s)	271(w)
422	38(s)	66(w)	95(s)	129(s)	141(w)	189(w)	217(w)	250(w)	264(w)
425	40(s)	66(w)	102(m)	136(w)		176(w)	220(w)	250(m)	266(w)
428	40(s)	69(w)	99(m)	135(m)		183(w)		251(m)	270(w)
433	40(s)	67(w)	100(m)	127(m)	153(w)	184(m)	223(w)	251(m)	268(w)
438	39(s)	70(w)	102(m)	126(m)	143(w)	185(w)	218(w)	252(m)	265(w)
Avg	40 ± 2	68 ± 2	95 ± 7	130 ± 4	149 ± 7	186 ± 4	221 ± 5	251 ± 1	269 ± 4

Excitation wavelength (λ_ex) is given in nm and mode frequencies are in cm⁻¹. The (s,m,w) denote (strong, medium, weak) intensity in the extracted power spectrum.

MbCN photoexcitation and photolysis

Several of the experimental results presented here suggest the appearance of a new photoproduct state soon after the excitation of the MbCN system. Previous studies considered the possibility of CN ligand photolysis, but suggested that this was unlikely (69). Moreover, numerical simulations of the MbCN structure have reached a similar conclusion (73). An alternative that has not received so much attention is the possibility that the proximal histidine (His⁹³) ligand may undergo rapid photolysis and rebinding. Although there are no definitive results on this subject, the idea of histidine photolysis has been discussed previously (98). Similar ultrafast experiments involving ferrous cytochrome c (cyt c) have been carried out (91,99), and photolysis of an iron axial ligand (Met⁸⁰) was detected with a quantum yield, Y_L, in excess of 80% and a rebinding timescale of ∼6 ps (91).

Photoexcitation of MbCN results in a significant amount of energy that is redistributed to the heme vibrational modes (22,100,102,103) and dispersed to the immediate environment of the heme through vibrational energy transfer. It is known that on the distal side of the heme, the CN ligand establishes a hydrogen bond with His⁶⁴ (104) and this could both stabilize the CN ligand and help transfer some of the excess energy from the heme to the bulk protein following that path. However, it is more likely that the deposition of vibrational energy into the solvent proceeds through the proprionate side chains (96,105). Energy deposition via ligand photolysis in MbCN is yet another possibility and this raises the question of which bond is most labile.

The relative strength of the two axial ligand bonds can be estimated from the preparation protocol for the Im-PPIX(Fe³⁺)-CN model compound (Im = imidazole), which suggests that, for ferric heme systems, the Fe-CN bond is stronger than Fe-His. Both of the axial ligands employed for the preparation of Im-PPIX(Fe³⁺)-CN (i.e., CN and Im) can form bis-heme structures, so an unavoidable step of the preparation protocol is to disrupt a bis-heme structure (either the bis-Im or the bis-CN). We observe that, when CN is added first to a solution (1% CTAB, pH = 8.5) of hemin, the bis-CN complex (Soret peak 432nm) formation is prompt and the subsequent addition of aliquots of saturated solution of Im does not result in a ligand exchange. On the other hand, we are able to prepare the Im-PPIX(Fe³⁺)-CN model by first forming the bis-Im-(Fe³⁺)PPIX (100 μM hemin, 0.5 M Im, Soret peak 414 nm) and then slowly adding small aliquots of a saturated solution of KCN. When the CN concentration reaches a threshold of ∼10 mM, a ligand switch takes place with the formation of Im-PPIX(Fe³⁺)-CN. The resulting model compound has a Soret absorption peak at 423 nm, matching closely the optical properties of the MbCN. If more KCN is added to the sample, it results in the formation of the bis-CN-(Fe³⁺)PPIX compound (λ_max = 433 nm). The ratio of relative concentrations of Im and CN needed to form the mixed ligand species is ∼50:1. Based on these observations, we conclude that the CN binding energy to the ferric heme is significantly larger than the binding energy of imidazole. Thus, in the context of ligand photolysis in MbCN, we must consider the photolysis of the weaker of the two axial ligands (namely, His⁹³).

Additional insight regarding photolysis can be obtained from a detailed analysis of the MbCN Soret band transient absorption shown in Fig. 9 B. The figure shows the calculated transient spectrum, which is a superposition of the photoproduct and the residual (unphotolyzed) hot six-coordinate MbCN. The transient absorption lineshape is found by the addition of the equilibrium MbCN absorption band to the observed difference spectrum using different weighting factors, so that the bleaching signal is eliminated. The weighting factors can be made to correspond to different quantum yields, Y_L, for photoproduct formation by referencing to the photolysis of MbCO under identical conditions (35) (after correction for relative concentration and absorption cross section at the excitation wavelength, as discussed in Materials and Methods).

The transient spectra shown in Fig. 9 B can be referenced to the wavelength where the phase jump and amplitude minima occur for the 40 cm⁻¹ mode, 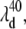and this is shown (arrow and dashed line) in the figure. Similarly, the amplitude minimum for ν₉ occurs near the maximum of the MbCN absorption and it is shown as 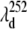in the figure. We simulated the set of transient lineshapes to help locate the photoproduct peak, 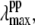of the putative five-coordinate photoproduct (pp) for each trial choice of Y_L. We fit the transient lineshape at each value of Y_L using two Gaussian lineshape functions, where the position of the hot six-coordinate MbCN lineshape was held fixed at 425 nm (at the point where the ν₉ mode experiences its amplitude minimum) with a full width at half-maximum (FWHM) of 31 nm (broader than the equilibrium spectrum by ∼20%), while the position of the photoproduct lineshape, 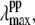was allowed to vary. The peak position found for each of the transient lineshapes in the figure is shown as an open circle on the respective transient absorption curve, where it can be seen that 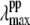moves systematically from ∼410 nm at Y_L ∼ 40% to ∼418 nm for Y_L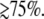

Since it is apparent that the 40 cm⁻¹ mode is coupled most strongly to the shifted photoproduct absorption band, its amplitude minimum and phase jump at 418 nm locate the likely maximum of this band. This, in turn, allows us to estimate the correct Y_L and the transient lineshape by choosing the scaling factor so that 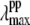∼ 418 nm. As can be seen in Fig. 9 B, the transient absorption bands constructed when Y_L > 75% all tend to have 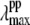close enough to 418 nm that they must be considered consistent with the observed phase and amplitude excitation profiles of the 40 cm⁻¹ mode. Thus, we can approximate the value of Y_L to be >75%. However, since the 252 cm⁻¹ mode is easily observable and indicates a significant population of hot six-coordinate material, absorbing at 425 nm, we suggest that the lower limit Y_L ∼ 75% is most probable.

It is possible that the 40 cm⁻¹ doming mode also couples to the hot six-coordinate MbCN, although we cannot be certain of this. Its appearance at both 400 nm and 438 nm excitation demonstrates that the excitation profile is quite broad and coupling to the red-shifted MbCN transition at 425 nm, as well as the blue-shifted photoproduct band at ∼418 nm, is possible. However, it appears that its coupling to the band centered at 425 nm is much weaker than its coupling to the band at 418 nm. This is because there is no obvious minimum in the 40 cm⁻¹ amplitude at 425 nm, although a small suppression in the amplitude profile can be discerned between 425 and 430 nm. Additionally, the small residual signal of this mode at 418 nm, and its upshift in frequency to ∼44 cm⁻¹ at this wavelength, could indicate weak doming activity of the six-coordinate MbCN species.

The possibility of CN photolysis can be tested by considering the optical absorption of the five-coordinated ferric heme species that must be produced. The optical absorption properties of the five-coordinate CN bound ferric heme are unknown, but for CN photolysis and histidine ligation the spectral properties should resemble those of the five-coordinate H64L metMb mutant. The H64L replacement of the distal histidine results in the elimination of the water molecule as a sixth axial ligand (106). The equilibrium optical absorption spectrum of H64L metMb has a broad Soret band that peaks at 390 nm (107). In contrast, the possible photoproduct absorption bands in Fig. 9 B display the presence of an absorbing species in the 410–420 nm region, depending on the value for Y_L that is assumed. Because the minimum of the 40 cm⁻¹ excitation profile occurs at 418 nm, we can fix the photoproduct absorption near this wavelength, which allows us to eliminate the possibility of CN photolysis because it should result in a transient absorption peak near 390 nm.

Based on this analysis, we assign the photoproduct band near 418 nm to a five-coordinate CN-bound product state, which has the His⁹³ transiently dissociated. This suggestion is reminiscent of the previous observation of methionine photolysis in ferrocytochrome c (91). The recovery of the His⁹³-Fe bond evidently takes place in ∼4 ps, which is somewhat faster than the ∼6 ps recovery reported for Met⁸⁰ in cyt c (91,99). The time constants associated with the full electronic and vibrational ground-state recovery (e.g., via nonradiative electronic decay, cooling, and ligand rebinding) are found in Fig. 8 where the FCS instrumentation was used to provide a significant improvement in the signal/noise. The three exponential time constants (0.2 ps, 1.2 ps, and 4.0 ps) in Fig. 8 are in excellent agreement with an earlier analysis (69) that found time constants of 0.23 ps, 1.3 ps, and 3.6 ps.

The interpretation of these time constants remains an open question and we suggest that the 200-fs response could involve either rapid cooling of a vibrationally hot electronic ground state, or an electronic intermediate on the nonradiative electronic decay pathway (which includes ligand photolysis). Although the possibility of hot electronic states cannot be completely excluded, the observation of prompt (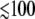 fs) electronic ground-state spectral signatures in several heme systems (7,35,90) suggests to us that the vibrational cooling assignment is more likely. Moreover, as pointed out by Helbing et al. (69), the ferric heme in MbCN is unlikely to participate in an iron-to-porphyrin charge transfer transition, which has been previously suggested as the source of the ∼200-fs signals in ferrous heme systems (56). Similarly, the 1.2–1.3 ps time constant is also likely to be associated with vibrational cooling of the heme in its electronic ground state (35,96,108).

The signal at 3.6–4.0 ps, on the other hand, is assigned to proximal histidine rebinding with a photolysis quantum yield of Y_L ∼ 75%. We select this value of Y_L based on both Fig. 9 B and on the independent infrared studies (69) that show a 25% residual MbCN bound-state IR absorption signal at the earliest detectible times. The IR measurements are consistent with, and help to constrain, the quantum yield limits deduced from the analysis in Fig. 9 B. It should be recalled that the observation of a strong coherence signal from six-coordinate MbCN (e.g., the ν₉ mode at 252 cm⁻¹), which displays its amplitude minimum at 425 nm, clearly demonstrates that the quantum yield for photolysis is <100%. All the evidence together points strongly to the lower limit of the quantum yield obtained from Fig. 9 B, namely Y_L ∼ 75%.

The assignment of proximal histidine photolysis and rebinding to the 3.6–4.0 ps transient also helps to explain several other IR observations (69). First, the IR response for MbCN is nearly identical to that of HbICN, another heme protein (from the clam Lucina pectinata) with a very different distal pocket. Histidine photolysis is consistent with this observation because, unlike CN photolysis, the histidine reaction would be expected to give a common IR signature in both proteins. For MbCN, the 3.6-ps decay of the transient infrared bleaching signal of the bound CN, along with the simultaneous decay of the weaker red-shifted (by 28 cm⁻¹) CN transient absorbance (69), is directly explained by the rebinding of the histidine ligand, assuming the red-shifted IR component is associated with the five-coordinate CN bound species. We have no direct method for testing this red-shifted frequency assignment, but the HCN species evidently has a frequency and oscillator strength that is consistent with the red-shifted absorbance (69). Thus, it seems possible that the removal of the trans histidine ligand, leaving behind the positively charged heme core, might evoke a similar spectral change. The shared thermal response of the two IR bands (reactant bleach and red-shifted product), as well as the lack of any detectible difference in the IR anisotropy of the bleach and the product CN oscillators during the return to equilibrium (69), all speak in favor of the CN ligand being bound to an initially hot heme that cools and undergoes a separate photophysical process, such as the rebinding of the histidine ligand.

The proposal (69,73) that the separate photophysical process might involve rapid nonradiative decay to an excited electronic state of the six-coordinate species, which transiently weakens the Fe-CN bond for ∼4 ps, cannot be completely ruled out. However, it is hard to understand why this would proceed with a quantum yield of only ∼75% and why there would be no relative changes in the Fe-CN bond angles, as determined from the IR anisotropy measurements (69). Moreover, the observation of strong coupling of the 40 cm⁻¹ mode to the photoproduct absorption band at 418 nm suggests that a five-coordinate species with a significantly domed structure appears in the 4-ps time window.

Phase measurements

A final observation that deserves discussion is the unexpected value for the phase of the 40 cm⁻¹ mode. As can be seen clearly in Figs. 5 and 6, its absolute phase in MbCN is close to ±π/2. For resonant conditions, the imaginary part of the complex lineshape function is much larger than the real part, so that coordinate (rather than momentum) displacements dominate the preparation of the initial nonequilibrium wavepacket (77,78). Under such conditions, we calculate the phases in the degenerate pump-probe experiment to be near 0 or π (77). Such calculations depend upon the use of the well-separated pulse approximation (77,78), so that the field-matter interactions of the pump and probe pulses do not intermingle. This means that the theory is only valid for those signals obtained at times longer than the autocorrelation pulse width. However, because the 40 cm⁻¹ mode has a recurrence time of ∼800 fs, its phase can be measured accurately by using the longer time data points and extrapolating back to time zero as shown by the dashed lines in Fig. 6. For harmonic modes, and a single electronic resonant state, a full quantum mechanical theoretical treatment of the wavepacket preparation step is possible (78). This approach leads to very good agreement with the measured phase behavior of the 220 cm⁻¹ (Fe-His mode) coherence of Mb, under either ground-state or product-state excitation conditions (77). On the other hand, the calculation of the absolute phase becomes a significant theoretical challenge outside of the harmonic Franck-Condon approximation, when electronic curve crossing and rapid photophysical phenomena are present.

Abnormal phase behavior, especially for the low-frequency mode near 40 cm⁻¹, has been reported before in both photolabile (MbNO) and photostable (deoxyMb) myoglobin samples (49). We have also found that the 40 cm⁻¹ mode shows the same unusual phase behavior in other heme species such as metMb, ferric and ferrous cytochrome c, ferric horseradish peroxidase-NO and cytochrome P450_cam, and various ferric model compounds (Figs. 1 and 2). The ±π/2 phase will arise when momentum transfer dominates the wavepacket preparation step. Because the period of oscillation for the 40 cm⁻¹ mode is ∼800 fs and the pump-probe autocorrelation is 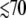fs, there is a relatively small error in zero time determination (±20 fs). Thus, we rule out experimental error as the source of this unusual phase behavior.

Theoretically, the absolute phase of the ground state wave packet is given by φ_g = −tan⁻¹[P_g0/Q_g0], where P_g0 and Q_g0 are the first moments of the momentum and position operators that are established in response to the pump pulse (77). Under normal resonant conditions, the initial wavepacket created by Raman-like interactions will be dominated by the coordinate shift (77,78). Either a hole is created in the ground state or a displaced wavepacket (with P_e0 = 0) is created on an excited-state surface (which can also be considered as a product state). Thus, the phase of the nonstationary state wavepacket is usually either 0 or π because Q_g0 ≫ P_g0. There is one exception for resonant conditions, and that occurs when the laser carrier frequency is tuned to the maximum of the resonant absorption band and the value of Q_g0 goes to zero. At this point, the ground-state wavepacket only receives a small momentum kick and the phase-excitation profile evolves from 0 to a ±π/2 discontinuity at the point where the coherence amplitude drops to its minimum value (77). (Usually, this discontinuity is washed out by inhomogeneous broadening so that the observed phase remains near zero across the entire excitation range (49).) Another exception occurs for nonresonant conditions, when the pulse carrier frequency is far to the red of the material electronic transitions and the birefringent response is dominant. Under this condition, the pump pulse primarily transfers momentum to the wavepacket and typically generates a signal phase of π/2 (78).

Thus, our observations suggest that the impulsive process that creates the 40 cm⁻¹ wavepacket must involve strong forces and momentum transfer that lie outside the standard theory of resonant impulsive stimulated Raman scattering (77–79,109). The phase jumps and amplitude minima observed in the excitation profile studies reported both here and elsewhere (90,91) demonstrate that this must be a resonant excitation process, therefore eliminating the nonresonant explanation. As a result, we have considered some other possibilities.

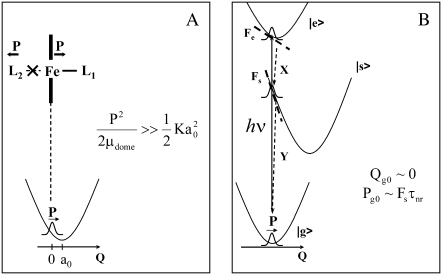
One such possibility (see Fig.10 A) is that momentum is transferred due to recoil, when an axial ligand bond is broken and the momentum of the ligand fragment leads to an opposing momentum kick to the heme iron. One problem with this explanation is that we have seen similar phase behavior for the 40 cm⁻¹ mode in other heme systems where it is thought that no photolysis is taking place. An additional problem is that the heme is initially in a planar configuration and, upon photolysis, the iron moves out of the plane along the doming coordinate. As a result, there is an inherent displacement of the coordinate that must be considered along with any momentum recoil that takes place. From the equation for the phase given above, we expect this to lead to a phase that is intermediate between 0 and π/2, because both P_g0 and Q_g0 are nonzero. However, the observed phase is almost exactly ±π/2 and this is indicative of dominant momentum transfer. Thus, the recoil model can only be applicable if the momentum transfer is very large and P_e0 ≫ Q_e0.

FIGURE 10.

(A) The recoil model for momentum transfer to the doming mode after photolysis. L₁ and L₂ are generic axial ligands of the central iron atom. The quantity a₀ represents the coordinate displacement. The momentum transfer must dominate the coordinate displacement for the wavepacket to have a phase of ±π/2. (B) The ultrafast nonradiative decay model for momentum transfer to the doming mode. |e> and |s> represent the optically excited and nonradiatively coupled intermediate electronic states, respectively. F_e and F_s are the electron-nuclear coupling forces felt by the wave packet on the corresponding potential surfaces and F_s ≫ F_e so that radiative-field-driven wavepacket preparation can be neglected. The quantity τ_nr is the timescale for sampling the intermediate potential energy surface during the nonradiative decay. The coordinates X and Y represent other higher-frequency motions that carry the system through conical intersections and back to the ground state on very rapid timescales that leave the low-frequency 40 cm⁻¹ mode (800-fs period) nearly undisplaced. Interesting quantum mechanical admixtures of the participating electronic states must be considered in a more formal theory.

The other possibility (see Fig.10 B) involves a novel mechanism for wavepacket generation and is focused on the ultrafast nonradiative electronic decay that is known to take place in the iron-based heme systems (83–87). Generally, it is thought that the electronic decay takes place on a timescale of tens of femtoseconds, leading to electronic damping factors of several hundred cm⁻¹. Since the period of the 40 cm⁻¹ oscillator is ∼800 fs, this means that rapid nonradiative decay along other coordinates (x,y) that lead to a conical intersection could bring the system back to the ground state, before any significant displacement of the low-frequency coordinate, Q. Insofar as the electrons pass through states that strongly couple to the 40 cm⁻¹ mode, it will receive an impulsive momentum transfer, ∼[dV/dQ]τ_nr, where τ_nr is the timescale for sampling the intermediate potential surfaces during the nonradiative decay (e.g., in the example of Fig. 10 B, F_s = −[dV/dQ]_s would be the coupling force that supplies the momentum impulse). Because the nonradiative decay channels in heme are thought to involve the open shell iron d-electrons, it is possible that very strong coupling forces at the iron atom may be generated during the nonradiative decay process. This, in turn, may be responsible for the large component of momentum that dominates the 40 cm⁻¹ wavepacket associated with the doming mode. Again, while other more quantitative models will be needed to explain the observed phase profiles in proper detail, it is generally required that P_g0 ≫ Q_g0 or P_eo ≫ Q_e0 (for coherences in either the ground or product state) to generate the ±π/2 absolute phase shift.

SUMMARY

In summary, we have presented the low-frequency spectra of a variety of ferric heme proteins and demonstrated that these spectra are sensitive to the protein environment. Systematic comparisons of the extracted frequencies with those determined from resonance Raman spectroscopy show very promising agreement in the region where there is overlap, validating the spectra found at lower frequencies. Detailed studies of the MbCN complex have shown the presence of a photophysical process that is coupled strongly to the mode at 40 cm⁻¹, associated with heme doming. We find that the data are consistent with the generation of a five-coordinate CN bound heme that has undergone histidine photolysis with a quantum yield of ∼75% and a rebinding time of ∼4 ps. The observation of an absolute phase of ±π/2 for the 40 cm⁻¹ mode indicates that momentum transfer dominates its preparation. This is not fully understood, but we suggest that iron recoil and/or ultrafast nonradiative decay, on timescales that are faster than the ∼800-fs period, might account for this unusual behavior.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.