Microfluidic high-throughput encapsulation and hydrodynamic self-sorting of single cells

Abstract

We present a purely hydrodynamic method for the high-throughput encapsulation of single cells into picoliter droplets, and spontaneous self-sorting of these droplets. Encapsulation uses a cell-triggered Rayleigh–Plateau instability in a flow-focusing geometry, and self-sorting puts to work two extra hydrodynamic mechanisms: lateral drift of deformable objects in a shear flow, and sterically driven dispersion in a compressional flow. Encapsulation and sorting are achieved on-flight in continuous flow at a rate up to 160 cells per second. The whole process is robust and cost-effective, involving no optical or electrical discrimination, active sorting, flow switching, or moving parts. Successful encapsulation and sorting of 70–80% of the injected cell population into drops containing one and only one cell, with <1% contamination by empty droplets, is demonstrated. The system is also applied to the direct encapsulation and sorting of cancerous lymphocytes from a whole blood mixture, yielding individually encapsulated cancer cells with a >10,000-fold enrichment as compared with the initial mix. The method can be implemented in simple “soft lithography” chips, allowing for easy downstream coupling with microfluidic cell biology or molecular biology protocols.

The postgenome era is stimulating a strong demand for high-throughput cell assays. Because genetically identical cells may display very heterogeneous behaviors (1, 2), bulk measurements on cell populations provide only partial information on cell metabolism, in particular from a dynamic point of view. Cell-to-cell variability is also of paramount importance for cancer research, developmental biology, drug screening (3), and stem cell research. Recent trends in cell biology thus put strong emphasis on studies at the single-cell level (4).

Microtechnologies raise the hope of dramatic breakthroughs in this field (5). For instance, compartmentalization of single cells in microchambers allows the analysis of stochastic protein expression at the single molecule level (6). In another approach, the capture of cells in microdroplets within double emulsions enables the screening of enzyme libraries with an unprecedented resolution and speed (7). In this perspective, combining encapsulation within droplets with microfluidic techniques may allow the observation and analysis of individual cells (e.g., with drugs or reagents) in a fully automated, time-resolved manner. These operations can be achieved using optical traps, but this approach remains complex and is hardly amenable to high throughput (8). In contrast, the use of classical continuous microdroplets generation techniques such as flow-focusing (9) or break-up at a T-junction (10) from a cell suspension offers potential for very high throughput, but could so far not warrant a controlled distribution of the cells in the drops (11). In these methods, the number of cells contained in the formed drops is dictated by the probability that a given volume of the initial cell suspension contains a given number of cells, following a Poisson distribution. It imposes a rather unfavorable compromise between the rate of encapsulation (total number of “positive drops,” containing one and only one cell, created per second) and the yield (fraction of the initial cell population ending up in a positive drop). A suspension containing one cell per three drops volume on average is generally used, resulting in an ≈22% rate of encapsulation for a 75% yield. To obtain reasonably pure populations of “positive” droplets, the steady-state generation of droplets from the suspension of cells is thus coupled with a detection and sorting of “positive” droplets by flow-cytometry-like technologies (12, 13). Active sorting can operate at very high frequencies, so that the presence of negative droplets does not raise serious problems regarding throughput, but it considerably increases the complexity and cost of the process. Also, in real systems, a perfectly random cell suspension is hard to achieve because of rapid sedimentation of cells in containers and pinning effects in microchannels (14). Therefore, the main issue when using these encapsulation devices in a routine mode lies in the number of droplets that contain no more than one cell. In summary, despite their strong interest for cell biology, current single-cell encapsulation processes remain delicate to tune and to maintain.

Here, we propose a different approach, relying entirely on passive hydrodynamic effects, in which picoliter droplets containing a single cell are prepared and self-sorted with high purity and yield. This system works even with highly concentrated suspensions, whatever the distribution of cells in the solution. It uses a triggered Rayleigh–Plateau instability in a jet flow (15), followed by shear-induced drift and excluded-volume-driven dispersion of the individual droplets. Its performance is characterized experimentally using a pure population of T-lymphocytes and described semi-quantitatively. We also demonstrate the robustness of the method for practical applications by directly encapsulating and sorting cancerous T-lymphocytes out of a whole-blood mixture. This method opens the route toward robust, low-cost and high-throughput molecular biology assays and diagnosis on single cells.

Design Principles

Fluidic Design.

The device consists in (i) a flow focusing region (9); (ii) a narrowed straight channel; and (iii) an expansion finally splitting into two symmetric outlets (Fig. 1A). By convention, “right” and “left” sides of the microfluidic channels are referenced to the flow direction. The stream of culture medium containing the cells is introduced in the center channel and is focused into the narrow channel downstream by two co-flowing streams of oil. The flow rate of the left oil stream Q_o is twice that of the right oil stream Q_o/2, and the flow rate of the central stream, Q_c, is always kept lower than Q_o. As discussed below, the asymmetry of the oil flow is a key feature of the system, instrumental in the hydrodynamic sorting of positive droplets.

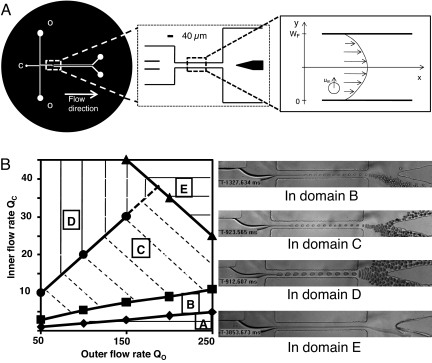
Fig. 1.

Characterization of the experimental setup. (A) Device geometry (top view). Rectangular channels with a uniform height of 30 μm. (Left) Complete circuit, c and o correspond to the cell suspension and oil inlet respectively. (Center) Zone of interest. Scale bar is 40 μm. (Right) Central channel with the coordinates used for calculating droplet migrations. Inferior (y-coordinates between 0 and W_F/2) and superior (y-coordinates between W_F/2 and W_F) regions of these schematics are denoted as right and left, respectively, in the text. The inlets are located on the low value side of the x axis, whereas outlets are located on its high value side. (B) Experimental phase diagram for droplet formation in the absence of cells as a function of oil and cell culture medium flow rates, Q_o and Q_c (μl/h). For Q_o < 50 μl/h, the device functions in dripping mode and individual droplets are formed without jetting. Domain A corresponds to unstable jetting. Above the filled triangles line (domain E), the cell medium stream is stable across the whole system. In the remainder of the diagram, the jet breaks at a stable position in the strait. The lines separating domains A–D correspond to different fixed droplet diameters: filled diamonds, Φ_N = 7 μm ± 10%; filled squares, Φ_N = 10 μm ± 10%; filled circles, Φ_N = 17 μm ± 10%. Micrographs in Right exemplify the flow stream's behavior in the different zones of the diagram.

Phase Diagram for the Jet Instability.

The hydrodynamic behavior of the system in the absence of cells (but with culture medium as the aqueous phase) is depicted in the phase diagram shown in Fig. 1B. We attribute the unstable jetting in region A of the diagram to flow oscillations due to discrete steps in the functioning of syringe pumps at very low flow rates, combined with PDMS elasticity. This domain is not useful for encapsulation and will not be discussed further. In regions B–D of the diagram, monodisperse droplets are generated at rates >1,000 s⁻¹ by jet break-up in the focusing channel. In regions B and C, the diameter Φ_N of the droplets generated by the spontaneous jet instability is smaller than or comparable to that of the cells, Φ_C. In domain E, no droplet is formed and the jet is stable through the whole fluidic system.

Mechanism of Cell Encapsulation.

When a cell suspension is used instead of empty culture medium as the aqueous phase, using flow rates corresponding to regions B or C of the phase diagram, the entrance of a cell in the focusing region induces a rupture of the jetting “neck” upstream of the position where the jet breaks in the absence of cells [Fig. 2A and supporting information (SI) Movie 1]. The cell gets encapsulated in a “positive” drop with diameter Φ_P, which is larger than that Φ_N of empty (“negative”) drops. Importantly, because the cell diameter is larger than the radial dimension of the jet, even if numerous cells flow in close vicinity, they are separated from each other by the elongational component of the flow in the focusing region. They get individually aligned with the center of the jet before encapsulation, which prevents encapsulation of multiple cells in a single droplet.

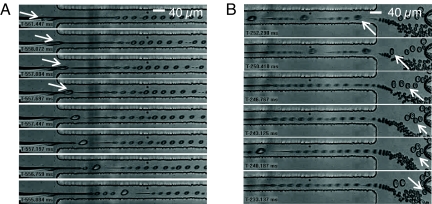
Fig. 2.

Images from video sequences of cell encapsulation obtained by high-speed videomicroscopy (negative timescale). Scale bar for each image sequence is 40 μm. Q_o = 150 μl/h; Q_c = 8 μl/h. (A) Jet neck breaking by the passage of a cell (white arrow), and consecutive destabilization of the jet (triggered Rayleigh–Plateau instability, see also SI Movie 1). (B) Sorting of positive droplets. The white arrow points to the mechanism by which some positive drops (generally those smaller than the average size of positive drops) can be “lost” when a series of closely spaced positive drops exits the focusing region: the positive droplet marked by the arrow is pushed down by the train of larger ones that follows it (see also SI Movie 2).

Single cell encapsulation can also take place in region E of the diagram because the continuous jetting is destabilized by the passage of a cell. However, this regime could not be used because this triggered instability at high flow rates also creates numerous negative “satellite” drops that perturb the subsequent sorting of positive drops.

Droplets Shear-Induced Migration.

The asymmetry in the incoming oil flow rates induces a shift of the jet position relative to the focusing channel axis. The flow in this region can be approximated by a parabolic Poiseuille profile (see Results and Discussion and SI Text for more details). Because of the small viscosity ratio between the aqueous solution and the oil (<10⁻²), the deformable droplets undergo a lateral shear-induced drift toward the center of the channel (16). The drift velocity is a strong function of the droplet diameter Φ (proportional to Φ³) and droplets spend only a few tenths of milliseconds in the narrow channel. Consequently, depending on their size, some droplets reach the focusing channel‘s center during that short time, whereas others remain on a streamline closer to the right wall (see calculations below and SI Text). This effect is used to initiate a self-sorting of cell-containing droplets in the focusing region. When working in zone B and C of the phase diagram (Fig. 1B), the size of the negative droplets formed by “natural” jet instability is smaller than that of the positive droplets, so that they exit the focusing region on a streamline closer to the right wall than the positive ones. A related effect was recently proposed in ref. 17 for the elimination of satellite droplets in microfluidic emulsification systems, but would hardly be sufficient for full separation of our drops, differing by a factor of only about two in diameter.

Drop–Drop Interactions.

We amplify the shear-induced migration sorting effect described above by a dispersion mechanism associated with steric interactions between droplets at the channel expansion (18). As the flow velocity decreases abruptly, droplets collide due to the thinning of the oil spacer initially separating them in the strait. These collisions induce a spreading of the droplets train in the transverse direction, often giving rise to “zigzag” patterns (see SI Movies 2 and 4) that strongly resemble those observed for the folding of a viscous thread in a diverging microchannel (19). The amplitude of this spreading depends on the expansion ratio of the microchannel (not shown here) and increases with the relative values of the buffer and oil flows Q_c and Q_o. This effect is instrumental in amplifying the partial segregation of positive droplets initiated in the focusing region. Indeed, in region B of the phase-diagram, negative droplets enter the expansion from streamlines closer to the right wall than positive ones, all exit by the right outlet, but push the positive droplets toward the left outlet (SI Movie 2).

Results and Discussion

Cells Encapsulation and Sorting.

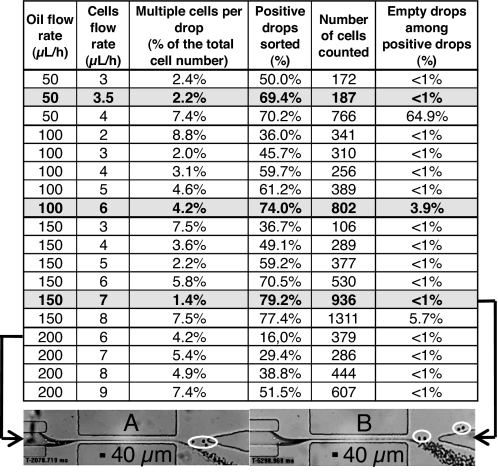
Quantitative results are provided in the table of Fig. 3. The flow combinations leading to the best yield in positive drops with minimal contamination by negative ones in the left outlet lie along the boundary between domains B and C (Fig. 1B). Decreasing Q_c, a lower fraction of positive drops gets correctly sorted: the size and volume fraction of negative droplets decrease, and their effect on positive ones becomes insufficient to drive the latter in the left outlet. Using optimal flow conditions (i.e., Q_o = 150 μl/h, Q_c = 7 μl/h), for a cell concentration around 10⁷ cells per ml, 80 ± 3% of the positive droplets are recovered in the left outlet channel with <1% of negative drops and an encapsulation rate superior to 20 cells per second (SI Movies 3 and 4).

Fig. 3.

Statistical results for cell sorting. Gray lines correspond to optimal encapsulation and sorting efficiencies at a given oil flow rate. Micrographs in A and B at the bottom of the table (20x magnification) exemplify situations of low and high efficiency cell sorting. (A) Q_o = 200 μl/h; Q_c = 6 μl/h (low part of region B in Fig. 1B): most positive droplets, circled in white, exit in the right outlet. (B) Q_o = 150 μl/h, Q_c = 7 μl/h: most positive drops, circled in white, exit in the left outlet.

Typically, 4 ± 3% of the injected cells are encapsulated as doublets or triplets in a single drop. Direct observation of the suspension in the inlet and outlet streams shows that this phenomenon is not due to the sorting process itself, but to cell–cell adhesion in the incoming stream, i.e., an intrinsic biological problem.

Noticeably, when cells arrive in the focusing region in direct contact but are not adhering, the high elongational strain separates them and leads to encapsulation of single cells in individual drops (SI Movies 3 and 4). Therefore, efficient single-cell encapsulation can be achieved even from highly concentrated solutions. With suspensions around 10⁸ cells per ml, sorting with a throughput around 160 ± 10 cells per second is achieved, without increasing the fraction of multiple cells in droplets. The relative yield of recovery of positive droplets at this concentration decreases moderately to 72 ± 3%. This “loss” is linked to a wrong addressing of some positive droplets, due to random steric interactions between them in the sorting area (Fig. 2B). These interactions lead to an extra dispersion of their position in the exiting flow, and to the delivery of some of them toward the wrong outlet. This effect is increased when the cells concentration increases, but remains marginal. Indeed, even at a concentration of 10⁸ cells per ml, positive droplets are most often separated by enough negative ones to render direct interaction between positive drops infrequent.

The recovery of positive drops is also affected by the inherent variability in size of the cell population: because the size of the final drop (and its consequent migration speed) is correlated with the size of the cell that initiated the Rayleigh–Plateau instability, smaller cells tend to exit the expansion in streamlines closer to the right side than larger ones. In the next section, we demonstrate how this effect can be used to sort the prepared droplets according to the size of the cells they contain. Specifically, we use it to sort cancerous cells out of a whole blood cell mix.

A further increase in throughput could be expected by simultaneously increasing the oil and cell medium flow rates. However, at oil flow rates above 200 μl/h, the sorting efficiency decreases due to increased deformations of positive drops, which perturb droplet–droplet interactions in the channel expansion. In addition, these strong deformations may damage certain cell types. For instance, subjecting T lymphocytes to high shear stress (although for periods of time much higher than the typical few tens of ms involved here) has been demonstrated to affect their proliferative response (20). Therefore, we avoided in the present study flow regimes likely to induce such high shear stresses.

Cells were checked for integrity and viability during and after encapsulation using a 40× objective. When using culture medium containing trypan blue, the fraction of cells collected in the outlet channel with a stained cytoplasm was equal, within experimental error, to that in the inlet (10%). This demonstrates that the cell membrane was not affected during the sorting. However, as compared with previous cell encapsulation methods, the present one leads to a small droplet volume. This is a definite advantage for the application of molecular biology protocols, for which dilution is detrimental. However, it is not advantageous for long-term cell viability, because the encapsulated cell must find in the aqueous drop the nutriments necessary for its survival. For combining this method with downstream protocols requiring live cells, it is important to add culture medium immediately after encapsulation. For this purpose, the present method can be associated with known droplet fusion methods (21). The surfactant used here (see Materials and Methods), which possesses an acid hydrophilic tail, may also be detrimental to the cell viability and interfere with some downstream cell biology or molecular biology protocols. In this case, it should be easy to transpose the technology to other biphasic systems, using e.g., a fluorinated oil with a PEG-terminated fluorosurfactant in a fluorosilanized system, to ensure more extensive biological compatibility (22). As demonstrated below, the mechanisms at play in our system are purely physical and should depend on the viscosities and interfacial tension of the oil and water phase only. Thus, they can be transposed to different fluids by adapting these two parameters.

Theoretical Estimation of the Lateral Distance Traveled by Droplets of Different Sizes.

A simple calculation for droplets shear induced migration can help understanding the striking positioning difference between positive and negative droplets in the focusing region. The behavior of deformable drops in a shear flow was described theoretically by Chan and Leal (16) for two simple geometries: a slit between two infinite walls and a circular pipe. The geometry of our strait does not correspond perfectly to any of these “solvable” cases, but we preferred to use an analytical solution clearly showing the physical processes at play rather than using difficult numerical simulations for biphasic flows (23). Thus, we model the focusing region as a slit between two infinite walls, separated by W_F = 40 μm. As shown in SI Text, using the other analytical solution and modeling the strait by a cylinder produces a comparable behavior.

Assuming a laminar Poiseuille flow, mass conservation applied to the two oil streams implies a location of their interface at ≈3/8 of the channel width (precisely 15.5 μm as measured from the right wall). Experimentally, droplets resulting from jet break-up are indeed initially located at this coordinate (15 ± 0.5 μm, Fig. 2).

Following the steps outlined by Chan and Leal (ref. 16 and SI Text) and using the coordinates of Fig. 1A, one gets for the droplets trajectory in the slit:

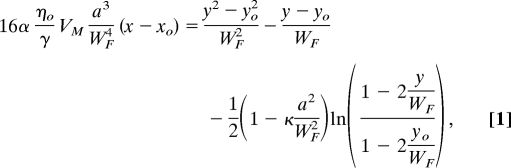where V_M is the maximum speed (at y = W_F/2), α ≈ 0.66 and κ ≈ 0.004 are dimensionless coefficients depending on the dispersed and continuous phase viscosity ratio, η_o is the oil viscosity, γ is the interfacial tension between oil and aqueous solution, and a is the drop radius.

Numerical results of Eq. 1 for lateral distances traveled by droplets starting from y_o = 15.5 μm and for (x − x_o) = 500 μm are summarized on a plot of droplet trajectories in Fig. 4, for various drop radii and an oil flow rate Q_o = 100 μl/h (γ = 5 mN/m; η_o = 120 mPa·s).

Fig. 4.

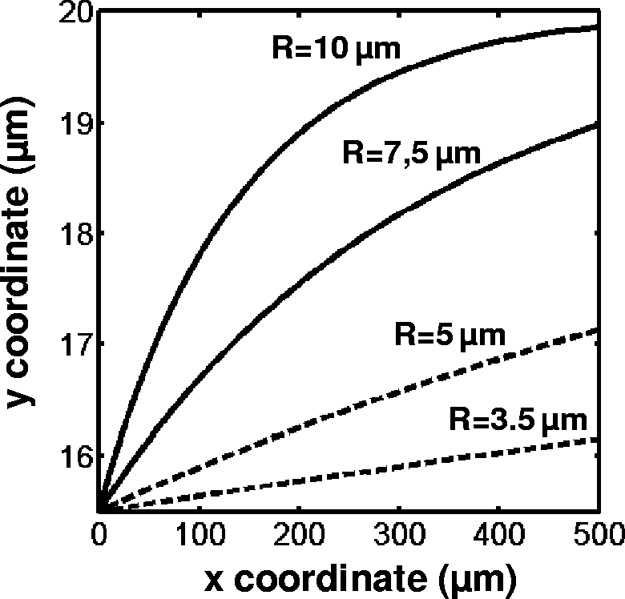
Trajectories of droplets with various radii in the focusing channel as predicted by ref. 16, assuming a 2D parabolic flow, the droplet center of mass starting from y = 15.5 μm.

These results correlate qualitatively well with our experimental observations. A clear-cut distinction appears between the positioning of negative drops (with a typical radius in the range of 3.5–5 μm), and that of positive ones (with a typical radius between 7.5 and 10 μm). Positive droplets are predicted to travel almost all of the way to the focusing region's center, whereas negative ones are predicted to travel no more than half of this distance. Moreover, Eq. 1 highlights the dependence of the droplet migration amplitude upon the maximum speed of the oil in the channel, and therefore upon the oil flow rate. That might explain the improved efficiency of our system at high oil flow rates (i.e., 150 μl/h) as compared with lower ones (50 μl/h).

It should be kept in mind that the theoretical model in ref. 16 assumes that the droplet dimension is small as compared with the microchannel's size, and that droplet deformations are small. In our experiments, the largest droplets can reach ≈1/2 of the channel's dimension, and they visibly deform in the narrow channel. Therefore, although they provide a good insight into the operation of our system, the above theoretical predictions must be considered as semi-quantitative only.

Encapsulation and Sorting of Cancerous Lymphocytes Out of Whole Blood.

The dependence of sorting efficiency upon cell size reported above suggests that our method can also allow a simultaneous encapsulation of single cells and sorting of the resulting droplets according to the size of the encapsulated cells.

To validate this approach, we use a model system consisting of a 10-fold dilution of whole blood in a buffer solution containing fluorescently labeled T lymphocytes from an immortalized cancer cell line (Jurkat). The proportion of Jurkat T cells relative to erythrocytes corresponds to the usual ratio of white cells to red cells in blood (1 Jurkat T lymphocyte per 1,000 red blood cells, RBC) and thus represents a realistic model of real-life applications.

Erythrocytes are smaller than Jurkat cells and disk-shaped. They tend to align in the jet along the disk axis, and get encapsulated into small droplets only slightly exceeding the size of negative ones. Erythrocytes-containing droplets therefore exit in the right outlet, although on the left of empty droplets (SI Fig. 6), leading to an extra spreading of the beam of negative droplets as compared with buffers containing Jurkat cells only. The leukocytes naturally present in the blood are also smaller than cancerous Jurkat cells (typically by >2 μm in radius) and also exit in the right outlet with a proper tuning of flow rates.

One Jurkat T cell is encapsulated and sorted every few seconds, against hundreds of RBC. The best compromise between purity and sorting efficiency is again obtained on the frontier between domain B and C in Fig. 1B. Starting from a population containing 99.8% RBC, 0.1% WBC, and 0.1% Jurkat T cells, we obtain in the left outlet a population containing 94 ± 3% droplets with a single Jurkat cell, and 6 ± 3% contamination by unwanted droplets (multiple encapsulation, empty drops, or drops containing normal leukocytes or RBC). Moreover, 60 ± 10% of the initial Jurkat cells are recovered. These purity and yield are slightly smaller than with pure Jurkat cells suspensions, due to the extra droplet stream spreading, but nevertheless represents a better than 10,000-fold enrichment in the cells of interest with regards to the initial cell population. This also demonstrates that the strong elongational flow at the entrance of the jet avoids encapsulation of smaller RBC together with Jurkat T cells, a very unique feature of the present method relative to earlier encapsulation processes.

Conclusions

We have proposed a microfluidic device for simultaneous cell encapsulation and sorting entirely based on hydrodynamic effects. A description of the physical mechanisms at play in the device, corroborated by a simplified theoretical model, fits our results semi-quantitatively. Using this model and the phase diagram provided in Fig. 1B, results obtained in the particular geometry used here can be extrapolated for the rapid design of other devices.

From a practical point of view, the system is low-cost, efficient, does not require any external sensing or feedback control, and, in its present version, can prepare up to 160 encapsulated cells per second with a 99% purity in positive droplets. The membrane of the cell remains intact after the encapsulation process, and the reaction of cells to various stimuli or reagents could then be screened at the single-cell level. This encapsulation process keeps the droplet volume to a minimal value (from two to eight times the initial volume of the cell) and is well suited for applying single cells molecular biology protocols adversely affected by dilution, such as PCR and enzymatic assays. Robust PCR (24) and sequencing (25) in microdroplets was recently demonstrated, and could be fruitfully combined with the present technology.

Moreover, unlike previous systems, this system operates very satisfactorily with strongly heterogeneous cell suspensions, provided that the cells do not undergo strong cell–cell adhesion, and is able to accurately sort the droplets according to the size of the encapsulated cell. This property allowed us to encapsulate single cancerous T cells out of a whole blood suspension with an enrichment yield >10,000. The sorting of cells from blood is presently a major challenge in applications of microfluidics to biology (26, 27). The enrichment and yield obtained here are not sufficient, e.g., for the direct search of micrometastasis in blood, but are high enough for molecular and genetic typing of HIV infected T cells, or for the typing of lymphomas from fine needle aspirates. Our encapsulate-and-sort method thus opens the route to a direct, high-throughput typing of single cells at the genome or transcriptome level.

Materials and Methods

Device and Materials Preparation.

The device is microfabricated in polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) using soft-lithography. The microchannel is sealed by plasma activation on a glass slide bearing a thin spin-coated PDMS layer (28). Before use, the constructed circuits are left at 65°C at least 24 h to ensure full recovery of the PDMS hydrophobicity.

Characterization experiments are carried out using human T lymphocytes (Jurkat). Cell lines are cultured in RPMI medium 1640 (Gibco) supplemented with 100 units/ml aqueous penicillin, 100 μg/ml streptomycin and 10% fetal bovin serum at 37°C in a 100% humidity atmosphere with 5% CO₂. Cell diameters range between 10 and 15 μm. Before injection in the microsystem, cells are taken from the incubator at an approximate concentration of 10⁶ cells per ml, centrifuged, and resuspended in their culture medium at a concentration of ≈10⁷ cells per ml, except when stated otherwise.

Whole blood is drawn by finger pricking in sterile conditions, diluted at 1:10 in PBS buffer with 2 mM EDTA to avoid coagulation and centrifuged. After removing of the supernatant, blood cells are resuspended (1:10 dilution relative to whole blood) in a suspension of Jurkat cells (PBS buffer with 2 mM EDTA and 1 wt% BSA, 5 × 10⁵ cells per ml) prestained with CFDMA cell tracker (Invitrogen), resulting in one Jurkat cell per 1,000 RBC on average.

We use a mineral oil (Rectapur, Prolabo) containing 5 wt% Span 80 surfactant (measured viscosity of the solution is η_o = 120 mPa·s). To ensure a good mixing of the oil and the surfactant, the oil containers are gently agitated when not in use.

Fluidic Controls.

The flow rate of the cell-containing medium is controlled using a single syringe pump (Harvard Apparatus) equipped with a Hamilton 250 μl syringe. The syringe pump is used vertically to limit the adverse consequences of cell sedimentation and adhesion on the walls of the syringe. Oil flow rates are controlled by using a double syringe pump (Harvard Apparatus) equipped with a 1-ml Exmire syringe (left channel) and a 500-μl Exmire syringe (right channel). The 500-μl syringe diameter is $\sqrt{2}$ that of the 1-ml one, and the flow rate in the right channel Q_o is thus twice the flow rate in the left channel. Syringes are connected to the circuit using Tygon tubes (inner diameter, 250 μm; outer diameter, 760 μm; Fisher Bioblock).

Data Acquisition.

Data are acquired by using high-speed video microscopy (Phantom 4.2 camera, Vision Research, mounted on an Olympus direct microscope BX41). Drop diameters in cell-free situations were calculated by automated counting of several hundred droplets using homemade macros under ImageJ (29) and comparing the throughput to the cell medium flow rate. This average diameter was consistent with the value obtained by direct image analysis of the droplet size under 40× magnification. Statistics for cell encapsulation and drop sorting were obtained by image analysis of high speed video sequences. Video observation was also used to determine the polydispersity of cells sizes, and the presence of cell–cell adhesion, occasionally leading to the encapsulation of cell doublets or triplets. All data points for cell encapsulation correspond to the statistical analysis of at least 100 cells.

Statistics for experiments on blood are carried out using high-speed fluorescence videomicroscopy to discriminate between droplets containing labeled Jurkat cells and others drops, and to visually assess the presence of a single cell in positive drops. Data correspond to counting on >100 lymphocytes (≈10⁵ cells sorted)