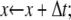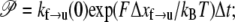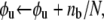Spectrin Folding versus Unfolding Reactions and RBC Membrane Stiffness

Abstract

Spectrin (Sp), a key component of the erythrocyte membrane, is routinely stretched to near its fully folded contour length during cell deformations. Such dynamic loading may induce domain unfolding as suggested by recent experiments. Herein we develop a model to describe the folding/unfolding of spectrin during equilibrium or nonequilibrium extensions. In both cases, our model indicates that there exists a critical extension beyond which unfolding occurs. We further deploy this model, together with a three-dimensional model of the junctional complex in the erythrocyte membrane, to explore the effect of Sp unfolding on the membrane's mechanical properties, and on the thermal fluctuation of membrane-attached beads. At large deformations our results show a distinctive strain-induced unstiffening behavior, manifested in the slow decrease of the shear modulus, and accompanied by an increase in bead fluctuation. Bead fluctuation is also found to be influenced by mode switching, a phenomenon predicted by our three-dimensional model. The amount of stiffness reduction, however, is modest compared with that reported in experiments. A possible explanation for the discrepancy is the occurrence of spectrin head-to-head disassociation which is also included within our modeling framework and used to analyze bead motion as observed via experiment.

INTRODUCTION

Simple flexible polymer chains extended near their contour length generally exhibit a pronounced nonlinear stiffening (see, for example, Weiner (1) who discusses a wide range of polymer elasticity models including those used herein). Multidomain proteins, such as RNA, titin, ankyrin, or spectrin, however, can undergo overstretching due to unfolding of domains or repeated folded segments (2–4). Unfolding of repeats moreover, is directly influenced by induced tension as documented in the AFM force tests reported in the literature (2–5) and as simulated via molecular dynamics (6–8). In the case of spectrin, Ortiz et al. (9) find that the unfolding process begins with the unfolding of the helical linker between repeats.

Despite the abovementioned efforts to characterize the constitutive behavior of spectrin, the effect of its unfolding on the mechanical response of a spectrin-based network such as the protein skeleton reinforcing the erythrocyte (red blood cell, or RBC) membrane remains unsolved. It is reasonable to expect that, as the membrane is sufficiently stretched, the Sp tetramers comprising the skeleton segments may lose stiffness. (Note that a loss in stiffness is meant that the derivative of force versus extension is diminished, yet remains distinctly positive as opposed to the extension-induced softening referred to in Lee and Discher (13), which has yet to be observed, and would result in network instability of a type also not yet reported.) This, in turn, implies that the entire skeletal response may be characterized as undergoing an extension unstiffening. This would be, notably, in contrast to most existing model analyses of RBC skeleton constitutive behavior which yield a continuous extension stiffening typical of flexible entropic polymer chains. Examples of such treatments are found in the literature (10–12).

Evidence for a loss of stiffness of the RBC skeleton with increasing strain has been reported by Lee and Discher (hereafter referred to as LD) (13), who experimentally resolved thermal fluctuations of single beads attached to the RBC skeleton. Essentially what they observed was that when the RBC, and thus the skeleton, was subjected to a shear strain characterized by principal stretches λ₁ > λ₂, λ₁λ₂ ≈ 1, the amplitude of fluctuation along the direction of λ₁ increased. Indeed, in a deformation with λ₁ ∼ 2, the amplitude of fluctuation in the stretching direction was observed to increase by as much as twofold compared with the unstressed state. On the other hand, along the direction of λ₂, the fluctuation amplitude decreased by 10–20%. Although full analysis of such interesting results is far from complete, and the observations remain limited, they do raise questions as to the importance of tension-induced dynamic unfolding ⇆ refolding of Sp during the deformation of RBCs. (Note that the analysis of the observations in Lee and Discher (13) was based on linear, isotropic, elastic analysis of the membrane skeleton. Moreover, no accounting was given of the connections of the beads whose motion was filmed, and thus of the dynamic response that would be affected by extension-induced changes in the behavior of such connections. Nonetheless, the fluctuations observed in Lee and Discher (13) were unquestionably increased in amplitude with stretching and this provides compelling evidence for possibility of network unstiffening, unless explained otherwise. The beads were 40 nm in diameter and bound to either glycophorin extracellularly, or to the cytoskeleton F-actin in cell ghosts.) We note, however, that there are other mechanisms that lead to reductions in membrane stiffness, and that may lead to reductions in strength. One such type of event is a shift in the dynamic equilibrium between Sp dimer head-to-head association (14,15). Comprehensive investigations are required to illustrate the mechanical consequence of each of these mechanisms and determine their contributions to membrane unstiffening.

We present a constitutive model for Sp force-versus-extension based on the notion that Sp tetramers, within the skeleton of the RBC membrane, undergo continuous transitions between the folded and unfolded states. We note that the tensile force required to completely unfold an Sp, estimated from the AFM studies of Rief et al. (4) to be ∼30 ± 5 pN, may well be beyond that achievable in the skeleton under ambient conditions prevailing during circulation. (Note also that peak loads were measured by Rief et al. (4) at extensions rates of 0.8 μm s⁻¹ and at 0.08 μm s⁻¹. As noted below, the unfolding process is thermally activated and thus rate-dependent. The peak loads thus decrease as the extension rate decreases. Rate dependence is controlled by an activation length as explained below.) Yet even at much lower tension a finite number, which is a finite fraction, of domains within an Sp will be unfolded; this fraction of domains will increase with the tensile force, F. As this happens, a reduction in compliance may result and it is this sort of phenomenology we aim to explore in the model. The process is rate-dependent and thermally activated, as explained below. Key issues that arise include 1), at what levels of Sp tension do significant rates of transition (i.e., the unfolding of repeats f ⇆ u) occur; and 2), at what rates do such transitions occur, and how do (or can) these rates affect, i.e., make their influence felt in, network response? As it happens, a pointed test of any such analysis is: can the formalism explain the observation of a decrease in fluctuation amplitude in the direction of decreasing stretch (i.e., λ₂ < 1) as observed in the experiments of LD? To do so requires that the Sp force would have had to have been, while the network was in its rest configuration, at the level where appreciable f ⇆ u transitions were in progress. Our analysis, in fact, indicates that Sp unfolding is likely to occur during biologically achievable deformations and that eventual unstiffening occurs. This happens, however, only after appreciable entropic stiffening which makes our results consistent with experimental observations that indicate such strain induced stiffening (16). Head-to-head disassociation is also explored within our framework as an alternative explanation of increased bead fluctuation amplitude. Both Sp unfolding and head-to-head association/disassociation are thereby two types of events, among others, that constitute a remodeling of the skeleton and that induce changes in constitutive response.

The rest of the article is organized as follows. In the next section, we briefly describe the molecular structure of Sp domains/repeats as used in our simulations. This is followed by the mathematical formulation describing folding/unfolding of these domains. The constitutive model is then detailed. Numerical results, including the equilibrium and dynamic responses of a stretched Sp, as well as the effect of Sp unfolding on the mechanical response of a RBC membrane skeleton, are presented. The skeleton response is studied via a hybrid model which incorporates the three-dimensional architecture of a basic unit of the skeleton, namely a junctional complex (JC), the dynamic interactions between this junctional complex and the lipid bilayer to which it is attached, and the fluid-structure interactions (17). Using this three-dimensional model, we will examine the effect of Sp unfolding on the three-dimensional configuration of the junctional complex, the shear modulus, and the thermal fluctuation of skeleton-attached beads. Finally, Discussion and Conclusions will be provided.

SPECTRIN (Sp) DOMAIN AND REPEAT STRUCTURE

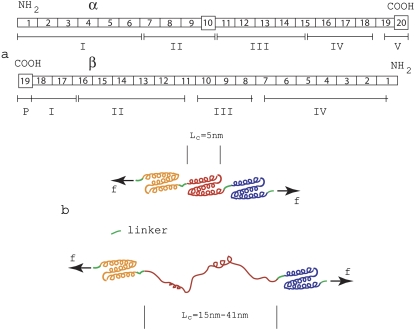
Speicher (18) has given a description of the domain/repeat structure of the α- and β-chains of spectrin proteins that we adopt herein; Fig. 1 a illustrates the domain/repeat α/β-structure as described there.

FIGURE 1.

(a) Domain/repeat structure of α- and β-spectrin (after Speicher (18)). The α- and β-units occur in antiparallel side-to-side orientation to form heterodimers that then associate via head-to-head association to form tetramers making up the segments involved within a spoked JC. Most repeat units (indicated by rectangles) are homologous and are 106 residues in length. The repeats are composed of triply folded α-helices. Repeats are connected by short linker peptides indicated in green. Nonhomologous segments are indicated by squares and have different lengths. Domains are indicated by Roman numerals and were derived via digestion and were established before amino-terminal orientation of the subunits were established. (b) Schematic illustrating a folded repeated Sp structure comprised mostly of the 106-residue repeats, and a peptide segment in which one repeat has unfolded.

Spectrin within the skeleton of an RBC, for instance, is composed of two similar peptide chains, α (with 2418 residues) and β (with 2137 residues). Sequence analysis indicates that both chains are composed mostly of repeats, 106-amino-acids long (see figure caption for further detail). The repeats are expected to fold into triply stranded α-helical coils as indicated on the top side of Fig. 1 b (19). Thus it may be estimated that the contour length, per 106 amino-acid repeat is 106/3 × 0.15 nm = 5.3 nm; the repeats are connected via a short linker adding additional length to the average repeat. (Note that, for α-helical segments, we take the rise to be 0.15 nm per residue, whereas, for nonhelical peptide segments, we assume the peptide length is 0.37 nm per residue (20).) For a completely unfolded repeat, it may be estimated that the contour length may be as large as 106 × 0.37 nm ≈ 39 nm plus the length contributed by the linker. Thus, upon unfolding, the net contour length gained may be as large as 39–5.3 nm ≈ 34 nm. Of course, the observed extension of the peptide chain is likely to be less than this as the unfolded segment will generally not be stretched to its full contour length. Indeed, the average forced extensions, estimated by fitting the wormlike chain (WLC) model to the measured force versus extension curves in the AFM tests of Sp were found to be 31.7 nm and 22 nm by Rief et al. (4) and Law et al. (5), respectively. In the case of the data of Rief et al. (4), the spacings thus estimated are seen to be quite close to the spacings observed between force peaks.

We note that Bennet and Gilligan (21) present a similar picture for the Sp structure, but with the addition of a 21st and 22nd domain (i.e., repeat) that are similar to the 106 amino-acid repeats with an eight-residue insertion. For analysis performed herein, either structural interpretation is adequate.

Unfolding versus refolding

General kinetic framework

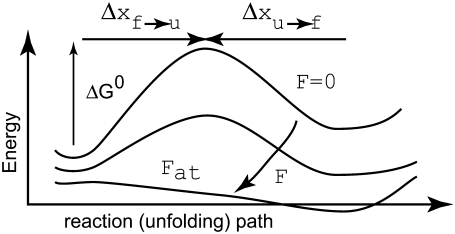
Consider Fig. 2, which illustrates the energy scheme for the transitions between the folded, f, and unfolded, u, states within an Sp domain; the caption explains the terms shown in the figure. We assume here that Sp unfolds in an all-or-nothing manner as originally envisioned by Rief et al. (4) and does not exhibit intermediate states of unfolding as described, for example, by Altmann et al. (22). Unfolding of tandem repeats, as suggested by the experiments of Law et al. (5) and analyzed via molecular dynamics (9) are possible, although statistically unlikely, events in the model presented below. Specific accounting for either phenomena is also possible within the framework of our model but, given the present level of quantitative understanding, we postpone such refinement to later reports.

FIGURE 2.

The figure illustrates the energy path along the folded ⇆ unfolded reaction path. 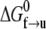is the activation energy for the process f → u when F = 0. With finite tension, the net activation energy is reduced so that 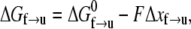where Δx_f→u is the activation length, akin to an activation volume for solid-state reactions. The activation length for the refolding transition is Δx_u→f; note Δx_u→f < 0. When F = F_at, ΔG = 0 and there is an athermal driving of all domains into the unfolded state.

We assume, following LD, that of the 76 repeats of an Sp tetramer there exist transitions, and possibly an equilibrium, between the folded versus unfolded repeats via

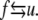(1)

Hereafter we use the subscript f to denote values corresponding to the folded state, and u the unfolded state. Similarly, f → u represents the unfolding process and u → f the refolding process. Each repeat possesses a constitutive response as described below. For now we note that the contour length of an unfolded repeat, L_u, is larger than that of a folded repeat, L_f; later we take L_f = 5.3 nm and L_u = 39 nm. The effect of this is that once an appreciable fraction of repeats reside in the unfolded state, a reduction in stiffness of the Sp is possible.

The rate of transition from the folded to unfolded state is described by an Arrhenius rate relation with an activation energy, ΔG_f→u(T,F), where T is temperature and F(>0) the force within the Sp. Now let ΔG_f→u be expressed as

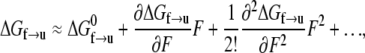(2)

where 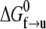is the activation energy at F = 0. An activation length may be defined as 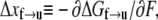with which 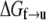may in turn be expressed as

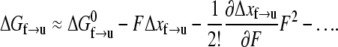(3)

For the f → u transition, we now assume that ∂Δ x_f→u/∂F is negligible along with its higher derivatives; the rate of transition then takes the form

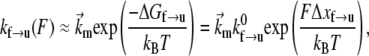(4)

where 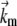is a frequency term that is related to the attempt frequency of the f → u transition and thus is dependent on the molecular (mechanical) configuration of the folded domain. The assumption of ignoring ∂Δx_f→u/∂F and higher derivatives is here similar to Bell's linear approximation (23) as recently discussed by Ng et al. (24) or to the assumption of a sharp barrier for unfolding as discussed by Evans and Ritchie (25) in their analysis of the unfolding of titin domains. The temperature-dependent quantity 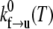is the exponential term containing the activation energy at zero F. Heuristically the activation length, Δx_f→u, may be seen as a measure of the distance through which the force acts in attaining the transition state along the f → u path. Neglecting terms involving the derivatives of Δx_f→u with respect to F appears reasonable, based on molecular dynamics simulations of Sp unfolding (6) that illustrate the localized nature of the transition state. However, more compelling justification for using the linear approximation in our present modeling rests upon the consistency it provides in describing the forced unfolding data of Rief et al. (3,4) and Law et al. (5), as described below. For the reverse transition, we use a similar approximate form

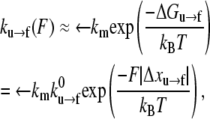(5)

where we have highlighted the fact that Δx_u→f < 0, which means that F ≠ 0 retards the refolding process, by placing |Δx_u→f| in the exponential. We note that the implied assumption of the simple exponential dependence on force that derives from the linear approximation made above is undoubtedly far more approximate for the refolding reaction. As explained below, however, refolding does not likely occur at appreciable rates during the sorts of deformations we simulate, and thus, the approximation appears justified, as long as Δx_u→f is approximated large enough to account for this fact.

We now let N be the total number of Sp domains, N_u be the number of those unfolded, N_f the number folded, φ_u = N_u/N the fraction unfolded, and φ_f = N_f/N the fraction folded; clearly φ_f = 1 − φ_u. At equilibrium we have balanced rates for f ⇆ u, or

(6)

which leads to

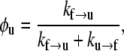(7)

or

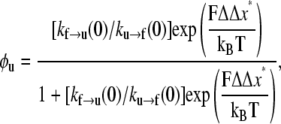(8)

where ΔΔx* = Δx_f→u − Δx_u→f. The terms k_f→u(0) and k_u→f(0) simply denote the expressions in Eqs. 4 and 5 evaluated at F = 0. Now define F_1/2 as the level of Sp tension such that φ_u = 1/2. We find from Eq. 8 that

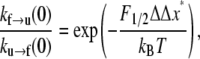(9)

which reveals the key role that the parameter F_1/2 plays in the constitutive response. To understand the numerology here, i.e., to assess the possible magnitudes that F_1/2 must have, note that k_u→f (0)/k_f→u(0) > 1 and in fact it is most likely that k_u→f(0)/k_f→u(0) ≫ 1, and thus F_1/2ΔΔx*/k_BT > 1. The assumption that k_u→f(0)/k_f→u(0) ≫ 1 is supported by the kinetic data of Clarke and co-workers (26,27), who report values of rate constants for the folding and unfolding of the 15th, 16th, and 17th repeats of chicken brain α-spectrin. Their data indicate that, at minimum (i.e., for repeat 17), k_u→f (0)/k_f→u(0) > 20; for repeats 15 and 16, the ratios are considerable larger. Accordingly, the requirement that F_1/2ΔΔx*/k_BT > 1 is meant to ensure that, at rest, the Sp are seen as mostly in the folded state. If, for example, ΔΔx* ≈ 12.6 nm is used as an estimate below, then F_1/2 ≈ 0.3 pN, just to make the ratio k_u→f (0)/k_f→u(0) = e. Thus F_1/2 = 0.3 pN would appear to be a lower limit. On the other hand, if F_1/2 = 5 pN, with the same value of ΔΔx* ≈ 12.6 nm for the net activation lengths, k_u→f (0)/k_f→u(0) = e¹⁵ ≈ 4 × 10⁶, high enough to ensure that almost all domains are folded at zero force.

For reference, we may also note that with the above we may express φ_u as

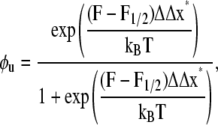(10)

with which we may explore the fraction, φ_u, at F = 0 via

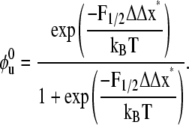(11)

We note that an equilibrium constant may be obtained for the reaction f → u defined as K_d = φ_u/φ_f, and from Eq. 10,

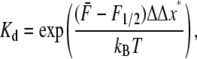(12)

where we have used the symbol 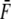in Eq. 12 to note that in a true ensemble of Sp the equilibrium constant would be determined from the average, or characteristic, force acting on the Sp. (Note that strictly speaking, in calculating the unfolded fraction for an ensemble of Sp molecules, one must consider the distribution of forces acting on different molecules and integrate over all forces.) From this we have

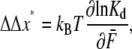(13)

which suggests an experimental method for obtaining values for the combined activation length, ΔΔ x*. The method has, in fact, been employed by Liphardt et al. (2) for RNA unfolding.

Rate constants and the activation length

Clearly knowledge of the activation lengths, Δx_f→u and Δx_u→f, is important for establishing the kinetics of f ⇆ u transitions, and in particular the force dependence. Limited data exists so only preliminary estimates may be made at this time. Rief et al. (4), however, performed their AFM pulling tests at two rates, 0.08 μm s⁻¹ and 0.8 μm s⁻¹. Let x be the end-to-end distance projected to the direction of F, and its time derivative 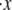represents the rate of extension. To estimate the activation length, Δx_f→u, we note that the force dependence of 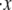due to the f ⇆ u transition is in the form 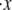∝ exp(F*Δ x_f→u/k_BT), where F* is the most probable unfolding force or a characteristic unfolding force, as defined in the analysis of Evans and Ritchie (28). Thus, the activation length may be obtained from

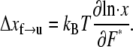(14)

In fact, given the linear approximation used here, Eq. 14 may also be extracted from the analysis of Evans and Ritchie (28) (see, for example, Eq. 7 of (24) who review the Evans and Ritchie theory as applied to protein unfolding). From the data in Rief et al. (4) (see their Fig. 6) it may be estimated from the first peaks in load that the difference in peak load was ∼5 pN. Thus from Eq. 14 we estimate Δx_f→u ≈ 2 ± 0.5 nm. We later compare our Monte Carlo simulations with the experimental measurements in Rief et al. (4) and show that Δx_f→u ≈ 2.1 nm yields a best match. Note that, as is typical in reaction rate theory, smaller activation volumes, and in our case activation lengths, imply a stronger rate dependence with respect to the value of force. This was noticed by Rief et al. (4) in connection with the difference in the magnitudes of the forces required (at comparable rates) to unfold titin molecules whose estimated activation lengths were approximately a factor of 5–6 smaller; in fact, the forces required to unfold titin were measured to be larger by the same factors. Unfortunately, at this time data that would allow estimates of Δx_u→f are unavailable. On the other hand, observations of refolding after unloading of Sp (4) indicate that Sp segments refold, but only after the extended segments are relaxed completely. (Note that the refolding observations of Rief et al. (4) were made by completely relaxing Sp segments. No partial unloading or fixed force tests were reported, however, that may have indicated refolding at reduced yet finite tension.) Similarly, Rief et al. (3) noted that refolding of titin was not observed until the extended chains were nearly completely relaxed. This, in turn, suggests that |Δx_u→f| is, in fact, almost certainly larger than Δx_f→u. Hereafter we assume that |Δx_u→f| = 5Δx_f→u. This explains the earlier estimate of ΔΔx* ≈ 12.6 nm. We note that we have determined that variations of |Δx_u→f| from the above estimate confirm that imperceptible differences result in all the results that we present below. For this reason, we ignore refolding events in our simulations of dynamic unfolding of Sp. We note herein that although the choice of Δx_u→f appears to be arbitrary, we have shown through numerical tests that if this value is sufficiently large it does not have a significant effect on the results. For example, in the equilibrium force-extension curves (see Fig. 3), we find that an increased Δx_u→f leads to flatter plateaus, while there is no significant change in the amount of extension related to unfolding.

FIGURE 6.

Schematic of a single JC unit coupled with its lipid bilayer. One end of the protofilament (the pointed end) is capped by E-Tmod and is marked by an asterisk.

FIGURE 3.

(a) Force versus extension response for the folded-unfolded Sp with various values of F_1/2 used. For all cases, p_f = 2.5 nm and p_u = 0.5 nm, L_f = 5.3 nm, L_u = 39 nm, Δx_f→u = 2.1 nm, |Δx_u→f| = 5Δx_f→u, and N = 19. Note that not until F_1/2 ≽ 2 pN does the response exhibit a reduction in stiffness with extension (for a limited range of extension). (b) Same as panel a, except that p_u = 0.8 nm.

As far as k_u→f (0) is concerned, we note from Eq. 9 that

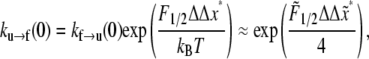(15)

where in the second expression on the right, and for convenience of association with the familiar units used for the parameters, 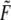is measured in pN and in nm and T ≈ 37°C. Also for the rates under the action of finite force,

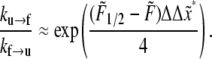(16)

THE CONSTITUTIVE MODEL

Equilibrium constitutive relations

We consider first the constitutive response of an Sp deformed slowly enough that local equilibrium between folded and unfolded domains prevails. In this case (and even if equilibrium does not prevail), the projected end-to-end length, x, of an Sp is just the sum of the lengths of its constituent domains, and thus

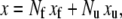(17)

where x_f and x_u are the projected extensions (i.e., the end-to-end length projected onto the direction of F) of folded and unfolded domains, respectively. When x is normalized by NL_f, for example, and noting that N_f = N − N_u, we have

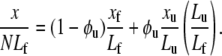(18)

Since all the domains are in series they share the same extension force F. Models are needed for the extension-versus-force response of both folded and unfolded domains, i.e., for x_f/L_f and x_u/L_u versus F. For this we use a freely jointed chain model, obtained from a stress ensemble (see e.g., Weiner (1)) and write

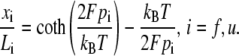(19)

In Eq. 19, p_i is the persistence length of either a folded or unfolded domain (i = f, u). We note that Eq. 19 may be expressed as x_i/L_i = ℒ(2Fp_i/k_BT) where ℒ(ζ) = coth ζ − 1/ζ is the Langevin function. The full constitutive response is then

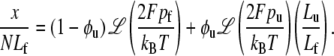(20)

The approximation of the Langevin function for small ζ is given as 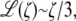so that for sufficiently small F, we extract a linear response

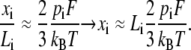(21)

Therefore, when Fp_i/k_BT ≪ 1, we have

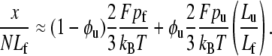(22)

In equilibrium, φ_u is given through Eq. 10.

Time-dependent response: Monte Carlo methods

An effective way to explore the potential influence of nonequilibrium, and thus rate-dependent, domain unfolding-refolding is to simulate the process via a Monte Carlo method. Below we list a simple algorithm that includes the kinetics of unfolding; refolding is not explicitly included as we intend this to be used only for monotonically increasing load where the incidence of refolding would be quite rare. The stochastic process is meant to simulate the monotonic AFM experiments of Rief et al. (3,4) and Law et al. (5). The procedure involves imposing a constant rate of stretching, and to perform this in time steps, Δt. After each time step, the force on the Sp is computed via Eq. 20 and the probability of unfolding, 𝒫(F), is computed from 𝒫(F) = k_f→u(0) exp (FΔx_f→u/k_BT)Δt. Each folded domain is then polled to judge whether it should be unfolded at the new time t = t + Δt. A simple algorithm implementing this scheme for an N repeat Sp segment is

• 0. Set the stretching rate,

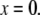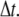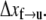• Set Set Set Set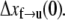

Do while

1. 

2. Calculate force, F, via Eq. 20;

3. Compute

4. Poll each folded domain for unfolding (n_b unfolds found?)

   • 4.1 update
   • 4.2 recompute force, F, via Eq. 20,
   • 4.3 record (F, x), loop to 1,

   end.

RESULTS

Equilibrium extension of individual Sp chains

Fig. 3 shows, via Eqs. 10 and 20, the force-versus-extension responses for a given set of the parameters p_f, p_u, and ΔΔx*, and the force-versus-extension responses for various levels of F_1/2. Note that the type of response, e.g., whether extension unstiffening is exhibited depends sensitively on the value of F_1/2. Such behavior is also sensitive to the values taken for the other parameters. For example, the two figures use identical parameters except for the value of p_u, which is chosen as 0.5 nm and 0.8 nm in Fig. 3, parts a and b, respectively. With the parameters described in the caption to Fig. 3, parts a or b, we note that only when F_1/2 ≽ 2 pN is significant, is extension unstiffening observed. Unstiffening per se, however, is observed at all values of F_1/2. Unstiffening occurs when F/F_1/2 ≿ 0.75 or at F ≈ 1.5 pN if F_1/2 = 2 pN. If F_1/2 = 3 pN, unstiffening begins when F ≈ 2.25 pN, and so on. To put this in perspective, we note that when F_1/2 = 5 pN, the Sp extension where unstiffening is first observed is at ∼x/NL_f ≈ 0.8. The extension of Sp in a junctional complex in the membrane of an RBC at rest is often taken as (x/NL_f) ≈ 0.33 (12); this would suggest that unstiffening is expected to set in at stretches corresponding to λ ≈ 2.4. In fact, inspection of Fig. 3, a and b, reveals that unstiffening effectively begins at values of extension near x/NL_f ≈ 0.7–0.8 for all the values of F_1/2 considered. To put this in the perspective of the time-dependent simulations described next, we recall from Eq. 4 that the unfolding rate is proportional to exp(FΔx_f→u/k_BT). But polymer-force-versus-extension relations of the type used to describe Sp are such that as the extension approaches the contour length, i.e., as x/NL_f→1, F ∼ 1/ε where ε = 1 − x/NL_f. Thus, as ε→0—that is, as the extension approaches the contour length—the rate and probability of unfolding dramatically increase, in fact as exp(1/ε) as ε→0. As is seen in what follows, this leads to the paradigm that “unfolding occurs at critical values of extension” and is further seen to be rather insensitive to other parameters in contrast. This could provide a consistent rationale for the results of LD, as noted above—assuming that enough time is elapsed during LD's loading of the RBC before the fluctuations are observed.

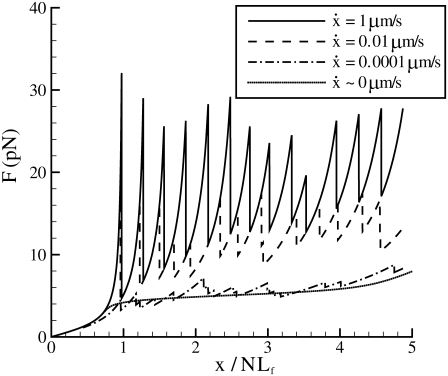
Dynamic unfolding of a single Sp monomer via Monte Carlo simulation

Monte Carlo simulations for single Sp were carried out via the simple algorithm given earlier. In these, simulations after the AFM forced unfolding observations of Rief et al. (4) and Law et al. (5) were conducted as described next. The parameters used were based on the spectrin structure mentioned above, as well as experimentally measured values (4,5). We have: p_u = 0.8 nm, p_f = 2.5 nm, L_u = 39 nm, L_f = 5.3 nm, k_f→u(0) = 3 × 10⁻⁵ s⁻¹, and Δx_f→u = 2.1 nm. As shown in Fig. 4, the computed force-versus-extension response clearly demonstrates sawtooth characteristics consistent with experimental observations. Quantitatively, the Monte Carlo results also compare well with experimental measurements. According to the AFM measurements by Rief et al. (4), the average unfolding force is ∼27 pN (at 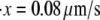), and 32 pN (at 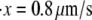) (measured from Fig. 7 in (4)). These measurements are close to our Monte Carlo simulations, which predict that at the two stretching rates, the numerical results are 26 pN (with a standard deviation of 3.8 pN) and 31.9 pN (with a standard deviation of 3 pN), respectively. In addition, according to the Monte Carlo simulations the average peak-to-peak distances in the force-versus-extension curve are 29.8 nm (at 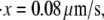with a standard deviation of 6.5 nm), and 30.7 nm (at 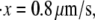with a standard deviation of 4.8 nm). As noted, these levels are consistent with those observed by Rief et al. (31.7 nm).

FIGURE 4.

Monte Carlo prediction of the force versus extension of an Sp with 19 repeats at different stretching rates. Also plotted is the equilibrium solution ().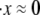

FIGURE 7.

(a) The natural state, (b) an anisotropically deformed state, and (c) an idealized picture of a single JC.

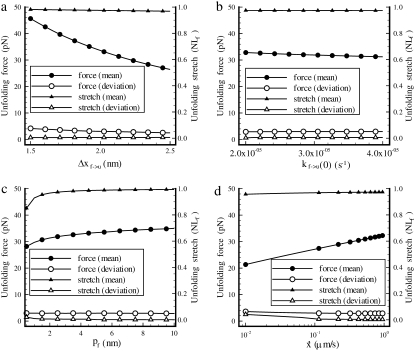
Sensitivity studies were performed with respect to key parameters including the persistence and activation lengths. Results for the effects of varying Δx_f→u, k_f→u(0), p_f, and 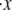are summarized in Fig. 5.

FIGURE 5.

Effects of variations in (a) Δx_f→u, (b) k_f→u(0), (c) p_f, and (d) 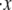to the unfolding force (in pN) and the amount of stretch where the unfolding occurs (normalized by NL_f). While changing one parameter, the other parameters are kept as: p_u = 0.8 nm, p_f = 2.5 nm, L_u = 39 nm, L_f = 5.3 nm, k_f→u(0) = 3 × 10⁻⁵ s⁻¹, Δx_f→u = 2.1 nm, and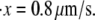

As expected, the effect of increasing the activation length on the observed unfolding force levels is to decrease the force peak levels with increasing Δx_f→u (Fig. 5 a). In fact, since the force and activation length appear in the rate relations as the product FΔx_f→u, we expect that the sensitivity curve may be of the form FΔx_f→u = constant; in fact, the relation FΔx_f→u ≈ 60 describes the curve well. The observed stretch at unfolding is, in contrast, markedly insensitive to varying Δx_f→u, as shown in Fig. 5 a. Instead, we observed that unfolding occurred when x ≈ 0.975NL_f ; the plotted standard deviation in the values of stretch indicates how insensitive the value of unfolding stretch is to Δx_f→u. The effects of varying persistence length, stretching rate 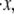and k_f→u(0) on the unfolding force and extension were explored via similar simulations as described next.

Fig. 5 b shows the effect of the rate constant k_f→u(0) on the unfolding force and the stretch at unfolding, respectively. As seen earlier with respect to sensitivity to activation length, the stretch at unfolding is insensitive to parameters that directly affect the transition rate. Unfolding is seen to occur when x ≈ 0.96NL_f. The force at unfolding is dependent on activation length and this dependence may be approximately described by setting k_f→u(0) exp(FΔx_f→u) = constant. The accuracy of such an approach to scaling this dependence is not as high as found earlier but does provide a reasonable guideline. The dependence on persistence length, p_f, is shown in Fig. 5 c. In this case, both the unfolding force and the stretch at unfolding are seen to be sensitive to p_f, since the tension generated within an Sp is inversely dependent on persistence length for a given stretch. Nonetheless, it is found that over the full range of p_f studied (see 0.5 nm ≤ p_f ≤ 10 nm), the stretch at unfolding varies only over the range 0.85NL_f ≤ x ≤ 0.99 NL_f.

Particularly revealing is the dependence of the average unfolding force and the stretch at unfolding on the rate of stretching, 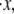shown in Fig. 5 d. The observed rate dependence of the unfolding force follows from what has been said earlier. Fig. 5 d, however, provides additional evidence for the validity of the paradigm of a critical stretch at unfolding; here again it is observed via the simulations that unfolding occurs, regardless of 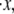when x ≈ 0.96NL_f, at least for the range of stretching rates included in the figure. We note, however, that for rates 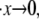the stretch at unfolding will decrease further and eventually toward values more like x ∼ 0.76NL_f as discussed in connection with Fig. 3.

In the perspective of the dynamic deformation of a RBC membrane skeleton at which the Sp segments would be expected to unfold, we note first that in the “rest (or natural) state,” an Sp dimer is stretched to the end-to-end lengths in the range 30 nm ≤ x₀ ≤ 44 nm (13). As it was seen that unfolding occurs when x → 0.9NL_f, this means that that the expected stretch at unfolding is in the expected range 2 ≤ λ ≤ 3. In the example simulations described next, x₀ is taken as x₀ ≈ 40 nm.

Quasi-static and dynamic shearing of a single JC

In the following simulations, we will apply our constitutive model and examine the shearing deformation of a single JC in the membrane of an erythrocyte.

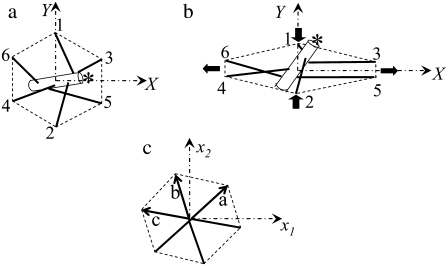
Unlike the complicated three-dimensional cytoskeletons of other cells, a mature human erythrocyte has only a thin (yet three-dimensional) skeletal protein network beneath the lipid bilayer. The network is composed of several major proteins: α- and β-spectrins, ankyrin, band 3, protein 4.1, protein 4.2, and actin, as well as some minor proteins such as myosin, tropomyosin, and tropomodulin (E-Tmod). Structurally, the network is organized into ∼33,000 repeating units (29–31). Each basic repeating unit is called a junctional complex (JC), including an actin protofilament, up to six pairs of αβ heterodimers, and suspension complexes that tether the JC to the lipid bilayer. Based upon a three-dimensional model of the JC (32,33), we have developed a hybrid model to simulate the fluid-structure interactions involved in the dynamics of the JC and its coupling with the lipid bilayer (17). This model combines a Brownian-dynamics model of the protofilament, a Fourier-Space-Brownian-Dynamics (FSBD) model of the lipid bilayer (34,35), and a WLC model of the Sp dimers (36). In the following, we outline the basic assumptions and the mathematical formulations of this hybrid model.

Hybrid modeling of a JC coupled with its lipid bilayer

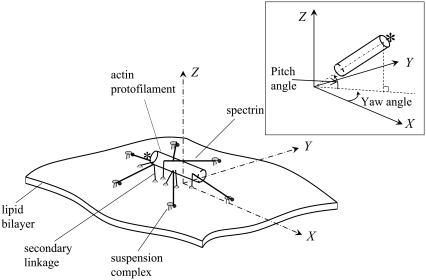
As shown in Fig. 6, we consider the dynamic response of a single JC, containing six long αβ spectrin dimers radiating from a central short actin protofilament, six suspension complexes (SC) (including ankyrin, band 3, and protein 4.2), and secondary linkages between the actin protofilament and the lipid bilayer via protein 4.1 and the transmembrane glycophorin C.

In the hybrid model, the actin protofilament is modeled as a rigid circular cylinder with length 35.75 nm and radius 4.5 nm (32,33). The Sps are modeled as entropic springs. The secondary linkages are modeled as linear springs. The heaving motion h of the lipid bilayer is governed by the nonlocal Langevin equation,

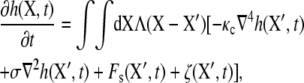(23)

where X = (X, Y) is the horizontal position vector in a global space-fixed Euler coordinate system (X, Y, Z) (see Fig. 6). The X,Y plane corresponds to the undisturbed lipid bilayer, and Z points toward the JC. Λ(X − X′) = 1/8πη|X − X′| is the diagonal component of the Oseen hydrodynamic tensor, η is the dynamic viscosity of the surrounding fluid, and κ_c the bending modulus of the bilayer (so that −κ_c∇⁴h is a force imposed on the lipid bilayer due to bending). Similarly, due to the existing tension, σ, there is an induced force σ∇²h in the bilayer. Following our previous work, we choose σ = 10⁻⁴ N/m so that the bending and the pretension contribute equally to the deformation of the bilayer. The values F_s(X′, t) and ζ(X′, t) are the interaction (steric) force and the random thermal fluctuation force, respectively (all forces are measured per unit area of the bilayer). A detailed description of these forces is found in Zhu et al. (17).

In this analysis, our focus is on membrane fluctuations with wavelengths comparable to or smaller than the size of a single JC (∼100 nm). Fluctuations with larger wavelengths (e.g., 0.1–1 μm) were studied by using a coarse-grained model assuming that the membrane skeleton behaves as a rigid shell (37); a similar model has been applied to examine correlations between skeleton defects and membrane fluctuation (38). The skeleton was found to have a dual effect. First, its presence imposes an overall confinement that restricts the elevation of the bilayer. This effect was conveniently modeled by replacing F_s in Eq. 23 with a harmonic potential. Second, the skeleton increases the tension inside the bilayer by two orders of magnitude, as confirmed later by measurements of membrane fluctuations using an optical interferometry technique (39).

The motion of the protofilament is described using an Euler-Lagrangian dual-coordinate system, including the Euler coordinate system (X, Y, Z) defined above, and a local actin-fixed Lagrangian reference frame (l₁, l₂, l₃). The origin of the Lagrangian coordinate system is at the center of the protofilament, l₁ is tangential to the protofilament aligned toward the pointed end capped by E-Tmod, and both l₂ and l₃ are perpendicular to l₁. The transformation between the Euler coordinate system and the Lagrangian coordinate system is performed through a robust Euler parameter approach, which eliminates the well-known singularity of the more conventional Euler angle method.

A Sp dimer connects with the protofilament near its tail end at the β-spectrin binding site (32). In the Lagrangian coordinate system (l₁, l₂, l₃), these binding sites on the surface of the protofilament are given in Zhu et al. (17). The other end of the Sp connects to the lipid bilayer through a SC, modeled as a mobile point inside the bilayer. The X, Y position of a SC within the lipid bilayer (the horizontal motion) is either fixed (in equilibrium simulations), or prescribed (in dynamic simulations). It then follows the heaving motion of the bilayer.

Due to the small length scale of the problem, the inertia of the protofilament is negligible so that its motion is determined by the balance among the hydrodynamic viscous drag exerted by the surrounding fluid, the Brownian force/moment, F^(ζ), M^(ζ), the force and moment exerted by Sp, F^(s), M^(s), and the repulsive force/moment due to its interaction with the lipid bilayer, F^(b), M^(b). Measured in the Lagrangian coordinate system, its translational velocity (u₁, u₂, u₃) and rotational velocity (ω₁, ω₂, ω₃) are thus given as

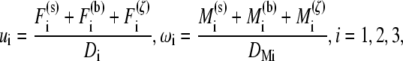(24)

where D₁ is the tangential drag coefficient along the protofilament and D₂ = D₃ are the normal drag coefficients. D_M1, D_M2, and D_M3 are the drag coefficients associated with rotations around the l₁, l₂, and l₃ axes, respectively. The exact value of these coefficients are obtained by using the Stokeslet approach (40) and the slender body approximation (41).

Equation 23 is solved by using an efficient FSBD algorithm. It is then coupled with the protofilament whose motion is described by Eq. 24. The details of the FSBD method, as well as the bilayer-protofilament interaction (including the parameters that characterize the intensity of this interaction), are given in Zhu et al. (17) and are thus skipped.

In our model, we replace the WLC model for the force-extension relation of an Sp dimer used in the previous study with the constitutive relation incorporating unfolding behavior as discussed before. A difficulty is that it is not straightforward to adopt the α (or β) monomer constitutive model developed above for simulation of αβ heterodimers. Apparently, the coiled-coil α- and β-subunits in a heterodimer are arranged as parallel springs. The detailed configuration of this structure (e.g., the different contour lengths of α- and β-subunits) suggests that it is quite unlikely that the extension force is distributed equally between the two subunits. A possible scenario is that during extension one of the subunits bears the bulk of the force until it unfolds. The unfolding will then trigger a force redistribution so that the mechanical loading may be shifted between the two subunits alternatively. This process is further complicated by the existence of side-bonds between the subunits. A comprehensive modeling of the Sp dimer in large deformations thus requires extensive studies via AFM, MD, or other techniques. Until such a model is available, we will use a simplified approach by assuming that the heterodimer behaves similarly to a monomer with some difference in kinetic parameters. In this approach, we choose most of the parameters to be consistent with those of the α- or β-spectrin monomers as given before. For our JC model to yield a prediction of the shear stiffness consistent with the reported value in the literature (see e.g., (42–44)), we use p_f = 8 nm. In addition, we assume F_1/2 = 5 pN, p_u = 0.8 nm, and the total number of repeats to be N = N_f + N_u = 19. It is helpful to note that although the p_f we use here is much larger than the one which yields best predictions of the unfolding force (p_f = 2.5 nm), it is still within a reasonable range since the unfolding force is relatively insensitive with respect to p_f according to our tests (see Fig. 5 c). It is further supported by the fact that the persistence lengths of each subunit in a heterodimer should be larger than those of a standalone subunit owing to the interaction between the two subunits which imposes a confinement on the fluctuations. It therefore is consistent with the scenario that at any given moment, the mechanical loading is sustained mostly by one subunit.

We also assume herein that that all repeats have identical unfolding/refolding characteristics. In fact, the evidence is that this is an approximation and that the various repeats along an Sp have different levels of stability (18,26,27). The repeats studied by forced AFM are more likely among the more stable and thus a full accounting for variable repeat stability will add additional precision to the model. Here we explore a range of parameter space to probe the effect of varying repeat stability.

The simplification of the heterodimer configuration may affect the accuracy of our model in describing the exact sequence of unfolding, and consequently the mechanical properties of the JC during dynamic deformations (see Fig. 8). However, based upon our discovery that unfolding starts whenever the Sp is stretched close to its fully folded contour length, it is reasonable to conclude that the simplified model will provide accurate predictions of the start of unfolding and unstiffening as discussed later, as well as the equilibrium mechanical responses.

FIGURE 8.

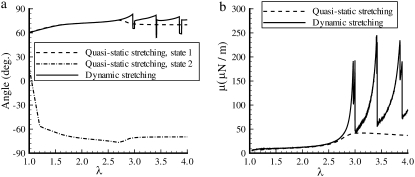
Equilibrium (quasistatic) and dynamic response (T_s = 0.01 s) of a single JC when it is stretched continuously from its natural state (λ = 1) to an anisotropically deformed state (λ = 4). The plotted are (a) the yaw angle and (b) the shear stiffness μ. The pitch angle is <3° in all cases.

Another important difference between this model and the one described in Zhu et al. (17) is that the secondary JC-bilayer linkages, consisting of six pairs of glycophorin C and protein 4.1, are now included and modeled as six linear springs with spring constant k_s. The top end of each spring is attached to the protofilament at the same location as the Sp-protofilament attachment (45). The bottom end is embedded in the lipid bilayer and follows the heaving motion of the bilayer. In addition, the bottom end (corresponding to glycophorin C) is modeled as horizontally mobile with mobility m_s. In the following simulations, we assume that k_s = 10 μN/m, which effectively limits the pitch angle to be <3° (without thermal fluctuations) in all the cases considered in our study. The choice of m_s is based upon the following estimation. Although glycophorin C (with one transmembrane domain) is a much smaller molecule than band 3 (with multiple transmembrane domains), its mobility should be just a little larger than that of band 3 owing to the logarithmic relation between the mobility of a membrane-embedded molecule and its size (46). The mobility of band 3 within the bilayer has been estimated to be 1.28 × 10⁸ m/Ns based on its short-range diffusivity (35). Thus in our simulations we choose m_s = 2 × 10⁸ m/Ns. For more accurate simulations, precise values of k_s and m_s are required, which unfortunately are not currently available.

In our previous study, we applied two different modes of Sp-protofilament junction, that is, a point attachment and a molecular wraparound type of connection. In a point-attachment junction, Sp dimers are connected to the protofilament at a single point corresponding to the proposed β-spectrin binding site on the G actin (32). Correspondingly, in our numerical model the six Sps are pinned at the outer surface of the circular cylinder representing the protofilament. In a wraparound junction, on the other hand, the α- and β-spectrins branch and reconnect at the backside of the protofilament, providing a possible mechanism of torque mitigation. In terms of JC response, the most pronounced difference between the point-attachment junction and the wraparound junction is that the latter effectively limits the pitch angle of the protofilament and is therefore more consistent with experiments (47,48). We see herein that even if the point-attachment junction is applied, by including the secondary linkages the pitch angle of the protofilament is also restricted. The computations hereafter are performed with the point-attachment model.

Equilibrium and dynamic response of the JC to in-plane deformations

We assume that in its natural state the six SCs in a JC form a regular hexagon with a radius of 40 nm (Fig. 7 a). A general in-plane stretch of the JC, corresponding to a topology-conserving redeployment of the SCs within the lipid bilayer, can be represented as a stretching along an arbitrary axis within the X,Y plane (denoted as axis 1) by a ratio λ₁, plus a stretching by a ratio λ₂ along an second axis which also lies within the X,Y plane and is normal to axis 1. The angle between axis 1 and the X axis, measured counterclockwise, is defined as the deformation angle. Two special cases, an equibiaxial deformation and an anisotropic deformation, have been considered. The equibiaxial deformation refers to an in-plane stretching in which λ₁ = λ₂ = λ. The anisotropic deformation corresponds to an area-preserving shearing, i.e., λ₁ = 1/λ₂ = λ (Fig. 7 b). Our current modeling efforts will be focused on anisotropic deformations with deformation angle 0°. To relate the deformation ratio λ to the Sp extension x/NL_f, we note that at the natural state (λ = 1), the extensions of Sp₁ to Sp₆ are, respectively, 0.46, 0.45, 0.40, 0.39, 0.36, and 0.36. As λ is increased, Sp₁ and Sp₂ are shortened and the other four are elongated. For example, at λ = 3, the extensions of Sp₃ to Sp₆ are all ∼1.0, close to the starting point of unfolding as shown in Fig. 3.

The shear modulus of the JC undergoing finite deformations is calculated by using the method described by Evans and Skalak (49) based upon the strain energy Φ^(s) stored in the Sp dimers. In this approach, an arbitrary deformation is characterized by two independent deformation parameters α = λ₁λ₂ − 1 and 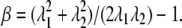Here α represents area change, and β a change of aspect ratio or eccentricity. The shear modulus, μ, is then given as

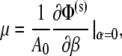(25)

where A₀ is the reference area, which is the projected area occupied by the JC (the hexagon). The value α = 0 corresponds to the anisotropic deformation. The potential energy stored inside each Sp dimer is calculated by integrating its internal tension timing the extension, starting from the natural state. Φ^(s) is then evaluated by summing up the total potential energy in the six dimers.

In the following, we consider a shearing process, in which the JC undergoes an anisotropic deformation starting from its natural state (λ = 1) to a deformed state (λ = 4) within a time interval T_s. To achieve this, we prescribe the X,Y locations of the six SCs as functions of time so that λ increases linearly with time from 1 to 4.

Fig. 8 shows results for the attitude of the protofilament, i.e., the yaw angle (see the inset of Fig. 6 for a definition), and the shear modulus μ of a JC in an anisotropic extension. No thermal fluctuations are included in the simulation. As shown in Fig. 8 a, in a quasistatic simulation (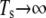), a bifurcation exists over the whole range of λ. One of the equilibrium states is characterized by a yaw angle at ∼70° (state 1) and the other at −70° (state 2). As we have illustrated in Zhu et al. (17), with thermal fluctuations included, the existence of bifurcation may cause mode switching (the frequent switching of JC configuration between the two equilibrium states). Our current results, as well as the results reported in Zhu et al. (17) indicate that the two equilibrium states are often approximately symmetric with respect to axis 1 (the stretching axis). Therefore, while considering the thermal fluctuation of a protofilament-attached bead as discussed below, this mode switching is expected to contribute to the motion of the bead along axis 2 (the compressing axis). The exact contribution depends on, for example, the location on the protofilament where the bead is mounted.

A dynamic simulation with T_s = 0.01 s yields a result close to the equilibrium state 1 until λ = 2.7. Beyond that, owing to the occurrence of unfolding, the quasistatic simulation predicts a smoothly reducing yaw angle, while abrupt changes in yaw angle are observed in the dynamic simulation. The shear modulus μ is plotted in Fig. 8 b. For small deformations (λ ∼ 1), both simulations predict that μ is ∼5–10 μN/m, a value consistent with other studies. Strain-stiffening is observed up to λ ∼ 2.7. At a larger stretching, and assuming an equilibrium-force-versus-extension response applies, however, the shear stiffness reaches a plateau. As seen from Eq. 25, the shear stiffness is determined by the slope of the strain energy Φ_s. Due to the occurrence of unfolding, if λ > 2.7, the tension inside an Sp reaches a almost steady value (see Fig. 3), while the elastic energy inside the Sp increases linearly with extension. Correspondingly, the derivative of Φ_s with respect to λ becomes nearly constant. With respect to the eccentricity parameter β, however, the derivative decreases and thus a reduction in μ is indeed observed. Additional discussion about this strain-unstiffening behavior is provided in the Discussion and Conclusions.

In the same figure, we also show μ predicted by the dynamic simulation, in which a sawtooth-like curve is observed and a peak value of 250 μN/m, much larger than the maximum value in the equilibrium stretching (∼45 μN/m), is recorded. Our dynamic simulation indicates that Sp₅ unfolds first at λ = 2.97. After that, the system experiences a sequence of unfolding events, occurring at λ = 3.0 (Sp₃), 3.41 (Sp₄, Sp₆), 3.85 (Sp₄), and 3.9 (Sp₆). After each unfolding event, significant variations and redistribution of tension inside the six Sp are observed (Fig. 9 b). The unfolding of one Sp usually leads to an abrupt plunge in tension both in itself and in other Sp.

FIGURE 9.

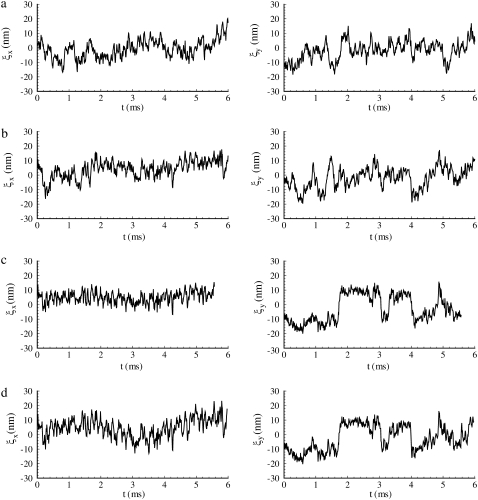
Thermal vibration of an protofilament-attached bead at (a) λ = 1, (b) λ = 2, (c) λ = 3, and (d) λ = 4.

Cases with different deformation angles have also been examined. The results are in general similar to those presented above. However, the sequence of unfolding was found to be case-dependent. For instance, with a deformation angle of 90°, in a dynamic anisotropic deformation from λ = 1 to 4 within 0.01 s, the first unfolding occurs at λ = 2.6 within Sp₁, followed by Sp₂ (λ = 3), Sp₁ (λ = 3.4), and Sp₂ (λ = 3.7). In addition, we inspected the effect of deformation time T_s. By increasing T_s, the peak tensions inside the Sp dimers as well as the peak values of the shear modulus are decreased, so that the results are closer to the equilibrium predictions.

Thermal fluctuation of a JC-attached bead

In the following, we apply the single-JC model and numerically investigate the thermal oscillation of a spherical bead attached to the protofilament (similar to the experiment done by LD as described in the Introduction). The intention here was to determine how Sp unfolding affects the magnitude of bead fluctuation, which is measurable through experiments. In a broader context, the analysis and simulations provide vital underpinning for future study via microrheology methods for measuring response that, in fact, rely on monitoring membrane motion as seen by marker movements either in response to thermal fluctuations or other external stimulation.

In our simulation, a bead of diameter D = 40 nm is connected to the pointed end of the protofilament through a stiff spring with spring constant 10³ μN/m. The motion of the bead is determined by the balance among the restoring force from the spring, the fluid drag (with drag coefficient 3πηD), and a random thermal fluctuation force following the dissipation-fluctuation law. By using the equilibrium constitutive relation for the Sp, the thermal vibration of the bead is recorded, from which the standard deviation is extracted. We note that by attaching the bead with a stiff spring we limit the fluctuation amplitude to what is allowed by the stiffness of the skeleton; otherwise the stiffness of this spring has to be considered in k_eff in Eq. 26.

To put the results to be now presented in perspective, we use a result obtained by LD via the analysis found in Chaikin and Lubensky (50), for the mean-square fluctuation amplitude, 〈ξ²〉 versus stiffness. This is

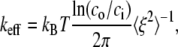(26)

where as explained below, is the square-magnitude of the fluctuation amplitude vector with components ξ_X and ξ_Y (i.e., the displacements from the mean position in X and Y directions). In Eq. 26, c_i and c_o are inner and outer cutoff ranges for fluctuation wavelengths. We take c_o to be on the order of the radius of a JC in its natural state (∼40 nm), and c_i to be on the order of a typical persistent length (∼8 nm); thus, ln(c_o/c_i)/2π ≈ 0.26. The effective stiffness from Chaikin and Lubensky (50) is k_eff = μ(κ + μ)/(κ + 2μ), where κ is the area modulus. Now, if the skeleton is thought to be mobile in the lipid membrane, reasonable because the SCs and glycophorin are mobile, we take κ to be the area modulus of the skeleton itself and therefore κ ≈ 2μ, as model studies have typically shown (e.g., (12)). Thus, k_eff ≈ 3/4μ. Then if μ ≈ 5–10 μN/m, as our model studies and experiments have found, the expectation is that 〈ξ²〉 ≈ 140–280 nm². In fact, we find that for a JC in its natural state, 〈ξ²〉 ≈ 142 nm², as presented just below.

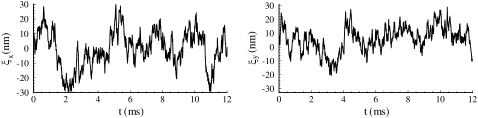
Fig. 9 displays the thermal fluctuations of the bead in both the X (stretching) and Y (compressing) directions at λ = 1, λ = 2, λ = 3, and λ = 4. The corresponding deviations are 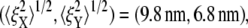(8.5 nm, 7.6 nm), (4.6 nm, 10.4 nm), and (7.4 nm, 11.4 nm), respectively. The decrease of 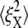until λ = 3 demonstrates the strain-stiffening before unfolding (see Fig. 8 b). The strain-unstiffening as a result of Sp unfolding leads to the increase in 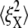at λ = 4. The variation of 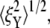on the other hand, cannot be explained solely by the change in skeleton stiffness. Instead, as we observe from Fig. 9, b–d, the onset of mode switching contributes to the increase of oscillation in Y direction. This finding highlights the importance of including the detailed three-dimensional structure of the network. Indeed, we created a simplified model by ignoring the protofilament and connecting the bead directly to the Sp dimers. With this setup, our simulations show that the variation of 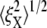is consistent with the three-dimensional model prediction, while 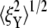decreases from ∼8 nm at λ = 1 to ∼5 nm at λ = 3, where it reaches a steady value. It is also necessary to note that the effect of mode switching on 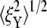strongly depends on the configuration, i.e., the exact location of the bead-protofilament attachment. For example, if the connection point is at the center of the protofilament instead of the pointed end, our simulations show that 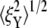is close to the prediction of the simplified model.

DISCUSSION AND CONCLUSIONS

Our dynamic and equilibrium analysis of Sp unfolding has suggested a new paradigm of a critical stretch, x_c, for unfolding. The forces existent within an Sp at unfolding are, as shown, dependent on stretching rate, yet at most rates of biological interest appreciable unfolding occurs only when the Sp extension is near, say, x → 0.8 – 0.9L, where L = N_f L_f + N_uL_u is the effective contour length of the partially folded/unfolded chain. For RBC skeletons stretched very slowly, this implies that appreciable unfolding is expected at principal stretches as low as, say, λ → 2, and certainly when the stretch is near λ → 2.5–3. The RBC skeleton, importantly, is routinely subject to stretches within this range and thus we clearly expect that Sp unfolding will be common events. The stiffness of the membrane skeleton is thereby apparently adaptive and, in a way, self-protective against damage from overstretching.

By employing a three-dimensional model of a single JC within the membrane skeleton coupled with the lipid bilayer, we simulated the anisotropic deformation of the skeleton and examined the effect of Sp unfolding on the shear modulus, μ. Strain-stiffening, i.e., the monotonous increase in shear modulus with the deformation ratio λ, is observed up until λ ∼ 2.7. If the deformation ratio is further increased, however, strain-unstiffening, manifested in the plateauing and the slow decreasing of μ in equilibrium deformations, or the abrupt plunging of μ in dynamic deformations, are observed. Each plunge in μ observed in the dynamic case corresponds to the occurrence of an unfolding event in one (or more than one) Sp. Unstiffening of the membrane skeleton, although expected to occur at a stretch λ > 2 as indicated by Fig. 8 b, is expected to be modest. Perspective on this may be obtained by first using a result of Dao et al. (12) who represented the stress, via the virial theorem, within a regular hexagonal skeleton, such as drawn in Fig. 7 and in particular sketched as an idealized JC in Fig. 7 c, as

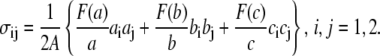(27)

Here, F(x) is the force-versus-extension relation used to describe the tension within a stretched Sp and a, b, and c represent the three vector Sp segments (tetramers) that exist on average per JC; A is interpreted as 4/3 the area of the JC unit as considered here, and a, b, and c represent the magnitudes of a, b, and c, respectively. Dao et al. (12) include a steric repulsive term that is unimportant here where we impose only an area preserving pure shear described by the deformation gradient

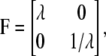(28)

and where the components of F are referred to the x₁, x₂ axes shown in Fig. 7 c. Here the stretch, λ, is set to unity when the JC is in an initial or rest state where, with reference to Fig. 3, x/NL_f ≈ 0.4 as estimated, for example, in Dao et al. (12). At sufficiently large stretches, say λ > 2 or so, the in-plane principle stresses obtained from Eq. 27 are dominated by terms of the form σ₁ – σ₂ ∼ λg(λ), or perhaps like σ₁ – σ₂ ∼ λg(λ – 1), depending on the form of the force-versus-extension law used. To see this, note that the stretch per unit length along a typical vector segment such as a is given as

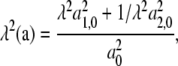(29)

where a₀ = (a_{1, 0}, a_{2, 0}) is the vector a in an initial state. As λ becomes large, λ(a) → λ|a_{1, 0}| and a → λ|a_{1, 0}|, a_i → λa_{i, 0}. This then implies that the maximum shear stress, τ = 1/2|σ₁ – σ₂|, is of that same form (viz. λg(λ)). We now recall that the shear modulus we define may be expressed via the relation (49)

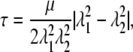(30)

where the conjugate shear strain is 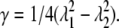For the pure shear being considered, of course, λ₁λ₂ = 1. Thus dimensionally we have, at sufficiently large stretch,

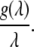(31)

To acquire the desired perspective, note that this also implies

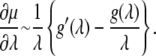(32)

For the simplest linear spring model for an Sp, the result implies that at large stretches μ becomes stationary, although during modest stretches it will undergo an increase as previous studies have documented (e.g., (10)). If, on the other hand, g(λ) is hyperlinear, μ may display continued stiffening as shown by others who use entropic Sp models (e.g., (12)). In our case, g(λ) displays a transition from hyperlinear to quasilinear behavior as shown in Fig. 3. Indeed the term in brackets becomes negative after the transition but only at values of λ sufficiently large to ensure that the magnitude of the negative slope is modest, which helps explain the modest effect of Sp unstiffening on predicted bead fluctuation amplitude. As a confirmation of the above dimensional analysis, we assume that λ = 3 is sufficiently large to apply Eq. 32 with confidence. We then set the value of a constant, ζ, in the relation μ ≈ ζg(λ)/λ by equating ζg(λ)/λ = 45 μN/m, the latter value obtained at λ = 3 from the quasistatic prediction for μ in Fig. 8 b; thus ζ ≈ 45/(g(λ)/λ) m⁻¹. Then, and again at λ = 3, ∂μ/∂λ ≈ 45/(g(λ)/λ)(g′/λ – g/λ)_λ=3. Now appealing to Fig. 3 b we estimate g′/f ≈ 0.2 at λ = 3. Thus we estimate (∂μ/∂λ)_λ=3 ≈ 6 μN/m. In fact, the drop in μ from λ = 3 to λ = 4 shown in Fig. 8 b is ∼7 μN/m, consistent with this estimate.

To further investigate the possibility that the unfolding might have been the cause of the reported deformation-induced increase in the thermal fluctuation of a skeleton-attached bead, we applied a single-JC model and carried out simulations of a bead connected to the protofilament. Our result does indicate that the unfolding causes increase in the amplitude of fluctuation as a result of reduced skeleton stiffness. The effect, however, is not large enough to explain the observed twofold increase (13). Moreover, the unfolding occurs at λ ∼ 3, while in the experiment the bead was located at a position with λ ∼ 2. Mode switching, the transition of the protofilament orientation between two equilibrium states, can increase the fluctuation in the compressing direction. However, mode switching does not have a considerable effect on the fluctuation in the stretching direction. We therefore conclude that the increased bead fluctuation cannot be solely interpreted by Sp unfolding or mode switching. Other factors, such as inter-protein interactions, may then play a pivotal role on Sp network stiffness, and may contribute to the phenomenon discussed above. We explore this briefly below.

Sp dimers within the skeleton network assemble via association at the N-terminal region of the α-subunit with the C-terminal region of the β-subunit. The vital role of this association has been demonstrated by various hereditary hemolytic anemia causing mutations that perturb tetramer formation (e.g., (51–54)). The moderate affinity of the head-to-head association between α and β is dynamic in vivo and will be affected by Sp tension. The disassociation process may be written as

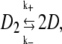(33)

where D₂ stands for a tetramer and D the two dimers α + β. The association constant, K_a, has been measured in the range K_a ≈ 1 – 3 × 10⁵ M⁻¹ at 37°C (53,55). (Note that the association constant is traditionally written for the tetramer formation reaction, i.e., the reverse of the disassociation reaction of Eq. 33.) With these definitions we have that

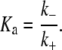(34)

DeSilva et al. (53) report a value of k₊ = 3.4 × 10⁻⁴ s⁻¹ at 23°. Ungewickell and Gratzer (55) report the value k₊ = 1.6 × 10⁻³ s⁻¹ at 37°.

Various measurements of K_a, e.g., (53,55), are consistent to within factors of 2–3, as are the measured rate constants. To assess the possibility of head-to-head disassociation affecting skeleton response, it is necessary to evaluate the tension affected term exp (FΔx_d/k_BT) where Δx_d is an activation length characterizing the head-to-head dissociation. With the tension measured in pN, 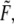and the activation length, 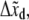in nm this factor is 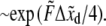Then, with the tension force in the range of several pN and the activation length of ∼2-4 nm, the rates are in the range of 10⁻² s⁻¹, or larger, and are clearly seen to be of possible importance. Data that directly address forced Sp dimer-tetramer association/disassociation are not available as yet. The results presented by An et al. (14), however, suggest that tetramer dissociation is promoted by even modest imposed levels of shear stress. In fact, when interpreted within the framework of our kinetic descriptions, we would estimate Δx_d to be certainly >2 nm, and most likely larger yet. An et al. (14) suggest, based on their results, “… that rupture of spectrin tetramers is a likely mechanism for the capacity of the membrane to adapt to very large distortions.” Moreover, the apposition of the association sites on the proteins attached to the membrane promotes reassociation so that modest amounts of disassociation need not cause a permanent remodeling of the network. In fact, that association is promoted by the geometrical constraint of being attached to the membrane, within the network, was an argument used in An et al. (14) to explain the preponderance of tetramers in the rest state of the membrane despite the relatively weak self-association in free solution, i.e., K_a ≈ 1 – 3 × 10⁵ M⁻¹ at 37°C. The implication is that the membrane skeleton undergoes a dynamic balance between head-to-head disassociation and reformation. A shear deformation, even if modest (within the range achievable in vivo), can disturb this equilibrium in favor of local disassociation from tetramers to dimers.

Our brief discussion of head-to-head Sp dimer disassociation certainly suggests that this may be another cause of phenomena such as strain unstiffening in such entropic systems as the RBC skeleton. Indeed, as shown in Fig. 10, by using the hybrid model our preliminary simulations show that the stretched Sp dimers (i.e., Sp₃ ∼ Sp₆ in Fig. 7) are removed at λ = 2, and the bead fluctuations are found to be 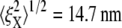and 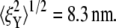Note that 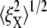is almost 50% larger than its value (9.8 nm) at the natural state (λ = 1), even at this more modest level of stretch. This indicates that large increases in thermal fluctuation in a sheared membrane skeleton along the stretching direction are possible with progressive Sp dimer disassociation. As noted above, the kinetics of head-to-head disassociation suggests timescales for such events that are comparable to those of Sp unfolding as demonstrated herein. Future analysis of the full effects await further study. Whether head-to-head disassociation would be seen to be reversible upon Sp unfolding remains to be seen, yet recent experiments (14) and model results (15) suggest this is indeed so. If so, both unfolding and disassociation would fit within a broader category of adaptive mechanical response as recently described by Chaudhuri et al. (56) for actin networks. Of course there, that is in (56), the elasticity is not thought to be entirely entropic but rather comprised of an interplay between entropic and enthalpic (energetic), the latter manifested in the elastic buckling of shorter actin filaments. The simulations of Li et al. (15), based on a tethered bead model (e.g., akin to that of Boey et al. (57)) assumed a range of binding energies for the Sp head-to-head connection. Indeed, when the binding energy was set sufficiently low, the shear stiffness was reduced by factors near 2 at low to modest strains, at least under the conditions of shear strain rate they imposed. At larger deformations the skeleton were observed to become fluidlike. Under such circumstances, the amplitude of bead fluctuation would be expected to indeed increase and eventually become diffusive.

FIGURE 10.

Thermal vibration of an protofilament-attached bead attached to a disassociated JC (with Sp₃ ∼ Sp₆ disconnected) at λ = 2.

Still another event that will cause a loss of stiffness in the membrane is Sp-actin disassociation. Such events may be described within the framework we have used here. Indeed, if such disassociation occurs at a sufficiently high density, the membrane's response will become fluidlike; such transitions in membrane behavior are in fact the topic of a forthcoming report. We note, however, that in that case, evidence indicates that direct metabolic energy input may help drive Sp-actin disassociation. Such events are readily accounted for in our kinetic models as direct reductions in the activation energy for disassociation.

The perspective gained from the studies presented herein demonstrates the most likely occurrence of Sp unfolding during normal RBC deformation. The effect of unfolding on membrane stiffness is seen, however, to be modest. The more significant effect of unfolding perhaps lies in its role as a remodeling phenomenon that mitigates the rise in tension during large deformations. Our preliminary results of the effects of Sp tetramer disassociation suggest that dimer-tetramer stability has a more pronounced influence on membrane stiffness. Here two requirements exist for further progress. The first is more direct experimental data on the role of stress on disassociation; the results of An et al. (14) are clearly a start in this direction. The second is the development of more quantitative models for forced disassociation calibrated by such data. The framework and model presented herein provides the quantitative capability to better interpret, and design, experiments, such as those that probe membrane dynamic motion, and to directly link such motion to the details of molecular connectivity.

As noted above, for simplicity, we have assumed that all domain repeats have identical unfolding/refolding characteristics. By accounting for the variable stability of different repeats (18), it is possible that additional reductions in stiffness may be displayed by our model. This refinement will certainly be included in future study. Finally, we note that the computational simulations presented here, based on our molecular-detailed model for the JC units and their connectivity to each other and the lipid bilayer, provide a valuable capability to interpret experiment as we have done herein as well as to “design-experiment”—for example, those that involve observations of the motion of attached markers. The results presented here demonstrate that such motions, as observed, are indeed influenced by many factors including the details of attachment itself.