Abstract
We have analyzed flash-induced period-four damped oscillation of oxygen evolution and chlorophyll fluorescence with the aid of a kinetic model of photosystem II. We have shown that, for simulation of the period-four oscillatory behavior of oxygen evolution, it is essential to consider the so-called intermediate S-state as an initial phase of each of the Sn-Sn+1, (n = 0, 1, 2, 3) transitions. The intermediate S-states are defined as [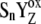 ]-states (n = 0, 1, 2, 3) and are formed with rate constant kiSn ∼1.5 × 106 s−1, which was determined from comparison of theoretical predictions with experimental data. The assumed intermediate S-states shift the equilibrium in reaction
]-states (n = 0, 1, 2, 3) and are formed with rate constant kiSn ∼1.5 × 106 s−1, which was determined from comparison of theoretical predictions with experimental data. The assumed intermediate S-states shift the equilibrium in reaction 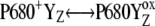 more to the right and we suggest that kinetics of the intermediate S-states reflects a relaxation process associated with changes of the redox equilibrium in the above reaction. The oxygen oscillation is simulated without the miss and double-hit parameters, if the intermediate S-states, which are not the source of the misses or the double-hits, are included in the simulation. Furthermore, we have shown that the intermediate S-states, together with
more to the right and we suggest that kinetics of the intermediate S-states reflects a relaxation process associated with changes of the redox equilibrium in the above reaction. The oxygen oscillation is simulated without the miss and double-hit parameters, if the intermediate S-states, which are not the source of the misses or the double-hits, are included in the simulation. Furthermore, we have shown that the intermediate S-states, together with 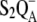 charge recombination, are prerequisites for the simulation of the period-four oscillatory behavior of the chlorophyll fluorescence.
charge recombination, are prerequisites for the simulation of the period-four oscillatory behavior of the chlorophyll fluorescence.
INTRODUCTION
It is well known that the oxygen-evolving complex (OEC), an integral part of the multicomponent pigment-protein complex called photosystem II (PSII), is responsible for the light-induced water splitting and release of protons and oxygen molecules from water molecules (1). When dark-adapted material (higher plants, algae, and cyanobacteria) is exposed to a series of single turnover flashes, oxygen evolution is detected with typical period-four damped oscillation with maxima on the third and seventh flashes and with minima on the first and fifth flashes (2–4).
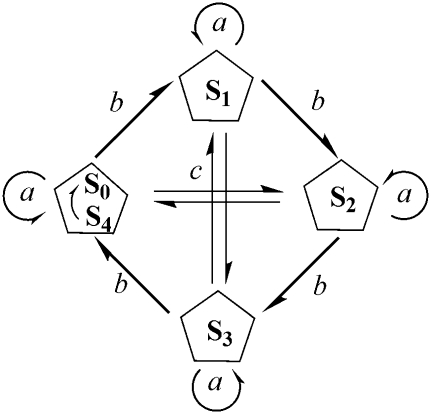
Several phenomenological models were proposed to describe and explain damped period-four oscillation in oxygen evolution (2,5,6). However, only one model that introduces a cycle of flash-induced transitions of the Sn-states (n = 0, 1, 2, 3), describing the four redox states of OEC, explains the results. This model, suggested by Kok and co-workers (5), is known as the Kok cycle or the Kok model (Scheme 1). By introducing two parameters—the so-called misses and double-hits—the Kok model describes damping of the period-four oscillation of oxygen evolution. However, positive proof or in silico analysis of molecular mechanisms, behind these parameters, is still being debated.
SCHEME 1.
Kok model for oxygen evolution which, for the purpose of successful description of damped period-four oscillation of oxygen evolution induced by flash-train, introduces two parameters: misses (a) that characterize a failure to advance from Sn-state to Sn+1-state and double-hits (c) which characterize transition from Sn-state to Sn+2-state. Parameter b characterizes the most likely transition from Sn-state to Sn+1-state.
It is generally accepted the misses, which, in fact, reflect decreases in the primary photochemical yield, have several sources. Some misses arise from the presence of the 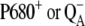 before the flash because of reversibility of the electron transport at the donor or acceptor side of PSII (7). However, the main source of the misses is the recombinational loss of the charge-separated state
before the flash because of reversibility of the electron transport at the donor or acceptor side of PSII (7). However, the main source of the misses is the recombinational loss of the charge-separated state 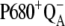 whose yield increases with a slowdown of the OEC oxidation in higher S-states (8). The influence of other mechanisms or electron transporters, which can contribute to misses, is often either neglected (YD, cytochrome b559) or implicitly included in the
whose yield increases with a slowdown of the OEC oxidation in higher S-states (8). The influence of other mechanisms or electron transporters, which can contribute to misses, is often either neglected (YD, cytochrome b559) or implicitly included in the 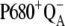 recombination (e.g., as a final state of
recombination (e.g., as a final state of 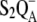 recombination). The majority of scientists agree that the misses should be unequal (4). Equal misses are, however, usually used in analysis of oxygen evolution because it provides a satisfactory fit of experimental data (9).
recombination). The majority of scientists agree that the misses should be unequal (4). Equal misses are, however, usually used in analysis of oxygen evolution because it provides a satisfactory fit of experimental data (9).
The meaning of the double-hits is not evident either, but there is some speculation as to what is hidden in this parameter to explain the significant oxygen yield after the second flash:
Longer flash duration (usually a 3 μs flash is used) might allow the two-step advancement of S-states in a certain part of PSII if
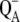 is reoxidized twice by QB during one flash (10);
is reoxidized twice by QB during one flash (10);The double-hits parameter might represent not only double but also triple turnover of PSII (9).
Double-hits parameter is higher for the freeze-intact chloroplasts than for the freeze-damaged chloroplasts (11).
The oxygen oscillation can also be successfully simulated using mathematical modeling. This approach provides the best fit of the model parameters to specific experimental data (9) and can also result in an interesting hypothesis such as the suggestion of two internal cycles of the PSII characterized by different transition probabilities (4,7). But the mathematical modeling based only on the Kok model cannot describe or explain the molecular mechanism of the OEC oxidation or the electron transport from the OEC to the P680.
In this article, we present a new kinetic model for the PSII (without considering the static heterogeneity correlated with the grana/stroma structure), which can flexibly and without artificial parameters (the misses and the double-hits) simulate damped period-four oscillation of oxygen evolution and chlorophyll fluorescence induced by a flash-train. The main aim of this article is to introduce a new view of the OEC oxidation and so provide a better explanation of the oxygen oscillation. In addition, this study serves as a starting point for a more detailed understanding of the flash-induced period-four oscillation of chlorophyll fluorescence.
METHODS
Software used
All simulations were run in GEPASI 3.30 software (12), which was designed for modeling of chemical and biochemical kinetics (13,14). GEPASI uses an integrative routine LSODA (Livermore Solver of Ordinary Differential Equations) for the solution of system of differential equations. LSODA is a sophisticated algorithm (15) that measures stiffness of equations and, when necessary, dynamically switches the integration method.
RESULTS AND DISCUSSION
Intermediate S-states: a way for kinetic description of period-four oscillation
We first simulated the flash-induced changes of the S-state distribution with the aid of a detailed kinetic model of PS II, which includes pheophytin, QA and QB at the acceptor side of PSII, and P680, YZ, and S0,1,2,3-states of the OEC at the donor side of PSII (16). We found that this kinetic model of PSII is not able to simulate the flash-induced damped period-four oscillation of the S-states of OEC (Fig. 1, open triangles). Since the model used (16) includes reactions and mechanisms responsible for the misses and the double-hits (see Introduction), we came to the conclusion that the existing kinetics description of the OEC oxidation (16) is insufficient. Therefore, we introduced the idea to determine the condition(s) for in silico S-state oscillation and thus for kinetic description of OEC oxidation.
FIGURE 1.
Simulations of the flash-induced changes of the S-state distribution. Initial conditions of simulations: 75% of OEC in the S1-state, 25% of OEC in the S0-state. Open triangles show simulations based on the earlier (16) kinetic model of PSII. Open and solid squares show simulations based on modified earlier model tested with two suggested kinetics (kiS3) of the incorporated S4-state, 5000 s−1 (as S3 → S4 → S0) or 1.5 × 106 s−1 (as S3 + 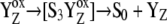 ), respectively (in text). Open and solid circles show simulations based on modified model with incorporated intermediate S-states (i.e., formation of [
), respectively (in text). Open and solid circles show simulations based on modified model with incorporated intermediate S-states (i.e., formation of [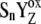 ] (n = 0, 1, 2, 3) during each Sn-Sn+1 transition) with rates of their formations kiS0 = kiS1 = kiS2 = kiS3 = kiSn = 3 × 104 s−1 or 1.5 × 106 s−1, respectively.
] (n = 0, 1, 2, 3) during each Sn-Sn+1 transition) with rates of their formations kiS0 = kiS1 = kiS2 = kiS3 = kiSn = 3 × 104 s−1 or 1.5 × 106 s−1, respectively.
We based our further analysis on the results of Fig. 1 (open triangles), showing it is the S3 state that mainly accumulates with increasing number of flashes; it seems obvious that it suggests almost zero efficiency of the S3-S0 transition. We therefore performed simulation where 100% of OEC was initially (in the dark) in the S3-state, and 500 ms after flash we observed 75.7% concentration of the S3-state (i.e., 75.7% misses during the S3-S0 transition, data not shown).
Our analysis suggests that the very high misses during the S3-S0 transition, a consequence of 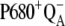 recombination, must be caused by accumulation of P680+ in a preceding reaction. This reaction is reversible reduction of P680+ by YZ leading to P680 and
recombination, must be caused by accumulation of P680+ in a preceding reaction. This reaction is reversible reduction of P680+ by YZ leading to P680 and 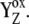 Even if the equilibrium of this reaction is to the right, the slow S3-S0 transition and the backward electron transport of
Even if the equilibrium of this reaction is to the right, the slow S3-S0 transition and the backward electron transport of 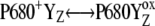 reaction that enables the accumulation of P680+ leads to the excessive
reaction that enables the accumulation of P680+ leads to the excessive 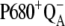 recombination in the model, so the high misses are obtained. We therefore tested all possible modifications of the model (see below).
recombination in the model, so the high misses are obtained. We therefore tested all possible modifications of the model (see below).
A decrease of the S3-state accumulation and thus shift of the equilibrium more to the right in the 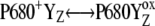 reaction during S3-S0 transition might be obtained by introduction of the S4-state into the model (S4-state is commonly ignored in the kinetic models of PSII). Since it is still not clear what should be labeled as the S4-state, we tested two possible rate constants suggested for the S4-state formation (see below). The first option is associated with the proposed irregular sequence model of alternating proton and electron abstraction from the Mn cluster of OEC (17–19), in which a state, caused by proton release and denoted as S4-state, is formed with a rate constant of 5000 s−1 during the S3-S0 transition. On the other hand, it has been suggested that the S4-state represents the formation of the
reaction during S3-S0 transition might be obtained by introduction of the S4-state into the model (S4-state is commonly ignored in the kinetic models of PSII). Since it is still not clear what should be labeled as the S4-state, we tested two possible rate constants suggested for the S4-state formation (see below). The first option is associated with the proposed irregular sequence model of alternating proton and electron abstraction from the Mn cluster of OEC (17–19), in which a state, caused by proton release and denoted as S4-state, is formed with a rate constant of 5000 s−1 during the S3-S0 transition. On the other hand, it has been suggested that the S4-state represents the formation of the 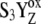 -state formed with a rate constant >106 s−1 (20,21). The S4-state was entered into the model either as a separated transient state (5000 s−1) or formation of the
-state formed with a rate constant >106 s−1 (20,21). The S4-state was entered into the model either as a separated transient state (5000 s−1) or formation of the 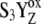 -state (1 × 106 s−1). Although we observed qualitative changes of the flash-induced S-state distribution (Fig. 1, open squares for kiS3 = 5000 s−1 and solid squares for kiS3 = 1.5 × 106 s−1), no period-four oscillation in the S-state distribution was simulated. Moreover, the low sensitivity of the PSII model to the value of rate constant of the S4-state formation (unchanged qualitative behavior of the S0,1-states distribution; Fig. 1) shows that this approach is not sufficient. We therefore concluded that the period-four oscillation of the S-state distribution is not associated with the modification of the one S-state transition in comparison with the earlier model (16).
-state (1 × 106 s−1). Although we observed qualitative changes of the flash-induced S-state distribution (Fig. 1, open squares for kiS3 = 5000 s−1 and solid squares for kiS3 = 1.5 × 106 s−1), no period-four oscillation in the S-state distribution was simulated. Moreover, the low sensitivity of the PSII model to the value of rate constant of the S4-state formation (unchanged qualitative behavior of the S0,1-states distribution; Fig. 1) shows that this approach is not sufficient. We therefore concluded that the period-four oscillation of the S-state distribution is not associated with the modification of the one S-state transition in comparison with the earlier model (16).
A possible way to shift the equilibrium in 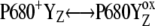 reaction during all S-states transitions more to the right, is consideration of P680+ reduction in a microsecond time-range, which was not considered in our original model (16). Because microsecond reduction of P680+ (i.e., only the microsecond component) was suggested to occur in ∼30% of PSII (22), we considered the microsecond reduction of P680+ by biphasic kinetics with half-times of 5 μs (15% of PSII) and 38 μs (15% of PSII). However, after comparison with results from the earlier model (Fig. 1, open triangles), we observed negligible changes of the S-state distribution (data not shown). For the irreversible/reversible option of microsecond reduction of P680+, we saw ∼±0.1/0.1% change of the S-state distribution after the first flash and ∼±0.1/0.001% change of the S-state distribution for the following flashes. This was the last possible modification of the existing kinetic description for the donor side of PSII.
reaction during all S-states transitions more to the right, is consideration of P680+ reduction in a microsecond time-range, which was not considered in our original model (16). Because microsecond reduction of P680+ (i.e., only the microsecond component) was suggested to occur in ∼30% of PSII (22), we considered the microsecond reduction of P680+ by biphasic kinetics with half-times of 5 μs (15% of PSII) and 38 μs (15% of PSII). However, after comparison with results from the earlier model (Fig. 1, open triangles), we observed negligible changes of the S-state distribution (data not shown). For the irreversible/reversible option of microsecond reduction of P680+, we saw ∼±0.1/0.1% change of the S-state distribution after the first flash and ∼±0.1/0.001% change of the S-state distribution for the following flashes. This was the last possible modification of the existing kinetic description for the donor side of PSII.
If we reject the possibility of an unknown intermediate between YZ and OEC, there is only one other possibility for shifting the equilibrium in 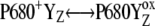 more to the right. This is an assumption of the kinetically identifiable intermediate S-states associated with some relaxation process at the donor side of PSII, which stabilizes
more to the right. This is an assumption of the kinetically identifiable intermediate S-states associated with some relaxation process at the donor side of PSII, which stabilizes 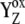 —i.e., the mechanism associated with the formation of
—i.e., the mechanism associated with the formation of 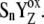 We therefore analyzed this possibility below, and attempted to identify the relaxation process in the next section. Since the intermediate S-states do not necessarily have to be involved with each of the S-state transitions, we tested all combinations. We have found that the option, where we consider the existence of intermediate S-state as an initial phase of the S0-S1, S1-S2, S2-S3, and S3-S0 transitions, leads to the desired in silico period-four oscillation in the S-state distribution (comparable with known course and damping of the oxygen oscillation; see example for the rate constant kiSn = 106 s−1 of the intermediate S-states in Fig. 1, solid circles). The period-four oscillation can be observed from value kiSn ∼ 3 × 104 s−1 of the rate constant of the intermediate S-states (Fig. 1, open circles). Since the rate constant 3 × 104 s−1 is comparable with the rate constant of the S0-S1 transition (∼2 × 104 s−1), we also tested the model without an intermediate S-state associated with the S0-S1 transition. We have found almost no-effect on the course of the oscillation, whether or not the intermediate S-state associated with the S0-S1 transition is omitted (data not shown). However, if we want to decrease damping of the S-state oscillation, we have to increase rate constant of the intermediate S-states and then the intermediate S-state as the initial phase of the S0-S1 transition must be considered.
We therefore analyzed this possibility below, and attempted to identify the relaxation process in the next section. Since the intermediate S-states do not necessarily have to be involved with each of the S-state transitions, we tested all combinations. We have found that the option, where we consider the existence of intermediate S-state as an initial phase of the S0-S1, S1-S2, S2-S3, and S3-S0 transitions, leads to the desired in silico period-four oscillation in the S-state distribution (comparable with known course and damping of the oxygen oscillation; see example for the rate constant kiSn = 106 s−1 of the intermediate S-states in Fig. 1, solid circles). The period-four oscillation can be observed from value kiSn ∼ 3 × 104 s−1 of the rate constant of the intermediate S-states (Fig. 1, open circles). Since the rate constant 3 × 104 s−1 is comparable with the rate constant of the S0-S1 transition (∼2 × 104 s−1), we also tested the model without an intermediate S-state associated with the S0-S1 transition. We have found almost no-effect on the course of the oscillation, whether or not the intermediate S-state associated with the S0-S1 transition is omitted (data not shown). However, if we want to decrease damping of the S-state oscillation, we have to increase rate constant of the intermediate S-states and then the intermediate S-state as the initial phase of the S0-S1 transition must be considered.
For accurate determination of the rate constant of the intermediate S-states and thus, determination of the mechanism associated with the intermediate S-states, it is necessary to compare our simulations with measured data (see next section). However, we can already conclude that the intermediate S-states seem to be a key assumption for in silico, period-four oscillation of the S-state distribution.
Kinetics and mechanism of the intermediate S-states
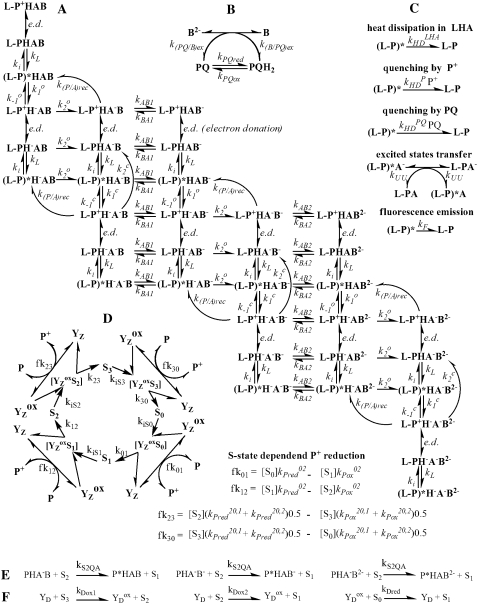
As we mentioned, presented kinetic model describes homogeneous population of PSII which is not exactly the case for higher plants and some algae. Therefore, for the purpose of comparison of simulated oxygen evolution with experimental data we have chosen the cyanobacterial sample where PSII heterogeneity may be neglected (23). In this respect, the main source of the experimental data is the thermophilic cyanobacterium Synechococcus elongatus and we chose suitable (i.e., without the addition of an exogenous electron acceptor or donor; accurate information about temperature of the measurement) experimental data (24) for testing the model. Since oxygen is evolved during the S3-S0 transition, we have assumed that an experimentally measured oxygen yield induced by a flash is quantitatively proportional to simulated maximal concentration of the intermediate S-state during the S3-S0 transition after the flash. This approach gives, as shown below, a suitable approximation of the oxygen evolution and the possibility of comparing theoretical and experimental data with ease. The final kinetic model of PSII used for all following simulations is described in Scheme 2 and Table 1, and the summary of rate constant values used in this model of PSII is given in Table 2 (see also (25–28); Appendix.)
SCHEME 2.
The introduced kinetic model of PSII used for simulations of flash-induced period-four oxygen and chlorophyll fluorescence oscillations (see Table 1 for definitions).
TABLE 1.
Definitions for Scheme 2
| Value | Description |
|---|---|
| L | All light harvesting antennas in PSII. |
| P | P680. |
| I | Pheophytin. |
| A | QA. |
| B | QB. |
| PQ | Oxidized plastoquinone molecules in the PQ pool. |
| PQH2 | Reduced and protonated PQ molecules in the PQ pool. |
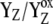 |
Reduced/oxidized state of tyrosine 161-D1. |
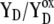 |
Reduced/oxidized state of tyrosine 160-D2. |
| Sn (n = 0, 1, 2, 3) | The S-states of OEC. |
[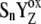 ] ] |
(n = 0, 1, 2, 3) and the intermediate S-states of OEC. |
| e.d. | In Part A, electron donation to P680+ by YZ as it is described by part D. |
| * | Excited state. |
| Scheme sections | |
| Part A | Includes: |
| 1. Formation of excited states, which is defined by rate constant kL and in our case simulate δ-flashes. | |
| 2. Reactions of primary photochemistry: charge separation, stabilization, electron transfer to QB, and charge recombination. | |
| Part B | Incorporates exchange of double-reduced QB by free plastoquinone molecule from the PQ pool. |
| Part C | Includes the loss of excited state by: |
| 1. Heat dissipation in the light harvesting antennas. | |
| 2. Heat dissipation by P680+. | |
| 3. Heat dissipation by oxidized PQ pool. | |
| 4. Energy transfer between closed and open reaction centers of PSII. | |
| 5. Chlorophyll fluorescence emission. | |
| Part D | Mainstream of the electron transfer at the donor side of PSII is represented in part D, which connects Kok cycle of the S-states advancement and electron transport through PSII with the help of newly introduced intermediate S-states. |
| Part E | Describes charge recombination between the S2-state of OEC and 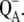
|
| Part F | Shows slow electron transfer at the donor side of PSII; specifically, redox reaction between YD and OEC. |
| Rate constants | |
| kL | Rate of excited states formation. |
| ki | Symbolic rate constant representing all processes of the excited state utilization except for the primary photochemistry as described in part C. |
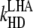 |
Overall nonradiative loss of excited states in light harvesting antennas in PSII. |
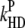 |
Nonradiative heat dissipation of excited states by P680+ (the fluorescence quenching by P680+). |
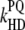 |
Nonradiative heat dissipation of excited states by PQ molecules (the fluorescence quenching by PQ molecules). |
| kUU | Excited states transfer between reaction centers of PSII. |
| kF | Fluorescence. |
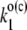 |
Overall electron transfer from P680 to Pheo (the charge separation) in the open (closed) reaction centers of PSII. |
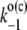 |
Backward electron transfer from Pheo− to P680+ (the charge recombination) in open (closed) reaction centers of PSII leading to formation of an excited state. |
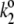 |
Electron transfer from Pheo− to QA (the charge stabilization) in open reaction centers of PSII. |
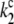 |
Backward electron transfer from Pheo− to P680+ (nonradiative charge recombination) in closed reaction centers of PSII leading to the ground state of P680 and Pheo. |
| kAB1(2) | Electron transfer from 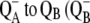 ). ). |
| kBA1(2) | Backward electron transfer from 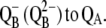
|
| k(B/PQ)ex | Exchange of double-reduced QB (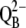 ) with an oxidized PQ molecule from the PQ pool. ) with an oxidized PQ molecule from the PQ pool. |
| k(PQ/B)ex | Backward exchange of reduced and protonated PQ molecule (PQH2) from the PQ pool with QB. |
| kPQox | Overall oxidation of reduced PQ molecules (PQH2) from the PQ pool. |
| kPQred | Overall reduction of oxidized PQ molecules from the PQ pool. |
| k(P/A)rec | Charge recombination between P680+ and 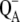 leading to the formation of a particular excited state. leading to the formation of a particular excited state. |
| kiS0, kiS1, kiS2, kiS3 | Proposed kinetics of the intermediate S-states. |
| k01, k12, k23, k30 | Electron donation from OEC to 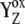 during the S0 → S1, S1 → S2, S2 → S3, and S3 → S0 transitions (Kok cycle), respectively. during the S0 → S1, S1 → S2, S2 → S3, and S3 → S0 transitions (Kok cycle), respectively. |
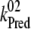 |
P680+ reduction by YZ in the S0 and S1 states of OEC. |
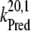 and and 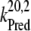
|
P680+ reduction (both rates contribute each by 50% to overall rate) by YZ in the S2 and S3 states of OEC. |
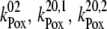 |
Backward electron transfers from P680 to 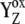 in previous reactions. in previous reactions. |
| kS2QA | Charge recombination of the 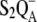 state. state. |
| kDox1/kDox2 | YD oxidation by S3/S2 state of OEC. |
| kDred |
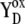 reduction by S0 state of OEC. reduction by S0 state of OEC. |
TABLE 2.
Values of the rate constants of the newly considered reactions (in comparison to the earlier model (16)) used in the simulations and in literature-reported values
| Rate constant | Used value [s−1] | Value in literature [s−1] |
|---|---|---|
| kL | 3,333,333 | Appendix |
| kiS0 | 1.5 × 106 | NA |
| kiS1 | 1.5 × 106 | NA |
| kiS2 | 1.5 × 106 | NA |
| kiS3 | 1.5 × 106 | >1 × 106 (21) |
| kS2QA | 0.66 | 0.66 (25) |
| kDox1 | 1.25* (0.62) | 0.62 (24)* (26) |
| kDox2 | 2.1* (0.7) | 0.7 (24)* (27) |
| kDred | 3.47 × 10−4* (1.38 × 10−3) | 0.83 − 3 × 10−3 (24)* (26,27) |
| kAB1 | 10,500* (3500)† | (24)* |
| kBA1 | 1050* (175)† | (24)* |
| kAB2 | 5250* (1750)† | (24)* |
| kBA2 | 210* (35)† | (24)* |
| k(P/A)rec | 1250* (10,000)† | (28)* |
Values of the rate constants, shown in parentheses, are characteristic for higher plants. See Scheme 2 for rate constants.
See literature references for suggested modifications of the rate constants and for description of the cyanobacterial samples.
This value of the rate constant describing higher plants was used in the earlier model (16).
The selected results of the comparison of the flash-induced in silico oxygen evolution (solid circles, and solid and open squares for three selected values of the rate constant of the intermediate S-states) with the experimental data (open circles) are shown in Fig. 2. From this comparison, it is evident that the rate constant 1.5 × 106 s−1 (solid circles) of the intermediate S-states allows quantitative description of the measured data. The kinetics of the assumed intermediate S-states regulate the appearance and the damping of the oxygen oscillation, caused by secondary reactions (see Introduction) and influenced by duration of flashes. If the rate constant of the intermediate S-states is increased (or decreased), the possibility of the backward electron transport in reaction 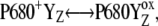 and hence, of the
and hence, of the 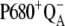 recombination, is decreased (or increased). Therefore, the value of the rate constant of the intermediate S-states regulates how much the misses, caused by
recombination, is decreased (or increased). Therefore, the value of the rate constant of the intermediate S-states regulates how much the misses, caused by 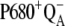 recombination, will occur. We emphasize that the intermediate S-states, changes in equilibrium in reaction
recombination, will occur. We emphasize that the intermediate S-states, changes in equilibrium in reaction 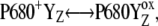 and the equilibrium itself, are not the sources of the misses or the double-hits.
and the equilibrium itself, are not the sources of the misses or the double-hits.
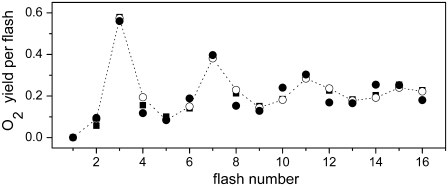
FIGURE 2.
Comparison of theoretical and experimental data of the period-four oxygen oscillation induced by eight (for unsatisfactory simulations) or 16 flashes. Initial conditions for simulations are the same as for measured data (24): 3-μs flash and 500-ms dark interval between the flashes, initially 89% of oxidized YD, 100% of OEC in the S1-state. Open circles show experimental data redrawn from Isgandarova et al. (24). Solid circles (kiSn = 1.5 × 106 s−1), solid (kiSn = 5 × 105 s−1) and open (kiSn = 2.5 × 106 s−1) squares, show simulations based on our introduced kinetic model of PSII which, in addition to the intermediate S-states (Scheme 2 D), includes the 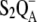 recombination, YD reduction/oxidation (Scheme 2, E and F, respectively), and assumes 25% of QB to be initially in the
recombination, YD reduction/oxidation (Scheme 2, E and F, respectively), and assumes 25% of QB to be initially in the 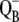 state. Values of rate constants are listed in Tables 2 and 3. Note that solid circles describing simulated oxygen yield after the second, third, and fifth flashes are hidden behind the open circles.
state. Values of rate constants are listed in Tables 2 and 3. Note that solid circles describing simulated oxygen yield after the second, third, and fifth flashes are hidden behind the open circles.
We note that the S4-state, as defined in the literature (20,21), can be considered, in our view, to be the intermediate S-state of the S3-S0 transition. This is not only because our intermediate S-states are defined as [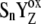 ] (which is the same as the S4-state previously defined (20,21)) but also because of the value used in our model, kiSn (1.5 × 106 s−1) (which agrees with the value of the S4-state formation from (20,21)).
] (which is the same as the S4-state previously defined (20,21)) but also because of the value used in our model, kiSn (1.5 × 106 s−1) (which agrees with the value of the S4-state formation from (20,21)).
We suggest that kinetics of the intermediate S-states reflects the relaxation process associated with changes of the redox equilibria [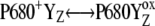 ]j (index j symbolizes one state of relaxation sequence (29–30)), which stabilizes the final product of YZ oxidation by P680+ (i.e.,
]j (index j symbolizes one state of relaxation sequence (29–30)), which stabilizes the final product of YZ oxidation by P680+ (i.e., 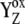 ) through the kinetically identifiable intermediate [
) through the kinetically identifiable intermediate [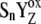 ]-state (n = 0, 1, 2, 3). The [
]-state (n = 0, 1, 2, 3). The [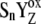 ]-state is then transformed to YZ and the Sn+1-state, which represents the S0-S1, S1-S2, S2-S3, and S3-S0 transitions of the Kok cycle. The presented assumption is based on our theoretical simulations (see above) compared with the experimental data and on the known fact that relaxation processes are important in the regulation of the redox reaction kinetics of biological systems (31,32). The detailed mechanism of the intermediate S-states associated with the considered relaxation process is unclear to us as yet, and further studies are required to clarify this point. However, we speculate that the mechanism comprises a rearrangement of the variable system of the hydrogen-bond network around YZ, caused by phenolic proton dissociated after YZ oxidation by P680+ (33–37).
]-state is then transformed to YZ and the Sn+1-state, which represents the S0-S1, S1-S2, S2-S3, and S3-S0 transitions of the Kok cycle. The presented assumption is based on our theoretical simulations (see above) compared with the experimental data and on the known fact that relaxation processes are important in the regulation of the redox reaction kinetics of biological systems (31,32). The detailed mechanism of the intermediate S-states associated with the considered relaxation process is unclear to us as yet, and further studies are required to clarify this point. However, we speculate that the mechanism comprises a rearrangement of the variable system of the hydrogen-bond network around YZ, caused by phenolic proton dissociated after YZ oxidation by P680+ (33–37).
S-state-dependency/independency of the intermediate S-states
We have shown so far that the assumption of the intermediate S-states led to the desired period-four oscillation in the S-state distribution and oxygen yield. In modeling this approach, we assumed that the rate constants of the intermediate S-states (kiSn, n = 0,1,2,3; without this and Scheme 2) were the same in each S-state, i.e., they were S-states-independent. Even if S-state-independent kinetics lead to the quantitative agreement with experimental data (Fig. 2), the S-state-dependent kinetics of the intermediate S-state cannot be a priori excluded, and, thus, it was also necessary to test this option. Here it is important to note that a change of the particular kiSn in fact results in a change of the Kok miss and double-hit parameters in the particular S-state (see examples below). As already described above, this is due to the fact that the intermediate S-states characterized by kiSn compete for usage of 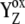 with backward electron transport from P680 to
with backward electron transport from P680 to 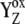 characterized by rate constants
characterized by rate constants 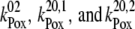 (Scheme 2). This backward electron transport leads to the formation of P680+ and thus to an increased possibility of
(Scheme 2). This backward electron transport leads to the formation of P680+ and thus to an increased possibility of 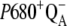 recombination, the main source of the misses (see Introduction).
recombination, the main source of the misses (see Introduction).
We at first tested kinetics of the intermediate S-states that were slightly different in the lower (S0, S1) and higher S-states (S2, S3; kiS0 = kiS1 = 6 × 106 s−1, kiS2 = kiS3 = 1.1 × 106 s−1). This idea is related to the different behavior shown by OEC in its higher and lower S-states (e.g., due to two different pathways of 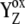 reduction by the OEC (33)). However, we found that this idea does not lead to an agreement with the experimental data because of a too-low simulated oxygen yield after the second flash (ratio of the measured/simulated yield is ∼1.56; Fig. 3, solid squares). Therefore, we rejected this possibility, even though the following simulated data fit the experimental data almost perfectly.
reduction by the OEC (33)). However, we found that this idea does not lead to an agreement with the experimental data because of a too-low simulated oxygen yield after the second flash (ratio of the measured/simulated yield is ∼1.56; Fig. 3, solid squares). Therefore, we rejected this possibility, even though the following simulated data fit the experimental data almost perfectly.
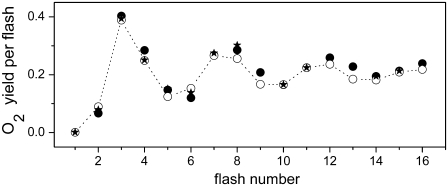
FIGURE 3.
Comparison of theoretical and experimental data of the period-four oxygen oscillation induced by 16 flashes. Initial conditions for simulations are the same as for measured data (24) (Fig. 2). Open circles show experimental data redrawn from Isgandarova et al. (24). Solid squares (different kinetics of the intermediate S-states in the lower and higher S-states) and solid circles (high misses during the S2-S3 transition) show theoretical simulations for S-state dependent kinetics of the intermediate S-states. Model used for simulations is the same as used for simulations of the oscillations presented by solid circles in Fig. 2.
Another idea was to suggest high misses (i.e., a decrease of kiSn) in only one S-state transition. Because high misses during the S0-S1 and S1-S2 transitions are generally unacceptable (8,24), we can only consider high misses during the S2-S3 or S3-S0 transition. In principle, both options should be acceptable because it is known that almost any permutation of the misses gives the same oxygen evolution (4). However, decrease of the kiS3 and thus higher misses during the S3-S0 transition are a priori unacceptable, because the value of kiS3 > 106 s−1 is a prerequisite for agreement between simulated and experimental data (tested for all possible combinations of S-state dependent kinetics of the intermediate S-states; data not shown). Therefore, we have further analyzed the concept of high misses during the S2-S3 transition where significant decrease of kiS2 could be explained by the accumulation of the positive charge on the Mn cluster associated with the structural changes of the D1 subunit of PSII in the S2-state (39). In addition, the S2-S3 transition is the most controversial S-state transition and the mechanism of OEC oxidation in this transition is still being discussed and explored (40). The best agreement with experiment was obtained for the following set of the rate constants: kiS0 = 6 × 106 s−1, kiS1 = 4.5 × 106 s−1, kiS2 = 0.3 × 106 s−1, and kiS3 = 1.5 × 106 s−1. From our results (Fig. 3, solid circles), satisfactory agreement of the theory with the experimental oxygen yield (open circles) is obvious for the first three flashes and significant differences between the simulated and the experimental data for the fourth and following flashes are apparent in comparison to the first S-state dependent option of the intermediate S-states kinetics (solid squares). Nevertheless, S-state independent kinetics of the intermediate S-states (Fig. 2, solid circles) generally agrees much better with the experimental data than the simulations based on the S-state dependent kinetics of the intermediate S-states. However, on the basis of presented results we accept that some S-state dependence of kinetics of the intermediate S-states cannot be excluded but it seems from our theoretical results that it is not necessary for the description of the experimental data.
We note that the S-state-independent kinetics of the intermediate S-states should not be connected with equal misses during S-state transitions. It is mainly because the oxidation of P680+ by YZ and consequently 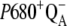 recombination, which is thought to be the main source of the misses (see Introduction), are S-state dependent. Also,
recombination, which is thought to be the main source of the misses (see Introduction), are S-state dependent. Also, 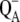 recombines only with the S2-state and YD redox activity occurs only in some of the S-states. All these reactions, considered in our model (Scheme 2), lead to a different kinetic equilibrium within the whole model when particular S-state is accumulated, and therefore also to different misses during particular Sn-Sn+1 transitions even in the case of the S-state independent kinetics of the intermediate S-states. Therefore, we conclude that equal misses are highly unrealistic.
recombines only with the S2-state and YD redox activity occurs only in some of the S-states. All these reactions, considered in our model (Scheme 2), lead to a different kinetic equilibrium within the whole model when particular S-state is accumulated, and therefore also to different misses during particular Sn-Sn+1 transitions even in the case of the S-state independent kinetics of the intermediate S-states. Therefore, we conclude that equal misses are highly unrealistic.
Dependence of oxygen oscillation on the high initial reduced YD concentration
Thus far, all simulations and analyses were performed with a 100% (S-state oscillation; Fig. 1) or 89% (oxygen evolution; Figs. 2 and 3) initial concentration of oxidized YD. Since reduced YD can significantly influence damping of the oxygen oscillation, we simulated the oxygen oscillation with high initial concentration of reduced YD and compared it with experimental data.
The result of our analysis is shown in Fig. 4, where simulation (solid circles) with high initial concentrations of reduced YD (55%) is presented, the same as in the experiment (open circles, data from (24)). Although the simulations qualitatively agree with the experimental data, some discrepancies can be found—it is obvious that our model cannot perfectly simulate the experimental data. Furthermore, another modification of the rate constants in the model is unacceptable because of conflict with the simulation performed before (Fig. 2; initially 89% of oxidized YD), which sufficiently describes the experimental data, mainly the characteristics points of oscillation, the Y2 (oxygen yield after the second flash determines double-hits), and Y3 (oxygen yield after the third flash determines global maximum of the oscillation). Therefore, another mechanism that particularly explains the difference between simulated and experimental Y2 in the cyanobacterial sample with the higher initial concentration of reduced YD should be considered.
FIGURE 4.
Comparison of theoretical and experimental data of the period-four oxygen oscillation induced by 16 flashes. Initial conditions for simulations are the same as for measured data (24): 3-μs flash and 500-ms dark interval between the flashes, initially 55% of reduced YD, 100% of OEC in the S1-state. Open circles show experimental data redrawn from Isgandarova et al. (24). Model used for simulations presented by solid circles (kiSn = 1.5 × 106 s−1) is the same as used for simulations of the oscillations presented by solid circles in Fig. 2. Solid stars show theoretical simulations based on fivefold slowdown of the intermediate S-states (kiSn = 3 × 105 s−1) in the presence of reduced YD.
It has been reported that the presence of reduced YD affects the YZ to P680+ electron donation (36,41). This is probably due to the complex changes of the redox equilibria and electron-transfer kinetics between cofactors at the donor side of PSII (24). Our theoretical results revealed (data not shown) that only deceleration or acceleration of the electron transfer from YZ to P680+ in PSII when both tyrosines (YZ and YD) are initially reduced (41) do not provide a better simulation of the experimental data of the oxygen oscillation. This theoretical result was expected because the effectivity of the S-state transitions is, in our model, also influenced by the rate of the intermediate S-states. However, in the real PSII, the role of reduced YD on the kinetics of the YZ oxidation is a consequence of yet unclear changes in the system of the hydrogen-bond network around YZ (33–37) caused by reduced YD (41)—a network which, in our approach, can be associated with intermediate S-states (see above). We therefore tested the consequences of the modification of the rate constants for the intermediate S-states which, to a certain extent, can describe broad kinetic changes at the donor side of PSII in the presence of reduced YD. The results shown in Fig. 4 (solid stars), based on a five-times deceleration of the intermediate S-states (kiSn = 3 × 105 s−1) in PSII with the reduced YD, give a better description of related experimental data (open circles in Fig. 4), especially in the Y2-Y4 (oxygen yield after the second, third, and fourth flashes). Therefore, an effect of the higher initial concentration of reduced YD to oxygen oscillation reported in the literature seems to be reasonable; our model also supports this hypothesis.
However, we note that it is not possible to simulate all experimental data with the same model of PSII, even if we focus only on the cyanobacteria. The main reasons are:
Lower reproducibility of the experiments (e.g., two measurements with the same sample preparation, the same measuring and subsequent fitting procedures can lead to an almost identical oxygen yield after the second flash (Y2) but significantly different Y3; (42,43)).
Almost no possibility of comparison with experimental results obtained by different authors (caused, e.g., by significant temperature-dependence of the damping of the oxygen oscillation, different time-course of the flash intensity).
The reason we present only one set of the oxygen oscillation measurements is because theoretical analysis of the large majority of the experiments must be done separately (and part of it is possible to simulate only qualitatively). Our goal is to introduce the assumption of the intermediate S-states and to describe kinetics of the period-four oscillation. In our opinion, it is more relevant to test the validation of our model in other ways (see following sections).
Dependence of oxygen yield on flash frequency
An analysis of the dependence of flash-induced oxygen yield on flash frequency is another way to test the validity of our model and thus of the intermediate S-states, which are assumed in our model. A comparison of experimental and theoretical oxygen yields induced by a flash-train, where the frequency of the flashes was 2 Hz, is shown in Figs. 2–4. However, this flash frequency is too high for marked changes of the oxygen oscillation due to the YD oxidation/reduction, which represents the main part of the S-states deactivation at longer timescales (i.e., lower flash frequencies), and is also included in our model (Scheme 2 F).
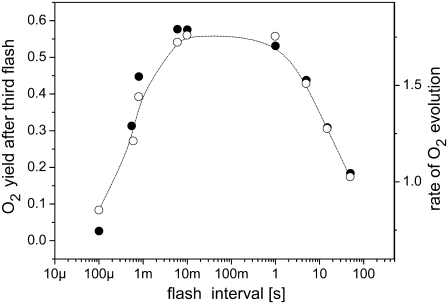
Since the highest oxygen yield is after the third flash, we calculated the oxygen yield after this flash (Y3) for a broad range of frequencies applied in the flash-train. However, no experimental data are yet available which could be compared directly with our data. Therefore, for comparison, we chose experimental data from Kok et al. (5), which represent the rate of oxygen evolution in continuous illumination, started 1 s after the second flash fired at variable time intervals after the first flash. The comparison of theoretical Y3 (solid circles) with the experimental data (open circles) is presented in Fig. 5. This figure shows a clear correlation between the experimental and theoretical data, and thus, a direct relation between the maximum of oxygen oscillation and the rate of oxygen evolution is evident. Therefore, we can conclude that the incorporation of the OEC-YD redox activities into our model successfully enables us to simulate the oxygen-yield independent of flash frequency.
FIGURE 5.
Comparison of simulated (solid circles) oxygen yield after the third flash (Y3) and experimentally measured rate of O2 evolution (open circles; data redrawn from (5)) as a function of flash frequency. Model, used here, is the same as that for simulations of the oscillations presented by solid circles in Fig. 2. The experimental rate of oxygen evolution was measured in continuous illumination which started 1 s after the second flash was fired at variable time intervals after the first flash.
We note that there are insufficient experimental data concerning the changes of S-state distribution in the dark. In addition to the known S-state decay kinetics caused by the YD reduction/oxidation or recombination of the S2-state with 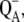 there are several unprobed mechanisms such as the S2-S1 passive relaxation in the presence of reduced YD (44) or the omitted recombinant deactivation of the S3-state (45). Therefore, the self-consistent quantitative simulations of oxygen evolution and S-states at any flash frequency and for any light/dark conditions are nearly impossible at this time, and we are primarily testing the experimental data of oxygen yield with known or mostly estimated initial distribution of the S-states.
there are several unprobed mechanisms such as the S2-S1 passive relaxation in the presence of reduced YD (44) or the omitted recombinant deactivation of the S3-state (45). Therefore, the self-consistent quantitative simulations of oxygen evolution and S-states at any flash frequency and for any light/dark conditions are nearly impossible at this time, and we are primarily testing the experimental data of oxygen yield with known or mostly estimated initial distribution of the S-states.
The interrelationship between period-four oscillations of chlorophyll fluorescence and oxygen evolution
The period-four oscillation induced by the flashes was also detected in chlorophyll fluorescence signal (46,47) which can be used, e.g., for indirect kinetic analysis of the oxygen evolution (48) or fluorescence quenching analysis (49). However, after the introduction of the intermediate S-states into the previous model (16), any simulated flash-induced, period-four oscillation in the fluorescence signal still did not appear (data not shown). It was therefore necessary to add a connecting link between the deactivation of the S-states and chlorophyll fluorescence to our model as suggested before (46), because the linear four-step mechanism of the OEC oxidation is insufficient for the explanation of the fluorescence oscillation (50).
There is only a speculation as to the origin of the fluorescence oscillation. For example, the reversible radical pair model of PSII, without consideration of static heterogeneity, cannot simulate this oscillation (51). We found that, besides the intermediate S-states, a sufficient condition for the period-four oscillation in chlorophyll fluorescence is the charge recombination between 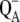 and the S2 state of OEC (Scheme 2 E) with a time constant of 1.5 s (25). We observed (data not shown) that, for a qualitative agreement with the experiments, it is necessary to consider 25% of QB to be initially in the
and the S2 state of OEC (Scheme 2 E) with a time constant of 1.5 s (25). We observed (data not shown) that, for a qualitative agreement with the experiments, it is necessary to consider 25% of QB to be initially in the 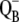 state as suggested before (52).
state as suggested before (52).
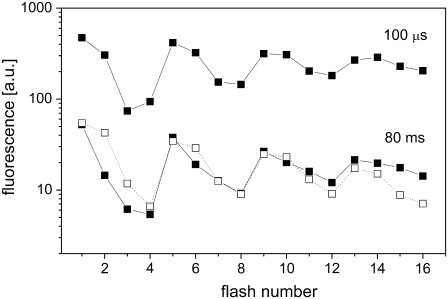
Fig. 6 (solid squares) shows flash-induced period-four oscillation in the signal of delayed fluorescence at two different times (100 μs and 80 ms) after application of the flashes as had resulted from simulations based on our model (Scheme 2). It is obvious from a comparison of the theoretical data with the related experimental data (open squares; redrawn from (53)) that the simulated oscillation of fluorescence at 80 ms is in qualitative agreement (position of the minima and maxima) with the experimental data. Moreover, the simulated oscillation of fluorescence signal has minima after the third flash at shorter times (100 μs) of fluorescence detection after the flashes, but after the fourth flash at longer times (80 ms) of the fluorescence detection after the flashes (39).
FIGURE 6.
Comparison of theoretical and experimental data of oscillation of delayed chlorophyll fluorescence emission induced by 16 flashes. Initial conditions for simulations are the same as for measured data (53): assumption of 5-min dark adaptation (25% of OEC in the S0-state and 75% of OEC in the S1-state), 3-μs flash and 630-ms dark interval between the flashes. Open squares show experimental data redrawn from Delrieu and Rosengard (53). Solid squares show theoretical simulations based on our model (Scheme 2).
We note that the experimental data shown in the Fig. 6 (open squares) were obtained from spinach, a higher plant where heterogeneity of PSII is well known. Therefore, for a detailed analysis and a better agreement between simulated and experimental fluorescence oscillation, it is necessary to consider the heterogeneity of the acceptor side of PSII or to measure flash-induced chlorophyll fluorescence from cyanobacteria where PSII may be considered as homogeneous (presented kinetic model describes homogeneous population of PSII). Among other things, our model cannot simulate the empty QB pocket after a long dark adaptation (several hours) and its effect on the binary oscillation of chlorophyll fluorescence. On the other hand, our model can be used, after some modifications, for further insight into the relationship between thermoluminescence and delayed fluorescence period-four oscillations (54).
All in all, the simulated fluorescence oscillations are presented here above all as an auxiliary result to check the correctness of our proposed model (the intermediate S-states assumption). It is important to note that chlorophyll fluorescence is defined in our model according to its true physical origin, as a radiative deactivation of the excited states via rate constant of fluorescence, kF (Scheme 2 C (55,56)). Therefore, our simultaneous simulations of oxygen and fluorescence signal can provide more valuable information about the function of PSII (and in the future about the heterogeneity of PSII) and the origin of studied phenomena than numerical models, where chlorophyll fluorescence is assumed to reflect, e.g., 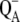 concentration (e.g., (52)) or fitted only to the Kok model (e.g., (53)).
concentration (e.g., (52)) or fitted only to the Kok model (e.g., (53)).
CONCLUSIONS
We have found that the existing kinetic description of the OEC oxidation (16) is insufficient because, thanks to the backward electron transport in reaction 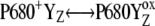 and relatively slow S-state transitions, P680+ is accumulated, which leads to excessive
and relatively slow S-state transitions, P680+ is accumulated, which leads to excessive 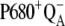 recombination in the kinetic model of PSII. As a result, the very high misses were obtained and it was not possible to simulate the period-four oscillation of the S-state distribution. We have shown that to shift the equilibrium in the above reaction more to the right, it is essential to consider an additional kinetic step as the initial phase of each of the Sn-Sn+1 (n = 0, 1, 2, 3) transitions. These steps, [
recombination in the kinetic model of PSII. As a result, the very high misses were obtained and it was not possible to simulate the period-four oscillation of the S-state distribution. We have shown that to shift the equilibrium in the above reaction more to the right, it is essential to consider an additional kinetic step as the initial phase of each of the Sn-Sn+1 (n = 0, 1, 2, 3) transitions. These steps, [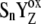 ]-states (n = 0, 1, 2, 3) named the intermediate S-states, are formed with rate constant kiSn ∼ 1.5 × 106 s−1. The [
]-states (n = 0, 1, 2, 3) named the intermediate S-states, are formed with rate constant kiSn ∼ 1.5 × 106 s−1. The [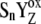 ]-state is then transformed to YZ and the Sn+1-state, which represents the S-state transitions of the Kok cycle. We suggest that kinetics of the intermediate S-states, which was determined from comparison of theoretical predictions with experimental data, reflects a relaxation process associated with changes of the redox equilibrium in the reaction
]-state is then transformed to YZ and the Sn+1-state, which represents the S-state transitions of the Kok cycle. We suggest that kinetics of the intermediate S-states, which was determined from comparison of theoretical predictions with experimental data, reflects a relaxation process associated with changes of the redox equilibrium in the reaction 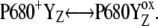 We speculate that the relaxation process comprises a rearrangement of the variable system of the hydrogen-bond network around YZ caused by phenolic proton dissociated after YZ oxidation by P680+ (33–37).
We speculate that the relaxation process comprises a rearrangement of the variable system of the hydrogen-bond network around YZ caused by phenolic proton dissociated after YZ oxidation by P680+ (33–37).
By consideration of the intermediate S-states in the model, we determined the conditions for in silico S-state oscillation and we have shown that the proposed kinetic model of PSII successfully describes flash-induced, period-four damped oscillations of oxygen evolution and partially also of chlorophyll fluorescence.
The oxygen oscillation is simulated without the Kok miss and double-hit parameters, as defined by Kok et al. (5), if the intermediate S-states are assumed. Moreover, the kinetics of the intermediate S-states regulate the appearance and the damping of the oxygen oscillation caused by secondary reactions and influenced by the duration of the flashes; i.e., the intermediate S-states are not the source of the misses or the double-hits. Further, several consequences resulting from our assumption of the intermediate S-states to the oxygen evolution were successfully tested in this article. In the future, we will incorporate PSII heterogeneity into the model to improve agreement between theoretical and experimental data, especially of the period-four fluorescence oscillation and for description of oxygen oscillation from higher plants.
Acknowledgments
The authors thank Govindjee, J. Naus, P. Ilik, and P. Pospisil for critical reading of the manuscript. We owe special thanks to Govindjee, who suggested significant changes at the time of the reviewing process that led to the improvement of this manuscript.
This work was financially supported by the Ministry of Education of the Czech Republic by grant No. MSM 6198959215 and by Grant Agency of the Czech Republic grant No. 522-08-H003.
APPENDIX: MODEL DESCRIPTION
The model proposed here is a kinetic model of the PSII and is derived from a model used for simulation of the chlorophyll fluorescence rise (16). A scheme of the model used in this work for simulations, as presented in Figs. 2–6, is shown in Scheme 2. This is divided into several parts: the main reaction scheme (Scheme 2 A); the exchange of a PQ molecule in the QB pocket (Scheme 2 B); pathways of deactivation for the excited state (Scheme 2 C); the donor side of PSII (Scheme 2 D); the recombination link between the acceptor and the donor side of PSII (Scheme 2 E); and the tyrosine D redox reactions (Scheme 2 F). The newly defined or changed rate constants with respect to the earlier model (16) are listed in Table 2. Values for the rate constants already used in the earlier model (16) are listed in Table 3. The earlier model (16), which was used for one simulation as presented in Fig. 1, does not consider Scheme 2, E and F, and the intermediate S-states of Scheme 2 D, i.e., a particular Sn-state is transformed to an Sn+1 state directly without going through a particular intermediate S-state (see also below).
TABLE 3.
Values of the rate constants of the reactions considered in the earlier model (16), and also used in our model (Scheme 2)
| Rate constant | Used value [s−1] |
|---|---|
| kF | 6.7 × 107 |
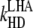 |
5 × 108 |
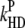 |
1 × 109 |
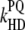 |
5.6 × 107 |
| kUU | 1 × 109 |
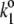 |
3 × 109 |
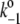 |
3 × 108 |
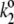 |
2.3 × 109 |
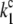 |
4.8 × 108 |
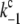 |
3.4 × 108 |
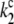 |
1 × 109 |
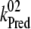 |
5 × 107 |
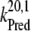 |
2 × 107 |
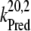 |
3.6 × 106 |
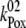 |
1.7 × 106 |
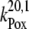 |
6.7 × 106 |
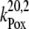 |
1.2 × 106 |
| k01 | 20,000 |
| k12 | 10,000 |
| k23 | 3330 |
| k30 | 1000 |
| k(B/PQ)ex | 250 |
| k(PQ/B)ex | 250 |
| kPQox | 10 |
| kPQred | 10 |
The main modification with respect to the earlier model (16), and also a keystone of our results, is the kinetic description of the donor side function in the model (Scheme 2 D). It is described in more detail now: P680+ formed by the charge separation is reduced by YZ leading to formation of P680 and 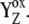 Kinetics of P680+ reduction by YZ is monophasic in the S0- and S1-states (rate constant
Kinetics of P680+ reduction by YZ is monophasic in the S0- and S1-states (rate constant 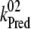 = 5 × 107 s−1 (22,57)) and biphasic in the S2- and S3-states (rate constants
= 5 × 107 s−1 (22,57)) and biphasic in the S2- and S3-states (rate constants 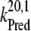 = 2 × 107 s−1 and
= 2 × 107 s−1 and 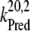 = 3.6 × 106 s−1; both rates contribute 50% to the overall rate (22,57)). The reduction of P680+ by YZ is reversible and the backward reaction keeps the same rules for mono- and biphasicity as for the forward reactions (for values of
= 3.6 × 106 s−1; both rates contribute 50% to the overall rate (22,57)). The reduction of P680+ by YZ is reversible and the backward reaction keeps the same rules for mono- and biphasicity as for the forward reactions (for values of 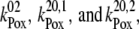 see Table 3).
see Table 3). 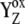 resulted from the reduction of P680+, then with a particular Sn-state forms a particular intermediate [
resulted from the reduction of P680+, then with a particular Sn-state forms a particular intermediate [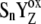 ]-state (n = 0, 1, 2, 3). This state reflects a relaxation process associated with changes of the redox equilibria [P680+ YZ ↔ P680
]-state (n = 0, 1, 2, 3). This state reflects a relaxation process associated with changes of the redox equilibria [P680+ YZ ↔ P680 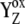 ]j (index j symbolizes one state of relaxation sequence (21,22), which stabilizes the final product of YZ oxidation by P680+, i.e.,
]j (index j symbolizes one state of relaxation sequence (21,22), which stabilizes the final product of YZ oxidation by P680+, i.e., 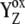 ). After relaxation, the [
). After relaxation, the [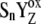 ]-state is then transformed to YZ and the Sn+1-state, which represents the Kok cycle described by rate constants k01, k12, k23, and k30 (Table 3). Comparison between experimental and simulated data supports the S-state independent rate constant of the intermediate S-states, kiSn = 1.5 × 106 s−1.
]-state is then transformed to YZ and the Sn+1-state, which represents the Kok cycle described by rate constants k01, k12, k23, and k30 (Table 3). Comparison between experimental and simulated data supports the S-state independent rate constant of the intermediate S-states, kiSn = 1.5 × 106 s−1.
We note that the model used here is based on the original model (16), which assumed that the primary electron donor in PSII is P680. Although accessory-chlorophyll Chlacc D1 (placed between P680 and Pheo) was recently identified as the primary electron donor in PSII (58,59), for simplicity's sake in our model, we considered P680 to be the primary electron donor in PSII.
We note that, in addition to the fast nanosecond P680+ decay through nonradiative charge recombination in the closed reaction centers of PSII (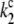 = 1/(1 ns)), through radiative charge recombination in the closed reaction centers of PSII (
= 1/(1 ns)), through radiative charge recombination in the closed reaction centers of PSII (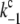 = 1/(2.9 ns)), and through radiative charge recombination in the open reaction centers of PSII (
= 1/(2.9 ns)), and through radiative charge recombination in the open reaction centers of PSII (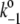 = 1/(3.3 ns)), our model also explicitly includes P680+ decay with time constants of 20 ns, 50 ns, 278 ns, and 100 μs. The first three time-constants reflect P680+ reduction by YZ (
= 1/(3.3 ns)), our model also explicitly includes P680+ decay with time constants of 20 ns, 50 ns, 278 ns, and 100 μs. The first three time-constants reflect P680+ reduction by YZ (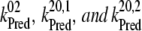 ), and the microsecond kinetics are due to
), and the microsecond kinetics are due to 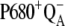 recombination (k(P/A)rec) (Scheme 2 A and Table 3). We also have shown that microsecond reduction of P680+ does not induce or remarkably influence the period-four oscillation associated with the OEC oxidation.
recombination (k(P/A)rec) (Scheme 2 A and Table 3). We also have shown that microsecond reduction of P680+ does not induce or remarkably influence the period-four oscillation associated with the OEC oxidation.
All reversible/irreversible monomolecular/bimolecular reactions entered into the model are assumed to be first-order reactions with respect to one reactant and are defined as mass action reactions. For illustration, if monomolecular reversible mass action reaction between substrate A and product B (e.g., (L-P)*HAB ↔ L-P+H−AB; Scheme 2 A)) is considered with forward (kf) and backward (kb) rate constants, the overall rate of reaction is v = kf[A](t) – kb[B](t). The overall rate of several mass action reactions is dependent on the concentration of certain modifiers (P680+/P680 reduction/oxidation by YZ depends on the S-state of the OEC; the quenching of the excited states by oxidized PQ pool and P680+ depends on a concentration of oxidized PQ molecules and P680+ (16)).
The excitation of L-P is defined in the model by the rate constant kL, which was 3,333,333 s−1 for simulating 3-μs saturation flashes (this value resulted from a condition of 100% concentration of P680+ in the model with inhibited OEC, at the end of a 3-μs flash, after dark adaptation). The successful simulation of experimental data (Figs. 2–6) show that consideration of the residual light intensity (tail), normal for a xenon flash lamp, is not a prerequisite for quantitative agreement between the simulation and the experimental results.
The oxygen signal in the model is defined as a maximum of the concentration of the intermediate S-state during the S3-S0 transition (Scheme 2 D) because oxygen is released during the S3-S0 transition and the [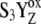 ]-state is the last state in the transition in our model. The fluorescence signal is defined as a radiative deactivation via rate constant kF (Scheme 2 C) of the sum of all excited states considered in the model (Scheme 2 A). The contribution of photosystem I fluorescence to the total fluorescence signal is neglected in our model.
]-state is the last state in the transition in our model. The fluorescence signal is defined as a radiative deactivation via rate constant kF (Scheme 2 C) of the sum of all excited states considered in the model (Scheme 2 A). The contribution of photosystem I fluorescence to the total fluorescence signal is neglected in our model.
In our theoretical approach we use theoretical simulations and not fitting. In the simulations, we fixed values of all model parameters (initial concentrations and values of rate constants) to values known from literature and followed the resulting simulations, which we have compared with experimental data. In the fitting, the model parameters are fitted to obtain the best agreement between theoretical and experimental data. However, in the fitting a change in one model parameter can be greatly compensated by a change in another model parameter (55), especially in such a complex model as presented here. Moreover, the best fit of the model parameters does not necessarily mean that the values of the fitted model parameters have correct physiological values (60). Further, in simulations of biological systems, which are usually very complex (as is our system) and hard to describe comprehensively and correctly, a qualitative agreement between theory and experiment is sufficient goal, in comparison to technical systems which can easily be correctly described and where a quantitative agreement is required between theory and experiments.
Editor: Ron Elber.
References
- 1.Wydrzynski, T., and K. Satoh. 2005. Photosystem II: The Water/Plastoquinone Oxido-Reductase in Photosynthesis. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- 2.Joliot, P., G. Barbieri, and R. Chabaud. 1969. A new model of photochemical centers in system 2. Photochem. Photobiol. 10:309–329. [Google Scholar]
- 3.Joliot, P. 2003. Period-four oscillations of the flash-induced oxygen formation in photosynthesis. Photosynth. Res. 76:65–72. [DOI] [PubMed] [Google Scholar]
- 4.Shinkarev, V. P. 2005. Flash-induced oxygen evolution and other oscillation processes in photosystem II. In Photosystem II: The Water/Plastoquinone Oxido-Reductase in Photosynthesis. T. Wydrzynski and K. Satoh, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- 5.Kok, B., B. Forbush, and M. McGloin. 1970. Cooperation of charges in photosynthetic O2 evolution. I. A linear four-step mechanism. Photochem. Photobiol. 11:457–475. [DOI] [PubMed] [Google Scholar]
- 6.Mar, T., and Govindjee. 1972. Kinetic models of oxygen evolution in photosynthesis. J. Theor. Biol. 36:427–446. [DOI] [PubMed] [Google Scholar]
- 7.Shinkarev, V. P., and C. A. Wraight. 1993. Oxygen evolution in photosynthesis: from unicycle to bicycle. Proc. Natl. Acad. Sci. USA. 90:1834–1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.deWijn, R., and H. J. van Gorkom. 2002. S-state dependence of the miss probability in photosystem II. Photosynth. Res. 72:217–222. [DOI] [PubMed] [Google Scholar]
- 9.Shinkarev, V. P. 2005. Flash-induced oxygen evolution in photosynthesis: simple solution for the extended S-state model that includes misses, double-hits, inactivation, and backward-transition. Biophys. J. 88:412–421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Messinger, J., W. P. Schröder, and G. Renger. 1993. Structure-function relations in photosystem II. Effects of temperature and chaotropic agents on the period four oscillation of flash-induced oxygen evolution. Biochemistry. 32:7658–7668. [DOI] [PubMed] [Google Scholar]
- 11.Jursinic, P. 1981. Investigation of double turnovers in photosystem II charge separation and oxygen evolution with excitation flashes of different duration. Biochim. Biophys. Acta. 635:38–52. [DOI] [PubMed] [Google Scholar]
- 12.Mendes, P. 2002. GEPASI, Ver. 3.30. The University of Wales, Aberystwyth, UK.
- 13.Mendes, P. 1993. GEPASI: a software package for modeling the dynamics, steady states and control of biochemical and other systems. Comput. Appl. Biosci. 9:563–571. [DOI] [PubMed] [Google Scholar]
- 14.Mendes, P. 1997. Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem. Sci. 22:361–363. [DOI] [PubMed] [Google Scholar]
- 15.Petzold, L., and A. Hindmarsh. 1997. LSODA (Livermore Solver of Ordinary Differential Equations). Computing and Mathematics Research Division, Lawrence Livermore National Laboratory, Livermore, CA.
- 16.Lazár, D. 2003. Chlorophyll a fluorescence rise induced by high light illumination of dark-adapted plant tissue studied by means of a model of photosystem II and considering photosystem II heterogeneity. J. Theor. Biol. 220:469–503. [DOI] [PubMed] [Google Scholar]
- 17.Haumann, M., P. Liebisch, C. Müller, M. Barra, M. Grabolle, and H. Dau. 2005. Photosynthetic O2 formation tracked by time-resolved x-ray experiments. Science. 310:1019–1021. [DOI] [PubMed] [Google Scholar]
- 18.Dau, H., and M. Haumann. 2006. Photosynthetic oxygen production: response. Science. 312:1470–1472. [DOI] [PubMed] [Google Scholar]
- 19.Dau, H., and M. Haumann. 2007. Eight steps preceding O-O bond formation in oxygenic photosynthesis—a basic reaction cycle of the photosystem II manganese complex. Biochim. Biophys. Acta. 1767:472–483. [DOI] [PubMed] [Google Scholar]
- 20.Rappaport, F., M. Blanchard-Desce, and J. Lavergne. 1994. Kinetic of electron transfer and electrochromic change during the redox transition of the photosynthetic oxygen-evolving complex. Biochim. Biophys. Acta. 1184:178–192. [Google Scholar]
- 21.Razeghifard, M. R., and R. J. Pace. 1999. EPR kinetic studies of oxygen release in thylakoids and PSII membranes: a kinetic intermediate in the S3 to S0 transition. Biochemistry. 38:1252–1257. [DOI] [PubMed] [Google Scholar]
- 22.Brettel, K., E. Schlodder, and H. T. Witt. 1984. Nanosecond reduction kinetics of photooxidized chlorophyll-aII (P-680) in single flashes as a probe for the electron pathway, H+-release and charge accumulation in the O2-evolving complex. Biochim. Biophys. Acta. 766:403–415. [Google Scholar]
- 23.Lavergne, J., and J.-M. Briantais. 1996. Photosystem II heterogeneity. In Oxygenic Photosynthesis: The Light Reactions. Govindjee, D. R. Ort and C. F. Yocum, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands.
- 24.Isgandarova, S., G. Renger, and J. Messinger. 2003. Functional differences of photosystem II from Synechococcus elongatus and spinach characterized by flash induced oxygen evolution patterns. Biochemistry. 42:8929–8938. [DOI] [PubMed] [Google Scholar]
- 25.Robinson, H. H., and A. R. Crofts. 1983. Kinetic of the oxidation-reduction reactions of the photosystem II quinone acceptor complex, and the pathway for deactivation. FEBS Lett. 153:221–226. [Google Scholar]
- 26.Vermaas, W. F. J., G. Renger, and G. Dohnt. 1984. The reduction of the oxygen-evolving system in chloroplasts by thylakoid components. Biochim. Biophys. Acta. 764:194–202. [Google Scholar]
- 27.Vass, I., Z. Deák, and É. Hideg. 1990. Charge equilibrium between the water-oxidizing complex and the electron donor tyrosine-D in photosystem II. Biochim. Biophys. Acta. 1017:63–69. [Google Scholar]
- 28.de Wijn, R., and H. J. van Gorkom. 2002. The rate of charge recombination in photosystem II. Biochim. Biophys. Acta. 1553:302–308. [DOI] [PubMed] [Google Scholar]
- 29.Renger, G. 2004. Coupling of electron and proton transfer in oxidative water cleavage in photosynthesis. Biochim. Biophys. Acta. 1655:195–204. [DOI] [PubMed] [Google Scholar]
- 30.Renger, G., and P. Kühn. 2007. Reaction pattern and mechanism of light induced oxidative water splitting in photosynthesis. Biochim. Biophys. Acta. 1767:458–471. [DOI] [PubMed] [Google Scholar]
- 31.Christophorov, L. N., A. R. Holzwarth, V. N. Kharkyanen, and F. van Mourik. 2000. Structure-function self-organization in nonequilibrium macromolecular systems. Chem. Phys. 256:45–60. [Google Scholar]
- 32.Goushcha, A. O., V. N. Kharkyanen, G. W. Scott, and A. R. Holzwarth. 2000. Self-regulation phenomena in bacterial reaction centers. I. General theory. Biophys. J. 79:1237–1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Vrettos, J. S., J. Limburg, and G. W. Brudvig. 2001. Mechanism of photosynthetic water oxidation: combining biophysical studies of photosystem II with inorganic model chemistry. Biochim. Biophys. Acta. 1503:229–245. [DOI] [PubMed] [Google Scholar]
- 34.Rappaport, F., and J. Lavergne. 2001. Coupling of electron and proton transfer in the photosynthetic water oxidase. Biochim. Biophys. Acta. 1503:246–259. [DOI] [PubMed] [Google Scholar]
- 35.Hays, A.-M. A., I. R. Vassiliev, J. H. Golbeck, and R. J. Debus. 1998. Role of D1-His190 in proton-coupled electron transfer reactions in photosystem II: a chemical complementation study. Biochemistry. 37:11352–11365. [DOI] [PubMed] [Google Scholar]
- 36.Ishikita, H., and E. W. Knapp. 2006. Function of the redox-active tyrosine in photosystem II. Biophys. J. 90:3886–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhang, Ch. 2006. Low-barrier hydrogen bond plays key role in active photosystem II—a new model for photosynthetic water oxidation. Biochim. Biophys. Acta. 1767:493–499. [DOI] [PubMed] [Google Scholar]
- 38.Reference deleted in proof.
- 39.Putrenko, I. I., S. Vasil'ev, and D. Bruce. 1999. Modulation of flash-induced photosystem II fluorescence by events occurring at the water oxidizing complex. Biochemistry. 38:10632–10641. [DOI] [PubMed] [Google Scholar]
- 40.Messinger, J., J. H. Robblee, U. Bergmann, C. Fernandez, P. Glatzel, H. Visser, R. M. Cinco, K. L. McFarlane, E. Bellacchio, S. A. Pizarro, S. P. Cramer, K. Sauer, M. P. Klein, and V. K. Yachandra. 2001. Absence of Mn-centered oxidation in the S2→S3 transition: implications for the mechanism of photosynthetic water oxidation. J. Am. Chem. Soc. 123:7804–7820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Faller, P., R. J. Debus, K. Brettel, M. Sugiura, A. W. Rutherford, and A. Boussac. 2001. Rapid formation of the stable tyrosyl radical in photosystem II. Proc. Natl. Acad. Sci. USA. 98:14368–14373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sugiura, M., F. Rappaport, K. Brettel, T. Noguchi, A. W. Rutherford, and A. Boussac. 2004. Site-directed mutagenesis of Thermosynechococcus elongatus photosystem II: the O2-evolving enzyme lacking the redox-active tyrosine D. Biochemistry. 43:13549–13563. [DOI] [PubMed] [Google Scholar]
- 43.Boussac, A., F. Rappaport, P. Carrier, J.-M. Verbavatz, R. Gobin, D. Kirilovsky, A. W. Rutherford, and M. Sugiura. 2004. Biosynthetic Ca2+/Sr2+ exchange in the photosystem II oxygen-evolving enzyme of Thermosynechococcus elongatus. J. Biol. Chem. 279:22809–22819. [DOI] [PubMed] [Google Scholar]
- 44.Ho, F. M., S. F. Morvaridi, F. Mamedov, and S. Styring. 2006. Enhancement of YD• spin relaxation by the CaMn4 cluster in photosystem II detected at room temperature: a new probe for the S-cycle. Biochim. Biophys. Acta. 1767:5–14. [DOI] [PubMed] [Google Scholar]
- 45.Diner, B. A. 1977. Dependence of the deactivation reactions of photosystem II on the redox state of plastoquinone pool A varied under anaerobic conditions—equilibria on the acceptor side of the photosystem II. Biochim. Biophys. Acta. 460:247–258. [DOI] [PubMed] [Google Scholar]
- 46.Delosme, R. 1971. New results about chlorophyll fluorescence “in vivo”. In Proceedings of the 2nd International Congress on Photosynthesis Research, Stresa, Italy. G. Forti, M. Avron, and A. Melandri, editors. 187–195.
- 47.Delosme, R., and P. Joliot. 2002. Period-four oscillations in chlorophyll a fluorescence. Photosynth. Res. 73:165–168. [DOI] [PubMed] [Google Scholar]
- 48.Shinkarev, V. P., C.H. Xu, Govindjee, and C. A. Wraight. 1997. Kinetics of the oxygen evolution step in plants determined from flash-induced chlorophyll a fluorescence. Photosynth. Res. 51:43–49. [Google Scholar]
- 49.Shinkarev V. P., and Govindjee. 1993. Insight into the relationship of chlorophyll a fluorescence yield to the concentration of its natural quenchers in oxygenic photosynthesis. Proc. Natl. Acad. Sci. USA. 90:7466–7469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Christen, G., and G. Renger. 1999. The role of hydrogen bonds for the multiphasic P680+• reduction by YZ in photosystem II with intact oxygen evolution capacity. Analysis of kinetic H/D isotope exchange effects. Biochemistry. 38:2068–2077. [DOI] [PubMed] [Google Scholar]
- 51.Vasil'ev, S., and D. Bruce. 1998. Nonphotochemical quenching of excitation energy in photosystem II. A picosecond time-resolved study of the low yield of chlorophyll a fluorescence induced by single-turnover flash in isolated spinach thylakoids. Biochemistry. 37:11046–11054. [DOI] [PubMed] [Google Scholar]
- 52.de Wijn, R., and H. J. van Gorkom. 2001. Kinetic of electron transfer from QA to QB in photosystem II. Biochemistry. 40:11912–11922. [DOI] [PubMed] [Google Scholar]
- 53.Delrieu, M. J., and F. Rosengard. 1991. Changes in the S0 and S1 properties during dark adaptation in oxygen-evolving photosystem II enriched thylakoid membranes. Biochim. Biophys. Acta. 1057:78–88. [Google Scholar]
- 54.Rutherford, A. W., Govindjee, and Y. Inoue. 1984. Charge accumulation and photochemistry in leaves studied by thermoluminescence and delayed light emission. Proc. Natl. Acad. Sci. USA. 81:1107–1111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Baake, E., and J. P. Schlöder. 1992. Modeling the fast fluorescence rise of photosynthesis. Bull. Math. Biol. 54:999–1021. [Google Scholar]
- 56.Zhu, X.-G, Govindjee, N. R. Baker, E. deSturler, D. R. Ort, and S. P. Long. 2005. Chlorophyll a fluorescence induction kinetics in leaves predicted from a model describing each discrete step of excitation energy and electron transfer associated with photosystem II. Planta. 223:114–133. [DOI] [PubMed] [Google Scholar]
-
57.Meyer, B., E. Schlodder, J. P. Dekker, and H. T. Witt. 1989. O2 evolution and Chl
 (P680+) nanosecond reduction kinetics in single flashes as a function of pH. Biochim. Biophys. Acta. 974:36–43. [Google Scholar]
(P680+) nanosecond reduction kinetics in single flashes as a function of pH. Biochim. Biophys. Acta. 974:36–43. [Google Scholar] - 58.Groot, M. L., N. P. Pawlowicz, L. J. G. W. van Wilderen, J. Breton, I. H. M. van Stokkum, and R. van Grondelle. 2006. Initial electron donor and acceptor in isolated photosystem II reaction centers identified with femtosecond mid-IR spectroscopy. Proc. Natl. Acad. Sci. USA. 102:13087–13092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Holzwarth, A. R., M. G. Müller, M. Reus, M. Nowaczyk, J. Sander, and M. Rögner. 2006. Kinetics and mechanism of electron transfer in intact photosystem II and in the isolated reaction center: pheophytin is the primary electron acceptor. Proc. Natl. Acad. Sci. USA. 103:6895–6900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Strasser, R. J., and A. D. Stirbet. 2001. Estimation of the energetic connectivity of PS II centres in plants using the fluorescence O-J-I-P. Fitting of experimental data to three different PS II models. Math. Comput. Simul. 56:451–461. [Google Scholar]