Skip to main content
PMC home page
Genomic Medicine logoLink to Genomic Medicine
. 2007 May 11;1(1-2):19–28. doi: 10.1007/s11568-007-9004-7

Deciphering modular and dynamic behaviors of transcriptional networks

Ming Zhan 1,✉
PMCID: PMC2276884  PMID: 18923925

Abstract

The coordinated and dynamic modulation or interaction of genes or proteins acts as an important mechanism used by a cell in functional regulation. Recent studies have shown that many transcriptional networks exhibit a scale-free topology and hierarchical modular architecture. It has also been shown that transcriptional networks or pathways are dynamic and behave only in certain ways and controlled manners in response to disease development, changing cellular conditions, and different environmental factors. Moreover, evolutionarily conserved and divergent transcriptional modules underline fundamental and species-specific molecular mechanisms controlling disease development or cellular phenotypes. Various computational algorithms have been developed to explore transcriptional networks and modules from gene expression data. In silico studies have also been made to mimic the dynamic behavior of regulatory networks, analyzing how disease or cellular phenotypes arise from the connectivity or networks of genes and their products. Here, we review the recent development in computational biology research on deciphering modular and dynamic behaviors of transcriptional networks, highlighting important findings. We also demonstrate how these computational algorithms can be applied in systems biology studies as on disease, stem cells, and drug discovery.

Keywords: Systems biology, Coexpression, Transcriptional module, Pathway dynamics, Transcriptional intervention, ModulePro, PathwayPro

Introduction

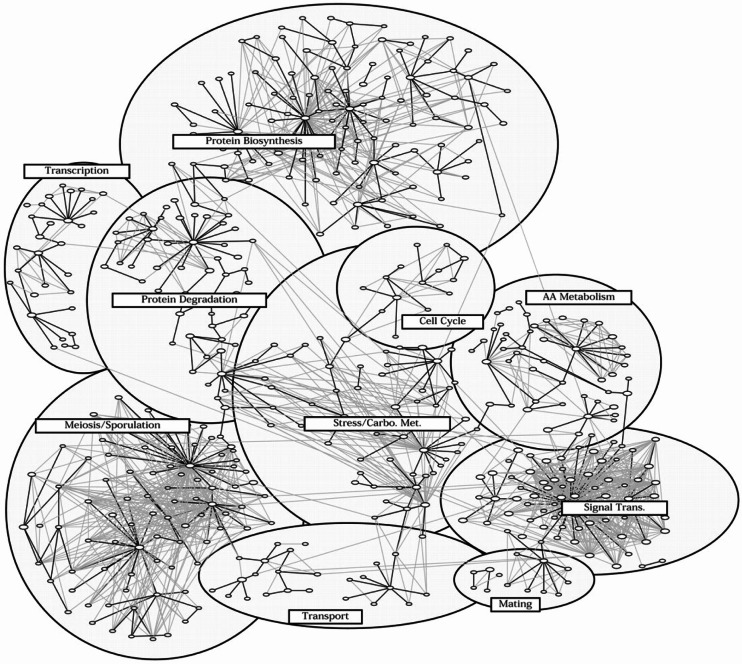
The coordinated and dynamic modulation or interaction of genes or proteins acts as an important mechanism used by a cell in functional regulation (Bar-Joseph et al. 2003; Hartwell et al. 1999; Ideker et al. 2001; Segal et al. 2004). It has been shown that many transcriptional networks exhibit a scale-free topology and hierarchical modular architecture (Barabasi and Bonabeau 2003; Ihmels et al. 2002; Jeong et al. 2000; Ravasz et al. 2002; Resendis-Antonio et al. 2005; Stuart et al. 2003; Tanay et al. 2004; van Noort et al. 2004). That implies that the networks are dominated by a few highly connected nodes (i.e., genes or proteins) which link the rest of less connected nodes to the system. It also implies that genes often closely interact with each other forming transcriptional modules, some of which further interact with each other forming larger modules, and this process may continue on several different scales. Such a hierarchical modular structure is exemplified by the yeast transcriptional network, as shown in Fig. 1 (Tanay et al. 2004). In addition to the static properties, transcriptional networks or pathways are also dynamic and behave only in certain ways and controlled manners in response to disease development, changing cellular conditions, and different environmental factors (Li and Zhan 2006; Luscombe et al. 2004; Nilsson et al. 2006; Qi and Ge 2006). The examination of the modular and dynamic behavior of genetic networks using microarray or other high-throughput data has begun systems-level exploration of how disease or cellular phenotypes arise from the connectivity or networks of genes and their products (Imoto et al. 2003; Li et al. 2007b; Li and Zhan 2006; Savoie et al. 2003; Sun et al. 2007). The study is particularly promising for identifying diagnostic biomarkers and drug targets, and for elucidating molecular mechanism of disease or cell development (Imoto et al. 2003; Li and Zhan 2006; Savoie et al. 2003).

Fig. 1.

Fig. 1

Open in a new tab

Hierarchical and modular organization of the yeast transcriptional network. Genes are clustered into different modules. Some of the modules (e.g., protein biosynthesis) are organized in more than two hierarchical levels; large modules are composed of several smaller modules, giving a star-like topology. (Reproduced from (Tanay et al. 2004))

In this article, we review the recent development in computational biology research on deciphering modular and dynamic behaviors of transcriptional networks from microarray data, highlighting important findings. We also demonstrate how these computational algorithms can be applied in systems biology studies as on disease, stem cells, and drug discovery.

Identification of transcriptional modules

Computational identification of transcriptional modules from microarray data has been conventionally conducted using clustering-based methods, such as hierarchical clustering, self-organizing maps, and k-means. Recently, different algorithms have been proposed to uncover biologically more meaningful transcriptional modules which may be featured with regulatory programs or hierarchical and contextual modularity.

Segal et al. proposed a class of probabilistic graphical models for inferring regulatory modules from gene expression data (Segal et al. 2003). In this framework, a regulatory module is a set of genes that are regulated in concert by a shared regulatory program. The regulatory program specifies the behavior of the genes in the module as a function of the express levels of regulators. The method allows identifying specific regulators for each module, their effects, and the experimental conditions under which the regulation occurs. Clearly, this approach relies on the assumption that the expression levels of regulated genes depend on the expression levels of regulators. The method was demonstrated for its ability to generate detailed testable hypotheses relating to both regulatory modules and their control programs. The experimental results supported their computationally generated results and suggested regulatory roles for previously uncharacterized proteins.

Similarly, Bar-Joseph et al. described an algorithm that uses gene expression data and transcription factor binding data to discover transcriptional modules (Bar-Joseph et al. 2003). The algorithm performs an exhaustive search over all possible combinations of transcription factors implied by the transcription factor binding data. Once a set of genes bound by a common set of transcription factors is found, the algorithm proceeds to find a smaller subset of genes that are coexpressed. The algorithm then seeks to add additional genes to the module that are similarly expressed and assumingly bound by the same set of transcription factors. The algorithm was applied to an analysis on yeast expression data from over 500 experiments and 106 yeast transcription factors profiled in rich medium conditions, and shown to be efficient in accurately clustering genes and regulators.

Zhou et al. introduced an approach, termed the second-order expression analysis, for the identification of transcriptional modules (Zhou et al. 2005). They defined the first-order expression analysis as the extraction of expression patterns from one microarray data set. They then proposed the second-order expression analysis as a study of the correlated occurrence of expression patterns across multiple data sets measured under different conditions. By analyzing yeast microarray data, they demonstrated that the second-order analysis could identify modules of genes with the same function yet without clear coexpression patterns. The approach could further reveal network relationships among different transcriptional modules.

Barkai’s group presented a method to assign genes into context-dependent and potentially overlapping regulatory units (Ihmels et al. 2004). They defined the transcriptional module as a self-consistent regulatory unit consisting of a set of co-regulated genes as well as the experimental conditions that induce their co-regulation, and proposed an efficient iterative signature algorithm to identify such modules. The proposed method is capable to reveal hierarchical organization of transcriptional modules and capturing overlapping modules in the presence of combinatorial regulation. The transcription modules identified by this method shows a high biological coherence, as measured by the conservation of putative cis-regulatory motifs between four related yeast species, in comparison to those by conventional methods.

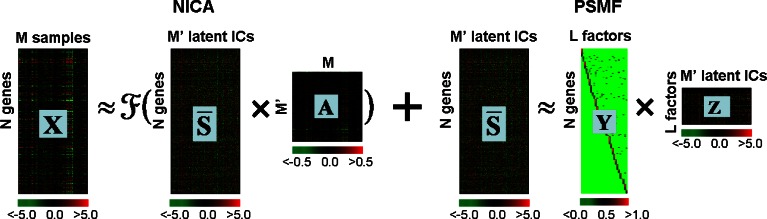
A variety of matrix decomposition methods have been introduced for uncovering transcriptional modules from microarray data, including singular value decomposition (Alter et al. 2000; Holter et al. 2001), independent components analysis (Frigyesi et al. 2006; Lee and Batzoglou 2003; Liebermeister 2002), non-negative matrix factorizations (Brunet et al. 2004; Gao and Church 2005; Kim and Tidor 2003; Lee and Seung 1999; Wang et al. 2006), network component analysis (Liao et al. 2003), and probabilistic sparse matrix factorization (Dueck et al. 2005). Recently, we presented a new matrix decomposition method, ModulePro, for transcriptional module discovery (Li et al. 2007b). The rationales behind our algorithm are: a) there may be nonlinear structure in transcriptional profiles, particularly between transcription factors and their target genes; and b) while many genes are involved in gene regulation, only a small set of genes (e.g., transcription factors or network hub genes) have predominant impact on the expression patterns of most genes. The new method is based on two-stage matrix decomposition on microarray data, as illustrated in Fig. 2. First, a nonlinear independent component analysis (NICA) is adopted to reduce the nonlinear distortion in the data and represent the data with independent latent components. Second, a probabilistic sparse matrix factorization (PSMF) approach is used to model the “fake” expression profiles of genes across the independent latent components as a linear weighted combination of a small number of predominant prototypes that represent the influence of different biological or experimental factors (e.g., transcription factors or network hub genes). The method treats microarray data as a mixture of biological sources unknown or hidden, and takes into account the nonlinear structure existed in the data. The method does not assume that genes with similar expression profiles share the same pathway or similar functions. A gene can be assigned to multiple modules if the gene has multiple functions or is active in multiple biological processes. In comparison with other approaches (e.g., hierarchical clustering, k-means, self-organizing maps, probabilistic sparse matrix factorization, and independent component analysis), the new method shows a higher performance in identifying biologically meaningful transcriptional modules (Li et al. 2007b).

Fig. 2.

Fig. 2

Open in a new tab

A two-stage matrix decomposition of a microarray data set X (N genes and M samples) is obtained by ModulePro. The NICA extracts nonlinear independent components (columns in 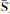Inline graphic) from X. At the PSMF stage, 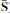Inline graphic is approximated by the product of sparse matrix Y and low-rank Z. The values of all matrices are color coded by using a color heatmap, from dark green (minimum) to dark red (maximum). (Reproduced from (Li et al. 2007b))

Cross-species analysis is important for identifying evolutionarily conserved and divergent transcriptional modules (Bergmann et al. 2004; Ihmels et al. 2005; Stuart et al. 2003; Zhou and Gibson 2004). We implemented an R-based program for the comparative analysis of transcriptional modules from two microarray data sets of different species (Zhan et al. unpublished). First, gene clustering is performed using a method such as self-organizing maps, k-means, or clustering analysis on the microarray data. The clustering results from two different species are then compared, and from the overlaps or non-overlaps of clustering results between two species, conserved or divergent transcriptional modules are identified. Using the program, we examined transcriptional profiles of embryonic stem cells (ESCs) and their earliest differentiated cells, embryoid bodies (EBs), from human and mouse (Sun et al. unpublished). Figure 3 shows the analysis results on the Oct4/Sox2/Nanog-directed network in ESCs and EBs. As illustrated by the combined pair-wise correlation matrices of gene expression in human and mouse (Fig. 3A), the conserved modules (C1 and C2) showed overlapping gene clustering between human and mouse, while the divergent modules (D1 through D7) showed non-overlaps on the gene clustering between the two species. As illustrated by the heatmap of gene expression values (Fig. 3B), the conserved module C1 showed elevated expression in ESCs, while the conserved module C2 showed repressed expression in ESCs, in comparison to EBs in both human and mouse. The conserved and divergent transcriptional modules underline fundamental and species-specific molecular mechanisms regulating stem cell development (Sun et al. unpublished).

Fig. 3.

Fig. 3

Open in a new tab

Results of cross-species transcriptional module analysis on the Oct4/Sox2/Nanog-directed regulatory network in human and mouse ESCs and EBs. (A) Heatmap presentation of the combined pair-wise correlation matrices of gene expression profiles in mouse (upper diagonal part) and human (lower diagonal part). Each column or row represents a human–mouse orthologous gene. Each block on the matrix presents the correlation level between the gene of the corresponding column and the gene of the row. The more reddish the color is, the more correlated the genes are on the expression profiles. The white color indicates zero correlation. (B) Heatmap of normalized gene expression values (red, over-expression in comparison to the mean expression value; green, under-expression, black, non change on the expression level). Each row represents an orthologous gene, and the position of the genes is the same as that on the row in the correlation matrix heatmap in A. The identified transcriptional modules are labeled as C1 through D7

Analysis of gene coexpression

Transcriptional modules are made up by coexpressed or co-regulated genes. With recent interests in genetic networks and modules, the study of gene coexpression has emerged as a novel holistic approach for microarray data analysis (Butte and Kohane 2000; Carter et al. 2004; Graeber and Eisenberg 2001; Lee et al. 2004; Stuart et al. 2003; van Noort et al. 2004). The coexpression of genes has been conventionally measured using the Pearson’s correlation coefficient (Graeber and Eisenberg 2001; Lee et al. 2004; Stuart et al. 2003). The linear model-based correlation coefficient provides a good first approximation of coexpression, but is also associated with certain pitfalls; it can not provide evidence of directional relationship in which one gene is upstream of another, and underestimates the degree of coexpression if the relationship between genes is nonlinear (Herrgard et al. 2003; Imoto et al. 2002). Mutual information is also used to measure gene coexpression (Basso et al. 2005; Butte and Kohane 2000; Margolin et al. 2006; Zhou et al. 2003), but not suitable for modeling directional relationships, either. The coefficient of determination (CoD), on the other hand, can measure how much the combination of given genes (predictors) predicts the behavior of the target gene by comparison to the absence of the predictors, capable of uncovering nonlinear relationship of coexpression and suggesting the directionality (Dougherty et al. 2000; Hashimoto et al. 2004; Kim et al. 2002; Shmulevich et al. 2002a). Recently, we proposed a new algorithm, CoexPro, which is based on B-spline approximation followed by CoD estimation (Li et al. 2007a). The computation by the new algorithm requires no quantization of microarray data, thus avoiding significant loss or misrepresentation of biological information, which would otherwise occur in the conventional application of CoD (Dougherty et al. 2000; Hashimoto et al. 2004). In comparison to correlation coefficient and CoD, the new algorithm reveals gene coexpression with higher biological relevance. Along with uncovering both linear and nonlinear relationships of coexpression and suggesting the directionality, the new algorithm provides a more biologically meaningful model for gene coexpression, particularly useful in determining connectivity and inferring topology in transcriptional network studies. We used CoexPro to analyze coexpression of ligands and their corresponding receptors in lung cancer, prostate cancer, leukemia, and their normal tissue counterparts (Li et al. 2007a). As seen in Table 1, the analysis revealed many ligand-receptor pairs that showed different patterns of coexpression in cancer and normal tissues. Between the ligand BMP7 and its receptor ACVR2B, for example, CoD-B (the coexpression estimated by CoexPro) was 0.76 (P-value <0.028) in lung cancer and 0.00 (P-value <0.58) in normal samples, while R2 (correlation coefficient) was 0.042 in cancer and 0.0012 in normal samples. This pattern suggests a nonlinear coexpression in lung cancer but no coexpression in normal samples, and possibility of negative feedback regulation in BMP7 and ACVR2B expression. Between the ligand CCL23 and its receptor CCR1, on the other hand, CoD-B was 0.85 in the normal tissue while 0.00 in lung cancer, and R2 was 0.91 in the normal tissue and 0.054 in lung cancer. This pattern suggests a high linear coexpression in the normal lung tissue but no coexpression in cancerous lung samples. Similarly, CCL23 and CCR1 were also highly coexpressed in normal prostate samples (CoD-B = 0.85) but not coexpressed in cancerous prostate samples (CoD-B = 0.0). However, CCL23 and CCR1 were not coexpressed in both leukemia samples (CoD-B = 0.0) and their normal tissue counterparts (CoD-B = 0.0). Thus, CCL23 and CCR1 show differential coexpression not only between cancerous and normal tissues, but also among different cancers. The coexpression analysis using CoexPro sheds new light to the understanding of cancer development.

Table 1.

List of ligand-receptor pairs which showed differential coexpression between cancers and normal tissue

Ligand Receptor CoD-B Pshuffle
Cancer Normal Cancer Normal
(A) Lung cancer
BMP7 ACVR2B 0.76 0.00 0.028 0.58
EFNA3 EPHA5 0.84 0.00 6.7E-06 0.69
FGF8 FGFR2 0.55 0.00 1.5E-07 0.66
IL16 CD4 0.62 0.031 2.7E-06 0.68
CCL23 CCR1 0.00 0.85 0.73 2.1E-09
IL1RN IL1R1 0.23 0.83 0.077 8.4E-07
IL18 IL18R1 0.18 0.71 0.097 4.5E-06
IL13 IL13RA2 0.00 0.69 0.62 1.5E-04
BMP5 BMPR2 0.00 0.61 0.69 1.7E-04
(B) Prostate cancer
BMP6 ACVR2B 0.63 0.081 0.0011 0.44
BTC EGFR 0.75 0.00 1.7E-11 0.28
TGFB2 TGFBR2 0.79 0.00 3.5E-04 0.49
INHA ACVR2A 0.59 0.019 1.1E-06 0.45
CCL23 CCR1 0.00 0.85 0.43 3.2E-09
IL1RN IL1R1 0.00 0.82 0.32 3.1E-07
TNFSF8 TNFRSF8 0.00 0.76 0.36 1.5E-06
IL18 IL18R1 0.00 0.70 0.39 2.1E-07
FIGF KDR 0.00 0.57 0.26 0.0023
CXCL5 IL8RB 0.00 0.58 0.41 1.1E-04
(C) Acute myeloid leukemia
FASLG FAS 0.90 0.14 3.6E-05 0.34
BMP7 BMPR1B 0.82 0.00 7.7E-04 0.59
EFNA5 EPHA1 0.85 0.00 2.5E-04 0.71
FGF3 FGFR2 0.81 0.00 7.4E-06 0.66
FGF13 FGFR4 0.75 0.059 0.0097 0.47
NRG1 ERBB3 0.95 0.00 1.7E-05 0.28
CCL4 CCBP2 0.99 0.24 9.6E-06 0.062
CCL7 CCR5 0.97 0.29 0.00476 0.41
IFNA8 IFNAR2 0.88 0.00 2.9E-05 0.70
IFNG IFNGR1 0.87 0.00 3.4E-04 0.68
IL13 IL4R 0.82 0.00 0.0041 0.70
INHBB ACVR2B 0.82 0.23 1.5E-04 0.11
AMH AMHR2 0.00 0.78 0.63 4.7E-05
CD40LG CD40 0.00 0.97 0.33 8.6E-05
TNFSF7 TNFRSF7 0.39 0.97 0.043 8.2E-05
EFNA1 EPHA4 0.065 0.86 0.59 1.6E-06
FGF1 FGFR4 0.00 0.93 0.32 1.6E-06
CXCL2 IL8RB 0.25 0.84 0.33 3.3E-06
FGF17 FGFR3 0.17 0.70 0.17 3.0E-04
DLK1 NOTCH4 0.00 0.89 0.55 2.5E-07
TNFSF4 TNFRSF4 0.00 0.92 0.67 3.3E-04
CXCL9 CXCR3 0.30 0.98 0.054 1.5E-04
TGFB1 TGFBR1 0.00 0.71 0.62 6.8E-05
Open in a new tab

(A) Lung cancer

(B) Prostate cancer

(C) Acute myeloid leukemia (AML)

Coexpression networks or relevance networks can be constructed by computing gene–gene association using indices such as correlation coefficient, mutual information from all genes in a microarray dataset (Basso et al. 2005; Butte and Kohane 2000; Carter et al. 2004; Davidson 2001; Stuart et al. 2003). Basso et al. described a statistical algorithm, ARACNE, for inferring pair-wise interactions among genes and constructing coexpression networks (Basso et al. 2005). ARACNE identifies statistically significant gene–gene interactions by mutual information and builds networks with the relationships showing a high probability of representing either direct regulatory interactions or interactions mediated by post-transcriptional modifiers. Using ARACNE, a regulatory network of human B-cells was recovered from the expression profile data, showing a typical scale-free and hierarchical architecture.

Zhang and Horvath presented a general framework for constructing and analyzing gene coexpression networks (Zhang and Horvath 2005). They proposed to use soft thresholding techniques to convert the gene coexpression similarity measure into the network connection strength and construct a weighted network. The soft thresholding is based the scale-free topology criterion that yields networks with high biological significance. They also distinguished intra-modular connectivity from whole network connectivity and showed that the intra-modular connectivity was more strongly correlated with functional significance than the whole network connectivity. Using the method, coexpression networks of human and chimpanzee brains were constructed, from which transcriptional modules were identified that correlated to the neuroanatomical structure of the brain (Oldham et al. 2006). Genes with the highest intra-modular connectivity were shown to be conserved between human and chimpanzee brains, underscoring the shared molecular bases of primate brain organization. Important differences in cerebral cortex between human and chimpanzee coexpression networks highlight the fact of rapid expansion of this brain region on the human lineage. The results provide insights into the molecular bases of primate brain organization and demonstrate the general utility of gene coexpression network analysis.

Exploring dynamics of transcriptional network

It is important to explore the dynamics of transcriptional coexpression or networks in response to disease development or changing cellular phenotypes. Various algorithms have been employed to explore the dynamics, including the conditional Markov chain model (Kim et al. 2002; Li and Zhan 2006), probabilistic Boolean network (Shmulevich et al. 2002b), liquid association model (Li et al. 2004), and a genomic scale approach for network dynamics analysis (Luscombe et al. 2004).

Li et al. proposed a liquid association model for systematical analysis of coexpression dynamics (Li et al. 2004). The model detects the association of the transcriptional increase or decrease of the gene Z with the increase or decrease in the transcriptional correlation between the genes X and Y. The model was used to reveal how the enzymes associated with the urea cycle were expressed to ensure a proper mass flow of the involved metabolites in yeast, showing that the correlation between ARG2 and CAR2 changed from positive to negative as the expression level of CPA2 increased (Li et al. 2004).

Luscombe et al. developed an approach for a genomic scale analysis of network dynamics (Luscombe et al. 2004). The approach combines well-known global topological measures, local motifs and newly derived statistics, uncovering significant changes in the network architecture that are unexpected from random simulation. An analysis on yeast gene expression data using this approach resulted in some interesting findings: a few transcription factors served as permanent hubs of the transcriptional network, whereas the most factors acted transiently only during certain conditions (Luscombe et al. 2004), and environmental responses facilitated fast signal propagation, whereas the cell cycle and sporulation directed temporal progression through multiple stages.

Recently, we developed an algorithm, PathwayPro, to mimic the dynamic behavior of transcriptional networks through a series of interventions made in silico on each gene or gene combination (Li and Zhan 2006). The inputs to the algorithm are experiment-specific regulatory network information and gene expression data. The outputs are the estimated probabilities of the behavior transition of a network in instances such as disease development, aging process, or cell differentiation. The algorithm can provide answers to two questions: 1) whether or how much a gene or external perturbation contributes to the behavior transition of a network across different conditions; 2) in what specific ways is this contribution manifested. The PathwayPro analysis is particularly valuable in its ability to in silico simulate the network behavior which may not be easy to recreate in vitro, and generate hypotheses for further in vitro investigation. The potential clinical impact of such analysis is tremendous as it can not only open up a window on the dynamic behavior of a pathway or disease progression, but also translate into accurate diagnosis, drug discovery, and effective preventive and therapeutic intervention of disease. We used PathwayPro to examine the dynamic behavior of the BCR-ABL pathway in response to the leukemia development, and to identify possible disease and drug targets of leukemia (Li and Zhan 2006). In this case study, in silico transcriptional intervention was conducted on each gene (referred to as single-gene intervention), each combination of two genes (double-gene intervention), and each combination of three genes (triple-gene intervention) on this pathway. In each intervention, the observed expression of a gene was altered to the opposite direction or remained unchanged. The probability of the network behavior transition between the normal condition and leukemia state under each of the transcriptional interventions was calculated. The probability of the network transition from normal to leukemia states suggests disease susceptibility of the genes involved. The higher the probability is, the more likely the gene or gene combination under a certain intervention is responsible for the disease development. On the other hand, the probability of the network transition from leukemia to normal states suggests the potential usefulness of a drug or therapeutic intervention. Table 2 lists parts of the analysis results. As shown, more genes and gene combinations had higher probabilities in the normal-to-leukemia network transition than the leukemia-to-normal transition. This result suggests that the chance is higher for human to develop leukemia than to recover from the disease. It was also showed that transcriptional interventions involving the genes BCR and ABL yielded high probabilities for the normal-to-leukemia transition and for the leukemia-to-normal transition, no matter in single-, double- and triple-gene interventions (Table 2). The result suggests that BCR and ABL are the most contributive genes to the network behavior transition between the normal condition and the leukemia state, and therefore the most susceptible for the development of leukemia as well as the recovery of the disease to a normal condition. The two genes can thus serve as good drug targets for the treatment of leukemia. This result, reached independently by the computational analysis, is in agreement with the conclusion by previous laboratory-based studies (Zou and Calame 1999). It has been shown that chronic myeloid leukemia (CML) is associated in most cases with the fusion of the genes ABL and BCR, and the activation of BCR-ABL represses apoptosis and allows transformed cells to divide, resulting in the development of CML. The drug Gleevec is a selective BCR-ABL inhibitor, effective in the treatment of CML (Druker et al. 2001). In addition, the PathwayPro analysis revealed that BAD and MYC played critical roles in the leukemia development while AKT appeared important in the leukemia recovery to a normal condition, shedding new light on the understanding of the leukemia disease.

Table 2.

Probabilities of the network behavior transition by serial interventions on the genes in the ABL-BCR pathway of human

Gene Transcriptional intervention Transition probability
(A) Transition from normal to CML states by single-gene interventiona
BCR 0⇒−1⇒1 0.00639
(B) Transition from CML to normal states by single-gene interventiona
ABL1 1⇒0⇒−1 0.000299
(C) Transition from the normal to CML states by double-gene interventionb
BCR ABL1 0 −1⇒1 1⇒1 1 0.0109
BCR BAD 0 1⇒−1 0⇒1 0 0.00639
BCR MYC 0 −1⇒−1 0⇒1 0 0.00639
BCR BAD 0 1⇒−1 −1⇒1 0 0.00639
BCR MYC 0 −1⇒−1 1⇒1 0 0.00639
BCR STAT5A 0 1⇒−1 −1⇒1 1 0.00639
BCR STAT5A 0 1⇒−1 0⇒1 1 0.00639
BCR STAT1 0 0⇒−1 1⇒1 0 0.00639
BCR STAT1 0 0⇒−1 −1⇒1 0 0.00639
BCR CRKL 0 −1⇒−1 1⇒1 0 0.00539
BCR CRKL 0 −1⇒−1 0⇒1 0 0.00399
BCR PIK3CG 0 −1⇒−1 0⇒1 −1 0.00384
BCR JAK2 0 0⇒ −1 1⇒1 0 0.00224
BCR AKT1 0 0⇒−1 −1⇒1 0 0.00107
(D) Transition from the CML to normal states by double-gene interventionb
ABL1 AKT1 1 0⇒0 1⇒−1 0 0.00185
ABL1 AKT1 1 0⇒0 −1⇒−1 0 0.00179
BCR ABL1 1 1⇒0 −1⇒0 −1 0.00111
(E) Transition from normal to CML states by triple-gene interventionc
BCR ABL1 BAD 0 −1 1⇒1 1 0⇒1 1 0 0.010936
BCR ABL1 MYC 0 −1 −1⇒1 1 0⇒1 1 0 0.010936
BCR ABL1 BAD 0 −1 1⇒1 1 −1⇒1 1 0 0.010933
BCR ABL1 MYC 0 −1 −1⇒1 1 1⇒1 1 0 0.010933
BCR ABL1 STAT5A 0 −1 1⇒1 1 0⇒1 1 1 0.010933
BCR ABL1 STAT5A 0 −1 1⇒1 1 −1⇒1 1 1 0.010933
BCR ABL1 STAT1 0 −1 0⇒1 1 −1⇒1 1 0 0.010933
BCR ABL1 STAT1 0 −1 0⇒1 1 1⇒1 1 0 0.010933
(F) Transition from CML to normal states by triple-gene interventiond
BCR ABL1 AKT1 1 1 0⇒0 −1 1⇒0 −1 0 0.00684
BCR ABL1 AKT1 1 1 0⇒0 −1 −1⇒0 −1 0 0.00662
ABL1 CRKL AKT1 1 0 0⇒0 −1 1⇒−1 −1 0 0.00297
ABL1 CRKL AKT1 1 0 0⇒0 −1 −1⇒−1 −1 0 0.00288
BCR ABL1 AKT1 1 1 0⇒−1 −1 1⇒0 −1 0 0.00274
BCR ABL1 AKT1 1 1 0⇒−1 −1 −1⇒0 −1 0 0.00265
ABL1 CRKL AKT1 1 0 0⇒0 1 1⇒−1 −1 0 0.00250
ABL1 CRKL AKT1 1 0 0⇒0 1 −1⇒−1 −1 0 0.00242
Open in a new tab

The gene expression profile of each state is presented as: initial state (e.g., normal state) ⇒ state after intervened ⇒ end state (e.g., disease state). Transcriptional intervention is presented as: initial state (e.g., normal state) ⇒ state after intervened ⇒ end state (e.g., disease state). In each state, expression levels of each gene are presented by ternary values

aProbability cutoff 1E-4

bProbability cutoff 1E-3

cProbability cutoff 1E-2

dProbability cutoff 2E-3

Closing remarks

Systems biology is aimed at elucidating how genes interact to each other to perform specific biological processes or functions, and how disease or cellular phenotypes arise from the connectivity or networks of genes and their products. The utilization of high-throughput data generated by microarray or other technologies provides scientists with a first step towards systems-level analyses of transcriptional networks, in particular their modular and dynamic behaviors. However, the current data quality and coverage of high-throughput datasets impose various limitations on the network studies. Recent studies suggest that regulatory networks learned from gene expression data alone can be considerably obscured by spurious interactions when the number of observations is small (Husmeier 2003). Integrating findings from multiple data sources (e.g., DNA sequences, gene and protein expression profiles, protein–protein interactions, protein structural information, and protein-DNA binding data) can overcome this drawback. Several research groups demonstrate that the recovery of transcriptional networks from multiple types of data is more accurate than that from each data type alone (Bar-Joseph et al. 2003; Bernard and Hartemink 2005; Li et al. 2006). By continuing multidisciplinary efforts on further technological innovations in both data generation and computational methodology, we are expecting for more effective exploration of transcriptional networks and systems biology studies on disease, cell development, and other biological phenomena.

Acknowledgements

This study was supported by the Intramural Research Program, National Institute on Aging, NIH.

Abbreviations

NICA

Nonlinear independent component analysis

PSMF

Probabilistic sparse matrix factorization

CoD

Coefficient of determination

ESC

Embryonic stem cell

EB

Embryoid body

Footnotes

Concise Summary

This article reviews the recent development in computational biology research on deciphering modular and dynamic behaviors of transcriptional networks, discussing important findings and demonstrating the applications in systems biology studies.

References

  1. Alter O, Brown PO, Botstein D. Singular value decomposition for genome-wide expression data processing and modeling. Proc Natl Acad Sci U S A. 2000;97:10101–10106. doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Bar-Joseph Z, Gerber GK, Lee TI, Rinaldi NJ, Yoo JY, Robert F, Gordon DB, Fraenkel E, Jaakkola TS, Young RA, Gifford DK. Computational discovery of gene modules and regulatory networks. Nat Biotechnol. 2003;21:1337–1342. doi: 10.1038/nbt890. [DOI] [PubMed] [Google Scholar]
  3. Barabasi AL, Bonabeau E. Scale-free networks. Sci Am. 2003;288:60–69. doi: 10.1038/scientificamerican0503-60. [DOI] [PubMed] [Google Scholar]
  4. Basso K, Margolin AA, Stolovitzky G, Klein U, Dalla-Favera R, Califano A. Reverse engineering of regulatory networks in human B cells. Nat Genet. 2005;37:382–390. doi: 10.1038/ng1532. [DOI] [PubMed] [Google Scholar]
  5. Bergmann S, Ihmels J, Barkai N. Similarities and differences in genome-wide expression data of six organisms. PLoS Biol. 2004;2:E9. doi: 10.1371/journal.pbio.0020009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bernard A, Hartemink AJ. Informative structure priors: joint learning of dynamic regulatory networks from multiple types of data. Pac Symp Biocomput. 2005;10:459–470. [PubMed] [Google Scholar]
  7. Brunet JP, Tamayo P, Golub TR, Mesirov JP. Metagenes and molecular pattern discovery using matrix factorization. Proc Natl Acad Sci U S A. 2004;101:4164–4169. doi: 10.1073/pnas.0308531101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Butte AJ, Kohane IS. Mutual information relevance networks: functional genomic clustering using pairwise entropy measurements. Pac Symp Biocomput. 2000;5:418–429. doi: 10.1142/9789814447331_0040. [DOI] [PubMed] [Google Scholar]
  9. Carter SL, Brechbuhler CM, Griffin M, Bond AT. Gene co-expression network topology provides a framework for molecular characterization of cellular state. Bioinformatics. 2004;20:2242–2250. doi: 10.1093/bioinformatics/bth234. [DOI] [PubMed] [Google Scholar]
  10. Davidson EH. Genomic regulatory systems: development and evolution. San Diego, CA: Academic Press; 2001. [Google Scholar]
  11. Dougherty ER, Kim S, Chen Y. Coefficient of determination in nonlinear signal processing. Signal Processing. 2000;80:2219–2235. doi: 10.1016/S0165-1684(00)00079-7. [DOI] [Google Scholar]
  12. Druker BJ, Sawyers CL, Kantarjian H, Resta DJ, Reese SF, Ford JM, Capdeville R, Talpaz M. Activity of a specific inhibitor of the BCR-ABL tyrosine kinase in the blast crisis of chronic myeloid leukemia and acute lymphoblastic leukemia with the Philadelphia chromosome. N Engl J Med. 2001;344:1038–1042. doi: 10.1056/NEJM200104053441402. [DOI] [PubMed] [Google Scholar]
  13. Dueck D, Morris QD, Frey BJ. Multi-way clustering of microarray data using probabilistic sparse matrix factorization. Bioinformatics. 2005;21(Suppl 1):i144–i151. doi: 10.1093/bioinformatics/bti1041. [DOI] [PubMed] [Google Scholar]
  14. Frigyesi A, Veerla S, Lindgren D, Hoglund M. Independent component analysis reveals new and biologically significant structures in microarray data. BMC Bioinformatics. 2006;7:290. doi: 10.1186/1471-2105-7-290. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Gao Y, Church G. Improving molecular cancer class discovery through sparse non-negative matrix factorization. Bioinformatics. 2005;21:3970–3975. doi: 10.1093/bioinformatics/bti653. [DOI] [PubMed] [Google Scholar]
  16. Graeber TG, Eisenberg D. Bioinformatic identification of potential autocrine signaling loops in cancers from gene expression profiles. Nat Genet. 2001;29:295–300. doi: 10.1038/ng755. [DOI] [PubMed] [Google Scholar]
  17. Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402:C47–C52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
  18. Hashimoto R, Kim S, Shmulevich I, Zhang W, Bittner ML, Dougherty ER. Growing genetic regulatory networks from seed genes. Bioinformatics. 2004;20:1241–1247. doi: 10.1093/bioinformatics/bth074. [DOI] [PubMed] [Google Scholar]
  19. Herrgard MJ, Covert MW, Palsson BO. Reconciling gene expression data with known genome-scale regulatory network structures. Genome Res. 2003;13:2423–2434. doi: 10.1101/gr.1330003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Holter NS, Maritan A, Cieplak M, Fedoroff NV, Banavar JR. Dynamic modeling of gene expression data. Proc Natl Acad Sci U S A. 2001;98:1693–1698. doi: 10.1073/pnas.98.4.1693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Husmeier D. Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics. 2003;19:2271–2282. doi: 10.1093/bioinformatics/btg313. [DOI] [PubMed] [Google Scholar]
  22. Ideker T, Galitski T, Hood L. A new approach to decoding life: systems biology. Annu Rev Genomics Hum Genet. 2001;2:343–372. doi: 10.1146/annurev.genom.2.1.343. [DOI] [PubMed] [Google Scholar]
  23. Ihmels J, Bergmann S, Barkai N. Defining transcription modules using large-scale gene expression data. Bioinformatics. 2004;20:1993–2003. doi: 10.1093/bioinformatics/bth166. [DOI] [PubMed] [Google Scholar]
  24. Ihmels J, Bergmann S, Berman J, Barkai N. Comparative gene expression analysis by differential clustering approach: application to the Candida albicans transcription program. PLoS Genet. 2005;1:e39. doi: 10.1371/journal.pgen.0010039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Ihmels J, Friedlander G, Bergmann S, Sarig O, Ziv Y, Barkai N. Revealing modular organization in the yeast transcriptional network. Nat Genet. 2002;31:370–377. doi: 10.1038/ng941. [DOI] [PubMed] [Google Scholar]
  26. Imoto S, Goto T, Miyano S. Estimation of genetic networks and functional structures between genes by using Bayesian networks and nonparametric regression. Pac Symp Biocomput. 2002;7:175–186. [PubMed] [Google Scholar]
  27. Imoto S, Savoie CJ, Aburatani S, Kim S, Tashiro K, Kuhara S, Miyano S. Use of gene networks for identifying and validating drug targets. J Bioinform Comput Biol. 2003;1:459–474. doi: 10.1142/S0219720003000290. [DOI] [PubMed] [Google Scholar]
  28. Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL. The large-scale organization of metabolic networks. Nature. 2000;407:651–654. doi: 10.1038/35036627. [DOI] [PubMed] [Google Scholar]
  29. Kim PM, Tidor B. Subsystem identification through dimensionality reduction of large-scale gene expression data. Genome Res. 2003;13:1706–1718. doi: 10.1101/gr.903503. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kim S, Li H, Dougherty ER, Chao N, Chen Y, Bittner ML, Suh EB. Can Markov chain models mimic biological regulation? J Biol Syst. 2002;10:337–357. doi: 10.1142/S0218339002000676. [DOI] [Google Scholar]
  31. Lee DD, Seung HS. Learning the parts of objects by non-negative matrix factorization. Nature. 1999;401:788–791. doi: 10.1038/44565. [DOI] [PubMed] [Google Scholar]
  32. Lee HK, Hsu AK, Sajdak J, Qin J, Pavlidis P. Coexpression analysis of human genes across many microarray data sets. Genome Res. 2004;14:1085–1094. doi: 10.1101/gr.1910904. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Lee SI, Batzoglou S. Application of independent component analysis to microarrays. Genome Biol. 2003;4:R76. doi: 10.1186/gb-2003-4-11-r76. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Li H, Sun Y, Zhan M. Analysis of gene coexpression by B-spline based CoD estimation. EURASIP J Bioinform Syst Biol. 2007;27:1–10. doi: 10.1155/2007/49478. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Li H, Sun Y, Zhan M. The discovery of transcriptional modules by a two-stage matrix decomposition approach. Bioinformatics. 2007;23:473–479. doi: 10.1093/bioinformatics/btl640. [DOI] [PubMed] [Google Scholar]
  36. Li H, Zhan M. Systematic intervention of transcription for identifying network response to disease and cellular phenotypes. Bioinformatics. 2006;22:96–102. doi: 10.1093/bioinformatics/bti752. [DOI] [PubMed] [Google Scholar]
  37. Li J, Li X, Su H, Chen H, Galbraith DW. A framework of integrating gene relations from heterogeneous data sources: an experiment on Arabidopsis thaliana. Bioinformatics. 2006;22:2037–2043. doi: 10.1093/bioinformatics/btl345. [DOI] [PubMed] [Google Scholar]
  38. Li KC, Liu CT, Sun W, Yuan S, Yu T. A system for enhancing genome-wide coexpression dynamics study. Proc Natl Acad Sci U S A. 2004;101:15561–15566. doi: 10.1073/pnas.0402962101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Liao JC, Boscolo R, Yang YL, Tran LM, Sabatti C, Roychowdhury VP. Network component analysis: reconstruction of regulatory signals in biological systems. Proc Natl Acad Sci U S A. 2003;100:15522–15527. doi: 10.1073/pnas.2136632100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Liebermeister W. Linear modes of gene expression determined by independent component analysis. Bioinformatics. 2002;18:51–60. doi: 10.1093/bioinformatics/18.1.51. [DOI] [PubMed] [Google Scholar]
  41. Luscombe NM, Babu MM, Yu H, Snyder M, Teichmann SA, Gerstein M. Genomic analysis of regulatory network dynamics reveals large topological changes. Nature. 2004;431:308–312. doi: 10.1038/nature02782. [DOI] [PubMed] [Google Scholar]
  42. Margolin AA, Nemenman I, Basso K, Wiggins C, Stolovitzky G, Dalla Favera R, Califano A. ARACNE: an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context. BMC Bioinformatics. 2006;7(Suppl 1):S1–S7. doi: 10.1186/1471-2105-7-S1-S7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Nilsson R, Bajic VB, Suzuki H, di Bernardo D, Bjorkegren J, Katayama S, Reid JF, Sweet MJ, Gariboldi M, Carninci P, Hayashizaki Y, Hume DA, Tegner J, Ravasi T. Transcriptional network dynamics in macrophage activation. Genomics. 2006;88:133–142. doi: 10.1016/j.ygeno.2006.03.022. [DOI] [PubMed] [Google Scholar]
  44. Oldham MC, Horvath S, Geschwind DH. Conservation and evolution of gene coexpression networks in human and chimpanzee brains. Proc Natl Acad Sci U S A. 2006;103:17973–17978. doi: 10.1073/pnas.0605938103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Qi Y, Ge H. Modularity and dynamics of cellular networks. PLoS Comput Biol. 2006;2:e174. doi: 10.1371/journal.pcbi.0020174. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Ravasz E, Somera AL, Mongru DA, Oltvai ZN, Barabasi AL. Hierarchical organization of modularity in metabolic networks. Science. 2002;297:1551–1555. doi: 10.1126/science.1073374. [DOI] [PubMed] [Google Scholar]
  47. Resendis-Antonio O, Freyre-Gonzalez JA, Menchaca-Mendez R, Gutierrez-Rios RM, Martinez-Antonio A, Avila-Sanchez C, Collado-Vides J. Modular analysis of the transcriptional regulatory network of E. coli. Trends Genet. 2005;21:16–20. doi: 10.1016/j.tig.2004.11.010. [DOI] [PubMed] [Google Scholar]
  48. Savoie CJ, Aburatani S, Watanabe S, Eguchi Y, Muta S, Imoto S, Miyano S, Kuhara S, Tashiro K. Use of gene networks from full genome microarray libraries to identify functionally relevant drug-affected genes and gene regulation cascades. DNA Res. 2003;10:19–25. doi: 10.1093/dnares/10.1.19. [DOI] [PubMed] [Google Scholar]
  49. Segal E, Friedman N, Koller D, Regev A. A module map showing conditional activity of expression modules in cancer. Nat Genet. 2004;36:1090–1098. doi: 10.1038/ng1434. [DOI] [PubMed] [Google Scholar]
  50. Segal E, Shapira M, Regev A, Pe’er D, Botstein D, Koller D, Friedman N. Module networks: identifying regulatory modules and their condition-specific regulators from gene expression data. Nat Genet. 2003;34:166–176. doi: 10.1038/ng1165. [DOI] [PubMed] [Google Scholar]
  51. Shmulevich I, Dougherty ER, Kim S, Zhang W. Probabilistic boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics. 2002;18:261–274. doi: 10.1093/bioinformatics/18.2.261. [DOI] [PubMed] [Google Scholar]
  52. Shmulevich I, Dougherty ER, Zhang W. Gene perturbation and intervention in probabilistic Boolean networks. Bioinformatics. 2002;18:1319–1331. doi: 10.1093/bioinformatics/18.10.1319. [DOI] [PubMed] [Google Scholar]
  53. Stuart JM, Segal E, Koller D, Kim SK. A gene-coexpression network for global discovery of conserved genetic modules. Science. 2003;302:249–255. doi: 10.1126/science.1087447. [DOI] [PubMed] [Google Scholar]
  54. Sun Y, Li H, Liu Y, Shin S, Mattson MP, Rao MS, Zhan M. Cross-species transcriptional profiles establish a functional portrait of embryonic stem cells. Genomics. 2007;89:22–35. doi: 10.1016/j.ygeno.2006.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Tanay A, Sharan R, Kupiec M, Shamir R. Revealing modularity and organization in the yeast molecular network by integrated analysis of highly heterogeneous genomewide data. Proc Natl Acad Sci U S A. 2004;101:2981–2986. doi: 10.1073/pnas.0308661100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. van Noort V, Snel B, Huynen MA. The yeast coexpression network has a small-world, scale-free architecture and can be explained by a simple model. EMBO Rep. 2004;5:280–284. doi: 10.1038/sj.embor.7400090. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Wang G, Kossenkov AV, Ochs MF. LS-NMF: a modified non-negative matrix factorization algorithm utilizing uncertainty estimates. BMC Bioinformatics. 2006;7:175. doi: 10.1186/1471-2105-7-175. [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Zhang B, Horvath S (2005) A general framework for weighted gene co-expression network analysis. Stat Appl Genet Mol Biol 4:Article17 [DOI] [PubMed]
  59. Zhou X, Wang X, Dougherty ER. Construction of genomic networks using mutual-information clustering and reversible-jump Markov-Chain Monte-Carlo predictor design. Signal Processing. 2003;83:745–761. doi: 10.1016/S0165-1684(02)00469-3. [DOI] [Google Scholar]
  60. Zhou XJ, Gibson G. Cross-species comparison of genome-wide expression patterns. Genome Biol. 2004;5:232. doi: 10.1186/gb-2004-5-7-232. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Zhou XJ, Kao MC, Huang H, Wong A, Nunez-Iglesias J, Primig M, Aparicio OM, Finch CE, Morgan TE, Wong WH. Functional annotation and network reconstruction through cross-platform integration of microarray data. Nat Biotechnol. 2005;23:238–243. doi: 10.1038/nbt1058. [DOI] [PubMed] [Google Scholar]
  62. Zou X, Calame K. Signaling pathways activated by oncogenic forms of Abl tyrosine kinase. J Biol Chem. 1999;274:18141–18144. doi: 10.1074/jbc.274.26.18141. [DOI] [PubMed] [Google Scholar]

Articles from Genomic Medicine are provided here courtesy of Springer Science+Business Media B.V.

RESOURCES