Calcium Transport Mechanisms of PC12 Cells

Abstract

Many studies of Ca²⁺ signaling use PC12 cells, yet the balance of Ca²⁺ clearance mechanisms in these cells is unknown. We used pharmacological inhibition of Ca²⁺ transporters to characterize Ca²⁺ clearance after depolarizations in both undifferentiated and nerve growth factor-differentiated PC12 cells. Sarco-endoplasmic reticulum Ca²⁺ ATPase (SERCA), plasma membrane Ca²⁺ ATPase (PMCA), and Na⁺/Ca²⁺ exchanger (NCX) account for almost all Ca²⁺ clearance in both cell states, with NCX and PMCA making the greatest contributions. Any contribution of mitochondrial uniporters is small. The ATP pool in differentiated cells was much more labile than that of undifferentiated cells in the presence of agents that dissipated mitochondrial proton gradients. Differentiated PC12 cells have a small component of Ca²⁺ clearance possessing pharmacological characteristics consistent with secretory pathway Ca²⁺ ATPase (SPCA), potentially residing on Golgi and/or secretory granules. Undifferentiated and differentiated cells are similar in overall Ca²⁺ transport and in the small transport due to SERCA, but they differ in the fraction of transport by PMCA and NCX. Transport in neurites of differentiated PC12 cells was qualitatively similar to that in the somata, except that the ER stores in neurites sometimes released Ca²⁺ instead of clearing it after depolarization. We formulated a mathematical model to simulate the observed Ca²⁺ clearance and to describe the differences between these undifferentiated and NGF-differentiated states quantitatively. The model required a value for the endogenous Ca²⁺ binding ratio of PC12 cell cytoplasm, which we measured to be 268 ± 85. Our results indicate that Ca²⁺ transport in undifferentiated PC12 cells is quite unlike transport in adrenal chromaffin cells, for which they often are considered models. Transport in both cell states more closely resembles that of sympathetic neurons, for which differentiated PC12 cells often are considered models. Comparison with other cell types shows that different cells emphasize different Ca²⁺ transport mechanisms.

INTRODUCTION

The PC12 clonal cell line is derived from a cancer of rat adrenal chromaffin cells, a pheochromocytoma (Greene and Tischler, 1976). Rapidly dividing PC12 cells are regarded as chromaffin cell–like, having dense-core secretory granules and the ability to release catecholamines upon stimulation. The cells undergo a marked phenotypic change in response to nerve growth factor (NGF) and certain other substances: they stop dividing, extend numerous neural processes (neurites), and up-regulate several neural markers (Greene and Tischler, 1976; Vaudry et al., 2002). Thus, PC12 cells also could be considered models of sympathetic neurons and of neural differentiation.

Almost 2,000 publications concern calcium effects in this cell line. Much is therefore known about protein expression, including Ca²⁺ channels and transporters, yet in neither undifferentiated nor differentiated PC12 cells is much known about the Ca²⁺ transport itself. This is surprising, as these excitable cells are so often used as models for chromaffin cells or sympathetic neurons. We have characterized Ca²⁺ transport in PC12 cells in order to answer the following questions. What are the principal pathways for Ca²⁺ clearance? Do they change in response to NGF? Does this Ca²⁺ clearance resemble clearance in chromaffin cells or in sympathetic neurons? We used Ca²⁺ photometry and electrophysiology to characterize Ca²⁺ buffering and transport in both undifferentiated and NGF-differentiated PC12 cells, and we focus on the four canonical transport mechanisms commonly found in mammalian cells: sarco/endoplasmic reticulum Ca²⁺ ATPases (SERCA), mitochondrial uniporter(s) (MtU), plasma membrane Ca²⁺ ATPases (PMCA), and Na⁺/Ca²⁺ exchangers (NCX).

MATERIALS AND METHODS

All chemicals were obtained from Sigma-Aldrich unless otherwise noted.

Culture and Differentiation of PC12 Cells

PC12 D19 cells were a gift from Sandra Bajjalieh in the Department of Pharmacology, University of Washington (the lineage of these cells is traced in the online supplemental material). Cells were cultured in Dulbecco's Modified Eagle Medium with high glucose, L-glutamine, pyridoxine hydrochloride, and sodium pyruvate (Invitrogen), supplemented with 10% horse serum (Gemini Bioproducts), 5% FBS (Gemini Bioproducts), 44 mM sodium bicarbonate, and 25 mM HEPES, pH to 7.3 with NaOH. Cells were maintained in a 5% CO₂ atmosphere and passaged 1:20 with Ca²⁺- and Mg²⁺-free PBS (Invitrogen) weekly. Cells were subcultured onto polyornithine-coated number 0 glass coverslips for experiments.

To differentiate cells, we subcultured them onto the coated coverslips at a low density and cultured them in the normal culture medium for 2 h. We then replaced this medium with medium supplemented with 50 ng/ml NGF (gift of M. Bothwell, University of Washington). NGF medium was renewed every third day for a minimum of 15 d. Neurite extension was evident as early as day 3, but we waited longer in order to reach a stage of differentiation in which all neural markers would be up-regulated.

Ca²⁺ Photometry

Cytoplasmic Ca²⁺ measurements were done at elevated temperature by ratiometric fura-2 or fura-4F (Invitrogen) photometry. Cells were loaded with the acetoxymethyl (AM) ester of the desired dye dispersed in 10% pluronic and diluted to 10 μM in modified Ringer's solution (in mM: 130 NaCl, 2.5 KCl, 1 MgCl₂, 2 CaCl₂, 10 glucose, and 10 HEPES, pH 7.3) at room temperature for 20–25 min and transferred into a recording chamber perfused with the modified Ringer's solution using a local perfusion device heated to 37°C. To determine the [fura-2] in PC12 cells, we loaded cells with known concentrations of fura-2 salt using whole-cell patch configuration (see below). By comparing the amount of light collected from resting cells so loaded to similarly sized cells loaded with fura-2-AM, we estimated that the average PC12 cell contains 300 nM fura-2 under our loading conditions. This number was used in our mathematical model and in translating the rate of change of [Ca²⁺]_cyt into absolute fluxes. We used a 3-s or, in Fig. 1 C only, 30-s exposure to high-K⁺ depolarizing solution to impose a cytoplasmic Ca²⁺ load. This solution contained in mM: 70 KCl, 67 NaCl, 2 CaCl₂, 1 MgCl₂, 10 glucose, and 10 HEPES, pH 7.3. In control experiments, a nominally Ca²⁺-free solution (modified Ringer's without CaCl₂) was applied to the cells as they recovered from depolarization. The composition of this clearance solution and of the high K⁺ solution was sometimes changed as noted. Nominally Ca²⁺-free Ringer's solution was adequate to prevent store-operated currents activated by thapsigargin from contaminating the measurements (Fig. S1). We recorded only from one cell on each coverslip to ensure that each recorded cell was “naïve” with respect to previous Ca²⁺ elevations.

Figure 1.

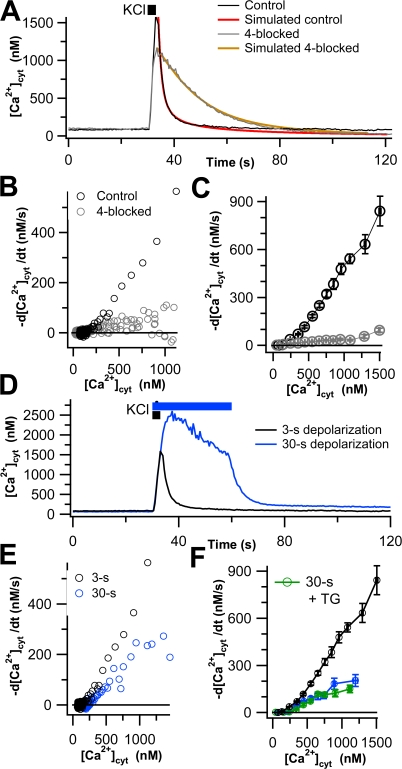
Four canonical Ca²⁺ transporters account for most Ca²⁺ clearance in undifferentiated PC12 cells. (A) Representative time course of [Ca²⁺]_cyt in two single undifferentiated PC12 cells in response to KCl depolarization (black bar). The control cell is shown in black, and the 4-blocked cell (see text) is in gray. Colored lines superimposed on these two traces are simulated time courses of Ca²⁺ clearance using a kinetic model with four canonical transport mechanisms and residual transport discussed in Appendix. (B) Transport curves of Ca²⁺ clearance, −d[Ca²⁺]_cyt/dt, calculated from the clearance phases of the cells in A and plotted against [Ca²⁺]_cyt. In 4-blocked cells, transport is greatly slowed. (C) Mean clearance rates for control (black open circles, n = 88) and 4-blocked (gray open circles, n = 62) cells. (D) Representative time course of [Ca²⁺]_cyt in single undifferentiated PC12 cells in response to 3-s (black line) and 30-s (blue line) KCl depolarizations. (E) Ca²⁺ clearance, plotted as in B, for the two cells shown in D. (F) Mean clearance rates for 3-s depolarized (black, n = 88), 30-s depolarized (blue, n = 12), and TG-treated and 30-s depolarized (green, n = 9) cells, shown as in C.

Fura fluorescence was excited by 10 ms of 340-nm illumination followed immediately by 10 ms of 380-nm illumination (TILL Photonics), and emission at 505 nm was collected by a photodiode controlled by PatchMaster software (HEKA Electronics). The first 2 ms of each collection was discarded to allow time for the optical transitions of the illuminator. [Ca²⁺]_cyt was calculated from the background-corrected fluorescence ratio R = F₃₄₀/F₃₈₀ using the standard calibration equation: [Ca²⁺]_cyt = K*[(R − R_min)/(R_max − R)], where R is the measured ratio, and the calibration parameters K*, R_min, and R_max were experimentally determined as previously reported (Chen et al., 2003). Fura-2 and fura-4F required separate calibrations. For Ca²⁺ transport measurements, which used fura-2, all points >1500 nM Ca²⁺ were discarded as unreliable.

The setup included a viewfinder that allowed us to exclude some regions of the field of view from the measurements. We took advantage of this to restrict measurements to the soma or to a field of neurites (in NGF-differentiated cells). Due to the larger volume of the somata, fura fluorescence collected from them was substantially larger than fluorescence collected from neurites. To prevent contamination of signals collected from neurites with nearby somata, we recorded from neurites only when we could exclude all somata completely from the field of view. It is likely that the neurites from several cells were in the same field of measurement.

Inhibition of Ca²⁺ Transporters

SERCA were inhibited by adding 1 μM thapsigargin (TG) to the fura-loading medium. After TG treatment, [Ca²⁺]_cyt became responsive to extracellular Ca²⁺, demonstrating activation of store-operated currents and indicating successful SERCA inhibition (Ufret-Vincenty et al., 1995). The MtU was inhibited by applying 2 μM CCCP to the cells both during the KCl depolarization and throughout Ca²⁺ clearance (Herrington et al., 1996). In later experiments, 5 μM oligomycin (EMD BioSciences) was added either concomitantly with CCCP or 30 s before depolarization and maintained through the rest of the experiment. For the inhibition of MtU in neurites, cells were pretreated with 10 μM Ru360 (EMD BioSciences) for 30 min before Ca²⁺ measurement (Thomas et al., 2006). For the inhibition of plasma membrane Ca²⁺ ATPases (PMCA), extracellular pH was raised to 9.0 during clearance by replacing the HEPES buffer in the nominally Ca²⁺-free modified Ringer's with 20 mM Trizma, pH 9.0 (Xu et al., 2000). NCX were inhibited by replacing the NaCl in the nominally Ca²⁺-free modified Ringer's with LiCl. Any experiment in which only one transporter is blocked is referred to as a “1-blocked” experiment. Our results are generally displayed as Ca²⁺ transport curves by plotting the rate of change of free Ca²⁺ (−d[Ca²⁺]_cyt/dt) as a function of [Ca²⁺]_cyt. To obtain the Ca²⁺ transport curve for the inhibited mechanism in a 1-blocked experiment, we subtracted the 1-blocked Ca²⁺ transport curve from the control Ca²⁺ transport curve. In many experiments, we combined two of these treatments (2-blocked), three of these treatments (3-blocked), or all four (4-blocked). When combining treatments, TG was always used to inhibit SERCA, CCCP to inhibit MtU (unless otherwise noted), pH 9.0 to inhibit PMCA, and LiCl to inhibit NCX. In some experiments, we added a fifth inhibitor to the 4-blocked protocol, 10 μM tert-butylhydroquinone (BHQ), to inhibit secretory pathway Ca²⁺ ATPases (SPCA), as well as SERCA. The Ca²⁺ peak heights and rise times were unaffected by these inhibitors of Ca²⁺ transport. Also, some cells were pretreated with 50 μM glycyl phenylalanyl β-napthylamide (GPN) for 20 min before Ca²⁺ measurements (Duman et al., 2006).

Determination of the Ca²⁺ Binding Ratio of Cytoplasm (κ_i)

For every free cytoplasmic Ca²⁺ ion, κ_i ions are bound reversibly to intracellular buffers. κ_i was determined using simultaneous fura-2 photometry and standard whole-cell recording of inward Ca²⁺ currents (I_Ca). The intracellular solution contained (in mM): 125 cesium glutamate, 5 NaCl, 2 Mg⋅ATP, 0.3 Na₂GTP, 1 MgCl₂, 0.2 fura-2, and 20 HEPES, pH 7.2 with CsOH. The extracellular solution contained (in mM): 140 NaCl, 2.8 KCl, 10 d-glucose, 1.2 MgCl₂, 2 CaCl₂, and 10 HEPES, pH 7.4 with NaOH. PC12 cells were clamped at −80 mV and depolarized to 0 mV for 1 s to elicit Ca²⁺ influx through voltage-gated Ca²⁺ channels. Whole-cell currents (with P/4 subtraction) and fura fluorescence (as above) were recorded, and κ_i was calculated using the equation:

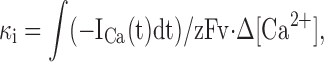(1)

where I_Ca(t) is empirically measured current using the patch clamp, z is the valence of Ca²⁺, F is Faraday's constant, v is cellular volume calculated from the capacitance of the cell assuming a sphere, and Δ[Ca²⁺] is the peak increase determined from the fura-2 measurements. κ_i represents the contributions of all buffers in the cell, including fura-2. To extract the contribution of endogenous buffers, we split κ_i into κ_{i endo} and the known fura-2 component:

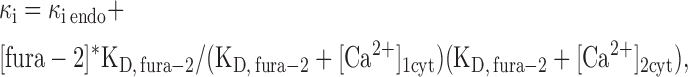(2)

where κ_{i, endo} is the endogenous Ca²⁺ binding ratio of the cytoplasm, and [Ca²⁺]_1cyt and [Ca²⁺]_2cyt represent [Ca²⁺]_cyt recorded before and after membrane depolarization (Zhou and Neher, 1993). The concentration of fura-2 in the intracellular pipette solution is 200 μM and its dissociation constant for Ca²⁺ (K_D) was taken as 224 μM.

Data Analysis

Fluorescence intensities were recorded using PatchMaster, corrected for background, and converted into ratios and then free Ca²⁺ using IGOR Pro (Wavemetrics). For each individual Ca²⁺ trace, we considered only the clearance phase that follows Ca²⁺ loading and used IGOR to calculate the derivative d[Ca²⁺]_cyt/dt for each data point during Ca²⁺ clearance. The derivative was calculated as the slope of the line between the point immediately before the desired point and the point immediately after; points were 0.5 s apart. The first two to three points on all traces were discarded. During net clearance, d[Ca²⁺]_cyt/dt has a negative value by convention. To simplify the presentation, we plot −d[Ca²⁺]_cyt/dt, so that as the rate of Ca²⁺ transport out of the cytoplasm falls, the curve falls. Fig. 1 A shows typical time courses of Ca²⁺ in cells that underwent KCl depolarization and clearance, and Fig. 1 B shows the derivatives obtained from these single cells.

The error bars and statistics given for means represent SEM. To combine data from multiple cells, we binned data points by the values of [Ca²⁺]_cyt. The bins were 100 nM wide from 0 to 1000 nM, and 200 nM wide above 1000 nM. We then averaged the binned data from a pool of cells—[Ca²⁺]_cyt for the abcissae and d[Ca²⁺]_cyt/dt for the ordinates—and report the average value in the figures. Note that due to a large spread in peak Ca²⁺ values (Fig. 5), not every cell that we measured contributed to every bin. All of these mean Ca²⁺ transport curves (d[Ca²⁺]_cyt/dt vs. [Ca²⁺]_cyt) are shown ± SEM of both x and y values. At times, we performed mathematical operations on Ca²⁺ transport curves. Most frequently, this involved addition and subtraction operations. To add or subtract curves, we averaged the concentrations and performed the desired operation on the transport rates for each bin. SEMs combined according to the standard formula for addition (Goldstein, 1964).

Figure 5.

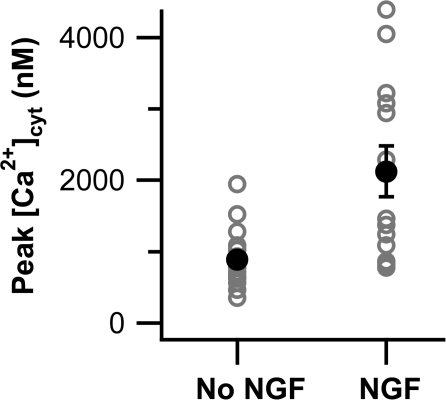
NGF-differentiated PC12 cells have greater Ca²⁺ rises in response to depolarization than undifferentiated cells. Peak [Ca²⁺]_cyt for PC12 cells loaded with fura-4F and depolarized with 70 mM KCl are shown for both undifferentiated (No NGF, n = 20) and differentiated (NGF, n = 13) cells. Open gray circles represent individual cells, and closed black circles are means.

Throughout the manuscript, curves that were obtained directly from experimental data are shown with open symbols and solid lines; the lines may connect the symbols or may represent output of a model. Points from mathematical operations performed on experimental results are shown with closed symbols and dotted lines. With the exception of the control Ca²⁺ transport curves, curves that have appeared in previous figures are shown as lines and error bars without symbols. In Fig. 9, we bypassed some of our rules and switched to closed symbols in panels A, B, C, and D for clarity.

Figure 9.

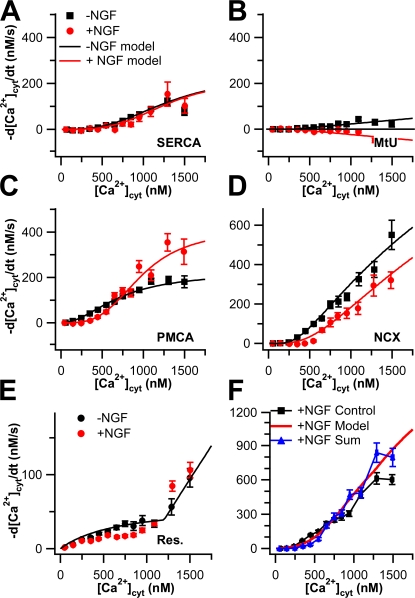
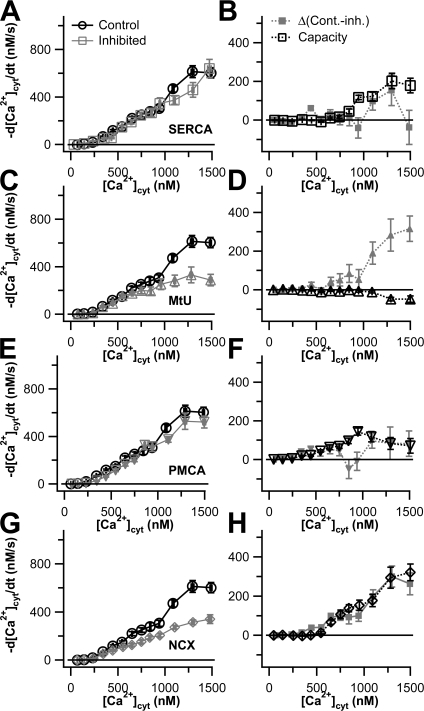
Comparison of Ca²⁺ transport capacities between undifferentiated and NGF-differentiated PC12 cells. Experimental Ca²⁺ transport curves (−d[Ca²⁺]_cyt/dt vs. [Ca²⁺]_cyt) are shown as symbols. Black symbols are from undifferentiated cells and red symbols are from NGF-differentiated cells. Capacity data from undifferentiated cells are reproduced from Fig. 2. The capacity data for MtU and residual Ca²⁺ transport in differentiated cells are reproduced from Figs. 8 and 7, respectively. Smooth black and red curves represent fitted functions from the mathematical model in Appendix using the same color code. (A) Capacities and fits of SERCA. The NGF-differentiated points result from 2-blocked experiments where PMCA and NCX were inhibited, corrected for MtU and residual Ca²⁺ transport (n = 11). (B) Capacities and fits of MtU. (C) Capacities and fits of PMCA. The NGF-differentiated curve is the result of 2-blocked experiments in which SERCA and NCX were inhibited, corrected for MtU and residual Ca²⁺ transport (n = 16). (D) Capacities and fits of NCX. The NGF-differentiated curve points result from 2-blocked experiments in which SERCA and PMCA were inhibited, corrected for MtU and residual Ca²⁺ transport (n = 12). (E) Capacities and fits of the residual Ca²⁺ transport. (F) The NGF-differentiated control values (black) are shown with the sum of the five capacity curves from NGF-differentiated cells (blue) from A–E and the sum of the fitted functions (red).

Online Supplemental Material

The online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.200709915/DC1. Figs. S1 and S2 show the responsiveness of baseline [Ca²⁺]_cyt to extracellular Ca²⁺ after TG treatment and theoretical calculations of local depletion of Ca²⁺ near the plasma membrane when Ca²⁺ transporters are at work. Additional supplementary text describes the provenance of the PC12 cells we used and lists the computer program used in the calculation of local Ca²⁺ depletion.

RESULTS

Preliminary Observation of Ca²⁺ Clearance

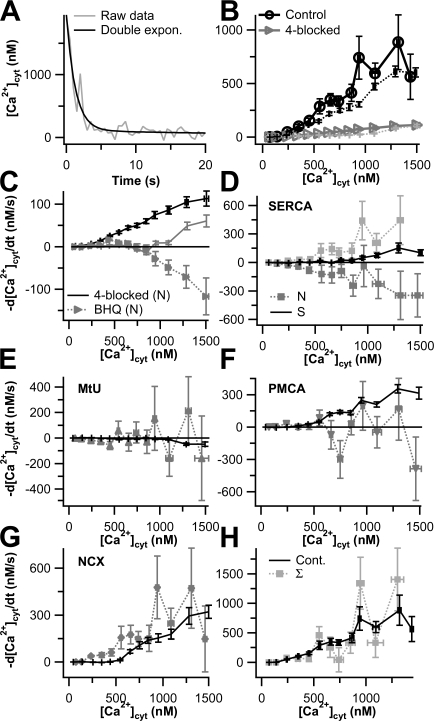
PC12 cells were depolarized with 3-s pulses of 70 mM KCl to induce Ca²⁺ entry, and the cytoplasmic Ca²⁺ ([Ca²⁺]_cyt) was monitored using fura-2 preloaded into cells in its acetoxymethyl ester form. Fig. 1 A shows the Ca²⁺ time course for an experiment on a single cell that exhibited average rates of Ca²⁺ clearance (black line, control). During KCl treatment, [Ca²⁺]_cyt increased rapidly, and then upon removal of KCl it fell back more slowly to the baseline, representing Ca²⁺ clearance. In this figure and elsewhere we have also drawn smooth curves (red, simulated control) derived from a mathematical model of the transport mechanisms described in Appendix. The black circles in Fig. 1 B (control) show the time derivative of [Ca²⁺]_cyt during the clearance phase plotted versus [Ca²⁺]_cyt as a Ca²⁺ transport curve for the same cell. As expected, the net clearance rate −d[Ca²⁺]_cyt/dt fell from its peak value (top right) as [Ca²⁺]_cyt fell. Results from many cells were pooled and binned by the [Ca²⁺]_cyt values in the abscissa to obtain the black curve in Fig. 1 C. This method of analysis allowed us to pool results from many cells despite differences in peak cytoplasmic Ca²⁺.

Before resolving the mechanistic components of this clearance, we need to consider whether Ca²⁺ transport rates depend only on instantaneous [Ca²⁺]_cyt or are also influenced by the past history of Ca²⁺ exposure. To look for history dependence, we lengthened the KCl pulse to 30 s (Fig. 1, D–F, blue line). As was typical of several repeats of this protocol, Ca²⁺ continued to increase well above the useful level for fura-2 for 8–10 s during the pulse and then “sagged” (Fig. 1 D). Fig. 1 D compares 30-s and 3-s depolarizations. After the 30-s depolarization, clearance was slower and Ca²⁺ _cyt remained above baseline, even 70 s later. Transport curves for these two cells are compared in Fig. 1 E, and mean values for pooled data from many cells are shown in Fig. 1 F. Clearance rates after 30 s are less that half those after 3 s. A possible explanation for the slowing is that the Ca²⁺ level in intracellular stores rises during prolonged Ca²⁺ elevation, altering their ability to continue to clear Ca²⁺ or even causing Ca²⁺ to be released from the stores, further blunting apparent Ca²⁺ clearance. We tested whether this might involve the ER by pretreating the cells with thapsigargin (TG) to inhibit SERCA and to empty ER Ca²⁺ stores; however, TG did not change the Ca²⁺ clearance seen after a 30-s depolarization (Fig. 1 F). These experiments indicate that (a) Ca²⁺ clearance in PC12 cells is slower after long depolarizations, (b) SERCA pumps do not serve to clear Ca²⁺ after 30-s depolarization (in contrast to 3-s depolarization, see below), and (c) release of Ca²⁺ from the ER during clearance does not contribute to the apparent slowing of Ca²⁺ clearance after long depolarizations. The unexplained slowing could be due to release of Ca from other stores that fill during the extended depolarization or to modifications (phosphorylations?) of transporters induced by the massive, unphysiological Ca²⁺ elevation. We chose to avoid these complications in the rest of this paper by focusing only on recovery after 3-s depolarizations and by using only “naive” cells that had never been exposed to previous KCl pulses.

Ca²⁺ Clearance in Undifferentiated PC12 Cells

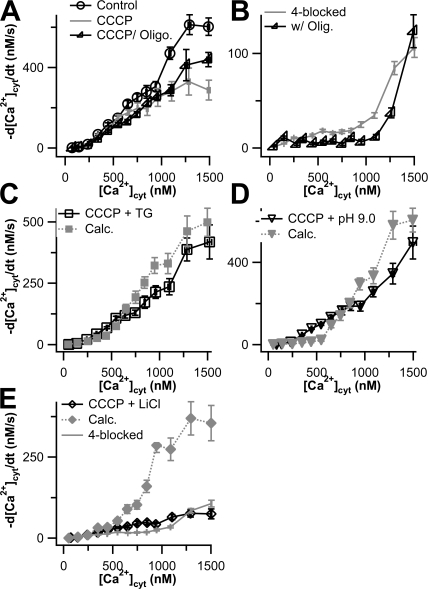
We dissected the contributions of various Ca²⁺ transporters to total Ca²⁺ clearance after 3-s depolarizations using the conditions described in Materials and methods to inhibit each mechanism. SERCA was inhibited by pretreatment with 1 μM thapsigargin (TG), MtU was inhibited by acute application of 2 μM CCCP, PMCA was inhibited by acutely lowering extracellular proton concentration (pH raised to 9.0), and NCX was inhibited by replacing extracellular Na⁺ with Li⁺. We started by blocking all four mechanisms simultaneously to determine whether they accounted for the observed Ca²⁺ transport. The results of these 4-blocked experiments are shown in Fig. 1 as gray symbols. Fig. 1 A shows a sample time course of intracellular Ca²⁺, and Fig. 1 B shows the derivatives obtained from that cell. Although Ca²⁺ transport is much slower in the 4-blocked cell, [Ca²⁺]_cyt does eventually return to baseline in this cell. Of the 62 cells treated with the 4-blocked protocol, 43 (∼70%) returned to baseline within 90 s, albeit with greatly slowed kinetics. The remaining cells arrested before reaching the baseline, at an average [Ca²⁺]_cyt of ∼650 nM. This arrest is not due to Ca²⁺ entering through a store-operated pathway activated by TG because the clearance phase was performed in nominally Ca²⁺-free Ringer's, and we observed that TG-treated cells maintained under this condition did not have elevated basal [Ca²⁺]_cyt. The pooled 4-blocked transport curve from the 62 experiments is compared with that for 88 controls in Fig. 1 C. Blocking the four transporters inhibits over 90% of the Ca²⁺ transport above 300 nM [Ca²⁺]_cyt. Thus most Ca²⁺ transport in PC12 cells is accounted for by the four classical mechanisms. We refer to the small remaining transport as “residual Ca²⁺ transport.” It could represent additional minor Ca²⁺ clearance mechanisms, possible slow binding to some cytoplasmic buffers, and imperfect block of the classical transport mechanisms. For example, pH 9.0 should block only 93% of the PMCA activity, leaving a residual of 7% (Xu et al., 2000).

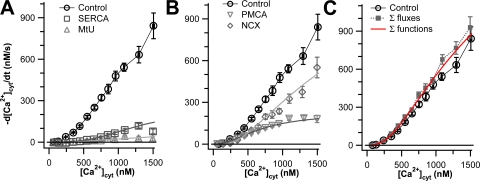
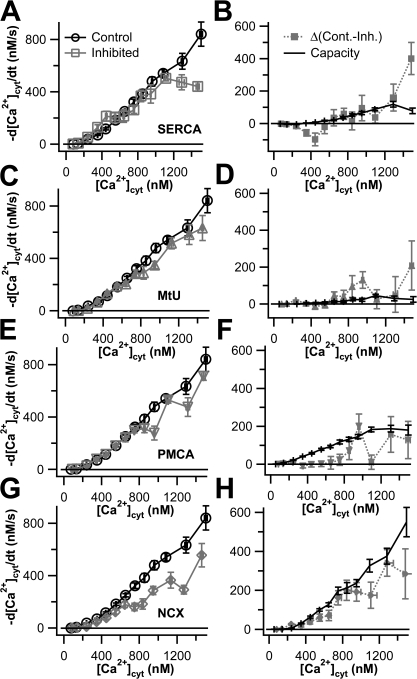
We then assessed the capacity of each of these classes of transporters by performing 3-blocked experiments in which we blocked three classes of transporters and examined the ability of the unblocked transporter to clear Ca²⁺. The results of these experiments are shown in Fig. 2. In each panel, the control curve represents transport in the absence of inhibitors, and the remaining curves in Fig. 2 (A and B) show the transport when only one of the classical mechanisms is operating alone; these curves have been corrected for the small residual Ca²⁺ transport that remains in the 4-blocked experiments (Fig. 1 C). We call the results of these experiments “capacity curves” because they show what one transport mechanism could accomplish essentially alone. Fig. 2 A shows the capacity of the two intracellular Ca²⁺ transporters. Compared with overall transport, the SERCA makes little contribution except above 800 nM [Ca²⁺]_cyt. The MtU component is practically negligible, being comparable to the residual transport component of 4-blocked experiments (Fig. 1). Fig. 2 B shows the capacities of the two plasma-membrane transporters. The PMCA and NCX each account for almost half of the total Ca²⁺ transport up to 900 nM [Ca²⁺]_cyt. In accordance with work on other cells, at higher concentrations, the PMCA appears to saturate, whereas the NCX rate continues to rise and accounts for ∼70% of the total Ca²⁺ transport. Fig. 2 C shows the sum of the capacity curves for these four transporters plus the residual Ca²⁺ transport compared with the observed transport in the control. Together, these data show that the Ca²⁺ transporting capacity of PC12 cells is dominated by the two plasma membrane transporters and that, up to 1000 nM [Ca²⁺], the transporters are operating near capacity.

Figure 2.

Plasma membrane Ca²⁺ transporters have higher capacities than intracellular Ca²⁺ transporters in undifferentiated PC12 cells. Clearance rate, −d[Ca²⁺]_cyt/dt, is plotted against [Ca²⁺]_cyt for cells treated with 3-blocked protocols that allow only one transporter to work at a time. All gray data points are corrected for residual Ca²⁺ transport after 4-blocked experiments. Black curves represent data from control cells, as shown in Fig. 1 (n = 88). (A) Capacities of the intracellular transporters, SERCA (squares, n = 15) and MtU (triangles, n = 24). (B) Capacities of the plasma membrane transporters, PMCA (inverted triangles, n = 16) and NCX (diamonds, n = 16). (C) The sum of the four capacity (gray) curves in A and B plus the residual Ca²⁺ transport from Fig. 1 is compared with the control curve. The smooth curves superimposed on the gray data points of A and B and on the black points of C are calculated from the individual functions of a kinetic model with four canonical transport mechanisms and residual transport discussed in Appendix.

Are Clearance Mechanisms Independent?

If the four clearance mechanisms operated independently, any combination of them should be additive. To verify additivity and to cross-check the conclusions of our 3-blocked measurements, we performed a series of 1-blocked experiments in which only one transporter was inhibited at a time. The “activity” of that transporter was determined by subtracting the 1-blocked curve from the control curve. We refer to the subtracted curves as “activity curves” (Fig. 3). An activity curve differs from a capacity curve in that the former is intended to show what a given transporter accomplishes while working in concert with other Ca²⁺ transporters, whereas the latter shows the results of that transporter working alone. The panels on the left show the 1-blocked transport curves in gray and the control curves in black. The panels on the right show the activity curves for each mechanism, i.e., the differences between the two curves in the left panel, in gray, compared with the capacity curves obtained from the 3-blocked experiments (Fig. 2) in black. The activity curves are quite noisy as each point represents a small difference between two large numbers. For SERCA pumps, the capacity and activity curves are not obviously different, transport remaining small until [Ca²⁺]_cyt rises above 1000 nM (Fig. 3, A and B). Likewise, for the MtU, the curves seem similar and small at all but high (≥800 nM) values of [Ca²⁺]_cyt (Fig. 3, C and D). For PMCA, on the other hand, the calculated activity falls well below the capacity for five consecutive data points below 800 nM [Ca²⁺]_cyt (Fig. 3, E and F). Under these 1-blocked conditions, the NCX was the most robust transporter of Ca²⁺, and it operated at capacity until ∼1000 nM Ca²⁺; where it fell below the capacity curve (Fig. 3, G and H). These calculations indicate that the canonical Ca²⁺ transporters transport at or a little below capacity over the tested range of [Ca²⁺]_cyt, explaining why the sum of individual transport capacities slightly exceeds the observed total transport at higher values of [Ca²⁺]_cyt (Fig. 2 C). The deviation from additivity for the NCX, for example, might imply that when the other transporters are operating, the NCX experiences a lower local [Ca²⁺]_cyt than the average value that fura-2 dye reports (see Discussion).

Figure 3.

Most Ca²⁺ transporters work at or near capacity in undifferentiated PC12 cells. In each panel of the left column (A, C, E, and G), Ca²⁺ transport curves from various 1-blocked experiments are shown in gray, and control Ca²⁺ transport curves from Fig. 1 (−d[Ca²⁺]_cyt/dt vs. [Ca²⁺]_cyt) are shown in black. In each panel in the right column (B, D, F, and H), the activity of a given transporter, calculated as the difference between the control Ca²⁺ transport curve and the 1-blocked Ca²⁺ transport curve to the left, is shown in gray. The capacity trace obtained from the 3-blocked experiments of Fig. 2 is shown in black. (A and B) SERCA was inhibited with 1 μM TG (n = 12). (C and D) MtU was inhibited by treatment with 2 μM CCCP (n = 16). (E and F) PMCA was inhibited by raising extracellular pH to 9.0 (n = 16). (G and H) NCX was inhibited by replacing extracellular Na⁺ with Li⁺ (n = 16).

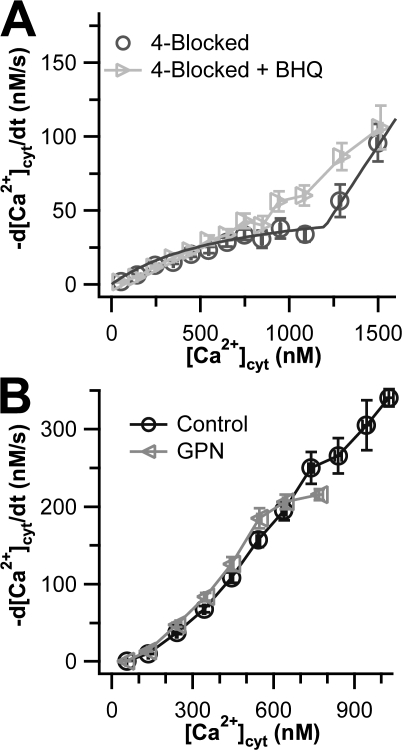
In addition to the four canonical mechanisms of Ca²⁺ transport, SPCAs can transport Ca²⁺ into the Golgi and perhaps into distal secretory compartments. SPCAs are not inhibited by TG but are reported to be inhibited by high concentrations of BHQ (Wuytack et al., 2002). We performed a 5-blocked experiment in which we blocked SPCA with added 10 μM BHQ after blocking the other four mechanisms of Ca²⁺ transport with the 4-block cocktail. Surprisingly, adding BHQ slightly speeded Ca²⁺ clearance above 800 nM [Ca²⁺]_cyt (Fig. 4 A). This might occur if SPCAs normally fill some compartment with Ca²⁺ that releases the Ca²⁺ when [Ca²⁺]_cyt is high; BHQ would prevent this compartment from being full, so that less Ca²⁺ is released into the cytoplasm during the clearance phase in the presence of BHQ. The effect is small. In a previous study, we observed that dense core secretory granules release Ca²⁺ after plasma membrane depolarization in pancreatic β cells and were disrupted by the dipeptide GPN (Duman et al., 2006). Therefore we wanted to see whether the BHQ-sensitive compartment in PC12 cells also was disturbed by pretreatment for 20 min with 50 μM GPN. Below 800 nM [Ca²⁺]_cyt, clearance was completely unaltered by GPN (Fig. 4 B). Unfortunately, we were unable to collect data from high Ca²⁺ ranges because these cells exhibited lower peak Ca²⁺ values than control cells did. The experiment was therefore not conclusive.

Figure 4.

Effects of BHQ and GPN on undifferentiated PC12 cells. Ca²⁺ transport curves (−d[Ca²⁺]_cyt/dt vs. [Ca²⁺]_cyt) are shown. (A) The light gray data points show cells treated with 10 μM BHQ in addition to the 4-blocked protocol (n = 15). The dark gray data points show residual transport in the 4-blocked cells of Fig. 1 with a superimposed smooth curve calculated from the residual transport function in a kinetic model discussed in Appendix. (B) The gray curve shows cells treated with GPN, whereas the black curve shows a truncated version of the control Ca²⁺ transport curve from Fig. 1.

Ca²⁺ Clearance from Somata of Differentiated PC12 Cells

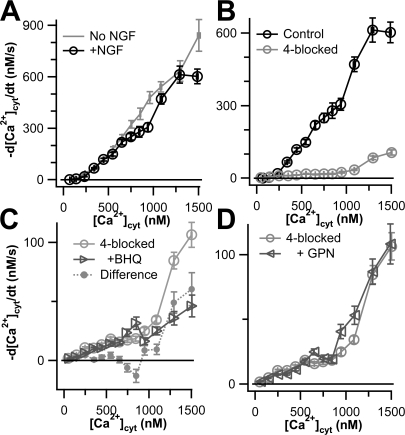
We next asked whether cellular Ca²⁺ clearance mechanisms are changed when PC12 cells are differentiated by >15 d culture in 50 ng/ml NGF (see Materials and methods). With undifferentiated cells, the KCl-induced peak of [Ca²⁺]_cyt sometimes rose above the reliable range of the fura-2 indicator; and with differentiated cells this happened more often. Therefore we turned to the lower-affinity Ca²⁺ dye fura-4F for more reliable measurements of the height of [Ca²⁺]_cyt peaks. Both differentiated and undifferentiated cells showed a wide range of peak heights in response to KCl depolarization (Fig. 5). The average, maximal, and range of peak heights were all markedly higher in NGF-differentiated cells. Higher [Ca²⁺]_cyt peaks might be expected from the greater surface-to-volume ratio of differentiated cells and from a reported increase in Ca²⁺ current (Black et al., 2003).

Fig. 6 A compares the Ca²⁺ transport curves for somata of NGF-differentiated (black line) and undifferentiated cells (gray line). They are very similar, with that for undifferentiated cells lying slightly above that for differentiated cells. When the 4-blocked protocol was applied to differentiated cells, we found that it abolished virtually all transport when [Ca²⁺]_cyt was <1000 nM but left some residual Ca²⁺ transport above this value (Fig. 6 B). Adding 10 μM BHQ on top of the 4-blocked protocol (i.e., a 5-blocked experiment) decreased residual Ca²⁺ transport by ∼50% (Fig. 6 C). Thus, differentiation introduces a measurable component of Ca²⁺ clearance flux (out of the cytoplasm) that is not eliminated by TG but is BHQ sensitive. This flux could represent SPCA transporters on non-ER organelles of the secretory pathway. Unlike undifferentiated cells, the differentiated cells showed no depression of maximal Ca²⁺ rise after GPN treatment. GPN pretreatment had no effect on Ca²⁺ transport (Fig. 6 D), suggesting that the putative SPCA-containing compartment is not lysosomal.

Figure 6.

Global Ca²⁺ transport in NGF-differentiated PC12 cells is similar to that in undifferentiated PC12 cells. (A) Total Ca²⁺ transport with no Ca²⁺ transporters blocked is shown for undifferentiated (gray curve, Fig. 1) and NGF-differentiated (black curve, n = 48) PC12 control cells. (B) Ca²⁺ transport is shown for control (black curve, from A) and 4-blocked (gray curve, n = 62) NGF-differentiated PC12 cells. (C) Ca²⁺ transport is shown for NGF-differentiated PC12 cells treated with the 4-blocked protocol (light gray circles, from B) or with the 4-blocked protocol plus 10 μM BHQ (dark gray triangles, n = 16). The difference between these two curves (gray circles) might represent SPCA activity. (D) Ca²⁺ transport is shown for NGF-differentiated cells treated with the 4-blocked protocol (circles, from B) or pretreated with 50 μM GPN and then treated with the 4-blocked protocol (triangles, n = 18).

We determined the capacity of the four canonical transporters in differentiated cells by performing 3-blocked experiments, and we determined their activities when other transporters were active using 1-blocked experiments. As shown in Fig. 7, the capacity curves nearly overlaid the noisier activity curves for SERCA, PMCA, and NCX in differentiated cells. However, the component of transport attributed to MtU is clearly discrepant between the two measures. Application of CCCP at the moment of the KCl treatment diminished subsequent Ca²⁺ transport by almost 50% at [Ca²⁺]_cyt values above 1000 nM (Fig. 7 C). At face value, this result contrasted with our 3-blocked experiments, which suggested that the mitochondria might even release a little Ca²⁺ into the cytoplasm at these high values of [Ca²⁺]_cyt and transported little net Ca²⁺ below 1000 nM [Ca²⁺]_cyt (Fig. 7 D). Clearly in differentiated cells the 1-blocked (CCCP) experiments are not correctly extracting the mitochondrial component of flux seen with the three blocked experiments (high pH, TG, Li⁺).

Figure 7.

Capacities and activities of Ca²⁺ transporters in NGF-differentiated PC12 cells. Results are shown as Ca²⁺ transport curves (−d[Ca²⁺]_cyt/dt vs. [Ca²⁺]_cyt). In the left column (A, C, E, and G), data from 1-blocked experiments for each of the four canonical Ca²⁺ transport mechanisms (gray lines and symbols) are compared with control NGF-differentiated cells (black lines and circles) from Fig. 6. In the right column (B, D, F, and H), the capacity of each transporter, obtained from 3-blocked experiments and corrected for residual Ca²⁺ transport, is shown in black. The activity of each Ca²⁺ transporter type, calculated as the difference between the two traces in the lefthand panel, is shown in gray: (A and B) SERCA (n = 33 for 1-blocked experiments, n = 17 for 3-blocked experiments); (C and D) MtU (n = 21 for 1-blocked experiments, n = 17 for 3-blocked experiments); (E and F) PMCA (n = 17 for 1-blocked experiments, n = 16 for 3-blocked experiments). (G and H) NCX (n = 19 for 1-blocked experiments, n = 16 for 3-blocked experiments).

Why does CCCP block so much clearance activity in the 1-blocked experiments? We suggest that even a short CCCP treatment stops not only the MtU but also the two ATP-requiring transporters. CCCP collapses the mitochondrial proton gradient, stopping formation of new ATP by mitochondria and allowing cellular ATP to deplete if glycolysis cannot keep up with ATP demand. Treatment with oligomycin can be used to keep the F₁F₀ ATPase from breaking down ATP once the proton gradient is gone (Babcock et al., 1997). However, addition of 5 μM oligomycin, either coincident with CCCP or as a 30-s preincubation before CCCP was added, only weakly restored some missing Ca²⁺ transport (Fig. 8 A). Oligomycin had little effect on residual Ca²⁺ transport in 4-blocked experiments (Fig. 8 B). To determine which non-MtU transporters were affected by CCCP, we performed a series of 2-blocked experiments, treating the cells with both CCCP and one other inhibitor and allowing the other two mechanisms to function. We compared these results to curves calculated from the 3-blocked experiments in Fig. 7. For example, in Fig. 8 C, we compare a 2-blocked experiment in which MtU and SERCA are inhibited (black line) with the calculated sum of the capacities of NCX, PMCA, and the residual Ca²⁺ transport (gray line). The two curves are similar, suggesting that the fluxes allowed to operate in this experiment are not strongly affected by CCCP. In Fig. 8 D, we inhibited both MtU and PMCA (black line) and compared the transport curve to the sum of the capacities of SERCA, NCX, and the residual Ca²⁺ transport. Once again, the curves are quite similar with CCCP being only slightly lower. However, when we inhibited NCX in addition to CCCP treatment, we obtained the unambiguous result that the remaining transport was far below that expected for the sum of SERCA, PMCA, and the residual Ca²⁺ transport (Fig. 8 E). In fact, the observed transport was virtually identical to residual Ca²⁺ transport. These results indicate that both SERCA and PMCA are inhibited by CCCP treatment, as might be expected since both require ATP, and that when only one of these two transporters is working, a differentiated cell can supply almost enough ATP to keep up, but when both are operating it cannot.

Figure 8.

CCCP inhibits primary active transporters in NGF-differentiated PC12 cells. Results are shown as Ca²⁺ transport curves (−d[Ca²⁺]_cyt/dt vs. [Ca²⁺]_cyt). (A) Data from control NGF-differentiated cells (from Fig. 7) are shown as black lines and circles, and data from 2 μM CCCP-treated cells (Fig. 7) are shown as a gray line. CCCP-treated cells were also concomitantly treated with 5 μM oligomycin (gray lines and triangles, n = 28). We obtained the same results when cells were treated with oligomycin for 30 s before application of CCCP as with continuing application of oligomycin (data not shown). (B) Residual Ca²⁺ transport in NGF-differentiated cells (gray line, from Fig. 6) and NGF-differentiated cells treated with 5 μM oligomycin (black line and triangles, n = 16). (C–E) Ca²⁺ transport curves for 2-blocked experiments (black lines and symbols) and estimated results of these experiments based on transporter capacities shown in Fig. 7 (gray lines and symbols). Residual Ca²⁺ transport (from Fig. 6) is shown as a gray line in E. In C, cells were treated with CCCP and TG (n = 15) and compared with the sum of the transport curves for NCX, PMCA, and residual Ca²⁺ transport. In D, cells were treated with CCCP and pH 9.0 (n = 16) and compared with the sum of the transport curves for NCX, SERCA, and residual Ca²⁺ transport. In E, cells were treated with CCCP and Li⁺ (n = 20) and compared with the sum of the transport curves for SERCA, PMCA, and residual Ca²⁺ transport.

The results in Fig. 8 cast suspicion on the capacity measurements made in Fig. 7, since some were based on 3-blocked experiments that contained CCCP. Therefore, we redetermined capacity for canonical transporters in differentiated cells using another series of 2-blocked experiments. (The capacity measurement for MtU was unaffected, however, because this was the one 3-blocked experiment that did not contain CCCP.) For determination of the capacity of each transporter, we inhibited the other two non-MtU transporters. We then corrected the resulting transport curve for the contributions of both MtU and residual Ca²⁺ transport. We compared these fluxes with capacity curves obtained from 3-blocked experiments performed on undifferentiated cells (Fig. 2). Strikingly, differentiation left many aspects of Ca²⁺ clearance unchanged. Not only are the overall control transport curves for undifferentiated and NGF-differentiated cells scarcely distinguishable from each other (Fig. 6 A), the capacity curves for SERCA are essentially the same in both undifferentiated and NGF-differentiated cells (Fig. 9 A), and they are small. The mitochondria remain a negligible component showing no net uptake in differentiated cells (Fig. 9 B). However, the capacities of both PMCA and NCX change appreciably and reciprocally with differentiation. PMCA capacity increases and NCX capacity decreases (Fig. 9, C and D). Finally, residual Ca²⁺ transport does not change appreciably after NGF differentiation (Fig. 9 E). As was the case for the undifferentiated cells, the sum of the four capacity traces and the residual Ca²⁺ transport trace for differentiated cells gives a reasonable estimate for observed total cellular Ca²⁺ transport (Fig. 9 F), although with some indication that transporters are working below capacity above 800 nM [Ca²⁺]_cyt.

To describe the changes between differentiated and undifferentiated cells quantitatively, we fitted the capacity curves with mathematical functions that describe Ca²⁺ transport due to each mechanism (see Appendix for details). The smooth lines in Fig. 2, Fig. 4 A, and Fig. 9 show these functions using the parameters given in Table I. A small increase in apparent cooperativity (reflected in the Hill coefficient, n_Hill) was the most marked change in SERCA caused by differentiation. PMCA underwent an almost twofold increase in maximal velocity (M _max), a decrease in Ca²⁺ affinity, and an increase in cooperativity. NCX affinity for activation by cytoplasmic Ca²⁺ affinity fell as did the rate of transport. Adding these theoretical capacity curves together also provided a reasonable estimate of total cellular Ca²⁺ transport (Fig. 9 F). When combined into a mathematical simulation of Ca²⁺ decay, these fits also replicated the observed time course of Ca²⁺ clearance in control cells and in 4-blocked cells (Fig. 1 A).

TABLE I.

Parameters for Model of Ca²⁺ Clearance in PC12 Cells

Mechanism	Parameter	Undifferentiated	Differentiated	Units
SERCA	Mmax	61	58	μmol⋅Ca2+ l−1⋅s−1
	Km	1.3	1.3	μM
	nHill	2.9	3.4
MtU	Slope	8	−8	μmol⋅Ca2+ l−1⋅s−1⋅μM−1
PMCA	M ma x	77	141	μmol⋅Ca2+ l−1⋅s−1
	K m	0.71	0.97	μM
	n Hill	2.0	3.4
NCX	M rate	560	470	μmol⋅Ca2+ l−1⋅s−1
	K CaAct	0.5	0.85	μM

Parameter values were obtained using the Virtual Cell model in Appendix to fit the empirical data collected in this study. Values are given for the MtU, but we regard these small numbers as being in the noise level and ill determined. These adjusted parameters were used to generate the smooth traces shown in Fig. 1 A and Figs. 2, 4, and 9. Units of M _max and M _rate are micromoles of Ca²⁺ pumped from the cytoplasm of a liter of cells per second. Because the cytoplasm contains Ca²⁺ buffers, these numbers are about 300 times higher than the observed rates of fall of free Ca²⁺ seen in transport curves and Table II. Referred to a unit area of the plasma membrane, the M _max of 77 μmol⋅Ca²⁺ l⁻¹⋅s⁻¹ for PMCA for example is about equivalent to 27,000⋅Ca²⁺ ions pumped⋅μm⁻²⋅s⁻¹ and might require 100-200 PMCA molecules μm⁻² of membrane and consumption of 77 μmol⋅ATP l⁻¹⋅s⁻¹.

Ca²⁺ Clearance from the Neurites of Differentiated PC12 Cells

We tried to measure Ca²⁺ transport in the extensive network of neurites that emerged from our cells upon NGF differentiation. The Ca²⁺ signals from thin neurites were quite noisy compared with those from the much larger somata because the fluorescence was much dimmer. Therefore, before taking the derivatives of these traces, we fitted the Ca²⁺ clearance phase for each field of neurites with a double exponential function (Fig. 10 A) and used these functions in our subsequent analysis instead of the original data. Even so, the variability in the Ca²⁺ transport curves was higher than for somata (Fig. 10 B, black lines) and the results must be regarded as somewhat qualitative. The control transport curve for neurites was statistically indistinguishable from the control curve for somata. The 4-blocked protocol showed that the residual Ca²⁺ transport of neurites and somata also are similar (Fig. 10 B, gray lines). We next compared the additional BHQ-sensitive transport. As shown in Fig. 10 C, BHQ increased Ca²⁺ clearance in neurites relative to the 4-blocked protocol. This effect is similar to that seen in undifferentiated PC-12 cells, but unlike that recorded from the somata of differentiated cells (Fig. 10 C). This was the first indication of differences in Ca²⁺ handling in the neurites versus the somata of differentiated PC12 cells.

Figure 10.

Ca²⁺ transport in neurites of NGF-differentiated PC12 cells. (A) Typical time course of Ca²⁺ clearance in neurites of a PC12 cell (gray line). Due to the noisiness of the traces, we fitted the original data with a double exponential (black line) to calculate Ca²⁺ transport curves. (B) Ca²⁺ transport curves for control and 4-blocked experiments in neurites (black lines with circles, and gray lines with triangles, respectively, n = 13). Data from cell somata are shown as well (broken black line is control from Fig. 10, broken gray line is 4-blocked from Fig. 10). (C) Ca²⁺ transport curves for the BHQ-dependent fluxes in NGF-differentiated cells. The dotted gray line and triangles are from neurites (n = 10), the solid gray line are from cell somata (Fig. 6), and the black line represents the residual Ca²⁺ transport for neurites (B). (D) Ca²⁺ transport capacity curves for SERCA. The two different shades of gray lines and squares represent the SERCA data for neurites sorted into two classes (n = 11 each) (N). The black line represents SERCA Ca²⁺ transport in soma from Fig. 9 (S). (E–G) Ca²⁺ transport curves for MtU (E), PMCA (F), and NCX (G). Gray line and symbols are from neurites (n = 16, 13, 11, respectively), and the black lines represent capacity data from somata (Fig. 9). (H) The control total Ca²⁺ transport curve from neurites (black line, Fig. 10 B) is compared with the sum of the individual activities obtained from neurites (gray line).

The SERCA transport data from 1-blocked experiments with TG-treated neurites clustered into two statistically distinct pools when [Ca²⁺]_cyt exceeded 400 nM. We split these two pools and plot both their ensemble Ca²⁺ transport curves in Fig. 10 D (gray symbols and lines), along with the somatic Ca²⁺ capacity curve due to SERCA. According to this dissection, in one population of neurites, Ca²⁺ is transported by SERCA pumps into the ER, aiding clearance, but in the other Ca²⁺ emerges from the TG-sensitive ER after depolarization, opposing Ca²⁺ clearance. Possibly the latter would represent Ca²⁺-induced Ca²⁺ release. Neglecting the two pools, the summed TG-sensitive transport in neurites is not statistically different from that in somata. The Ca²⁺ transport data did not fall into multiple pools in any of the other 1-blocked experiments. For MtU (Fig. 10 E), PMCA (Fig. 10 F), and NCX (Fig. 10 G), overall Ca²⁺ clearance in neurites was statistically indistinguishable from that in the cell soma, but the power of the test was poor because of the standard errors. Adding the Ca²⁺ transport curves representing SERCA, MtU, PMCA, NCX, and residual Ca²⁺ transport together gave a reasonable approximation of total transport in neurites if we chose the SERCA Ca²⁺ transport curve that shows positive values of clearance (Fig. 10 H). These results show that the Ca²⁺ transport due to MtU, PMCA, and NCX is similar in cell soma and neurites, but that due to SERCA may vary in different neurites.

Endogenous Ca²⁺ Binding Ratio of the Cytoplasm in PC12 Cells

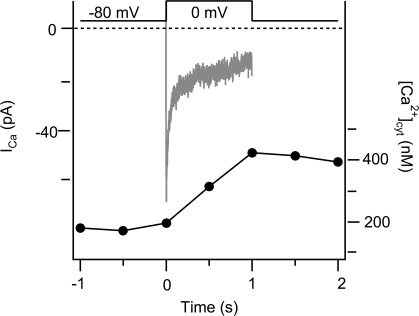
Finally, we determined the endogenous Ca²⁺ binding ratio of PC12 cytoplasm. Only a small fraction of Ca²⁺ in cells is free; the rest is bound to and buffered by a number of intracellular species. The Ca²⁺ binding ratio (κ) is the number of bound Ca²⁺ ions per free Ca²⁺ ion. To lower the free Ca²⁺ of a buffered cell by a given amount, the Ca²⁺ transport machinery of the cell must move 1 + κ times as many Ca²⁺ ions out of the cytoplasm as it would if there were no buffer. We determined κ for PC12 cells by measuring Ca²⁺ currents and [Ca²⁺]_cyt simultaneously in cells under the whole-cell configuration. Current measurements give the total amount of Ca²⁺ that entered the cell (Fig. 11, gray line), and fura-2 measurements give the change in free Ca²⁺ that occurred as a result (Fig. 11, black line). Using this technique and Eqs. 1 and 2 of Materials and methods, we determined that the endogenous κ in undifferentiated PC12 cells is 268 ± 85 (n = 9).

Figure 11.

Determination of κ in PC12 cells. Time courses of simultaneous fura-2 photometry and standard whole-cell recording used to determine κ in PC12 cells. Cytoplasmic Ca²⁺ (black line, left axis) and Ca²⁺ current (gray line, right axis) were monitored before and after depolarization from −80 to 0 mV for 1 s as described in Materials and methods. The black arrow marks the onset of the depolarization, and the gray arrow indicates the baseline for the current measurement. This result is typical of nine cells used for such experiments.

DISCUSSION

Using Ca²⁺ photometry and a pharmacological dissection, we have measured the contributions of several Ca²⁺ transport mechanisms to Ca²⁺ dynamics in PC12 cells. In these cells, the two plasma membrane transporters, NCX and PMCA, account for the majority of the clearance from cytoplasm. As [Ca²⁺]_cyt rises above 900 nM, the PMCA tends to saturate, whereas the NCX continues to speed up, becoming dominant at the highest [Ca²⁺]_cyt. This is in accord with the oft-repeated generalization that the PMCA is a high-affinity, low-capacity transporter, whereas the NCX is a low-affinity, high-capacity transporter. The two organellar transporters, SERCA and MtU, contribute less. SERCA pumps account for a small but significant component of clearance, and the MtU contributes little. There is also a residual Ca²⁺ clearance activity even with our cocktail to block the four canonical mechanisms that is larger than we have seen in other cells. The overall transport remains virtually unchanged by differentiation with NGF. The NCX contribution is lowered, the PMCA contribution is raised, and the apparent Ca²⁺ affinity decreases for both transporters. In differentiated cells, half of the residual Ca²⁺ transport is inhibited by addition of BHQ to the 4-block cocktail, suggesting SPCA activity. The NGF-differentiated cells show more Ca²⁺ influx with depolarization and have a higher dependence on oxidative metabolism than undifferentiated cells. Finally, neurites of differentiated cells show similar overall Ca²⁺-transporting activity to somata, but the SERCA component and a BHQ-sensitive cellular compartment show differences in detail.

In two cases, we found small differences between the transport capacity curves obtained from 3-blocked experiments and the activity curves obtained from 1-blocked experiments. The capacity curves were slightly higher than the activity curves for the PMCA and NCX in undifferentiated cells (Fig. 2 C and Fig. 3, F and H). A plausible explanation considers possible local Ca²⁺ gradients. The PMCA and the NCX are the fastest transporters, and they are both in the plasma membrane. When two of them are operating, [Ca²⁺] near the plasma membrane would be reduced below the mean cytoplasmic level reported by the fura dye, and both mechanisms will be slightly slowed. When one of the two transporters (NCX or PMCA) is inhibited, the other will speed up since the local Ca²⁺ depletion is reduced. This will have the effect that capacity curves will be overestimated and activity curves will be underestimated. In the Appendix and the online supplemental material (available at http://www.jgp.org/cgi/content/full/jgp.200709915/DC1) we develop calculations showing that the local [Ca²⁺] at the cell surface can be reduced 7–36% by pumping at the membrane under various assumptions. As described there, the predicted reduction depends strongly on the actual diffusion coefficient for free calcium in the cytoplasm and on the equilibration time for the reaction between Ca²⁺ and buffering molecules (Fig. S2). Hence, the calculation shows plausibility of the concept but not the exact amount of the effect. This effect, which occurs even without postulating restricted spaces in the cytoplasm, may need to be considered in other transport work.

We saw that the massive Ca²⁺ loads induced by 30-s depolarizations reduced total clearance rates compared with those after the 3-s depolarizations that we have emphasized in this paper. It is already known that components of transporters can be regulated through changes of phosphorylation state (Toyofuku et al., 1993; Bozulic et al., 2007). The summed model equations we give describe the clearance after 3-s well. We hope that they can be used for other physiological stimulus protocols but have not tested the limits of their use.

Strategies for Ca²⁺ Clearance in Excitable Cells

We can now compare Ca²⁺ transport properties of PC12 cells with those of other excitable cells including two rat cells from related catecholaminergic lineages: chromaffin cells (Herrington et al., 1996) and superior cervical ganglion (SCG) neurons (Wanaverbecq et al., 2003). Table II summarizes the overall rates of Ca²⁺ clearance and the contributions of the four classical mechanisms to clearance measured at 1000 nM [Ca²⁺]_cyt for a variety of excitable cells.

TABLE II.

Rates of Ca²⁺ Clearance in Five Excitable Cell Types

			Rate of [Ca2+]cyt fall (nM/s) @ 1000 nM Ca2+
Cell type	T (°C)	τ (s)	Total	SERCA	MtU	PMCA	NCX
PC12 cells (undiff.)	37	2.5	520	75	22	148	275
PC12 cells (diff.)	37	2.7	420	67	−22	214	153
Chromaffin cells	27	2–3	575	0	440	80	55
SCG neurons	33	2.2	320	110	<40	80	120
β-cells	35	1.7	500	290	0	105	105
Sperm	21–23	45–55	8	0	1.5	4.9	1.6

Time constants of [Ca²⁺]_cyt decay τ were obtained from exponential fits of Ca²⁺ clearance time courses. The rates of [Ca²⁺]_cyt fall at 1000 nM Ca²⁺ were obtained from smoothed transport curves. Mitochondrial values from the present study are small and in the noise level. The results for mouse sperm (Wennemuth et al., 2003), rat pancreatic β cells (Chen et al., 2003), rat chromaffin cells (Herrington et al., 1996), and PC12 cells (this article) were collected in this laboratory. The results for rat superior cervical ganglion (SCG) neurons are from Wanaverbecq et al. (2003).

Initial Ca²⁺ clearance in rat chromaffin cells is dominated by the mitochondria above 500 nM [Ca²⁺]_cyt. The Ca²⁺ accumulated by mitochondria later returns to the cytoplasm and exits the cell via the slower PMCA and NCX (Herrington et al., 1996). In contrast, in undifferentiated PC12 cells, mitochondria take up little Ca²⁺ over most of the range of [Ca²⁺]_cyt that we measured (Fig. 3, C and D), and each of the other mechanisms of transport is more than twice as fast as in chromaffin cells at 1000 nM [Ca²⁺]_cyt. Thus the balance of Ca²⁺ transport mechanisms is remarkably different between undifferentiated PC12 cells and chromaffin cells, although the overall Ca²⁺ clearance rate during initial clearance is about the same.

NGF-differentiated PC12 cells are a somewhat closer mimic of the Ca²⁺ transport properties of SCG neurons, but significant differences remain. Both have at most minor mitochondrial transport components. The neurons have almost equal contributions from PMCA, NCX, and SERCA pumps, whereas differentiated PC12 cells have PMCA > NCX > SERCA. It is possible that different isoforms of NCX are present in these different cells and/or that NCX is differentially regulated since the dependence on [Ca²⁺]_cyt looks different. At high values of [Ca²⁺]_cyt, −d[Ca²⁺]_cyt/dt for NCX rises with negative curvature (sublinear) in PC12 cells and with positive curvature (supralinear) in SCG neurons (Wanaverbecq et al., 2003).

Table II includes Ca²⁺ transport rates for two more cell types, pancreatic β cells and sperm, for comparison. They differ from the others. In β cells the overall transport rate is like the other cells, but SERCA pumps dominate for initial Ca²⁺ clearance (Chen et al., 2003). In sperm, overall transport is only 1/25 as fast as in the other cells, and SERCA pumps may make no contribution (Wennemuth et al., 2003). We see at least two major lessons from these comparisons. First, PC12 cells and by extension other cancer cells are not quantitative models for the normal differentiated cells whose initial lineage they are thought to share. They may have many of the right molecules and be good systems for study of molecular mechanisms, but they are not close mimics of physiological responses that depend on the quantitative balance of signals. Probably they have gone through many generations of selection as cancer and cultured cells that give them properties molded by a niche quite unlike that of the “parent” cell. That said, PC12 cells do resemble SCG neurons in their mix of Ca²⁺ transporters. Second, different differentiated cells differ markedly in the balance of Ca²⁺ transport mechanisms. Presumably the mix of transporters is complementary to the sources of Ca²⁺ signals in each cell type. Cells that signal largely by Ca²⁺ entry from the outside eventually will need to clear that Ca²⁺ to the outside, and cells that signal largely by Ca²⁺ release from intracellular stores eventually will have to replenish those stores. The number and mix of transporters and the relative importance of organelles vs. the plasma membrane also help to determine whether a Ca²⁺ signal in that cell is local or widespread, fast or long lasting, large or small, and steady vs. oscillatory. It seems to us that the relation between these factors and cellular physiology still needs much clarification.

Nonmitochondrial Ca²⁺ Transporters in PC12 Cells

Studies using PC12 cells as a model for neural differentiation have examined the expression patterns of various Ca²⁺ transporters and how NGF changes them. NGF increases the N- and P/Q-type Ca²⁺ current (as well as Na⁺ current) in PC12 cells (Black et al., 2003); Ba²⁺ currents are tripled. There is an increased transcription of N-type but not of P/Q-type channel genes (Colston et al., 1998). Such observations agree with our finding that NGF differentiation more than doubles the peak [Ca²⁺]_cyt evoked by KCl depolarization (Fig. 6). PC12 cells express SERCA2b and SERCA3 (Rooney and Meldolesi, 1996), the general housekeeping and neuroendocrine-specific mammalian SERCA isoforms, respectively (Wuytack et al., 2002), and NGF is reported to reduce overall SERCA protein levels (Keller and Grover, 2000). This accords with our finding that the SERCA component of transport activity falls a little with differentiation (Table I). PMCAs 1b, 2b, 3a, 3b, 3c, and 4b are present in undifferentiated PC12 cells, and NGF causes up-regulation of PMCAs 1c, 2a, 2c, and 4a (Hammes et al., 1994). Overall, PMCA protein is increased in NGF-differentiated cells (Hammes et al., 1994; Keller and Grover, 2000). This fits with our finding of a 70% increase in PMCA transport rate at 1000 nM Ca²⁺. Little is known about NCX isoforms in PC12 cells, except that an NCX-mediated Ca²⁺ influx was observed in Na⁺-loaded, NGF-differentiated PC12 cells (Ay et al., 2005). The large slowing of Ca²⁺ clearance upon removal of extracellular Na⁺ in our experiments indicates that NCX is the most significant component of the Ca²⁺ transport machinery of undifferentiated PC12 cells and its activity falls a little during NGF differentiation whereas the PMCA rises (Table II).

In summary, the effects of differentiating PC12 cells on Ca²⁺ transport are subtle. The overall transport rate remains the same. New isoforms of some of the transporters appear and the balance of rates changes a little and the details of [Ca²⁺] dependence change appreciably (Table I). Presumably some of the changes of gene expression reflect groups of genes regulated by the neural differentiation program. Some of the genes may be essential for differentiation since reducing expression of PMCAs 2 and 3 by antisense methods slows neurite extension and promotes cell death in NGF-treated PC12 cells (Szemraj et al., 2004).

Metabolism in PC12 Cells

A striking difference between the differentiated and undifferentiated cells in our study was that treatment with CCCP slowed PMCA and SERCA pumps in differentiated cells but not in undifferentiated cells. We suggest that the slowing arises because of rapid CCCP-induced ATP depletion in differentiated cells and reflects a switch to dependence on oxidative metabolism in those cells. The published literature supports that interpretation. Treatment of undifferentiated PC12 cells with the protonophore carbonyl cyanide 4-(trifluoromethoxy)phenylhydrazone (FCCP) depletes cellular ATP with a long half-time of 30–100 min (Luo et al., 1997; Kubota et al., 2005), too slow to affect our experiments. This is consistent with the general notion that undifferentiated, rapidly dividing (cancerous) cells rely chiefly on glycolysis for their ATP supply (Racker and Spector, 1981). Treatment with NGF changes metabolism of PC12 cells. After 30 h of NGF, PC12 cells increase glucose consumption threefold, increase lactate and pyruvate production twofold, and increase CO₂ production four- to sixfold (Morelli et al., 1986). Levels of all nucleotides including ATP increase, and oxidative respiration increases (Morelli et al., 1986; Davis and Kauffman, 1987). This should make the cells more sensitive to CCCP. They also become more neuron-like in the sense that production of ATP by oxidative phosphorylation and glycolysis occurs in both somata and neurites of sympathetic neurons, with oxidative metabolism predominating (Tolkovsky and Suidan, 1987). Our observation that oligomycin “rescues” the effect of CCCP only a little indicates that ATP pools in the differentiated cells turn over rapidly.

SPCA and Organellar Ca²⁺ Transport

The results of our experiments using BHQ on top of the 4-block cocktail implicate SPCA as a mechanism of Ca²⁺ transport in PC12 cells. Although BHQ is also a SERCA inhibitor, cells treated with BHQ were pretreated with TG, so most SERCA activity should have been inhibited already (Wuytack et al., 2002). SPCA was identified as a pump that imports Ca²⁺ and Mn²⁺ into the Golgi (Wuytack et al., 2002) and subsequently found immunologically in membrane preparations enriched in dense-core secretory granules (Mitchell et al., 2004). The dense-core secretory granules of insulinoma cells possess a vanadate-sensitive but thapsigargin-insensitive Ca²⁺-importing ATPase, suggesting a non-SERCA P-type ATPase (Mitchell et al., 2001), which could be SPCA. The transgranular pH gradient should also be considered in our experiments. It might contribute to Ca²⁺ accumulation by secretory granules and would be collapsed whenever we applied CCCP. While dense core secretory granules can transport Ca²⁺ in the absence of a pH gradient, the transport can be blunted (Mahapatra et al., 2004). All of our BHQ experiments were conducted in the presence of 2 μM CCCP, which would have collapsed the granular H⁺ gradient and perhaps led to underestimation of the importance of SPCA-containing compartments to overall Ca²⁺ dynamics. Our data also do not rule out the possibility that the change in behavior of the BHQ-sensitive compartment(s) due to NGF results from the increased size of the Ca²⁺ peak in response to depolarization rather than from some molecular change(s) of transporters. Identification of BHQ-sensitive compartments other than the ER and elucidation of the precise nature of the changes that they undergo during NGF differentiation are challenges for the future.

Spatial Differences in Cellular Ca²⁺ Transport

In differentiated cells, individual dye-filled neurites were too dim to record from reliably. Therefore, we selected fields of view containing up to 20 neurites. The observed Ca²⁺ transport differed in several ways from that in somata. First, the small BHQ-sensitive Ca²⁺ transport remaining in neurites of 4-blocked cells had the opposite sign from BHQ-sensitive transport in the soma. Evidently BHQ-sensitive stores take up Ca²⁺ after depolarization in somata but release Ca²⁺ in neurites. Perhaps there are different BHQ-sensitive stores in different regions of the cell. Second, we find two behaviors of TG-sensitive stores. In some fields of neurites the ER stores clear Ca²⁺ and in others they release Ca²⁺ during clearance. Finally, the dichotomy in SERCA responses is accompanied by an overall excess of variability in the neurites. We feel this is not accounted for fully by the intrinsic noisiness of the neurite data, or by any contamination with soma signals, or by the smaller statistical sample. Rather, we believe that the excess variability reflects a variety of modes of Ca²⁺ transport present in different neurites.

Conclusions

PC12 cells provide a poor mimic of the balance of Ca²⁺ transporters observed in primary rat chromaffin cells. Instead, the Ca²⁺ transporters of both differentiated and undifferentiated PC12 cells more closely resemble those in sympathetic neurons. In particular, a high NCX activity distinguishes Ca²⁺ clearance in PC12 cells from Ca²⁺ clearance in chromaffin cells or sympathetic neurons, and the near absence of mitochondrial Ca²⁺ uptake in PC12 cells is in marked contrast with chromaffin cells where the MtU is by far the dominant transporter. Differentiation with NGF causes some changes in the kinetic details of Ca²⁺ transport in PC12 cells. Changes in Ca²⁺ transporter expression conceivably contribute to the neuronal differentiation of PC12 cells. However, although there are switches in transporter isotypes and changes in the observed kinetic constants, there is little net change in total transport. Hence, any effects of these changes must be local rather than global. Indeed, we provided indirect evidence for differences in local gradients at the plasma membrane between undifferentiated and NGF-differentiated cells. Further, undifferentiated PC12 cells are resistant to ATP depletion by CCCP, but differentiated PC12 cells may lose ATP rapidly in response to CCCP; this may lead to rapid inhibition of those Ca²⁺ transporters that directly consume ATP. A BHQ-sensitive mechanism compatible with SPCA-containing Ca²⁺ stores apparently provides small contributions to Ca²⁺ release in undifferentiated cells and to Ca²⁺ clearance in differentiated cells. As this store could be dense-core secretory granules, it merits further investigation.

APPENDIX

Modeling Four Transporters and Residual Transport

We modeled Ca²⁺ clearance in PC12 cells using mathematical functions for the four canonical Ca²⁺ transporters that we had used in earlier studies of sperm and pancreatic β-cells (Wennemuth et al., 2003; Chen et al., 2003) plus a function for residual transport. The functions for flux M were:

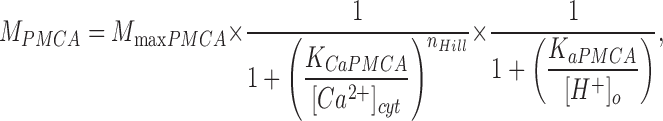(3)

where M _PMCA is a Hill function of the internal Ca²⁺ and a saturation function of the external H⁺. The acid dissociation constant K _aPMCA is 13.8 nM, corresponding to pH 7.86.

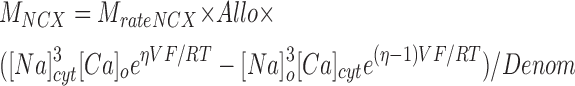(4a)

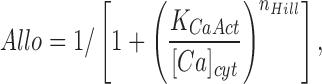(4b)

where M _NCX depends on the membrane potential V and the usual thermodynamic constants and Denom is a complex function with many terms (Weber et al., 2001). Values for all parameters except M_rateNCX and K_CaAct are taken without change from Weber et al. (2001) assuming V = −65 mV.

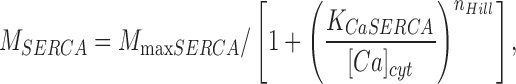(5)

where M _SERCA is a Hill function of the internal Ca²⁺.

M_MtU is a broken line:

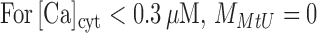(6a)

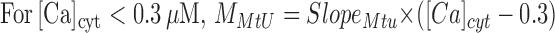(6b)

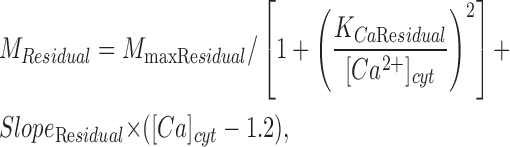(7)

where M _Residual is a Hill function of the internal Ca²⁺ plus a linear rising function that is added in only when internal Ca²⁺ is >1.2 μM. This purely empirical formulation used the following parameters: M _maxResidual = 15.8 μmol⋅Ca²⁺ l⁻¹⋅s⁻¹; K _CaResidual = 0.7 μM; and Slope _Residual = 44 μmol⋅Ca²⁺ l⁻¹⋅s⁻¹μM⁻¹.

The equations were entered into the Virtual Cell on-line modeling environment, solved for transport curves (Figs. 2, 4, and 9), and integrated together with the buffer equation (Eq. 2) for simulations of Ca²⁺ time course during clearance (Fig. 1 A). Parameters for the individual functions (Table II) were optimized by comparing predicted transport curves to measured transport curves for individual mechanisms. The optimization was done by eye, giving no consideration to points >1500 nM Ca²⁺. The simulated Ca²⁺ decays in Fig. 1 A are from individual cells rather than from averages, so it was acceptable to scale the transport rates for best agreement. For the control cell the scale factor is 1.0 (no scaling) and for the 4-blocked curve the M_Residual was multiplied by 1.65 and the four canonical transporters were multiplied by 0.0 (turned off).

The Virtual Cell model is available in the public domain at http://www.vcell.org/ under the shared username hillelab. The units of transport fluxes there are molecules transported per second per square micrometer and all concentrations are in micromolar. These units were translated into the practical clearance units of Table I by the conversion factors: for PMCA and NCX, 360 Ca²⁺ ions μm²s⁻¹ = 1 μmol⋅Ca²⁺ l⁻¹⋅s⁻¹; for SERCA and MtU, 1,851 Ca²⁺ ions μm²s⁻¹ = 1 μmol⋅Ca²⁺ l⁻¹⋅s⁻¹

Modeled transport curves were scaled by the same factors and further divided by 1 + κ_i (Eq. 2) to account for the buffering effects of binding to endogenous buffers and fura.

Modeling Local Gradients

We asked whether transporters acting at the cell surface can deplete local [Ca²⁺] near the plasma membrane in comparison to the bulk [Ca²⁺] measured by dyes. The problem was simulated by a multicompartmental planar-diffusion model making many approximations to simplify the calculations. Cytoplasm from cell surface to cell center was represented by a 1-μm-long cylindrical (not conical) column 1 μm² in cross section and divided into 50 equal thin slices 0.02 μm thick. The first planar compartment was at the cell surface. This model had approximately the same surface-to-volume ratio as our cells. Calcium and a mobile, nonsaturable Ca²⁺ buffer were allowed to “diffuse” between compartments in successive time increments of 20 ns, using Euler integration. The assumed calcium binding ratio κ for the buffer was 300 and the equilibration time for the reaction of Ca²⁺ with buffer was varied. The correctness of the equations was verified by showing that a calculation for applying instantaneous point sources of Ca²⁺ or buffer at the origin resulted in diffusion profiles within 1% of the well-known analytical solution and that mass was conserved within 0.0001%.

The pump problem was simulated by starting with 1 μM Ca²⁺ throughout the “cell” and continuously removing calcium from the juxta-membrane compartment. According to Table II the PMCA and NCX together reduce free [Ca²⁺]_cyt in PC12 cells at a rate of 423 nM per second at 1000 nM Ca²⁺. For a cell with κ = 300, this requires removal of 127 μM total calcium per second (see Table I). Our model “cell” starts with 301 μM calcium, free and bound, and the two “pumps” (if linear) would clear the calcium with an appropriate time constant of 301/127 = 2.4 s. As is illustrated in the online supplemental material, activating the “pumps” established a local drop of free [Ca²⁺]_cyt near the membrane that stabilized within a few milliseconds (Fig. S2 A). It extended ∼200 nm into the cytoplasm while the cell center was hardly depleted. The amplitude of the local drop increased if diffusion was slowed (Fig. S2 B), and it increased if the equilibration time of the Ca buffer was slowed (Fig. S2 C). The spatial extent of the gradient decreased when the buffer reaction was speeded. Making the calcium buffer mobile or immobile changed the calculations very little. We express the local drop as a percent of the [Ca²⁺]_cyt at the cell center. For example, with a buffer equilibration time constant of 1 ms, the relative surface drop of free [Ca²⁺]_cyt after 3 ms of pumping was 37%, 23%, and 18% using diffusion coefficients of 0.1, 0.2, and 0.3 × 10⁻⁵ cm²/s for free Ca²⁺ and buffer. Similarly, with a diffusion coefficient of 0.2 × 10⁻⁵ cm²/s, the relative surface drop at 3 ms was 39%, 23%, and 8% for buffer equilibration time constants of 10, 1, or 0.1 ms.